Multiscale Polymer Dynamics in Hierarchical Carbon Nanotube Grafted Glass Fiber Reinforced Composites

Abstract

Carbon nanotube (CNT) grafted glass fiber reinforced epoxy nanocomposites (GFRP) present a range of stiffnesses (MPa to GPa) and length scales (μm to nm) at the fiber–matrix interface. The contribution of functionalized CNT networks to the local and bulk polymer dynamics is studied here by using a combination of torsion dynamical mechanical thermal analysis (DMTA), positron annihilation lifetime spectroscopy (PALS), and neutron scattering (NS) measurements. DMTA measurements highlight a reduction in the storage modulus (G′) in the rubbery region and an asymmetric broadening of the loss modulus (G″) peak in the α-transition region. NS measurements show a suppressed hydrogen mean-square displacement (MSD) in the presence of glass fibers but a higher hydrogen MSD after grafting functionalized CNTs onto fiber surfaces. PALS measurements show greater free volume characteristics in the presence of the functionalized CNT modified composites, supporting the view that these interface layers increase polymer mobility. While NS and DMTA are sensitive to different modes of chain dynamics, the localization of functionalized nanotubes at the fiber interface is found to affect the distribution of polymer relaxation modes without significantly altering the thermally activated relaxation processes.

Graphical Abstract

INTRODUCTION

Addition of nanoscale reinforcements, such as CNTs, to polymer matrices has been shown to improve the structural, electrical, and thermal properties of the polymer. The large surface area of CNTs result in increased CNT–polymer interactions that improve the load transfer properties between the CNTs and the host matrix, while the interconnected nanotube contacts increase the electrical and thermal conductivities of typically insulating polymeric materials.^1–4 Traditional approaches for manufacturing CNT-based polymer nanocomposites and CNT-based fiber reinforced polymer nanocomposites rely on directly dispersing CNTs into polymer matrices via ultrasonication,^5,6 surfactant assisted/surface modified dispersions,^3,7 three-roll mill,⁸ and high-speed shear mixing.⁹ Despite having success at lower CNT mass fractions (typically <1%), these methods are not effective in uniformly dispersing higher CNT mass fractions (>1%) because of the strong van der Waals interactions between the nanotube surfaces.^8,10 This can lead to large-scale CNT agglomeration within the polymer matrix and cause processing issues due to increased resin viscosities and CNT screening from continuous fiber surfaces in the fiber reinforced polymer nanocomposites.¹¹ Hence, the improvement in mechanical, thermal, and electrical properties of polymer nanocomposites and fiber reinforced polymer nanocomposites are often lower than theoretical predictions. Directly grafting CNTs onto microfiber surfaces presents a viable alternative to introduce a hierarchical composite architecture where CNT mass fractions (up to ≈20%) are localized on continuous fiber surfaces.^12,13 The CNT networks impart a gradient in stiffness from the fiber to the matrix, thereby increasing the interfacial load transfer and toughness, and readily form a percolated network that increases electrical conductivity of fiber reinforced polymer nanocomposites.^10,12,13 Two scalable approaches for directly grafting CNTs onto fiber surfaces include chemical vapor deposition (CVD) of carbon precursors¹⁰ and electrophoretic deposition (EPD) of functionalized CNTs.¹² The latter approach has been found to preserve fiber sizing that allows covalent bonding between the fiber and polymer surfaces on commonly used continuous fiber surfaces (carbon¹² and glass¹³) and is therefore adopted for CNT incorporation in this study.

Multifunctional application of CNT-based fiber reinforced polymer nanocomposites include utilizing the percolated CNT network for structural health monitoring, thermal transport, structural batteries, or antennae, which requires a knowledge of CNT–polymer interactions over long time durations or elevated temperatures.^10,12,13 Furthermore, a thorough understanding of structure–interphase–property relationships (SIPR) is essential for designing and modeling the properties of hierarchical CNT-based fiber reinforced polymer nanocomposites. However, developing SIPR for hierarchical systems is challenging, as a single characterization technique does not adequately capture the structural influence of CNTs across bulk and nanoscale lengths. The polymer nanocomposite community has recognized the importance of understanding the role of reinforcement–polymer interactions via viscoelasticity and polymer dynamics for dispersions of 1-D (CNTs) and 2-D nanoscale reinforcements in thermoplastic or thermoset matrix.^16–31 We first establish a framework for the effect of CNTs on polymer dynamics and viscoelasticity by summarizing both CNT-based polymer nanocomposites and CNT-based fiber reinforced polymer nanocomposites research literature.

The use of covalent and noncovalent functionalization to modify the surface properties of CNTs (to match the surface energy of the polymer matrix) is found to improve wetting and dispersion in thermoplastic polymers and increase the stiffness and the electrical conductivity of the matrix.^20,21,32,33 In thermosets, optimizing CNT dispersion is challenging due to reinforcement induced increases in viscosity,³⁴ potential for reaggregation and flocculation during cure, and the possible impact of nanoscale reinforcements on cure kinetics.¹⁶ Therefore, the results tend to be highly dependent on the system and processing conditions.^14,17 Amine functionalization of the CNT surface improves dispersion and covalent bonding with the network,^18,19 but the presence of excess surface amines distorts the local stoichiometry during curing and alters the viscoelastic properties of the epoxy.²² Viscoelastic property indicators of strongly bonded CNT–polymer systems are enhancements in the glassy and rubber moduli along with increases in the glass transition temperature (T_g).^20–31 An increase in the glassy modulus is generally attributed to the improvements in stress transfer between the polymer and the CNTs, while an increase in the rubbery plateau modulus and polymer T_g is attributed to reduced polymer mobility at the surface of high-aspect-ratio CNTs (length/diameter up to 1000). The presence of CNTs has also been found to increase the stiffness of the matrix and reduce its damping properties (as measured by the area under the loss tangent (tan δ) peak).^{24,25,27,30,31} Nonbulk interphase domains of varying thicknesses are formed based on the chemical functionality,^22,27,29 length,^23,30 and rigidity²⁷ of the functional groups on CNT surfaces that affect the polymer relaxation characteristics in these systems. Generally, favorable interactions between the matrix and the CNT functionality are found to increase²¹ and broaden segmental relaxation times,^22,27,29 while unfavorable interactions cause reductions in segmental relaxation times.²³

SIPR in hierarchical CNT–GFRPs involves a complex array of interactions beyond just the CNT (functionalization, geometry, dispersion) and polymer chemistry. The high CNT mass fraction–polymer interphase is localized at the rigid fiber substrate and becomes a third phase of the composite between the bulk polymer and the rigid fiber substrate with effects beyond controlling fracture and failure. The presence of the CNTs, extending hundreds of nanometers radially from the fiber surface, leads to a blurring of elastic and viscoelastic properties as one moves across the composite cross section. In this work, the nano- to mesoscale polymer properties are captured by characterizing the physical structure, the bulk viscoelasticity, and the polymer dynamics using a host of techniques. We show that within the time scales ranging between 10⁻¹² and 10⁶ s the viscoelastic behavior of a hierarchical CNT–GFRP is influenced by complex interactions of the topological constraints of the nanotubes, CNT–amine–epoxide chemical interactions, and continuous fiber surface constraints. Furthermore, the combination of metrologies used herein provides a pathway for understanding time-dependent properties of the fiber–matrix interphase in engineered multifunctional composites.

MATERIALS AND METHODS³⁶

Sample Preparation.

Epoxy specimens were prepared by using a stoichiometric mixture (approximately 100:26.4, by mass) of bisphenol-F epichlorohydrin epoxy monomer (Epon 862; Hexion Specialty Chemicals) and an aromatic diamine curing agent (Epikure Curing Agent W; Hexion Specialty Chemicals). The liquid constituents were hand mixed, degassed, and drawn into approximately 1 mm thick films and cured in a convection oven. GFRP specimens were manufactured via a vacuum resin transfer process. The resin mixture was infused into four layers of unidirectional, E-glass fibers, where ≈15% of the overall fabric mass consisted of stitched fibers aligned perpendicular to the unidirectional fibers (Thayercraft, aminopropylsilane (APS) sizing). A multistep procedure is required for the manufacture of CNT–GFRP specimens. Multiwall CNTs (about 10–20 nm in diameter and over 200 nm in length) are dispersed in water and oxidized by a combination of ultrasonication–ozonolysis for about 16 h. After ozone treatment, hyperbranched polyethylenimine (PEI, M_w ≈ 25000 g/mol) was dissolved to a concentration of ≈1 g/L, and the dispersion was sonicated for about 4 h. Following this, the pH of the solution was adjusted to nominally 6 to facilitate the protonation of the amine groups and to form a stable dispersion of positively charged CNTs. The PEI-functionalized carbon nanotubes (CNT–PEI) were then deposited onto unidirectional E-glass fibers that were placed in direct contact with a stainless steel anode by using an electrophoretic deposition (EPD) process. The mass fraction of CNT–PEI on the glass fiber was determined by weighing the fabric before and after deposition on an analytical balance with a minimum resolution of 0.1 mg. The resulting CNT–PEI coating formed on the fibers is ≈25 mass % PEI.¹³ Because of the electrostatic interaction between the oxidized CNTs and protonated PEI molecules, it is noted that the CNT-rich layer (e.g., CNT, CNT–PEI, etc.) contains a PEI, epoxy, and diamine component. The CNT-coated fiber laminates (four layers) were processed similarly to the GFRP materials. A detailed description of this process is outlined in previous work by An et al.¹³ All materials were cured at ≈130 °C for ≈6 h and postcured at ≈150 °C for about 24 h. The samples were then machined using a high-speed water lubricated saw to approximately 35 mm by 4 mm by 1 mm for DMTA and approximately 50 mm by 30 mm by 1 mm for NS measurements.

Thermal Characterization.

Thermogravimetric analysis (TGA) was performed on the GFRP and CNT–GFRP to establish the fiber mass fraction in the composites. Samples weighing around 10 mg were heated to about 800 °C at a heating rate of nominally 10 °C/min in a platinum pan with an air purged volumetric flow rate of around 60 mL/min and maintained at that temperature for ≈30 min to remove any organic content. The residual mass content is nominally assigned to the fiber mass fraction. The experimentally determined mass fraction percentages of fiber content in GFRP and CNT–GFRP specimens are found to be similar (≈57%) and the mass fraction percentages of CNT and PEI were calculated to be ≈1.3% and ≈0.4%, respectively (details in Table S1).

Differential scanning calorimetry (DSC) was used to measure the limiting fictive temperature,³⁵ on heating after cooling at the same rate, which is equivalent to T_g (within 1 °C) defined on cooling.³⁷ We refer to limiting fictive temperature as the calorimetric T_g throughout the article. Two samples for each specimen, weighing ≈11 mg each, were sealed in an aluminum hermetic pan and cycled twice between about T_g − 65 °C and T_g + 40 °C at a heating rate of ≈10 °C/min and a nitrogen purge volumetric flow rate of nominally 50 mL/min. Prior to the start of each cooling cycle, the samples were held at around T_g + 40 °C for 30 min to remove the thermal history. The heat flow curve of the second heating cycle was then utilized to calculate the specimen T_g, as outlined by Moynihan et al.³⁸ (FigureS1).

Dynamic Mechanical Thermal Measurements.

Dynamic mechanical thermal measurements were conducted on the specimens using an ARES-G2 rheometer equipped with a stainless steel rectangular torsion fixture and a liquid-nitrogen-cooled forced-convection oven. Prior to sample evaluation, the rheometer was calibrated as per manufacturer specifications to confirm that the standard uncertainties in the frequency and the modulus responses were within ±5% and ±8%, respectively. For temperature measurements, a standard uncertainty of ±0.1 °C was assumed. GFRP and CNT–GFRP specimens were mounted with the principal fiber direction parallel to the torsion axis to minimize their contribution to the shear modulus measurement. Multiple temperature sweeps (up to 3) were conducted between approximately T_g + 40 °C and −140 °C at an oscillating frequency of nominally 1 Hz and a cooling rate of 1 °C/min. Prior to the sweeps, all samples were held at about T_g + 40 °C for ≈1 h to remove thermal history. Strain sweeps were performed prior to the experiments to confirm that the initially set strain percentages at T_g + 40 °C (Epoxy: 1%; GFRP: 0.25%; CNT–GFRP: 0.35%) were within the linear viscoelastic range with sufficient signal/noise in the torque signal (minimum 200 μN·m) above T_g. The set strain values were automatically controlled (reduced) at each temperature step by the instrument to stay within a specified torque limit (200–500 μN·m).

Based on the maximum of the α-transition peak observed in G″ at 1 Hz, frequency sweeps were performed between about T_g + 40 °C and T_g − 65 °C. The temperature steps were nominally assigned to 8 °C intervals and reduced to 4 °C intervals in the transition region to increase data overlap for time–temperature superposition (TTS). At each temperature step, data were obtained across a frequency range of about 0.3 to 30 rad/s. For test temperatures that were equal to or above approximately T_g + 10 °C, all samples were thermally conditioned at the specified temperature for around 30 min to remove any thermal history. Below T_g + 10 °C, the samples were first held at approximately T_g + 10 °C for about 15 min to reset the thermal history and then isothermally held at the test temperature for about 1 h (≈10 times the testing time per Struik’s protocol)³⁹ to minimize the effects of physical aging during data acquisition. Upon completing frequency sweeps for the entire test range, the frequency sweep measurement was repeated at approximately T_g + 40 °C to confirm the absence of sample degradation during experimentation. The method adopted by Dessi et al.⁴⁰ was employed to verify that the instrument compliance did not significantly influence the measurement. By use of TTS, master curves were constructed by first reducing the tan δ using horizontal shifts (a_T); subsequent vertical shifts were then performed with the aid of van Gurp–Palmen plot to reduce the G′ and G″ responses by using the a_T obtained from tan δ shifts.³⁵ T_ref was chosen based on the T_g obtained from DSC measurements. This was similar to the α-transition temperature (T_α) obtained from single-frequency (1 Hz) G″–temperature sweeps.

Thermally activated processes in the glassy region (T < T_g − 150 °C) were investigated by performing frequency sweeps (nominally from 0.3 to 30 rad/s) between about 0 and −136 °C at an 8 °C temperature interval. As the effect of physical aging is considered minimal this far from the glass transition temperature,³⁹ all samples were conditioned for ≈30 min at each temperature step prior to the measurements. After completion of frequency sweeps for the entire temperature range, the temperature step at 0 °C was repeated to confirm the validity of the frequency data. The TTS principle, described previously, was applied to generate master curves at a T_ref ≈ −80 °C based on the maximum G″ response in the frequency sweep in the low temperature range.

Neutron Scattering.

Small-angle neutron scattering (SANS) measurements were performed to characterize the structure of the fiber–CNT–polymer interphase. The experiments were conducted on the NG-B 30m SANS instrument at the National Institute of Standards and Technology (NIST) Center for Neutron Research (NCNR). The samples were placed between quartz windows, and the measurements were performed with sample-to-detector distances of nominally (1, 4, and 13 m) and a neutron wavelength λ ≈ 6 Å to cover the Q-range from ≈0.004 to ≈0.5 Å⁻¹, Q = 4π/λ sin(θ/2), λ being the incoming neutron wavelength and θ the scattering angle. Q represents the inverse of the length scale at which the structure of the system is probed and roughly corresponds to length scales of ≈13 to 1571 Å here. All scattering profiles were corrected for background, empty cell, and sample transmission to generate scattering patterns using Igor-based SANS packages developed at the NCNR.⁴¹

Elastic neutron scattering probes the nanoscale dynamics of polymers as a function of temperature. It is a nondestructive technique that uses a low-energy neutron beam to characterize atomic displacements by measuring changes in neutron energy upon scattering with the sample. Because of the high scattering cross section of hydrogen in NS techniques, it is well suited to probe relevant polymer dynamic processes at the nanoscale with characteristic times between 10⁻⁸ and 10⁻¹² s. Here, only neutrons scattered elastically within the instrument resolution of ≈1 μeV (where |ΔE| = |E_f − E_i| ≲ 0.5 μeV, E_i and E_f being the initial and final energy of the scattered neutron, respectively) are recorded as a function of Q. The measurements were conducted on the high-flux backscattering (HFBS)⁴² spectrometer on NG-2 at the NCNR. The samples were wrapped with aluminum foil and placed in a sealed aluminum cylinder with a helium environment. The samples were isothermally kept at around 150 °C in this environment for about 12 h prior to measurement. The cylinder was placed in a top-loader closed-cycle thermal chamber that controls the sample temperature to an accuracy better than 1 °C. During the scans the temperature was varied between approximately −258.15 and 276.85 °C (14 and 550 K) at a heating rate of 1 °C/min. The intensity was collected across 16 detectors in a Q-range of ≈0.25 to ≈1.75 Å⁻¹ that corresponds to length scales of ≈25.1 to ≈3.59 Å.

Electron Microscopy.

Prior to electron imaging, freshly cleaved cross sections (perpendicular to the glass fibers) of the CNT–GFRP laminate were wet polished using silicon carbide paper in the following order of grit size: 600, 800, 1200, and 2000. Scanning gallium ion microscopy (SGIM) imaging was conducted using a 30 kV electron-beam voltage at a 24 pA beam current. To obtain SEM images at magnifications greater than 1000×, the sample surfaces were sputter coated with a gold/palladium target for ≈40 s, which resulted in a nominal 4 nm thick conductive coating on the sample surfaces. The sample surfaces were then imaged using an electron beam with a 5 kV electron-beam voltage at a 100 pA beam current.

Positron Annihilation Lifetime Spectroscopy (PALS).

PALS is an electron/positron annihilation-based measurement that is often utilized to understand free-volume characteristics in polymeric materials. In materials with low electron densities, such as polymers and composites, thermalized positrons form a metastable bound state with an electron, termed positronium, which are largely confined to the pore structures/free volume.⁴³ In fiber-composite specimens, this is assumed to occur at the fiber–polymer interfacial region and the polymer-rich regions.⁴⁴ Under a vacuum environment, the triplet state of positronium, namely orthopositronium (o-Ps), has a lifetime of 142 ns. In polymers, this lifetime is often shortened to a few nanoseconds because of interactions between o-Ps and other electrons.⁴³ The o-Ps lifetime (τ₃) can be directly related to the cavity radius (R) and the cavity volume (V_c) via the Tao–Eldrup model⁴⁵ via eqs 1 and 2, and the intensity of the o-Ps annihilation (I₃) is often used as an indicator of the number density of interchain porosity. However, in commercial systems that contain a variety of chemical additives, the propensity of thermalized positrons to form positronium is affected by chemical moieties having high electron affinity, which consequently reduces I₃.⁴⁶ Hence, the product of τ₃ and I₃ or the relative free volume is not considered as a reliable metric to compare specimen porosity in this study; instead, only τ₃ values are used.

$${\tau }_3=0.5{\left[1-\frac{R}{R+0.166}+\frac{1}{2\pi }\text{sin}\left(\frac{2\pi R}{R+0.166}\right)\right]}^{-1}$$ (1)

$$V_{\text{c}}=\frac{4}{3}\pi R^3$$ (2)

Samples with approximate dimensions of 25 mm by 25 mm by 1.5 mm were tightly clamped on either side of a positron emission source. The source consists of ²²NaCl salt (activity: 10 μCi) placed between two Kapton foils that are ≈50 μm thick and sealed using a commercial adhesive. The sample–source–sample assembly was wrapped in an aluminum foil and placed between two photomultiplier tubes (PMTs) coupled with plastic scintillators. The PMTs were designated to detect the γ-ray signatures corresponding to the positron emission process (≈1.27 MeV) and the subsequent positron/positronium (Ps) annihilation processes (≈0.511 MeV). The time difference in the positron production and the annihilation within the sample is recorded to generate the positron annihilation time spectrum, which was analyzed using a commercially available software. For each specimen, nearly 8 million counts of annihilation data were collected at room temperature conditions and atmospheric pressure.

The lifetime data obtained from each specimen are convoluted with the timing resolution (≈270 ps) of the spectrometer. Prior to sample measurements, the timing-resolution function of the spectrometer was estimated from an undoped, polycrystalline Si wafer having known positron lifetimes. A nominal source correction from positron annihilation within the ²²NaCl salt and the surrounding Kapton film was applied to the specimen data by using an empirical relationship derived by McGuire et al.⁴⁷ For each specimen, the PALS spectra were analyzed by assuming three discrete exponential lifetime components using PALSfit3.⁴⁸ The shortest lifetime (τ₁) is nominally assigned to the self-annihilation of parapositronium (p-Ps), the middle lifetime (τ₂) to the free-positron annihilation, and the longest lifetime (τ₃) to the orthopositronium (o-Ps) annihilation.

RESULTS AND DISCUSSION

Structural Characterization: Microscopy and SANS.

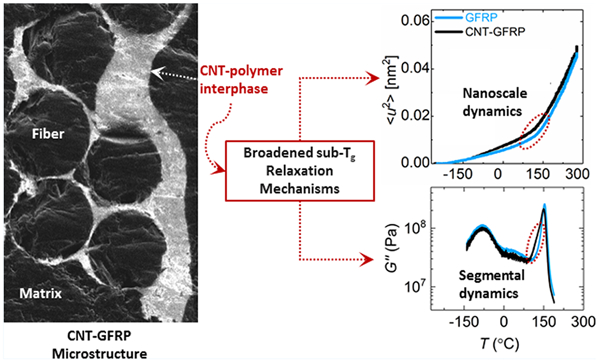
A key attribute of CNT–GFRP is the hierarchical microstructure surrounding fiber surfaces, as previously described by An et al.¹³ and represented in Figure 1a. It is difficult to observe the location and uniformity of the CNT layer across a large area at lower magnifications using SEM (Figure 1b). Stitching together high-magnification SEM images is time-consuming and requires a conductive coating that may alter the appearance of the deposited CNT layer. SGIM is a focused ion-beam technique that has been previously used to image large areas (up to 300 μm × 400 μm) in CNT-based polymer nanocomposites by applying a charge contrast between CNT-rich areas and the polymer-rich areas.⁸ Briefly, SGIM uses positively charged gallium ions which upon interaction with conductive and nonconductive surfaces alter the local surface electronic states. The Ga⁺ ions prevent the release of secondary electrons (SE) from epoxy- and glass-fiber-rich areas and cause them to appear dark, while the CNT-rich areas readily release SEs that neutralize the Ga⁺ and appear bright.⁸ This enables the visualization of the CNT–polymer interphase and provides a qualitative assessment of CNT confinement to fiber surfaces in the final composite, as shown in Figure 1c.

Figure 1.

(a) Illustration of a CNT–GFRP composite with the CNTs uniformly coating the glass fiber surfaces. (b) SEM image of the CNT–polymer interphase region where CNT-rich areas are not clearly visible. (c) SGIM image of CNT–polymer interphase shown in (b), where the charge contrast enables visualization of CNT-rich areas within the composite.

A thin CNT coating of about 100–200 nm was observed on individual fiber surfaces within a fiber bundle. Fibers situated in the outer regions of a ply show thicker CNT films (≈5 μm) than the fibers situated inside a ply (Figure 1c and Figure S2). This is attributed to the diffusion/deposition kinetics of CNTs during the EPD process. CNT deposition is typically initiated at the surface of the electrode, and the CNTs readily form a film around glass fibers that are in direct contact with the electrode. These CNT-coated glass fiber layers act as an extension of the electrode and promote further film growth. However, upon reaching a certain coating thickness on the outer layers, the diffusion of CNTs to the inner fiber layers within a ply is reduced. This is described in greater detail by An et al.¹³ An assumption of a minimum layer thickness ≈100 nm and a calculated mass percentage of deposited CNTs of 1.7% leads to an interphase volume of ≈2% of the total composite volume in the materials investigated here.

SANS measurements were conducted to characterize the averaged CNT morphology at length scales between approximately 1 and 200 nm, which is comprised mainly of the CNT layers internal to the composite. The coherent scattering intensity in SANS results from the differences in scattering length densities of the constituent atoms in each component, which includes any organic polymer (C, H, O, N), glass fibers (Si, O), and CNTs (C). Based on the length scale investigated, the mesh size between fibers and the textile laminates is too large to be resolved; the relevant structural feature probed is the roughness of the fiber–polymer interface. Figure 2a shows the 2-D neutron detector data for the GFRP and CNT–GFRP samples. Well-defined, ordered glass fiber structures arranged in a mesh result in highly anisotropic patterns with bands separated by 90° and with a higher intensity in the principal fiber direction of the unidirectional composite. The power law dependence of SANS intensity with exponent ≈−4 (Porod scattering)⁴⁹ in the GFRP system (Figure 2b) suggests a sharp, smooth interface formed between the epoxy and the fibers, in agreement with the microscopy images (Figure S3). CNT–GFRP shows a diffuse, isotropic scattering in addition to the ordered fiber structure of the GFRP at higher length scales (lower Q), as shown in 2-D detector image in Figure 2b. The CNT features are present in the intermediate Q range. Subtracting the intensity of CNT–GFRP from the intensity of GFRP yields the profile shown in Figure 2c, which corresponds to form factor contributed only by the CNT–polymer interphase. There are multiple length scales associated with the tube-like 2-D structures of CNTs that crossover at Q ≈ 0.03 Å⁻¹, which is a length scale associated with the CNT diameter (≈2π/Q) of 20 nm. At larger length scales, or lower Q, the rod-like nature of CNTs yields the power-law exponent of −1.5, which is consistent with previous observations.⁸ Note that this exponent is observed to be −1 only in the case of perfect individual rods, which is not expected for functionalized CNTs deposited on fiber surfaces. Similarly, at smaller Q, the scaling deviates from −4, an ideal case for rods.

Figure 2.

Small-angle neutron scattering measurements on fiber composite specimens. (a) 2-D detector images obtained from GFRP and CNT–GFRP showing highly ordered bare fiber structure (left) and additional diffuse scattering due to CNT coating on fiber (right). (b) Scattering intensity–wavevector profiles from the GFRP and CNT–GFRP samples clearly showing the CNT contribution in the intermediate Q-range. (c) Intensity of CNT–GFRP subtracted by the intensity of GFRP showing the bare contribution of CNTs. The numbers in the figure correspond to exponents from the power law scattering dependence.

Several conclusions may be drawn about the structure of the CNT–GFRP system from microscopy and SANS. The functionalized CNT network is preferentially distributed at the interface of the majority of glass fibers and has a varying coating thicknesses that is infiltrated by the epoxy matrix. Moving outward from the glass fiber interface, there is a transition from the CNT–PEI–epoxy interphase to the bulk epoxy matrix. SANS data show that a sharp interface formed between the glass fibers and the polymer matrix is modified into a rougher interface in the presence of CNTs. Based on these structural observations, the CNT–GFRP composite is expected to exhibit different viscoelastic properties and polymer dynamics than the GFRP, and any differences are expected to be localized in the nonbulk, polymer–CNT–fiber interphase layer (composed of CNT–PEI–epoxy) in this system.

Viscoelastic Properties as a Function of Temperature at a Single Frequency.

The temperature dependence of G′ and G″ in the presence/absence of grafted CNT networks and glass fibers was evaluated at a fixed frequency, i.e., nominally 1 Hz, for CNT–GFRP, GFRP, and Epoxy specimens, as shown in Figure 3 and Figure S4. G′ increases by nearly 2 orders of magnitude when the specimens undergo a transition from a rubbery to a glassy state (Figure 3a). An α-transition (segmental relaxation) is observed between 100 and 190 °C and a β-transition (side-chain motion or sub-T_g dynamics) between 0 and −140 °C, as shown from the G″ response in Figure 3b.^50,51 The temperatures corresponding to the maximum value of G″ in the α- and β-transition regions are designated as the α- and β-transition temperatures (T_α and T_β), respectively. The widths of the β-transition peaks are ≈2 times broader than the α-transition peaks (Figure 3b), and the T_β occurs at ≈−80 °C for all specimens. A T_α of ≈149 °C was observed in the CNT–GFRP, which is about 5 °C lower than that observed for the GFRP and the Epoxy specimens (≈154 °C) (Figure 3b and Table 1). The T_α measured from DMTA was compared against the T_g measured using a DSC (Table 1). The calorimetric T_gs of the CNT–GFRP and the GFRP specimens differ by only about 2 °C. A good agreement (difference of <1%) between T_α and T_g was observed for all specimens in this study (Table 1), although both techniques may capture relaxation time distributions differently.³⁵

Figure 3.

(a) Storage (G′) and (b) loss (G″) moduli of Epoxy, GFRP, and CNT–GFRP represented as a function of temperature, measured at a single frequency (nominally 1 Hz) and a cooling rate of about 1 °C/min. The standard uncertainty on the frequency and the modulus responses were found to be within ±5% and ±8%, respectively. For temperature measurements a standard uncertainty of ±0.1 °C is assumed based on manufacturer specifications.

Table 1.

Transition Temperatures (T_g and T_α) Pertaining to the Segmental Relaxation of the Specimens Determined by Using Thermal (DSC) and Dynamic Mechanical (DMTA) Measurements^a

sample	Tg, DSC (°C)	Tα, DMTA (°C)
Epoxy	153.2 ± 0.2	154.5 ± 0.3
GFRP	152.9 ± 0.6	153.3 ± 0.1
CNT-GFRP	151.0 ± 0.1	149.4 ± 0.4

^aThe standard deviations in DSC measurements are derived from testing two samples from each specimen, and the standard deviations in DMTA measurements are obtained by averaging peak intensities over two consecutive measurements.

Both CNT–GFRP and GFRP specimens exhibit higher G′ and G″ than the Epoxy specimen over the entire temperature range. This is attributed to the presence of continuous, microscale glass fibers (≈57 mass %) that increase both the torsional stiffness (G′) and the frictional losses (G″) at the fiber–polymer interface (Figure 3a,b). However, the tan δ peak intensity (Figure S4) is lower in GFRP and CNT–GFRP compared to the Epoxy system, indicating that the purely elastic reinforcements of glass fibers (magnitude of G′) dominate any frictional losses at the fiber–polymer interface (magnitude of G″).^52,53 The CNT–GFRP specimen exhibits marginally lower dynamic moduli (G′ and G″) (Figure 3a,b) and a significantly wider α-transition peak than the GFRP specimen (Figure 3b and Figure S4). A single-frequency temperature sweep evaluates the moduli responses weighted strongly to relaxation processes closest to 1/ω at each temperature. At low temperatures, the technique is sensitive to the shortest relaxation times and at high temperatures toward the longest relaxation times. Because the interfacial properties of the hierarchical microstructure are expected to exhibit a range of viscoelastic responses over different relaxation times, multiple frequency sweep measurements were conducted over a large temperature range to probe these relaxation processes.

Viscoelastic Properties as a Function of Temperature and Frequency.

Frequency scans were conducted in the α and β transition temperature ranges for all specimens to explore the origins of broadening in the α-transition peak observed in the single-frequency temperature scan of the CNT–GFRP. The frequency range was fixed between nominally 0.3 and 30 rad/s (2 orders of magnitude) to reduce measurement time and limit instrumental errors associated with long data collection.⁵⁰ Frequency sweeps conducted on the CNT–GFRP between T_g + 40 °C and T_g − 65 °C are shown in Figure 4. The frequency sweeps of the Epoxy and the GFRP specimens are shown in Figures S5 and S6.

Figure 4.

(a) Storage (G′) and (b) loss (G″) moduli as a function of frequency (ω) between 0.3 and 30 rad/s over the α-transition range for a CNT–GFRP specimen. The standard uncertainty on the frequency and the modulus responses were found to be within ±5% and ±8%, respectively. For temperature measurements a standard uncertainty of ±0.1 °C is assumed based on manufacturer specifications.

TTS was used to construct the G′, G″, and tan δ master curves over a relaxation time range of ≈10 decades. Time–temperature equivalence in commercial epoxy formulations is often an approximation;⁵⁴ its feasibility to this study is verified as part of the data reduction process. We briefly describe the shifting process in the interest of clarity. In the first step of data reduction, tan δ responses at various temperatures (as a function of frequency) were shifted to a reference temperature (T_ref) along the frequency axis, by applying a set of horizontal shift factors, a_T. For TTS shifts in the α-transition region, T_ref was equal to T_g for all specimens by DSC. In the case of β-transition, T_ref was assigned to the temperature corresponding to the peak G″ response (T_β ≈ −80 °C for all samples). Subsequent vertical shifts (b_T) were performed with the aid of van Gurp–Palmen plots and applied to the G′ and G″ master curves. An example of the shifting process performed in the α-transition region is shown for the Epoxy specimen in Figure S7, and the van Gurp–Palmen plots for GFRP and CNT–GFRP specimens in the α-transition region are shown in Figure S8.³⁵ The overlap of complex moduli shifts in the van Gurp–Palmen plot was also used to assess thermorheological complexity of the specimens. Both Figures S7 and S8 highlight a minor mismatch in data overlap at the maximum in the α-transition peak and at the highest temperatures. Because of the reasonable overlap across the majority of the G′, G″, and tan δ master curves, a TTS approximation may be considered valid for comparing relaxation characteristics in these materials.

Trends in b_T for the α-relaxation process are presented in Figure 5a. Vertical shifts during TTS are governed by physical aging in the glassy region and the temperature to density ratio of samples in the rubbery region. Corrections for changes in magnitude of G′ and G″ are typically small (or negligible) for simple polymers.⁵⁵ Though the commercially formulated epoxy resin and the presence of micro- and nanoscale reinforcements may introduce variations in b_T, the magnitude of b_T for all specimens is found to be much smaller than a_T, as observed in Figure 5 and Figure S9. It is also observed that the magnitude of b_T for the CNT–GFRP is lower than that observed for the GFRP and the Epoxy specimens, especially in the glassy region. This may be attributed to the presence of strong interfacial interactions between CNT–PEI and the epoxy matrix, which has previously been shown to reduce composite expansion in the glassy–rubbery transition region.⁵⁶

Figure 5.

Variation of (a) vertical shift factors (b_T) and horizontal shift factors (a_T) as a function of temperature for all specimens. In (b), the fit line represents a WLF fit above T_ref and shows a departure from equilibrium conditions below the α-transition temperature. The adjusted R² values for WLF fit was at least 99% for all specimens.

Trends in a_T as a function of temperature are shown in Figure 5b. Above T_ref (≈T_g), trends in a_T for all specimens are found to obey the Williams–Landel–Ferry (WLF) equation:⁵⁵

$$\text{log\hspace{0.17em}}{a}_T=\frac{-C_1\left(T-T_{\text{ref}}\right)}{C_2+\left(T-T_{\text{ref}}\right)}$$ (3)

where C₁ and C₂ are the WLF fit constants, T is the measurement temperature, and T_ref is the reference temperature (≈ T_g). The constants C₁ and C₂ are found to be similar for all specimens, and the values are reported in Table S2.

Below T_ref, a_T deviates from the WLF model as the polymer chain dynamics approach a nonequilibrium glassy state. The deviation from equilibrium is found to be smaller in magnitude (larger a_T) in the CNT–GFRP specimen as compared to GFRP and Epoxy specimens (Figure 5b). As all samples were subjected to similar thermal conditioning, it is likely that the relaxation characteristics of the epoxy are altered in the presence of functionalized CNT networks. At lower temperatures near β-transition, a_T was fit by using an Arrhenius model, as shown in Figure S10. The activation energy (E_a) for the β-relaxation process is ≈16 kcal/mol for all specimens, which is similar to the E_a reported by Hunston et al.⁵⁰ for a commercial epoxy-amine system.

The reduced master curves obtained after TTS are presented in Figure 6. General trends in G′ over the entire frequency range show an increase in the magnitude of G′ for both the GFRP and the CNT–GFRP specimens as compared to the Epoxy specimen (Figure 6a). This is attributed to the inclusion of glass fibers and was previously observed in the single frequency (1 Hz), temperature sweeps. In this study, glass shear modulus (G_g) is defined as the storage shear modulus measured at (T_ref − 65 °C) and the highest frequency (30 rad/s), while rubbery shear modulus (G_r) is defined as the storage shear modulus measured at (T_ref + 40 °C) and the lowest frequency (0.3 rad/s). The G_g and G_r of the GFRP and CNT–GFRP specimens are presented in Table 2. A minor increase in G_g and a reduction in G_r are observed for the CNT–GFRP as compared to the GFRP specimen. The increase in G_g is likely due to an increase in sample stiffness caused by the presence of interfacial CNT networks while the reductions in G_r are less clear. We attribute this decrease to reduced epoxy cross-linking reactions or increased polymer segmental mobility within the CNT–PEI–epoxy–fiber interface. Further study is underway to elucidate this observation.

Figure 6.

Reduced master curves generated after horizontal shifts of frequency and vertical shifts of dynamic moduli at T_ref. (a) Reduced storage (b_TG′) and (b) reduced loss (b_TG″) moduli versus reduced frequency (a_Tω). (c) Normalized loss tangent (tan δ) versus normalized reduced frequency. The tan δ axis was normalized against its maximum value while the frequency axis was normalized against the reduced frequency corresponding to the maximum tan δ. The fits shown for (a) and (b) are based on Maxwell’s equations for generating a discrete relaxation spectrum. The standard deviations for the fits are <0.02% for all specimens.

Table 2.

Glassy (G_g) and Rubbery (G_r) Shear Modulus of the GFRP and CNT–GFRP Specimens^a

sample	Gg (MPa) at Tref − 65 °C	Gr (MPa) at Tref + 40 °C
GFRP	1945 ± 5	168 ± 4
CNT-GFRP	2144 ± 5	124 ± 5

^aThe standard deviations on the G_g data were calculated from the scatter in limiting high-frequency, and the standard deviation in G_r was estimated based on scatter in limiting low-frequency from two independent measurements at T_ref + 40 °C.

G″ master curves for all specimens are shown in Figure 6b. Both the GFRP and the CNT–GFRP specimens show a significantly broader α-relaxation characteristic compared to the Epoxy specimen, originating from the frictional losses caused by increased physical and chemical interactions between the glass fiber and the polymer surfaces at the interface. The CNT–GFRP exhibits additional broadening at both high- and low-frequency regions of the G″ curve, asymmetrically stretching further in the high-frequency (glassy) region, similar to that observed in G″ response at 1 Hz (Figure 3b).

To better understand the magnitude of broadening observed in the α-transition region, the tan δ peak was normalized against its maximum value (tan δ_max) and is presented as a function of frequency for all specimens in Figure 6c.⁵⁷ The addition of glass fibers in the GFRP results in a nearly 5-fold increase in the full width at half-maximum (fwhm) of normalized tan δ as compared to the Epoxy specimen. This may be due to the shifting of the dominant rubbery and glassy relaxation modes introduced by interfacial interactions between the fiber sizing and the epoxy resin.⁵⁸ The fwhm of the normalized tan δ response further broadens asymmetrically by nearly 2-fold, specifically into the glassy region upon grafting PEI-functionalized CNTs (≈1.7 mass %) onto the fiber surfaces. The observation of this type of broadening in α-relaxation characteristics is not uncommon in CNT-based polymer nanocomposites. It has been previously reported that covalent interactions between dispersed CNTs and polymer matrices result in the formation of nonbulk interphase domains around nanotube surfaces, and their viscoelastic properties often differ from bulk polymer characteristics, along with changes in polymer T_g.^21,23,59 A similar treatment of CNT–resin interaction can be extrapolated to this study; however, it is important to note that some of the key differences between this study and its predecessors include the presence glass fibers, the differences in resin chemistry, CNT morphologies, CNT mass fractions, CNT functionality, and importantly the localization of the CNTs to the fiber–polymer interface. As the CNT–PEI–epoxy interactions are largely restricted to interphase regions, which are estimated to be around only 2% of the total composite volume, the role of the interphase in affecting bulk polymer dynamics may be less drastic as compared to previous studies.

The relaxation characteristics of the CNT–GFRP system are represented as a function of time by fitting a sum of Maxwell elements (eqs 4 and 5) to the master curves (G′ and G″) using a commercial software developed by Winter et al.^55,60,61

$$G^{\prime }\left(\omega \right)=G_{\text{e}}+\sum _{i=1}^n{g}_i\frac{{\omega }^2{\tau }_i{}^2}{1+{\omega }^2{\tau }_i{}^2}$$ (4)

$$G^{″}\left(\omega \right)=\sum _{i=1}^n{g}_i\frac{\omega {\tau }_i}{1+{\omega }^2{\tau }_i{}^2}$$ (5)

where G_e is the equilibrium modulus (G_e > 0 for solids), ω is the angular frequency in rad/s, g_i is the series coefficient, and τ_i is the relaxation time of the ith coefficient, to develop discrete relaxation spectra shown in Figure S11. The model fits to their respective master curves are shown in Figure 6a,b. The standard deviations for the fits are <0.02% for all specimens.

The trends observed in the relaxation spectrum fit (Figure 7) are similar to that observed in frequency space presented in Figure 6. The relaxation spectra have been normalized to the highest series coefficient to facilitate comparison of the shapes between specimens. The Epoxy specimen exhibits relaxation processes spanning nearly 10 orders of magnitude, similar to that observed previously by Brien et al.⁶² in an identical resin–hardener combination. In GFRP and CNT–GFRP, the presence of glass fibers retards the polymer chain relaxation primarily at the interfacial region, leading to an increase in the influence of longer relaxation times (10⁰−10⁷ s) in the rubbery region. Similar to the behavior in frequency space, the changes in viscoelastic properties of the CNT–GFRP is localized to fast relaxation time processes (τ/τ_max < 1).

Figure 7.

Normalized relaxation spectra calculated using dynamic moduli master curves shown in Figure 6. The relaxation spectra have been normalized based on the highest series coefficient.

Several potential factors, based on the influence of the CNT–polymer interphase, could contribute to the broadening observed in the viscoelastic characteristics (identified in Figures 3, 6, and 7). The surface functionality on CNTs consist of high-molecular-weight (25000 g/mol), flexible, hyperbranched amine groups. Faster PEI–epoxy segmental mobility at the interphase (as compared to the bulk of the polymer) may lead to reductions in T_α (and T_g) and broadened relaxation characteristics, as observed by Chen et al. in a CNT–epoxy system consisting of large molecular weight (≈2000 amu) amine grafts on CNTs.²³ The presence of excessive amine groups in the PEI may also affect the local nanoscale cure kinetics within the CNT–PEI–epoxy interphase and, thus, modify its relaxation characteristics. For all specimens, the ratio of epoxy resin to aromatic hardener was maintained at stoichiometry. We assume that within the CNT interphase region the presence of hyperbranched PEI increases the equivalent hydrogens available for the epoxide ring-opening reactions. The stoichiometric offset in reaction chemistry between amine and epoxide groups may cause minor reductions in T_g because of an increase in the chain ends, which leads to excessive free volume at the CNT–PEI–epoxy interphase, similar to that observed by Palmese et al.⁶³ Another possible effect on the cure chemistry may be due to the topological constraints associated with the hyperbranched amine structure that reduces the accessibility to the internal amine groups of PEI and decreases the kinetics of the cross-linking reactions between the PEI and the epoxy.⁶⁴ Reduced covalent interactions can result in increased noncovalent interactions (van der Waals and hydrogen bonding) between the CNT–PEI–epoxy–fiber constituents that are analogous to thin polymer films enclosed within nonwetting, hard surfaces (or free surfaces), where the relaxation characteristics along with the T_g are affected.^65,66 Further study is underway to understand whether PEI-influenced cure changes are likely to increase, decrease, or broaden relaxation times.

Regardless of the specific physical or chemical nature of the heterogeneity introduced into the epoxy relaxation mechanisms, the incorporation of grafted CNTs on glass-fiber surfaces has achieved a change in viscoelastic characteristics of the CNT–GFRP that is unique to this commercially relevant, hierarchical composite architecture. The time dependence of the polymer segmental relaxation has been altered without significant changes to the temperature dependence. This is evident from the lack of significant changes to the T_g (or T_α) of the polymer matrix before and after CNT–PEI addition, which are different from the trends observed in poor²³ or strongly²¹ interacting CNT–polymer systems. Therefore, the overall influence of the CNT–PEI–epoxy interphase on the polymer dynamics is highly localized and less drastic as compared to dispersed CNT-based polymer nanocomposites, as mentioned earlier.

Nanoscale Polymer Dynamics and Free-Volume Characterization.

The HFBS spectrometer was used to characterize the nanoscale polymer chain dynamics in the Epoxy, GFRP, and CNT–GRFP specimens and ascertain the role of CNT–PEI–epoxy interphase. These measurements capture both incoherent and coherent scattering of neutrons from the sample. Incoherent scattering is related to the spatial correlations of the same atom at different times and gives a measure of the self-motion, while coherent scattering is due to spatial correlations between different atoms at different times and gives a measure of the collective motion. The scattering intensity is dominated by the self-motion of H atoms since the incoherent scattering cross section of H atoms is very large when compared to coherent and incoherent cross sections of other atoms in the samples. Therefore, incoherent scattering measured on the HFBS instrument provides information about the self-motion of H in polymer chains, both in the bulk phase and in the interphase.

A temperature scan of the elastic scattered intensity provides information about the motions and thermal transitions occurring in the samples (Figure 8a). The elastic intensity I_el(Q,T) is dominated by the hydrogen dynamics slower than ≈1 ns (instrumental resolution). Differences in sample volume or polymer weight fraction are eliminated by normalizing intensities to those obtained at the lowest temperature I_el(Q,T)/I_el(Q, T ≈ −258.15 °C) which allows a direct comparison between the samples as shown in Figure 8a. At the lowest temperature T ≈ −258.15 °C, all motions are essentially frozen at the time scale of the instrument (≈1 ns). Increasing temperature decreases the elastic intensity as the atoms on the pendant functional groups vibrate or rotate faster than the instrument resolution. The stepwise decrease in slope at ≈127 °C is a signature of the glass transition indicative of main chain motion. Above the T_g, the chain segments in the backbone contribute to faster hydrogen dynamics (lower elastic intensity and larger MSDs) due to translational motion. In the region of glass transition, α (side chain) and β (main chain) relaxation merges whereas at temperatures well above the T_g, the localized dynamics are too fast, and the observed intensity change at the highest temperature is solely due to segmental dynamics of the epoxy chains. From the Q dependence of the elastic intensity, the mean-square displacement (MSD) of the hydrogen atoms, 〈u²〉, is estimated by eq 6^67,68 and shown in Figure 8b.

$$\frac{I_{\text{el}}(Q,T)}{I_{\text{el}}(Q,T\to 0)}={\text{e}}^{\left(Q^2\langle u^2\rangle \right)/3}$$ (6)

On the basis of the results shown in Figure 8, we see that the MSD within the range of the temperature–frequency sweep measurements follows the following trend: Epoxy > CNT–GFRP > GFRP. Increasing the fraction of interfacial area within the specimens via the addition of fillers widens the transition region between sub-T_g dynamics and segmental dynamics as observed in Figure 8b. Above 177 °C, the contribution of the interphase weakens and the MSDs of GFRP and CNT–GFRP merge. The inclusion of rigid fiber fillers in both glass and CNT-coated glass fiber composites retard the overall polymer dynamics, in both the glassy and the rubbery regime.

Figure 8.

Elastic neutron scattering results. (a) Normalized elastic intensity–temperature scans for the polymer, GFRP, and CNT–GFRP samples. (b) Mean-square-displacement of H atoms determined from the Q dependence of the elastic scattering intensity (see the text) as a function of temperature.

The differences in the o-Ps lifetimes and their corresponding intensities as measured by PALS is shown in Table 3. The normalized spectra and the complete analysis are shown in the Supporting Information (Figure S12 and Table S3). At room temperature conditions, the lifetime values follow the trend Epoxy > CNT–GFRP > GFRP, which indicates that the average pore-size in the polymer reduces upon addition of fibers. This is similar to the trend observed for the MSD at room temperature conditions. The reduction of pore size in the fiber composite specimens may be attributed to increased polymer chain confinement between densely packed fibers due to physical and chemical interactions between the fiber surfaces and the polymer.⁶⁹ Upon comparison of GFRP and CNT–GFRP specimens, the CNT–PEI interface is found to increase the average size of free-volume sites. As discussed previously, this is likely due to a variety of reasons including increased polymer chain ends from nonstoichiometric cure process at the interface, higher flexibility (reduced chain frustration) of the PEI molecule, and increased surface roughness due to addition of CNTs.

Table 3.

Orthopositronium Annihilation Lifetime (τ₃) and Its Corresponding Intensity (I₃) for the Various Test Specimens^a

sample	τ3 (ns)	I3 (%)	reduced χ2
Epoxy	1.700 ± 0.005	26.7 ± 0.1	0.99 ± 0.02
GFRP	1.643 ± 0.007	17.5 ± 0.2	1.03 ± 0.02
CNT-GFRP	1.684 ± 0.008	16.6 ± 0.2	1.01 ± 0.02

^aThe standard deviations for all the samples are based on the nonlinear least-squares fitting process carried out using a commercial software, with reduced χ² values shown in the table.

The I₃ values in the Epoxy sample are found to be higher than the fiber composite samples. This is attributed to the lower polymer mass fraction (≈40%) in the fiber composite samples, as compared to the 100% Epoxy sample. Though a minor reduction in I₃ was observed in CNT–GFRP specimen as compared to GFRP specimen, the origins of this reduction were not explored due to potential interference from positronium quenching mechanisms in these samples.

CONCLUSIONS

Direct attachment of CNTs to the surface of microscale glass fibers is a commercially viable, alternate route to produce hierarchical, multifunctional nanocomposites. The effects of CNTs on viscoelastic properties are not as well understood as the mechanical or fracture properties due to the complex nature of the CNT–PEI–epoxy interphase localized to fiber surfaces. A combination of DMTA temperature–frequency measurements and NS techniques was used to interrogate the GFRP and CNT–GFRP materials—in particular, the interphase contribution to viscoelasticity and polymer dynamics throughout the glassy-to-rubbery transition region. Results from both techniques, despite their differences in sensitivity to length and time scales, suggest that the polymer viscoelasticity is influenced by the presence of PEI-functionalized CNT layers. The combination of techniques provides a unique insight into the effects of confining an anisotropic interphase layer on the dynamic properties of bulk CNT–GFRP that have not been previously reported. These insights are summarized below.

(1) The localization of the CNT complex at the fiber interface does not significantly alter the T_g of the composite. DSC, DMTA, and HFBS provide a slightly different estimate of T_g; e.g., the transition occurs at ≈127 °C for HFBS, which is ≈5% smaller compared to the values obtained from the DSC and DMTA. More importantly, the addition of neither glass fibers nor CNT–PEI causes a substantial change in T_g. This is consistent with the results observed in highly filled attractive polymer nanocomposites where the changes in T_g remain within 10%.⁷⁰

(2) The introduction of nonbulk interphase domains broadens the glassy–rubbery transition region of the epoxy across both the measured frequency and time scales, as evidenced by both DMTA and HFBS measurements. The α-transition peak of the epoxy is observed to undergo broadening with the addition of both micro- and nanoscale reinforcing constituents, i.e., glass fibers (≈58 mass %) and CNT–PEI (≈1.7 mass %). In the DMTA measurements, the broadening in α-relaxation process is more significant right below T_g (or T_α), while in HFBS measurements, the broadening is consistent across the entire transition region. This translates into increased contribution of short time-scale relaxation process (or high frequency in TTS) due to the CNT–PEI complex. The fact that the MSD of CNT–GFRP is larger than that of GFRP near-T_g and in the sub-T_g region suggests that the localized dynamics of the epoxy are faster in the presence of CNT–PEI coating. The broadening is likely related to the heterogeneity in local environments experienced by the epoxy due to the presence of the CNT–PEI complex extending a significant distance out from the fiber surfaces.

(3) While the CNTs increase the elastic stiffness of the composite deeper in the glassy region, they alternatively result in a more compliant material above the glass temperature. The G_r of CNT–GFRP is ≈26% lower than GFRP. This indicates higher mobility of cross-links or lower cross-link density in the rubbery region and is supported by higher MSD of the CNT–GFRP in this temperature range. The nano- to microscale roughness introduced by CNT deposition (as shown by SGIM and SANS) on the glass fiber surfaces may induce topological constraints that result in a higher free volume (as shown by PALS measurements at room-temperature conditions) and faster local hydrogen dynamics (HFBS measurements). Alternatively, the stoichiometric offset by the presence of excessive hydrogen from the PEI may reduce interfacial covalent bonding between CNT–PEI and the epoxy and thereby reduce G_r.

The specific origin of viscoelastic broadening and influences on MSD are difficult to isolate in this complex system. Overall, the results suggest that the PEI-functionalized CNT coating on the glass fibers increases the contribution of the interphase to the mechanical relaxation of the composites without altering a key engineering specification, the T_g. In the broader context with respect to engineering applications of these materials, the changes in relaxation properties may not be inconsequential. The transport of small molecules (water, solvent, etc.) through the fiber reinforced composites, creep and stress relaxation, electrical conductivity, and thermal expansion may be influenced by the structural and viscoelastic variations identified here. The ability to measure both structure and interfacial viscoelastic properties will guide engineering of the percolated CNT networks for various multifunctional applications.