The Quantum Hall Effect in the Era of the New SI

Abstract

The quantum Hall effect (QHE), and devices reliant on it, will continue to serve as the foundation of the ohm while also expanding its territory into other SI derived units. The foundation, evolution, and significance of all of these devices exhibiting some form of the QHE will be described in the context of optimizing future electrical resistance standards. As the world adapts to using the quantum SI, it remains essential that the global metrology community pushes forth and continues to innovate and produce new technologies for disseminating the ohm and other electrical units.

1. Introduction and background on the requirements for absolute units

The recent, global celebration of World Metrology Day on May 20, 2019 reflects historic changes to the International System of Units, or SI. In establishing the new SI, representatives of the world’s governmental metrology community, along with the International Committee for Weights and Measures (CIPM), decided that all units of measure should be traceable to fundamental constants of nature. The seven base units are now linked to seven fixed values, four of which have been modified to represent an exact value: the Planck constant (h), the elementary charge (e), the Boltzmann constant (k_B), and the Avogadro constant (N_A).

The changes to the constants h and e have direct ramifications on how the electrical units of the ohm, volt, and ampere are defined. In the context of the quantum Hall effect (QHE), the von Klitzing constant underwent a change from its conventional value set in 1990 (R_K-90 = 25 812.807 Ω) to the most recent scientifically-produced value of h/e² (R_K = 25 812.807 459 304 5 Ω).

1.1. Historical context

At the turn of the 20^th century, Italian physicist Giovanni Giorgi advocated for the use of a unit to represent physical constants predicted by Maxwell’s equations, namely the magnetic or electric constant (μ₀ and ε₀, respectively, where μ₀ε₀ = c⁻² ), mostly relevant to electromagnetism. The MKS system of units was combined with the ampere, formerly an empirical electrical unit, to complete the archaic MKSA system adopted by the CIPM in 1946 [1].

The ampere was inherently difficult to realize based on its definition in 1946, and would be realized through Ohm’s law, as asserted by the General Conference on Weights and Measures (CGPM) [2]. Over the next 40 years, quantum phenomena such as the Josephson effect and the quantum Hall effect were discovered [3, 4], and electrical standards would soon become universally accessible. Two derived constants, R_K-90 and the Josephson constant K_J-90, were created in 1990 and thus quantum phenomena made a global appearance in conventional electrical unit definitions. Since then, exploration of two-dimensional electron systems (2DES) where the QHE is measured, typically silicon metal-oxide semiconductor field-effect transistors (MOSFETs), GaAs/AlGaAs heterostructures, and single-atomic-layer epitaxial graphene, and in Josephson effect superconducting microwave-frequency circuits, have significantly impacted the metrology community.

1.2. Modern day realizations

To achieve highly precise measurements of the ohm, GaAs/AlGaAs became the primary material for the unit’s representation after 1990. For about two decades, electronic and semiconductor technologies advanced and both GaAs-based resistance standards and cryogenic measurement methods became more and more developed [5, 6], increasing the applicability to electrical metrology but limited by the availability of suitable GaAs heterostructures tailored by molecular-beam epitaxy.

By the end of the 2000s, with the dawn of research in two-dimensional materials like graphene, the QHE became truly accessible to metrology researchers. Experimental quantized Hall resistance (QHR) standards were soon being fabricated by chemical vapor deposition (CVD) [7], epitaxial growth [8], and mechanical exfoliation of bulk graphite [9]. Throughout the 2010s, researchers gradually improved devices to overcome various obstacles and reached a point where graphene was set to replace its predecessor [10].

Present-day efforts include the global implementation of graphene-based devices as resistance standards and the replacement of artefact kilogram standards of mass with quantum-based mass determinations using the Kibble balance and atomic-mass-based standards [11]. The SI-90 representations failed to adequately encompass and link together the energy-wavelength equivalence principle, physiochemical constants (Avogadro, Boltzmann, Faraday, etc.), or electromagnetic constants of nature – many of these were quite inexact [12]. And with such considerations, the 2019 definitions of just seven constants stands to correct these failures and to place quantum electrical standards into exact agreement with the SI [13].

1.3. Future directions

As the new SI, or more colloquially the quantum SI, takes hold on our everyday lives, future directions are plentiful and are of interest to the metrology and scientific community. The QHE will continue to serve as the foundation of the ohm and may possibly contribute to the development of more sophisticated devices suitable for alternating current (AC) resistance standards. This is inextricably linked to standards for impedance typically obtained from systems like a calculable capacitor [14–16].

Variants of graphene-based devices, like those prepared in array geometries or as p-n junctions (pnJs) may provide a rapid expansion of available quantized resistance values. And for devices taking on array geometries, the parameter space for applied current may drastically increase, paving the way for the establishment of a benchtop quantum current standard. In other potential directions, it may be possible to use very different materials called topological insulators to develop resistance standards exhibiting the quantum anomalous Hall effect (QAHE), which essentially removes the need for a strong magnetic field.

2. Development of the 1990 SI

2.1. Early 2DES devices

Traditionally, resistance measurements involved standard resistors made of copper-manganese-nickel and other alloys, but due to their unpredictable and time-dependent variation [17], a resistance standard that did not depend on physical artifacts was strongly desired. With the discovery of the integer QHE in the early 1980s, the electrical metrology community immediately sought to develop a resistance standard based on the observed relation: R_H = h/ie². With i taking on an integer value (within the scope of this review), multiple quantized resistance steps could be observed as the Hall effect was measured in 2DES under large magnetic fields.

These observations were made in a variety of systems starting out with silicon MOSFETs and quickly moving to GaAs/AlGaAs heterostructures [18]. In GaAs systems, a two-dimensional layer of electrons is formed when an intrinsic electric field forces electrons to an interface between semiconductor layers. For the case of the less-frequently used silicon systems, the electric field is generated by a gate and is separated from the surface of the semiconductor by an oxide layer with insulating properties. One of the large disadvantages of MOSFETs was the high magnetic field requirement needed to produce a wide plateau in resistance as well as a smaller operating current. In some cases, currents as low as 10 μA would cause the QHE to break down [19–21].

2.2. Using GaAs-based heterostructures

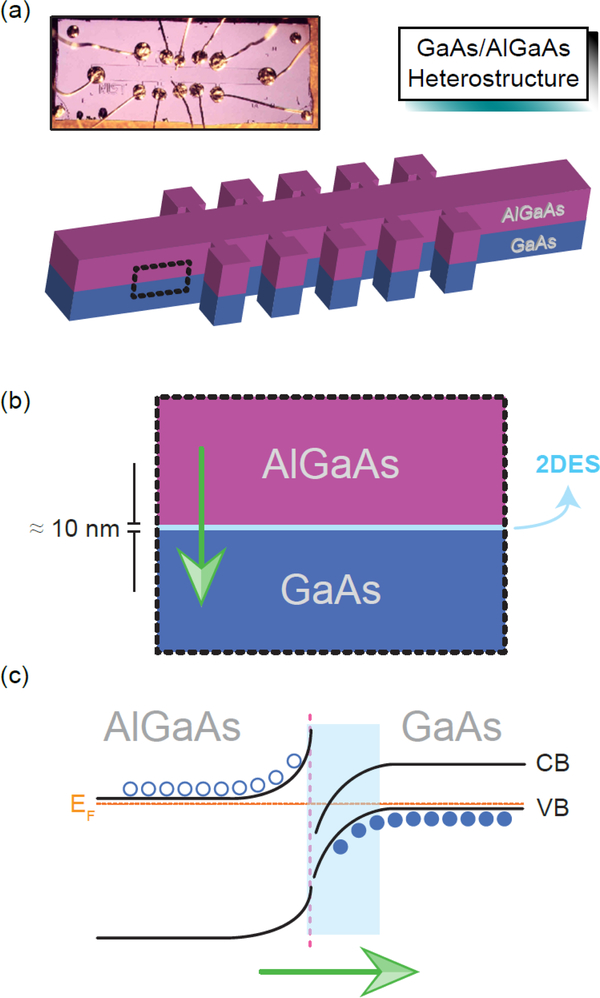
For many heterostructure devices, the 2DES is created by growing interface layers via molecular beam epitaxy. For the GaAs-based device shown in Figure 1, a 2DES is formed at low temperature when confinement potentials result from the positively charged ions present in the AlGaAs (insulating) layer [22–29]. Similar 2DES heterostructures have been developed in InGaAs/InP, which is obtained via metal-organic chemical vapor deposition [30].

Figure 1.

(a) Example of a GaAs-based device used as a QHR standard. A photo of an actual device accompanies the illustration of the heterostructure. (b) Upon magnifying the heterostructure cross-section, the AlGaAs/GaAs interface provides the region in which a 2DES can form. (c) The confinement is depicted in terms of the local band structure of the interface. The region in light blue indicates the approximate confinement in the horizontal direction, typically on the order of 10 nm.

A 2DES exhibits the QHE when placed under a strong magnetic field, with the field vector orthogonal to the 2DES plane. Experimentally, the measured Hall resistance R_xy perpendicular to the direction of the current becomes quantized and the diagonal resistivity ρ_xx vanishes. In the quantum Hall regime, electronic states at the Fermi energy become localized, and the localization length diverges as the Fermi energy approaches the center of a Landau subband. In the case of GaAs, the states at the center of the Landau level have a slight dispersion along the growth direction. These 3D effects would not become experimentally clear until the rise of graphene decades later.

These types of devices have been grown with such homogeneity and general quality that high mobilities (on the order of 200 000 cm²V⁻¹s⁻¹) at 4 K temperatures and below were easily achievable. It was during the 1980s that metrologists took advantage of the new high-quality devices to make determinations of the von Klitzing constant R_K. By many difficult experiments, various national metrology institutes (NMIs) improved the uncertainty of R_K and imparted momentum to the eventual approval of R_K-90 by the Consultative Committee for Electricity (CCE) [31].

The recommended value for international reference was obtained by using a weighted average of determinations made around the world, and in 1988 a global agreement was made – R_K would become R_K-90 = 25 812.807 Ω [32]. This value was also rounded to eight significant digits and was exact in practical usage, however the ohm unit was assigned an uncertainty relative to the best SI value to account for the statistical disagreements present in the global realizations. Despite the drastic, part-per-million changes that propagated through NMIs’ standard resistors from the 1990 redefinition, an order of magnitude better agreement in worldwide resistance intercomparability was achieved [33].

3. The evolving role of the quantum Hall effect in determining absolute units

3.1. Arrays and AC QHR in GaAs

In the earlier decades of developing QHR standards, the many NMI efforts had succeeded in implementing new standards based on GaAs devices [34–43], and metrologists commenced to explore the extent to which these devices could accommodate other values of resistance, namely through the construction of quantum Hall array resistance standards (QHARS) [44–52]. In conjunction, pursuits of standardized impedances from the QHE were well on their way at various NMIs to avoid using a difficult-to-construct calculable capacitor [53–62].

3.2. Overcoming limitations of GaAs-based devices

3.2.1. Looking to expand the parameter space

Although the establishment of QHR standards throughout major NMIs and a few primary laboratories have been successful, considerations had to be made regarding two important factors in metrology: simplicity of operation and total accessible parameter space. In the case of GaAs, whose available parameter space is graphically represented in Figure 2, the required infrastructure to achieve well-quantized resistances was demanding and approximated a basic research and development program in cost.

Figure 2.

A compilation of various studies involving GaAs-based and epitaxial graphene (EG)-based standards. The metrics of magnetic field, temperature, and applied current are shown as a basis of comparison. The labelled GaAs devices can be traced to the following references: A – [39], B – [91], C – [18], D – [27]. The labelled EG devices can be traced to the following references: A – [91], B – [75], C – [77], D – [92], E to G – [73], H – [92].

3.2.2. Graphene as a promising successor

The discovery of graphene and its anomalous QHE at restricted values (i = 2, 6, 10, …) due to spin and pseudo-spin degeneracies present in its Landau levels has ignited a paradigm shift in resistance metrology [63–70]. With the various methods of synthesizing graphene, many parameters including the crystal growth method could be adjusted to optimize this material’s utility for metrological purposes.

In a majority of cases, exfoliated graphene is understood to exhibit the highest of mobilities and cleanest of crystallinity. These reasons motivated an initial effort to evaluate the accuracy of quantization in such devices [8]. The devices made from exfoliated flakes of graphene were small and achieved low breakdown currents on the order of 1 μA at best. Furthermore, these were assembled one-by-one and could not achieve high yields. The first breakthrough came in 2010 when researchers at Linkoping and Chalmers Universities produced structures made from epitaxial graphene on SiC substrates and provided them to the RISE Research Institutes of Sweden and the National Physical Laboratory (NPL) of Great Britain. These lithographically grown devices achieved quantization uncertainties of 8.6 × 10⁻¹¹ μΩ/Ω in comparisons with a GaAs QHR standard from the International Bureau of Weights and Measures (BIPM). Notably, these measurements were direct comparisons and were limited by the breakdown current of the GaAs device, not the graphene standard. Epitaxial graphene (EG) can also be synthesized by chemical vapor deposition on SiC, and in 2015, exploration of this material achieved standards-quality at temperatures up to 10 K [71, 72].

3.3. Exploring the v=2 plateau in epitaxial graphene

Figure 2 highlights the present-day parameter space over which one can realize the extraordinary precision of the QHR value in a 2D material [73–81]. It has been established that graphene-based QHE devices can exhibit a distinct advantage over GaAs-based devices when attempting to use low magnetic fields, higher temperatures, and larger currents [10]. Improvement of devices to expand accessibility is expected to correlate with the reduction in cost and complexity of QHR resistance standards for metrology as well as the associated laboratory measurement apparatus.

4. The modern generation of measurements and devices

4.1. Graphene as a new standard

Since 2017, EG has been used as part of the electrical resistance dissemination service in the United States. The preceeding years were primarily dedicated to optimizing the technology and fabrication processes such that EG-based QHR devices could be deployed into US and global industries. A summary of this optimization process is illustrated in Figure 3 and represents years of efforts directed by multiple institutes [82–90]. In short, EG-based devices, to be deployable for metrological implementation and general global usage, required the quality of the graphene to be of high order, the device scalability to be of appreciable range (from micrometers to centimeters), the stability of electrical properties to be simple to achieve, and for more complex structures’ fabrication and testing to be demonstrated (i.e. arrays).

Figure 3.

(a) The optimization process for EG-based devices made at NIST took several years to accomplish, with the first crucial milestone being the successful growth of uniform single layer EG as opposed to overgrown or undergrown (i.e. disordered) material. (b) With successful growth came the need to increase the scalability from the micron to the centimeter scale. This was accomplished with polymer-assisted sublimation growth (PASG) [79]. (c) Once devices can be fabricated from large-scale growths, their stability, typically of the carrier density and longitudinal resistivity, must be ensured by one of a few modern-day techniques like functionalization with Cr(CO)₃. Other methods of carrier density adjustment include encapsulation with a polymer containing a dopant, i.e., F4TCNQ [88, 89]. (d) As fully functioning QHR standards become easier to produce, fabricating more complex devices to pursue different quantized resistance values becomes a feasible reality [93].

4.2. EG recent breakthroughs

The recent breakthroughs in using EG as a national resistance standard are best embodied by several works recently published indicating that EG has surpassed GaAs as a user-friendly material [72, 78, 91, 92]. In addition to outperforming GaAs-based devices, EG-based devices have added advantages: their fabrication methods allow simple electrical contacting [88, 89]; production can be taken over by the NMIs; and, most recently, they are compatible with contact pads made from superconducting materials (NbN, NbTiN) with high critical temperature (approximately 10 K) and high critical field (greater than 20 T) [93]. These breakthroughs enable further work summarized in 4.4.

4.3. CCC and DCC improvements

As the devices for resistance standards improved, so did the corresponding measurement systems with which one can disseminate the ohm. To provide reliable traceability, the measurement of the ratio between the QHR and a resistor must achieve uncertainties comparable to the stability of the standard resistors of the laboratory. Frequent measurements produce better results because such ratios are well-maintained, and room-temperature bridge systems like direct current comparators (DCCs) are able to deliver an improved frequency of measurements year-round because they can be operated without the need for cryogens [94]. Moreover, these bridges have been developed into user-friendly and automated systems, removing the dependence on specialized knowledge typically required of the more complex cryogenic counterparts [6, 95]. For some NMIs, the automated, binary-ratio cryogenic current comparator (CCC) has near-perfect ratio accuracy and improved Type B uncertainties for more precise ratios in QHR comparisons [96–101].

Moving forward, NMIs have anticipated the following goals for EG-based standards: (1) Precise resistance scaling to the reference 10 kΩ level from the QHR using larger voltages than the usual bridge voltages of 0.5 V to 1 V (DCC and CCC). (2) Streamlining of compact measurement systems including cryogen-free (closed-loop) cryostats to provide turn-key traceability, thereby reducing the operational costs significantly. That said, the already-achieved improvements and user-friendly commercialization of both types of bridges have undoubtedly accelerated dissemination efforts.

4.4. Ongoing work

Ongoing work in implementing EG-based devices as national standards includes a careful analysis of the process of traceability [72, 92, 102]. With the metrology community in agreement that a comparison against GaAs-based devices was accomplished, next steps became clearer as far as how the basic EG-based QHR could be further developed. Interconnections between QHR devices have been a subject of special research interest since the early 1990s [103]. This is due to the surprising ability of the QHE state to strongly suppress current from entering or leaving the device at all but one set of contacts.

5. Future of the quantum Hall effect and its effect on the quantum SI

5.1. Array devices

If the device contact resistances are much smaller than R_K, it is straightforward to achieve an equivalently precise resistance of R_K/2 or 2R_K using two QHE devices interconnected at three or more such pairs of contacts. By using series and parallel connections as fundamental units, construction of an EG-based QHARS has become feasible, enabling high-precision access to multiple quantized resistance values [93, 104–105]. One of the challenges for complex arrays might be the accumulation of resistances at electrical contact pads and interconnections when large numbers of devices are used in such an array. The use of superconducting contact metals together with various device geometries promoting multiple-series connections [93, 106], may pave a smooth path to the next generation of QHR devices.

With the complexity of EG-based devices increasing, coupled with the capability of having effectively zero contact resistance, much larger arrays can be constructed having an abundance of new quantized resistance values. Examples of such devices are shown in Figure 4 (a) and (b), where may select any two arbitrary points between which to measure an effective quantized resistance whose exact value can be determined by various models like Kwant, a simulation program with integrated circuit emphasis (SPICE, LTspice), or other generalized parametric analyses [107–109].

Figure 4.

(a) Using superconducting contacts and small EG QHR elements, grid arrays can be constructed as rectangles or (b) Corbino-type geometries. Determining the expected value between any arbitrary pair of points can be done with various modeling techniques done for similar systems. (c) Unlike the previous two configurations, which presumably use unipolar regions, a bipolar and complex pnJ device in the quantum Hall regime could be used to externally program various values of resistance without changing lead connections.

5.2. p-n Junctions

Another alternative for moving forward is the pnJ construction. For EG-based devices on the order of 100 μm or less, it is possible to implement top gates to adjust the carrier density in various regions, as has been demonstrated using a hexagonal boron nitride dielectric layer. Additionally, because of the underlying physics of graphene p-n junctions (pnJs), it is feasible to construct devices that can access quantized resistance values that are either multiples or fractions of R_K, and metrologically useful resistance quantization has been recently shown [110–113]. The obtainable values in the measured longitudinal resistivity arise from the equilibration of various Landauer-Büttiker edge states [114–116].

If implementing controllable gates on EG-based devices becomes possible, then revolutionary devices like the programmable QHR may become future milestones (see Figure 4 (c)). And although pnJs for metrology need to be further developed in terms of gating, the scalability of that gating has already been demonstrated for semi-permanent gating [108]. Furthermore, the latter devices, when fed multiple sources of current at arbitrary points, have been demonstrated to exhibit electric potential redistributions resulting in atypical values of resistance [108].

These convenient and rather unique properties of pnJs demonstrate a second, more fundamental path to avoid resistance from the metallic contacts and multiple device interconnections. And unlike the superconducting contacts, more devices can be connected in series using a minimum surface area and the 100 nm-scale junctions between bipolar regions.

5.3. DC quantum current standard and AC QHR

The calibration of capacitors, inductors, or AC resistors, essentially being a measurement of complex ratios of impedance, can be performed with traceability from a calculable capacitor as described earlier. Practical construction and use of the calculable capacitor are challenging because of unavoidable fringe fields and general deviations of the electrodes from ideal geometries.

The utilization of EG-based QHARS can be applied to the possible realization of the quantum ampere, which is now based on the elementary charge. The ampere lacks accurate traceability to within 10⁻⁸ despite many efforts made for the development of single-electron tunneling devices. By combining the QHR and a programmable Josephson junction voltage standard, a quantum circuit can be built, leading to the attainment of a programmable quantum current generator (PQCG) and resulting in a direct way of disseminating the ampere at the milliampere range and above [117].

The pursuit of AC QHR standards opened new avenues enabling a way to realize units such as the farad and henry by using fundamental constants rather than dimensional measurements [118–119]. AC QHR measurements performed with EG-based devices, as opposed to the GaAs-based counterparts, were demonstrated to be a feasible reality because of improved device characteristics. Consequently, research groups have been able to directly access the units of capacitance and inductance with high precision [120–122].

In the quantum SI, the permittivity of free space will no longer be exact and will have an inconsequential uncertainty associated with it. Considering these factors, it may be time to use existing quantum electrical standards to a better advantage. Efforts are ongoing to utilize several Josephson arbitrary waveform synthesizers jointly with an EG-based AC QHR device to construct a quantum LCR meter that can be used to calibrate any two-terminal impedance standard.

5.3. Topological Insulators

To remove the need for strong magnetic fields, new materials, like topological insulators (TIs), that exhibit the QAHE could be improved. This next generation of resistance standards would, at most, need small permanent magnets to activate a quantized resistance value. And an added advantage to using TIs includes being able to operate them at zero-field for measurements, as has been shown in some recent work [123–126]. In the ideal case, TI-based QHR devices would make disseminating the ohm more economical and portable, as these types of devices could be combined in a single cryostat with other components of the quantum metrology triangle, like the previously-mentioned programmable Josephson junction voltage standard.

5.4. Conclusions

As the world adapts to using the quantum SI, the QHE will continue to serve as the foundation of the ohm while also expanding its territory into other SI derived units. This growth appears promising in the form of new and more complex EG-based devices, including arrays and pnJs, as well as potentially new materials developed for the QAHE. Devices exhibiting some form of the QHE will provide a robust way of optimizing future electrical measurements and may even appear in instruments designed for end-users with very demanding applications.

Figure 5.

An example illustration of an EG-based device usable for AC QHR measurements. The graphene layer is effectively shielded in this design configuration.