An experimental and modelling study of water vapour adsorption on SBA-15

Abstract

Many publications have been dedicated to the study of water vapour adsorption on the ordered silica-based material Santa Barbara Amorphous-15 (SBA-15). However, two aspects still need to be clarified: whether the solid is stable under repeated adsorption-desorption cycles and whether the experimental data can be predicted with a simple yet accurate analytical equilibrium model. In this study, SBA-15 showed good long-term structural stability when exposed to repeated adsorption-desorption cycles using water vapour as adsorptive up to 90 % relative humidity at 288 K, 298 K and 308 K. The reproducibility of the equilibrium isotherm was investigated using different commercial gravimetric instruments designed for water vapour adsorption measurements. The experimental measurements show a modification of the microporous structure of the solid after the first full isotherm measurement. Some water is strongly adsorbed and trapped during the first experiment on a fresh sample. After the first adsorption-desorption cycle, the water isotherm is characterized by a low value of the Henry law constant and by a nearly vertical capillary condensation and evaporation branches. Quite interestingly, the experimental scanning curves do not simply cross from one branch to the other as would be expected for cylindrical independent pores. The experimental data are correlated using new analytical models able to predict the amount adsorbed in the entire concentration range for the main adsorption-desorption branches and for the adsorption-desorption scanning curves.

Graphical Abstract

1. Introduction

The ordered structured silica-based mesoporous material Santa Barbara Amorphous-15 (SBA-15) was synthesized twenty years ago for the first time [1]. Considering the innovative and promising characteristics, it has been one of the most studied mesoporous solids in the literature [2]. The synthesis and preparation [3] are well-known, and the material has revealed some interesting differences when compared to the similarly structured precursor Mobil Composition of Matter-41 (MCM-41) [4]. Due to the possibility of obtaining a solid with an ordered structure made of independent cylindrical pores and customized pore size and length [5], SBA-15 has been used and tested for several different studies or applications [2,3]: adsorption; gas storage; catalysis; bio-sensing; and drug release are the most common fields in which the solid has been studied and evaluated.

The interaction between SBA-15 and either liquid or vapour water has been extensively studied in the literature [6–9]. These studies are mostly focused on three aspects: the phase behaviour of water confined in mesoporous channels of well-known dimensions; the hydrothermal stability of SBA-15 when exposed to liquid or vapour water; and the hydrophobicity-hydrophilicity nature of the solid surface.

The stability of SBA-15 for water adsorption applications has been studied under several different conditions, including in the presence of water vapour or when dispersed in liquid water [7,8]. However, clear indications about the stability of the solid to high relative humidity are still missing. The main reasons might be due to the different procedures used in the preparation of the solid, which lead to samples with different properties. As a general consideration, the main structure of the SBA-15 seems to be reasonably stable when exposed to moisture or liquid water, especially when compared to the similarly structured MCM-41[9]. However, some modification of the SBA-15 microporous structure has been reported in the literature [7]. The micro-porosity, usually present in SBA-15, has been considered as the main cause for the change in the structure of the solid when exposed to liquid water. An increase of the temperature synthesis up to 130 °C will eventually lead to a solid with no micropores and it will avoid a possible modification of the structure when the solid is exposed to water [7]. The modifications that affect the structure of SBA-15 in presence of micropores have been studied also at higher liquid and vapour water temperature up to 150 °C. The observed dissolution of silica and consequent re-deposition on the pores walls is present with both vapour and liquid water. However, the process occurs more rapidly in the presence of liquid water. In both cases, most of the microporous volume of the material is lost and some water is permanently trapped in the microporous structure [8,10]. The same process of dissolution of the pore surface silica in water has also been observed at 60 °C. In this case, the dissolution rate of silica in water has been observed to decrease until the dynamic equilibrium between dissolution and redeposition is reached [9]. In some cases, repeated cycles of water vapour adsorption-desorption on SBA-15 performed at 5 °C have also shown strong modifications of the mesoporous structure [11]. Not only does the permanently-trapped-in water drastically reduce the microporous volume, but the capillary pressure of liquid water has also been responsible for the collapsing of some of the inner walls of the pores. Thus, this process can lead to even more water trapped within the mesoporous volume of the solid [11]. Ordered silica-based materials, such as MCM-41 and SBA-15, have been proven to be hydrophobic materials. This has clearly been demonstrated in a study in which the simultaneous adsorption of water and organic solvents, onto several ordered silica-based materials, has been investigated [12]. The organic compounds were able to displace the water. The hydrophobicity of these materials depends mainly on the pores size [13,14], the superficial concentration of silanol and siloxane groups, and the micropore volume [6,15]. The diameter of the mesopores can be tailored by adjusting the temperature adopted during the synthesis [16], meanwhile, the surface polarity can be tailored either by varying the synthesis conditions [15] or by changing the post-treatment temperature [16].

In this contribution, firstly, the stability of SBA-15 when exposed to repeated adsorption-desorption cycles up to high relative humidity at three different temperatures is investigated. Our particular interest is in the stability of the material after the first adsorption-desorption cycle as this will be the condition of SBA-15 in practical applications. We will aim to determine under which conditions the irreversible loss of the micropores occurs as a result of water adsorption.

The adsorption-desorption equilibrium isotherm of condensable vapours on silica-based mesoporous materials such as MCM-41, SBA-15, and similarly ordered solids has been modelled by following several approaches [17,18]. Historically, the modelling has been particularly challenging due to the complex shape of the equilibrium isotherm, which contains a characteristic hysteresis loop. Today, it is quite clear that the shape of the adsorption isotherm is mainly correlated to three factors: the geometric structure of the solid, the surface chemistry of the solid, and the physical status of the adsorptive inside the pores [19]. The modern molecular simulation approaches, e.g. GCMC and DFT, represent the state of the art in the field of porous solid characterization via adsorption and they can consider all these factors. Indeed, these techniques are capable of microscopically simulating the interactions that occur when considering an adsorptive molecule confined inside a nanoporous solid [19–21]. However, simple analytical expressions for these theories do not exist and they cannot be easily incorporated into the simulations of traditional semi-continuous adsorption processes, e.g., PSA (pressure swing adsorption) or TSA (temperature swing adsorption). These analytical expressions are also necessary for the investigation of adsorption kinetics [22,23].

One of the first attempts to predict type IV or type V isotherms [24] was presented in as a modification of the BET theory [17]. The model was proposed as an alternative to the capillary condensation phenomena with the more general intent of covering all the types of isotherms present in the literature. This approach does not reproduce with sufficient accuracy water adsorption on SBA-15 as will be demonstrated in this study.

The modified BET model has been replaced by more accurate approaches based on the widely accepted capillary condensation theory [19]. The systematic study conducted by Everett [18] on the hysteresis phenomena gave birth to the “independent domain theory”. This theory has been used for the interpretation of the hysteresis loops arising from adsorption of condensable vapours on ordered mesoporous solids made of independent pores. The theory is based on the main assumption that any physical system showing hysteresis can be considered as made of non-interacting domains. Each domain can be characterized by a distribution function in which only two discrete conditions are permitted, completely empty or completely full in case of adsorption phenomena. The amplitude and the shape of the distribution functions give a characteristic shape to the main adsorption-desorption curves and to the scanning curves of the hysteresis loop. This approach is quite accurate for ordered solids made of independent pores, such as MCM-41 and SBA-15. The adsorption equilibrium isotherms of vapours on these types of solids are generally characterized by a hysteresis loop with parallel adsorption and desorption branches. This confirms the main assumption of Everett’s theory. The shape of the scanning curves can be used to collect exceptional and crucial indications about the internal structure of the solid [25]. For solids made of cylindrical independent pores, the scanning curves are expected to depart from one branch of the isotherm, cross the hysteresis loop and join the other branch in an almost straight line. However, this behaviour has rarely been observed experimentally in the literature [26]. The unusual behaviour of the scanning curves has been predicted by considering a solid made of independent pores with different diameters along the same pore [27–31]. This attempt is meant to represent the probable roughness on the inner surface of the mesopores which is usually present in SBA-15 [32]. The presence of irregularities in the SBA-15 mesoporous channels was also suggested from diffusion studies by means of pulse field gradient nuclear magnetic resonance [33]. In this view, the sub-domains inside the same pore can no longer be considered independent of each other and the predicted isotherms resemble the isotherms usually obtained on solids characterized by disordered pore networks [34]. To account for the interactions among the sub-domains, the phenomena of advanced adsorption/condensation and pore blocking have been introduced respectively for the adsorption and desorption mechanisms. The advantage of this innovative approach, which was already partially introduced in Everett’s theory [35], is due to enhanced flexibility in predicting the different behaviour of the scanning curves and sub-loops. Starting from Everett’s theory, it is possible to derive analytical adsorption equilibrium models to interpret the adsorption of condensable vapours on ordered mesoporous solids [36–38]. The key point of these models is to consider a multilayer surface adsorption sequentially followed by the capillary condensation of the liquid inside a distribution of mesopores. Oh et al. [39] implemented a simpler approach by using more traditional expressions for the adsorption isotherms. In this case, two distinct types of isotherms have been combined for a good correlation of the experimental data: a linear isotherm from low concentration up to the onset of capillary condensation combined with the Sips isotherm for the capillary condensation and saturation part of the equilibrium isotherm. However, the equilibrium isotherm of water vapour on SBA-15 is not perfectly linear up to the condensation threshold, as it shows a small curvature low-pressure region. In addition, the Sips isotherm is not designed for the prediction of capillary condensation phenomena. An analysis of the S-shaped isotherms (type IV-V) which do not include capillary condensation phenomena can be found in [40]. Other authors have used the Dubinin-Astakhov model for the main adsorption curves and the scanning curves [41]. An important weak point of these approaches is due to the lack of thermodynamic consistency at low pressures, where the models should reduce to Henry’s law. In addition, these approaches generate mathematical discontinuities in the derivative of the isotherm (cusps) between the adsorption and desorption branches at the upper and lower closure points of the hysteresis loop. Firstly, such discontinuities are not observed experimentally. Secondly, these discontinuities can result in mathematical instabilities when used in the simulation of dynamic adsorption processes. The scanning curves can be predicted by the same models although a set of different parameters is required for each scanning curve.

In this study, the analytical expressions for two adsorption-desorption equilibrium models are introduced. The models are capable of consistently predicting the main adsorption-desorption branches and the scanning curves and can be used to interpolate the experimental data at different temperatures. The first formulation of the model considers a solid made of regular independent cylindrical pores. The second formulation of the model considers non-regular independent cylindrical pores for an improved correlation of the scanning curves, which is similar to the serially connected pore model [34].

2. Materials and Methods

The synthesis and preparation of the adsorbent material used in this work can be found in [42]. The pore size distribution of the material was obtained through the measurement of the argon adsorption-desorption isotherm at 87 K [24]. The argon adsorption-desorption isotherms up to the saturation pressure of argon at 87 K were performed in a low-pressure volumetric sorption instrument (Quantachrome Instruments Autosorb iQ MP)¹. The temperature was kept at 87 K using a liquid argon bath. Before the measurement, the sample was activated at 393 K for 3 h. Both fresh sample and used sample, which had previously been used for the water adsorption experiments, were characterized.

Two different gravimetric systems, designed for water vapour adsorption, were used for the measurement of the water equilibrium isotherms: a Quantachrome Instruments Aquadyne DVS; and a TA Instruments VTI-SA+ vapour sorption analyser. Both instruments are dynamic vapour sorption systems in which a dry nitrogen flow is continuously mixed with a humid nitrogen flow to reach the desired humidity value. For the experiments conducted on the Aquadyne system, the fresh sample was activated at 393 K for 3h under vacuum in a separate system and then loaded on the crucible of the gravimetric system. Before starting the run, the sample was held for 24h under a pure nitrogen flow at the same temperature of the experimental run. For the following runs, the sample was regenerated in situ at the same temperature of the experiment and under nitrogen flow for 24 h. For the experiments conducted on the VTI-SA+ system, the sample was regenerated in situ on the crucible of the instrument at 393 K for 3h under a constant flow of pure nitrogen before starting each experiment. Two complete adsorption-desorption isotherms were measured at three different temperatures of 288 K, 298 K, and 308 K. A complete adsorption-desorption isotherm with two scanning desorption curves and two scanning adsorption curves were measured at 298 K. The complete adsorption-desorption cycles were repeated several times on the same sample at 308 K to assess the long-term stability of the solid. Each water vapour adsorption measurement is fairly time-consuming and the time needed to complete a measurement was never less than a week as it is possible to observe in Fig. 1 where the uptake curves for a complete adsorption-desorption cycle at 298 K are reported.

Fig. 1.

Experimental uptake curves and relative humidity at 298 K. Sample dry mass 7.6 mg.

3. Experimental results and discussion

3.1. Solid stability

The first experimental runs were meant to evaluate the stability of SBA-15 in contact with high concentrations of water vapour and the eventual reproducibility of the adsorption-desorption equilibrium isotherm. The relative amount adsorbed was calculated as:

$$M_a=\frac{m_s-m_{dry}}{m_{dry}}$$ (1)

Where m_s is the mass of the sample on the crucible and m_dry is the mass of the dry sample at the beginning of the experiments. Fig. 2 shows the first adsorption-desorption run on a fresh sample immediately after the activation. The hydrophobic nature of the silica surface is visible from the shape of the adsorption isotherm at low concentrations. The adsorption branch of the isotherm is characterized by an almost linear region going from zero loading up to the onset of the capillary condensation. This clearly results in a low value for the Henry’s law constant. The first adsorption-desorption cycle clearly shows that the desorption curve does not reach the initial dry state. This is the first indication that some water is strongly adsorbed and/or trapped inside the solid during the first experiment on a fresh sample. The irreversibility at low pressures was previously observed in [6] where the authors decided to always use a fresh SBA-15 sample for each measurement.

Fig. 2.

Adsorption-Desorption runs on SBA-15 fresh sample at 298 K. The continuous lines are only a guide for the eyes.

Two more experimental runs were performed immediately afterward on the same sample using the same temperature and concentration steps. For each of the following experiments, the sample was regenerated at 393 K for 3 h under a nitrogen purge flow. Fig. 3 shows all the water adsorption-desorption experiments performed on the same sample. The second and the third run are reproducible and confirm that some water is strongly adsorbed and cannot be removed by simply degassing the solid with pure nitrogen or by increasing the temperature up to 393 K. The initial mass of the solid at the beginning of the second and the third run increased compared to the dry mass of the fresh sample used in the first run by approximately 1 %, see Fig. 2. The dry mass of the fresh sample was used as dry mass for all the following runs to have a consistent comparison between the experiments. In contrast to the first experiment on the fresh sample, the successive experiments show complete reversibility of the isotherm. A possible explanation for these results is that some water is trapped inside the microporous regions of the solid. After the first experimental run, these regions are no longer available for reversible adsorption.

Fig. 3.

Adsorption-Desorption runs on SBA-15 fresh sample and replications on the same sample at 298 K. The continuous lines are only a guide for the eyes.

To test this hypothesis, Ar isotherms at 87 K were measured as shown in Fig. 4. The pore size distribution for each sample (fresh and used) was calculated from the equilibrium branch using the NLDFT method (Argon at 87 K zeolites/silica, spherical/cylindrical pore, equilibrium) [24]. The corresponding results are shown in Fig. 5. The mesoporous volumes of the two samples are practically the same, while there is a clear difference in the microporous region as shown more clearly in Fig. 6. It is interesting to note that in our study the mesopore volume remains unchanged and, therefore, we can conclude that the mesopores have not collapsed. Other studies reported in the literature [8,10,11] observed some loss of mesopore volume resulting from water adsorption. Systematic removal of the strongly adsorbed water might be achieved at temperatures higher than 673 K up to 1073 K [6] without compromising the structural stability of the solid [43]. However, there is no further evidence to claim whether the removal of water will also involve the microporous regions.

Fig. 4.

Adsorption-Desorption isotherm of Ar on SBA-15 fresh sample and used sample. The continuous lines are only a guide for the eyes.

Fig. 5.

Comparison between the fresh sample and the water-used sample. PSD and pore volume of SBA-15 from argon adsorption-desorption at 87 K.

Fig. 6.

Comparison between the fresh sample and the water-used sample. PSD of the microporous region.

What remains to be determined is whether the entrapment of water is achieved at low partial pressures or if the water molecules need to be in the capillary condensed state. It has been suggested in the literature [8] that the irreversible interaction between water and the solid surface occurs during or after the capillary condensation process. This hypothesis can be confirmed by running an adsorption and desorption cycle on a fresh sample but limiting the vapour pressure so that the onset of capillary condensation is avoided. The results of this experiment can be observed in Fig. 7, together with the first complete adsorption-desorption cycle. The reversibility of the experimental data when the onset of capillary condensation is avoided confirms the fact that in order to understand the water adsorption isotherm on SBA-15 a knowledge of the history of the sample is required.

Fig. 7.

Adsorption-Desorption runs on SBA-15 fresh sample at 308 K. The continuous lines are only a guide for the eyes.

It is also important to note the fact that reproducible isotherms are obtained after the first occurrence of the hysteresis loop, indicating that in practical applications one needs to consider only the water that is reversibly adsorbed. To confirm the stability of the material and the reproducibility of the isotherm, a complete adsorption-desorption experiment was performed on a sample two months after the first experiment, as shown in Fig. 8. This sample was used for two months in five different adsorption-desorption cycles before the repeated experiment. The isotherm is unchanged from zero loading to the full saturation of the pores.

Fig. 8.

Stability test for water vapour adsorption on SBA-15 at 308 K. The repeat run was performed after 2 months and five adsorption-desorption cycles.

In conclusion, the equilibrium adsorption-desorption isotherms for water vapour on SBA-15 are characterized by three main aspects: a moderately high hydrophobicity which results in a small amount adsorbed at low concentrations, almost stepwise capillary condensation and evaporation branches in the hysteresis region, and the irreversible adsorption of some water within the micropores in the first condensation loop.

3.2. Experimental scanning curves

Once the stability of the SBA-15 for repeated water adsorption-desorption cycles was assessed, the attention was focused on the study of the scanning behaviour of the hysteresis region. It is important to point out that in the case of almost vertical adsorption and desorption branches a slight change in the gas phase concentration can cause a sudden increase in the amount adsorbed. Therefore, it is not straightforward to choose the starting point for a scanning curve a priori. Several runs need to be performed to evaluate the appropriate concentration and equilibration time for the starting points. In addition, the hysteresis region is the irreversible part of the isotherm, and it is important to have a stable concentration of water in the gas phase to avoid an irreversible change in the amount adsorbed.

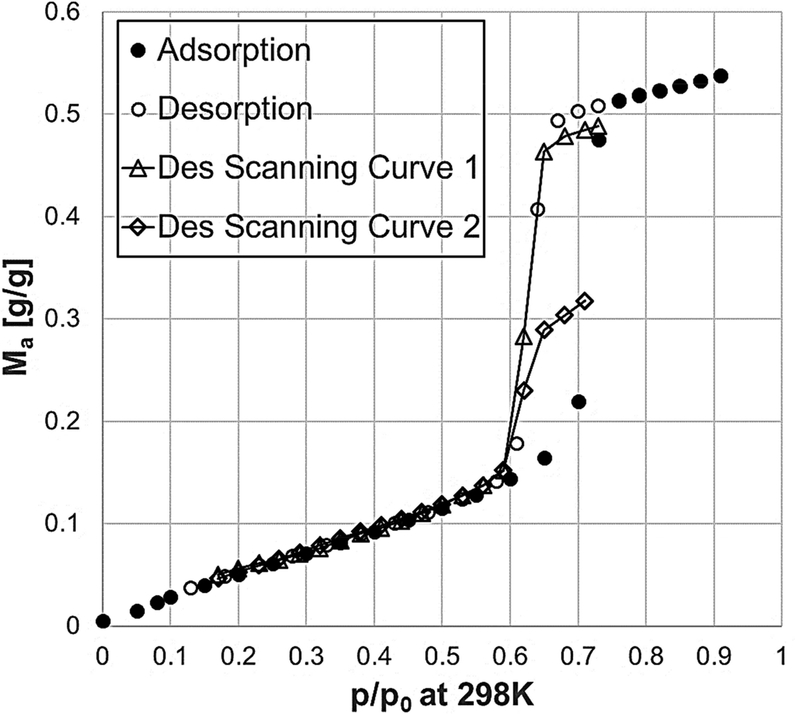
Two adsorption and two desorption scanning curves were measured on the same sample as shown in Figs 9 and 10. The desorption scanning curves seem to be initially in agreement with the theoretical behaviour expected for a solid made of cylindrical independent pores [20], by exhibiting an almost straight crossing behaviour from the main adsorption branch up to the main desorption branch. However, the curves start to deviate from a straight-line trajectory when approaching the desorption branch. The adsorption scanning curves show similar and even clearer behaviour. Indeed, the curves seem to join the main adsorption branch with a nonlinear and smoother trajectory rather than a crossing straight line. The non-crossing behaviour of the scanning curves on SBA-15 has already been observed in the literature [27–29]. The theoretical explanation of such a behaviour has been attributed to the possible presence of imperfections and/or constrictions inside the mesopores.

Fig. 9.

Experimental desorption scanning curves for water vapour adsorption on SBA-15 at 298 K. The continuous lines are only a guide for the eyes.

Fig. 10.

Experimental adsorption scanning curves for water vapour adsorption on SBA-15 at 298 K. The continuous lines are only a guide for the eyes.

4. Regression of the experimental data

4.1. Literature models

As discussed in the introduction section, we are interested in correlating the experimental data with an analytical adsorption isotherm, which can then be used in the interpretation of adsorption kinetics and the simulation of adsorption separation processes. The key challenge is to provide a reasonably simple analytical model able to accurately predict the experimental data throughout the range of concentration. The task is difficult if one considers the complex shape of the equilibrium isotherm and the presence of the hysteresis loop. In addition, it would be advantageous to have the same analytical expression for the main adsorption-desorption branches and the scanning curves. The analytical models in the literature most likely to be able to reproduce the main adsorption-desorption branches and the scanning curves for water vapour on SBA15 [36] are the ones formulated by Brunauer et al. [17]; Rajniak et al. [41]; Moore et al. [44]; Liu et al. [36]. The analytical expressions of these models can be found in Table 1. These models have been used for the simulation of pressure swing adsorption processes in packed beds for water vapour removal [45–48]. Therefore, such models are probably considered the most appropriate analytical expressions for the correlation of type IV isotherms.

Table 1.

Analytical expressions of the literature isotherm models considered in this study.

Ref.	Model expression
Brunauer et al. [17]	$V_{ml}=V_m\frac{Cx}{(1-x)}\frac{1+\left(0.5n_{max}g-n\right)x^{n_{max}-1}-\left(n_{max}g-n_{max}+1\right)x^{n_{max}}+0.5n_{max}g{x}^{n_{max}+1}}{1+(C-1)x+(0.5Cg-C)x^{n_{max}}-0.5Cg{x}^{n_{max}+1}}$
Rajniak et al. [41]	$V_{ads}=V_{sat}\text{exp}\left[-{\left(Kln\left(\frac{1}{x}\right)\right)}^n\right]$
Moore et al. [44]	$q_{ads}=q_{s1}{x}^{k_{1}T}+\left(q_{s2}-q_{s1}\right)x^{k_{2}T}$
Liu et al. [36]	$q_{ads}=q_m{x}^{k_{m}T}+\left(q_s-q_m\right)\text{erf}\left[\frac{-k_c}{Tln(x)}\right]$

Figs 11–14 show the experimental data and the correlation obtained by using the models of Brunauer et al. [17], Rajniak et al. [41], and Liu et al. [36] for several concentration ranges. In general, these models are capable of reproducing a limited range of adsorbed phase concentrations, but all fail in describing the entire adsorption isotherm as discussed in this section.

Fig. 11.

Correlation of the experimental data with the BET model [17] for different concentration ranges.

Fig. 14.

Correlation of the experimental data with the model of Liu et al. [36] for different concentration ranges.

4.2. Independent cylindrical pores model

The adsorption of condensable vapours on a micro-mesoporous solid can be described through different adsorption mechanisms depending on the relative saturation value of the vapour phase x = p/p₀ in equilibrium with the adsorbed phase. In general, at very low pressures (p/p₀ < 0.05), the micropores will be filled first and a prevalently monolayer adsorption will occur in the mesopores. All the adsorptive molecules will therefore adsorb on the free surface. These adsorption mechanisms can be represented with the Langmuir model for the micropores and the BET model for the mesopores. At values of p/p₀ > 0.05, the adsorptive molecules will simultaneously adsorb on the free surface and on the adsorbate phase in the mesopores. The multilayer adsorption described by the BET model will be the predominant adsorption mechanism. By increasing the value of p/p₀ in the gas phase, the thickness of the multilayer adsorbed phase or clusters will increase and at a given value of partial pressure, the pores will be filled with a capillary condensed phase. The condensation pressure will mainly depend on the size of the mesoporous channel. A specular mechanism can be considered for a desorption scenario in which the pores are initially filled with capillary condensed liquid. The evaporation pressure will again mainly depend on the size of the mesoporous channels.

Two analytical expressions for the adsorption-desorption equilibrium isotherm of water vapour on SBA-15 were derived. The mathematical derivations of the models are reported in the appendix. The first model considers a solid made of cylindrical independent pores. In this model, the pores are filled and emptied in an ordered sequence from the smallest to the largest and vice versa. The mathematical formulation of the first model can be expressed as:

$$\frac{m_{ads}}{m_{sat}}=\frac{d\frac{Cx}{(1-Jx)[1+(C-1)x]}{\int }_{r_C(x)}^{r_{max}}{f}_r(2r-d)dr+{\rho }_r(x){\int }_{r_{min}}^{r_C(x)}{f}_r{r}^{2}dr}{{\int }_{r_{min}}^{r_{max}}{f}_r{r}^{2}dr}+\frac{m_{res}}{m_{sat}}$$ (2)

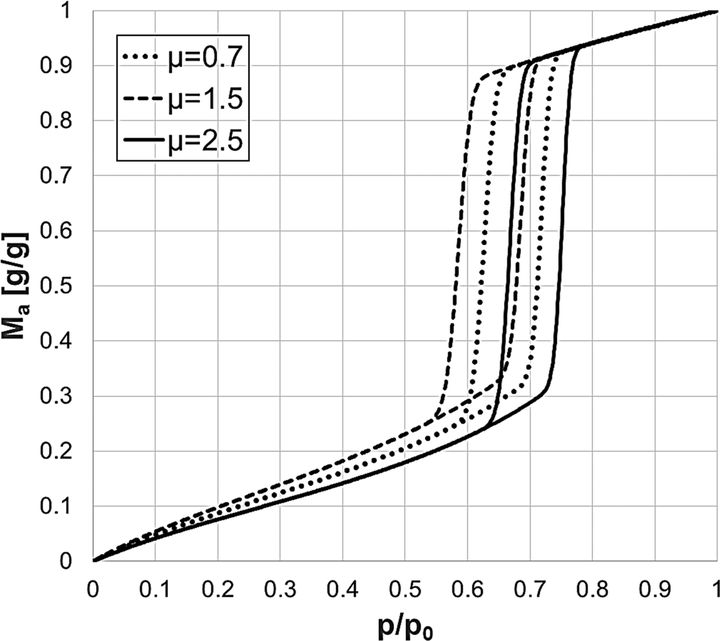
Where m_ads is the amount of water adsorbed divided by the dry mass of the solid. m_sat is the amount of water adsorbed at saturation, i.e. x = p/p₀ = 1, divided by the dry mass of the solid. M_res is the mass of residual water trapped inside the solid. C is the equilibrium constant of the BET model and takes into account the temperature and the difference between the heat of adsorption on the free surface and the heat of condensation of the vapour. C is responsible for the slope of the isotherm at low concentration. J is the surface reduction coefficient introduced by Anderson [49]. J influences the shape of the multilayer adsorption region and it also limits the amount adsorbed at medium-high concentrations. d is the thickness of the first adsorbed layer. f_r is the pore size distribution of the mesopores expressed as a numerical fraction of pores with radius r. For the radii of the mesopores, a truncated log-normal distribution was adopted with r_min and r_max respectively as lower and upper bounds of the distribution. The two parameters of the pore size distribution σ and μ influence the slope and the position of the capillary condensation and evaporation branches with respect to the x-axis. r_c(x) is the radius of the pore condensing at the relative pressure x. The condensation and evaporation pressures are calculated using the Kelvin equation respectively for cylindrical and hemispherical meniscus as reported in Eq. (20) and Eq. (26). ρ_r(x) is the relative density of the capillary condensed liquid and it is expressed in Eq. (34). ρ_r(x) influences the slope of the top part of the isotherm after the capillary condensation and before the onset of capillary evaporation. The relative density change depends on the packing factor of the liquid condensed phase inside the pores which is defined in the appendix as κ. The desorption branch of the model is represented by the same mathematical expression of Eq. (2). r_c(x) is replaced by r_e(x) which gives the radius of the pore evaporating at the relative pressure x. For the desorption branch, there is one more parameter given by the evaporation angle θ between the solid surface and the liquid hemispherical meniscus. The parameter θ is defined in Eq. (29) and influences the position of the desorption evaporation branch with respect to the x-axis. An angle θ equal to 0° corresponds to a semi-spherical equilibrium meniscus, while, an angle θ equal to 90° corresponds to a flat equilibrium meniscus. Consequently, the desorption evaporation branch will respectively be shifted to the lowest and the highest possible evaporation pressures. The effect of the model parameters on the shape of the calculated equilibrium isotherm are shown in Figs 15–21.

Fig. 15.

Effect of the parameter J on the shape of the equilibrium isotherm model.

Fig. 21.

Effect of the parameter κ on the shape of the equilibrium isotherm model.

These plots clearly demonstrate that while Eq. 2 contains several physical parameters, each parameter influences in a clear way different portions of the adsorption isotherm. This facilitates the evaluation of the parameters since each one can be determined independently by focussing on different regions in sequence. Once good estimates for all the parameters are obtained, a final non-linear regression ensures a close match with the experimental results. The model in Eq. (2) was used to regress the experimental data at three different temperatures as shown in Fig. 22.

Fig. 22.

Experimental adsorption-desorption runs and model correlation at 288 K, 298 K, and 308 K.

The parameters of the model, reported in Table 2, were calibrated by using the data at 298 K. The same temperature independent parameters were then used to predict the experimental data at 308 K and 288 K with an excellent agreement.

Table 2.

Parameters used for the regression of the experimental data with the model expressed in Eq. (2)

	298 K
d (nm)	0.153
J	0.839
C	3.66
θ° (desorption)	36.5
σ	0.045
μ	0.663
msat (g/g)	0.55
κ (Pa−1)	4.42*10−9

m_res is set equal to zero given that in process applications only the reversibly adsorbed water contributes. If for completeness one wishes to include this, m_res can be measured independently from the first adsorption-desorption run.

The theoretical modelling of the scanning curves is quite straightforward under the assumption of a solid made of cylindrical independent pores. This basic assumption permits one to model the adsorption process in a single pore independently from all the other pores. For each pore, the condensation and the evaporation pressures will only be a function of the radius of the specific pore. Each pore is allowed to condense and evaporate independently of the status of the other pores. A given point on the vertical part of the adsorption branch corresponds to a point in which only part of the pores is filled with condensed liquid and the rest of the pores still have a multilayer adsorbed phase on the pore walls. If a desorption process is originated from that specific point, the amount adsorbed will not go back reversibly on the adsorption branch, but it will rather cross the hysteresis loop and eventually join the desorption branch. When doing this, the pores will evaporate independently from each other. The first pore to evaporate will be the last pore condensed during the adsorption process. Therefore, as long as the partial pressure of water does not reach the evaporation pressure of that specific pore, the only desorption mechanism happening will be the shrinkage of the liquid condensed phase in the condensed pores and the decrease of the multilayer adsorbed phase in the non-condensed pores. The amount adsorbed will theoretically follow a trajectory similar to the multilayer and saturation part of the isotherm. The scanning curves will eventually cross the hysteresis loop and join the main desorption branch at the evaporation pressure of the last pore condensed. A specular scenario can be considered for the adsorption scanning curves.

This theoretical behaviour predicts a discontinuity at the contact point between the scanning curves and the main branches. However, such behaviour has not been observed experimentally unless some cavitation phenomenon is present [19,50]. Indeed, it has been observed in the literature that the most common behaviour for experimental scanning curves on solids made of cylindrical independent pores is to approach the desorption curve with a smoother curvature instead of a straight crossing line.

4.3. Irregular cylindrical pores model

The difference between the experimental data and the model prediction has been attributed to irregular cylindrical pores [27,29,51]. The presence of imperfections or restrictions on the internal surface of the cylindrical pores has theoretically been demonstrated to give a different behaviour to the scanning curves and to the main adsorption and desorption curves. An increase of either the number or the amplitude of the size distribution of imperfections along the pore leads to scanning curves characterized by a less crossing and more converging behaviour. The converging behaviour of the scanning curves can be confirmed from our data.

The comparison between the theoretical predictions using the independent cylindrical pores model in Eq. (2) and the experimental desorption and adsorption scanning curves is shown in Fig. 23 and Fig. 24. The theoretical model for cylindrical independent pores is not able to capture the actual behaviour of the scanning curves in the entire range of concentration, yet it provides a good match.

Fig. 23.

Experimental desorption scanning curves and perfectly cylindrical pores model correlation at 298 K

Fig. 24.

Experimental adsorption scanning curves and perfectly cylindrical pores model correlation at 308 K.

The second derivation of the equilibrium model was designed considering the particular structure of SBA-15. The adsorption in the interconnecting microporous channels is neglected, and it is assumed that the solid is made of independent cylindrical mesopores, which are defined in this work as the main pores N. The mesopores are made of an ensemble of cylindrical constrictions or sub-pores n as illustrated in Fig. 25. According to the new formulation of the model, the amount of mass adsorbed as a function of the relative humidity x = p/p₀ is given by:

$$\frac{m_{ads}(x)}{m_{sat}}=\frac{d\frac{cx}{(1-Jx)[1+(c-1)x]}{\sum }_{i=0}^N{f}_i{\sum }_{j=0}^n{g}_j{F}_j\left(2r_j-d\right)+{\rho }_r{\sum }_{i=0}^N{f}_i{\sum }_{j=0}^n{g}_j\left(1-F_j\right)r_j^2}{{\sum }_{i=0}^N{f}_i{\sum }_{j=0}^n{g}_j{r}_j^2}$$ (3)

Where f_i is the numerical fraction of the main pore i. g_j is the numerical fraction of the sub-pore j inside each main pore i. A normal distribution was assumed for the average radii of the main pores. A normal distribution was also assumed for the radii of the sub-pores inside each main pore. The average radius of each main pore was used as mean for the normal distributions of the sub-pores correlated to each main pore. The radii and the sequence of the sub-pores inside each main pore were chosen randomly after imposing a standard deviation value. The same standard deviation was used for the size distributions of all the sub-pores inside each main pore. F_j is the function used to designate whether a sub-pore is filled with capillary condensed liquid or with a multilayer adsorbed phase. F_j is zero if the sub-pore j is filled with condensed adsorbate while it is one for non-condensed sub-pores. The sub-pores are no longer independent of each other and a collaborative effect is assumed for the evaporation mechanism of each condensed sub-pore. The condensation of the vapour in a sub-pore occurs when the pressure is equal or higher than the equilibrium pressure given by the Kelvin equation for a cylindrical meniscus expressed in Eq. (23). The advanced adsorption/condensation phenomenon [31] was not considered in this study. The evaporation from a condensed pore occurs if at least one of the two adjacent sub-pores is empty and if the pressure is equal to or less than the equilibrium pressure given by the Kelvin equation for a hemispherical meniscus expressed in Eq. (24). If both the adjacent sub-pores are filled with condensed liquid and the pressure is equal or less than the equilibrium pressure, the pore will not empty according to the pore blocking mechanism. The cavitation mechanism was not considered in this study.

Fig. 25.

Qualitative representation of the sub-pores inside each main pore of the SBA-15.

In Fig. 26 and Fig. 27, the predictions of the second formulation of the model given in Eq. (3) are shown. The new formulation of the model can qualitatively represent the correct behaviour of the scanning curves. The minor inconsistency between the model predictions and the experimental data can be explained by the main assumptions about the geometrical structure used for the formulation of the model. It is reasonable to assume that the solid is characterized by discrete size distribution of main pores or in this case by a distribution of the average size of the main pores. It is also reasonable to assume that each of the main pores has the same length. Cylindrical shape and same length are the assumptions used for the geometry of the sub-pores. These assumptions are mathematically convenient for the modelling of the adsorption in the sub-pores. However, firstly, it is probably more realistic to assume defects of different lengths. Secondly, it is probably more common to find smoother and gradual transitions between each constriction rather than a sudden change in the diameter of the pore. These two factors might influence the trajectory of the theoretical scanning curves and give a better correlation of the experimental data. Their implementation can be considered for future investigations.

Fig. 26.

Desorption scanning curve and non-perfectly cylindrical pores model correlation at 298 K.

Fig. 27.

Adsorption scanning curves and non-perfectly cylindrical pores model correlation at 298 K.

The parameters of the irregular cylindrical pores model expressed in Eq. (3) and used for the regression of the experimental data shown in Fig. 26 and Fig. 27, are reported in Table 3.

Table 3.

Additional parameters used for the regression of the experimental data with the model given by Eq. (3).

	298 K
θ° (desorption)	39.5
σ main pores	0.06
μ main pores	1.89
σ sub – pores	0.08
n	50
N	60

5. Conclusions

The structural stability of the silica-based ordered material SBA-15 when exposed to highly concentrated water vapour was investigated. The sample was exposed to several relative humidities up to 90 % at 288 K, 298 K and 308 K. Complete adsorption-desorption cycles were used for the evaluation of the long-term stability of the solid. After the first adsorption-desorption cycle, the equilibrium isotherm is reproducible and the solid appears to be stable to repeated water vapour adsorption-desorption cycles. The structural stability of the solid was confirmed by the measurement of argon adsorption at 87 K. The comparison between the pore size distribution of the fresh sample and the water-used sample showed an unaltered mesoporous volume and a decrease in the microporous volume for the water-used sample.

The first experimental adsorption run with water vapour on a fresh sample resulted in some water trapped inside the microporous structure. The irreversible interaction between water and the solid surface occurs during or after the capillary condensation of the water inside the mesopores. This was verified by running a reversible adsorption-desorption experiment up to a concentration value located right before the onset of the capillary condensation in the pores. The equilibrium isotherms are characterized by three main aspects: the relative hydrophobicity of the solid surface which results in a small amount adsorbed at low concentrations; the hysteresis loop due to the capillary condensation phenomenon in the mesopores; the presence of non-crossing scanning adsorption and desorption curves.

The experimental data were correlated using two different analytical models for the equilibrium isotherms. The first model assumes independent cylindrical pores. This model can consistently and accurately correlate the main adsorption and desorption branches in the entire range of concentration at different temperatures. However, the model fails to qualitatively predict the behaviour of the scanning curves inside the hysteresis loop, since the model predicts perfect crossing behaviour. However, the experimental scanning curves show a crossing behaviour at first and a converging trajectory when approaching the opposite branch of the isotherm. This phenomenon can be predicted by assuming irregular cylindrical pores. The second model included such non-ideal pores and was successfully used for the correlation of both the main adsorption and desorption curves and the scanning curves.

The equilibrium models can be adopted in future adsorption process simulations and kinetics studies. The relatively simple analytical expressions of the models would allow for implementation in adsorption simulation software packages.

Fig. 12 –

Correlation of the experimental data with the model of Rajniak et al. [41] for different concentration ranges.

Fig. 13.

Correlation of the experimental data with the model of Moore et al. [44] for different concentration ranges.

Fig. 16.

Effect of the first layer thickness d (nm) on the shape of the equilibrium isotherm model.

Fig. 17.

Effect of the BET equilibrium constant C on the shape of the equilibrium isotherm model.

Fig. 18.

Effect of the desorption angle θ on the shape of the equilibrium isotherm model.

Fig. 19.

Effect of the PSD dispersion σ on the shape of the equilibrium isotherm model.

Fig. 20.

Effect of the PSD mean value μ on the shape of the equilibrium isotherm model.

Highlights.

• SBA-15 water adsorption irreversibility after first condensation.

• Accurate adsorption desorption data including scanning curves.

• Development of novel analytical adsorption model for the entire concentration range.

• Adsorption model parameters can be obtained from analysis of different sections of the isotherms.

Notation

C

Equilibrium constant of the BET model

d

Thickness of a single adsorbed layer (nm)

dA

Adsorbate differential surface (nm²)

dV

Adsorbate differential volume (nm³)

f_i

Numerical fraction of the main pore i

f_r

Numerical fraction of pores with radius r

F_j

Condensation-evaporation function of the sub-pore j

g_j

Numerical fraction of the sub-pore j

J

Anderson surface reduction coefficient

K

Langmuir equilibrium constant (Pa⁻¹)

L

Length of the mesopores (nm)

m_dry

Mass of the dry sample (mg)

m_res

Mass fraction or residual water trapped inside the solid

m_s

Mass of the wet sample (mg)

m_sat

Saturation capacity of the solid (mg/mg)

m_s–micro

Saturation capacity of the micropores (mg/mg)

M_a

Relative amount adsorbed (mg/mg)

n

Number of sub-pores inside each main pore

N

Number of mesopores

N_max

Maximum number or allowed adsorbed layers

N_r

Number of pores with radius r

P₀

Saturation pressure of water (Pa)

r

Radius of the mesopore (nm)

r_c

Radius condensation function (nm)

r_e

Radius evaporation function (nm)

r_m

Radius of curvature of the meniscus (m)

r_max

Maximum radius of the pore size distribution (nm)

r_min

Minimum radius of the pore size distribution (nm)

R

Gas constant (J/mol K)

S_i–equi

Equilibrium surface occupied by an adsorbate molecule on the layer i (nm²)

S_i–geom

Geometrical surface occupied by an adsorbate molecule on the layer i (nm²)

V_cond

Volume of capillary condensed liquid in the mesopores (nm³)

V_i

Volume of the adsorbate layer i (nm³)

V_m

Volume of the first adsorbed layer (nm³)

V_meso

Mesoporous volume (nm³)

V_micro

Microporous volume (nm³)

V_ml

Volume of the adsorbed multilayer phase (nm³)

V_mol

Molar volume (m²/mol)

V_s–tot

Total pore volume of the solid (nm³)

V_total

Total volume of adsorbate in the mesopores (nm³)

v_i

Specific volume of an adsorbate molecule on the layer i (nm³/nm²)

t

Thickness of the multilayer phase (nm)

x

Relative humidity

Greek letters

γ

Surface tension (J/m²)

ΔH_Condensation

Enthalpy of condensation (J/mol)

ΔH_{first layer}

Enthalpy of adsorption of the first layer (J/mol)

θ

Contact angle between the solid and liquid surface ()

κ

Isothermal compressibility or liquid packing coefficient (Pa⁻¹)

μ

Median of the log-normal or normal distribution

ρ

Capillary condensed liquid density (Kg/m³)

ρ₀

Bulk density (Kg/m³)

ρ_r

Relative density

σ

Standard deviation of the log-normal or normal distribution

6. Appendix

In this appendix, the mathematical derivation of the two analytical equilibrium models used in this contribution is reported. The models are based on traditional macroscopic approaches to the adsorption phenomena. These methods are likely obsolete if used for the fully accurate characterization of porous materials. However, they provide a reasonable representation of the real adsorption mechanisms and more significantly, they allow for the introduction of a relatively simple but accurate analytical expression for type IV and type V equilibrium isotherms.

In the first instance, it is feasible to assume a solid made of micropores and mesopores. The mesopores are assumed to be cylindrical with the same diameter and length. The saturation capacity of such a solid is:

$$V_{s-tot}=V_{meso}+V_{micro}=NL\pi r^2+V_{micro}$$ (1)

Where N is the number of mesopores, L is the length of the mesopores and r is the radius of the mesopores. If the adsorbed phase is uniformly distributed on the surface of the mesopores, the multilayer phase adsorbed on the wall of each pore will be given by the difference between the total volume of the pore and the volume of the empty part of the pore. If t(x) is the thickness of the adsorbed phase on the wall, the volume of the multilayer adsorbed phase V_ml as a function of the relative partial pressure x = p/p₀ can be expressed as:

$$V_{ml}(x)=N\pi L\left[r^2-{(r-t(x))}^2\right]=N\pi Lt(x)[2r-t(x)]$$ (2)

From Eq. (2), the thickness of the multilayer adsorbed phase can be found as a function of the partial pressure x. Eq. (2) has two roots. Only one root can physically be valid, as the thickness of the amount adsorbed cannot be greater than the radius of the pore. The thickness of the multilayer adsorbed phase can be expressed as:

$$t(x)=r-\frac{\sqrt{\pi {(NLr)}^2-LN{V}_{ml}(x)}}{LN\sqrt{\pi }}$$ (3)

The multilayer adsorption can be theoretically represented with one of the many multilayer adsorption models present in the literature. The original BET model [52] represents an extension of the monolayer Langmuir model in which the molecules can adsorb both on the free surface and on the molecules already adsorbed. This model assumes a flat surface and an infinite adsorbed amount at saturation. The model was later modified by several authors to consider a more realistic adsorption process in a confined environment. The total amount of adsorbed phase was limited to a certain value using different approaches: limited adsorption volume [17], different energetic interactions between the first adsorbed layer and the following layers[49,53], and a continuously decreasing surface [49,54].

The assumptions made for the formulation of the original BET theory can be modified to model the adsorption process on a cylindrical surface. The original BET theory assumes the adsorption to occur on a flat surface and that the surface available for all the layers remains constant. The multilayer volume of the adsorbed phase V_ml can be calculated as:

$$V_{ml}={\sum }_{i=0}^{\infty }{v}_{i}i{S}_{i-equi}={\sum }_{i=1}^{\infty }\frac{V_i}{S_{i-geom}}i{S}_{i-equi}$$ (4)

Where v_i is the specific volume of an adsorbate molecule. V_i is the absolute volume occupied by an adsorbate molecule. S_i–geom is the actual geometrical surface occupied by a molecule of adsorbate. S_i is the equilibrium surface covered only by the i layers of adsorbate. S_i is given by the dynamic equilibrium relationship for each layer. For flat surfaces v_i is constant and Eq. (4) leads to the BET model expressed as:

$$V_{ml}=\frac{V_0}{S_{0-geom}}{\sum }_{i=1}^{\infty }i{S}_{i-equi}$$ (5)

If the adsorption occurs inside cylindrical channels and the adsorbed layer has constant thickness d, as represented in Fig. A1, the specific volume v_i will depend on the specific layer i. The specific volume v_i of the generic layer i is given by:

$$v_i=\frac{d[2r-(2i-1)d]}{2[r-(i-1)d]}$$ (6)

By combining Eq. (4) and Eq. (6), the multilayer adsorbed amount can be expressed as:

$$V_{ml}={\sum }_{i=0}^{N_{max}}{v}_{i}i{S}_{i-equi}={\sum }_{i=1}^{N_{max}}\frac{d[2r-(2i-1)d]}{2[r-(i-1)d]}i{S}_{i-equi}$$ (7)

Where N_max is the maximum number of adsorption layers permitted in the pore. N_max can easily be calculated if d is known. From a comparison between Eq. (5) and Eq. (7), the amount adsorbed is now limited to a certain amount and it also depends on the size of the channel. In the same way, the amount adsorbed on the cylindrical pore surface when this is completely covered by a single layer of adsorbate can be defined as:

$$V_m={\sum }_{i=0}^{N_{max}}{v}_i{S}_{i-equi}=v_0{S}_{0-equi}+{\sum }_{i=1}^{N_{max}}\frac{d[2r-(2i-1)d]}{2[r-(i-1)d]}{S}_{i-equi}$$ (8)

From the derivation of the original BET model [52], S_i–equi is given by the dynamic equilibrium relationship for each layer i and can be expressed as a function of the relative saturation pressure x = p/p₀ as:

$$S_{i-equi}(x)=C{S}_{0-equi}{x}^i$$ (9)

Where C is the equilibrium constant of the BET model defined as:

$$C=exp\left(\frac{\mathrm{\Delta }{H}_{firstlayer}-\mathrm{\Delta }{H}_{condensation}}{RT}\right)$$ (10)

By combining Eqs (7–9) the multilayer amount adsorbed can be expressed as:

$$\frac{V_{ml}}{V_m}=\frac{{\sum }_{i=0}^{N_{max}}\frac{r}{r-(i-1)d}i{S}_{i-equi}}{{\sum }_{i=0}^{N_{max}}\frac{r}{r-(i-1)d}{S}_{i-equi}}=\frac{C{S}_{0-equi}{\sum }_{i=0}^{N_{max}}\frac{d[2r-(2i-1)d]}{2[r-(i-1)d]}i{x}^i}{v_0{S}_{0-equi}+C{S}_{0-equi}{\sum }_{i=1}^{N_{max}}\frac{d[2r-(2i-1)d]}{2[r-(i-1)d]}{x}^i}$$ (11)

Dividing by S_0–equt and considering the explicit expression for v₀:

$$\frac{V_{ml}}{V_m}=\frac{C{\sum }_{i=0}^{N_{max}}\frac{d[2r-(2i-1)d]}{2[r-(i-1)d]}i{x}^i}{\frac{d(2r-d)}{2r}+C{\sum }_{i=1}^{N_{max}}\frac{d[2r-(2i-1)d]}{2[r-(i-1)d]}{x}^i}$$ (12)

By expressing V_m as a function of the radius of the pore and thickness of the adsorbed layer, the final expression for the multilayer adsorbed amount for N pores of radius r is given by:

$$V_{ml}(x,r)=N\pi Ld(2r-d)\frac{C{\sum }_{i=0}^{N_{max}}\frac{d[2r-(2i-1)d]}{2[r-(i-1)d]}i{x}^i}{\frac{d(2r-d)}{2r}+C{\sum }_{i=1}^{N_{max}}\frac{d[2r-(2i-1)d]}{2[r-(i-1)d]}{x}^i}$$ (13)

A comparison between the traditional BET model and Eq. (13) is shown in Fig. A2. The multilayer adsorption model presented in this study and the original BET model [17] are compared using the same parameters, assuming a pore radius of 2 nm and a thickness of the adsorbed layer of 0.3 nm. As expected, the two models provide the same results at low pressures. At higher pressures, Eq. (13) diverges due to the cylindrical adsorption surface which limits the volume available for each following layer.

The thickness of the multilayer adsorbed amount for a pore of radius r will be:

$$t(x)=r-\frac{\sqrt{\pi {(NLr)}^2-LN{V}_{ml}(x)}}{LN\sqrt{\pi }}=r-\sqrt{r-d(2r-d)\frac{C{\sum }_{i=0}^{N_{max}}\frac{d[2r-(2i-1)d]}{2[r-(i-1)d]}i{x}^i}{\frac{d(2r-d)}{2r}+C{\sum }_{i=1}^{N_{max}}\frac{d[2r-(2i-1)d]}{2[r-(i-1)d]}{x}^i}}$$ (14)

If the solid is characterized by discrete size distribution of mesopores and N_r is the number of mesopores with radius r and same length L, the saturation capacity of the solid will be:

$$V_{s-tot}=V_{micro}+{\sum }_{i=1}^N{V}_{mesoi}=V_{micro}+L\pi {\sum }_{r_{min}}^{r_{max}}{N}_r{r}^2$$ (15)

Where n is the total number of mesopores. The multilayer adsorbed amount for a solid characterized by a discrete distribution of mesopores N_r of different radius r and same length L will be:

$$V_{ml}(x)={\sum }_{i=1}^N{V}_{mli}=\pi Ld{\sum }_{r_{min}}^{r_{max}}\left[N_r(2r-d)\frac{C{\sum }_{i=0}^{N_{max}}\frac{d[2r-(2i-1)d]}{2[r-(i-1)d]}i{x}^i}{\frac{d(2r-d)}{2r}+C{\sum }_{i=1}^{N_{max}}\frac{d[2r-(2i-1)d]}{2[r-(i-1)d]}{x}^i}\right]$$ (16)

At a given value or relative pressure, each pore will eventually be filled with capillary condensed liquid. For the evaluation of the condensation pressure, the Kelvin equation can be used considering a cylindrical interface between the gas phase and the multilayer adsorbed phase as shown in Fig. A3.

Therefore, the condensation pressure is obtained from:

$$\frac{\frac{dV}{dt(x)}}{\frac{dA}{dt(x)}}=-\frac{\gamma V_{mol}}{RTln(x)}$$ (17)

Where dV and DA are respectively the differential volume and the differential surface of the cylindrical meniscus. The derivative of the volume is given by:

$$\frac{dV}{dt(x)}=\frac{d\left(\pi L{(r-t(x))}^2\right)}{dt(x)}=2\pi L(r-t(x))$$ (18)

The derivative of the surface is given by:

$$\frac{dA}{dt(x)}=\frac{d(2\pi L(r-t(x)))}{dt(x)}=2\pi L$$ (19)

As a result, the condensation pressures for each pore will be given by the solution of the following equation:

$$\frac{\frac{dV}{dt(x)}}{\frac{dA}{dt(x)}}=r-t(x)=-\frac{\gamma V_{mol}}{RTln(x)}$$ (20)

For the calculation of the evaporation pressure, the Kelvin equation can be used considering a hemispherical meniscus as shown in Fig. A4. The evaporation pressure is obtained from:

$$\frac{\frac{dV}{d\left(r_m\right)}}{\frac{dA}{d\left(r_m\right)}}=-\frac{\gamma V_{mol}}{RTln(x)}$$ (21)

Where r_m is the radius of curvature of the meniscus. The derivative of the volume is given by:

$$\frac{dV}{d\left(r_m\right)}=\frac{d\left(4/3\pi r_m{}^3\right)}{d\left(r_m\right)}=4\pi r_m{}^2$$ (22)

The derivative of the surface is given by:

$$\frac{dA}{d\left(r_m\right)}=\frac{d\left(4\pi r_m{}^2\right)}{d\left(r_m\right)}=8\pi r_m$$ (23)

As a result, the evaporation pressures for each pore will be given by the solution of the following equation:

$$\frac{\frac{dV}{d\left(r_m\right)}}{\frac{dA}{d\left(r_m\right)}}=\frac{r_m(x)}{2}=-\frac{\gamma V_{mol}}{RTln(x)}$$ (24)

Where r_m(x) is given by:

$$\frac{r_m(x)}{2}=\frac{r}{2cos(\theta )}=-\frac{\gamma V_{mol}}{RTln(x)}$$ (25)

θ is the angle between the solid and liquid surface. If the first layer of adsorbate is assumed to behave as a stationary adsorbed layer, the evaporation pressure can be obtained from:

$$\frac{r_m}{2}=\frac{r-d}{2cos(\theta )}=-\frac{2\gamma V_{mol}}{RTln(x)}$$ (26)

In a particular concentration range, some of the pores will have a multilayer adsorbed phase and others a condensed liquid phase inside. To distinguish between the two groups, a function r_c(x) is needed. This function gives the value of the pore radius condensing at each relative pressure x. If the solid is made of cylindrical independent pores, at a given pressure x, all the pores with a radius less or equal to r_c(x) will be filled with capillary condensed liquid, while, the pores with a radius higher than r_c(x) will have multilayer adsorbed phase. The same mechanism can be considered for the desorption using a similar function r_e(x). To evaluate the functions r_c(x) and r_e(x), Eq. (20) and Eq. (26) can respectively be used. The volume of capillary condensed liquid inside the pores can be expressed as:

$$V_{cond}=\pi L{\sum }_{r_{min}}^{r_c(x)}{N}_r{r}^2$$ (27)

Therefore, the total amount of adsorbate inside the mesopores is given by:

$$V_{total}=V_{ml}(x)+V_{cond}$$ (28)

Dividing the total amount of adsorbate in the mesopores by the total volume of the mesopores, the following expression for the relative amount adsorbed in the mesopores is obtained:

$$v_{ads-meso}(x)=\frac{d{\sum }_{r_c(x)}^{r_{max}}\left[N_r(2r-d)\frac{C{\sum }_{i=0}^{N_{max}}\frac{d[2r-(2i-1)d]}{2[r-(i-1)d]}i{x}^i}{\frac{d(2r-d)}{2r}+C{\sum }_{i=1}^{N_{max}}\frac{d[2r-(2i-1)d]}{2[r-(i-1)d]}{x}^i}\right]+{\sum }_{r_{min}}^{r_c(x)}{N}_r{r}^2}{{\sum }_{r_{min}}^{r_{max}}{N}_r{r}^2}$$ (29)

This can be rearranged by dividing both numerator and denominator by the total number of pores. In this way, the equation will contain the numerical fraction of pores of radius as f_r rather than the absolute amount N_r. f_r can be considered as the pore size distribution of the solid.

$$v_{ads-meso}(x)=\frac{d{\sum }_{r_c(x)}^{r_{max}}\left[f_r(2r-d)\frac{C{\sum }_{i=0}^{N_{max}}\frac{d[2r-(2i-1)d]}{2[r-(i-1)d]}i{x}^i}{\frac{d(2r-d)}{2r}+C{\sum }_{i=1}^{N_{max}}\frac{d[2r-(2i-1)d]}{2[r-(i-1)d]}{x}^i}\right]+{\sum }_{r_{min}}^{r_c(x)}{f}_r{r}^2}{{\sum }_{r_{min}}^{r_{max}}{f}_r{r}^2}$$ (30)

The relative mass of adsorbate is obtained by multiplying and dividing Eq. (30) by the density of the adsorbed phase. The density of the multilayer adsorbed phase is assumed to be equal to the bulk liquid density ρ₀. The density of the capillary condensed phase is assumed to depend on the relative pressure according to the ideal liquid law [55]. The capillary condensed phase density reaches the bulk liquid density value when p/p₀ = 1. The relative liquid density ρ_r of the capillary condensed phase can be expressed as:

$${\rho }_r(x)=\frac{\rho (x)}{{\rho }_0}=exp\left[\frac{\kappa \gamma }{-r_m(x)}\right]$$ (31)

Where ρ(x) is the density of the capillary condensed phase as a function of the relative pressure. κ is the isothermal compressibility of the liquid which, in this case, can be considered as a packing coefficient of the liquid condensed phase inside the solid. γ is the surface tension at the interface. r_m is the radius of curvature of the meniscus expressed in Eq. (25). For a real solid, the pore size distribution will be a discrete stepwise function. However, for practical aims, the discrete pore size distribution can be approximated with a continuous function f_r and the sum operator can be substituted with a continuous integral as follows:

$$m_{ads-meso}(x)=\frac{d{\int }_{r_c(x)}^{r_{max}}{f}_r(2r-d)\frac{c{\sum }_{i=0}^{N_{max}}\frac{d[2r-(2i-1)d]}{2[r-(i-1)d]}i{x}^i}{\frac{d(2r-d)}{2r}+C{\sum }_{i=1}^{N_{max}}\frac{d[2r-(2i-1)d]}{2[r-(i-1)d]}{x}^i}dr+{\rho }_r(x){\int }_{r_{min}}^{r_c(x)}{f}_r{r}^{2}dr}{{\int }_{r_{min}}^{r_{max}}{f}_r{r}^{2}dr}$$ (32)

The desorption branch can be defined in the same way by substituting r_e(x) to r_c(x). If the solid contains also micropores, the Langmuir equation can be introduced for a better correlation of the adsorbed amount at low pressures. The amount adsorbed in the micropores can be expressed as:

$$m_{ads-micro}(x)=m_{s-micro}\frac{Kx}{\frac{1}{p_0}+Kx}$$ (33)

The total relative amount adsorbed in the solid is given by:

$$m_{ads}(x)=\frac{m_{s-micro}\frac{Kx}{\frac{1}{p_0}+Kx}+d{\int }_{r_c(x)}^{r_{max}}{f}_r(2r-d)\frac{c{\sum }_{i=0}^{N_{max}}\frac{d[2r-(2i-1)d]}{2[r-(i-1)d]}i{x}^i}{\frac{d(2r-d)}{2r}+C{\sum }_{i=1}^{N_{max}}\frac{d[2r-(2i-1)d]}{2[r-(i-1)d]}{x}^i}dr+{\rho }_r(x){\int }_{r_{min}}^{r_c(x)}{f}_r{r}^{2}dr}{m_{s-micro}\frac{K}{\frac{1}{p_0}+K}+{\int }_{r_{min}}^{r_{max}}{f}_r{r}^{2}dr}$$ (34)

Where m_s–micro is the capacity of the micropores and K is the equilibrium constant. Eq. (34) is similarly structured to other models already present in the literature [37,56]. However, the model presented in Eq. (34) is more detailed and the complete analytical expression is reported. The model includes the possibility of having micropores in the solid structure as in the case of the SBA-15 and its applicability can be extended to other adsorptives other than water. The multilayer adsorption is limited by the size of the cylindrical pore and it is also consistent with the cylindrical surface and pore size distribution of the mesopores. In addition, the increase in the adsorbed amount after the capillary condensation can be predicted by the shrinkage or expansion of the liquid condensed phase.

The model can correlate type IV and type V isotherms for vapours adsorption in cylindrical pores. Some assumptions can be made to obtain a simpler analytical expression, while the model can still provide an excellent correlation of the experimental data. The multilayer adsorption can be assumed to occur on a surface which constantly decreases by a factor J [49]. For the case of water vapour adsorption on SBA, the most of the microporosity of the solid is lost during the first experiment on a fresh sample. Therefore, considering only the adsorption in the mesopores can provide a good correlation of the experimental data. According to these assumptions, Eq. (34) can be modified to provide the amount of water adsorbed as:

$$\frac{m_{ads}(x)}{m_{sat}}=\frac{d\frac{cx}{(1-Jx)[1+(C-1)x]}{\int }_{r_c(x)}^{r_{max}}{f}_r(2r-d)dr+{\rho }_r(x){\int }_{r_{min}}^{r_c(x)}{f}_r{r}^{2}dr}{{\int }_{r_{min}}^{r_{max}}{f}_r{r}^{2}dr}$$ (35)

Where m_sat is the amount adsorbed at saturation and m_ads(x) is the amount adsorbed. Eq. (35) does not consider the empty hemispherical volumes generated by the equilibrium liquid menisci at the two ends of the pores. For SBA-15, these volumes are negligible as the diameter of the pores is much smaller than the pores lengths [5]. The adsorption model for cylindrical independent pores can be modified to consider the converging behaviour of the experimental scanning curves. This kind of scanning curves is typical of disordered solids characterized by a pore structure made of interconnected channels or pore networks [20,25]. However, considering the pore structure of the SBA-15, a three-dimensional pore network effect can certainly be excluded for such a solid. Also, the eventual microporous connections between the mesoporous cylindrical channels are permanently filled with strongly adsorbed water as discussed beforehand. The most likely theoretical explanation able to predict the non-crossing behaviour of the scanning curves is given by the presence of cylindrical constrictions along the longitudinal axis of the pore [27–29,34]. Therefore, the solid can be assumed as made of N irregular cylindrical main mesopores. Each single main mesopore of average radius $\overline{r}$ can be considered as an ensemble of n cylindrical subpores or constrictions of different radius r and same length L. In this view, the mechanisms of adsorption and desorption can be represented as in Figs A5 and A6. In such a scenario Eq. (35) can be rewritten as:

$$\frac{m_{ads}(x)}{m_{sat}}=\frac{d\frac{cx}{(1-Jx)[1+(c-1)x]}{\sum }_{i=0}^N{f}_i{\sum }_{j=0}^n{g}_j{F}_j\left(2r_j-d\right)+{\rho }_r{\sum }_{i=0}^N{f}_i{\sum }_{j=0}^n{g}_j\left(1-F_j\right)r_j^2}{{\sum }_{i=0}^N{f}_i{\sum }_{j=0}^n{g}_j{r}_j^2}$$ (36)

Where f is the size distribution of the main mesopores, g is the sub-pores size distribution and F is a function that can assume only two values: 1 for the non-condensed pores and 0 for the condensed pores. The function F is designed to consider the adsorption-condensation and the desorption-evaporation mechanisms. The latter also includes the pore blocking effect. The role of the function F has been introduced beforehand in the section 4.3.

Fig. A1.

Representation of the adsorbed layers on a cylindrical surface.

Fig. A2.

Comparison between the original BET model and the multilayer adsorption model on cylindrical surface given in Eq. (13).

Fig. A3.

Cylindrical meniscus of the multilayer adsorbed phase.

Fig. A4.

Hemispherical meniscus of the capillary condensed phase.

Fig. A5.

Representation of the adsorption-condensation mechanism when increasing the partial pressure of water vapour.

Fig. A6.

Representation of the desorption-evaporation mechanism when decreasing the partial pressure of water vapour.