Association analysis of loci implied in “buffering” epistasis

Abstract

The existence of buffering mechanisms is an emerging property of biological networks, and this results in the buildup of robustness through evolution. So far, there are no explicit methods to find loci implied in buffering mechanisms. However, buffering can be seen as interaction with genetic background. Here we develop this idea into a tractable model for quantitative genetics, in which the buffering effect of one locus with many other loci is condensed into a single statistical effect, multiplicative on the total additive genetic effect. This allows easier interpretation of the results and simplifies the problem of detecting epistasis from quadratic to linear in the number of loci. Using this formulation, we construct a linear model for genome-wide association studies that estimates and declares the significance of multiplicative epistatic effects at single loci. The model has the form of a variance components, norm reaction model and likelihood ratio tests are used for significance. This model is a generalization and explanation of previous ones. We test our model using bovine data: Brahman and Tropical Composite animals, phenotyped for body weight at yearling and genotyped at high density. After association analysis, we find a number of loci with buffering action in one, the other, or both breeds; these loci do not have a significant statistical additive effect. Most of these loci have been reported in previous studies, either with an additive effect or as footprints of selection. We identify buffering epistatic SNPs present in or near genes reported in the context of signatures of selection in multi-breed cattle population studies. Prominent among these genes are those associated with fertility (INHBA, TSHR, ESRRG, PRLR, and PPARG), growth (MSTN, GHR), coat characteristics (KIT, MITF, PRLR), and heat resistance (HSPA6 and HSPA1A). In these populations, we found loci that have a nonsignificant statistical additive effect but a significant epistatic effect. We argue that the discovery and study of loci associated with buffering effects allow attacking the difficult problems, among others, of the release of maintenance variance in artificial and natural selection, of quick adaptation to the environment, and of opposite signs of marker effects in different backgrounds. We conclude that our method and our results generate promising new perspectives for research in evolutionary and quantitative genetics based on the study of loci that buffer effect of other loci.

Introduction

The availability of high-density single nucleotide polymorphism (SP) genotypes in livestock species allows for the exploration of nonadditive effects to a degree not often captured by pedigree relationships alone. In particular, epistasis—the interaction between loci—is thought to play a key role in defining the genetic architecture of complex traits (Mackay, 2014). However, exploring all possible SNP to SNP combinations is computationally prohibitively and statistically underpowered. Hence, alternative compromises are being proposed such as the identification of the interaction between one SNP and the polygenic background (Crawfor et al., 2017).

Epistasis against the polygenic background is one of the biological phenomena in which epistasis is likely implied in “buffering” (Visser et al., 2003; Flatt, 2005), a mechanism that would allow the buildup of robustness through evolution (see Flatt, 2005, for examples). A known example is chaperones (Visser et al., 2003; Kitano, 2004). Loci implied in buffering would mitigate heritable perturbations. For instance, for a trait with intermediate optima, too high total genotypic values would not be expressed.

Inspired by these models, here we present a unique computational approach for the rapid identification of buffering epistatic SNPs based on those with a significant effect on the phenotype, however with an opposed effect depending on the genetic background of the sampled population. Preliminary derivations were presented by Reverter et al. (2018) with a mechanical heuristic and a fast approximate numerical method applied to one population of Brahman (BB) cattle. Here, we expand that work by deriving an exact maximum likelihood method and using a second larger population of Tropical Composite (TC) cattle.

Materials and Methods

Animal Care and Use Committee approval was not obtained for this study because historical data were used and no animals were handled as part of the study. Analyses were performed on phenotypic data and DNA samples that had been collected previously as part of the Australian Cooperative Research Centre for Beef Genetic Technologies (Beef CRC; http://www.beefcrc.com/).

Animals, phenotypes, and genotypes

Animals, phenotypes, and genotypes used in this study were a subset of those recently described in Raidan et al. (2018). In brief, we used body yearling weight (YWT) data of 2,111 BB and 2,550 TC cows and bulls genotyped using either the BovineSNP50 (Matukumalli et al., 2009) or the BovineHD BeadChip array (Illumina Inc., San Diego, CA). Animals that were genotyped with the lower density array had their genotypes imputed to higher density as described previously by Bolormaa et al. (2014). The imputation was performed on 30 iterations of BEAGLE 3.3 (Browning and Browning, 2011), within breed using as reference 519 BB and 351 TC genotyped using the BovineHD chip. SNPs were mapped to the UMD3.1 bovine genome assembly (Zimin et al., 2009). The SNP positions were based on the Bos taurus genome assembly ARS-UCD1.2 (https://www.animalgenome.org/repository/cattle/UMC_bovine_coordinates/). After selecting autosomal SNP with minor allele frequency > 1%, we retained 651,253 SNPs for BB and 689,818 SNPs for TC.

The average, minimum, and maximum of YWT (kg) were 227.7, 115, and 353 kg for BB, and 247.07, 120.5, and 394.5 kg for TC. Moreover, the average, minimum, and maximum of age at YWT was 360, 302, and 416 days for BB, and 361, 319, and 403 days for TC.

Genome-wide association study (GWAS) for epistasis: one locus against the polygenic background

A typical model is $\mathit{y}=\dots +\mathit{W}\mathit{u}+\dots$ where $\mathit{u}$ is estimated as a vector with additive polygenic effects. Let $Var\left(\mathit{u}\right)=\mathit{G}{\sigma }_u^2$ and assume that there is an epistatic deviation quantitative trait loci (QTL) at position $i$ with statistical (not biologically functional) effect ${\left(\alpha \alpha \right)}_i$ and that the epistasis is against the polygenic background. A model for total genotypic value is: $\mathit{g}=\mathit{u}+\mathit{i}=\mathit{u}+{\left(\alpha \alpha \right)}_i{\mathit{z}}_i\odot \mathit{u}$ (Jannink, 2007), where ${\mathit{z}}_i$ is a centered vector with $\{2-2p,1-2p,0-2p\}$ for genotypes $\{aa,Aa,AA\}$^, and the symbol ⨀ indicates de Hadamard product.

Equivalently, $\mathit{g}=\mathit{u}+{\left(\alpha \alpha \right)}_i{\mathit{Z}}_i^{*}\mathit{u}$, where ${\mathit{Z}}_i^{*}$ is a matrix whose diagonal contains the coding of the different genotypes at locus i. Thus, ${\left(\alpha \alpha \right)}_i$ can be seen as the regression of the remaining genetic value once the polygenic additive effect $u$ has been removed from $g$.

Imagine for instance the epistatic effect is ${\left(\alpha \alpha \right)}_i=-0.2$ and $p=freq\left(a\right)=0.6$. For an individual with $u=20$ and carrier of $aa$ genotype, the epistatic effect is negative: ${\left(\alpha \alpha \right)}_i{z}_{i}u=-0.2\times 0.8\times 20=-3.2$, 2 – 2p = 0.8, and the total genetic value is $g=20-3.2=16.8$. Similarly, for an individual with $u=0$, the epistatic QTL has no effect; for an individual with $u=-20$, the epistatic effect is positive.

Mechanical heuristics

In layman terms, our proposed approach proceeds in five main steps as follows (Reverter et al., 2018):

• (1) Rank individuals from lowest to highest genomic estimated breeding value (GEBV);

• (2) Divide the ranked list into five equally sized bins with BIN1 containing the 20% of individuals with the lowest GEBVs, BIN2 the next 20% of individuals based on GEBVs, and so on until BIN5 containing the 20% individuals with the highest GEBVs;

• (3) Perform a GWAS of SNPs on phenotypes, within bin, and with the whole population. Note that because relationships are considered when estimating GEBVs, bins should contain similar individuals;

• (4) Collect SNPs with significant yet opposed effect in BIN1 and BIN5 and a monotonic pattern of effect from BIN1 to BIN5 (e.g., strong positive, mild positive, zero, mild negative, and strong negative);

• (5) Confirm the SNPs collected are not significant in the GWAS with the whole population.

The interpretation of the heuristic is that we try to find SNPs with significant and opposing effect in the extreme populations, but that are not significant in the current population when analyzed as a whole.

Fast approximate numerical method

The quantity of interest is the regression of $\mathit{y}$ on ${\mathit{Z}}_i^{*}\mathit{u}$, which can be approximated as follows:

• (1) Run a GBLUP model with additive effect;

• (2) Extract residuals $\widehat{e}$ and GEBVs $\widehat{\mathit{u}}$ from the output;

• (3) For each SNP marker $i$:

• a) Multiply $\widehat{\mathit{u}}$ by centered gene contents to obtain ${\mathit{Z}}_i^{*}\widehat{\mathit{u}}$

• b) Run a single marker regression $\widehat{\mathit{e}}=1\mu +{\left(\alpha \alpha \right)}_i{\mathit{Z}}_i^{*}\widehat{\mathit{u}}+ϵ$ to estimate ${\left(\alpha \alpha \right)}_i$

• c) Obtain a t-test and associated P-value from the output.

This approximate method is very fast, but ignores the uncertainty in the estimation of $\widehat{\mathit{e}}$ and $\widehat{\mathit{u}}$, and therefore it will be accurate for informative datasets—that is, for moderate to highly heritable traits or large datasets. It may be used for a fast screening followed by a restricted maximum likelihood (REML) analysis (Jannink, 2007; Crawford et al., 2017) for a subset.

Exact maximum likelihood method

A GWAS model would be:

$${\displaystyle \begin{array}{l}{\displaystyle \mathit{y}=\mathit{X}\mathit{b}+\mathit{u}+k_i{\mathit{Z}}_i^{*}\mathit{u}+\mathit{e}}\end{array}}$$ (1)

Where y are quantitative phenotypes of interest, $\mathit{b}$ is the fixed effects vector (e.g., herd-sex-year contemporary group), $\mathit{X}$ is a design matrix relating records to fixed effects, ${\mathit{Z}}_i^{*}$ is a diagonal matrix whose diagonal contains ${\mathit{z}}_i$, the coding of the different genotypes at locus i, and k_i is the buffering effect of locus i, expressed as a regression of phenotype on the product gene content at i multiplied the additive polygenic effect. Note that the term $k_i{\mathit{Z}}_i^{*}\mathit{u}=k_i\sum _{j=1,n}{\mathit{z}}_i\odot {\mathit{z}}_j{\alpha }_j$ is equivalent to equation 1 in Crawford et al. (2017) and their terms ${\alpha }_j$ are equivalent to our terms $k_i{\alpha }_j$. However, they do not present their model in terms of buffering, and their matrices $x$ ($z$ in our notation) are not centered, which leads to a lack of orthogonality of their model (Alvarez-Castro and Carlborg, 2007; Vitezica et al., 2017).

Our model in equation 1 is not usable because both the terms $k_i$ and $\mathit{u}$ implied in the regression are unknown. However, the epistatic component $\varphi =k_i{\mathit{Z}}_i^{*}\mathit{u}$ defines a covariance matrix for$\varphi$ in the i-th locus:

$${\displaystyle \begin{array}{l}{\displaystyle Cov\left(\varphi \right)={\mathit{Z}}_i^{*}\mathit{G}{\sigma }_u^2{k}_i^2{\mathit{Z}}_i^{{*}^{\prime }}}\end{array}}$$

which suggests a linear model with the form $\mathit{y}=\mathit{X}\mathit{b}+\mathit{u}+\varphi +\mathit{e}$, with covariance as above (Jannink, 2007; Crawford et al., 2017). Unfortunately, GWAS tests with this formulation imply computing and inverting $Cov\left(\varphi \right)$ matrix at each locus (which is computing intensive) and can result in lack of convergence (Crawford et al., 2017). We instead propose an equivalent formulation that uses:

$${\displaystyle \begin{array}{l}{\displaystyle \mathit{g}=\mathit{u}+\varphi =\mathit{u}+{\mathit{Z}}_i^{*}{\mathit{u}}^i}\end{array}}$$

where ${\mathit{u}}^i=k_i\mathit{u}$. We have, therefore, defined a random effect, ${\mathit{u}}^i$, which multiplies real values given by the covariable ${\mathit{Z}}_i^{*}$. This is known as a reaction norm or random regression model (Laird and Ware, 1982; Schaeffer, 2004). Using this formulation, there are two additive genetic traits in this model: a general additive trait $\mathit{u}$ with variance $\mathit{G}{\sigma }_u^2$, where G is a relationship matrix (Wright, 1922; VanRaden, 2008) and a transformation of the buffering action of locus i into another additive trait: ${\mathit{u}}^i=\mathit{u}{k}_i$, $Var\left({\mathit{u}}^i\right)=\mathit{G}{\sigma }_u^2{k}_i^2$. The joint covariance matrix is:

$${\displaystyle \begin{array}{l}{\displaystyle Var\left(\begin{array}{l}\mathit{u}\\ {\mathit{u}}^i\end{array}\right)=\left(\begin{array}{cc}{\sigma }_u^2& {\displaystyle k_i{\sigma }_u^2}\\ k_i{\sigma }_u^2& {\displaystyle k_i^2{\sigma }_u^2}\end{array}\right)\otimes \mathit{G}={\mathit{G}}_0\otimes \mathit{G}}\end{array}}$$

where $\left(\begin{array}{cc}{\sigma }_u^2& k_i{\sigma }_u^2\\ k_i{\sigma }_u^2& k_i^2{\sigma }_u^2\end{array}\right)$ is a non-full rank matrix because ${\mathit{u}}^i=\mathit{u}{k}_i$, and ⨂ indicates the Kronecker product. The final linear model, considering the epistatic interaction of locus i with all other loci, is:

$${\displaystyle \begin{array}{l}{\displaystyle \mathit{y}=\mathit{X}\mathit{b}+\mathit{u}+{\mathit{Z}}_i^{*}{\mathit{u}}^i+\mathit{e}}\end{array}}$$

with $\left({}_{u^i}^u\right)=\left(\begin{array}{cc}{\sigma }_u^2& k_i{\sigma }_u^2\\ k_i{\sigma }_u^2& k_i^2{\sigma }_u^2\end{array}\right)$ . This model can be used in an exact method as described below.

The exact method proceeds by likelihood ratio test of the two alternative hypothesis, using random regression with the Model $H_1$:

$${\displaystyle \begin{array}{l}{\displaystyle \mathit{y}=\mathit{X}\mathit{b}+{\mathit{z}}_i{\alpha }_i+\mathit{u}+{\mathit{Z}}_i^{*}{\mathit{u}}^i+\mathit{e}}\end{array}}$$ (2)

and a simpler model excluding random regression with the Model $H_0:$

$${\displaystyle \begin{array}{l}{\displaystyle \mathit{y}=\mathit{X}\mathit{b}+{\mathit{z}}_i{\alpha }_i+\mathit{u}+\mathit{e}}\end{array}}$$ (3)

Where the actual parameter being tested is $k_i^2{\sigma }_u^2\ne 0$. The regression on gene content $z_i{\alpha }_i$ corrects for eventual statistical additive (not epistatic) effects of locus i. Parameters are estimated by REML (Patterson and Thompson, 1971).

After fitting the two models, the likelihood ratio test of the competing models is distributed as a mixture of 0 and 1 degrees of freedom chi-square, from which P-values can be obtained. In addition, from the estimated covariance matrix ${\mathit{G}}_0$ estimated under $H_1$, the estimated buffering epistatic effect can be obtained as:

$${\displaystyle \begin{array}{l}{\displaystyle {{\displaystyle \widehat{k}}}_i={{\displaystyle \widehat{G}}}_0[2,2]/{{\displaystyle \widehat{\mathit{G}}}}_0[1,2]}\end{array}}$$ (4)

Contrary to Crawford et al. (2017), the matrix $\mathit{G}$ has to be computed and inverted only once, because the inclusion of the $i$-th locus has zero influence on the result (Gianola et al., 2016) and the matrix ${\mathit{Z}}_i^{*}\mathit{G}{\sigma }_u^2{\mathit{Z}}_i^{{*}^{\prime }}$ is never explicitly computed. This results in great savings of computing time. Matrix ${\mathit{G}}_0$ is a non-full rank matrix, which slows down convergence. An easy solution is to use a reduced rank model fitting one principal component (Meyer and Kirkpatrick, 2005) as implemented in Wombat (Meyer, 2007). Convergence takes a few iterations in this case compared with hundreds using a standard REML algorithm.

False discovery rate

Following Bolormaa et al. (2014) and with equivalent original derivations from Storey (2002), false discovery rate (FDR) was calculated as:

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{F}\mathrm{D}\mathrm{R}=\frac{P(1-\frac{A}{T})}{\left(\frac{A}{T}\right)(1-P)}}\end{array}}$$

Where P is the P-value tested, A is the number of SNPs that were significant at the P-value tested, and T is the total number of SNP tested (T = 651,253 and 689,818 for BB and TC, respectively).

Analytical implementation

We implemented the analyses using shell scripts to manipulate the data, Wombat (Meyer, 2007) for the REML analyses (see Supplementary Appendix), and our own programs for the fast approximate analyses. Scripts and source code are available from the corresponding author upon request. The GWAS was performed in a high-performance cluster computer (Genotoul Toulouse bioinfo platform), in which the epistatic effect of each marker (k_i) was estimated separately from each other. Wall clock computing time was approximately 4 d for the exact analysis run in parallel and a few minutes for the fast approximate one.

Results and Discussions

Figure 1 shows the steps of the mechanical heuristics proposed to identify SNPs with buffering epistatic effect. For the BB population, the distribution of GEBV averaged 4.26 × 10^–7 kg and ranged from −43.08 to 41.12 kg (Figure 1A). Similarly, for the TC population, the distribution of GEBV averaged −6.27 × 10^–7 kg and ranged from −58.50 to 57.53 kg (Figure 1A). We split the animals into five equally sized bins according to their GEBV (Figure 1B). Using a nominal P < 0.05 from the GWAS within the extreme bins (BIN1 and BIN5) with opposite effect sign, plus a monotonic pattern of effect across bins as well as a P > 0.10 in the GWAS using the whole data, we found 243 and 143 epistatic SNPs in the BB and TC population, respectively (Figure 1C).

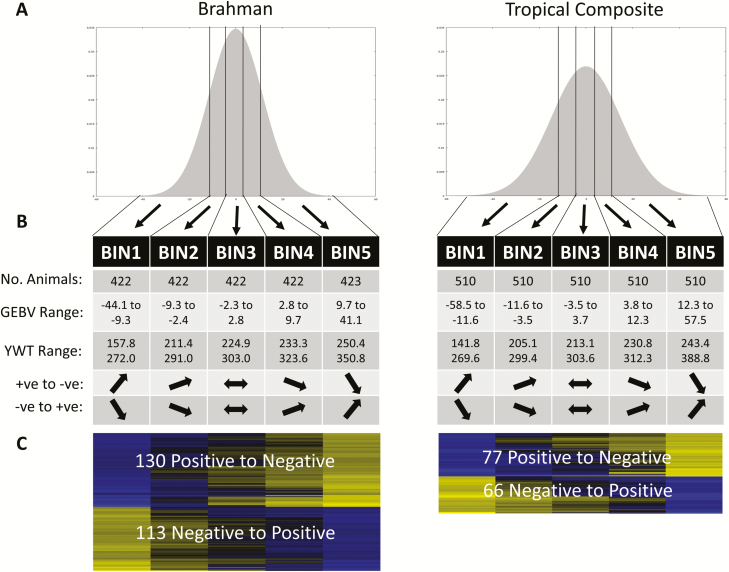
Figure 1.

Schematic flowchart of the mechanical heuristic to identify buffering epistatic SNP: (A) Distribution of yearling weight GEBV for 2,111 BB and 2,550 TC cattle with five equally sized bins clearly demarked, BIN1 to BIN5; (B) Across bins the range of GEBV are by construct nonoverlapping, but the range of phenotypes overlap across bins. A GWAS of SNP genotype on phenotype is performed with the intention to capture SNPs with significant yet opposed additive effects in BIN1 and BIN5, and with a monotonic pattern of effects across bins; (C) We find 243 and 143 buffering epistatic SNPs in the BB and TC population, respectively.

For each population, six of these SNPs, including three of each pattern (positive to negative, and negative to positive), are listed in Table 1. Table 1 also lists the effect of an SNP in the coding regions of PLAG1 (pleomorphic adenoma gene 1), a well-known locus affecting stature in humans (Gudbjartsson et al., 2008), as well as growth and fertility traits in cattle (Karim et al., 2011; Fortes et al., 2013). The SNP on PLAG1 was found to be significant only in the GWAS of the middle bins (BIN3 and BIN2 in BB and TC, respectively) as well as the GWAS of the whole dataset in both the populations.

Table 1.

Mechanical heuristics: estimated SNP effects in t-statistic units (estimated effect divided by standard error) in the GWAS within BINs and across the whole population: three examples each of “Negative to Positive” and “Positive to Negative” pattern as well as for a SNP in the PLAG1 coding region for BB and TC populations.

SNP Chr:Mb (Gene)	BIN1	BIN2	BIN3	BIN4	BIN5	Whole
	Brahman
18:56.5 (CPT1C)	−7.58*	−1.38	−0.86	2.67	4.84*	0.60
23:50.0 (PRPF4B)	−4.50*	0.91	1.39	2.14	3.58*	1.28
28:23.3 (CTNNA3)	−8.00*	−3.05	−1.93	1.55	5.06*	−0.05
4:71.4 (OSBPL3)	5.95*	1.45	−0.50	−1.89	−6.01*	0.29
5:54.9 (LRIG3)	4.86*	−0.30	−0.79	−2.05	−3.94*	1.18
27:1.1 (CSMD1)	4.53*	1.18	−0.66	−0.69	−2.37*	0.58
14:25.0 (PLAG1)	0.74	2.07	3.46*	2.15	2.02	4.71*
	Tropical Composite
14:84.3 (SNTB1)	−4.21*	0.25	1.69	1.93	3.42*	0.64
16:28.5 (CNIH3)	−3.39*	−2.00	0.65	1.10	2.74*	0.52
23:15.3 (FOXP4)	−6.20*	−1.94	−0.76	1.87	5.14*	−0.26
1:5.39 (GRIK1)	2.90*	0.74	0.16	−0.83	−2.98*	1.58
10:75.6 (KCNH5)	3.56*	2.07	1.00	−0.12	−3.63*	−0.54
22:57.3 (PPARG)	3.49*	1.12	−0.09	−2.66*	−2.81*	1.01
14:25.0 (PLAG1)	−0.08	2.83*	2.47	1.02	0.44	6.16*

*indicates significance at P < 0.001.

Among the genes listed in Table 1, we highlight LRIG3 (Leucine-rich repeats and immunoglobulin-line domains protein 3), a body size-related gene found to be under positive selection in a study of five bovine breeds including BB (Xu et al., 2015). This finding is of most relevance because genes found under selection in a breed comparison study are bound to have little variation in their coding region and/or no additive effect in any given breed, and are only identified as relevant, such as harboring signatures of selection, in a multi-breed comparison.

Table 2 presents the number of significant SNP and FDR at various P-value thresholds. At any given P-value, the number of significant SNP was lower in BB than in TC. As a result, the FDR was lower in TC than in BB for a given P-value. For instance, at P-value < 0.0001, the FDR was 9.83% and 4.38% for BB and TC, respectively. The higher number of epistatic SNPs identified in the TC compared with the BB population was attributed to the distinct allele frequencies observed in the two populations. Across all SNPs, the first (reference) allele was found to be either mostly absent (reference allele frequency near 0) or nearly fixated (reference allele frequency near 1) in the BB population, while intermediate allele frequencies (highly polymorphic and hence more informative SNP) were predominant in the TC population (Figure 2 in (Reverter et al. 2017)). In other words, the distribution of allele frequencies in BB are U-shaped.

Table 2.

Number of significant buffering epistatic SNP (N) and false discovery rate (FDR) at decreasing levels of P-value for the BB and TC populations

P-value	Brahman		Tropical Composite
	N	FDR, %	N	FDR, %
< 0.05	66,789	46.06	87,545	36.21
< 0.01	20,542	31.01	30,803	21.61
< 0.005	12,503	25.67	19,831	16.98
< 0.001	3,679	17.62	6,972	9.80
<0.0005	2,186	14.85	4,484	7.64
<0.0001	662	9.83	1,571	4.38
<0.00005	384	8.47	1,028	3.35
<0.00001	91	7.15	342	2.02

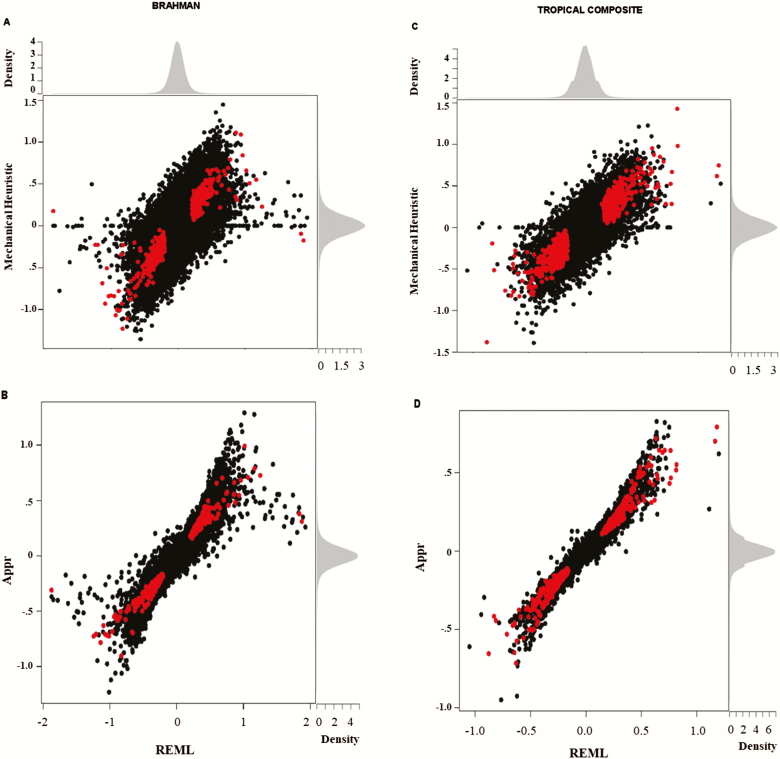
Figure 2.

Methods comparison: relationship between the SNP buffering epistatic effects estimated via the bivariate REML analyses and the mechanical heuristic (A and C), and between the bivariate REML analyses and the approximation based on the regression of residuals on GEBV (B and D) for the Brahman (A and B) and Tropical Composite (C and D) populations. Highlighted red are the significant SNP (P < 0.0001) according to REML.

Figure 2 illustrates the two-way relationship between the mechanical heuristics and the exact test based on bivariate random regression REML analyses (Figure 2A and C), and between the numerical approximation based on the regression of residuals on GEBV and the exact text (Figure 2B and D). In the BB population, we observed a correlation of r = 0.728 (Figure 2A) between SNP epistatic effects according to the mechanical heuristics and the exact test, while a correlation of r = 0.979 (Figure 2B) was found between the approximation and the exact test. In the TC population, the same pair of values were r = 0.805 (Figure 2C) and r = 0.990 (Figure 2D). These results corroborate the superiority of the numerical approximation compared with the mechanical heuristics, with the latter being affected by arbitrary parameters, including the number of bins and the criteria for the identification of epistatic SNPs (e.g., monotonic pattern of effects from the first to the last bin).

The performance of the mechanical heuristics could be further affected if only GEBV with an accuracy beyond a nominal threshold were to be employed. Also, issues related to the sensitivity of the mechanical heuristics to GEBV accuracies, number of bins and relatedness of individuals within bin have not been considered with any degree of detail. Obviously, the minimum number of bins would be two (for negative and positive GEBVs), but that would likely result in many false positives. On the other extreme, a large number of bins can only be considered with large sample sizes so that a within-bin GWAS can be undertaken with sufficient statistical power. At this stage, we acknowledge that the mechanical heuristics lacks theoretical formality and its value is limited to provide a graphical understanding of buffering epistasis.

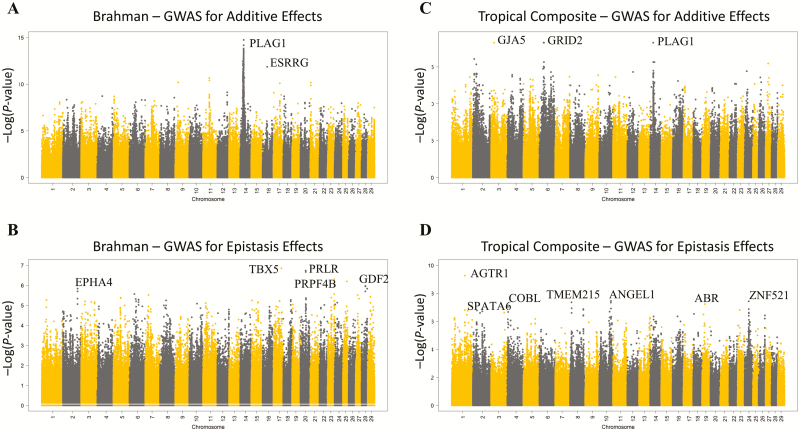
Figure 3 shows the Manhattan plots for the GWAS for additive and epistatic effects in the BB and TC populations. The most likely candidate genes in the most significantly associated regions are also given in Figure 3. It can already be noted that additive and epistatic gene effects are mutually orthogonal.

Figure 3.

Genome-wide additive and epistasis association: Manhattan plots of the additive (A and C) and buffering epistatic (B and D) association of SNPs across the 29 bovine autosomal chromosomes for the Brahman (A and B) and Tropical Composite (C and D) populations. The most likely candidate genes in the most significantly associated regions are annotated where an obvious candidate could be identified according to the bovine reference genome assembly ARS-UCS1.2. SNPs on odd-numbered chromosomes are in black and those on even-numbered chromosomes are in yellow.

In the BB population, the strongest significance for epistatic effect corresponded to SNP BovineHD1700017822 mapped to 60,216,894 bp of BTA17 at 11,627 bp of the coding region of TBX5 (T-box 5 transcription factor) and with an estimated epistatic effect of −0.533 (−Log₁₀(P-value) = 6.849). The corresponding human chromosome segment is involved in ulnar–mammary syndrome (Klopocki et al., 2006), and a recent large meta-GWAS study reveals TBX5 as a candidate gene for mammary gland morphology in Fleckvieh cattle (Pausch et al., 2016).

Following TBX5, we found the second strongest signal for buffering epistasis in BB to SNP BovineHD2000011094 (estimated epistatic effect of −0.282 and −Log₁₀(P-value) = 6.669) mapped to 38.97 Mb of BTA20 and 2.6 kb downstream of prolactin receptor (PRLR). PRLR is in a region captured by selection signatures for adaptation in beef cattle (Boitard et al., 2016) and mutations on this gene have been found to have a major genetic effect on hair length and coat structure characteristics of cattle (Littlejohn et al., 2014; Porto-Neto et al., 2018).

The third strongest signal corresponded to SNP BovineHD2300014569 mapped to 50.10 Mb of BTA23 in the coding region of PRPF4B (pre-mRNA processing factor 4B) with an estimated effect of 0.324 (−Log₁₀(P-value) = 6.309). With no reported function in the context of bovine breeding and genetics, PRPF4B is an essential kinase induced by estrogen (Lahsaee et al., 2016) and its loss promotes sustained growth factor signaling (Corkery et al., 2018). Quite strikingly, loci on the coding region of SPEN (SNP BovineHD1600014616, epistatic effect = 0.213, −Log₁₀(P-value) = 2.137) and GHR (SNP BovineHD2000009203, epistatic effect = 0.782, −Log₁₀(P-value) = 2.234) were found to be significantly epistatic in our study. SPEN is an estrogen receptor cofactor and a key regulator of fat deposition and energy balance (Hazegh et al., 2017). Furthermore, an SNP-based co-association gene network by our group previously identified ESRRG and PPARG as key regulators of age at puberty in BB cows (Fortes et al., 2013).

In the TC population, we found the strongest signal in SNP BovineHD0100028404 (epistatic effect = 0.294, −Log₁₀(P-value) = 9.261) mapped to 98.71 Mb of BTA1 in the coding region of LOC100139843 (mCG140927-like) with limited information known about its function, but quite strikingly, recently reported to be associated with age at puberty in Angus bulls (Fernández et al., 2016). We found the second and third strongest signal in the coding region of ZNF521 (SNP BovineHD2400008618 mapped to BTA24:31,439,030 with an estimated epistatic effect = −0.260, −Log₁₀(P-value) = 7.432) and AGTR1 (SNP BovineHD0100034098 mapped to BTA1: 119,483,491 with an estimated epistatic effect = −0.194, −Log₁₀(P-value) = 3.204), respectively. The loci on ZNF521 has been found to associate with female fertility in Nordic Red cattle, consisting of three different populations from Finland, Sweden, and Denmark (Höglund et al., 2015). Whereas the role in bovine fertility of AGTR1 (angiotensin II receptor type 1) has long been documented (Portela et al., 2008; Marey et al., 2016) including its differential expression at the level of the oviduct between Bos taurus and Bos indicus cattle (Fontes et al., 2018).

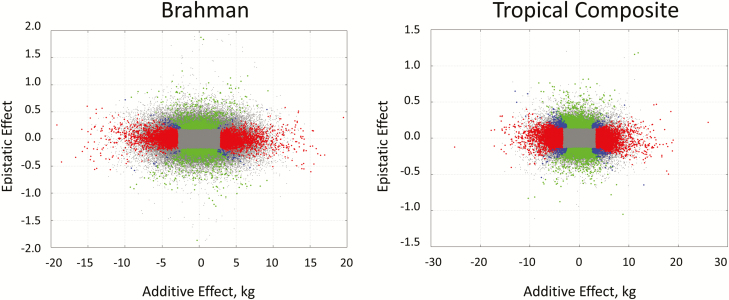
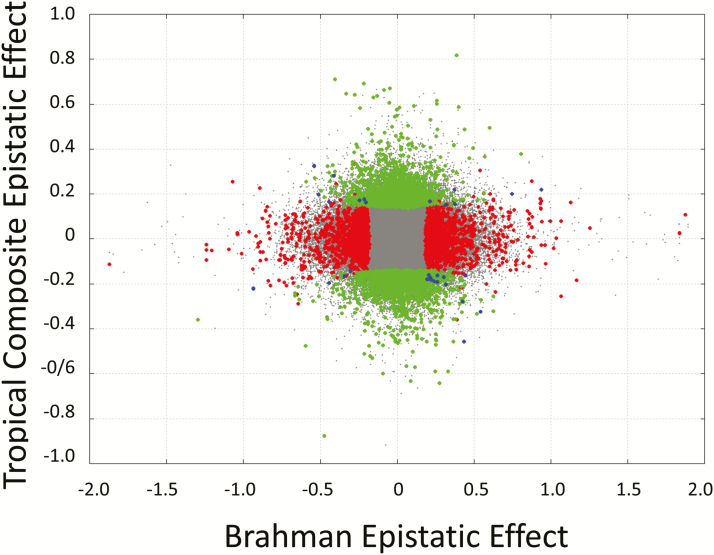
The relationship between epistatic and additive effect in each population is illustrated in Figure 4. It can be seen that effects are empirically orthogonal as expected. Note that unlike additive effects, epistatic effects have no units as they are defined as a multiplier on additive effects. Figure 5 shows the relationship between the epistatic effects in both populations, BB and TC. Significant simultaneously in both populations were 42 SNPs of which 24 where located within 50 kb of the coding region of known genes and these are listed in Table 3. Porto-Neto et al. (2014) showed that Linkage disequilibrium dropped below 0.2 at distances of 50 kb.

Figure 4.

Scatter plot of the relationship between SNP additive (x-axis) and buffering epistatic effects (y-axis) for the Brahman (left panel) and Tropical Composite (right) populations. Red, green, and blue indicate significance (P-value < 0.001) for additivity, epistatic and both, respectively.

Figure 5.

Scatter plot of the relationship between SNP buffering epistatic effect in the Brahman (x-axis) and Tropical Composite (y-axis) populations. Red, green, and blue indicate significance (P-value < 0.001) in the Brahman, Tropical Composite, and both populations, respectively.

Table 3.

Annotation of SNP with significant (P < 0.001) buffering epistatic effect in both populations (BB and TC) including genome position, distance to nearest gene, gene (according to the bovine reference genome assembly ARS-UCS1.2), reference allele frequency (RAF), estimated effect, and significance (−Log(P))

SNP	Chr	Bp	Distance	Gene	Brahman			Tropical Composite
					RAF	Effect	−Log(P)	RAF	Effect	−Log(P)
BovineHD0200001651	2	5,747,611	38,487	NEMP2	0.0263	−0.5406	3.0404	0.0729	0.3258	3.5760
BovineHD0200001652	2	5,748,515	37,583	NEMP2	0.0263	−0.5406	3.0404	0.0727	0.3237	3.5065
BovineHD0200001654	2	5,757,112	28,986	NEMP2	0.9737	0.5433	3.0404	0.9272	−0.3234	3.5297
ARS-BFGL-NGS-100083	8	11,133,497	0	SCARA3	0.9528	−0.5113	3.4369	0.6920	0.1975	4.1983
BovineHD0800014800	8	49,143,207	36,501	ALDH1A1	0.9820	0.7474	3.5992	0.7831	0.2002	3.9915
BovineHD0800015819	8	52,427,816	8,480	PCSK5	0.0452	−0.4416	3.3439	0.2349	−0.1963	3.6686
Hapmap48089-BTA-81187	8	52,524,895	0	GCNT1	0.9403	0.3760	3.0638	0.6829	0.1562	3.2041
BovineHD1000026980	10	92,312,649	0	TSHR	0.6054	0.2160	3.5761	0.4686	−0.1712	4.0605
BovineHD1000026985	10	92,331,573	0	TSHR	0.3946	−0.2140	3.5761	0.5317	0.1779	4.1064
BovineHD1000030828	10	92,335,071	0	TSHR	0.4216	−0.2017	3.2507	0.7002	0.1623	3.2973
BovineHD1200025989	12	84,830,432	15,785	5S_rRNA	0.7141	0.2066	3.2041	0.6998	−0.1603	3.0872
BovineHD1400011237	14	37,055,691	0	ENSBTAG00000002076	0.1033	−0.3042	3.0404	0.5288	−0.1442	3.0872
BovineHD1400011280	14	37,211,716	0	ENSBTAG00000050514	0.9095	0.3733	3.9915	0.6543	0.2204	5.9710
BovineHD1400013234	14	44,638,868	5,792	PMP2	0.6080	0.1951	3.0169	0.6512	−0.1791	3.9225
BovineHD1600016214	16	56,665,443	0	TNR	0.1409	0.2618	3.0872	0.6231	−0.1635	3.6917
BovineHD1700009805	17	35,070,459	0	IL21	0.9377	0.4452	3.7841	0.7129	−0.1633	3.2973
BovineHD1700009807	17	35,079,284	8,519	IL21	0.0623	−0.4429	3.7610	0.2859	0.1659	3.2274
BovineHD1700009808	17	35,083,771	13,006	IL21	0.0623	−0.4429	3.7610	0.2859	0.1659	3.2274
BovineHD1700009811	17	35,094,499	23,734	IL21	0.9377	0.4452	3.7841	0.7131	−0.1626	3.2740
BovineHD1900012991	19	45,742,542	18,774	ENSBTAG00000053203	0.2399	0.2629	3.5297	0.3921	−0.1908	4.5416
BovineHD4100015365	21	65,988,493	33,080	bta-mir-656	0.0559	0.4343	3.1340	0.0502	−0.4564	5.9259
BovineHD2500009619	25	34,418,988	0	SSC4D	0.1843	0.3028	3.6455	0.4378	−0.1702	3.8764
BovineHD2500009621	25	34,427,964	0	SSC4D	0.1831	0.3168	3.8764	0.3959	−0.2030	4.9974
BovineHD2800005959	28	22,571,976	0	CTNNA3	0.1338	0.3147	3.1807	0.3500	0.1516	3.2973

Among those listed in Table 3, prominent genes for their reported role in mammalian fertility including bovine are: ALDH1A1 (aldehyde dehydrogenase 1 family member A1), PCSK5 (proprotein convertase subtilisin/kexin type 5), and TSHR (thyroid-stimulating hormone receptor), and IL21 (Interleukin-21).

The role of ALDH1A1 during bovine ovarian development has recently been established (Hatzirodos et al., 2019; Hummitzsch et al., 2019). Antenos et al. (2011) reported the role of PCSK5 in mouse ovarian follicle development. Similarly, TSHR is a well-known regulator of growth, fat metabolism, and fertility. Dias et al. (2017) identified a candidate QTL in TSHR affecting puberty in five cattle breeds across the taurine and Indicine lineages: Brangus, BB, Nellore, Angus, and Holstein. Also, one of the most prominent selective sweeps found in all domestic chickens occurred at the locus for TSHR (Rubin et al., 2010). Finally, the immune system response gene IL21 has been shown to harbor selection signatures among divergently selected subpopulations of Polish Red cattle (Gurgul et al., 2019), and among goats and sheep indigenous to a hot arid environment (Kim et al., 2016).

The existence of buffering mechanisms is an emerging propriety of networks (Mackay, 2014), and, therefore, because biochemical and gene networks are pervasive in nature, buffering loci must exist. Moreover, the existence of segregating (not fixed) buffering epistatic loci would explain several phenomena that are not well understood: environmental robustness, release of additive variance after disturbing events, (Visser et al., 2003; Flatt, 2005), maintenance of genetic variance in selected populations previously under stabilizing selection (Gimelfarb, 1989), and opposite signs of GWAS associations in different populations (Huang et al., 2012).

A simulated dataset would assist in understanding the implications of the analytical approach presented here, but we argue about the difficulty of simulating a dataset in a realistic fashion. Jannink (2007) simulated a trait with a genetic variance of 60 and a phenotypic variance of 100. An epistatic variance of 20 was generated with the marked QTL interacted with nine other unlinked loci based on a compound epistatic network proposed in the context of plant breeding (Cooper et al., 2002). Further research is warranted to understand how and if this approach could work to simulate buffering epistasis by which a set of QTLs have opposing effects on the extremes of the additive polygenic value and in the presence of selection. Importantly, in his simulations, Jannink (2007) observed the conversion of additive-by-additive epistasis to additive variance which is what we hypothesize based on our mechanical heuristics and the empirical results.

In multi-generation selection programs, the continued response has been seen, classically for over 100 generations in the Illinois maize kernel content lines [38], and there have been large and still continuing genetic improvements in livestock populations, notably in broiler chickens [39]. Whilst the obvious source of continued response is de novo mutation, some of the additive variation being utilized may have derived from existing mutations whose behavior changes from epistatic to additive in response to changes in the remainder of the genome. Paixão and Barton (2016) argued that “epistasis sustains additive genetic variance for longer: Alleles that were initially deleterious or near-neutral may acquire favorable effects as the genetic background changes, ‘converting’ epistatic variance into additive, and so prolonging the response to selection.” Similarly, Hill (2017) concluded that “It seems better to concentrate on utilizing additive variance, and hope for a bonus from converting epistatic variance.” These assessments beg the questions: 1) how would one go about strategically increasing this conversion? and 2) are some functional groups and/or genomic regions more likely to convert than others? We hypothesize the epistatic SNPs found here are in effect “dormant” with an additive effect waiting to be “released” when selection moves the population to either tail of the genetic value distribution. Consistent with the argument of Carlborg et al. (2006), we further argue that these SNPs provide an answer to the long-standing paradox by which genetic variation does not diminish with selection as fast as theory would anticipate, and instead epistasis is responsible for the release of genetic variation during long-term selection.

Conclusions

We have developed three novel analytical methodologies to identify and estimate the effect of an SNP with an epistatic effect against the polygenic background. Two of the approaches require the use of previously computed GEBV, which makes them particularly suited to domestic species of agricultural importance that have adopted genomic selection for their breeding purposes.

Glossary

Abbreviations

BB

Brahman

FDR

false discovery rate

GEBV

genomic estimated breeding value

GWAS

genome-wide association study

PLAG1

pleomorphic adenoma gene 1

PRLR

prolactin receptor

PRPF4B

pre-mRNA processing factor 4B

QTL

quantitative trait loci

REML

restricted maximum likelihood

SP

single nucleotide polymorphism

TBX5

T-box 5 transcription factor

TC

Tropical Composite

YWT

yearling weight

Conflict of interest statement

The authors declare no real or perceived conflicts of interest.