Motion Artifact Reduction Using a Convolutional Neural Network for Dynamic Contrast Enhanced MR Imaging of the Liver

Abstract

Purpose:

To improve the quality of images obtained via dynamic contrast enhanced MRI (DCE-MRI), which contain motion artifacts and blurring using a deep learning approach.

Materials and Methods:

A multi-channel convolutional neural network-based method is proposed for reducing the motion artifacts and blurring caused by respiratory motion in images obtained via DCE-MRI of the liver. The training datasets for the neural network included images with and without respiration-induced motion artifacts or blurring, and the distortions were generated by simulating the phase error in k-space. Patient studies were conducted using a multi-phase T₁-weighted spoiled gradient echo sequence for the liver, which contained breath-hold failures occurring during data acquisition. The trained network was applied to the acquired images to analyze the filtering performance, and the intensities and contrast ratios before and after denoising were compared via Bland–Altman plots.

Results:

The proposed network was found to be significantly reducing the magnitude of the artifacts and blurring induced by respiratory motion, and the contrast ratios of the images after processing via the network were consistent with those of the unprocessed images.

Conclusion:

A deep learning-based method for removing motion artifacts in images obtained via DCE-MRI of the liver was demonstrated and validated.

Introduction

Dynamic contrast enhanced magnetic resonance imaging (DCE-MRI) of the liver is widely used for detecting hepatic lesions and distinguishing malignant from benign lesions. However, such images often suffer from motion artifacts due to unpredictable respiration, dyspnea, or mismatches in k-space caused by rapid injection of the contrast agent.^1,2 In DCE-MRI, a series of T₁-weighted MR images is obtained after the intravenous injection of a gadolinium-based MR contrast agent, such as gadoxetic acid. However, acquiring appropriate datasets for arterial phase DCE-MR images is difficult owing to the limited scan time available in the first pass of the contrast agent. Furthermore, it has been reported that transient dyspnea can be caused by gadoxetic acid at a non-negligible frequency,^1,2 which results in degraded image quality due to respiratory motion-related artifacts such as blurring and ghosting.³ Especially, coherent ghosting originating from the anterior abdominal wall decrease the diagnostic value of the images.⁴

Recently, many strategies have been proposed to avoid motion artifacts in DCE-MRI. Of these, fast acquisition strategies using compressed sensing may provide the simplest way to avoid motion artifacts in liver imaging.^5–7 Compressed sensing is an acquisition and reconstruction technique based on the sparsity of the signal, and the k-space undersampling results in a shorter scan time. Zhang et al.⁶ demonstrated that DCE-MRI with a high acceleration factor of 7.2 using compressed sensing provides significantly better image quality than conventional parallel imaging. Other approaches include data acquisition without breath-holding (free-breathing method) using respiratory triggering and respiratory triggered DCE-MRI, which is an effective technique to reduce motion artifacts in the case of patients who are unable to suspend their respiration.^4,8 In these approaches, sequence acquisitions are triggered based on respiratory tracings or navigator echoes, and typically provide a one-dimensional projection of the abdominal images. Chavhan et al. and Vasanawala et al. found that the image quality in acquisitions with navigator echoes under free-breathing conditions is significantly improved. Although triggering based approaches successfully reduce the motion artifacts, it is not possible to appropriately time arterial phase image acquisition due to the long scan times required to acquire an entire dataset. In addition, miss-triggers often occur in the case of unstable patient respiration, which cause artifacts and blurring of the images. Recently, a radial trajectory acquisition method with compressed sensing was proposed,^9,10 which enabled high-temporal resolution imaging without breath-holding in DCE-MRI. However, the image quality of the radial acquisition without breath-holding was worse than that with breath-holding even though the clinical usefulness of the radial trajectory acquisition has been demonstrated in many papers.^11–13

Post-processing artifact reduction techniques using deep learning approaches have also been proposed. Deep learning, which is used in complex non-linear processing applications, is a machine learning technique that relies on a neural network with a large number of hidden layers. Han et al.¹⁴ proposed a denoising algorithm using a multi-resolution convolutional network called “U-Net” to remove the streak artifacts induced in images obtained via radial acquisition. In addition, aliasing artifact reduction has been demonstrated in several papers as an alternative to compressed sensing reconstruction.^15–17 The results of several feasibility studies of motion artifact reduction in the imaging of brain,^18–20 abdomen,²¹ and cervical spine²² have also been reported. Although these post-processing techniques have been studied extensively, no study has ever demonstrated practical artifact reduction in DCE-MRI of the liver.

In this study, a motion artifact reduction method was developed based on a convolutional network (Motion artifact reduction method based on convolutional neural network [MARC]) for DCE-MRI of the liver, which that removes motion artifacts from input MR images. Both simulations and experiments were conducted to demonstrate the validity of the proposed algorithm.

Materials and Methods

Network architecture

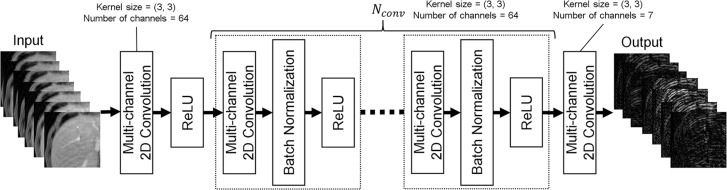
In this paper, a MARC with multi-channel images is proposed, as shown in Fig. 1. It is based on the network originally proposed by Zhang et al.²³ for Gaussian denoising, JPEG deblocking, and super-resolution of natural images. A patch-wise approach was adopted for training the MARC. The patch-wise training has advantages in extracting large training datasets from limited images and has efficient memory usage on host PCs and GPUs. Residual learning approach was adopted to achieve effective training of the network.²⁴ The network relies on two-dimensional convolutions, batch normalizations, and rectified linear units (ReLU) to extract the artifact components from images with artifacts. To utilize the structural similarity of the multi-contrast images, a seven-layer patched image with varying contrast was used as the input to the network. The layers corresponded to the temporal phases acquired in a time-series with multi-phase sequence. In the first layer, 64 filters with kernel size of 3 × 3, and ReLU as an activation function, were applied to the input layer, which had seven channels. Then, 64 filters with kernel size of 3 × 3, followed by batch normalization and ReLU, were used in the convolution layers. The number of convolution layers (N_conv) was determined as shown in the subsection “Analysis”. In the last layer, seven filters with a kernel size of 3 × 3 with 64 channels were used. Finally, a seven-channel image was predicted as the output of the network. The total number of parameters was 268423. Artifact-reduced images could then be generated by subtracting the predicted image from the input. The developed network can be used for images of arbitrary size in the same way as conventional convolution filters.

Fig. 1.

Network architecture for the proposed convolutional neural network, two-dimensional convolutions, batch normalizations, and ReLU. The network predicts the artifact component from an input dataset. The number of convolution layers in the network was determined by simulation-based method. ReLU, rectified linear unit.

Imaging

Following the Institutional Review Board approval, patient studies were conducted from May 15th through June 30th, 2018. All patients underwent DCE-MRI for the purpose of screening or diagnosis of hepatocellular carcinomas. MR images were acquired using a 3T MR750 system (GE Healthcare, Waukesha, WI, USA); a whole-body coil and a 32-channel torso array were used for radio-frequency (RF) transmission and receiving, and self-calibrated parallel imaging (Autocalibrating Reconstruction for Cartesian sampling [ARC]) was used with an acceleration factor of 2 × 2. A 3D T₁-weighted spoiled gradient echo sequence with a dual-echo bipolar readout and variable density Cartesian undersampling (differential subsampling with Cartesian ordering [DISCO]) was used for the acquisition,²⁵ along with an elliptical-centric trajectory with pseudo-randomized sorting in k_y − k_z. Dixon-based reconstruction method was used to suppress fat signals.²⁶ A total of seven temporal phase images, including pre-contrast and six arterial phases, were obtained using gadolinium contrast with end-expiration breath-holdings of 10 and 21 s. The standard dose (0.025 mmol/kg) of contrast agent (EOB Primovist, Bayer HealthCare, Osaka, Japan) was injected at the rate of 1 mL/s followed by a 20-mL saline flush using a power injector. The arterial phase scan was started 30 s after the start of the injection. The acquired k-space datasets were reconstructed using a view-sharing approach between the phases and a two-point Dixon method to separate the water and fat components. The following imaging parameters were used: flip angle = 12°, receiver bandwidth = ±167 kHz, TR = 3.9 ms, TE = 1.1/2.2 ms, acquisition matrix size = 320 × 192, FOV = 340 × 340 mm², total number of slices = 56, slice thickness = 3.6 mm. The acquired images were cropped to a matrix size of 320 × 280 after zero-filling to 320 × 320.

For the network training, arterial phase images were successfully acquired without artifact from 14 patients (M/F, mean age: 51, range: 34–69) selected by a radiologist with 3 years of experience in abdominal. In addition, 20 patients (M/F, mean age: 65, range: 46–79) were retrospectively included for the volunteer experiments. The patients for the volunteer experiments were randomly selected from a series of 132 patients, excluding those selected for the network training.

Respiration-induced artifact simulation

A respiration-induced artifact was simulated by adding simulated errors to the k-space datasets generated from the magnitude-only image. The training; required the preparation of pairs of input and output of the network, namely, images with and without motion artifact. In the case of abdominal imaging, it is difficult to obtain such pairs from the experimental imaging because respiratory motion induces a misregistration between them. Therefore, the datasets were generated based on simulation with a simple assumption, as described below. Generally, a breath-holding failure causes phase errors in the k-space, which results in an artifact along the phase-encoding direction. In this study, rigid motion along the anterior–posterior direction was assumed for the simplicity, as shown in Fig. 2. In this case, the phase error was induced in the phase-encoding direction and was proportional to the motion shift. Motion during readout can be neglected because it is performed within a millisecond order. Then, the in-phase and out-of-phase MR signals, which are derived from water and fat components and have phase error ϕ, can be expressed as follows:

$$\begin{array}{ccc}{S}_{\text{I}}^{\prime }(k_x,k_y)& =& S_{\text{I}}(k_x,k_y)e^{-j\phi (k_y)}\\ S_{\text{O}}^{\prime }(k_x,k_y)& =& S_{\text{O}}(k_x,k_y)e^{-j\phi (k_y)}\end{array},$$

where S_I and S_O are the in-phase and out-of-phase signals, respectively, without the phase error; S′_I and S′_O are the corresponding signals with the phase error, and k_x, k_y represent the k-space co-ordinate (−π < k_x < π, −π < k_y < π) in the readout and the phase-encoding directions, respectively. Finally, k-space of the water signal (S_w) with the phase error can be expressed as follows:

$$\begin{array}{ll}{S}_{\text{w}}\hfill & =\frac{S_{\text{I}}^{\prime }+S_{\text{O}}^{\prime }}{2}\hfill \\ \hfill & =\frac{S_{\text{I}}+S_{\text{O}}}{2}{e}^{-j\varphi (k_y)},\hfill \\ \hfill & =ℱ[I_{\text{w}}]e^{-j\varphi (k_y)}\hfill \end{array}$$

where ℱ is the Fourier operator, and I_w denotes the water image. Hence, artifact simulation can be implemented by simply adding the phase error components to the k-space of the water image. In this study, the k-space datasets were generated from magnitude-only water images. To simulate the background B₀ inhomogeneity, the magnitude images were multiplied by B₀ distributions derived from polynomial functions up to the third order as below.

$$B_0(x,y)=\sum _{i=0}^3\sum _{j=0}^3{c}_{ij}{x}^i{y}^j,$$

where c_ij are linear combination coefficients, and x and y are the spatial coordinates. The coefficients c_ij were determined randomly so that the peak-to-peak value of the B₀ distribution was within ±5 ppm (±4.4 radian).

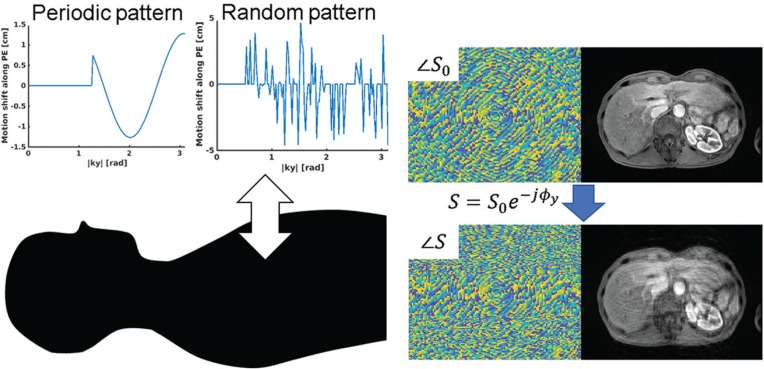
Fig. 2.

(Left) Example of a simulation of the respiratory motion artifact by adding phase errors along the phase-encoding direction in k-space. (Right) The k-space and image datasets before and after adding simulated phase errors.

To generate a motion artifact in the MR images, we used two kinds of phase error patterns: periodic and random. Generally, severe coherent ghosting artifacts are observed along the phase-encoding direction. Although there are several factors that generate artifacts in the acquired images during DCE-MRI including respiratory, voluntary motion, pulsatile arterial flow, view-sharing failure, and unfolding failure,^3,27 the artifact from the abdominal wall in the phase-encoding direction is mainly recognizable. In the case of centric-order acquisitions, the phase mismatching in the k-space results in high-frequency and coherent ghosting. An error pattern using simple sine wave with random frequency, phase, and duration was used to simulate the ghosting artifact. It was assumed that motion oscillations caused by breath-hold failures occurred after a delay as the scan time proceeded. The phase error can be expressed as follows:

$$\varphi (k_y)=\{\begin{array}{ll}0\hfill & \left(\left|k_y\right|<k_{y0}\right)\hfill \\ 2\pi \frac{k_y\mathrm{\Delta }\text{sin}(\alpha k_y+\beta )}{N}\hfill & (\text{otherwise}),\hfill \end{array}$$

where Δ denotes the significance of motion, α is the period of the sine wave which determines the frequency, β is the phase of the sine wave, and k_y0, (0 < k_y0 < π) is the delay time for the phase error. In this study, the values of Δ (from 0 to 20 px, which equals 2.4–2.6 cm depending on the FOV), α (from 0.1 to 5 Hz), β (from 0 to π/4), and k_y0 (from π/10 to π/2) were selected randomly. The period α was determined such that it covered the normal respiratory frequency for adults and elderly adults, which is generally within 0.2–0.7 Hz.²⁸ In addition to the periodic error, random phase error pattern was also used to simulate non-periodic irregular motion as follows. First, the number of phase-encoding lines, which have the phase error, was randomly determined as between 10 and 50% of all phase-encoding lines except at the center region of the k-space (− π/10 < k_y0 ≤ π/10). Then, the significance of the error was determined randomly line-by-line in the same manner as used for the periodic phase error.

Network training

The processing was implemented in MATLAB 2018b (The MathWorks, Inc., Natick, MA, USA) on a workstation running Ubuntu 16.04 LTS (Canonical Ltd., London, UK) with an Intel Xeon CPU E5-2630, 128 GB DDR3 RAM (Intel Corporation, Santa Clara, CA, USA), and an NVIDIA Quadro P5000 graphics card (NVIDIA Corporation, Santa Clara, CA, USA).

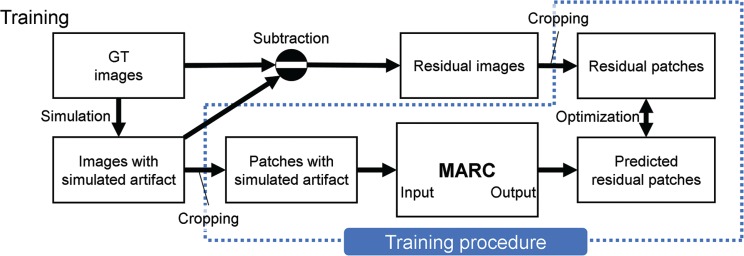
The data processing sequence used in this study is summarized in Fig 3. Training datasets containing patches with simulated artifact and residual components were generated using multi-phase magnitude-only ground truth (GT) images (readout [RO] × phase-encoding [PE] × slice-encoding [SL] × Phase: 320 × 280 × 56 × 7) acquired from 14 patients. For creating the multi-phase slices (320 × 280 × 7) of the images, 127730 patches 48 × 48 × 7 in size were randomly cropped as illustrated in Fig. 4. The resulting patches that contained only background signals were removed from the training datasets. Images with simulated artifact were generated using the reference images, as explained in the previous subsection. The patches with simulated artifact, which were used as inputs to the MARC, were cropped from the images with simulated artifact using the same method as that for the reference patches. Finally, residual patches, which were the output of the network, were generated by subtracting the reference patches from the artifact patches. All patches were normalized by dividing them by the maximum value of the images with simulated artifact.

Fig. 3.

Process diagram of the network training. The datasets for the input and output were generated from the GT images. Images with simulated artifact were calculated using the respiratory motion simulation with the GT images. The residual images were derived from the subtraction of the images with simulated artifact from the GT images. Finally, patches for the input and output were generated by cropping these images. The training was performed using the pair of patches. GT, ground truth; MARC, Motion artifact reduction method based on convolutional neural network.

Fig. 4.

Data processing for the training. The images with simulated artifact were generated from the GT images. Residual images were calculated by subtracting the reference patches from the patches the simulated artifact. A total of 127730 patches were generated by randomly cropping small images from the acquired image. GT, ground truth.

Network training was performed using Keras with TensorFlow backend (Google, Mountain View, CA, USA), and the network was optimized using the Adam algorithm with an initial learning rate of 0.001.²⁹ The optimization was conducted with a mini-batch of 64 patches. A total of 100 epochs with an early-stopping patience of 10 epochs was completed for convergence purposes. The L1 loss function was used as the residual component between the simulated artifact patches and the outputs were assumed to be sparse.

$$\text{Loss}\left(I_{\text{art}},I_{\text{out}}\right)=\frac{1}{N}\sum _i^N{\Vert I_{\text{art}}-I_{\text{out}}\Vert }_1,$$

where I_art represents the patches with simulated artifact, I_out represents the outputs predicted using the MARC, and N is the number of data points. Validation for L1 loss was performed using K-fold cross validation (K = 3).

The N_conv used in the network was determined by maximizing the structural similarity (SSIM) index between the GT and artifact-reduced patches of the validation datasets. Here, the SSIM index is a quality metric used for measuring the similarity between two images, and is defined as follows:

$$\text{SSIM}\left(I_{\text{ref}},I_{\text{den}}\right)=\frac{\left(2{\mu }_{\text{ref}}{\mu }_{\text{den}}+c_1\right)\left(2{\sigma }_{\text{ref},\text{den}}+c_2\right)}{\left({\mu }_{\text{ref}}^2+{\mu }_{\text{den}}^2+c_1\right)\left({\sigma }_{\text{ref}}^2+{\sigma }_{\text{den}}^2+c_2\right)},$$

where, I_ref and I_den are input and artifact-reduced patches, μ is the mean intensity, σ denotes the standard deviation (SD), and c₁ and c₂ are constants. In this study, the values of c₁ and c₂ were as reported by Wang et al.³⁰ The number of patients used for the training versus the L1 loss with 100-epoch training was plotted to investigate the relationship between the size of the training datasets and the training performance. The training datasets with 95359 data were generated from 11 patients, whereas 32371 patches for the validation datasets were obtained from another three patients.

Analysis

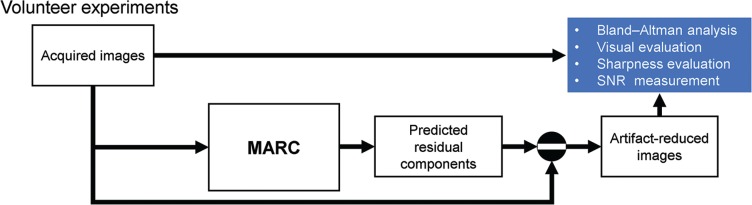
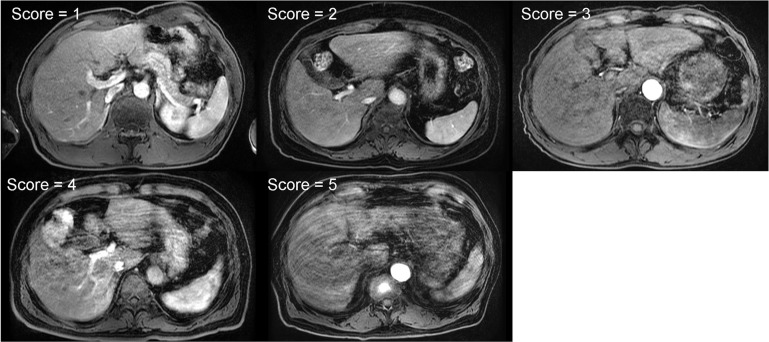
To demonstrate the performance of the MARC in reducing the artifacts in the DCE-MR images acquired during unsuccessful breath-holding, the following experiments were conducted using the data from the 20 patients in the study as shown in Fig. 5. The acquired images were directly inputted to the MARC to generate the predicted residual and artifact-reduced images. The processing using the MARC was performed with an image-wise approach. All the images were normalized using the maximum value of the acquired images for each patient. To identify biases in the intensities and liver-to-aorta contrast between the reference and artifact-reduced images, a Bland–Altman analysis, which plots the differences between the two images versus their average, was used in which the intensities were obtained from the central slice in each phase. The Bland–Altman analysis for the intensities was conducted in the subgroups of high (mean intensity ≥ 0.46) and low (mean intensity < 0.46) intensities. For convenience, half of the maximum mean intensity (0.46) was used as the threshold. The mean signal intensities of the liver and aorta were measured by manually marking the ROI on the MR images, and the ROI of the right lobe of the liver was carefully placed to exclude vessels. The same ROIs were applied to all other phases of the images. The quality of images before and after applying the MARC were visually evaluated by two radiologists (readers A and B) with 11 and 3 years of experience in abdominal radiology, respectively, who were unaware of whether each image was generated before or after the MARC was applied. The radiologist evaluated the images using a five-point scale based on the significance of the artifacts (1 = no artifact; 2 = mild artifacts; 3 = moderate artifacts; 4 = severe artifacts; 5 = non-diagnostic), as shown in Fig. 6. The evaluation was performed phase-by-phase for the 20 patients and resulted in 140 samples. To evaluate the improvement in the scores after using the MARC, the cases with artifact scores of >1 for the acquired images were analyzed statistically using the Wilcoxon signed rank test. As a result, 37 samples were excluded. The readers evaluated the images twice (A1, A2, B1 and B2) in a randomized order with a week’s interval between the two evaluations. Inter- and intra-observer agreements were calculated by Cohen’s kappa statistics with 95% confidence intervals. The calculation for the intra-observer agreement was performed based on A1 versus A2 and B1 versus B2. The inter-observer agreement was calculated separately for the first and second evaluations. Kappa <0.20 was regarded as indicating poor; 0.21–0.40 fair; 0.41–0.60, moderate; and >0.60, good agreement in this study. To confirm the validity of the anatomical structure after applying the MARC, the artifact-reduced images in the arterial phase were compared with those without the motion artifact, which were obtained from separate MR examinations performed 71 days apart in the same patients. The same sequence and imaging parameters were used for the acquisition. To evaluate the sharpness of the images, full width at half maximum (FWHM) of the line spread function (LSF)³¹ were compared between the acquired and artifact-reduced images. The LSF derived from the edge response roughly characterizes the spatial resolution of the images. The edge response was obtained by fitting the one-dimensional profile measured across the liver to the hepatic vein with the error function expressed as below.

$$\begin{array}{c}\text{ERF}(x^{\prime })=\frac{2}{\sqrt{\pi }}\underset{0}{\overset{x^{\prime }}{\int }}{e}^{-t^2}dt\\ x^{\prime }=\frac{x-x_0}{\sigma }\end{array},$$ (1)

where x is the spatial position of the profile, x₀ is the edge position, and σ denotes the SD for the error function. Then, the LSF can be defined as the deviation of the error function.

$$\text{LSF}=\frac{d}{dx}\text{ERF}(x^{\prime })=\frac{2}{\sqrt{\pi }}{e}^{-x^2}$$ (2)

Finally, the FWHM can be calculated as below.

$$\text{FWHM}=2\sqrt{2\text{ln}2\sigma }$$ (3)

Fig. 5.

Process diagram of volunteer experiments using volunteers. Bland–Altman analysis, visual evaluation, sharpness evaluation, and signal-to-noise ratio (SNR) measurement were performed for the artifact and the artifact-reduced images. The artifact-reduced images were the subtraction of the predicted residual components from the acquired images. Sharpness of the images was quantified using the line spread function approach. MARC, Motion artifact reduction method based on convolutional neural network.

Fig. 6.

Example images for five-point scale grading based on the significance of the artifacts (1 = no artifact; 2 = mild artifacts; 3 = moderate artifacts; 4 = severe artifacts; 5 = non-diagnostic).

The profiles with length of 20 px were extracted manually from the acquired images. The signal intensity of the profiles was normalized to the range [−1, 1]. The fitting was implemented using the non-linear least-squares method to determine the parameters of x₀ and σ. The squared norm of the residual <0.1 was considered as the convergence criterion because the LSF approach is sensitive to signal-to-noise ratios of the profiles. The profiles that did not meet the criterion were excluded from the analysis. The range for σ was limited from 0 to 25 px to prevent divergence of the parameters. Signal-to-noise ratios of the artifact and the artifact-reduced images were measured. The ROIs for the measurement were placed on the right lobe. The signal-to-noise ratios (SNRs) were calculated by dividing the signal intensities by the SDs of the same ROIs. The measured values of the FWHM and SNR were analyzed using the paired t-test.

Results

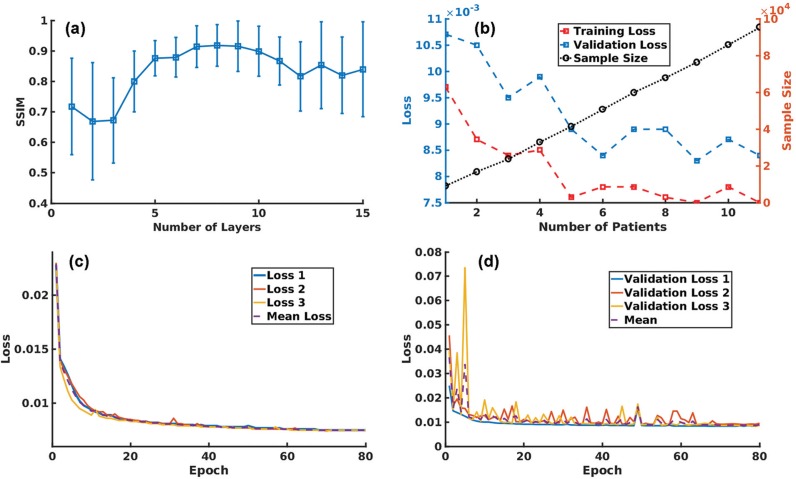
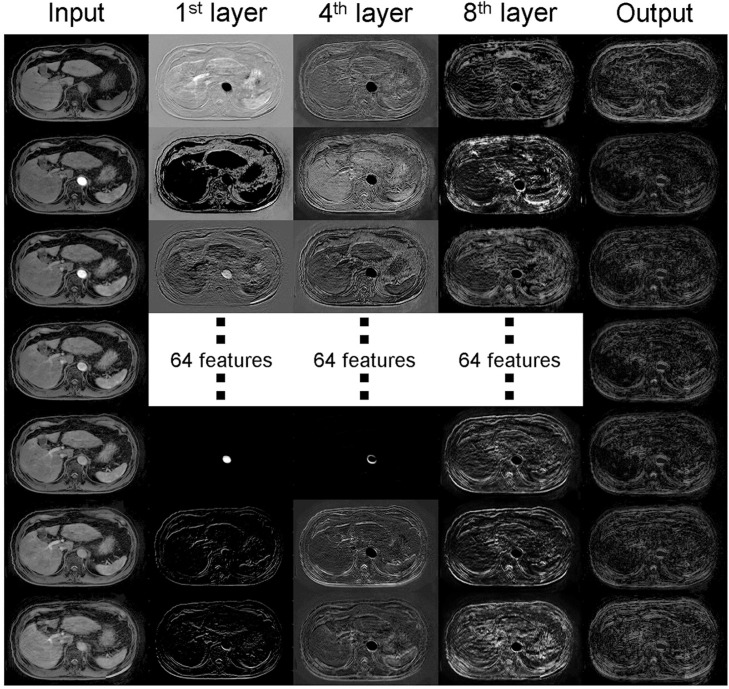
The changes in the mean and SD (μ) of the SSIM index between the reference and artifact-reduced images are plotted against N_conv in Fig. 7a, and the results show that the network with N_conv of >4 exhibited a better SSIM index, whereas networks with N_conv <4 had a poor SSIM index. In this study, an N_conv of seven was adopted in the experiments as this value maximized the SSIM index (mean: 0.91, μ: 0.07). Figure 7b shows the number of patients used for the training versus the training and validation losses, and the sample size. The results implied that stable convergence was achieved when the sample size was three or more although the training with few patients gave inappropriate convergence. The training was successfully terminated by early stopping in 70 epochs, as shown in Fig. 7c and 7d. The features using the trained network extracted from the 1st, 4th, and 8th intermediate layers corresponding to specific input and output are shown in Fig. 8. Higher frequency ghosting-like patterns were extracted from the input in the 8th layer.

Fig. 7.

(a) SSIM changes depending on the number of layers (N_conv). The highest SSIM (0.91) was obtained with N_conv of 7. (b) Validation loss, training loss, and sample size were plotted against the number of patients. Smaller loss was observed as the sample size and number of patients increased. (c and d) The L1 loss decreased in both the (c) training and (d) validation datasets as the number of epochs increased. The training was implemented three times to perform K-fold validation with K = 3. No further decrease was visually observed after 70 epochs. The training was terminated by early stopping in 80 epochs. Error bars on the validation loss represent the standard deviation for K-fold cross validation. SSIM, structural similarity.

Fig. 8.

Features extracted from the 1st, 4th, and 8th layers of the developed network corresponding to specific input and output. Low- and high-frequency components were observed in the lower layers. On the other hands, an artifact-like pattern was extracted from the higher layer.

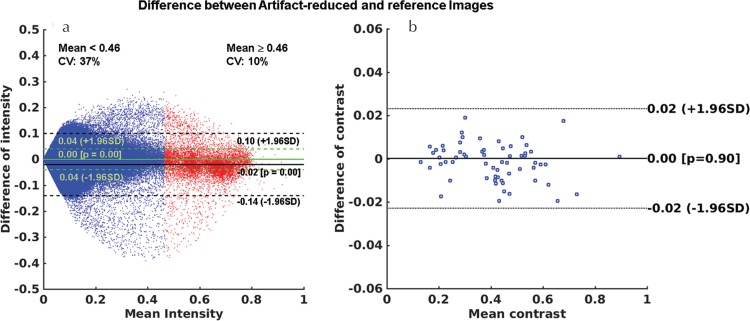
Figure 9a and 9b show the Bland–Altman plots of the intensities and liver-to-aorta contrast ratios between the reference and artifact-reduced images. The differences in the intensities between the two images (mean difference = 0.04 (95% confidence interval [CI], −0.04 to 0.04) for mean intensity <0.46 and mean difference = −0.02 (95% CI, −0.14 to 0.10) for mean intensity ≥0.46) were heterogeneously distributed, depending on the mean intensity. The intensities of the artifact-reduced images were lower than that of the references by 15% on average, which can be seen in the high signal intensity areas shown in Fig. 9a. A Bland–Altman plot of the liver-to-aorta contrast ratio (Fig. 9b) showed no systematic errors in contrast between the two images.

Fig. 9.

Bland–Altman plots for (a) the intensities and (b) the liver-to-aorta contrast ratio between the reference and artifact-reduced images in the validation dataset. The mean difference in the intensities was 0.00 (95% CI, −0.04 to 0.04) in the areas corresponding to mean intensity of <0.46 and −0.02 (95% CI, −0.14 to 0.10) in the parts with mean intensity of ≥0.46. Mean difference in the contrast ratio was 0.00 (95% CI, −0.02 to 0.02). These results indicated that there were no systematic errors in the contrast ratios, whereas the intensities of the artifact-reduced images were lower than that of the reference images owing to the effect of artifact reduction, especially in the area with high signal intensities. CI, confidence interval; CV, coefficient of variation.

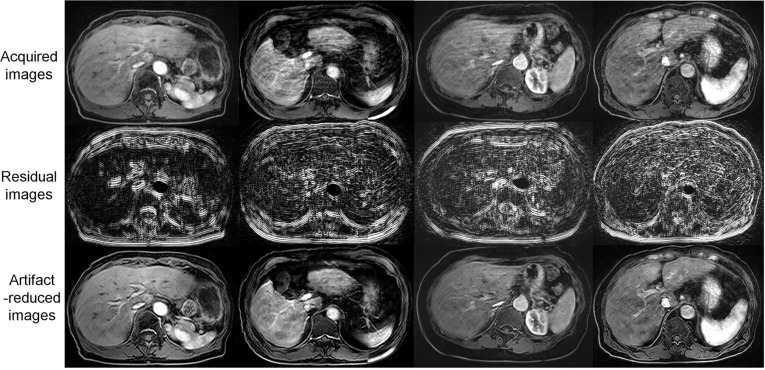
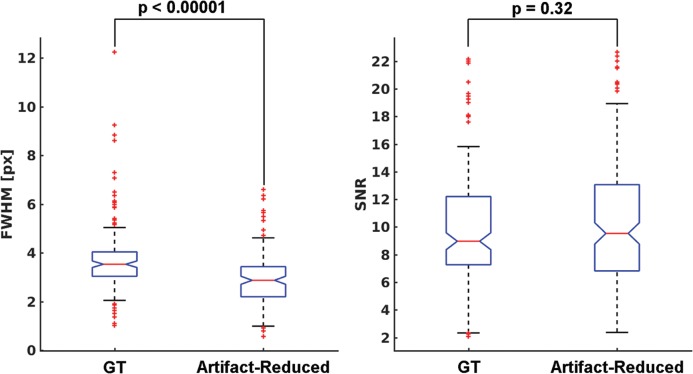
As shown in Table 1, the image quality of the artifact-reduced images [mean (SD) score = 3.14–3.23] was significantly better (P < 0.05) than that of the acquired images [mean (SD) score = 2.59–2.86] in the evaluations by all readers because respiratory motion-related artifacts (Fig. 10 top row) were reduced by applying MARC (Fig. 10 bottom row). The middle row in Fig. 10 shows the extracted residual components for the input images. The MARC caused no significant change in image quality in the case of score of 1. The inter- and intra-observer agreements are shown in Table 2. Intra-observer reliability was good for all readers. The inter-observer agreements were good or moderate. FWHMs and SNRs of the acquired and artifact-reduced images are shown in Fig. 11. There was no significant difference in the SNR, whereas the image sharpness was improved significantly after applying the MARC.

Table 1.

Mean scores of the artifact for the acquired and artifact-reduced images.

	A1	A2	B1	B2
Acquired	3.23	3.22	3.14	3.15
Artifact-reduced	2.86	2.85	2.59	2.62
	P = 0.0250	P = 0.0230	P = 0.0012	P = 0.0020

The evaluation was performed twice by each of the two radiologists (A1, A2, B1 and B2) in randomized-order

Fig. 10.

Examples of artifact reduction with MARC for patient data from the datasets that were not used for the training or validation. The motion artifacts in the images (upper row) were reduced (lower row) using the MARC. The residual components are shown in the middle row. MARC, Motion artifact reduction method based on convolutional neural network.

Table 2.

Intra- and inter-observer reliability of the visual evaluation.

	Acquired	Artifact-reduced
Intra-observer	Kappa [95% CI]	Kappa [95% CI]
Reader A	0.75 [0.66–0.84]	0.77 [0.70–0.86]
Reader B	0.95 [0.91–0.99]	0.93 [0.87–0.97]
Inter-observer
A1 versus B1	0.68 [0.59–0.78]	0.80 [0.72–0.88]
A2 versus B2	0.59 [0.48–0.69]	0.65 [0.55–0.74]

The analyses were performed using Cohen’s kappa statistics with 95% confidence intervals. CI, confidence interval.

Fig. 11.

FWHMs and SNRs of the images with and without the MARC. The FWHM was derived from the line spread function which was estimated from the one-dimensional profile across the liver to the hepatic vein. SNR was calculated by placing ROIs on the right robe. FWHM of the artifact-reduced images was significantly reduced compared with that of the images without the application of MARC. There was no significant difference in SNR between the images with and without the application of MARC. FWHM, full width at half maximum; MARC, Motion artifact reduction method based on convolutional neural network; SNR, signal-to-noise ratio.

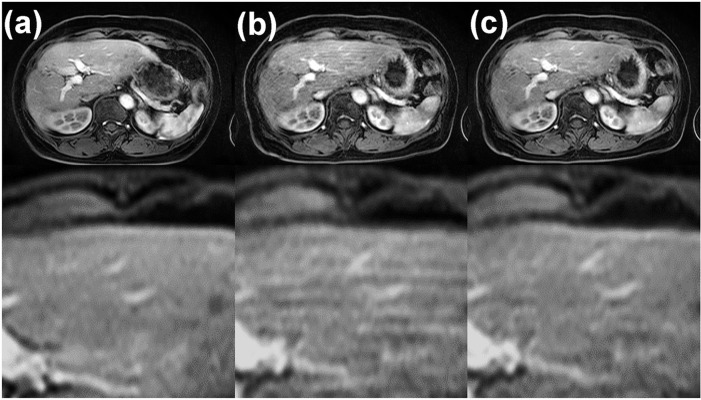
The images with and without breath-hold failure are shown in Fig. 12a and 12b. The motion artifact in Fig. 12b was partially reduced using MARC, as shown in Fig. 12c. This result indicated that there was no loss of critical anatomical details, and no additional blurring was observed although moderate artifact on the right lobe remained.

Fig. 12.

Gadoxetic acid-enhanced arterial phase MR images obtained in two separate examinations. (a) The arterial phase image acquired in the first examination, in which the patient succeeded in holding the breath. (b) The arterial phase image acquired in another examination 1 month later, in which the patient failed to hold the breath. (c) The artifact-reduced image of (b). These images were acquired with the same imaging parameters.

Discussion

In this paper, an algorithm to reduce the number of motion-related artifacts after data acquisition was developed using a deep convolutional network, and was then used to extract artifacts from local multi-channel patch images. The network was trained using reference MR images acquired with appropriate breath-holding, and noisy images were generated by adding phase error to the reference images. The number of convolution layers in the network was semi-optimized in the simulation. Once trained, the network was applied to MR images of patients who failed to hold their breath during the data acquisition. The results of the experimental studies demonstrate that the MARC successfully extracted the residual components of the images and reduced the amount of motion artifacts and blurring without affecting the contrast and SNR of the images. However, further research is required to verify the accuracy of quantitative imaging after applying the MARC. No study has ever attempted to demonstrate blind artifact reduction in abdominal imaging, although many motion correction algorithms with navigator echoes or respiratory signal have been proposed.^8,32,33 In these approaches, additional RF pulses and/or longer scan time are required to fill the k-space signal whereas MARC enables motion reduction without sequence modification or additional scan time. The processing time for one slice was 4 ms, resulting in approximately 650 ms for processing all slices of one patient. This computational cost is acceptable for practical clinical use compared with previous studies using retrospective approaches.^34–36 Although the processing was implemented off-line with the workstation used for the training, the algorithm can be executed on the reconstruction machine of the scanner.

In the MRI of the liver, DCE-MRI is mandatory to identify hypervascular lesions, including hepatocellular carcinoma,^37,38 and to distinguish malignant from benign lesions. At present, almost all DCE-MR images of the liver are acquired with a 3D gradient echo sequence owing to its high spatial resolution and fast acquisition time within a single breath-hold. Despite recent advances in imaging techniques that improve the image quality,^39,40 it remains difficult to acquire uniformly high quality DCE-MRI images without respiratory motion-related artifacts. In terms of reducing motion artifacts, the unpredictability of a patient’s breath-holding ability is the biggest challenge to overcome, as the patients who will fail to hold their breath are not known in advance. One advantage of the proposed MARC algorithm is that it is able to reduce the magnitude of artifacts in images that have been already acquired, which will have a significant impact on the efficacy of clinical MR.

In this study, an optimal N_conv of seven was selected based on the SSIM indexes of the reference image and the artifact-reduced image after applying MARC. The low SSIM index observed for small values of N_conv was thought to be due to the difficulty in modeling the features of the input datasets with only a small number of layers. On the other hand, a slight decrease in the SSIM index was observed for N_conv of >12. This result implies that overfitting of the network occurred using too many layers. To overcome this problem, a larger number of learning datasets and/or regularization and optimization of a more complicated network will be required.

Several other network architectures have been proposed for the denoising of MRI images. For example, U-Net,⁴¹ which consists of upsampling and downsampling layers with skipped connections, is a widely used fully convolutional network for the segmentation,⁴² reconstruction, and denoising⁴³ of medical images. This architecture, which was originally designed for biomedical image segmentation, uses multi-resolution features instead of a max-pooling approach to implement segmentation with high localization accuracy. Most of the artifacts observed in MR images, such as motion, aliasing, or streak artifacts, are distributed globally in the image domain because the noise and errors usually contaminate the k-space domain. It is known that because U-Net using the whole image has a large receptive field, these artifacts can be effectively removed using global structural information. Generative Adversarial Networks (GANs),⁴⁴ which are comprised of two networks, called the generator and discriminator, are another promising approach for denoising MR images. Yang et al.¹⁶ proposed a network to remove aliasing artifacts in compressed sensing MRI using a GAN-based network with a U-Net generator. We used patched images instead of a full-size image because of the difficulty in implementing appropriate training with limited number of datasets as well as owing to computational limitation. However, we believe this approach is reasonable because the pattern of artifact due to respiratory motion looks similar in every patch, even though the respiratory artifact is distributed globally. Although it should be studied further in the future, we consider that MARC from the patched image can be generalized to a full-size image from our results. Recently, the AUtomated TransfOrm by Manifold APproximation (AUTOMAP) method, which uses full connection and convolution layers, was proposed for MRI reconstruction.⁴⁵ The AUTOMAP method directly transforms the domain from the k-space to the image space, and thus enables highly flexible reconstruction for arbitrary k-space trajectories. Three-dimensional convolutional neural networks (CNNs) which are network architectures for 3D images,^46,47 are also a promising method. However, these networks require large number of parameters, huge memory on GPUs and host computers, and long computational time for training and hyperparameter tuning. Therefore, it is still challenging to apply these approaches in practical applications. These network architectures may be combined to achieve more spatial and temporal resolution. It is anticipated that further studies will be conducted on the use of deep learning strategies in MRI.

Limitations

The limitations of this study are as follows. First, clinical significance was not fully assessed. Although the image quality appeared to improve in almost all cases, it will be necessary to confirm that no anatomical/pathological details were removed by MARC before this approach can be clinically applied. Second, simple centric acquisition ordering was assumed when generating the training datasets, which means that MARC can only be applied to a limited sequence. Additional training will be necessary before MARC can be generalized to more pulse sequences and vendors because the appearance of artifact depends on the sequence and its parameters such as TR, TE, and acquisition order. Because it is difficult to obtain pairs of images with and without artifacts to train the filter, we used simulation-based images as the images with artifact. There was a concern whether the training was appropriate to reduce the artifact in the real MR images. Fortunately, the results indicated that our approach worked even with images obtained from real patients, although the simulation model used in this study assumed simple rigid motion of the body. Therefore, realistic simulation including non-rigid and 3D motion can offer further improvement of our algorithm because it could be challenging to remove artifact induced by a complicated situation. Dataset generation based on numerical phantoms could be a promising solution.^48,49 Wissmann et al.^48,49 proposed a simulation with deformable and four-dimensional motion model for cardiac imaging. More practical artifact simulation can be achieved by utilizing these approaches although the computation cost to generate datasets of large size may be high. Moreover, the artifact was simulated in the k-space data generated from images for clinical use. Simulation with the original k-space data may offer different results. We need further researches to reveal which approach would be appropriate for artifact simulation. The proposed filter was trained with the datasets of patients who were referred for an MRI for the purpose of hepatocellular carcinoma (HCC) screening. Because the background liver of these patients is typically cirrhotic, the filter may not be applicable to a liver without chronic liver disease. To show the clinical usefulness, investigation of lesion detectability will be required as a future study.

The research on diagnostic performance using deep learning-based filters has not been performed sufficiently in spite of considerable effort spent for the development of algorithms. Our approach can provide additional structures and texture to the input images using the information learned from the trained datasets. Further research on diagnostic performance will be required to prove the clinical validity.

Conclusion

In this study, a deep learning-based network was developed to remove motion artifacts in DCE-MRI images. The results of the experiments showed that the proposed network effectively removed the motion artifacts from the images. These results indicate that the deep learning-based network has the potential to also remove unpredictable motion artifacts from images.