Cost-Effectiveness Analysis and Decision Modelling: A Tutorial for Clinicians

Abstract

Cost-effectiveness analysis (CEA) provides information on how much extra do we need to spend per unit gain in health outcomes with introduction of any new healthcare intervention or treatment as compared to the alternative. This information is crucial to make decision regarding funding any new drug, diagnostic test or determining standard treatment protocol. It becomes even more important to consider this evidence in resource constrained low-income and middle-income country settings. Generating evidence on costs and consequences of a treatment or intervention could be performed in the setting of a randomized controlled trial, which is the perfect platform to evaluate efficacy or effectiveness. However, we argue that randomized controlled trial (RCT) offers an incomplete setting to generate comprehensive data on all costs and consequences for the purpose of a CEA. Hence, it is needed to use a decision model, either in combination with the evidence from RCT or alone. In this article, we demonstrate the application of decision model–based economic evaluation using 2 separate techniques – a decision tree and a Markov model. We argue that application of a decision model allows computation of health benefits in terms of utility-based measure such as a quality-adjusted life year or disability-adjusted life year which is preferred for a CEA, measure distal costs and consequences which are much more downstream to the application of intervention, allows comparison with multiple intervention and comparators, and provides opportunity of making use of evidence from multiple sources rather than a single RCT which may have limited generalizability. This makes the use of such evidence much more acceptable for clinical use and policy relevant.

Economic Evaluation (EE) or cost-effectiveness analysis (CEA) is one of the important aspects of a health technology assessment. Classically, CEA is defined as a comparative assessment of two or more interventions, in terms of their costs and consequences.¹ As the definition suggests, any CEA would comprise two measurements – costs and consequences, which has to be carried out for both the intervention and the comparator/s. Ultimately, it generates the evidence that how much extra do we need to spend per unit gain in health outcomes with introduction of any new healthcare intervention or treatment as compared with the alternative. In the entire process, the key factor which determines the quality of a CEA is how comprehensive are the methods to measure both costs and consequences and is the valuation standardized across interventions. In other words, do we measure all the important costs and consequences which accrue as a result of a given intervention? Consequently, such an assessment can be performed alongside any epidemiological or clinical study which is being used to measure the effectiveness or efficacy, if we also piggy-back measurement of costs alongside. However, an epidemiological study may not be able to measure all costs and consequences comprehensively, in a manner which may be considered appropriate for a CEA. This leads to the need for decision modelling.

Section 1 of this article describes the limitations of undertaking CEA alongside a clinical trial which necessitates use of a decision model. Subsequently, in section 2, we describe how a decision model is able to bridge the limitations of an epidemiological or clinical study in undertaking CEA. We also introduce the 2 types of decision models which are used for CEA, i.e., the decision tree and Markov model. Section 3 uses an illustration of each of the two types of decision models for explanation. A hypothetical example of implementation of special newborn care units (SNCUs) at district hospitals to treat sick newborns is used to explain a decision tree. Similarly, a published CEA of use of sorafenib – drug used for treatment of hepatocellular carcinoma (HCC) is used to explain the Markov model. Finally, we conclude on what caution should be exercised by the clinicians while undertaking a CEA.

Can Randomized Controlled Trial Alone be Used to do an Economic Evaluation?

As introduced previously, the measurement of costs and consequences in a CEA can be undertaken alongside an epidemiological or clinical study. Classically, a randomized controlled trial (RCT) is considered the epidemiological design with highest degree of rigour for internal validity, hence the word RCT will be used as a proxy for an epidemiological study.

An RCT is generally carried out to evaluate the clinical efficacy of a drug, device, treatment or healthcare intervention (Table 1). If alongside the measurement of the health consequences, which is used to measure efficacy, data on cost of delivering the intervention and comparator is also collected, this information can then be synthesized to produce the results for CEA. This appears to be a very good approach for undertaking CEA, as there are numerous RCTs carried out to assess clinical efficacy, and all it needs is an additional data collection for cost of care. However, there are several limitations to using an RCT for doing CEA.

Table 1.

Differences in the Approach of Randomized Controlled Trial and Economic Evaluation.

Characteristic	Approaches for undertaking economic evaluation
	RCT	Decision model
Focus of assessment	Internal validity	External validity
Time horizon	Usually short – enough to estimate proximal clinical endpoints	Usually long – to comprehensively estimate downstream costs and consequences
Measure of outcome	Usually proximal clinical endpoint, eg. reduction in blood pressure	Utility-based measure such as quality-adjusted life year (QALY)
Number of comparators	Limited	No limitation

RCT: randomized controlled trial, QALY: quality-adjusted life year.

First, the focus of RCT is to determine the clinical efficacy. In view of this objective, careful selection criteria are applied to recruit subjects and the interventions are delivered in the most optimal manner. Although this may be perfectly justifiable to produce results which have high internal validity, there may be some limitation to generalizability. For example, a trial performed to evaluate the vaccine efficacy ensured that all the kids who were immunized were previously healthy, vaccine was potent and injected in the recommended manner in correct dose and route of administration. However, in reality, when immunization is introduced in a public health program setting, not all children may be vaccinated. Similarly, there may be breakdowns of cold chain leading to lowered potency of vaccine, and some babies may be given vaccine using suboptimal dose or incorrect route. Hence, the effectiveness may be lower than the efficacy reported in RCT. For a CEA which is dealing with a policy question of whether to introduce the vaccine in national immunization schedule, the data on pragmatic real-world effectiveness is more useful than efficacy.

Second, several trials may be carried out for determining clinical effectiveness in terms of outcomes which may be perfectly rational to a particular health condition but may not solve the needs for a CEA. For example, an RCT for determining clinical effectiveness of new antihypertensive drug compared with the existing treatment measured its effectiveness in terms of reduction in blood pressure. However, the appropriate outcome measure which is recommended for a CEA is a generic utility-based measure such as quality-adjusted life year (QALY) or disability-adjusted life year (DALY). Use of such utility-based outcome measures allows comparison of efficiency across a range of different types of interventions applicable for different diseases in different types of patient population. This makes evidence useful for policymaking at a macro level. Hence again, RCT falls short of providing solution for CEA.

Third, on grounds of feasibility, most of the trials are run for short periods which is appropriate enough to demonstrate clinical effectiveness. However, a CEA aims at measuring all the costs and consequences which are a result of the intervention. For example, a clinical trial which may be carried out for a hemophilus influenza type ‘b’ (Hib) vaccine (given to children at 6,10 and 14 weeks of age) which offers protection against pneumonia and meningitis due to the said organism, measured the episodes of Hib disease among vaccinated and unvaccinated cohorts during a 1-year period after vaccine administration. Although this may be sufficient for measuring the vaccine efficacy, however, the protection against Hib disease continues as long as child is susceptible, which is generally about 5 years, and to a lesser degree as long as 15 years.² Hence there is a reduction of disease episodes much longer than the trial period. So, although a trial in this case may measure all costs accurately – as all costs related to vaccination are incurred in year 1, it underestimates the overall downstream health benefits as well as cost savings (due to decrease in treatment costs). To overcome this problem of measuring benefits, RCTs will need to be extended till the time intervention continues to be beneficial, so that all costs and consequences are valued credibly. However, this can sometime become unfeasible because of constraints of funding a long-term RCT. This may become even more difficult when the effects of an intervention are much more distant in time, since the application of intervention. For example, in case of a preventive intervention such as vaccine for human papillomavirus (HPV) to protect against cervical cancer among women, although the vaccination is recommended to be carried out around the age of 10–12 years, reduction in the cancer cases continues to happen as late as 60 or 70 years or even later.³ And it may not be feasible to have resources to follow-up a trial cohort for a lifetime. Hence, RCTs may not offer the medium to generate data for CEA.

Fourth, a trial is generally conducted to evaluate a few alternative options for treatment or addressing a particular health problem. However, decision-making in the field of policy is full of possible scenarios which need to be evaluated for potential implementation. For example, a single question of which is the most appropriate way to screen women for cervical cancer can be further stratified into several scenarios based on which method should be used (pap smear, visual inspection with acetic acid or HPV DNA), which population should be screened (30–65 years, 40–65 years and 50–65 years), how frequently (annual, 3 yearly, 5 yearly, 10 yearly, once in a lifetime). Together these can constitute 16 possible scenarios. However, it may be difficult to have a single RCT with 16 arms to evaluate all possible scenarios. In view of this limitation again, RCT alone cannot be used to generate evidence for CEA.

Bridging the Limitations of RCT: Role for Decision Modelling

A solution to bridge the limitations of RCT is to either undertake decision modelling alone, or use decision model alongside the evidence generated in RCT. A decision model used for CEA is a biologically plausible sequence of occurrence of health consequences as a result of the decision of undertaking an intervention. The model so prepared does not only shows relationships but also mathematically quantifies the probability of occurrence of such a health consequence or outcome as a result of an intervention. In the mathematical parameterization of a decision model, the researcher can use pragmatic data on effectiveness from a real-word study rather than an RCT. Alternatively, an assumption which justifies the constraints of program implementation or treatment administration in real-world could be incorporated to generate an output which is more acceptable. For example, one may consider findings of a national evaluation which shows that the coverage of routine immunization is not likely to be more than 90% in the best possible scenario, and hence the efficacy of treatment derived from RCT could be modelled on only 90% of the intervention cohort to generate the health consequences. Similarly, data from a universal treatment program of HCV treatment could be used to determine sustained virological response, rather than efficacy data from trial.

Second, the evidence from a 1-year trial of antihypertensive drug on reduction in blood pressure could then be used along with evidence from other studies for effect of lowering blood pressure on long-term consequences such as coronary artery disease (CAD) or mortality or quality of life, to model long-term consequences of the antihypertensive drug on survival, life years and QALY.

The third limitation of an RCT was its inability to have a longer time horizon to capture all cost consequences satisfactorily. A decision model can use a lifetime study horizon to capture all costs and consequences which can accrue as a result of the intervention. Having said that, however, it does not mean that this can be generated without a previous evidence. Hence, a model synthesizes evidence from various inputs to predict long-term costs and consequences. Finally, a model construction is not limited in terms of the number of scenarios which it can potentially evaluate. Thus, it overcomes the last limitation of an RCT by enabling comparison with several possible treatment or program interventions to deal with a given health problem.

Two most commonly used decision models in CEA are a decision tree and a Markov model. Classically, a decision tree is a unidirectional flow of events which begins with the decision of giving an intervention or not. This is followed by occurrence of different sequence of outcomes which may continue to happen with a given probability or chance at each step in a unidirectional way. The tree ultimately ends with a terminal event in which individual may return to full health or may die. The major limitation of a decision tree is its unidirectional flow. This may be suitable for acute disease conditions which follow a particular course because their onset and the patient may either recover completely and live or may live with some long-term sequelae or may die.

However, this may not be the case with chronic noncommunicable diseases. For example, a patient diagnosed with hypertension may not necessarily remain hypertensive all his life. He may recover back to be normotensive with treatment or may progress to a worse off health state such as CAD. Modelling such chronic diseases requires application of a Markov model which differs from a decision tree in allowing transition from any one health state to any other health state, which is biologically plausible as per the scientific understanding of disease course.

The subsequent sections illustrate the use of a decision tree and a Markov model for better understanding.

Decision Model 1: Decision Tree

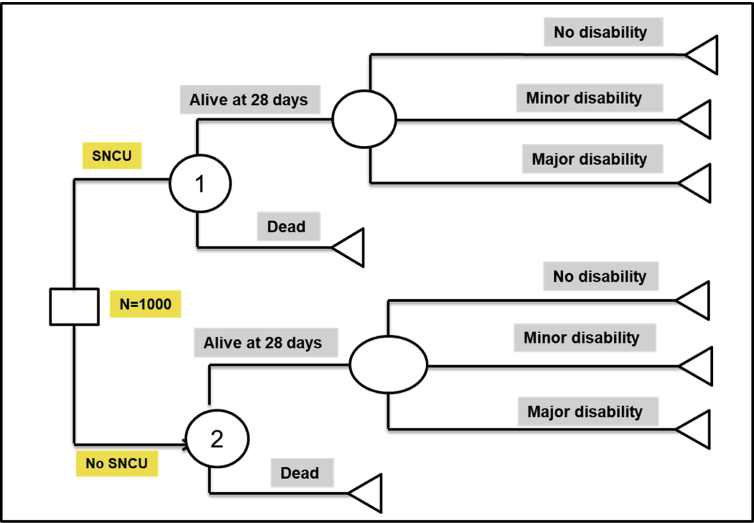
Let us consider a policy choice between whether to construct a SNCU – a level II intensive care unit, at the level of district hospitals and continue routine care through existing paediatric services. The following hypothetical example illustrates estimation of incremental cost per QALY gained with implementation of a strategy to create SNCU at the level of district hospitals, against a comparator of routine management of sick newborns in these hospitals. A decision tree was constructed for comparing these 2 policy options as shown in Figure 1.

Figure 1.

Decision tree structure to evaluate the cost-effectiveness of treatment of sick newborns in special newborn care units versus routine paediatric care. *SNCU: Sick newborn care unit.

The square box on the extreme left represent a decision node – i.e. whether or not to build an SNCU. Subsequently, it was assumed that the sick newborns could be treated in either of the 2 scenarios, either SNCU or routine paediatric care services. Each of the round circles represents a chance node, where there is a probability of either of the subsequent events. For example, it was assumed that the sick newborns after treatment in either SNCU or based on routine management as per standard practice could either die or remain alive within 28 days of birth. If the newborn dies within 28 days, it signifies the end of outcome or event and is represented by a terminal node (triangle). However, if sick newborn remains alive till 28 days of birth, there is again a probability that the baby may become fully cured with no disability, or may develop minor disability, or develops a major disability and continue to live in that health state. This course of events is similar in both the scenarios. Further, there is a cost of alternative courses of actions, which include treatment in SCNU or routine care, which is summarized in Table 2. Furthermore, table 2 shows each of these probabilities at different chance nodes, quality of life for each state, average life expectancy and cost of being in each state. This hypothetical data in a typical model-based CEA is sourced from either a single or multiple clinical studies or a meta-analysis based on systematic review.

Table 2.

Parameter Values for Decision Tree.

Parameter	Parameter definition	Hypothetical values
Transition Probabilities	Probability of dying after treatment in sick newborn care unit	0.3
	Probability of dying after treatment based on current practice	0.6
	Probability of developing minor disability after treatment in sick newborn care unit	0.43
	Probability of developing major disability after treatment in sick newborn care unit	0.29
	Probability of developing minor disability after treatment based on current practice	0.25
	Probability of developing major disability after treatment based on current practice	0.5
Cost parameters (in Indian Rupees)	Cost of treating a newborn in sick newborn care unit who develops no disability	818
	Cost of treating a newborn in sick newborn care unit who develops minor disability	1024
	Cost of treating a newborn in sick newborn care unit who develops major disability	1200
	Cost of treating a newborn (who develops no disability) based on current practice	1000
	Cost of treating a newborn (who develops minor disability) based on current practice	1100
	Cost of treating a newborn (who develops major disability) based on current practice	1400
Quality of life	With no disability	1
	With minor disability	0.7
	With major disability	0.4
Life expectancy (in years)	With no disability	64
	With minor disability	60
	With major disability	55

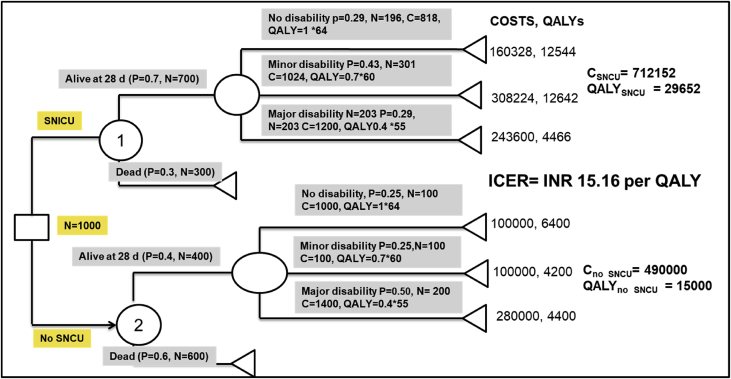
In this hypothetical example, it is assumed that 1000 sick newborns with less than 1800 gms birth weight were treated with either of the competing treatment practice. Assigning all the probabilities and costs to each of the arms in the decision tree, total cost of treating 1000 newborns with each of the treatment strategy is shown in Figure 2. Multiplying the number of newborns treated with probability of a given outcome, life expectancy of that outcome, and quality of life of that outcome provides an estimate of total number of QALYS for that outcome branch. Similarly, QALYs via all outcome possibilities (alive, minor disability and major disability) were summated to derive the total QALYs for 1000 sick newborns with either of the two policy options or treatment choices. The cost of each outcome branch was estimated using the number of newborns in that branch and the unit cost. Finally, it was observed that treating 1000 babies in SNCU resulted in a gain of 14,652 more QALYs at an additional cost of INR 222,152 as compared with routine management (absence of SNCU). This implies that creation of SNCU will incur an incremental cost of INR 15.16 per QALY gained. Compared with the threshold for considering cost-effective, the incremental cost per QALY gained for treating babies in SNCU is very cost-effective in Indian context and hence should be chosen as the treatment option.

Figure 2.

Solved Decision tree analysis to evaluate the cost-effectiveness of treatment of sick newborns in special newborn care units versus routine paediatric care. *SNCU, Sick newborn care unit; QALYs, Quality-adjusted life years; ICER, Incremental cost-effectiveness ratio; P, Probability; C, Cost; N, Number of sick newborn.

Decision Model 2: Markov Model

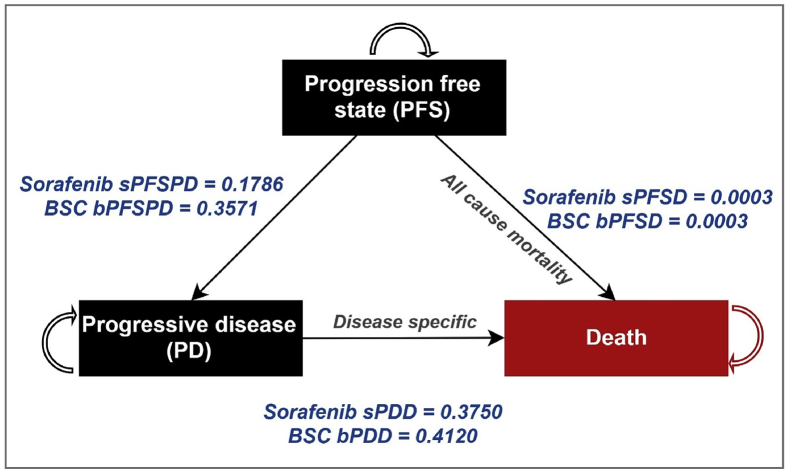
In this, we use an example of a CEA which was used to evaluate sorafenib – a drug used to treat HCC.⁴ HCC is the primary malignant neoplasm of the liver. Majority (70%) cases of HCC in India present at advanced stage (Barcelona Clinic Liver Cancer [BCLC] stage C and D) in which curative resection is not possible. For these unresectable, advanced HCC cases with extrahepatic spread or vascular invasion, treatment options are limited. Targeted molecular therapy – sorafenib, is indicated for such patients with advanced BCLC stage C and HCC. Sorafenib has been reported to have an increased median overall survival and time to progression in advanced HCC as compared with best supportive care (BSC). The alternative to giving sorafenib is BSC which comprises standard routine care and management of complications. Sorafenib and BSC arms are considered as intervention and control, respectively. To model life-term costs and consequences, patients are segregated into two alive health transition states termed as progression-free state (PFS) and progressive disease (PD) in intervention and control arm, respectively. As shown in Figure 3, patients with HCC diagnosed in PFS health state can advance to PD or death from all-cause mortality health states. Death from HCC happens from PD health state only. Figure 3 is next converted to Table 3, Table 4 which shows a transition matrices which represents the probability of moving from each health state to the next state in sorafenib and BSC arm, respectively.

Figure 3.

Markov model to evaluate the cost-effectiveness of sorafenib for treatment of hepatocellular carcinoma.

Table 3.

Markov Transition Matrix for Sorafenib Arm.

Table 4.

A Schematic to Illustrate the Mathematical Computation of Markov Trace in Excel.

Sorafenib (Intervention) arm – How to implement in excel
	A	B	C	D	E	F
1	Cycle	PFS	PD	Death from disease	All-cause mortality	Check
2	1	1000	0	0	0	=Sum (B2:E2)
3	2	=B2*(1-sPFSPD-sPFSD)	=(B2*sPFSPD) +(C2*(1-sPDD))	=C2*sPDD	=B2*sPFSD	= Sum (B3:E3)
4	3	=B3*(1-sPFSPD-sPFSD)	=(B3*sPFSPD) +(C3*(1-sPDD))	=C3*sPDD	=B3*sPFSD	=Sum (B4:E4)

PFS, progression-free state; PD, progressive disease.

Let us decipher intervention transition matrix. Before we begin the calculation, it is important to understand that sum of the probabilities to move from any one health state to either of the other health states in a given row must be equal to one. For example, the sum of probability to move from PFS to either PD or death or to remain in PFS with treatment from sorafenib in Table 3 (row 1):

• •Horizontal row for PFS in Table 3 = 0.8211 + 0.1786 + 0 + 0.0003 = 1

To understand how other probabilities are taking place in the matrix, it is important to keep in mind the markov schematic and the flow of one state to another. For PFS to PFS probability is mentioned as 0.8211 which is derived in terms of 1 − (0.1786 + 0 + 0.0003). Similarly, for remaining in the PD state the probability of 0.6250 is deduced from 1 − (0 + 0.3750 + 0). The values 0 describe no movement between the respective health states. As for death from disease and all-cause mortality which is a terminal state because patients cannot move to any health state once they die so the probability to remain in the same health state is always 1.

Using the Markov schematic as shown in the following paragraph, we will illustrate the steps involved in building Markov trace and further calculations to arrive at incremental cost-effectiveness ratio (ICER). The following illustration (Figure 3) is shown for sorafenib arm only.

Then, we show to convert the Markov model to a transition matrix which again describes the probabilities for a given case of HCC to move from one state to another (Table 3).

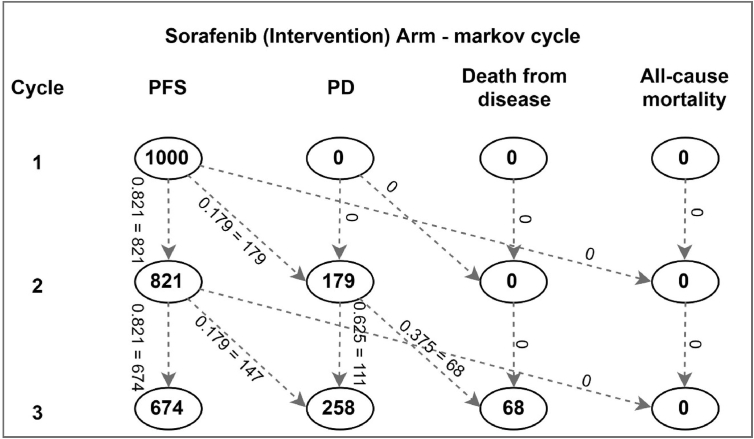
Figure 4 and Table 4 shown in the following mathematically describes the movement of an HCC case from one transition state to another. Here, each cycle represents one year. In the first year, all 1000 cases are assumed to be detected in PFS stage. Based on the probability of progression, 179 cases move to the PD stage, whereas remaining 821 cases remain in the same PFS stage. Similarly, in cycle 3, although 68 of the 179 PD cases die, 111 continue to remain in the PD stage. Another 147 PFS cases progress to PD stage, thus making the total PD cases in year 3 –258. A total of 674 cases are thus left in PFS stage. This calculation is extended in each cycle, till all cases have died. This implies a lifetime study horizon. One may note that the total number of cases in each row remains 1000. Table 4 shows how the mathematical computation takes place in excel to derive these numbers. Similar calculation is also undertaken for the control or BSC arm to evaluate the outcomes.

Figure 4.

Illustration to depict the movement from one health state to another in the sorafenib arm.

Once we have the cohort in each cycle for each health state in our Markov trace, we use the number of individuals in each health state to multiply with annual cost of being in each health state, as well as the utility or quality of life in the respective health states to arrive at total costs and QALYs for each cycle. Finally, we add the lifetime costs and QALYs in each scenario by summing the costs and QALYs in each year or cycle. Similar analysis is undertaken for the BSC arm as well. To arrive at the ICER, we will use the following formula:

$$ICER=\frac{TotalSorafeni{b}_{\mathit{costs}}-TotalBS{C}_{\mathit{costs}}}{\mathit{Total}Sorafeni{b}_{\mathit{QALYs}}-\mathit{Total}\mathit{BS}{C}_{\mathit{QALYs}}}$$

Overall, an EE needs measurement on costs and effects for 2 or more possible alternative which are being compared. An important consideration for a robust CEA is that both costs and consequences (in terms of QALY or DALY) of alternative courses of action need to be measured comprehensively. This implies that the time horizon should be sufficiently long enough. The measurement of such costs and consequences could be performed alongside a clinical trial. However, as we discussed, an RCT may have limitations in certain context to generate robust evidence for a CEA.

As a result, application of decision models becomes imperative. However, it needs to be recognized that decision models are not free of inaccuracy. These decision models can lead to erroneous findings due to several reasons – first, if the model structure if incorrect and is not biologically plausible, then it leads to incorrect output. Second, a model is as good as the values of parameters which are fed to generate output. Hence, any uncertainty in the values of these parameters can lead to uncertainty in estimate of the ICER. This is not an unthinkable option, as each epidemiological study also has some uncertainty around the sample estimate which it generates because of sampling variation. As a result, just as the 95% confidence interval is computed around the estimate found in an RCT, similarly it calls for a sensitivity analysis in a decision model–based CEA to compute 95% confidence intervals around the ICER. Subsequently, it needs to be assessed whether the null value for the ICER lies within the 95% bounds. Third, the population group which is considered in a decision model may not be representative of the certain population groups. Subgroup analysis is the way forward in such situations.

To conclude, one can say that each of the methodology has certain limitations. However, the decision modelling does overcome several limitations of an RCT-based CEA. As a result, gradually, there is a trend towards CEA which is carried out using a decision model alone, or using a decision model alongside an RCT.^5,6 Such as decision model would need evidence for parameters, which could be limited. However, the key would be to use as much robust data to parameterize the model and then take a decision. After all, a policy maker or program manager or a clinician can have 2 options to make a decision about the appropriate intervention – either wait for the best possible data to be generated or make the best possible decision (using a model) with the available data! There can always be options to revisit the decision when better data are generated.

Author contributions

All authors contributed substantially to the design and undertaking of the study, its analysis, and in the writing of this manuscript. All authors approved the final manuscript. S.P. is the guarantor. Specific roles of authors are as follows: NG, SP and RKD conceived the study and designed the article. N.G. and S.P. wrote the first draft of the article. R.V. contributed to a section of the first draft paper. All authors critically reviewed the article and revised the manuscript. All authors approved the final version of the manuscript submitted. All authors take responsibility for the integrity of the data and accuracy of the data analysis and their presentation.

Conflicts of interest

All authors have none to declare.

Funding

We did not receive any funding for this study.

Ethical approval

This article does not involve any primary research and did not require any ethics approval.