Abstract
Ultra-high field functional magnetic resonance imaging (fMRI) has allowed us to acquire images with submillimetre voxels. However, in order to interpret the data clearly, we need to accurately correct head motion and the resultant distortions. Here, we present a novel application of Boundary Based Registration (BBR) to realign functional Magnetic Resonance Imaging (fMRI) data and evaluate its effectiveness on a set of 7T submillimetre data, as well as millimetre 3T data for comparison. BBR utilizes the boundary information from high contrast present in structural data to drive registration of functional data to the structural data. In our application, we realign each functional volume individually to the structural data, effectively realigning them to each other. In addition, this realignment method removes the need for a secondary aligning of functional data to structural data for purposes such as laminar segmentation or registration to data from other scanners. We demonstrate that BBR realignment outperforms standard realignment methods across a variety of data analysis methods. For instance, the method results in a 15% increase in linear discriminant contrast, a cross-validated estimate of multivariate discriminability. Further analysis shows that this benefit is an inherent property of the BBR cost function and not due to the difference in target volume. Our results show that BBR realignment is able to accurately correct head motion in 7T data and can be utilized in preprocessing pipelines to improve the quality of 7T data.
Highlights
-
•
We carried out a visual attention fMRI study at 7T, looking at both early and higher visual areas.
-
•
We demonstrated a novel application of BBR coregistration to realign the fMRI time series (BBR realignment).
-
•
BBR realignment was shown to be better than VBR realignment across multiple metrics, including a 15% increase in LDC.
-
•
We further showed that the benefit of BBR realignment was a property of the BBR cost function itself.
1. Introduction
Participant motion is a significant confound in functional magnetic resonance imaging (fMRI) (Andre et al., 2015), and this problem is exacerbated when data is acquired at higher field strengths and submillimetre resolution (Maclaren et al., 2010). Even the best trained participants will often have unavoidable drift and unconscious motions due to respiratory (~1 mm) and cardiac activity (~100μm) (Maclaren et al., 2012) which can impact data quality (Hutton et al., 2011). Participant motion is a multi-faceted problem that is persistent in fMRI studies (Friston et al., 1996) and results in degrading data quality in a multitude of ways. Participant motion can affect the magnetic field, in turn causing distortions (Jezzard and Clare, 1999) and intensity variations (Friston et al., 1996) in the acquired volumes. This is a large confound since such motion artefacts affect the image in non-rigid ways and hence, standard rigid body realignment techniques might not be sufficient. Since field inhomogeneities scale with field strength, the aforementioned distortions will also become amplified at higher fields.
In addition to distortions due to field inhomogeneities, submillimetre resolution voxels also worsen the problem. While smaller voxel sizes are useful for analysis of brain substructures (e.g. cortical layers), smaller voxels also mean that any analysis would be more susceptible to motion, as the magnitude of the motion becomes larger relative to the voxel size. The presence of motion will invalidate the assumption that the same voxel corresponds to the same location in the brain throughout a fMRI time series and thus, can result in missed effects and/or false positives (Field et al., 2000; Schulz et al., 2014). Moreover, studies acquiring data at sub-millimetre resolutions generally only obtain partial brain volumes to maintain a reasonable repetition time (TR). This compounds the problem because the reduced field-of-view provides less information to drive the realignment. As such, we believe that the conventional realignment methods currently used might be insufficient to ensure the quality of ultra high-resolution data. Numerous improvements have been suggested and implemented, both at the acquisition stage (Frost et al., 2019; Huang et al., 2018; Todd et al., 2015) and the post-processing stage (Gallichan et al., 2016; Yarach et al., 2015).
There are two main categories of motion correction methods: Prospective Motion Correction (PMC) and Retrospective Motion Correction (RMC). In PMC, real-time motion information of the participant’s head is obtained concurrently with the acquisition of the imaging volume. This information is used to update the coordinates of the acquisition volume before each radiofrequency (RF) pulse to ensure that the exact same voxels are being acquired across time. Recent reviews (Maclaren et al., 2013; Zaitsev et al., 2016) provide a good overview of the PMC field and highlight some of the most promising techniques. The estimation of real-time motion information can be done by either using external tracking modules, such as an optical camera in the bore of the scanner (Callaghan et al., 2015; Stucht et al., 2015), or using the internal MR data, such as k-space navigators (Van Der Kouwe et al., 2006) or fat-based navigators (Engstrom et al., 2015). In RMC, rigid body translations and rotations are applied to each volume post-scan to align all volumes to the same scan (Ashburner and Friston, 2003). Currently, most RMC methods utilize a cost function relying on intensity differences per voxel across the volumes to drive realignment, henceforth referred to as Voxel-Based Registration (VBR) methods. There have also been attempts to address the non-rigid body nature of motion artefacts through more advanced realignment methods (Andersson et al., 2001; Chambers et al., 2015).
Both PMC and RMC come with their own set of advantages and disadvantages. PMC ensures that edge voxels are consistently captured in cases of partial brain volume acquisition and can also correct for intra-volume motion since the real-time motion information is updated for every k-space line. However, PMC is still a relatively novel field. Specialized equipment (such as an in-bore optical camera, dentist-molded mouthpieces for marker attachment, etc) is often not widely available and implementation requires modifications to standard scanning sequences. In contrast, RMC has consistently been part of post-processing pipelines for over 15 years, such as that in the SPM software (www.fil.ion.ucl.ac.uk/spm). It also does not require any specialized equipment. However, RMC has shown to be less than perfect, especially when compared to PMC data (Huang et al., 2018; Stucht et al., 2015).
In this paper, we proposed a novel application of Boundary-Based Registration (BBR) to generate an accurate realignment of an fMRI time series to improve on conventional RMC techniques. BBR (Greve and Fischl, 2009) was originally developed to coregister images across different imaging modalities or functional contrasts, and was shown to be more effective than standard VBR methods. However, to the best of our knowledge, BBR has not been used to realign time series data. We utilized the Freesurfer (https://surfer.nmr.mgh.harvard.edu/) implementation of BBR in our realignment pipeline by coregistering each fMRI volume to the same structural volume, thereby aligning each fMRI volume to every other fMRI volume. We evaluated the performance of BBR realignment against a standard VBR approach, in this case SPM’s conventional fMRI realignment, which has been used for high-resolution 7T data (O’Brien et al., 2017; Tak et al., 2018).
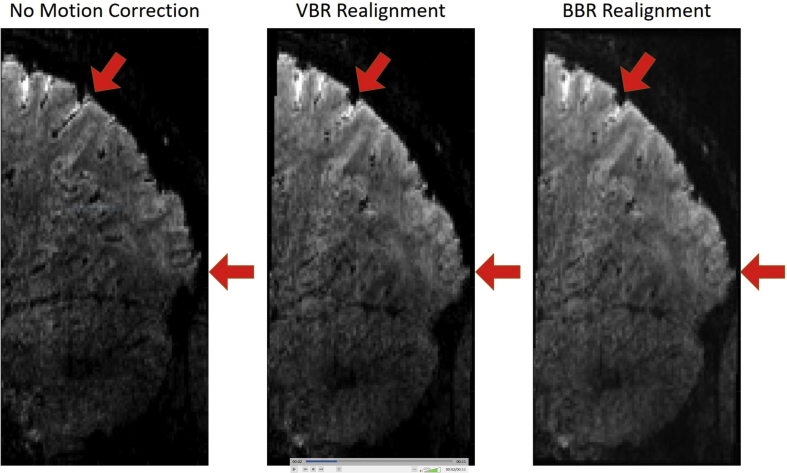
In BBR, the white matter-grey matter boundaries are generated from the Freesurfer cortical surface reconstruction and used to align the EPI image such that the direction of the maximum change of intensity across voxels in the EPI image is perpendicular to the boundary. Because the BBR cost function depends only on the grey matter-white matter boundary, we hypothesised that it would benefit alignment of 7T sub-millimetre data. We expected BBR realignment to be more robust to distortions at medial white-matter and subcortical locations (as seen in Supplementary Video 1) due to their distance from the boundaries.
Supplementary video related to this article can be found at https://doi.org/10.1016/j.neuroimage.2020.116542.
The following is/are the supplementary data related to this article:
We conducted a visual attention task on six participants at 7T and analysed the same data using the two different realignment methods (BBR vs SPM’s VBR). We looked at four different metrics of data quality: three univariate metrics – temporal signal to noise ratio (tSNR), functional contrast to noise ratio (fCNR) and the coefficient of determination for the model fit (R2) – and the cross-validated linear discriminant contrast (LDC) as a multivariate metric (Huang et al., 2018). The stimuli were designed to probe multiple regions of interest (ROIs), in both early and higher visual areas, so as to compare the realignment methods in different parts of the brain. Furthermore, we carried out three additional realignment approaches that are intermediary between the two main methods, in order to attempt to isolate the source of any differences between the two realignment methods. These intermediary methods utilized 1) a brain mask for SPM realignment (reducing the influence of non-brain voxels on the realignment), 2) a reduced brain mask for SPM realignment and 3) realignment via coregistering each fMRI volume to the structural image, analogous to BBR, but using SPM’s between-modality, voxel-based coregistration (where the cost function is based on mutual information rather than sum-of-squares). Finally, we also applied the BBR realignment technique to 3T data from a previous study (Huang et al., 2018), in an attempt to establish whether any differences or improvements are restricted to high-field 7T data, or generalizable to other types of fMRI data.
2. Methods
2.1. 7T Experiment
2.1.1. 7T experimental design
The task conformed to a 2x2 factorial design, with factors of spatial attention (along one of two directions) and stimulus category at the attended location (faces vs houses). On each trial, the participant was prompted to attend to either the positive diagonal (45°/225°) or negative diagonal (135°/315°). The attended diagonal contained two images of the same category of stimuli, either faces or houses. Thus, there were four different conditions: attending to houses along the positive diagonal (H+), attending to houses along the negative diagonal (H-), attending to faces along the positive diagonal (F+) and attending to faces along the negative diagonal (F-). The four conditions were illustrated in Fig. 1, Panel A. This allowed us to test for location selectivity and categorical selectivity by contrasting the corresponding pair of conditions, i.e. H+ and F+ versus H- and F- to investigate location selectivity, or H- and H+ against versus F- and F+ to investigate category selectivity. We expected strong location selectivity but weak or no categorical selectivity in early visual ROIs (V1, V2 and V3), and strong category selectivity but weak location selectivity in higher visual ROIs (scene-selective transverse occipital sulcus [TOS] and parahippocampal place area [PPA], plus face-selective occipital face area [OFA] and fusiform face area [FFA]).
Fig. 1.
Panel A illustrates the four different conditions. Each condition was presented for five blocks per run. Panel B details the timecourse of each block. At the start of the block, two white dots appear for 350 ms to indicate the two regions that the participant should attend to. This is followed by 10 repeats of stimuli presentation, where the participants was required to make a same different judgement.
2.1.2. 7T stimuli design
All stimuli were created using Matlab (2009a, The MathWorks, Natwick, MA, USA) and presented in the scanner using Presentation (v17.2, https://www.neurobs.com/). For the main experiment, the stimuli were presented in a circular patch at four locations, diagonally from the fixation cross at 45°, 135°, 225° and 315° respectively and spanning 0.16o-2.42° visual angle. There were a total of 20 faces and houses used as the category stimuli. All images were presented in greyscale and histogram matched across the board to equate both luminance and root mean squared contrast. This prevents any decoding due to mismatch of brightness or contrast.
A total of 20 blocks (five blocks for each of the four conditions) were presented during each run of the main experiment. At the start of each block, two white dots (visual angle = 0.10°) appeared for 350 ms indicating the pair of patches (either 45° and 225° or 135° and 315°) to which the participant should attend. This was followed by a 550 ms of fixation. The stimuli then appeared at the two attended locations for 950 ms, during which the participant made a same-difference judgement between the two stimuli, followed by 550 ms of fixation. This was repeated for a total of 10 trials per block, with a 1000 ms rest block of fixation between each block.
In addition to the main experiment, we also acquired six runs of a population receptor field (pRF) retinotopic localizer and four runs of a categorical-selective localizer at 3T. The pRF localizer was based on (Dumoulin and Wandell, 2008; Kay et al., 2013). Both stimuli presentation and analysis scripts are available here: https://github.com/kendrickkay/knkutils/. The raw stimuli were taken from (Kriegeskorte et al., 2008). Three runs of translating bars and three runs of rotating wedges and expanding/contracting rings were presented in an alternating order. The stimulus was presented within a circular patch (radius = 7.15°) centred on fixation with a mid-grey background.
The category-selective localizer task comprised 16-s blocked presentations of faces, scenes, objects, scrambled objects, and fixation. Each of these 5 block types appeared in a random order in each run. There was a total of 20 blocks per run (4 presentations of each block type). Within each block, 20 random stimuli from the current category were presented consecutively for 800 ms each. Participants carried out a 1-back matching task while fixating on a black dot in the middle of the screen.
2.1.3. Data acquisition
Fixation is very important in this experiment to ensure that any contrast observed between blocks is not due to eye movement. Due to the inability to perform eyetracking within the 7T scanner (equipment not available), a behavioral pre-training session was carried out to ensure adequate fixation during the scan session itself, using a SMI high speed eye tracker (https://www.inition.co.uk/product/sensomotoric-instruments-iview-x-hi-speed/). Participants performed the scanner task and received feedback on their fixation performance after each run. This was repeated until the participant was able to fixate consistently (<0.05° visual angle difference between the attended and non-attended axis) for two runs.
The main experimental data was acquired on a Siemens 7 T Terra scanner using the Nova Medical 1TX/32RX head coil. Localizer data for this experiement were acquired on a Siemens 3 T Prisma-Fit scanner using a standard 32-channel head coil. Participants provided informed consent under a procedure approved by the institution’s local ethics committee (Cambridge Psychology Research Ethics Committee). A total of six healthy participants were scanned (two females, age range 25–41; two participants were authors of this study).
For the main experimental acquisition, MP2RAGE structural images were acquired first (TR = 4,300 ms, TE = 1.99 ms, TI 1 = 840 ms, TI 2 = 2370 ms, GRAPPA = 3, FOV = 240 mm*240 mm*168 mm, Matrix size = 320*320*224, FA 1 = 5°, FA 2 = 6°).
This was followed by four runs of task fMRI acquisition with the following scan parameters: 0.8 mm isotropic voxels, TR = 2390 ms (2440 ms for two participants), TE = 24 ms (24.4 ms for two participants), GRAPPA = 3, FA = 80°, Matrix size = 200*168*84, TA = ~11mins. The two participants used longer TE and TR due to the peripheral nerve stimulation threshold being exceeded in the scanner.
For the localizer session, MPRAGE structural images were acquired first (TR = 2,250 ms, TE = 3.02 ms, TI = 900 ms, GRAPPA = 2, FOV = 256 mm*256 mm*192 mm, Matrix size = 256*256*192, FA = 9°, TA = ~5 min).
This was followed by six runs of a pRF retinotopic localizer and four runs of a categorical-selective localizer. The EPI parameters for all localizer runs were as follows: 3 mm isotropic voxels, TR = 2000 ms, TE = 30 ms, FA = 78°, Matrix size = 64*64*32, TA = ~5mins.
2.2. 3T Experiment
2.2.1. Experimental design
In addition to the main 7T dataset, we investigated the effect of BBR realignment on a previous 3T dataset (Huang et al., 2018) to determine whether similar effects would be observable at other resolutions and field strengths. The 3T dataset consisted of a total of 18 participants and investigated the decoding of orientation gratings in V1. Each participant was scanned on three separate occasions (for full details, see Huang et al., 2018). The three sessions varied in whether the mouthpiece (necessary for PMC) was present (M+) or not (M-), and whether the PMC was turned on (P+) or not (P-). Note that the three sessions only consisted of P + M+, P-M+, P-M- as PMC cannot be carried out without the mouthpiece. If BBR did confer any advantages in post-processing correction of motion under normal conditions, this might not be expected when PMC is turned on (P+), given that PMC has been shown to reduce motion-related artefacts (Callaghan et al., 2015; Huang et al., 2018). Within each session, the participants underwent one 11-min run of task-based fMRI at 3 mm isotropic resolution, and another run at 1.5 mm isotropic resolution. The participants were asked to fixate on a blue dot in the center of the screen for the duration of the task and respond to any color changes via button press. Diagonal gratings were presented in an annulus around the fixation dot during active blocks.
2.2.2. 3T data acquisition
The 3T data were acquired on a Siemens 3 T Prisma-Fit scanner using a standard 32-channel head coil. Imaging parameters for the 3 mm isotropic EPI were: TR = 1260 ms, TE = 30 ms, FA = 78°, Matrix size = 64*64*20, TA = ~11mins. Imaging parameters for the 1.5 mm isotropic EPI were: TR = 3050 ms, TE = 30 ms, GRAPPA = 2, FA = 78°, Matrix size = 128*128*40, TA = ~11mins. Field-of-view (FOV) parameters for both 3 mm and 1.5 mm EPI sequences were chosen such that the same volume was imaged across scans. For further details on the 3T study, refer to (Huang et al., 2018).
2.3. Data analysis
First, the dataset underwent temporal interpolation in SPM 12 to correct for differences in slice acquisition times. The images then underwent distortion correction using TOPUP in FSL. The distortion was calculated using five reverse phase encode (PE) images, acquired at the start of each run, and the first five images of the fMRI time series. We chose to carry out TOPUP prior to realignment so as to ensure that any difference observed were solely due to the differences between the realignment methods and not due to any complex interaction between the realignment methods and TOPUP. Nonetheless, we demonstrated that the specific order of TOPUP and realignment does not have a significant effect on the results (Supplementary Fig. 1).
Distortion correction was not carried out for the 3T images.
2.3.1. Realignment methods
After initial pre-processing, the volumes then underwent five different realignment methods: two main methods and three subsidiary methods.
2.3.1.1. Main realignment methods
The two main methods were functional-structural BBR realignment and functional-functional VBR realignment in SPM. For functional-structural BBR realignment, we applied the Freesurfer implementation of the BBR function in a two-step process. First, the fMRI images were averaged across volumes, and the mean fMRI image aligned to the structural using BBR to generate an initial realignment matrix. Next, each fMRI volume was aligned to the structural using BBR with the initial realignment matrix as the seed, to reduce computation time and the probability of convergence failures due to local minima. This operation combined the motion correction of functional images with coregistration to the structural image into a single processing step. Note that the BBR realignment uses a 6 degrees of freedom transform, similar to the VBR realignment method.
For functional-functional VBR realignment, we used standard rigid-body realignment based on a sum-of-squares cost function as implemented in SPM12, which we call here the functional-functional VBR approach. Previous studies (Morgan et al., 2007; Oakes et al., 2005) have shown that while there are subtle differences between the various software packages (SPM, Analysis of Functional Neuroimages (AFNI), BrainVoyager and FMRIB Software Library (FSL)), the packages all performed similarly overall. To minimize resampling of the functional data, the structural was then coregistered to the functional data using BBR, analogous to the BBR fMRI method above, and this transform was applied on the ROIs and masks to transform them to functional space.
2.3.1.2. Subsidiary realignment analyses
To further probe the cause of the differences between the two main realignment methods, we evaluated three additional realignment methods. First, we performed a variant of the functional-functional VBR realignment method where the motion estimation was restricted to a full brain mask (both shaded areas in Fig. 2). Second, we carried out a similar analysis with a smaller brain mask (the red area in Fig. 2), in which the cortical surface was further eroded (functional-functional VBR realignment with small brain mask). The definition of both masks is described in Section 2.3.3. Lastly, we repeated the BBR realignment pipeline, however, utilizing SPM between-modality coregistration instead of the BBR coregistration. We refer to this realignment method as functional-structural VBR. In this method, we realigned every fMRI volume at each timepoint to the structural using the default normalized mutual information cost function. Note that we first realigned the average functional volume to the structural and used that as the initial seed for the realignment of individual volumes, similar to what was done for BBR realignment.
Fig. 2.
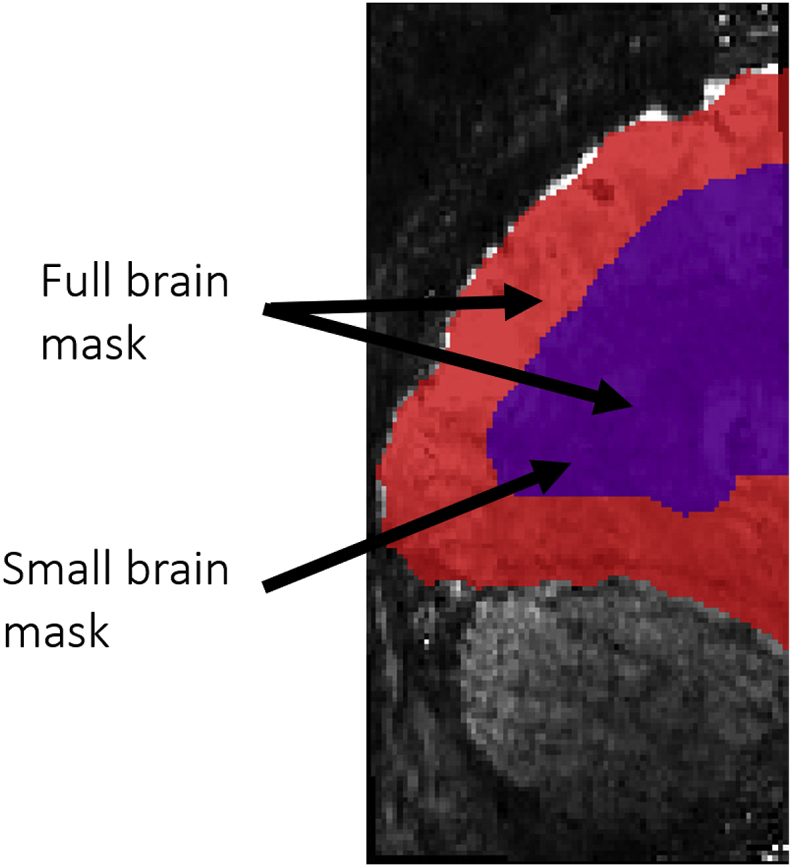
An illustration of the two brain masks utilized for the subsidary realignment methods. The full brain mask consists of both the red and purple areas while the small brain mask consists of only the purple area.
The two functional-functional VBR realignments with brain masks served to remove the potential confound of non-brain voxels harming the standard SPM realignment. Note that since BBR realignment is driven solely by inner brain boundaries, this method already ignores out of brain volumes. A smaller brain mask (in which more voxels outside the brain surface were removed; see below for details) was also utilized because anecdotal reports have shown this method to result in better realignment. Comparisons with the functional-structural VBR realignment would isolate whether differences between the two main methods were due to a methodological difference (realigning within a time series vs realigning via a structural template) or whether the benefit was inherent to the different cost functions (brain features) used.
We hypothesised that masking out-of-brain voxels should improve the accuracy of the realignment relative to standard functional-functional VBR realignment without masking. In contrast, we expected that function-structural VBR to perform worse than that of any other realignment methods. This is because we expected that functional-structural realignments would be generally less accurate due to different spatial distortions across modalities. While the same criticism applies for BBR realignment, it is possible that the benefits of BBR realignment discussed above would outweigh the drawbacks of cross-modality realignment.
2.3.2. Regions of interest (ROIs)
Seven distinct ROIs were analysed: three retinotopic (V1, V2, V3) and four category-selective (FFA, OFA, PPA and TOS).
Retinotopic ROIs were defined in Freesurfer 6.0.0. Retinotopic activation maps were generated from the retinotopic pRF localizer. The maps were then projected onto a polygon-mesh reconstruction of the individual participants’ cortical surfaces. These maps were then used to manually segment out V1 to V3 on the cortex. Each individual visual area was also manually segmented into ventral and dorsal regions (e.g. V1 into V1v and V1d) for the purposes of fCNR analysis.
For the category-specific ROIs, activation t-maps were obtained using SPM by fitting a GLM to the fMRI data from the categorical localizer runs. The face-selective areas (FFA and OFA) were obtained from a contrast map by subtracting the object activation t-maps from the face activation t-maps. Similarly, the scene-selective areas (TOS and PPA) were obtained from a contrast map by subtracting the object activation t-maps from the scene activation t-maps. For each ROI, we took the 100 most activated contiguous voxels in regions that correspond to their expected locations on a brain atlas.
As all localizer data were obtained at 3T, coregistration to the 7T dataset was needed. This was done by first coregistering the 3T functional data to the 3T structural data using SPM’s between-modality coregistration. The 3T structural data were then coregistered to the 7T structural data, again using the SPM coregistration. The transformations from both coregistration steps were then applied to the ROI data. For the BBR realignment method, no further transformation was necessary since the BBR realignment process realigns the functional 7T data to the structural data. However, for the standard SPM realignment method, BBR was used to coregister the 7T structural data to the 7T functional data and the corresponding transform was applied to the ROI data. All ROI data were only resliced once all transforms have been applied.
2.3.3. Brain masks
The full brain mask was obtained by combining the grey matter and white matter voxels from the Freesurfer reconstruction and was coregistered to the functional volumes with BBR, using the structural data as a reference. Then the full brain mask underwent dilation and erosion by two voxels to fill in the sulci voxels. The small brain mask was obtained by eroding the full brain mask by 10 voxels. A sample volume of both brain masks superimposed on the mean fMRI image is shown in Fig. 2.
We also created a grey matter mask solely for tSNR analysis. This was obtained by combining all the grey matter voxels from the Freesurfer reconstruction. In addition, we excluded all the visual ROIs (V1, V2, V3, FFA, OFA, PPA and TOS) from the tSNR mask to remove potential confounds due to task-related activations. The grey matter mask also underwent BBR coregistration to the functional volume using the structural volume as a template.
2.4. Data analysis
The processed data were analysed using the following four metrics (tSNR, fCNR, R2 and LDC):
2.4.1. Temporal signal-to-noise ratio (tSNR)
The tSNR for each voxel was obtained by dividing the mean voxel intensity across the entire time course by the standard deviation of the voxel intensity. The mean tSNR was obtained by averaging across all the voxels in the grey matter mask. In the further analysis, the mean tSNR of the central brain region was obtained by averaging across all voxels in the small brain mask.
2.4.2. Functional contrast-to-noise ratio (fCNR)
The postprocessed fMRI data was fit by a GLM that modeled responses to each of the four different attention conditions. For each block in the GLM, a boxcar model was used and then convolved with the canonical SPM HRF. Motion covariates were not included in the GLM due to the difficulty in parsing the BBR motion covariates. Thus, we excluded motion covariates from all realignment methods to ensure a fair comparison. Nonetheless, to address the issue of motion covariates, we show in Supplementary Fig. 2 that fitting the VBR realignment to GLMs with and without motion covariates generated similar results. Linear and first-order sinusoidal detrending were applied to the data to remove signal drift. For each voxel, the fCNR was calculated by dividing the contrast of interest by the standard deviation of the noise. For the early retinotopic ROIs, the contrast of interest was obtained by subtracting the two conditions where the stimulus was absent in the retinotopic area from the two conditions where the stimulus is present (i.e. H+ and F+ against H- and F- or vice versa depending on the ROI). For categorical ROIs, the contrast was obtained by subtracting the two conditions where the stimulus was of the other category from the two conditions where the stimulus was of the category for which the ROI was selective for (i.e. H+ and H- against F+ and F- or vice versa depending on the ROI). The standard deviation of the noise was obtained from the standard deviation of the residuals of the GLM.
2.4.3. Goodness of fit (R2)
The R2 value was calculated from same GLM as for the fCNR analysis. For each voxel, the R2 was obtained by dividing the variance of the model fit by the total variance of the processed data. The model fit was obtained by multiplying the design matrix with the beta estimates for the four attention conditions. This represents the percentage of variance explained by the model. A higher R2 value indicates that the model is able to explain more of the variance in the data.
2.4.4. Linear discriminant contrast (LDC)
In addition to the three univariate measures, we also investigated the effect of the different realignment methods on multivariate activation patterns using the cross-validated LDC. The cross-validated LDC (Kriegeskorte et al., 2007; Walther et al., 2016) is a contrast estimate between two conditions measured using a discriminant, which is made up of a weighted combination of the ROI voxels. An independent set of data is used to generate the weights so as to maximize the sensitivity of the LDC to differences between the two conditions of interest. Cross-validation is performed to remove the positive bias in the distance estimate due to noise (which is by definition positive) (Walther et al., 2016). This measure is also referred to as the cross-validated Mahalanobis (crossnobis) distance (Kriegeskorte and Diedrichsen, 2016).
For this paper, three of the four runs were utilized as the independent training set, and the data was cross-validated using the remaining run as the testing set. For the training set, all presentations of each condition (H+, F+, H-, F-) from the three runs were modeled as a single regressor in the design matrix. Both the data and the design matrix underwent linear, first order sinusoidal detrending. The detrended data matrix was then fit to the detrended design matrix to generate contrast estimates for the four conditions. For the early retinotopic areas, we contrasted the H+ and F+ blocks against the H- and F- blocks to produce the representational distance metric. For the categorically selective areas, we contrasted the H+ and H- blocks against the F+ and F- blocks to generate the representational distance metric. This representational distance metric was normalized using the sparse covariance matrix of the noise residuals to produce the weights vector from the independent data set (Ledoit and Wolf, 2003). The data from the remaining task run underwent the same detrending and fitting to generate a test contrast estimate. The LDC test statistic is calculated by taking the dot product of the representational distance metric and the test contrast estimate. We repeated this procedure four times, utilizing a different task run to generate the test contrast estimate for each iteration. We averaged across the four LDC test statistics to generate a final continuous performance estimate, which is centred on zero under the null hypothesis of no reliable differences between the two groups of conditions. As the number of voxels used in this analysis varied across participants and ROIs, the LDC was normalized by dividing the metric by the square root of the number of voxels.
2.4.5. Wilcoxon signed-rank test
Since six datapoints (participants) is not sufficient to check the normality assumption of Gaussian error that is assumed by parametric tests, the tSNR, fCNR, R2 and LDC data were analysed using a non-parametric, pairwise Wilcoxon signed-rank test. The Wilcoxon signed-rank test only requires that the data is on an interval scale and each pair of observations are random samples from a symmetric distribution. Significance was defined with an alpha level of 0.05. Due to the small sample size (six participants), our results will only be significant (p = 0.0313) if all six participants demonstrate changes in the same direction. In all other cases, the results would not be significant (p > 0.0625).
3. Results
To visualize the effects of each realignment method, we generated a video that animates the transitions between the first volume in each run of the experiment for one representative example participant (Supplementary Video 1). Inspection of this video indicated that BBR resulted in a visibly-improved registration of the grey-matter voxels over time relative to VBR. In the subsequent analyses we quantify this apparent improvement by characterizing tSNR, fCNR, model fit (R2), and multivariate discrimination performance (LDC).
3.1. Analysis of the two main realignment methods
3.1.1. tSNR analysis of 7T fMRI data
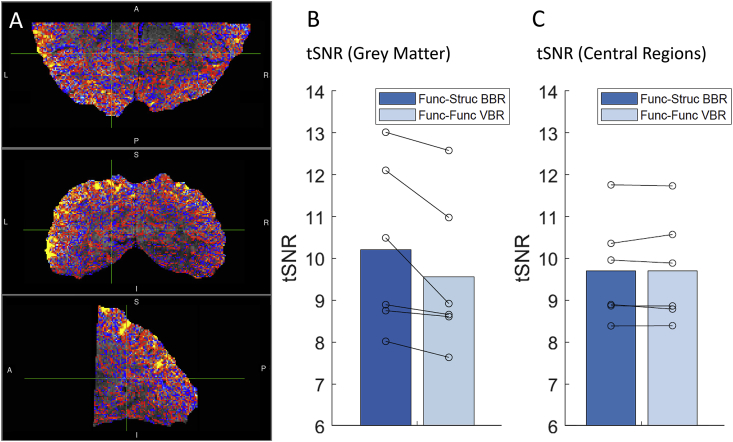
We analysed the tSNR for the two main realignment methods (see Fig. 3, Panel A for a comparison map between the two methods on a sample participant). Improvements due to BBR realignment were heavily localized on the brain surface, which concurs with our expectations since BBR is boundary driven. In central regions of the brain, there is no visually discernible advantage of any methods, and the voxels showing preference for either method are most likely reflecting random fluctuations.
Fig. 3.
Panel A showed a comparison of the tSNR of the two main methods using a sample participant. The heatmap was generated by subtracting the functional-functional VBR tSNR from the functional-structural BBR tSNR. Red-yellow areas indicate regions where functional-structural BBR performed better while blue-teal areas show regions where functional-functional VBR performed better. Panel B showed the tSNR of the grey matter across all 6 participants when the two main realignment methods are used. Panel C showed the tSNR of the two main realignment methods when the small brain mask (Fig. 2) is applied. For both Panel B and C, each pair of connected circles indicated single participant results while the bar showed the group average.
By averaging over all grey-matter voxels, we found that BBR significantly outperforms VBR under the Wilcoxon signed-rank test (Fig. 3, Panel B). In contrast, averaging over the central (mostly white matter) brain regions using the small brain mask, both methods yielded very similar results (mean = 9.69 for both, Fig. 3, Panel C). These results are consistent with what we observed from the heatmap in Fig. 3, Panel A and with our expectations that BBR realignment are more beneficial towards voxels near the boundaries.
3.1.2. fCNR analysis of 7T fMRI data
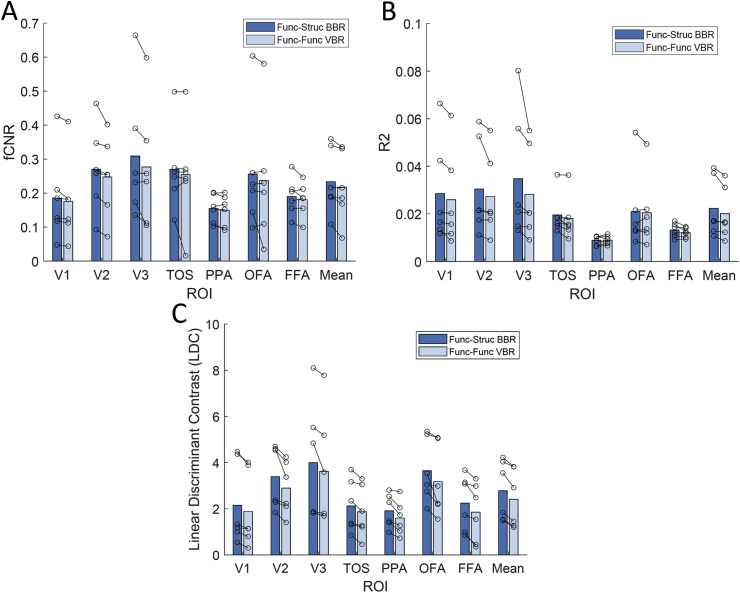
Analysis of fCNR in visual ROIs provided further evidence that BBR realignment outperformed the standard VBR approach (Fig. 4, Panel A). When the fCNR was averaged across all ROIs within each participant, the Wilcoxon signed-rank test indicated that BBR realignment significantly benefits our data relative to VBR realignment. For individual ROIs, only V1 and V2 ROIs showed significant differences under Wilcoxon signed-rank testing. All other ROIs demonstrated a general trend of BBR realignment being better than standard VBR realignment, although this improvement was not consistent across all participants.
Fig. 4.
These plots compare functional-structural BBR against functional-functional VBR across multiple metrics— fCNR (Panel A), R2 (Panel B) and Linear Discriminant Contrast (Panel C). Each pair of connected circles indicate single participant results while the bar shows the group average.
3.1.3. R2 analysis of 7T fMRI data
The R2 results were shown in Fig. 4, Panel B, and exhibited a very similar trend to that of the fCNR results since these metrics are closely related. Averaging the R2 results across all ROIs within each participant showed that BBR realignment significantly outperforms VBR realignment under the Wilcoxon signed-rank test. Individual ROI results showed significant differences for V1, V2, V3 and TOS while all other ROIs showed a small, but non-significant, benefit of BBR realignment over standard realignment.
3.1.4. LDC analysis of 7T fMRI data
The LDC results were plotted in Fig. 4, Panel C. Similar to the R2 and fCNR results, the average LDC across all ROIs showed a significant improvement under Wilcoxon signed-rank test when BBR realignment was used. Moreover, for all individual ROIs, the LDC from the BBR realignment data was significantly higher than that of VBR realignment data. This suggested that there is a consistent benefit of BBR realignment across all ROIs. Across all ROIs and participants, there was an average of 15.23% increase in LDC when utilizing BBR realignment over conventional VBR realignment.
3.1.5. tSNR analysis of 3T fMRI data
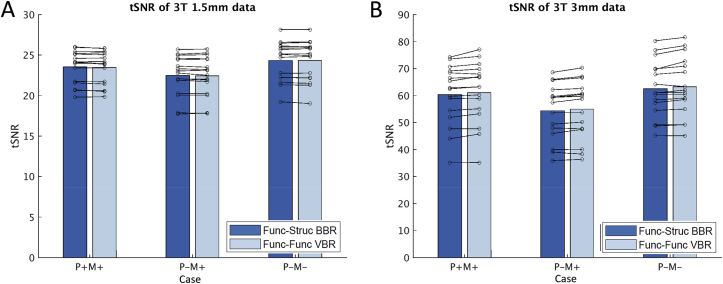
Applying the two main realignment methods to the 3T data told a very different story (Fig. 5). At 1.5 mm (Fig. 5, Panel A), both methods showed very similar tSNR results across all three sessions and no significant differences were observed when the Wilcoxon signed rank test was carried out (p = 0.47). At 3 mm (Fig. 5, Panel B), BBR realignment performed significantly worse than standard VBR realignment for all 3 sessions (p = 0.00049 under Wilcoxon signed rank test). Note that these findings applied regardless of whether PMC was active (P+) or not (P-), and whether a mouthpiece was present (M+) or not (M-); see Huang et al. (2018) for details of the three conditions. These results indicated that there is no benefit in using BBR for 3T data and it could even be detrimental (in the case of 3 mm isotropic fMRI data). Given that we did not observe any benefit at the level of tSNR, we did not carry out further analysis with the other metrics or subsidiary methods. Moreover, due to the differences in the nature of the task, we would be unable to make any meaningful comparison between the 3T and the 7T data for fCNR, R2 and LDC.
Fig. 5.
These plots compared the tSNR of functional-structural BBR against functional-functional VBR for 3T data at 1.5 mm isotropic resolution (Panel A) and 3 mm isotropic resolution (Panel B). The three cases on the x-axis corresponds to the type of PMC used- PMC On, Mouthpiece On (P + M+); PMC Off, Mouthpiece On (P-M+); PMC Off, Mouthpiece Off(P-M-). The fourth condition (PMC On, Mouthpiece Off) was not carried out because PMC was unreliable in the absence of the mouthpiece. Each pair of connected circles indicated single participant results while the bar showed the group average.
3.2. Subsidiary analyses of 7T fMRI data
To probe for the source of the difference between the VBR and BBR realignment results, we designed three subsidiary analyses to help bridge the gap between the two main analyses. These analyses were not included in Section 2.3.1 as they are not standalone methods of improving fMRI realignment, but rather a way of understanding the differences between the functional-functional VBR and functional-structural BBR results. The three methods were: functional-functional VBR realignment with a full brain mask, functional-functional VBR realignment with a smaller brain mask and functional-structural VBR realignment. These analysis methods were discussed in detail in Section 2.3.1.
3.2.1. tSNR analysis
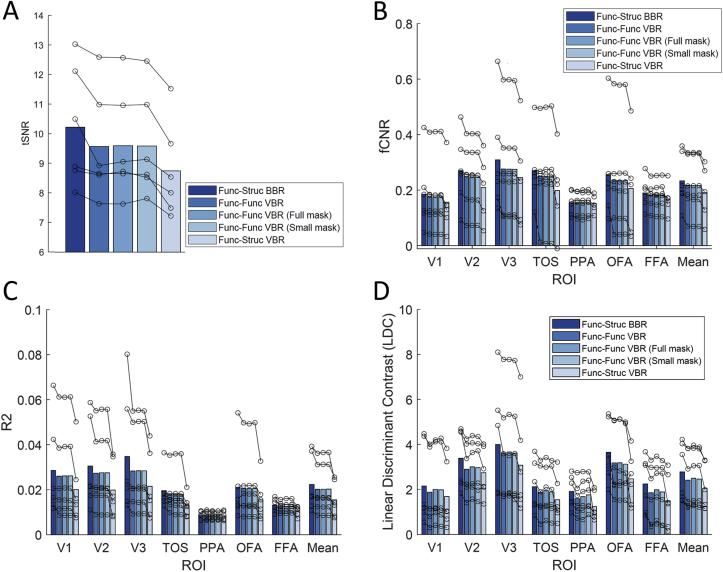
The tSNR results of the three subsidiary methods were plotted alongside the two main methods in Fig. 6, Panel A. The functional-structural BBR realignment (leftmost bar) was significantly better than the other four methods. The results from the functional-functional VBR realignment using SPM with the two masks (full brain and smaller brain, middle and second bar from the right) were very similar to that of the standard VBR realignment results with no mask applied (second bar from the left). Indeed, Wilcoxon signed rank test also showed no significant difference between the VBR realignment with and without mask in SPM, indicating that there was no significant benefit of removing non-brain voxels.
Fig. 6.
These plots compared the five different realignment methods across multiple metrics-tSNR (Panel A), fCNR (Panel B), R2 (Panel C) and Linear Discriminant Contrast (Panel D). Each set of connected circles indicated single participant results while the bar showed the group average.
When the functional-structural VBR realignment process (rightmost bar) was used, the tSNR results become significantly worse than both the functional-structural BBR realignment and the functional-functional VBR realignment results. Thus, the benefit of BBR realignment was not due to the functional-structural nature of the realignment process, but rather an inherent benefit of the BBR cost function.
3.2.2. fCNR and R2 analysis
Subsidiary analyses on the fCNR and R2 measures produced qualitatively similar results as the tSNR results (Fig. 6, Panels B and C). The results using functional-functional VBR realignment with either mask (middle and second bar from the right) were similar to that of VBR realignment without mask (second bar from the left) and no significant difference was detected across all ROIs between the three methods via pairwise comparison using Wilcoxon signed-rank test for both fCNR and R2. Moreover, comparisons between the results from BBR realignment (leftmost bar) and the two functional-functional VBR realignments with masks yielded similar results to that of the comparison between BBR realignment and functional-functional VBR realignment without mask, with significant improvements in the early visual areas but no significant differences in the higher visual areas. Functional-structural VBR realignment (rightmost bar) produced results that were significantly worse than either of the main methods for most ROIs for both R2 and fCNR analysis. These results concur with the tSNR results that BBR was the best realignment method of all five used, at least for high-resolution.
3.2.3. LDC analysis
Subsidiary analysis using the multivariate LDC measure showed that utilizing a mask (middle and second bar from the right) improves the quality of the data relative to VBR realignment without mask (second bar from the left) slightly. This improvement was consistent, but not significant, across all ROIs except OFA and does not fully account for the differences between the main BBR and VBR realignment methods. Functional-structural VBR realignment (rightmost bar) produced results that were significantly worse than all other methods for all ROIs. The full results were plotted in Fig. 6, Panel D.
4. Discussion
Retrospective motion correction (RMC) is a critical step for ensuring data quality. Our results showed that BBR realignment outperforms more conventional VBR methods for realigning the grey-matter portion of 7T submillimetre data. With an increasing focus in functional activations across different cortical layers and fine-scale functional specialization, it is important to ensure proper data realignment to prevent the masking of real effects or being misled by false positives.
Initial comparisons of 7T submillimetre data using the two main methods (BBR realignment and standard whole-image VBR) showed a benefit of using BBR realignment and this benefit was observed across all four metrics used, tSNR, fCNR, R2 and LDC. All benefits were shown to be significant according to Wilcoxon signed-rank testing when averaged across all ROIs. Probing individual ROIs with fCNR and R2 showed greatest numerical improvements in ROIs near the surface of the brain, namely the early visual areas. This agreed with the tSNR comparison heatmap, which showed the greatest benefit of BBR realignment being on and near the surface of the brain. Restricting our analysis to the central region of the brain showed that both methods yielded similar tSNR results. This is expected since BBR is driven by realigning the boundaries of the brain and hence the largest benefit should be observed on and near the boundaries. However, in the LDC analysis, all ROIs showed significant improvements when BBR realignment was utilized. Given that LDC, which combines information across multiple voxels, is likely the most sensitive metric, we interpreted these results to mean that while the major benefits of BBR realignment were localized to the brain’s surface, there were also more subtle improvements in other brain regions. We theorized that the benefit of BBR realignment arose because it only considered a small subset of voxels in the neighbourhood of the grey matter-white matter boundary and thus would be robust against any distortions not in those regions (such as in the medial white matter and subcortical regions). Furthermore, as fMRI analyses are generally concerned with grey matter voxels, realignment using the grey matter boundary will likely be beneficial when non-linear distortions are present, as seen in Supplementary Video 1.
Repetition of the tSNR analysis on 3T data showed no difference between realignment methods for 1.5 mm isotropic data, plus a significant decrease in tSNR for BBR realignment for 3 mm isotropic data. This was in line with our expectation that BBR realignment should be most beneficial at high resolutions. Since BBR uses the brain boundaries to drive realignment, the benefit would be most apparent at higher resolutions, where the boundaries are more clearly defined. The lack of fine detail in 3 mm isotropic voxels would mean that the BBR algorithm would not be able to accurately identify boundaries in the fMRI data, thus potentially leading to misalignments. Moreover, the smaller voxels at higher resolution would also cause the data to be more sensitive to small differences in realignment. Geometric distortions due to field inhomogeneities were worse at higher field strengths and this could explain why BBR is more beneficial at 7T relative to 3T. Lastly, it should also be noted that the 7T data utilized a MP2RAGE sequence to obtain the structural volume whereas the 3T data utilized a MPRAGE sequence. The different sequences use different contrasts, which could translate to a difference in accuracy of boundary definition and hence, a difference in BBR performance across the datasets.
We then attempted to probe for the source of the benefit for BBR realignment. By running standard SPM realignment with a full brain mask and also with a smaller brain mask, we obtained similar results to standard realignment without a mask for univariate analysis. LDC analysis on functional-functional VBR realignment with masks showed a slight benefit of masking over simple functional-functional VBR but was still significantly worse than functional-structural BBR realignment. Taken together, these results showed that masking out non-brain voxels achieved a slight benefit on realignment, but only when using a more sensitive multivariate measure. However this was a small benefit and insufficient to explain the much larger overall advantage of BBR realignment, suggesting that the advantage of BBR realignment does not simply reflect the smaller subset of brain voxels used but rather reflects an inherent improvement due to the BBR cost function.
Functional-structural VBR generated much poorer realignment of data as compared to the other four methods. This was reflected by a significant decrease in tSNR, as well as significantly worse fCNR and R2 values across most ROIs. This was in line with our expectations as we expected that functional-structural realignments would be generally less accurate due to different spatial distortions across modalities and different contrasts in images. Nonetheless, it confirmed that the advantage of BBR realignment is not an artefact arising from realigning to the structural rather than between fMRI volumes.
Given that functional-structural VBR was the worst performing realignment method, it is worth considering if we could attempt functional-functional BBR. This would allow us to utilize the benefit of BBR cost function, while potentially removing the cost of a functional-structural coregistration across modalities (e.g, from images that may have different spatial distortions). However, BBR requires at least one of the images to have good definition of grey matter boundaries (normally the higher-resolution structural image) and we believe that the fMRI volumes do not typically have sufficient contrast to define those boundaries for matching. Moreover, in the Freesurfer implementation of BBR, we need to generate a surface reconstruction for the definition of boundaries. This requires either a structural image from MP2RAGE or a structural-like image from newer methods such as multi-inversion-recovery time echo planar imaging (MI-EPI) (Kashyap et al., 2018).
Our study has shown that BBR realignment is beneficial for 7T submillimetre data, especially if the region of interest for the study is near the surface of the brain. We also demonstrated that the benefits of BBR realignment is inherent to that of its realignment cost function and not due to other differences from the standard realignment approach.
However, there are definitely limitations to our study. Firstly, we used a relatively unconventional field of view (FOV) due to the need to capture both higher and early visual areas with minimal repetition time (TR). Future studies using different FOVs could help further establish the advantages of using BBR realignment. Secondly, BBR realignment does not, on its own, deal with other artefacts caused by head motion, such as within-volume motion and interactions with field inhomogeneities, which cause non-rigid deformations of the image. Slice-based PMC (Huang et al., 2018; Schulz et al., 2014) is necessary to handle within-volume motion, while more sophisticated methods would be needed to model field inhomogeneities (Andersson et al., 2003; Chambers et al., 2015; Yarach et al., 2015). Next, BBR realignment is also more computationally intensive and takes a few hours per participant for realignment. It also requires a Freesurfer surface reconstruction, which would add to the computational time if the surface reconstruction is not needed for other purposes (such as ROI or laminar segmentation). Lastly, BBR realignment requires good grey matter-white matter contrasts in both the structural and functional data to help drive the cost function. Thus, BBR would benefit from optimizing the acquisition sequences to maximize grey matter-white matter contrasts. Otherwise, performance might degrade when the boundaries are less clearly defined (such as in multiband sequences, which has shorter TR).
5. Conclusion
As the field shifts towards higher resolutions, participant motion during fMRI will remain an important and pertinent problem. In this paper, we presented results that show BBR realignment of fMRI volumes helps to remove inter-volume motion for fMRI time sequences and thereby improves the quality of the data by 15%, as measured by LDC. We also showed benefits in three other different metrics (tSNR, fCNR and R2). We believe that this, together with other motion correction tools, will be critical as we move towards higher resolutions.
CRediT authorship contribution statement
Pei Huang: Conceptualization, Methodology, Software, Investigation, Formal analysis, Writing - original draft. Johan D. Carlin: Conceptualization, Formal analysis, Writing - review & editing, Supervision. Richard N. Henson: Conceptualization, Formal analysis, Writing - review & editing, Supervision. Marta M. Correia: Resources, Project administration, Formal analysis, Writing - review & editing, Supervision.
Acknowledgements
This work was supported by the Agency for Science, Technology and Research, Singapore funding to PH and UK Medical Research Council funding to JC, RH and MC (SUAG/046 G101400).
The authors would also like to thank Chris Rodgers, Catarina Rua and the radiographers at WBIC for assisting with the scans and all volunteers for their time and patience.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.neuroimage.2020.116542.
Appendix A. Supplementary data
The following are the Supplementary data to this article:
figs1.
References
- Jezzard P., Clare S. Sources of distortion in functional MRI data. Hum. Brain Mapp. 1999;8:80–85. doi: 10.1002/(SICI)1097-0193(1999)8:2/3<80::AID-HBM2>3.0.CO;2-C. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersson J.L.R., Hutton C., Ashburner J., Turner R., Friston K. Modeling geometric deformations in EPI time series. Neuroimage. 2001;13:903–919. doi: 10.1006/nimg.2001.0746. [DOI] [PubMed] [Google Scholar]
- Andersson J.L.R., Skare S., Ashburner J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. Neuroimage. 2003;20:870–888. doi: 10.1016/S1053-8119(03)00336-7. [DOI] [PubMed] [Google Scholar]
- Andre J.B., Bresnahan B.W., Mossa-Basha M., Hoff M.N., Patrick Smith C., Anzai Y., Cohen W.A. Toward quantifying the prevalence, severity, and cost associated with patient motion during clinical MR examinations. J. Am. Coll. Radiol. 2015;12:689–695. doi: 10.1016/j.jacr.2015.03.007. [DOI] [PubMed] [Google Scholar]
- Ashburner J., Friston K. Human Brain Function. second ed. 2003. Rigid body registration and interpolation; pp. 635–653. [Google Scholar]
- Callaghan M.F., Josephs O., Herbst M., Zaitsev M., Todd N., Weiskopf N. An evaluation of prospective motion correction (PMC) for high resolution quantitative MRI. Front. Neurosci. 2015;9:1–9. doi: 10.3389/fnins.2015.00097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chambers M.C., Bhushan C., Haldar J.P., Leahy R.M., Shattuck D.W. Correcting inhomogeneity-induced distortion in FMRI using non-rigid registration. Proc. - Int. Symp. Biomed. Imaging. 2015:1364–1367. doi: 10.1109/ISBI.2015.7164129. 2015-July. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dumoulin S.O., Wandell B.A. Population receptive field estimates in human visual cortex. Neuroimage. 2008;39:647–660. doi: 10.1016/j.neuroimage.2007.09.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engstrom M., Martensson M., Avventi E., Norbeck O., Skare S. Collapsed fat navigators for brain 3D rigid body motion. Magn. Reson. Imaging. 2015;33:984–991. doi: 10.1016/j.mri.2015.06.014. [DOI] [PubMed] [Google Scholar]
- Field A.S., Yen Y.F., Burdette J.H., Elster A.D. False cerebral activation on BOLD functional MR images: study of low-amplitude motion weakly correlated to stimulus. Am. J. Neuroradiol. 2000;21:1388–1396. [PMC free article] [PubMed] [Google Scholar]
- Friston K.J., Williams S., Howard R., Frackowiak R.S.J., Turner R. Movement-related effects in fMRI time-series. Magn. Reson. Med. 1996;35:346–355. doi: 10.1002/mrm.1910350312. [DOI] [PubMed] [Google Scholar]
- Frost R., Wighton P., Karahanoğlu F.I., Robertson R.L., Grant P.E., Fischl B., Tisdall M.D., van der Kouwe A. Markerless high-frequency prospective motion correction for neuroanatomical MRI. Magn. Reson. Med. 2019;82:126–144. doi: 10.1002/mrm.27705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallichan D., Marques J.P., Gruetter R. Retrospective correction of involuntary microscopic head movement using highly accelerated fat image navigators (3D FatNavs) at 7T. Magn. Reson. Med. 2016;75:1030–1039. doi: 10.1002/mrm.25670. [DOI] [PubMed] [Google Scholar]
- Greve D.N., Fischl B. Accurate and robust brain image alignment using boundary-based registration. Neuroimage. 2009;48:63–72. doi: 10.1016/j.neuroimage.2009.06.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang P., Carlin J.D., Alink A., Kriegeskorte N., Henson R.N., Correia M.M. Prospective motion correction improves the sensitivity of fMRI pattern decoding. Hum. Brain Mapp. 2018;39:4018–4031. doi: 10.1002/hbm.24228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutton C., Josephs O., Stadler J., Featherstone E., Reid A., Speck O., Bernarding J., Weiskopf N. The impact of physiological noise correction on fMRI at 7T. Neuroimage. 2011;57:101–112. doi: 10.1016/j.neuroimage.2011.04.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kashyap S., Ivanov D., Havlicek M., Sengupta S., Poser B.A., Uludağ K. Resolving laminar activation in human V1 using ultra-high spatial resolution fMRI at 7T. Sci. Rep. 2018;8 doi: 10.1038/s41598-018-35333-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kay K.N., Winawer J., Mezer A., Wandell B.A. Compressive spatial summation in human visual cortex. J. Neurophysiol. 2013;110(2):481–494. doi: 10.1152/jn.00105.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kriegeskorte N., Diedrichsen J. Inferring brain-computational mechanisms with models of activity measurements. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2016;371:489–495. doi: 10.1098/rstb.2016.0278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kriegeskorte N., Formisano E., Sorger B., Goebel R. Individual faces elicit distinct response patterns in human anterior temporal cortex. Proc. Natl. Acad. Sci. U. S. A. 2007;104:20600–20605. doi: 10.1073/pnas.0705654104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kriegeskorte N., Mur M., Ruff D.A., Kiani R., Bodurka J., Esteky H., Tanaka K., Bandettini P.A. Matching categorical object representations in inferior temporal cortex of man and monkey. Neuron. 2008;60:1126–1141. doi: 10.1016/j.neuron.2008.10.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ledoit O., Wolf M. Improved estimation of the covariance matrix of stock returns with an application to portfolio selection. J. Empir. Financ. 2003;10:603–621. [Google Scholar]
- Maclaren J., Speck O., Stucht D., Schulze P., Hennig J., Zaitsev M. Navigator accuracy requirements for prospective motion correction. Magn. Reson. Med. 2010;63:162–170. doi: 10.1002/mrm.22191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maclaren J., Armstrong B.S.R.R., Barrows R.T., Danishad K.A., Ernst T., Foster C.L., Gumus K., Herbst M., Kadashevich I.Y., Kusik T.P., Li Q., Lovell-Smith C., Prieto T., Schulze P., Speck O., Stucht D., Zaitsev M. Measurement and correction of microscopic head motion during magnetic resonance imaging of the brain. PLoS One. 2012;7 doi: 10.1371/journal.pone.0048088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maclaren J., Herbst M., Speck O., Zaitsev M. Prospective motion correction in brain Imaging : a review. Magn. Reson. Med. 2013;636:621–636. doi: 10.1002/mrm.24314. [DOI] [PubMed] [Google Scholar]
- Morgan V.L., Dawant B.M., Li Y., Pickens D.R. Comparison of fMRI statistical software packages and strategies for analysis of images containing random and stimulus-correlated motion. Comput. Med. Imag. Graph. 2007;31:436–446. doi: 10.1016/j.compmedimag.2007.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oakes T.R., Johnstone T., Ores Walsh K.S., Greischar L.L., Alexander A.L., Fox A.S., Davidson R.J. Comparison of fMRI motion correction software tools. Neuroimage. 2005;28:529–543. doi: 10.1016/j.neuroimage.2005.05.058. [DOI] [PubMed] [Google Scholar]
- O’Brien T.J., Wong Y.T., Moffat B.A., Grayden D.B., Cleary J.O., Oxley T.J., Yoo P.E., Mulcahy C.B., Opie N.L., Ordidge R.J., Ng A., John S.E., Farquharson S. 7T-fMRI: faster temporal resolution yields optimal BOLD sensitivity for functional network imaging specifically at high spatial resolution. Neuroimage. 2017;164:214–229. doi: 10.1016/j.neuroimage.2017.03.002. [DOI] [PubMed] [Google Scholar]
- Schulz J., Siegert T., Bazin P.L., Maclaren J., Herbst M., Zaitsev M., Turner R. Prospective slice-by-slice motion correction reduces false positive activations in fMRI with task-correlated motion. Neuroimage. 2014;84:124–132. doi: 10.1016/j.neuroimage.2013.08.006. [DOI] [PubMed] [Google Scholar]
- Stucht D., Danishad A., Schulze P., Godenschweger F., Zaitsev M., Speck O., Danishad K.A., Schulze P., Godenschweger F., Zaitsev M., Speck O. Highest resolution in vivo human brain MRI using prospective motion correction. PLoS One. 2015;10 doi: 10.1371/journal.pone.0133921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tak S., Noh J., Cheong C., Zeidman P., Razi A., Penny W.D., Friston K.J. A validation of dynamic causal modelling for 7T fMRI. J. Neurosci. Methods. 2018;305:36–45. doi: 10.1016/j.jneumeth.2018.05.002. [DOI] [PubMed] [Google Scholar]
- Todd N., Josephs O., Callaghan M.F., Lutti A., Weiskopf N. Prospective motion correction of 3D echo-planar imaging data for functional MRI using optical tracking. Neuroimage. 2015;113:1–12. doi: 10.1016/j.neuroimage.2015.03.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Der Kouwe A.J.W., Benner T., Dale A.M. Real-time rigid body motion correction and shimming using cloverleaf navigators. Magn. Reson. Med. 2006;56:1019–1032. doi: 10.1002/mrm.21038. [DOI] [PubMed] [Google Scholar]
- Walther A., Nili H., Ejaz N., Alink A., Kriegeskorte N., Diedrichsen J. Reliability of dissimilarity measures for multi-voxel pattern analysis. Neuroimage. 2016;137:188–200. doi: 10.1016/j.neuroimage.2015.12.012. [DOI] [PubMed] [Google Scholar]
- Yarach U., Luengviriya C., Danishad A., Stucht D., Godenschweger F., Schulze P., Speck O. Correction of gradient nonlinearity artifacts in prospective motion correction for 7T MRI. Magn. Reson. Med. 2015;73:1562–1569. doi: 10.1002/mrm.25283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaitsev M., Akin B., LeVan P., Knowles B.R. Prospective motion correction in functional MRI. Neuroimage. 2016;154:33–42. doi: 10.1016/j.neuroimage.2016.11.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.