Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Feb 4;20(3):1883–1889. doi: 10.1021/acs.nanolett.9b05101

Multiband Hypersound Filtering in Two-Dimensional Colloidal Crystals: Adhesion, Resonances, and Periodicity

Bartlomiej Graczykowski †,‡,*, Nicolas Vogel §, Karina Bley §, Hans-Jürgen Butt ‡, George Fytas ‡
PMCID: PMC7068716  PMID: 32017578

Abstract

graphic file with name nl9b05101_0006.jpg

The hypersonic phonon propagation in large-area two-dimensional colloidal crystals is probed by spontaneous micro Brillouin light scattering. The dispersion relation of thermally populated Lamb waves reveals multiband filtering due to three distinct types of acoustic band gaps. We find Bragg gaps accompanied by two types of hybridization gaps in both sub- and superwavelength regimes resulting from contact-based resonances and nanoparticle eigenmodes, respectively. The operating GHz frequencies can be tuned by particle size and depend on the adhesion at the contact interfaces. The experimental dispersion relations are well represented by a finite element method model enabling identification of observed modes. The presented approach also allows for contactless study of the contact stiffness of submicrometer particles, which reveals size effect deviating from macroscopic predictions.

Keywords: Colloidal crystals, phononics, acoustic band gap, Lamb waves, Brillouin light scattering, GHz signal filtering

Phonons, quanta of acoustic field, similarly as photons and electrons, are carriers of energy, momentum, and information. High-frequency phonons in the GHz-THz regime corresponding to submicrometer wavelengths are responsible for hypersound and heat transport, thus having importance for wireless communication, optomechanics, and thermal energy harvesting.1 Periodically structured materials that take advantage of the wave-like nature of phonons, such as phononic crystals (PnCs) and acoustic metamaterials, have been shown to enable new mechanical and acoustic features, including negative effective moduli and densities, frequency filtering, and acoustic cloaking.2−7 Recently, this field has experienced a tremendous growth of research in topological PnCs showing unidirectional propagation of sound immune to structural imperfections.8,9

To date, the majority of studies on PnCs and acoustic metamaterials has involved macroscopic structures aimed to affect Hz-kHz acoustic waves/phonons. Nowadays, however, there is a significant need in developing PnCs in the nanoscale and operating in GHz as well as THz frequency regimes.6,10,11 Nevertheless, nanofabrication of hypersonic PnCs faces several practical challenges preventing their implementation in everyday devices. The patterning needs to be performed over large areas/volumes of matrices being CMOS compatible for easy integration without sophisticated instrumentation. Furthermore, fabricated materials should keep structural order and coherence of GHz acoustic signals over long length scales. Self-assembly of nanoparticles has emerged as a solution for low-cost mass production.12 Propagation of GHz phonons in three-dimensional (3D) self-assembled PnCs, typically known as colloidal crystals, composed of glass or polymer nanoparticles was initially investigated by means of Brillouin light scattering (BLS).13−17 More recently, contact-based modes of colloidal crystals have been extensively studied using the pump–probe technique.18−25 This approach, unlike BLS, is limited to sub-GHz frequencies and often requires additional fabrication of a transducer for the acoustic wave generation.

Two-dimensional (2D) self-assembled PnCs, known as colloidal monolayers,12 offers a low-cost and large-area platform for harnessing high-frequency phonons. These materials, if supported by ultrathin membranes, can overcome the issue of signal/energy losses into the substrate. The use of inorganic membranes provides a mechanically robust framework serving as a waveguide for a discrete set of dispersive (Lamb) waves that can be tuned by the membrane thickness.26,27 The monolayer-membrane architecture enables use of stiff and low-losses materials which can maintain signal coherence, adding functionality to PnC. This solution goes hand in hand with new features of PnCs, that is, elastic and thermal size effects, unexplored schemes of band gap opening, as well as with experimental challenges related to their investigation and understanding in the high-frequency regime.

In this work, we study the phonon propagation in large-area 2D PnCs composed of spherical polystyrene (PS) nanoparticles self-assembled on an ultrathin Si3N4 membrane (Figure 1). We use micro BLS (μBLS)28,29 to record the dispersion of thermally populated GHz phonons. To interpret the experimental results, we develop a finite element method (FEM) model. We find significant modification of the phonon dispersion revealing three types of band gaps that are related to nanoparticle: membrane contact resonance (hybridization), lattice period (Bragg), and local resonances of nanoparticles (hybridization). The latter type, unlike for the vast majority of PnCs and metamaterials, appears above the Bragg band gap frequency, that is, in the superwavelength regime.2,3,30 All these mechanisms contribute to multiband filtering of hypersound that can be easily tailored by means of the nanoparticle size governing lattice spacing, frequencies of local resonances, and adhesion forces. Noteworthy, for the latter, we find a size effect and significant discrepancy from macroscopic predictions.

Figure 1.

Figure 1

Open in a new tab

(a) Schematic illustration of the sample and the μBLS experiment. (b) Optical image of the sample. PS monolayer is deposited over the whole top surface of Si3N4 chip, while the central bright 3 × 3 mm2 square is fully suspended. Top view SEM images of samples with nanoparticle diameter (c) d = 333 nm and (d, e) d = 430 nm. Dashed line lighter circle in (c) indicates approximately the area measured in the BLS experiment. In (d) light rhombus and cyan circles denote the lattice unit cell and the first nearest neighbors, respectively. Scale bars in (c), (d), and (e) are 2 μm, 1 μm and 100 nm, respectively.

The samples were made of hexagonally close-packed (hcp) monolayers of PS nanoparticles deposited on 3 × 3 mm2 and t = 50 nm-thick Si3N4 membranes (Figure 1b). We used emulsion polymerization31 to prepare monodispersed dispersions of PS nanoparticles, which were self-assembled on the membranes using a pre-assembly at the air/water interface and subsequent transfer to the target membrane.32 We fabricated monolayer-membrane samples with nanoparticle diameters d = 2R = 245, 333, and 430 nm, which are labeled samples B, C, and D, respectively. A pristine membrane, labeled sample A, was used as a reference. In addition, we prepared three reference samples using PS nanoparticles of the same size as those of monolayer-membrane samples albeit assembled into 3D fcc clusters by means of drop cast evaporation. Such structures were extensively investigated in prior studies13,33 and here are utilized to highlight similarities and foremost differences with 2D hcp monolayer-membrane structures. Figure 1a–e shows a schematic view of the experiment, representative optical image, and SEM images from large to small length scales, respectively. A schematic side view, representative optical, and SEM images of the monolayer-membrane samples are shown in Figure 1a–e), respectively. Typically, the in-plane translational symmetry extends over tens of micrometers.

We recorded the dispersion of acoustic waves propagating in the samples at room temperature by means of angle-resolved μBLS in p–p (TM–TM) backscattering geometry, as shown schematically in Figure 1a. The incident laser light at λ0 = 532 nm was focused on the sample by means of 10× microscope objective with 0.25 numerical aperture. The scattered light was collected by the same objective and analyzed by a tandem type Fabry–Perot interferometer. The laser spot size on the sample and the corresponding power were in the order of a few micrometers and <500 μW, respectively. BLS probes the frequency shift f of the laser light inelastically scattered by thermally populated acoustic phonons. For a pristine membrane, which is well-approximated as a homogeneous elastic continuum, the scattering wave vector q is the same as the wave vector k of the acoustic phonons. However, for periodic structures the momentum conservation defines the scattering wave vector as q = k ± G. In particular, for the hexagonal lattice 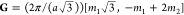Inline graphic is a reciprocal lattice vector with lattice parameter a and integers m1, m2. Following previous studies29 of thin membranes, we define the magnitude of the scattering wave vector q as q = 4π sin θ/λ0 and assume the superposition of photoelastic and moving-interface (surface ripple) effects contributing to BLS spectra. Figure 2a,b displays BLS spectra obtained for samples A and B at q = 10 μm–1, which were normalized by the thermal population factor.34 The single peak present in the spectrum of the bare membrane can be assigned to a fundamental antisymmetric (flexural, A0) Lamb plate wave mode.26 PS monolayer on top of the membrane results in increased complexity of the spectrum, as evident in Figure 2b. However, the latter spectrum is distinct from that of the corresponding 3D control sample showed in Figure 2c. Two peaks in Figure 2c are attributed to the dipolar (low frequency) and quadrupolar (higher frequency) spheroidal Lamb modes of nanoparticles.14,33 In principle, the contribution of spheroidal Lamb modes to BLS is due to the photoelastic effect and depends on deformation field and dimensionless magnification factor qR.35 For a free homogeneous sphere, eigenfrequencies of Lamb modes are given by the formula fn,l = An,lvT/d, where n and l are integers defining radial and angular dependence of the displacement, respectively, vT is the transverse speed of sound in bulk PS, and An,l is a dimensionless mode- and material-dependent parameter.33,36 The low-frequency peak in Figure 2c originates in (1,1) mode, which is nonzero as one would expect for a single sphere due to nanoparticle–nanoparticle interactions. The peak line shape resembles phonon density of states (DOS) of propagating waves in the fcc cluster, as q is ill-defined due to the light multiple scattering from the 3D cluster.14 The second peak is associated with (1,2) mode, the expected frequency of which is indicated by an arrow in Figure 2c. The asymmetry of this peak is due to contact-induced splitting of (1,2) mode into weakly dispersive branches.33 In principle, the BLS spectra of 3D clusters characterize spheroidal Lamb modes (torsional remain silent) and contain information about interparticle forces. By comparing Figure 2b,c, we notice that the asymmetric peak of (1,2) mode in the 3D fcc cluster turns into two peaks in the 2D hcp monolayer-membrane. The difference between the spectra in Figure 2b,c is even more evident in the low frequency range. The broad asymmetric peak of (1,1) mode in the 3D sample is replaced by three distinct peaks recorded in the monolayer-membrane. A similar comparison of the BLS spectra of the other samples can be found in Supporting Information (SI).

Figure 2.

Figure 2

Open in a new tab

Measured (circles) normalized BLS spectra at q = 10 μm–1 obtained for samples (a) A [membrane] and (b) B [d = 245 nm]. (c) BLS spectrum of self-assembled 3D fcc cluster made of PS nanoparticles with d = 245 nm. Solid lines correspond to Lorentzian multipeak fits of the experimental data.

Figure 3 summarizes angle-resolved μBLS measurements for all membrane-monolayer samples as dispersion relations f(q). Here, the color scale refers to the normalized intensity of the scattered light, and the circles stand for the frequencies at the peak positions. The dispersion relation of sample A displayed in Figure 3a shows only one branch that we identified as a flexural (A0) wave of a bare membrane.26 The fundamental symmetric (dilatational, S0) and shear-horizontal (SH0) modes are not BLS active due to zero (SH0) or small (S0) out-of-plane displacement (u3) for the measured range of wave numbers q.29 As follows from Figure 3b–d, the adhered monolayers in the samples B–D result in severely modified and complex dispersion relations compared to the dispersion of sample A.

Figure 3.

Figure 3

Open in a new tab

Experimental phonon dispersion relations f(q) for (a) bare 50 nm-thick Si3N4 membrane [sample A] and 50 nm membrane coated with a PS nanoparticle monolayer with diameters (b) d = 245 nm [sample B], (c) d = 333 nm [sample C], and (d) d = 430 nm [sample D]. Right-hand side bars denote band gaps (shading), where BG, CR, and LR stand for Bragg, nanoparticle–membrane contact resonance, and local resonance gap, respectively. Vertical solid lines denote the Brillouin zone boundary (ZB) at the M point. Dashed curves indicate the calculated dispersion of the fundamental antisymmetric Lamb mode (A0) of the bare membrane. Color scale indicates the BLS signal intensity normalized by the thermal phonon population factor. Circles stand for the peak position fitted by a Lorentzian function. Arrows indicate frequencies of particle–membrane contact resonance (fpm) and unperturbed spheroidal Lamb modes (fn,l).

At first glance, we can indicate three distinct effects and corresponding partial gaps related to the measured bands, that is, (i) Bragg reflections, hybridization of A0 mode with (ii) nanoparticle–membrane contact-based resonance, or (iii) spheroidal modes of nanoparticles. In each case, we define the band gaps for the modes of predominant out-of-plane displacement and indicate them only for the measured range of wave numbers q. For samples C and D, we identify clear zone folding and Bragg band gaps (BG) at frequencies f ≈ 2.5 GHz and f ≈ 1.5 GHz, respectively. This observation confirms the presence of wave-like/coherent effects and long-range order of PnCs extending over distances larger than the measured wavelengths. This phenomenon was neither observed nor modeled in previous works on similar, albeit sub-GHz, structures. Figure 3c,d suggests that the spectral position of BG can be estimated at the crossing of A0 mode and zone boundary (ZB). This provides simple geometric means for tunability of this type of a stop band, as A0 and ZB can be adjusted by the membrane thickness and nanoparticle diameter, respectively.

The horizontal branches that appear above f ≈ 2 GHz in dispersion relations of samples B–D can be attributed to the spheroidal (n,l) modes of PS nanoparticles.35,36 This assignment is supported by BLS spectra of the reference fcc clusters showing similarities with the accumulative spectra of the corresponding monolayer-membrane samples (SI, Figure S1). We use the calculated frequencies of spheroidal modes of free PS nanoparticles (arrows in Figure 3c,d) for a preliminary identification of these branches.

In Figure 3b,d, we observe a split of the f1,2 mode that is represented by two distinct branches. A similar split was not captured for sample C, probably due to adverse qR magnification factor and thereby weak scattering intensity for the (1,2) mode.35 The (1,2) mode split can be explained by the presence of nanoparticle–nanoparticle and nanoparticle–membrane contacts.23,33 We will discuss this phenomenon in more detail later in this work, making use of FEM modeling. In the case of higher order (n,l) modes, as those in the dispersion relation of sample D, it cannot be clearly stated that the mode split is experimentally resolved. Although anticipated, it could be masked by a close neighborhood of branches as for instance those related to (2,1) and (1,3) modes. Despite this ambiguity, we observe a clear hybridized interaction of the spheroidal modes with the flexural wave at frequencies above BG, as evident in Figure 3d. This results in a unique feature of membrane-based PnCs, namely, opening of the local resonance band gaps (LR) in the superwavelength regime. This phenomenon was studied theoretically for pillared membranes in terms of the impact on heat transport at THz frequencies37 and, more recently, demonstrated experimentally in the kHz regime for a macroscopic trampoline metamaterial.38

Band diagrams of samples B–D reveal contact-based modes falling below BG that is in the subwavelength regime typical for acoustic metamaterials.3,5,39 These branches are a consequence of the hybridization and avoided crossing between A0 wave and the nanoparticle–membrane contact resonance. As we will further show using FEM, this resonance originates from the spheroidal (1,1) mode. From Figures 3b–d we can conclude that corresponding contact resonance (CR) stop bands appear in the hypersonic regime but at wavelengths longer than the lattice parameter. That type of a band gap was previously observed in the sub-GHz range for acoustic metamaterials18,19,21,22,24 and modeled using Hertzian contact40,41 and van der Waals-type adhesive forces.42

The frequency of the nanoparticle–membrane resonance denoted as fpm in Figure 3 yields information about the nanoparticle–membrane adhesion force. Assuming q → 0 and negligible effect of nanoparticle–nanoparticle contacts, the normal contact stiffness KN can be determined from the two-mass oscillator equation 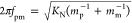Inline graphic, where mp and mm denote masses of the PS nanoparticle and corresponding fraction of the membrane, respectively (Figure 4a). Based in the latter expression, the contact resonance gap depends on the nanoparticles mass, lattice packing, and strength of the nanoparticle–membrane bonding. The determined KN is plotted in Figure 4d and compared with expected values calculated by means of Johnson–Kendall–Roberts (JKR) model.43 For small displacements around the equilibrium point in JKR model, the linearized contact stiffness KJKR (Figure 4b) is given by41,43,44

graphic file with name nl9b05101_m003.jpg 1

where Epm = 5.91 GPa is the nanoparticle–membrane effective modulus, Wpm = 0.103 J/m2 is the work of adhesion of PS-Si3N4, and R is the nanoparticle radius. Both values are derived in SI (Section II). As we can infer from Figure 4d, for each sample, the measured contact stiffness KN is about five times higher than what is predicted by JKR model. This deviation stems from additional physical bonding due to liquid or solid bridges resulting from impurities in the fabrication that are evident in SEM image in Figure 1e.25 Notably, the deviation from the model increases as the nanoparticle diameter becomes smaller. Conclusively, this manifests the impact of the real size of the contact interfaces on the phonon propagation in hypersonic colloidal PnCs in addition to the geometry and bulk elastic properties.

Figure 4.

Figure 4

Open in a new tab

(a) Schematics of the nanoparticle–membrane contact stiffness KN and (b) JKR model of nanoparticle–membrane and nanoparticle–nanoparticle contacts. (c) 3D scheme of FEM unit cell (see text). (d) Measured (BLS) and predicted (JKR) contact stiffness KN. (e) Fitted (FEM) from the experiment and predicted (JKR) contact radii of the nanoparticle–nanoparticle and nanoparticle–membrane interfaces.

Theoretical models used in previous studies18,20,45 did not consider two phenomena evident in our measurements, namely, interaction of the propagating waves with local resonances and periodicity of the material. Therefore, to capture these features and explain (1,2) mode split we developed a FEM model. Figure 4c schemes FEM 3D unit cell that includes lateral periodicity and assumes fused contacts with fully deformable spheres and membrane. PS spheres of radius R are connected to each other and to a membrane of thickness t by fully deformable circular interfaces with radii rpp and rpm, respectively. The periodicity of the structure in the x1x2 plane is implemented by applying Bloch–Floquet periodic boundary conditions to all vertical walls of the unit cell. In the fitting procedure, we used two adjustable parameters, radii of nanoparticle–membrane (rpm) and nanoparticle–nanoparticle (rpp) contact areas. In addition to the dispersion relation, we used FEM to determine the contribution of surface ripple and photoelastic mechanisms to BLS by means of two parameters ξ3 and ξR, respectively (SI, Section V). The superposition of these effects as well as size effects (membrane thickness, qR factor) are beyond the scope of this work. Further details and material properties used in the FEM model can be found in the SI (Section V).

Figure 5a shows good agreement of the calculated dispersion relation with the experimental data obtained for sample C (d = 333 nm). In addition, the experimental BLS intensity follows the calculated ξ3 that is related to the magnitude of the BLS surface ripple mechanism. The discrepancies above about 2.5 GHz can result from the simplification, that is, neglected contribution of the photoelastic effect and its interference with the moving-interface effect, which can enhance as well as cancel the BLS signal.28,29 Nevertheless, FEM allows sorting of (n,l) modes in terms of the sphere radial displacement. For that purpose we define the ξR parameter, which resembles BLS activity of Lamb modes due to photoelastic effect (SI, Section V).35 We note that this approach does not include the effect of the qR magnification factor.35Figure 5b shows the dispersion relation calculated for sample C with a color scale overlaid reflecting the magnitude of ξR. The frequency levels illustrate the split of 2l + 1 degenerate vibrations of (n,l) modes of a free sphere resulting from nanoparticle–membrane and nanoparticle–nanoparticle contacts and thereby symmetry lowering.22,33,46 For transparency, we limit the analysis to BLS active modes at q = 0. To identify the modes, we utilized FEM displacement fields showed in Figure 5c which are sorted with respect to (n,l) parent mode and the azimuthal number m. The example of (1,2) mode at q = 0 shows a split into two doublets (m = 1, m = 2) and one singlet (m = 0), which we resolve as two peaks by means of BLS. The situation is much more complex for q ≠ 0. Namely, the degeneracy is not present, and all five modes are of different frequencies. Furthermore, they interact with propagating waves in the membrane and their BLS activity varies with q. A similar analysis can be performed for all spheroidal modes undergoing mode split as schemed in Figure 5b,c. Here, for instance, (1,1) m = 0 mode with nanoparticle and membrane vibrating out-of-phase in the out-of-plane direction is the nanoparticle–membrane contact resonance. The comparison of experimental and calculated dispersion relations for samples B and D can be found in SI (Section V).

Figure 5.

Figure 5

Open in a new tab

(a, b) Dispersion relations (dashed lines) calculated for sample C [d = 333 nm] with overlaid color intensity plots indicating (a) out-of-plane displacement (ξ3) and (b) radial displacements (ξR). Circles in (a) stand for BLS experimental data. Right-hand panel of (b) schemes 2l + 1 hybridization of BLS active spheroidal (n,l) modes at q = 0 due to nanoparticle–membrane and nanoparticle–nanoparticle contacts, where m stands for the azimuthal number. Corresponding FEM displacement fields are displayed in (c).

The contact radii fitted by FEM and plotted in Figure 4e reveal a trend that follows the JKR model,33,41,42 namely 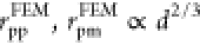Inline graphic. In principle, the JKR model allows us to predict the contact radii from the formula (Figure 4b):

graphic file with name nl9b05101_m005.jpg 2

where for the nanoparticle–membrane interface, the work of adhesion is W = Wpm = 0.1036 J/m2, effective radius is Reff = R, and Eeff = Epm = 5.91 GPa is the effective moduli. In the case of the nanoparticle–nanoparticle contact in eq 2, we substitute W = Wpp = 0.064 J/m2, Reff = R/2, and Eeff = Epp = 3.01 GPa (see SI, Sections III and IV). From Figure 4e, we can conclude that for both types of interfaces, the JKR model predicts over twice lower contact radii as compared to values fitted by FEM model for all samples. This goes along with the already mentioned underestimation of the contact stiffnesses by JKR model with respect to those measured by BLS. In principle, our results call into question the applicability of JKR model to assemblies of submicrometer particles with unavoidable fabrication imperfections.

In summary, we investigated the propagation of hypersonic phonons in large-area self-assembled 2D colloidal PnCs utilizing nondestructive μBLS technique. We showed that these materials can simultaneously host three distinct mechanisms for the phonon dispersion modification toward opening of stop bands for GHz acoustic waves. Each mechanism can be tailored by simple geometrical means as they result from (i) the lattice period, (ii) nanoparticle–membrane adhesion, and (iii) mechanical eigenmodes of nanoparticles. We found Bragg band gaps accompanied by subwavelength (contact resonance) and, noteworthy, multiple superwavelength (local resonance) gaps. We developed a finite element method model, which captured the physical phenomena with nanoparticle–nanoparticle and nanoparticle–membrane contact areas as fitting parameters. On the experimental side, we showed that μBLS provides a new means for contactless characterization of the interface mechanics at the submicrometer scale. We envision self-assembled 2D PnCs as a robust, chip-scale platform to study GHz signal processing for next-generation telecommunication devices, for tailoring sub-Kelvin thermal transport by coherent effects,47 for light–sound interaction in optomechanics and for nonlinear effects.45,48,49 These materials hold promise for downscaling topological acoustics to the hypersonic regime.

Acknowledgments

B.G. acknowledges the support from the Foundation for Polish Science (POIR.04.04.00-00-5D1B/18), Polish National Science Centre (UMO-2018/31/D/ST3/03882). The work was supported by the ERC AdG SmartPhon (grant no. 694977).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.9b05101.

  • Material properties; acumulative BLS spectra; work of adhesion; effective contact elastic constant and radius; and finite element method model (PDF)

The authors declare no competing financial interest.

Supplementary Material

nl9b05101_si_001.pdf (5.6MB, pdf)

References

  1. Volz S.; Ordonez-Miranda J.; Shchepetov A.; Prunnila M.; Ahopelto J.; Pezeril T.; Vaudel G.; Gusev V.; Ruello P.; Weig E. M.; et al. Nanophononics: state of the art and perspectives. Eur. Phys. J. B 2016, 89, 15. 10.1140/epjb/e2015-60727-7. [DOI] [Google Scholar]
  2. Hussein M. I.; Leamy M. J.; Ruzzene M. Dynamics of phononic materials and structures. Historical origins, recent progress, and future outlook. Appl. Mech. Rev. 2014, 66, 040802 10.1115/1.4026911. [DOI] [Google Scholar]
  3. Deymier P. A.Acoustic metamaterials and phononic crystals; Springer Science+Business Media: New York, 2013; Vol. 173. [Google Scholar]
  4. Laude V.Phononic crystals: artificial crystals for sonic, acoustic, and elastic waves; Walter de Gruyter GmbH & Co KG: Berlin, 2015; Vol. 26. [Google Scholar]
  5. Khelif A.; Adibi A.. Phononic Crystals; Springer Science+Business Media: New York, 2015. [Google Scholar]
  6. Maldovan M. Phonon wave interference and thermal bandgap materials. Nat. Mater. 2015, 14, 667. 10.1038/nmat4308. [DOI] [PubMed] [Google Scholar]
  7. Graczykowski B.; Sledzinska M.; Alzina F.; Gomis-Bresco J.; Reparaz J.; Wagner M.; Torres C. S. Phonon dispersion in hypersonic two-dimensional phononic crystal membranes. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 91, 075414 10.1103/PhysRevB.91.075414. [DOI] [Google Scholar]
  8. Mousavi S. H.; Khanikaev A. B.; Wang Z. Topologically protected elastic waves in phononic metamaterials. Nat. Commun. 2015, 6, 8682. 10.1038/ncomms9682. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Wang P.; Lu L.; Bertoldi K. Topological Phononic Crystals with One-Way Elastic Edge Waves. Phys. Rev. Lett. 2015, 115, 104302. 10.1103/PhysRevLett.115.104302. [DOI] [PubMed] [Google Scholar]
  10. Benchabane S.; Reinhardt A.. Fundamentals and Applications of Acoustic Metamaterials; John Wiley & Sons, Ltd: Hoboken, NJ, 2019; Chapter 8, pp 207–262. [Google Scholar]
  11. Yazdani N.; Jansen M.; Bozyigit D.; Lin W. M.; Volk S.; Yarema O.; Yarema M.; Juranyi F.; Huber S. D.; Wood V. Nanocrystal superlattices as phonon-engineered solids and acoustic metamaterials. Nat. Commun. 2019, 10, 4236. 10.1038/s41467-019-12305-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Vogel N.; Retsch M.; Fustin C.-A.; del Campo A.; Jonas U. Advances in colloidal assembly: the design of structure and hierarchy in two and three dimensions. Chem. Rev. 2015, 115, 6265–6311. 10.1021/cr400081d. [DOI] [PubMed] [Google Scholar]
  13. Cheng W.; Wang J.; Jonas U.; Fytas G.; Stefanou N. Observation and tuning of hypersonic bandgaps in colloidal crystals. Nat. Mater. 2006, 5, 830. 10.1038/nmat1727. [DOI] [PubMed] [Google Scholar]
  14. Mattarelli M.; Montagna M.; Still T.; Schneider D.; Fytas G. Vibration spectroscopy of weakly interacting mesoscopic colloids. Soft Matter 2012, 8, 4235–4243. 10.1039/c2sm07034k. [DOI] [Google Scholar]
  15. Akimov A. V.; Tanaka Y.; Pevtsov A. B.; Kaplan S. F.; Golubev V. G.; Tamura S.; Yakovlev D. R.; Bayer M. Hypersonic Modulation of Light in Three-Dimensional Photonic and Phononic Band-Gap Materials. Phys. Rev. Lett. 2008, 101, 033902 10.1103/PhysRevLett.101.033902. [DOI] [PubMed] [Google Scholar]
  16. Wu S.; Zhu G.; Zhang J. S.; Banerjee D.; Bass J. D.; Ling C.; Yano K. Anisotropic lattice expansion of three-dimensional colloidal crystals and its impact on hypersonic phonon band gaps. Phys. Chem. Chem. Phys. 2014, 16, 8921–8926. 10.1039/c4cp00498a. [DOI] [PubMed] [Google Scholar]
  17. Still T.; Cheng W.; Retsch M.; Sainidou R.; Wang J.; Jonas U.; Stefanou N.; Fytas G. Simultaneous Occurrence of Structure-Directed and Particle-Resonance-Induced Phononic Gaps in Colloidal Films. Phys. Rev. Lett. 2008, 100, 194301. 10.1103/PhysRevLett.100.194301. [DOI] [PubMed] [Google Scholar]
  18. Boechler N.; Eliason J. K.; Kumar A.; Maznev A. A.; Nelson K. A.; Fang N. Interaction of a Contact Resonance of Microspheres with Surface Acoustic Waves. Phys. Rev. Lett. 2013, 111, 036103 10.1103/PhysRevLett.111.036103. [DOI] [PubMed] [Google Scholar]
  19. Khanolkar A.; Wallen S.; Abi Ghanem M.; Jenks J.; Vogel N.; Boechler N. A self-assembled metamaterial for Lamb waves. Appl. Phys. Lett. 2015, 107, 071903 10.1063/1.4928564. [DOI] [Google Scholar]
  20. Wallen S. P.; Maznev A. A.; Boechler N. Dynamics of a monolayer of microspheres on an elastic substrate. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 92, 174303. 10.1103/PhysRevB.92.174303. [DOI] [Google Scholar]
  21. Hiraiwa M.; Abi Ghanem M.; Wallen S. P.; Khanolkar A.; Maznev A. A.; Boechler N. Complex Contact-Based Dynamics of Microsphere Monolayers Revealed by Resonant Attenuation of Surface Acoustic Waves. Phys. Rev. Lett. 2016, 116, 198001. 10.1103/PhysRevLett.116.198001. [DOI] [PubMed] [Google Scholar]
  22. Vega-Flick A.; Duncan R.; Wallen S.; Boechler N.; Stelling C.; Retsch M.; Alvarado-Gil J.; Nelson K.; Maznev A. Vibrational dynamics of a two-dimensional microgranular crystal. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 96, 024303 10.1103/PhysRevB.96.024303. [DOI] [Google Scholar]
  23. Vega-Flick A.; Duncan R.; Wallen S.; Boechler N.; Stelling C.; Retsch M.; Alvarado-Gil J.; Nelson K.; Maznev A. Contact-based and spheroidal vibrational modes of a hexagonal monolayer of microspheres on a substrate. Wave Motion 2018, 76, 122–133. 10.1016/j.wavemoti.2017.10.010. [DOI] [Google Scholar]
  24. Otsuka P. H.; Mezil S.; Matsuda O.; Tomoda M.; Maznev A. A.; Gan T.; Fang N.; Boechler N.; Gusev V. E.; Wright O. B. Time-domain imaging of gigahertz surface waves on an acoustic metamaterial. New J. Phys. 2018, 20, 013026 10.1088/1367-2630/aa9298. [DOI] [Google Scholar]
  25. Abi Ghanem M.; Khanolkar A.; Wallen S. P.; Helwig M.; Hiraiwa M.; Maznev A. A.; Vogel N.; Boechler N. Longitudinal eigenvibration of multilayer colloidal crystals and the effect of nanoscale contact bridges. Nanoscale 2019, 11, 5655. 10.1039/C8NR08453J. [DOI] [PubMed] [Google Scholar]
  26. Lamb H. On waves in an elastic plate. Proc. R. Soc. London, Ser. A 1917, 93, 114–128. [Google Scholar]
  27. Graczykowski B.; Gomis-Bresco J.; Alzina F.; Reparaz J.; Shchepetov A.; Prunnila M.; Ahopelto J.; Torres C. S. Acoustic phonon propagation in ultra-thin Si membranes under biaxial stress field. New J. Phys. 2014, 16, 073024 10.1088/1367-2630/16/7/073024. [DOI] [Google Scholar]
  28. Graczykowski B.; Sledzinska M.; Placidi M.; Saleta Reig D.; Kasprzak M.; Alzina F.; Sotomayor Torres C. Elastic Properties of Few Nanometers Thick Polycrystalline MoS2Membranes: A Nondestructive Study. Nano Lett. 2017, 17, 7647–7651. 10.1021/acs.nanolett.7b03669. [DOI] [PubMed] [Google Scholar]
  29. Graczykowski B.; Gueddida A.; Djafari-Rouhani B.; Butt H.-J.; Fytas G. Brillouin light scattering under one-dimensional confinement: Symmetry and interference self-canceling. Phys. Rev. B: Condens. Matter Mater. Phys. 2019, 99, 165431. 10.1103/PhysRevB.99.165431. [DOI] [Google Scholar]
  30. Liu Z.; Zhang X.; Mao Y.; Zhu Y.; Yang Z.; Chan C. T.; Sheng P. Locally resonant sonic materials. Science 2000, 289, 1734–1736. 10.1126/science.289.5485.1734. [DOI] [PubMed] [Google Scholar]
  31. Qiu D.; Cosgrove T.; Howe A. M. Narrowly Distributed Surfactant-Free Polystyrene Latex with a Water-Soluble Comonomer. Macromol. Chem. Phys. 2005, 206, 2233–2238. 10.1002/macp.200500306. [DOI] [Google Scholar]
  32. Vogel N.; Goerres S.; Landfester K.; Weiss C. K. A Convenient Method to Produce Close-and Non-close-Packed Monolayers using Direct Assembly at the Air–Water Interface and Subsequent Plasma-Induced Size Reduction. Macromol. Chem. Phys. 2011, 212, 1719–1734. 10.1002/macp.201100187. [DOI] [Google Scholar]
  33. Kim H.; Cang Y.; Kang E.; Graczykowski B.; Secchi M.; Montagna M.; Priestley R. D.; Furst E. M.; Fytas G. Direct observation of polymer surface mobility via nanoparticle vibrations. Nat. Commun. 2018, 9, 2918. 10.1038/s41467-018-04854-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. YU P.; Cardona M.. Fundamentals of Semiconductors: Physics and Materials Properties, 4th ed.; Graduate Texts in Physics; Springer-Verlag: Berlin, 2010. [Google Scholar]
  35. Still T.; Mattarelli M.; Kiefer D.; Fytas G.; Montagna M. Eigenvibrations of submicrometer colloidal spheres. J. Phys. Chem. Lett. 2010, 1, 2440–2444. 10.1021/jz100774b. [DOI] [Google Scholar]
  36. Lamb H. On the Vibrations of an Elastic Sphere. Proceedings of the London Mathematical Society 1881, s1–13, 189–212. 10.1112/plms/s1-13.1.189. [DOI] [Google Scholar]
  37. Davis B. L.; Hussein M. I. Nanophononic metamaterial: Thermal conductivity reduction by local resonance. Phys. Rev. Lett. 2014, 112, 055505 10.1103/PhysRevLett.112.055505. [DOI] [PubMed] [Google Scholar]
  38. Bilal O. R.; Foehr A.; Daraio C. Observation of trampoline phenomena in 3D-printed metamaterial plates. Extreme Mechanics Letters 2017, 15, 103–107. 10.1016/j.eml.2017.06.004. [DOI] [Google Scholar]
  39. Maznev A. A.; Gu G.; yuan Sun S.; Xu J.; Shen Y.; Fang N.; yi Zhang S. Extraordinary focusing of sound above a soda can array without time reversal. New J. Phys. 2015, 17, 042001 10.1088/1367-2630/17/4/042001. [DOI] [Google Scholar]
  40. Hertz H. On the contact of elastic solids. J. reine angew. Math 1881, 92, 156. [Google Scholar]
  41. Johnson K. L.Contact mechanics; Cambridge university press: Cambridge, UK, 1987. [Google Scholar]
  42. Israelachvili J.Intermolecular and Surface Forces; Elsevier Science: Amsterdam, 2015. [Google Scholar]
  43. Johnson K. L.; Kendall K.; Roberts A. Surface energy and the contact of elastic solids. Proceedings of the royal society of London. A. mathematical and physical sciences 1971, 324, 301–313. 10.1098/rspa.1971.0141. [DOI] [Google Scholar]
  44. Saeedi Vahdat A.; Azizi S.; Cetinkaya C. Nonlinear dynamics of adhesive micro-spherical particles on vibrating substrates. J. Adhes. Sci. Technol. 2013, 27, 1712–1726. 10.1080/01694243.2012.751521. [DOI] [Google Scholar]
  45. Wallen S.; Lee J.; Mei D.; Chong C.; Kevrekidis P.; Boechler N. Discrete breathers in a mass-in-mass chain with Hertzian local resonators. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 2017, 95, 022904 10.1103/PhysRevE.95.022904. [DOI] [PubMed] [Google Scholar]
  46. Girard A.; Gehan H.; Mermet A.; Bonnet C.; Lermé J.; Berthelot A.; Cottancin E.; Crut A.; Margueritat J. Acoustic mode hybridization in a single dimer of gold nanoparticles. Nano Lett. 2018, 18, 3800–3806. 10.1021/acs.nanolett.8b01072. [DOI] [PubMed] [Google Scholar]
  47. Zen N.; Puurtinen T. A.; Isotalo T. J.; Chaudhuri S.; Maasilta I. J. Engineering thermal conductance using a two-dimensional phononic crystal. Nat. Commun. 2014, 5, 3435. 10.1038/ncomms4435. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Bunyan J.; Vakakis A. F.; Tawfick S. Mechanisms for impulsive energy dissipation and small-scale effects in microgranular media. Phys. Rev. E 2015, 92, 062206 10.1103/PhysRevE.92.062206. [DOI] [PubMed] [Google Scholar]
  49. Wallen S. P.; Boechler N. Shear to longitudinal mode conversion via second harmonic generation in a two-dimensional microscale granular crystal. Wave Motion 2017, 68, 22–30. 10.1016/j.wavemoti.2016.08.009. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl9b05101_si_001.pdf (5.6MB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES