Simultaneous Training on Overlapping Grapheme Phoneme Correspondences Augments Learning and Retention

Abstract

An important component of learning to read is the acquisition of letter-to-sound- mappings. The sheer quantity of mappings and many exceptions in opaque languages such as English suggests that children may use a form of statistical learning to acquire them. However, while statistical models of reading are item-based, reading instruction typically focuses on rule-based approaches involving small sets of regularities. This discrepancy poses the question of how different groupings of regularities, an unexamined factor of most reading curricula, may impact learning. Exploring the interplay between item statistics and rules, this study investigated how consonant variability, an item-level factor, and the degree of overlap among the to-be-trained vowel strings, a group-level factor, influence learning. English-speaking first graders (N = 361) were randomly assigned to be trained on vowel sets with high overlap (e.g., EA, AI) or low overlap (e.g., EE, AI); this was crossed with a manipulation of consonant frame variability. While high vowel overlap led to poorer initial performance, it resulted in more learning when tested immediately and after a two-week-delay. There was little beneficial effect of consonant variability. These findings indicate that online letter/sound processing impacts how new knowledge is integrated into existing information. Moreover, they suggest that vowel overlap should be considered when designing reading curricula.

1. Introduction

1.1. The Complexity of Learning to Read

Literacy is correlated with academic success (National Reading Panel, 2000) and life outcomes (e.g., Beck, McKeown, & Kucan, 2002). However, 60% of students in the United States lack basic reading skills (U.S. Department of Education, National Center for Education Statistics, 2010). This may in part be due to the complexity of the problem children face: Reading a sentence requires word recognition, use of text conventions, and syntactic and semantic processing. Even the most elemental aspect of reading—isolated word recognition—is complex, as the sound-spelling system of many languages is irregular and children must sort through a large number of lexical candidates.

There are too many words for children to memorize their forms. As a result, in alphabetic languages phonics-based curricula teach children to map letters to sounds. This mapping offers children generalizable regularities (so-called grapheme-phoneme-correspondence [GPC] regularities) that allow a child to access the sound of an unfamiliar word from its spelling. For example, once a child learns that EA makes the /i/ sound, he or she can read a variety of words like MEAT and GLEAM. Thus, one critical aspect of learning to read is acquiring GPC regularities.¹

There has been growing interest in applying principles of learning from cognitive science to education (e.g., Apfelbaum, Hazeltine, & McMurray, 2013; Kellman, Massey, & Son, 2010; Rohrer, Dedrick, & Stershic, 2015). The present study builds on this effort to examine the acquisition of GPC mappings to support decoding skills. We focus on a disconnect between statistical learning theories of reading acquisition that emphasize exposure to large numbers of items and common classroom approaches that emphasize teaching rules.

1.2. Statistical Learning

In English and other orthographically deep languages, GPC regularities are only quasi-regular. For any “rule” (e.g., EA→/i/), there are many exceptions (e.g., STEAK) and sub-regularities (e.g., HEAD, DEAD; Seidenberg, 2005). Thus, acquiring these regularities can be challenging.

This quasi-regularity of many languages motivates the hypothesis that GPC mappings are acquired via statistical learning mechanisms that track predictive relationships among letters, and between letters and sounds (Seidenberg, 2005). Supporting this, statistical learning ability (in isual and auditory domains) is correlated with reading outcomes (Arciuli & Simpson, 2012; Qi, Sanchez Araujo, Georgan, Gabrieli, & Arciuli, 2019; Raviv & Arnon, 2018; Spencer, Kaschak, Jones, & Lonigan, 2015). Moreover, the pattern of children’s spelling errors often conforms to the statistical structure of the input (Pollo, Kessler, & Treiman, 2009; Thompson, Fletcher-Flinn, & Cottrell, 1999; Treiman, Gordon, Boada, Peterson, & Pennington, 2014; but see Sénéchal, Gingras, & L’Heureux, 2016) and children are sensitive to consonantal context when spelling vowels in nonwords (Treiman & Kessler, 2006). Together, these data suggest that the acquisition of sound/spelling correspondence may derive from statistical learning. While the general relationship between statistical learning and reading is well-supported, it is not clear how it develops and/or what other factors influence the extent to which statistical learning occurs (see recent special issues Alt, 2018; Elleman, Steacy, & Compton, 2019 as well as Schmalz, Moll, Mulatti, & Schulte-Körne, 2018 for a discussion).

In models of statistical learning, learning is fundamentally item-based and GPC regularities are not explicitly stored: Learning a GPC regularity is conceptualized as emergent from experience with individual words. In this case, children are not acquiring individual regularities, but a system of mappings that “works” across all words. Supporting this, Armstrong et al. (2017) showed that after adults are taught a small set of nonwords with irregular pronunciations, they spontaneously generalize this to a new set of untrained nonwords.

While this documents a potential role of statistical learning, it is unclear how to use this to improve instruction or remediation. Apfelbaum, Hazeltine, & McMurray, 2013 offered a first step by manipulating item-level statistics (e.g., within the set of words used in training) to promote acquisition of GPC regularities for vowels. In English, vowels are most challenging for early readers, as they are less regular than consonants (Fowler, Liberman, & Shankweiler, 1977; Näslund, 1999) and may be harder to process (New, Araújo, & Nazzi, 2008).

When confronted with a whole word (e.g., TEAM), a child must learn that the vowel letters (EA) are most predictive of the vowel pronunciation, not the consonants. However, if children initially weighted all letters equally, this could create problems. If the child was trained on words with similar consonants (as is typical in many curricula), they might acquire spurious associations between the vowel pronunciation and the consonants. This could impair learning and hinder generalization (see Juel & Roper-Schneider, 1985). For example, after exposure to HAT, CAT and MAT, the child could learn that the /æ/ sound is predicted by AT, not by A. The solution to this problem is to train on items that are more variable on irrelevant dimensions (Rost, and McMurray, 2009; Gómez, 2002), so that only the vowels consistently predict pronunciation.

To test this, Apfelbaum, Hazeltine, & McMurray, 2013 trained children on six GPC regularities (three digraphs and three short vowels) using a computer-based reading intervention that implemented a variety of sound/spelling tasks (Foundations in Learning, 2010). Target vowels were embedded in training word-lists in which consonants were either similar (e.g., MET, PET, MOAT, POT) or variable (e.g., MET, LEG, LOAF, TOP). Children in the variable condition showed larger gains at post-test for trained and novel words. Thus, manipulations at the item-level—motivated by a learning theory—can benefit instruction.

Apfelbaum, Hazeltine, & McMurray, 2013 findings are consistent with a naïve associative account of statistical learning (i.e., the blind tracking of items’ co-occurrence): Variability impedes the formation of incorrect associations between consonant letters and the vowel phonemes, while similarity in the consonant frames reinforces them.

1.3. Explicit Teaching of Regularities

Where statistical learning focuses on statistics across items, reading instruction is typically structured around regularities. The emphasis on regularities offers practical benefits: Explicit regularities can be easily described and conceptualized explicitly, allowing students to bootstrap learning. However, there are too many GPC regularities to teach them all. Thus, curricula often focus on GPC regularities that generalize to a large number of words (c.f., Fry, 1964), permitting children to learn many new words independently (Share, 1995). Further constraining the space, typical curricula focus on only a subset of these regularities at a time (e.g., short vowels) to make it easier to conceptualize the regularities.

In contrast, statistical learning emphasizes properties of individual items and only treats regularities as emergent. In this case, the optimal training set for instruction should mirror the distribution of letters in the language (e.g., in the extreme, all possible items). Consequently, the groupings imposed by typical curricula limit the range of statistics that children are exposed to and may bias learning. Importantly, because these groupings are brief and change over the course of the curricula (e.g., children are exposed to short vowels for a week or two and then long vowels), this can create further local biases in the statistics.

1.4. Structuring Items and Regularities to Promote Learning

Little research has examined how the grouping of GPC regularities affects learning. For example, the short vowels E (as in MET) and A (CAP) are typically grouped in most curricula. However, discriminating different GPCs within a class (e.g., short vowels) may be a trivial memorization process since they have no letters in common. In contrast, a harder problem may be discriminating a word that includes an E and makes the /ε/ sound (like MEN) from one that includes an E and makes the /i/ sound (like MEAN). Thus, grouping GPC regularities that have no letters in common may not offer any benefits. As this example illustrates, understanding how learning is impacted by structure at the level of the generalizable regularities (in addition to structure at the item-level) may have consequences for the basic understanding of how children learn to read, as well as implications for structuring curricula.

The present study examined this issue, focusing on whether or not instruction should group GPC regularities whose orthographic forms “overlap”. In digraph vowels, letters can combine to represent a phoneme(s) (as in EA, AI, OI). Unlike the consonant manipulations of Apfelbaum, Hazeltine, & McMurray, 2013, where the consonants need to be ignored, here the conjunction of letters is critical, and the challenge is to map the combination of letters to a sound that may not be associated with either individual letter. For example, OA and EA both contain an A, and A can also function in isolation. All three strings however map to different phonemes, making the interpretation of A contextually dependent. Most curricula do not systematically consider this type of overlap, instead grouping regularities by conceptually related regularities (e.g., long vowels).

We contrast two predictions. First, the naïve associative account (Gough & Juel, 1991; Juel & Roper-Schneider, 1985) suggests overlapping vowels may be more difficult to learn, as the same individual letters must be associated with different sounds. However, variability in consonant frames could highlight the overlapping vowels as a unit, potentially mitigating the effect of overlap. Alternatively, statistical learning has also been conceptualized in terms of acquiring a system of mappings (e.g., as in connectionist models). Here, overlap may be advantageous: Connectionist modeling suggests that new information that is consistent with established knowledge may be more easily integrated with existing schemas (McClelland, 2013). This “schema-based” account predicts that simultaneous training on overlapping GPC should benefit learning. It is unclear whether consonant variability will interact with overlap under this view.

1.5. The Present Study

To distinguish these hypotheses, we taught first graders a small number of GPC regularities for short vowels and digraphs over several days. Overlap was manipulated via the sets of vowels children were trained and tested on. These either maximized shared letters across the set (EA, OA, OI, AI, E, O) or minimized them (AI, OO, EE, OU, I, U). To relate this regularity-based manipulation to an item-based factor, we further asked if the role of overlap is moderated by consonant variability. Consonant variability was manipulated by selecting words that either had variable or similar consonant frames. This led to a 2×2 between-subjects design.

To deliver training and testing, we repurposed an internet-based reading intervention program (Foundations in Learning, 2010). We tested first graders for two reasons. First, they match the children tested in Apfelbaum, Hazeltine, & McMurray, 2013, allowing us to follow-up on the effect of variability. Second, they are still in the process of acquiring these GPC mappings, so they were unlikely to perform at ceiling but had sufficient skills to perform the tasks.

Students’ baseline ability was first assessed with a pre-test, incorporating a variety of simple tasks tapping the six GPC regularities. They then completed training with feedback on each trial over approximately one week, followed by a post-test. We also included a third testing point one to two weeks later to assess retention. Unlike Apfelbaum, Hazeltine, & McMurray, 2013, GPCs were fully interleaved across training to improve learning and maximize the effect of overlap (Carvalho & Goldstone, 2014).

2. Method

2.1. Overview

The experiment included four phases: pre-test, training, post-test and retention. Pre-test, post-test and retention had an identical design. There were four experimental conditions (high overlap/low overlap GPCs × similar/variable consonants). These were crossed with two conditions for counterbalancing task order (A/B). Overlap was manipulated throughout the experiment, whereas variability was only manipulated during training.

2.2. Participants

Participants were 316 first-grade students (average age: 6.46 years) from eight elementary schools in the [removed for review]. All first-grade students without an Individualized Education Plan for a learning disability were invited to participate. Approximately 50% of first graders in the eight schools participated, yielding a wide distribution of reading abilities. Of the 316 students enrolled in the study, 281 completed pre-test, training and post-test. The remaining 35 withdrew during pre-test or training or were excluded based on behavioral issues reported by the research staff (who were not aware of the hypotheses or students’ conditions). Two children did not complete post-test immediately after training but did complete retention; their data was analyzed for the retention phase only. Two additional children completed post-test data five days after end of training (and they completed retention shortly after). We excluded their post-test, but kept their retention data in the analysis. Thus, data from 277 children were analyzed at post-test, and from 267 at retention.

The final sample included 32 non-native English speakers, roughly equally distributed across conditions. These children’s data were included, as English language learner status did not interact with experimental factors in similar work (Apfelbaum, Hazeltine, & McMurray, 2013). Table 1 shows the demographic breakdown of the groups.

Table 1.

Demographic breakdown of participants across conditions for the final dataset.

		High Overlap		Low Overlap		Total
		Variable	Similar	Variable	Similar
Gender	Boys	35	33	33	38	139
	Girls	37	32	38	35	142
First Language	English	67	57	62	63	249
	Other	5	8	9	10	32

We obtained children’s reading assessment scores on the Fountas and Pinnell Benchmark Assessment System from the school district. Letter scores (A through Y) were converted to an ordinal scale, ranging from 0 to 23 with an average of 6.74 (SD = 4.08). A score of 6 or 7 (equivalent to letter scores F and G) roughly maps onto the upper level of what is expected for first graders (Fountas & Pinnell, 2011). Moreover, the range and standard deviation of scores suggest a fair amount of variability in students’ reading ability. Participants’ reading scores were used as a between-subject factor for moderator analyses (see Supplemental Online Materials S2).

2.3. Design

2.3.1. Overlap

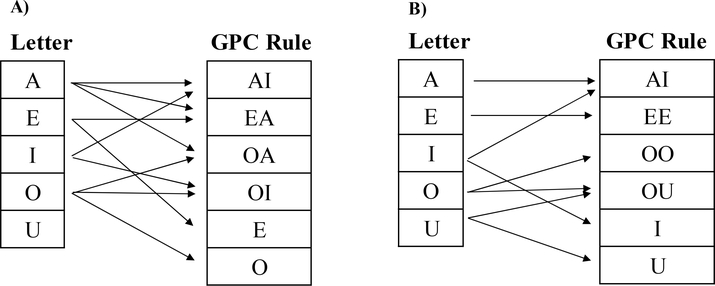
Children learned one of two sets of six GPC regularities (high overlap/low overlap). These GPC regularities captured common digraphs and monographs of English that have high spelling-sound consistency. Each set included two short vowels (e.g. E as in MEN or O as in POT) and four digraphs (e.g. EA as in MEAN or AI as in MAIL; Figure 1, Table 2). One vowel (AI) was used in both overlap conditions. Each GPC regularity represented the dominant pronunciation for the given letter string (see Table 2, Supplement S1). Thus, our investigation focuses on learning the most regular GPCs (not exception or secondary pronunciations).

Figure 1:

Visual depiction of vowel overlap in A) high overlap and B) low overlap condition.

Table 2.

GPC regularities used.

Group	Letters	Sound (Phoneme)	Examples	Percent Consistent	n	N Overlaps
High Overlap	AI+	eɪ	bait, gain, mail	98.7	87	3
	EA*	i	mean, heat, beam	77.4	164	3
	OA*	ou	coal, goat soap	98.1	53	4
	OI	ɔɪ	foil, coin, soil	100	35	3
	E*	ɛ	red, met, pen	100	272	1
	O*	ɑ	pot, hot, rod	82.4	267	2
Low Overlap	AI+	eɪ	bait, gain, mail	98.7	87	1
	OO*	u	food, roof, pool	76.7	133	1
	EE*	i	feel, feed, teen	100	127	0
	OU	aʊ	hour, noun, loud	54.8	146	2
	I*	ɪ	lid, hit, tin	93.0	491	1
	U*	ʊ	but, mud, run	96.4	305	1

Note. N refers to the number of monosyllables in the MRC psycholinguistic database that include that vowel string; regularity is the proportion of monosyllables that include that string and are pronounced with the target phoneme.

⁺indicates GPC rule that appears in both groups

^*’s indicate GPC regularities for which screener data was available. While OU’s regularity may seem low, it had a total of six pronunciations, and the next highest only appeared in 19.2% of the items.

Given only five vowel letters, it was not possible to construct completely non-overlapping sets. On average, each GPC regularity in the high overlap set shared a letter with 2.67 others (range 1–4), where each regularity in the low overlap set shared a letter with 1.0 other regularities (range 0–2). The GPC regularities in each condition were balanced on overall difficulty using procedures outlined in Supplement S1.

2.3.2. Variability

Within each overlap condition, there were two item lists that differed in the amount of variability in the consonants. Similar item lists included words that shared one or both consonants (e.g. MEAL, MOAN, PEN, MEN); words in the variable group were selected to minimize the number of shared consonants. For more information on how variability was manipulated and items were selected, see Supplement S1.

2.3.3. Relation of Overlap and Variability to Phase

The overlap manipulation was based on the set of GPCs children were trained on (not individual items). Thus, overlap condition controlled the words used in all experiment phases (training and tests). In contrast, variability was an item-level manipulation of the consonants that did not affect the GPCs. Consequently, the variability manipulation only affected the items used in training.

This led to a hybrid random assignment scheme. First, participants were assigned to the overlap condition at the onset of the experiment, balancing gender, school, and language status. After pre-test, we performed random assignment to the respective variability condition. Since pre-test ability was known at this point, assignment for variability could balance pre-test scores in addition to demographic factors and task set. This procedure meant that while pre-test scores were well-matched within variability conditions, pre-test scores were not matched across overlap condition as anticipated (also see Results section).

2.3.4. Tasks

To ensure that training and testing tapped a robust ability and to keep students engaged, eight tasks were used (Table 3). For any given subject, two tasks were not included in training, and only appeared in testing to assess generalization. We counterbalanced which tasks were held out for generalization testing with two sets (A/B).

Table 3.

Tasks used. Two of the testing tasks could also appear in training; these are marked as ‘trained’. Tasks that only appeared in testing are marked as ‘generalization’.

Experiment Phase	Task	Description	Task-Type	Testing Role
				A	B
Testing	Find the Word	Hear a word played and find that word among ten displayed alternatives.	Recognition	Generalization	Trained
	Fill in the Blank (Nonword)	Hear a nonword and see a consonant frame and ten vowel options. Choose which vowel completes the played nonword.	Spelling	Generalization	Trained
	Make the Word	Hear a word and choose the letters to spell it from ten displayed alternatives for each position.	Spelling	Trained	Generalization
	Nonword Family	Hear the vowel and coda consonant of a nonword and find the nonword that contains those sounds among ten alternatives.	Recognition	Trained	Generalization
Training	Word Family	Hear the vowel and coda consonant of a word and find the word that contains those sounds among ten alternatives.	Recognition	Not applicable
	Change the Word (Vowel)	See a consonant frame and ten vowel options. Asked aurally to change one word to another.	Spelling
	Find the Nonword	Hear a word played and find that nonword among ten displayed alternatives.	Recognition
	Change the Nonword (Initial)	See vowel and offset consonant and ten onset consonants. Asked to change one nonword to another.	Spelling

Students performed each closed set task in multiple blocks of 10 trials, switching frequently. Tasks were grouped into “cycles”; each cycle included a task selection screen. After completing the tasks in a cycle, they advanced to the next. Half of the tasks used real words and the other half nonwords. Nonwords allowed a more thorough manipulation of the overall amount of consonant variability and a more direct test of grapheme→phoneme knowledge, since children cannot perform well by “memorizing” the word. Each trial included ten response options (chance = 10%). Foil responses were drawn from other items within that block, unless this would have led to repetitions. In the latter case, additional foils were added to create ten unique options.

2.3.4. Testing

Each test (pre-test, post-test and retention) consisted of three cycles of four tasks, resulting in 120 total trials. Items differed between overlap conditions to reflect the different GPC regularities but were identical between the similar and variable conditions. For each GPC regularity and item-type (word/nonword), five types of items were tested: two trained words, two untrained (generalization) words from the same GPC regularity, and a baseline word not from any of the trained GPC regularities. Items were presented three times during test.

Words were randomly assigned to block in a fixed order for each student, roughly balancing the number of items from each GPC regularity within a block. Within a block, item order was random. During testing, students did not receive feedback.

Testing sessions were run over two days; participants were logged out automatically of the program after completing 60 trials (halfway through cycle 2). The following day, they completed the remaining 60 trials. Pre-test generally occurred on Thursday and Friday to allow for the second phase of random assignment over the weekend, though some children missed a day, and pre-test was extended to the following week. Post-test was conducted on the day immediately after the last day of training (or the following Monday, if training finished on a Friday). Retention was conducted at least a week after post-test (though typically two weeks), depending on the school’s schedule.

2.3.5. Training

Training consisted of five cycles of six tasks, for a total of 300 training trials. Training items differed as a function of overlap and similarity. There were an equal number of trials for each GPC regularity, roughly equal within tasks. For each GPC regularity, five words and five nonwords were selected (60 items total). Each item was repeated five times during training.

During training, children always received feedback via three mechanisms. First, they heard a high tone for correct answers, and a low tone for incorrect ones. Second, on incorrect trials, students repeated the trial after hearing “Try again!”. On repetitions, the initial choice was removed from the screen, and for spelling tasks, buttons were added to allow the child to hear the sound corresponding to each response. Use of the buttons was optional and infrequent. If the child responded incorrectly twice, they were told the correct answer. A score accumulated across trials within each task. Children received 10 points for a correct answer on the initial attempt, and 5 on the second.

On each training day, participants ran for a fixed period of 20 minutes at which point they were automatically logged out of the system, and would continue where they had left of the following day. When participants completed the total number of training trials, they were done.

2.4. Items and Stimuli

Items were matched on frequency, imageability, concreteness and neighborhood density across conditions (Supplement S1). All words, training instructions, letter cues as well as carrier sentences were recorded by a phonetically trained native speaker of English. Recordings were conducted in a sound-attenuated room using a Kay Elemetrics CSL 4300b (Kay Elemetrics Corp., Lincoln Park, NJ) at 44,100-Hz sampling rate. For each item, the speaker produced 3–5 exemplars in a neutral carrier phrase. These recordings underwent noise reduction using Audacity (Audacity Team, 2014), to remove background noise. Next, the clearest exemplar of a given item was selected from the phrase. 50msec of silence was then spliced onto the onset and offset of each word, followed by amplitude normalization using Praat (Boersma & Weenink, 2016).

2.5. Procedures

The study was conducted between February and May 2014. Pre-test, training and post-test lasted for about 1.5 weeks at a given school with an additional two days of retention testing. Stimuli were presented over high-quality headphones to minimize disruption from other students taking part in the study at the same time.

After logging in, children saw a task selection screen which displayed icons for all possible tasks. Completed tasks were marked with a checkmark and showed how many points were awarded within that task (during training). After completing a cycle, participants were presented with a new task selection screen in a new color.

Each task began with auditory instructions. Trials started with a carrier sentence that included the target stimulus. For instance, in the Find the Word task, students were told to “Find the word MEAT”. This was accompanied by ten written responses. Children responded with a mouse. Students received positive reinforcement (e.g. hearing, “Thank you for working so hard!” or “Great job!”) during both testing and training; these were given approximately every five trials and were independent of accuracy on a particular trial.

2.6. Analysis

The dependent measure in all analyses was accuracy². Baseline words (untrained words from untrained GPC classes) were not analyzed. There was a large effect of vowel overlap at pre-test (Table 4). Thus, to quantify the amount of learning (rather than differences in post-learning performance), we focused on change scores (post-test – pre-test). To investigate learning in practical terms, we calculated untransformed change scores between pre-test and either post-test or retention. This captures meaningful differences in performance, much as classroom learning would be evaluated. However, this analysis could also reflect ceiling or floor effects (larger gains are possible when pre-test scores are low than high). Thus, we also scaled scores using an empirical logit scale using the empirical logit transformation (which stretches the space near 0 and 1), and computed change scores between logit scaled pre-test and post-test (or retention) accuracy. The empirical logit transformation is a standard statistical solution to overcome differences in where two groups are in the learning curve, as it is easier to improve when one is in a medium accuracy range than when one is close to ceiling. Thus, it allowed us to counteract the anticipated accuracy differences at pre-test.

Table 4.

Percent correct and standard error of the mean (SEM) at pre-test.

	Variable	Similar
High Overlap	57.01 (2.23)	58.12 (1.81)
Low Overlap	62.46 (2.19)	63.40 (2.26)

3. Results

3.1. Pre-test

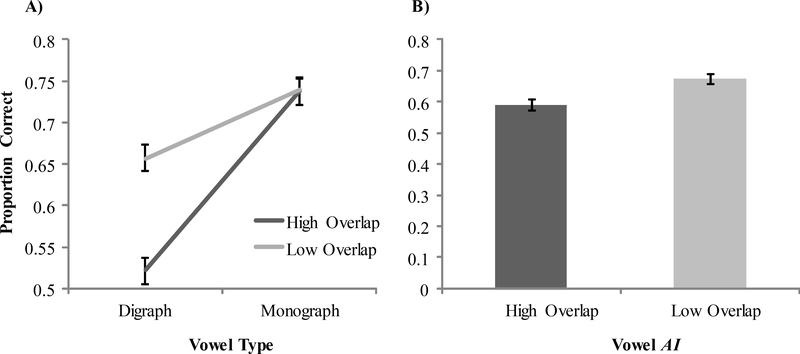
We first examined pre-test to detect differences in baseline performance due to overlap (Table 4). Participants in the high overlap × variable condition and the high overlap × similar condition performed lowest, whereas low overlap × variable condition and low overlap × similar condition did better. There was relatively little variability in how well students performed (SEM always < 3%).

As there were no main effects or interactions with variability, analyses of pre-test collapse across this condition. We performed an ANOVA examining overlap and vowel-type (monograph vs. digraph, within-subject). We found a significant main effect of overlap (F(1, 279) = 10.53, p = 0.001, η_p² = 0.036) with lower performance in the high overlap condition. We also found a significant main effect of vowel-type (F(1, 279) = 258.24, p < 0.001, η_p² = 0.481), supporting overall lower performance for digraphs (Figure 2A). There was a significant interaction between overlap and vowel-type (F(1, 279) = 31.38, p < 0.001, η_p² = 0.101). This was driven by a significant effect of overlap for digraphs (F(1, 279) = 34.79, p < 0.001, η_p² = 0.111), but not for monographs (F < 1).

Figure 2:

Proportion correct at pre-test for both high overlap and low overlap conditions A) separated by vowel-type and B) for vowel AI only. Both figures include the SEM as error bars.

While GPC regularities were balanced on initial difficulty (Supplement S1), it is possible that differences between groups were due to the GPC regularities in the high and low overlap conditions. We tested this by examining performance on AI, which appeared in both conditions (Figure 2B), though the specific items differed. AI showed a similar pattern with about a 10% decrement in performance for the high overlap group (F(1, 279) = 17.89, p < 0.001, η_p² = 0.060). This suggests that the differences between conditions were unlikely to have derived from the difficulty of the individual GPC regularities, but rather emerged from interrelationships among GPC regularities in the set. To determine if these effects could have arisen from spurious differences between the students, we conducted a 2 × 2 (overlap × variability) ANOVA with reading scores (collected by the district) as the dependent variable. We found no significant differences in reading score as a function of overlap (F(1, 277) = 1.81, p = 0.179, η_p² = 0.006) or variability (F< 1), and there was no interaction (F< 1). Thus the effect of overlap at pre-test is not a consequence of pre-existing differences between groups.

3.2. Post-test

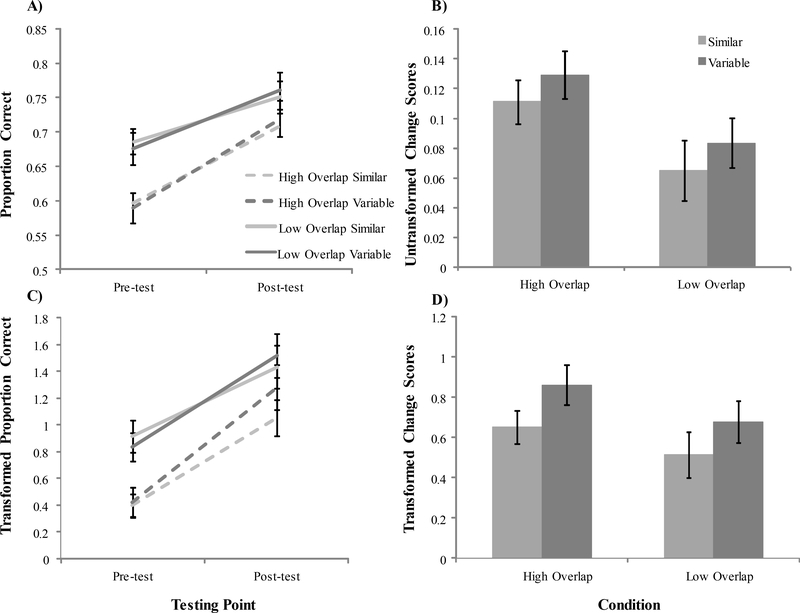
We next examined learning gains (change in performance) at post-test as a function of condition (vowel overlap and consonant variability). Figure 3A shows accuracy for each group at pre- and post-test. First, we examined post-test change scores using untransformed accuracy with a 2×2 between-subjects (overlap × variability) ANOVA. We found a significant effect of overlap (F(1, 273) = 7.05, p = 0.008, η_p² = 0.025), with larger learning gains in the high overlap than the low overlap condition. Variability was not significant (F(1, 273) = 1.09, p = 0.297, η_p² = 0.004), and did interact with overlap (F(1, 273) < 1) (Figures 3A, 3B). In an item analysis, a mixed 2 × 2 (overlap × variability) ANOVA was used (with variability as within-item and overlap as between-item). Overlap remained significant (F(1, 94) = 8.09, p = 0.005, η_p² = 0.079). There was a significant effect of variability (F(1, 94) = 9.64, p = 0.003, η_p² = 0.093), with more learning after variable than similar training, but no interaction (F(1, 94) < 1). Note that variability may have been significant by-item (but not-subject) because in this analysis variability is within-item (whereas it was between-subject).

Figure 3:

A) Proportion correct at pre-test and post-test across all the overlap × variability conditions including SEM error bars. B) Untransformed post-test change scores for all conditions. C) Empirical logit transformed proportion correct at pre-test and post-test across all conditions. D) Transformed post-test change scores for all conditions.

We next applied the empirical logit transformation to accuracy and recalculated the difference score (Figure 3C, D). This showed no significant effect of overlap (F(1, 273) = 2.44, p = 0.120, η_p²= 0.009). The effect of variability (F(1, 273) = 3.35, p = 0.068, η_p²= 0.012) was marginally significant, showing slight advantages in variable conditions. Overlap and variability did not interact (F < 1). The item analysis found significant effects of overlap (F(1, 94) = 8.18, p = 0.005, η_p²= 0.080) and variability (F(1, 94) = 6.10, p = 0.015, η_p²= 0.061), but no interaction (F< 1). These results are similar to those of the untransformed item analysis: There was a tendency toward better learning with high overlap or variable consonants.

We followed up on these analyses by asking whether a variety of moderating factors influenced any of these factors (Supplement S2). These included whether tasks and items were trained or generalization, word/nonword, gender and reading ability. Only a few moderators were identified (vowel-type was significant, and there was a marginal interaction with reading ability). This suggests that this pattern held across a variety of conditions.

Finally, given the small learning gains in the low overlap group, untransformed change scores were used to investigate whether there was measurable learning in each sub-condition. We compared the untransformed change scores to zero using a one-sample t-test (Table 5). We found significant learning in all groups. Learning gains ranged from 6.5 to 12.9%, considerable given the relatively short amount of training.

Table 5.

Planned comparisons of post-test change scores to test learning.

Overlap Group	Variability Group	Mean ± SD	Statistics
High Overlap	Similar	0.112 ± 0.119	t(64) = 7.57, p < 0.001
	Variable	0.129 ± 0.133	t(68) = 8.07, p < 0.001
Low Overlap	Similar	0.065 ± 0.176	t(72) = 3.16, p = 0.002
	Variable	0.084 ± 0.142	t(69) = 4.90, p < 0.001

3.3. Retention

Finally, we examined retention (Figure 4). We first examined untransformed retention change scores (retention – pre-test) in a 2×2 ANOVA. A significant effect of overlap was observed (F(1, 263) = 9.67, p = 0.002, η_P² = 0.035), with better retention in the high overlap than low overlap conditions. No other effect reached significance (variability: F < 1; variability × overlap: F(1,263) = 1.20, p = 0.275 η_P² = 0.005).

Figure 4:

A) Raw proportion correct at pre-test and retention across all the overlap × variability conditions including SEM as error bars (as all other panes). B) Untransformed retention change scores for all conditions. C) Transformed accuracy at pre-test and retention across all conditions. D) Transformed retention change scores across all conditions.

The item analysis replicated the significant effect of overlap (F(1, 94) = 18.87, p < 0.001, η_P² = 0.167). As with post-test, the item analysis also showed evidence for a variability effect (F(1, 94) = 7.51, p = 0.007, η_P² = 0.074), but this time there was a significant interaction (F(1, 94) = 16.38, p < 0.001, η_P² = 0.148). We examined this by separating the data by overlap condition and comparing similar and variable condition within each (with a factorial ANOVA adjusted using the Bonferroni correction, α = 0.025). For the low overlap condition, there was no effect of variability (F < 1). However, for the high overlap condition, there was a significant effect of variability (F(1, 47) = 28.37, p < 0.001, η_P² = 0.376). Unlike at post-test, retention was better with similar than variable consonants for high overlap students.

We next evaluated retention with logit transformed scores. We again found a significant effect of overlap (F(1, 263) = 4.17, p = 0.042, η_p² = 0.016), but no effect of variability (F <1) or interaction (F < 1). An item analysis using the transformed change scores also found a significant effect of overlap (F(1, 94) = 22.97, p < 0.001, η_p² = 0.196). There was also a significant effect of variability (F(1, 94) = 9.86, p = 0.002, η_p² = 0.095) and a significant interaction (F(1, 94) = 15.58, p < 0.001, η_p² = 0.142). We split the data by overlap condition, and adjusted for repeated tests using the Bonferroni correction, α = 0.025. Again, we found a significant effect of variability in the overlap condition only (high overlap: F(1, 47) = 34.29, p < 0.001, η_P² = 0.422; low overlap: F(1, 47) < 1) with better retention for similar consonants in the high overlap condition.

Finally, we asked whether students in each group showed non-zero retention (Table 6). Only students in the high overlap groups exhibited significant retention. In fact, change scores for overlap were similar to those at post-test, suggesting only minimal loss over the testing delay.

Table 6.

Planned comparisons of retention change scores.

Overlap Group	Variability Group	Mean ± SD	Statistics
High Overlap	Similar	0.114 ± 0.143	t(61) = 6.27, p < 0.001
	Variable	0.072 ± 0.160	t(66) = 3.71, p < 0.001
Low Overlap	Similar	0.018 ± 0.226	t(69) = 0.68, p = 0.500
	Variable	0.026 ± 0.199	t(67) = 0.68, p = 0.278

Overall, retention was better with high overlap GPCs than low overlap. This was true for both untransformed and transformed scores, suggesting advantages for long-term retention with overlapping materials. There was also an overall benefit of similarity, though item analyses indicate this benefit may be restricted to the high overlap condition. Moderator analyses (Supplement S2) indicated that the only significant moderator was word/nonword status. The effect of overlap on retention appeared to be driven by the words. Other task, item and subject factors showed little effect.

4. Discussion

4.1. Overview

A marked effect of overlap was evident before training: At pre-test, children performed worse on the high-overlap GPC than low-overlap. That pattern was more complex after training (Table 7 for a summary). At immediate post-test, larger learning gains were observed with high overlap in raw change scores but evidence was less robust with the empirical logit transformation. More importantly, retention was consistently better for students in the high overlap condition than low overlap. This overlap benefit is notable given that initial performance in the high overlap condition was much lower. Clearly there is no cost to training overlapping items simultaneously, and students may learn more.

Table 7.

Summary of major findings: For factors (overlap/variability [here shortened to ‘var.’]), a capital letter indicates significant effect, lower case is marginal; O: overlap>no overlap; V: variable>similar; S: similar>variable; * indicates presence of interaction with overlap; ⁺ indicates marginal interaction with moderator (see S2).

		Post		Retention
		Subject	Item	Subject	Item
Overlap	Raw	O	O	O	O
	Logit	-	O	O	O
	Moderators	Digraphs/ Monographs Reading ability+		Word/NW
Var.	Raw	-	V	-	S*
	Logit	v	V	-	S*
	Moderators	Spelling/Rec. Task+
Groups showing Learning / Retention		All		O only

Evidence for the variability effect was mixed. At post-test, the variability benefit was significant by items. By subjects, it was not significant with raw scores, but marginally significant with transformed scores. This suggests a small learning advantage for variable consonants, though this is weaker evidence than prior studies. At retention, the effect was significant but reversed and restricted to the high overlap condition.

4.2. Limitations

Several limitations are worth noting. Many are unavoidable consequences of the structure of English and the items available for first graders. First, overlap was manipulated by training students on distinct sets of English regularities. Thus, we cannot eliminate the possibility that effects were driven by the particular GPC regularities selected for each condition. Pilot data with a large sample (Supplement S1) do not suggest numerically large differences for four of the six GPC regularities which were tested, and one regularity was shared between conditions. Moreover, items were balanced on frequency and neighborhood density between conditions. Thus it is unlikely that differences in the inherent difficulty of the items or the GPC regularities were a large factor.

Second, we tested only a small subset of English GPCs. Digraphs were selected because they offer a clear way to instantiate and manipulate overlap. While there is no reason to believe that they are not representative, it is important to replicate these findings with other classes of GPC regularities to test their general applicability.

Third, it is also possible that these factors work differently or are less critical for other languages that are more orthographically transparent (Nigro, Jiménez-Fernández, Simpson, & Defior, 2015). This should be investigated in future research. However, these factors are likely to be relevant to these languages. For example, in German—a transparent language—the vowel E can be used in isolation (as in ENTE [DUCK]) but can also be combined with U to create the new digraph EU (as in EULE [OWL]). Thus, even in a language with no quasi-regularity, children must still confront overlap (and variability may still be important in isolating the even more regular GPCs). In addition, our study used only the most regular pronunciation of each digraph. Thus, it is reasonable that these findings would generalize to orthographically transparent languages.

Finally, we note that all of our testing used closed set tasks in which children selected the correct choice from a range of options. This contrasts with open set tasks like oral reading which are more standard in classroom and assessment work. Open set responding was not possible with our procedures, and it remains to be seen whether overlap benefits these tasks. However, in other work with older children we have found strong correlations (r>0.6) between closed set tasks and oral reading suggesting that these results would likely hold (Roembke, Reed, Hazeltine, and McMurray, 2019).

4.3. Consonant Variability

The effect of variability was small (Table 7). At immediate post-test (the closest comparison to Apfelbaum, Hazeltine, & McMurray, 2013), effects were consistent with a variability benefit, but statistical evidence was not robust, significant by items and marginal by subject with logit transformed scores. These statistically weak effects were surprising given Apfelbaum, Hazeltine, & McMurray, 2013 results, and evidence from other areas of learning that variability in irrelevant elements leads to robust learning benefits (e.g., Rost, and McMurray, 2009; Gómez, 2002).

Several differences between Apfelbaum, Hazeltine, & McMurray, 2013 and our study could explain this discrepancy. First is statistical power: Apfelbaum, Hazeltine, & McMurray, 2013 split their similarly-sized sample along only one factor (variability), not two (variability and overlap). This may explain why some by-subject analyses were not significant, but by-item analyses were (since variability was manipulated between subjects but within-items). However, it does not account for the relatively small magnitude of the effect.

Second, our manipulation of variability may have been inadvertently weaker than that of Apfelbaum, Hazeltine, & McMurray, 2013. Similar items in that study shared the full consonant frame with 2.4 other items (variable=0.2); compared with only 1.99 here (variable=0.31). To ensure overlap between vowels, we used vowels from a small pool of appropriate words, affording less flexibility to maximize variability. Thus, the smaller difference between the variability conditions may have led to a smaller effect.

Third, the Apfelbaum, Hazeltine, & McMurray, 2013 training regime blocked trials by vowel while we interleaved all vowels during training. The decision to interleave was motivated by findings that interleaving items may maximize learning (Carvalho & Goldstone, 2014; Vlach, Sandhofer, & Kornell, 2008). However, fully interleaved GPC regularities might have helped eliminate spurious associations between consonant graphemes and vowel pronunciations to isolate the respective vowels without requiring consonant variability.

This was investigated in a follow-up study by McMurray, Roembke, and Hazeltine, (2018), which simultaneously manipulated consonant variability and training blocked by vowels. They showed a variability benefit when blocking highlighted the overlapping strings, but no variability benefit for interleaved training. These findings offer a unifying explanation as to why the observed variability effect was smaller than in Apfelbaum, Hazeltine, & McMurray, 2013 and suggest that how vowels are blocked impacts whether variability benefits learning or not. These types of interactions suggest that children’s statistical learning is sensitive to other factors in the input (particularly factors local to a sequence of training), and should not be conceptualized as simple co-occurrence counting across the entire training set.

It remains unclear why the variability effect was reversed at retention and only significant in the high overlap condition. The follow-up study by McMurray, Roembke, and Hazeltine, (2018) observed a similarity benefit at retention under some blocking conditions. This is likely some form of consolidation, and may be related to the schema-based learning approach we discuss below.

4.4. Vowel Overlap

4.4.1. Pre-test

Performance at pre-test was lower in the high overlap than the low overlap condition. This was likely due to two factors. First, on a trial-to-trial basis simply alternating between similar GPC strings could add difficulty, analogous to phenomena like cumulative semantic interference (e.g., Oppenheim, Dell, & Schwartz, 2010). Second, items or letters that were assigned to the same task served as each other’s foils. Consequently, foil items were more likely to overlap with the target item in the high overlap condition than in the low overlap condition³. Thus, accurately selecting the target in the high overlap condition required both adequate understanding of the relevant GPC regularities but also the ability to inhibit competitors in the moment (McMurray, Horst, and Samuelson, (2012) for an analogy in word learning).

However, the pre-test effect of overlap was only observed for digraphs. This is likely because digraphs are more difficult. Monographs are typically introduced first in reading curricula and thus would have been practiced the most. This early, and often isolated, exposure may lead to more robust mappings that are more resilient to interference from overlapping strings later. It is also possible that digraphs are not perceived as a unit: The two letters may therefore compete with a larger number of foils on each trial than a monograph with only one letter. This could explain why accuracy for digraph vowels was particularly low in the high overlap condition, in which foils were more likely to be closer competitors.

4.4.2. Learning and retention

Even though the high overlap condition was harder at pre-test, there were larger learning gains with high overlap than low overlap training. This difference was particularly pronounced at retention where no retention was observed after low overlap training. Overlapping vowels, which introduced difficulties during pre-test (and presumably during training), may help in the long run.

4.4.3. Theoretical Accounts

The naïve associative account does not predict these findings. The fact that individual letters must be mapped to more than one sound was expected to impede learning, but this was not observed. So why was vowel overlap helpful for learning and retention?

Connectionist instantiations of statistical learning (McClelland, 2013) show that new materials can be more rapidly and robustly integrated into an existing network if they share schematic structure with already learned items than if they are inconsistent with what is known. In this case, the learning system is not characterized as isolated associations between elements like letters and sounds, but rather between sounds, letters and most importantly, complex intermediate representations. In situations in which new material can be better integrated because of similarity to existing items, learning is more efficient. This could also explain the similarity benefit at retention—similar consonants may be an additional way to build schemas (though it is unclear why would not be observed at immediate post-test).

At a broader level, our work offers clear evidence that statistical learning in reading must be considered as part of a complex network (e.g., Seidenberg, 2005): Students are not learning an entirely novel set of associations from scratch. Rather, new associations are embedded in a rich network of existing knowledge. When we consider statistical or associative accounts in this light—as part of a developmental process, not a laboratory learning exercise—the nature of learning may change. These interactions might also relate to why it has sometimes been difficult to find a relationship between domain-general statistical learning and reading (e.g., Schmalz et al., 2018). That is, statistical learning in reading development maybe more than just a matter of whether a child is a good statistical learner. Moreover, learning depends on more than the cumulative statistics to which the child is exposed. Local groupings of items or GPCs likely matter, and this can vary markedly across curricula and the corpora of text to which a child is exposed. This may explain why there is no straightforward relationship between, for example, sequence learning and reading ability.

4.5. Moderators

Supplement S2 presented extensive analyses on potential factors that may moderate these effects at the level of task, item and subject. For the most part, few of these were significant. However, there were notable exceptions.

First, the effect of overlap did not differ in generalization tasks and items. Although caution is warranted when interpreting null effects, it suggests that overlap not only improved learning, but that learning gains are not fragile or specific to the items/tasks that were used. Critically, it suggests the bulk of learning is at the level of generalizable regularities, and not item-specific.

Second, at the level of item, the word/nonword distinction moderated the effect of overlap on retention, with a larger effect of overlap for words than nonwords. This could speak to a schema-based account in that the effect of overlap helps the child not only learn the regularities but store words in an orthographically organized lexicon.

Finally, at the subject level, we found that reading ability was a marginal moderator of the overlap effect. Here, stronger readers showed a larger effect of overlap. This may also support schema-based learning, as these readers would have had a larger and more robust set of GPC schemas at the onset of the experiment. Unfortunately, we did not have access to other person-level factors. It would be particularly important to examine variation in statistical learning (Arciuli & Simpson, 2012; Elleman et al., 2019) or other types of learning. However, there was little variability in learning gains (Tables 5–6). This suggests that in highly supervised classroom- style learning, there may be less variability than in unsupervised or naturalistic learning settings. At the broadest level, the lack of strong moderators suggests that over the long-haul most students, independently of their individual differences, would benefit similarly from orthographic overlap.

4.5. Implications for Teaching

Our goal was to identify principles by which materials can be structured to improve learning, considering both implications from statistical learning and from typical reading instruction. This work was motivated by the fact that current statistical learning theories make competing predictions for what should benefit learning when we consider the real-world of grouping GPC regularities for instruction. Rather than testing a full curriculum, we conducted a rapid “field test” of these principles. This type of study may offer an important addition to our understanding of instructional practice, given the dearth of work on the microstructure of curricula (e.g., the specific groupings of items or regularities in a curriculum; McMurray, Roembke, and Hazeltine, (2018)).

In this light, our findings suggest why vowels may be particularly hard for early readers (e.g., Treiman, 1993). While clearly part of the difficulty lies in the fact that most digraph rules have several alternative pronunciations (e.g., EA can be /i/ MEAT, /ɛ/ in THREAT, and /eɪ/ in STEAK), our work indicates that the overlap among digraphs may also contribute to their in-the-moment difficulty (e.g., at pre-test).

Despite this, our study suggests that it may not be effective to avoid overlap in reading curricula that target subsets of the GPC regularities. At immediate post-test, high overlap training led to learning gains that were at least as large, if not larger, than low overlap training, and retention was more robust. This principle can easily be incorporated into curricula by reworking the way GPC strings are introduced, though clearly such curricula require randomized control testing for efficacy.

One potential caveat may be that participants in this study already had some knowledge on the GPC regularities they were trained on (mean pre-test accuracy>55% correct). In addition, the interaction between overlap and reading ability was marginally significant at post-test (Supplement S2), as lower performing children had a tendency to benefit less from high overlap than highly performing ones. This could indicate that high overlap groupings may not be effective from the beginning of reading instruction, but will be useful later. Future research should investigate in more detail to what extent individual differences in reading ability and statistical learning impact the success of curricular manipulations at the item and groupings level.

More broadly, the findings highlight the power of systematically manipulating how items are grouped during training. Computer-based training may be helpful in enacting these principles, as they can efficiently instantiate controlled manipulations of items, stress different forms of overlap at different times, and provide immediate feedback (which might be important for some forms of implicit learning, Maddox, Ashby, & Bohil, 2003). While this cannot replace real teachers, computer-based training may supplement the curriculum and traditional school media (e.g., worksheets) by leveraging learning principles for better outcomes. Future research might investigate the extent to which the computer interface facilitated students’ learning: For example, was the provided feedback during training necessary for children’s learning?

Most children completed the training portion of the experiment within three to five days of daily 20-minute-sessions. While improvements were impressive at post-test, only the high overlap group’s performance remained above pre-test at retention. This suggests two things: First, relatively little time may be needed to harness the positive effects of item-level manipulations (e.g., one could imagine a child completing a couple of tasks each day after school). Second, these effects are only longer-lasting (i.e., at least 1–2 weeks) if the statistics are well-tuned to the child’s needs.

If one takes statistical learning seriously as a mechanism of reading acquisition, it must be considered in the context of how reading instruction is structured. Our findings offer clear recommendations for how curricula could be designed, both on the item level as well as at the level of grouping regularities that are taught simultaneously, while providing evidence for a network view of statistical learning.