Measuring the Affinity of Protein-Protein Interactions on a single-molecule level by Mass Photometry

Abstract

Measurements of biomolecular interactions are crucial to understand the mechanisms of the biological processes they facilitate. Bulk-based methods such as ITC and SPR provide important information on binding affinities, stoichiometry, and kinetics of interactions. However, the ensemble averaging approaches are not able to probe the intrinsic heterogeneity often displayed by biological systems. Interactions that involve cooperativity or result in the formation of multicomponent complexes pose additional experimental challenges. Single-molecule techniques have previously been applied to solve these problems. However, single-molecule experiments are often technically demanding and require labeling or immobilization of the molecules under study. A recently developed single-molecule method, mass photometry (MP), overcomes these limitations. Here we applied MP to measure the affinities of biomolecular interactions. We have demonstrated how MP allows the user to study multivalent complexes and quantify the affinities of different binding sites in a single measurement. Results obtained from this single-molecule technique have been validated by ITC and BLI. The quality and information content of the MP data, combined with simple and fast measurements and low sample consumption makes MP a new preferred method for measuring strong protein-protein interactions.

Graphical Abstract

1. Introduction

Protein-protein interactions play key roles in a wide range of biological processes, from metabolism and signal transduction to cytoskeleton formation and cell migration [1–3]. The outcomes of those processes depend on the strength of their underlying interactions [4], making the evaluation of the interaction affinities essential for their understanding. In many cases, protein interactions are complex and multivalent [5], involving cooperativity of ligand binding to different sites [6]. The detailed characterization of binding affinities may be challenging and require probing populations of several reaction complexes.

Many methods are used to determine affinities of protein-protein interactions, including isothermal titration calorimetry (ITC) [6], light scattering [7, 8], analytical ultracentrifugation (AUC) [9], fluorescence intensity [10], and fluorescence polarization [11]. Measuring affinities using those methods often requires a relatively large amount of material and is time consuming. Other approaches, like microscale thermophoresis (MST) [12], surface plasmon resonance (SPR) [13], and biolayer interferometry (BLI) [14] usually require a smaller sample size than ITC or AUC but, in most cases, proteins have to be immobilized or fluorescently labeled, which may significantly affect the binding process [15]. Most importantly, signals observed in the bulk methods listed above reflect the sum or the average of contributions from all detectable components. For multiple binding sites with similar affinities, it becomes challenging to distinguish signals from different partially occupied states and precisely determine association constants of individual binding sites. In the study of the interaction of α-chymotrypsin with its double-headed inhibitor (soybean trypsin inhibitor, SBTI) Zhao and Schuck [6] demonstrated that single ITC, SPR, or fluorescence anisotropy experiments are not sufficient to precisely determine affinities of the two chymotrypsin binding sites of the SBTI. However, they were able to determine both affinities using global analysis of data from four ITC experiments performed along different titration trajectories.

In recent decades, single-molecule techniques have developed rapidly and provided data essential for a detailed understanding of protein-protein interactions both in vivo and in vitro [16–19]. With the help of single-molecule techniques, individual molecular complexes can be detected, enabling a detailed investigation of ligand interactions with multiple binding sites. However, single-molecule techniques often require sophisticated instrumentation and advanced statistical data analysis. Moreover, molecules under study usually have to be fluorescently labeled or immobilized.

Recently, Young at al. [20] developed the mass photometer (MP), a new single-molecule method based on interferometric scattering microscopy (iSCAT) [21]. MP detects single protein molecules nonspecifically binding to the microscope coverslips. Signals from these binding events consist of the incident laser light reflected from the glass-buffer interface combined with light scattered by individual molecules. After the intensity of the reflected light is selectively attenuated by the partial reflector in the MP optical system, the images are recorded by the camera. Those images are processed to obtain the ratio (contrast) of the signal generated by molecules landing on the coverslips to the signal from the surrounding static background. Contrast values are proportional to the intensity of light scattered by individual particles which is a function of their refractive index and molecular mass. For the majority of proteins, the refractive index increment is narrowly distributed with a small variation (<2%) [22]. This enables the use of the contrast values obtained by MP to directly measure molecular mass of individual particles. In a typical mass photometry experiment, the landing events of several thousands of molecules are recorded to obtain the molar mass distribution plot. Mass distribution reflects sample homogeneity and purity and enables the analysis of oligomerization and formation of molecular complexes.

For a simple case of 1:1 binding, A + B ↔ AB, the association equilibrium constant K_a is given by [AB]/([A][B]). The relative populations of bound and unbound states can be directly obtained from the MP contrast distributions, enabling the determination of the binding constant K_a. In a more complicated interaction system that involves multiple binding sites, MP is able to distinguish different binding states populated in the binding process. Detailed population information obtained from this data can be used to calculate association equilibrium constants for each binding site. As long as each complex formed in the reaction is sufficiently populated in the reaction mixture, and the population of each component is well defined in the contrast distribution, binding affinities can be determined from the MP analysis of a single sample. A typical MP experiment requires only 10 μL of sample volume at approximately 20 nM protein concentration. Mass photometry measurements can be performed within a few minutes, and do not require labeling or the immobilization of molecules. These properties make mass photometry a promising alternative for studying protein-protein interactions.

In this study, we applied MP to measure binding affinities of two protein-protein interaction systems; an antigen-antibody complex with a 2:1 stoichiometry (human thrombin binding to anti-human thrombin antibody), and the 1:1 interaction of CD16a/FCGR3A binding to IgG. The association equilibrium constants calculated from MP were validated by the ITC and BLI.

2. Materials and Methods

2.1. Proteins and chemicals.

Human α-thrombin (HT) and mouse monoclonal anti-human thrombin antibody (AHT) were purchased from Hematologic Technologies (Essex Junction, VT). The biotinylated CD16a/FCGR3A (CD16) was from Sino Biological (Wayne, PA). The polyclonal anti-ubiquitin antibody (IgG) was purchased from Abcam (Cambridge, UK), and the bovine serum albumin (BSA) was from Sigma. All experiments were performed in a PBS buffer.

2.2. Mass Photometry:

The MP experiments were carried out on a OneMP instrument (Refeyn, UK) at room temperature, i.e. approximately 24°C. Microscope coverslips (24×50 mm, Fisher Scientific, and 24×24 mm, Globe Scientific) were prepared by rinsing them consecutively with isopropanol and H₂O and drying them under a stream of clean nitrogen. The high concentration protein stocks were diluted with the PBS buffer and filtered through 0.22 μm filters. A series of solutions containing AHT (25 nM) and HT (0 – 120 nM) were incubated for approximately 10 minutes before being loaded into flow chambers formed by stacked coverslips. Considering the typical reaction rates of antigen-antibody binding, this incubation time was long enough to allow the solutes to reach chemical equilibrium while avoiding significant protein loss through surface adsorption. Similarly, CD16 was mixed with the IgG antibody at a 1:1 molar ratio and diluted with PBS to obtain samples of 80 nM total protein concentration. Data from the 3 μm × 10 μm instrument field of view were collected for 100 s at a 1 kHz frame rate. At least 5×10³ particles were detected in each acquisition. Images were processed as previously described [20], using the LabView software provided by the instrument manufacturer (Refeyn, UK).

2.3. Equilibrium constant calculations from the MP data:

To calculate populations of interaction components, contrast distribution histograms obtained from the MP data were plotted using 1×10⁻⁴ contrast bin size and fitted with Gaussian functions (Fig. S1a):

$$Ct(cntr)=\sum a_i\exp \left[-\frac{{\left(cntr-{\mu }_i\right)}^2}{2{\sigma }_i^2}\right]$$ (1)

where Ct is the number of molecules counted at the corresponding contrast value cntr, and a_i, μ_i, and σ_i, represent the amplitude (peak height), mean contrast (peak position), and the standard deviation (peak width) of the distribution of component i, respectively.

For the experimental data considered here, all distribution peaks represent the free and bound forms of the same protein preparation with a relatively small molecular mass increase and consequently exhibit similar contrast heterogeneity. It is therefore reasonable to assume that all distribution peaks can be fitted with Gaussian functions with the same standard deviation (peak width) parameter value (σ_i = σ). Consequently, the relative population of each distribution component i is represented by a_i. Introducing this constraint doesn’t substantially affect the final fit (Fig. S2), but it is necessary to eliminate correlations in some parameters in Eq. (1) that preclude obtaining accurate species population estimates from contrast distributions with multiple overlapping peaks.

The mean contrast value of the component i is linearly correlated with its molecular mass Mw_i (Fig. S1b):

$$M{w}_i=slope\times {\mu }_i+intercept$$ (2)

where slope and intercept are the instrument calibration parameters. In the global analysis of contrast distributions from the titration experiment, Eq. (2) introduces a constraint by linking the mean contrast values of species i between different distributions. The Mw_i values are fixed at the expected molecular masses of the interaction components i, while allowing the calibration parameters to optimize. This also constrains the ratios of the μ_i parameters when distribution peaks representing more than two species are present.

2.3.1. One-site binding.

For the commercially available MP instrument used in this study, the low molecular weight detection limit is approximately 50 kDa. The light scattering signal from a molecule smaller than the detection limit cannot be distinguished from the image background noise and therefore is not detected by the data analysis software. In the case of CD16 and IgG binding considered here, the molecular mass of the free CD16 (48 kDa) is close to the MP detection limit. Therefore, the number of the free CD16 molecules detected in the MP experiments is significantly affected by the image noise levels, rendering the population determination of this component from the contrast histograms inaccurate. For this reason, the MP detection threshold cutoff was set during data analysis to exclude the peak corresponding to the free CD16 population from the association constant calculations. The association equilibrium constant for the CD16 and IgG binding, K_a, and the CD16 total concentration, (c_CD16)_tot, are given by the relationships:

$$K_a=\frac{a_{IgG\cdot CD16}}{a_{IgG}\times c_{CD16}}$$ (3-a1)

$${(c_{CD16})}_{tot}=c_{CD16}+\frac{a_{IgG\cdot CD16}}{a_{IgG}+a_{IgG\cdot CD16}}\times {(c_{IgG})}_{tot}$$ (3-a2)

where c_CD16 and (c_IgG)_tot represent the free CD16 concentration and the total IgG concentration, respectively.

2.3.2. Two-site binding.

Herein, we will consider antigen binding to a bivalent monoclonal antibody. Since the two paratopes of the antibody are identical, we will assume that their microscopic binding constants are equal and apply the macroscopic binding model. The molecular mass of the antigen used in this study (HT, Mw = 37 kDa) is lower than the MP detection limit, and only three components appear in the distributions: The free AHT and the single and double complexes, AHT·HT and AHT·HT₂, respectively (Fig. S2). The macroscopic association constants can be defined as:

$$K_{a1}=\frac{a_{AHT\cdot HT}}{a_{AHT}\times c_{HT}},K_{a2}=\frac{a_{AHT\cdot H{T}_2}}{a_{AHT\cdot HT}\times c_{HT}}$$ (3-b1)

where c_HT represents the concentration of the free HT. The total HT concentration is given by:

$${(c_{HT})}_{tot}=c_{HT}+\frac{a_{AHT\cdot HT}+2a_{AHT\cdot H{T}_2}}{a_{AHT}+a_{AHT\cdot HT}+a_{AHT\cdot H{T}_2}}\times {(c_{AHT})}_{tot}$$ (3-b2)

In the titration series, the total number of molecules recorded for each sample will vary. In the global fit of the titration data, a scaling factor for the free AHT peak amplitude is included as a local fitting parameter to account for this variation.

2.3.3. MP distributions fitting procedure.

The distribution data were fitted by combining Eqs. (1) - (3) and optimizing the values of association constants, slope, intercept, and σ. Least-square analysis of the experimental data using the Levenberg-Marquardt algorithm was applied to find the best-fit values of all variable parameters. All calculations were implemented as MatLab scripts. Fitting parameter errors were obtained by the error projection method and represent the 68.3% confidence intervals of the best-fit values.

2.4. Isothermal titration calorimetry:

Proteins for the ITC experiments were dialyzed overnight in the PBS buffer. The AHT sample at the concentration of 3 μM was loaded into the cell of the iTC200 microcalorimeter (Malvern Panalytical, UK), and titrated with the 60 μM HT solution. Titrations were performed in triplicate at 25°C. Experimental binding isotherms obtained by processing the ITC thermograms in NITPIC [23] were fitted in SEDPHAT [24] as described in the Results section.

2.5. Biolayer Interferometry:

BLI experiments were performed in the Octet RED96 instrument (Molecular Devices, CA). The biotinylated CD16 at the concentration of 5 μg/ml was immobilized on the streptavidin coated SA sensors (Molecular Devices, CA) using the 120 s contact time. After the immobilization step, the unreacted streptavidin was blocked using the 50 μg/ml biocytin solution. The association and dissociation kinetics were recorded for 120 s and 180 s, respectively, at the 11.3 nM to 360 nM concentration range of the IgG analyte. To prevent nonspecific binding of the analyte, all solutions and the running buffer were supplemented with 0.02% v/v of Polysorbate 20. All BLI measurements were performed at 30°C, the lowest temperature setting of the Octet RED96 temperature control system. Reference sensors were prepared following the same procedure, replacing the biotinylated CD16 with buffer in the immobilization step. No significant nonspecific analyte interaction was detected in the control experiments (Fig. S3). Binding sensograms were fitted using the EVILFIT software [25].

3. Results

3.1. Global analysis of AHT-HT binding.

One of the main advantages of Mass Photometry, when compared with other biophysical methods, is its ability to relatively easily probe populations of different multivalent molecular species in solution. We used the bivalent antigen-antibody system to investigate how MP data can be used to obtain the association equilibrium constants for multiple binding sites. Fig. 1 shows the MP contrast distribution histograms for samples with a constant 25 nM AHT concentration, and the HT concentration increasing from 0 to 120 nM. The first panel (Fig. 1a) shows a single peak representing the free AHT (Mw = 149 kDa). A very low particle count shoulder at the higher contrast values of this distribution might represent a small percentage of AHT dimers, aggregates, or impurities. With the increasing HT concentration the AHT liganded states populations increase (Fig. 1b-f), and two higher molecular mass peaks form. These two peaks represent the AHT·HT (Mw = 186 kDa) and AHT·HT₂ (Mw = 223 kDa) complexes. The MP distribution for the 25 nM HT, 60 nM AHT mixture (Fig. 1e) clearly shows all three comparably populated interaction components (AHT, AHT·HT and AHT·HT₂, left to right, respectively). The last titration mixture (25 nM HT, 120 nM AHT, Fig. 1f) is dominated by the high contrast peak representing the AHT·HT₂ species. To perform a global analysis of the titration data, MP distributions were fitted with the two-site binding model with three Gaussian peaks (solid red lines in Fig. 1) as defined by Eqs. (1–2), Eq. (3-a1) and Eq. (3-a2).

Figure 1:

Global analysis of the AHT and HT binding data obtained from mass photometry. (a-f) MP contrast distribution histograms for 25 nM AHT solutions containing HT at 0, 7.5, 15, 30, 60, and 120 nM concentration, respectively. Distribution peaks in panels b to f represent the free AHT, AHT·HT and AHT·HT₂, left to right, respectively. Red lines represent the best global fit of all six measurements simultaneously using Eqs. (1)-(3).

The global fit of all six contrast distributions (Fig. 1) yields estimates of the association constants values for the two binding sites with relatively narrow confidence intervals (Table 1). To assess the repeatability of the MP experiment, the AHT/HT titrations were repeated five times and the best fit parameters obtained from the global analysis of each titration were averaged (Table 2). The averaged values of the association equilibrium constant for the first and second antibody binding site are logK_a1 = 7.59 ± 0.10 and logK_a2 = 7.42 ± 0.16, respectively. The standard deviations of the averages are small when compared with the confidence intervals of affinities obtained from the global fit of a single titration (Table 1). This indicates good repeatability of the binding affinity estimations from the mass photometry data.

Table 1.

Best-fit association equilibrium constants obtained from different experimental methods. Numbers in parenthesis indicate the 68.3% confidence intervals.

	AHT-HT	CD16-IgG
MP	logKa1 = 7.59 (7.50, 7.66) logKa2 = 7.47 (7.41, 7.55)	logKa = 6.49 (5.81, 6.78)
ITC	logKa1 = 8.04 (7.76, 8.37) *logKa2 = 7.44	--
BLI	--	logKa = 6.67

^*For ITC logK_a1 is a fitting parameter and logK_a2 is linked to logK_a1 by the relationship: logK_a2 = log(K_a1/4) = logK_a1 − 0.6

Table 2.

Association equilibrium constants for AHT-HT binding obtained from five replicate MP titrations. Numbers in parenthesis indicate the 68.3% confidence intervals.

logKa1	logKa2
7.59 (7.50, 7.66)	7.47 (7.41, 7.55)
7.70 (7.56, 7.76)	7.64 (7.56, 7.72)
7.42 (7.35, 7.48)	7.20 (7.12, 7.28)
7.62 (7.51, 7.73)	7.43 (7.34, 7.51)
7.60 (7.47, 7.73)	7.38 (7.28, 7.48)

In a model with two microscopically identical and independent binding sites, the macroscopic K_a1 equals 4K_a2. The best fit value of the association equilibrium constant K_a1 for the AHT-HT binding is only slightly larger than K_a2, which might indicate a weak positive cooperativity of binding, i.e. an increase of the antibody binding affinity for binding of the second ligand. Similar positive cooperativity between the two antibody binding sites was reported previously [26, 27].

Association equilibrium constant values obtained from the MP measurements were validated by the Isothermal Titration Calorimetry (Fig. 2a). The ITC isotherm appears largely uniphasic, precluding precise estimation of the two association constants values and four additional thermodynamic parameters required by the general ITC fitting model [28]. Consequently, the ITC data were first analyzed assuming that the second binding site is microscopically identical with the first, (Fig. 2b), and linking the K_a1 and K_a2 fitting parameters. The best-fit values of the association constants obtained from this analysis are in good agreement with the MP results (Table 1). To further validate the association equilibrium constants obtained from the MP data, the ITC isotherm was also fitted with the K_a1 and K_a2 fixed at values previously obtained from the MP analysis while optimizing all the remaining thermodynamic parameters. Both methods fit the ITC data equally well, and the line representing the best fit with linked K_a values, (blue line in Fig. 2b, fit root-mean-square deviation, RMSD = 153) overlays with the line representing the best fit with fixed K_a values (red line in Fig. 2b, RMSD = 146).

Figure 2:

ITC analysis of the AHT-HT binding. (a) Representative thermogram of 60 μM HT titrated into 3 μM AHT. (b) Integrated heats and error bars calculated by NITPIC. The blue line represents best-fit to a model with two identical binding sites, rmsd = 153; the red line shows the best-fit to a two-site model with association equilibrium constants fixed at values obtained from the MP experiment (logK_a1 = 7.59 and logK_a2 = 7.47), and optimizing the remaining fitting parameters, rmsd = 146. The adjoined lower panel shows the fit residuals.

3.2. Calculations of the association binding constants from individual MP distributions.

When the populations of the free and bound species of the molecular interaction are known, they can be used to directly calculate the association equilibrium constants for each binding site. In the MP experiment, the population of each species is determined by the relative peak height of its Gaussian component in the contrast distribution plot. As long as the peaks representing all the interaction components can be discerned from the contrast distribution, the K_a values for this interaction can be calculated from a single MP measurement. To assess the accuracy of these calculations, we performed individual fits of contrasts distributions obtained for the AHT-HT mixtures at different HT concentrations (Fig. 3a-e). The best-fit values and the 68.3% confidence intervals for K_a1 and K_a2 are shown in Fig. 3f and Table 3. For the majority of analyzed distributions, all three species are sufficiently populated to determine the K_a1 and K_a2 values from a single experiment. Since the ligand concentration range for those samples is relatively wide, this type of analysis can be very useful for fast measurements of unknown association equilibrium constants.

Figure 3:

Association equilibrium constants calculated from individual MP distributions. (a-e) MP contrast distributions for the AHT/HT titration from Fig. 1, with red lines representing the best-fit of each individual data set using equations (1)-(3). Panels show contrast distributions for 25nM AHT solutions containing HT at 7.5, 15, 30, 60 and 120 nM concentration, respectively. (f) Association equilibrium constant values obtained from best fits of individual MP distributions shown in panels a-e (vertical blue dashed lines) and their 68.3% confidence intervals (blue rectangles). Orange dashed lines and orange rectangles represent the best-fit values and 68.3% confidence intervals obtained from the global analysis shown in Fig. 1, respectively. Arrows indicate unbounded confidence intervals. To fit the contrast distribution in panel e, fixed slope and intercept calibration values were used. In analyses of the remaining individual samples and in the global fit, calibration values were treated as fitting parameters.

Table 3.

Association equilibrium constants for AHT-HT binding obtained from fitting individual MP measurements. Numbers in parenthesis indicate the 68.3% confidence intervals.

cHT (nM)	logKa1	logKa2
7.5	7.28 (7.02, 7.54)	7.82 (--, --)
15	7.30 (7.14, 7.51)	7.51 (6.81, 8.16)
30	7.21 (7.14, 7.29)	7.20 (6.96, 7.40)
60	7.57 (7.47, 7.66)	7.41 (7.32, 7.51)
120	7.76 (7.07, --)	7.73 (7.54, 8.06)

Association equilibrium constants cannot be precisely determined from contrast distributions obtained for the two samples with the highest and lowest HT concentration. For the mixture of 25 nM AHT and 7.5 nM HT (Fig. 3a), the population of the double-bound AHT·HT₂ species is very low, leading to poor determination of the K_a2 association constant. Similarly, in the mixture of the 25 nM AHT with 120 nM HT, the antibody is almost completely saturated with the antigen. This increases the uncertainty of the free AHT population determination. Additionally, the concentration of the free HT in this sample is relatively high. Despite the fact that the molecular mass of the free HT is just below the MP detection limit, a large number of the HT particles in solution increases the background noise of the raw MP data. To fit the data in Fig. 3e, we fixed the slope and intercept parameters at values obtained from the MP mass calibration.

3.3. Single-site interaction: CD16 receptor binding to the IgG antibody.

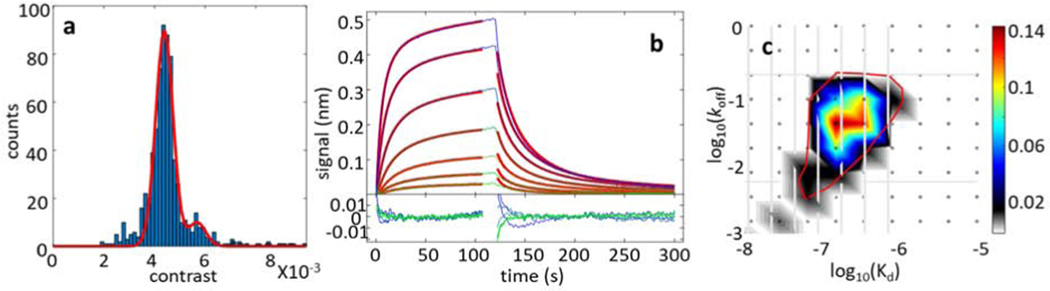
We used the CD16 binding to the Fc region of the IgG antibody as a single-site protein-protein interaction system for the MP study. The value of the CD16-IgG association constant is approximately an order of magnitude smaller than that for the AHT-HT interaction, which also allows us to test the accuracy of the estimation of weaker interaction affinities from the MP distributions. The contrast distribution obtained for the equimolar CD16 and IgG mixture at 80 nM total protein concentration is dominated by a large peak representing the free antibody with a smaller CD16·IgG complex peak at the higher contrast position. The molecular mass of CD16 (48 kDa) is close to the MP detection limit, and the free CD16 species peak is not shown in the distribution (see Methods).

The association equilibrium constant for the CD16-IgG interaction was determined from a single contrast distribution (Fig. 4a and Table 1) as described in Methods. The 80 nM total protein concentration is optimal for obtaining a high-quality MP contrast distribution with a sufficient population of the CD16·IgG complex species. Samples with higher total protein concentrations exceed the high concentration mass photometry detection limit and yield noisy MP data with unresolved antibody and complex distribution peaks (Fig. S4).

Figure 4:

Analysis of the CD16 and IgG binding. (a) MP contrast distribution histogram for 40 nM CD16 and 40 nM IgG mixture. Red curve shows the best fit using equations (1)-(3). The major distribution peak represents the free IgG, and the small peak to the right of the main peak represents the CD16·IgG complex. (b) BLI sensograms for the immobilized CD16 binding to IgG at 11.3, 22.5, 45, 90, 180, 360, and 720 nM concentrations (green to blue lines). Red lines represent the global best fit using EVILFIT, and the adjoined panel below the binding data shows the fit residuals. (c) Distribution of the K_d and k_off values for the best global fit of the BLI data. Vertical gray lines represent IgG concentrations at which the BLI sensograms were collected. The red line indicates the region integrated to determine the logK_a = 6.67.

The affinity equilibrium constant obtained from the MP analysis was validated in the BLI experiments. The association and dissociation kinetics of the IgG binding to the biotinylated CD16 immobilized on the streptavidin-coated sensors was measured in the 11.3 nM to 720 nM antibody concentration range (Fig. 4b). BLI control experiments show no significant non-specific binding or excessive baseline drifts (Fig. S3). The association equilibrium constant obtained from the global fit of the BLI data for the immobilized CD16 (Figure 4b and 4c, Table 1) is comparable to the K_a obtained from the MP contrast distribution fit.

4. Discussion

Mass Photometry, a novel label-free single-molecule technique, generates high resolution molecular mass distributions in solution. In the current study, MP was successfully applied to determine binding affinities for mono- and multivalent protein-protein interactions. A typical MP data acquisition and analysis takes less than 5 minutes and requires 10 μL of sample at the approximately 20 nM concentration. Both the amount of time and sample used for MP experiments is small in comparison with the requirements of other techniques, such as ITC or BLI (Fig. 5). The advantage of mass photometry is even more evident in studies of multivalent interactions. Affinities of multiple binding sites can be determined from a single MP measurement (Fig. 3) while a global analysis of multiple experiments is necessary when using other techniques [6, 24].

Figure 5:

Total amount of material (left panel) and time (right panel) required to determine the K_a values using different experimental methods in the current study. Bar heights represent the total amount of material and time required by MP (blue), ITC (orange), and BLI (yellow). Values shown for ITC are for only one titration and are not sufficient to determine the affinities of the two binding sites independently. Values for the AHT-HT experiment (MP vs ITC) represent the total time and protein required for six MP measurements at different HT concentrations; values for the CD16-IgG experiment (MP vs BLI) represent the requirements for a single MP measurement.

When the molecular mass of one of the binding partners is small, the contrast distribution peaks for bound and unbound states may be unresolved, precluding application of Eqs. 1-3. For this kind of data, the association equilibrium constants can be obtained from the analysis of the concentration dependence of the MP distribution’s average contrast values. Fig. 6 shows the average contrast values for each distribution in Fig. 3 plotted as a function of the HT concentration. The averaged contrast values do not contain information on the population of each interaction species but can still be analyzed with the two-state binding model when the known calibration parameters are applied (Fig S1b). The best-fit association equilibrium constants values for the AHT-HT interaction are logK_a1 = 7.34 (<8.43) and logK_a2 = 7.78 (>6.91), but only one 68.3% confidence interval boundary can be found for the association constants in the two-state binding model. Despite the fact that this analysis requires MP measurements of samples with several ligand concentrations, the overall sample consumption and analysis time is still smaller than required by other methods, such as ITC or BLI.

Figure 6:

Analysis of the average contrast values for the AHT-HT binding. Points represent the average contrast values of the MP distributions shown in Fig. 2, plotted as a function of the HT concentration. The solid red line shows the best fit to the two-site binding model with independent K_a1 and K_a2 fitting parameters.

To allow precise determination of the association equilibrium constant values, relative species populations measured by mass photometry must accurately reflect their populations in solution. Mass photometry detects molecules as they bind to the surface of the cover glass. The frequency of those events decreases during the measurement [20], and minor corrections might be required to account for all binding events for each detected species (Fig. S5). To assess the overall experimental error of the species population determination by mass photometry, we acquired contrast distributions of the non-interacting mixture of the IgG and glutamic dehydrogenase at the 1:1 molar ratio (Fig. S6). The experimental species population ratio obtained by fitting and integrating the MP contrast distribution peaks is 1:1.14. The small difference in the expected and experimentally recovered values is also a result of protein concentration determination errors and may be affected by the protein adsorption to the plastic labware at the low sample concentrations. The 14% error in the MP population determination will change the estimated logK_a by less than 0.06, a value smaller than the width of the K_a1 and K_a2 confidence intervals (Tab. 1 and Tab. 2).

Examples of the mono- and bivalent interaction analysis presented here demonstrate the advantages of mass photometry applications for binding affinity measurements. Currently, those applications are restricted by the limitations in the concentration range, and the molecular mass range of samples that can be measured by the MP. The MP sample concentration has to be low enough to provide spatial separation of the landing events within the field of view of the mass photometer. For the untreated glass coverslips, the optimum concentration of the detectable protein fraction is usually in the 20 nM to 50 nM range. This limits the MP to measurements of only relatively strong binding interactions. Typically, the binding complex peak in the contrast distribution should constitute at least 5% of the total protein concentration to reliably measure the species populations. For a 1:1 protein mixture at a 50 nM total concentration, this requirement corresponds to the maximum measurable K_d value of approximately 500 nM. This limitation can be partially overcome by using passivated glass coverslips [20].

The low molecular mass detection limit of mass photometry is approximately 50 kDa. To obtain the free and bound species ratio from the MP contrast distributions, at least one binding partner should have a molecular mass higher than the detection limit. The minimum molecular mass detection limit might be advantageous for studying interactions with small-MW protein ligands. The sample concentration of those ligands, undetectable by mass photometry, might be above the typical 50 nM concentration limit as demonstrated for the AHT-HT system in the current study.

The antigen-antibody interactions are a prime example of molecular systems that fit very well into the optimum mass photometry sample requirements range. Considering the importance of antibodies in both scientific and therapeutic applications, mass photometry can play an important role in antibody testing. In a single experiment, mass photometry can provide information not only on the antibody purity and activity, but also allow researchers to estimate its antigen binding affinity.

Conclusions

The affinities of mono- and bivalent protein-protein interactions were successfully measured in solution using mass photometry. In comparison with other methods, MP uses an extremely small amount of material, significantly shortens experimental time, and doesn’t require sample labeling or immobilization. Additionally, MP can estimate affinities of different binding sites of multivalent interactions. These properties make MP a promising alternative for studying protein-protein interactions.

Highlights:

• -Mass photometry can be used to measure protein-protein interaction affinities in solution on a single-molecule level without sample labeling or modification.
• -MP can easily estimate the cooperativity of multivalent interactions.
• -MP requires much less material and time to measure affinities than traditional methods.

Abbreviations:

MP

Mass photometry

HT

Human α-thrombin

AHT

anti-human thrombin antibody

BLI

Biolayer Interferometry