Computationally aided, entropy-driven synthesis of highly efficient and durable multi-elemental alloy catalysts

We developed a computationally aided alloy synthesis in the multi-element space toward highly efficient and durable catalysts.

Abstract

Multi-elemental alloy nanoparticles (MEA-NPs) hold great promise for catalyst discovery in a virtually unlimited compositional space. However, rational and controllable synthesize of these intrinsically complex structures remains a challenge. Here, we report the computationally aided, entropy-driven design and synthesis of highly efficient and durable catalyst MEA-NPs. The computational strategy includes prescreening of millions of compositions, prediction of alloy formation by density functional theory calculations, and examination of structural stability by a hybrid Monte Carlo and molecular dynamics method. Selected compositions can be efficiently and rapidly synthesized at high temperature (e.g., 1500 K, 0.5 s) with excellent thermal stability. We applied these MEA-NPs for catalytic NH₃ decomposition and observed outstanding performance due to the synergistic effect of multi-elemental mixing, their small size, and the alloy phase. We anticipate that the computationally aided rational design and rapid synthesis of MEA-NPs are broadly applicable for various catalytic reactions and will accelerate material discovery.

INTRODUCTION

The chemical industry and emerging electrochemical energy conversion technologies are generally either thermally or electrically energy intensive and therefore require efficient catalysts to reduce the reaction temperature, pressure, or electrochemical overpotentials (1–3). In particular, clean energy based on hydrogen (H₂), despite being very promising for the replacement of fossil fuels, is largely dependent on advanced catalysts that substantially improve the energy conversion efficiency and decrease material cost (4, 5). To address these needs, multi-elemental alloy nanoparticles (MEA-NPs) demonstrate great potential for catalyst discovery and property optimization, with an expansive and underexplored compositional space (6, 7). In addition, the uniform mixing of multiple elements increases the system entropy and provides an entropy-driven, thermodynamically (ΔG = ΔH − T*ΔS) and kinetically (sluggish diffusion) stabilized structure that can sustain harsh service environments (high temperature, corrosion, and high electrochemical potential) (8–10), which have been also verified in other high-entropy materials (11–14). Preliminary experimental results have shown the enhanced catalytic performance of MEA-NPs compared with existing unary or binary systems (6, 7, 15, 16). However, few MEA-NPs have been reported in the literature due to the intrinsic complexity in multi-elemental synthesis and the ease of phase separation/elemental segregation among multiple different elements, posing a synthesis challenge.

Furthermore, although experimentally driven trial-and-error synthesis is possible, it requires substantial time and laboratory work to explore a virtually unlimited compositional space, particularly without any guidance or prescreening. Recently, computationally aided material discovery has made notable progress in the prediction of crystal structures and their catalytic properties (7, 17–21). However, the development of simulation models for increasingly complex structures, like MEA-NPs, is not yet readily available, forming a computational challenge. Therefore, despite being very promising, the study of MEA-NPs is still at the infancy stage and requires further advancements in both theoretical and experimental tools for the rational design and controllable synthesis of MEA-NP catalysts for accelerated materials discovery.

Here, we report the computationally aided, entropy-driven design and synthesis of MEA-NPs featuring a uniform alloy structure made up of traditionally immiscible elements. The multi-elemental system has an increased entropy that drives the uniform mixing toward alloy formation, whose compositions were analyzed in a million scale for phase selection. The formation energies of MEA-NPs were predicted using density functional theory (DFT) calculations, and their structures were simulated via a hybrid Monte Carlo and molecular dynamics (MC-MD) approach. Experimentally, we used a rapid and high-temperature method (e.g., 1500 K in 0.5 s) that enables the synthesis of MEA-NPs with an alloy structure that contains fragmented domains and rich interfaces. The synthesized MEA-NPs show excellent thermal stability in terms of both particle size and structure. In addition, we demonstrate the use of these materials for catalytic NH₃ decomposition with outstanding performance. We believe that this computationally aided rational design and controllable synthesis method can be generally used to accelerate catalyst discovery in multi-elemental materials.

RESULTS

We used the catalytic NH₃ decomposition reaction as a model system for developing MEA-NP catalysts. NH₃ is an ideal H₂ carrier that is CO free, has a high storage capacity, and is easy to handle. However, the release of H₂ from NH₃ is only energetically favorable when effective catalysts are present (Fig. 1A), among which Ru shows the best performance, while Ni is very active as a non-noble catalyst [Fig. 1B, derived from (22)] (22–24). Because different metals have different reactivity, MEA-NPs composed of multiple elements enable us to continuously tune the surface structure and chemistry for optimized catalytic performances. Below, guided by the computational methods, we will explore the large composition space among active metals (Ru, Rh, Co, Ni, Ir, Pd, Cr, Fe, Cu, and Mo) and construct several alloy compositions for detailed study.

Fig. 1. Computationally-aided compositional screening and alloy formation prediction of MEA-NPs.

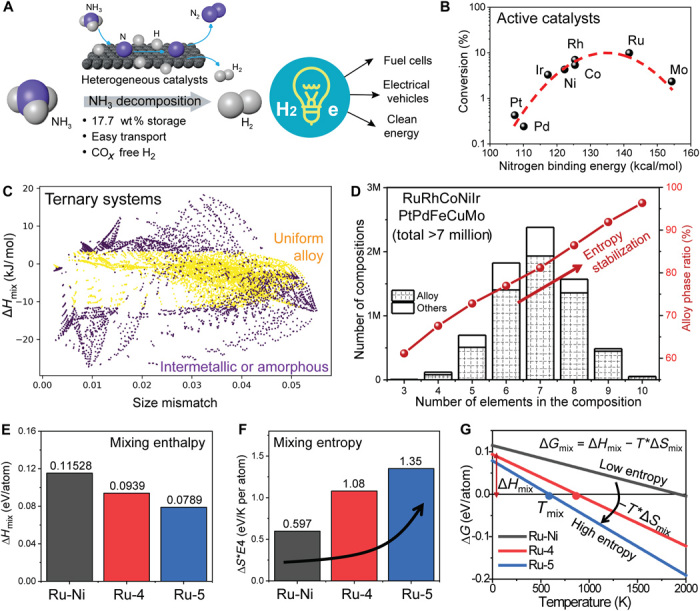
(A) The NH₃ decomposition reaction is critical to provide CO-free H₂ for fuel cell applications but can only be economically favorable with effective catalysts. (B) Reaction efficiencies of unary metal catalysts for NH₃ decomposition as a function of nitrogen desorption energy [derived from (22)]. (C) Ternary alloy screening from the 10 active elements (Ru, Rh, Co, Ni, Ir, Pd, Cr, Fe, Cu, and Mo) at 1500 K synthesis with compositions of each element ranging from 5 to 50% at a 5% step size (i.e., 7740 compositions). Yellow, uniform solid solution phase; purple, intermetallic, phase-separated, or amorphous structures. (D) Numbers of the compositions (left) and the ratio of the alloy phase in these compositions (right) as a function of the multi-elemental systems, showing a total of >7 million compositions and the steady increase of the alloy ratio due to entropy stabilization. (E) The mixing enthalpy, (F) mixing entropy, and (G) temperature-dependent Gibbs free energy of Ru-Ni, Ru-4, and Ru-5 MEA-NPs derived from DFT calculations. Systems with a higher mixing entropy can form an alloy phase at a relatively low temperature due to the entropy-driven effect (−T*ΔS_mix). %, molar percent.

Step 1: Composition prescreening for phase selection

The different physiochemical properties among the above elements often lead to phase separation (e.g., Ru-Ni, immiscible phase diagram in fig. S1). We launched a composition prescreening process to identify solid solution structures based on the phase formation rules derived in well-studied bulk high-entropy alloy materials (8, 25, 26), where the solid solution phase usually meets the following criteria: (i) atomic differences (δ ≤ 6.5%), (ii) mixing enthalpy (−11.6 < ΔH_mix < 3.2 kJ/mol), and (iii) Gibbs free energy (alloy mixing ΔG_mix = ∆H_mix − T∆S_mix < intermetallic ΔG_IM = ∆H_IM − T∆S_IM). With these criteria, we have explored the composition space of 10 active elements (Ru, Rh, Co, Ni, Ir, Pd, Cr, Fe, Cu, and Mo) with the ratio of each element ranging from 5 to 50%, with a 5% step size. As shown in Fig. 1C, for the ternary alloys derived from 10 active elements (7740 compositions), we can identify the solid solution (alloy) phase by calculating the above parameters: (i) atomic differences, (ii) mixing enthalpy (ΔH_mix), and (iii) ΔG_mix and ΔG_IM at 1500 K (our later synthesis temperature). The statistical data show that ~61% of the ternary compositions are alloys (yellow dots), while the others are intermetallic, phase-separated, or amorphous structures (purple dots). With more elements in the multi-elemental system, the number of total screened compositions increases exponentially to >7 million (Fig. 1D and fig. S2, A and B). In addition, the ratio of the alloy phases in the screened compositions increased steadily with increase in elements (i.e., increasing mixing entropy), indicating a strong entropy-driven single-phase stabilization. This prescreening process covers the whole composition map of the 10 elements studied and helped us to identify potential compositions that could lead to alloy phases well before synthesis.

Step 2: Composition design and DFT estimation for thermodynamic alloy formation

Although having the highest catalytic performance, Ru and Ni present a large immiscible gap (fig. S1), making the continuous tuning of Ru-Ni binary alloys impossible. However, through entropy engineering (i.e., increasing the entropy of the system), the immiscible combinations could be made into the alloy phase due to the entropy-driven effect. We therefore designed two MEA-NP compositions starting from Ru-Ni, including (i) RuRhCoNi (Ru-4 MEA-NPs), by incorporating Rh and Co that are also highly active for NH₃ decomposition, and (ii) RuRhCoNiIr (Ru-5 MEA-NPs), by further incorporating the dissimilar yet active element Ir. Both compositions were within our phase selection for alloy formation by 1500 K synthesis.

We then evaluated the thermodynamic parameters of the binary Ru-Ni and Ru-4 and Ru-5 MEA-NPs using DFT calculations with disordered face-centered cubic (fcc) alloy structures modeled by special quasi-random structures (SQS) (5 × 5 × 4 supercells containing 100 atoms) (27). Accordingly, we calculated the mixing enthalpy (ΔH_mix) and entropy (ΔS_mix) for alloy phase formation (Fig. 1, E and F): for Ru-4 and Ru-5 MEA-NPs, while the calculated mixing enthalpy decreases a little, the ideal mixing entropy increases nearly two to three times as compared with the bimetallic Ru-Ni system. The Gibbs free energy was drawn (ΔG_mix = ΔH_mix − T*ΔS_mix) by further considering the temperature effect (Fig. 1G). We found that the mixing enthalpy (ΔH_mix) acts as the barrier to alloy formation, but the entropy-driven effect (−T*ΔS_mix) favors an alloy phase, particularly at high temperatures. As a result, the alloy formation temperature for Ru-Ni bimetallic is around 2000 K, while it drastically decreases to 871 and 584 K for Ru-4 and Ru-5 MEA-NPs, respectively, suggesting the promise of entropy engineering for alloy formation in multi-elemental systems (28, 29). Note that our DFT calculations did not take into account the vibrational energy and surface-energy effect in the NPs, and the predicted formation temperature represents a thermodynamic lower limit for alloy formation. The calculation is also capable to predict systems that cannot form a homogeneous alloy structure in the multi-element space, as demonstrated in an RuRhCoNiCu system (fig. S2, C to E).

Step 3: Kinetic structural simulation and high-temperature synthesis

The above computation prescreening and DFT calculations are mostly thermodynamic rationale, while the kinetic formation of MEA-NPs remains unknown. We have performed a hybrid MC-MD method to simulate the high-temperature synthesis process and the probable structure of Ru-based MEA-NPs (details in the Supplementary Materials). We developed the interatomic potential for the Co-Ni-Ru-Rh-Ir alloy system within the framework of the second nearest-neighbor modified embedded atom method (MEAM) (30, 31). The parameters of the cross-potentials for each element pair were fitted so that the MEAM predictions of physical quantities, such as the enthalpy of formation and lattice constants, matched the DFT calculation results (table S1).

As shown in Fig. 2A, an NP with a cuboctahedra shape (Ru-5: Ru_0.25Rh_0.25Co_0.2Ni_0.2Ir_0.1, 4033 atoms, ~5 nm) was first generated by randomly assigning elements to each atom site, having a similar composition of Ru-5 MEA-NPs measured by inductively coupled plasma mass spectrometry (ICP-MS; table S2). Subsequently, 2 million MC diffusion steps at 1500 K were performed to relax the initial random structure to reach the compositional equilibrium, which shows a uniform alloy structure. The resulting structure was then quenched to 298 K and further thermally equilibrated through 20 million MD steps, after which the alloy structure was still maintained, demonstrating the successful formation and stabilization of the MEA-NP using a high-temperature synthesis. A similar simulation was also performed for Ru-4 MEA (Ru_0.44Rh_0.30Co_0.12Ni_0.14) (fig. S2F), and our computation predicted that both Ru-4 (Ru_0.44Rh_0.30Co_0.12Ni_0.14) and Ru-5 (Ru_0.25Rh_0.25Co_0.2Ni_0.2Ir_0.1) MEA-NPs would have well-mixed alloy structures.

Fig. 2. Kinetic formation simulation and high-temperature synthesis of MEA-NPs.

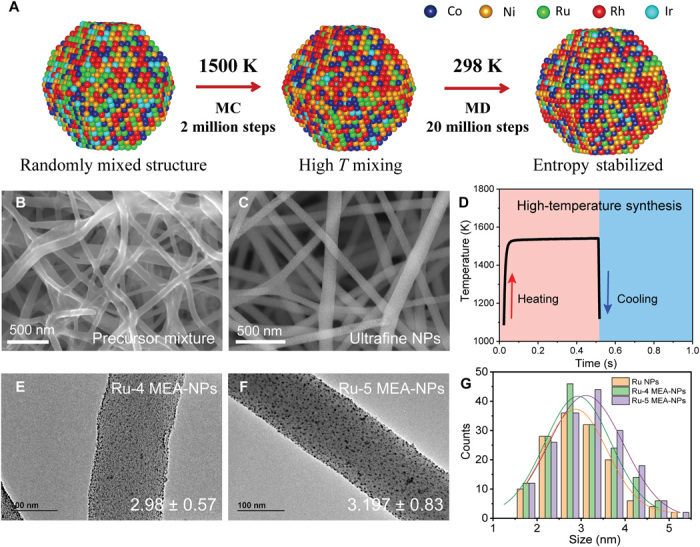
(A) The hybrid MD-MC simulation approach for the formation of an Ru-5 MEA-NP at 1500 K. The high temperature promotes the uniform mixing, while the high entropy stabilizes the structure. (B and C) SEM images of the Ru precursor–loaded carbon nanofibers (B) before and (C) after high-temperature synthesis. (D) The temporal temperature evolution during the high-temperature synthesis, which features a high temperature of 1500 K for 500 ms. (E and F) TEM images show the uniform size and dispersion of (E) Ru-4 and (F) Ru-5 MEA-NPs on carbon nanofibers and (G) the associated size distribution.

High-temperature synthesis of MEA-NPs

To experimentally realize the computational predictions, we used a unique high-temperature synthesis enabled by electrical Joule heating in which the temperature and its duration can be precisely controlled for the formation of MEA-NPs (16, 32). In a typical experiment, the multi-elemental salt precursor mixture (0.05 M in ethanol) was first deposited on an activated carbon nanofiber matrix (see Methods in the Supplementary Materials) with uniform wetting (Fig. 2B). After applying the rapid high-temperature heating (500 ms, 1500 K) to the substrate, the precursor salt mixture was thermally reduced into metals and well mixed at high temperature; upon quenching, the uniform mixing self-assembled into small NPs dispersed on the substrate (Fig. 2C). Figure 2D displays the temporal evolution of the temperature during the synthesis, showing featured rapid heating and cooling that enable the alloy NP formation. Note that although the mixing temperature predicted by the DFT calculation (T_mix) is relatively low, a higher temperature is still needed for the successful synthesis of MEA-NPs to promote uniform mixing and overcome diffusion barriers. Also, a higher-temperature synthesis is accompanied by superfast kinetics as compared with low-temperature syntheses, which usually take several hours or even days to complete the particle synthesis.

Figure 2 (E to G) further demonstrates the transmission electron microscopy (TEM) images of Ru-4 and Ru-5 MEA-NPs and their corresponding size distributions. We obtained NPs with an ultrasmall size and high-density dispersal. Despite containing different elements, these NPs show an unexpectedly uniform particle size distribution of ~3 to 5 nm (Fig. 2G and high-resolution images in fig. S3A). The ultrafine size of the MEA-NPs may be attributed to two reasons: (i) the high-temperature duration of the rapid synthesis is only 0.5 s, thus limiting the particle diffusion and coalesce to ensure a uniform distribution; (ii) the use of defective carbon substrates allows the defects to stabilize the particles during synthesis and prevent aggregation. The size uniformity by our synthesis approach is critical for property evaluation among these compositionally different NPs.

Alloy phase characterization in MEA-NPs

We characterized the detailed alloy structure of these MEA-NPs by energy-dispersive x-ray spectroscopy (EDS), Fourier transform extended x-ray absorption spectroscopy fine structure (FT-EXAFS), and scanning TEM (STEM) (Fig. 3). The microscopic EDS elemental maps provide direct evidence of alloy formation at the single NP level. As shown in Fig. 3A, synthesizing bimetallic Ru-Ni NPs using the same heating conditions (~1500 K, 500 ms) leads to phase separation between Ru and Ni, which confirms our DFT calculation that Ru-Ni requires a temperature of at least 2000 K for alloy formation. Figure 3 (B and C) shows that the synthesized Ru-4 MEA-NPs contain all four elements (Ru, Rh, Co, and Ni) and all five elements (Ru, Rh, Co, Ni, and Ir) for the Ru-5 MEA-NPs. In addition, each element is uniformly distributed throughout the particles without elemental segregation or the formation of immiscible phases. The uniform elemental distribution in these MEA-NPs, especially between the immiscible elements of Ru and Ni, demonstrates the successful alloying in Ru-based MEA-NPs at the particle level.

Fig. 3. The alloy structure of Ru-based MEA-NPs.

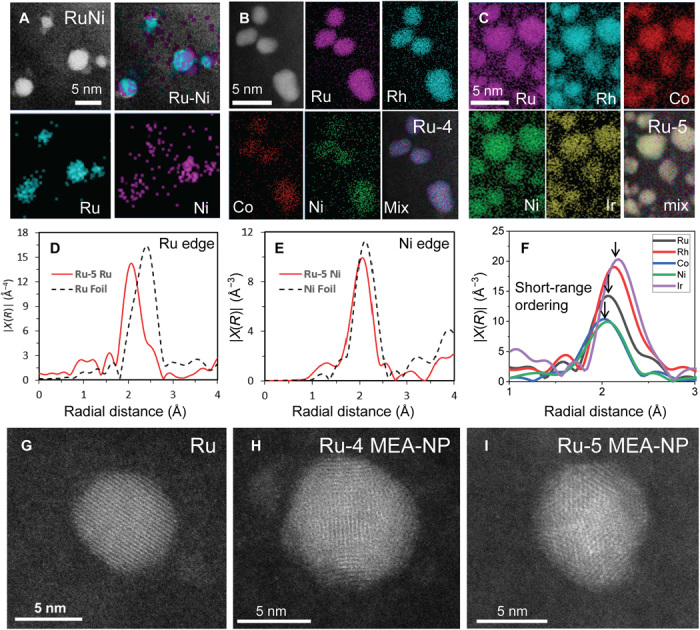
(A) Elemental maps of bimetallic Ru-Ni NPs showing that Ru separated from Ni due to their immiscibility. EDS elemental maps of (B) Ru-4 and (C) Ru-5 MEA-NPs, which demonstrate a homogeneous alloy structure with uniform distribution of each element. FT-EXAFS spectra for representative (D) Ru and (E) Ni elements in Ru-5 MEA-NPs, showing a slight shift relative to their corresponding metallic bonds, indicating that the elements are in a metallic state but surrounded by different elements, suggesting an alloy structure. (F) FT-EXAFS spectra of Ru, Rh, Co, Ni, and Ir in Ru-5 MEA-NPs showing a slight difference in bond lengths among the different elements, indicating the existence of short-range ordering in the MEA-NPs. High-angle annular dark-field (HAADF)–STEM images of (G) Ru, (H) Ru-4, and (I) Ru-5 MEA-NPs. While the Ru NP displays a single domain structure, the MEA-NPs show a fragmented domain structure with rich interfaces.

In addition, we used macroscopic x-ray diffraction (fig. S3, B and C) and X-ray absorption spectroscopy (XAS) to confirm the alloy formation at the macroscopic level. The x-ray absorption near-edge structure (XANES) provides information on the valence state of elements in the Ru-5 MEA-NPs by comparing with reference metal foils. The preabsorption edge features for Co and Ni and the absorption edge for Ru, Rh, and Ir all have a similar profile to their metallic reference, indicating that all the elements in the Ru-5 MEA-NPs are in a metallic state (XANES profiles in fig. S4A). In addition, the slight deviation in the shape and intensity of the postedge features indicates alloy formation, rather than elemental segregation into pure/unary metals, which would show the same length as metal foils. EXAFS provides further structural information of the Ru-5 MEA-NPs, as determined through the fitting of the Fourier transform (FT) spectra. In the FT-EXAFS spectra (Fig. 3, D and E, and fig. S4B for other elements), the bond structure reveals that the average bond length of Ru and Ni in the Ru-5 MEA-NPs is considerably different from the metallic bond in their bulk references, indicating that those elements are surrounded by different metallic species, i.e., a random alloy structure.

Through EXAFS fitting, we have summarized the bond length (R) and coordination numbers of each bond type in the Ru-5 MEA-NP system (Table 1). Because of the similar atomic number of the 3d (Co and Ni) and 4d (Ru and Rh) metals, bonds to them could not be distinguished from each other, so they were treated as the same for the purposes of the EXAFS fitting. The overall trend for the bond distances shows that in each bond type, with the exception of the 3d-3d interaction, the derived metal-metal bond is shorter than the bond present in the bulk reference. This indicates unique homogeneous mixing and supports the formation of an alloy structure. The reliability of the fitting method is supported by smaller R factors. Because of the relatively small amount (~5 to 10 atomic %) of Ir present in the Ru-5 sample, the coordination number for the bonds with Ir was found to be negligible during the fitting, and therefore, the fitting paths were removed to ensure a high-quality fit.

Table 1. The fitted coordination number (CN) and bond length (R) from the XAS profiles of the Ru-5 MEA-NP system (σ² is the Debye-Waller factor, and E₀ is the edge energy shift; the R factor indicates the goodness of fit (<0.03 is considered acceptable)].

Bond	CN	R (Å)	σ2 (Å) ×10−3	E0 (eV)	R factor
Ru-Co/Ni	7(2)	2.54(3)	5(3)	1(2)	0.0067
Ru-Rh	4.5(8)	2.59(5)	8(3)	1(2)	0.0067
Rh-Co/Ni	6.6(7)	2.54(2)	3.0(8)	1(2)	0.0088
Rh-Ru	4.0(7)	2.57(4)	7(4)	1(2)	0.0088
Co-Ni	6(1)	2.51(1)	4.8	−6(1)	0.0079
Co-Rh/Ru	3.4(5)	2.52(3)	4.8	−6(1)	0.0079
Ni-Co	5.0(6)	2.520(9)	7(2)	−7.6(8)	0.0075
Ni-Rh/Ru	2.1(3)	2.54(2)	7(2)	−7.6(8)	0.0075
Ir-Co/Ni	6(2)	2.55(3)	4(3)	5(3)	0.0226
Ir-Ru/Rh	4(2)	2.62(5)	8(7)	5(3)	0.0226

We also observed that the first shell peaks in the FT-EXAFS of all five elements have little mismatch (Fig. 3F), which means that the alloy is not completely random and some short-range chemical ordering exists. We have confirmed this short-range ordering using high-angle annular dark-field (HAADF) imaging in STEM mode to observe the atomic structure of the NPs. As shown in Fig. 3G, a single-element Ru NP displays a uniform and single domain structure, which is more energy favorable at the nanoscale. However, when the alloyed elements increased to Ru-4 and Ru-5 MEA-NPs, the particles start to show a fragmented domain structure with rich interfaces, which may come from the multi-elemental mixing among immiscible combinations that leads to the short-range ordering: The atomic size mismatch (table S3) and the complex composition lead to a multidomain structure to accommodate the lattice distortion and strain effect. These fragmented domains with rich interfaces are believed to have improved catalytic performance, as more active sites are exposed in these NPs (33, 34).

Stability of MEA-NPs

The stability of the MEA-NPs is critical for their practical application at elevated temperatures. We, therefore, performed an in situ stability test in the electron microscope from room temperature up to 873 K, annealing the NPs at each test point for at least 30 min. As shown in Fig. 4A, the ultrafine Ru-5 MEA-NPs maintain their uniform dispersion throughout the in situ tests up to 873 K and demonstrate superior size stability after high-temperature annealing. In addition, the NPs are still in a homogeneous alloy structure without elemental segregation or phase separation (Fig. 4B), showing their structural stability. Note that the Co and Ni after annealing are slightly less than the nominal composition, which is likely due to metal evaporation at high temperature in the microscope vacuum. We also confirmed the alloy structure macroscopically by powder and synchrotron x-ray diffraction, showing a single-phase fcc structure with a fitted lattice constant of 3.673 Å (fig. S3, B and C).

Fig. 4. Structural stability of the MEA-NPs.

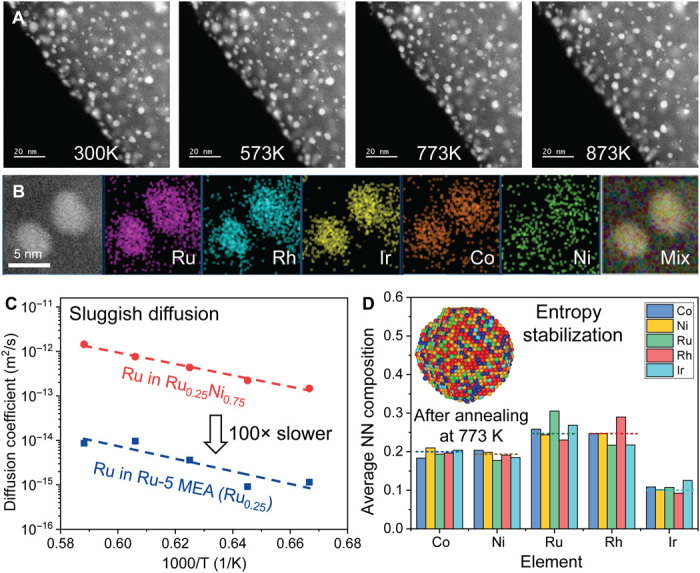
(A) In situ thermal stability of Ru-5 MEA-NPs from room temperature up to 873 K, holding at each temperature for >30 min, demonstrating the size and dispersion stability of the MEA-NPs. (B) EDS mapping of the Ru-5 MEA-NPs after the in situ stability test, showing a homogeneous alloy structure without elemental segregation (i.e., structural stability). (C) The MD simulated diffusion coefficient for Ru in binary Ru-Ni versus Ru in Ru-5 MEA; the latter is two orders (100×) slower, suggesting that the sluggish diffusion effect in the MEA-NPs enhances their structural stability. (D) Compositional analysis of Ru-5 MEA-NPs annealed at 773 K through coupled MD-MC simulation, further demonstrating the structural stability. The system’s high entropy helps to stabilize the alloy structure against segregation. NN, nearest neighbor.

The dispersion stability of the MEA-NPs can be explained by the following two reasons. First, we used high temperatures for the MEA-NP synthesis, and as a result, they naturally have high thermal stability. Second, the defects of the carbon nanofibers help to anchor these MEA-NPs onto the substrate with improved thermal stability. In terms of the observed structural stability, we believe that it originates from the entropy stabilization effect. Thermodynamically, multi-elemental mixing increases the mixing of entropy and favors an alloy structure. Kinetically, the mixing among different elements also leads to increased lattice distortion (table S3 for Ru MEA-NPs) and, therefore, sluggish diffusion, which prevents phase separation and elemental segregation (8, 10).

To further verify the structural stability, we performed MD simulations to calculate the self-diffusion coefficient of the Ru element in Ru-5 MEA and compared it with Ru in a binary Ru-Ni alloy. We found that the Ru atoms in the Ru-Ni alloy diffuse about two orders of magnitude (100×) faster than in Ru-5 MEA (Fig. 4C), indicating that the sluggish diffusion in the MEA-NPs is due to the multi-elemental mixing and the resultant lattice distortion, which contributes to the enhanced thermal stability. The diffusion coefficient of Ru in Ru-5 MEA has a slightly larger slope, suggesting higher activation energy (i.e., larger diffusion barrier) according to the Arrhenius equation.

We also simulated the overall diffusion in the MEA-NP using a hybrid MC + MD simulation approach, in which the MC swaps were attempted at a constant frequency during the MD simulation to model the annealing conditions at 773 K. The entropy-stabilized structure has less atom diffusion due to high diffusion barriers and sluggish kinetics, resulting in uniform elemental distribution after annealing. Figure 4D shows the statistical probability of the nearest composition distributions for each element in Ru-5 MEA-NPs, displaying its microscopic/atomic arrangement of different elements. We found the nearest-neighbor sites of each element equal to its nominal composition with only short-range fluctuations. As a comparison, when it is fully diffusion equilibrated, clear elemental segregation, especially for Ru, Rh, and Ni, is observed (fig. S5A), indicating that the entropy-induced slow kinetics are the key to stabilize the structure for thermal annealing. Similar entropy-stabilization results were also found when there is an extension of MC + MD’s time scale to 50 ns (fig. S5B) and in the Ru-4 MEA-NPs (fig. S5, C and D). The confirmation of the structural stability of the MEA-NPs is critical for catalytic application at high temperatures and demonstrates the importance of the high entropy-stabilization effect.

Application of MEA-NPs in catalytic NH₃ decomposition

We demonstrated the application of the uniform and ultrafine MEA-NPs for catalyzing the NH₃ decomposition reaction. We designed two sets of control samples: (i) Ru and RhCoNi control samples that featured the same composition ratio and loading as in the Ru-4 (RuRhCoNi) MEA-NPs synthesized separately by high-temperature heating at 1500 K, and (ii) a RuRhCoNiIr sample made by the impregnation method (Ru-5 IMP; annealed at 300°C for 1 hour), featuring the same composition as the Ru-5 MEA-NPs (size distribution and elemental maps in fig. S6). As shown in Fig. 5A, the performance of the Ru-4 and Ru-5 MEA-NP samples was substantially higher than the corresponding controls. The Ru-4 MEA-NPs reached 100% NH₃ decomposition at ~470°C, while the Ru sample with the similar Ru loading only showed a 30% conversion, indicating the importance of composition control and homogeneous mixing for performance optimization. In addition, despite the same composition, the Ru-5 MEA-NPs obviously outperformed the Ru-5 IMPs sample, indicating that the improved performance mostly comes from the alloy structure rather than the simple element blending. Figure 5B shows that the conversion efficiency of RuRhCoNi-MEA is much higher compared with the simple addition of Ru + RhCoNi, indicating a strong synergistic effect in the RuRhCoNi MEA sample that leads to enhanced performances (7, 35). The substantial increase in the catalytic performance of both MEA-NPs demonstrates the advantage of using multi-elemental composition in an alloy structure for the discovery of high-performance catalysts.

Fig. 5. Catalytic performance of Ru-4 and Ru-5 MEA-NPs in the NH₃ decomposition reaction.

(A) Polarization curves of Ru-4 and Ru-5 MEA-NPs compared with Ru, RhCoNi, and Ru-5 IMP samples, respectively. Both MEA-NP systems show substantial improvement compared with the controls. (B) Conversion efficiency for Ru-4 MEA-NPs compared with the addition of Ru + RhCoNi, indicating a strong synergistic effect in the Ru-4 MEA sample that leads to enhanced performances. (C) HAADF and (D) EDS maps of Ru-4 MEA-NPs after high-temperature catalytic study, demonstrating their good dispersion and alloy structure without phase separation. (E) Performance comparison of Ru-based MEA-NPs with the literature (data in table S4), showing the higher performance of the MEA-NPs (450°C with a GHSV ≥30,000).

We have characterized the MEA-NPs after the catalytic reaction, where the MEA-NPs were still well dispersed and continued to feature the alloy structure (Fig. 5, C and D), confirming the high thermal stability of the MEA-NPs. We also compared our results with previous reports of Ru-based catalysts for NH₃ decomposition in the literature (normalized by the Ru loading) and found that our catalysts are among the superior catalysts [Fig. 5E, data in table S4: reaction temperature 450°C with a gas hourly space velocity (GHSV) of ≥30,000] (23, 24, 36). The outstanding performance of the MEA-NPs is likely a synergistic effect from the ultrafine size of the NPs (3 to 5 nm), their multi-elemental composition, and their homogeneous alloy structure.

DISCUSSION

In this work, we report the computationally aided design and rapid synthesis of MEA-NPs as highly active and durable catalysts. Composition prescreening, DFT calculations, and hybrid MD-MC modeling help to predict and simulate the MEA-NP formation, both thermodynamically and kinetically, which serves as an important guide for rational composition design before synthesis. Moreover, a high-temperature approach enables the synthesis of MEA-NPs with an ultrasmall size and uniform dispersion. We further confirmed the dispersion and alloy structural stability of the MEA-NPs after thermal annealing, which is critical for practical applications. The ultrafine, well-dispersed, and thermally stable MEA-NPs showed high performance and durability in catalyzing NH₃ decomposition. We believe that this work has developed a viable approach for guided catalyst discovery in MEA-NPs and can be generally applied to various catalytic reactions to largely accelerate material discovery in multi-elemental space.

MATERIALS AND METHODS

MEA-NP synthesis

The carbon substrate was derived from electrospinning of polyacrylonitrile, which was then stabilized in air at 260°C for 6 hours, carbonized at 1000°C for 2 hours in argon, and activated at 750°C for 3 hours in CO₂ to obtain CO₂-activated carbon nanofibers (CA-CNFs) (16). Metal precursors (chlorides, 0.05 M in ethanol) were uniformly dripped on the CA-CNFs (~ 100 μl/cm²). The high-temperature synthesis was triggered by electric Joule heating with a highly controllable high-temperature duration and ramp rate using a Keithley 2425 SourceMeter (500-ms pulse). We have used a time-resolved pyrometer to capture the emitted light from the sample for temperature characterization (16).

Compositional prescreening

To screen the possible structures for the MEA-NPs, two sets of rules, derived from well-studied high-entropy alloy materials, were applied for size mismatch, mixing enthalpy, and Gibbs free energy (details in the Supplementary Materials) (8, 25, 26, 37). We scanned all possible alloys by selecting n (3 ≤ n ≤ 10) of the 10 active metal elements (Ru, Rh, Co, Ni, Ir, Pd, Cr, Fe, Cu, and Mo) and changing the composition of each element from 5 up to 50%, with a 5% step size increment.

DFT calculations

The thermodynamic evaluation of the alloy formation was carried out using the DFT calculation method. All the calculations were performed using plane-wave basis and the projector-augmented wave method, as implemented in the Vienna Ab-initio Simulation Package (38). The exchange-correlation energy was described by the Perdew-Burke-Ernzerhof (GGA-PBE) functionals (39). A kinetic energy cutoff of 500 eV was used for plane-wave expansion. During structural optimization, the energy and force convergence criteria were set to 10⁻⁶ eV and 0.01 eV/Å, respectively. The equilibrium lattice parameters were determined by fitting the total energy to the Murnaghan equation of state (40). MEA-NPs and disordered Ru-Ni in fcc structures were modeled by SQS (27) of 5 × 5 × 4 supercells containing 100 atoms. The mcsqs code in the Alloy Theoretic Automated Toolkit (41) was used to find the best SQS that most satisfies the correlation function of random solutions (details of calculations are in the Supplementary Materials). It should be noted that the DFT calculations were performed without taking the vibrational energy and surface energy effect of the NP into consideration. Also, the real configurational entropy in the NP should be lower than ideal configurational entropy due to short range ordering. As a result, the formation temperature predicted by our DFT is a lower limit.

Atomistic modeling by MD-MC

The interatomic potential for the Ru-based MEA-NPs was developed within the framework of the second nearest-neighbor MEAM (30, 31). The cross-potentials for each element pair were fitted so that the MEAM predictions of physical quantities, such as the enthalpy of formation and lattice constants, match the DFT calculation results. In the current formulism of the MEAM potential, the reference structure between all pairs of elements was chosen to be the B2 structure (ordered body-centered cubic). The predicted physical properties of the binary alloys are tabulated in table S1. All the MD simulations were executed in the NVT ensemble (N: number of particles; V: system volume; T: absolute temperature) with a Nosé-Hoover thermostat, as implemented in the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) package (details of modeling can be found in the Supplementary Materials) (42).

Structural characterization

The microstructure was characterized by SEM (Hitachi SU-70 FEG-SEM at 10 kV) and TEM (JEOL 2100F FEG TEM/STEM operated at 200 kV, and JEOL TEM/STEM ARM 200CF). The elemental distribution and maps were measured using an Oxford X-max 100TLE windowless x-ray detector. ICP-MS was measured on a PerkinElmer NexION 300D ICP-MS.

X-ray absorption measurement and analysis

Ir L₃-edge and Ru, Rh, Co, and Ni K-edge XAFS data were collected from the CLS@APS (Sector 20-BM) beamline at the Advanced Photon Source (operating at 7.0 GeV) in Argonne National Labs, Chicago, IL, USA. The sample was measured in fluorescence mode simultaneously with a reference for each element (powder for Ir and metal foil for Ru, Rh, Co, and Ni) at room temperature and ambient pressure, protected from exposure with oxygen. EXAFS data were transformed and normalized into k-space and R-space using the Athena program, with conventional procedures. A k-range of 2.6 to 13.6 Å⁻¹ for Ir, 2.8 to 13.4 Å⁻¹ for Ru, 2.8 to 13.3 Å⁻¹ for Rh, 2.4 to 11.3 Å⁻¹ for Co, and 2.4 to 12.9 Å⁻¹ for Ni was used to obtain all FT-EXAFS spectra with a k weighting of 3. Self-consistent multiple-scattering calculations were performed using the FEFF6 program to obtain the scattering amplitudes and phase-shift functions used to fit various scattering paths with the Artemis program. In the fitting, an R-window of 1.5 to 3.7 Å for Ir, 1.4 to 3.4 Å for Ru, 1.3 to 3.6 Å for Rh, 1.2 to 3.4 Å for Co, and 1.5 to 3.4 Å for Ni was used. In the fitting of each element, the E₀ values of each path were correlated together to minimize the number of independent variables and ensure high fitting quality. For the fitting of Co and Ni, the σ² values were also correlated together to further minimize the number of independent variables due to the shorter k-range.

NH₃ decomposition

Catalytic decomposition of NH₃ was conducted in a fixed-bed flow reactor at atmospheric pressure. Typically, 50 mg of catalyst was loaded into a quartz tube reactor (7-mm internal diameter). The catalyst was heated to 300°C at a rate of 5°C/min under He (20 ml/min). At 500°C, the gas flow was switched to the reaction gas containing 5% NH₃, balanced by He. The space velocity was adjusted to 3600 ml g_cata⁻¹ hour⁻¹ by tuning the flow rate. The reaction was then carried out at various temperatures, which was increased stepwise from 300° to 550°C, and steady state was allowed to reach before the product analysis. To determine the conversions of reactants and the yields of products, an FTIR (Fourier transform infrared) spectrometer (Nicolet 6700, Thermo Scientific) equipped with a long path (5 m) gas cell and a mercury cadmium telluride detector (with a resolution of 8 cm⁻¹) were used to analyze NH₃ (964 cm⁻1). The NH₃ conversions were calculated using the following equation

$$\text{NH}3 \text{conversion}=\frac{{[\text{NH}3]}_{\text{inlet}}‐{[\text{NH}3]}_{\text{outlet}}}{{[\text{NH}3]}_{\text{inlet}}}\times 100\%$$

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/11/eaaz0510/DC1

Simulation details

Table S1. Predicted lattice constant a and enthalpy of formation ∆H for relevant binary and quaternary alloys using DFT and MEAM.

Table S2. ICP-MS result for our samples in the NH₃ decomposition experiment.

Table S3. Simulated lattice distortion of the Ru-4 and Ru-5 MEA-NPs.

Table S4. Catalytic performance of NH₃ decomposition and comparison with the literature.

Fig. S1. Equilibrium phase diagram of Ru-Ni, showing a large immiscible gap.

Fig. S2. MEA-NP composition screening and prediction.

Fig. S3. Size distribution and macro structure of Ru-MEA NPs.

Fig. S4. X-ray absorption spectra for Ru-5 MEA-NPs.

Fig. S5. Hybrid MC + MD simulation on MEA-NP stability after annealing.

Fig. S6. Ru-5 control samples prepared by impregnation method.

Reference (43)