An investigation of elastic waves producing stone fracture in burst wave lithotripsy

Abstract

Burst wave lithotripsy is a method to noninvasively fragment urinary stones by short pulses of focused ultrasound. In this study, physical mechanisms of stone fracture during burst wave lithotripsy were investigated. Photoelasticity imaging was used to visualize elastic wave propagation in model stones and compare results to numerical calculations. Epoxy and glass stone models were made into rectangular, cylindrical, or irregular geometries and exposed in a degassed water bath to focused ultrasound bursts at different frequencies. A high-speed camera was used to record images of the stone during exposure through a circular polariscope backlit by a monochromatic flash source. Imaging showed the development of periodic stresses in the stone body with a pattern dependent on frequency. These patterns were identified as guided wave modes in cylinders and plates, which formed standing waves upon reflection from the distal surfaces of the stone model, producing specific locations of stress concentration in the models. Measured phase velocities compared favorably to numerically calculated modes dependent on frequency and material. Artificial stones exposed to bursts produced cracks at positions anticipated by this mechanism. These results support guided wave generation and reflection as a mechanism of stone fracture in burst wave lithotripsy.

I. INTRODUCTION

The outputs of modern shock wave lithotripters used to fragment kidney stones vary in focal pressure amplitude and beam dimensions.¹ However, all produce similar shock waveforms consisting of a primary compressive phase followed by a tensile phase with a total duration of 5–10 μs, delivered at a rate of 1 to 2 shocks per second. Numerical models of elastic wave propagation indicate that shear waves produced by the incident shock are a dominant cause of fracture—assertions supported by experiments observing fractures in model stones.^2–4 More specifically, the incidence of the focused shock along the edges of the stone produces mode conversion, resulting in shear waves generated within the stone body.^5,6 In a cylindrical model, these waves converge on-axis which focuses the stress.² Shear wave production is enhanced when the shear waves in the stone closely match the sound speed of the surrounding fluid. In addition, a longitudinal wave propagates through the stone and reflects at the distal surface to create a tensile wave. The coincidence of these two waves creates a localized stress, and an initial fracture in the stone is observed at this location after multiple shock wave exposures. Cavitation bubbles at the stone surface, which grow and collapse in response to the incident tensile wave in the fluid, also contribute to fracture by initiating surface cracks.⁷ Repeated shocks cause the stone to fracture first into several large fragments, then section further into smaller fragments.⁸ As the fragments become smaller, the boundary conditions limit the amplitude of elastic waves that can be generated within a fragment, but cavitation can further erode the stone to passable fragments.

An alternative emerging technology under clinical trials for noninvasive stone fragmentation is burst wave lithotripsy (BWL). In contrast to SWL, BWL employs multicycle sinusoidal bursts of focused ultrasound.⁹ While the general principle of treatment is similar, several observations of stones exposed to shocks and bursts differ. For one, stones exposed to BWL show periodic fracturing throughout the stone prior to fragmentation. Further, fragmentation in BWL primarily proceeds by small pieces ejecting from the larger body of the stone, as opposed to sequential bisection observed in SWL. The periodicity of fractures in BWL appears proportionate to the wavelength of the ultrasound, resulting in smaller fragments for higher frequency exposures.⁹ These features may be beneficial in producing a treatment that generates only small fragments that will readily and asymptomatically pass through the urinary tract.^10,11 Cavitation activity with BWL pulses is also different; the multicyclic nature of the pulse (versus a single, trailing negative phase in SWL) limits expansive growth of the bubbles during tension.¹² At amplitudes sufficient to fracture stones, BWL pulses can be delivered at rates considerably higher than a typical shock wave lithotripter (10–100 Hz vs 1–2 Hz) without producing detectable cavitation in vivo.¹³ The rate at which pulses can be delivered in SWL is limited by cavitation that may shield the stone from effective energy transfer^14,15 and produce tissue injury.¹⁶ The selected amplitude and rate of BWL pulses may therefore prevent such cavitation-induced injury that is common in SWL.¹⁷

The differences in stone fracture between BWL and SWL motivate further investigation of the physical interactions that lead to high levels of stress and fracture of stones. The present study considers elastic waves in stone models in the frame of guided waves propagating along the acoustic axis. We hypothesize that stone fracture is a result of stresses created through (1) generation of specific wave modes and (2) reflection of these modes from the distal surfaces or cracks in the stone to create localized standing waves that result in a cycle of repeated stressing that initiates and propagates fractures over several cycles or bursts. In this article, the hypothesis is examined by dynamic photoelasticity imaging to visualize stress patterns in model stones, numerical calculations of guided wave propagation, and experiments detailing fracture formation.

II. EXPERIMENTAL METHODS

A. Focused ultrasound system

Three piezoelectric focused ultrasound transducers were used to produce BWL pulses in experiments. The transducers had nominal frequencies of 170, 340, and 800 kHz. The three transducers also have different aperture and focal length (Table I). Each source was electrically driven by a class D switching amplifier^18,19 controlled by an FPGA timing board. The pulsing settings on the timing board were programmed through a USB connection to a desktop computer by matlab (The Mathworks, Natick, MA). Each transducer element was connected to the amplifier through an L-bridge matching circuit that transformed the element impedance to a lower value to increase the voltage that could be applied to the elements.

TABLE I.

Characteristics of the three transducers used in experiments.

Center frequency (kHz)	Aperture (mm)	Focal length (mm)	Axial beam width (mm)	Lateral beam width (mm)
170	80	54	32.4	7.6
340	180	150	29.0	5
800	147	140	17.0	2.6a

^aStones are exposed 1 cm prefocal to the peak pressure position where the lateral beam width was ∼ 6 mm.

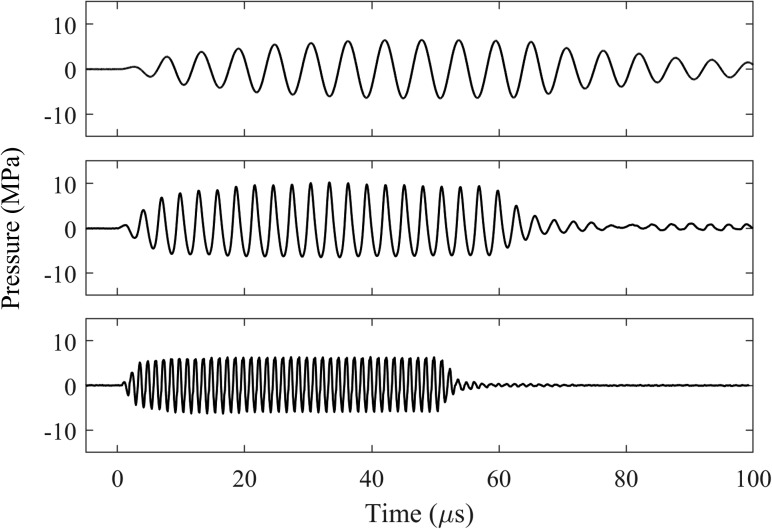
The transducers were all calibrated using a fiber optic probe hydrophone (FOPH2000; RP Acoustics, Leutenbach, Germany)²⁰ in a bath with degassed, deionized water. The focal beam dimensions were measured along and transverse to the axes (Table I). The 170 and 340 kHz transducers had focal beam widths near the width of the stone models used in this study, but the 800 kHz transducer had a much narrower focus. In order to produce a reasonable comparison for exposures with similar beam widths, all stones exposed to the 800 kHz transducer were aligned in the prefocus 1 cm, where the −6 dB beam width was approximately 6 mm. In the following experiments, photoelastic imagers were captured at multiple focal pressure amplitudes ≤6.5 MPa. Pressure waveforms recorded by FOPH at 6.5 MPa peak negative pressure at displayed in Fig. 1. All are nearly sinusoidal, although there is some nonlinear distortion evident at 340 kHz. The second harmonic amplitudes relative to the fundamental amplitudes are −44, −14, and −22 dB for the 170, 340, and 800 kHz waveforms, respectively.

FIG. 1.

Waveforms recorded by fiber optic probe hydrophone at 170 kHz (top), 340 kHz (middle), and 800 kHz (bottom) with peak negative pressure of 6.5 MPa. The 170 and 340 kHz waveforms are captured at the focus, while the 800 kHz waveform is captured 1 cm prefocally along the acoustic axis of the transducer.

B. Stone models

Since only certain materials display stress birefringence, specific models were selected for photoelastic imaging that encompass the range of acoustic properties for stones.²¹ An epoxy (INF 114/212; West System, Bay City, MI) and borosilicate glass were selected as two materials. The properties of each material are listed in Table II, along with ranges for natural human urinary stones and the artificial stone model used in experiments of stone fracture. Properties for natural stones, artificial stones, and borosilicate glass are acquired from literature (see references in Table II). Acoustic properties of epoxy (sound speeds and attenuation) were acquired by measurement via a pulse echo measurement²² using longitudinal and shear transducers (V303-SU and V153-RB, Olympus NDT, Center Valley, PA) on a bulk sample. The epoxy sound speeds are 10%–15% below the lower end of the range for human urinary stones, while those in glass are about 20%–35% higher than the upper end, with similar density. Urinary stones requiring intervention are commonly between 5–20 mm along their largest dimension.²³ For these studies, epoxy rectangular plates (1 mm thickness) and cylinders with 6.35 mm width (diameter) and 6–26 mm length were cast in silicone molds after degassing the liquid resin for 1 h. While human urinary stones will have irregular geometry, these idealized models serve as a structure where the stress can be quantified and compared against numerical models. Some cast plate samples were further machined to create other nonuniform shapes as 1 mm thick epoxy plates—a “star” shape and an “N” shape, both approximately 7–8 mm vertical dimension by 9 mm along the acoustic axis. These shapes tested whether the general hypotheses for regular geometries extend to nonuniform shapes. Borosilicate glass rods (Part No. 8477K98, McMaster-Carr, Princeton, NJ) with 7 mm diameter and lengths of 10, 14, or 22 mm were sectioned using a dicing saw (MTI Corporation, Richmond, CA) to create cylindrical sections. For experiments in stone fracture, artificial stones^24,25 made from Begostone Plus plaster (Bego USA, Lincoln, RI) were formed as cylinders of different lengths between 6 to 26 mm with a diameter of 6.35 mm.

TABLE II.

Properties of model materials used in this study and ranges for human urinary stones.

	Human urinary stonesa	Epoxyb	Borosilicate glassc	Artificial stonesd
Density (kg/m3)	1550–2040	1100	2200	2040
Longitudinal wave speed (m/s)	2800–4550	2440	5640	3640
Shear wave speed (m/s)	1460–2130	1295	3300	2035
Longitudinal attenuation (dB/MHz/cm)	N/A	3.0	0.15	2.8
Optical index of refraction	N/A	1.58	1.48	N/A
Immersion liquid density (kg/m3)	1000	1100	1230	1000
Immersion liquid sound speed (m/s)	1500	1493	1880	1500

^aData acquired from Ref. 21.

^bData for benzyl benzoate acquire from Ref. 47.

^cData acquired from Refs. 48 and 49.

^dArtificial stones are made from Begostone Plus plaster (Bego USA, Lincoln, RI).

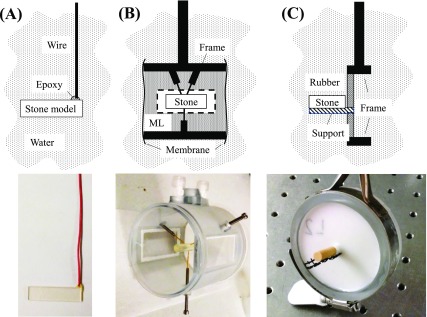
The distal end of each rectangular plate was attached with a small amount of epoxy to a 22-gauge solid copper wire (Fig. 2) to suspend it in the transducer beam field in water. The optical index of refraction of both glass and epoxy is higher than water, thus, cylindrical samples had to be contained in an index-matched fluid to avoid light distortion when viewing them. An 85 mm × 85 mm cylindrical chamber was fabricated to house the stone and fluid (Fig. 2). For epoxy, the chamber was filled with benzyl benzoate (Sigma-Aldrich, St Louis, MI). For glass, a solution of 80% glycerol (Sigma-Aldrich, St Louis, MI) with 20% deionized water by weight was mixed to match the refractive index of glass. Both immersion liquids were degassed for 1 h in a bell jar held at a partial vacuum of 6.5 kPa prior to adding them to the chamber. Each cylindrical stone model was held in the center of the chamber by three 0.6 mm-diameter spring-loaded pins. Two flat glass windows in the sides of the chamber allowed visualization of the model during experiments. The ends of the chamber were sealed with a 0.5-mm silicone rubber membrane at the distal end and a 12 μm thick LDPE sheet at the proximal end to isolate the liquid but serve as acoustic windows. Acoustic losses from the LDPE sheet were found to be negligible. The differences in fluid impedance for different cases caused changes in transmitted pressure by ≤20%. For stone fracture experiments, artificial cylindrical stones were placed in a plastic frame in the water bath that minimized contact with the stone and disruption of the acoustic field, but provided support along the length of the stone (Fig. 2).

FIG. 2.

(Color online) Stone holders for each model in this study. The top shows a schematic diagram and the bottom shows a photograph of each. (A) A rectangular stone model held by a small amount of epoxy attached to a 22-gauge wire. These models were directly submerged in degassed water. (B) A chamber for containing an optical-matching fluid and fixing a cylindrical stone model. An acoustically transparent membrane is placed over the front face to contain the liquid while the optical windows on the side allow visualization with a camera. The model is held by three spring-loaded pins in the center of the chamber. ML = Matching liquid. (C) A small plastic frame (black) extending from a tissue-mimicking material holding a cylindrical artificial stone made from Begostone Plus plaster. This holder was used to suspend and support the length of the stone during fracture formation.

Experiments were performed in a 110 L bath of degassed, filtered water. A transducer was suspended in the water bath from a manual three-axis linear stage (Velmex, NJ). The chamber was suspended in the tank on a separate three-axis positioning system with the proximal cylinder end facing the transducer. Each stone model was aligned with the transducer focus (or prefocus for the 800 kHz transducer) prior to sonication.

C. Dynamic polariscopic imaging

To visualize stress created by BWL pulses in the stone models, a dynamic photoelasticity imaging system was developed. Photoelasticity imaging relies on the stress-birefringence of certain materials in which the indices of refraction for light polarization along orthogonal axes change with differences in stress between axes. Two light rays traveling through the material under stress with polarization along axes 1 and 2 will travel at different speeds, creating a phase shift between them. For a sample with thickness d through which light travels at optical wavelength λ_o, the principal stress difference along these axes can be determined in terms of observed phase shift δ as

$${\sigma }_1-{\sigma }_2=\frac{{\lambda }_o}{2\pi Cd}\delta ,$$

where ${\sigma }_1$ and ${\sigma }_2$ are the principal stresses and C is the material-specific stress-optic coefficient.²⁶ The phase shift between light rays at different points in the sample creates interference appearing as bright and dark fringes for monochromatic light similar to those observed in other forms of interferometry. In a thin, uniform sample, this interference can be interpreted as the relative magnitude of this stress difference based on the intensity of a single fringe at low magnitude, or the number of fringes at high magnitude when the optical phase shift may be greater than π. Similar systems have been used for stress analyses of ultrasound, shock waves, and laser pulses^27–29 or visualization of guided waves during ultrasound exposure.³⁰ However, the magnitude is difficult to directly interpret in a sample of nonuniform thickness such as a cylinder.³¹ Nevertheless, we use both plate and cylindrical models here to examine wave propagation and compare with model stones fractured during BWL.

A 450-nm 1-W light emitting diode (LED) was used for backlighting. LED lighting was chosen because monochromatic LEDs have a bandwidth of ∼10 nm, which is narrow enough to consider a single wavelength for this application, but broad enough to avoid nonuniformity of the field due to a speckle pattern, as would occur with a laser light source.²⁷ In addition, the LED can be driven beyond its rated power for a short time with a rapid pulse to produce a flash. A triggerable LED driver was designed and constructed in our lab to provide timed, staggered flashes of ∼200 ns duration and a peak electrical power of approximately 200 W. The LED was strobed once per BWL pulse, with the delay between the transducer output and the LED flash incremented to capture a different time point in the wave progression in a stroboscopic fashion.^29,32 Since the transducer output was highly consistent between pulses, the resulting image sequence effectively replicated the temporal sequence of the stress development in the stone model during and after the incidence of the pulse on the model. The LED light was shaped by two condenser lenses to produce a nearly collimated beam.

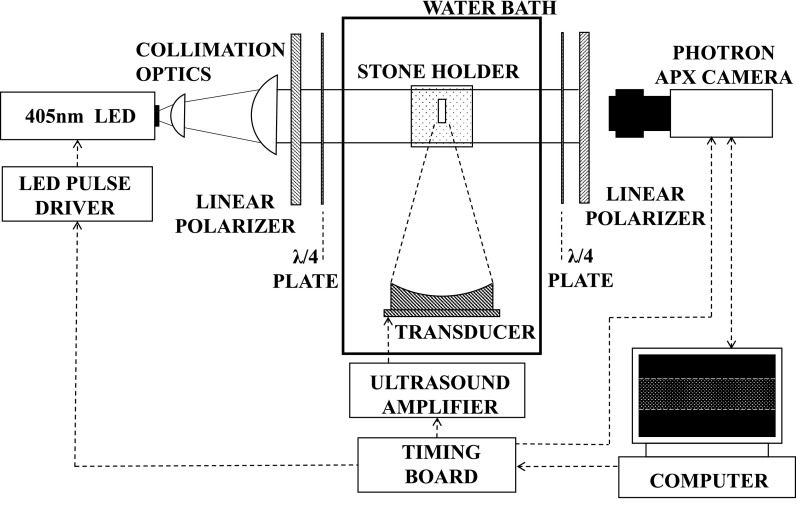
The light was passed through a circular polariscope on either side of the tank (Fig. 3). The brightfield circular polariscope was formed by passing the light through a linear polarizer, then a quarter-wave plate with fast/slow axes 45° from the linear polarization direction to create circularly polarized light.²⁶ This light then passed through the water bath and sample. On the opposing side of the bath, a quarter-wave plate with axes 90° to the first was aligned, followed by another linear polarizer with the same orientation as the first. This apparatus served to measure the component of the light polarized along the axis of the linear polarizer on the camera side. If the light propagated through the sample under zero stress, the circularly polarized light would be converted back to linear polarization and the field appears bright. Under stress, dark fringes appear indicating the phase change between axes and thus the magnitude of the photoelastic effect. By using circular polarization, the field is made independent of the orientation of the linear polarizers removing the isoclinic field and preserving the isochromatic field.

FIG. 3.

Experimental setup with the stone model aligned with the transducer focus in a water bath. A high-speed camera is used to record stroboscopic images of the stone model, backlit by a 450 nm LED flash source. A timing board controls triggering of the ultrasound pulse, light source, and camera with staggered triggers for the camera and light producing stroboscopic images of the ultrasound pulse interaction with the stone.

A high-speed camera (APX RS; Photron, Tokyo, Japan) was positioned facing the light source and focused on the stone. Both the camera and LED source were triggered by the FPGA timing board controlling the transducer amplifier (Fig. 3). The camera was triggered to capture one frame each pulse, synchronized so that the exposure of the 200 ns LED flash determined the effective exposure time of each camera frame. The BWL transducer was driven to produce bursts with duration of about 60 μs at a pulse repetition frequency (PRF) of 10 Hz. The PRF was kept low to minimize cavitation in the fluid that would affect consistency of elastic wave propagation in the stone model. At 170 and 340 kHz, the time was staggered by 100 ns per frame over a 100 μs period during and after the incident of the acoustic pulse on the stone, producing an effective frame rate of 10⁷ frames per second. At 800 kHz, the exposure time and staggering were reduced by half the listed values to adequately capture faster oscillations at these frequencies.

D. Image and numerical analysis

The raw photoelastic images from the camera were captured in a bright field configuration. Further image manipulation and analysis was performed in matlab. The image background intensity were normalized across the image and subtracted from an initial frame prior to the ultrasound exposure to produce a uniform image containing only the photoelastic changes. From these images, the wave phase velocities along the length of the stone models were calculated in two ways. First, the phase velocity of a guided wave mode traveling along the axis of the stone model was found by computing the lag of the image cross-correlation between sequential frames during the initial cycles of the burst prior to reflection from any distal surface. Second, the phase velocity was estimated from the wavelength of the standing wave patterns produced after the pulse impingement on the distal surface. For this measurement, images between initial impingement of the pulse on the distal surface and the end of the pulse were temporally integrated over the duration of the ultrasound exposure to obtain a single image. The peak intensity in the 2 D fast Fourier transform of the image was used to estimate wavenumbers and corresponding phase velocities present in the image along the horizontal (acoustic) axis for standing wave images. The phase velocities measured by these two methods were used to compare to modes calculated by a numerical model (see below). Distances between the surfaces and areas of constructive interference were measured from the images manually in matlab.

A free software package, the Graphical User Interface for Guided Waves (guiguw)³³ was used to calculate guided wave mode phase velocities and wavenumbers in rectangular and cylindrical cross sections for comparison to measurements. The program utilizes semi-analytical finite-element formulations of wave propagation to numerically calculate the dispersive characteristics of the model in simulation, including phase velocity. Mode shapes illustrated in the results were separately generated in a separate software package (disperse).³⁴ The properties for the epoxy and glass stone models (Table II) were input into their respective models with either rectangular cross section of 6.35 mm × 1 mm or cylindrical diameters of 6.35 mm (epoxy) or 7 mm (glass). Cylindrical artificial stones were also modeled and compared to experimental observations from photoelasticity imaging and stone fracture. The phase velocity vs frequency was calculated from 50 to 850 kHz in rectangular samples and to 1000 kHz in cylinders. The models are considered to be in a vacuum rather than in liquid in this simulation, thus they do not consider leakage of energy from the stone into the surrounding environment, although damping due to attenuation in the material itself is included in the formulation. However, preliminary simulations found that inclusion of the liquid did not significantly alter the modal phase velocity profiles, and we use the simulation here only to identify expected phase velocities rather than the strength of different modes.

E. Stone fragmentation

To determine the location of initial fractures in an artificial stone, stones were fragmented in a water bath with the 170 kHz transducer. The stone was supported in a small plastic frame [Fig. 2(c)] to hold the fragments in place during the initial fracturing of the stone. The frame was backed by a silicon rubber membrane. The center of the stone was aligned to the BWL transducer by a mechanical indicator attached to the transducer that was removed prior to exposure. A video camera was used to capture high-definition frames of the stone during exposure and the sequence and position of initial crack formation along the stone. Stones were exposed to 10-cycle bursts with 6.5 MPa focal pressure amplitude at a pulse repetition frequency of 200 Hz, until fractures had developed and fragments started to fall from the stone. At this point, exposure was terminated and the stones were photographed to record the fracture patterns.

III. RESULTS

To illustrate the behavior of elastic waves in stones, we describe results in simple geometries that suggest a mechanism for kidney stone fracture, and then present results for how the process is affected by relevant deviations from the simple models. The first section provides the photoelastic observations and interpretations of wave propagation in a rectangular stone model. In this model, the uniform thickness of the plate makes the stress pattern easy to interpret and can be simulated by numerical models for comparison. Following this analysis, effects of different frequencies on guided wave modes are compared to those calculated numerically. Further data present the behavior of elastic waves in cylindrical and irregular stone models in two different materials, and similarities to the rectangular plate model. Finally, additional experiments demonstrate the formation of fractures in BWL and the relation to elastic wave propagation in stones.

A. Elastic wave progression in simple models

1. Rectangular plate model

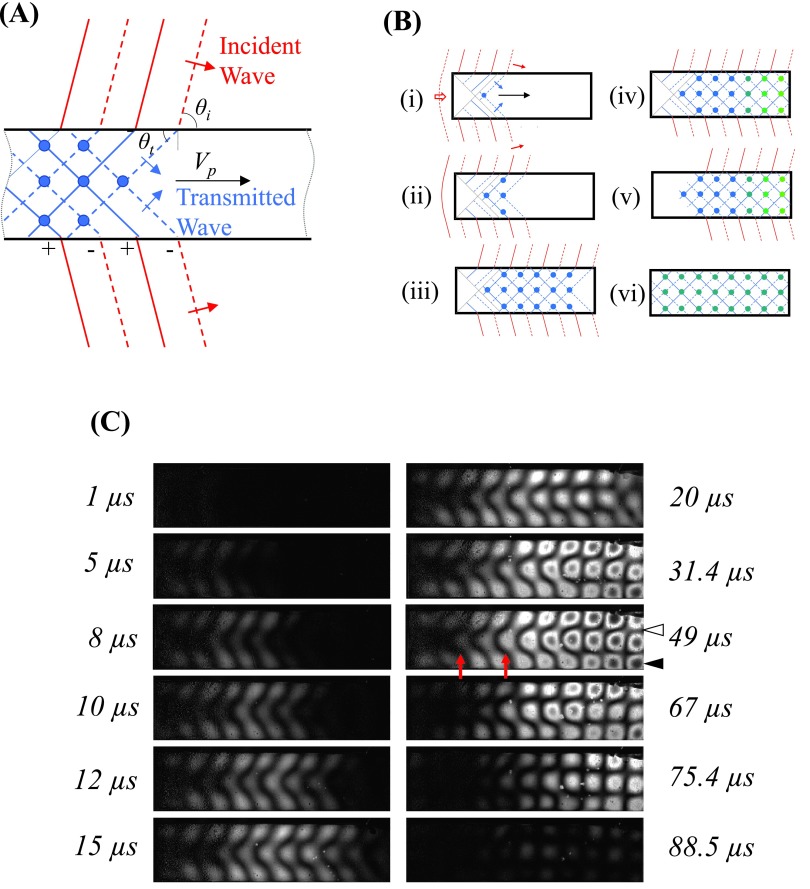
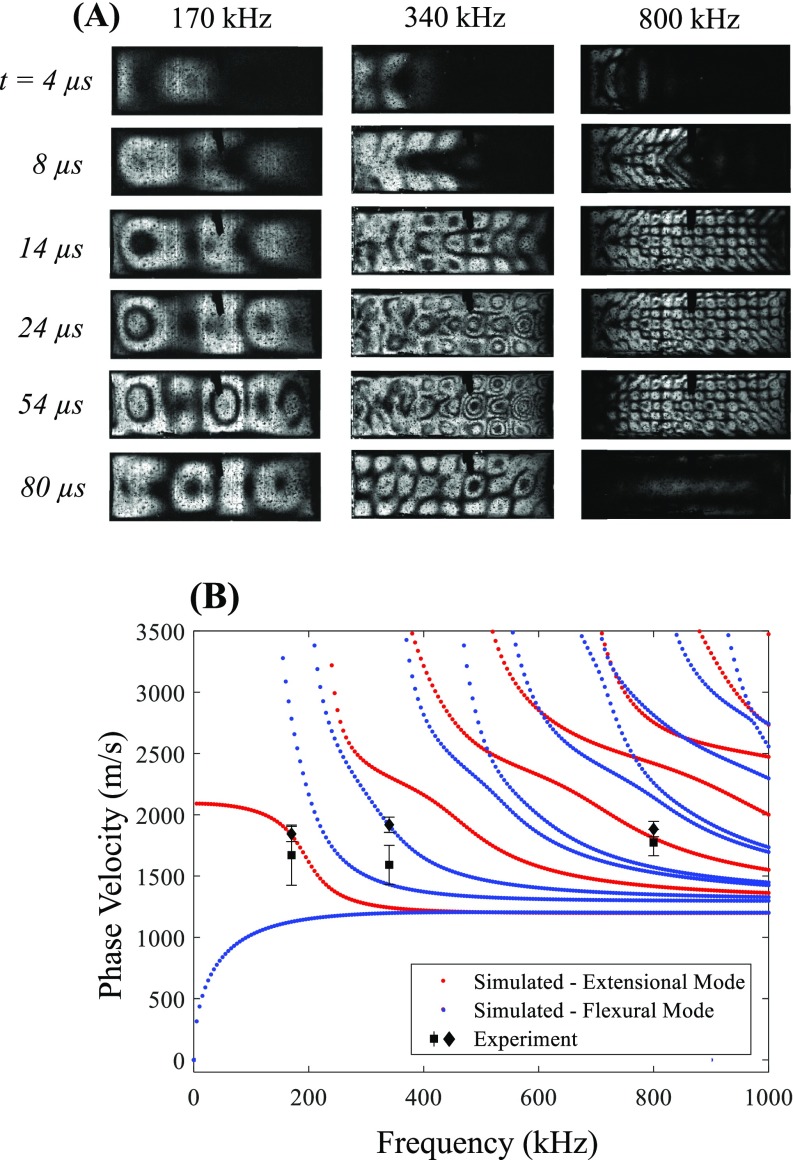
Photoelasticity imaging was used to visualize elastic waves during a BWL pulse impinging on 1-mm thick rectangular plates. An example of wave progression at 340 kHz for a 26 mm length stone is shown in Fig. 4 (see also Mm. 1), along with diagrams interpreting the images. When the focused burst first hits the stone, the wave propagates around and into the stone at the end nearest to the transducer. At the boundaries, shear and longitudinal waves may be generated propagating at different angles. The first waves are visualized propagating at an angle converging toward the center of the model, similar to the case in SWL for shear waves.³ The transmitted waves propagate at angles (θ_t) experimentally measured to be between θ_t = 53°–61° at 340 kHz and θ_t = 45°–51° at 800 kHz from the normal to the upper and lower surfaces. This angle could not be measured at lower frequency (170 kHz). These angles are calculated to be refracted angles for shear waves generated on the lateral (top and bottom) surfaces of the model by mode conversion for incidence angles (θ_i) between θ_i = 90° (parallel to surface) and θ_i = 55° (the angle of incidence for both 340 and 800 kHz transducers covers a range from θ_i = 54°–90°).

FIG. 4.

(A) Schematic of the formation and progression of guided waves modes during BWL. Red denotes the incident wave in the liquid travelling at angle θ_i, and blue denotes transmitted or reflected wave in the stone model traveling at θ_t. The blue dots indicate positions of constructive interference of the propagating guided wave mode. (B) Impinging focused ultrasound waves transmit into a stone and form a guided wave mode (i)–(ii). The modes travel towards the distal end of a stone (iii) and reflect from the surface, forming periodic stress points (iv)–(v). The green dots indicate antinodes with higher stress due to reflection from the distal surface. After the pulse, elastic waves reverberate at a lower amplitude within the stone and decay from attenuation or radiation (vi). (C) Photoelastic images showing the development of elastic waves in a 26-mm epoxy plate at 340 kHz, with the BWL pulse incident from the left and propagating to the right. The images are subtraction images from a still frame at the start of the sequence. Between 1 and 15 μs, the formation of the guided wave mode is seen propagating through the plate, with areas of brightness indicating intensity. The red arrows indicate locations where the transmitted waves converge at the center and opposing edges of the model. By 20 μs, the mode reflects from the distal surface and a periodic standing wave is formed that remains until the end of the pulse (67 μs). During this time, the photoelastic intensity is further increased in the distal area of the stone, appearing as a dark fringe within each bright zone (black arrowhead), indicating an optical birefringent shift greater than π/2 radians in phase (i.e., greater photoelastic effect). These are differentiated from stress minima, the areas between the bright circular regions (white arrowhead). After the pulse, the photoelastic intensity declines. For a more complete visualization of the progression, see the accompanying video Mm. 1.

Mm. 1.

Download video file ^{(7.3MB, mp4)}

DOI: 10.1121/10.0000847.1

A video of photoelasticity imaging in a rectangular epoxy stone model at 340 kHz showing the progression of elastic waves, corresponding with Fig. 4(c). This is a file of type “mp4” (7.3 MB).

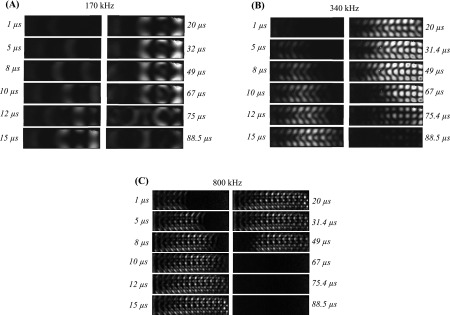
When the waves incident on the top and bottom surfaces of the stone interfere, a guided wave is established in the transverse direction while the axial component of the wave propagates down the plate. At 340 kHz, the waves converge at the center at 5.9 mm while at 800 kHz convergence occurs at 3.3 mm. The pattern is fully developed after 10.0 mm at 340 kHz [t = 10 μs, Fig. 5(b)] and 5.4 mm at 800 kHz [t = 5 μs, Fig. 5(c)] (see also Mm. 2 and Mm. 3). Assuming these shear waves initiate at the proximal corner of the rectangular model, the pattern would theoretically be expected to converge at the center at 3.1 mm and at the edges at 6.3 mm for a theoretical angle of 45°, and 5.4 and 10.8 mm for 61°. Thus, the data indicate shear waves are generated in the model by the incident BWL pulse.

FIG. 5.

Temporal sequences of elastic wave propagation in rectangular models 26 mm length at (A) 170, (B) 340, and (C) 800 kHz. The images show the development of wave modes in the model at each frequency, with the BWL pulse incident from the left and propagating to the right. The images are subtraction images from a still frame at the start of the sequence, and brightness indicates photoelastic intensity. Each pulse is 50–60 μs in duration (10 cycles at 170 kHz, 20 cycles at 340 kHz, and 40 cycles at 800 kHz). A mode forms and propagates down the acoustic axis in the model, reaching the end at 10–15 μs. After reaching the distal surface, the spatial pattern near the distal end becomes constant for the remainder of the pulse (for example, compare images at 32 and 67 μs for 170 kHz pulse). Then energy then dissipates after the end of the pulse (last three frames in each sequence). The dissipation is faster at 800 kHz likely due to greater attenuation in the material at that frequency. The video sequence for (A) is available as Mm. 2. The video sequence for (C) is available as Mm. 3.

Mm. 2.

Download video file ^{(1.3MB, mp4)}

DOI: 10.1121/10.0000847.2

A video of photoelasticity imaging in a rectangular epoxy stone model at 170 kHz showing the progression of elastic waves, corresponding with Fig. 5(a). This is a file of type “mp4” (1.3 MB).

Mm. 3.

Download video file ^{(3.1MB, mp4)}

DOI: 10.1121/10.0000847.3

A video of photoelasticity imaging in a rectangular epoxy stone model at 800 kHz showing the progression of elastic waves, corresponding with Fig. 5(c). This is a file of type “mp4” (3.1 MB).

The established stress pattern is a guided wave mode.³⁵ In Fig. 4, two nodes are fixed along the vertical dimension between three stress peaks. As the incident pulse duration is 20 cycles, the mode continues to propagate down the plate producing stresses along the entire length. When the burst reflects at the distal end of the stone, the reflected wave creates constructive and destructive interference resulting in a standing wave in the axial direction as well. The lateral nodes remain in the same position, but axial nodes and antinodes along the distal portion of the model become spatially stationary and are amplified by constructive interference. These nodes increase in amplitude over the initial 3–5 cycles of the pulse and then reach a steady amplitude for the remainder of the pulse. The stresses oscillated in this grid pattern until the end of the pulse, when the photoelastic intensity declined to a quiescent state over ∼30 μs. These results indicate that specific spatial regions receive amplified cyclic stressing, while areas located along the nodes are subject to minimal stressing and the highest effect was present near the distal end of the model during the pulse. These effects occurred specifically due to the periodic nature of the burst waveform as opposed to a single-cycle pulse as with SWL.

Excitations of rectangular plates at different frequencies are shown in Fig. 5. A similar “grid” of stresses was formed for each of the three frequencies. Given the end of the pulse occurred about 50–60 μs after initial exposure, the stresses in the 170 and 340 kHz cases diminish but are detectable for tens of microseconds after the pulse. At 800 kHz, the angled shear waves can be visualized in the first frames converging to form the mode pattern. The mode at this frequency was quickly attenuated after reflection from the distal surface, thus a standing wave only occurred for a few wavelengths near the distal surface and the model became quiescent quickly after the pulse ends. The distance between the back surface and the most distal antinode was constant for a given frequency regardless of stone length: 2.2 ± 0.1 mm from the back at 170 kHz, 0.86 ± 0.1 mm at 340 kHz, and 0.31 ± 0.08 mm from the back at 800 kHz. Relative to the wavelength associated with the mode, λ_p, these correspond with λ_p/4 for 170 kHz, ∼λ_p/5 at 340 kHz, and ∼λ_p/6 at 800 kHz. We might therefore expect that the stone will initially fracture at these antinodes near the back of the stone.

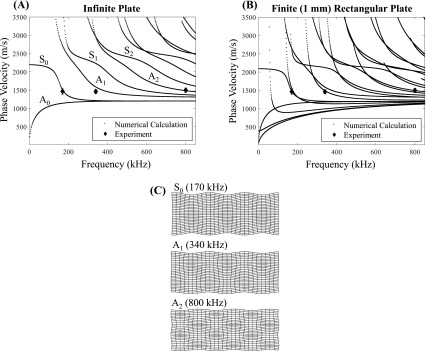
guiguw, a numerical software package,³³ was used to calculate the dispersion curves (phase velocity vs frequency) for rectangular samples with a 6.35 mm × 1 mm cross section. They were compared to the measured values for stones of 6, 14, and 26 mm length at the three frequencies. Measurements of the traveling phase velocity extracted from the initial propagation of the mode through the plates are also recorded as points for different frequencies on the plot. Symmetric and antisymmetric Lamb wave modes are plotted in Fig. 6 for both an infinite and finite plate. It is worth noting the consistency of the measured phase velocity, which is roughly the same in the models at all frequencies. However, this is likely a consequence of the near-matching of the shear wave speed in the epoxy and the sound speed in the water. Under this condition, the incident wave travels at a trace velocity along the surface that reinforces and continues to generate shear waves along the length of the stone, similar to shear wave generation in SWL.

FIG. 6.

Guided wave mode phase velocities for an infinite (A) and 1-mm finite thickness (center) rectangular plate. On the left, the symmetric (S_n) and antisymmetric (A_n) Lamb wave modes are listed for each curve. The black diamonds denote measured phase velocities for different rectangular models of varying length at 170, 340, and 800 kHz. In (B), the same experimental data are plotted over the finite (1-mm thick) plate, indicating close agreement with specific modes in the model used in experiments. Illustrations in (C) show the displacement patterns for the identified guided wave modes in an infinite plate (scaled in magnitude for visibility).

2. Cylindrical model

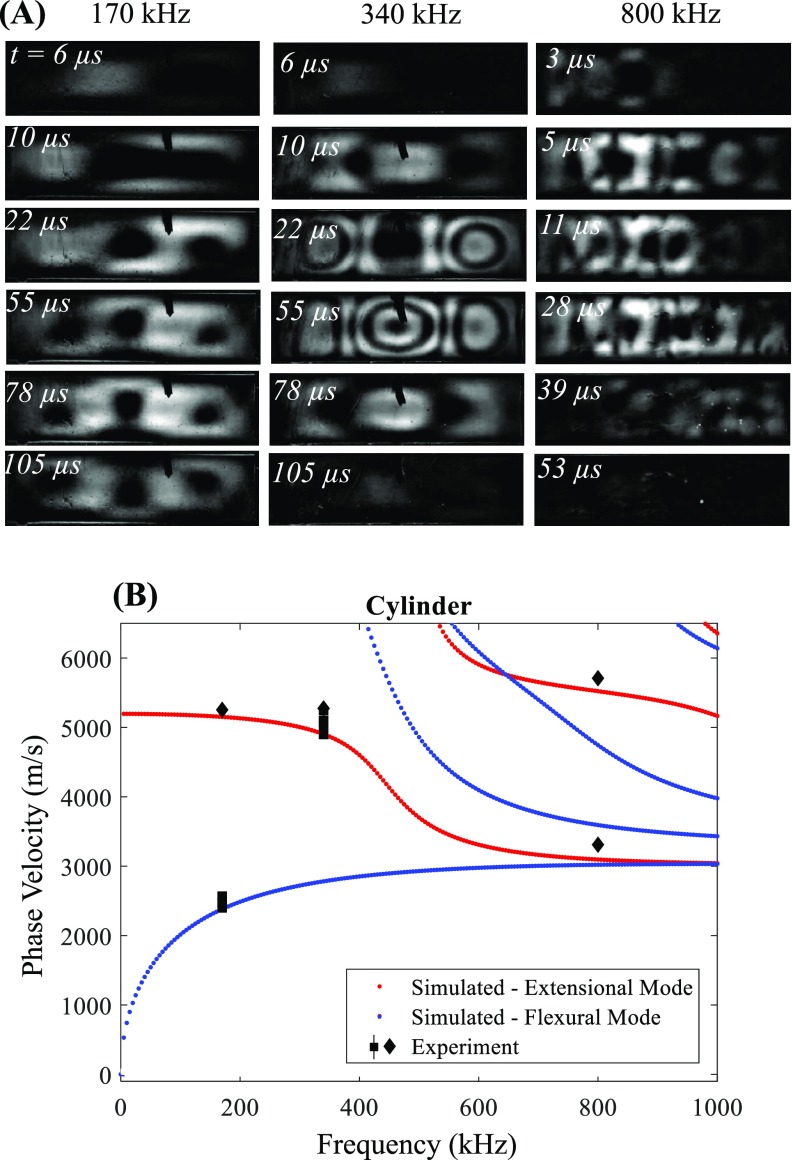
Cylindrical models were also analyzed for wave propagation for different lengths of 10–26 mm. In these experiments, the models were submerged in an index-matched fluid to minimize distortion. However, the nonuniform cross section obfuscates the relationship between stress and photoelastic effects in the cylinders. Nonetheless, cylinders represent a volumetric body more akin to a stone (compared to a thin plate), and are common for stone models in lithotripsy research.^24,36 Further, the photoelastic effect in the cylinders is larger than a thin plate and thus is sensitive enough to compare in different materials (epoxy and glass).

Similar to the rectangular models, guided wave modes were formed from the incident wave, initially propagating from left to right. Reflection of the modes at the distal surfaces created similar standing waves with spatially defined nodes and antinodes (Fig. 7; see also Mm. 4). One difference observed with cylindrical models is that the on-axis component of the photoelastic effect was stronger compared to off-axis, particularly at low frequency (compare Fig. 7 with Fig. 5), which is expected as the photoelastic effect is integrated through the cross section of the model.

FIG. 7.

(Color online) (A) Temporal progression of photoelastic patterns in 6.35-mm diameter 22-mm length epoxy cylinders exposed to BWL pulses with 170, 340, and 800 kHz frequency. Similar stress patterns as those observed in the rectangular plates are seen, although the photoelastic effect is greater, because of the larger thickness particularly on axis. Images are shown with ultrasound incident from the left. (B) Phase velocities vs frequency calculated by GUIGUW in epoxy stone models. Extensional modes are displayed in red and flexural modes are displayed in blue. Experiments show higher phase velocities in epoxy cylinders as those in plates. Diamonds indicate initial phase velocity estimate during propagation and squares indicate standing wave estimate from measured wavelength. A video of the photoelastic imaging sequence in (A) at 340 kHz is available as Mm. 4.

Mm. 4.

Download video file ^{(7.2MB, mp4)}

DOI: 10.1121/10.0000847.4

A video of photoelasticity imaging in a cylindrical epoxy stone model at 340 kHz showing the progression of elastic waves, corresponding with Fig. 7(a). This is a file of type “mp4” (7.2 MB).

In epoxy cylinders, the extensional mode was dominant at 170 kHz. At 340 kHz, two potential higher-order flexural modes were found to match the observed phase velocities. Here, the pattern was nearly the same as the pattern formed at 340 kHz in the rectangular plate (A1) asymmetric mode. Finally, at 800 kHz, the phase velocity corresponds with the third longitudinal mode in epoxy and formed a similar ‘grid’ of stresses during initial propagation. A similar standing wave pattern was observed near the back of the stone, and as with the rectangular plate, it was limited to only the distal 1–2 mm. For all data, the measured phase velocities were close to numerically calculated modes.

B. Effect of variations in the models

The observations above lead to a hypothesis that guided wave mode generation, propagation, and reflection are important in the production of stresses causing fractures in stones during BWL. As kidney stones vary significantly in composition, size, and shape, several experiments were considered to further investigate the generality and validity of this hypothesis under changes in these characteristics.

1. Effect of stone composition

In glass cylinders, two modes were identified and observed at 170 kHz (Fig. 8; see also Mm. 5). First, the initial propagation speed was close to the fundamental extensional mode. However, the steady state pattern indicated a phase velocity much lower, close to the flexural mode (Fig. 8). This possibly demonstrates a mode conversion due to repeated reflections within the cylinder. Only the fundamental extensional mode was excited at 340 kHz, which formed a standing wave condition along the entire length of the cylinder. This was particularly noticeable in the 22 mm cylinder at which the length is 3λ_p/2. At 800 kHz, there were two initial wave velocities, one propagating near the bulk longitudinal wave speed and one propagating close to the bulk shear wave speed in the stone model during the initial propagation. Although photoelastic effects were clearly present throughout the pulse, no periodic standing wave pattern could be distinguished at this frequency. In summary, these results indicate different modes may be excited by the incident wave based on the material properties, and can undergo mode conversion from internal reflections.

FIG. 8.

(Color online) (A) Temporal progression of photoelastic patterns in 26 mm length glass cylinders exposed to BWL pulses with 170, 340, and 800 kHz (subtraction images). Note at 170 kHz the progression of the stress pattern from about 1 wavelength (10 μs) along the length of the cylinder to about 3/2 wavelengths (55 μs). The 340 kHz pattern similarly shows about 3/2-wavelength pattern, indicative of a higher phase velocity than the final pattern at 170 kHz. (B) Phase velocities vs frequency calculated by GUIGUW and estimated from initial wave speeds (diamonds) or standing wave patterns (squares) in glass stone models. Extensional modes are displayed in red and flexural modes are displayed in blue. Measurements indicate multiple significant modes for a given frequency. For instance, at 170 kHz, it is apparent that the initial propagation is extensional but undergoes mode conversion to a flexural state after repeated reflections. At 800 kHz, two separate modes traveling at different speeds are visible. A video of the photoelastic imaging sequence in (A) at 340 kHz is available as Mm. 5.

Mm. 5.

Download video file ^{(3MB, mp4)}

DOI: 10.1121/10.0000847.5

A video of photoelasticity imaging in a cylindrical glass stone model at 340 kHz showing the progression of elastic waves, corresponding with Fig. 8(a). This is a file of type “mp4” (3.0 MB).

2. Effect of stone size and shape

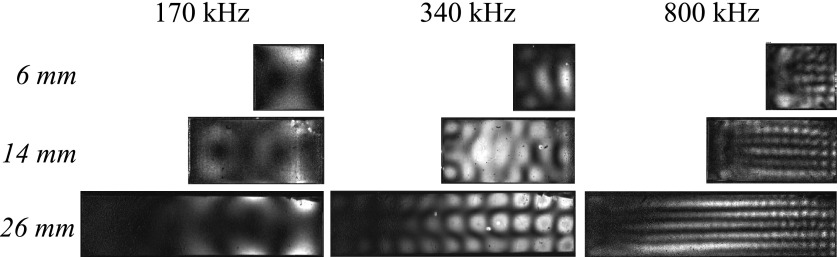
Several different lengths of stone models as well as two nonsymmetric geometries were tested to determine if similar elastic wave behavior would be observed to that described above. To visualize where standing waves occur in the models and where the photoelastic effects are strongest, the photoelastic intensity integrated over the duration of the burst was computed for 6, 14, and 26 mm length plates at 170, 340, and 800 kHz (Fig. 9). The images indicate guided wave mode patterns appear in both shorter and longer stones. These images show that provided the stone is larger than a relevant wavelength, modes are established. Additionally, the standing wave pattern was strongest near the back surface in most cases, and the distance between the back surface and first antinode is similar between lengths.

FIG. 9.

Time-averaged photoelastic intensity in rectangular models of different lengths and frequencies. Ultrasound is incident from the left. Time averaging emphasizes areas where the amplitude is constant vs time, thus areas of localized standing wave antinodes appear bright and nodes appear dark. The images show strong constructive interference near the distal surface in most models with similar spacing for a given frequency.

Given that the symmetries of the stone models produce particular modes, it is natural to question how well these translate to stones of an arbitrary shape or nonuniform cross-section. It has been shown that shear waves are generated in both axisymmetric³ and non-axisymmetric³⁷ stones, thus it is expected that similar activity may occur in irregular stones (i.e., stones of irregular geometry will have high stress magnitudes near the distal interfaces where reflections can occur). To test this idea, two shapes were created as epoxy plates—a “star” shape and an “N” shape. Similar time-integrated photoelasticity images were captured for both of these shapes at 340 kHz, and show the greatest photoelastic effect occurred near the distal surfaces of the stone model (see arrows in Fig. 10), indicating similar reflection and stressing is present in irregular shapes.

FIG. 10.

Integrated (time-averaged) photoelastic effect in star (A) and “N shaped” (B) models exposed to 340 kHz BWL burst. Ultrasound impinges from the left side of the models. Both show photoelastic stresses strongest near the distal surfaces of the model (arrows), indicating standing wave formation due to reflections from these surfaces. The distance from the interfaces is similar to that for the rectangular and cylindrical interfaces. The scale bar shows a 1 mm distance.

C. Interactions of elastic waves with fractures

We hypothesized that guided wave reflection could occur not only from the distal surfaces of stones, but also from cracks formed during previous bursts, causing a reconfiguration of stresses in the stone. This hypothesis was tested by introducing gaps in the photoelastic stone models and validated through observations of fracture in artificial stones.

1. Photoelastic models containing cracks

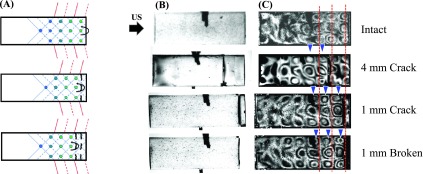
Cylindrical epoxy stones containing a ∼300 μm gap either 1 or 4 mm from the distal surface of the stone were created to simulate a crack in the stone. The two cylindrical sections were tacked together with a small amount of epoxy in two regions to maintain the gap while keeping the total length ∼18 mm in each.

Stones exposed to 340 kHz bursts displayed similar formation and propagation of guided wave patterns. However, the position of the largest photoelastic effect shifted with the introduction of the gap (Fig. 11). In particular, the peak occurred 0.86 ± 0.1 mm proximal to the back surface for the intact stone, 1.0 ± 0.1 mm proximal to the gap (5.4 ± 0.1 mm from the back surface) for the stone with a 4-mm gap, and 1.0 ± 0.1 mm proximal to the gap (2.4 ± 0.1 mm from the back surface) for a 1-mm gap. Although difficult to evaluate in the case of the 1-mm gap, some stress still occurred in the distal section of the 4-mm gap stone, indicating that the reflection from the crack was incomplete, or waves at the lateral surfaces of the stone reinforce these stresses regardless of the reflection of the wave in the stone. However, these data confirm that cracks can significantly alter the guided wave reflection and cause changes in the stress distribution as they form.

FIG. 11.

(A) Schematic diagram of the alteration of stress patterns caused by cracks in the stone. The pattern is shifted forward as a crack is generated, creating a new position for the peak stress just in front of the crack. (B) Photoelastic images in an 18 mm cylinder intact (top), with an artificially created crack at 4 mm (upper center) and 1 mm (lower center) from the back surface and with the 1-mm back section broken off (bottom). The photos show brightfield images of the stone models prior to insonation and the photos in (C) show a transient photoelastic image during the last cycle of the ultrasound pulse. The black bars in the middle of each image are pins holding the cylinder in place. The red lines in the right image indicate axial positions of peak photoelastic effect in the intact cylinder, while the blue arrowheads indicate the positions of peak stress in the modified cylinders. When a crack was introduced, the peaks shift to be proximal to the crack, indicating significant reflection from the crack which was similar to that formed when the back section is removed (bottom).

2. Fragmentation of artificial stone cylinders

Cylindrical artificial stones used to model kidney stones for SWL studies were exposed to BWL bursts at 170 kHz in a water bath to determine the initial locations of circumferential cracks along their length for different lengths of stones. guiguw was used to model the dispersion curves for the artificial stone material.

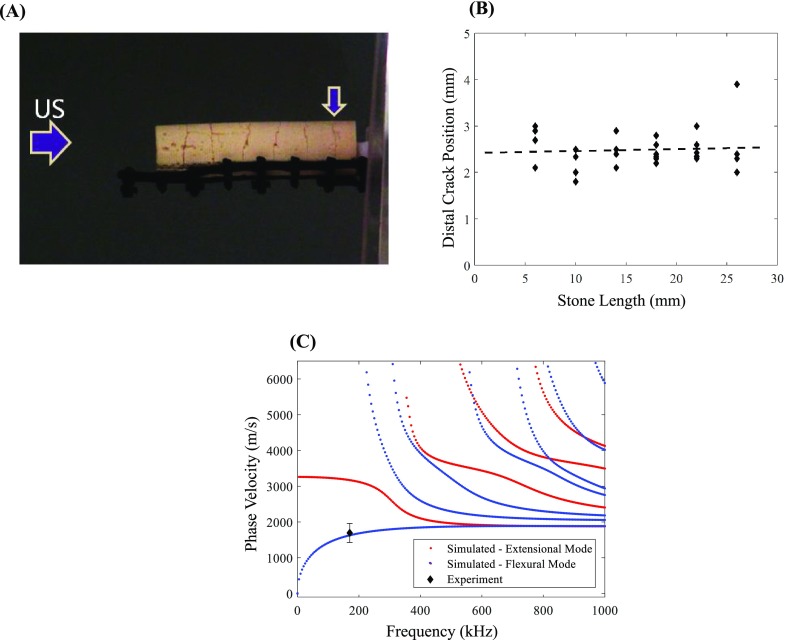
The distal crack position was measured for stone lengths between 6 and 26 mm. The initial cracks formed in the stones within the first few seconds of exposure to BWL pulses were usually circumferential cracks. Often, a crack near the distal surface formed first followed by another crack proximal to its position, propagating a series of cracks forward towards the transducer. Notably, the most distal circumferential crack position was consistent regardless of stone length (Fig. 12; see also Mm. 6), 2.4 ± 0.4 mm from the distal surface. A one-way analysis of variance between groups with nominal lengths of 6, 10, 14, 18, 22, and 26 mm (n = 4–6 per group) performed in matlab did not indicate significant differences between groups (P = 0.49). The distance between adjacent cracks in the stones was also fairly consistent, although it increased slightly between the most distal crack and proximal cracks to 2.9–3.4 mm. A one-way analysis of variance demonstrated a significant increase between the distal crack and proximal cracks (P = 0.0012), but no significant difference between any of the four cracks adjacent to the distal crack (P = 0.46). With further BWL exposure, axially oriented cracks formed and fragments began to separate from the cylindrical body usually initiating at the proximal face, consistent with previous observations.⁹

FIG. 12.

(Color online) (A) An artificial stone containing several cracks after initial BWL exposure. The vertical arrow shows the location of the distal crack. (B) Position of the distal circumferential crack observed during a short BWL exposure vs stone length. A linear regression fit indicates minimal variation between lengths. (C) Simulated phase velocity curves and anticipated phase velocity based on the measured position of the crack, assuming a soft boundary condition at the distal stone surface. An example video of stone fracture over the first 100 s of an exposure is available as Mm. 6.

Mm. 6.

Download video file ^{(4.2MB, mp4)}

DOI: 10.1121/10.0000847.6

A video of stone fracture in a cylindrical stone model at 170 kHz showing the progression of fractures over the first 100 seconds of exposure. The video is sped up by a factor of 30. This is a file of type “mp4” (4.3 MB).

Assuming a soft boundary condition at the distal surface, a standing wave antinode position λ_p/4 = 2.4 mm corresponds with a phase velocity of V_p^f = 1632 m/s. Numerical simulations calculate the phase velocity for the fundamental flexural mode of the cylinder at 170 kHz to be V_p^f = 1624 m/s, the extensional mode to be V_p^e = 3162 m/s, and the torsional mode (which is nondispersive) the same as the shear wave speed, V_p^t = c_s = 2035 m/s. These results suggest the fundamental flexural mode was dominant in this stone material and geometry (Fig. 12).

For the remaining crack spacings, two boundary conditions may be considered. In the case that the cracks are acoustically insignificant, the antinode spacing may be considered to be λ_p/2, and the cylinder maintains acoustic integrity regardless of crack formation. In this situation, the spacing 2.9–3.4 mm corresponds with phase velocity between 985–1156 m/s, a range below that of any calculated mode in the cylinder. In the case that the cracks produce a perfect (soft) reflection, the antinode adjacent to the crack is λ_p/4, giving V_p = 1970–2312 m/s. As demonstrated in the results of photoelasticity imaging, likely the boundary condition is mixed and the true node position lie between these two extremes, however, the soft boundary condition appears to be closer to the likely condition given the results in the above experiments and simulations. Overall, the results suggest under certain circumstances, the location of fractures can be predicted from the mechanism proposed.

IV. DISCUSSION

In this work, we observed the formation of guided wave modes in stone models exposed to BWL focused ultrasound pulses. Results in rectangular and cylindrical epoxy models showed similar patterns of propagation that matched well with numerical simulations of particular modes in their respective shapes. The formation appeared to be initiated with the generation of shear waves in epoxy and artificial stones, while both longitudinal waves and shear waves were identified in glass. This difference is expected behavior as the generation of shear waves in glass from water is much weaker because of the difference in sound speeds. In SWL, these shear waves converge in a cylindrical stone and constructively interfere to produce a single region of high tensile stress in conjunction with a direct longitudinal wave reflected from the back of the stone (spallation). With BWL, the periodic nature of the wave produces a grid of stress points within the model that reflect and propagate along the acoustic axis as guided waves. While SWL reaches a maximum stress from elastic waves during the initial cycle of the pulse, BWL required several cycles for the photoelastic effect to reach a peak amplitude as the off-axis constructive interference occurs between consecutive cycles. Because the shear angle is essentially independent of frequency (although dependent on the aperture angle of each transducer), V_p was similar over a range of frequencies as well, giving rise to the notion that specific modes are pronounced when their dispersion curve aligns with this anticipated V_p based on this angle.

As the wave reached the distal part of the stone model, it was partially reflected. This reflection formed a standing wave at the lowest frequency throughout the stone length. At high frequency, the mode was attenuated very near to the distal surface, thus the standing wave was limited to this area. Numerical models suggest that certain Lamb wave modes are preferentially reflected from a surface.³⁸ In particular, vertically polarized shear waves propagating at an angle of 45° achieve a perfect reflection from the surfaces of a plate and undergo no mode conversion.³⁹ These special characteristics lead to “Lamè modes,” which are identified notably in the 340 and 800 kHz rectangular plates (Figs. 4 and 5) and give rise to a near-perfect standing wave that is only mitigated by the attenuation of the model material. Given that the stone model is surrounded by fluid not supportive of shear waves, it is considered a soft boundary and thus a node occurs at the distal surface, while an antinode occurs near λ_p/4 from the surface. However, some modes are not perfectly reflected and the antinode may lie in a different position, which may explain the measurements at higher frequencies where the stress peak occurred at a distance smaller the λ_p/4. In addition, end resonance effects or trapped modes can complicate the diffraction of modes from a surface of an elastic structure.^40,41 The observed localization of the standing-wave stresses in the irregular stone models in the present study are consistent with such trapped modes. Another potential explanation for this discrepancy could be nonlinear distortion of the waveforms at higher frequencies, which alters the position of constructive interference compared to a linear wave.

The data in artificial stones indicate that fractures are promoted at this distal location, but also at several regular intervals along the stone. Further, the position relative to the distal end is independent of stone length, in contrast to similar experiments in SWL.³ The periodicity of fracture can be explained by our experiment with photoelastic models containing a gap: the introduction of a fracture produces a new boundary condition for reflection of wave modes, relocating the peak stress to a position proximal to the crack. Such cracks already exist within some human urinary stones prior to any intervention.⁴² With artificial stones, it was sometimes observed that several fractures formed in rapid succession, although not always starting at the most distal position. However, within ∼10 s, a distal fracture was observed in all stones exposed. Such succession of crack formation is strongly reminiscent of a mechanism of cavitation in fluids or soft solids, where scattering of waves from cavitation bubbles incites further cavitation forming in nearly equidistant layers as a cloud.⁴³ As fractures can serve as pressure-release boundaries, new fractures may not develop between the existing network as there are no volumes large enough in which to produce the same stress amplitudes as those in the intact stone.

Such an effect may explain why fracture density on the surface increases with the ultrasound frequency in BWL. The results also offer an explanation for the observed fragment sizes produced during BWL, which range from 3 to 4 mm for 170 kHz to 0.6 mm at 800 kHz in artificial stones, and similar sizes in human urinary stones. For instance, an in vivo study of BWL in a porcine model fragmented COM stones at 350 kHz,⁴⁴ producing many fragments in the 1–2 mm range as expected from in vitro data.⁹ The fragment sizes are too small to be described by a simple explanation of cracks forming at antinodes from a standing wave. For instance, at 170 kHz in the artificial stone models, the expected antinode separation would produce λ_p/2 = 4.8–9.3 mm between cracks. In reality, we see approximately half the smallest distance, near λ_p/4, suggesting the cracks are generated at the antinode near a soft boundary from either the distal surface of the stone or a crack, which can act as a soft boundary particularly to modes with a strong shear component. In experiments, fractures are also limited in depth for higher frequencies. This is explainable from the photoelastic results where the stresses are limited in depth; null points are observed along the vertical axis in both the cylindrical and rectangular models. While these features are consistent with the observations in this study, the relationship between the produced modes, frequency, and stone shape are more complex than the suggestion of a simple inverse trend between fragment size and frequency.

Are there methods to promote specific guided wave modes or higher stresses that could lead to faster comminution? Models and experiments in SWL suggest the propagation of the wave around the stone are responsible for the generation of shear wave leading to initial fracture of the stone.^2,27 Generating shear waves was similarly important in this study, and there are theoretically ideal angles of incidence to produce strong shear waves. In the epoxy rectangular plate, there is a range of angles between about 40°–70° relative to normal incidence. In the case of a human urinary stone, the surface consists of many angles, but it may be prudent to use a transducer that impinges a broad angular spectrum upon the stone (i.e., is strongly focused). However, the position of the focus relative to the stone may become important in such a scenario. In the present study and in previous work,⁹ the 800 kHz transducer had the stone aligned in a prefocal position, where the beamwidth was similar to the other two transducers.

A notable limitation of this study is that the stone models used for photoelastic imaging have characteristics that differ from those of actual kidney stones. The epoxy stones have density and sound speed ∼20% lower than soft stones like struvite or uric acid, while glass has a higher sound speed than the hardest stones.²¹ While quantitatively these differences may result in different modal amplitudes, the general results are still valid, as highlighted by the experiment using artificial stone materials with properties similar to COM stones. A remaining challenge in assessing the mechanism is to quantify the acoustic attenuation of urinary stones, which affects the reverberation of waves within the stone and ultimately the stresses that can be achieved. Nonetheless, even stones with significant attenuation could still be described by the mechanism outlined in this paper, as it only requires that the wave travels the length of the stone once to achieve a reflection and fracture-inducing stresses. The symmetry of the stones supports easily identified and modeled modes, which were valuable in identifying the modes (and fractures) quantitatively. Although the exposure is also symmetric for these experiments, such modes will be excited by an oblique excitation as well (Fig. 13), although their relative amplitudes will change, but does not reflect the complexity of acoustic propagation in a quasi-random geometry of a real stone with oblique incidence of the wave. Human urinary stones do not fragment with the uniformity of artificial cylinders, but other studies show that the same trends in fragment size dependency on wavelength hold for real stones as artificial stones, supporting the generality of the hypothesis.⁴⁴ Further, our irregular-shaped models displayed strongest stressing in the distal area similar to regular geometries.

FIG. 13.

Brightfield photoelasticity images of a cylindrical epoxy stone with 26 mm length exposed to 170 kHz BWL with a symmetric (A) and asymmetric (exposure) angle relative to the cylinder axis. Similar modes appear in both cases, although the photoelastic amplitude and exact distribution of stresses differs. The scale bar is 1 cm.

A further limitation was that the experiments in cylinders were necessarily conducted in liquids dissimilar to water or urine. These liquids are more viscous and somewhat suppress cavitation. The similarity of the results in the rectangular plates (in water) vs those in the cylinder indicate that the liquid surrounding the stone model did not strongly impact the results. In fact, we changed the glycerol/water mixture for glass cylinders to determine if the viscosity affected the reverberation or amplitude of photoelastic effect induced in the stone, but found nearly identical results in two mixtures that have more than an order of magnitude difference in viscosity.

Finally, we did not assess here the role of cavitation in stone comminution, which undoubtedly is a contributing factor to fragmentation in both BWL and SWL. Previous data suggest that stone materials of different strength (by a factor of 3)^25,45 have nearly identical thresholds for fracture in vitro,⁹ inconsistent with the notion that only elastic modes are responsible for initiating and propagating fractures. Instead, the cavitation at the stone surface is likely similar between different stone types and cavitation is likely necessary to initiate fracture. In addition, the level of dissolved gases in the liquid strongly influences the rate of fragmentation. This may be due to damping effects on the violence of collapse as the gas level increases.⁴⁶ Alternatively, models and other BWL experiments suggest an abundance of cavitation can generate a cloud of bubbles that shield acoustic energy from propagating into the stone and producing elastic waves.¹² The photoelastic imaging showed some disruption of the stress pattern/amplitude when cavitation was present, although clouds were not intentionally generated in this study. Further experiments will elucidate the seemingly delicate balance of cavitation activity needed to promote fracture without restricting energy delivery.

V. CONCLUSIONS

We examined the temporal progression of stresses created in stone models subjected to BWL ultrasound bursts using a custom high-speed photoelasticity imaging apparatus. Observations show the development of regular patterns corresponding with specific guided wave modes in models with rectangular and circular cross section, arising notably from shear waves generated by the burst. The identified modes changed with ultrasound frequency and stone material. The reflection of guided waves from the distal surfaces of the models in the stone produced the strongest stresses at the antinodes of a periodic standing wave. We hypothesized that a crack formed in the model causes a redistribution of these stresses to create an antinode approximately λ_p/4 from the defect (where λ_p is modal wavelength). Experiments in artificial stones showed the sequential formation of nearly equally spaced cracks, supporting this mechanism of fracture formation. This mechanism explains the consistency of fractures and fragment sizes observed in previous studies as a function of frequency in BWL.