Abstract
High entropy alloys (HEA) are an unusual class of materials where mixtures of elements are stochastically arrayed on a simple crystalline lattice. These systems exhibit remarkable functionality, often along several distinct axes: e.g., the examples [TaNb]1-x(TiZrHf)x are high strength and damage resistant refractory metals that also exhibit superconductivity with large upper critical fields. Here we report the discovery of an f-electron containing HEA, [TaNb]0.31(TiUHf)0.69, which is the first to include an actinide ion. Similar to the Zr-analogue, this material crystallizes in a body-centered cubic lattice with the lattice constant a = 3.41(1) Å and exhibits phonon mediated superconductivity with a transition temperatures Tc ≈ 3.2 K and upper critical fields Hc2 ≈ 6.4 T. These results expand this class of materials to include actinide elements, shows that superconductivity is robust in this sub-group, and opens the path towards leveraging HEAs as functional waste forms for a variety of radioisotopes.
Subject terms: Physics, Condensed-matter physics, Electronic properties and materials, Structure of solids and liquids, Superconducting properties and materials
Introduction
High entropy alloys (HEA) are multicomponent mixtures of randomly combined elements where, instead of producing disordered mixtures of lower order crystalline compounds (binaries, ternaries, etc.), solid solutions with simple structures (e.g., body center cubic, face center cubic, or hexagonal close packed) are formed1–5. This occurs when the mixing entropy overrides simple stoichiometric/crystalline phase selection, and leads to a large chemical compositional space that is distinct from that of traditional alloys where a few molar percent of one element is added to another (e.g., as for sterling silver, modern steels, and Be-Cu). Many attractive behaviors are observed in HEAs, including fracture resilience at cryogenic temperatures6,7, excellent mechanical properties at elevated temperatures8, high strength9,10, and high resistance to radiation damage11–14. An emerging class of HEAs are those hosting 4d and 5d transition metals that exhibit phonon mediated superconductivity with large upper critical fields5,15,16. Importantly, many HEAs are functional in multiple distinct ways, making them attractive as candidates for a variety of applications; e.g., as next generation wires for superconducting magnets or for use under extreme conditions1–5.
Most studies have focused on combinations of transition metal elements to produce HEAs, but it is interesting to ask whether lanthanide or actinide elements can be introduced as well. This would have several advantages with both practical and basic science implications. For instance, f-electron elements such Ce, Yb, U, Np, Pu, and Am exhibit valence flexibility, have a tendency to hybridize with conduction electrons and have large spin anisotropy17. Other examples such as Nd, Sm, Gd-Tm, and Cm-Cf feature well localized f-states with associated magnetism18. These characteristics often lead to novel properties that include unconventional magnetic order, complex electronic order, topologically protected states, structural instabilities, and superconductivity19–21. Indeed, recent studies of HEAs that are composed entirely of lanthanide elements show that they exhibit complex magnetism with evidence for spin-glass behavior22–24. It was also recently shown that the presence of a high entropy alloy-type blocking in the series REO0.5F0.5BiS2 enhances the superconductivity of this system25. Actinide based alloys are also of interest for development of solid solutions (i) that form under extreme conditions, (ii) as radiation resistant cladding and robust waste forms, or (iii) for long term storage of hazardous radioisotopes.
Here we report results for the HEA system [TaNb]0.31(TiUHf)0.69, which is a variant of the alloy series [TaNb]1-x(TiZrHf)x5,15,16. To our knowledge, this is the first examples of an actinide containing HEA, but point out that its existence is readily anticipated given that in many cases zirconium and uranium can be considered as chemical and electronic analogues to each other; they both can adopt a tetravalent electronic configuration and have similar atomic sizes. Therefore, we expect that this will merely be the first of many such examples and that other lanthanides and actinides with multi-configurational valences (e.g., Ce, Np and Pu) will readily be introduced into such environments. Similar to the Zr analogues, X-Ray diffraction measurements show that this material crystallizes in the cubic space group Imm and occupies a body-centered cubic lattice (BCC) with the lattice constant a = 3.41(1) Å. Elemental mapping using energy dispersive spectroscopy shows a uniform distribution of the elements throughout the arc-melted samples. The alloy is difficult to abrade or cut, is readily cold worked into thin plate, and is resistant to many destructive environments including concentrated acids. We also show that, similar to the Zr containing analogues, the material exhibits bulk superconductivity with an onset transition temperatures Tc ≈ 3.2 K and large upper critical field Hc2 ≈ 6.4 T, exceeding what is seen for most uranium based superconductors. Like other HEA superconductors, this occurs in a highly disordered environment which likely provides pinning centers for superconducting vortices. Bulk electrical transport, magnetization, heat capacity, thermopower, and thermal conductivity measurements reveal other similarities to the Zr-analogues, where we find that the f-electrons are delocalized and that the chemical disorder results in a large and nearly temperature independent electrical resistivity and a small thermal conductivity. [TaNb]0.31(TiUHf)0.69 thus emerges as a representative of what likely is a much larger family of actinide materials that would be of importance for both technological (e.g., development of durable waste forms) and basic science (reservoir for superconductivity) reasons.
Results
Structural and chemical characterization of [TaNb]0.31(TiUHf)0.69
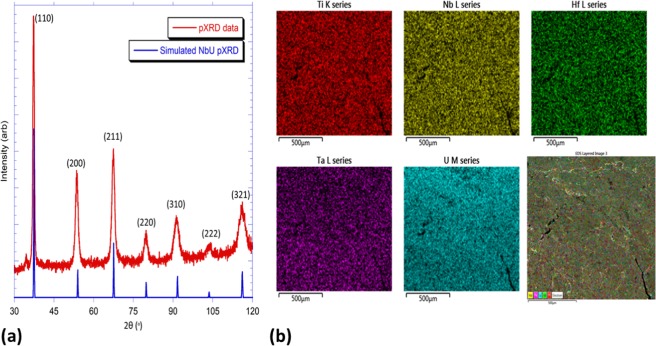
Polycrystalline specimens were produced using the arc furnace method. The resulting boules are difficult to abrade, cut, or reduce to a granular form, which required that powder X-Ray diffraction measurements be performed on pieces that were pounded flat in liquid nitrogen. The resulting diffraction pattern (Fig. 1a) is isomorphous with a series of Group IV/V alloys such as NbU26, HfTa27, TaTi28, and NbZr29 and related “type A” HEAs5. All of these alloys form in the Cubic space group Imm and occupy a body-centered cubic lattice (BCC). These results are consistent with the literature, and the notation of Group V metals given in brackets and Group IV metals given in parentheses is maintained from ref. 5. The unit cell axis length is determined to be 3.41(1) Å, which is slightly larger than the NbU analogue employed for powder diffraction comparisons, and at the upper end of the range observed for an alloy which employed Zr instead of U. There is some indication of an impurity phase, likely uranium, as indicated by a weak peak at 2θ = 34.5°. However, this peak is so small as to be unquantifiable. As noted previously, the reflections are exceptionally broad (FWHM 2–3% of peak position) due to disorder in the HEA and inherent limitations of powder diffraction on a single block. Energy Dispersive Spectroscopy was used to identify inhomogeneity in the sample and quantify the elements (Fig. 1b). Elemental mapping of both the flattened sample and chips cut from the bulk indicated a homogenous mixture of Ti, Nb, Hf, Ta, and U, with no enriched zones. While standard-less quantification is only approximate, we obtain the stoichiometries listed in Table S1. These data were calculated from 29 spectra on a flat polycrystalline surface, and there was no statistical difference between quantification on the flat surface or on small chips. Phase matching found no minor phases to be present when a surface approximately 4 mm2 was examined. The deficiency in Nb and Ta is persistent, whether the quantification was on the flat surface or razor-cut chips off the bulk product. Therefore, we conclude that the product is approximately [TaNb]0.31(TiUHf)0.69.
Figure 1.
Summary of structural and chemical data for [TaNb]0.31(TiUHf)0.69. (a) X-ray diffraction pattern for the as-cast [TaNb]0.31(TiUHf)0.69. The pattern was collected for a small piece removed from the very hard alloy, which was impossible to reduce to a powder even when cooled using liquid nitrogen. The pattern is isomorphous with a series of Group IV/V alloys such as NbU20, HfTa21, TaTi22, and NbZr23 and related “type A” HEAs5, which form in the Cubic space group Imm and occupy a body-centered cubic lattice (BCC). The unit cell axis length is calculated to be 3.41(1) Å. (b) Energy Dispersive Spectroscopy data for an as-cast piece of [TaNb]0.31(TiUHf)0.69. These data were used to identify inhomogeneity in the sample and quantify the apparent elements. Elemental mapping of both the flattened sample and chips cut from the bulk indicated a homogenous mixture of Ti, Nb, Hf, Ta, and U, with no enriched zones.
In order to assess the chemical stability of the alloy it was immersed in several acidic solutions for a period of two minutes and observed for evidence of degradation or chemical reactivity. The sample was thoroughly rinsed with deionized water after each reactivity test. We find that it does not immediately dissolve in: nitric acid at 0.001 M, 1 M, 3 M, 6.5 M, or concentrated (16 M); 5 M hydrochloric acid; 6 M sulfuric acid; 9 M hydrobromic acid; aqua regia; or 9 M perchloric acid. It does dissolve readily in 29 M hydrofluoric acid. This is in agreement with earlier results for other HEAs; for instance, Al0.5CoCrCuFeNiBx was reported to be more resistant to corrosion than stainless steel in a 1 N sulfuric acid solution30.
Superconductivity in [TaNb]0.31(TiUHf)0.69
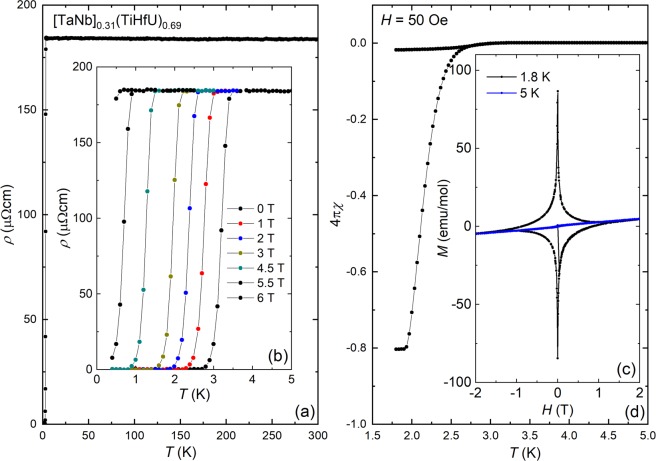
The temperature dependent electrical resistivity data are presented in Fig. 2a,b, where it is seen that ρ(T) increases slowly with decreasing temperature to reach a residual resistivity value near ρ0 = 183 μΩcm. Below Tc ≈ 3.2 K there is an abrupt drop to a zero resistance state which indicates the onset of superconductivity. As seen in the inset, the transition has a width of approximately Δ = 0.4 K, and together with the large ρ0 this suggests that the chemical disorder impacts both the normal state behavior and superconductivity. Similar behavior was earlier seen for the Zr analogues16, although the value of ρ0 for the U case is somewhat increased by comparison. The magnetic field dependence of the transition is shown in the inset, where Tc is gradually suppressed with increasing H and is fully suppressed for values above 6 T. We also examined the pressure dependence of Tc (Fig. S1), where we find that it almost completely insensitive to hydrostatic pressure for P < 2.3 GPa. This is like what is seen for other HEA superconductors, where Tc remains nearly constant up to hundreds of GPa5,31.
Figure 2.
Summary of electrical transport and magnetization data for [TaNb]0.31(TiUHf)0.69. (a) Electrical resistivity ρ between the temperatures T = 2–300 K for [TaNb]0.31(TiHfU)0.69. (b) Magnetic field H dependence of ρ(T) for H = 0–6 T, focusing on the superconducting phase transition Tc. (c) DC magnetization data collected in an applied magnetic field of H = 50 Oe showing both the zero field cooled and field cooled temperature T dependence, which reveal bulk superconductivity. (d) Magnetization M vs. H loop at temperatures T = 1.8 and 5 K. For T = 1.8 K, the behavior is consistent with expectations for a type 2 superconductor where magnetic flux penetrates the bulk of the sample. At 5 K the M(H) curve is consistent with expectations for a Pauli paramagnet where the U f-states are delocalized. DC magnetic susceptibility χ = M/H collected in H = 0.5 T for T = 1.8–300 K are shown in Fig. S1, where the weak temperature dependence and lack of Curie-Weiss behavior also indicate that the uranium f- electrons are not well localized.
The magnetic susceptibility χ(T) data measured in a field of 50 Oe for both field cooled and zero field cooled conditions are shown in Fig. 2c,d. Below about Tc ≈ 2.5 K the ZFC curve shows a strong diamagnetic response due to the Meissner effect, which yields almost the ideal diamagnetic value −4πχ that is expected for a bulk superconductor. For the FC curve the small recovery of the diamagnetic signal may indicate that the material exhibits strong vortex pinning. Isothermal magnetization M(H) curves for 1.8 and 5 K are shown in Fig. 2c. Here, the linear response of the Meissner state at low fields is rapidly followed by a decrease in the magnitude of M with increasing H, as is expected due to flux penetration in the vortex state for a type-II superconductor. The χ(T) and M(H) data in the normal state (Figs. S2 and 2c) indicate that the uranium f-electrons are not well localized in this system. In particular, χ(T) is not described by a Curie-Weiss law and instead is weakly temperature dependent, while M(H) for T > Tc shows a weak linear response.
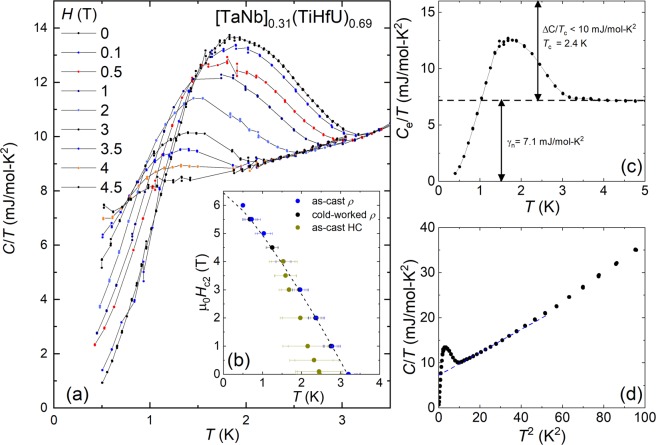
The heat capacity divided by temperature C/T data for temperatures spanning Tc and for magnetic fields between 0–4.5 T are summarized in Fig. 3a. For H = 0, the superconducting phase transition appears as a broadened lambda-shaped feature where Tc = 2.4 K is defined as the midpoint of the rise in C/T (Fig. 3c), although its onset is found at Tc,onset = 3.2 K. The size of the jump ΔC/Tc < 10 mJ/mol-K2 is estimated using an equal entropy construction, but the broadness of the peak prevents determination of a definitive value. As shown in Fig. 3d, a fit to the data for T > Tc using the expression γ + βT2 yield the values γ = 7.1 mJ/mol-K2 and β = 0.26 mJ/mol-K4 and from this we estimate that ΔC/γ Tc is slightly less than 1.43, consistent with expectations from the BCS theory for a phonon-mediated superconductor in the weak electron-phonon coupling limit. We also calculate a Debye temperature near ΘD = (12π4R/5β)1/3 = 193 K, where R is the ideal gas constant. Within the superconducting state C/T extrapolates towards zero, suggesting that the gap is isotropic and does not include nodes. This is in contrast to what is seen for some other strongly correlated f-electron superconductors with likely non-s-wave superconductivity19 but similar to results for the Zr containing HEA analogues5,16. In order to assess the gap size, we consider the BCS expression 2Δ(0)/kBTc = 3.52, from which we estimate Δ(0) ≈ 0.36 meV. Taken together, these results reveal a close similarity to the Zr-based analogues15,16.
Figure 3.
Heat capacity data for [TaNb]0.31(TiUHf)0.69. (a) Temperature dependent heat capacity measurements for temperatures T = 0.5–3.5 K and magnetic fields H = 0–4.5 T. The bulk superconducting phase transition at Tc is seen as a broadened lambda-like peak that is suppressed with increasing H. (b) The upper critical field Hc2 vs T defined both from the lambda feature in the heat capacity and as the 50% value of the electrical resistivity (see Fig. 2). Results are shown both for an as-cast sample and for a piece that was cold worked under liquid nitrogen into a thin sheet. The dotted line is a fit to the data, as described in the text. (c) The electric contribution to the heat capacity divided by T, where the phonon contribution (shown in panel d as a dotted line) has been subtracted. The electronic coefficient of the heat capacity γ and the size of the jump ΔC/Tc are shown. (d) C/T vs. T2 showing that over a broad T range the data are described by the expression γ + βT2.
In Fig. 3b we show the temperature dependence of the upper critical field curve Hc2 determined from both electrical resistivity and heat capacity measurements. We also compare results from electrical transport studies of both an as-cast specimen and one that was cold worked into a flattened plate, where there is no discernable change in the behavior. There is a notable difference in Tc determined from the electrical resistivity and the heat capacity - the 50% resistive transition precedes the midpoint of the heat capacity lambda feature by 0.6 K - but we point out that the onset of the lambda transition overlaps with the 50% resistive transition. From this, we suggest that the significant disorder in the system broadens the superconducting transition, with the bulk transition occurring near Tc ≈ 2.4 K. From the resistive transitions, an upper limit for Hc2(0) is determined using the expression Hc2(T) = Hc2(0)(1-(T/Tc) n), where Hc2(0) = 6.4 T and n = 1.27. This value of Hc2(0) is similar to Pauli-paramagnetic limit for weak electron-phonon coupling, Hc2(0) = 1.84Tc ≈ 5.7 K. As suggested earlier for the Zr-based analogue, this may suggest that strong spin-orbit coupling plays a role in determining the properties of the superconducting state16. The superconducting coherence length ζ is estimated using the expression (dHc2/dT)Tc = −Φ0/2πTcζ2, where Φ0 = 2.07 × 10−7 G/cm2 is the flux quantum. From (dHc2/dT)Tc = 2.4 T/K and Tc = 3.2 K we find that ζ = 117 Å.
Thermal properties of [TaNb]0.31(TiUHf)0.69
In order to address the thermal properties, we investigated the temperature dependent Seebeck coefficient S(T) and thermal conductivity κ(T). The Seebeck coefficient (Fig. 4a) is nearly temperature independent and exhibits small values across the entire temperature range. This indicates typical metallic behavior, similar to what is seen in other HEAs such as YxCoCrFeNi, AlxCoCrFeNi, and (BiSbTe1.5Se1.5)1-xAgx32–34. This supports our conclusion that the uranium f-states are delocalized and thus do not significantly impact the electrical transport behavior. At lower temperatures, S(T) exhibits a weak peak around 50 K, which we propose is due to phonon drag effect, as is seen in other HEAs due to plastic deformation at high strain rates35–37. The thermal conductivity (Fig. 4b) next suggests that phonon scattering mechanisms dominate the thermal transport, as would be anticipated based on the disordered arrangement of atoms on the lattice. This is seen by considering that κ is given by a summation of the electronic and lattice thermal conductivity κ = κE + κL. κE can be estimated using the Wiedemann-Franz law where κE = LσT (L = 2.44 × 10−8 WΩK−2 and σ is the electrical conductivity). From this, we find that that κL (solid dots in Fig. 4b) dominates the total κ at all temperatures. Below 50 K, where phonon scattering is dominated by grain boundaries, a broad peak in κ(T) appears, which is consistent with a small phonon mean free path. At higher temperatures, κ(T) is further suppressed by both point-defect scattering and Umklapp scattering. As a result, the resulting κ(T) is quite small for a metal.
Figure 4.
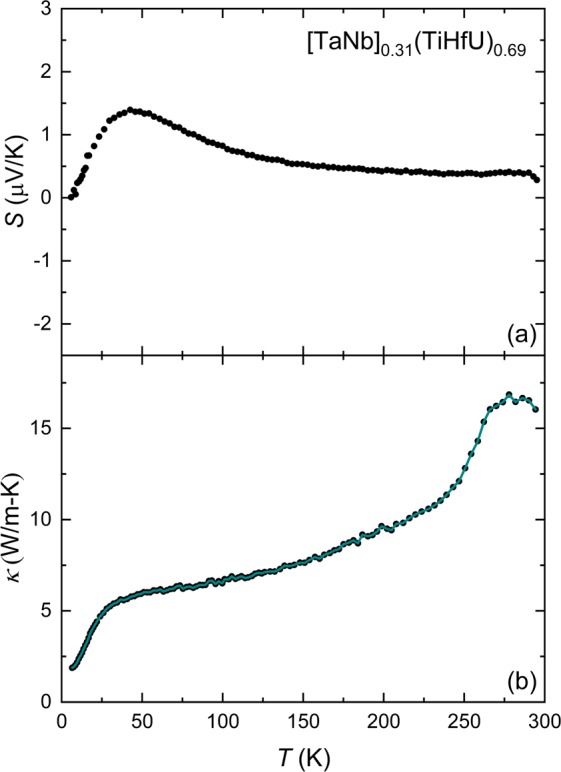
Thermal properties data for [TaNb]0.31(TiUHf)0.69. (a) Temperature-dependent Seebeck coefficient S(T) for [TaNb]0.31(TiHfU)0.69. (b) Temperature-dependent thermal conductivity κ(T) for [TaNb]0.31(TiHfU)0.69. The cyan line shows the lattice contribution to the thermal conductivity κL, which was calculated from the expression κ = κE + κL, where κE is estimated using the Wiedemann-Franz law where κE = LσT (L = 2.44 × 10−8 WΩK−2 and σ is the electrical conductivity determined from Fig. 2).
Discussion and Conclusion
From these measurements we conclude that [TaNb]0.31(TiUHf)0.69 is a disordered type II superconductor with a bulk superconducting phase transition at Tc = 2.4 K and upper critical field Hc2 = 6.4 T. Analysis of the data indicates that the superconducting state is described by the BCS theory within the weak electron-phonon coupling regime, although there is evidence that the strong spin orbit coupling impacts some of the properties. In general, these results are similar to what was earlier reported for the Zr-containing analogues, which is consistent with the conclusion that the uranium f-electrons are delocalized and do not (i) carry a well-defined magnetic moment or (ii) result in strong electronic correlations. Thus, it is appealing to consider the behavior of this system in the context of the framework proposed by Cava et al.5,16, where Tc for the Zr-based analogue system evolves mainly as a function of the valence electron count. For those systems, it can be estimated that [TaNb]0.31(TiZrHf)0.69 would exhibit 4.5 K < Tc < 6.5 K with an upper critical field 9 T < Hc2 < 11 T, and that the Zr → U analogue behave the same way.
However, Tc and Hc2 for [TaNb]0.31(TiUHf)0.69 are suppressed from the values extrapolated from the Zr analogue; i.e., the presence of the uranium ions has the effect of weakening the superconducting state. There could be several reasons for this, including that the typical effect of introducing uranium ions into conventional phonon mediated superconductors is to break Cooper pairs19. We also point out that earlier work in the d-electron analogues shows that there are several other important parameters that can impact the superconductivity, including the electron count and the degree of disorder. Regarding electron count, it might be anticipated that uranium would adopt a tetravalent electronic configuration. However, tetravalent uranium would be expected to produce a Curie-Weiss temperature dependence of the magnetic susceptibility and such behavior is not observed. This may indicate that the uranium ions exhibit intermediate valence behavior that quenches the local moment17,38,39 and that the effective electron count is smaller than anticipated. It is also possible that the introduction of an f-element in the place of a d-element, with its distinct orbitals and shape, enhances the disorder and suppresses Tc. Prior work has shown that there is a positive correlation between crystallinity and the superconducting state5. Further work will be needed to address these questions; e.g., including X-Ray absorption spectroscopy to quantify the uranium valence and scanning tunneling electron microscopy to image the disorder.
[TaNb]0.31(TiUHf)0.69 thus emerges as an example of a small but growing family of f-electron materials with both practical and fundamental implications. Earlier work revealed that the Zr-based analogues and other HEAs exhibit high strength, ductility, and damage resistant properties across a broad range of temperatures, and the work presented here demonstrates that this extends to the actinide family. This suggests that this and other HEAs may provide a next generation waste form for radioactive isotopes, similar to other HEA systems11–14. We also anticipate that the [TaNb]1-x(TiAHf)x HEA series will accommodate other radioactive elements (A = actinide) in the place of A = U. This has the advantage that it will enable studies of the direct impact of natural radiation damage and the long term robustness of these materials. It is also appealing to consider that variation of the stoichiometry may improve the superconducting properties and the introduction of other actinide or even lanthanide elements may induce novel behavior that might include magnetism, as has already been observed for other f-element HEAs22–25. This sets the stage for these systems to emerge as a next generation of novel materials with functionality along multiple axes.
Methods
Synthesis
Specimens were produced using the arc furnace technique, as earlier described for the Zr-based analogues5,13,14. The starting materials were metallic niobium (purity 99.9%), tantalum (purity 99.9%), uranium (purity 99.9%), hafnium (purity 99.9%), and titanium (purity 99.99%). The reaction took place under an argon atmosphere that was purified prior to the growth by heating a zirconium getter. After melting, the sample was rapidly cooled on a water-chilled copper plate. The sample was melted five times and turned over each time to encourage homogeneity.
Elemental analysis
Elemental analysis was performed by scanning electron microscopy using energy dispersive spectroscopy (SEM-EDS) on an FEI NOVA 400. Samples were analyzed at an accelerating voltage of 20 kV for 60 seconds at a working distance of 10 mm. Both a large mechanically-flattened piece and small chips from the rough bottom of the boule were examined, and no statistically-significant elemental difference was observed between them.
X-ray diffraction
Attempts at single-crystal X-Ray Diffraction (XRD) failed for even the smallest samples cut off the boule, with inherent multicrystallinity even with samples on the order of 5 μm per axis. Powder XRD was conducted on a PANalytical X’Pert PRO diffractometer with a Cu Kα source. Extracted peaks were then assigned to d-spacings using a Microsoft Excel Spreadsheet and the Solver Tool to minimize sum-squared errors to determine the unit cell dimensions.
Electrical resistivity, heat capacity, and magnetic measurements
DC electrical resistivity ρ measurements were performed in a four wire configuration for flattened specimens using a Quantum Design Physical Properties Measurement Systems with He3 option down to temperatures T > 0.4 K and magnetic fields H < 9 T. Specific heat C measurements were also performed in the same system using a conventional thermal relaxation technique. DC magnetic susceptibility χ = M/H and magnetization measurements were carried out at temperatures T = 1.8–300 K under an applied magnetic field of H = 5 kOe and at T = 1.8 K and 5 K for H < 7 T using a Quantum Design VSM Magnetic Property Measurement System. The samples were embedded in GE-varnish and attached to a quartz rod for the measurement. Electrical resistance R(T) measurements under applied pressure were performed using a piston cylinder pressure cell with Daphne 7575 oil as the pressure transmitting medium. The pressure was determined by the shift in ruby flourescence peaks as measured below T = 10 K.
Thermopower and thermal conductivity measurements
The thermal conductivity was measured using the conventional one-heater-two-thermometer method. Two Cernox bare chip sensors were used for the thermometer and a polished thin metal chip resistor was used for the heater. A step-wise increasing heater power (dP) to the chip resistor generated step-wise thermal gradient across the sample. The temperature gradient (dT) and the corresponding thermoelectric voltage (dV) were simultaneously measured when dT was stabilized at different heater power. The thermal conductivity and the Seebeck coefficient were obtained by the relations, κ ~ dP/dT and S = dV/dT, respectively.
Supplementary information
Acknowledgements
Synthesis and material characterization was supported by CAST, an EFRC funded by the US DOE under Award DE-SC0016568. KW acknowledges support from the Jack E. Crow NHMFL postdoctoral fellowship. This work was performed at the NHMFL which is supported by NSF Cooperative Agreement DMR-1644779 and the State of Florida.
Author contributions
R.B. led the project by designing the work and overseeing/contributing to the synthesis of materials, acquisition and interpretation of data and preparation of the manuscript. W.L.N. contributed to the work by synthesizing samples, collecting data (magnetization, electrical resistivity, and heat capacity), and writing the manuscript. A.T.C., M.H., and S.L. contributed to the manuscript by collecting and interpreting X-Ray diffraction and EDS data. E.C. and K.W. contributed to the manuscript by collecting and interpreting thermopower and thermal conductivity data. D.G. contributed to this project by performing electrical transport measurements under applied pressures. T.A.S. contributed to the manuscript by advising MH and ATC in their analysis of data, by providing raw materials (depleted uranium). All authors reviewed the manuscript.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
is available for this paper at 10.1038/s41598-020-61666-z.
References
- 1.George EP, Raabe D, Ritchie RO. High Entropy Alloys. Nature Reviews. 2019;4:515. [Google Scholar]
- 2.Chen J, et al. A review on fundamental of high entropy alloys with promising high-temperature properties. Journal of Alloys and Compounds. 2018;760:15. doi: 10.1016/j.jallcom.2018.05.067. [DOI] [Google Scholar]
- 3.Miracle DB, Senkov ON. A Critical Review of High Entropy Alloys and Related Concepts. Acta Materialia. 2017;122:448. doi: 10.1016/j.actamat.2016.08.081. [DOI] [Google Scholar]
- 4.Tsai MH, Yeh JW. High Entropy Alloys: A critical Review. Materials Research Letters. 2014;2(3):107. doi: 10.1080/21663831.2014.912690. [DOI] [Google Scholar]
- 5.Sun L, Cava RC. High entropy alloy superconductors: Status, opportunities, and challenges. Physical Review Materials. 2019;3:090301. doi: 10.1103/PhysRevMaterials.3.090301. [DOI] [Google Scholar]
- 6.Gludovatz B, et al. A fracture-resistant high-entropy alloy for cryogenic applications. Science. 2014;345:1153–1158. doi: 10.1126/science.1254581. [DOI] [PubMed] [Google Scholar]
- 7.Gludovatz B, et al. Exceptional damage-tolerance of a medium-entropy alloy CrCoNi at cryogenic temperatures. Nature Communications. 2016;7:10602. doi: 10.1038/ncomms10602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zou Y, Ma H, Spolenak R. Ultrastrong ductile and stable high-entropy alloys at small scales, Nature. Communications. 2015;6:7748. doi: 10.1038/ncomms8748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Youssef KM, Zaddach AJ, Niu C, Irving DL, Koch CC. A novel low-density, high hardness, high-entropy alloy with close-packed single-phase nanocrystalline structures. Materials Research Letters. 2016;3:95. doi: 10.1080/21663831.2014.985855. [DOI] [Google Scholar]
- 10.Kou H, Lu J, Li Y. High-strength and high-ductility nanostructured and amorphous metallic materials. Advanced Materials. 2014;26:5518. doi: 10.1002/adma.201401595. [DOI] [PubMed] [Google Scholar]
- 11.Yang T, et al. Precipitation behavior of AlxCoCrFeNi high entropy alloys under ion irradiation. Scientific Reports. 2016;6:32146. doi: 10.1038/srep32146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lu C, et al. Enhancing radiation tolerance by controlling defect mobility and migration pathways in multicomponent single-phase alloys. Nature Communications. 2016;7:13564. doi: 10.1038/ncomms13564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Granberg F, et al. Mechanism of radiation damage reduction in equiatomic multicomponent single phase alloys. Physical Review Letters. 2016;116:135504. doi: 10.1103/PhysRevLett.116.135504. [DOI] [PubMed] [Google Scholar]
- 14.El-Atwani O, et al. Outstanding radiation resistance of tungsten-based high-entropy alloys. Science Advances. 2019;5:eaav2002. doi: 10.1126/sciadv.aav2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kozelj P, et al. Discovery of a superconducting high entropy alloy. Physical Review Letters. 2014;113:107001. doi: 10.1103/PhysRevLett.113.107001. [DOI] [PubMed] [Google Scholar]
- 16.von Rohr F, Winiarski MJ, Tao J, Klimczuk T, Cava RJ. Effect of electron count and chemical complexity in the Ta-Nb-Hf-Zr-Ti high-entropy alloy superconductor. Proceedings of the National Academy of Sciences USA. 2016;113:E7144. doi: 10.1073/pnas.1615926113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Moore KT, van der Laan G. Nature of the 5f states in actinide metals. Reviews of Modern Physics. 2009;81:235. doi: 10.1103/RevModPhys.81.235. [DOI] [Google Scholar]
- 18.Gschneidner, K. A. & Eyring, L. (eds.) Handbook on the Physics and Chemistry of Rare Earths, Vol. 1 (North Holland, Amsterdam, 1978).
- 19.Pfleiderer C. Superconducting phases of f-electron compounds. Reviews of Modern Physics. 2009;81:1551–1624. doi: 10.1103/RevModPhys.81.1551. [DOI] [Google Scholar]
- 20.Maple MB, Baumbach RE, Butch NP, Hamlin JJ, Janoschek M. Non-Fermi Liquid Regimes and Superconductivity in the Low Temperature Phase Diagrams of Strongly Correlated d- and f-Electron Materials. Journal of Low Temperature Physics. 2010;161:4. doi: 10.1007/s10909-010-0212-5. [DOI] [Google Scholar]
- 21.Dzero M, Sun K, Galitski V, Coleman P. Topological Kondo Insulators. Physical Review Letters. 2010;104(March):106408. doi: 10.1103/PhysRevLett.104.106408. [DOI] [PubMed] [Google Scholar]
- 22.Luznik J, et al. Complex magnetism of the Ho-Dy-Y-Gd-Tb hexagonal high-entropy alloy. Physical Review B. 2015;92:224201. doi: 10.1103/PhysRevB.92.224201. [DOI] [Google Scholar]
- 23.Yuan Y, et al. Rare-earth high-entropy alloys with giant magnetocaloric effect. Acta Materialia. 2017;125:481. doi: 10.1016/j.actamat.2016.12.021. [DOI] [Google Scholar]
- 24.Qiao JW, et al. Rare-earth high entropy alloys with hexagonal close packed structure. Journal of Applied Physics. 2018;124:195101. doi: 10.1063/1.5051514. [DOI] [Google Scholar]
- 25.Sogabe R, Goto Y, Mizuguchi Y. Superconductivity in REO0.5F0.5BiS2 with high entropy alloy type blocking layers. Applied Physics Express. 2018;11:053102. doi: 10.7567/APEX.11.053102. [DOI] [Google Scholar]
- 26.Rogers BA, Atkins DF, Manthos EJ, Kirkpatrick ME. Uranium columbium alloy diagram. Transactions of the Metallurgical Society of AIME. 1958;212:p387. [Google Scholar]
- 27.Krug MP, Oden LL, Romans PA. The solid state portion of the Hf-Ta phase diagram. Metallurgical Transactions. 1975;6:997. doi: 10.1007/BF02645523. [DOI] [Google Scholar]
- 28.Summers-Smith D. The constitution of tantalum titanium alloys. Journal of the Institute of Metals. 1953;81:73. [Google Scholar]
- 29.Knapton AG. Constitution, structure, and physical properties of niobium and tantalum alloys. Journal of the Less Common Metals. 1960;2:113. doi: 10.1016/0022-5088(60)90006-0. [DOI] [Google Scholar]
- 30.Lee CP, Chen YY, Hsu CY, Yeh JW, Shih HC. The Effect of Boron on the Corrosion Resistance of the High Entropy Alloys Al0.5CoCrCuFeNiBx. Journal of the Electrochemical Society. 2007;154:C424. doi: 10.1149/1.2744133. [DOI] [Google Scholar]
- 31.Guo J, et al. “Robust zero resistance in a superconducting high entropy alloy at pressures up to 190 GPa. Proceedings of the National Academy of Sciences USA. 2017;114:13144. doi: 10.1073/pnas.1716981114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Shafeie S, et al. High-entropy alloys as high-temperature thermoelectric materials. Journal of Applied Physics. 2015;118:184905. doi: 10.1063/1.4935489. [DOI] [Google Scholar]
- 33.Fan Z, Wang H, Wu Y, Liu XJ, Lu ZP. Thermoelectric high-entropy alloys with low lattice thermal conductivity. RSC Advances. 2016;6:52164. doi: 10.1039/C5RA28088E. [DOI] [Google Scholar]
- 34.Dong W, et al. Effects of Y, GdCu, and Al Addition on the Thermoelectric Behavior of CoCrFeNi High Entropy Alloys. Metals. 2018;8:781. doi: 10.3390/met8100781. [DOI] [Google Scholar]
- 35.Kumar N, et al. High strain-rate compressive deformation behavior of the Al0.1CrFeCoNi high entropy alloy. Mater. Des. 2015;86:598. doi: 10.1016/j.matdes.2015.07.161. [DOI] [Google Scholar]
- 36.Wang B, Yao X, Wang C, Zhang X, Huang X. Mechanical Properties and Microstructure of a NiCrFeCoMn High-Entropy Alloy Deformed at High Strain Rates. Entropy. 2018;20:892. doi: 10.3390/e20110892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.F. J. Blatt, P. A. Schroeder, C. L. Foiles, and D. Greig, Thermoelectric Power in Metals, Springer US, (1976).
- 38.Varma CM. Mixed Valence Compounds. Reviews of Modern Physics. 1976;48:219. doi: 10.1103/RevModPhys.48.219. [DOI] [Google Scholar]
- 39.Booth CH, et al. Multiconfigurational nature of 5f orbitals in uranium and plutonium intermetallics. Proceedings of the National Academy of Sciences USA. 2012;109:10205. doi: 10.1073/pnas.1200725109. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.