Measuring Entropy in Molecular Recognition by Proteins

Abstract

Molecular recognition by proteins is fundamental to the molecular basis of biology. Dissection of the thermodynamic landscape governing protein–ligand interactions has proven difficult because determination of various entropic contributions is quite challenging. Nuclear magnetic resonance relaxation measurements, theory, and simulations suggest that conformational entropy can be accessed through a dynamical proxy. Here, we review the relationship between measures of fast side-chain motion and the underlying conformational entropy. The dynamical proxy reveals that the contribution of conformational entropy can range from highly favorable to highly unfavorable and demonstrates the potential of this key thermodynamic variable to modulate protein–ligand interactions. The dynamical so-called entropy meter also refines the role of solvent entropy and directly determines the loss in rotational–translational entropy that occurs upon formation of high-affinity complexes. The ability to quantify the roles of entropy through an entropy meter based on measurable dynamical properties promises to highlight its role in protein function.

INTRODUCTION

How the fundamental forces of chemistry and physics combine to define the energy landscape of proteins remains a difficult and complex question to unravel and dissect through experiment, simulation, or theory. This is particularly true in the context of the residual conformational (configurational) entropy of the protein and the entropy of solvent. For nearly half a century, the magnificent but largely monolithic atomic-scale views of protein molecules primarily obtained by crystallography have provided deep insight into the energetic (enthalpic) origins of their function. For decades, theoretical explorations, molecular simulations, and a variety of spectroscopic approaches have emphasized that protein molecules are nevertheless dynamic and explore a range of microstates. It is now clear that the internal conformational entropy of proteins is significantly larger than that indicated by common representations of the native-state well of their energy landscapes. The availability of large reservoirs of entropy in the native states of proteins makes it critical to determine whether this entropy is coupled to the energetics of functions that exist beyond those involved in the folding and stability of protein molecules. Here, we focus on the development of a new approach to measuring changes in conformational entropy using what is referred to as a dynamical proxy provided by advanced nuclear magnetic resonance (NMR) relaxation methods. Over the past decade or so, this approach has emerged to allow quantitative access to the contribution of conformational entropy to protein molecular recognition, which is one of the most fundamental roles carried out by proteins in biology. In addition, experimental access to conformational entropy has also allowed refinement of the calculation of the contribution of solvent entropy based on changes in solvent-accessible surface area and the direct determination of the reduction in rotational–translational entropy upon formation of high-affinity complexes.

THERMODYNAMICS AND DYNAMICS OF MOLECULAR RECOGNITION

Experimental investigation of the thermodynamics of molecular recognition by proteins often begins from a calorimetric perspective where the heat or enthalpy (ΔH_total) and free energy (ΔG_total) are measured and the total binding entropy (ΔS_total) is determined by

$$\mathrm{\Delta }{G}_{\text{total}}=\mathrm{\Delta }{H}_{\text{total}}-T\mathrm{\Delta }{S}_{\text{total}}=\mathrm{\Delta }{H}_{\text{total}}-T\left(\mathrm{\Delta }{S}_{\text{conf}}^{\text{protein}}+\mathrm{\Delta }{S}_{\text{conf}}^{\text{ligand}}+\mathrm{\Delta }{S}_{\text{solvent}}+\mathrm{\Delta }{S}_{\text{r}–\text{t}}+\mathrm{\Delta }{S}_{\text{other}}\right).$$ 1.

Detailed atomic resolution structural models provide great insight into the origins of the enthalpy of binding. Much less certain are the various contributions to the total binding entropy. In principle, several types of entropy are potentially important (see right side of Equation1). Historically, entropy has most often entered the discussion in terms of the changes in the entropy of solvent water (ΔS_solvent) and framed in terms of the so-called hydrophobic effect (3, 14, 32, 98). ΔS_solvent has, with some success, been related empirically to changes in accessible surface area (ΔASA) of the protein and ligand upon complexation (32). Changes in the conformational entropy (ΔS_conf) and the rotational–translational entropy (ΔS_r–t) of the interacting species have received far less attention, presumably because they have resisted experimental measurement. ΔS_other refers to other processes, such as proton binding or release, that may contribute to the total binding entropy (50). The goal is to measure these contributions to the binding of ligands by protein molecules. It turns out that an indirect approach utilizing a dynamical proxy obtained by NMR relaxation methods has proven quite successful.

CHARACTERIZATION OF MOTION BY NMR RELAXATION METHODS

Solution NMR spectroscopy has emerged as a powerful means for the site-resolved measurement of internal motion in protein molecules over an impressive range of timescales in proteins of significant size and complexity (88). NMR spectroscopy has a bounty of capabilities to characterize time-dependent phenomena and can access time regimes from picoseconds to days (8, 90). As is apparent below, motion on the fast timescale is anticipated to be rich in the underlying conformational entropy, and we focus on the features of solution NMR relaxation that sample this time regime. Here, we are ultimately most focused on those motions that express large contributions to protein conformational entropy (i.e., motions that extensively sample the many states available to the folded native state of the protein molecule). It has long been recognized from early simulations that the extremely fast soft-mode torsional oscillations of amino acid side chains contain significant entropy and that vibrational entropy will vary little as proteins move from state to state (41). Classical NMR relaxation phenomena will probe the interconversion of these states on the picosecond–nanosecond timescale.

Mechanisms of NMR Relaxation

Very briefly, an ensemble of nuclear spins can relax from a nonequilibrium state via a range of potential interactions. For example, the internuclear dipole–dipole interaction between spatially proximal hydrogens gives rise to the nuclear Overhauser effect (NOE), which is likely familiar to the nonexpert reader as a means to measure interatomic distances for the determination of molecular structure in solution (70, 114). The strength of this interaction depends on the time average of the distance between the nuclei and of the angle of the internuclear vector with the applied magnetic field. In favorable situations, such as when the two nuclei are bonded, the distance dependence is effectively constant (though see 30, 82) and the interaction is temporally modified only by the change in the orientation of the bond vector with respect to the magnetic field. Examples include the ¹⁵N–¹H amide bond (38) and the ¹³C–¹H bond in a variety of contexts, such as in a methyl group (34). Other nuclear spin interactions are perhaps more obscure to the reader. These include chemical shift anisotropy, which reflects the interaction of the nuclear spin with the asymmetric distribution of electrons around it (91), and the interaction between the nuclear quadrupolar moment of spin quantum number of one or greater and the surrounding electric field gradient (37). In some cases, the interference between relaxation mechanisms can offer insight into motion (e.g., 17, 68, 84, 107, 111, 116).

Relaxation to an equilibrium distribution of nuclear spins in a liquid sample is mediated by the fluctuation of local fields arising from chemical shielding anisotropy, dipole–dipole, and quadrupolar interactions brought about by local (internal) motion and by macromolecular tumbling. Internal protein motion results in time modulation of the local fields that, in turn, contribute to relaxation. The theoretical connection between the observed relaxation phenomena and motion is complicated. The interested reader is referred to a recent monograph on this and related subjects (8). Very briefly, the density matrix formalism is employed to represent the properties of the statistical ensemble of spins in a liquid sample, while the surroundings (or lattice) are generally treated classically (1, 33). To obtain the correct behavior of the density matrix as it evolves in time, it is replaced by its nonequilibrium value through the action of a definable propagator. Once the time behavior of the density matrix is known, the behavior of an observable is obtained by taking a trace of the product between its matrix representation and the corresponding density matrix operators. Examples can be found elsewhere (34).

Measures of NMR Relaxation

NMR observables that are measured can be expressed as linear combinations of the so-called spectral density functions. The spectral densities are related to the time dependence of the orientation of the vector defining the particular type of interaction. Consider a ¹³C nucleus with a single attached ¹H (e.g., a methine alpha carbon of an amino acid). The motion of the ¹³C–¹H interaction vector (along the rigid bond between them) can be described by the autocorrelation function of the dot product of the interaction vector’s orientation at some time t and its orientation at some time t′. The time dependence will have two components: a contribution from the slower global tumbling of the protein and an assumed faster component due to motion within the molecular frame. The global tumbling of the protein in solution defines the upper limit of the timescale that can be investigated by these types of measurements. The spectral densities are linearly combined as required by the physics of the specific NMR relaxation mechanism to define an observable relaxation (see 34 for illustrative derivations). For example, the longitudinal relaxation rate (1/T₁ or R₁) of the ¹³C nucleus by a single bonded ¹H nucleus is given by

$$R_1=\frac{d^2}{4}\left[J({\omega }_{\text{H}}-{\omega }_{\text{C}})+3J({\omega }_{\text{C}})+6J({\omega }_{\text{H}}+{\omega }_{\text{C}})\right],$$ 2.

where d² is composed of fundamental constants and the effective C–H bond length and ω_H and ω_C are the resonance frequencies of ¹H and ¹³C nuclear spins, respectively.

Primary Interpretation of NMR Relaxation

The dominant procedure for describing the essential character of the motion that gives rise to NMR relaxation phenomena of the type considered here is the so-called model-free approach of Lipari & Szabo (66, 67). The Lipari-Szabo (L-S) form of the spectral density is remarkably robust (20). In the simplest case, the L-S treatment leads to three parameters: a correlation time for isotropic macromolecular reorientation (τ_m), an effective correlation time (τ_e), and a measure of the angular disorder of the interaction vector termed the squared generalized order parameter (O²)¹ expressed as

$$J(\omega )=\frac{O^2{\tau }_{\text{m}}}{1+{\omega }^2{\tau }_{\text{m}}^{\text{2}}}+\frac{(1-O^2)\tau }{1+{\omega }^2{\tau }^2},$$ 3.

where ${\tau }^{-1}={\tau }_{\text{m}}^{-\text{1}}+{\tau }_{\text{e}}^{-\text{1}}$.

The order parameter by definition ranges from zero to one, corresponding to complete isotropic disorder and complete rigidity of the interaction vector within the molecular frame, respectively. It is this motional parameter that provides access to conformational entropy. The effective correlation time, however, is too model dependent to be used as a robust descriptor of the time constant(s) for the underlying motion (66).

For each site of interest, there are two unknowns (O² and τ_e) plus one global variable (τ_m) defining isotropic tumbling of the protein in solution. The situation can become more complicated, of course. For example, the character of the tumbling of the macromolecule may be anisotropic to some degree. This is directly handled using appropriate diffusion equations and data filtering (46, 55, 83, 103).

Some cases may require (justify) more complex forms of the model-free spectral density shown above (10, 72). Nevertheless, the experimental prescription is clear: Resolve relaxation data at n individual sites in a protein and measure as many relaxation parameters (e.g., T₁, T₂) at as many magnetic fields (to vary ω_H, ω_C) as needed to provide a robust determination of the 2n + 1 (in the case of isotropic macromolecular tumbling) parameters.

The advent of multidimensional NMR spectroscopy provides a means to resolve literally hundreds of probe sites for motion in proteins. To realize a comprehensive use of NMR relaxation phenomena to characterize protein internal motion requires several key steps. Increasingly sophisticated isotopic labeling schemes have been introduced to simplify the complexity of the NMR relaxation as much as possible to make its measurement and subsequent analysis more robust (e.g. 21, 22, 27, 40, 45, 53, 56, 62–65, 75, 76, 81, 88, 92, 102, 109). The basic strategy is to reduce the number of relaxation mechanisms (interactions) as much as possible. Finally, the cornerstone was the development of NMR experiments that prepared so-called pure NMR observables of NMR relaxation that could be directly interpreted. Lewis Kay and colleagues are largely identified as the developers of the NMR machinery necessary to measure ¹⁵N (16, 44), ²H (77, 80), and ¹³C (81) autorelaxation in proteins. Tugarinov and coworkers (61) have extended the number of deuterium relaxation experiments that provide a context for extracting even more fundamental relaxation rate constants at a single magnetic field. Notable contributions for implementing ¹³C relaxation in the context of proteins came from Torchia and colleagues (36) in their unraveling of the complexity of this particular mechanism of relaxation in the context of proteins. More recently, cross-correlated relaxation in ¹³CH₃ groups has emerged as a highly sensitive though perhaps not as accurate route to measures of protein motion in even very large protein systems (99, 100, 105). Finally, computational strategies were needed to confidently extract the desired model-free parameters (12, 72, 103).

Preparation of Samples

Unfortunately, it turns out the relaxation properties of most ¹³C nuclei with bonded hydrogen(s) in proteins of significant size are unfavorable for detailed quantitative analysis. This has important ramifications as is discussed below. The important general exception is the methyl carbon, which, owing to the fast rotation of the methyl group, can be used as a relaxation probe in even very large proteins (88, 104). Isotopic labeling is designed to render relaxation in the methyl group as simple and tractable as possible. The CHD₂ isotopomer is targeted for ¹³C relaxation and the CH₂D isotopomer for deuterium relaxation. In the case of deuterium methyl relaxation, which is most suited for smaller proteins, the CH₂D isotopomer is created by expression of the protein on minimal media in ~55% D₂O. For ¹³C-methyl relaxation studies, the labeling strategy has evolved significantly over the past two decades. A simple approach is to employ randomly partially deuterated ¹³C₃-pyruvate as a general carbon source and the appropriate spin systems isolated by low-pass filtering (53). A better approach is to express the target protein during growth on unlabeled glucose and appropriately labeled metabolic precursors for valine, leucine, and isoleucine (27). Protein expression is carried out in “100%” D₂O to ensure elimination of ¹H spins at nonmethyl sites in the protein (35).

Proteins produced in this manner are largely deuterated with selective ¹H and ¹³C labeling in methyl groups. The methyl groups are mixtures of isotopomers (i.e., CD₃, CHD₂, CH₂D, CH₃). Only the three carrying at least one hydrogen are observed in the two-dimensional ¹H–¹³C chemical shift correlation spectrum and give cross-peaks that are at slightly different positions. The appropriate isotopomer, in this case the CHD₂, is selected by spectroscopic manipulation (104). Recently, new precursors (21) and expression strategies (78) have become available for increasingly precise and efficient introduction of appropriate combinations of nuclear spins into proteins.

The NMR relaxation experiment is designed to follow the return of a particular type of magnetization from a nonequilibrium state back to equilibrium. For carbon relaxation in proteins, longitudinal and transverse relaxation processes are most useful and are likely familiar to the nonspecialist reader as T₁ and T₂ relaxation, respectively. The NOE is not so useful in the context of carbon relaxation in proteins of significant size since this observable reaches a limit as molecular tumbling slows. Relaxation at a specific methyl is quantified by the variation of the intensity of the corresponding ¹H–¹³C cross-peak with the relaxation time period. These types of data are then used to determine the L-S order parameter, which includes the effects of the fast rotation of the methyl group about its symmetry axis and the motion of the symmetry axis itself. Since the geometry of the methyl group can be assumed, the L-S order parameter for the symmetry axis,$O_{\text{axis}}^{\text{2}}$, is obtained directly.

PRELUDE TO A DYNAMICAL PROXY FOR CONFORMATIONAL ENTROPY

As described above, various technical barriers to obtaining accurate and interpretable measures of site-resolved relaxation phenomena have been surmounted. Analytical strategies for analyzing these data are now largely established with the L-S model-free approach, providing the dominant framework. The next task was to try to make sense of the physical significance of measured squared generalized order parameters and, to a lesser extent, obtained effective correlation times.

A Model-Independent Statistical View

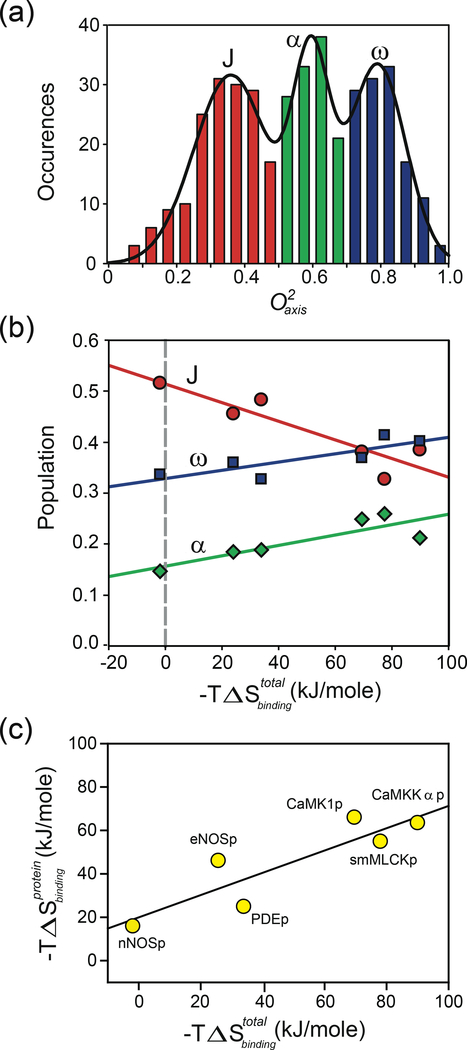
Analysis of the first dozen or so comprehensive examples of methyl dynamics in proteins suggested that there are three basic classes or types of motion of methyl groups in proteins. Individual proteins often, though not always, displayed a distinct trimodal distribution centered roughly on $O_{\text{axis}}^{\text{2}}$values of ~0.35, ~0.6, and ~0.8 (34). The trimodal distribution is exemplified by the calmodulin complexes (19, 51, 54) (Figure 1a). It now seems clear that the three classes correspond to distinct types of methyl-bearing side-chain motion, which have only a modest relationship with the length of the side chain and are determined mostly by local context (93). The low order-parameter distribution centered at ~0.35 is identified as having extensive rotamer interconversion that leads to averaging of J-coupling constants (52) and is termed the J-class (34). The distribution of order parameters centered at ~0.8 is identified with highly restricted motion within a single rotameric well reminiscent of the rigidity of the protein backbone and is termed the ω-class (34). Molecular dynamics (MD) simulations also suggest a slight narrowing of the rotamer potential at high $O_{\text{axis}}^{\text{2}}$values (93). The intermediate band centered on an $O_{\text{axis}}^{\text{2}}$value of ~0.6 is suggested to involve larger amplitude motion within a rotamer well with occasional rotamer jumps (52, 93).

Figure 1.

Correlation of the apparent contribution of conformational entropy to the binding of target domains by calmodulin with total binding entropy. The apparent contribution reported by a model-dependent local interpretation of changes in methyl side-chain dynamics in calmodulin in complex with six different calmodulin-binding domains (19). (a) Summed histogram of the distribution of methyl group $O_{\text{axis}}^{\text{2}}$values of calmodulin in various complexes. (b) Correlation of the fractional population of the three classes of methyl-group motion with the total binding entropy measured by isothermal titration calorimetry for the six calmodulin complexes: J-class (red circles), α-class (green diamonds), and ω-class (blue squares). (c) Application of the oscillator inventory approach to assess the role of conformational entropy of calmodulin in the binding of calmodulin-binding domains. The harmonic oscillator potential was used to convert changes in methyl-group motion to estimates of changes in local side-chain entropy. The simple sum of apparent entropies is plotted against the total binding entropy. A The p at the end of the terms in panel c signifies that the various calmodulin-binding domains are represented by peptides. dapted from Reference 19. Abbreviations: CaMK1p, calmodulin-binding domain of calcium/calmodulin-dependent protein kinase1; CaMKKαp, calmodulin-binding domain of calcium/calmodulin-dependent protein kinase kinase alpha; eNOSp, calmodulin-binding domain of endothelial nitric oxide synthase; nNOSp, calmodulin-binding domain of neuronal nitric oxide synthase; PDEp, calmodulin-binding domain of phosphodiesterase; smMLCKp; calmodulin-binding domain of smooth muscle myosin light chain kinase.

This interpretation of the trimodal distribution of methyl-bearing side-chain motion also brings with it the notion that the different classes of motion correspond to different quantities of conformational entropy. A calmodulin complex provided the first clear insight into the response of a protein to binding a high-affinity ligand. Calmodulin interacts with literally hundreds of proteins in the course of eukaryotic signaling (39). Most calmodulin-binding domains of protein regulated by calmodulin are satisfactorily represented by relatively short peptides that generally have an amphiphilic character (e.g., 47). Using deuterium relaxation, it was found that there is a significant redistribution and loss of methyl-bearing side-chain motion in calmodulin upon binding a peptide corresponding to the calmodulin-binding domain of the smooth-muscle myosin light chain kinase (51). From this perspective, Wand and coworkers (19) measured the variation in methyl-bearing side-chain dynamics across six calmodulin–peptide complexes. The startling result was the population of J, α, and ω classes of methyl side-chain motion varied linearly with the total binding entropy (Figure 1b) (19). This provided a relatively model-independent view of the potential role for conformational entropy in protein–ligand interactions and led subsequently to a more quantitative interpretation.

The Model-Dependent Oscillator Inventory Approach

One can imagine an approach that uses a specific potential energy function to obtain a quantitative connection between the motion interconverting states and the corresponding entropy. There is a long history of employing dynamical models to interpret experimental NMR relaxation data (e.g., 113 and references therein). The formal definition of the L-S squared generalized order parameter indicates how this might be done (66):

$$O^2=\iint \text{d}{\mathrm{\Omega }}_i\text{d}{\mathrm{\Omega }}_j{p}_{\text{eq}}({\mathrm{\Omega }}_i)P_2(cos{\theta }_{ij})p_{\text{eq}}({\mathrm{\Omega }}_j),$$ 4.

where Ωi is the polar angles for the ith orientation of the interaction vector and θ_ij is the angle between them. The key is p_eq(Ω), which describes the probability distribution of the orientations. Knowledge of p_eq(Ω) provides the partition function of the system and hence gives access to fundamental thermodynamic quantities such as entropy. A particularly influential contribution came from Akke and coworkers (2), who illustrated how, using a specific potential, one could make a connection to the thermodynamics of the system. Taking this view, Yang & Kay (115) and Li and coworkers (60) employed free diffusion in an infinite square well and a harmonic oscillator potential, respectively, to make a parametric connection between entropy and the L-S order parameter. Importantly, it also turns out that vastly different potentials give roughly the same change in entropy with a change in motion (order parameter) (52).

It is obvious that there are many difficulties and qualifications with using what we term the oscillator inventory approach. To name but a few, (a) the true nature of the potential governing motion is uncertain and may vary within and among proteins; (b) current NMR methods provide routine access to the dynamics of only a limited number of sites (e.g., the amide N–H bond vector and the methyl symmetry axis); (c) NMR relaxation has a distinct geometric dependence (see Equation 4) and so may not sense all internal motions to the same degree; and (d) motions of different NMR probes may be correlated. Notwithstanding these strong criticisms, application of the oscillator inventory analysis to the calmodulin complexes recapitulated the linear correlation between the apparent change in conformational entropy of calmodulin and the total binding entropy (Figure 1c). This once again strongly suggested that the entropy represented by the change in internal motion of the protein constituted a significant fraction of the total entropy of binding.

CONSTRUCTION OF A DYNAMICAL PROXY FOR CONFORMATIONAL ENTROPY

To avoid the various limitations of the oscillator inventory approach, we embarked on a strategy that would empirically calibrate the relationship between changes in internal motion of methyl-bearing side chains and the corresponding change in total side-chain conformational entropy. Here, the view changes. We now seek to use the methyl group as a reporter not only of its own disorder but also as a response to the disorder of its surrounding.

The Model-Independent Entropy Meter

The construction of the entropy meter rests on two fundamental assumptions: (a) that methyl-bearing side chains are numerous enough to provide good coverage throughout the protein and (b) that they are sufficiently coupled to neighboring side chains to report on the local disorder (entropy). This results in a simple relationship between what can be measured (protein motion) or calculated (solvent entropy) and what is desired (conformational entropy) (42, 74), expressed as

$$\left(\mathrm{\Delta }{S}_{\text{tot}}-\mathrm{\Delta }{S}_{\text{sol}}\right)=s_d\left[\left(a•{\langle \mathrm{\Delta }{O}_{\text{axis}}^2\rangle }^{\text{protein}}+b•{\langle \mathrm{\Delta }{O}_{\text{axis}}^{\text{2}}\rangle }^{\text{ligand}}\right)\right]+\mathrm{\Delta }{S}_{\text{RT}}+\mathrm{\Delta }{S}_{\text{other}},$$ 5.

where ΔS_tot, ΔS_sol, ΔS_conf, ΔS_r−t, and ΔS_other are the changes in total system entropy, solvent entropy, conformational entropy, rotational–translational entropy, and undocumented entropy, respectively. By postulate, ΔS_conf is linearly related to the weighted change in the dynamics of the ligand and the protein upon binding. The weighting factors (a and b) serve to project the measured changes in motion of the methyl-group reporters across the entire protein and ligand. In its original formulation (74), the weighting factors were simply the number of amino acid residues [the ligand was a peptide; nonpeptide ligands may require more detailed analysis (see 13, for example)], but this has subsequently been shown to be insufficient (42, 108), as is described below. A linear relationship between changes in the L-S order parameter and entropy appears to persist for order parameters between 0.1 and 0.9 (34). The scaling factor s_d is what we desire. In effect, the objections that might be made against the oscillator inventory approach are subsumed into this empirical parameter.

Initial application of this approach to the aforementioned calmodulin complexes proved most convincing (74). A high linear correlation for Equation 5 was observed. Subsequent use of this strategy in the analysis of various mutants of the catabolite activator protein binding DNA resulted in an even more impressive linearity and precision of the scaling factor s_d (106). However, comparison of the calmodulin and catabolite activator protein studies revealed that the two independently determined s_d values differed greatly (108). On one hand, perhaps they truly are different, but, on the other hand, one suspects that the relationship between motion and the underlying conformational entropy is a universal property of protein molecules.

Insights from Computation and Simulation

To gain insight into this apparent discrepancy, we turned to MD simulations. MD simulations have improved greatly over the past decade in their ability to recapitulate experimental order $O_{\text{axis}}^{\text{2}}$values, and multi-nanosecond-length simulations are now sufficiently accurate to provide useful guidance (e.g., 5, 15, 25, 42, 48, 49, 57–59, 87). Utilizing a set of proteins with a range of dynamical properties, we examined some of the basic assumptions of the entropy meter approach outlined above (42, 95).

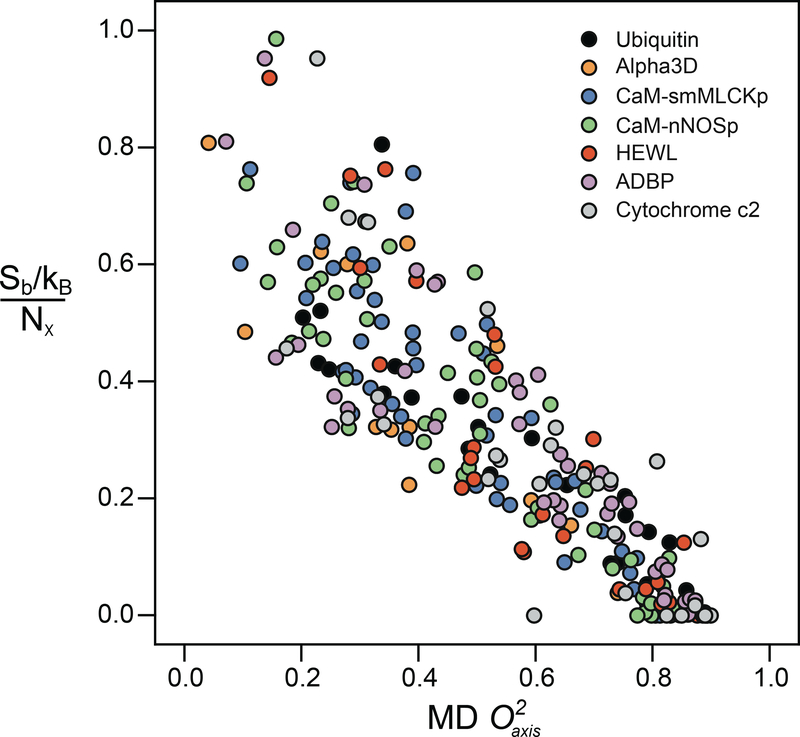
Perhaps the strongest premise of the entropy meter is the need for a quantitative linkage between the motional averaging of the methyl-group symmetry axis and the underlying conformational entropy. To examine this question, the rotamer population distributions of all the methyl-containing amino acids were calculated from the MD trajectories of each protein (42). An excellent linear correlation was seen between the rotamer entropy (S_b) of each methyl-containing amino acid normalized by the number of side-chain torsion angles (N_χ) in that residue and the corresponding methyl side-chain order parameters calculated from the MD simulations (Figure 2). Local normalization by the number of torsion angles (soft modes) has been recommended by earlier simulations (57, 58). Importantly, it turns out that this linearity extends globally when the coupling between side chains is weak (95). Moreover, as might be expected, the distributions from the different proteins overlay one another, strongly suggesting that the empirical scaling of motion to the corresponding entropy should be universal.

Figure 2.

Correlation of the methyl rotamer entropy versus$O_{\text{axis}}^{\text{2}}$ from molecular dynamics (MD) simulations. Normalized entropy S_b/Nχ given for every side-chain methyl probe. The correlation was highly linear (R² of 0.77) with a slope of −0.88 ± 0.03 and an intercept of 0.78 ± 0.02. The different proteins are color coded as indicated in the inset key. Modified from Reference 42, copyright American Chemical Society. Abbreviations: ADBP, porcine procarboxypeptidase B; CaM, calmodulin; k_B, Boltzmann constant; HEWL, hen egg white lysozyme; nNOSp, calmodulin-binding domain of neuronal nitric oxide synthase; Nχ, total number of side-chain torsion angles; S_b, rotamer entropy; smMLCKp, calmodulin binding domain of the smooth muscle myosin light chain kinase.

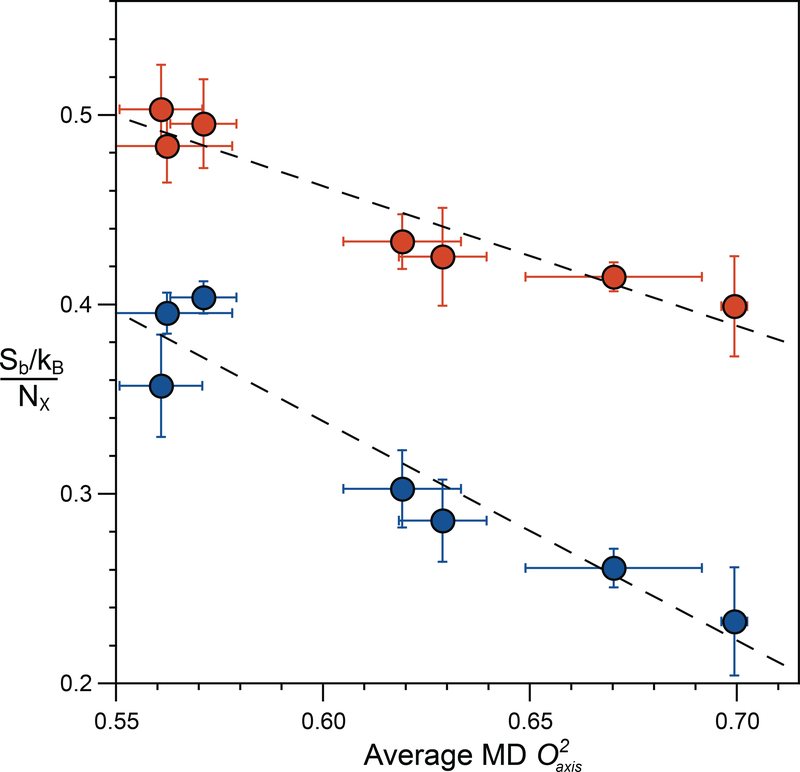
A second critical assumption in the construction of the entropy meter is that the motion of the methyl group is sufficiently coupled to its surroundings to faithfully report on local disorder (74). This central issue was explored by comparing the rotamer entropy from the probability distributions for all side-chain torsion angles to the dynamical proxy (i.e., methyl-group motion). An excellent linear correlation was found indicating that methyl motions (disorder) do indeed report quantitatively on the disorder of surrounding amino acid side chains (Figure 3). The final factor is the extent to which motions of individual side chains are coupled and to what extent this coupling reduces the total internal conformational entropy. Again, MD simulations provide the insight that this coupling primarily manifests as a linear scaling, reducing the side-chain entropy by a constant factor of about 17% (42).

Figure 3.

The dynamic proxy of methyl groups is an excellent reporter of both methyl and total side-chain rotameric entropy. (Blue circles) The normalized methyl rotameric entropy for each protein is calculated as the summation of S_b for individual methyl-bearing amino acids divided by the number of associated rotamer angles (Nχ). (Red circles) The total rotameric entropy for each protein is calculated as the summation of S_b for all residues and is normalized by the respective total number of rotamer angles (Nχ). The average methyl $O_{\text{axis}}^{\text{2}}$parameter for all methyl-bearing residues, including Ala, is that obtained from MD simulations. A very high linear correlation is observed for both methyl side-chain rotamer entropy (slope = −1.16 ± 0.17, R² = 0.90) and total rotamer entropy (slope = −0.74 ± 0.10, R² = 0.91), indicating that methyl-group motion is a good predictor of total side-chain conformational entropy. Adapted from Reference 43.

Experimental Calibration of the Entropy Meter

We have recently experimentally tested the hypothesis that the entropy meter is universally applicable—in other words, that the scaling (s_d) between changes in fast motion and changes in conformational entropy is constant (7). The 28 protein–ligand complexes used for the calibration span a broad range of binding affinities (K_d: 10⁻⁴ to 10⁻¹⁰ M) and ligand types, including nucleic acids, enzyme substrates and cofactors, carbohydrates, peptides, and proteins.

Usually, the contribution of solvent entropy to the thermodynamics of an equilibrium is calculated using empirically determined coefficients relating changes in accessible polar and apolar surface area (32). These coefficients have been derived with various assumptions about the nature of conformational entropy in the folded state. It is important to note that significant heat capacity changes accompany hydration of apolar and polar groups. This temperature variation is well described experimentally by the relations a₁ = dC_p1 ln(T / 385 K) (3) and a₂ = dC_p2 ln(T / 176 K) (71), where dC_p1 and dC_p2 are the hydration heat capacities per unit area of apolar and polar surface, respectively. The unprecedented extent of the dynamical data set used (7) allowed us to fit directly for these solvent entropy coefficients. In addition, the intercept of Equation 5 contains the loss in rotational–translational entropy upon formation of the complex ΔG_r–t. We therefore recast Equation 5 as

$$\begin{gathered} \mathrm{\Delta }{S}_{\text{total}}=s_d\left[\left(N_{\chi }^{\text{protein}}\mathrm{\Delta }{\langle O_{\text{axis}}^{\text{2}}\rangle }^{\text{protein}}\right)+\left(N_{\chi }^{\text{ligand}}\mathrm{\Delta }{\langle O_{\text{axis}}^2\rangle }^{\text{ligand}}\right)\right] \\ +\left[\text{d}{C}_{p_1}\ln (T/385K)\mathrm{\Delta }{\text{ASA}}_{\text{apolar}}+\text{d}{C}_{p_2}\ln (T/176K)\mathrm{\Delta }{\text{ASA}}_{\text{polar}}\right]+\left[\mathrm{\Delta }{S}_{\text{r}–\text{t}}+\mathrm{\Delta }{S}_{\text{other}}\right] \end{gathered}$$ 6.

Equation 6 is written for the situation of having a ligand with soft torsional modes and would be modified for a rigid molecule. Violations of the few assumptions used to construct the calibration line for the entropy meter will tend to result in deviation from linearity. These include the assumptions that methyl groups are sufficiently numerous, are well distributed, and are adequately coupled to non-methyl-bearing amino acids such that their motions provide comprehensive coverage of internal motion in the protein. As discussed above, these assumptions are strongly supported by simulation (42).

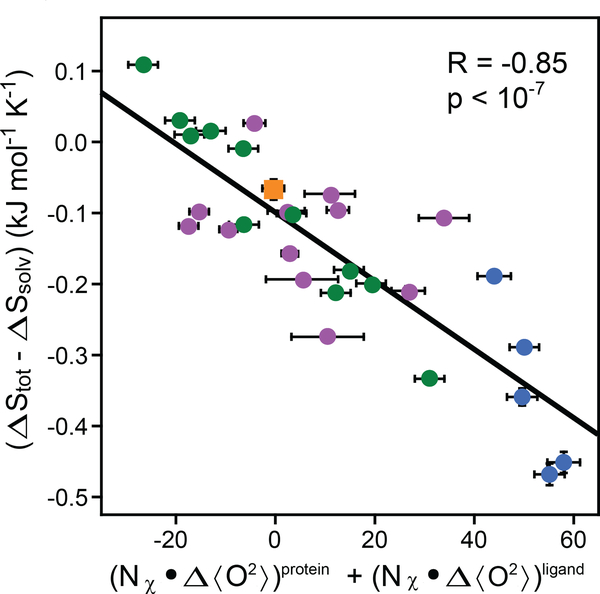
Fitting of Equation 6 to the database of 28 protein complexes gives an R of 0.85 and p of ~10⁻⁸. The fitted values of s_d, ΔS_r–t, dC_p1, and dC_p2 are listed in Table 1. The parameter of central interest (s_d) is well determined to be –4.8 ± 0.5 J mol⁻¹ K⁻¹ and provides for the first time a robust and apparently general means to experimentally obtain the change in conformational entropy upon protein–ligand association. It is important to appreciate that the effects of correlated motion noted above in the context of MD simulations are inherently taken care of by the experimental calibration of s_d. It is also notable that, in this treatment, we have ignored the contribution to the binding entropy from the backbone of the protein. Recent simulations suggest that the binding of ligands by structured proteins will involve little contribution from the polypeptide chain (95). Unfortunately, only six of the complexes used have sufficiently characterized dynamics to allow backbone motion be included in our analysis. However, when analyzed in a similar fashion, this subset indicates that the contribution by the backbone to the binding entropy is less than 5% (7).

Table 1.

Calibration of the dynamical proxy for conformational entropy^a

Parameter	Value
Ordinate intercept (ΔSr–t + ΔSother)	−(0.10 ± 0.01) × 10−1 kJ mol−1 K−1
Slope (sd)	−(4.8 ± 0.5) × 10−3 kJ mol−1 K−1
Hydration heat capacity—apolar (dCp1)	+(37 ± 11) × 10−5 kJ mol−1 K−1 Å−2
Hydration heat capacity—polar (dCp2)	−(5.2 ± 1.0) × 10−5 kJ mol−1 K−1 Å−2
Solvent entropy coefficient—apolar (a1) at 298 K	−(9.6 ± 2.9) × 10−5 kJ mol−1 K−1 Å−2
Solvent entropy coefficient—polar (a2) at 298 K	−(2.7 ± 0.5) × 10−5 kJ mol−1 K−1 Å−2

^aDerived from a global fit of nuclear magnetic resonance–derived dynamical data. Precision determined by Monte Carlo sampling. See Reference 7 for details. a₁ = dC_p1 ln(T / 385 K) (3) and a₂ = dC_p2 ln(T / 176 K) (71), where dC_p1 and dC_p2 are the hydration heat capacities per unit area of apolar and polar surface, respectively. Substituting these relations for a₁ and a₂ into Equation 6, the parameters dC_p1, dC_p2, ΔS_r–t, and s_d are obtained from a global fit using the experimental binding entropy changes, order parameter changes, and temperatures.

ENTROPY IN MOLECULAR RECOGNITION BY PROTEINS

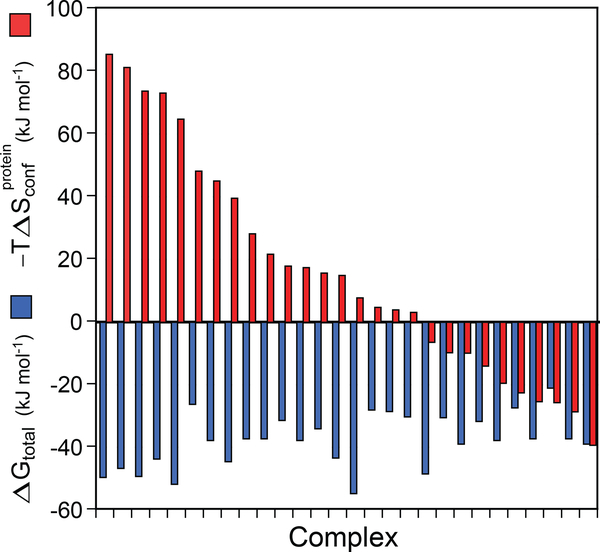
Utilizing the determined value of s_d, we can establish that the contribution of conformational entropy to molecular recognition by proteins is quite variable among complexes. Conformational entropy can highly disfavor, have no effect on, or strongly favor association and is often a large determinant of the thermodynamics of binding (Figure 5). The structural origins of this behavior remain a mystery, but the sheer variation will undoubtedly motivate many future investigations.

Figure 5.

Contribution of protein conformational entropy to the free energy of ligand binding to proteins. The broad range of contributions available to proteins for high-affinity binding of ligands is illustrated by the protein–ligand complexes used to calibrate the entropy meter (Figure 4). The 28 protein–ligand complexes are arranged in descending order of the contribution of conformational entropy (red bars) to the total free energy of binding (blue bars). Conformational entropy contributed by the response of amino acid side chains to the binding of a ligand can vary from highly unfavorable to negligible to highly favorable. In some cases, conformational entropy is essential for high-affinity binding. The structural origins of the variable utilization of conformational entropy in molecular recognition are unknown. In most cases, the change in solvent entropy remains a dominant contribution. Note that −TΔS_r–t, ΔS_ligand, and ΔS_solvent are not shown here. Adapted from Reference 7

Other entropic contributions to protein–ligand associations are also made accessible. The entropy meter represented by Equation 6 allows that there may be other unknown sources of entropy. These might include, for example, (de)protonation events associated with binding (50). Clearly, if ΔS_other is both significant and varies between complexes or if ΔS_r–t varies greatly between complexes, then the linearity of Equation 6 will be degraded. The observed linear correlation strongly suggests that neither of these occur. In this case, the ordinate intercept represents the loss in rotational–translational entropy (ΔS_r–t) upon formation of high-affinity complexes. The change in rotational–translational entropy accompanying formation of complexes involving proteins has been the subject of extensive theoretical debate (e.g., 6, 18, 23, 24, 29, 31, 69, 89, 97, 101, 117) but, like conformational entropy, has largely resisted experimental definition. From the fitted ordinate intercept in Figure 4, the apparent ΔS_r–t is found to be ~0.10 ± 0.01 kJ mol⁻¹ K⁻¹, which is somewhat higher than that recently obtained through MD simulations (29). Because it is a freely fitted parameter, the rotational–translational entropy term serves as an internal control for the veracity of the entropy meter, and it is satisfying that the obtained value is largely in agreement with modern treatments. It is interesting to note that the dynamic response of a weak complex (K_d ≈ 4 mmol) between serotonin and a mutant histamine-binding protein binary complex with histamine falls near the calibration line (Figure 4). This suggests that even for weak-associating ligands, the loss of translational–rotational entropy remains close to that obtained for the higher-affinity complexes used in the calibration (7).

Figure 4.

Calibration of the dynamical proxy for protein conformational entropy. Fitting of Equation 6 to data provided by 28 protein–ligand associations. The difference in the measured total binding entropy and calculated solvent entropy is plotted against the change in the dynamical proxy upon binding of ligands. The dynamical proxy is the average Lipari-Szabo squared generalized order parameter of methyl-group symmetry axes (<$O_{\text{axis}}^{\text{2}}$>). The fitted slope (s_d) of −4.8 ± 0.5 J mol⁻¹ K⁻¹ allows for the conversion between measured changes in methyl-bearing side-chain motion and the associated conformational entropy. Other parameters of the entropy meter are summarized in Table 1. The CaM (calmodulin) and CAP (calmodulin-associated peptide) data subsets are shown in blue and green, respectively. Purple circles represent other binary complexes, as summarized elsewhere (7). The orange square represents the HBP(D24R)–histamine binary complex binding to serotonin, which has a dissociation constant in the millimolar range and was not used in the calibration. See text for details. Adapted from Reference 7.

Finally, the contribution of solvent entropy to processes involving proteins has usually been obtained from empirical relationships related to changes in solvent-accessible surface area. Underlying such approaches have been strong assumptions regarding conformational entropy in the folded state (32), which are not required by the entropy meter. Simultaneous fitting of the heat capacity coefficients in Equation 6 indicate that the burial of apolar and polar surfaces upon binding both produce a positive (favorable) change in solvent entropy. This is because hydration of polar groups, like that of apolar groups, has a negative entropy of hydration, in agreement with a wide range of thermodynamic data on solute, ion, and protein hydration (4, 71, 73). The surface area coefficients for apolar (a₁) and polar (a₂) desolvation entropy at 298 K are found to be −0.096 ± 0.029 J mol⁻¹ K⁻¹ Å⁻² and −0.027 ± 0.005 J K⁻¹ Å⁻², respectively (Table 1). The corresponding hydration heat capacity surface area coefficients are also listed in Table 1. Burial of hydrophobic area stabilizes the complex through the usual hydrophobic effect. Concomitantly, burial of polar area also provides a stabilizing entropic contribution to the complex via release of its hydrating water into the bulk, less ordered state. The coefficients are smaller than those obtained previously (26, 32) and, in part, reflect the impact of inadequately assessing the contribution of residual side-chain entropy in the folded state of proteins in prior work. Also interesting to note is that the smaller magnitude also likely arises from a difference in the nature of solvation. Previously, solvation entropies have been estimated from group transfers between water and organic solvents or global unfolding of globular proteins (e.g., 3, 26, 32, 71, 85, 86, 96), which involves complete solvation of side chains. In contrast, the studies here focus on the (de)solvation of more extended protein surfaces and may reflect differences in length scale, detailed geometry, and inherent dynamics of protein surfaces (e.g., 9, 94, 110). This remains to be further explored.

LOOKING FORWARD

To see what the contribution of conformational entropy to ligand binding by proteins might be, we can turn to results from the proteins used to calibrate the entropy meter (Figure 5). This group of protein complexes shows that conformational entropy contributed by the response of amino acid side chains to the binding of a ligand can vary from highly unfavorable to negligible to highly favorable. In some cases, conformational entropy is essential for high-affinity binding. Indeed, it is important to note that, without the favorable contribution by conformational entropy, one quarter of these complexes would be reduced to biologically meaningless affinities. The structural origin of the variable utilization of conformational entropy in molecular recognition remains unknown and will undoubtedly be the focus of future investigation. The entropy meter will allow investigation of the role of entropy in context, including transition state and Michaelis complexes in enzymology, extremely high-affinity binding interactions such as those seen in immunology, and the underlying mechanisms of allostery guided by entropic forces (11, 28, 79, 112).

SUMMARY POINTS.

1. Solution nuclear magnetic resonance (NMR) relaxation methods can provide extensive site-resolved measurement of internal dynamics of proteins, which can be interpreted in a robust, relatively model-free way using the Lipari-Szabo formulation.

2. The dynamical proxy for protein conformational entropy provided by NMR relaxation has been empirically calibrated. The resulting entropy meter allows the estimation of changes in conformational entropy upon a change in state (e.g., the binding of a ligand).

3. The entropy meter has revealed an unexpectedly broad range of responses by proteins to the binding of high-affinity ligands.

FUTURE ISSUES.

1. How can the entropy meter be expanded to incorporate slow timescales and additional probes, such as aromatic and polar side chains?

2. What strategies need to be developed for molecular dynamics simulations to reach quantitative agreement with nuclear magnetic resonance relaxation?

3. How does conformational entropy participate in very high- and low-affinity interactions?

4. What is the nature of protein surface hydration and its contribution to the thermodynamics of protein–ligand interactions?

5. Does conformational entropy participate in the activation entropy of enzyme catalysis or modulate the affinities of various Michaelis complexes?

6. How has conformational entropy contributed to the evolution of protein structure–function relationships?

TERMS AND DEFINITIONS

Binding entropy

the change in total system entropy upon the formation of a protein–ligand complex

Configurational entropy

the distribution of states accessed by both soft modes (torsions) and hard modes (vibrations) of motion

Conformational entropy

entropy largely associated with distribution of rotameric (soft modes) states of amino acid side chains

Dynamical proxy

the use of motion between states to implicitly count the states visited

Entropy meter

the empirically calibrated conversion of the dynamical proxy into a quantitative statement about conformational entropy

Hard modes

the motions (vibrations) involving atoms in fixed covalent geometry (e.g., bonds, germinal angles)

Nuclear magnetic resonance relaxation

the process of returning nonequilibrium distribution of spin states to equilibrium; intimately related to motion

Rotational–translational entropy

the entropy associated with the rotational and translational freedom that is lost when a protein and ligand combine to form a complex

Soft modes

the motions associated with torsion angles connecting different rotameric states

Solvent entropy

change in the entropy of water due to release from the protein and ligand surfaces to form a dry intermolecular interface