Timing of fungal spore release dictates survival during atmospheric transport

Significance

Fungi move between habitats by dispersing small spores through the atmosphere. We ask what causes some species to release spores at a specific time every day versus irregularly. We find that timing of spore release dictates how long spores remain in the atmosphere before returning to the ground: Spores released at night are likely to travel for hours while spores released during the day may linger for days. Drivers are stronger in lower, warmer latitudes. Because spores in the open atmosphere are likely to die from prolonged exposure to light and air, the timing of spore release will impact survival. We have discovered a constraint likely to shape observed patterns of spore liberation.

Abstract

Fungi disperse spores to move across landscapes and spore liberation takes different patterns. Many species release spores intermittently; others release spores at specific times of day. Despite intriguing evidence of periodicity, why (and if) the timing of spore release would matter to a fungus remains an open question. Here we use state-of-the-art numerical simulations of atmospheric transport and meteorological data to follow the trajectory of many spores in the atmosphere at different times of day, seasons, and locations across North America. While individual spores follow unpredictable trajectories due to turbulence, in the aggregate patterns emerge: Statistically, spores released during the day fly for several days, whereas spores released at night return to ground within a few hours. Differences are caused by intense turbulence during the day and weak turbulence at night. The pattern is widespread but its reliability varies; for example, day/night patterns are stronger in southern regions. Results provide testable hypotheses explaining both intermittent and regular patterns of spore release as strategies to maximize spore survival in the air. Species with short-lived spores reproducing where there is strong turbulence during the day, for example in Mexico, maximize survival by releasing spores at night. Where cycles are weak, for example in Canada during fall, there is no benefit to releasing spores at the same time every day. Our data challenge the perception of fungal dispersal as risky, wasteful, and beyond control of individuals; our data suggest the timing of spore liberation may be finely tuned to maximize fitness during atmospheric transport.

A careful reading of the natural history of fungal spore liberation reveals nontrivial patterns. Spores may be released at specific times of day, perhaps driven by an internal clock, or may be released irregularly, perhaps triggered by local fluctuations in the environment. Some fungi display regular, nearly circadian rhythms (Table 1). Spores of powdery mildews are often released at midday (ref. 1 and references therein), while other fungi release spores at night or in the early morning, e.g., the plant pathogens Mycosphaerella spp. (causing leaf blotch in wheat and black leaf streak in bananas) (2–4), Giberella zeae (causing rots in cereals) (5, 6), and Venturia inequalis (the apple scab) (7, 8). Tropical fungi also appear to release spores at night (9, 10). Or patterns may be more complex: The causal agent of blackleg, Leptosphaeria maculans, seems to follow different diurnal rhythms in different regions and seasons, with most spores liberated in the morning in England (11) or at night in Canada (12) or in early afternoon in Western Australia (13). In other studies of the same species in Western Australia, spores appear to be released intermittently, regardless of location or month (14, 15).

Table 1.

Data on spore release patterns compiled from the literature

Species	Peak release time	Location	Season	Spore type	Source
Alternaria spp.	Noon or later/detached by wind	n/a	n/a	Conidia	(ref. 20, p. 138)
Amanita muscaria var. alba	Night	Avon, CT	September to October	Basidiospores	(88)
Cladosporium spp.	Early afternoon	Harpenden, UK	June to July	Conidia	(89)
Claviceps purpurea	Early afternoon	Herminston, OR	May to July	Ascospores	(90)
Coprinus spp.	0500 to 0600	Havana, Cuba	Entire year	Basidiospores	(91)
Erysiphe spp. (and other powdery mildews)	Midmorning to early afternoon	Various	Various	Conidia	(ref. 1, p. 32 and cited literature)
Giberella zeae (Fusarium graminearum)	Peak usually before midnight	Quebec, Canada	June	Ascospores	(5)
	Night: 1900 to 0700	Blacksburg, VA	April to June		(6)
	Peak at 2100	Manitoba, Canada	July to August		(92)
Ganoderma boninense	Early evening	Lima Puluh, Indonesia	n/a	Basidiospores	(93)
Helminthosporium maydis (now Bipolaris maydis)	Early morning/detached by wind	Mt. Carmel, CT	July	Conidia	(18, 19)
Hymenoscyphus pseudoalbidus	0600 to 0800	Ås, Norway	July to August	Ascospores	(94)
Microcyclus ulei	0800 to 1500	Pointe Combi, French Guiana	Entire year	Ascospores	(95)
	1000 to 1600			Conidia
Mycosphaerella fijiensis	0530 to 0830, abrupt cutoff at 0830	Turrialba, Costa Rica	May to August	Ascospores and conidia	(3)
	Maximum at 0600	Kua’i, HI and Nausori, Fiji	June to March	Ascospores	(2)
Mycosphaerella graminicola	After rain	Horsham, Australia	March to November	Ascospores	(58)
Mycosphaerella pinodes	1700 to 0400	Manitoba, Canada	June	Ascospores and pycnidiospores	(4)
Peridiopsora mori	1200 to 1400	Berhampore, India	October to November	Basidiospores	(96)
Puccinia psidii	Night/early morning	Viçosa, Brazil	July to November	Urediniospores	(21)
Sclerotinia sclerotiorum	1200	Harpenden, UK	July	Ascospores	(97)
Tropical fungi	Several hours before sunrise	Manaus, Brazil	Wet season	n/a	(10)
	Nocturnal	Cape Tribulation, Australia	Early rainy season	n/a	(9)
Rhizoctonia solani (Thanatephorus cucumeris)	Midnight to dawn	Hokkaido, Japan	August	Basidiospores	(61)
Leptosphaeria maculans	Early morning	Rothemsted, UK	October to November	Ascospores	(11)
	2100 to 0400	Manitoba, Canada	July	Ascospores and pycnidiospores	(12)
	Afternoon	Western Australia	June to August	Ascospores	(13)
	Intermittent	Western Australia	n/a	n/a	(14, 15)
Polyporus albellus	Before midnight	Manhattan, KS	November	Basidiospores	(98)
Venturia inaequalis	Day, rain is a driver	Ferrara, Italy	March to May	Ascospores	(7)
		Fletcher, NC	April to May		(8)

n/a, not available.

Many authors have attempted to connect the diversity of spore liberation patterns to specific environmental cues by testing for correlations between liberation and local temperature, humidity and wind speed, etc. (reviewed in refs. 1, 16, and 17). Correlations are sometimes found; for example, asexual spores of Helminthosporium maydis (now Bipolaris maydis) and Alternaria spp. are detached from supporting structures by intense wind gusts (e.g., refs. 18–20). Often there are no obvious correlations. Despite a wealth of data describing different diurnal or nocturnal patterns of spore liberation and a nascent awareness of their significance for spore dispersal (21–23) the drivers of observed patterns remain obscure (13, 16).

Dispersal through the atmosphere is assumed to be both common and dangerous. Cellular material makes up about 25% of atmospheric particulate and 3 to 11% by weight (24, 25), with crucial implications for human health, agriculture, and climate. But only a small fraction of the estimated $\sim 10^{21}$ cells riding the atmosphere annually survive the journey. The main threats limiting the lifespan of spores are exposure to UV light and harsh temperatures and humidities (26, 27).

Research on atmospheric dispersal often focuses on the reach of a spore; in other words, biologists pay attention to distances traveled and seek to understand how far a spore will move before settling. Long-distance dispersal remains a particular concern (22, 28–30). But a spore that dies in the atmosphere will have zero fitness, even if it ultimately settles back to the ground, and an equally important facet of successful dispersal is survival. Spores in the atmosphere may survive for days or weeks or possibly longer (31–34). Careful data tracking the lifetimes of individual spores in the air are lacking; spores are not easy to observe or manipulate in nature. But laboratory experiments suggest the spores of many other species are in fact quite sensitive to sunlight. The mean half-life of the thin-walled basidiospores of wood decay fungi is 1.5 h after exposure to simulated sunlight (26). Twelve hours of natural sunlight kill 99% of the conidia of Botrytis cinerea (35). Rhizoctonia solani basidiospores appear unable to tolerate more than 60 min of exposure (36) (Table 2).

Table 2.

Data on spore longevity compiled from the literature

Species	Longevity	Spore type	Source
Alternaria macrospora	4 d in natural sunlight kills >95% individual spores (30% of spore aggregates)	Conidia	(35)
Aspergillus niger	12 h in natural sunlight kills over 85% individual spores (mimimal impact on spore aggregates)	Conidia	(35)
Mycosphaerella pinodes	Two 12-h exposures to natural sunlight kills over 90% individual spores	Pycnidiospores	(35)
Botrytis cinerea	12 h in natural sunlight kills 99% of individual spores (and 50% of spore aggregates)	Conidia	(35)
Mycosphaerella graminicola	24 h in sunlight kills over 90% spores; 1 to 2 wk viability in shade or darkness	Ascospores	(58)
Mycosphaerella fijiensis	Exposure to simulated sunlight for >6 h kills spores	Ascospores	(62)
Puccinia graminis	About 20 h exposure to sunlight results in greater than 90% mortality	Urediniospores	(99)
Puccinia striiformis	6 to 10 h exposure to sunlight results in greater than 90% mortality	Urediniospores	(99)
Rhizoctonia solani	60 min in direct sunlight results in death	Basidiospores	(36)
Sclerotinia sclerotiorum	Field experiment: steep mortality within first 2 to 7 d, depending on temperature	Ascospores	(100)
Sirococcus clavigignenti-juglandacearum	Field experiments: 2 to 3 h decreased viability to less than 10% in warm days; greatest survival in any experiment “35% after 8 h on a cool, rainy day with overcast skies”	Conidia	(101)
Wood decay fungi (multiple species)	4 h in simulated sunlight causes germinability to drop to <20% of maximum	Basidiospores	(26)

While a spore must settle back to the ground before it dies from exposure, turbulence makes the duration of a spore’s journey in the atmosphere inherently unpredictable: Two identical spores released from a single sporocarp may take radically different paths (37). But the average flight time for a group of spores released simultaneously from the same location may follow a specific pattern, which is widely studied in the context of aerosol science (and named residence time or flight time; e.g., refs. 38 and 39). We use principles taken from atmospheric science to model spore flight time. The underlying dynamics are well understood: The flight time of large aerosols (diameter 5 to 20 $\mathrm{\mu }$m, similar to a typical fungal spore) results from a balance between two opposing forces: gravity causes particles to sediment downward, and turbulence keeps them aloft (38, 39). Hence residence times for larger particles are shorter (38, 40, 41). To facilitate quantitative models, aerosol science often assumes that the dynamics have reached equilibrium, for example assuming particles take off from a large area consistently over time. But this assumption cannot hold for fungi, which are discrete organisms distributed in irregular patches, often reproducing at one or a few time points. While a recent model (42) considers particles released at one time in the idealized case of a vertically infinite neutral atmosphere (where the intensity of turbulence increases linearly with altitude and does not change in time), it cannot capture how flight times vary with geography and season. More realistic analyses of spore flight time considering variations of the state of the atmosphere in space and time require massive numerical simulations using meteorological data.

By combining state-of-the-art numerical simulations of atmospheric particle transport drawn from real weather data with simplified models of atmospheric turbulence, and by explicitly considering spore lifespan, we discover that the timing of spore liberation dramatically influences the reach of living spores. Manipulating the timing of spore liberation will dramatically influence fitness. We find the following: 1) The average duration of a spore’s flight depends on when it is released. 2) By explicitly defining fitness as the fraction of spores that return to ground while alive (within their lifetimes) we discover that patterns of spore liberation shape fitness. 3) Turbulence dominates vertical transport and thus dictates flight time in realistic conditions. 4) Turbulence is cyclical and typically stronger during the day versus at night. But the strength and reliability of its diurnal cycle vary with geography and season. 5) When and where the diurnal cycle is strong, releasing spores at specific times of day will allow a fungus to shape the duration of a spore’s journey through the atmosphere. But if the cyclical pattern of turbulence is unreliable, a direct measure of the local intensity of turbulence will be a better guide than time of day to shaping flight time and maximizing fitness. Results provide a set of testable hypotheses to understand observed patterns of spore release: 1) A regular, rhythmic release of spores is beneficial for species living in regions where the atmosphere cycles regularly. 2) For these species, short-lived spores should be released at night, while long-lived spores can be released during the day. 3) Intermittent patterns of spore release may emerge as an adaptation to an environment where the diurnal cycle of turbulence is disrupted.

Atmospheric transport is assumed to be unpredictable, and fungi are assumed to have little control over dispersal, but spore discharge itself appears finely tuned to maximize individual fitness (43–48). Our results demonstrate that although after leaving a sporocarp individual spores follow unpredictable trajectories, a fungus may still maximize survival of its progeny in the atmosphere by strategizing the timing of spore release.

Results

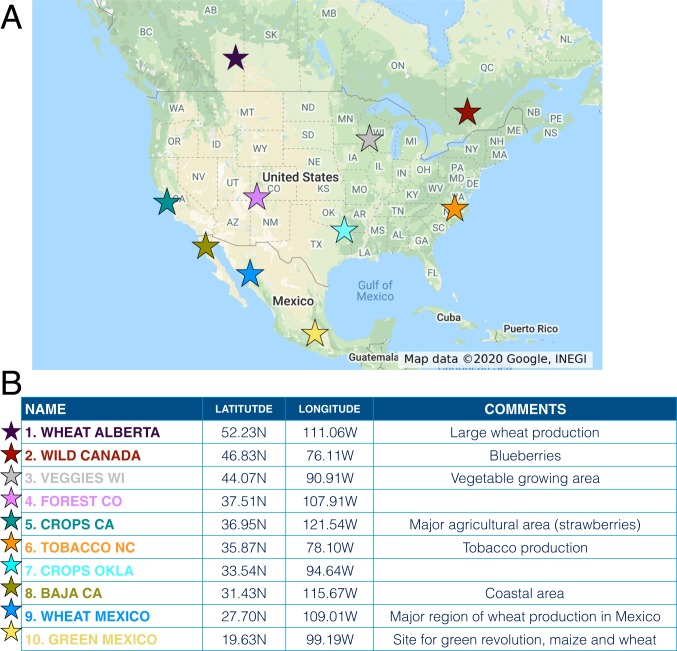
The duration of a spore’s flight in the atmosphere can be controlled by the timing of its release. To determine the statistics of spore flight time, we follow the trajectories of many spores released instantaneously from different sites. We model an array of 10 locations in North America (Fig. 1), releasing groups of 100,000 spores from each site from the first layer of the atmosphere closest to the soil, running independent simulations every 3 h over the entire course of 4 different months (January, April, July, and October 2014), resulting in a total of 9,600 numerical simulations. Our simulations track the Lagrangian trajectories of spores in the atmosphere using meteorological data publicly available from the National Oceanic and Atmospheric Administration (NOAA) and the Hybrid Single-Particle Lagrangian Integrated Trajectory (HYSPLIT) model (49–53); see Materials and Methods and SI Appendix. In essence, we are using HYSPLIT to model the movement of spores in the real weather recorded along their path in the atmosphere in 2014. Particles are modeled as tracers carried across the atmosphere both vertically and horizontally, with a specific gravitational settling velocity. Spores are carried by the large-scale wind field, coming from meteorological datasets, and are additionally kicked and buffeted by turbulent fluctuations. Turbulence is modeled as a correlated stochastic process akin to a simple diffusion, with an effective diffusivity (eddy diffusivity) that depends on height. To mimic dry deposition, spores remaining or returning to the first layer closest to the soil are randomly removed from the simulation and returned to the ground using a constant rate proportional to the deposition velocity. The fascinating interaction of deposition with rain (54, 55) will be analyzed elsewhere. Moreover, our simulations focus on the large-scale journey of spores traveling in the open air and do not resolve the details of release and deposition within the canopy. We record the duration of each particle’s trajectory in the atmosphere from takeoff to landing and analyze the statistics of each group of 100,000 spores. We consider deposition velocity equal to gravitational settling velocity, a reasonable assumption for large particles (38), and we set both velocities to 6 mm/s (corresponding to an equivalent sphere of radius 7 $\mathrm{\mu }$m and density equal to the density of water). We follow each group of spores for 6 wk; by then, most spores have returned to the ground. A fraction of spores, on average 16%, never return to the ground within our simulation: These spores typically escape into the stratosphere and outside of the simulated domain. The escape fraction depends on gravitational settling and affects fitness of long-lived spores but not of short-lived spores because it occurs over timescales of weeks (SI Appendix, Figs. S1–S3).

Fig. 1.

Starting locations for our series of HYSPLIT numerical simulations described in the text. (A) Map of the locations. (B) Details for each location.

Spore release at different times of the same day results in dramatic oscillations in flight time ranging from less than 1 h to several days (Fig. 2, Top row), consistent with previous results in the context of aerosol science (38). Longer flight times are observed in the summer (Fig. 2, Top row), confirming a previously observed seasonal pattern in the residence time of abiotic particles (56). While flight times depend only on the physical properties of the spore, the impact of spore travel on mortality depends on the typical lifetimes of spores, which we indicate with $\tau$. We define one aspect of fitness (57) as the fraction of spores deposited within their lifetime $\tau$, in other words, the fraction of spores reaching the ground while still alive, and indicate it with the symbol ${\chi }_{\tau }$ ($w$ is commonly used for fitness in evolutionary biology but here we reserve the symbol $w$ for velocity, as is standard in the physics literature). Different spores of the same species will live for shorter or longer lifespans in part because of the different environments each spore encounters along its path. While demographic data describing spore longevity in nature are lacking, laboratory manipulations suggest spores are sensitive to sunlight (26, 35, 36) (Table 2); a spore of, e.g., Mycosphaerella graminicola exposed to the sun may not live as long as a spore traveling at night (58). A comprehensive analysis of what shapes the survival kernel, i.e., the distribution of lifetimes across spores of the same species, is the focus of ongoing work. Here, to illustrate the effects of flight time on survival, we pick a constant lifetime $\tau =6$ h motivated by available data on survival times (Table 2) and we indicate the fitness of spores with a 6-h lifetime as ${\chi }_{6\text{h}}$. Fitness also undergoes oscillations, similar to the oscillations observed for flight time (Fig. 2, Bottom row). Note that peaks in flight time correspond to minima in fitness.

Fig. 2.

Spore survival depends on time of liberation. (Top row) Average flight time (solid lines) from liberation to deposition as a function of the time of day, $\pm$SD (shading). Eight takeoffs were simulated each day at 10 locations for the entire months of January, April, July, and October 2014. (Bottom row) Average fitness ${\chi }_{6h}$ (solid lines) $\pm$ SD (shading), defined as the fraction of spores deposited within their lifetime $\tau$: ${\chi }_{6h}={\int }_0^{\tau }p\left(t\right)dt$ with $\tau \hspace{0.17em}=$ 6 h.

The explanation for these oscillations is straightforward: Maximum flight times are on the order of several days and in these conditions most of our short-lived spores die in flight. Conversely at night flight times are shorter, on the order of hours, and therefore spore survival is maximized. Hence short-lived spores should be released at night to maximize fitness. Similar relationships hold for different choices of lifetime $\tau$, but fitness tends to flatten out for longer-lived spores, which can survive even very long flights (see SI Appendix, Fig. S2 for results with $\tau =2$ d and $\tau =2$ wk). Hence the timing of spore release only weakly affects the survival of long-lived spores, which may be released at any time of the day: Other aspects of fitness may shape their liberation patterns, for example the need to maximize dispersal range. In the aggregate our models identify demographic variables, and specifically lifespan, as a potentially underappreciated control on successful dispersal.

Flight time and fitness oscillate for different values of gravitational settling and deposition. Varying these parameters, however, shifts the oscillations up or down. Doubling deposition and settling (Fig. 3A) results in shorter flight times and therefore increases in fitness. Deposition is responsible for this variation; indeed, when deposition velocity is kept constant, fitness ${\chi }_{6\text{h}}$ is insensitive to variation in gravitational settling from 0 to 12 mm/s (SI Appendix, Fig. S3), consistent with previous results (59). The relationship between deposition velocity and flight time is described as relevant to fungal spores in an older literature (e.g., ref. 40) and is well known in the context of aerosol science (e.g., ref. 38). A substantial difference occurs when we set deposition and settling to the much larger value of 60 cm/s (corresponding to a sphere with diameter 140 $\mathrm{\mu }$m) (Fig. 3A). In this parameter range sedimentation dominates the dynamics of flight time and all spores return to ground within 6 h. This result is well understood in the context of seeds (60), but even the smallest seeds are orders of magnitude larger than fungal spores (47), and we do not consider these larger sedimentation values further but instead focus on the more typical case of spores smaller than $\sim 20\hspace{0.17em}\mathrm{\mu }$m in diameter, for which gravitational settling plays a minor role.

Fig. 3.

Fitness depends only weakly on deposition efficiency, on large-scale wind, and on the details used to model turbulence: Turbulence intensity robustly dictates fitness. In all panels, gray dotted lines represent fitness averaged across all simulations performed in the same month, as a function of the timing of spore release with $\tau =$ 6 h, computed from the full HYSPLIT simulations described in the text. Gray shading represents $\pm$SD of fitness over all simulations. Solid colored lines and colored shading represent mean fitness $\pm$SD, calculated from (A) HYSPLIT simulations where deposition velocity and gravitational settling are doubled (set to 12 mm/s), (B) simplified HYSPLIT simulations without large-scale meteorological winds, (C) HYSPLIT simulations with an eddy diffusivity that varies in time but not in z for the entire troposphere, and (D) one-dimensional finite-volume simulations implementing the eddy diffusivity model only (no gravitational settling, no large-scale meteorological winds, no horizontal displacement). We represent the entire month—rather than the average day—to illustrate that this model that implements only turbulence reproduces nearly exactly the full model. Dashed gray line in A represents fitness for spores with gravitational settling and deposition velocities both set to 60 cm/s. All simulations start from the same location (10) in Mexico (Fig. 1).

In fact, the flight times and fitnesses of spores depend mainly on turbulence. Flight time and fitness are only weakly sensitive to the wind experienced by spores during travel (Fig. 3B) because typically, turbulence dominates over vertical wind; horizontal winds do not affect the vertical dynamics either, because meteorological parameters vary slowly in space. To test the robustness of our turbulence model, we implemented two closures for subgrid fluctuations (Materials and Methods). Both closures result in the same qualitative results (SI Appendix, Fig. S4). We next tested whether the exact profile of these phenomenological expressions affects the flight time. In this test, we further simplified the HYSPLIT simulation by using a vertically uniform eddy diffusivity resulting from the average over the entire boundary layer; the results are a good match to the full numerical simulation (Fig. 3C). The overall intensity of turbulence appears to dictate fitness almost entirely. To test this hypothesis, we temporarily left the HYSPLIT framework and modeled the rate of change of spore concentration as a function of time and distance from the ground, using only the model of turbulence extracted from HYSPLIT (an Eulerian eddy diffusivity model; Materials and Methods). Fitness is well approximated by this bare bones model (Fig. 3D), confirming the intensity of turbulence as the single major parameter dictating fitness.

Observed oscillations in flight time and fitness are caused by alternations between strong turbulence during the day and weak turbulence at night. During the day the sun warms the soil, and the soil in turn warms the lowest layers of the atmosphere. Because warm air rises, it powers thermal convection and intense turbulence. Releasing spores during the day causes them to be carried into the upper layers of the atmosphere, resulting in long flights. Conversely, during the night, the absence of sunlight quickly cools the soil and hence the lowest layers of air, typically causing stable stratification of the air and weak turbulence. Spores released at night never reach high altitudes and return to the ground more rapidly.

To probe the geography of the diurnal cycle and define where it may be strongest, we extracted measures of the intensity of turbulent fluctuations from the full meteorological dataset: We use $w$ to indicate the SD of fluctuations in vertical air speed, mediated in height and computed within HYSPLIT. Larger values of $w$ correspond to greater intensities of turbulent fluctuations. In Fig. 4A we show $w$ measured from location 10 in Mexico during the first 2 wk of January. Turbulence displays regular diurnal oscillations over the entire 2 wk. To quantify the consistency of this diurnal cycle, we define an index $p_w$ as the autocorrelation of turbulence $w$ at 24 h (Fig. 4B). The index ranges from 1 for a perfectly periodic signal to 0 for an irregular or intermittent signal. We next compute $p_w$ for the entire North American continent during the months of January, April, July, and October 2014. We approximate $w$ as the convective velocity, a parameter available from the meteorological dataset and not requiring HYSPLIT computations (SI Appendix). Although the diurnal cycle is widespread, its consistency or reliability varies with geography and season (Fig. 4C).

Fig. 4.

Atmospheric turbulence undergoes a diurnal cycle that varies according to geography and season. (A) Magnitude of vertical turbulent velocity (w) during 2 wk in January in Mexico (in 2014 at location 10 in Mexico, Fig. 1), showing oscillations with period 24 h (14 peaks in 14 d). (B) The corresponding autocorrelation function $<\left(w\left(t\right)-\overline{w}\right)\left(w\left(t+t\prime \right)-\overline{w}\right)/{\sigma }_w^2>$, where $<.>$ denotes average over 10 d. We define an index $p_w$ (for periodicity) measuring the autocorrelation at $t\prime =24$ h, a measure of the reliability of the diurnal cycle. For a perfectly periodic signal $p_w=1$, whereas for an intermittent signal $p_w=0$. (C) Map of $p_w$ computed from meteorological datasets, color coded from yellow (regular) to purple (intermittent), for the entire North American continent and different seasons. (D and E) Regular oscillations of fitness ${\chi }_{6h}$ (D) and its autocorrelation $<\left({\chi }_{6h}\left(t\right)-{\overline{\chi }}_{6h}\right)\left({\chi }_{6h}\left(t+t\prime \right)-{\overline{\chi }}_{6h}\right)/{\sigma }_{\chi }^2>$ (E) calculated for the same simulations and as described for turbulence in B. The autocorrelation of ${\chi }_{6h}$ at 24 h defines the index $p_{\chi }$ for fitness, similar to the index $p_w$ for turbulence. (F) Index $p_{\chi }$ for fitness at 6 h is positively correlated to index $p_w$ for turbulence. The lower left corner corresponds to highly intermittent cases (purple diamond is location 1 in Canada in January), while the upper right corresponds to extremely regular conditions (yellow star is location 10 in Mexico in January, shown in A and D).

To confirm the diurnal cycle of turbulence as the main driver of fitness, we compute a second index $p_{\chi }$, analogous to $p_w$ but measuring the periodicity of fitness for each of our 10 starting locations during the same 4 mo. Fig. 4 D and E shows one example of fitness $\chi$ and its autocorrelation $p_{\chi }$, for the same location/weeks illustrated in Fig. 4 A and B. Next we correlate $p_w$ with $p_{\chi }$ and find a strong correlation between the periodicity of turbulence and periodicity of fitness (Fig. 4F). Because $p_{\chi }$ is strongly correlated with $p_w$, $p_w$ can be used to estimate $p_{\chi }$ directly, with no need of elaborate simulations of spore trajectories, indeed the index $p_w$ is computed directly from meteorological data. Moreover, the analysis implies that when and where turbulence is periodic $p_w\sim 1$, fitness is also periodic $p_{\chi }\sim 1$ and in these regions (marked in yellow/green in Fig. 4C) releasing spores at specific times of the day will enable fungi to control flight time and maximize fitness.

However, releasing spores at the same time every day may not always be a good strategy; if turbulence is difficult to predict, rhythmic patterns of spore release may not maximize fitness. In our pool of simulations, the weakest diurnal cycle is found in location 1, in Canada during the month of January (Fig. 5 A–D). Although January is not the typical season for sporulation, we use this simulation as an extreme example to illustrate maximum intermittency of turbulence. In this simulation, both turbulence and fitness vary irregularly from day to day and the indexes $p_w$ and $p_{\chi }$ are close to zero (purple diamond in Fig. 4F; Fig. 5 B and D). Every day is different. But even in environments where there is no periodicity, intense turbulence at liberation will cause spores to be carried into higher altitudes, increasing flight times and constraining the fitness of short-lived spores. Indeed, note negative fluctuations in fitness (troughs in Fig. 5C) often occur when turbulence is intense (peaks in Fig. 5A). To maximize fitness in intermittent environments, species may still evolve to liberate spores when turbulence is weak, but may require tools to measure turbulence directly.

Fig. 5.

Releasing spores at the same time every day is not efficient when the intensity of turbulence is intermittent. (A–D) Magnitude of vertical turbulent velocity $w$ (A), its autocorrelation function (B), fitness ${\chi }_{6h}$ (C), and its autocorrelation (D). A–D are the same as Fig. 4 A, B, D, and E, for the same 2 wk but a different location (no. 1 in Canada; Fig. 1). (E) Fitness (solid lines) $\pm$SD (shading) as a function of turbulence intensity, where all simulations are pooled together by month. (F) Difference between goodness of fit for fitness as a function of turbulence and fitness as a function of time of day, $r^2\left(w\right)-r^2\left(t\right)$, for each of the 40 simulated months. Squares correspond to the five more Northern locations (nos. 2, 4, 6, 7, 10) and circles to the five more southern locations; months are color coded as in E. Goodness of fit is defined as $r^2\left(w\right)=1-<{\left[g\left(w\right)-\chi \right]}^2>/{\sigma }_{\chi }^2$, and similarly $r^2\left(t\right)=1-<{\left[f\left(t\right)-\chi \right]}^2>/{\sigma }_{\chi }^2$, where ${\sigma }_{\chi }$ is the variance of the fitness over the test set. Note how turbulence intensity is a better predictor of fitness than time of the day for small values of $p_w$ corresponding to intermittent conditions, whereas time of the day and turbulence are nearly equally accurate in predicting fitness when the atmosphere cycles regularly between weak and intense turbulence.

To test whether measuring turbulence may be useful to time spore liberation, we compare two alternative models. In the first model, we consider fitness as a function of the time of the day (Fig. 2, Bottom row). In the second model, we consider fitness as a function of the intensity of turbulence (Fig. 5E). In both models, we use nonlinear regressions to obtain either a function $f$ that predicts fitness $\chi =f\left(t\right)$ as a function of the time of the day or a second function $g$ that predicts fitness $\chi =g\left(w\right)$ as a function of turbulence (Materials and Methods). We then compute the mean square error of each prediction. For each of our 40 simulated locations/months, we compare the goodness of fit of the two models $r^2\left(w\right)=1-<{\left[g\left(w\right)-\chi \right]}^2>/{\sigma }_{\chi }^2$ and $r^2\left(t\right)=1-<{\left[f\left(t\right)-\chi \right]}^2>/{\sigma }_{\chi }^2$. Time of day and turbulence are nearly equally accurate in predicting fitness where and when the diurnal cycle is regular ($p_w\gtrsim 0.8$; Fig. 5F), but where and when the cycle is disrupted, the intensity of turbulence predicts fitness more accurately than time of the day (Fig. 5F). In intermittent environments, spores should be liberated whenever the intensity of turbulence is low, regardless of whether it is day or night. This is especially true for our most intermittent simulation, which is an outlier (purple diamond in Fig. 5F), but it is also true for other simulations, for example Colorado in April and Wisconsin in July.

Discussion

Our results demonstrate that the time of the day when spores are released dramatically affects their fitness. Spores released during the day tend to be transported higher up in the atmosphere and return to the ground after several days. But many spores can survive only a few hours in the open atmosphere and would die before returning to the ground. Hence, we predict that to maximize survival short-lived spores should be typically launched at night. Many tropical fungi release spores preferentially at night or in the early morning (9, 10), as do pathogens including Mycosphaerella fijiensis (2, 3), and R. solani (61) (Table 1). Measures of M. fijiensis and R. solani’s survival after exposure to sunlight suggest spores’ lifetimes in the open atmosphere are in fact very short, consistent with our prediction (36, 62).

But why are some species releasing spores during the day? Our results show that fitness peaks at night for short-lived spores; however, fitness flattens out as spores are more long lived (see SI Appendix, Fig. S2 for results with $\tau =2$ d and $\tau =2$ wk). In other words, spores that are adapted to survive in the atmosphere for weeks can be released at any time of the day including when turbulence is maximum during the day. Because survival in the air is not limiting, long-lived spores may be released in conditions that maximize a different aspect of fitness, for example, distance traveled. To maximize distance traveled, these spores should be released in strong turbulent conditions, typically found during the day. Consistent with this hypothesis, asexual spores of various species including Alternaria spp. are liberated by winds in the afternoon (Table 1); Alternaria spores may also be long lived (63) [e.g., Alternaria porri spores can survive for hundreds of days (64)]. B. cinerea also appears to liberate spores predominantly during the day (65, 66); however, its conidia do not appear particularly long lived (35): This species may have evolved different adaptations to return to the ground in timely fashion.

Releasing spores at a specific time of the day modulates the expected fraction of spores surviving the journey, suggesting that fungi may tie spore liberation to an internal clock. Interestingly, spore production in species like Neurospora crassa is indeed regulated by a circadian clock (67, 68), but whether this provides any selective advantage has been hitherto unclear. Our results suggest that producing spores at certain times of the day may be instrumental to releasing them at times that maximize chances of survival.

A clock is not always a useful predictor of fitness: In cases where the atmospheric cycle is disrupted, turbulence varies irregularly, and releasing spores at the same time every day may lead to massive losses. In regions where the cycle is disrupted, short-lived spores should be released intermittently, whenever turbulence is weak, whereas long-lived spores can be released in conditions of intense turbulence. Interestingly, intermittent patterns of spore liberation are observed for many species (ref. 17 and references therein). A particularly clear correlation is observed between long-lived asexual spores and wind. Asexual spores of the species H. maydis (now B. maydis) are among those considered to be capable of withstanding atmospheric conditions experienced during continental-scale dispersal (69). Abscission of these spores occurs only when wind velocity exceeds 10 m/s (70). This is consistent with our hypothesis, because large air speed close to a substrate is usually associated to intense turbulent wind gusts. Whether other meteorological variables, e.g., temperature and humidity, are sensed by the fungi and how they dictate spore release is still poorly understood (16).

Whether a clock-based or a sensation-based strategy is more effective will depend on the environment that a species is adapted to live within. To compare these two alternative strategies, we introduced the parameter $p_w$ which distinguishes between regions with regular vs. intermittent atmospheric conditions. If patterns of spore liberation are shaped by the need to maximize spore survival in the atmosphere, species adapted to regions where the diurnal cycle is strong (where $p_w\sim 1$) may release spores at the same time every day, for example releasing short-lived spores at night. In these regions, spores may be released at the same time every day either by using time of the day as a cue or by responding to, e.g., temperature or wind speed, which will also vary regularly. But species adapted to regions with a weak diurnal cycle (where $p_w\sim 0$) will be more likely to liberate spores intermittently in response to local cues that provide information about turbulence intensity directly. The value of $p_w$ that marks the transition from clock-based to sensation-based strategies will vary from species to species, but the qualitative pattern is robust.

Globally distributed fungi may adapt to local environments by evolving different patterns of spore liberation in different parts of the world. The genetic model N. crassa would provide an ideal test of whether species can evolve different spore liberation patterns at different latitudes. It grows as far north as Alaska but also in New Mexico and Louisiana and near the equator in places like Indonesia, India, and the Caribbean. Spores are produced according to an intrinsic circadian rhythm, but whether the fungus uses different spore liberation strategies across its range is to the best of our knowledge an unasked question.

Spore dispersal is generally regarded as dangerous and fundamentally wasteful. Our results demonstrate that although fungi do lose control over individual spores, they can still maximize fitness in the atmosphere by manipulating the timing of spore release. Indeed, the timing of spore liberation dictates the fraction of spores that survive their journey in the open atmosphere. In other words, the ensemble statistics of spore flight time keep memory of the initial conditions that spores meet when they first reach the open air.

These results partially reconcile two contrasting aspects of fungal spore dispersal: microscopic optimization vs. large-scale uncertainty. On the one hand, at micrometer to centimeter scales, fungi have evolved fascinating adaptations to maximize the efficiency of the microscopic mechanism of discharge (reviewed in ref. 48). The ascomycetes, an enormously large and diverse phylum, fire sexual spores from a pressurized cell finely tuned to minimize dissipation (43–47). The basidiomycetes, a similarly diverse phylum, eject spores using a surface tension catapult and achieve precise control of spore range immediately after discharge (71–77). These adaptations suggest spore dispersal is under considerable selective pressure. But optimization during spore discharge appears a stark contrast to the fact that, once spores reach dispersive airflows, their fate is dictated by a series of stochastic events and appears entirely out of control of any individual parent. Fungi may acknowledge uncertainty by producing extraordinarily large numbers of propagules; fungal migration appears wasteful and fundamentally different from the ordered migration of mammals (78). But fungi may also use their exquisite control of discharge to release spores when the chances of spores’ survival in the atmosphere are greatest. Our study points to a previously unsuspected connection between patterns of diurnal or nocturnal release and longevity. But release and longevity are rarely considered simultaneously. There is a great need for data, and these data may confirm fungal movements through the atmosphere as less chaotic than they appear.

Materials and Methods

Lagrangian Simulations with Meteorological Data Using HYSPLIT.

To compute the statistics of flight times, we follow many particles released from a given location at different times using the HYSPLIT model (79), an open source code developed at the Air Resource Laboratory of the NOAA (ARL-NOAA) in the United States. We modeled spores as passive tracers with an additional gravitational settling velocity. Spores are transported by the wind, whose velocity is obtained from meteorological datasets on a large-scale grid with resolution 32 km, and turbulence on smaller scales is modeled as a correlated stochastic process, so spore trajectories can be computed through a Langevin equation

$$\frac{d\mathbf{P}\left(t\right)}{dt}={\mathbf{V}}_{\text{meteo}}\left[\mathbf{P}\left(t\right),t\right]+\mathbf{V}\prime \left[\mathbf{P}\left(t\right),t\right]+{\mathbf{V}}_G,$$ [1]

where $\mathbf{P}$ is the three-dimensional instantaneous location of a spore, ${\mathbf{V}}_{\text{meteo}}$ is the large-scale wind velocity from the North American Regional Reanalyses (NARR) (80), $\mathbf{V}\prime$ is a realization of the stochastic turbulent fluctuation (81), and ${\mathbf{V}}_G$ is the gravitational settling velocity. NARR is an extended dataset of meteorological variables on a regular grid covering the whole North American continent resulting from a matching procedure between outputs of numerical models and sparse observations of many atmospheric variables. NARR data are given on a Lambert conformal grid with 309 × 237 horizontal points and 24 levels on a vertical pressure-sigma coordinates system. The nominal horizontal resolution is 32 km. Starting from 1979 to today the state of the atmosphere is available at a time resolution of 3 h. The variance of turbulent fluctuations in the vertical direction depends on height and is modeled with semiempirical expressions that vary with the state of the atmosphere, i.e., stable vs. unstable (see SI Appendix for details) (82, 83). The specific choice for the closure as well as the dependence on altitude only weakly affects fitness (SI Appendix).

Spores settle with a constant downward speed or gravitational settling velocity, $V_G$. Fitness at 6 h is insensitive to $V_G$ for typical spores, $V_G\lesssim 12$ mm/s (SI Appendix, Fig. S3). As a reference, this value of gravitational settling velocity corresponds to a sphere with the density of water and diameter 20 $\mathrm{\mu }$m. Gravitational settling affects the process of escape into the stratosphere relevant for fitness of long-lived spores (SI Appendix, Figs. S1 and S2). Finally, dry deposition to the ground is computed assuming that the flux of spores $j\left(\mathbf{x},t\right)$ to the ground is proportional to concentration of spores close to the soil $\theta \left(\mathbf{x},t\right)$: $j\left(\mathbf{x},t\right)=V_d\theta \left(\mathbf{x},t\right){|}_{z=0}$, where $V_d$, the deposition velocity, was taken equal to the gravitational settling, as appropriate for spherical particles larger than about 1 $\mathrm{\mu }$m (38). A more detailed modeling of deposition on the canopy including dependence on spore shape is left for future studies. Fig. 3 shows that deposition velocities affect fitness quantitatively, but do not affect the qualitative patterns. In our model, the gravitational/deposition velocity is the only parameter of the dynamics that depends on the fungal species. Wet deposition may decrease the flight time in daytime releases, but does not change the general conclusions unless fungi are able to release spores right before rain. There is some evidence that this may be true for some species, and we will treat this fascinating possibility elsewhere.

One-Dimensional Model of Spore Transport.

In the Eulerian framework, the concentration of passive tracers advected by a short-correlated velocity field in one dimension follows the well-known Fokker–Plank equation ${\partial }_t\theta \left(z,t\right)={\partial }_z\left[D\left(z\right){\partial }_z\theta \right]+v_D{\partial }_z\theta$ (37, 84), where $\theta \left(z,t\right)$ is the average concentration of spores at altitude $z$ and time $t$; $D\left(z\right)$ is the vertical eddy diffusivity, for which we use the closures implemented in the HYSPLIT simulations (SI Appendix); and $v_D$ is the sedimentation velocity. We compared fitness obtained through this simplified one-dimensional model that neglects the horizontal dynamics entirely to the results of the full HYSPLIT model. The one-dimensional model captures well the importance of stability in determining fitness and reproduces the oscillations observed in the full simulations. We impose reflecting boundary conditions at the top of the domain (25 km), and we remove a fraction of spores localized at $z<50\hspace{0.17em}\mathrm{m}$ according with the deposition velocity, as done by the HYSPLIT model. We adopt a finite-volume scheme with regular cells of $\mathrm{\Delta }z=5\hspace{0.17em}\mathrm{m}$ and a Runge–Kutta algorithm of fourth order for time marching, with time step $\mathrm{\Delta }t$ chosen according to the Courant criterion $\mathrm{\Delta }t=\underset{D_i}{min}\frac{\mathrm{\Delta }{z}^2}{8D_i}$, where $D_i=D\left(z_i\right)$ is the eddy diffusivity evaluated at the center of the ith vertical cell.

Regression.

To determine whether time of the day or vertical turbulence holds the most reliable information about fitness, we perform nonparametric regression using regularized least squares with kernels (85–87). We target a function that predicts fitness $\chi$ from input data $x$, where $x$ represents either time of day or turbulence intensity at spore release. A kernel function defines similarity between different input points; here we use a Gaussian kernel $k\left(x,x\prime \right)=e^{-\Vert x-x\prime {\Vert }^2/\left(2\pi {\beta }^2\right)}$. Given a training set $\left(\mathbf{x},\chi \right)=\left(x_1,..,x_N,{\chi }_1,\dots ,{\chi }_N\right)$, the solution to the regularized least-squares problem predicts fitness for a new value of the input data $x_{\text{new}}$,

$$f\left(x_{\text{n}ew}\right)=k\left(x_{\text{n}ew},\mathbf{x}\right){\left(K+\lambda nI\right)}^{-1}\chi ,$$ [2]

where $K$ is the matrix whose entries are the values of the kernel function calculated over the training points $K_{ij}=k\left(x_i,x_j\right)$. We use Eq. 2 to predict fitness and evaluate the error as the square difference between the prediction $f\left(x_{\text{new}}\right)$ and the actual value of fitness computed through our HYSPLIT simulations, ${\chi }_{\text{new}}$. We choose the hyperparameters of the model, $\lambda$ and $\beta$, to minimize the validation error using fourfold cross-validation. We split our 9,600 simulations (10 locations $\times$ 4 mo $\times$ 30 d $\times$ 8 releases per day) into 240 test points (1 location $\times$ 1 mo $\times$ 30 d $\times$ 8 releases per day) and a random subsample from the remaining 9,360 simulations was split 3:1 between training and validation. We use a random subsample of 1,000 (for $t$) and 1,500 (for $w$) simulations. We compute the mean square error over the validation set using Eq. 2 and repeat the procedure varying systematically the hyperparameters to identify the region in the parameter space that provides minimum validation error.

We then compute the mean square error on the test data and we repeat the procedure over the 40 different ways to split the dataset into test and training, and we average to obtain the test error. The difference in the test error, defined as $<{\left({\chi }_{\text{test}}-f\left(x_{\text{test}}\right)\right)}^2>$, for $x\hspace{0.17em}=$ time of day and $x\hspace{0.17em}=$ turbulence intensity, with the hyperparameters selected as above, is plotted in Fig. 5F, normalized with the variance of fitness calculated over the test set.

Data Availability.

All data and scripts are available in SI Appendix, and the list and content of files are described in SI Appendix. Simulations of spore transport in the atmosphere are generated through the HYSPLIT transport and dispersion model, freely available from the NOAA ARL: https://www.ready.noaa.gov/HYSPLIT.php. Data on turbulence intensity are obtained from the National Centers for Environmental Prediction (NCEP) Reanalysis dataset, which is freely available from the NOAA/Office of Oceanic and Atmospheric Research (OAR)/Earth System Research Laboratory (ESRL) Physical Sciences Division (PSD), Boulder, CO: https://www.esrl.noaa.gov/psd/.