Bioinspired underwater locomotion of light-driven liquid crystal gels

Significance

Untethered dynamic shape programming and control of soft materials have significant applications in technologies such as soft robots, medical devices, organ-on-a-chip, and optical devices. Here, we present a solution to remotely actuate and move soft materials underwater in a fast, efficient, and controlled manner using photoresponsive liquid crystal gels (LCGs). LCG constructs with engineered molecular alignment show a low and sharp phase-transition temperature and experience considerable density reduction by light exposure, thereby allowing rapid and reversible shape changes. We demonstrate different modes of underwater locomotion, such as crawling, walking, jumping, and swimming, by localized and time-varying illumination of LCGs. The diverse locomotion modes of smart LCGs can provide a new toolbox for designing efficient light-fueled soft robots in fluid-immersed media.

Abstract

Soft-bodied aquatic invertebrates, such as sea slugs and snails, are capable of diverse locomotion modes under water. Recapitulation of such multimodal aquatic locomotion in small-scale soft robots is challenging, due to difficulties in precise spatiotemporal control of deformations and inefficient underwater actuation of existing stimuli-responsive materials. Solving this challenge and devising efficient untethered manipulation of soft stimuli-responsive materials in the aquatic environment would significantly broaden their application potential in biomedical devices. We mimic locomotion modes common to sea invertebrates using monolithic liquid crystal gels (LCGs) with inherent light responsiveness and molecular anisotropy. We elicit diverse underwater locomotion modes, such as crawling, walking, jumping, and swimming, by local deformations induced by selective spatiotemporal light illumination. Our results underpin the pivotal role of the physicomechanical properties of LCGs in the realization of diverse modes of light-driven robotic underwater locomotion. We envisage that our results will introduce a toolbox for designing efficient untethered soft robots for fluidic environments.

The physical intelligence of numerous aquatic organisms is integrated in their soft and anisotropic stimuli-responsive bodies that have been selectively evolved during their morphogenesis. Such physical intelligence facilitates a chain of sensing, actuation, and adaptation events in response to environmental cues, which leads to a rich repertoire of shape-morphing, locomotion, and propulsion mechanisms (1). The evolutionary success of these organisms has inspired an ever-increasing body of research to develop bioinspired soft-bodied robots as artificial analogs that can operate in fluid-immersed conditions (2, 3). Hence, soft materials with shape-morphing abilities are envisioned to play a pivotal role in this quest (4). However, diverse underwater manipulation of common stimuli-responsive materials with anisotropic morphology in an untethered soft robotic construct still remains a challenge.

The use of soft smart materials in robots also promises their untethered manipulation with less need for traditional rigid and bulky on-board powering, sensing, and actuation components (5, 6). Toward this end, the state-of-the-art aquatic soft robots have employed a range of remote stimulation strategies like electrical (7, 8) and magnetic (9) fields, light (10), and chemical signals (11). The replication of multiscale and often spatially anisotropic morphological features of aquatic organisms is usually achieved by water-friendly materials, such as myocytes and hydrogels. Biohybrid robotic systems (7, 8, 10) and spatially gradient (12–17) and composite (18–20) assemblies from hydrogels are some of the successful examples with a morphological resemblance to soft-bodied aquatic organisms. However, morphological anisotropy in the majority of such assemblies is obtained via elaborate or nonfacile multimaterial fabrication procedures (21). Moreover, the spatiotemporal control of shape morphing in these assemblies, especially for hydrogel-based materials, is dictated by relatively slow diffusion and mass transfer processes (22–24).

Cross-linked liquid crystal (LC) polymers have gained much attention thanks to their inherent coupling of stimuli responsiveness and molecular anisotropy. Typically, LC elastomers (LCEs) contain loosely cross-linked flexible polymer chains with LC mesogenic units either in their backbone or attached to them. The cross-linking density in LC networks (LCNs) is notably larger (25). These materials are sensitive to a variety of cues, such as light and temperature, and their molecular alignment can be programmed through different techniques (26, 27) to induce anisotropy for programmed shape morphing. Swelling both LCNs and LCEs with low-molecular-weight LCs forms liquid crystalline gels (LCGs) that are more sensitive to external stimuli (25). Previously, the relatively accurate spatiotemporal control over molecular alignment and programmable shape morphing of LCNs and LCEs have enabled numerous terrestrial robot locomotion systems in dry conditions, such as walking (28), crawling (29, 30), and jumping (31). However, only few robotic locomotion systems are reported at interaction with liquids (32–35). This is mainly due to the relatively high stiffness and transition temperature and the gradual phase change behavior of common LCEs and LCNs. In addition, higher drag force and lower energy conversion efficiency in water yield inefficient and slow underwater actuation.

Herein, we broaden the dexterity of LC-based materials by using extremely soft, light-sensitive LCGs with low actuation temperatures. We demonstrate how LCGs enable various locomotion modes inspired by those of benthic invertebrates, particularly members of the phylum Mollusca, beyond dry environments to fluid-immersed media. We show that the LCGs can create untethered underwater locomotion modes such as crawling, walking, jumping, and swimming. Our simulation and experimental results provide a method for the development of untethered soft robots with mobility in environments flooded with liquids.

Results and Discussion

Inspiration and Design.

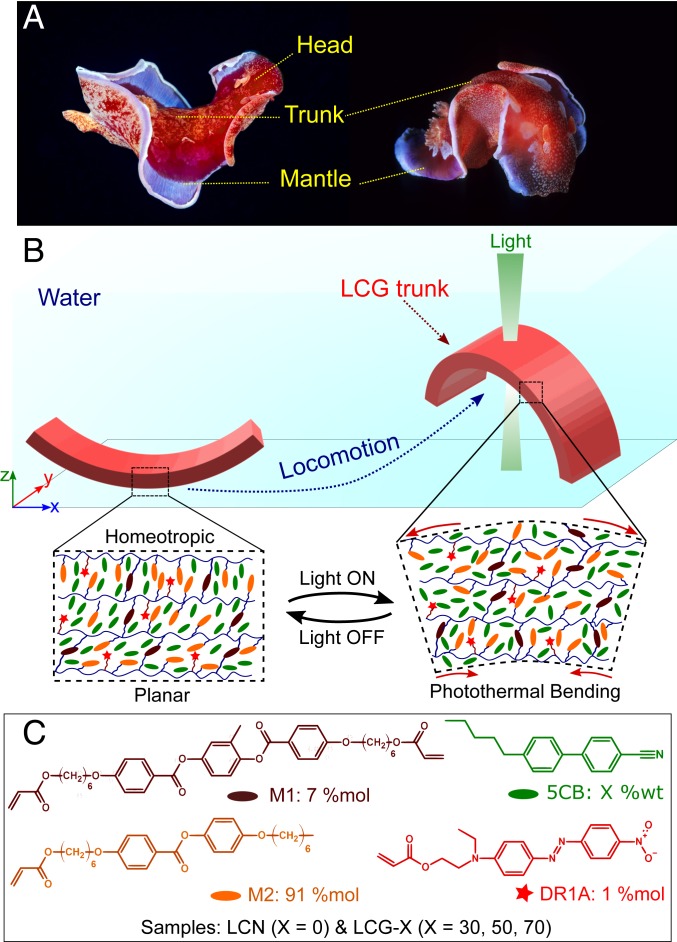
Benthic invertebrates, such as sea slugs and snails, have evolved a great variety of underwater locomotion modes, either on or away from the seabed, in adaptation to the density and viscosity of seawater. In contrast to ground-locomotion animals, marine creatures utilize their milieu to move in a three-dimensional (3D) framework in a controlled manner. For instance, the higher density of seawater (∼1.02 to 1.05 g⋅cm⁻³) provides buoyancy, which acts against sinking imposed by gravity. Programmed dynamic shape morphing of these creatures and interaction of the fluid and possibly seabed with such local body deformations enable thrust and locomotion. In general, the primary locomotion mechanism of these species is based on crawling on the seabed. A few species can also walk, jump, or even swim. The swimming is usually based on flapping, undulation, lateral bending, breaststroke movement, jet propulsion, or a combination of these modes (36–41). In the majority of these modes, the presence of spatiotemporally changing body curvature is a common geometrical feature during the locomotion. For instance, Hexabranchus sanguineus (Spanish dancer) is a famous sea slug that can move both on the seabed and swim away from it (Fig. 1A). The swimming mechanism of this species is essentially based on a large-scale bending undulation along its central trunk (41).

Fig. 1.

Shape morphing in a sea slug and artificial monolithic analogs from LCGs. (A) An H. sanguineus (Spanish dancer) swimming with the bending undulation of its central trunk. (B) Schematic view of an artificial analog of the Spanish dancer’s central trunk made from LCG constructs that move by repeating shape morphing. The relaxed state on the left side corresponds to a splay molecular alignment, while the bent state on the right side corresponds to the photothermally deformed LCG construct with disordered molecules. (C) The chemical structure of mesogenic monomers and the photothermal agent used to realize the light-fueled deformation of LCNs and LCGs; X represents the amount of the 5CB added to the original LCN precursor mixture in weight percentage.

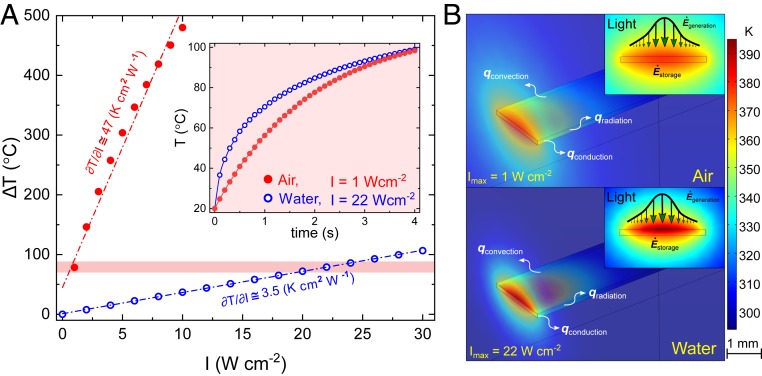
We propose that light-fueled LCGs can be employed to create artificial constructs with aquatic locomotion mechanisms inspired by sea slugs and snails. Fig. 1B illustrates a schematic of an artificial monolith with hybrid molecular alignment, which can in a simplistic manner recapitulate the undulating flexion of the trunk in a number of sea slugs. In this model, photothermally induced decrease in molecular alignment is translated into temporal macroscopic shape morphing of the monolith and the storage of elastic energy. We anticipate that the release of such stored elastic energy during the relaxation can result in the displacement of the surrounding fluid. As such, locomotion can be realized by the repeated formation and relaxation of local curvatures. However, in order to remotely and efficiently actuate the common LCEs and LCNs underwater, one needs to decrease both their stiffness and phase-transition temperature. It is known that, in air, the magnitude of thermally induced deformations decreases with increasing stiffness (42). Moreover, our crude approximation shows that the temperature increase of an LCN cantilever upon exposure to a certain light intensity is much less in quiescent water than in air (Fig. 2 A and B). This is partly due to the greater overall heat transfer coefficient of water that makes both rates of energy storage in and thermal dissipation from the LCN much faster inside water than in air (SI Appendix, section S1 and Fig. S1). As a result, the energy conversion efficiency, the ratio between the stored energy inside the LCN cantilever and energy received by it, is much less in water than in air (SI Appendix, section S1 and Fig. S2, Inset), and much higher energy input is required to create a similar temperature increase in water than in air.

Fig. 2.

FE simulation of light-induced heating of an LCN cantilever in water and air. (A) Variation of the average temperature with illuminating light intensity for photothermal heating of an LCN cantilever (9 × 1.5 × 0.1 mm³). (Inset) The kinetics of light-induced heating, where a light intensity of almost 20 times larger is required to increase the LCN temperature to 100 °C in water. (B) Spatial temperature gradient inside the LCN is drastically larger in water due to higher thermal dissipation.

We postulate that anisotropic plasticized LCNs (i.e., LCGs) can alleviate these problems. Previously, the electro-optical behavior of these materials in confined geometries has been extensively studied (43–45), and a few reports have focused on their potential as free-standing actuators (23, 46, 47). In LCGs, the LC molecules and cross-linked networks self-assemble into nanoscale composites with a highly coupled thermomechanical response (44). Consequently, LCGs benefit from easier manipulation of director orientation, as well as lower and relatively sharper isotropic-to-nematic temperature $T_{NI}$. We anticipate that the lower degree of cross-linking in LCGs compared to their LCN counterparts will render them softer. Such characteristics could lead to a higher fidelity in fast shape morphing with greatly reduced input energies. We also expect that the lower density of LCGs compared to their LCN counterparts enhances their buoyancy, which is beneficial for locomotion under immersed conditions.

LCGs as Thermal Actuators.

The control LCN consists of a mixture of a biacrylate- (M1) and a monoacrylate- (M2) reactive mesogens and Disperse Red 1 acrylate (DR1A) as a reactive photothermal heating agent. Plasticized LCNs were prepared by adding certain amounts of 5CB, as a compatible nematogenic solvent, to the LCN precursor. Hereafter, we refer to all samples containing X weight percentage of 5CB as LCG-X (Fig. 1C and Materials and Methods). Both stiffness and density (ρ) of the control LCN drastically reduce by the gradual addition of 5CB, promising a larger magnitude of thermal actuation and buoyancy. The density of the LCG-70 was particularly close to that of water. Rheology tests also showed a reduction of shear modulus (G′) by up to two orders of magnitude for LCG-70, without sacrificing the elasticity (SI Appendix, section S2 and Table S1).

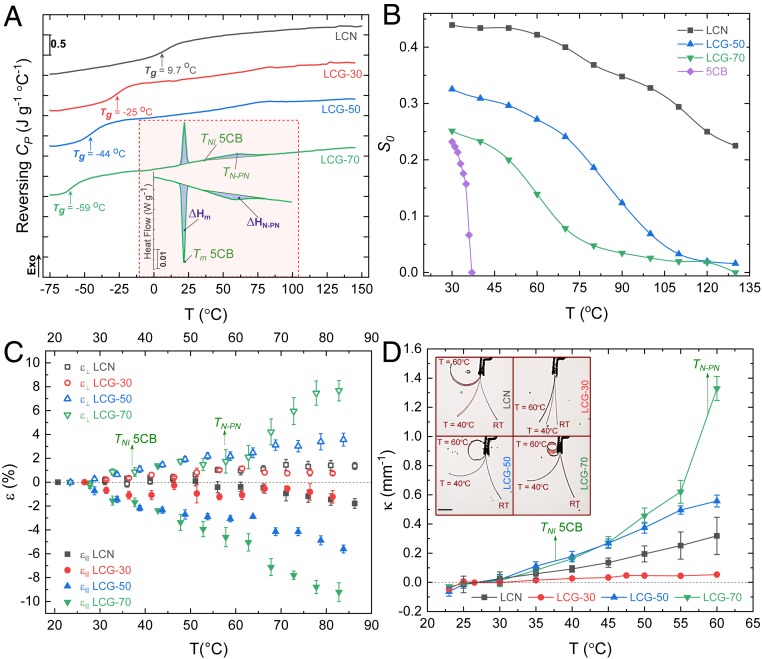
The enhanced softness of the LCG can be partly attributed to the reduction of the glass transition temperature (T_g). We used differential scanning calorimetry (DSC) to determine the transition temperatures of LCN and LCG constructs (SI Appendix, section S2). As can be seen in Fig. 3A and SI Appendix, Table S1, T_g is well below the ambient temperature for all samples. No sign of first-order nematic-to-isotropic transition was observed in any of the samples up to 150 °C heating. This can be attributed to the presence of a supercritical state imposed by the existence of a residual orientational order even at high temperatures. In the supercritical state, the material experiences a continuous nematic-to-paranematic (T_N-PN) phase change and suppression of the first-order nematic-to-isotropic discontinuity, which is a common property of nematic LCs in a subcritical state (48, 49). Heating LCG-70 showed a sharp peak at ∼22 °C, followed by a broad peak starting at ∼35 °C, corresponding to the melting (T_m) and nematic-to-isotropic (T_NI) temperature of 5CB, respectively. For LCG-70, a broad T_N-PN peak centered at ∼57 °C is observed (Fig. 3 A, Inset), suggesting that the presence of 5CB has shifted the supercritical behavior of the native LCN toward a subcritical behavior (48). Similar to previous reports (44), LCG-70 seems to have a mobile molecular assembly with two populations of 5CB, one in the free form and the other fixed onto the native LC network.

Fig. 3.

Thermal actuation behavior of LCNs and LCGs. (A) The variation of reversing heat capacity (C_P) with temperature in a temperature-modulated DSC measurement confirms the reduction of T_g of LCN by the addition of 5CB. The peak at 57 °C is attributed to the nematic-to-paranematic transition of the LCG-70. (Inset) The evolution of reversing heat flow and integration under the peaks show that ΔH_m ≈ 2.9 J⋅g⁻¹ and ΔH_N-PN ≈ 2.05 J⋅g⁻¹. (B) The variation of order parameter from dichroism (S₀) with temperature indicating the range of nematic-to-paranematic phase transition temperature for each sample; the drop in S₀ around 57 °C is more pronounced for LCG-70, which is reminiscent of a phase transition similar to subcritical conditions. S₀ of LCG-30 is not reported due to persistent inconsistencies in measurement attributed to its proximity to the eutectic point. (C) The thermally induced shape change of planar samples in water parallel and perpendicular to the director; coefficient of expansion (∂ε/∂T) of LCG-70 experiences a drastic change close to 57 °C. (D) The thermal bending of LCN and LCG cantilevers (9 × 1.5 × 0.1 mm³) exposed to homogenous heat in a water tank; the bending curvature (κ) of LCN and LCG-30 varies linearly with temperature. This is not the case particularly for the LCG-70, where a pronounced change in the slope takes place in the vicinity of 57 °C. Both LCG-50 and LCG-70 experience a full-turn bending at 60 °C (superimposed photos shown in the inset). RT, room temperature. (Scale bar, 3 mm.)

All samples were birefringent up to 150 °C, confirming the existence of a residual orientational order at high temperatures (48, 49) (SI Appendix, section S2 and Fig. S5). We estimated the order parameter of the samples (S₀) from the dichroism of the DR1A dye and observed gradual phase change from a nematic to a paranematic phase as a function of temperature. In contrast to LCN, S₀ of LCG-50 and LCG-70 reduced with temperature with a sharper slope, reaching zero at elevated temperatures (Fig. 3B and SI Appendix, section S2). The gradual and continuous phase change of the LCN corresponds to gradual thermomechanical response and could be deemed as the main challenge in their thermal actuation underwater. It is worth noting that light-driven LCN oscillators with high amplitude and frequency have been thoroughly investigated in air using a variety of mechanisms such as self-oscillation by rapid trans–cis–trans isomerization (50, 51), self-shadowing (52), and time delay in material photothermal response (53). However, we could not achieve such oscillatory motion using the LCN in water, most probably due to fluidic drag and high thermal dissipation inside water impeding thermal actuation. We expect that doping the LCN with a sufficient amount of 5CB alters the phase-change behavior toward a faster thermomechanical response.

The experimental characterization of the thermal actuation of the planar and splay samples in water is shown in Fig. 3C. The fairly linear increase in strain, $\epsilon =\left(l-l_0\right)/l_0$, with temperature does not hold for LCG-70, for which the slope (∂ε/∂T) suddenly changes at around 60 °C, similar to the transition point observed in DSC. l and l₀ represent the current and the initial length of samples, respectively. The thermal bending behavior of splayed LCN and LCG constructs in water is shown in Fig. 3D. All samples became flat at the polymerization temperature. Again, the linear trend for the bending curvature (κ) versus temperature does not hold for LCG-70. In line with the DSC results and strain measurements, LCG-70 experiences a sudden increase in the curvature at around 60 °C.

Photothermal Actuation of LCGs.

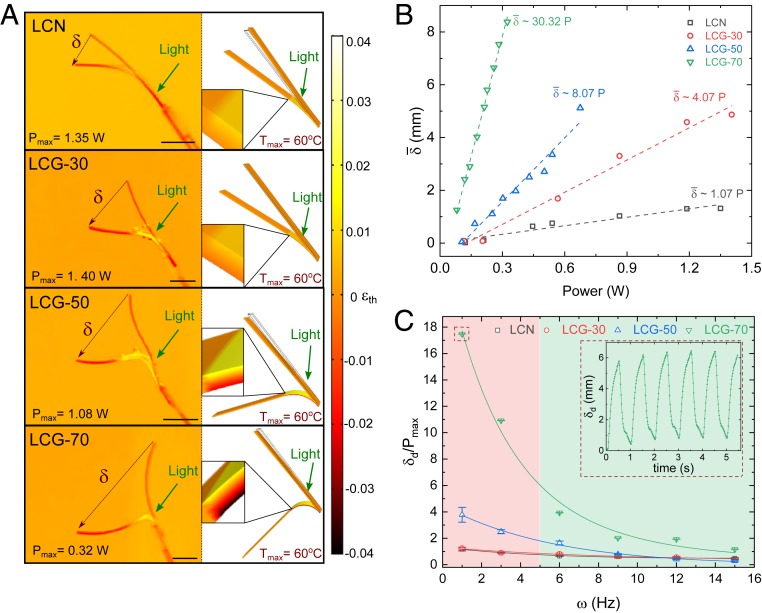
Using thermal actuation results in our finite-element (FE) simulations, we predicted a relatively large and fast photothermal actuation of LCG samples in water at room temperature (23 °C), despite their high thermal dissipation (SI Appendix, sections S1 and S4). Fig. 4A shows the underwater bending of the LCN and LCG constructs illuminated with a 532-nm laser beam with different input powers $\left(P\right)$. The mean quasi-static tip displacement $\left(\overline{\delta }\right)$ is linearly proportional to the input power (Fig. 4B). We define the photothermal response as the ratio of the mean tip displacement to the input power $\left(\overline{\delta }/P\right)$. We found that the photothermal response of LCG-70 is almost 30 times higher than that of the pure LCN, which enables larger underwater deformation for a given input energy.

Fig. 4.

Underwater light-induced actuation of LCN and LCG constructs. (A, Left) The photothermal bending of LCN and LCG cantilevers (9 × 1.5 × 0.1 mm³) exposed to 532-nm laser in a water tank; laser spot: 6 mm in diameter. (A, Right) The results obtained by the finite-element simulation of beams that are locally heated to 60 °C. (Insets) The thermal strain profile on an arbitrary spot on cantilevers. (B) The variation of the tip displacement $\overline{\delta }$ with the input power of laser indicates the higher sensitivity of LCG-70 to light compared to the pure LCN counterpart. (C) Oscillatory photothermal bending by using 532-nm laser chopped at different frequencies; the tip displacement is normalized by the maximum input power shown in B during the oscillation. (Inset) The tracking of the cantilever tip with time. (All scale bars, 3 mm.)

Undulation between stimulated and relaxed states is a common trait of aquatic locomotion, leading to a complex interplay between the kinematics of swimmers and their surrounding flow (54). Beating amplitude and frequency (ω) are the two main parameters to describe swimmers’ undulating body kinematics. In our system, the tip displacement ${\delta }_d$ corresponds to the beating amplitude. In Fig. 4C, we demonstrate the variation of photothermal dynamic response at maximum input power $\left({\delta }_d/P_{max}\right)$ with the beating frequency (Movies S1 and S2). The dynamic responses of LCG-70 and LCG-50 were consistently larger than those of pure LCN and LCG-30. At ω = 1 Hz, ${\delta }_d/P_{max}$ of LCG-70 and LCG-50 was ∼15 and 3.2 times larger than that of LCG-30 and pure LCN, which further demonstrates their superior suitability for underwater actuation.

Notably, the photothermal dynamic response at maximum input power $\left({\delta }_d/P_{max}\right)$ for all LCG samples at 1 Hz is much lower than the corresponding values $\left(\overline{\delta }/P\right)$ measured with constant input power in quasi-static experiments shown in Fig. 4B. We also did not notice a meaningful correlation between these two values. This indicates that the mechanical response time for our LCGs to reach the maximum amplitude (i.e., a full stroke–relaxation cycle interval), is larger than 1 s. However, when oscillating with reduced amplitude, the stroke and relaxation times were nearly the same for LCGs (Fig. 4 C, Inset) until ω ≈ 5 Hz, where the illumination and actuation become out of phase, particularly for LCG-70 and LCG-50. This suggests a limit of ∼0.2 s for their mechanical relaxation times in oscillatory mode. This is anticipated to be due to lower cross-linking density as a result of the addition of 5CB. Thus, we conservatively use ω <5 Hz for the actuation of our materials to render undulatory locomotion.

Aquatic Locomotion Modes of LCGs.

Crawling is the dominant locomotion mode of sea slugs and snails on the seabed. Using external or internal solids as support, these creatures can generate muscular traveling waves on their pedals to move (38). The seminal work by Broer and coworkers (30) demonstrated that photoactive LCNs can create undulatory traveling waves similar to terrestrial gastropods through the self-shadowing effect of static illumination at a certain angle. In a similar configuration attached to a passive frame or a substrate as solid constraints, we demonstrated self-shadowing undulatory motion on a confined LCG-50 cantilever for underwater propulsion. We could generate such traveling waves only for LCG-50, as the given light intensity was not sufficient for ample deformation on LCN and LCG-30 constructs (Fig. 5A and Movie S3). LCG-70, in turn, was too soft to withstand the attachment to a passive solid frame.

Fig. 5.

Underwater walking, crawling, and jumping locomotion modes. (A) Self-sustained wave-like deformation for propulsion by shining a stationary beam of a 532-nm laser to a cantilever construct from LCG-50 (21 × 3 × 0.1 mm³); the cantilever is fixed to a frame with the length of 16 mm. In this design, the continuous displacement of the wave leads to a change in the position of the exposed and unexposed areas to a stationary beam (i–iv). (B) Crawling of the sample through undulatory traveling waves created by scanning 532-nm laser (input power ∼ 0.4 W). Note that the altered mode of illumination in our design leads to different transient geometries in the state iv of wave formation in A and B. (C) Walking of an LCG-50 cantilever (21 × 3 × 0.1 mm³) on a ratchet surface; the light is shone from a high-pressure mercury vapor short-arc lamp with an intensity of almost 1.5 W⋅cm⁻². (D) Jumping of an LCG-70 cantilever (21 × 3 × 0.1 mm³) on a ratchet surface; the light is shone from the same source in C but with an intensity of 1.2 W⋅cm⁻². The left side in all figures shows predictions obtained from finite-element simulations. All inset figures show the thermal strain profile through the thickness of an arbitrary spot on corresponding cantilevers. The maximum temperature is 60 °C. All experiments were performed in water at room temperature (23 °C). h, homeotropic; p, planar. (All scale bars, 4 mm.)

In our experiments, maintaining the correct illumination angle for the self-shadowing on an object moving in water proved to be arduous. We changed the illumination geometry and shone the light from above the sample, which was beyond the self-shadowing angle. In this geometry, we achieved undulatory traveling waves of LCG-50 as well as crawling, by scanning the light along LCG length (with a range of ca. 4 mm). As shown in Movie S4, the exposed part of the sample bends and pushes the unexposed part along the soft axis of the construct (Fig. 5 B, i–iv). The geometrical constraint imposed by the passive frame then leads to the abrupt transfer of the center of the mass and sudden release of stored elastic energy. The repetition of this process leads to locomotion. The overall speed of the locomotion depends on how fast localization, illumination, and scanning processes take place.

Besides locomotion by pedal waves in snails, some mollusks can move on the seabed by mechanisms similar to walking. Walking-like motion in a monolithic material can be achieved without a passive frame. Fig. 5C and Movie S5 show the two-step walking of the LCG-50 construct upon undulatory light illumination on a ratchet surface. Light irradiation to a point away from the geometrical center of LCG results in an outward flexion (stroke) and the storage of elastic energy. Accordingly, the leg closer to the illuminated spot deforms to a larger extent than the other and finds an anchoring point on the solid substrate ahead of its prior location (Fig. 5 C, ii). When the light is turned off the stored elastic energy on the bent spot is released (relaxation) and the LCG construct is pushed forward by leaning against the anchoring point (Fig. 5 C, i). The illumination spot, the frequency of stroke and relaxation, and the speed of motion of the light source determine the locomotion direction and speed. Asymmetry in bending and friction on the substrate are crucial for the forward locomotion. Movement on a flat surface was also possible, albeit slow.

Interestingly, repeating the same experiment on the LCG-70 construct resulted in another mode of locomotion that included also jumping (Fig. 5D and Movie S6). Unlike LCG-50, the locomotion mode for the LCG-70 construct has three stages. The first two stages are based on the flexion upon illumination (Fig. 5 D, i and ii). However, the elastic energy stored in the first two stages is large enough to lift the object from the substrate during a sudden relaxation (Fig. 5 D, iii). We attribute this sudden release of the stored elastic energy to the sharper phase transition in LCG-70 (Fig. 3A). A similar type of locomotion is used by some gastropods that dig their operculum into the ground to catapult themselves forward on the seabed (39, 40). In addition, we believe that the lower density of the LCG-70 and its decrease upon illumination plays a key role in buoyancy during relaxation. We confirmed this by measuring the density of LCG-70 before and during illumination. Similar to a report by Liu et al. (55), when shone by light our LCG-70 undergoes almost 8% density reduction, while no discernable density change is observed for isotropic counterparts (SI Appendix, section S3). By repeating the jumping locomotion this time on flat terrain with much lower anchoring support we confirmed the effective role of light-triggered density reduction for lifting the LCG-70 in water (Movie S7).

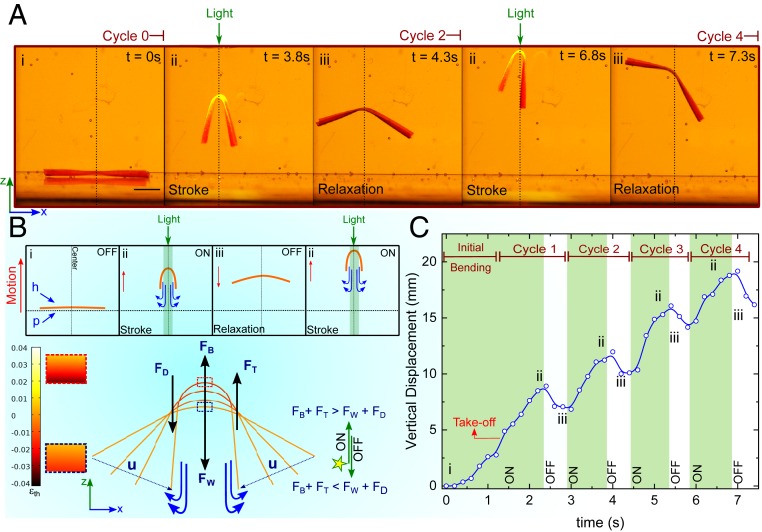
In addition to crawling, walking, and jumping, a few members of sea slugs are also capable of swimming. Undulatory bending of the body is a recurring theme during the swimming of these species, which can be mimicked with our LCG construct, albeit in a much simplified form. By slightly salting the water to increase its density (∼1.03 g⋅cm⁻³), we could overcome gravity and eventually make the LCG-70 construct swim by consecutive arrhythmic stroke (Fig. 6 A, ii) and relaxation (Fig. 6 A, iii) cycles. The reduction of density upon illumination enables larger buoyancy force (F_B) that compensates for sinking gravitational force (F_W). Such locomotion away from the bottom surface continues as long as F_B + F_T ≥ F_W + F_D, where F_T and F_D are thrust and drag forces acting for and against propulsion of the LCG construct, respectively (Fig. 6B and Movie S8). In our system, comparable to moving paddles in fluids, the net thrust is produced by the drag acting on the legs. The propulsive thrust persists as long as the drag during the stroke is greater than during the relaxation (56). The undulatory bending of LCG ceases when the illumination fails to target the middle part of the construct. Spatiotemporal tracking of the geometrical center of the LCG-70 with a typical swimming performance shown in Fig. 6C indicates that the stroke period (∼1 s) is almost twice as long as the relaxation period (∼0.5 s), resulting in the LCG-70 construct swimming upward with a constant velocity of ∼4.9 mm⋅s⁻¹ (∼0.3 body length⋅s⁻¹). Assuming that gravity is compensated by the light-induced buoyancy, we can conclude that F_T ≈ F_D. Our crude approximation of the Reynolds number (Re) of the LCG construct (22 < Re < 80) indicates that both inertial and viscous forces play a significant role in the dynamics of locomotion. With respect to the Stokes number (Stk) of our swimmer, we found that Stk ∼ 1,072, which is in the same range as that of juvenile H. sanguineus with a comparable size (SI Appendix, section S5) (41).

Fig. 6.

Underwater swimming locomotion mode. (A) Swimming of an LCG-70 cantilever construct (16 × 3× 0.1 mm³) in consecutive illumination cycles (ii and iii). The upward locomotion continues until the illumination is able to target the center of the mass. (Scale bar, 4 mm.) (B) The net upward motion is the result of light-induced buoyancy (F_B) and the propulsive thrust (F_T) during the 1-s period of stroke in state ii. Upon illumination, the two ends of cantilever move toward each other with the speed of u, leading to the downward propulsion of water. When the light is OFF during the 0.5-s period of relaxation, the cantilever does not fully relax in state iii. Time-resolved actuation profiles are obtained by the FE modeling and the thermal strain profile at the stroke and relaxation periods are shown on the left side of the swimmer. The net displacement is positive in the z-direction. (C) Tracking the center part of the LCG-70 construct shows that the initial buoyancy and shape change for the take-off takes place in less than 1.5 s ,followed by vertical swimming with an almost constant velocity of 4.9 mm⋅s⁻¹ during the stroke period. Maintaining a constant light intensity in this experiment was difficult due to the manual control of the distance between the light source and the cantilever. However, the light intensity was always below 1.8 W⋅cm⁻². The swimming experiment was done in salt-water brine with a density of 1.03 g⋅cm⁻³.

Conclusions

We have designed and demonstrated a soft-bodied robot with a number of locomotion modes, inspired by those of sea slugs and snails in an aqueous environment. For this, we leveraged the stimuli-responsive properties of LCGs and the versatile nature of light as an external source of stimulation. Intrinsic molecular anisotropy and higher molecular mobility of LCGs enabled us to create predesigned localized shape morphing of monolithic soft constructs upon optical stimulation. The transition temperature of the LCGs, well below the boiling point of water, enabled shortened relaxation times and thus fast and large underwater photothermal response. This is particularly advantageous over the use of purely photochemically driven systems, which may need either higher temperatures or multiple light sources with different wavelengths for fast relaxation (33). As a result of these characteristics, spatiotemporally dynamic illumination of LCGs results in the formation of undulatory traveling waves and localized bending, essential for the propulsion and aquatic locomotion. Our experiments demonstrate an overly simplified case of swimming based on macroscale body undulation. Nonetheless, mimicking other swimming modes in submillimeter scales is also possible using advanced alignment and 3D fabrication techniques, such as two-photon lithography (57).

One of the immediate applications of our LCG-based soft constructs is the development of untethered aquatic soft robots, where elastic but highly deformable materials with anisotropic physicomechanical properties are highly in demand. In this regard, adaptation to media with diverse, dynamic, and complex properties, such as biological fluids and fluid–air interfaces, is a challenging task for the next generation of such robots (3). Toward this end, it is imperative to improve the toughness of such LC-based materials without sacrificing versatile touchless molecular programming and fast thermomechanical response at reduced temperatures. With respect to the stimulation technique, like previous reports on light-fueled swimmers (32, 34), our results buttress the crucial role of optical stimulation in providing not only energy but also positional information for the precise control of the speed and direction of locomotion. The ability to locally decrease the LCG density enhances the buoyancy, leading to a higher degree of freedom for locomotion away from the solid–liquid interface. We believe that by the use of algorithmic and finely controlled local shape and density changes, more intricate modes of light-fueled locomotion, such as turning, maneuvering, and targeted locomotion, can also be achieved.

Materials and Methods

Materials.

Bifunctional monomer 1,4-Bis-[4-(6-acryloyloxyhexyloxy)benzoyloxy]-2-methylbenzene (M1), monofunctional monomer 4-(6-Acryloxy-hex-1-yl-oxy)phenyl 4-(hexyloxy)benzoate (M2), and short-chain nonreactive LC 4-Cyano-4′-n-pentylbiphenyl (5CB) were purchased from SYNTHON Chemicals GmbH & Co. KG. DR1A, 2,2-dimethoxy-2-phenylacetophenone (Irgacure651), and N, N-dimethylformamide (DMF) were purchased from Sigma-Aldrich. Brilliant yellow (BY) was purchased from TCI. Polyimide SE-1211 was donated by Nissan Chemical Industries. All reagents and solvents were used as received without further purification.

LC Alignment and Cell Preparation.

To induce planar molecular alignment, precleaned glass slides were spin-coated with 1 wt % solution of BY in DMF, baked at 90 °C for 30 min, and exposed to polarized blue light (λ ∼ 447 nm and I ∼ 125 mW⋅cm⁻²). The in-plane orientation of the director field was determined by the orientation of polarized light. To induce homeotropic surface anchoring, glass slides were spin-coated with ∼120 nm of polyimide SE-1211 (3,000 rpm for 35 s) and baked at 180 °C for 1 h. The film thickness was measured by a laser profilometer (Keyence VK-X210). Planar cells were assembled using two planar treated glass slides placed parallel to each other. Splay cells were made by placing one planar and one homeotropic treated glass slide on top of each other. The cell gap was kept constant at 100 μm in all experiments using polystyrene spacer particles (Cospheric LLC).

Preparation of LCN and LCG Constructs.

LCN precursor mixture in all samples consisted of 7.7 mol % M1 as the mesogenic cross-linker, 90.3 mol % M2 as the monofunctional mesogenic monomer, 1 mol % DR1A as a reactive photothermal reagent, and 1 mol % Irgacure651 as the photoinitiator. Covalent bonding of the DR1A to the LCN network reduces the chance of leaching and its short cis half-life at room temperature leads to a more efficient photothermal response (30). LCG precursor mixtures were obtained by adding 5CB to the original LCN mixture with 30 wt %, 50 wt %, and 70 wt % of the LCN mixture total mass. All mixtures were melted to their isotropic phase at 100 °C, stirred for 1 h, and then injected into cells of different alignment configurations. The filled cells were cooled down to 25 °C (∼1 °C⋅min⁻¹) and were exposed to 365-nm ultraviolet (UV) light (Herolab) with an intensity of ∼5 mW⋅cm⁻² for 30 min for cross-linking. Afterward, LCN and LCG samples were cut to desired shapes and sizes using a laser cutter (Proto Laser R cutter; LPKF Laser and Electronics) and harvested by immersion in water. All samples were conditioned in water for several days prior to any experiments. Note that our method in the synthesis of LCGs slightly differs from some techniques reported in previous studies where a prepolymerized LCN becomes swollen with a low-molecular-weight nematogen (46, 47). This slight change enables us to obtain better control over the initial molecular alignment and shape of the LCG construct, especially for samples with local splay alignment.

Characterization and Actuation.

The density (ρ) of LCN and LCGs was measured by immersing 2- × 2-mm² pieces of each sample in brines of salt water with different densities. Absorption spectra and order parameter vs. temperature were measured with a microspectrometer (PIXIS 256; Princeton Instruments) equipped with a polarization controller and a heating stage (Polaviz heater and temperature controller; APSYS Inc.).

A polarized optical microscope equipped with a heating stage was used to observe the phase behavior of the precursor mixtures and polymerized samples. As shown in SI Appendix, Table S1, the T_NI of the prepolymerized mixtures decreases with the higher content of 5CB. We noticed an inconsistent phase behavior for the prepolymerized LCG-30 mixture that can be attributed to its proximity to a eutectic concentration (44). This adversely affected all other data obtained for the actuation of LCG-30.

DSC (DSC2500; TA Instruments) was used to measure heat capacity (C_P) and transition temperatures of LCN and LCGs (T_g and T_NI). Mechanical properties of the LCN and LCGs, such as storage shear modulus (G′), were measured by a rheometer (TA Instruments) in a plate–plate geometry in a frequency sweep test performed at room temperature.

Thermal expansion and contraction of planar LCN and LCG samples were performed using the same heating stage. Samples were cut in squares and immersed in water poised on superhydrophobic glass substrates with reduced adhesion. The variation of length with temperature was monitored by a digital microscope (Dino-lite) and measured with a custom-developed computer code. The thermal bending of splay LCNs and LCGs was performed by mounting and immersing rectangular cantilever beams in water. We increased the temperature in our actuation tests up to the point that the actuation of LCGs was fairly reversible. The temperature of the water was varied with a hot plate and controlled with a probe thermocouple. The variation of bending curvature (κ) with temperature was monitored by the same digital microscope and measured manually using the Fiji image processing package.

Photothermal actuation of LCN and LCGs was achieved by using a continuous-wave laser (DPSS, 532 nm, 2 W; Riothner) and a high-pressure mercury vapor short arc UV lamp (Omnicure S2000; Excelitas Technologies). Oscillatory actuation of samples was achieved by chopping the incident laser beam with different frequencies (optical chopper with MC1F2 blade; Thorlabs). Photoinduced bending and oscillation were monitored by a Canon 5D Mark III camera with a 100-mm lens and a long-pass filter, cut-on wavelength 550 nm. Tip displacement vs. time, frequency, and light intensity were measured using open-source software (Tracker 5.1.0). We increased the light intensity to the point at which LCG-50 and LCG-70 showed discernable leaching of 5CB. Frame-assisted locomotion of LCG-50 cantilever was attained by manual positioning of the laser beam. The actuation of free-standing LCG-70 on a flat substrate was obtained by chopping the incident light from the laser source. All other actuation and locomotion tests were carried out by the manual positioning and oscillation of the incident light from the UV source.

FE Simulations.

The FE simulations of photothermal heating of an LCN construct were carried out using the Heat Transfer module of COMSOL Multiphysics 5.4. The Beer–Lambert law was employed to model the incident light and energy absorption inside an LCN cantilever. The incident beam with a Gaussian distribution was applied on the top surface of the cantilever through a Dirichlet boundary condition interface. Next, the time-domain simulations were performed to obtain the temperature profile within the material surrounded by air and water media. The thermomechanical analysis of the LCN and LCG cantilevers was conducted in the Solid Mechanics module of COMSOL Multiphysics 5.4. The elastic bending of the heated splay cantilever was modeled using the anisotropic thermal strain assumption across their thickness, while they were treated as isotropic hyperelastic material (58, 59). The external thermal strain values for the parallel and normal to the nematic director were extracted from the experimental results (Fig. 3C) and imported directly to the FE model.

Data Availability.

All data, materials, and associated protocols that support the findings of this study are shown in Materials and Methods and SI Appendix.