Visualizing Structure and Transitions in High-Dimensional Biological Data

Abstract

The high-dimensional data created by high-throughput technologies require visualization tools that reveal data structure and patterns in an intuitive form. We present PHATE, a visualization method that captures both local and global nonlinear structure using an information-geometric distance between datapoints. We compared PHATE to other tools on a variety of artificial and biological datasets, and find that it consistently preserves a range of patterns in data, including continual progressions, branches, and clusters, better than do other tools. We define a manifold preservation metric called ‘Denoised Embedding Manifold Preservation’ (DEMaP) and show that PHATE produces quantitatively better denoised lower-dimensional embeddings compared with existing visualization methods. An analysis of a newly generated scRNA-seq dataset on human germ layer differentiation demonstrates how PHATE reveals unique biological insight into the main developmental branches, including identification of three previously undescribed subpopulations. We also show that PHATE is applicable to a wide variety of data types, including mass cytometry, single-cell RNA-sequencing, Hi-C, and gut microbiome data.

Introduction

High dimensional, high-throughput data are accumulating at a staggering rate, especially of biological systems measured using single-cell transcriptomics and other genomic and epigenetic assays. Because humans are visual learners, it is important that these datasets are presented to researchers in intuitive ways to understand both the overall shape and the fine granular structure of the data. This is especially important in biological systems, where structure exists at many different scales and a faithful visualization can lead to hypothesis generation.

There are many dimensionality reduction methods for visualization [1-11], of which the most commonly used are PCA [11] and t-SNE [1-3]. However, these methods are suboptimal for exploring high-dimensional biological data. First, they tend to be sensitive to noise. Biomedical data is generally very noisy, and methods like PCA and Isomap [4] fail to explicitly remove this noise for visualization, rendering fine grained local structure impossible to recognize. Second, nonlinear visualization methods such as t-SNE often scramble the global structure in data. Third, many dimensionality reduction methods (e.g. PCA and diffusion maps) fail to optimize for two-dimensional visualization as they are not specifically designed for visualization.

Furthermore, common implementations of dimensionality reduction methods often lack computational scalability. The volume of biomedical data being generated is growing at a scale that far outpaces Moore’s Law. State-of-the-art methods such as MDS and t-SNE were originally presented (e.g., in [1, 7]) as proofs-of-concept with somewhat naïve implementations that do not scale well to datasets with hundreds of thousands, let alone millions, of data points due to speed or memory constraints. Although some heuristic improvements may be made (see, for example, [3, 8]), most available packages still follow the original implementation and thus cannot run on big data, which severely limits the usability of these methods in the medium to long term.

Finally, we note that some methods try to alleviate visualization challenges by directly imposing a fixed geometry or intrinsic structure on the data. However, methods that impose a structure on the data generally have no way of alerting the user whether the structural assumption is correct. For example, any data will be transformed to fit a tree with Monocle2 [12] or clusters with t-SNE. While such methods are useful for data that fit their prior assumptions, they can generate misleading results otherwise, and are often ill suited for hypothesis generation or data exploration.

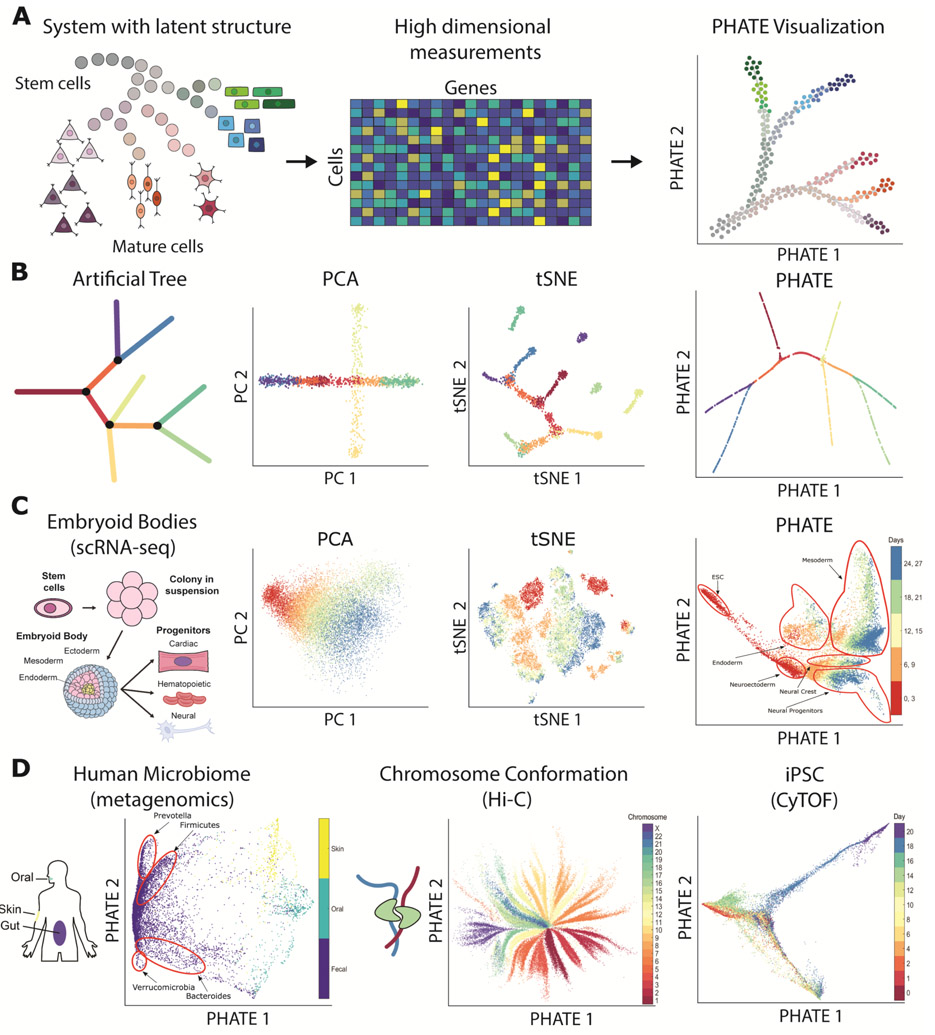
To address the above concerns, we have designed a dimensionality reduction method for visualization named Potential of Heat-diffusion for Affinity-based Transition Embedding (PHATE). PHATE generates a low-dimensional embedding specific for visualization which provides an accurate, denoised representation of both local and global structure of a dataset in the required number of dimensions without imposing any strong assumptions on the structure of the data, and is highly scalable both in memory and runtime. To achieve this, we combine ideas from manifold learning, information geometry, and data-driven diffusion geometry and integrate them with current state-of-the-art methods. The result is that high-dimensional and nonlinear structures, such as clusters, nonlinear progressions, and branches, become apparent in two or three dimensions and can be extracted for further analysis (Figure 1A).

Figure 1.

Overview of PHATE and its ability to reveal structure in data. (A) Conceptual figure demonstrating the progression of stem cells into different cell types and the corresponding high dimensional single-cell measurements rendered as a visualization by PHATE. (B) (Left) A 2D drawing of an artificial tree with color-coded branches. Data is uniformly sampled from each branch in 60 dimensions with Gaussian noise added (see Methods). (Right) Comparison of PCA, t-SNE, and the PHATE visualizations for the high-dimensional artificial tree data. PHATE is best at revealing global and branching structure in the data. In particular, PCA cannot reveal fine-grained local features such as branches while t-SNE breaks the structure apart and shuffles the broken pieces within the visualization. See Figure S3 for more comparisons on artificial data. (C) Comparison of PCA, t-SNE, and the PHATE visualizations for new embryoid body data showing similar trends as in (B). (D) PHATE applied to various datatypes. Left: PHATE on human microbiome data shows clear distinctions between skin, oral and fecal samples, as well as different enterotypes within the fecal samples. Middle: PHATE on Hi-C chromatin conformation data shows the global structure of chromatin. The embedding is colored by the different chromosomes. Right: PHATE on induced pluripotent stem cell (iPSC) CyTOF data. The embedding is colored by time after induction. See Figures 5, S8, S10, and S11 for more applications to real data.

We develop a new metric called ‘Denoised Embedding Manifold Preservation’ (DEMaP) to quantify the ability of an embedding to preserve denoised manifold distances, we show that PHATE consistently outperforms 11 other methods on synthetically generated data with known ground truth. We also use PHATE to visualize several biological and non-biological real world datasets, showing PHATE’s capacity to visualize datasets with many different underlying structures including trajectories, clusters, disconnected and intersecting manifolds, and more (Figure 1). To demonstrate the ability of PHATE to reveal new biological insights, we apply PHATE to a newly generated single-cell RNA-sequencing dataset of human embryonic stem cells grown as embryoid bodies over a period of 27 days to observe differentiation into diverse cell lineages. PHATE successfully captures all known branches of development within this system as well as differentiation pathways that have—to the best of our knowledge—not been described before, and enables the isolation of rare populations based on surface markers, which we validate experimentally.

Results

Visualizing complex, high-dimensional data in a way that is both easy to understand and faithful to the data is a difficult task. Such a visualization method needs to preserve local and global structure in the high-dimensional data, denoise the data so that the underlying structure is clearly visible, and preserve as much information as possible in low (2-3) dimensions. Additionally, a visualization method should be robust in the sense that the revealed structure of the data is insensitive to user configurations of the algorithm and scalable to the large sizes of modern data.

Popular dimensionality reduction methods are deficient in one or more of these attributes. For example, t-SNE [1] focuses on preserving local structure, often at the expense of the global structure (Figure 1B-C), while PCA focuses on preserving global structure at the expense of the local structure (Figure 1B-C). Although PCA is often used for denoising as a preprocessing step, both PCA and t-SNE provide noisy visualizations when the data is noisy, which can obscure the structure of the data (Figure 1B-C). In contrast, diffusion maps [13] effectively denoises data and learns the local and global structure. However, diffusion maps typically encodes this information in higher dimensions [14], which is not amenable to visualization, and can introduce distortions in the visualization under certain conditions (see Figures S1 and S2A).

PHATE is designed to overcome these weaknesses and provide a visualization that preserves the local and global structure of the data, denoises the data, and presents as much information as possible into low dimensions. There are three major steps in the PHATE algorithm.

1. Encode local data information via local similarities (Figure 2A-C).

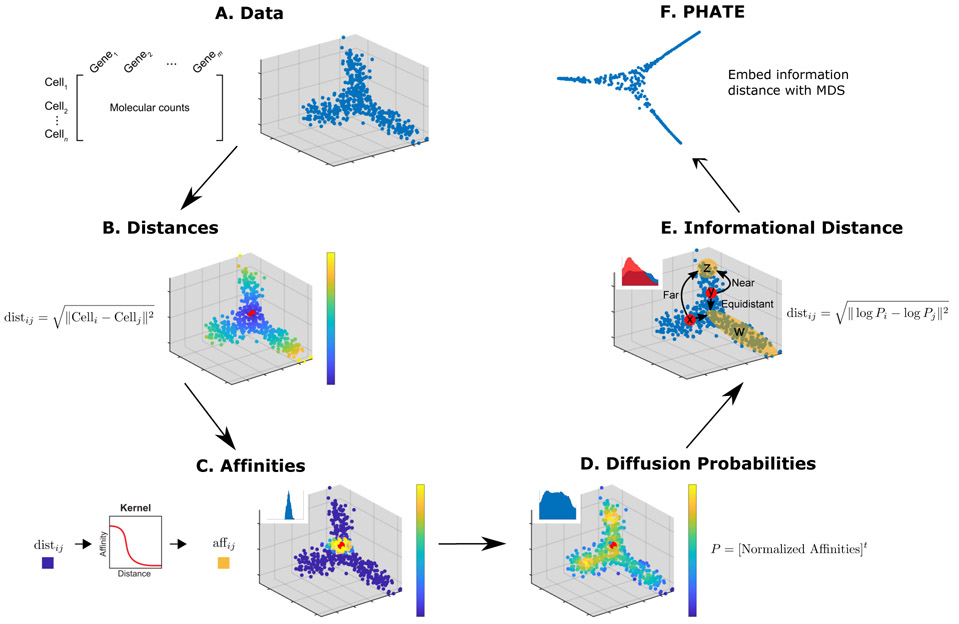
Figure 2.

Steps of the PHATE algorithm. (A) Data. (B) Euclidean distances. Data points are colored by their Euclidean distance to the highlighted point. (C) Markovnormalized affinity matrix. Distances are transformed to local affinities via a kernel function and then normalized to a probability distribution. Data points are colored by the probability of transitioning from the highlighted point in a single step random walk. (D) Diffusion probabilities. The normalized affinities are diffused to denoise the data and learn long-range relationships between points. Data points are colored by the probability of transitioning from the highlighted point in a t step random walk. (E) Informational distance. An informational distance (e.g. the potential distance) that measures the dissimilarity between the diffused probabilities is computed. The informational distance is better suited for computing differences between probabilities than the Euclidean distance. See the text for a discussion. (F) The final PHATE embedding. The informational distances are embedded into low dimensions using MDS. Note that distances or affinities can be directly input to the appropriate step in cases of connectivity data. Therefore, the Euclidean distance or our constructed affinities can be replaced with distances or affinities that best describe the data. For example, in Figure S11D we replace our affinity matrix with the Facebook connectivity matrix.

For some data types, such as Hi-C chromatin conformation maps [15], the local relationships are encoded directly in the measurements. However, for most data types, the local similarities must be learned. We assume that component-wise, the data are well-modeled as lying on a manifold. Effectively this means that local relationships between data points, even noisy, are meaningful with respect to the overall structure of the data as they can be chained together to learn global relationships along the manifold. We apply a kernel function we developed (called the α-decay kernel) to Euclidean distances to accurately encode the local structure of the data even when the data is not uniformly sampled along the underlying manifold structure.

2. Encode global relationships in data using the potential distance (Figure 2D).

Diffusing through data is a concept that was popularized in the derivation of Diffusion Maps (DM) [13]. Diffusion is performed by first transforming the local similarities into probabilities that measure the probability of transitioning from one data point to another in a single step of a random walk and then powering this operator to t steps to give t-step walk probabilities. Thus both the local and global manifold distances are represented in the newly-calculated multi-step transition probabilities, referred to as the diffusion probabilities. For example, two points that have multiple potential, short paths that connect them will have a higher diffusion probability than two points that either have only long paths or relatively few paths connecting them. By considering all possible random walks, the diffusion process also denoises the data by downweighting spurious paths created by noise. However, directly embedding the diffusion probabilities into 2 or 3 dimensions via eigenvalue decomposition results in either a loss of information (Figure S1) or an unstable embedding (Figures S2A and S3D, respectively). In PHATE we interpret the diffusion probability of each point to all other points as the “global context of the datapoint,” and derive an information-theoretic potential distance between each pair of cells that compares the entire global context. Potential distance is computed as a divergence between the associated diffusion probability distributions of the two cells to all other cells. Thus the relationship of each cell to both near neighbors and distant points is accounted for in this distance. Notably, many divergences use a sublinear transformation of probability distributions (such as a logscale transformation) which prevents nearest neighbors from dominating the distance.

3. Embed potential distance information into low dimensions for visualization (Figure 2E-F).

The information in the potential distances are then squeezed into low dimensions for visualization via metric MDS, which creates an embedding by matching the distances in the low-dimensional space to the input distances. Unlike PCA, this ensures that all variability is squeezed into the two dimensions for a maximally informative embedding.

These steps are outlined in Table 1. All of these steps are necessary to create a good visualization that preserves local and global structure in the high-dimensional data, denoises the data, and presents as much information as possible in low dimensions. Further details on all of the steps of PHATE are included in Online Methods, Table S1, and Supplementary Note 1. PHATE is also robust to the choice of parameters (Online Methods and Figure S4) and produces the same results every time it is run, regardless of random seed (Figure S5).

Table 1:

General steps in the PHATE algorithm.

Input: Data matrix, algorithm parameters (see Online Methods) Output: The PHATE visualization
1:	Compute the pairwise distances from the data matrix.
2:	Transform the distances to affinities to encode local information.
3:	Learn global relationships via the diffusion process.
4:	Encode the learned relationships using the potential distance.
5:	Embed the potential distance information into low dimensions for visualization.

In addition to the exact computation of PHATE, we developed an efficient and scalable version of PHATE that produces near-identical results. In this version, PHATE uses landmark subsampling, sparse matrices, and randomized matrix decompositions. For more details on the scalability of PHATE see Online Methods, Table S2, and Figure S6, which shows the fast runtime of PHATE on datasets of different sizes, including a dataset of 1.3 million cells (2.5 hours) and a network of 1.8 million nodes (12 minutes).

Extracting Information from PHATE

PHATE embeddings contain a large amount of information on the structure of the data, namely, local transitions, progressions, branches or splits in progressions, and end states of progression. Here we present new methods that provide suggested end points, branch points, and branches based on the information from higher dimensional PHATE embeddings. These may not always correspond to real decision points, but provide an annotation to aid the user in interpreting the PHATE visual.

• Branch Point Identification with Local Intrinsic Dimensionality. In biological data, branch points often encapsulate switch-like decisions where cells sharply veer towards one of a small number of fates (see Figure S7A for an example). Identifying branch points is of critical importance for analyzing such decisions. We make a key observation that most points in PHATE plots of biological data lie on low-dimensional progressions with some noise as demonstrated in Figure 3Aii. Since branch points lie at the intersections of such progressions, they have higher local intrinsic dimensionality and can thus be identified by estimating the local intrinsic dimension. Figure 3Aii shows that points of intersection in the artificial tree data indeed have higher local intrinsic dimensionality than points on branches.

• Endpoint Identification with Diffusion extrema. We identify endpoints in the PHATE embedding as those that are least central and most distinct by computing the eigenvector centrality and the distinctness of a cellular state relative to the general data by considering the minima and maxima of diffusion eigenvectors (see Figure 3Ai). After identifying branch points and endpoints, the remaining points are assigned to branches between two branch points or between a branch point and endpoint using an approach based on the branch point detection method in [14] that compares the correlation and anticorrelation of neighborhood distances. Figure 3Aiii gives a visual demonstration of this approach and details are given in Online Methods. Figure 3B shows the results of our approach to identifying branch points, endpoints, and branches on an artificial tree dataset, a scRNA-seq dataset of bone marrow [16], and an iPSC CyTOF dataset [17]. Our procedure identifies the branches on the artificial tree perfectly and defines biologically meaningful branches on the other two datasets which we will use for data exploration.

Figure 3.

Extracting branches and branchpoints from PHATE. (A) Methods for identifying suggested endpoints, branch points, and branches. (i) PHATE computes a specialized diffusion operator as an intermediate step (Figure 2D). We use this diffusion operator to find endpoints. Specifically we use the the extrema of the corresponding diffusion components (eigenvectors of the diffusion operator) to identify endpoints [56]. (ii) Local intrinsic dimensionality is used to find branchpoints in a PHATE visual. As there are more degrees of freedom at branch points, the local intrinsic dimension is higher than through the rest of a branch. (iii) Cells in the PHATE embedding can be assigned to branches by considering the correlation between distances of neighbors to reference cells (e.g. branch points or endpoints). (B) Detected branches in the (i) artificial tree data, (ii) bone marrow scRNA-seq data from [16], and (iii) iPSC CyTOF data from [17].

Comparison of PHATE to Other Methods

Here we compare PHATE to multiple dimensionality reduction methods. We provide quantitative comparisons on simulated data where the ground truth is known, and provide a qualitative comparison using both simulated and real biological data.

Quantitative Comparisons.

Quantifying the accuracy of a dimensionality reduction for visualization is an open problem in machine learning [18-20] as it is generally impossible to greatly reduce the dimensionality of a dataset without loss of information. To quantify the quality of a visualization, we need a metric that judges whether a method preserves the information that is necessary for visual understanding. Prior work has focused on preserving pairwise distances or local neighborhoods [5, 21, 22]. However, these quantifications are not strictly desirable. For example, classical MDS is analytically the optimal solution to pairwise distance preservation in n dimensions [7]. However, MDS, as is visible in Figures S8 and S3, often does not produce clear or insightful visualizations for complex, nonlinear data. On the other hand, preserving local neighborhoods is the basis of the objective function for t-SNE [1], which fails to incorporate global structure and is hence insufficient for our purposes (Figure S3).

Prior work has also emphasized the utility of geodesic distances in computing both dimensionality reductions [4] and associated metrics [19]. Similar computations have been used to compare the output of trajectory inference algorithms [23]. However, this metric is insufficient for our use for two reasons: 1. unlike in trajectory inference, the raw data is noisy, and we wish to quantify the ability of a visualization method to denoise the data; and 2. geodesic distances on low-dimensional visualizations fail to capture the inherent meaning of curvature. Since visualizations do not suffer from the curse of dimensionality, we are able instead to use Euclidean distances, which capture the difference between straight and curved lines which are also meaningful to the human eye.

Hence, to quantitatively compare PHATE to other visualization methods, we formulated the Denoised Embedding Manifold Preservation (DEMaP) metric. DEMaP is designed to encapsulate the desirable properties of a dimensionality reduction method that is intended for visualization. These include: 1. the preservation of relationships in the data such that cells close together on the manifold are close together in the embedded space and cells that are far apart on the manifold are far apart in the embedding, including disconnected manifolds (e.g. clusters) which should be as well separated as possible; and 2. denoising, such that the low-dimensional embedding accurately represents the ground truth data and is as invariant as possible to biological and technical noise. DEMaP encapsulates each of these properties by comparing the geodesic distances on the noiseless data to the Euclidean distances of the embedding extracted from noisy data. An overview of DEMaP is presented in Figure 4A. See Online Methods for details.

Figure 4.

PHATE most accurately represents manifold distances in a 2D embedding. (A) Schematic description of performance comparison procedure. For each method and each type of corruption, Euclidean distances in the 2D embedding are compared to geodesic distances in an equivalent noiseless simulation by Spearman correlation. (B) Performance of 12 different methods across varying levels of corruption by dropout, decreased signal-to-noise ratio (BCV), randomly subsampled cells (subsample) and randomly subsampled genes (n_genes). Mean correlation of 20 runs for each configuration is shown. For further details see Table S3.

To compare the performance of PHATE to 12 dimensionality reduction methods, we simulated scRNA-seq data from Splatter [24]. Splatter uses a parametric model to generate data with various structures, such as branches or clusters. This simulated data provides a ground truth reference to which we can add various types of noise. We then use this noisy data as input for each dimensionality reduction algorithm, and quantify the degree to which each representation preserves local and global structures and denoises the data using DEMaP. To generate a diverse set of ground truth references, we simulated 50 datasets containing clusters and 50 datasets containing branches. See Online Methods for simulation details.

For each method, we used the default parameters and calculated DEMaP on each simulated dataset using different noise settings. The results are presented in Figure 4B and Table S3. We found that PHATE had the highest DEMaP score in 22/24 comparisons and was the top-performing method overall. UMAP was the second best performing method overall but had the highest DEMaP score in only two of the comparisons, one of which is equal with PHATE. We ran further tests on cluster data using the adjusted Rand Index [25] and found that on average PHATE preserves local cluster structure as well or better than t-SNE, UMAP, and PCA. The results are presented in Figure S9. From all of these results, we conclude that PHATE captures the true structure of high dimensional data more accurately than existing visualization methods.

Qualitative Comparisons.

In addition to the quantitative comparison, we can visually compare the embeddings provided by different methods. Figure 5 shows a comparison of the PHATE visualization to seven other methods on five single-cell datasets with known trajectory (Fig. 5A,D,E) and cluster (Fig. 5B-C) structures. We see that PHATE provides a clean and relatively denoised visualization of the data that highlights both the local and global structure: local clusters or branches are visually connected to each other in a global structure in each of the PHATE visualizations. Many of these branches are consistent with cell types or clusters validated by the authors [16, 17, 26, 27] and are also present in other visualizations such as force-directed layout and t-SNE, suggesting that the structures in the PHATE embedding reflect true structure in the dataset. However, force-directed layout tends to give a noisier visualization with fewer clear branches. Additionally, t-SNE [21] tends to shatter trajectories into clusters, creating the false impression that the data contain natural clusters. We characterize each of these visualizations in detail in Supplementary Note 2.

Figure 5.

Comparison of PHATE to other visualization methods on biological datasets. Columns represent different visualization methods, rows different datasets.

We obtained similar results by comparing PHATE to eleven methods on nine non-biological datasets, including four artificial datasets where the ground truth is known (Figure S3). Expanded comparisons on single-cell data, including additional datasets and visualization methods, are also included in Figure S8. See Supplementary Note 2 for a full discussion of each method in all of these comparisons.

Data Exploration with PHATE

PHATE can reveal the underlying structure of the data for a variety of datatypes. Supplementary Note 3 discusses PHATE applied to multiple different datasets, including SNP data, microbiome data, Facebook network data, Hi-C chromatin conformation data, and facial images (Figures S10 and S11). In this section, however, we show the insights gained through the PHATE visualization of this structure for single-cell data. See Online Methods for details on preprocessing steps.

We show that the identifiable trajectories in the PHATE visualization have biological meaning that can be discerned from the gene expression patterns and the mutual information between gene expression and the ordering of cells along the trajectories. We analyze the mouse bone marrow scRNA-seq [16] and iPSC CyTOF [17] datasets described previously. Our analysis of the iPSC CyTOF data is presented here while the analysis of the mouse bone marrow data is presented in Supplementary Note 3. For both of these datasets, we used our new methods for detecting branches and branch points. We then ordered the cells within each trajectory using Wanderlust [28] applied to higher-dimensional PHATE coordinates. We note that ordering could also be based on other pseudotime ordering software such as those in [14, 29-32]. To estimate the strength of the relationship between gene expression and cell ordering along branches, we estimated the DREMI score (a weighted mutual information that eliminates biases to reveal shape-agnostic relationships between two variables [33]) between gene expression and the Wanderlust-based ordering within each branch. Genes with a high DREMI score within a branch are changing along the branch. We also use PHATE to analyze the transcriptional heterogeneity in rod bipolar cells to demonstrate PHATE’s ability to preserve cluster structure (see Supplementary Note 3 and Figure S12A).

Figure S7C shows the mass cytometry dataset from [17] that shows cellular reprogramming with Oct4 GFP from mouse embryonic fibroblasts (MEFs) to induced pluripotent stem cells (iPSCs) at the single-cell resolution. The protein markers measure pluripotency, differentiation, cell-cycle and signaling status. The cellular embedding (with combined timepoints) by PHATE shows a unified embedding that contains five main branches, further segmented in our visualization, each corresponding to biology identified in [17]. Branch 2 contains early reprogramming intermediates with the correct set of reprogramming factors Sox2⁺/Oct4⁺/Klf4⁺/Nanog⁺ and with relatively low CD73 at the beginning of the branch. Branch 2 splits into two additional branches. Branches 4 and 6 (Figure S7) show the successful reprogramming to ESC-like lineages expressing markers such as Nanog, Oct4, Lin28 and Ssea1, and Epcam that are associated with transition to pluripotency [34]. Branch 5 shows a lineage that is refractory to reprogramming, does not express pluripotency markers, and is referred to as “mesoderm-like” in [17].

The other branches are similarly analyzed in Supplementary Note 3. In addition, the data features can be reweighted to obtain specific “views” of the data (see Supplementary Note 3 and Figure S13).

PHATE Analysis of Human ESC Differentiation Data

To test the ability of PHATE to provide novel insights in a complex biological system, we generated and analyzed scRNA-seq data from human embryonic stem cells (hESCs) differentiating as embryoid bodies (EB) [35], a system which has never before been extensively analyzed at the single-cell level. EB differentiation is thought to recapitulate key aspects of early embryogenesis and has been successfully used as the first step in differentiation protocols for certain types of neurons, astrocytes and oligodendrocytes [36-39], hematopoietic, endothelial and muscle cells [40-48], hepatocytes and pancreatic cells [49, 50], as well as germ cells [51, 52]. However, the developmental trajectories through which these early lineage precursors emerge from hESCs as well as their cellular and molecular identities remain largely unknown, particularly in human models.

We measured approximately 31,000 cells, equally distributed over a 27-day differentiation time course (Figure S14A and Online Methods). Samples were collected at 3-day intervals and pooled for measurement on the 10x Chromium platform. The PHATE embedding of the EB data revealed a highly ordered and clean cellular structure dominated by continuous progressions (Figures 1C and 6A), unlike other methods such as PCA or t-SNE (Figure S8). Exploratory analysis of this system using PHATE uncovered a comprehensive map of four major germ layers with both known and novel differentiation intermediates that were not captured with other visualization methods.

Figure 6.

PHATE analysis of embryoid body scRNA-seq data with n = 16, 285 cells. (A) i) The PHATE visualization colored by clusters. Clustering is done on a ten dimensional PHATE embedding. The number of cells in each cluster is given in Table S5. ii) The PHATE visualization colored by estimated local intrinsic dimensionality with selected branch points highlighted. iii) Branches and sub-branches chosen from contiguous clusters for analysis. (B) Lineage tree of the EB system determined from the PHATE analysis showing embryonic stem cells (ESC), the primitive streak (PS), mesoderm (ME), endoderm (EN), neuroectoderm (NE), neural crest (NC), neural progenitors (NP), and others. Red font indicates novel cell precursors. See supplemental videos S1, S2, and S3 for 3D PHATE visualizations of each stage in the tree. (C) PHATE embedding overlaid with each of the populations in the lineage tree. Other abbreviations include lateral plate ME (LP ME), hemangioblast (H), cardiac (C), epicardial precursors (EP), smooth muscle precursors (SMP), cardiac precursors (CP), and neuronal subtypes (NS). (D) Heatmap showing the EMD score between the cluster distribution and the background distribution for each gene. Relevant genes for identifying the main lineages were manually identified. Genes are organized according to their maximum EMD score. The number of cells in each cluster is given in Table S5. (E) The EMD scores of the top scoring surface markers in the targeted sub-branches (sub-branches iii and vii). (F) Scatter plots of the bulk transcription factor expression vs. the mean single-cell transcription factor expression in sub-branches iii (left, n = 2,537 cells) and vii (right, n = 1,314 cells). The Spearman correlation coefficients are calculated for n = 1,213 transcription factors.

A Comprehensive Lineage Map of Embryoid Bodies from PHATE

Importantly, PHATE retained global structure and organization of the data as is evidenced by the retention of a strong time trend in the embedding, although sample time was not included in creating the embedding. Further, PHATE revealed greater phenotypic diversity at later time points as seen by the larger space encompassed by the embedding at days 18 to 27 (Figure 1C).

This phenotypic heterogeneity was further analyzed by both an automated analysis (see Supplementary Note 4, Figure 6A, and Tables S4 and S5) and by manual examination of the embedding in conjunction with the established literature on germ layer development (Figure S14B). For the manual analyses, we used 80 markers from the literature to identify populations along the PHATE map which gave rise to a detailed germ layer specification map (Figure 6B, Videos S1, S2, and S3). These populations are shown on the PHATE visualization in Figure 6C. In the lineage tree, the dots are the populations and the arrows represent transitions between the populations. Our map shows in detail how hESCs give rise to germ layer derivatives via a continuum of defined intermediate states.

Novel Transitional Populations in Embryoid Bodies

The comprehensive nature of the lineage map generated from the PHATE embedding allowed us to identify novel transitional populations that have not yet been characterized. Three novel pre-cursor states were identified in both manual and automated analyses: a bi-potent NC and NP pre-cursor, a novel EN precursor, and a novel cardiac precursor.

Within the ectodermal lineage, differentiation begins with the induction of pre-NE state characterized by downregulaton of POU5F1 and induction of OTX2. This state is resolved into two precursors, NE-1 (GBX2+ZIC2/5+) and NE-2 (GBX2+OLIG2+HOXD1+). While NE-1 neuroectoderm appeared to develop along the canonical NE specification route and expressed a set of well established anterior NE markers (ZIC2/5, PAX6, GLI3, SIX3/6), the NE-2 neuroectoderm gave rise to a bi-potent HOXA2+HOXB1+ precursor that subsequently separated into the NC branch and neural progenitor (NP) branch. Given its potential to generate both NE and NC cell types, the HOXA2+HOXB1+ precursor could represent the equivalent of the neural plate border cells that have been defined in model organisms [53, 54].

Within the EN branch, the canonical EOMES+FOXA2+SOX17+ EN precursor was clustered together with the novel EOMES−FOXA2−GATA3+SATB1+KLF8+ precursor, which further differentiated into cells expressing posterior EN markers NKX2-1, CDX2, ASCL2, and KLF5. Finally, a novel T+GATA4+ CER1+PROX1+ cardiac precursor cell was identified within the ME lineage that gave rise to TNNT2+ cells via a GATA6+HAND1+ differentiation intermediate.

A more detailed analysis of the novel and canonical cell types derived from the PHATE embedding is given in Supplementary Note 4.

Experimental Validation of PHATE-Identified Lineages

We next used the ability of PHATE to extract data on specific regions within the visualization to define a set of surface markers for the isolation and molecular characterization of specific cell populations within the EB differentiation process.

We focused on two specific regions that correspond to the NC branch (sub-branch iii, Figure 6Aiii) and cardiac precursor sub-branch within the ME branch (sub-branch vii, Figure 6Aiii). Differential expression analysis identified a set of candidate markers for each region (Figures 6D-E). We focused on markers with a high Earth Mover’s Distance (EMD) [55] score in the targeted sub-branch, and low EMD scores in all other sub-branches (see Online Methods for more details on the EMD). Based on these analyses and the availability of antibodies, CD49D/ITGA4 was chosen for the neural crest (the highest scoring surface marker for sub-branch iii) while CD142/F3 and CD82 were chosen for cardiac precursors (among the top 6% of surface markers and the top 3% of all genes by EMD). We FACS-purified CD49d+CD63− and CD82+CD142+ and performed bulk RNA-sequencing (Figure S14F) on these sorted populations.

To verify that we isolated the correct regions, we calculated the Spearman correlation between the gene expression pattern of each cell and the bulk RNA-seq data from the CD49d+CD63− sorted cells (Figures 6F and S14D). The correlation coefficient was the highest in the neural crest branch (branch iii), which corresponds to the highest expression of CD49d. Similar results were obtained for the cardiac precursor cells (Figures 6F and S14E).

Taken together, our analyses show that PHATE has the potential to greatly accelerate the pace of biological discovery by suggesting hypotheses in the form of finely grained populations and identifying markers with which to isolate populations. These populations can be probed further using alternative measurements such as epigenetic or protein expression assays.

Discussion

With large amounts of high-dimensional high-throughput biological data being generated in many types of biological systems, there is a growing need for interpretable visualizations that can represent structures in data without strong prior assumptions. However, most existing methods are highly deficient at retaining structures of interest in biology. These include clusters, trajectories or progressions of various dimensionality, hybrids of the two, as well as local and global nonlinear relations in data. Furthermore, existing methods have trouble contending with the sizes of modern datasets and the high degree of noise inherent to biological datasets. PHATE provides a unique solution to these problems by creating a diffusion-based informational geometry from the data, and by preserving a divergence metric between datapoints that is sensitive to near and far manifold-intrinsic distances in the dataspace. Additionally, PHATE is able to offer clean and denoised visualizations because the information geometry created in PHATE is based on data diffusion dynamics which are robust to noise. Thus, PHATE reveals intricate local as well as global structure in a denoised way.

We applied PHATE to a wide variety of datasets, including single-cell CyTOF and RNA-seq data, as well as Gut Microbiome and SNP data, where the datapoints are subjects rather than cells. We also tested PHATE on network data, such as Hi-C and Facebook networks. In each case, PHATE was able to reveal structures of visual interest to humans that other methods entirely miss. Moreover, we have implemented PHATE in a scalable way that enables it to process millions of datapoints in a matter of hours. Hence, PHATE can efficiently handle the datasets that are now being produced using single-cell RNA sequencing technologies.

To showcase the ability of PHATE to explore data generated in new systems, we applied PHATE to our newly generated human EB differentiation dataset consisting of roughly 31,000 cells sampled over a differentiation time course. We found that PHATE successfully resolves cellular heterogeneity and correctly maps all germ layer lineages and branches based on scRNA-seq data alone, without any additional assumptions on the data. Through detailed sub-population and gene expression analysis along these branches we identified both canonical and novel differentiation intermediates. The insights obtained with PHATE in this system will be a valuable resource for researchers working on early human development, human ES cells, and their regenerative medicine applications.

We expect numerous biological, but also non-biological, data types to benefit from PHATE, including applications in high-throughput genomics, phenotyping, and many other fields. As such, we believe that PHATE will revolutionize biomedical data exploration by offering a new way of visualizing, exploring and extracting information from large scale high-dimensional data.

Methods

Here we present an expanded explanation of our computational methods, experimental methods, and data processing steps. For the computational details, we first provide a detailed overview of the PHATE algorithm followed by a robustness analysis of PHATE with respect to the parameters and the number of datapoints. We then provide details on the scalable version of PHATE, identifying branch points and branches, and the EMD score analysis.

The embedding provided by PHATE is designed for visualizing global and local structure in the data in exploratory settings with the following properties in mind: 1) The visualization should capture the relevant structure in low (2-3) dimensions. 2) The visualization should preserve and emphasize global and local structure including transitions and clusters. 3) The visualization is denoised to enable data exploration. 4) The visualization is robust in the sense that the revealed structure is insensitive to user configurations.

The mathematical steps of PHATE are provided in Table S1. We now provide further details about each of the steps in the PHATE algorithm and we explain how these steps ensure that PHATE meets the four properties described above. For even further mathematical details of the algorithm, see Supplementary Note 1.

Distance Preservation

Consider the common approach of linearly embedding the raw data matrix itself, e.g., with PCA, to preserve the global structure of the data. PCA finds the directions of the data that capture the largest global variance. However, in most cases local transitions are noisy and global transitions are nonlinear. Therefore, linear notions such as global variance maximization are insufficient to capture latent patterns in the data, and they typically result in a noisy visualization (Figure S3, Column 2). To provide reliable structure preservation that emphasizes transitions in the data, we need to consider the intrinsic structure of the data. This implies and motivates preserving distances between data points (e.g., cells) that consider gradual changes between them along these nonlinear transitions (Figure 2A-B).

Local Affinities and the Diffusion Operator

A standard choice of a distance metric is the Euclidean distance. However, global Euclidean distances are not reflective of transitions in the data, especially in biological datasets that have nonlinear and noisy structures. For instance, cells sampled from a developmental system, such as hematopoiesis or embryonic stem cell differentiation, show gradual changes where adjacent cells are only slightly different from each other. But these changes quickly aggregate into nonlinear transitions in marker expression along each developmental path. Therefore, we transform the global Euclidean distances into local affinities that quantify the similarities between nearby (in the Euclidean space) data points (Figure 2C).

A common approach to transforming global (e.g. Euclidean) distances to local similarities is to apply a kernel function to all pairs of points. A popular kernel function is the Gaussian kernel k_ε(x, y) = exp(∓∥x – y∥²/ε) that quantifies the similarity between the two points x and y based on their Euclidean distance. The bandwidth ε determines the radius (or spread) of neighborhoods captured by this kernel. Let $\mathcal{X}\subset {\mathbb{R}}^d$ be a dataset with N points sampled i.i.d. from a probability distribution $p:{\mathbb{R}}^d\to [0,\infty )$ (with ∫ p(x)dx = 1) that is essentially supported on a low dimensional manifold ${\mathcal{M}}^m\subseteq {\mathbb{R}}^d$, where m is the dimension of $\mathcal{M}$ and m ≪ d. A kernel matrix that includes all pairwise measures of local affinity is constructed by computing the kernel function between all pairs of points in $\mathcal{X}$.

Embedding local affinities directly can result in a loss of global structure as is evident in t-SNE (Figures 1, 5, S8, and S3) or kernel PCA embeddings. For example, t-SNE only preserves data clusters, but not transitions between clusters, since it does not enforce any preservation of global structure. In contrast, a faithful structure-preserving embedding (and visualization) needs to go beyond local affinities (or distances), and also consider global relations between parts of the data. To accomplish this, PHATE is based on constructing a diffusion geometry to learn and represent the shape of the data [13, 57, 58]. This construction is based on computing local similarities between data points, and then walking or diffusing through the data using a Markovian random-walk diffusion process to infer more global relations (Figure 2D).

The initial probabilities in this random walk are calculated by normalizing the row-sums of the kernel matrix. In the case of the Gaussian kernel described above, we obtain the following:

$${\nu }_{\epsilon }(x)=\Vert k_{\epsilon }(x,\cdot ){\Vert }_1=\sum _{z\in \mathcal{X}}{k}_{\epsilon }(x,z)$$ (1)

resulting in a N × N row-stochastic matrix

$$[P_{\epsilon }{]}_{(x,y)}=\frac{k_{\epsilon }(x,y)}{{\nu }_{\epsilon }(x)},x,y\in \mathcal{X}.$$ (2)

The matrix P_ε is a Markov transition matrix where the probability of moving from x to y in a single time step is given by Pr[x → y] = [P_ε]_(x,y). This matrix is also referred to as the diffusion operator.

The α-decaying Kernel and Adaptive Bandwidth

When applying the diffusion map framework to data, the choice of the kernel K and bandwidth ε plays a key role in the results. In particular, choosing the bandwidth corresponds to a tradeoff between encoding global and local information in the probability matrix P_ε. If the bandwidth is small, then single-step transitions in the random walk using P_ε are largely confined to the nearest neighbors of each data point. In biological data, trajectories between major cell types may be relatively sparsely sampled. Thus, if the bandwidth is too small, then the neighbors of points in sparsely sampled regions may be excluded entirely and the trajectory structure in the probability matrix P_ε will not be encoded. Conversely, if the bandwidth is too large, then the resulting probability matrix P_ε loses local information as [P_ε]_(x,·) becomes more uniform for all $x\in \mathcal{X}$, which may result in an inability to resolve different trajectories. Here, we use an adaptive bandwidth that changes with each point to be equal to its kth nearest neighbor distance, along with an α-decaying kernel that controls the rate of decay of the kernel.

The original heuristic proposed in [13] suggests setting ε to be the smallest distance that still keeps the diffusion process connected. In other words, it is chosen to be the maximal 1-nearest neighbor distance in the dataset. While this approach is useful in some cases, it is greatly affected by outliers and sparse data regions. Furthermore, it relies on a single manifold with constant dimension as the underlying data geometry, which may not be the case when the data is sampled from specific trajectories rather than uniformly from a manifold. Indeed, the intrinsic dimensionality in such cases differs between mid-branch points that mostly capture one-dimensional trajectory geometry, and branching points that capture multiple trajectories crossing each other.

This issue can be mitigated by using a locally adaptive bandwidth that varies based on the local density of the data. A common method for choosing a locally adaptive bandwidth is to use the k-nearest neighbor (NN) distance of each point as the bandwidth. A point x that is within a densely sampled region will have a small k-NN distance. Thus, local information in these regions is still preserved. In contrast, if x is on a sparsely sampled trajectory, the k-NN distance will be greater and will encode the trajectory structure. We denote the k-NN distance of x as ε_k(x) and the corresponding diffusion operator as P_k.

A weakness of using locally adaptive bandwidths alongside kernels with exponential tails (e.g., the Gaussian kernel) is that the tails become heavier (i.e., decay more slowly) as the bandwidth increases. Thus for a point x in a sparsely sampled region where the k-NN distance is large, [P_k]_(x,·) may be close to a fully-supported uniform distribution due to the heavy tails, resulting in a high affinity with many points that are far away. This can be mitigated by using the following kernel

$$K_{k,\alpha }(x,y)=\frac{1}{2}\text{exp}\left(-{\left(\frac{\Vert x-y{\Vert }_2}{{\epsilon }_k(x)}\right)}^{\alpha }\right)+\frac{1}{2}\text{exp}\left(-{\left(\frac{\Vert x-y{\Vert }_2}{{\epsilon }_k(y)}\right)}^{\alpha }\right),$$ (3)

which we call the α-decaying kernel. The exponent α controls the rate of decay of the tails in the kernel K_k,α. Increasing α increases the decay rate while decreasing α decreases the decay rate. Since α = 2 for the Gaussian kernel, choosing α > 2 will result in lighter tails in the kernel K_k,α compared to the Gaussian kernel. We denote the resulting diffusion operator as P_k,α. This is similar to common utilizations of Butterworth filters in signal processing applications [59]. See Figure S2B for a visualization of the effect of different values of α on this kernel function.

Our use of a locally adaptive bandwidth and the kernel K_k,α requires the choice of two tuning parameters: k and α. k should be chosen sufficiently small to preserve local information, i.e., to ensure that [P_k,α]_(x,·) is not a fully-supported uniform distribution. However, k should also be chosen sufficiently large to ensure that the underlying graph represented by P_k,α is sufficiently connected, i.e., the probability that we can walk from one point to another within the same trajectory in a finite number of steps is nonzero.

The parameter α should also be chosen with k. α should be chosen sufficiently large so that the tails of the kernel K_k,α are not too heavy, especially in sparse regions of the data. However, if k is small when α is large, then the underlying graph represented by P_k,α may be too sparsely connected, making it difficult to learn long range connections. Thus we recommend that α be fixed at a large number (e.g. α ≥ 10) and then k can be chosen sufficiently large to ensure that points are locally connected. In practice, we find that choosing k to be around 5 and α to be about 10 works well for all the data sets presented in this work. However, the PHATE embedding is robust to the choice of these parameters as discussed later in the Online Methods.

In addition to progression or trajectory structures, the recommendations provided in this section work well for visualizing data that naturally separate into distinct clusters. In particular, the α-decay kernel ensures that relationships are preserved between distinct clusters that are relatively close to each other.

Propagating Affinities via Diffusion

Here we discuss diffusion, i.e., raising the diffusion operator to its t-th power as shown in Table S1 (Figure 2D). To simplify the discussion we use the notation P for the diffusion operator, whether defined with a fixed-bandwidth Gaussian kernel or our adaptive kernel. This matrix is referred to as the diffusion operator, since it defines a Markovian diffusion process that essentially only allows single-step transitions within local data neighborhoods whose sizes depend on the kernel parameters (ε or k and α). In particular, let $x\in \mathcal{X}$ and let δ_x be a Dirac at x, i.e., a row vector of length N with a one at the entry corresponding to x and zeros everywhere else. The t-step distribution of x is the row in $P_{\epsilon }^t$ corresponding to x:

$$p_x^t\triangleq {\delta }_x{P}^t=[P^t{]}_{(x,\cdot )}.$$ (4)

These distributions capture multi-scale (where t serves as the scale) local neighborhoods of data points, where locality is considered via random walks that propagate over the intrinsic manifold geometry of the data. This provides a global and robust intrinsic data distance that preserving the overall structure of the data. In addition to learning the global structure, powering the diffusion operator has the effect of low-pass filtering the data such that the main pathways in it are emphasized and small noise dimensions are diminished, thus achieving the denoising objective of our method as well.

Choosing the Diffusion Time Scale t with Von Neumann Entropy

The diffusion time scale t is an important parameter that affects the embedding. The parameter t determines the number of steps taken in a random walk. A larger t corresponds to more steps compared to a smaller t. Thus, t provides a tradeoff between encoding local and global information in the embedding. The diffusion process can also be viewed as a low-pass filter where local noise is smoothed out based on more global structures. The parameter t determines the level of smoothing. If t is chosen to be too small, then the embedding may be too noisy. On the other hand, if t is chosen to be too large, then some of the signal may be smoothed away.

We formulate a new algorithm for choosing the timescale t. Our algorithm quantifies the information in the powered diffusion operator with various values of t. This is accomplished by computing the spectral or Von Neumann Entropy (VNE) [60, 61] of the powered diffusion operator. The amount of variability explained by each dimension is equal to its eigenvalue in the eigendecomposition of the related (non-Markov) affinity matrix that is conjugate to the Markov diffusion operator. The VNE is calculated by computing the Shannon entropy on the normalized eigenvalues of this matrix. Due to noise in the data, this value is artificially high for low values of t, and rapidly decreases as one powers the matrix. Thus, we choose values that are around the ”knee” of this decrease.

More formally, to choose t, we first note that its impact on the diffusion geometry can be determined by considering the eigenvalues of the diffusion operator, as the corresponding eigenvectors are not impacted by the time scale. To facilitate spectral considerations and for computational ease, we use a symmetric conjugate

$$[A{]}_{(x,y)}=\sqrt{\nu (x)}[P{]}_{(x,y)}∕\sqrt{\nu (y)}$$

of the diffusion operator P with the row-sums ν. This symmetric matrix is often called the diffusion affinity matrix. The VNE of this diffusion affinity is used to quantify the amount of variability. It can be verified that the eigenvalues of A^t are the same as those of P^t, and furthermore these eigenvalues are given by the powers $\{{\lambda }_i^t{\}}_{i=1}^{N-1}$ of the spectrum of P. Let η(t) be a probability distribution defined by normalizing these (nonnegative) eigenvalues as $[\eta (t){]}_i={\lambda }_i^t∕{\sum }_{j=0}^{N-1}{\lambda }_j^t$. Then, the VNE H(t) of A^t (and equivalently of P^t) is given by the entropy of η(t), i.e.,

$$H(t)=-\sum _{i=1}^N[\eta (t){]}_i\log [\eta (t){]}_i,$$ (5)

where we use the convention of 0 log(0) ≜ 0. The VNE H(t) is dominated by the relatively large eigenvalues, while eigenvalues that are relatively small contribute little. Therefore, it provides a measure of the number of the relatively significant eigenvalues.

The VNE generally decreases as t increases. As mentioned previously, the initial decrease is primarily due to a denoising of the data as less significant eigenvalues (likely corresponding to noise) decrease rapidly to zero. The more significant eigenvalues (likely corresponding to signal) decrease much more slowly. Thus the overall rate of decrease in H(t) is high initially as the data is denoised but then low for larger values of t as the signal is smoothed. As t → ∞, eventually all but the first eigenvalue decrease to zero and so H(t) → 0.

To choose t, we plot H(t) as a function of t as in the first plot of Figure S2C. Choosing t from among the values where H(t) is decreasing rapidly generally results in noisy visualizations and embeddings (second plot in Figure S2C). Very large values of t result in a visualization where some of the branches or trajectories are combined together and some of the signal is lost (fourth plot in Figure S2C). Good PHATE visualizations can be obtained by choosing t from among the values where the decrease in H(t) is relatively slow, i.e. the set of values around the “knee” in the plot of H(t) (third plot in Figure S2C and the PHATE visualizations in Figure 1). This is the set of values for which much of the noise in the data has been smoothed away, and most of the signal is still intact. The PHATE visualization is fairly robust to the choice of t in this range, as discussed later in this section.

In the code, we include an automatic method for selecting t based on a knee point detection algorithm that finds the knee by fitting two lines to the VNE curve [62]. This algorithm calculates the error between the VNE plot and two lines fitted to the data. The first line has endpoints at the first VNE value and the suggested knee point. The second line has endpoints at the suggested knee point and the last VNE value. The suggested knee point with the minimum error is selected.

Potential Distances

To resolve instabilities in diffusion distances and embed the global structure captured by the diffusion geometry in low (2 or 3) dimensions, we use a novel diffusion-based informational distance, which we call potential distance (Figure 2E). It is calculated by computing the distance between log-transformed transition probabilities from the powered diffusion operator. The key insight in formulating the potential distance is that an informational distance between probability distributions is more sensitive to global relationships (between far-away points) and more stable at boundaries of manifolds than straight point-wise comparisons of probabilities (i.e., diffusion distances). This is because the diffusion distance is sensitive to differences between the main modes of the diffused probabilities and is largely insensitive to differences in the tails. In contrast, the potential distance, or more generally informational distances, use a submodular function (such as a log) to render distances sensitive to differences in both the main modes and the tails. This gives PHATE the ability to preserve both local and manifold-intrinsic global distances in a way that is optimized for visualization. The resulting metric space also quantifies differences between energy potentials that dominate “heat” propagation along diffusion pathways (i.e., based on the heat-equation diffusion model) between data points, instead of simply considering transition probabilities along them.

The potential distance is inspired by information theory and stochastic dynamics, both fields where probability distributions are compared for different purposes. First, in information theory literature, information divergences are used to measure discrepancies between probability distributions in the information space rather than the probability space, as they are more sensitive to differences between the tails of the distributions as described above. Second, when analyzing dynamical systems of moving particles, it is not the point-wise difference between absolute particle counts that is used to compare states, but rather the ratio between these counts. Indeed, in the latter case the Boltzmann Distribution Law directly relates these ratios to differences in the energy of a state in the system. Therefore, similar to the information theory case, dynamical states are differentiated in energy terms, rather than probability terms. We employ the same reasoning in our case by defining our potential distance using localized diffusion energy potentials, rather than diffusion transition probabilities.

To go from the probability space to the energy (or information) space, we log transform the probabilities in the powered diffusion operator and consider an L² distance between these localized energy potentials in the data as our intrinsic data distance, which forms an M-divergence between the diffusion probability distributions [63, 64]. Mathematically, if $U_x^t=-\log (p_x^t)$ for $x\in \mathcal{X}$, then the t-step potential distance is defined as

$${\mathfrak{V}}^t(x,y)=\Vert U_x^t-U_y^t{\Vert }_2,x,y\in \mathcal{X}.$$ (6)

To give a more intuitive view, consider two points x and y that are on different sides of a line of points W = {w₁, w₂,… ,w_n} (See Figure 2E), suppose that there is a small set of distant points Z = {z₁, z₂,…, z_n} that are on the same side of W as y but opposite side as x such that they are twice as far from x as from y. The representation of each point x is as its t-step diffusion probability to all other points. So to compute the potential distance between x and y we compare these probabilities. What is the right type of distance to measure the distinction between these two probability distributions? One solution has been the diffusion distance which is simply the Euclidean distance between these probability distributions. However, in the example mentioned above the diffusion distance would be dominated by larger probabilities and the probabilities to the Z points would not affect the distance from x to y perhaps making them seem close. But instead, we take a divergence between the probabilities from x and y by first log-scale transforming the probabilities and then taking their Euclidean distance, which makes the distance sensitive to fold-change. Thus, if a probability of 0.01 from x to a point z_i is changed to 0.02 from y then this has the same effect as if the probabilities had been 0.1 and 0.2. Thus, PHATE is sensitive to small differences in probability distribution corresponding to differences in long-range global structure, which allows PHATE to preserve global manifold relationships using this potential distance.

We note that the potential distance is a particular case of a wider family of diffusion-based informational distances that view the diffusion geometry as a statistical manifold in information geometry. See Supplementary Note 1 for details on this family of distances.

Embedding the Potential Distances in Low Dimensions

A popular approach for embedding diffusion geometries is to use the eigendecomposition of the diffusion operator to build a diffusion map of the data. However, this approach tends to isolate progression trajectories into numerous diffusion coordinates (i.e., eigenvectors of the diffusion operator; see Figure S1). In fact, this specific property was used in [14] as a heuristic for ordering cells along specific developmental tracks. Therefore, while diffusion maps preserve global structure and denoise the data, their higher intrinsic dimensionality is not amenable for visualization. Instead, we squeeze the variability into low dimensions using metric multidimensional scaling (MDS), a distance embedding method (Figure 2F).

There are multiple approaches to MDS. Classical MDS (CMDS) [7] takes a distance matrix as input and embeds the data into a lower-dimensional space as follows. The squared potential distance matrix is double centered:

$$B=-\frac{1}{2}J{\mathfrak{V}}^{t(2)}J,$$ (7)

where ${\mathfrak{V}}^{t(2)}$ is the squared potential distance matrix (i.e. each entry is squared) and $J=I-\frac{1}{N}{11}^T$ with 1 a vector of ones with length N. The CMDS coordinates are then obtained by an eigendecomposition of the matrix B. This is equivalent to minimizing the following “strain” function:

$$\text{Strain}({\widehat{x}}_1,\dots ,{\widehat{x}}_N)=\sqrt{\sum _{i,j}(B_{ij}-\langle {\widehat{x}}_i,{\widehat{x}}_j\rangle {)}^2/\sum _{i,j}{B}_{ij}^2},$$ (8)

over embedded m-dimensional coordinates ${\widehat{x}}_i\in {\mathbb{R}}^m$ of data points in $\mathcal{X}$. We apply CMDS to the potential distances of the data to obtain an initial configuration of the data in low dimension m.

While classical MDS is computationally efficient relative to other MDS approaches, it assumes that the input distances directly correspond to low-dimensional Euclidean distances, which is overly restrictive in our setting. Metric MDS relaxes this assumption by only requiring the input distances to be a distance metric. Metric MDS then embeds the data into lower dimensions by minimizing the following “stress” function:

$$\text{Stress}({\widehat{x}}_1,\dots ,{\widehat{x}}_N)=\sqrt{\sum _{i,j}{\left({\mathfrak{V}}_{(x_i,x_j)}^t-\Vert {\widehat{x}}_i-{\widehat{x}}_j\Vert \right)}^2/\sum _{i,j}{\left({\mathfrak{V}}_{x_i,x_j}^t\right)}^2}.$$ (9)

over embedded m-dimensional coordinates ${\widehat{x}}_i\in {\mathbb{R}}^m$ of data points in $\mathcal{X}$.

If the stress of the embedded points is zero, then the input data is faithfully represented in the MDS embedding. The stress may be nonzero due to noise or if the embedded dimension m is too small to represent the data without distortion. Thus, by choosing the number of MDS dimensions to be m = 2 (or m = 3) for visualization purposes, we may trade off distortion in exchange for readily visualizable coordinates. However, some distortion of the distances/dissimilarities is tolerable in many of our applications since precise dissimilarities between points on two different trajectories are not important as long as the trajectories are visually distinguishable. By using metric MDS, we find an embedding of the data with the desired dimension for visualization and the minimum amount of distortion as measured by the stress. When analyzing the PHATE coordinates (e.g. for clustering or branch detection), we use metric MDS with m chosen to explain most of the variance in the data as determined by the eigenvalues of the diffusion operator (as is done for von Neumann entropy). In this case, minimal distortion is introduced into the analysis.

A naïve approach towards obtaining a truly low dimensional embedding of diffusion geometries is to directly apply metric MDS, from the diffusion map space to a two dimensional space. However, as seen in Figures S3 (Column 5) and S8, direct embedding of these distances produces distorted visualizations. Embedding the potential distances (defined in Def. 1) is more stable at boundary conditions near end points compared to diffusion maps, even in the case of simple curves that contain no branching points. Figure S2A shows a half circle embedding with diffusion distances versus distances between log-scaled diffusion. We see that points are compressed towards the boundaries of the figure in the former. Additionally, this figure demonstrates that in the case of a full circle (i.e., with no end points or boundary conditions), our potential embedding (PHATE) yields the same representation as diffusion maps.

PHATE achieves an embedding that satisfies all four properties delineated previously: PHATE preserves and emphasizes the global and local structure of the data via: 1. a localized affinity that is chained via diffusion to form global affinities through the intrinsic geometry of the data, 2. denoises the data by low-pass filtering through diffusion, 3. provides a distance that accounts for local and global relationships in the data and has robust boundary conditions for purposes of visualization, and 4. captures the data in low dimensions, using MDS, for visualization.

We have shown by demonstration in Figures S3 and S8 that all of the steps of PHATE, including the potential transform and MDS, are necessary, as diffusion maps, t-SNE on diffusion maps, and MDS on diffusion maps fail to provide an adequate visualization in several benchmark test cases with known ground truth (even when using the same customized α-decaying kernel we developed for PHATE). We have also shown that PHATE is robust to the choice of parameters.

Robustness Analysis of PHATE

Here we show that the PHATE embedding is robust to subsampling and the choice of parameters. We demonstrate this both qualitatively and quantitatively. For the quantitative demonstrations, we simulated scRNA-seq data using the Splatter package [24] as in Section . We first calculated the geodesic pairwise distances for the noiseless data. Then for each setting, we calculated the pairwise Euclidean distances in the 2-dimensional embedding. We then compared the geodesic distances with the embedded distances via the Spearman correlation coefficient to compute DEMaP. We used both the paths and groups options of the Splatter package. Simulation details are discussed later in Online Methods.

Table S3 shows that PHATE is robust to subsampling on the Splatter datasets. For the paths dataset, the average Spearman correlation is the same when 95% and 50% of the data points are retained. For the groups dataset, the correlation drops slightly when going from 95% retention to 50% retention. Additionally, the correlation coefficient is still quite high (and better than all other methods) when only 5% of the data points are retained. Thus, quantitatively, PHATE is robust to subsampling.

We also demonstrate this visually. We ran PHATE on the iPSC mass cytometry dataset from [17] with varying subsample sizes N. Figure S4A shows the PHATE embedding for N = 1000, 2500, 5000, 10000. Note that the primary branches or trajectories that are visible when N = 50000 (Figure S7C) are still visible for all subsamples. Thus, PHATE is robust to the subsampling size. Similar results can be obtained on other datasets.

We also show that the PHATE embedding is robust to the choice of t, k, and α. Figure S4B shows the PHATE embedding on the iPSC mass cytometry dataset from [17] with varying scale parameter t. This figure shows that the embeddings for 50 ≤ t ≤ 200 are nearly identical. Thus, PHATE is very visually robust to the scale parameter t. Similar results can be obtained on other datasets and with the k and α parameters.

The embedding is also quantitatively robust to the parameter choices. Figure S4C-D shows heatmaps of the Spearman correlation coefficient between geodesic distances of the ground truth data and the Euclidean distances of the PHATE visualization applied to the simulated Splatter datasets for different values of k, t, and α. For α ≤ 10, the correlation coefficients are very similar for all values of k, t, and α. This demonstrates that PHATE is robust to the choices of these parameters.

Scalability of PHATE

The native form of PHATE is limited in scalability due to the computationally intensive steps of computing potential distances between all pairs of points, computing metric MDS, and storing in memory the diffused operator. Thus, we describe here, and in Table S2, an alternative way to compute a PHATE embedding that is highly scalable and provides a good approximation of the native PHATE described previously. The scalable version of PHATE uses a slight difference in computing t-step diffusion probabilities between points. It requires that every other step that the diffusion takes goes through one of a small number of “landmarks.” Each landmark is selected to be a central point that is representative of a portion of the manifold, selected by spectrally clustering manifold dimensions.

First, we construct the α-decaying kernel on the entire dataset. This can be calculated efficiently and stored as a sparse matrix by using radius-based nearest neighbor searches and thresholding (i.e., setting to zero) connections between points below a specified value (e.g., 0.0001), as we regard them numerically insignificant for the constructed diffusion process. The resulting affinity matrix K_k,α will be sparse as long as α is sufficiently large (e.g., α ≥ 10) to enforce sharp decay of the captured local affinities. The full diffusion operator P is constructed from K_k,α by normalizing by row-sums as described previously.

However, powering the sparse diffusion operator would result in a dense matrix, causing memory issues. To avoid this, we instead perform diffusion between points via a series of M landmarks where M < N. We select the landmarks by first applying PCA to the diffusion operator and then using k-means clustering on the principal components to partition the data into M clusters. This is a variation on spectral clustering. We then calculate the probability of transitioning in a single step from the i-th point in $\mathcal{X}$ to any point in the j-th cluster for all pairs of points and clusters. Mathematically, we can write this as

$$P_{NM}(i,j)=\sum _{\xi \in C_j}P(i,\xi )$$ (10)

where C_j is the set of points in the jth cluster. Thus, we can view each cluster as being represented by a landmark and the (i, j)-th entry in P_NM gives the probability of transitioning from the ith point in $\mathcal{X}$ to the j-th landmark in a single step. Similarly, we construct the matrix P_MN where the (j, i)-th entry contains the probability of transitioning from the j-th landmark to the i-th point in $\mathcal{X}$. In this case, we cannot simply sum the transition probabilities P(ξ, i), ξ ∈ C_j, since we also have to consider the prior probability Q(j, ξ) of the ξ-th point (with ξ ∈ C_j) being the source of a transition from a cluster C_j. For this purpose we use the prior proposed in [65], and write

$$P_{MN}(j,i)=\sum _{\xi \in C_j}Q(j,\xi )P(\xi ,i)$$ (11)

with Q(j, ξ) = ∑_i K_k,α (ξ, i)/∑_ζ∈Cj ∑_i K_k,α (ζ, i).

We use the two constructed transition matrices to compute P_MM = P_MNP_NM, which provides the probability of transitioning from landmark to landmark in a random walk by walking through the full point space. Diffusion is then performed by powering the matrix P_MM. This can be written as

$$P_{MM}^t=P_{MN}{P}_{NM}{P}_{MN}{P}_{NM}\dots P_{MN}{P}_{NM}.$$ (12)

From this expression, we see that powering the matrix P_MM is equivalent to taking a random walk between landmarks by walking from landmarks to points and then back to landmarks t times.

We then embed the landmarks into the PHATE space by calculating the potential distances between landmarks and applying metric MDS to the potential distances. Denote the resulting embedding as Y_landmarks. We then perform an out of sample extension to all points from the landmarks by multiplying the point to landmark transition matrix P_NM by Y_landmarks to get

$$Y_{\text{points}}=P_{NM}{Y}_{\text{landmarks}}.$$ (13)

Since M is chosen to be vastly less than N, the memory requirements and computational demands of the powering the diffusion operator and embedding the potential distances are much lower.

The described steps are summarized in Table S2. In Figure S6A-E we show that this constrained diffusion preserves distances between datapoints in the final PHATE embedding, with the scalable version giving near-identical results to the exact computation of PHATE. Further, in Figure S6B we show that the embedding achieved by this approach is robust to the number of landmarks chosen.

We note that if the only computational bottleneck were in computing MDS, scalable versions of MDS could be used [8, 66, 67]. However, since storing the entries of the powered diffusion operator in memory is also an issue, we employ the use of landmarks earlier in the process. It has also been shown that “compressing” the process of diffusion through landmarks in the fashion described here performs better than simply applying Nystrom extension (which includes landmark MDS [66]) to diffusion maps [68].

The fast version of PHATE was used in Figures 5, S8, S3, S2D, S6A-E, S13, and S12. All other plots were generated using the exact version of PHATE.

To demonstrate the scalability of PHATE for data exploration on large datasets, we applied PHATE to the 1.3 million mouse brain cell dataset from 10x [69]. Figure S6C shows a comparison of PHATE to t-SNE, colored by 10 of the 60 clusters provided by 10x. We see that PHATE retains cluster coherence while t-SNE shatters some of the cluster structure.

Branch Identification

Here we describe the methods we developed for identifying branches in a PHATE visualization and selecting representative branch- and endpoints.

We use the estimated local intrinsic dimensionality to identify branch points. We can regard intrinsic dimensionality in terms of degrees of freedom in the progression modeled by PHATE. If there is only one fate possible for a cell (i.e. a cell lies on a branch as in Figure 3Aii) then there are only two directions of transition between data points—forward or backward—and the local intrinsic dimension is low. If on the other hand, there are multiple fates possible, then there are at least three directions of transition possible—a single direction backwards and at least two forward. This cannot be captured by a one dimensional curve and will require a higher dimensional structure such as a plane, as shown in Figure 3Aii. Thus, we can use the concept of local intrinsic dimensionality for identifying branch points.

We used the local intrinsic dimension estimation method derived in [70, 71] to provide suggested branch points. This method uses the relationship between the radius and volume of a d-dimensional ball. The volume increases exponentially with the dimensionality of the data. So as the radius increases by δ, the volume increases by δ^d where d is the dimensionality of the data. Thus the intrinsic dimension can be estimated via the growth rate of a k-nn ball with radius equal to the k-nn distance of a point. The procedure is as follows. Let Z_n = (z₁,…, z_n} be a set of independent and identically distributed random vectors with values in a compact subset of ${\mathbb{R}}^d$. Let ${\mathcal{N}}_{k,j}$ be the k nearest neighbors of z_j; i.e. ${\mathcal{N}}_{k,j}=\{\mathbf{z}\in {\mathbf{Z}}_n\setminus \{{\mathbf{z}}_j\}:\Vert \mathbf{z}-{\mathbf{z}}_j\Vert \le {ϵ}_k({\mathbf{z}}_j)\}$. The k-nn graph is formed by assigning edges between a point in Z_n and its k-nearest neighbors. The power-weighted total edge length of the k-nn graph is related to the intrinsic dimension of the data and is defined as

$${\mathbf{L}}_{\gamma ,k}({\mathbf{Z}}_n)=\sum _{i=1}^n\sum _{\mathbf{z}\in {\mathcal{N}}_{k,i}}\Vert \mathbf{z}-{\mathbf{z}}_i{\Vert }^{\gamma },$$ (14)

where γ > 0 is a power weighting constant. Let m be the global intrinsic dimension of all the data points in Z_n. It can be shown that for large n,

$${\mathbf{L}}_{\gamma ,k}({\mathbf{Z}}_n)=n^{\beta (m)}c+{ϵ}_n,$$ (15)

where β(m) = (m–γ)/m, ϵ_n is an error term that decreases to 0 as n → ∞, and c is a constant with respect to β(m) [70]. A global intrinsic dimension estimator $\widehat{\mathbf{m}}$ can be defined based on this relationship using non-linear least squares regression over different values of n [70, 71].

A local estimator of intrinsic dimension $\tilde{\mathbf{m}}(i)$ at a point z_i can be defined by running the above procedure in a smaller neighborhood about z_i. This approach is demonstrated in Figure 3A, where a k-nn graph is grown locally at each point in the data. However, this estimator can have high variance within a neighborhood. To reduce this variance, majority voting within a neighborhood of z_i can be performed:

$$\widehat{\mathbf{m}}(i)=\underset{\ell }{\text{arg}\max }\sum _{{\mathbf{z}}_j\in {\mathcal{N}}_{k,i}}1(\tilde{m}(j)=\ell ),$$ (16)

where $1(\cdot )$ is the indicator function [71].

We note that other local intrinsic dimension estimation methods could be used such as the maximum likelihood estimator in [72].

We also identify endpoints in the PHATE embedding. These points can correspond to the beginning or end-states of differentiation processes. For example, Figure S7A shows the PHATE visualization of the iPSC CyTOF dataset from [17] with highlighted endpoints, or end-states, of the reprogrammed and refractory branches. While many major endpoints can be identified by inspecting the PHATE visualization, we provide a method for identifying other endpoints or end-states that may be present in the higher dimensional PHATE embedding. We identify these states using data point centrality and distinctness as described below.

First, we compute the centrality of a data point by quantifying the impact of its removal on the connectivity of the graph representation of the data (as defined using the local affinity matrix K_k,α). Removing a point that is on a one dimensional progression pathway, either branching point or not, breaks the graph into multiple parts and reduces the overall connectivity. However, removing an endpoint does not result in any breaks in the graph. Therefore we expect endpoints to have low centrality, as estimated using the eigenvector centrality measure of K_k,α.

Second, we quantify the distinctness of a cellular state relative to the general data. We expect the beginning or end-states of differentiation processes to have the most distinctive cellular profiles. As shown in [56] we quantify this distinctness by considering the minima and the maxima of diffusion eigenvectors (see Figure 3Ai). Thus we identify endpoints in the embedding as those that are most distinct and least central.

After identifying branch points and endpoints, the remaining points can be assigned to branches between two branch points or between a branch point and endpoint. Due to the smoothly-varying nature of centrality and local intrinsic dimension, the previously described procedures identify regions of points as branch points or endpoints rather than individual points. However, it can be useful to reduce these regions to representative points for analysis such as branch detection and cell ordering. To do this, we reduce these regions to representative points using a “shake and bake” procedure similar to that in [73]. This approach groups collections of branch points or endpoints together into representative points based on their proximity.

Let ${\mathcal{V}}_n=\{v_1,\dots ,v_n\}$ be the set of branch points and endpoints in the high-dimensional PHATE coordinates that we wish to reduce. We create a Voronoi partitioning of these points as follows. We first permute the order of ${\mathcal{V}}_n$, which we denote as ${\mathcal{V}}_n^{\prime }=\{v_{1^{\prime }},\dots ,v_{n^{\prime }}\}$. We then take the first point v_1′ and find all the points in ${\mathcal{V}}_n^{\prime }$ that are within a distance of h, where h is a scale parameter provided by the user. These points (including v_1′) are assigned to the first component of the partition and removed from the set ${\mathcal{V}}_n^{\prime }$. This process is then repeated until all points in V_n are assigned to the partition. To ensure that each point is assigned to the nearest component of the partition (as measured by proximity to the centroid), we next calculate the distance of each point to all centroids of the partition, and reassign the point to the component with the nearest centroid. This reassignment process is repeated until a stable partition is achieved. This completes the process of constructing the Voronoi partition.

The Voronoi partition constructed from this process may be sensitive to the ordering of the points in ${\mathcal{V}}_n^{\prime }$. To reduce this sensitivity, we repeat this process multiple times (e.g., 40-100) to create multiple Voronoi partitions. We then construct a distance between points by estimating the probability that two points are not in the same component from this partitioning process. This provides a notion of distance that is robust to noise, random permutations, and the scale parameter h. We then partition the data again using the above procedure except we use these probability-based distances. The representative points are then selected from the resulting centroids of this final partition.

A representative point is labeled an endpoint if the corresponding collection of points contains one or more endpoints as identified using centrality and distinctness. Otherwise, the representative point is labeled a branch point.

After representative points have been selected, the remaining points can be assigned to corresponding branches. We use an approach based on the branch point detection method in [14] that compares the correlation and anticorrelation of neighborhood distances. However, we use higher dimensional PHATE coordinates instead of the diffusion maps coordinates. Figure 3Aiii gives a visual demonstration of this approach. Here we consider two reference cells X and Y. We wish to determine if cells Q1 and Q2 belong to the branch between X and Y or not. Consider Q1 first which does belong to this branch. If we move from Q1 towards X, we also move farther away from Y. Thus the distances to X and Y of a neighborhood of points around Q1 (which will be located on the branch) are negatively correlated with each other. Now consider Q2 which does not belong to the branch between X and Y. In this case, if we move from Q2 towards Y, we also move closer to X. Thus the distances to X and Y of a neighborhood of points around Q2 are positively correlated with each other. In practice, these distance-based correlations are computed for each possible branch and the point is assigned to the branch with the largest anticorrelation (i.e. the most negative correlation coefficient).

EMD Score Analysis

The EMD is measure of dissimilarity between two probability distributions that is particularly popular in computer vision [74]. The EMD was chosen to perform differential expression analysis in the EB scRNA-seq data due to its stability in estimation compared to other divergence measures. Intuitively, if each distribution is viewed as a pile of dirt, the EMD can be thought of as the minimum cost of converting one pile of dirt into the other. If the distributions are identical, then the cost is zero. When comparing univariate distributions (as we do as we only consider a single gene at a time), the EMD simplifies to the L¹ distance between the cumulative distribution functions [55]. That is, if P and Q are the cumulative distributions of densities p and q, respectively, then the EMD between p and q is ∫ ∣P(x) – Q(x)∣dx. While the EMD is nonnegative, we assign a sign to the EMD score based on the difference between the medians of the distributions.

Biological Methods

The processes for generating the EB data and for preprocessing the biological data are described here.

Generation of Human Embryoid Body Data

Low passage H1 hESCs were maintained on Matrigel-coated dishes in DMEM/F12-N2B27 media supplemented with FGF2. For EB formation, cells were treated with Dispase, dissociated into small clumps and plated in non-adherent plates in media supplemented with 20% FBS, which was prescreened for EB differentiation. Samples were collected during 3-day intervals during a 27 day-long differentiation timecourse. An undifferentiated hESC sample was also included (Figure S14A). Induction of key germ layer markers in these EB cultures was validated by qPCR (data not shown). For single cell analyses, EB cultures were dissociated, FACS sorted to remove doublets and dead cells and processed on a 10x genomics instrument to generate cDNA libraries, which were then sequenced. Small scale sequencing determined that we have successfully collected data on 31,161 cells distributed throughout the timecourse. After preprocessing the data as described below, we are left with 16,825 cell measurements for data analysis. See also the Life Sciences Reporting Summary for further details.

Data Preprocessing

Here we discuss methods we used to preprocess the various datasets.

Data Subsampling: The full PHATE implementation scales well for sample sizes up to approximately N = 50000. For N much larger than 50000, computational complexity can become an issue due to the multiple matrix operations required. All of the scRNAseq datasets considered in this paper have N < 50000. Thus, we used the full data and did not subsample these datasets. However, the mass cytometry datasets have much larger sample sizes. To aid in branch analysis, we randomly subsampled these datasets for analysis in Section using uniform subsampling. For the comparison figures (Figures 5, S3, and S8), scalable PHATE was used and subsampling was not performed except as indicated in the figures. The PHATE embedding is robust to the number of samples chosen, which we demonstrated in Section .

Mass Cytometry Data Preprocessing: We process the mass cytometry datasets according to [75].

Single-Cell RNA-Sequencing Data Preprocessing: This data was processed from raw reads to molecule counts using the Cell Ranger pipeline [76]. Additionally, to minimize the effects of experimental artifacts on our analysis, we preprocess the scRNAseq data. We first filter out dead cells by removing cells that have high expression levels in mitochondrial DNA. In the case of the EB data which had a wide variation in library size, we then remove cells that are either below the 20th percentile or above the 80th percentile in library size. scRNA-seq data have large cell-to-cell variations in the number of observed molecules in each cell or library size. Some cells are highly sampled with many transcripts, while other cells are sampled with fewer. This variation is often caused by technical variations due to enzymatic steps including lysis efficiency, mRNA capture efficiency, and the efficiency of multiple amplification rounds [77]. Removing cells with extreme library size values helps to correct for these technical variations. We then drop genes that are only expressed in a few cells and then perform library size normalization. Normalization is accomplished by dividing the expression level of each gene in a cell by the library size of the corresponding cell.

After normalizing by the library size, we take the square root transform of the data and then perform PCA to improve the robustness and reliability of the constructed affinity matrix K_k,α. We choose the number of principal components to retain approximately 70% of the variance in the data which results in 20-50 principal components.

Gut Microbiome Data Preprocessing: We use the cleaned L6 American Gut data and remove samples that are near duplicates of other samples. We then preprocess the data using a similar approach for scRNA-seq data. We first perform “library size” normalization to account for technical variations in different samples. We then log transform the data and then use PCA to reduce the data to 30 dimensions.

Applying PHATE to this data reveals several outlier samples that are very far from the rest of the data. We remove these samples and then reapply PHATE to the log-transformed data to obtain the results that are shown in Figure 1D.

ChIP-seq Processing for Hi-C Visualization: We used narrow peak bed files and took the average peak intensity for each bin at a 10 kb resolution. For visualization, we smoothed the average peak intensity values based on location using a 25 bin moving average.

DEMaP

To quantitatively compare each dimensionality reduction tool, we wish to calculate the degree to which each method preserves the underlying structure of the reference dataset and removes noise. Since single-cell RNA-sequencing and other biological types of data are highly noisy, visual renderings of the data that can offer denoised embeddings that reveal the underlying structure of the data are desirable. Therefore, the goal of our accuracy metric is to quantify the correspondence between distances in the low-dimensional embedding and manifold distances in the ground truth reference.

To define a quantitative notion of manifold distance we use geodesic distances. Geodesic distances are shortest path distances on a nearest-neighbor graph of the data weighted by the Euclidean distances between connected points [4]. In cases where points are sampled noiselessly from a manifold, such as in our ground truth reference, geodesic distances converge exactly to distances along the manifold of the data [4, 78]. Thus we reason that if geodesic distances between points on the noiseless manifold are preserved by an embedding computed on the noisy data then the data is sufficiently denoised and the manifold structure is also preserved.

We take this approach to formulate our ground-truth manifold distance as a quantification of the degree to which each dimensionality reduction method preserves the pairwise geodesic distances of the noiseless data after low-dimensional embedding of the corresponding noisy data. Since the low dimensional embedding is often a result of a non-linear dimensionality reduction, curves and major paths in the data are “straightened” such that Euclidean distances in the embedding space correspond to manifold distance in the high dimensional space [7]. Thus we quantify the preservation of manifold distances as the correlation between geodesic distance in the noiseless reference dataset and Euclidean distances in the embedding space as a measure of structure preservation which we call Denoised Embedding Manifold Preservation (DEMaP). An overview of DEMaP is presented in Figure 4A.

Construction of the Artificial Tree Test Case

The artificial tree data shown in Figure 1B is constructed as follows. The first branch consists of 100 linearly spaced points that progress in the first four dimensions. All other dimensions are set to zero. The 100 points in the second branch are constant in the first four dimensions with a constant value equal to the endpoint of the first branch. The next four dimensions then progress linearly in this branch while all other dimensions are set to zero. The third branch is constructed similarly except the progression occurs in dimensions 9-12 instead of dimensions 5-8. All remaining branches are constructed similarly with some variation in the length of the branches. We then add 40 points at each endpoint and branch point and add zero mean Gaussian noise with a standard deviation of 7. This construction models a system where progression along a branch corresponds to an increase in gene expression in several genes. Prior to adding noise, we also constructed a small gap between the first branch point and the orange branch that splits into a blue and purple branch (see the top set of branches in the left part of Figure 1B). This simulates gaps that are often present in measured biological data. We also added additional noise dimensions, bringing the total dimensionality of the data to 60.

Splatter Simulation Details

Splatter is a scRNA-seq simulation package that uses a parametric model to generate data with various structures, such as branches or clusters [24]. We use Splatter to simulate multiple ground truth datasets for multiple experiments. To select parameters for the simulation, we fit the Splatter simulation to the EB data, and then modified the resulting dataset from both the Splatter ”paths” and the Splatter “groups” simulations as described in Section . Note that we do not make use of Splatter’s built-in dropout function, since it uses a zero-inflated model; multiple studies have shown that an undersampling (binomial) model is more appropriate [79-83]. Each simulation is performed with 3000 simulated cells. The mean correlation coefficient and standard deviations are calculated from 20 trials.

To generate a diverse set of ground truth references, we simulated 50 datasets containing clusters and 50 datasets containing branches. In each of these simulated datasets, the number and size of the clusters of branches as well as the global position of the clusters or branches with respect to each other is random. Furthermore, the local relationships between individual cells on these structures is random. Finally, the changes in gene expression within clusters or along branches is random. The output of this simulation is the ground truth reference.

Next, we add biological and technical noise to the reference data. First, to simulate stochastic gene expression we use Splatter’s Biological Coefficient of Variation (BCV) parameter, which controls the level of gene expression in each cell following an inverse gamma distribution. Second, to simulate the inefficient capture of mRNA in single cells, we undersample from the true counts using the default BCV. Third, to demonstrate robustness to varying of total genes measured, we randomly remove genes from the data matrix. Finally, to demonstrate robustness to the number of cells captured, we randomly remove cells from each dataset. We vary each of these parameters, including by default some degree of biological variation and mRNA undersampling to each simulation.

The default parameters used in the simulation are the following:

• batchCells=3000	• out.prob=0.016
• nGenes=17580	• out.facLoc=5.4
• mean.shape=6.6	• out.facScale=0.90
• mean.rate=0.45	• bcv.common=0.18
• lib.loc=9.1	• bcv.df=21.6
• lib.scale=0.33	• de.prob=0.2

We also set dropout.type="none", with a post-hoc binomial dropout of 50%. For the groups simulation we drew the number of groups n from a Poisson distribution with rate λ = 10, and then drew the group.prob parameter from a Dirichlet distribution with n categories and a uniform concentration α₁ = ⋯ = α_n = 1. For the paths simulation, we set group.prob as above, and additionally set the ith entry in the parameter path.from as a random integer between 0 and i – 1, drew the parameter path.nonlinearProb from a uniform distribution on the interval (0, 1), and drew the parameter path.skew from a beta distribution with shape α = 10, β = 10. Note that here the library size was doubled from the fit value, since the EB data itself suffers from dropout. To reduce the number of genes for the n_genes simulation, we randomly removed genes post-hoc in order to avoid changing the state of the random number generator in building the simulation.

For the ground truth simulations, we set bcv.common to 0, did not perform binomial dropout, and did not remove genes or cells. For the BCV simulation, we performed 50% post-hoc binomial dropout, did not remove genes or cells, and set bcv.common to 0, 0.25, and 0.5. For the dropout simulation, we set bcv.common to 0.18, did not remove genes or cells, and performed 0%, 50%, and 95% post-hoc binomial dropout. For the subsample simulation, we set bcv.common to 0.18, performed 50% post-hoc binomial dropout, did not remove genes, and subsampled rows of the matrix to retain 95%, 50%, and 5% of the total cells. For the n_genes simulation, we set bcv.common to 0.18, performed 50% post-hoc binomial dropout, did not remove cells, and subsampled columns of the matrix to retain 17000, 10000, and 2000 genes.

PHATE Experimental Details

For all of the quantitative comparisons, we have used the default parameter settings for the PHATE plots. For the majority of the qualitative comparisons in Figures 5, S8, and S3, we also used the default parameter settings for all methods. Exceptions to this are the artificial tree (Figure S3A), the intersecting circles (Figure S3D), and the MNIST dataset (Figure S3I). In these cases, the PHATE parameters have been tuned to give a clearer separation of the branches. However, in general, the default PHATE settings give good results on most datasets, especially those that are complex, high-dimensional, and noisy as demonstrated empirically in Section . The default settings are also used in Figures S2D, S6A-E, S13, and S12. For all other PHATE plots, the parameters were tuned slightly to better highlight the structure of the data.

Data Availability

The embryoid body scRNA-seq and bulk RNA-seq datasets generated and analyzed during the current study are available in the Mendeley Data repository at:

http://dx.doi.org/10.17632/v6n743h5ng.1 Figure S14A contains images of the raw single cells while Figure S14F contains scatter plots showing the gating procedure for FACS sorting cell populations for the bulk RNA-seq data.

Code Availability

Python, R, and Matlab implementations of PHATE are available on GitHub, for academic use: https://github.com/KrishnaswamyLab/PHATE

Supplementary Material

Supp. Video 1

Supplemental Video S1: Rotating video of 3D PHATE visualizations of the endoderm branch of the EB scRNA-seq data colored by the geometric mean of selected genes at each stage of the lineage specification tree in Figure 6B.

Supp. Video 2

Supplemental Video S2: Rotating video of 3D PHATE visualizations of the mesoderm branch of the EB scRNA-seq data colored by the geometric mean of selected genes at each stage of the lineage specification tree in Figure 6B.

Supp. Video 3

Supplemental Video S3: Rotating video of 3D PHATE visualizations of the neuroectoderm branches of the EB scRNA-seq data colored by the geometric mean of selected genes at each stage of the lineage specification tree in Figure 6B.

Supp. Video 4

Supplemental Video S4: Video showing the PHATE visualization (left) for the Frey Face datase used in Roweis and Saul (Science, vol. 290, no. 5500, pp. 2323-2326, 2000) (right). PHATE reveals multiple branches in the data that correspond to different poses. Two of the branches are highlighted in this video. The corresponding point in the PHATE visualization is highlighted as the video progresses.

Supp. Video 5

Supplemental Video S5: Rotating 3D PHATE visualization of chromosome 1 in the Hi-C data from Darrow et al. (Proceedings of the National Academy of Sciences, p. 201609643, 2016) at 10 kb resolution. Multiple folds are clearly visible in the visualization.

Supp. Video 6

Supplemental Video S6: Rotating 3D PHATE visualization of all chromosomes in the Hi-C data from Darrow et al. (Proceedings of the National Academy of Sciences, p. 201609643, 2016) at 50 kb resolution. The embedding resembles the fractal globule structure proposed in Lieberman-Aiden et al. (Science, vol. 326, no. 5950, pp. 289-293, 2009).