Abstract
Long non-coding RNAs (long ncRNAs, lncRNAs) of all kinds have been implicated in a range of cell developmental processes and diseases, while they are not translated into proteins. Inferring diseases associated lncRNAs by computational methods can be helpful to understand the pathogenesis of diseases, but those current computational methods still have not achieved remarkable predictive performance: such as the inaccurate construction of similarity networks and inadequate numbers of known lncRNA–disease associations. In this research, we proposed a lncRNA–disease associations inference based on integrated space projection scores (LDAI-ISPS) composed of the following key steps: changing the Boolean network of known lncRNA–disease associations into the weighted networks via combining all the global information (e.g., disease semantic similarities, lncRNA functional similarities, and known lncRNA–disease associations); obtaining the space projection scores via vector projections of the weighted networks to form the final prediction scores without biases. The leave-one-out cross validation (LOOCV) results showed that, compared with other methods, LDAI-ISPS had a higher accuracy with area-under-the-curve (AUC) value of 0.9154 for inferring diseases, with AUC value of 0.8865 for inferring new lncRNAs (whose associations related to diseases are unknown), with AUC value of 0.7518 for inferring isolated diseases (whose associations related to lncRNAs are unknown). A case study also confirmed the predictive performance of LDAI-ISPS as a helper for traditional biological experiments in inferring the potential LncRNA–disease associations and isolated diseases.
Keywords: disease similarity, lncRNA similarity, space projection, computational prediction model
1. Introduction
Long non-coding RNAs (LncRNAs) are a type of RNA, defined as being transcripts with lengths exceeding 200 nucleotides that are not translated into protein, which exist in all kinds of organisms widely [1,2]. A growing number of studies have found that mutations and dysregulations of lncRNAs cause a variety of diseases, including cervical cancer [3,4], colorectal cancer [5,6], ovarian cancer [7,8,9], prostate cancer [10,11], and diabetes [12,13]. Therefore, lncRNAs could be used as biomarkers for the early diagnosis and prognosis of corresponding cancers, which motivates the identification and confirmation of the associations between lncRNAs and diseases to become a research focus. The lncRNA related databases (such as LncRNAdb [14], LncRNADisease [15], NRED [16], and NONCODE [17]) provide strong data support on which the computational prediction models can be built to provide more accurate experimental targets as well as an effective supplement to biological experiments [18,19,20,21,22]:
Provide guidance with less cost and time for the subsequent biological experimental verification related to complex diseases;
Speed up our understanding on the pathogenesis of complex diseases;
Give new ideas for disease prevention, diagnosis, treatment, and prognosis;
Have a profound implication on drug development and medical improvement.
The computational models used for inferring lncRNA–disease associations have been divided into two main categories: machine learning-based inference and network-based inference.
In recent years, machine learning has been used to infer lncRNA–disease associations [23,24,25,26,27,28,29]. Zhao et al. [30] integrated multi-omic data, genomic, regulome, and transcriptome with naïve Bayesian classifier models to predict lncRNA–cancer associations, and successfully identified 707 potential cancer-related lncRNAs. Yu et al. [24] utilized the naïve Bayesian classifier to predict lncRNA–disease associations after constructing the global tripartite network and the global quadruple network. Lan et al. [31] used bagging support vector machine (SVM) to predict lncRNA–disease association based on multiple biological data resources fused by the matrix geometric mean. How to obtain the negative samples is the huge challenge that all of the above-mentioned machine learning based methods have to face. Normally, the unlabeled lncRNA–disease associations are those that cannot be found in a finite number of biological experiments, which are selected randomly to be the negative samples. Therefore, selecting the unknown associations as the negative samples randomly is unreasonable and will undoubtedly have a serious impact on the accuracy of prediction results, because it cannot mean that these associations do not exist. For overcoming that the negative sample cannot be obtained accurately, Chen et al. [32] proposed a semi-supervised learning framework (LRLSLDA) based on Laplacian Regularized Least Squares, without needing negative samples. LRLSLDA still has some defects, like needing too many parameters and low prediction accuracy. Considering that the accurate similarity network construction is beneficial to improve the prediction accuracy, Chen et al. [33] used the hyper geometric distribution to infer lncRNA–disease associations (HGLDA) without relying on known experimentally verified lncRNA–disease associations, but HGLDA cannot be used for isolated diseases and new lncRNAs.
The hypothesis that lncRNAs with similar functions tend to be related to similar diseases is the foundation of those network-based methods [34,35,36]. Chen et al. [37] proposed a new method named LNCSIM that only used the information of common ancestors to calculate the similarity without retaining the hierarchical structure of Directed Acyclic Graphs (DAGs) of diseases, which led to being more vulnerable to information bias in DAGs. Huang et al. [38] proposed an edge-based computational model ILNCSIM by integrating lncRNA–disease associations and disease DAGs. However, the prediction results of ILNCSIM were affected for lack of unlabeled but existing associations. Chen et al. [39] proposed a fuzzy measure-based lncRNA functional similarity calculation model (FMLNCSIM) that achieved better performance but still suffered from the information bias in DAGs. Inspired by social network analysis, Chen et al. [40] utilized Katz Centrality on network topology to predict lncRNA–disease associations. The predicted results were biased toward those diseases that had more related lncRNAs found from the known associations. Cheng et al. [41] proposed an integrative framework to predict novel lncRNA–disease associations, but the prediction result heavily relied on the integrated network and was easily affected by data incompleteness. Ding et al. [42] inferred the lncRNA–disease associations via lncRNA–disease–gene tripartite graph (TPGLDA), but TPGLDA depended on the topology of a tripartite graph whose data incompleteness may affect the predictive performance. Shi et al. [43] proposed a graph regression-based unified framework (GRUF) for the inference of lncRNA–disease associations including the inference of isolated diseases and new lncRNAs. GRUF provided more information on the relationships between a pair of lncRNA and disease instead of only a binary result. However, the prediction results may be affected by the quality of the dataset as well as those lncRNAs with low expression level. Numerous researchers introduced random walk into the prediction of lncRNA–disease associations [44,45,46,47,48,49,50,51,52,53,54]. Sun et al. [55] executed random walk with restart (RWR) on lncRNA functional similarity network to infer lncRNA–disease associations. Zhou et al. [56] implemented RWR on a heterogeneous network, which cannot avoid producing some biased predictions. Yao et al. [57] integrated genes, lncRNAs, phenotypes, and their associations into a multi-level composite network with which they implemented a RWR algorithm to identify candidate lncRNA–disease associations. Although this method can be used for isolated disease prediction, its prediction accuracy depended on the topology of the composite network and was affected by incompleteness and biases of data. The selection of a seed vector that was produced from known lncRNA–disease associations had a great influence on the predictive performance of the above-mentioned random walk algorithms. It caused the prediction results of the models that used the random walk algorithms to heavily depend on the known lncRNA–disease associations. Therefore, identifying diseases-related lncRNAs is still in its initial phase with following limitations:
Most of the off-the-shelf computational models cannot be used for inferring isolated diseases and new lncRNAs directly;
Supervised learning of machine learning needs a negative sample to train the class classifier, but such negative sample cannot be obtained;
Those that only rely on the known network topology will produce biased prediction results.
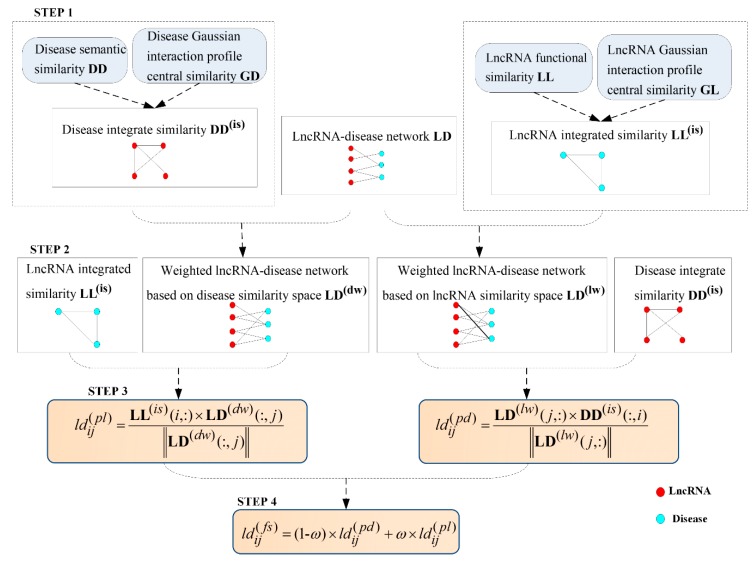
Considering above limitations, we proposed a novel lncRNA–disease associations inference based on space projections of integrated networks (LDAI-ISPS) that contained the following four steps: step one, reconstruct the disease (lncRNA) integrated similarities network via integrating multiple network information; step two, change the Boolean network of known experimentally verified associations into the weighted network for further inferring the associations between lncRNAs and diseases accurately; step three, utilize the vector projections of the vectors coming from the networks of the above two steps to construct space projection scores; step four, obtain the final prediction results by integrating two kinds of space projection sores. Finally, LOOCV experiments and the case study showed that, without needing negative samples, LDAI-ISPS not only achieved excellent predictive performance, but also can be used for isolated diseases and new lncRNAs.
2. Results
2.1. Influence of Parameter Selection on Performance
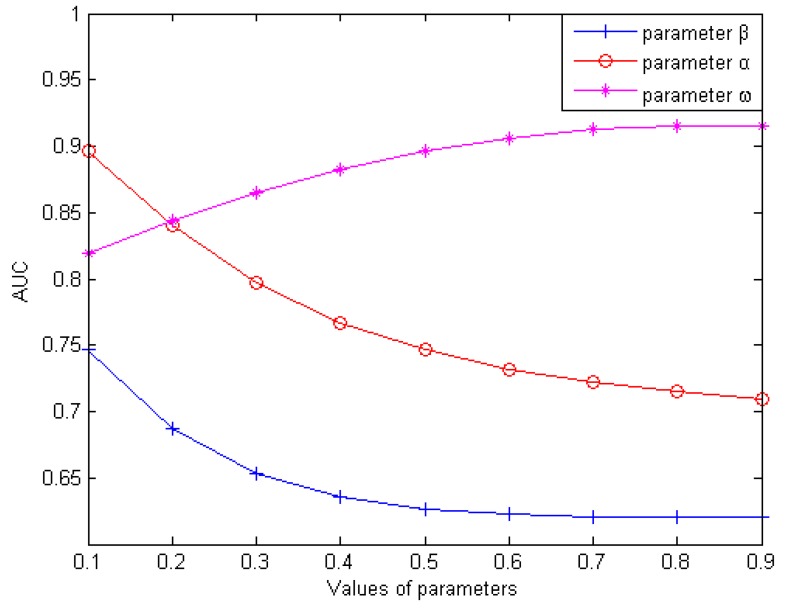
In this section, we mainly discuss how to obtain the optimum values that were the values when corresponding AUC values were highest with three weighting parameters (weighting parameter used for the reconstruction of , weighting parameter used for the reconstruction of , weighting parameter used for the integration of and ). Firstly, we analyzed how the value of influenced the predictive validity of LDAI-ISPS with setting and as 0.5 for simplicity. With increasing the value of from 0.1 to 0.9 (with a step size of 0.1), we performed LOOCV on the dataset to calculate the AUC values (can be seen in Figure 1). We found that AUC was obtained the optimum value of 0.7463 when was set to 0.1, and then AUC values decreased gradually. AUC obtained the minimum value of 0.6204 when was set to 0.9. Secondly, after setting to be 0.1 and to be 0.5, we performed LOOCV to observe the corresponding AUC values with increasing from 0.1 to 0.9 (with step size of 0.1). Similarly, we found that AUC obtained the optimum value of 0.893915 when was set to 0.1, and then AUC values decreased gradually. Based on above two steps (setting ), we performed LOOCV to calculate the corresponding AUC values with increasing from 0.1 to 0.9 (with step size of 0.1). We found that AUC obtained the optimum value of 0.9154 when was set to 0.8. In conclusion, we set and to obtain the corresponding optimal AUC values.
Figure 1.
Influence of parameter variation on model prediction accuracy.
2.2. Comparison with Other Methods
2.2.1. Evaluation Metrics of Performance
LOOCV experiments were implemented for evaluating the predictive performance of LDAI-ISPS in inferring the latent lncRNA–disease associations. We divided the dataset into two parts. In one part, each known association in was observed in turn as a test data, and in the other part, the remaining known associations were used as the training data. Under the framework of LOOCV, we compared the prediction results with on some specific threshold to obtain the following four metrics: true positive (TP), false positive (FP), false negative (FN), true negative (TN). Furthermore, according to some specified thresholds, we calculated the true positive rate () against false positive rate () with which we plotted out the receiver operating characteristic curve (ROC). The area under the ROC curve (AUC) was finally calculated to assess the overall predictive performance of LDAI-ISPS.
2.2.2. Comparison Results on Performance
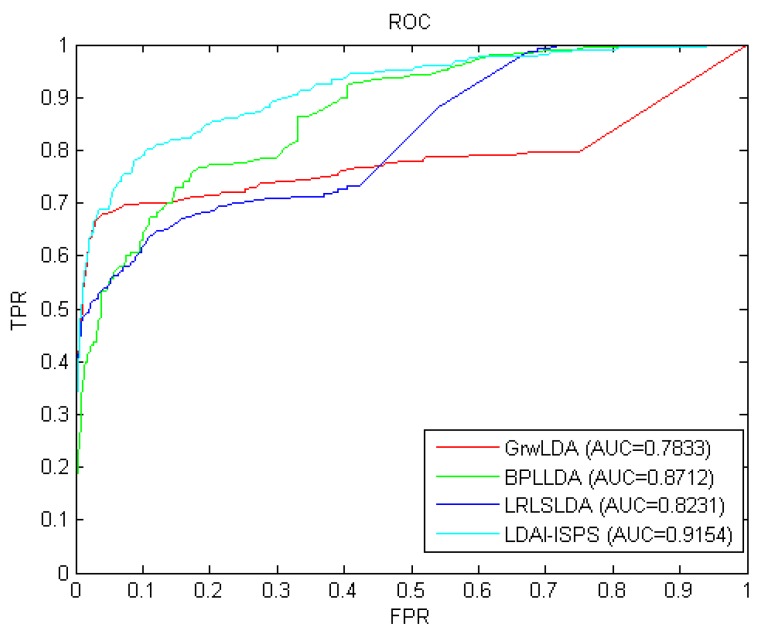
Considering that the information used by GrwLDA [46], BPLLDA [58], and LRLSLDA [32] is similar to that of LDAI-ISPS and these four methods can all be used for isolated diseases and new lncRNAs, we compared LDAI-ISPS with GrwLDA, BPLLD, and LRLSLDA on predictive performance. In order to make an unbiased comparison, we used the same parameter values described in corresponding papers of GrwLDA, BPLLD, and LRLSLDA. The comparison results from LOOCV can be seen in Figure 2, where AUC values of GrwLDA, BPLLDA, LRLSLDA, and LDAI-ISPS were 0.7833, 0.8712, 0.8231, and 0.9154, respectively. Obviously, LDAI-ISPS obtained the optimum AUC value, which was higher than GrwLDA (16.84%), BPLLDA (5.07%), and LRLSLDA (11.21%).
Figure 2.
The receiver operating characteristic (ROC) curves and AUC values of the long non-coding RNA (lncRNA)–disease associations inference based on integrated space projection scores (LDAI-ISPS) compared with other methods.
2.3. Prediction for New lncRNAs and Isolated Diseases
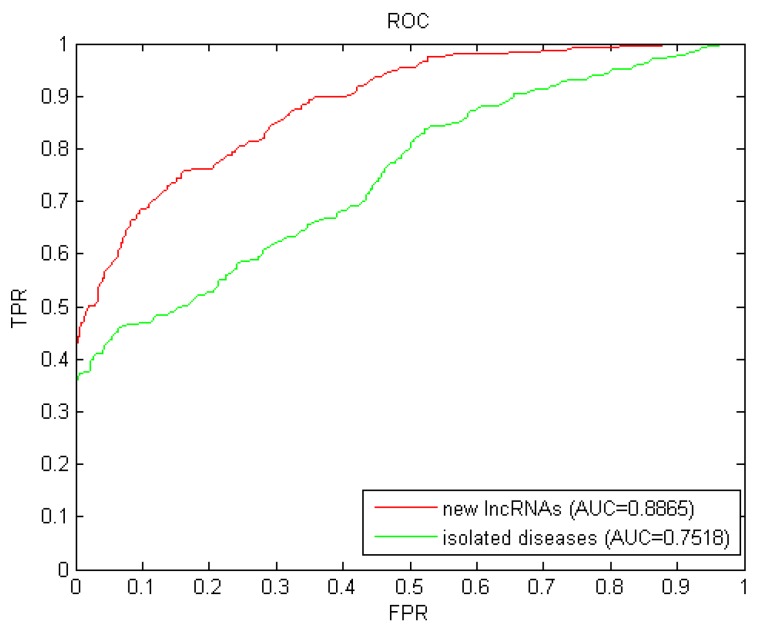
New lncRNAs are those whose associations related to diseases are unknown. How to pair new lncRNAs with diseases remains an urgent challenge, and the solutions will certainly advance our understanding of disease molecular mechanisms. Firstly, although more and more new lncRNAs were discovered, their associations with diseases could not be identified by the time they were discovered. Secondly, no known association can be used directly to predict the potential associations. Thirdly, most of the existing computational methods cannot infer the potential associations between new lncRNAs and diseases. Therefore, we continuously removed all known related associations of each candidate lncRNA with diseases to simulate new lncRNAs and performed LOOCV to evaluate the predictive performance of LDAI-ISPS.
Isolated diseases are those whose associations related to lncRNAs are unknown. The prediction for isolated diseases faced the similar challenge of new lncRNAs as mentioned before. We simulated each candidate disease as an isolated disease by removing all known related associations with lncRNAs, and then implemented LOOCV with these simulated isolated diseases. The AUC value of 0.7518 (shown in Figure 3) further confirmed the excellent predictive performance of LDAI-ISPS for isolated diseases.
Figure 3.
Results of LDAI-ISPS for new lncRNAs and isolated diseases.
2.4. Case Study
2.4.1. Case Study for Potential Associations
Cervical cancer is a deadly threat to a woman’s life and health. It is estimated that there are 528,000 new cases and 266,000 deaths from cervical cancer worldwide every year [59]. Type 2 diabetes is one kind of metabolic disorder. So far, more than 415 million people have suffered terribly from type 2 diabetes. Therefore, identifying some specific diseases related lncRNAs is important for understanding the pathogenesis, treatment, and prognosis. We took cervical cancer and type 2 diabetes as the cases to further confirm the performance of LDAI-ISPS by using the known lncRNA-disease associations in as the training data.
The top five out of the prediction results for each of these two diseases are listed in Table 1, where two out of the top five predicted associations were found evidence in database LncRNADisease [15] and the remaining three out of the top five predicted associations were found supporting evidence in relevant literatures. Only one predicted association listed in Table 1 was not found any supporting evidence, which confirmed the excellent performance of LDAI-ISPS in inferring the potential associations between lncRNAs and diseases.
Table 1.
The top five results predicted for cervical cancer and type 2 diabetes.
| Disease | lncRNA Name | Evidence | Rank |
|---|---|---|---|
| Cervical cancer | LSINCT5 | Ref. [60] | 1 |
| Cervical cancer | HOTAIR | LncRNADisease | 2 |
| Cervical cancer | MEG3 | LncRNADisease | 3 |
| Cervical cancer | EPB41L4A-AS1 | Ref. [61] | 4 |
| Cervical cancer | PANDAR | Ref. [3] | 5 |
| Type 2 diabetes | IGF2-AS | Ref. [62] | 1 |
| Type 2 diabetes | MEG3 | LncRNADisease | 2 |
| Type 2 diabetes | PINK1-AS | Ref. [63] | 3 |
| Type 2 diabetes | Gas5 | LncRNADisease | 4 |
| Type 2 diabetes | PCAT-1 | Unconfirmed | 5 |
2.4.2. Case Study for Isolated Diseases
We took prostate cancer and Alzheimer’s disease as the cases to further confirm the predictive performance of LDAI-ISPS for isolated diseases. As for prostate cancer, we removed 13 known associations related to it to simulate the isolated disease. As for Alzheimer’s disease, we removed eight known associations related to it to simulate the isolated disease. The top five out of the predicted results of both diseases were listed in Table 2, where all of the top five predicted associations related to prostate cancer were found evidence in database LncRNADisease, and four out of the top five predicted associations related to Alzheimer’s disease were found evidence in database LncRNADisease except CDKN2B-AS10. However, Tedde et al. [64] found that CDKN2A/CDKN2B genes/loci associated with late-onset Alzheimer’s disease, which proved the credibility of our LDAI-ISPS.
Table 2.
The top five results predicted for specific isolated diseases (e.g., prostate cancer and Alzheimer’s disease).
| Disease | lncRNA Name | Evidence | Rank |
|---|---|---|---|
| Prostate cancer | PCAT-1 | LncRNADisease | 1 |
| Prostate cancer | C1QTNF9B-AS1 | LncRNADisease | 2 |
| Prostate cancer | CBR3-AS1 | LncRNADisease | 3 |
| Prostate cancer | PCA3 | LncRNADisease | 4 |
| Prostate cancer | PCAT1 | LncRNADisease | 5 |
| Alzheimer’s disease | BACE1-AS | LncRNADisease | 1 |
| Alzheimer’s disease | GDNFOS | LncRNADisease | 2 |
| Alzheimer’s disease | SNHG3 | LncRNADisease | 3 |
| Alzheimer’s disease | SOX2-OT | LncRNADisease | 4 |
| Alzheimer’s disease | CDKN2B-AS10 | Ref. [64] | 5 |
3. Discussion
The research of a computational model for inferring lncRNA–disease associations is still a hot topic. On one hand, the prediction of lncRNA–disease associations is helpful to explore the complex pathogenesis of diseases; on the other hand, the traditional biological methods are tedious and time-consuming, therefore, many computational methods have emerged in recent years used for inferring massive lncRNA–disease associations. Those computational methods still have some limitations that motivated us to propose a new lncRNA–disease association inference (LDAI-ISPS), whose main contribution consists of the following points: made full use of network topology characters instead of needing negative samples; LOOCV results showed that AUC value of LDAI-ISPS in inferring disease related lncRNAs was 0.9154, which was 16.86%, 5.07%, and 11.21% higher than that of GrwLDA, BPLLDA, and LRLSLDA, respectively. Additionally, the AUC value for new lncRNAs and isolated diseases were 0.8865 and 0.7518, respectively, which further evaluated the stronger predictive performance of LDAI-ISPS.
The following reasons helped our LDAI-ISPS achieve good predictive performance: first, we integrated Gaussian interaction profile central similarity to calculate disease similarity and lncRNA similarity, which made up the incompleteness of similarity network construction only with sematic similarity. Second, we reconstructed the Boolean network of known experimentally verified lncRNA–disease associations to be the weighted network of lncRNA–disease associations. The weighted network can exactly describe the association strength not just showing the existence of an association. Third, the global information (all the disease similarities, lncRNA similarities, and lncRNA–disease associations), even those diseases and lncRNAs without any known association, were utilized to improve the predictive ability of LDAI-ISPS including the ability on new lncRNAs and isolated diseases.
Our method still has following limitations that need to be improved in future: the predicted results were biased towards the diseases with more related lncRNAs or the lncRNAs with more related diseases; the prediction accuracy needs to be enhanced further through fusing different data. In conclusion, LDAI-ISPS can be a useful helper for inference of lncRNA–disease associations.
4. Materials and Methods
4.1. Materials
4.1.1. LncRNA–Disease Association Network
The data source of our dataset used came from the LncRNADisease database [15] composed of experimentally supported lncRNA–disease association data and predicting novel lncRNA–disease associations. After preprocessing, the dataset was composed of 352 known associations that involved 156 lncRNAs (denoted by set ) and 190 diseases (denoted by set ), as shown in Supplementary Materials S1–S3. A Boolean matrix including the 352 known lncRNA–disease associations was used to represent the adjacency matrix of the lncRNA–disease associations, where represented the number of lncRNAs with value of 156 and represented the number of diseases with value of 190. If lncRNA has a known association with disease checked from the 352 known lncRNA-disease associations, is set to 1, otherwise is set to 0.
4.1.2. Disease Semantic Similarity
The method proposed by Wang et al. [65] defined the semantic contribution value of disease according to the layer structure of corresponding direct acyclic graph (DAG). A similar way was used as described in [65] to calculate the disease semantic similarity, where nodes set denoted the disease itself and its ancestors, and edges set denoted the relations between the nodes in DAG. For each node in set , its contribution to was numerically defined as the following:
| (1) |
where is the contribution factor of connecting edges between and its children , with the optimum value of 0.5 described in [65]. Additionally, the sematic score of disease was defined in Equation (2):
| (2) |
A matrix (can be seen in Supplementary Materials S4) represented the disease semantic similarities, where denoted the semantic similarity between disease and , with the calculation shown in Equation (3):
| (3) |
4.1.3. LncRNA Functional Similarity
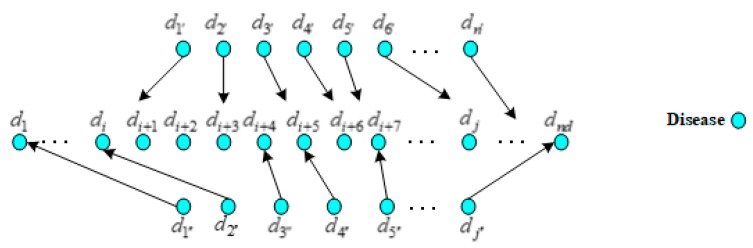
By far, there have been many methods for lncRNA similarity network construction. We used the similar method like that proposed by Sun et al. [55], it calculated the functional similarity of paired lncRNAs by measuring the semantic similarity of diseases related to these two lncRNAs. As shown in Figure 4, it supposed that lncRNA and related to m diseases and n diseases out of 190 diseases, respectively, which formed the sets and . The actual value of subscript () was the subscript of each element in set () that was composed of m (n) diseases relating to lncRNA ().
Figure 4.
The mapping relations of the diseases associated with different lncRNAs.
The similarity between one disease element in the set and the whole set was calculated as shown in Equation (4):
| (4) |
where the actual value of the subscripts and were the subscripts of the corresponding diseases mapped by the diseases in set , as mentioned before.
We defined a matrix (can be seen in Supplementary Materials S5), similar to the detailed calculation process described in ref. [55]. The functional similarities between lncRNAs were represented in matrix , where denoted the functional similarity between lncRNA and lncRNA , with the calculation shown in Equation (5):
| (5) |
where m and n refer the number of diseases related to lncRNA and lncRNA respectively.
4.2. Disease (LncRNA) Gaussian Interaction Profile Central Similarity
There are many zeros in matrix (and matrix ) because of few number of known associations as mentioned before; it means that the similarities related to these zeros between diseases (lncRNAs) cannot be found out from originally obtained information. Therefore, in order to further calculate the similarities between diseases (lncRNAs) accurately, the Gaussian interaction profile central similarities between lncRNAs were defined as with the calculation shown in Equation (6):
| (6) |
where denotes the Gaussian interaction profile central similarity between lncRNA and lncRNA , denotes the row of matrix , the optimal value of parameter that controlled the kernel bandwidth of Gaussian interaction profile in a similar way as described in ref. [66].
| (7) |
where parameter is set to 1 normally.
Similarly, the Gaussian interaction profile central similarity between diseases was defined as with the calculation shown in Equation (8):
| (8) |
where denotes the column of matrix , the optimal value of parameter that controlled the kernel bandwidth was calculated as the following:
| (9) |
where parameter is set to 1 normally.
4.3. Disease (LncRNA) Integrated Similarities
Considering that only semantic similarity is not able to describe all the relationships between diseases accurately, we integrated disease semantic similarity and disease Gaussian interaction profile central similarity to further construct the disease integrated similarities network (denoted by ). It means that the Gaussian interaction profile central similarity is utilized to measure the similarity between two diseases when the corresponding element value in a disease semantic similarity matrix related to these two diseases is 0. Similarly, we integrated lncRNA functional similarity and lncRNA Gaussian interaction profile central similarity to construct the lncRNA integrated similarities network (denoted by ). The detailed formula description is shown as the following for clarity:
| (10) |
| (11) |
4.4. LDAI-ISPS Workflow Model
After finishing the related data preparation, the detailed inferring process of LDAI-ISPS was explained in following flowchart (can be seen in Figure 5). Additionally, the numerical calculation results with each step are demonstrated in Supplementary Figure S1.
Figure 5.
The flowchart of LDAI-ISPS.
4.4.1. Construction of lncRNA-Disease Weighted Network
Boolean network of known associations can only indicate whether the associations between lncRNAs and diseases exist, without showing the strength of associations. We utilized , , and to construct two weighted networks of lncRNA–disease associations (denoted by and , respectively) for inferring the potential lncRNA–disease associations, with detailed calculation shown as the following:
| (12) |
where the weighting parameter , used for the lncRNA–disease weighted network reconstruction based on disease semantic similarities, is set to [0, 1].
| (13) |
where the weighting parameter , used for the lncRNA–disease weighted network reconstruction based on lncRNA functional similarities, is set to [0, 1].
4.4.2. Space Projection Scores of lncRNA–Disease Associations
Based on above two weighted lncRNA–disease networks ( and ), we defined the space projection scores of lncRNA–disease associations (denoted by and , respectively) by utilizing the concept of vector projection to infer the associations between lncRNAs and diseases more accurately.
| (14) |
where indicates one of the space projection scores obtained from the disease similarity network , and is the 2-norm based on row vector .
| (15) |
where indicates one of the space projection scores obtained from the lncRNA integrated similarities network , and is the 2-norm based on column vector .
4.4.3. Prediction Score Based on Space Projection Scores
The final prediction score of lncRNA–disease associations (denoted by ) was composed of two parts, space projection score and space projection score :
| (16) |
where the weighting parameter that represents the importance degree of is set to , the larger value of means the greater probability of an association existing between lncRNA and diseases .
Acknowledgments
The authors thank the anonymous reviewers for suggestions that helped improve the paper substantially.
Abbreviations
| LOOCV | leave-one-out cross validation |
| ROC | receiver operating characteristic |
| AUC | area under the ROC curve |
| FPR | false positive rate |
| TPR | true positive rate |
Supplementary Materials
The following are available online at https://www.mdpi.com/1422-0067/21/4/1508/s1, Figure S1: Numerical calculation results of LDAI-ISPS workflow model, Table S1: Known lncRNA-disease associations, Table S2: LncRNA names, Table S3: Disease names, Table S4: Disease semantic similarity matrix, Table S5: LncRNA functional similarity matrix.
Author Contributions
Conceptualization, Y.Z. and M.C.; Data curation, A.L.; Formal analysis, H.J.; Funding acquisition, M.C. and X.C.; Methodology, Y.Z. and M.C.; Software, A.L.; Validation, X.C., H.J. and Y.L.; Writing—original draft, Y.Z. and M.C.; Writing—review and editing, Y.Z. and M.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Nature Science Foundation of China (Grant No. 61772192, 61672223, 61662017, 61762031), Nature Science Foundation of Hunan Province, China (Grant No. 2018JJ2085, 2018JJ40064), scientific research project of education department of Hunan province, China (19A125), major cultivation projects of Hunan Institute of Technology (Grant No. 2017HGPY001), science and technology innovative research team of Hunan Institute of Technology (Grant No. TD18005).
Conflicts of Interest
The authors declare no conflict of interest.
References
- 1.Wapinski O., Chang H.Y. Corrigendum: Long noncoding RNAs and human disease. Trends Cell Biol. 2011;21:354–361. doi: 10.1016/j.tcb.2011.04.001. [DOI] [PubMed] [Google Scholar]
- 2.Song X., Cao G., Jing L., Lin S., Wang X., Zhang J., Wang M., Liu W., Lv C. Analysing the relationship between lnc RNA and protein-coding gene and the role of lnc RNA as ce RNA in pulmonary fibrosis. J. Cell. Mol. Med. 2014;18:991–1003. doi: 10.1111/jcmm.12243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Huang H., Xie H., Ma X., Zhao F., Gao Y. Upregulation of LncRNA PANDAR predicts poor prognosis and promotes cell proliferation in cervical cancer. Eur. Rev. Med. Pharmacol. Sci. 2017;21:4529–4535. [PubMed] [Google Scholar]
- 4.Zou R., Chen X., Jin X., Li S., Ou R., Xue J., Yan X., Chen L., Hu Y., Zhu H. Up-regulated BCAR4 contributes to proliferation and migration of cervical cancer cells. Surg. Oncol. 2018;27:306–313. doi: 10.1016/j.suronc.2018.05.013. [DOI] [PubMed] [Google Scholar]
- 5.Zhu Y., Ding L., Chen B.-F., Song J.-G., Yao Y.-S. Oncogenic activity of Wrap53 in human colorectal cancer in vitro and in nude mouse xenografts. Med. Sci. Monit. 2018;24:6129–6136. doi: 10.12659/MSM.910214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Liang W.-C., Fu W.-M., Wong C.-W., Wang Y., Wang W.-M., Hu G.-X., Zhang L., Xiao L.-J., Wan D.C.-C., Zhang J.-F. The lncRNA H19 promotes epithelial to mesenchymal transition by functioning as miRNA sponges in colorectal cancer. Oncotarget. 2015;6:22513–22525. doi: 10.18632/oncotarget.4154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tripathi M.K., Doxtater K., Keramatnia F., Zacheaus C., Yallapu M.M., Jaggi M., Chauhan S.C. Role of lncRNAs in ovarian cancer: Defining new biomarkers for therapeutic purposes. Drug Discov. Today. 2018;23:1635–1643. doi: 10.1016/j.drudis.2018.04.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chen Z., Zhang Z., Xie B., Zhang H. Clinical significance of up-regulated lncRNA NEAT1 in prognosis of ovarian cancer. Eur. Rev. Med. Pharmacol. Sci. 2016;20:3373–3377. [PubMed] [Google Scholar]
- 9.Jin Y., Feng S., Qiu S., Shao N., Zheng J. LncRNA MALAT1 promotes proliferation and metastasis in epithelial ovarian cancer via the PI3K-AKT pathway. Eur. Rev. Med. Pharmacol. Sci. 2017;21:3176–3184. [PubMed] [Google Scholar]
- 10.Cai Z., Wu Y., Li Y., Ren J., Wang L. BCAR4 activates GLI2 signaling in prostate cancer to contribute to castration resistance. Aging (Albany NY) 2018;10:3702–3712. doi: 10.18632/aging.101664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sun S., Zhao H., Liu R., Wang B., Liu Y., Zhao Y., Shi Z. Expression of long non-coding RNA H19 in prostate cancer and its effect on the proliferation and glycometabolism of human prostate cancer cells. Zhonghua Nan Ke Xue. 2017;23:120–124. [PubMed] [Google Scholar]
- 12.Kameswaran V., Golson M.L., Ramos-Rodríguez M., Ou K., Wang Y.J., Zhang J., Pasquali L., Kaestner K.H. The Dysregulation of the DLK1-MEG3 Locus in Islets From Patients With Type 2 Diabetes Is Mimicked by Targeted Epimutation of Its Promoter With TALE-DNMT Constructs. Diabetes. 2018;67:1807–1815. doi: 10.2337/db17-0682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Thomas A.A., Biswas S., Feng B., Chen S., Gonder J., Chakrabarti S. lncRNA H19 prevents endothelial-mesenchymal transition in diabetic retinopathy. Diabetologia. 2019;62:517–530. doi: 10.1007/s00125-018-4797-6. [DOI] [PubMed] [Google Scholar]
- 14.Quek X.C., Thomson D.W., Maag J.L., Bartonicek N., Signal B., Clark M.B., Gloss B.S., Dinger M.E. lncRNAdb v2. 0: Expanding the reference database for functional long noncoding RNAs. Nucleic Acids Res. 2014;43:D168–D173. doi: 10.1093/nar/gku988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chen G., Wang Z., Wang D., Qiu C., Liu M., Chen X., Zhang Q., Yan G., Cui Q. LncRNADisease: A database for long-non-coding RNA-associated diseases. Nucleic Acids Res. 2012;41:D983–D986. doi: 10.1093/nar/gks1099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Dinger M.E., Pang K.C., Mercer T.R., Crowe M.L., Grimmond S.M., Mattick J.S. NRED: A database of long noncoding RNA expression. Nucleic Acids Res. 2008;37:D122–D126. doi: 10.1093/nar/gkn617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bu D., Yu K., Sun S., Xie C., Skogerbø G., Miao R., Xiao H., Liao Q., Luo H., Zhao G. NONCODE v3. 0: Integrative annotation of long noncoding RNAs. Nucleic Acids Res. 2011;40:D210–D215. doi: 10.1093/nar/gkr1175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chen X., Sun Y.-Z., Guan N.-N., Qu J., Huang Z.-A., Zhu Z.-X., Li J.-Q. Computational models for lncRNA function prediction and functional similarity calculation. Brief. Funct. Genom. 2018;18:58–82. doi: 10.1093/bfgp/ely031. [DOI] [PubMed] [Google Scholar]
- 19.Chen X., Yan C.C., Zhang X., You Z.-H. Long non-coding RNAs and complex diseases: From experimental results to computational models. Brief. Bioinform. 2016;18:558–576. doi: 10.1093/bib/bbw060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Barracchia E.P., Pio G., Malerba D., Ceci M. New Frontiers in Mining Complex Patterns. Springer; Berlin/Heidelberg, Germany: 2015. Identifying lncRNA-disease relationships via heterogeneous clustering; pp. 35–48. [Google Scholar]
- 21.Li J., Gao C., Wang Y., Ma W., Tu J., Wang J., Chen Z., Kong W., Cui Q. A bioinformatics method for predicting long noncoding RNAs associated with vascular disease. Sci. China Life Sci. 2014;57:852–857. doi: 10.1007/s11427-014-4692-4. [DOI] [PubMed] [Google Scholar]
- 22.Liu M.-X., Chen X., Chen G., Cui Q.-H., Yan G.-Y. A computational framework to infer human disease-associated long noncoding RNAs. PLoS ONE. 2014;9:e84408. doi: 10.1371/journal.pone.0084408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Xuan P., Sheng N., Zhang T., Liu Y., Guo Y. CNNDLP: A Method Based on Convolutional Autoencoder and Convolutional Neural Network with Adjacent Edge Attention for Predicting lncRNA-Disease Associations. Int. J. Mol. Sci. 2019;20:4260. doi: 10.3390/ijms20174260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Yu J., Ping P., Wang L., Kuang L., Li X., Wu Z. A novel probability model for LncRNA-Disease association prediction based on the naïve bayesian classifier. Genes. 2018;9:345. doi: 10.3390/genes9070345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Xuan P., Jia L., Zhang T., Sheng N., Li X., Li J. LDAPred: A method based on information flow propagation and a convolutional neural network for the prediction of disease-associated lncRNAs. Int. J. Mol. Sci. 2019;20:4458. doi: 10.3390/ijms20184458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Xuan Z., Li J., Yu J., Feng X., Zhao B., Wang L. A probabilistic matrix factorization method for identifying lncRNA-disease associations. Genes. 2019;10:126. doi: 10.3390/genes10020126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Biswas A.K., Kang M., Kim D.-C., Ding C.H., Zhang B., Wu X., Gao J.X. Inferring disease associations of the long non-coding RNAs through non-negative matrix factorization. Netw. Model. Anal. Health Inform. Bioinform. 2015;4:9. doi: 10.1007/s13721-015-0081-6. [DOI] [Google Scholar]
- 28.Fu G., Wang J., Yu G., Domeniconi C. Matrix factorization-based data fusion for the prediction of lncRNA–disease associations. Bioinformatics. 2017;34:1529–1537. doi: 10.1093/bioinformatics/btx794. [DOI] [PubMed] [Google Scholar]
- 29.Lu C., Yang M., Luo F., Wu F.-X., Li M., Pan Y., Li Y., Wang J. Prediction of lncRNA-disease associations based on inductive matrix completion. Bioinformatics. 2018;34:3357–3364. doi: 10.1093/bioinformatics/bty327. [DOI] [PubMed] [Google Scholar]
- 30.Zhao T., Xu J., Liu L., Bai J., Xu C., Xiao Y., Li X., Zhang L. Identification of cancer-related lncRNAs through integrating genome, regulome and transcriptome features. Mol. Biosyst. 2015;11:126–136. doi: 10.1039/C4MB00478G. [DOI] [PubMed] [Google Scholar]
- 31.Lan W., Li M., Zhao K., Liu J., Wu F.-X., Pan Y., Wang J. LDAP: A web server for lncRNA-disease association prediction. Bioinformatics. 2016;33:458–460. doi: 10.1093/bioinformatics/btw639. [DOI] [PubMed] [Google Scholar]
- 32.Chen X., Yan G.-Y. Novel human lncRNA-disease association inference based on lncRNA expression profiles. Bioinformatics. 2013;29:2617–2624. doi: 10.1093/bioinformatics/btt426. [DOI] [PubMed] [Google Scholar]
- 33.Chen X. Predicting lncRNA-disease associations and constructing lncRNA functional similarity network based on the information of miRNA. Sci. Rep. 2015;5:13186. doi: 10.1038/srep13186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Zhang J., Zhang Z., Chen Z., Deng L. Integrating Multiple Heterogeneous Networks for Novel LncRNA-disease Association Inference. IEEE/ACM Trans. Comput. Biol. Bioinform. 2018. [DOI] [PubMed]
- 35.Yang X., Gao L., Guo X., Shi X., Wu H., Song F., Wang B. A network based method for analysis of lncRNA-disease associations and prediction of lncRNAs implicated in diseases. PLoS ONE. 2014;9:e87797. doi: 10.1371/journal.pone.0087797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wang P., Guo Q., Gao Y., Zhi H., Zhang Y., Liu Y., Zhang J., Yue M., Guo M., Ning S. Improved method for prioritization of disease associated lncRNAs based on ceRNA theory and functional genomics data. Oncotarget. 2017;8:4642. doi: 10.18632/oncotarget.13964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Chen X., Yan C.C., Luo C., Ji W., Zhang Y., Dai Q. Constructing lncRNA functional similarity network based on lncRNA-disease associations and disease semantic similarity. Sci. Rep. 2015;5:11338. doi: 10.1038/srep11338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Huang Y.-A., Chen X., You Z.-H., Huang D.-S., Chan K.C. ILNCSIM: Improved lncRNA functional similarity calculation model. Oncotarget. 2016;7:25902. doi: 10.18632/oncotarget.8296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Chen X., Huang Y.-A., Wang X.-S., You Z.-H., Chan K.C. FMLNCSIM: Fuzzy measure-based lncRNA functional similarity calculation model. Oncotarget. 2016;7:45948. doi: 10.18632/oncotarget.10008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Chen X. KATZLDA: KATZ measure for the lncRNA-disease association prediction. Sci. Rep. 2015;5:16840. doi: 10.1038/srep16840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Cheng L., Shi H., Wang Z., Hu Y., Yang H., Zhou C., Sun J., Zhou M. IntNetLncSim: An integrative network analysis method to infer human lncRNA functional similarity. Oncotarget. 2016;7:47864. doi: 10.18632/oncotarget.10012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ding L., Wang M., Sun D., Li A. TPGLDA: Novel prediction of associations between lncRNAs and diseases via lncRNA-disease-gene tripartite graph. Sci. Rep. 2018;8:1065. doi: 10.1038/s41598-018-19357-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Shi J.-Y., Huang H., Zhang Y.-N., Long Y.-X., Yiu S.-M. Predicting binary, discrete and continued lncRNA-disease associations via a unified framework based on graph regression. BMC Med. Genom. 2017;10:65. doi: 10.1186/s12920-017-0305-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Liu Y., Zhang R., Qiu F., Li K., Zhou Y., Shang D., Xu Y. Construction of a lncRNA-PCG bipartite network and identification of cancer-related lncRNAs: A case study in prostate cancer. Mol. Biosyst. 2015;11:384–393. doi: 10.1039/C4MB00439F. [DOI] [PubMed] [Google Scholar]
- 45.Ganegoda G.U., Li M., Wang W., Feng Q. Heterogeneous network model to infer human disease-long intergenic non-coding RNA associations. IEEE Trans. Nanobiosci. 2015;14:175–183. doi: 10.1109/TNB.2015.2391133. [DOI] [PubMed] [Google Scholar]
- 46.Gu C., Liao B., Li X., Cai L., Li Z., Li K., Yang J. Global network random walk for predicting potential human lncRNA-disease associations. Sci. Rep. 2017;7:12442. doi: 10.1038/s41598-017-12763-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Yu G., Fu G., Lu C., Ren Y., Wang J. BRWLDA: Bi-random walks for predicting lncRNA-disease associations. Oncotarget. 2017;8:60429. doi: 10.18632/oncotarget.19588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Hu Y., Zhou M., Shi H., Ju H., Jiang Q., Cheng L. Measuring disease similarity and predicting disease-related ncRNAs by a novel method. BMC Med. Genom. 2017;10:71. doi: 10.1186/s12920-017-0315-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Xu C., Ping Y., Zhao H., Ning S., Xia P., Wang W., Wan L., Li J., Zhang L., Yu L. LncNetP, a systematical lncRNA prioritization approach based on ceRNA and disease phenotype association assumptions. Oncotarget. 2017;8:114603. doi: 10.18632/oncotarget.23059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Wang L., Xiao Y., Li J., Feng X., Li Q., Yang J. IIRWR: Internal Inclined Random Walk With Restart for LncRNA-Disease Association Prediction. IEEE Access. 2019;7:54034–54041. doi: 10.1109/ACCESS.2019.2912945. [DOI] [Google Scholar]
- 51.Chen M., Zhang Y., Li A., Li Z., Liu W., Chen Z. Bipartite Heterogeneous Network Method Based on Co-neighbour for MiRNA–Disease Association Prediction. Front. Genet. 2019;10:385. doi: 10.3389/fgene.2019.00385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Chen M., Liao B., Li Z. Global Similarity Method Based on a Two-tier Random Walk for the Prediction of microRNA–Disease Association. Sci. Rep. 2018;8:6481. doi: 10.1038/s41598-018-24532-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Chen M., Peng Y., Li A., Li Z., Deng Y., Liu W., Liao B., Dai C. A novel information diffusion method based on network consistency for identifying disease related microRNAs. RSC Adv. 2018;8:36675–36690. doi: 10.1039/C8RA07519K. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Chen M., Lu X., Liao B., Li Z., Cai L., Gu C. Uncover miRNA-Disease Association by Exploiting Global Network Similarity. PLoS ONE. 2016;11:e0166509. doi: 10.1371/journal.pone.0166509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Sun J., Shi H., Wang Z., Zhang C., Liu L., Wang L., He W., Hao D., Liu S., Zhou M. Inferring novel lncRNA-disease associations based on a random walk model of a lncRNA functional similarity network. Mol. Biosyst. 2014;10:2074–2081. doi: 10.1039/C3MB70608G. [DOI] [PubMed] [Google Scholar]
- 56.Zhou M., Wang X., Li J., Hao D., Wang Z., Shi H., Han L., Zhou H., Sun J. Prioritizing candidate disease-related long non-coding RNAs by walking on the heterogeneous lncRNA and disease network. Mol. Biosyst. 2015;11:760–769. doi: 10.1039/C4MB00511B. [DOI] [PubMed] [Google Scholar]
- 57.Yao Q., Wu L., Li J., Guang Yang L., Sun Y., Li Z., He S., Feng F., Li H., Li Y. Global prioritizing disease candidate lncRNAs via a multi-level composite network. Sci. Rep. 2017;7:39516. doi: 10.1038/srep39516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Xiao X., Zhu W., Liao B., Xu J., Gu C., Ji B., Yao Y., Peng L., Yang J. BPLLDA: Predicting lncRNA-disease associations based on simple paths with limited lengths on a heterogeneous network. Front. Genet. 2018;9:411. doi: 10.3389/fgene.2018.00411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Ferlay J., Soerjomataram I., Dikshit R., Eser S., Mathers C., Rebelo M., Parkin D.M., Forman D., Bray F. Cancer incidence and mortality worldwide: Sources, methods and major patterns in GLOBOCAN 2012. Int. J. Cancer. 2015;136:E359–E386. doi: 10.1002/ijc.29210. [DOI] [PubMed] [Google Scholar]
- 60.Silva J.M., Boczek N.J., Berres M.W., Ma X., Smith D.I. LSINCT5 is over expressed in breast and ovarian cancer and affects cellular proliferation. RNA Biol. 2011;8:496–505. doi: 10.4161/rna.8.3.14800. [DOI] [PubMed] [Google Scholar]
- 61.Chen W., Chen X., Wang Y., Liu T., Liang Y., Xiao Y., Chen L. Construction and analysis of lncRNA-mediated ceRNA network in cervical squamous cell carcinoma by weighted gene co-expression network analysis. Med. Sci. Monit. 2019;25:2609. doi: 10.12659/MSM.913471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Mercader J.M., Liao R.G., Bell A.D., Dymek Z., Estrada K., Tukiainen T., Huerta-Chagoya A., Moreno-Macías H., Jablonski K.A., Hanson R.L. A loss-of-function splice acceptor variant in IGF2 is protective for type 2 diabetes. Diabetes. 2017;66:2903–2914. doi: 10.2337/db17-0187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Ghayori B., Rashki A., Motaleb G., Dahmardei M. Association of PINK1gene polymorphism Ala340Thr with type 2 diabetes in sistan and Baluchistan province. J. Ilam Univ. Med. Sci. 2015;23:127–133. [Google Scholar]
- 64.Tedde A., Piaceri I., Bagnoli S., Lucenteforte E., Ueberham U., Arendt T., Sorbi S., Nacmias B. Association study of genetic variants in CDKN2A/CDKN2B genes/loci with late-onset Alzheimer’s disease. Int. J. Alzheimer’s Dis. 2011;2011:374631. doi: 10.4061/2011/374631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Wang D., Wang J., Lu M., Song F., Cui Q. Inferring the human microRNA functional similarity and functional network based on microRNA-associated diseases. Bioinformatics. 2010;26:1644–1650. doi: 10.1093/bioinformatics/btq241. [DOI] [PubMed] [Google Scholar]
- 66.Liu Y., Feng X., Zhao H., Xuan Z., Wang L. A novel network-based computational model for prediction of potential lncrna-disease association. Int. J. Mol. Sci. 2019;20:1549. doi: 10.3390/ijms20071549. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.