Human versus Machine: Comparing a Deep Learning Algorithm to Human Gradings for Detecting Glaucoma on Fundus Photographs

Alessandro A Jammal; Atalie C Thompson; Eduardo B Mariottoni; Samuel I Berchuck; Carla N Urata; Tais Estrela; Susan M Wakil; Vital P Costa; Felipe A Medeiros

doi:10.1016/j.ajo.2019.11.006

. Author manuscript; available in PMC: 2021 Mar 1.

Published in final edited form as: Am J Ophthalmol. 2019 Nov 12;211:123–131. doi: 10.1016/j.ajo.2019.11.006

Human versus Machine: Comparing a Deep Learning Algorithm to Human Gradings for Detecting Glaucoma on Fundus Photographs

Alessandro A Jammal ^1,³, Atalie C Thompson ¹, Eduardo B Mariottoni ¹, Samuel I Berchuck ^1,², Carla N Urata ¹, Tais Estrela ¹, Susan M Wakil ¹, Vital P Costa ³, Felipe A Medeiros ¹

PMCID: PMC7073295 NIHMSID: NIHMS1542870 PMID: 31730838

INTRODUCTION

Glaucoma is a progressive optic neuropathy that is the leading cause of irreversible blindness worldwide.¹ The number of people with glaucoma is predicted to increase by 74% from 2013 to 2040, and will disproportionally impact underserved regions of the world, such as Africa and Asia.² Moreover, it is estimated that in developing countries up to 90% of glaucoma patients do not know they have the disease.³ Therefore, there is a pressing need for developing effective screening strategies that can be used for early detection of glaucoma.

The development of imaging technologies such as spectral-domain optical coherence tomography (SD OCT) has enabled accurate and reproducible quantification of early glaucomatous damage on optic nerve images.^{4, 5} However, although routinely used in clinical practice, SD OCT is too expensive to be used for widespread screening and requires experienced operators for image acquisition. Fundus photography is a low-cost and easy to acquire method to identify signs of glaucomatous damage to the optic nerve.⁶ However, detection of glaucoma on fundus photographs requires subjective grading by human experts, which can be laborious and costly. More importantly, previous studies have shown that human graders, even those with extensive clinical experience, tend to over- or underestimate glaucomatous damage when assessing fundus photographs.⁷ The requirement for subjective human grading of photos has thus resulted in poor reproducibility and accuracy, greatly limiting the use of fundus photos for glaucoma screening.^8–12

Artificial intelligence, by the use of deep learning (DL) convolutional neural networks (CNN), has recently become the state-of-the-art method for computer vision tasks, such as image classification, with performance that can sometimes even surpass those of humans.^13–15 In ophthalmology, DL algorithms have been successfully used to detect signs of diabetic retinopathy and age-related macular degeneration on fundus photographs.^{16, 17} DL algorithms have also been developed to detect signs of glaucomatous damage on photographs.^{18, 19} To provide the ground-truth or reference standard to train the deep-learning network, these previous approaches have used human labeling of the same photographs. However, when a DL classifier is trained to replicate subjective human gradings, it is bound to make the same mistakes that humans do when attempting to detect glaucoma on fundus photos.

In a previous study, we proposed a new machine-to-machine (M2M) approach to train DL algorithms to detect glaucomatous damage on fundus photographs.²⁰ Rather than using subjective human gradings as the reference label, we used objective SD OCT-derived measurements of retinal nerve fiber layer (RNFL) thickness for training the networks. We showed that the M2M algorithm was able to successfully predict RNFL thickness measurements from SD OCT by using simple color fundus photographs. Training a network with objective SD OCT data could eliminate the need to rely on subjective, error-prone photo labels by human graders.

In the present work, we compared the ability of the M2M DL algorithm to that of human graders in detecting eyes with glaucomatous visual field loss. We hypothesized that the SD OCT-trained M2M predictions would have a stronger correlation with visual field metrics than subjective gradings by human experts, thus providing an additional required validation of this approach as a method to screen for glaucomatous damage.

METHODS

This was a cross-sectional study with data drawn from the Duke Glaucoma Repository, a database of electronic medical and research records developed by the Vision, Imaging and Performance (VIP) Laboratory from the Duke Eye Center. The Duke Institutional Review Board approved this study. A waiver of informed consent was granted due to the retrospective nature of this work. All methods adhered to the tenets of the Declaration of Helsinki for research involving human subjects and were conducted in accordance with regulations of the Health Insurance Portability and Accountability Act.

The database contained information on comprehensive ophthalmologic examinations during follow-up, diagnoses, medical history, visual acuity, slit-lamp biomicroscopy, intraocular pressure measurements, results of gonioscopy, and dilated slit-lamp funduscopic examinations. In addition, the repository contained optic disc photographs (Nidek 3DX, Nidek, Japan), Spectralis SDOCT (Software version 5.4.7.0, Heidelberg Engineering, GmbH, Dossenheim, Germany) scans and standard automated perimetry (SAP) acquired with the 24–2 Swedish interactive threshold algorithm (Humphrey Field Analyzer II, Carl Zeiss Meditec, Inc., Dublin, CA). Visual fields were excluded if they had more than 33% fixation losses or more than 15% false-positive errors.

Spectral-Domain Optical Coherence Tomography

Images of the peripapillary RNFL were acquired using the Spectralis SD OCT. The device has been previously described in detail,⁵ and employs a dual-beam SD OCT and a confocal laser-scanning ophthalmoscope with a super luminescent diode light (center wavelength of 870 nm) as well as an infrared scan to provide simultaneous images of ocular microstructures. The global RNFL thickness measurement from a peripapillary 12-degree circular optic nerve head (ONH) scan with 100 averaged consecutive circular B-scans (diameter of 3.45 mm, 1536 A-scans) was used for this study. The center of rotation for the B-scans was the center of the ONH as it appeared within the infrared fundus image acquired at the time of SD OCT B-scan relative to the angle between the fovea and the center of Bruch’s membrane opening. Corneal curvature and axial length measurements were entered into the instrument’s software to ensure accurate scaling of all measurements. In addition, the device’s eye-tracking capability was used during image acquisition to adjust for eye movements. All images that had a quality score lower than 15 or that were inverted or clipped were excluded.

The M2M DL Algorithm

A previously described SD OCT-trained DL algorithm was used to predict RNFL global thickness from fundus photos.²⁰ In brief, the dataset consisted of 32,820 pairs of fundus photos and SD OCT scans from 2,312 eyes of 1,198 subjects. As multiple pairs of SD OCT and disc photos were available for each subject, the whole dataset was randomly split at the patient level into a training plus validation (80%) and test (20%) sample. This was important to ensure that no data for a given patient was present in both the training and the test samples in order to prevent leakage and biased estimates of test performance.

All of the available optic disc photographs were matched to the closest SD OCT RNFL scan acquired within 6 months from the photo date. The optic disc photographs were initially downsampled to 256 × 256 pixels and pixel values were scaled to range from 0 to 1. To increase the heterogeneity of the photographs and reduce overfitting, data augmentation (random lighting, random rotation, and random flips) was performed.

The Residual deep neural Network architecture (ResNet34), pre-trained on the ImageNet dataset,²¹ was further tuned with the pairs of fundus photos and SD OCT scans from the training sample, where the average RNFL thickness value given by the SD OCT was used as a label (target) for each photo. As the task of the present work largely differs from that of ImageNet, further training was performed by initially unfreezing the last 2 layers. Subsequently, all layers were unfrozen, and the network was fine-tuned with training performed using differential learning rates, so that a lower rate is used in the earlier layers and the rate is gradually increased in later layers. Minibatches of size 64 and Adam optimizer were used to train the network^{22, 23} and the best learning rate was found using the cyclical learning method with stochastic gradient descent with restarts.²⁴ Further details on the development and validation of the algorithm can be found elsewhere.²⁰

Human grading of fundus photos

For the present study, a subset of 490 monoscopic fundus photographs was randomly drawn from the test sample to form the “grading sample”. These images were presented to two independent glaucoma specialists. Both graders were masked to all patient clinical information and to the grades assigned by the other evaluator. Human graders were asked to assign an integer from 0 to 10 to each fundus photograph according to an ascending probability of glaucomatous optic neuropathy (GON), i.e., 0 if an optic disc was unlikely to have GON and 10 if GON was likely. The scores were later transformed to a percentage scale for analysis. Features such as enlarged cup-to-disc ratio (C/D), localized RNFL defects or rim thinning, and the presence of disc hemorrhages in the fundus photos were used as indicators of glaucomatous damage. Graders were also asked to estimate the vertical and horizontal C/D. For each metric, the scores from the two graders were averaged to give the final score for each eye.

Repeatable glaucomatous visual field loss

In order to compare the discriminatory ability of human graders and the M2M DL algorithm to detect perimetric glaucoma, we defined the presence of reproducible glaucomatous defects using SAP as the reference outcome. An additional four reliable SAP tests (two preceding and two following the photo-matched SAP) were extracted from the repository for each eye and manually reviewed by two graders who reached a consensus agreement when there were disagreements. Eyes with clear patterns of glaucomatous visual field loss (e.g., arcuate scotomas, nasal steps) consistently present throughout the visual field series were marked as eyes with repeatable glaucomatous field defects. Functional loss on SAP was used as the sole reference for a glaucoma diagnosis since definitions of the disease based on assessment of structural losses (e.g., presence of GON or loss of RNFL) would potentially favor predictions from the human graders or DL algorithm, respectively. Therefore, this classification targeted primarily to discriminate between eyes with and without repeatable glaucomatous visual field loss. Due to the lack of a perfect independent reference in diagnosing glaucoma, it is possible however, that some eyes with pre-perimetric glaucoma may have been included in the normal visual field group (see Discussion).

Statistical Analyses

We evaluated the ability of the human graders versus the DL algorithm to detect GON on fundus photos by comparing their outputs (i.e. probability of GON and C/D ratios by human graders vs. DL-predicted RNFL thickness) with visual field loss. The Spearman correlation coefficient was used to evaluate the correlations of human gradings and DL-predictions with both SAP mean deviation (MD) and pattern standard deviation (PSD). The SAP date was matched to within six months of the date of the fundus photograph acquisition. A test of hypothesis was conducted for the equality of correlation coefficients.²⁵ Generalized estimating equations (GEE) were used to account for the fact that both eyes from the same patient could be included in the sample.

The area under the receiver operating characteristic (ROC) curve (AUC) was used to evaluate the performance of the human graders and the M2M DL algorithm in order to discriminate eyes with perimetric glaucoma versus eyes with normal fields. ROC curves were plotted to demonstrate the tradeoff between the sensitivity and 1 – specificity. The AUC was used to assess the diagnostic accuracy of each parameter, with 1.0 representing perfect discrimination and 0.5 representing chance discrimination. In addition, the partial AUC (pAUC) of the DL algorithm and human gradings were calculated to evaluate performance of human and machine outputs in the region of 85–100% specificity,^{26, 27} which would be clinically relevant for screening. As the dataset included multiple images from the same eye and, in some cases, both eyes of the same subject, a bootstrap resampling procedure was used to derive 95% confidence intervals (CI) and P-values, where the patient level was considered as the unit of resampling to account for the presence of multiple correlated measurements within the same subject.²⁸ The difference in the AUC of two curves was compared using a Wald test based on the bootstrap covariance.²⁹Additionally, to account for any possible unbalanced distribution of eyes with and without repeatable glaucomatous visual field loss, we also plotted precision-recall (PR) curves.³⁰ PR curves evaluate the fraction of true positives among positive predictions by presenting the positive predictive power (precision, i.e., ratio of the number of true positives divided by the sum of the true positives and false positive) in function of sensitivity (recall). This approach avoids any overly optimistic assessment of the model’s performance in unbalanced data.³¹ Similarly to the AUC for ROC curves, values for an area under the PR curve (AUPR) closer to 1 represent perfect discrimination.

DL models were implemented using Keras (version 2.1.4), an open-source Python library. All statistical analyses were completed in Stata (version 15, StataCorp LP, College Station, TX). The alpha level (type 1 error) was set at 0.05.

RESULTS

The M2M DL algorithm was able to estimate RNFL thickness from the fundus photos with a mean absolute error (MAE) of 7.39 μm. There was a strong correlation between the predicted and the observed RNFL thickness values (Pearson’s r = 0.832; P<0.001). Further details on the performance and validation of the algorithm can be found in our previous work.²⁰ Results are presented below for the performance of the algorithm in the grading sample.

The grading sample consisted of 490 fundus photographs acquired from 490 eyes of 370 subjects, randomly drawn from the testing sample. Table 1 shows a summary of the demographic and clinical characteristics of the grading sample overall and stratified by the presence or absence of a repeatable glaucomatous visual field defect (i.e., perimetric glaucoma). While there was no statistically significant difference in age, race, or sex between the two groups (all P > 0.05), those with perimetric glaucoma had a significantly more negative SAP MD (−8.59 ± 7.10 vs. −1.12 ± 1.69, P < 0.001). In addition, presence of perimetric glaucoma was associated with a greater probability of GON according to human graders (69.4 ± 25.9 % vs. 40.3 ± 22.0 %, P < 0.001), and thinner predicted global RNFL thickness according to the DL algorithm (76.4 ± 15.0 % vs. 91.6 ± 9.7 %, P < 0.001).

Table 1.

Demographics and clinical characteristics of eyes included in the grading sample.

	Grading sample			P-value
		Presence of repeatable visual field loss
	Overall	No	Yes
Number of eyes	490	280	210	-
Number of subjects	370	233	262	-
Age (years)	60.5 ± 13.9	58.4 ± 14.3	63.4 ± 13.1	0.146^a
Female gender (%)	52.7	57.5	46.2	0.014^b
Race (%),
Caucasian	58.6	62.1	53.8	0.078^b
African-American	41.4	37.9	46.2
SAP MD (dB)^*	−4.32 ± 6.07	−1.12 ± 1.69	−8.59 ± 7.10	<0.001^a
	[−2.05 (−5.53, −0.52)]	[−0.81 (−1.93, −0.05)]	[−6.21 (−11.77, −3.75)]
Probability of GON by human graders (%)	52.3 ± 27.5	40.3 ± 22.0	69.4 ± 25.9	<0.001^a
Vertical C/D by human graders	0.63 ± 0.20	0.57 ± 0.18	0.72 ± 0.19	<0.001^a
Horizontal C/D by human graders	0.60 ± 0.18	0.56 ± 0.18	0.68 ± 0.18	<0.001^a
M2M DL-predicted global RNFL Thickness (μm)	85.1 ± 14.0	91.6 ± 9.7	76.4 ± 15.0	<0.001^a

Open in a new tab

^a

generalized estimating equations (GEE);

^b

Fisher’s exact test Values are given as mean ± standard deviation, unless otherwise noted.

^*

mean ± standard deviation [median (interquartile range)]

C/D = cup-to-disc ratio; GON = glaucomatous optical neuropathy; M2M DL = machine to machine deep learning; MD = mean deviation; SAP = standard automated perimetry; RNFL = retinal nerve fiber layer.

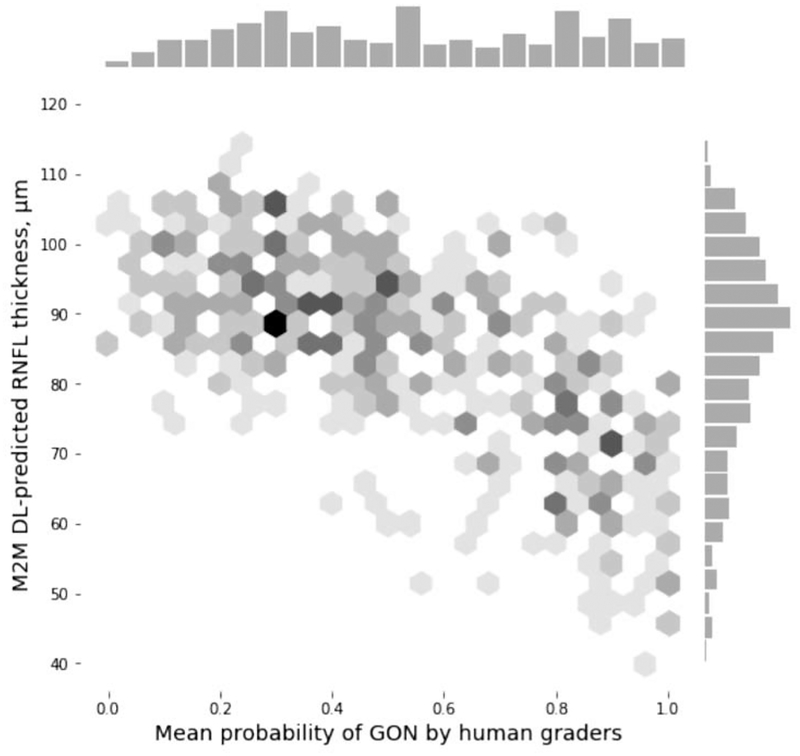
There was a significant correlation between the M2M DL-predicted global RNFL thickness and the mean probability of GON given by the human graders (absolute Spearman’s rho = 0.65, P < 0.001; Figure 1). Lower predicted RNFL thickness was associated with higher probability of GON given by human graders. However, the correlation with SAP MD was significantly stronger for the M2M DL model predictions than for the probability of GON given by human graders (absolute Spearman’s rho = 0.54 vs. 0.48, respectively; P < 0.001; Supplemental Figure 2, available at AJO.com). With SAP PSD, correlations were also stronger for the M2M DL predictions (absolute Spearman’s rho = 0.52 vs. 0.45, respectively; P = 0.001; Table 2).

Figure 1. — Scatterplot and histograms illustrating the relationship between predictions obtained by the machine to machine (M2M) deep learning (DL) algorithm evaluating optic disc photographs and the mean probability of glaucomatous optic neuropathy (GON) assessed by human graders.

Table 2.

Absolute Spearman correlations of the mean gradings by humans and the machine to machine (M2M) deep learning (DL) retinal nerve fiber layer (RNFL) thickness predictions with standard automated perimetry (SAP) mean deviation (MD).

Measure	SAP MD		SAP PSD
Measure	Correlation	P-value	Correlation	P-value
M2M DL RNFL thickness	0.540	< 0.001	0.521	< 0.001
Probability of GON	0.479	< 0.001	0.445	< 0.001
Vertical C/D	0.431	< 0.001	0.379	< 0.001
Horizontal C/D	0.332	< 0.001	0.281	< 0.001

Open in a new tab

C/D = cup-to-disc ratio; GON = glaucomatous optical neuropathy; M2M DL = machine to machine deep learning algorithm; MD = mean deviation; PSD = pattern standard deviation; RNFL = retinal nerve fiber layer; SAP = standard automated perimetry.

We compared the ability of the human graders and the M2M DL algorithm to discriminate reproducible glaucomatous visual field loss from no visual field loss by plotting the ROC and PR curves for each method (Figure 3). The overall AUC for the M2M DL-predicted RNFL thickness was similar to that of the probability of GON given by human graders [AUC = 0.801 (95% CI: 0.757, 0.845) versus 0.775 (95% CI: 0.728, 0.823), respectively; P = 0.222], and both of them performed significantly better than the vertical C/D [AUC = 0.732 (95% CI: 0.680, 0.784)] or horizontal C/D ratio [AUC = 0.683 (95% CI: 0.628, 0.739); all comparisons P < 0.05]. The performance of the M2M algorithm was also similar to the probability of GON by human graders in the PR curves [AUPR = 0.810 (95% CI: 0.765, 0.851) vs. 0.761 (95% CI: 0.703, 0.819), respectively]. In the region of clinically meaningful specificity (85–100%), the pAUC for the M2M DL algorithm was significantly higher than the probability of GON by human graders (pAUC = 0.529 vs. 0.411, respectively; P = 0.016).

Figure 3. — **(A)** Performance of the human gradings [probability of glaucomatous optical neuropathy (GON), and vertical and horizontal cup-to-disc ratio (C/D)] and deep learning (DL)-predicted retinal nerve fiber layer (RNFL) thickness to discriminate eyes with repeatable glaucomatous visual field loss. **(B)** Partial areas under the receiver operating characteristic curves (pAUC) at specificity of 85–100% and **(C)** precision-recall curves for the DL-predicted RNFL thickness and the probability of GON given by human graders. *AUC = area under the receiver operating characteristic curve; AUPR = area under the precision-recall curve*.

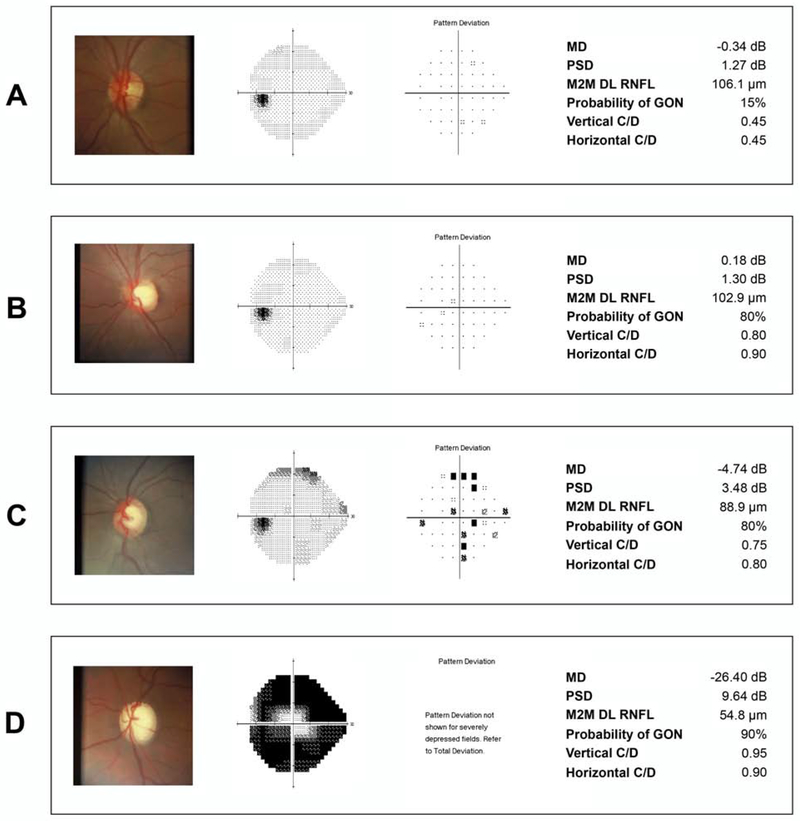
Figure 4 provides several examples of fundus photographs from the grading dataset, with the corresponding SAP, probability of GON and C/D given by the human graders and the M2M DL-predicted RNFL thickness.

DISCUSSION

In this study, we compared the performance of an objective DL algorithm to that of subjective human gradings in detecting glaucomatous damage on fundus photographs. We showed that predictions from the M2M DL algorithm had a significantly stronger correlation with visual field metrics than human gradings. In addition, in the range of clinically relevant specificity, the M2M DL predictions performed significantly better than human gradings in discriminating eyes with visual field loss from those with normal fields. Hence, our findings suggest that an automated objective method to quantify neural damage may perform at least as good as, if not better than, subjective human gradings in detecting signs of glaucomatous damage on fundus photographs.

The motivation for the development of the M2M model came from the realization that subjective gradings of optic disc photographs by human experts may have a limited accuracy in detecting glaucomatous damage. In a previous study, we have shown that cross-sectional human grading of photographs, even by fellowship-trained glaucoma specialists, had a poor accuracy in predicting risk of future visual field loss.³² Another study showed that glaucoma specialists tend to frequently under- or overestimate signs of glaucoma damage when assessing photographs.⁷ Eyes with large physiologic cups, for example, are frequently diagnosed as having glaucoma, whereas eyes with small optic discs but showing significant rim loss may go undetected.^{7, 33} A fundamental aspect of the development of a deep learning network is establishing a reliable “ground-truth” or reference label that can be used to train the algorithm. If the reference standard is biased, the same biases will be learned by the network. Therefore, training a DL network to learn to replicate subjective gradings by humans may lead to an algorithm that will have limited applicability in clinical practice or in screening situations.

In contrast to subjective human gradings, SD OCT can provide reliable quantitative measurements of neural loss in glaucoma. A previous study has shown that RNFL thickness measurements by SD OCT may be able to detect signs of glaucomatous damage 5 to 6 years before the earliest visual field defect.³⁴ In addition, for eyes with moderate or severe glaucoma, SD OCT has been shown to have excellent diagnostic accuracy.^{35, 36} Our M2M DL model was trained to predict RNFL thickness measurements using simple color photographs. The predictions showed excellent correlation with actual SD OCT measurements, with r of 0.832 and MAE of only 7.39 μm. In the present work, we expanded our observations by showing that such predictions outperformed glaucoma specialists’ gradings in detecting eyes with glaucomatous visual field loss in our sample. The M2M model had stronger correlations with visual field metrics and in greater diagnostic accuracy in the region of high specificity compared to an overall probability of glaucoma given by the average score from human graders. In a disease with a relatively low prevalence such as glaucoma, a screening test should have a high specificity to avoid an overwhelming number of normal subjects being referred with a diagnosis of glaucoma.

We observed that the estimation of the C/D ratio by human graders had the lowest correlation with both SAP MD and PSD and the lowest performance in discriminating eyes with glaucomatous visual field loss. The C/D ratio was first popularized as an indicator of GON by Armaly,³⁷ but estimates of the C/D, even among experts, may lack sufficient reliability to be a generalizable measure for screening. Individual graders may differ by >0.2 in their C/D ratio estimates in up to 76% of cases.¹⁰ Moreover, for C/D less than 0.7, there is a tendency to overestimate a larger C/D ratio by 10 to 20% on clinical examination as compared with the photographs.³⁸ Subjective grading of C/D ratio and of the probability of glaucoma is also influenced by variation in optic disc characteristics such as disc size, cup depth, peripapillary atrophy, and different angles of implantation of the optic disc to the sclera.⁷

The M2M DL model may offer several additional advantages compared to previous DL models trained based on subjective gradings. Most importantly, previous models have been trained to output a binary classification decision, i.e., yes or no, for the presence of glaucomatous damage. In contrast, the M2M model is able to provide a quantitative output. This makes it easier to set up cut-offs according to desired levels of specificity, for example. In addition, it is possible that the quantitative measurements might be useful for tracking changes over time, although this still requires validation.

This study has limitations. A study that attempts to compare a new diagnostic test with human gradings of fundus photographs offers some challenges, notably with regard to the gold standard used for diagnosis. We used the presence of visual field defects as the gold standard for glaucoma in this work. We attempted to avoid using clinical optic disc appearance as a diagnostic criterion, as this would most likely favor the performance of human gradings. However, as the population from this study was recruited from a tertiary hospital, it is likely that subjective clinical assessments played an important role in determining whether the patients were being followed in the glaucoma clinic. However, although this may have favored the diagnostic accuracy estimates of subjective human gradings, our results showed that the M2M model still showed significantly greater accuracy for detecting glaucoma. As another limitation, it is likely that some eyes with pre-perimetric glaucoma, but normal visual fields may have been included in the control group, resulting in artificially lower accuracies for detection of glaucoma. However, this potential bias would most likely affect results from both subjective grading and the DL model. Finally, clinicians may not be used to routinely provide a score of probability of GON like the one employed in this study. Although clinicians are trained to identify features that are indicative of glaucomatous damage (e.g. enlarged C/D ratio, localized RNFL defects, rim thinning) and are expected to make judgments of higher or lower probability of glaucoma on a routine basis. The scores are a direct measurement of this judgment, and therefore are likely to be a suitable metric to compare with the continuous metric yielded by the DL algorithm. However, clinicians are not formally trained to give a final score in the form of a probability and this should be taken into consideration when interpreting the results of our study.

Further refinement is desirable before the M2M DL algorithm can be applied in either clinical or screening settings. In particular, it will be important to define cut-offs suitable for screening according to the desirable level of specificity and the stage of the disease that one wants to detect. External assessment of the validity of our test results in external datasets will be an important next step. Also, the algorithm may underappreciate subtle sectoral RNFL losses given that it was trained with a global RNFL parameter. Thus, further refinement may include training the algorithm for detection of localized RNFL or rim loss.

In conclusion, a DL algorithm outperformed human graders in detecting signs of glaucomatous damage on fundus photographs. The algorithm provides objective and quantitative assessment of neural damage that could potentially be used for glaucoma diagnosis and screening, avoiding the biases and labor of human subjective gradings.

Supplementary Material

1

NIHMS1542870-supplement-1.tif^{(6.7MB, tif)}

2

Figure 2 (Supplemental). Scatterplots of standard automated perimetry (SAP) mean deviation (MD) and (Left) mean probability of glaucomatous optical neuropathy (GON) given by human graders and (Right) the retinal nerve fiber layer (RNFL) thickness predicted by the machine to machine (M2M) deep learning (DL) algorithm.

NIHMS1542870-supplement-2.tif^{(592.3KB, tif)}

ACKNOWLEDGEMENTS/DISCLOSURE

a. Funding/Support: Supported in part by the National Institutes of Health/National Eye Institute grants EY029885 (FAM), and the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior, Brazil (AAJ). The funding organizations had no role in the design or conduct of this research.

b. Disclosures: A.A.J.: none. A.C.T.: none. E.B.M.: none. S.I.B.: none. C.N.U: none. T.E.: none. S.M.W.: none. V.P.C.: Alcon Laboratories (C, F); Allergan (C, F, R); Aerie (C, F). F.A.M.: Alcon Laboratories (C, F, R), Allergan (C, F), Bausch&Lomb (F), Carl Zeiss Meditec (C, F, R), Heidelberg Engineering (F), Merck (F), nGoggle Inc. (F), Sensimed (C), Topcon (C), Reichert (C, R).

c. Other Acknowledgments: none.

Footnotes

The coauthors have seen and agree with each of the changes made to the manuscript in this revision and to the way his or her name is listed.

Supplemental Material available at AJO.com

REFERENCES

1.Mariotti SP. Global Data on Vision Impairments 2010 Bull World Health Organ. Switzerland: World Health Organization, 2012:1–14. [Google Scholar]
2.Tham YC, Li X, Wong TY, Quigley HA, Aung T, Cheng CY. Global prevalence of glaucoma and projections of glaucoma burden through 2040: a systematic review and meta-analysis. Ophthalmology 2014;121(11):2081–90. [DOI] [PubMed] [Google Scholar]
3.Sakata K, Sakata LM, Sakata VM, et al. Prevalence of glaucoma in a South brazilian population: Projeto Glaucoma. Invest Ophthalmol Vis Sci 2007;48(11):4974–9. [DOI] [PubMed] [Google Scholar]
4.Mwanza JC, Oakley JD, Budenz DL, Anderson DR, Cirrus Optical Coherence Tomography Normative Database Study G. Ability of Cirrus HD-OCT optic nerve head parameters to discriminate normal from glaucomatous eyes. Ophthalmology 2011;118(2):241–8 e1. [DOI] [PMC free article] [PubMed] [Google Scholar]
5.Leite MT, Rao HL, Zangwill LM, Weinreb RN, Medeiros FA. Comparison of the diagnostic accuracies of the Spectralis, Cirrus, and RTVue optical coherence tomography devices in glaucoma. Ophthalmology 2011;118(7):1334–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
6.Caprioli J, Prum B, Zeyen T. Comparison of methods to evaluate the optic nerve head and nerve fiber layer for glaucomatous change. Am J Ophthalmol 1996;121(6):659–67. [DOI] [PubMed] [Google Scholar]
7.Chan HH, Ong DN, Kong YX, et al. Glaucomatous optic neuropathy evaluation (GONE) project: the effect of monoscopic versus stereoscopic viewing conditions on optic nerve evaluation. Am J Ophthalmol 2014;157(5):936–44. [DOI] [PubMed] [Google Scholar]
8.Tielsch JM, Katz J, Quigley HA, Miller NR, Sommer A. Intraobserver and interobserver agreement in measurement of optic disc characteristics. Ophthalmology 1988;95(3):350–6. [DOI] [PubMed] [Google Scholar]
9.Jampel HD, Friedman D, Quigley H, et al. Agreement among glaucoma specialists in assessing progressive disc changes from photographs in open-angle glaucoma patients. Am J Ophthalmol 2009;147(1):39–44 e1. [DOI] [PMC free article] [PubMed] [Google Scholar]
10.Varma R, Steinmann WC, Scott IU. Expert agreement in evaluating the optic disc for glaucoma. Ophthalmology 1992;99(2):215–21. [DOI] [PubMed] [Google Scholar]
11.Gaasterland DE, Blackwell B, Dally LG, et al. The Advanced Glaucoma Intervention Study (AGIS): 10. Variability among academic glaucoma subspecialists in assessing optic disc notching. Trans Am Ophthalmol Soc 2001;99:177–85. [PMC free article] [PubMed] [Google Scholar]
12.Parrish RK 2nd, Schiffman JC, Feuer WJ, et al. Test-retest reproducibility of optic disk deterioration detected from stereophotographs by masked graders. Am J Ophthalmol 2005;140(4):762–4. [DOI] [PubMed] [Google Scholar]
13.Hinton G Deep Learning-A Technology With the Potential to Transform Health Care. JAMA 2018;320(11):1101–1102. [DOI] [PubMed] [Google Scholar]
14.Shen D, Wu G, Suk HI. Deep Learning in Medical Image Analysis. Annu Rev Biomed Eng 2017;19(1):221–248. [DOI] [PMC free article] [PubMed] [Google Scholar]
15.He K, Zhang X, Ren S, Sun J. Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification. ArXiv e-prints 2015, https://arxiv.org/abs/1502.01852. Accessed 11.01.18.
16.Gulshan V, Peng L, Coram M, et al. Development and Validation of a Deep Learning Algorithm for Detection of Diabetic Retinopathy in Retinal Fundus Photographs. JAMA 2016;316(22):2402–2410. [DOI] [PubMed] [Google Scholar]
17.Lee CS, Baughman DM, Lee AY. Deep learning is effective for the classification of OCT images of normal versus Age-related Macular Degeneration. Ophthalmol Retina 2017;1(4):322–327. [DOI] [PMC free article] [PubMed] [Google Scholar]
18.Li Z, He Y, Keel S, Meng W, Chang RT, He M. Efficacy of a Deep Learning System for Detecting Glaucomatous Optic Neuropathy Based on Color Fundus Photographs. Ophthalmology 2018;125(8):1199–1206. [DOI] [PubMed] [Google Scholar]
19.Christopher M, Belghith A, Bowd C, et al. Performance of Deep Learning Architectures and Transfer Learning for Detecting Glaucomatous Optic Neuropathy in Fundus Photographs. Sci Rep 2018;8(1):16685. [DOI] [PMC free article] [PubMed] [Google Scholar]
20.Medeiros FA, Jammal AA, Thompson AC. From Machine to Machine: An OCT-Trained Deep Learning Algorithm for Objective Quantification of Glaucomatous Damage in Fundus Photographs. Ophthalmology 2019;126(4):513–521. [DOI] [PMC free article] [PubMed] [Google Scholar]
21.Deng J, Dong W, Socher R, Li L-J, Li K, Fei-Fei L. Imagenet: A large-scale hierarchical image database. IEEE Conference on Computer Vision and Pattern Recognition, 2009: IEEE, 2009:248–255. [Google Scholar]
22.Kingma DP, Ba J. Adam: A method for stochastic optimization. ArXiv e-prints 2014, https://arxiv.org/abs/1412.6980. Accessed 11.01.18.
23.Ruder S An overview of gradient descent optimization algorithms. ArXiv e-prints 2016, https://arxiv.org/abs/1609.04747. Accessed 11.01.18.
24.Smith LN. Cyclical Learning Rates for Training Neural Networks. ArXiv e-prints 2017, https://arxiv.org/abs/1506.01186. Accessed 05.01.18.
25.Myers L, Sirois MJ. Spearman correlation coefficients, differences between In: Kotz S, Read CB, Balakrishnan N, Vidakovic B, Johnson NL, editors. Encyclopedia of statistical sciences. Hoboken: Wiley, 2006. [Google Scholar]
26.Berchuck SI, Mwanza JC, Tanna AP, Budenz DL, Warren JL. Improved Detection of Visual Field Progression Using a Spatiotemporal Boundary Detection Method. Sci Rep 2019;9(1):4642. [DOI] [PMC free article] [PubMed] [Google Scholar]
27.Zhu H, Russell RA, Saunders LJ, Ceccon S, Garway-Heath DF, Crabb DP. Detecting changes in retinal function: Analysis with Non-Stationary Weibull Error Regression and Spatial enhancement (ANSWERS). PLoS One 2014;9(1):e85654. [DOI] [PMC free article] [PubMed] [Google Scholar]
28.Medeiros FA, Sample PA, Zangwill LM, Liebmann JM, Girkin CA, Weinreb RN. A statistical approach to the evaluation of covariate effects on the receiver operating characteristic curves of diagnostic tests in glaucoma. Invest Ophthalmol Vis Sci 2006;47(6):2520–7. [DOI] [PubMed] [Google Scholar]
29.Alonzo TA, Pepe MS. Distribution-free ROC analysis using binary regression techniques. Biostatistics 2002;3(3):421–32. [DOI] [PubMed] [Google Scholar]
30.Davis J, Goadrich M. The relationship between Precision-Recall and ROC curves. Proceedings of the 23rd International Conference on Machine learning; 2006; Pittsburgh, Pennsylvania, USA. [Google Scholar]
31.Saito T, Rehmsmeier M. The Precision-Recall Plot Is More Informative than the ROC Plot When Evaluating Binary Classifiers on Imbalanced Datasets. PLoS ONE 2015;10(3):e0118432. [DOI] [PMC free article] [PubMed] [Google Scholar]
32.Medeiros FA, Alencar LM, Zangwill LM, Bowd C, Sample PA, Weinreb RN. Prediction of functional loss in glaucoma from progressive optic disc damage. Arch Ophthalmol 2009;127(10):1250–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
33.O’Neill EC, Gurria LU, Pandav SS, et al. Glaucomatous optic neuropathy evaluation project: factors associated with underestimation of glaucoma likelihood. JAMA Ophthalmol 2014;132(5):560–6. [DOI] [PubMed] [Google Scholar]
34.Kuang TM, Zhang C, Zangwill LM, Weinreb RN, Medeiros FA. Estimating Lead Time Gained by Optical Coherence Tomography in Detecting Glaucoma before Development of Visual Field Defects. Ophthalmology 2015;122(10):2002–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
35.Leite MT, Zangwill LM, Weinreb RN, et al. Effect of disease severity on the performance of Cirrus spectral-domain OCT for glaucoma diagnosis. Invest Ophthalmol Vis Sci 2010;51(8):4104–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
36.Dong ZM, Wollstein G, Schuman JS. Clinical Utility of Optical Coherence Tomography in Glaucoma. Invest Ophthalmol Vis Sci 2016;57(9):OCT556–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
37.Armaly MF. Genetic determination of cup/disc ratio of the optic nerve. Arch Ophthalmol 1967;78(1):35–43. [DOI] [PubMed] [Google Scholar]
38.Tielsch JM, Sommer A, Katz J, Royall RM, Quigley HA, Javitt J. Racial variations in the prevalence of primary open-angle glaucoma. The Baltimore Eye Survey. JAMA 1991;266(3):369–74. [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

1

NIHMS1542870-supplement-1.tif^{(6.7MB, tif)}

2

Figure 2 (Supplemental). Scatterplots of standard automated perimetry (SAP) mean deviation (MD) and (Left) mean probability of glaucomatous optical neuropathy (GON) given by human graders and (Right) the retinal nerve fiber layer (RNFL) thickness predicted by the machine to machine (M2M) deep learning (DL) algorithm.

NIHMS1542870-supplement-2.tif^{(592.3KB, tif)}

[R1] 1.Mariotti SP. Global Data on Vision Impairments 2010 Bull World Health Organ. Switzerland: World Health Organization, 2012:1–14. [Google Scholar]

[R2] 2.Tham YC, Li X, Wong TY, Quigley HA, Aung T, Cheng CY. Global prevalence of glaucoma and projections of glaucoma burden through 2040: a systematic review and meta-analysis. Ophthalmology 2014;121(11):2081–90. [DOI] [PubMed] [Google Scholar]

[R3] 3.Sakata K, Sakata LM, Sakata VM, et al. Prevalence of glaucoma in a South brazilian population: Projeto Glaucoma. Invest Ophthalmol Vis Sci 2007;48(11):4974–9. [DOI] [PubMed] [Google Scholar]

[R4] 4.Mwanza JC, Oakley JD, Budenz DL, Anderson DR, Cirrus Optical Coherence Tomography Normative Database Study G. Ability of Cirrus HD-OCT optic nerve head parameters to discriminate normal from glaucomatous eyes. Ophthalmology 2011;118(2):241–8 e1. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R5] 5.Leite MT, Rao HL, Zangwill LM, Weinreb RN, Medeiros FA. Comparison of the diagnostic accuracies of the Spectralis, Cirrus, and RTVue optical coherence tomography devices in glaucoma. Ophthalmology 2011;118(7):1334–9. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R6] 6.Caprioli J, Prum B, Zeyen T. Comparison of methods to evaluate the optic nerve head and nerve fiber layer for glaucomatous change. Am J Ophthalmol 1996;121(6):659–67. [DOI] [PubMed] [Google Scholar]

[R7] 7.Chan HH, Ong DN, Kong YX, et al. Glaucomatous optic neuropathy evaluation (GONE) project: the effect of monoscopic versus stereoscopic viewing conditions on optic nerve evaluation. Am J Ophthalmol 2014;157(5):936–44. [DOI] [PubMed] [Google Scholar]

[R8] 8.Tielsch JM, Katz J, Quigley HA, Miller NR, Sommer A. Intraobserver and interobserver agreement in measurement of optic disc characteristics. Ophthalmology 1988;95(3):350–6. [DOI] [PubMed] [Google Scholar]

[R9] 9.Jampel HD, Friedman D, Quigley H, et al. Agreement among glaucoma specialists in assessing progressive disc changes from photographs in open-angle glaucoma patients. Am J Ophthalmol 2009;147(1):39–44 e1. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R10] 10.Varma R, Steinmann WC, Scott IU. Expert agreement in evaluating the optic disc for glaucoma. Ophthalmology 1992;99(2):215–21. [DOI] [PubMed] [Google Scholar]

[R11] 11.Gaasterland DE, Blackwell B, Dally LG, et al. The Advanced Glaucoma Intervention Study (AGIS): 10. Variability among academic glaucoma subspecialists in assessing optic disc notching. Trans Am Ophthalmol Soc 2001;99:177–85. [PMC free article] [PubMed] [Google Scholar]

[R12] 12.Parrish RK 2nd, Schiffman JC, Feuer WJ, et al. Test-retest reproducibility of optic disk deterioration detected from stereophotographs by masked graders. Am J Ophthalmol 2005;140(4):762–4. [DOI] [PubMed] [Google Scholar]

[R13] 13.Hinton G Deep Learning-A Technology With the Potential to Transform Health Care. JAMA 2018;320(11):1101–1102. [DOI] [PubMed] [Google Scholar]

[R14] 14.Shen D, Wu G, Suk HI. Deep Learning in Medical Image Analysis. Annu Rev Biomed Eng 2017;19(1):221–248. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R15] 15.He K, Zhang X, Ren S, Sun J. Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification. ArXiv e-prints 2015, https://arxiv.org/abs/1502.01852. Accessed 11.01.18.

[R16] 16.Gulshan V, Peng L, Coram M, et al. Development and Validation of a Deep Learning Algorithm for Detection of Diabetic Retinopathy in Retinal Fundus Photographs. JAMA 2016;316(22):2402–2410. [DOI] [PubMed] [Google Scholar]

[R17] 17.Lee CS, Baughman DM, Lee AY. Deep learning is effective for the classification of OCT images of normal versus Age-related Macular Degeneration. Ophthalmol Retina 2017;1(4):322–327. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R18] 18.Li Z, He Y, Keel S, Meng W, Chang RT, He M. Efficacy of a Deep Learning System for Detecting Glaucomatous Optic Neuropathy Based on Color Fundus Photographs. Ophthalmology 2018;125(8):1199–1206. [DOI] [PubMed] [Google Scholar]

[R19] 19.Christopher M, Belghith A, Bowd C, et al. Performance of Deep Learning Architectures and Transfer Learning for Detecting Glaucomatous Optic Neuropathy in Fundus Photographs. Sci Rep 2018;8(1):16685. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R20] 20.Medeiros FA, Jammal AA, Thompson AC. From Machine to Machine: An OCT-Trained Deep Learning Algorithm for Objective Quantification of Glaucomatous Damage in Fundus Photographs. Ophthalmology 2019;126(4):513–521. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R21] 21.Deng J, Dong W, Socher R, Li L-J, Li K, Fei-Fei L. Imagenet: A large-scale hierarchical image database. IEEE Conference on Computer Vision and Pattern Recognition, 2009: IEEE, 2009:248–255. [Google Scholar]

[R22] 22.Kingma DP, Ba J. Adam: A method for stochastic optimization. ArXiv e-prints 2014, https://arxiv.org/abs/1412.6980. Accessed 11.01.18.

[R23] 23.Ruder S An overview of gradient descent optimization algorithms. ArXiv e-prints 2016, https://arxiv.org/abs/1609.04747. Accessed 11.01.18.

[R24] 24.Smith LN. Cyclical Learning Rates for Training Neural Networks. ArXiv e-prints 2017, https://arxiv.org/abs/1506.01186. Accessed 05.01.18.

[R25] 25.Myers L, Sirois MJ. Spearman correlation coefficients, differences between In: Kotz S, Read CB, Balakrishnan N, Vidakovic B, Johnson NL, editors. Encyclopedia of statistical sciences. Hoboken: Wiley, 2006. [Google Scholar]

[R26] 26.Berchuck SI, Mwanza JC, Tanna AP, Budenz DL, Warren JL. Improved Detection of Visual Field Progression Using a Spatiotemporal Boundary Detection Method. Sci Rep 2019;9(1):4642. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R27] 27.Zhu H, Russell RA, Saunders LJ, Ceccon S, Garway-Heath DF, Crabb DP. Detecting changes in retinal function: Analysis with Non-Stationary Weibull Error Regression and Spatial enhancement (ANSWERS). PLoS One 2014;9(1):e85654. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R28] 28.Medeiros FA, Sample PA, Zangwill LM, Liebmann JM, Girkin CA, Weinreb RN. A statistical approach to the evaluation of covariate effects on the receiver operating characteristic curves of diagnostic tests in glaucoma. Invest Ophthalmol Vis Sci 2006;47(6):2520–7. [DOI] [PubMed] [Google Scholar]

[R29] 29.Alonzo TA, Pepe MS. Distribution-free ROC analysis using binary regression techniques. Biostatistics 2002;3(3):421–32. [DOI] [PubMed] [Google Scholar]

[R30] 30.Davis J, Goadrich M. The relationship between Precision-Recall and ROC curves. Proceedings of the 23rd International Conference on Machine learning; 2006; Pittsburgh, Pennsylvania, USA. [Google Scholar]

[R31] 31.Saito T, Rehmsmeier M. The Precision-Recall Plot Is More Informative than the ROC Plot When Evaluating Binary Classifiers on Imbalanced Datasets. PLoS ONE 2015;10(3):e0118432. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R32] 32.Medeiros FA, Alencar LM, Zangwill LM, Bowd C, Sample PA, Weinreb RN. Prediction of functional loss in glaucoma from progressive optic disc damage. Arch Ophthalmol 2009;127(10):1250–6. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R33] 33.O’Neill EC, Gurria LU, Pandav SS, et al. Glaucomatous optic neuropathy evaluation project: factors associated with underestimation of glaucoma likelihood. JAMA Ophthalmol 2014;132(5):560–6. [DOI] [PubMed] [Google Scholar]

[R34] 34.Kuang TM, Zhang C, Zangwill LM, Weinreb RN, Medeiros FA. Estimating Lead Time Gained by Optical Coherence Tomography in Detecting Glaucoma before Development of Visual Field Defects. Ophthalmology 2015;122(10):2002–9. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R35] 35.Leite MT, Zangwill LM, Weinreb RN, et al. Effect of disease severity on the performance of Cirrus spectral-domain OCT for glaucoma diagnosis. Invest Ophthalmol Vis Sci 2010;51(8):4104–9. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R36] 36.Dong ZM, Wollstein G, Schuman JS. Clinical Utility of Optical Coherence Tomography in Glaucoma. Invest Ophthalmol Vis Sci 2016;57(9):OCT556–67. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R37] 37.Armaly MF. Genetic determination of cup/disc ratio of the optic nerve. Arch Ophthalmol 1967;78(1):35–43. [DOI] [PubMed] [Google Scholar]

[R38] 38.Tielsch JM, Sommer A, Katz J, Royall RM, Quigley HA, Javitt J. Racial variations in the prevalence of primary open-angle glaucoma. The Baltimore Eye Survey. JAMA 1991;266(3):369–74. [PubMed] [Google Scholar]

PERMALINK

Human versus Machine: Comparing a Deep Learning Algorithm to Human Gradings for Detecting Glaucoma on Fundus Photographs

Alessandro A Jammal, MD

Atalie C Thompson, MD, MPH

Eduardo B Mariottoni, MD

Samuel I Berchuck, PhD

Carla N Urata, MD

Tais Estrela, MD

Susan M Wakil, MD

Vital P Costa, MD, PhD

Felipe A Medeiros, MD, PhD

INTRODUCTION

METHODS