Estimation of backscatter coefficients using an in situ calibration source

Abstract

The objective of this work is to demonstrate the feasibility of estimating the backscatter coefficient (BSC) using an in situ calibration source. Traditional methods of estimating the BSC in vivo using a reference phantom technique do not account for transmission losses due to intervening layers between the ultrasonic source and tissue region to be interrogated, leading to increases in bias and variance of BSC-based estimates. To account for transmission losses, an in situ calibration approach is proposed. The in situ calibration technique employs a titanium sphere that is well-characterized ultrasonically, biocompatible and embedded inside the sample. A set of experiments was conducted to evaluate embedded titanium spheres as in situ calibration targets for BSC estimation. The first experiment quantified the backscattered signal strength from titanium spheres of three sizes: 0.5-, 1- and 2-mm in diameter. The second set of experiments assessed the repeatability of BSC estimates from the titanium spheres and compared these BSCs to theory. The third set of experiments quantified the ability of the titanium bead to provide an in situ reference spectrum in the presence of a lossy layer on top of the sample. The final set of experiments quantified the ability of the bead to provide a calibration spectrum over multiple depths in the sample. All experiments were conducted using a L9–4/38 linear array connected to a SonixOne system. The strongest signal was observed from the 2-mm titanium bead with an SNR of 11.6 dB with respect to the background speckle. Using an analysis bandwidth of 2.5 to 5.5 MHz, the mean differences between experimentally derived BSCs and BSCs derived from Faran theory were 0.54 dB and 0.76 dB using the array and a single-element transducer, respectively. The BSCs estimated using the in situ calibration approach without the layer, with the layer and using the reference phantom approach with the layer were compared to the reference phantom approach without the layer present. The mean differences in BSCs were 0.15 dB, 0.73 dB and −9.69 dB, respectively. The mean differences of the BSCs calculated from data blocks located at depths that were either 30 pulse lengths above or below the actual bead depth compared to the BSC calculated at bead depth were −1.55 dB and −1.48 dB, respectively. The results indicate that an in situ calibration target can account for overlaying tissue losses thereby improving the robustness of BSC-based estimates.

I. Introduction

Quantitative ultrasound (QUS) techniques have demonstrated the ability to characterize tissues, classify disease state, detect cancer and identify the response of cancer to therapy [1], [2], [3], [4], [5], [6], [7]. Among these techniques, spectral-based QUS utilizing the backscatter coefficient (BSC) has demonstrated success and continues to garner interest. In spite of the success of QUS to date, there remains a fundamental challenge with acquiring consistent QUS estimates when imaging in vivo, especially using the BSC. The challenge with a spectral-based estimation of the BSC in vivo is the inability in most cases to account for intervening losses between the transducer and the region of tissue to be interrogated. These losses can occur through transmission losses between different tissue layers and from frequency-dependent attenuation in the tissues.

Currently, two methods have been adopted for estimating the BSC: the planar reference technique [8], [9], [10], [11] and the reference phantom technique [12], [13]. In both cases an averaged power spectrum is acquired from raw radiofrequency (RF) backscattered ultrasound located spatially from a data block within a sample or tissue. The backscattered signals in the data block consist of several scan lines gated with a windowing function. The signals in the data block are assumed to arise from a random spatial arrangement of scatterers with uniform scattering statistics. To calculate the BSC, the averaged power spectrum is divided by a reference spectrum that accounts for the diffraction and system-dependent effects. The bias and variance of the BSC estimates depend on several factors including the size of the data block used, the analysis bandwidth, the windowing function and accounting for system-dependent effects and losses incurred between the transducer and data block [14], [15], [16], [17].

Conventional methods of calibration for QUS require collecting signals from a well-characterized reference phantom or from a planar reflector, which are external to the tissue being imaged. The long recognized problem with this approach is that transmission losses and attenuation through intervening layers between the transducer and the data block are unknown. Currently, there is no method available to account for both the transmission losses and frequency-dependent attenuation that occur as ultrasound propagates through tissues. Several methods have been proposed to estimate the total attenuation to a tissue region [18], [19], [20], [21], [22]. However, these techniques suffer from large variance of estimates and do not account for transmission losses. In one recent paper, the variance of attenuation estimation was greatly reduced by incorporating prior information into a regularization scheme [20]. In an interlaboratory comparison of BSC estimation approaches, to enable accurate BSC estimates the transmission coefficient was provided to the participants to account for losses induced by layers on the phantom materials used in the study [23]. Therefore, the interlaboratory study demonstrates the importance of accounting for transmission losses to obtain accurate estimates of the BSC.

The inability to account for these losses results in a reduction in the diagnostic capabilities of spectral-based QUS techniques. When scanning different tissues from different patients or even the same patient over time, the intervening layers between the transducer and the region of interest may not be the same. This can result in an increase in variance of QUS estimates from one scan to the next and between different patients despite methods in hand to partially correct for attenuation. In spectral-based QUS techniques for tissue classification, it is important to reduce the variance of estimates [24] which improves the ability to uniquely classify a tissue or tissue state.

In this study, we demonstrate that an in situ calibration approach can provide improved estimates of BSCs by accounting for ultrasonic transmission losses and attenuation encountered in a tissue. Specifically, the proposed in situ calibration approach employs a biocompatible sphere embedded in the vicinity of a tissue to be scanned. Because the sphere is in the tissues being scanned, the sphere will encounter similar losses and diffraction as the investigated tissue and can be used to generate a reference spectrum to provide a more precise estimation of the BSC. The in situ calibration approach offers several advantages over techniques like [18]. First, the in situ calibration technique allows compensation of transmission losses due to reflection/transmission through several layers, whereas the attenuation estimation techniques do not provide the ability to compensate for transmission losses. Second, the in situ calibration technique does not require a specific model for both attenuation and the BSC. Third, the in situ calibration technique does not require a large amount of data to reduce estimate variance. Example applications may include embedding spheres within a breast tumor during a biopsy and before chemotherapy. Current standard of practice before neoadjuvant chemotherapy is to embed fiducial markers into the breast tumor and lymph nodes suspected to contain cancer for future imaging. In these applications, the sphere would be used to register the tumor location and provide a calibration target that takes into accounts the overlaying layers. QUS could then be used to monitor the tumor or provide a means of identifying response of the tumor to therapy over time [25].

The purpose of the current study is to evaluate the performance of an in situ calibration bead for providing a reference spectrum for BSC estimation. Note that the purpose of the study is not to estimate the transmission and attenuation losses to some sample region, but to account for these losses through a calibration target embedded in the sample. In this study, three important features of the new calibration approach were assessed. First, the strength of the signal was tested for a variety of bead sizes relative to a wavelength. Second, the accuracy and the repeatability of the BSC estimates from the bead were evaluated using a single-element transducer and a linear array from a clinical ultrasound system and size of the bead relative to the transducer beamwidth. Third, the ability to replace the external reference phantom in the presence of unknown transmission losses was assessed. Finally, the accuracy of the calibration procedure was quantified for BSC estimation in the tissue at different depths compared to the depth of the calibration bead.

II. Theory

The BSC is defined as the differential backscattered cross section per unit volume [26]. The scattered intensity, as a function of frequency, is estimated from an averaged power spectrum of the RF signal corresponding to ultrasound backscatter from a data block. The power spectrum can be calculated from each windowed scan line of the data block through the magnitude squared of the Fourier transform of the RF signal. Assuming a single scattering approximation and that the data block is at least one aperture diameter away from the transducer surface, the power spectrum can be represented as [27]

$$W(f,\mathbf{x})=T(f,\mathbf{x})A(f,\mathbf{x})D(f,\mathbf{x})H(f,\mathbf{x})S(f,\mathbf{x}),$$ (1)

where T(f, x) incorporates the transmission losses between tissues, A(f, x) is the frequency dependent attenuation, D (f, x) represents the diffraction effects of the transducer, H (f, x) is the impulse response of the transducer system and incorporates effects of the windowing function, the electromechanical response and time gain compensation (TGC), and S(f, x) is the scattering function describing the underlying tissue microstructure. Note that each of the terms are spatially dependent.

The parameter of interest is the scattering function because it can be used to describe and possibly identify the state of the tissue. Therefore, it is necessary to account for all of the loss terms and system-dependent effects in the power spectrum estimate. Two methods have been adopted to account for the system-dependent effects in the power spectrum: 1) the planar reflector technique [8], [9], [10], [11] and 2) the reference phantom technique [12], [13]. For the planar reflector technique, a smooth plate of known reflectivity is placed at the focus of the transducer and the signal from the reflector is recorded. Using the planar reflector signal as a reference will only account for D (f, x) and H (f, x) near the focus of a weakly focused source.

Similarly, the reference phantom technique utilizes the power spectrum from a well-characterized tissue-mimicking phantom to account for system-dependent effects. Like the planar reflector technique, the reference phantom technique accounts for D (f, x) and H (f, x) but does not implicitly account for attenuation or transmission losses because the attenuation and transmission losses are in general unknown for a tissue in vivo. The attenuation correction in the reference phantom method can be incorporated through backscatter-based attenuation estimation methods described earlier or by using values of attenuation for overlying layers extracted from the literature. However, utilizing literature values of attenuation for different tissue layers still provides uncertainty for the exact corrections. The reference phantom technique can calibrate for system effects outside of the focus and for more highly focused sources including array transducers using delay and sum beamforming. Therefore, the reference phantom technique is more versatile in the ability to calibrate for different transducer configurations; however, ensemble averaging is required to reduce variance of the BSC introduced by the reference spectrum.

For an in situ calibration approach using a single spherical bead the following assumptions are made. First, it is assumed that the signal, i.e., scattered intensity, from the calibration bead is much larger than signal from the surrounding soft tissues (in our case we selected a bead that would be 10 dB above the background). Second, transmission and attenuation losses to the bead location in the tissue are close to transmission and attenuation losses encountered at a similar depth in the tissue not containing the bead. This is valid when the tissue layers above the bead and above a data block to be analyzed are similar in thickness, number and attenuation properties. The more this varies the larger the error in the BSC estimate from the data block. Figure 1 illustrates how the in situ calibration bead works in practice. The power spectrum from the bead is first acquired and then a power spectrum from a data block near the same depth as the bead in the sample is acquired. Under the two assumptions stated above, the power spectrum from the bead is given by,

$$W_{bead}(f,\mathbf{x})\approx T(f,\mathbf{x})A(f,\mathbf{x})D(f,\mathbf{x})H(f)S_{bead}(f,\mathbf{x}),$$ (2)

where S_bead (f, x) is the scattering function from the calibration bead. Therefore, the BSC can be estimated by dividing the power spectrum of the sample by the power spectrum from the bead and multiplying by the BSC of the bead,

$${\sigma }_{bsc}(f,\mathbf{x})=\frac{W(f,\mathbf{x})}{W_{bead}(f,\mathbf{x})}{\sigma }_{bsc}^{bead}(f,\mathbf{x}).$$ (3)

By estimating the power spectrum from the bead and utilizing the BSC from the bead, estimates of the BSC from a tissue can be acquired with the system-dependent terms, transmission losses and frequency-dependent attenuation approximately taken into account. Once the BSC of a bead of known size and material is estimated, that BSC can be used in subsequent experiments without having to take additional BSC estimates each time that type of bead is used.

Fig. 1.

Illustration of the in situ calibration technique. A transducer captures signal from a data block inside a tissue and the power spectrum is calculated from the backscattered ultrasound signal, W(f). Signals are also captured from the in situ calibration bead located at a similar depth as the data block of tissue signal.

III. EXPERIMENTAL METHODS

In the first set of experiments, titanium spheres of size 0.5, 1 and 2 mm in diameter were purchased (BalTec, Los Angeles, CA). These spheres are biocompatible and compatible with MRI making them desirable for clinical applications. The spheres were embedded in the middle of tissue-mimicking phantoms. A phantom was made of 200 mL of degassed water and 5 g of noble agar powder. The signal intensity from the titanium bead was calculated and compared to the background speckle. Specifically, we calculated the signal-to-noise ratio (SNR) as,

$$\mathrm{SNR}=10\log \left(\frac{{\sigma }_{bead}^2}{{\sigma }_{speckle}^2}\right),$$ (4)

where ${\sigma }_{bead}^2$ and ${\sigma }_{speckle}^2$ are the variances of the envelope signal at the bead location and of the speckle background, respectively. To calculate the SNR, the variance was calculated from envelope data from a block surrounding the bead and surrounding a bead free region at the same depth. The block size was 5 mm by 5 mm. The smallest titanium bead that was 10 dB above the background tissue signal was chosen as the calibration bead for subsequent experimental evaluation. The 10 dB was chosen because it allowed us to utilize the analysis bandwidth of our transducer.

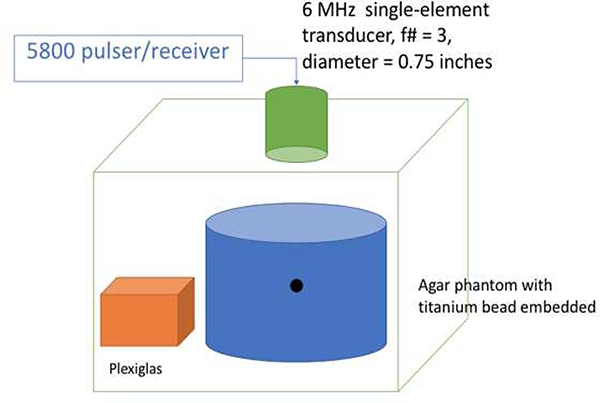
In the second set of experiments, BSCs were estimated from measurements from the titanium bead selected from the first set of experiments and compared to Faran theory [28]. A single-element transducer and the first phantom were submerged in a water tank (see Fig. 2 for illustration). The phantom was scanned in order to isolate the scattering from the calibration bead alone to compare with theory, i.e., Faran. The single-element transducer was an f/3 6-MHz focused transducer with a focal length of 2.25 inches (or 57.15 mm). The beamwidth was estimated to be 0.771 mm. The bead was at a depth of 35 mm from the top surface of the phantom as confirmed by B-mode imaging of the phantom. The focused transducer was connected to a Panametrics 5800 pulser/receiver (Olympus NDT, Waltham, MA) to excite the transducer and record the received data via an UF3 A/D card (Strategic Test, Boston, MA) sampled at 250 MHz. After scanning the phantom, the transducer scanned a planar reflector (a piece of plexiglass) at the same depth as the calibration bead in the phantom to obtain a reference spectrum. The planar reference was used to remove the diffraction and system effects in order to compare the scattering from the titanium bead to Faran’s theory for scattering from a sphere. The properties used for the Faran model and titanium were: mass density (4.5 g/cc), Poisson’s ratio (0.34) and sound speed (6,100 m/s). A −10 dB analysis bandwidth of 2.5 to 5.5 MHz was used. Next, the linear array was used to scan the same phantom to estimate the BSC of the bead, which subsequently was used as a calibration spectrum for later experiments. A reference phantom with known attenuation and BSC was scanned with the same system setup to remove the diffraction and system effects [29]. The array was touching the phantom surface. The experimental configuration was taken down and set up three separate times to test the repeatability of the BSC estimates from the bead.

Fig. 2.

Experimental testing configuration for estimating BSC from titanium bead.

In both experiments with the single-element and the linear array, the attenuation of the phantom was first estimated using the spectral difference method [30] to be α(f) = 0.2826f^1.249(dB/cm), which was then used to compensate for losses in the phantom to the depth of the bead for estimation of the BSCs. The differences between the BSCs estimated from the sphere using either the single-element or the array compared to Faran theory was calculated. Following [11], the fit between two BSCs was quantified using the first and second moments of the difference function:

$$D({\sigma }_{bsc1}(f,x),{\sigma }_{bsc2}(f,x))=10{\log }_{10}\frac{{\sigma }_{bsc1}(f,x)}{{\sigma }_{bsc2}(f,x)},$$ (5)

where σ_bsc2(f, x) was taken to be the baseline. The functions D_σ and D_μ were defined as follows where the averaging was over the analysis bandwidth:

$$D_{\mu }(x)=\frac{1}{N}\sum _{i=1}^{N}D({\sigma }_{bsc1}(f_i,x),{\sigma }_{bsc2}(f_i,x)),$$ (6)

$$D_{\sigma }(x)=\sqrt{\frac{1}{N}\sum _{i=1}^N[D({\sigma }_{bsc1}(f_i,x),{({\sigma }_{bsc2}(f_i,x)-D_{\mu }(x)]}^2.}$$ (7)

The quantities D_μ and D_σ are measures of the amplitude and frequency dependence agreements between the two BSCs σ_bsc1(f, x) and σ_bsc2(f, x).

In the third set of experiments, the titanium bead selected from the first experiment was implanted in a homogenous tissue-mimicking phantom with glass beads or in a chicken breast phantom. The glass bead phantom was fabricated similarly to the graphite phantoms from the first experiments except that 2 g of glass beads (of size 50–90 μm) were also added as a source of speckle to mimic in vivo conditions and have a ground truth for estimates of scatterer size. In the chicken breast phantom, the chicken breast was suspended in agar to provide extra depth from the phantom surface. The glass bead phantom and chicken breast phantom were scanned using the L9–4/38 array transducer connected to the SonixOne system with and without a layer of fatty pork placed between the transducer and the phantom. The chicken and pork samples were purchased from a local grocery store and kept in cold storage until preparation for scanning. The local attenuation of the phantom material was estimated using the spectral difference method [30] to be α(f) = 0.14184f^1.7975(dB/cm). Local attenuation estimation within the fatty layer could not be obtained using the method from [30] because we could not obtain sufficient-sized data blocks with uniform scattering within the fatty layers. BSCs from the samples were from data blocks at the same depth as the calibration bead in the sample. The BSCs were calculated from data blocks of size 9 beamwidths (10 mm) laterally by 30 pulse lengths axially (10 mm). BSCs were calculated with and without the layers on top and using the bead as a calibration target and the traditional reference phantom technique. The BSCs were compared between the different calibration approaches and differences of the BSCs were computed between the estimates with and without the layers present using Eq. (5). The baseline BSC was the BSC calculated without the layer and using the reference phantom. For the glass bead phantom, the effective scatterer diameter (ESD) of the glass beads was estimated using the theory of Faran and the minimum average squared deviation approach [10].

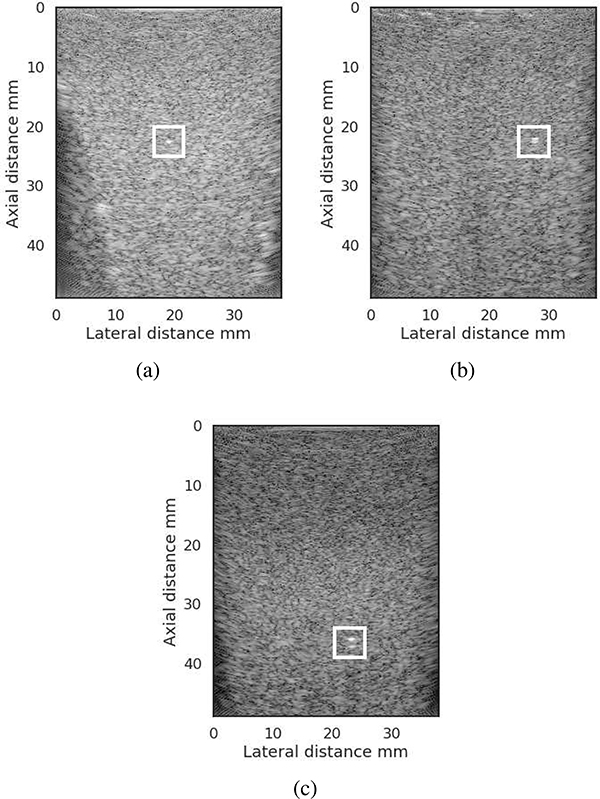
In the final set of experiments, the same phantoms were used to quantify the error in the BSC estimate when the depth of the data block used for analysis was either at a greater depth or shallower depth than the titanium bead. The data block location was stepped from one full data block axial length above the bead to one full data block axial length below the bead depth (see Fig. 3). The upper data block was within the depth of field of the imaging array and the lower data block was just outside of the depth of field. To account for differences in the total attenuation of the data blocks at depths different from the bead depth, the total attenuation loss was assumed to be accounted for up to the bead depth and only local attenuation corrections were needed to account for the offset of the data block from the bead depth. The local attenuation of the phantom was estimated using the spectral difference method [30]. Estimates of the BSC were acquired with and without the fatty layer on top and using the titanium bead as a reference and using the reference phantom technique. The mean differences between BSCs estimated at the depth of the calibration bead and BSCs estimated at different depths were calculated using Eq. (5).

Fig. 3.

a) Data block around the bead to calculate the ref spectrum, (b) data block to calculate the BSC at bead depth and (c) and (d) data blocks above and below the bead to compare with BSC estimates from (b). The dynamic range of the images was 60 dB.

IV. Results

Figure 4 shows B-mode images of the three different titanium beads (0.5-, 1-, and 2-mm diameter) embedded in graphite and agar phantom. The intensity of the signal scattered from each bead was calculated and compared to the background speckle at the same depth. Table I lists the values of the SNR for each bead size in the phantom computed using Eq. (4). From the B-mode images of Fig. 4, the larger the bead size, the more visible the target. Based on the results from the SNR for each bead size examined, the 2-mm diameter titanium bead with SNR of 11.61 dB was chosen for subsequent experiments. In addition to the SNR values, when there are fatty pork layers on top of the phantoms or the bead is embedded inside the chicken breast, the 2-mm diameter bead was also more visible and distinct compared to other small hyperechoic targets in the samples.

Fig. 4.

B-mode images from phantoms embedded with a single (a) 0.5-mm titanium bead, (b) a 1-mm diameter titanium bead and (c) 2-mm diameter titanium bead.

TABLE I.

SNR values from signals scattered from the titanium beads in the phantoms from Fig. 5.

Bead diameter	SNR
0.5 mm	2.65 dB
1 mm	5.69 dB
2 mm	11.61 dB

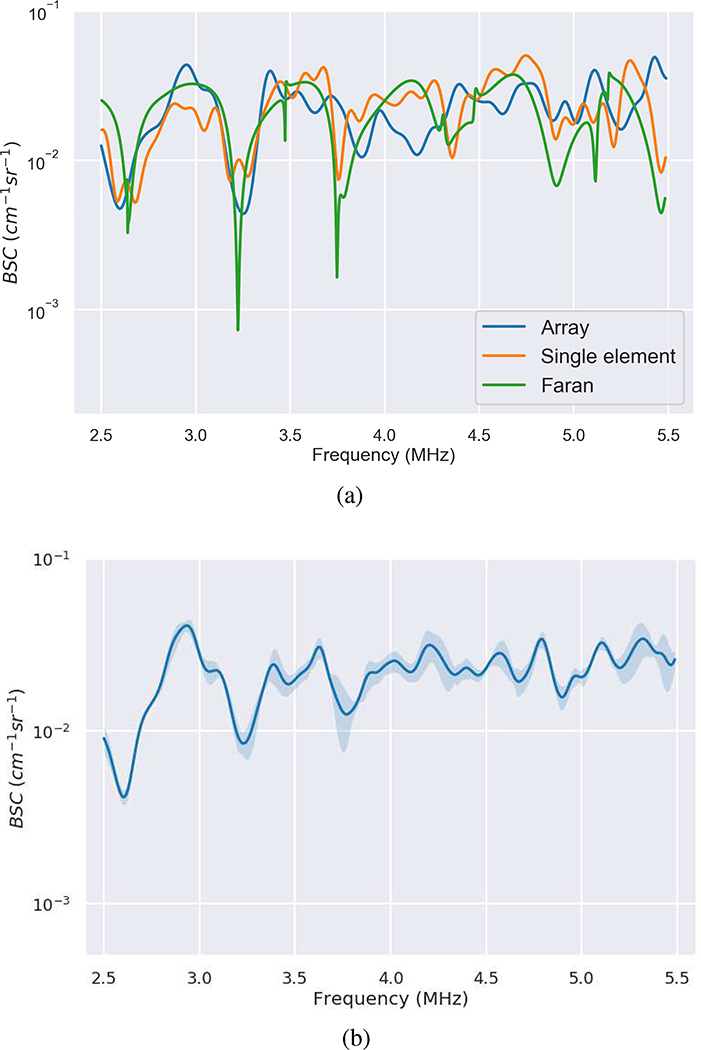
The BSCs for the 2-mm diameter titanium bead acquired using the single-element transducer and the linear array are plotted in Fig. 5(a) along with a curve derived from the Faran theory. The BSC estimated using the single-element transducer was derived from power spectra averaged across a 2 mm by 2 mm grid centered at the bead with the lateral step size of 100 microns. The data block for BSC estimate using the array was 10 mm by 10 mm. Although the beamwidths of the single-element and the linear array were estimated to be 0.771 and 1.11 mm, respectively, which are smaller than the bead size, the measured BSC captured most of the features of the curve predicted by Faran’s theory. The means differences of the BSCs between Faran curve fit and the BSCs of the single-element transducer and the linear array were 0.76 dB and 0.54 dB, respectively. Figure 5(b) shows the mean and standard deviation of the BSC of the titanium bead estimated using the linear array with the reference phantom technique where the experiment was repeated three times (over a period of two weeks).

Fig. 5.

(a) Comparison of Faran theory of scattering from a 2-mm diameter titanium sphere compared with measurements from the sphere using a single-element transducer and from using the linear array L9–4/38. (b) The mean and standard deviation of the BSCs of the bead measured by the linear array over three different experimental time points.

Figure 6 shows B-mode images of the tissue-mimicking phantom containing the titanium bead with and without a fatty layer placed on top of the phantom. The layer acted to change the transmission and attenuation losses to the data block used for analysis. The attenuation of the fatty layer was estimated using a substitution method and found to be 1.04 dB MHz⁻¹ cm⁻¹. The BSC was calculated for the phantom using the calibration bead and the reference phantom approach. The estimated ESD values are provided in Table II. The ESD was averaged from three data blocks centered at the same depth as the bead and the standard deviation was calculated from the three ESD estimates. Using a Kruskal-Wallis test, no significant differences were observed between the ESDs estimated using the bead with a layer present and the ESDs estimated using the reference phantom with no layer present. In addition, mean differences for the BSCs between the different calibration approaches (compared to the baseline of the BSC calculated with no layer present and using the reference phantom) are also listed in Table II.

Fig. 6.

B-mode images of phantoms (a) without and (b) with the layer on top.

TABLE II.

Error estimates and estimated glass bead characteristics using the different reference techniques with and without the layer present.

	ESD (glass bead phantom)	Dμ (glass bead phantom)	Dσ (glass bead phantom)	Dμ (chicken phantom)	Dσ (chicken phantom)
No layer - reference phantom (baseline)	75.2 ± 1.7	0	0	0	0
No layer - in situ bead	71.2 ± 1.6	0.15	2.29	−3.71	2.32
Layer - in situ bead	76.5 ± 0.9	0.73	3.19	0.46	3.71
Layer - reference phantom	45.5 ± 4.0	−9.69	3.08	−10.19	4.71

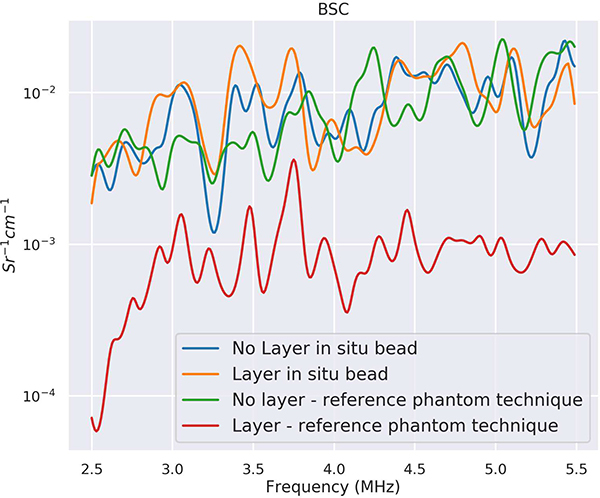
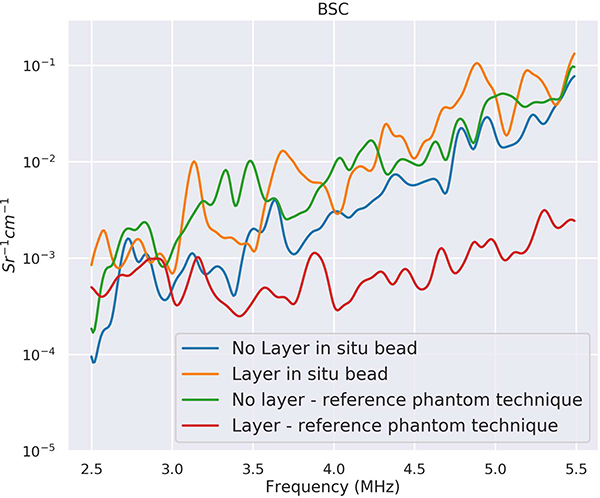
Plots of the BSCs versus the calibration approaches are provided in Fig. 7. Figure 7 shows the BSCs estimated using the traditional reference phantom technique and the in situ calibration approach and with and without the layer present. The BSCs estimated using the in situ calibration approach with and without the layer present overlapped with the BSC estimated using the traditional reference phantom approach without the layer present. The BSC estimated using the traditional reference phantom approach with the layer present, without attempting to correct for attenuation and transmission losses through the layer, did not overlap with the other curves. The BSC using the traditional reference phantom technique (red curve), without layer attenuation correction, was underestimated when the fatty layer was placed on top. Use of attenuation and transmission correction, either through attenuation estimates from the backscatter or through the use of literature values of attenuation, would make the BSC curve closer to the BSC curves estimated without the lossy layer present. However, the BSC using the in situ calibration bead (orange curve) when the layer was on top was close to the BSC estimates without the fatty layer.

Fig. 7.

BSCs from phantom using calibration bead and reference phantom technique.

A B-mode image from a chicken breast having an embedded 2-mm diameter titanium bead is shown in Fig. 8 with a fatty layer placed on top. BSC estimates from the chicken breast are provided in Fig. 9 using the reference phantom and calibration bead approaches with and without a fatty layer placed on top. The means differences of the BSC estimates are provided in the last column of Table II. The SNR of the bead estimated from the chicken breast was 11.7 dB. Estimates of the BSC when varying the interrogation depth are provided in Fig. 10. The mean differences between BSCs calculated at the same depth of the calibration bead and at different depths are provided in Table III.

Fig. 8.

B-mode of titanium bead in a chicken breast sample.

Fig. 9.

BSCs from chicken breast using calibration bead and reference phantom technique.

Fig. 10.

BSCs from data blocks located at different depths relative to the bead depth.

TABLE III.

Error estimates between the BSC at bead depth and BSCs above and below the bead depth

	Dμ (dB)	Dσ (dB)
BSC at bead depth (baseline)	0	0
BSC above the bead	−1.55	1.56
BSC below the bead	−1.48	1.42

V. Discussion

Currently, the reference phantom technique is the gold standard for acquisition of a calibration spectrum for calculating the BSC when using a clinical system and an array probe. However, the reference phantom technique for estimating spectral-based QUS parameters can result in high bias and high variance in QUS parameters due to the inability to account for the losses incurred from intervening layers. The in situ calibration technique presented in this study removes the need to use a reference phantom in cases where an embedded bead could be used. The embedded bead can also be used to compensate for the attenuation and transmission losses at depth due to intervening layers. To evaluate the suitability of an in situ calibration target for spectral-based QUS analysis, we scanned titanium beads embedded in different samples with and without lossy layers placed on top of the samples.

In the first set of experiments, we assessed the importance of bead size on the ability to acquire sufficient SNR. The SNRs for the smaller beads, 0.5- and 1-mm diameter, were not sufficient to get good QUS estimates. These beads are also difficult to handle due to their size and not easily differentiated in the B-mode images from other impurities or structures giving rise to large specular signals. Therefore, our results suggest that a bead size of at least 2 mm be used. The SNR for the 2-mm titanium sphere was also confirmed in the chicken with a value of 11.7 dB, which suggests that smaller beads might not have been clearly visible in the chicken breast.

In the next set of experiments, the ability to accurately estimate a BSC from the embedded bead compared to theory was assessed. Overall, as Fig. 5(a) demonstrates, we were able to accurately estimate the BSC from the embedded 2-mm diameter titanium bead. The BSC accuracy was observed even though the bead was larger than the beamwidth of the transducer (−6-dB pulse-echo beamwidth of the single-element and of the linear array are estimated to be 770 μm and 1.1 mm, respectively). The 3 dB standard deviation of the error function was due to the sharp dips in the theoretical Faran curve, which were not as prominent in the measured BSCs of the bead, which makes it suitable to use as a reference spectrum. The BSC calculated from measurements from the bead in 5(a) contains noise and does not always match the theoretical BSC from the bead, especially near 5.5 MHz where the signal energy is closer to the noise floor. For the reference phantom technique, noise in the reference spectrum can be reduced by averaging over many independent scan lines. This is not possible with the calibration bead. On the other hand, the noise present in the BSC of the bead can be characterized by high frequency oscillations on top of a smoother BSC curve. Parameterization of the BSC for estimates like the ESD typically involves fitting a slope to the BSC, which in effect low pass filters the BSC curve. Therefore, the nature of the noise added from the bead spectrum has little effect on the accuracy of estimates of ESD, as shown in Table II.

Previous results from [31] demonstrated that accurate estimates of the BSC from large scatterers compared to a beamwidth could be acquired as long as the power spectrum was averaged from scan lines that traversed across the lateral length of the scatterer. Kemmerer et al. [31] demonstrated this effect with caviar eggs, which are fluid spheres that supported little to no shear wave. The titanium bead did support a shear wave contribution to the scattering, as accounted for in the theory of Faran. Therefore, the present results demonstrate that accurate BSCs can be estimated from high contrast scatterers that are larger than a beamwidth and that support shear waves. These results suggest that the use of a large bead in situ for calibration is acceptable because it: 1) provides larger SNR than a smaller bead and 2) can provide accurate estimates of BSC at depth assuming the beams traverse the width of the bead in the imaging field. The BSC measured from the bead using the linear array was also shown to be highly repeatable, i.e., the mean standard deviation of the BSCs across experiments was 1.32 dB.

In the third set of experiments, we assessed the performance of the in situ calibration approach compared to the traditional reference phantom approach when lossy layers were placed on top of samples. The experimental results for the phantoms indicated that the reference phantom technique, without attenuation correction, could not faithfully reproduce the BSC when a fatty layer was placed on top of the phantom samples. The presence of the layer caused the BSC from the reference phantom to both change its shape, i.e., slope, and overall magnitude, i.e., the magnitude of the BSC was lower. The mean differences of the BSCs, using the BSC from the reference phantom without a layer as baseline, were 0.15 dB, 0.73 dB and −9.69 dB using the in situ calibration approach without the layer, with the layer and using the reference phantom approach with the layer, respectively. When using the in situ calibration bead, only small changes in the BSC were observed between the estimates of BSC with and without the layer present. Therefore, the use of the in situ calibration target provided the ability to account for losses incurred from the lossy layer. Similar results were observed for BSC estimates from the chicken breast sample. In addition, the layer above the phantom was approximately 1 cm in thickness whereas the fatty layer above the chicken was almost 1.5 cm and a small agar layer was also between the fatty layer and the chicken. This confirms that the in situ calibration approach can handle different layer thicknesses and multiple layers.

In the final set of experiments, we quantified the errors in the BSC that accumulate when the data blocks used for estimating the BSC occurred at different depths from the bead depth, i.e., the distance between the probe surface and the bead. The differences in the BSCs from the data blocks located at different depths were small compared to the data block centered at the bead depth (see Table III). These findings suggest that over a limited range, the in situ bead could properly account for losses, system effects and diffraction effects in a homogeneous scattering region. The depth ranges over which the calibration from the bead is usable will depend on the specific scan configurations of the probe (e.g., focal properties). Because there can be a large number of possible focal and scan configurations with an array probe, we limited our analysis to simple linear sequential scanning with constant f-number focusing. These results demonstrate the versatility of the in situ calibration approach.

The limitation of the study lies in the assumption that the transmission and attenuation losses at the bead location are close to the transmission and attenuation losses of the data block in the sample under investigation. Ideally, the data block around the bead and for the interrogated sample are close axially and laterally. Axially, the transmission losses can be assumed to be constant, and only the local attenuation needs to be estimated. In Fig. 10, the local attenuation was compensated based on estimated local attenuation at the bead depth multiplied by the depth difference between the data blocks. The BSCs from the data block above and below the data block at the bead depth in Fig. 10 are similar, which shows the local attenuation compensation is accurate. However, the local attenuation in the phantom is uniform and simpler to estimate, compared to the attenuation changes in in vivo conditions, which might be difficult to estimate and could introduce error in the BSC estimation. Laterally, as the distance between the interrogated data block and the bead increases, the corrections for the transmission and attenuation losses may grow worse. The quality of the correction will depend on the shape of the overlying layers for the particular imaging task. For layers of constant thickness, the corrections from the bead would potentially be valid for greater distances laterally.

Finally, the in situ calibration approach in this study was not evaluated in vivo. The implantation of a bead in vivo can cause inflammation and fibrous growth around the marker location. If the bead size is on the order of the size of the lesion, scar tissue from the bead placement and inflammation may radically alter the tissue characteristics of the lesion being examined. Because the bead is made of metal and has a much higher impedance than the surrounding tissue, local changes in tissue microstructure due to the bead placement should not greatly affect the ability to get signal from the bead. Future studies in vivo should include analysis of the effects of the bead on local microstructure and how this could affect estimates of the BSC. However, currently biocomatible metal fiducial markers of similar size are already placed in tumors for image registration purposes without much concern for tissue effects [32], [33].

VI. Conclusion

In this study, we evaluated the performance of an in situ calibration bead for calculating the BSC. The important feature of the in situ calibration bead is the ability to account for transmission and attenuation losses due to intervening tissue layers between the region of interest and the transducer surface. Accounting for these losses will reduce variance in QUS estimates from one sample to the next. The performance of the bead approach was assessed versus bead size relative to a beamwidth and wavelength and the depth of the bead in the sample. The results indicate that the in situ calibration bead provides robust calibration spectra. The in situ calibration bead requires a minimally invasive procedure to place the bead initially. Therefore, utilization of the bead for QUS analysis makes more sense for applications involving ongoing monitoring of tissue state for things like detection and quantification of response of tissue to therapy over time. Radiological markers are already used for these purposes and clinically the implantation of a calibration bead for QUS monitoring is not unfeasible.