Deep learning in single-molecule microscopy: fundamentals, caveats, and recent developments [Invited]

Abstract

Deep learning-based data analysis methods have gained considerable attention in all fields of science over the last decade. In recent years, this trend has reached the single-molecule community. In this review, we will survey significant contributions of the application of deep learning in single-molecule imaging experiments. Additionally, we will describe the historical events that led to the development of modern deep learning methods, summarize the fundamental concepts of deep learning, and highlight the importance of proper data composition for accurate, unbiased results.

1. Introduction

Deep learning is a class of machine learning techniques that employs artificial neural networks (NNs). [1] The term “learning” indicates in this context that the deep learning algorithm extracts a representation for some analysis task solely from the data with which it is provided. This is possible because NNs are universal function approximators, that is, when the parameters of the algorithm are correct, any continuous function can be represented. [2,3] Typical analysis tasks aim to extract some parameter(s) from data. If a function exists, be it more or less complex, which is able to map the data to the correct value of the parameter(s), NNs can be used to approximate that function.

For example, consider a camera image of a single molecule as is typically encountered in 2D single-molecule fluorescence microscopy (for an introduction to single-molecule microscopy, see section 5). [4–6] In principle, such an image transports all information on the extractable parameters of the molecule, e.g. the (sub-pixel) position of the molecule within the camera frame, orientation, etc. Therefore, one can imagine a function that takes the pixel intensities of the camera image as input and directly returns the parameters of interest. Writing down this function analytically is extremely challenging if not impossible, but NNs are an excellent tool to approximate it.

Progress both in computer hardware performance and in algorithms has immensely expedited the application of NNs as universal function approximators in real-world contexts. Importantly, advances in the development of software libraries have brought deep learning from a specialized technique to a broad audience of researchers in recent years. [7–9]

One of the earliest areas where deep learning proved to be very powerful was image analysis. [10–14] In particular, the advent of deep learning has been especially impactful for application areas that heavily rely on imaging such as astronomy, biology, and medicine. More recently, single-molecule microscopy, which takes the detection sensitivity to the ultimate level by studying signals of individual molecules one at a time, has started to employ tailored deep learning-based analysis to improve the ability to extract information from photon-limited images or measurements.

In this review, we will briefly describe the history of NNs before discussing their basic concepts and commonly used architectures, focusing on image analysis. Then, we will demonstrate the key importance of sample space coverage when training a NN. Finally, we will survey significant contributions to the field of single-molecule microscopy that apply deep learning-based analysis routines. We will define all key concepts within the review and additionally include a glossary of important terms in Table 1.

Table 1. Glossary of key concepts.

Term	Explanation
Architecture	The general layout of the neural network (layer type, sequence, etc.).
Hyperparameter	Design parameters of the neural network that are set externally by the user before training.
Input (data)	The data to be analyzed, e.g. an optical microscopy image of a fluorescently labeled cell.
Output (data)	The parameter to be extracted from the input data, e.g. the outline of the cell or the position of the centroid of the cell.
Layer	An individual layer within a neural network constitutes one hierarchical level when the data is processed by the neural network.
Loss	A metric to determine how strongly the prediction of the neural network differs from the ground truth.
Neural network	A universal function approximator, consisting of connected neurons and other building blocks, loosely inspired by neurons and synapses in the brain.
Node/Neuron	Inspired by biological neurons, a node/neuron in a neural networks is a function that receives a certain number of scalar inputs, processes them, and returns a single scalar as output.
Testing	The final assessment of neural network performance after all hyperparameter optimization etc. is completed and the final training has been completed.
Test set	The dataset that is set aside at the very beginning of the project, which is used for final testing. It is not part of the training set, and, in contrast to the validation set, is also not used for hyperparameter optimization and other tasks like that. This is done to ensure robustness and avoid focusing on the validation set as benchmark.
Training	The process of modifying the parameters (weights and biases) of a neural network in such a way that it yields a result closer to the correct output.
Training set	The dataset that is used to train the neural network.
Validation	The process of accessing the performance of the trained neural network.
Validation set	The dataset that is used to perform the validation. Crucially, this dataset was not part of the training set, i.e. the validation set was not used to train the neural network.

2. Historical overview

2.1. Initial developments and obstacles

Today, NN-based approaches are employed in an immense variety of applications. The speed with which these approaches rose to prominence in the last two decades, specifically outside the scientific community in the general public, might suggest that its concepts were derived equally recently. This, however, is not true.

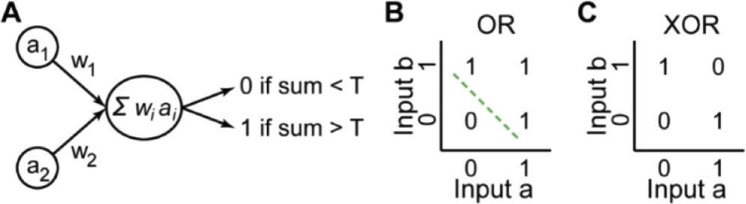
The birth of NNs and machine learning dates back to 1957, when the psychologist Frank Rosenblatt working in the Cornell Aeronautical Laboratory, developed what he called the Perceptron: A simplified, mathematical model of neurons in the brain (Fig. 1(A)). [15,16] Although he was not the first to investigate such model neurons, his approach would be the first to be useful for what we consider machine learning today. [17]

Fig. 1.

A simple Perceptron and the problem of linear separation. A) A simple Perceptron with two inputs a₁ and a₂ and the associated weights w₁ and w₂. B) Linear separation of the OR operator (green line). C) The XOR operator is not linearly separable.

The Perceptron bears similarity to what today is known as a “node” in NNs (see Table 1 and Section 3.1). It receives a set of real-valued inputs, multiplies each of these inputs with a number, sums the weighted inputs, and returns either 1 or 0, dependent on whether the sum is above or below some threshold, respectively. Notably, no non-linear activation function is applied, in contrast to the modern version of artificial neurons (see Section 3.1). The biological inspiration as well as the simplification of the biological case are evident: The input of the Perceptron corresponds to nearby neurons, the number or weight with which each input is multiplied corresponds to the strength of the synapse to other neurons, and the threshold corresponds to the required bias needed to be overcome in order for a neuron to fire. As a single Perceptron has only a single output – 1 or 0 –, several Perceptrons were used according to the requirements of the problem to be addressed. For example, in order to employ Perceptrons for the classic model application of handwritten digit recognition, one would use ten Perceptrons, where the output of each Perceptron stands for the function implementing classification of the input handwritten digit as one of the ten digits, i.e. one Perceptron returns 1 and the other nine all 0. Just as modern NNs, these early NNs consisting of a single layer of Perceptrons could be trained on data. Similar to today, training was done by modifying the weights and thresholds to make the output of the Perceptron layer match the correct class (see also section 3.2). Then, the trained network could be confronted with data to analyze it. Thus, for the first time, a method was found to make an algorithm “learn” according to the requirements posed by a dataset.

It is hard to overestimate the initial excitement caused by the introduction and experimental implementation of machine learning approaches with Perceptrons in the late 1950s and early 1960s. Not only Rosenblatt, but also many other scientists were convinced that the basis for the creation of a machine that thinks like humans was established, and some felt that it would just be a matter of further optimization to realize this goal. For example, when Rosenblatt presented the Perceptron at a press conference on 7 July 1958, he boasted so much about the potential of this approach that an infamous article in the New York Times, published the next day, reported on the “embryo of an electronic computer”, expected to “walk, talk, see, write, reproduce itself, and be conscious of its existence”. [18] It seems like the naïve fascination with machine learning was not completely different from today – some of the statements made back then seem strangely familiar now.

However, not all scientists researching machine learning at that time agreed. In fact, Rosenblatt was soon harshly criticized for overstating his results and making unrealistic promises. Such skepticism of potentially groundbreaking results is perhaps not too uncommon and may occasionally be fueled by some envy, but in this case, the criticism was justified. It became quickly clear that the Perceptron was not able to solve a range of problems.

Probably the most famous example is the exclusive or (XOR). [17,19] In contrast to the OR operator, the XOR operator cannot be linearly separated (Fig. 1(B) and (C)), and because of this, neither a single Perceptron nor a single-layer Perceptron are able to learn this simple function (for the case of an individual Perceptron, this can be easily rationalized by starting from a weight and threshold combination that represents the OR operator and then trying to modify the weights and the threshold in such a way that the XOR operator is represented, which inevitably leads to a contradiction).

The inability of the both an individual Perceptron and a single-layer Perceptron to learn the XOR operator was first conclusively demonstrated by Marvin Minsky and Seymour Papert in their 1969 book “Perceptrons – An Introduction to Computational Geometry”. [19] Although they were early critics of Rosenblatt and his visions – and not the only ones – this investigation is generally assumed to be the nail in the coffin for the initial hype around machine learning. Likely, the disillusion after a period of giant expectations contributed to a more or less complete abandonment of ideas related to NN-based machine learning for almost two decades. [17]

2.2. Reinventing neural networks

What caused the renaissance of machine learning with NNs? To recall: The approach proposed by Rosenblatt involved a single layer of Perceptrons, each receiving the whole instance of data and directly yielding an output. Training meant manipulation of the (linear) weights and threshold in each Perceptron to tune the output according to the instance of data.

But what happens when there is not a single layer of Perceptrons (or, as it is today, other model neurons)? That is, what happens if the first layer of neurons doesn’t directly return the output, but forwards its output into another layer of model neurons, which potentially feeds its output into another layer, until at some point an output is returned?

Such a multi-layered layout is indeed able to address and, at least partially, solve the problems of the original single-layer Perceptron architecture; and it was this realization that slowly resulted in the rediscovery of NN-based machine learning during the 1980s. It may seem surprising from today’s point-of-view that the extension from a single- to a multiple-layer architecture took so long, especially since Minsky and Papert already pointed out that a multilayer Perceptron is capable to learn the infamous XOR operator. [19] Interestingly, recent evidence suggests that this is also true for networks of biological neurons. [20] However, things were not so simple. First, the disappointment after the initial hopes manifested in a strong conviction that NNs were a dead-end, and for a while, virtually nobody was willing to invest time or money in research related to them. [17] Second, the mathematical requirements of training multilayered networks – even though discoveries related to them dated back to the 1960s and 1970s – needed to be transferred to the situation of NNs. [21,22] Innovation on that front was absolutely crucial: for a single-layer architecture, it is obvious how weights and thresholds need to be adjusted in order to make each Perceptron return the desired result, however, this is not the case for a multilayer architecture. [23,24] Third, datasets in sufficient size and quality had to be easily accessible. And finally, more neurons and more layers meant more computational demand – which was available, but certainly not as easily accessible as today.

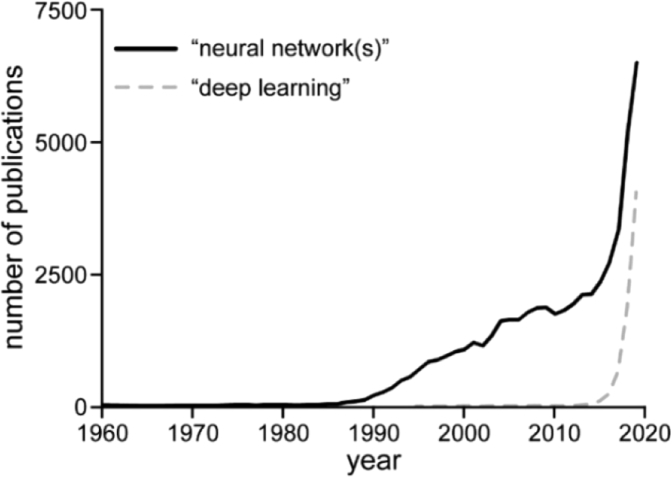
Thus, a renewal of openness to the idea and algorithmic programming advances were key requirements which had to be met before machine learning with NNs could return to the stage – and return they did. The timeline of the number of published results when searching Pubmed for “neural network(s)” or “deep learning”, shown in Fig. 2, illustrates this impressively. Evidently, after a period of virtually no research in this area, interest rises in the late 1980s. Spectacular successes in the early 2010s, such as the landslide victory of AlexNet in the ImageNet Large Scale Visual Recognition Challenge (ILSVRC) in 2012 [12,25] or the development of AlphaGo in 2016, a Go-playing program based on NNs that defeated world-class professional Lee Sedol, [26,27] caused the continuing spike in research on NNs.

Fig. 2.

Number of publications found on Pubmed when searching for “neural network(s)” (black line) or “deep learning” (dashed grey line) per year.

3. Fundamentals

3.1. Building blocks, training procedure, and validation

The demonstration of deep learning-based approaches to address challenges that could not be attempted with previous methods led to continual interest in this powerful tool. Consequently, deep learning is applied in such diverse fields as image analysis, speech recognition, financial day trading, chemical synthesis design, autonomous vehicle control, analysis of patch-clamp traces and single-particle trajectories, and even the generation of music and paintings. [28–41] This versatility sometimes evokes the impression of an almost magical, artificial consciousness. However, it is important to note that all aspects of deep learning-based approaches, from architecture design to the choice of the training algorithm, are set by the user and usually based on empirical observations.

A deep learning-based analysis routine consists of two major steps: first, training of the NN and validation, and second, processing of experimental data by the trained NN, yielding the parameter(s) to be extracted from the data (often called “inference”). The most time-consuming component in this process is the first step, i.e. training and validation. The second step, the application of the trained algorithm, nevertheless requires careful observation to avoid artifacts (see Section 4). To exemplify the training and validation procedure, we will describe in this section the fundamental building blocks used to engineer convolutional NNs, a family of NNs relevant for image processing tasks. Furthermore, the concept of convolutional NNs is also applicable in the context of more advanced architectures, which we will discuss in the following.

A basic NN can be constructed using mathematical operations defined by a fundamental building block, the “node” or “neuron”. Neurons can be considered an expansion of the Perceptron discussed in section 2. While a Perceptron receives a binary set of inputs (either 1 or 0) and outputs a binary value, the neuron is not limited to a binary set of inputs and outputs. Rather, it can receive any number of inputs with a continuous value. Equally, the resulting output is also a continuous value. Importantly, the output of each neuron may serve as input for a second set of neurons. One hierarchical level of neurons is termed a “layer”. Thus, NNs often build multiple layers until the desired output is reached. A layer of neurons in which each neuron is connected to all neurons in the previous layer or input nodes is termed a “fully-connected” or “dense” layer.

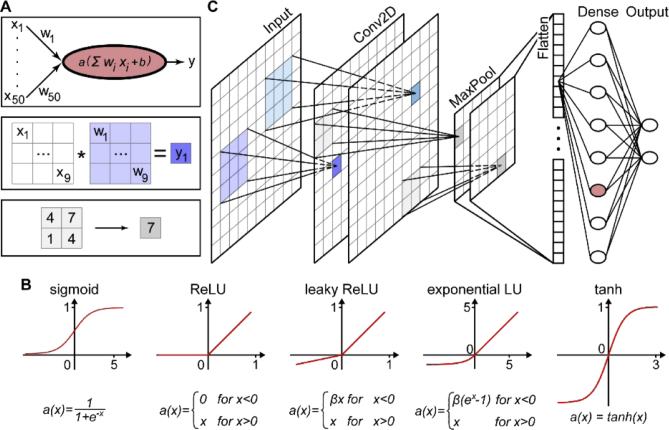
Figure 3(A), top, depicts a neuron which receives 50 inputs, each with a specific value x_i. Similar to the Perceptron, the neuron is simply a weighted average of all the inputs, but with some additional complexity. First, each input x_i is multiplied with a continuous number, w_i, called “weight”. Then these weighted inputs are summed and another number is added, called the “bias”. The weights and biases are the parameters that are adjusted during the training process – they are the “knobs” to turn. After this, the intermediate result is processed by a so-called “activation function”. The activation function is a mathematical function that mainly serves to introduce non-linearity. Many activation functions are used, and Fig. 3(B) presents the most common ones.

Fig. 3.

Building blocks of convolutional NNs and key mathematical concepts. A) Key mathematical operations executed in NNs: Fully-connected node, convolution, 2 × 2 MaxPooling (top to bottom). Note that activation is also performed for the convolution operation. B) Common activation functions and their definition. C) A simplified convolutional NN. The input image is passed to multiple (in this case: two) convolutional layers. After this, a 2 × 2 MaxPooling is performed, followed by flattening into a one-dimensional vector (which has, in this case, 50 elements). One fully-connected layer follows before the final layer returns the output (in this case: two scalars).

While NNs that consist only of fully-connected layers are effective for computationally tractable problems, they lose effectiveness for more complex data such as images. As image processing is critical in many fields such as biology, astronomy, microscopy, and bio-medical imaging, a NN designed to analyze images is a powerful tool. Convolutional NNs, conceived in the late 1980s and 1990s, [10,11] are NNs that are able to analyze images in order to extract specific features of interest with high speed and accuracy. In contrast to fully-connected layers, convolutional NNs convolve subimages with kernels that are composed of trainable weights with images (Fig. 3(A), middle). The resulting output can then, after activation, be processed in deeper convolutional or fully-connected layers of the network.

Figure 3(C) depicts a simplified, representative example of a small convolutional NN. The input, commonly an image with some number of values at each pixel (for instance, color or polarization), is provided to the network. Then, kernels are convolved with the input image. The number and dimensions of the kernels are hyperparameters, i.e. they are set by the user in advance. For instance, in Fig. 3(C), the 3 × 3 blue kernel (also often called “filter”) is convolved with a specific 3 × 3 region of the input image where the resulting value is the blue pixel demarcated in the next layer (see also Fig. 3(A), middle). This blue kernel is scanned through the entire input image. A distinct 3 × 3 kernel is shown in teal.

The two images labeled “Conv2D” in Fig. 3(C) are the final results after the two kernels/filters have been applied to the whole input image. These output images are then the inputs for the next layer of the NN, e.g. another convolutional layer. For simplicity, Fig. 3(C) depicts only one convolutional layer with two filters. Note that using only one convolutional layer when designing a NN is rare in most applications and that typically at least a few are used. The number of convolutional layers is another key hyperparameter.

Spatial downsampling is a common feature of almost all NN architectures. It both saves computational power and forces a more robust representation of the information content of the data. In Fig. 3(C), (a) MaxPooling layer follows the convolutional layer with a 2 × 2 kernel. That is, the pixel with the highest value in any 2 × 2 sub-region is retained (also see Fig. 3(A), bottom). Another commonly used pooling method is AveragePooling, retaining the average pixel value of the sub-region.

Frequently, NNs are used to extract a vector of scalar parameters from a 2D image (for example, considering handwritten digit identification, a 10 × 1 vector represents the 10 different digits). Thus, as depicted after the MaxPooling layer in Fig. 3(C), layers are at some point flattened into a vector. Subsequently, this vector can be provided to a fully-connected layer for further computation. Importantly, the last dense layer outputs a vector with a size equivalent to the number of desired parameters that shall be extracted from the net. For instance, the last layer in Fig. 3(C) is a dense layer with two nodes, which would correspond to two outputs.

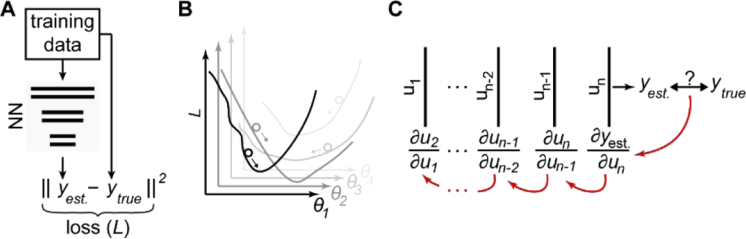
The weights and biases are the parameters to be optimized during training. Now we describe the key ideas underlying this crucial process. Figure 4(A) shows the basic training procedure where training data, labeled with the ground truth feature of interest, is first supplied to the network. Before training, the network is initialized with random weights and biases. At any point during training, the performance of the network is assessed by calculating the “loss” using an appropriate “loss function”, for example mean squared error (MSE). Training serves to minimize this loss by iteratively modifying the weights and biases. Typically, the whole training dataset is grouped into “batches”. For example, a training set with 1000 instances of data (e.g. 1000 images) could be divided into 50 batches with 20 instances each. The batch size is another hyperparameter. Each instance of one batch is provided to the network and the loss is calculated. After all elements of the batch have been processed, the average loss is determined. This is repeated until the whole training set has been processed once, which is termed an “epoch”. Training is not finished after a single epoch, but typically lasts for tens up to thousands of epochs. After training, the user must always perform careful assessment of the network on data which was not part of the training set; this essential step is termed “validation”.

Fig. 4.

Key concepts of training a NN. A) Loss. The loss function (here MSE) is a metric for the deviation of the prediction of the NN from the (known) ground truth. B) Gradient descent. The loss is reduced with respect to variation of all trainable parameters of the NN. C) Backpropagation. Each trainable parameter is iteratively adjusted backwards through the NN.

The main goal of training is to minimize the loss, i.e. training the network is an optimization problem in which the parameter combination is to be found that minimizes the loss. To achieve this, deep learning methods often use stochastic optimization algorithms such as the ADAM optimizer. [42] Schematically depicted in Fig. 4(B), the loss, which is dependent on all trainable parameters of the network, initially exists on some point in a multi-dimensional space (the dimensionality is determined by the number of trainable parameters). The loss, depicted by the circles, decreases most quickly in the direction of the negative gradient. Thus, the parameters (weights and biases) during each iteration of optimization are modified according to the negative gradient. How much each parameter is modified during training is therefore dependent on the gradient. In addition, the “learning rate” controls the actual step size that is taken in the direction of the negative gradient. The learning rate is a key hyperparameter. Typically it is changing in the course of training: initially, the network performs poorly and requires large adjustments of the trainable parameters, but as the network approaches some minimum, the learning rate needs to be reduced.

NNs often contain a substantially large sample space and thus, efficient algorithms to calculate the gradients must be employed. The mathematical framework employed for this process is called “backpropagation”, a concept that is rooted in research from the 1960s and 70s which was translated to NNs in the mid-80s. [21–23,43] First, the gradient of each parameter with respect to the loss in the very last layer of the network is calculated. Next, as depicted in Fig. 4(C), the algorithm iterates backwards from the last layer to the penultimate layer, and so on, until the first layer is reached. The gradient of each weight and bias with respect to the loss in all layers along the way through the network is calculated using the chain rule, essentially turning gradient calculation into many matrix multiplications. This allows for the computation of the gradients of each layer without redundancy, leading to significantly decreased computational cost, making it possible to train multi-layer NNs easily.

NNs feature a huge number of trainable parameters. Finding a parameter combination that matches the input to the desired output is therefore a strongly overdetermined problem. The consequence of this is that one may train a NN “too well”: In this case, the training set is perfectly processed and always yields an output very close to the ground truth. However, when the capability of the network is benchmarked with data that was not part of the training set, the trained network performs poorly. This problem is called “overfitting”. Numerous strategies exist to mitigate this unwanted effect. One common approach is “dropout”. [44] Here, a random subset of neurons is set to 0 after processing a batch. This is done on one or multiple layers of the NN. Dropout essentially forces the NN to learn a robust representation of the analysis task to be carried out, which improves the performance of trained NNs as well as generalization capabilities and robustness on new data.

3.2. Relevant modern neural network architectures

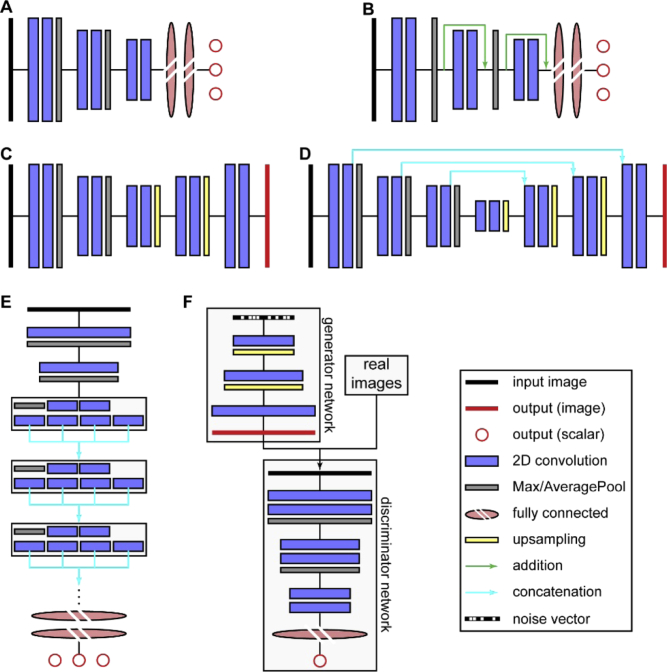
In recent years, a large variety of NN architectures have been developed. In this section, we will present several important layouts which are relevant for analysis tasks typically encountered in single-molecule imaging experiments. Schematic depictions for the discussed architectures are shown in Fig. 5.

Fig. 5.

Modern NN architectures relevant for image analysis in single-molecule experiments. A) Convolutional neural net (ConvNet). B) Residual net (ResNet). C) Encoder-decoder architecture. D) U-net. E) Inception architecture. F) Generative adversarial network. Note that all depicted network types exhibit considerable variations in the exact architecture, e.g. number of layers or layer sequence.

The first architecture used for image analysis are convolutional neural networks (Fig. 5(A)), which were developed in the late 1980s and 1990s and unleashed their full potential in the early 2010s thanks to increased computational power and the increasing availability of data. [10–12] Here, the input image is passed through one or more 2D convolutional layers, followed by spatial downsampling. The downsampling factor depends on the size of the input data and is typically between 2 and 7. Usually, deeper layers feature more filters than earlier layers. This sequence of convolution and spatial downsampling is repeated few or several times, again dependent on the input data. Eventually, the output of the last convolutional layer is flattened, and a few fully-connected layers follow before the last fully-connected layer returns the (scalar) output(s). The number of outputs depends on the problem to be addressed. For example, one could train a convolutional NN to count the number of cells within a microscopy image.

As more and more complex problems were addressed with convolutional NNs, an interesting observation was made. Intuitively, more complex problems call for deeper architectures (i.e. architectures featuring more layers). However, it became apparent that at some point, additional layers do not improve the performance. [45] Quite to the contrary, the performance deteriorated. This unexpected behavior originates from the backpropagation steps during training. As discussed above, backpropagation attenuates the value of each weight. This attenuation is proportional to the gradient of the loss function with respect to the weights. As the multivariate chain rule is used to calculate the derivatives of early layers from the derivatives of deeper layers, essentially many multiplications are performed. Thus, when one of the gradients from the deeper layer is very small, the gradients for all the previous layers become very small, too, which is not helpful to direct the network towards an improved parameter state, causing the network to stop learning or even change parameters erratically.

To address this so-called “vanishing gradient” problem, Residuals Nets (ResNets) have been developed (Fig. 5(B)). [45] They feature so called “skip connections” between earlier and deeper layers, which allows for residual mapping. These skip connections, in this case residual skip connections, provide a deeper layer with the output x of an earlier layer, forming a so called “residual block”. The output is also processed by the layers in between, yielding F(x). Then, these two outputs are added, yielding H(x) = F(x) + x. Thus, during training, F(x) adjusts x to reduce the residual between ground truth and prediction, which means that the gradient of a deep layer no longer influences the whole network, solving the vanishing gradient problem.

Both convolutional NNs and ResNets typically return scalar outputs. However, for many applications, an image as output is desirable – e.g. to perform segmentation of an image, such as finding the outlines of cells in a microscopy image. An important architecture that implements this is the encoder-decoder architecture (Fig. 5(C)). [46] Here, the input image is first passed through a series of 2D convolutions and spatial downsampling steps. As for convolutional NNs, the spatial downsampling usually goes hand in hand with an increasing number of filters. Then, this process is reversed: The spatially condensed representation is upsampled until the original spatial scale is reached while the filter space is reduced. The last step returns an image with the same size (and, in case of multichannel images, depth) as the input image. A related architecture that in some sense combines encoder-decoder architectures with the benefits of ResNets are U-nets (Fig. 5(D)). [47] Their main layout is the same as for encoder-decoder architectures. In addition, the output of each 2D convolutional layer that precedes a downsampling on the left arm is concatenated along the filter axis with the output of each spatial upsampling on the right arm (concatenation skip connections). As for encoder-decoder architectures, the output of the network is an image with the same spatial scale and channel depth as the input image.

Inception-type networks are an advanced architecture that is characterized by Inception modules, shaded boxes in Fig. 5(E). [48] The input image first passes through initial 2D convolution and spatial downsampling before entering the Inception blocks. Each Inception block performs multiple separate 2D convolutions which are concatenated after the Inception block along the filter axis. Typically, the following four operations are performed: 2D convolution with a 1 × 1 kernel (which is essentially tuning of the filter number without performing any spatial convolution); 2D convolution with a 1 × 1 kernel, followed by 2D convolution with a 3 × 3 kernel; 2D convolution with a 1 × 1 kernel, followed by 2D convolution with a 5 × 5 kernel; 3 × 3 MaxPooling, followed by 2D convolution with a 1 × 1 kernel. The 2D convolutions with 3 × 3 and 5 × 5 kernels are typically replaced by computationally less costly sequences of 2D convolutions with 1 × 3 and 3 × 1 kernels. The number of Inception modules vary according to the problem complexity. As for convolutional NNs and ResNets, the output are typically scalars.

Finally, generative adversarial networks (GANs, Fig. 5(F)) [49] have the capability to create images that mimic the appearance of a dataset of real images, which is an interesting avenue for e.g. image restoration. [50] GANs consist of two NNs: The generator network creates images from a noise vector (i.e. a vector of random numbers) by spatial upsampling and 2D convolution. The obtained output image is provided to the discriminator network alongside real images. The discriminator network is trained to differentiate between the real and the artificially created images. Essentially, GANs are therefore two networks in a tug of war situation: The generator network tries to create artificial images while the discriminator tries to discriminate the output produced by the generator.

3.3. Software and Hardware

In recent years, deep learning has developed from a specialized technique, requiring extensive knowledge of programming and of the hardware necessary to run the final code, into a generally available tool. In this section, we will first describe the currently used software to develop and train NNs and then discuss relevant hardware considerations.

Today, one can chose from a range of software libraries for the implementation of NNs. Most popular are probably TensorFlow [51] and PyTorch, [52] but many other libraries are also frequently used, for example, MXNet, [53] Theano, [54] CNTK, [55] and others. All mentioned software libraries have in common that they can be interfaced with Python, which emphasizes the current prominence of Python as a programming language for deep learning. In addition, Python-based Application Programming Interfaces (APIs) such as Keras [56] considerably simplify the complexity of architecture implementation and training. The mentioned libraries and many others are free of charge and open source, facilitating quick dissemination. Taken together, the software to implement NN architecture is nowadays readily available and reasonably straightforward to setup.

All applications of deep learning have in common that they typically require processing of large amounts of data. Thus, the hardware setup must be optimized for this task. Above all, the use of graphics processing units (GPUs) is more or less mandatory. This is because the training process consists essentially of countless matrix multiplications, an operation that benefits immensely from the parallelization capability of GPUs. [57,58] Thus, when installing a designated high-end setup for deep learning, one would likely opt for one of the latest GPUs with large memory, e.g. Nvidia’s RTX-2080 Ti. Multiple GPUs or GPU clusters can drastically speed up training, but they require careful parallelization design (e.g. via NV-Link by Nvidia), otherwise, the improvement in computation power is absorbed by latency. GPUs, however, are not the ultimate solution to deep learning. Dedicated hardware has been and is currently developed (e.g. Tensor Processing Units (TPUs) by Google).

Regarding random-access-memory (RAM), it is important to note that execution of GPU code might be slowed down if not enough RAM is available. A common rule of thumb is to provide the CPU at least with the same RAM as the GPU memory. Furthermore, handling of large datasets trivially benefits from larger RAM. Therefore, in practice, one would likely equip the setup with an ample amount of RAM.

Considering the central processing unit (CPU), the required performance mainly depends on the chosen training layout. Typically, the training data must be somehow preprocessed (e.g. normalized or other operation) before it is supplied to the NN. Data augmentation (i.e. rotating images or cropping to make the training more robust) is performed on the CPU as well. Fundamentally, one can either fully preprocess the training data before the training is started or preprocess on the fly, i.e. load a batch of data, preprocess it, and train. In the first case, the CPU performance is important, but does not directly affect the training performance, whereas in the second case, the CPU performance is an integral part of the training performance, thus the CPU must preprocess the batch quickly, which mandates multicore CPUs (in this scenario, however, the RAM is quickly cleared and can be smaller). Most truly intensive computations are carried by the GPU, therefore, the CPU clock rate is not a central determinant of the overall performance.

The GPU, the CPU, and the RAM are the most important components to be decided when setting up a hardware system for deep learning. The fourth central component, the storage device, must certainly be considered as well, but since fast solid state drives (SSDs) with large capacity have become affordable, they are probably the best choice nowadays. Finally, the motherboard must have the proper layout to host the GPU(s), the CPU(s), and the RAM. Other components such as cooling units or power supply can be chosen as needed. Generally, hardware optimization is a new problem for each setup, and discussion of individual experiences are can be easily found online. [59,60] In addition, training “on the cloud” (cloud computing), e.g. via Amazon Web Services (AWS), Microsoft Azure, or the Google Cloud Platform are increasingly used for deep learning.

Distribution of deep learning models is not standardized at the moment, but several approaches have been introduced, e.g. CDeep3M or ImJoy. [61,62] Certainly, as the field progresses, improvements will be made on this front.

4. The crucial role of data composition

4.1. Covering the sample space

Any analysis method requires careful benchmarking to ensure that the developed algorithm does not introduce major biases or artifacts. This is especially true for NN-based analysis. Why is this? Consider a NN that was trained on some training data which covers a certain sample space, the “input space”. The target output, which the network was trained to return, covers another sample space, which we will call the “result space”. After successful and validated training, the network is confronted with unknown instances of experimental data. First, suppose these instances of data are within the input space. In this case, the network will likely return an output within the result space (Fig. 6, case (i)). Now, suppose they are outside the input space. Very likely, the network will still return a result within the result space (Fig. 6, case (iii); see also the following section). [29] Conventional analysis approaches, when faced with data outside the input space, will likely exhibit strange features in the output and generally unpredictable behavior. Certainly, this will not be true for all instances, but typically, conventional algorithms, unlike NNs, do not preferentially return data within the result space when faced with data outside the input space. More generally, recent examples have pointed out the fragility of seemingly robustly trained networks via, for example, adversarial attacks or real-world perturbations. [63–67] It should be noted that input data that deviates greatly from the input space can also produce completely unpredictable results (case (iv)), but these erroneous results are usually straightforward to identify and should not be too problematic for a careful experimentalist.

Fig. 6.

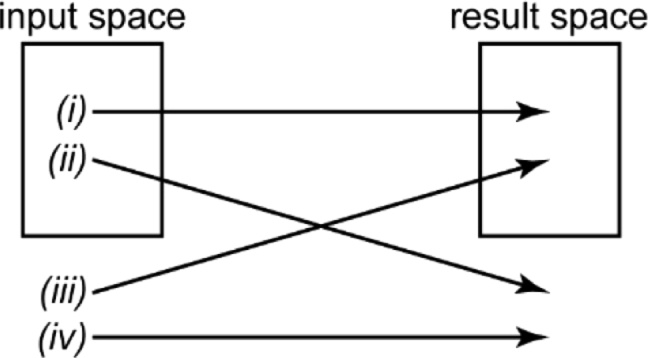
The four scenarios for the relationship between data analyzed and data returned by an algorithm. Data can be within the input space of the algorithm and be mapped within the result space (i) or outside the result space (ii). Conversely, data can be not within the input space and mapped within the result space (iii) or outside the result space (iv).

Thus, common network architectures return a seemingly valid, meaningful result, even though the training data did not cover the data the network received. If it is possible to verify that the result obtained is valid with other methods, then this is an indication that the network is robust against a certain amount of deviation from the input space. If the output fails the test with other methods, it will be discarded. However, if such verification is omitted or fundamentally impossible, there is a high risk for the creation of artifacts: there will be instances of data not within the input space of the trained network that might yield results not within the result space. Even more concerning, these potential artifacts may remain undetected as the result space is expected, thus, the data will appear completely reasonable.

It is therefore critical to ensure that the input space of the training data fully covers the sample space of the experimental data the network will be confronted with after training. Note that this requirement is fundamentally different from proper validation. The essential validation step after training of the network merely ensures that the training procedure was successful, i.e. that no overfitting occurred, for example. In contrast, even sample space coverage is conceptually situated prior to network design and training. It is a decision to be made by the researcher who develops the NN.

The necessity of sample space coverage is quite intuitive. A single instance of data contains a certain amount of information, and it is not possible to extract more than that information. A NN merely infers laws which it extracted from the training data. The underlying assumption when using NNs in this fashion is that the instances of experimental data the network analyzes after training are covered by the extractable information contained in the training data. If this assumption does not hold, the output of the network will not report on it.

The issue described is also relevant for the discussion whether it is possible to make fundamentally new discoveries using NNs. Consider an example: A NN processes low-resolution images of DAPI-stained nuclei to return a higher-resolution image. Let’s say an intricate feature appears in the higher-resolution output image that was invisible before. Has the NN made a discovery? Certainly, it inferred the feature from the input image, which did not contain the feature, but to do so, it used the information extracted from the training data; and this data must have been present before the network was trained. NNs are tools that rapidly apply previously established laws or correlations to new scenarios. Thus, the researcher investigating that new scenario plays an active role in the process: it is the researcher who opts whether or not it is justified to apply the NN to the given problem, i.e. whether or not the scenario is covered by the sample space of the training data and if the output represents reasonable results.

4.2. Artifact considerations

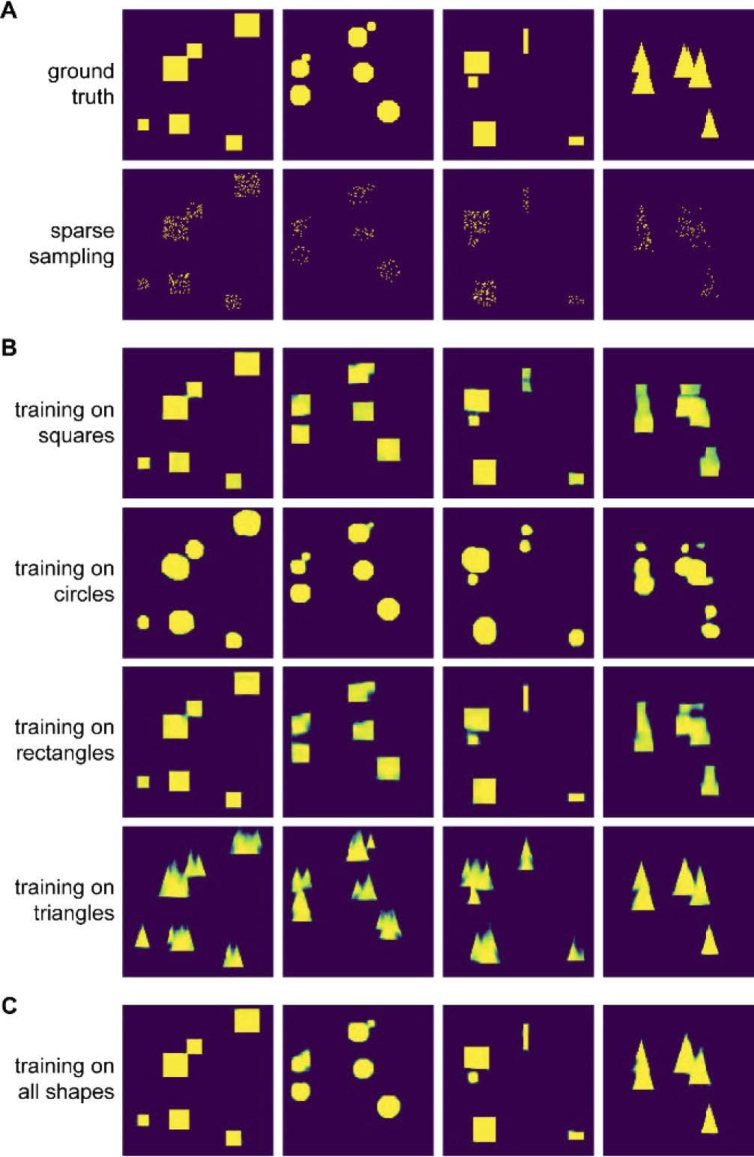
What are the consequences when coverage of the sample space in the training data is not ensured? To visualize the problems arising, we trained small encoder-decoder NNs to recover shapes from noisy or sparsely sampled observations. We included four shapes in the training data and, consequently, trained four networks: One network on squares, one on circles, one on rectangles, and one on isosceles triangles. Representative examples are shown in Fig. 7(A).

Fig. 7.

Influence of covering the sample space. A) Binary masks of squares, circles, rectangles, and triangles and sparse sampling of the masks (sampling rate: 10-20%). B) Output of four NNs trained on either squares, circles, rectangles, or triangles when the sparse square, circle, rectangle, or triangle dataset is supplied as input. C) Output of a NN that was trained on all four shapes when the four sparse datasets are supplied as input.

As expected, the networks performed very well when they were faced with sparse data that corresponded to the data they were trained on (Fig. 7(B), diagonal elements). However, when the networks were faced with data not present in the respective training sets, they returned results that resembled more or less the data they were trained on. For example, the triangle network returned triangles not only for the sparse representation of the triangle data, but also for the sparse representations of square, circle, and rectangle data; and the square and circle networks expected equal aspect ratios, thus, they split the rectangle at the top with high aspect ratio into two shapes.

Note that the rectangle network performed well for the square dataset. This makes sense as squares are a subset of rectangles, and thus, the input space for the rectangle network fully covers the square dataset. To further demonstrate the relevance of coverage of the sample space, we trained another network on a dataset that combined all four shapes. This network returns the correct shapes for all cases (Fig. 7(C)).

This simple example illustrates the key importance to cover the sample space of the experimental situation fully in order to avoid artifacts. Notably, the artifacts for this example are easy to identify since the ground truth is known, but problems might arise when the ground truth is not known. Consider a biological sample in which three features have been observed frequently. Data from previous investigations is used to train a network. If a new feature appears in an instance of data that the network analyzes after training, it will not return that feature – rather, it will return something close to one of the three features it was trained on.

In summary, proper assessment of the training data space is crucial to mitigate the risk of inaccurate predictions and artifacts. Such assessment allows for independent verification of the performance of the deep learning-based analysis. This verification is mandatory to ensure unbiased results.

5. Examples for recent applications of deep learning in single-molecule microscopy

5.1. Motivation

Recently, single-molecule microscopy studies have gradually reported on using NNs to analysis data to extract parameters at unprecedented speeds and precisions. The single-molecule field was established in 1989 when the first single molecule in a condensed phase sample was detected optically. [68] Since then, a plethora of studies have investigated single molecules to measure their properties without ensemble averaging. One powerful application of imaging single-molecule emitters is super-resolution (SR) fluorescence microscopy. As one of the approaches awarded the 2014 Nobel Prize, [69–71] SR fluorescence microscopy circumvents the diffraction limit: as first derived by Ernst Abbe, even under ideal conditions, the emission pattern of an infinitesimally small emitter recorded on a camera (called point spread function, or PSF), is limited by diffraction. Thus, the width of that emission pattern cannot be smaller than approx. 250 nm for visible wavelengths. Correspondingly, the best achievable resolution is around 250 nm. This lower bound is too high to study biological systems in detail, where resolution on the single-digit nanometer scale are frequently required to identify intricate features.

“Single-molecule active control microscopy”, SMACM, also frequently called “single molecule localization microscopy”, SMLM, is a class of SR methods that analyzes the PSF of single molecules to achieve 10-20 nm precision or better. [72–74] This approach to SR relies on two key principles. First, after detecting the PSF of an emitter using a sensitive camera, the PSF is fit to a model function that describes its shape appropriately. For example, in case of the standard open aperture PSF, the typically used model function is a two-dimensional Gaussian, where the position of the peak of the Gaussian serves as the estimate for the position of the molecule. Importantly, the precision of the position estimate scales with the inverse square root number of photons detected. Thus, with a sufficient amount of detected photons, the precision can easily reach 10-20 nm. However, biological structures of interest will usually be densely labeled with fluorophores. Thus, the PSFs of the emitters will overlap spatially. Such overlap prevents the fitting approach described above, which assumes the PSF of a single emitter. To solve this problem, the second key principle of SMACM is employed: a mechanism is actively chosen to ensure that only a sparse subset of emitters labeling the structure of interest are emissive, typically by optical or chemical means. [6] This ensures that PSFs are not overlapping in any one imaging frame. The PSF images are recorded, and in the next camera frame, another subset of emitters is activated or becomes emissive by blinking processes, for example. This processes is repeated, the individual PSFs in each frame are super-localized (that is, their position is determined with a precision better than the diffraction limit), and the positions of the fittings are recorded. Together, the recorded positions yield a point-by-point reconstruction of the structure with super-resolution detail. [75]

While the open aperture PSF shape can be well-approximated by a Gaussian, complex PSFs whose shape encodes parameters such as the 3D positions are difficult to approximate with a well-defined mathematical function. These 3D PSFs have been designed using PSF engineering methods where a transmissive quartz phase mask is inserted in the pupil or Fourier plane of the microscope. This phase mask modulates the light in the pupil plane that results in a PSF with the desired shape on the camera. Examples of 3D PSFs with axial ranges of 800 nm, 2 µm, and 4-6 µm include the astigmatic, double-helix, and the Tetrapod PSFs respectively. [76–79]

3D PSFs such as the astigmatic and the double-helix PSF have been modeled with elliptical and double Gaussian functions, respectively, but approximating the PSF with a well-defined function is not possible for more complex PSFs such as the Tetrapod PSFs. Moreover, using simple model functions to localize the open aperture and astigmatic PSFs (such as the two-dimensional Gaussian), does not reach the Cramer-Rao Lower Bound (CRLB), a metric for the highest achievable localization precision. [80,81] A more experimentally representative model of the PSF is scalar diffraction theory and, more complex but also more accurate, vectorial diffraction theory. [82] These models describe how the electric fields emitted from single molecules propagate to the detector and can easily incorporate the addition of a phase mask to account for PSF engineering schemes. The PSF model derived from scalar or vectorial diffraction theory serves as a much better approximation to the PSF shape found under experimental conditions.

Maximum likelihood estimation (MLE) in combination with a given PSF model (in this case, a PSF model derived from scalar or vectorial diffraction theory), [83] is therefore a superior approach to localize emitters. However, MLE analysis as well as other algorithms used to identify and fit PSFs (e.g. least squares) are computationally demanding, which severely reduces throughput. The main reason for this reduced throughput originates from the requirement of many precisely localized molecules that are acquired over many frames (typically 100,000s to millions of PSFs acquired in 10,000s of frames). Without a sufficient number of localizations, the resolution of the image and the image quality will severely degrade. As the exposure time for each frame is typically 15 to 100 ms, the total data acquisition time for a single SR image can be tens of minutes to hours. Thus, a tradeoff exists between throughput and resolution.

In contrast to many other deep learning applications, generating a sufficiently large training data set is rapid for SMACM experiments. To create this large training set quickly, the studies described below often leverage the mathematically well-characterized model of the PSF to simulate desired PSF shapes. Naturally, the simulated PSFs must be representative of PSFs found in experimental conditions. Otherwise, if the experimental PSF are outside the input space of the trained net, the trained net will not be able to extract parameters of interest with high accuracy from experimental data. Therefore, the studies described below often incorporate aberrations found in their microscope into their simulations to allow the simulations to more closely reflect experimental conditions.

The trained nets are then benchmarked with both simulated and experimental data sets to access their performance. For instance, multiple studies have recently simulated PSFs using models such as scalar diffraction theory to generate the data sets used to train and benchmark NNs. The trained NNs were then used to extract parameters such as position from experimental SMACM data sets with higher or comparable precision and with far more rapid speeds compared to conventional methods such as MLE. Clearly, the NNs are a promising new method in the single-molecule field as they improve on conventional analytical techniques and can easily be properly trained and benchmarked using physical models that describe single-molecule behavior accurately. The studies described below demonstrate the power of NNs mainly in localization based single-molecule super-resolution microscopy. In each section, we summarize the key features of the presented methods at the beginning (Table 2,3, and 4).

Table 2. Presented methods in section 5.2.

Name	Reference	Network type	Input	Output
DeepSTORM	Nehme, Shechtman, et al. [84]	Encoder-decoder	Camera frame with multiple open-aperture PSFs	Super-localized PSFs in 2D
smNET	Zhang, Liu, Huang, et al. [85]	ResNet	Images of individual astigmatic and double-helix PSFs	3D coordinates of PSFs, orientation
DeepLoco	Boyd, Jonas, Recht, et al. [86]	Convolutional	Images of open aperture, astigmatic, and double-helix PSFs in camera frames	3D coordinates of PSFs
—	Zelger, Jesacher, et al. [87]	Convolutional	Images of individual open aperture PSFs	3D coordinates of PSFs
DECODE	Speiser, Turaga, and Macke [88]	Two stacked U-Nets	Camera frame with multiple open aperture or 3D PSFs	3D coordinates of PSFs
ANNA-PALM	Ouyang, Zimmer, et al. [89]	Combination of U-net and GAN	Widefield image and camera frame sequence with multiple open-aperture PSFs	Super-resolved 2D image
—	Kim, Moon, and Xu [90]	Fully-connected	Images of individual open-aperture PSFs	Axial position of emitter and color channel

Table 3. Presented methods in section 5.3.

Name	Reference	Network type	Input	Output
—	Hershko, Weiss, Shechtman, et al. [95]	1) Convolutional (for color channel identification of open-aperture PSFs)	Images of individual open-aperture PSFs	Color channel
		2) Small architecture	Simulated point sources, mismatch between net 3 prediction and ground truth	PSFs, used to optimize SLM pattern in combination with output from net 3
		3) Encoder-decoder (for analysis of PSFs after SLM optimization)	Camera frame with multiple PSFs	Color channel, 2D coordinates of PSFs
DeepSTORM3D	Nehme, Shechtman, et al. [96]	1) Convolutional with skipped connections	Simulated point sources, mismatch between net 2 prediction and ground truth	PSFs, used to optimize phase mask pattern in combination with output from net 2
		2) Convolutional with skipped connections and upsampling	Camera frame with multiple 3D PSFs	3D coordinates of PSFs

Table 4. Presented methods in section 5.4.

Name	Reference	Network type	Input	Output
—	Xu, Fang, et al. [100]	Convolutional with LSTM layers	Fluorescence intensity traces	Stoichiometry of fluorescently labeled protein complexes
—	Paine and Fienup [101]	Inception v3	Images of individual arbitrary PSFs	Zernike coefficients of order 2 to 5 as starting guesses for subsequent phase retrieval
smNET	Zhang, Liu, Huang, et al. [85]	ResNet	Images of individual biplane PSFs	Zernike coefficients of order 1 to 5
—	Zelger, Jesacher, et al. [87]	Convolutional	Images of individual open aperture PSFs	Zernike coefficients for first order astigmatism and spherical aberration
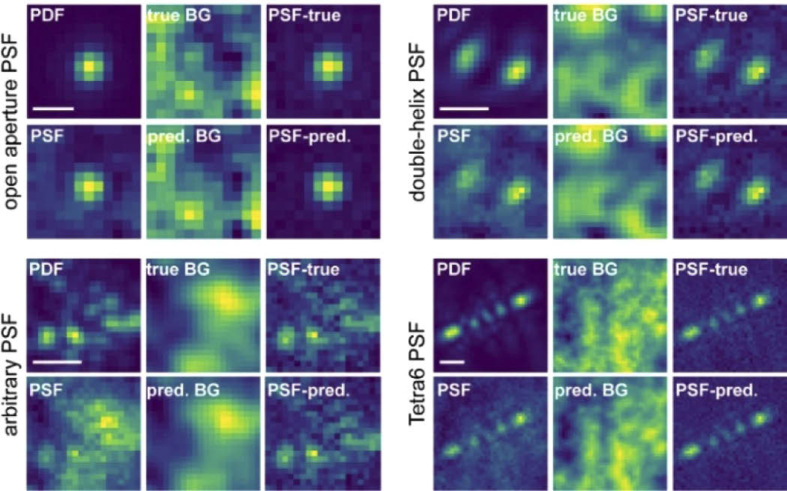
—	Möckl, Moerner, et al. [102]	ResNet	Stack of five z-slices of an individual arbitrary PSF	Zernike coefficients of order 1 to 6
BGnet	Möckl, Roy, Moerner, et al. [103]	U-net	Images of individual arbitrary PSFs	Structure and intensity of background

Generally, we would like to emphasize that a developing field like deep learning for single-molecule experiments frequently suffers from unestablished standards. We believe that the best approach to circumvent this problem is benchmarking against the current gold standard in the field. It should not be simply assumed that deep learning-based approaches are always superior to conventional methods.

5.2. Localization microscopy

The first deep learning method applied to localization microscopy is Deep-STORM. [84] DeepSTORM uses the rapid speed of NNs to obtain super-resolution reconstruction of microtubules from DL images consisting of single or overlapping PSFs. While previous multi-emitter fitting algorithms have been implemented to localize overlapping PSFs typically found in samples with high emitter density, [91–93] these methods can suffer from large computational time and sample-dependent parameter tuning. In particular, sample-dependent parameter tuning must be carefully determined through trial and error and, thus, requires user expertise and additional time to analyze the single-molecule data.

To alleviate issues found in multi-emitter fitting algorithms, Nehme et al. engineered an encoder-decoder NN which generated SR images from full-field-of-view image stacks of single or overlapping PSFs. [84] To first generate data to train Deep-STORM, DL images were generated by simulating PSFs with experimentally relevant signal and background levels at various positions in the image. Next, the DL images were up-sampled by a factor of 8 and the emitter positions were projected onto the newly spawned high resolution grid. The simulated DL and SR images were then supplied to Deep-STORM during the training phase as the input and output respectively. Once trained to convergence, Deep-STORM was first validated using simulated data consisting of DL images of horizontal lines and microtubules and experimental data of fluorescently labeled microtubules and quantum dots. Strikingly, Deep-STORM generated the SR reconstructions more rapidly and more accurately compared to conventional algorithms that localize overlapping emitters for both simulated and experimental data. Thus, Deep-STORM is a prime example of using a well-defined model of the PSF to train a NN with simulated data that is then validated with both simulated and experimental data.

Since the initial conception and validation of Deep-STORM, several methods have recently been developed to more accurately and rapidly analyze the PSFs of single molecules. For example, unlike Deep-STORM, which returns a complete 2D SR image from the diffraction limited image, smNet localizes astigmatic PSFs of single emitters from experimental data to extract 3D position. [85] Commonly, the astigmatic PSF is localized using to an elliptical Gaussian fit, which can be a poor approximation of the PSF as described earlier. In contrast to conventional fitting methods, smNet does not approximate the shape of PSFs with a well-defined function such as an elliptical Gaussian. Instead, Zhang et al. first simulated PSFs that are generated from scalar diffraction theory. These simulated PSFs also incorporate aberrations present in the microscope that were extracted through a phase retrieval protocol [83] and sample a wide range of experimentally relevant parameters such as position, signal, and background levels to more closely reflect PSFs shapes found in an experimental setting. Equipped with realistic PSF simulations, Zhang et al. trained smNet using the simulated PSFs as training data and the ground truth x/y/z position as the labels for each PSF image.

After completion of training, Zhang et al. benchmarked the performance of the smNet using both simulated and experimental data. First, they demonstrate that smNet localizes simulated single molecules far more precisely compared to conventional elliptical Gaussian fitting. In fact, the localization precision of smNet reaches the CRLB of the entire axial range for the astigmatic and, even, the double-helix PSF. Next, smNet was used on a more complex problem, localizing experimental astigmatic single-molecule PSFs of labeled mitochondria in cells. Remarkably, the 3D SR reconstructions reveal a well-resolved mitochondrial membrane with higher image quality compared to reconstructions of the same data set using conventional Gaussian fitting methods. In addition, while smNet was demonstrated experimentally only on the astigmatic PSF, in theory, any experimental arbitrary PSF shape may be analyzed using a similar deep learning method given appropriate benchmarking. In addition, smNET is also able to return other parameters such as the orientation of the molecule and wavefront distortions.

We note that other methods, such as DeepLoco, [86] have also recently been developed that model the PSF mathematically to train NNs to perform precise localizations. DeepLoco simulates OA, astigmatic, and DH PSFs in a camera frame via a well-defined mathematical model to generate data. Then, a neural network is trained to super-localize the simulated emitters in 2D and 3D. In addition, Zelger et al. trained a NN with training data generated from simulations using vectorial diffraction theory to localize emitters in 3D. [87] Importantly, they directly compared the performance and speed of their net to MLE fitting approaches. They observed that their trained net can localize molecules with similar precision to MLE fitting but with far greater speeds, showcasing the improvements possible with a NN.

Using a distinct method compared to the approaches described earlier, Speiser, Turaga, and Macke trained a NN using supervised learning to first generate data consisting of PSF shapes (DECODE). [88] Then they trained a secondary network with unsupervised learning to localize simulated and experimental emitters. The use of unsupervised learning is particularly a novel method to analyze single-molecule data. Potentially, unsupervised learning can be implemented in other single-molecule methods and analysis such as extracting diffusion behavior from single-molecule tracking trajectories. In addition, this work also includes information that is typically not in the focus of other approaches, e.g. time information from adjacent frames and the whole image stack.

Deep-STORM, smNet, and the other methods described above leverage the well characterized mathematical model of the PSF to simulate data that covers a large experimental sample space to train the nets. As an alternative approach that strictly uses only experimental data in the training phase of a NN, ANNA-PALM generates SR images using a diffraction-limited image in combination with a SR image reconstructed with a sparse number of localized molecules (henceforth termed sparse SR image). [89] As described earlier, conventional SMACM methods suffer from low throughput as many precisely localized molecules are required to reconstruct a high quality super-resolution image. Without acquiring sufficiently number of localizations to sample the structure of interest, the image quality and resolution will degrade. To mitigate the tradeoff found between throughput and resolution, ANNA-PALM was designed to reconstruct SR images with high throughput without sacrificing image quality and resolution.

To train ANNA-PALM, a SMACM data set of blinking single molecules that can be used to reconstruct a SR image of a specific structure with high image quality is acquired. A small subset of the frames in the entire data set is then used to generate the sparse SR image. The sparse SR image along with the diffraction-limited image and the knowledge which structure was imaged are fed as inputs into the network. The SR image reconstructed using the entire SMACM data set serve as labels for the sparse SR and diffraction-limited image. For example, Ouyang et al. trained ANNA-PALM to reconstruct SR images for microtubules, the nuclear pore complex, and mitochondria.

Once properly trained for the biological structure of interest, ANNA-PALM was benchmarked using simulated and experimental data similar to the approaches discussed with Deep-STORM and smNet. ANNA-PALM reconstructs SR images of simulated images and experimental microtubules, mitochondria, and the nuclear pore complex from sparse SR and DL images with comparable image quality but with much higher speeds compared to conventional SMACM methods. Impressively, Ouyang et al. applied ANNA-PALM to image a large 1.8 mm x 1.8 mm field of view of labeled microtubules in cells with high throughput. For future experiments, ANNA-PALM may be used for live-cell SR imaging and for imaging even larger fields of view with high throughput.

The deep learning PSF analysis methods described previously were chiefly interested in generating SR reconstructions from low resolution images. However, in a properly designed microscope, the PSF shape is sensitive to other parameters apart from the position of the emitter. Thus, in principle, parameters such as color of the single emitter, its orientation, [94] or the aberrations found in the microscope may also be extracted from PSF image of single molecules. For example, two recent studies published in close proximity utilized trained NNs to extract the color of single molecule from their PSF shape. [90,95] The trained networks allow for imaging two colors in the same channel simultaneously, a highly advantageous benefit for two-color SR experiments.

For conventional two-color SR experiments, the collected fluorescence light is split into two channels using two cameras or two regions of the same camera. Super-imposing the SR reconstructions from the two channels involves registration of the channels using a mathematical algorithm that might suffer from limited robustness and high computational demand, especially in 3D, leading to errors and thus reduced image quality. Although imaging the two colors sequentially using the same channel is possible, the acquisition time is doubled, substantially decreasing throughput. Moreover, issues of photobleaching and increased background may arise. Thus, imaging both colors simultaneously in the same channel is highly desirable for two color SR experiments. While previous schemes using PSF engineering methods have been implemented to achieve this, the use of NNs to discern colors represents an alternative approach that requires minimal optical modifications to a microscope.

Kim et al. engineered an artificial NN that discerned the color (either red or green) of PSFs. [90] They obtained many PSF images at each color through many SMACM imaging experiments, and implemented these experimental PSFs as part of their training data. Thus, the covered experimental sample space is implicitly encoded in their experimental training data. Once trained, the net was validated on simulated PSFs with high accuracy. Kim et al. then demonstrated the practicality of their net by reconstruction of two-color 3D SR reconstructions of microtubules and mitochondria. The axial position was extracted using a separate NN that was trained on experimental open apertures PSFs where the ground truth axial position was obtained from a z-scan measurement. Their two-color 3D SR reconstructions show nicely resolved microtubules and mitochondria that are clearly distinguishable.

5.3. PSF design for optimized localization microscopy

Using a similar approach as Kim et al., Hershko et al. trained a convolutional NN using experimental data of two quantum dot (QD) types emitting at two distinct colors (red and green). [95] Their trained NN exhibited high accuracy on a validation set of experimental PSFs of QD emitters. However, while discerning two colors with deep learning approaches is highly accurate, NNs may have a greater challenge in discriminating between multiple colors (i.e. 3-4 colors). The challenge stems mainly from the moderate influence of chromatic aberrations on the OA PSF shape. Therefore, a NN can have challenges differentiating between many colors from PSF images that appear similar.

A PSF engineering approach that increases the sensitivity of the PSF shape on wavelength-dependent aberrations is a potential solution to this issue. However, the newly designed PSF shape must also be able to localize emitters with high precision. This problem can be concisely stated as a question initially formulated by Hershko et al.: what is the optimal PSF shape that achieves both precise localizations of single molecules and equally precise classification of emitter color? Fisher information has previously been implemented as a metric to maximize the information content of a PSF shape to design an optimal PSF for a specific problem [97,98]. However, an analogous approach that considers both emitter position and color is challenging to define mathematically, making Fisher information hard to apply to this problem.

To still address this PSF-design challenge, Hershko et al. developed a unique deep learning approach that retrieves a phase pattern which can generate PSF shapes optimally encoded with emitter position and color. Hershko et al. engineered a NN comprised of two components: a spatial light modulator optimizer (SLM-optimizer) and a reconstruction net. To train the net, simulated point sources in a full-field-of-view image were first supplied to the SLM-optimizer as input training data. Each input image was also demarcated with a color (3-5 potential colors were used in this study). The simulated point sources were then convolved with a PSF unique to each color. The color-dependent PSFs were generated by using models that simulate the image of the pupil plane of the microscope with a phase mask. Importantly, the image in the pupil plane is wavelength dependent and thus, the shape of the PSF will be sensitive to the specific colors of the emitter as was shown earlier. [99] The phase mask used to generate an image of the pupil plane was chosen to be simply a matrix with weights that are optimized during the training process of the net. Thus, once trained to completion, the phase pattern, which is encoded in the matrix, could be extracted from the net to be used in later experiments.

The resulting PSFs were then degraded with Poisson noise to reflect realistic experimental environments and were then fed to a reconstruction net which predicts the original point sources position in the full-field-of-view image and its color. Next, the cost function was optimized over these parameters to train the reconstruction net and the SLM-optimizer simultaneously. Thus, as the reconstruction net improves, the SLM-optimizer will also improve in a co-dependent process. Once trained to completion, the phase pattern was retrieved from the net, and a SLM aligned in the pupil plane of the microscope was adjusted to encode the extracted, optimized pattern.

Hershko et al. demonstrated with simulated data that using their newly designed PSF recovers color with high accuracy with minimal deterioration of localization precision (the reconstruction net was used to recover color and to localize optimal PSFs). The colors of various experimental immobile QDs and diffusing beads were also recovered at high accuracy using the optimal PSF. Importantly, the optimal PSF was able to recover color more accurately compared to the OA PSF at all colors investigated.

Deep learning methods can be used to engineer PSFs that are optimal for other specific experiments. For instance, as described above, localizing overlapping emitters is a difficult computational problem that becomes more pronounced for PSFs that encode 3D information. These 3D PSFs usually have a large spatial footprint on the camera and thus, the probability of PSFs overlapping dramatically increases. To resolve this obstacle, Nehme et al. first engineered a convolutional NN that localizes many overlapping tetrapod PSFs with an axial range of 4 microns. [96] Training data was generated by simulating overlapping tetrapod PSF images with known ground truth x/y/z positions.

The performance of the trained net was accessed with simulated validation data with high accuracy over a range of densities of overlapping tetrapod PSFs. Strikingly, their net was also able to localize experimentally overlapping tetrapod PSFs of TOM20 labeled mitochondrial membranes to reconstruct a 3D SR images with high quality. While these results were encouraging, the tetrapod PSF was initially designed to achieve optimal 3D localization precision under single emitter fitting conditions. Likely, there is a more optimal PSF shape that localizes overlapping emitters in 3D over a large axial range more effectively than the tetrapod. To this end, Nehme et al. implemented a deep learning-based approach similar to the one described above to identify a phase mask that yields optimal performance for densely overlapping emitters. This deep learning approach also trains a reconstruction net that retrieves the positions of emitters from an image of overlapping PSFs.

This PSF, termed the learned PSF, has a much smaller spatial footprint compared to the tetrapod PSF. Furthermore, the PSF rapidly rotates throughout the axial range to encode z information. Nehme, Freedman, et al. compared the performance of the learned PSF to the tetrapod using simulated overlapping emitters at various densities. Encouragingly, the localization of the overlapping emitters was much more accurate using the learned PSF compared to the Tetrapod PSF. Finally, the performance of the two PSFs investigated in this study were compared with experimental data of fluorescently labeled DNA telomeres with known ground truth positions. Again, the learned PSF performed more accurately and with fewer false positives than the Tetrapod PSF, thus validating their approach to design a more optimal PSF.

The approaches developed by Hershko et al. and Nehme et al. are unique methods because they excellently make use of the ability of NNs to optimize parameters in high-dimensional space. This allowed problems to be tackled that are currently hard or even impossible to address with exact mathematical analyses. Future directions may investigate the sensitivity of optimal PSF designed from deep learning approaches to hyperparameters in the net. For instance, how does the choice of the cost function or net architecture influence the shape of the final PSF? Is the resulting PSF a global solution? If not, how can the net be modulated to reach a global solution?

5.4. PSF analysis for extraction of molecular and imaging parameters

Another area where deep learning is of high relevance is in the analysis of individual PSF images for extraction of quantitative parameters and signal characterization. The advantage of applying NNs in this area is clear: the photophysical processes during fluorophore excitation and photon emission as well as the process of PSF image formation via a microscope on the camera have been investigated extensively and are understood at a high level of detail. [76,82,97,104–106] Thus, it is possible to simulate realistic datasets of PSF images, providing a verifiable ground truth for training and validation.

A recent example employed a deep NN to perform stoichiometry analysis from fluorescence intensity trances. [100] Information on the stoichiometry of protein complexes in cells often yields direct insights into fundamental biological processes. Since it is desirable to study protein interactions in the context of the cellular environment, a method is required to monitor them non-invasively with high sensitivity. Fluorescence microscopy is therefore one of the most important techniques for these analyses. A common approach is to gradually bleach the fluorophores labeling a multiunit protein complex. As each fluorescent label contributes a discrete amount of fluorescence signal to the total signal, counting the steps in the bleaching curve acquired over time allows in principle direct extraction of the number of individual units in the complex. However, this process is often not so easy in practice. The main reason for this is that the fluorescence traces are usually quite noisy due to Poisson shot noise and background from the cellular environment. Also, a fluorophore might blink, i.e. transiently turn off and then back on again, further complicating the intensity trace.

In their paper, Xu et al. simulate realistic intensity traces for protein complexes with zero to four labeled subunits, including Poisson shot noise and various signal-to-noise ratios. They explain the limited number of subunits by stating that in the experimental data they are interested in, more than four subunits occur rarely, and that more than four bleaching steps are hard to identify by eye. It seems that this choice is quite arbitrary and that inclusion of higher step numbers, explicitly because they may be challenging to identify and analyze, could be a promising endeavor.

The simulated intensity traces were used to train a NN to return the number of steps in the noisy input trace. After a convolutional section, Xu et al. implemented long short-term memory (LSTM) layers. [107,108] These layers add the temporal axis to the analysis, since LSTM layers exhibit feedback connections, which allows them to identify temporal patterns in the input data. Finally, after passing the output from the LSTM to a fully-connected layer, the output layer returns the number of steps in the trace, i.e. a number between 0 and 4. The performance is assessed both with simulated validation data and experimental data, investigating epidermal growth factor dimerization, which verified that especially for low signal-to-noise ratios, the NN-based analysis performed superior to hidden Markov modeling.

A fundamental task in optical microscopy and especially single-molecule localization microscopy is phase retrieval (PR). PR is the reconstruction of the (usually pupil plane) phase information from intensity information (images). As detectors typically employed in optical measurements rely on the conversion of electrical fields to electrons, the phase information is usually lost and only the intensity information is recorded. However, it is possible to still extract phase information from the intensity information, a process that is collectively termed PR. As the phase information is important for many applications, PR is crucial for numerous investigations, ranging from crystallography over astronomy to electron and optical microscopy. Unfortunately, PR typically requires iterative optimization schemes, which are computationally demanding and thus slow. This is especially detrimental for experiments that involve a large number of PR calculations, for example characterization of phase aberrations varying through the field of view.

PR has been addressed several times with deep learning-based methods. For example, Paine et al. employ an adapted Inception v3 architecture to estimate good initial Zernike coefficient estimates for PR with gradient-based optimization algorithms from images of strongly aberrated PSFs. [101] With this combination of deep learning and conventional PR approaches, they were able to estimate the phase accurately and more effectively than using previous strategies, for example many random starting guesses. Zhang et al. performed estimation of wavefront distortions by training a NN to return the first 12 or 21 Zernike coefficients with amplitudes between -160 and +160 mλ. [85] Finally, Zelger et al. and trained a NN to localize PSFs, but noticed that aberrations can have a strong effect on the performance. [87] Thus, they trained the network to additionally return first order astigmatism and primary spherical aberration (Zernike coefficients Z₅, Z₆, and Z₁₁), which improved the localization precision of their approach.

Our lab has recently put forward another strategy to perform PR with deep learning. It was our goal to combine a compact architecture to enable rapid, real-time PR with large Zernike coefficient amplitude ranges. [102] Additionally, we wanted to ensure that the approach is purely based on the NN, i.e. that there is no requirement for refinement of the predictions of the NN. To this end, we simulated PSFs from a point emitter positioned at the coverslip by means of vectorial diffraction theory at focal positions of -1, -0.5, 0, 0.5, and 1 µm. To introduce phase information, we multiplied the Fourier plane fields with random Zernike coefficients with values between –λ to λ, using Zernike coefficient orders 1 to 6 (Noll indices 2 to 28). Such a large Zernike coefficient range yields very complex PSF shapes with rapidly varying appearance upon changes in focal position.

We employed a deep residual network to directly extract the values of the Zernike coefficient from the PSF images. The input layer receives the five PSF slices at the five focal positions and the last layer returns the values of the 27 Zernike coefficients of order 1 to 6. This compact architecture provides fast analysis, enabling real-time PR of PSF images. We quantified the performance of the NN with exact PSF simulations, which verified that the extracted Zernike coefficients match the ground-truth Zernike coefficients very closely. As a result, the shape of the retrieved PSFs resembles the shape of the ground-truth PSFs excellently, underscoring successful PR (Fig. 8)

Fig. 8.

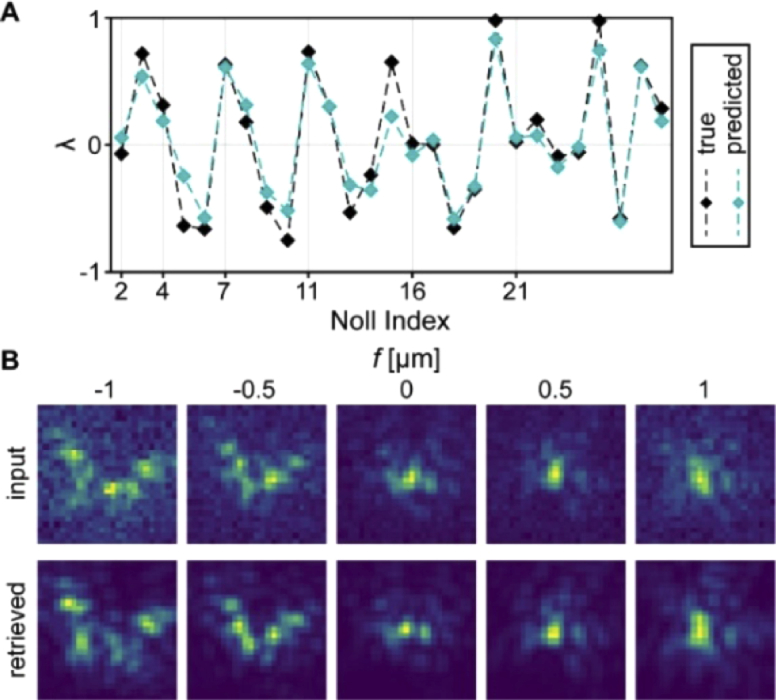
Phase retrieval of a general PSF with a residual network. A) The predicted Zernike coefficients (teal) match the ground-truth Zernike coefficients (black) very well. B) Correspondingly, the retrieved PSFs (bottom line) match the input PSF (top line) throughout the whole focal range.

A second recent project from our lab focused on the identification and quantitative extraction of background fluorescence from PSF images, a key issue in all single-molecule-based fluorescence imaging methods. [103] Background fluorescence is an umbrella term for any contributions to a fluorescence image that does not originate from the species investigated, but from other sources. For example, background fluorescence in biological samples frequently is caused by unspecific binding of labeling agents to other cellular components than the one that should be labeled. Cellular autofluorescence is another source. Background fluorescence results in reduced image quality and is therefore unwanted. However, it cannot be completely avoided in experimental settings, thus, proper background correction is necessary.

Unfortunately, background correction is a very challenging task. The main reason for this is that the background fluorescence is almost never uniform in a fluorescence image. For example, if unspecific binding of the labeling agent to different cellular components occurs, then the resulting background fluorescence will resemble the spatial length scales that these cellular components exhibit – which are distributed over a broad range, inducing structured background.

Structured background is very problematic in single-molecule localization microscopy, especially when using engineered PSFs for e.g. extracting 3D information. This is because the analysis algorithms that extract information from the PSF image are very sensitive to shape, thus, the presence of structured background can strongly affect the result of the analysis in an unpredictable fashion. Therefore, successful background correction requires the differentiation between desired signal from the PSF and unwanted signal from background. Our work provided the field for the first time with an algorithm to perform this task.

Our approach uses accurate PSF simulations that include all relevant experimental parameters such as signal level, amount of background, or focal position, implemented over a wide range of values. To include structured background, we turned to Perlin noise for training, covering the relevant spatial frequencies encountered in experimental situations. This allowed us to include structured background directly in our PSF simulations covering various spatial frequencies, each contributing arbitrarily to the total background, yielding a wide range of background shapes.

The NN we implemented, called BGnet, has a U-net-type architecture. It can be thought of as a combination of an encoder-decoder architecture, which first performs two-dimensional convolution and spatial downsampling while increasing the filter space, and then two-dimensional convolution and spatial upsampling while decreasing the filter space. Importantly, the outputs of the convolutional steps during spatial downsampling are concatenated with the inputs for the convolutions during spatial upsampling, which is somewhat reminiscent of residual nets.

BGnet receives PSF images corrupted with background and was trained to directly return the structure of the underlying background as well as the corresponding intensity of the background in each pixel, allowing for straightforward background correction. We investigated four PSFs: the standard, unmodified open-aperture PSF, the double-helix PSF, the Tetrapod PSF with 6 µm range, and an arbitrary PSF that did not exhibit a well-defined structure. Visual inspection of the predicted background structure and intensity was very promising (Fig. 9): using quantitative measures, the prediction of BGnet matched the ground-truth cases quite well. [103]

Fig. 9.

Estimation of arbitrary structured background from images of various PSFs. Shown are the probability density function of the PSF (i.e. the noise-free, theoretical PSF), the PSF with background, the true underlying background in the PSF image, the prediction of BGnet, and the background-corrected PSFs, using either the true or the predicted background. Scale bar: 500 nm (open aperture PSF), 1 µm (other PSFs).

Strikingly, both the localization precision, i.e. the spread of the localization cloud when repeatedly localizing identical PSFs that only differ in their Poisson noise structure, as well as localization accuracy, i.e. the distance of a single localization to the ground truth position, dramatically decreased by factors of approx. 2 to 50 when background correction with BGnet was employed compared to background correction with a constant background estimate. Furthermore, background correction with BGnet also significantly improved the quality of super-resolution reconstructions acquired from biological samples. The results from the experimental data also verify that the chosen artificial background simulations match the experimentally encountered background structures well.

6. Summary and outlook

Deep learning has become a generally available, powerful tool in many areas of scientific research. Rapid improvements both in software design for implementation and computational power for training and analysis have enabled spectacular results in recent years. The capability of NNs to process image data has been especially useful in fields that heavily rely on imaging and microscopy such as medicine, astronomy, and biology. Specifically in single-molecule microscopy, deep learning proved to be a highly valuable tool for data analysis. Several factors contribute to this: First, NNs can process data rapidly after training is completed, thus, the large amounts of imaging data typically generated in single-molecule microscopy are no longer the bottleneck of the analysis. Second, the formation of single-molecule signals by a microscope is largely understood and can be simulated using established mathematical models. This allows the generation of virtually unlimited amounts of accurate training data, a resource of invaluable significance for any type of machine learning approach. Finally, NNs are versatile and can be applied broadly to the many different challenges of single-molecule studies without the requirement to develop each approach from scratch.

Considering the remarkable success of deep learning-based analysis in single-molecule optical research, it is even more important to be aware of the pitfalls that are specific to NNs. Namely, deep learning algorithms can often be prone to return outputs that match the sample space of the training data. This behavior, which is less pronounced for conventional analysis approaches, mandates rigorous external benchmarking and careful evaluation of the use case to avoid artifacts. Generally, we hope that new thrusts to make NNs more robust, an area of research that currently receives increasing attention, will eventually penetrate applications of deep learning in single-molecule experiments and related fields.

Overall, deep learning algorithms have already had tremendous impact on many areas of scientific research. We expect that this story of success will continue and are confident that increasing general awareness will result in a range of creative, not yet foreseen applications.

Funding

National Institute of General Medical Sciences10.13039/100000057 (R35GM118067).

Disclosures

The authors declare that there are no conflicts of interest related to this article.