Deep learning segmentation for optical coherence tomography measurements of the lower tear meniscus

Abstract

The tear meniscus contains most of the tear fluid and therefore is a good indicator for the state of the tear film. Previously, we used a custom-built optical coherence tomography (OCT) system to study the lower tear meniscus by automatically segmenting the image data with a thresholding-based segmentation algorithm (TBSA). In this report, we investigate whether the results of this image segmentation algorithm are suitable to train a neural network in order to obtain similar or better segmentation results with shorter processing times. Considering the class imbalance problem, we compare two approaches, one directly segmenting the tear meniscus (DSA), the other first localizing the region of interest and then segmenting within the higher resolution image section (LSA). A total of 6658 images labeled by the TBSA were used to train deep convolutional neural networks with supervised learning. Five-fold cross-validation reveals a sensitivity of 96.36% and 96.43%, a specificity of 99.98% and 99.86% and a Jaccard index of 93.24% and 93.16% for the DSA and LSA, respectively. Average segmentation times are up to 228 times faster than the TBSA. Additionally, we report the behavior of the DSA and LSA in cases challenging for the TBSA and further test the applicability to measurements acquired with a commercially available OCT system. The application of deep learning for the segmentation of the tear meniscus provides a powerful tool for the assessment of the tear film, supporting studies for the investigation of the pathophysiology of dry eye-related diseases.

1. Introduction

Dry eye disease (DED) is a frequent disease of the ocular surface in which tear film instability plays a major role [1–3]. In an effort to assess the state of the tear film in DED, the tear meniscus, which is the concave tear surface at the upper and lower eyelid margins, has been widely studied [4–6]. A variety of quantitative parameters describing the tear meniscus, ranging from tear meniscus volume (TMV) [7] and radius of curvature (TMR) [8] to tear meniscus height (TMH) [9], depth (TMD) [10] and tear meniscus area (TMA) [11] have been studied, employing different devices and methods.

Optical coherence tomography (OCT) is based on interferometric principles. By measuring the echo time delay of the back-scattered light, OCT can acquire high-resolution cross-sectional images of a sample. Being non-invasive, the technology has become a clinical standard in ophthalmological care, where it is routinely used to investigate the anterior and posterior segment of the eye [12].

When evaluating quantitative parameters in images, manual segmentation is often time consuming and can introduce operator bias [3]. Automatic assessment, on the other hand, is hampered by the high inter- and intra-individual variability that comes with in vivo measurements. Depending on the application, conventional segmentation algorithms, e.g. based on thresholding and edge detection, can provide robust results, but at the price of high complexity [13].

Although known for a long time [14], machine learning has been increasingly used only in the past decade to solve image classification [15] and segmentation [16] tasks, mainly driven by advances in the parallelization capabilities of graphics processing units (GPUs) [17]. Using OCT data, segmentation applications can range from detection of retinal layer boundaries [18,19], macular edema [20] and macular fluid [21] to corneal layers [22] and intradermal volumes [23].

Class imbalance in deep learning describes the problem of having too few samples of a certain class as compared to other classes in the dataset. For image segmentation, this means that the structure of interest (foreground) covers only a small area in the image and therefore consists of far less pixels than the background. This kind of class imbalance usually leads to neural networks being very good at the detection of background pixels, while being worse at the detection of relevant foreground structures. Currently there are two main approaches to mitigate this effect: weighted loss functions and cascading (two-stage) networks. Weighted loss functions include weights that emphasize the foreground pixels or introduce scaling factors that focus the training on misclassified examples. They can reach complexities that consider smoothness constraints, topological relations or valid shapes [24–26]. The main concept of cascading networks is the employment of a series of neural networks, where the following model uses the output prediction map of the previous one. This can, for example, be accomplished by a fully convolutional network (FCN) segmenting within the segmented area of a previous one [27] or by segmenting within a previously regressed bounding box [28].

In this manuscript, we present a new application of neural networks for the localization and segmentation of the lower tear meniscus in ultrahigh-resolution (UHR-)OCT measurements. The current dataset of healthy subjects with a normal tear film provides a low support of tear meniscus pixels, an effect that will be even worse in DED patients. We therefore put the focus on investigating the class imbalance in these types of measurements. In the following, we will consider two deep learning segmentation approaches. One directly segments the tear meniscus in the original image, while the second approach first localizes the tear meniscus and then segments within the higher resolution region of interest (ROI). The goal is to investigate whether the two-stage segmentation is necessary, and if so, if the localization is possible with a very simple convolutional neural network (CNN). We will compare the localization results with a state of the art network and the segmentation outputs with our previously published thresholding-based segmentation algorithm (TBSA) [29], both quantitatively and qualitatively, and test the two deep learning approaches on a measurement acquired with a commercially available OCT system.

2. Material and methods

2.1. Subjects

The tear meniscus measurements were obtained from ten healthy subjects (five female, five male, age 31 ± 10 years). The study protocol was approved by the Ethics Committee of the Medical University of Vienna and the study was performed in adherence to the guidelines of the Declaration of Helsinki as well as Good Clinical Practice guidelines. All participants gave their written informed consent.

2.2. Data acquisition

Cross-sectional images of the lower tear meniscus were obtained using a custom-built UHR-OCT system described in detail elsewhere [30]. In short, the Ti:Sa laser source with a central wavelength of 800 nm provides an axial resolution of 1.2 µm in tissue, while the optics of the setup produce a lateral resolution of 21 µm. Measurements were centered on the lower eyelid margin and covered a volume of 2.9 × 4 × 2 mm³ (height × width × depth, in air).

An additional measurement was acquired with a commercially available Cirrus HD-OCT 4000 system (Carl Zeiss Meditec, Inc., Dublin, California, USA) in combination with a dedicated anterior segment lens. The system has a lateral resolution of 20 µm and an axial resolution of 5 µm in tissue. The depth-ranges of the UHR-OCT and the Cirrus HD-OCT are approximately 1.5 and 2.1 mm in tear fluid, respectively, assuming a tear film group index of 1.341 for the wavelength band of the light source [31].

2.3. Dataset

All images were obtained from volumetric measurements of ten different subjects and segmented using the TBSA presented elsewhere [29]. In order to increase the pixel resolution of the image, in a first step, the spectral signal was zero-padded before the discrete Fourier transform. While the axial resolution that is given by the central wavelength and bandwidth of the laser light source [32] remains unchanged, the larger number of axial pixels can be advantageous for image segmentation tasks. In brief, the TBSA then uses cross-correlation to identify the ROI. Next, it applies thresholding, detects the upper and lower tear meniscus boundaries and uses them to estimate the tear meniscus area.

After the segmentation by the TBSA, all images were evaluated by an experienced grader and only those with a suitable segmentation were retained. The final dataset consisted of 6658 images from all ten subjects with a resolution of $8192\times 512\text{pixel}$ (height × width). The average support of the tear meniscus, which is the amount of tear meniscus pixels divided by the amount of background pixels, was 0.71%.

2.4. Comparison of two segmentation approaches

In order to use both the segmentation and the localization data obtained from the TBSA, we decided to compare two different approaches. The first approach employs an FCN to segment the tear meniscus area in a down-scaled $512\times 512\text{pixel}$ version of the initial $8192\times 512\text{pixel}$ OCT image. Since the actual tear meniscus is relatively small in respect to the full cross sectional image, only a limited area in the image contains relevant information. The second approach, therefore, first localizes the tear meniscus and crops a ROI from the initial image in which the tear meniscus covers a larger part of the image section. This ROI is then scaled to $512\times 128\text{pixels}$ and segmented by a FCN. In this manuscript, these methods will be referred to as direct segmentation approach (DSA) and localized segmentation approach (LSA) (Fig. 1). The LSA is similar to Mask R-CNN [28], but differs in that the localization in our case is handled by a very simple and fast CNN.

Fig. 1.

Schematic of both investigated segmentation approaches. The DSA rescales and directly segments the initial image while the LSA first localizes the meniscus before segmentation. FCN512 and FCN128 have similar architectures and only differ in their image input dimensions (see also Fig. 3).

2.5. Data augmentation

Since most tear meniscus images that originate from a single subject are related, we used data augmentation during the training phase to increase the variability of our dataset. For the localization, the ground truth is modeled as the coordinates of the top left and bottom right corner of a rectangular bounding box. These bounding boxes all have the same dimensions of $3000\times 130\text{pixels}$, which we chose empirically while designing the TBSA to allow for larger tear menisci. We introduced some variation during the training process by multiplying in every epoch each coordinate by a random value between 0.95 and 1 or 1 and 1.05, chosen so that the bounding box can only increase in area. Reducing the area could cut off parts of the tear meniscus and falsify the ground truth data. For the segmentation we used Augmentor [33] to apply random rotations of up to five degrees and slight random skewing to the images, each with a probability of 50% per epoch. This generally increases the performance of a neural network, since it provides a wider range of training data.

2.6. Network architectures

In the following paragraph, the neural network architectures for the localization and the segmentation of the tear meniscus will be presented. All neural networks were implemented using the Keras library [34] with TensorFlow [35] backend.

2.6.1. Meniscus localization.

For the localization of the tear meniscus, a network with a single convolutional layer was used (Fig. 2). The ROI is modeled as a rectangular bounding box and the output of the network are the x and y coordinates of the top left and bottom right corner of this bounding box. Before being fed to the network, the initial $8192\times 512\text{pixel}$ image was rescaled to $64\times 64\text{pixels}$. This design aims to keep training and evaluation times very short. In order to prevent overfitting, L1 norm regularization is applied to the convolutional layer and a dropout layer [36] is introduced before the flattening. Batch normalization [37] is added before the rectified linear unit (ReLU) activation layer to increase the training stability. The last fully connected layer uses a linear activation function. For training, we used the mean squared error as loss function and stochastic gradient descent with a learning rate of $1\ast {10}^{-5}$, a Nesterov momentum of 0.999 and a batch size of 32. To compare the localization performance with a state of the art network, we trained YOLOv3 and Tiny YOLOv3, a smaller version of YOLOv3, on our dataset [38]. Best results were obtained using the available pre-trained weights as initialization and by employing stochastic gradient descent with a learning rate of $3\ast {10}^{-5}$ and a Nesterov momentum of 0.999.

Fig. 2.

Architecture of the neural network for the localization of the tear meniscus. The notation h x w x f represents the shape of the layer (h: height, w: width, f: number of feature channels). Conv2d 3x3: 2-dimensional convolution with a 3x3 kernel, L1 reg: L1 norm regularization, batchnorm: batch normalization, ReLU: rectified linear unit, maxpool: maximum pooling, FC: fully connected layer.

2.6.2. Meniscus segmentation

The segmentation of the tear meniscus was performed with a U-Net-like architecture [16] modified as shown in Fig. 3. Except for the layer dimensions, the network is very similar to our previously published segmentation network [23]. In short, the main differences to Ronneberger’s U-Net are a reduction in the amount of feature channels, a batch normalization layer before every rectified linear unit (ReLU) activation layer, application of image padding for every convolution and a sigmoid activation function instead of a softmax function for the last network layer.

Fig. 3.

Architecture of the two neural networks for the segmentation of the tear meniscus. The notation h x w x f represents the shape of the layer (h: height, w: width, f: number of feature channels). The DSA uses FCN512 with n = 512 and the LSA uses FCN128 with n = 128.

For training, a differentiable version of the Jaccard distance, as described in [23], was employed as loss function. We used stochastic gradient descent with a learning rate of $3.5\ast {10}^{-5}$ and $5\ast {10}^{-4}$ for DSA and LSA, respectively, a Nesterov momentum of 0.999 and a batch size of 4.

3. Results

3.1. Tear meniscus localization

The localization of the tear meniscus was evaluated by employing two different metrics. The Jaccard index is defined as the intersection of the ground truth bounding box with the predicted bounding box, divided by their union. The second metric will be referred to as $p_{inc}$ in the following paragraphs and is defined as the ratio of the number of tear meniscus pixels within the bounding box $(N_{box})$ and the total number of tear meniscus pixels in the image $(N_{image})$:

$$p_{inc}=\frac{N_{box}}{N_{image}}.$$ (1)

We used five-fold cross-validation and split the 6658 images into five subsets of 1179 to 1543 images, each fold consisting of images from two of the ten subjects. We then trained the network on four of the five folds and predicted the localization on the fifth. The results are shown in Table 1 for our proposed network and in Table 2 for YOLOv3 and Tiny YOLO. An average Jaccard index of 78.85 % as well as an average $p_{inc}$ of over 99.99% indicate a successful localization of the ROI by our proposed localization network. Although the CNN architecture for the localization is very simple, it reached a $p_{inc}$ of 100% in three out of five validation-folds. In comparison, YOLOv3 and Tiny YOLO reached an average Jaccard index of 58.95% and 55.32% and an average $p_{inc}$ of 98.50% and 92.24%, respectively. The average localization times for a single image were 310 µs, 1 ms and 5 ms for our proposed network, Tiny YOLOv3 and YOLOv3, respectively, using an Nvidia GeForce GTX 1080 Ti graphics card.

Table 1. Five-fold cross-validation results of the proposed network for the tear meniscus localization.

Fold		1	2	3	4	5	mean
Jaccard	mean	0.7974	0.7909	0.7968	0.7793	0.7739	0.7885
	std	0.0854	0.0804	0.0884	0.1061	0.1027	0.0927
${\mathit{p}}_{\mathit{i}\mathit{n}\mathit{c}}$	mean	0.9999	1.000	1.000	0.9998	1.000	0.9999
	std	0.0017	0.0000	0.0000	0.0081	0.0000	0.0035

Table 2. Five-fold cross-validation results of YOLOv3 and Tiny YOLOv3 for the tear meniscus localization.

YOLOv3
Fold		1	2	3	4	5	mean
Jaccard	mean	0.6197	0.6199	0.5403	0.5892	0.5749	0.5895
	std	0.1354	0.1477	0.1672	0.1152	0.1191	0.1533
${\mathit{p}}_{\mathit{i}\mathit{n}\mathit{c}}$	mean	0.9785	0.9948	0.9748	0.9986	0.9811	0.9850
	std	0.0920	0.0371	0.0879	0.0296	0.0522	0.0719

Tiny YOLOv3
Fold		1	2	3	4	5	mean
Jaccard	mean	0.5829	0.5135	0.5910	0.5771	0.4898	0.5532
	std	0.1560	0.1651	0.1426	0.1928	0.1161	0.1615
${\mathit{p}}_{\mathit{i}\mathit{n}\mathit{c}}$	mean	0.9558	0.8937	0.9892	0.8998	0.8542	0.9224
	std	0.1406	0.2146	0.0467	0.2154	0.2918	0.1998

3.2. Tear meniscus segmentation

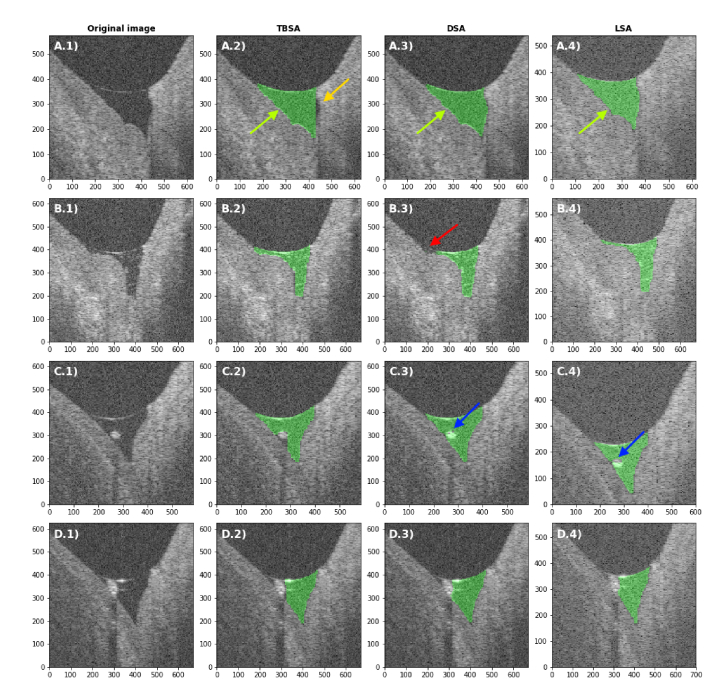
The image segmentation was performed using two different approaches. The one-step DSA rescales the initial OCT image to $512\times 512\text{pixels}$ and feeds it into the FCN512. The two-step LSA first localizes the ROI in the initial image and then uses a $512\times 128\text{pixel}$ image of the ROI to segment the tear meniscus with the FCN128. The segmentations obtained from both approaches in comparison to the TBSA are shown in Fig. 4 in the case of a typical lower tear meniscus measurement. In Fig. 5, the comparison between the TBSA, DSA and LSA in the context of challenging segmentation tasks is depicted. These instances are rare in healthy subjects but present a good opportunity to visualize the algorithm's behavior in edge cases.

Fig. 4.

Comparison between the thresholding-based segmentation algorithm (TBSA), the direct segmentation approach (DSA) and the localized segmentation approach (LSA) in an example case. The axes represent µm in tear fluid.

Fig. 5.

Comparison between the TBSA (column 2), DSA (3) and LSA (4) in rare cases of challenging segmentation tasks (1). None of the images were part of the training dataset. (A) Not segmented lateral cavity (orange arrow), (B) irregular meniscus shape, (C) small debris and (D) larger debris cutting the tear meniscus area in two parts. Green arrows indicate example areas where the bordering pixels are included in or excluded from the tear meniscus area. The red arrow indicates a non-segmented region of the tear meniscus area. The blue arrows indicate holes in the segmented area, where debris is present. Images in columns 1-3 are cropped from a $512\times 512\text{pixel}$ image, while images in column 4 are cropped from a $512\times 128\text{pixel}$ image. The axes represent µm in tear fluid.

The different performance metrics were calculated using five-fold cross-validation and are given in Table 3 along with the estimated absolute areas. Each fold consisted of 1179 to 1543 images from two of the ten subjects. Results for each individual subject are shown in Appendix 1 (Table 4) and 2 (Table 5) for the DSA and LSA, respectively. The average support of the tear meniscus, which is the amount of meniscus pixels in relation to background pixels, was 0.71% and 4.18% for the DSA and LSA, respectively. The mean sensitivity was 96.36% and 96.43%, the mean specificity was 99.98% and 99.86% and the mean Jaccard index was 93.24% and 93.16% for DSA and LSA, respectively, which indicates a good performance of both approaches overall. The segmentation time of a single image is on average 25 ms for the DSA and 7 ms for the LSA using an Nvidia GeForce GTX 1080 Ti graphics card, which is 64 times or 228 times faster than the TBSA requiring 1.6 s.

Table 3. Cross-validated results for the tear meniscus segmentation. Values are averages over all folds weighted by the number of images in the fold. Std is the standard deviation.

Metric		DSA	LSA
Support	mean	0.0071	0.0418
	std	0.0021	0.0136
Jaccard index	mean	0.9324	0.9316
	std	0.0432	0.0474
Dice coeff.	mean	0.9644	0.9638
	std	0.0261	0.0318
Accuracy	mean	0.9995	0.9972
	std	0.0003	0.0027
Sensitivity	mean	0.9636	0.9643
	std	0.0361	0.0262
Specificity	mean	0.9998	0.9986
	std	0.0001	0.0024

Metric	DSA	LSA	TBSA
Absolute area $(m{m}^2)$
mean	0.01895	0.01826	0.01832
std	0.00827	0.00842	0.00848
relative to TBSA	1.034	0.997	1.000

3.3. Segmentation of a measurement from a commercial system

In Fig. 6, a cross-sectional image acquired with a commercially available Cirrus HD-OCT 4000 system (Carl Zeiss Meditec, Inc., Dublin, California, USA) and the corresponding segmentation results employing the DSA and LSA are depicted. As can be seen in Fig. 6(A), the network correctly segmented the tear meniscus in the center of the image, but, in addition, falsely identified pixels in the lower left corner of the image that includes part of the iris. This can be explained by the larger depth range of the Cirrus HD-OCT system as compared to the UHR-OCT, which generates images that contain deeper lying structures of the anterior eye segment. These structures were not present in the training dataset that was entirely acquired with the UHR-OCT. However, when only considering the segmentation within the bounding box, the DSA accurately determines the tear meniscus region. The LSA depicted in Fig. 6(B), being limited to the ROI, provides a correct segmentation of the tear meniscus.

Fig. 6.

Segmentation of a lower tear meniscus image acquired with a commercially available Cirrus HD-OCT system. A) The initial image has been scaled to 512x512 pixels and was segmented with the DSA (green). The result of the tear meniscus localization is shown as a yellow bounding box. B) Segmentation of the image by the LSA (yellow). Both networks had only been trained on UHR-OCT images. The axes represent µm in tear fluid.

4. Discussion

In this manuscript, we presented the segmentation of the tear meniscus based on two different approaches with FCNs that have been trained on images processed with the previously published TBSA. For the DSA, after the standard OCT post-processing procedures and rescaling, the images were used for training without any further modification. For the LSA, involving an initial search of the ROI, the localization of the tear meniscus reached 99.99 % $p_{inc}$ with a very simple CNN architecture, indicating that almost every tear meniscus pixel was correctly surrounded by the bounding box. Comparing the localization results of the introduced network with those of the more complex YOLOv3 and Tiny YOLOv3 revealed that, in our case, this simple architecture was sufficient and even performed better when regarding Jaccard index and $p_{inc}$. Evidently these networks are designed for more advanced tasks, involving a multitude of classes, and would outperform our network in more complex cases. As a result of the localization, the support of tear meniscus increased approximately by a factor of six.

The mean Jaccard index of 93.24% and 93.16% and the mean sensitivity of 96.36% and 96.43% for DSA and LSA, respectively, indicate a good agreement between the training data and the segmentations. In most cases, the difference between the two approaches is the exclusion or inclusion of pixels at the edge of the tear meniscus area (see Fig. 4). Two factors influence this local difference: first, the TBSA is based on Otsu’s method, which creates a separate threshold value for the binarization of each image. Depending on the signal-to-noise ratio of the image, the cutoff-value might include or exclude these border pixels. Second, the two different processes of, on the one hand, downscaling the ground-truth area (TBSA) and, on the other hand, segmenting the downscaled images (DSA and LSA), do not necessarily yield the same results, given that the resolution on the depth axis is reduced by a factor of 16. Although the performance metrics of DSA and LSA are very similar, an analysis of the relative and absolute areas (Table 3) revealed an overestimation by the DSA and a slight underestimation by the LSA when compared to the TBSA. This can be explained by the fact that the deviation of a single pixel from the ground truth represents more area in the case of the DSA than in the LSA. The over- and underestimation can also be seen when visualizing the segmented area (e.g. see green arrows Fig. 5). The overall difference between both approaches, however, is negligible compared to other factors like intra-subject variability [10].

The neural networks show a large improvement in processing times compared to the TBSA, which can be attributed to the fact that the neural networks run on the GPU whereas the TBSA runs on the CPU. Although the LSA consists of more steps, it is faster than the DSA. The additional localization time of the LSA of 310 µs is negligible, while the lower image resolution requires fewer computationally demanding convolution operations. Nonetheless, both methods have the potential for video-rate and real-time segmentation applications.

In our previous work [29], we presented lower tear meniscus images that were challenging for the TBSA. These cases, which have not been part of the training dataset, are depicted in Fig. 5 and show the behavior of the segmentation in rare edge cases. The first case (Fig. 5(A)) demonstrates an advantage of the neural networks compared to the TBSA. While the TBSA was limited by proceeding in each A-scan from the top until it encountered tissue, the neural network is not and correctly segments the whole tear meniscus area. In the case of an irregular tear meniscus shape (Fig. 5(B)), the TBSA already performed well and so does the LSA, whereas the DSA omits part of the tear meniscus area. For case C (Fig. 5(C)) it is important to mention that the training dataset only contained images where the debris was small enough to not be considered by the TBSA, which was achieved by removing islets from the thresholded image. The network has therefore only seen cases of a single continuous area as training data, where, if present, debris was included in the tear meniscus area. Interestingly, in the present case, on one hand, both approaches included parts of the debris in the area, which the TBSA did not, but, on the other hand, also created small holes in the segmentation. Fortunately, this problem could easily be solved with a flood-fill operation, that would not alter correctly segmented images and only improve the segmentations containing holes. In Fig. 5(D), different depth-ranges the debris is probably too large to be considered part of the segmented area, since it borders not only the surrounding tissue, but also the air-tear-interface at the top of the image. Although the DSA and LSA slightly improve upon the segmentation of the area under the debris, this case still remains an open challenge.

Further improvements to the networks could be made by increasing the number of images from different subjects in the training dataset. Potentially including measurements of non-healthy subjects, e.g. DED patients, would make the application more robust in a wider range of cases. Furthermore, measurements acquired with different OCT-systems would reduce the device-dependency of the networks. As long as there is a good representation of different devices, the application could be used on data from systems it has not been trained on, which might reduce the problem of device-dependant measurements [39,40]. This is possible because the tear meniscus can be resolved with a standard resolution OCT, like the Cirrus HD-OCT system, and does not require the superior axial resolution of an UHR-OCT. Although in some cases different depth-ranges of different systems could lead to a false positive segmentation (Fig. 6), using networks in cascade like the LSA could reduce this erroneous detection. However, on such a multi-system scale, it might be necessary to use a more complex CNN than the one presented here for the localization.

In summary, both DSA and LSA provided good results close to the ground truth and performed better than the TBSA regarding segmentation time and segmentation of atypical cases. Given the good performance metrics of the DSA, the problem of class imbalance does not strongly affect the segmentation of measurements from healthy subjects. This might still change in the case of DED patients, where the tear meniscus dimensions are much smaller, which reduces the support even further. Comparing DSA and LSA, the future employment of the LSA seems favourable due to the shorter segmentation time and the potentially higher robustness in unseen cases, as shown by the challenging segmentation cases and the Cirrus HD-OCT measurement example. This presumes that the localization continues to perform robustly across different devices, which still requires further investigation and potential adjustments.

5. Conclusion

Deep learning was employed for the segmentation of the lower tear meniscus in healthy subjects. Two different segmentation approaches were developed and provided a segmentation performance close to the ground truth. Robust localization of the tear meniscus was achieved with a very simple CNN architecture. Segmentation times of the neural networks were up to two orders of magnitude faster than the previous algorithm and showed better performance in rare edge cases. Future improvements of the dataset could include data from non-healthy subjects and data from different OCT systems. When considering multi-system training for the segmentation of OCT-measurements, cascading localization and segmentation networks shows great potential.

A. Appendix

A.1. Performance metrics of the DSA for individual subjects

Table 4. Performance metrics of the DSA for individual subjects. Std is the standard deviation.

Subject		Jaccard	Dice	Accuracy	Sensitivity	Specificity
1	mean	0.9566	0.9778	0.9995	0.9802	0.9997
	std	0.0143	0.0076	0.0002	0.0111	0.0001
2	mean	0.9296	0.9630	0.9995	0.9594	0.9998
	std	0.0418	0.0236	0.0003	0.0270	0.0001
3	mean	0.9342	0.9654	0.9996	0.9660	0.9998
	std	0.0420	0.0386	0.0003	0.0425	0.0001
4	mean	0.8856	0.9380	0.9990	0.9263	0.9996
	std	0.0639	0.0386	0.0005	0.0506	0.0001
5	mean	0.9322	0.9647	0.9995	0.9630	0.9998
	std	0.0264	0.0151	0.0002	0.0261	0.0001
6	mean	0.9418	0.9699	0.9995	0.9603	0.9998
	std	0.0219	0.0119	0.0002	0.0233	0.0001
7	mean	0.9043	0.9464	0.9992	0.9234	0.9998
	std	0.0999	0.0652	0.0009	0.1017	0.0001
8	mean	0.9401	0.9690	0.9996	0.9651	0.9998
	std	0.0155	0.0083	0.0001	0.0165	0.0001
9	mean	0.9244	0.9605	0.9997	0.9558	0.9999
	std	0.0276	0.0154	0.0001	0.0243	0.0001
10	mean	0.9091	0.9510	0.9997	0.9734	0.9998
	std	0.0665	0.0406	0.0002	0.0233	0.0002

A.2. Performance metrics of the LSA for individual subjects

Table 5. Performance metrics of the LSA for individual subjects. Std is the standard deviation.

Subject		Jaccard	Dice	Accuracy	Sensitivity	Specificity
1	mean	0.9594	0.9792	0.9974	0.9825	0.9984
	std	0.0146	0.0078	0.0008	0.0091	0.0008
2	mean	0.9347	0.9658	0.9972	0.9579	0.9990
	std	0.0379	0.0211	0.0015	0.0287	0.0007
3	mean	0.9338	0.9657	0.9976	0.9675	0.9988
	std	0.0203	0.0110	0.0006	0.0153	0.0006
4	mean	0.8729	0.9275	0.9920	0.9389	0.9952
	std	0.1085	0.0815	0.0103	0.0596	0.0106
5	mean	0.9280	0.9625	0.9968	0.9542	0.9987
	std	0.0220	0.0120	0.0012	0.0220	0.0007
6	mean	0.9402	0.9689	0.9968	0.9593	0.9989
	std	0.0309	0.0184	0.0023	0.0192	0.0023
7	mean	0.9161	0.9548	0.9955	0.9442	0.9982
	std	0.0648	0.0408	0.0048	0.0345	0.0037
8	mean	0.9350	0.9663	0.9977	0.9567	0.9992
	std	0.0202	0.0109	0.0007	0.0225	0.0005
9	mean	0.9213	0.9587	0.9983	0.9664	0.9990
	std	0.0311	0.0176	0.0005	0.0247	0.0005
10	mean	0.9044	0.9457	0.9981	0.9670	0.9987
	std	0.1037	0.0759	0.0028	0.0242	0.0029

Funding

Christian Doppler Research Association10.13039/501100006012; Austrian Federal Ministry for Digital and Economic Affairs 10.13039/501100012416; National Foundation for Research, Technology, and Development10.13039/100010132; Carl Zeiss Meditec Inc. as industrial partner of the Christian Doppler Laboratory for Ocular and Dermal Effects of Thiomers.

Disclosures

The authors declare no conflicts of interest.