Estimation of vocal fold physiology from voice acoustics using machine learning

Abstract

The goal of this study is to estimate vocal fold geometry, stiffness, position, and subglottal pressure from voice acoustics, toward clinical and other voice technology applications. Unlike previous voice inversion research that often uses lumped-element models of phonation, this study explores the feasibility of voice inversion using data generated from a three-dimensional voice production model. Neural networks are trained to estimate vocal fold properties and subglottal pressure from voice features extracted from the simulation data. Results show reasonably good estimation accuracy, particularly for vocal fold properties with a consistent global effect on voice production, and reasonable agreement with excised human larynx experiment.

1. Introduction

Solving the inverse problem in voice production, i.e., estimating vocal fold properties (geometry, stiffness, and position) and the subglottal pressure from the produced voice, has many important applications. In the clinic, currently diagnosis of voice disorders relies heavily on the experience of the physician. A physics-based voice inversion system would allow clinicians to better evaluate the underlying physiological state of the vocal system, thus improving diagnosis of voice disorders. Voice inversion would also provide insight into physiologic control of voice in the communication of linguistic and paralinguistic information, and may provide a means to monitor the emotional state of the speaker. Such information on the physiologic control of voice may also be used as inputs to physically-based speech synthesis systems for natural speech synthesis (Zhang, 2016a).

Previous studies often solved the inverse problem through optimization of vocal fold properties that minimizes the difference between target voice production and voice production predicted by a voice production model (e.g., Dollinger et al., 2002; Hadwin et al., 2016, 2019; Gómez et al., 2018). Such an optimization-based voice inversion approach often requires a very large number of voice production simulations during voice inversion in order to find the optimized solution. As a result, this approach is currently limited to lumped-element models of phonation, or more recently a two-dimensional phonation model, due to their fast computational speed.

A different approach is to use neural networks to directly map voice production output to physiologic parameters of the vocal system. Unlike optimization which often involves a large number of numerical simulations of voice production, neural networks, once trained, do not require voice production simulations at the time of voice inversion and thus are computationally much more efficient than optimization (Gomez et al., 2019). Due to the lack of reliable methods to measure vocal fold geometry and stiffness in humans, this approach will have to rely on data generated from computer simulations in the foreseeable future. For example, using a long short-term memory network, Gomez et al. (2019) estimated the subglottal pressure from vocal fold trajectory data generated from a two-mass vocal fold model. They showed that their neural network can achieve performance similar to that by optimization.

Ideally, toward practical applications, three-dimensional continuum models of voice production with realistic, directly measurable model parameters should be used, particularly for clinical applications. However, the high computational cost associated with three-dimensional simulations has prevented their use in voice inversion systems based on either optimization or machine learning.

We have recently developed a reduced-order three-dimensional continuum body-cover model of voice production (Zhang, 2016b, 2017), and a large dataset of voice production data is available from a series of ongoing large-scale parametric simulations using this model (Zhang, 2017, 2018). The goal of the present study is to explore the feasibility of applying neural networks to this large set of simulation data to estimate vocal fold properties (geometry, stiffness, and position) and the subglottal pressure from the produced acoustics. Unlike lumped-element models parameterized by masses and springs which are of less clinical interest, this three-dimensional model is parameterized by realistic, directly measurable vocal fold properties, such as length, thickness, depth, transverse and longitudinal stiffness, vocal fold approximation, and subglottal pressure. Unlike Gomez et al. (2019) which used vocal fold trajectory data to train their neural network, in this study we use extracted features of voice production as input to network training, with the hope that such carefully selected features would help the network better capture the relationship between model control parameters and voice production, in particular fine details that are perceptually important but may not be well represented in objective functions based on vocal fold trajectory or glottal area functions.

2. Method

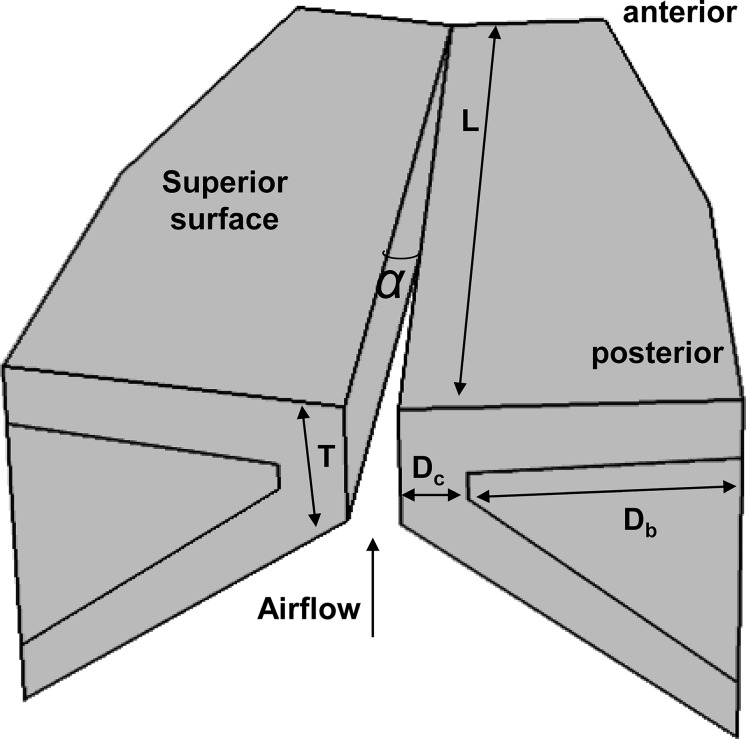
Data used for neural network training are from ongoing voice simulations using a three-dimensional, body-cover, continuum model of voice production (Zhang, 2016b, 2017). The reader is referred to these previous studies for details of the model. Briefly, the vocal fold is modeled as a transversely isotropic linear material with a plane of isotropy perpendicular to the longitudinal direction. The glottal flow is modeled as a one-dimensional quasi-steady flow taking into consideration of viscous loss. Simulations have been performed with parametric variations in nine model controls, including the vocal fold length L, medial surface vertical thickness T, medial-lateral depths of the body and cover layers D_b and D_c, initial glottal angle α controlling the degree of vocal fold approximation, transverse vocal fold stiffness in the coronal plane E_t, longitudinal vocal fold stiffness in the body and cover layers G_apb and G_apc, and the subglottal pressure P_s (Fig. 1). The ranges of parametric variation are listed in Table 1. These ranges are determined based on previous experiment and computational studies (Hollien and Curtis, 1960; Titze and Talkin, 1979; Hirano and Kakita, 1985; Alipour-Haghighi and Titze, 1991; Zhang, 2017, 2018). In total the dataset includes 162 000 simulations, each simulating a half-second voice production. Simulations that do not produce sustained phonation are excluded from this study, resulting in a total of 95 028 phonating conditions for this study.

Fig. 1.

Geometric control of the three-dimensional body-cover vocal fold model.

Table 1.

Ranges of parametric variations in the voice production model control parameters used to generate the dataset of this study.

Vocal fold length	L = [6, 10, 17] mm
Medial surface vertical thickness	T = [1, 2, 3, 4.5] mm
Depths of vocal fold cover and body layers	Dc = [1, 1.5] mm; Db = [4, 6, 8] mm
Initial glottal angle (vocal fold approximation)	α = [0, 1.6, 4]°
Transverse stiffness	Et = [1, 2, 4] kPa
Longitudinal stiffness in vocal fold cover and body layers	Gapc = [1, 10, 20, 30, 40] kPa; Gapb = [1, 10, 20, 30, 40] kPa
Subglottal pressure	Ps = 50–2400 Pa (18 values)

For each phonating simulation, voice features as listed in Table 2 are extracted from the output acoustics and glottal flow waveform. Initially, 11 features (set 1) are used, including fundamental frequency (F0), sound pressure level (SPL), closed quotient (CQ) of the glottal flow waveform, the amplitude differences between the first harmonic and the second harmonic (H1–H2), the fourth harmonic (H1–H4), the harmonic nearest 2 kHz (H1–H2 k), and the harmonic nearest 5 kHz (H1–H5 k) in the spectrum of the time derivative of the glottal flow waveform, the mean glottal flow rate (Qmean), perturbations in the period and peak amplitude of the glottal flow waveform (Zhang, 2018), and the maximum flow declination rate (MFDR). To improve voice inversion accuracy, two additional feature sets are added, including the maximum flow acceleration rate (MFAR), peak-to-peak amplitude of the glottal flow waveform (Qamp), cepstral peak prominence (CPP), harmonic to noise ratio (HNR), and subharmonic to harmonic ratio (SHR; Sun, 2002). We intentionally include only features that can be calculated from the output sound pressure alone, either directly or indirectly (e.g., glottal flow-based measures estimated from the output acoustics using inverse filtering), so that application of the trained network does not require data that may not be readily available outside the clinic (e.g., recordings of vocal fold vibration).

Table 2.

The three voice feature sets used in neural network training. See text for definition of individual features.

Set 1 (11 features)	Set 2 (13 features)	Set 3 (16 feature)
F0, SPL, CQ, H1–H2, H1–H4, H1–H2 k, H1–H5 k, Qmean, period perturbation, amplitude perturbation, MFDR	Set 1 + MFAR and Qamp	Set 2 + CPP, HNR, and SHR

The 95 028 conditions are first z-score normalized, and then randomly divided into three sets, each for training (70%, 66 520 conditions), validation (15%, 14 254 conditions), and testing (15%, 14 254 conditions), respectively. The training set of data, including both voice features and model controls, are used to train a feedforward neural network. Briefly, the network consists of an input layer (voice features), an output layer (estimated vocal fold properties or control parameters), and a number of hidden layers of interconnected neurons in between. Each neuron receives inputs from the preceding layer, transforms them using an activation function, and passes them as inputs to the next layer. The goal of the training process is to find parameters of the activation functions that minimize the difference between the target output and the network estimate in the training data. In other words, the training process is similar to conventional curve fitting, except that with an increasing number of hidden layers the neural network is able to curve fit increasingly complex nonlinear processes such as phonation. For a review of neural networks and their applications in acoustics and speech, the reader is referred to Bianco et al. (2019) and King et al. (2007). In this study, we experiment with neural networks of one, two, and three hidden layers, all with a hyperbolic tangent activation function. Each network is trained using the Levenberg-Marquardt algorithm, using the matlab Deep Learning Toolbox.

The performance of the neural network on the testing dataset is evaluated by the mean absolute error (MAE) or the average absolute differences between the target outputs (truth) and the network estimations, and the Pearson product-moment correlation between the target and estimated values. The Pearson product-moment correlation r (referred to correlation below) between a target output vector t and an estimation vector e is calculated as

$$r=\frac{\sum _{i=1}^n(t_i-\overline{t})(e_i-\overline{e})}{\sqrt{\sum _{i=1}^n{(t_i-\overline{t})}^2}\sqrt{\sum _{i=1}^n{(e_i-\overline{e})}^2}},$$ (1)

where n = 14 254 is the number of conditions in the testing dataset, and the bar indicates the mean value averaged over the 14 254 conditions in the testing dataset. The use of MAE instead of the root mean squared error is to facilitate comparison to results from previous studies (e.g., Gomez et al., 2019). In this study, the performance trends are similar whether they are evaluated using MAEs or root mean squared errors.

3. Results

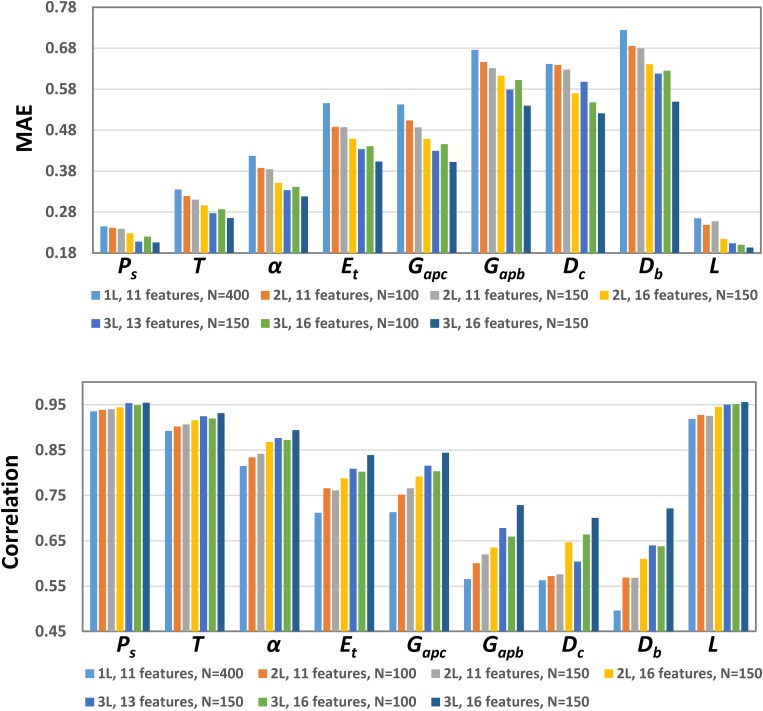
Figure 2 shows the MAE and correlation for different network configurations and feature sets used. In general, more hidden layers and more voice features lead to reduced MAE and increased correlation. The improvement is the most noticeable when the number of hidden layers is increased. Due to constraints of computational resources we are not able to train neural networks with four or more hidden layers. An increase in the number of neurons in each layer appears to have only a small improvement, and in some cases even slightly increases the MAEs on the testing dataset. Note that due to z-score normalization, the MAEs are mean-variance normalized.

Fig. 2.

(Color online) MAE and correlation for each of the nine model parameters using neural networks of different number of hidden layers (1 L, 2 L, 3 L), number of voice features, and number of neurons in each hidden layer (N).

Figure 2 also shows that estimations of the subglottal pressure, vertical thickness, and vocal fold length consistently have much lower MAEs and higher correlations than other control parameters, with MAEs around 0.25 and correlations above 0.93. In contrast, the MAEs are much higher for vocal fold stiffness, both transverse and longitudinal, and vocal fold depths. In particular, properties (stiffness and depth) associated with the body layer consistently have higher MAEs than those of the cover layer. These trends of the estimation accuracy are consistent across different network configurations.

Table 3 shows the best performance, i.e., highest correlation and lowest MAE, achieved in this study for the nine control parameters, obtained using a three-hidden layer neural network with 150 neurons in each hidden layer and 16 voice features (set 3 in Table 2). Note again that the MAE is mean-variance normalized. Table 3 also shows the MAE in real unit, to facilitate a more straightforward evaluation of the voice inversion performance, and as a percentage of the range of variation of the corresponding control parameter listed in Table 1. The MAE is generally within 15% of the range of variation of the corresponding control parameter, except for vocal fold depths and body-layer longitudinal stiffness, and is significantly lower for the subglottal pressure, vertical thickness, and vocal fold length, all of which are below about 9% of the range investigated. While better accuracy is clearly preferred, this accuracy allows at least monitoring the general trends of changes in vocal fold properties (e.g., consistent use of higher subglottal pressure or excessive thickening of the vocal folds), which often is more important than estimating the exact values (e.g., improving the MAE for the subglottal pressure from 137 Pa to 10 Pa likely will not affect clinical diagnosis or treatment plans).

Table 3.

Best estimation performance for the nine model control parameters.

Model control parameter	Correlation	MAE	MAE (real unit)	MAE (% of range)
Subglottal pressure Ps	0.954	0.206	137.3 (Pa)	5.8%
Vertical thickness T	0.931	0.265	0.32 (mm)	9.2%
Initial glottal angle α	0.894	0.318	0.51 (degree)	12.7%
Transverse stiffness Et	0.839	0.403	0.49 (kPa)	16.2%
Longitudinal stiffness, cover layer Gapc	0.844	0.402	5.33 (kPa)	13.7%
Longitudinal stiffness, body layer Gapb	0.729	0.539	7.18 (kPa)	18.4%
Cover layer depth Dc	0.700	0.521	0.12 (mm)	23.3%
Body layer depth Db	0.721	0.549	0.79 (mm)	19.8%
Vocal fold length L	0.956	0.183	0.86 (mm)	7.8%

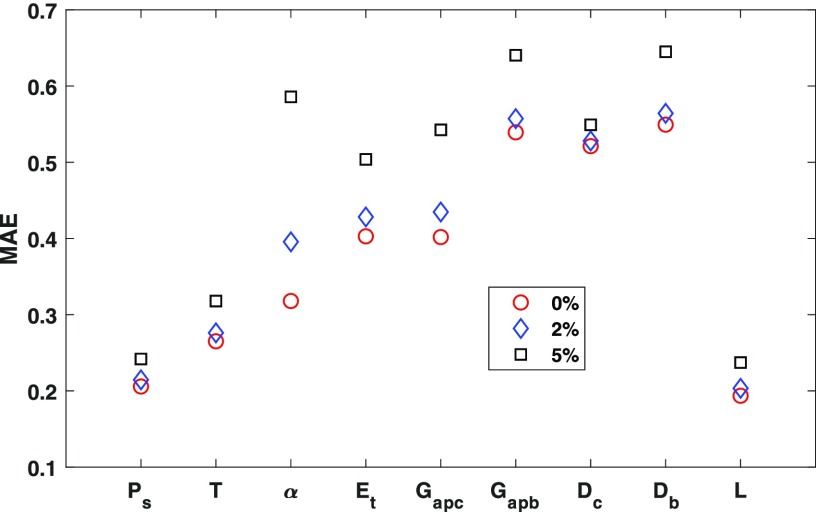
Speech recording is often contaminated by measurement noise during data collection. To evaluate the effect of noise on network performance, Gaussian noise with a standard deviation equivalent to 2% and 5% of the standard deviation of the corresponding voice feature in the entire dataset is added to the testing data. Figure 3 shows the MAEs for the nine control parameters under these noise conditions. In general, the effect of the added noise is smaller for control parameters (P_s, T, and L) with a small MAE in the absence of noise, but it is much larger for control parameters with an already high MAE in the absence of noise.

Fig. 3.

(Color online) The effect of added noise in the testing dataset on the MAEs for the nine control parameters, for a 3-hidden layer neural network with 150 neurons in each hidden layer and 16 voice features (set 3 in Table 2).

4. Comparison to human larynx experiment

To evaluate how well the trained network performs when applied to data generated by other models, voice feature data are extracted from sound pressure data obtained from a phonating excised human larynx (female, age 54). The larynx was adducted by tightening the arytenoid cartilages together using sutures attached to the muscular processes, which completely closed the cartilaginous glottal gap but left a small membranous glottal gap. During the experiment, the airflow was increased in steps and at each step the radiated sound pressure, the mean glottal flow, and the mean subglottal pressure were recorded. After the phonation experiment, the adducted larynx was scanned using magnetic resonance imaging (MRI) to determine its length, thickness, medial-lateral depths of the body layer (the thyroarytenoid muscle) and cover layer (lamina propria), and the initial glottal angle (estimated from the resting glottal area), similar to that in Wu and Zhang (2019). Unfortunately, no mechanical testing was performed in the experiment. Voice features (set 3) as listed in Table 2 are extracted from the recorded sound pressure at each step. Since no vocal tract was attached and no instantaneous glottal flow rate measurement was made during the experiment, the glottal volume flow is obtained by first calculating the sound source from the sound pressure assuming a monopole sound source model and then integrating the sound source. The extracted voice features are then used as input to the trained neural network to estimate control parameters.

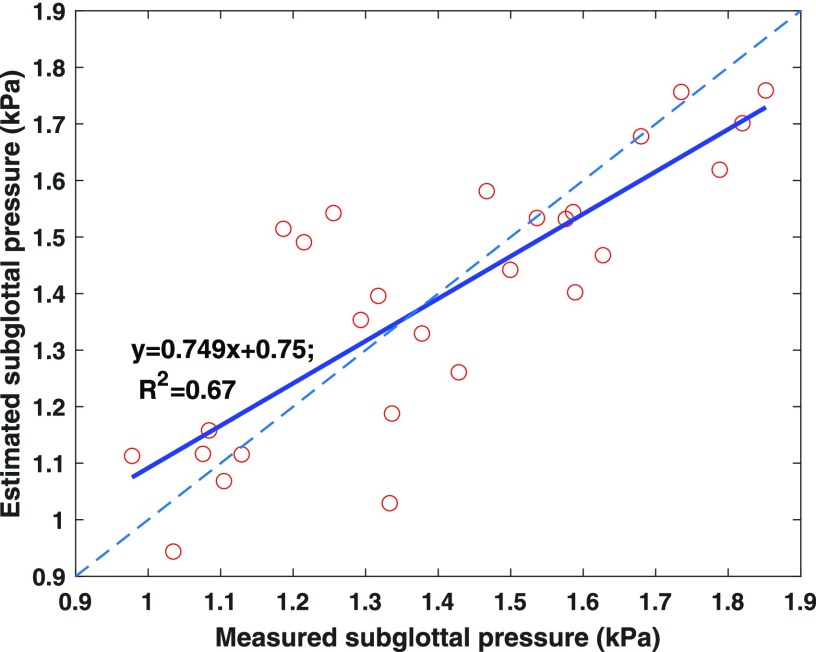
Figure 4 compares the estimated and measured subglottal pressures. Overall the estimated subglottal pressure follows closely the measured subglottal pressure. The average absolute difference between estimation and measurement is 115 Pa with a standard deviation of 95 Pa. The estimated geometric control parameters are generally close to their values from MRI measurement. The estimated vocal fold length is 15.5 mm, slightly larger than the membranous length of 14.3 mm from MRI. The initial glottal angle is 0.96°, smaller than 1.57° from the MRI measurement. The estimated depths of the cover and body layers are 1.4 and 5.8 mm, compared to the MRI measurement of 1.0 and 5.2 mm, respectively. One exception is that the estimated vertical thickness, 2.4 mm, is much larger than the 1.0 mm from MRI.

Fig. 4.

(Color online) Comparison between experimentally measured subglottal pressure and the subglottal pressure estimated from the trained network (3-hidden layer, 150 neurons in each layer, and 16 voice features). The solid line indicates linear regression between the estimated and measured subglottal pressure with the linear regression equation and the R² value. The dashed line is a line through the origin with a slope of 1.

5. Discussion and conclusion

The goal of this study is to explore the feasibility of combining neural networks with three-dimensional vocal fold modeling to infer realistic, directly measurable properties of the vocal system such as vocal fold geometry and stiffness, vocal fold approximation, and the subglottal pressure. Our results show reasonable accuracy that allows us to at least qualitatively infer from voice acoustics how vocal fold posture changes during voice production, which often is sufficient in many applications in which it is more important to monitor the trend of changes rather than the absolute amount of changes. The comparison between network estimation and excised human larynx experiment also suggests that networks trained using data from our computational model may be applicable to human phonation. While much work is required to improve estimation accuracy, we believe this approach has the potential to be useful in the clinic and other speech technology applications.

The contributions of this study include combining three-dimensional phonation modeling with neural networks, and the use of a small number of selected voice features instead of the large amount of vocal fold trajectory data used in previous studies. The advantage of neural networks over optimization methods is that once the neural network is trained, voice inversion does not require additional voice production simulations, which otherwise could be very time consuming especially if three-dimensional models are used for practical applications. The use of the three-dimensional models allows us to estimate realistic physiological variables that can be manipulated in the clinic. With the current approach, the neural network can be continuously improved by including more voice conditions, both healthy and pathological, whenever new simulation data become available, or refining the model by adding more physiological controls. We expect the same approach can be applied to data generated from subject-specific vocal fold models based on realistic vocal fold geometry (e.g., geometry based on MRI or computed tomography; Wu and Zhang, 2019), thus moving one step closer toward clinical applications.

Compared with the study by Gomez et al. (2019) which used vocal fold trajectory data to train their neural networks, in the present study we use pre-selected voice features, which has significantly reduced the amount of input data (16 features compared to thousands of vocal fold trajectory data points) and improved the training efficiency. The sets of voice features include many features that have been shown to be perceptually relevant (Kreiman et al., 2014). Use of these voice features in the training would thus facilitate the neural network to focus on perceptually-relevant relationship between voice acoustics and model control parameters. Although vocal fold trajectory or the glottal area function as extracted from high-speed imaging of vocal fold vibration is often used in previous voice inversion studies, voice inversion based on the entire waveforms may overlook fine details (e.g., glottal closure pattern) of the waveform that are perceptually important but may not be well represented in the objective function.

As far as we know, there have been no prior studies attempting to estimate both vocal fold geometry and stiffness as well as the subglottal pressure in a three-dimensional vocal fold model. Nevertheless, the estimation accuracy of this study is lower than those in previous studies using lumped-element models or two-dimensional vocal fold models. For example, Gomez et al. (2019) reported a MAE of slightly less than 80 Pa, which compares with the MAE of 137.3 Pa in the testing dataset and 115 Pa in the excised larynx experiment of this study. Hadwin et al. (2019) reported an even higher accuracy (3% for most parameters, and a maximal differences of 9.6%) between experiments and their predictions based on a two-dimensional vocal fold model. One important factor that may have contributed to the relatively high MAEs in our study is that while the training data set we use is large, it may still be relatively small in order to estimate nine model control parameters, considering that only 16 voice features from each condition are fed into the network. Also, the training data are obtained from parametric simulations with a small number of parametric values for each model parameters (e.g., three values for the initial glottal angle and transverse stiffness, two values only for the cover layer depth). It is reasonable to expect the voice inversion performance to significantly improve when training data at more intermediate values of vocal fold geometry and stiffness are included and more voice features are extracted, particularly for vocal fold depths and transverse stiffness.

The results also show that some properties, e.g., vocal fold stiffness and depths, are inherently more difficult to estimate than others. This is consistent with the findings in our previous studies on the cause-effect relation between vocal fold properties and voice production (Zhang, 2016b, 2017). These studies showed that the subglottal pressure and vertical thickness have consistent global effects on voice production, particularly the voice features used in this study, whereas the effect of vocal fold stiffness, particularly the longitudinal stiffness, is generally inconsistent and varies depending on the values of other vocal fold control parameters. One future goal is thus to identify voice features that would allow better inference of vocal fold stiffness and depth. Although in this study we only consider features that can be derived from the sound pressure alone, it is possible that inclusion of kinematic information based on recordings of vocal fold vibration, which is often available in the clinic, will significantly increase estimation accuracy, as demonstrated in Hadwin et al. (2019). On the other hand, if the stiffness and body depth have inconsistent effects on perceptually relevant acoustic measures, accurate estimation of these properties are likely to be less important in clinical applications.

Although our study shows reasonable agreement between network estimate and experiment, a more systematic comparison to human larynx experiments is required to better understand the performance of the trained network in difference voice conditions and how to improve the transferability of the trained network to human phonation, which will be the focus of future work.