Abstract
The Generalized Born with Molecular Volume (GBMV2) implicit solvent model provides an accurate description of molecular volume and has the potential to accurately describe the conformational equilibria of structured and disordered proteins. However, its broader application has been limited by the computational cost and poor scaling in parallel computing. Here, we report an efficient implementation of both the electrostatic and surface area (SA) components of GBMV2/SA on Graphics Processing Unit (GPU) within the CHARMM/OpenMM module. The GPU-GBMV2/SA is numerically equivalent to the original CPU-GBMV2/SA. The GPU acceleration offers ~60 to 70-fold speedup on a single NVIDIA TITAN X (Pascal) graphics card for molecular dynamic simulations of both folded and unstructured proteins of various sizes. The current implementation can be further optimized to achieve even greater acceleration with minimal reduction on the numerical accuracy. The successful development of GPU-GBMV2/SA greatly facilitates its application to biomolecular simulations and paves the way for further development the implicit solvent methodology.
Keywords: CHARMM, Generalized Born, OpenMM, protein conformation, solvation
Graphic abstract
Implicit solvent arguable provides an optimal balance between efficiency and accuracy for simulating large-scale conformational transitions of biomolecules. A GPU-accelerated version of one of the best implicit solvent models, GBMV2/SA, has been implemented in CHARMM/OpenMM program, offering ~60 to 70-fold speedup on a single GPU. The GPU-GBMV2/SA will greatly facilitate its application to biomolecular simulations in general.
Introduction
It is crucial to provide an accurate description of the solvent environment during biomolecular simulations, where the solvent plays a vital role in governing the conformational fluctuations and transitions.1–3 Conventionally, explicit solvent models provide a relatively detailed and accurate description on interactions between the solvent molecules and solutes, and are regarded as standard approaches to explore the influence of solvent on the solute molecule.4 However, it dramatically increases the computational cost of a simulation, and the solvent friction further adds to the difficulty of sampling the solute conformations. Implicit solvent is a viable alternative that captures the effective influence of solvent on the solute by direct estimation of the solvation free energy as a function of the solute coordinates.5 Implicit treatment of solvent substantially reduces the system size, thus allowing significant reduction of computational cost and faster sampling of solute conformations.6–10
There are many approaches for estimating the solvation free energy in implicit solvent treatment, including the Poisson-Boltzmann (PB) and generalized Born (GB) models. Both PB and GB are based on continuum electrostatics treatment of solvent environment.11–15 Compared with the PB model, the GB approximation allows the analytical evaluation of molecular forces and is more suitable for molecular dynamics (MD) simulations. The most important task in GB models is to evaluate the effective Born radius of each atom, which is dependent on all solute coordinates. GB models can be numerically equivalent to the underlying PB calculations, given accurate effective Born radii.5, 14 Numerous approaches have been developed for efficient calculations of effective Born radii, including the Fast Analytical Continuum Treatment of Solvation (FACTS)16, the Generalized Born Surface Area from Onufriev, Bashford, and Case (GBSA/OBC)17, Analytical Generalized Born plus NonPolar 2 (AGBNP2)18, and numerical integration-based ones such as the Generalized Born with Simple Smoothing function (GBSW)19–21 and Generalized Born with molecular volume22–29 models. The GBMV2 model, in particular, contains an analytical approximation of the Lee-Richards molecular volume and avoids unphysical solvent-inaccessible high dielectric protein interior regions.23–24, 29–30 It can reproduce the first solvent peak in the potentials of mean force (PMFs) of interactions between polar chemical groups.21 A comparison of several implicit solvent models has also suggested that the GBMV2 model provides the best agreement with the experimental data, such as hydration free energies of small molecules.31–32 Recently, it was demonstrated that an optimized GBMV2 model could provide a reliable description of both folded and unfolded protein conformations. 29 In particular, it shows minimal over-compaction bias in simulation of disordered proteins frequently associated with many implicit and explicit solvent protein force fields.29, 33–36 A key limitation to broader application of GBMV2, however, is that it is ~10 times slower than vacuum calculations and scales poorly to parallel multi-core executions.
One powerful technique to improve the efficiency is the use of graphics processing units (GPUs) that can have thousands of parallel processing cores. GPU-accelerated algorithms available in many MD engines, such as CHARMM37, AMBER38–39, GROMACS40, NAMD41–42, and OpenMM43, have offered up to two orders of magnitude speedup over traditional CPU-based codes. Some efforts have also been made on the GPU acceleration of GB implicit solvent models. The GB/OBC model in Amber has been implemented and achieved routine microsecond molecular dynamics simulations.44 The GBSW model has also been implemented in a CHARMM/OpenMM module that displays around 100-fold improvement on the efficiency while maintaining similar numerical accuracy.45 Notably, these early implementations only include the electrostatic solvation energy and thus might not be directly deployed for biomolecular simulations without the contribution of nonpolar solvation energy. Recently, an efficient pair-wise approximation of the solvent accessible surface area (SASA) was added into the GBSA/OBC GPU model, albeit with limited accuracy.46 The correlation between atomic SASAs calculated by the GPU model and exact numerical results varies significantly from the 0.54 to 0.91 for a number of test proteins.
Here, we report the implementation of an efficient GPU-accelerated GBMV2/SA algorithm in a CHARMM/OpenMM module. The implementation takes advantage of the similarities between GBMV2 and GBSW algorithms and builds on several existing kernels of the GPU-GBSW module. The numerical scheme for computing Born radii also allows for implementation of an efficient algorithm for calculating atomic surface areas. Together, the current implementation provides a complete realization of the GBMV2/SA model on GPUs, making it appropriate for general MD simulations of biomolecules. In the below sections of this paper, the detailed methodologies of GPU-GBMV2/SA algorithm are discussed in Section II, including the treatment of electrostatic and nonpolar solvation contributions, the lookup table algorithm for efficient volume integration, and the scheme of GPU implementations. Key points of the original GBMV2 model are highlighted. In the Results and Discussion Section III, the accuracy and efficiency of GPU-GBMV2/SA are benchmarked against the CPU-GBMV2/SA implementation, and the remaining computational bottlenecks are also discussed. Finally, the conclusions and an outlook towards future work are given in Section IV.
Method
In GB models, the total solvation free energy is generally divided into electrostatic and nonpolar contributions,
| (1) |
where the nonpolar component involves the free energy cost of creating the solute cavity in the solvent and turning on the nonpolar solute-solvent interaction, and the electrostatic component corresponds to the free energy cost of the subsequent step of charging up the solute.9 The nonpolar contribution is often estimated directly from SASA, even though it has been shown that this approximation limited its ability to capture conformational dependence of the nonpolar free energy.9, 47–48
Electrostatic solvation free energy and forces
The GB approximation developed by Still and coworkers49 allows the electrostatic energy to be written as a pairwise summation,
| (2) |
where qi and are the atomic charge and effective Born radius of the atom i, respectively, and Ks is an empirical constant that is set to 8 in the GBMV2 model.23–24 which provides an effective description of the salt screening effects with κ being a Debye-Hückel screening parameter.50 The effective Born radius is defined as the radius of an equivalent spherical cavity that yields the same atomic self-polarization free energy. It is thus a function of the positions of all solute atoms. The pair-wise GB expression allows analytical evaluation of atomic forces and is thus particularly suitable for MD simulations.
The GB forces with respect to the atomic positions include two terms,
| (3) |
where
| (4) |
| (5) |
It can be seen from Eqs. (2–5) that the GB energy and forces depend on the effective Born radii, , and their derivatives with respect to atomic positions, .
Born radii and their derivatives
Computing the effective Born radius of each solute atom is the key step for calculating the GB electrostatic solvation free energy. In GBMV2 model, the calculation of a given Born radius considers the contributions from the Coulomb field approximation and an empirical high-order correction term:
| (6) |
| (7) |
where P1 and P2 are empirical fitting coefficients, Ri are atomic coordinates, and V(r) is the molecular volume function.23–24 Optimal values of P1 and P2 are obtained by linear regression fitting of atomic GB radii of model proteins to the reference values obtained from high-resolution PB calculations.19–21, 29 Detailed expressions for derivatives of Born radii are given in the Supporting Information (SI).
Numerical integration
The important component of computing Born radius is to evaluate the 3-dimension integrals shown in the Eq. (7). In the GBMV2 and GBSW models, the integrals are evaluated using numerical quadrature, where they are split up into radial and angular components.19, 23–24 The radial integral is approximated by Riemann-Stieltjes summation with the standard set of radial grid points, while the angular integral is calculated by the Lebedev quadrature.
| (8) |
where is the weight of each grid point rmn and is an effective integration starting point less than the van der Waals (vdW) radius of each atom, in order to avoid the singularity of integrals. It is noted that the precise definition of the (solute) molecular volume in Eq. (8) is a key quantity in determining the Born radii. The vdW-like volume employed in GBSW is simple and efficient to evaluate, and it provides stable forces.19 However, it generates small and unphysical solvent-inaccessible high dielectric regions inside the solute, leading to an over-estimation of solvation free energy and a systematic over-stabilization of nonspecific compact conformations.20–21 This critical shortcoming is effectively solved by adopting an approximate Lee-Richards molecular volume in GBMV2.
Analytical approximation of the molecular volume
The molecular volume (MV) is defined as the solute volume that is formed by rolling a water probe on the solute.30 Two methods have been previously implemented in the CPU version of GBMV2.23–24 One is to use arbitrarily precise numerical grids for a highly accurate calculation of Born radii; but this method is computationally expensive, does not provide an analytical gradient, and thus is not suitable for efficient MD simulations. The other method introduces an efficient analytical approximation to the MV with comparable precision of calculating Born radii, which is also suitable for GPU acceleration. The molecular volume is given by a Fermi-Dirac switching function from a preprocessed “raw” molecular volume, S(r),
| (9) |
where β and λ are the parameters that represent the width and midpoint of the switching function, respectively.
The expression of S(r) in the GBMV2 model involved two terms,
| (10) |
where SvdW (r) is the vdW volume contribution and SMV2(r) includes a vector-based scaling term to account for the discrepancy between vdW and MV volumes. There are two significant points: One is that the atomic volume function, FMV2 (r), has a longer tail compared to the FvdW (r), in order to probe more overlap regions between atoms. The other is that the representation of MV. For the vdW volume, because SvdW (r) is a monotonic function with the number of atoms, the summation can be immediately terminated when its value exceeds a certain cutoff. SMV2(r), however, contains vector-based scaling approximation (VSA) term that helps to distinguish the “gap” (between atoms) and “open” (otherwise) regions, which is required to consider all atoms in proximity. As such, GBMV2 is considerably more expensive that GBSW, especially for small systems.
Additional details of the GBMV2 algorithms can be found in the SI equations and the original paper.24 Importantly, from Eq. (10) it can be seen that the next step is to calculate the S(r) at each numerical integration grid point (Eq. 8), which can be accelerated by a lookup table algorithm.
SASA nonpolar solvation free energy and forces
The nonpolar energy can be decomposed into a short-range repulsive energy and long-range solute-solvent dispersion energy, and is, in the first order approximation, proportional to SASA.9, 24 Thus, the nonpolar energy in the GBMV2 model is estimated as,
| (11) |
where the γi and Ai is the effective surface tension coefficient and SASA of each atom, respectively. The surface coefficient is often assumed to be same for all atom types, reducing Eq. (11) to . This linear approximation has been shown to provide an adequate description of nonpolar solvation energy for many biomolecular applications. 9, 24
The atomic SASA can be expressed as:
| (12) |
where the excluded volume involves volumes for all atoms except for atom i, and the smooth function f represents the exposed rate at r point, which should be one if the excluded volume is zero, and it should be zero if the sum of excluded volume is one. In the GBMV2/SA model, an analytic expression of the vdW volume is used,
| (13) |
the uj and exposed function f are written as,
| (14) |
| (15) |
where is the vdW radius of j atom and Rw is the radius of solvent molecule, for the water molecule, which is 1.4 Å. The switching widths, and , have been optimized to 1.2 and 1.5 Å, respectively, for Rw = 1.4 Å.
The general integral of Eq. (12) cannot be solved analytically. However, a straightforward numerical expression is given as follows,
| (16) |
where the excluded molecular volume at each grid point is determined quickly by the lookup table algorithm described below. Detailed derivations of the nonpolar energy and forces term can be found in the SI.
Lookup table algorithm
The numerical volume integrations in GBMV2 (and GBSW) require quick access of all atoms within a certain distance that could contribute to the volume function. This is enabled by constructing a lookup table.19, 23–24 Specifically, the lookup table contains a spatially uniform cubic grid enclosing all solute atoms. At each grid point, all the atoms that are less than a certain distance, Rmax, are stored in a lookup table array,
| (17) |
where c is the width of the grid cell, the value 2.1 Å is the length of the tail of the atomic function FMV2 (r), and Rbuffer is an adjustable length that determines how far any atom can move before rebuilding the lookup table. The default value of Rbuffer is zero, meaning the lookup table will be updated at each simulation step. By using the lookup procedure, the cost of computing the molecular volumes is reduced to linear scaling with the number of the grid points. It is noted that the number of neighbor atoms at each grid point is much larger in GBMV2 than GBSW due to the longer tail of atomic function, which contributes to a two to three-fold computational cost increase.
Parallelization and CUDA implementation
The existing GBSW kernels were adapted for the implementation of GPU-GBMV2/SA. As a plugin of CHARMM/OpenMM program, the overall design of the GPU-GBSW model is considered as a stand-alone solvent model in the OpenMM library.45 It contains eight kernels, four of which are used to implement the lookup table, and the other four are used to calculate the electrostatic solvation energies and forces of hydrogen and non-hydrogen atoms. Kernels to support the lookup table were directly modified to support a larger value of Rmax and the greater table depth required for GBMV2. In GBMV2, hydrogens have non-zero input radii and do not need to be treated separately. As such, the GBMV2 electrostatic term only requires three kernels (see Table 1). A new kernel, calcSASA, was developed to calculate atomic SASA and forces. The GPU algorithm for computing SASA terms is similar, where the number of blocks is equal to the number of atoms and threads loop over all quadrature integration grip points. Note that the calcSASA kernel is an independent kernel that can be used for both GPU-GBMV2 and GPU-GBSW models. Pseudo codes illustrating GPU algorithms for computing the electrostatic solvation energies and forces are provided in the SI. Similar algorithms are implemented for the calculations of nonpolar solvation energies and forces, and the pseudo codes thus not provided. A difference between the current implementation and previous GBSW CUDA plugin is that 256 threads are used to loop over all quadrature points per block, which provides optimal computational efficiency in our tests. Another difference is that the Born radii gradients are not saved, because the number of contributing atoms is much larger due to the longer tail of atomic volume function (2.6 Å in GBMV2 vs. 0.3 Å in GBSW). Instead, compact intermediate arrays are saved in the global memory to reduce the computational complexity and cost of electrostatic solvation forces (see the pseudo code in SI “CUDA algorithm for computing the electrostatic solvation forces”, arrays S, S, X1, X2, X3, and X4).
Table 1.
Layout of key kernels for GPU GBMV2/SA. Kernels for lookup table are similar to those used in GPU GBSW45 and thus not listed.
| Kernels | Description |
|---|---|
| calcBornR | To calculate the Born radius of each atom and save the temporary variables for the rapid calculations of the electrostatic forces. Each block is assigned to one atom, and 256 threads are used to loop over all the grid points. The equations can be found in the electrostatic energies part of SI. |
| computeGBMVForce | To calculate the GB electrostatic energies and the derivatives with respect to atomic coordinates. |
| reduceGBMVForce | To calculate the electrostatic forces. Each block is assigned to one atom, and 256 threads are used to loop all the grid points. The equations can be found in the electrostatic force part of SI. |
| calcSASA | To calculate the nonpolar energies and forces. Each block is assigned to one atom, and 256 threads are used to loop all the grid points. The equations can be found in Eqs. (12–16) and nonpolar force part of SI. |
Computational details
The correctness and accuracy of GPU-GBMV2/SA were mainly assessed by its ability to reproduce atomic energies and forces of the original CPU-GBMV2/SA implementation in CHARMM as well as PB-derived atomic self-solvation free energies. The model systems include the set of 22 small proteins previously used for the numerical parametrization of the original GBSW and GBMV models.21, 24 The accuracy of GPU-GBMV2/SA was also validated by examining the interaction energy profiles between selected sidechains, in comparison to explicit solvent results from previous works.20–21 The numerical stability of the GPU-GBMV2/SA model was assessed by examining the energy conservation properties under different configurations. Furthermore, a small helical model peptide, (AAQAA)5, was used to examine the stability of GPU-GBMV2/SA in long-time MD simulations and its ability to recapitulate the peptide conformational equilibrium. For this purpose, two distinct initial structures, an ideal helix and a fully extended conformation, were used to initiate independent control and folding simulations, allowing a rigorous diagnosis of convergence. A time step of 2 fs was used. The previously optimized GBMV2/SA protein force field29 was used and the results were directly compared with those from CPU simulations.
The efficiency of the GPU versus CPU versions of GBMV2/SA was benchmarked using five folded proteins ranging from 856 to 77,304 atoms as well as an intrinsically disordered protein, the N-terminal transactivation domain (TAD) of p53 (926 atoms). The initial structures of folded proteins were downloaded from the Protein Data Bank (PDB) and then energy minimized followed by 5,000 steps of NVT equilibration. The initial structure of p53-TAD was taken from a previous study.33 Default GBMV2/SA parameters were used in all calculations, except for three keywords, beta = −12, P3 = 0.65, P6 = 8, which correspond to β, S0, and Ks, in Eq. 2 and 9, respectively. The atomic input radii are from the previously optimized GBMV2 force field.29 The cutoff distance for nonbonded interactions was set at 20 Å and a time step of 2 fs was used. All GPU simulations were done on an NVIDIA TITAN X (Pascal) graphics card, and CPU calculations were carried out on an Intel Xeon E5–2620 v4 2.10GHz CPU. Performance of key GPU kernels was analyzed using the nvvp and nvprof tools. The result reports are provided in Figure S1, which includes threads per block, registers per thread, and theoretical vs. achieved occupancy etc.
Results and Discussion
Electrostatic solvation energies and forces
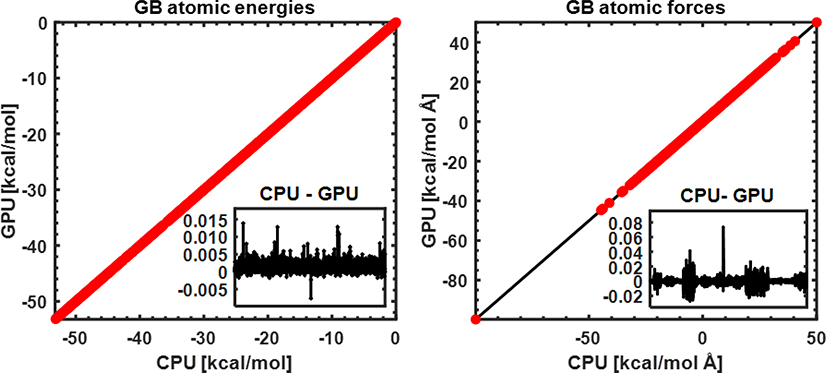
Proper GPU implementation of the GBMV2 is first assessed by its ability to reproduce the atomic electrostatic self-solvation energies and forces. As summarized in Figure 1, atomic self-solvation energies and forces of all 22 small proteins are essentially identical between the GPU and original CPU implementations. The numerical differences between CPU and GPU results (see inserts) are extremely small, completely negligible compared to the absolute GB electrostatic energies and forces. This demonstrates that the electrostatic solvation term of GPU-GBMV2/SA has been implemented correctly in the CUDA platform.
Figure 1.
Accuracy of GPU-GBMV2/SA atomic electrostatic self-solvation energies (left) and forces (right), compared with those of CPU-GBMV2. The diagonal line (y=x) is shown for reference. All atoms of 22 small proteins are included in this comparison. The inserted panels show the difference between CPU and GPU results (in the same unit, kcal/mol or kcal/mol Å for each of all atoms from the protein test set.
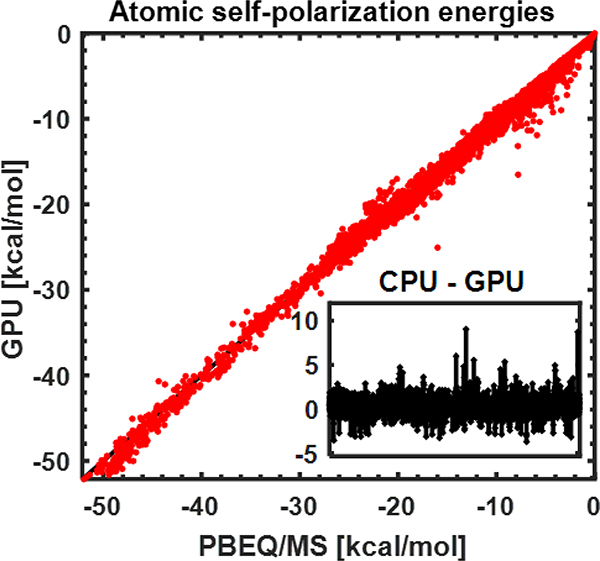
We also validated that atomic self-solvation energies provided by GPU-GBMV2 are consistent with PB-derived results, which is a key indicator of the quality of a GB implicit solvent model. Given the numerical equivalence of GPU- and CPU-GBMV2 models, GPU-GBMV2 should achieve a similar correlation with PB. Indeed, as summarized in Figure 2, the correlation coefficient between effective Born radii derived from PB and GPU-GBMV2 is 0.9985, consistent with the results of CPU-GBMV2.24 We note that the superb ability of GBMV2 to reproduce PB is attributed to both the higher order correction to the Coulomb field approximation (Eq. 7) and effective approximation of SMV (Eq. 10).24
Figure 2.
Atomic electrostatic self-solvation energies derived from GPU-GBMV2 versus PB. All atoms from 22 small proteins are included. The insert shows the difference for each atom.
Nonpolar solvation energy and forces
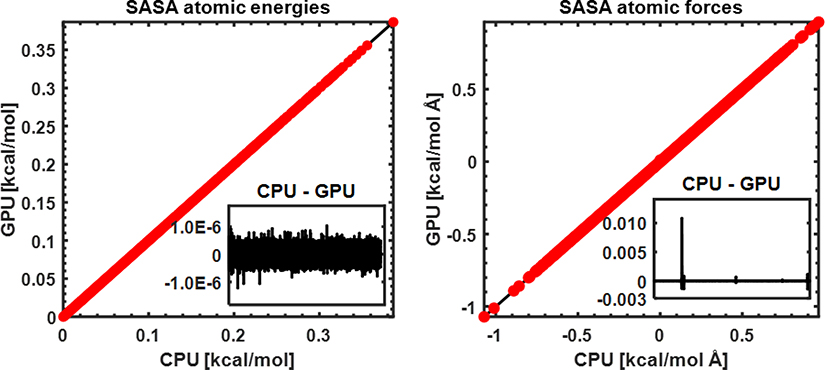
Nonpolar solvation energy plays important roles in driving the conformations of proteins, although it makes smaller contributions to the total solvation energies compared to the GB term. Figure 3 shows that the nonpolar energies and forces of GPU-GBMV2/SA are also numerically equivalent to those calculated by the original CPU-GBMV2/SA, indicating that both SASA energies and forces have been implemented in the present CUDA platform correctly. As such, it can be expected that the errors of nonpolar energies are on the order of 1 – 2% comparing with the exact SASA analytic model for proteins.24 The successful implementation of the SASA term in the CUDA platform provides a complete GPU-GBMV2/SA implicit solvent model that can now be readily deployed for biomolecular simulations. In addition, it also paves the way for the future development of better nonpolar solvation models, such as by including the dispersion contribution.9
Figure 3.
The accuracy of GPU and CPU-GBMV2/SA in calculating atomic SASA energies (left) and forces (right). The surface tension coefficient is 5 cal/mol Å2. All atoms from 22 small proteins are included. The inserted panels show the difference between CPU and GPU results (in the same unit, kcal/mol or kcal/mol/Å for each of all atoms from the protein test set.
Energy conservation and numerical stability
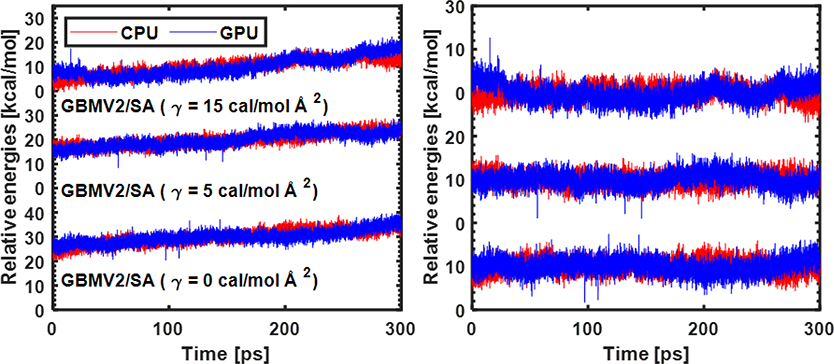
After establishing the correctness of the GPU implementation, we evaluated the numerical stability of GBMV2/SA by examining the energy conservation properties in NVE simulations with three different surface tension parameters (γ). As summarized in Figure 4, the energies from CPU and GPU calculations display similar trends for all three cases, suggesting that the GPU version has similar numerical stability compared to the CPU version. The energy drifts over 300 ps are significant, but in line with a previous analysis of the numerical stability of GBMV2 on CPU.25 The energy fluctuations in GPU calculations (after removing the linear drift) are slightly higher than those in CPU runs, likely due to the use of mixed single/double precisions. Comparison of the energy conservation properties from simulations with different γ show that SASA as implemented is numerically highly stable. We note that GBMV2 is numerically less stable compared to GBSW because of the sharp molecular surface definition as well as the VSA term. Nonetheless, peptide simulations suggest that GBMV2 can be reliable even with a 2 fs time step with a proper thermostat in NVT simulations, showing no sign of numerical instabilities or any significant artifacts in the resulting trajectories.29
Figure 4.
Energy conservation of MD simulations for a small protein (PDB: 1BDC) in CPU- and GPU-GBMV2/SA. Energies versus simulation time before (left) and after (right) removing the linear drift. The time step was set to 1 fs. The relative CPU/GPU energy drift rates are 0.0072/0.0085, 0.0048/0.0068 and 0.0071/0.0110 (unit: % / ps) for three cases (γ = 0, 5, 15 cal / mol Å2), respectively. The standard fluctuations of CPU/GPU energies (after removing the linear drift) are 1.5434/1.5942, 1.4566/1.5963, and 1.5934/2.0047 kcal/mol), for three cases, respectively. Only the last 100 ps trajectories were included in the energy drift analysis.
Sidechain interaction and peptide folding simulations
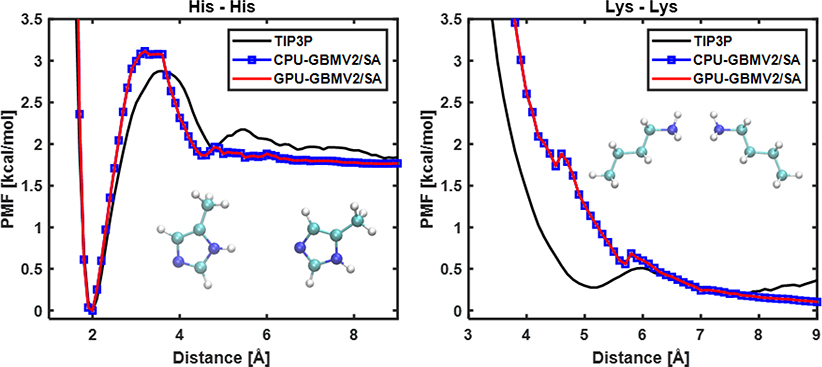
Before applying GPU-GBMV2/SA to protein simulations, we first validated its ability to accurately describe interactions between various backbone and side chain chemical groups. The balance of these interactions governs the ability of a force field to properly capture the protein conformational equilibria. Figure 5 compares the free energy profiles of two representative sidechains pairs. It demonstrates that GPU-GBMV2/SA exactly reproduce CPU-GBMV2/SA as expected, and the implicit solvent results also closely match the profiles derived from free energy calculations in TIP3P explicit solvent.20
Figure 5.
Free energy profiles of interactions for two sidechain pairs, (left) His – His and (right) Lys – Lys, in TIP3P, CPU- and GPU-GBMV2/SA solvent. γ = 5 cal/mol Å2 was used.
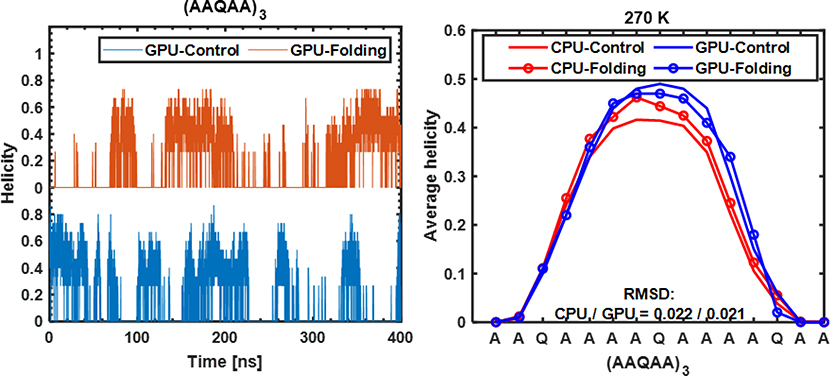
The peptide (AAQAA)3 has been widely used as a model flexible peptide for force field evaluation and calibration.20–21, 29 Figure 6 shows the time evolution of helicity of (AAQAA)3 during two independent control and folding simulations at 270 K in GPU-GBMV2/SA. It can be observed that several reversible conformational transitions between the (partial) helices and unfolded structures were sampled in both simulations within 200 ns, indicating that the implicit treatment of solvent using the GBMV2/SA model greatly facilitates protein conformational sampling without the friction from explicit solvent molecules. The resulting average residue helicity profiles are well- converged; the RMSD value between results from control and folding GPU runs are only 0.021. These results are comparable to results derived from previous replica exchange simulations on a CPU platform.29
Figure 6.
Left: Helicity of (AAQAA)3 during folding and control GPU-GBMV2/SA simulations at 270 K. Right: Average residue helicity profiles calculated from GPU simulations in comparison with previous results derived from CPU simulations.26 The RMSD values shown are the root-mean-square differences between profiles derived from control and folding simulations.
Computational efficiency
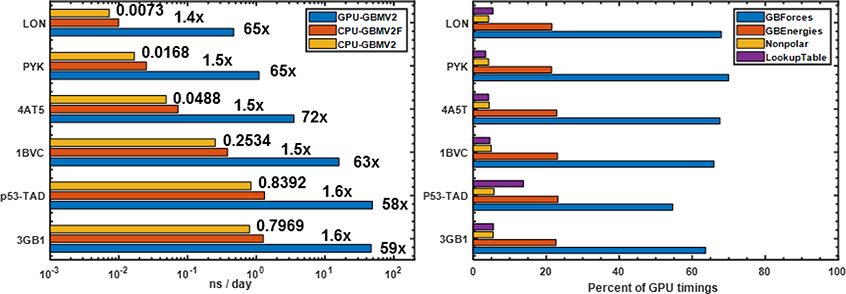
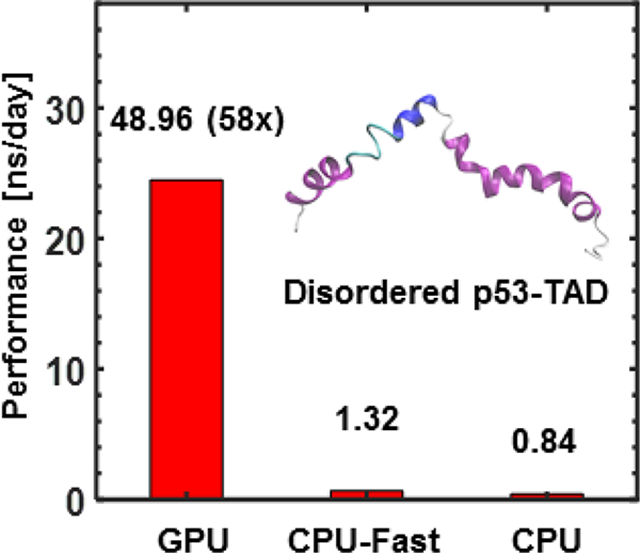
Figure 7 summarizes the performance of GPU-GBMV2/SA in comparison to the CPU version for six folded and unfolded proteins of various sizes and topologies. It shows that the GPU version offers ~ 60 to 70-fold speed up, with the larger systems exhibiting slightly superior efficiency. We note that a faster version of CPU-GBMV2/SA has been previously developed,25 which extensively utilizes pre-calculated data arrays to speed up the evaluation of Born radii and derivatives. Our current testing shows that the fast CPU version is ~50% more efficient than the standard one. We also note that the current multi-core parallel implementation of GBMV2/SA scales poorly beyond over 8 cores, with the speedup maxing out ~6X using 16 Intel Xeon E5–2620 v4 2.10GHz CPU cores (see Table S1). We have also profiled the timing distribution of each kernel in GPU-GBMV2/SA. The four kernels associated with the lookup table account for only ~5% of the time, although it is memory-intensive. The calculations of electrostatic and nonpolar terms take up around 85% and 7% of the total time, respectively. Thus, the bottleneck of the GBMV2/SA algorithm is clearly the calculation of Born radii and their derivatives. The reason is that the calculation of the Born radius for each atom involves a complicated expression based on around 800 numerical quadrature points and 100 neighbor atoms for each grid point; the derivatives of Born radii involve even more extensive operations (see detailed expressions in the SI). Consequently, the GB force calculations are about three-fold slower than the GB energies calculations.
Figure 7.
(Left) Timings of CPU- and GPU-GBMV2/SA simulations. The numbers next to the CPU-GBMV2/SA bars are the production time in ns/day, and the ratios next to the fast CPU-GBMV2/SA and GPU-GBMV2/SA are folds of speedup compared to CPU-GBMV2/SA. The production rates of GPU simulations are (in ns/day): 47.00 (3GB1), 48.96 (p53-TAD), 15.93 (1BVC), 3.52 (4AT5), 1.10 (PYK) and 0.47 (LON). (Right) Percentages of time spent in various parts of GPU-GBMV2/SA calculation, including constructing and updating the lookup table (“Lookup Table”), nonpolar energies and forces (“Nonpolar”) and electrostatic energies and forces calculations (“GBEnergies” and “GBForces”). The GPU and CPU calculations were done on one NVIDIA TITAN X (Pascal) and one core of Intel Xeon E5–2620 v4 2.10GHz CPU, respectively.
Conclusion
A GPU-accelerated GBMV2/SA model has been implemented within the CHARMM/OpenMM interface, including both the GB electrostatic and SASA nonpolar solvation terms. The GB term has been implemented based on the existing CUDA kernels of the GPU-GBSW model.42 Together with a SASA nonpolar term, it provides a complete and accurate GBMV2/SA implicit solvent model that is suitable for protein simulations. Results show that the GPU-GBMV2/SA solvation energies and forces are essentially the same as those in the original CPU-GBMV2/SA model with negligible errors, giving rise to similar energy conservation properties. Benchmarks based on a set of folded and unfolded proteins show that the current implementation of GPU-GBMV2/SA offers about 60 to 70-fold speedup on a single NVIDIA TITAN X graphics card compared to a single core of an Intel Xeon E5–2620 v4 2.10GHz CPU. While the speedup is somewhat modest compared to those achieved by GBSW or GBSA/OBC in Amber, it is still quite substantial and will enable the application of GBMV2 for MD of larger systems and for longer timescales. for both folded and unfolded proteins.
We note that there is still room for further improvement of the computational efficiency of GPU-GBMV2/SA. For example, a key bottleneck is the large lookup table required for evaluating the volume integrals due to longer tails required for analytical approximation of MV. The numbers of atoms within the proximity of each grid point can be as high as ~100. It is likely that the list can be truncated without significant reduction to the numerical accuracy. One can also optimize the usage of computational memory of lookup table array, e.g., by using the flexible allocation or avoiding the allocation by looping neighbor grid boxes. Development of the GPU-GBMV2/SA algorithm will also allow one to perform extensive folding simulations of model proteins and peptides to critically evaluate the ability of the simple SASA nonpolar model for describing the conformation equilibria.9 This will pave the way for further development of better treatments of the nonpolar solvation that can more accurately capture the conformational dependence of solvation free energies.
Supplementary Material
Acknowledgment
This work was supported by National Science Foundation (MCB 1817332 to JC) and National Institutes of Health (R35 GM130587 to CLB and R35GM126948 to MF).
Reference
- 1.Vaiana SM; Manno M; Emanuele A; Palma-Vittorelli MB; Palma MU, J Biol Phys 2001, 27 (2–3), 133–145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ponder JW; Case DA, Adv Protein Chem 2003, 66, 27–85. [DOI] [PubMed] [Google Scholar]
- 3.Mackerell AD, J. Comput. Chem. 2004, 25 (13), 1584–1604. [DOI] [PubMed] [Google Scholar]
- 4.Wagoner J; Baker NA, J. Comput. Chem. 2004, 25 (13), 1623–9. [DOI] [PubMed] [Google Scholar]
- 5.Onufriev A; Case DA; Bashford D, J Comput Chem 2002, 23 (14), 1297–1304. [DOI] [PubMed] [Google Scholar]
- 6.Cramer CJ; Truhlar DG, Chem. Rev. 1999, 99 (8), 2161–2200. [DOI] [PubMed] [Google Scholar]
- 7.Roux B; Simonson T, Biophys Chem 1999, 78 (1–2), 1–20. [DOI] [PubMed] [Google Scholar]
- 8.Feig M; Brooks CL, Curr. Opin. Struct. Biol. 2004, 14 (2), 217–224. [DOI] [PubMed] [Google Scholar]
- 9.Chen J; Brooks CL, Phys Chem Chem Phys 2008, 10 (4), 471–481. [DOI] [PubMed] [Google Scholar]
- 10.Chen JH; Brooks CL; Khandogin J, Curr Opin Struc Biol 2008, 18 (2), 140–148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Baker NA, Curr. Opin. Struct. Biol. 2005, 15 (2), 137–43. [DOI] [PubMed] [Google Scholar]
- 12.Gilson MK; Davis ME; Luty BA; Mccammon JA, J Phys Chem-Us 1993, 97 (14), 3591–3600. [Google Scholar]
- 13.Nicholls A; Honig B, J. Comput. Chem. 1991, 12 (4), 435–445. [Google Scholar]
- 14.Bashford D; Case DA, Annu Rev Phys Chem 2000, 51, 129–152. [DOI] [PubMed] [Google Scholar]
- 15.Tsui V; Case DA, Biopolymers 2001, 56 (4), 275–291. [DOI] [PubMed] [Google Scholar]
- 16.Haberthur U; Caflisch A, J Comput Chem 2008, 29 (5), 701–715. [DOI] [PubMed] [Google Scholar]
- 17.Onufriev A; Bashford D; Case DA, Proteins 2004, 55 (2), 383–394. [DOI] [PubMed] [Google Scholar]
- 18.Gallicchio E; Paris K; Levy RM, J Chem Theory Comput 2009, 5 (9), 2544–2564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Im WP; Lee MS; Brooks CL, J. Comput. Chem. 2003, 24 (14), 1691–1702. [DOI] [PubMed] [Google Scholar]
- 20.Chen JH; Im WP; Brooks CL, J Am Chem Soc 2006, 128 (11), 3728–3736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chen JH, J Chem Theory Comput 2010, 6 (9), 2790–2803. [DOI] [PubMed] [Google Scholar]
- 22.Ghosh A; Rapp CS; Friesner RA, J Phys Chem B 1998, 102 (52), 10983–10990. [Google Scholar]
- 23.Lee MS; Salsbury FR; Brooks CL, J. Chem. Phys. 2002, 116 (24), 10606–10614. [Google Scholar]
- 24.Lee MS; Feig M; Salsbury FR; Brooks CL, J. Comput. Chem. 2003, 24 (11), 1348–1356. [DOI] [PubMed] [Google Scholar]
- 25.Chocholousova J; Feig M, J. Comput. Chem. 2006, 27 (6), 719–729. [DOI] [PubMed] [Google Scholar]
- 26.Mongan J; Simmerling C; McCammon JA; Case DA; Onufriev A, J Chem Theory Comput 2007, 3 (1), 156–169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Nguyen H; Roe D; Simmerling C, Abstr Pap Am Chem S 2012, 244. [Google Scholar]
- 28.Nguyen H; Roe DR; Simmerling C, J Chem Theory Comput 2013, 9 (4), 2020–2034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lee KH; Chen JH, J. Comput. Chem. 2017, 38 (16), 1332–1341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Richards FM, Annu Rev Biophys Bio 1977, 6, 151–176. [DOI] [PubMed] [Google Scholar]
- 31.Juneja A; Ito M; Nilsson L, J Chem Theory Comput 2013, 9 (1), 834–846. [DOI] [PubMed] [Google Scholar]
- 32.Knight JL; Brooks CL, J Comput Chem 2011, 32 (13), 2909–2923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Liu XR; Chen JH, J Chem Theory Comput 2019, 15 (8), 4708–4720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Best RB; Zheng WW; Mittal J, J Chem Theory Comput 2014, 10 (11), 5113–5124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Piana S; Klepeis JL; Shaw DE, Curr Opin Struc Biol 2014, 24, 98–105. [DOI] [PubMed] [Google Scholar]
- 36.Piana S; Donchev AG; Robustelli P; Shaw DE, J Phys Chem B 2015, 119 (16), 5113–5123. [DOI] [PubMed] [Google Scholar]
- 37.Brooks BR; Brooks CL; Mackerell AD; Nilsson L; Petrella RJ; Roux B; Won Y; Archontis G; Bartels C; Boresch S; Caflisch A; Caves L; Cui Q; Dinner AR; Feig M; Fischer S; Gao J; Hodoscek M; Im W; Kuczera K; Lazaridis T; Ma J; Ovchinnikov V; Paci E; Pastor RW; Post CB; Pu JZ; Schaefer M; Tidor B; Venable RM; Woodcock HL; Wu X; Yang W; York DM; Karplus M, J. Comput. Chem. 2009, 30 (10), 1545–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Case DA; Cheatham TE; Darden T; Gohlke H; Luo R; Merz KM; Onufriev A; Simmerling C; Wang B; Woods RJ, J Comput Chem 2005, 26 (16), 1668–1688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Salomon-Ferrer R; Gotz AW; Poole D; Le Grand S; Walker RC, J Chem Theory Comput 2013, 9 (9), 3878–3888. [DOI] [PubMed] [Google Scholar]
- 40.Hess B; Kutzner C; van der Spoel D; Lindahl E, J Chem Theory Comput 2008, 4 (3), 435–447. [DOI] [PubMed] [Google Scholar]
- 41.Phillips JC; Braun R; Wang W; Gumbart J; Tajkhorshid E; Villa E; Chipot C; Skeel RD; Kale L; Schulten K, J Comput Chem 2005, 26 (16), 1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Tanner DE; Phillips JC; Schulten K, J Chem Theory Comput 2012, 8 (7), 2521–2530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Eastman P; Friedrichs MS; Chodera JD; Radmer RJ; Bruns CM; Ku JP; Beauchamp KA; Lane TJ; Wang LP; Shukla D; Tye T; Houston M; Stich T; Klein C; Shirts MR; Pande VS, J Chem Theory Comput 2013, 9 (1), 461–469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Gotz AW; Williamson MJ; Xu D; Poole D; Le Grand S; Walker RC, J Chem Theory Comput 2012, 8 (5), 1542–1555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Arthur EJ; Brooks CL, J Comput Chem 2016, 37 (10), 927–939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Huang H; Simmerling C, J Chem Theory Comput 2018, 14 (11), 5797–5814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Levy RM; Zhang LY; Gallicchio E; Felts AK, J Am Chem Soc 2003, 125 (31), 9523–9530. [DOI] [PubMed] [Google Scholar]
- 48.Chen JH; Brooks CL, J Am Chem Soc 2007, 129 (9), 2444-+. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Still WC; Tempczyk A; Hawley RC; Hendrickson T, J. Am. Chem. Soc. 1990, 112 (16), 6127–6129. [Google Scholar]
- 50.Srinivasan J; Trevathan MW; Beroza P; Case DA, Theor. Chem. Acc. 1999, 101 (6), 426–434. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.