Allelic Heterogeneity in Genetic Association Meta-Analysis: An Application to DTNBP1 and Schizophrenia

Abstract

Background/Aims:

Meta-analysis of genetic association studies is a useful approach when individual investigations do not yield studywise significant results but the evidence across studies is modest and homogeneous. Current meta-analysis methods account for heterogeneity by down-weighting studies as a function of between-study variance. We contend that current approaches may obscure interesting phenomena in genetic association data. However, an appropriate approach to examining heterogeneity across studies is lacking.

Methods:

We develop a novel approach, based on the EM algorithm, to detect allelic heterogeneity, identify subpopulations and assign studies to those subpopulations. We then apply these methods to the association between DTNBP1 and schizophrenia (Scz), one of the most studied relationships in complex disease genetics. We examined 32 published and unpublished population and family-based association studies containing up to 14 SNPs spanning the DTNBP1 locus.

Results:

We explored heterogeneity in several ways including meta-regression and approaches aimed at exploring the mixture of heterogeneous studies at a particular SNP. We found significant evidence for a mixture of association distributions at multiple loci.

Conclusion:

We propose a novel approach that is broadly applicable and may be useful in large scale genetic association meta-analyses to detect significant allelic heterogeneity.

Introduction

Replication is the sine qua non for establishing an association between a particular gene or variant and a complex disease [1, 2]. Support for this requirement has been bolstered by the rise of genomewide association studies (GWAS) and the subsequent realization that even in adequately powered samples, the relative rank of true signals may not permit their easy recognition [3]. In instances where several or more studies have generated equivocal or modest results, meta-analysis may be used to provide ample power to detect true positive signals [4]. However, such approaches assume etiologic homogeneity and may miss true effects in the presence of even modest between-study heterogeneity [5].

Assessment of heterogeneity is part of nearly all meta-analytic procedures. Generally, heterogeneity is perceived as a difficulty in meta-analysis and standard procedures account for its presence. Unlike in clinical trials, where it may indicate bias in underlying data, heterogeneity is a realistic expectation in genetic association studies [6, 7, 8]. A common pattern of extreme, early, contradictory results, often termed the Proteus effect, has been described in the context of genetic association studies [9].

A form of heterogeneity unique to genetic association studies is allelic heterogeneity, that is, non-random population-specific allelic effects. Lin and colleagues [10], in describing allelic heterogeneity, term it the ‘Flip-Flop' phenomenon and provide several examples. They explore, via simulation, several models which can explain flip-flops. They conclude that flip-flops can be observed under intralocus interaction models and suggest that flip-flops are a real phenomenon between interacting loci in weak linkage disequilibrium. More recently, Zaykin [11] presented a set of reasonable scenarios under which allelic heterogeneity can be generated, due to underlying haplotypic heterogeneity, without varying linkage disequilibrium between markers. This phenomenon has been observed in Drosophila by Gruber and colleagues [12] who chronicle their experience with an initially-replicated association between achaete-scute complex polymorphisms and a bristle number quantitative trait. Subsequent to their initial finding in an isogenic strain and replication in a wild-caught sample, they attempted replication in a laboratory-kept but out-bred sample. In this sample, they found a significant result in the opposite direction. In an attempt to understand these results, they tested the association in an additional wild-caught sample and found no association. They discuss several possible explanations for this result including linkage disequilibrium, sampling variation, and gene-gene or gene-environment interaction.

An important, but unanswered question regarding meta-analysis of genetic association data is whether these methods can deal effectively with allelic heterogeneity − that is different alleles at the same locus having true associations with the disease in distinct populations. A key feature of standard meta-analytic approaches is their ability to account for heterogeneity when present and validly combine odds ratios allowing for heterogeneity. While it is important to account for usual sources of heterogeneity (diagnosis, ethnicity, mode of ascertainment, etc.), it remains unclear how to provide power in meta-analyses where allelic effects at a particular variant are significantly nonzero but in opposite directions in different samples. The current paradigm of a unit of replication precludes anything but loci with inter-population homogeneous effects [1]. Moreover, the level of heterogeneity at a locus may in itself be an interesting phenomenon [6], especially in instances where that heterogeneity is non-random. Importantly, current prima facie approaches to meta-analysis do not seek to detect, exploit or even explain this heterogeneity. We contend that allelic heterogeneity is a detectable and interesting phenomenon.

A particular well-studied complex disease-gene relationship is that between schizophrenia (Scz) and DTNBP1. Scz [MIM 181500] is a disease of complex etiology with a lifetime population prevalence approaching 1%. Genetic contributions to Scz have long been recognized. Consequently, the exact nature of this contribution has been investigated using a range of approaches with varying degrees of success. Through linkage and candidate gene association studies, hosts of potentially interesting regions have been identified. While a small handful of these have been replicated with differing degrees of success and some verified meta-analytically [13], one of the most interesting of these is the region on 6p22.3 including DTNBP1, the dystrobrevin binding protein 1 gene. This region of 6p22 and the DTNBP1 locus have both been subject to numerous attempts at replicating initial findings of linkage to Scz in a set of Irish multiplex Scz pedigrees [14] and the subsequent report of association with Scz from the same sample. To date, DTNBP1 is among the most studied Scz candidate genes [15].

An interesting feature of the DTNBP1-Scz results is the equivocal nature of the association at any single variant. Often one allele at a SNP is highly significantly associated in one sample while in other samples either no association is observed or an association is seen but with the other allele. Debate has emerged as to whether such an observation results from true signals and thereby represents a ‘true replication' − or result from chance and reflects a ‘non-replication'.

The picture using haplotypes is no clearer. Similar to results with single markers in DTNBP1, the haplotype data generates a muddled pattern of findings, with one set of haplotypes associated in one study but not in others. Such a pattern could be due to true haplotypic heterogeneity or systematic error in haplotype inference. Mutsuddi and colleagues [16], noting the confusing pattern of haplotypic heterogeneity at DTNBP1, explored the Hapmap CEPH haplotype structure and verified consistency with the haplotype frequencies in the literature indicating that systematic error in haplotype inference across the region is an unlikely source of the haplotypic heterogeneity. Given their observation, they conclude that the evidence for association in DTNBP1 with Scz is equivocal and unconvincing.

Methods

Sample

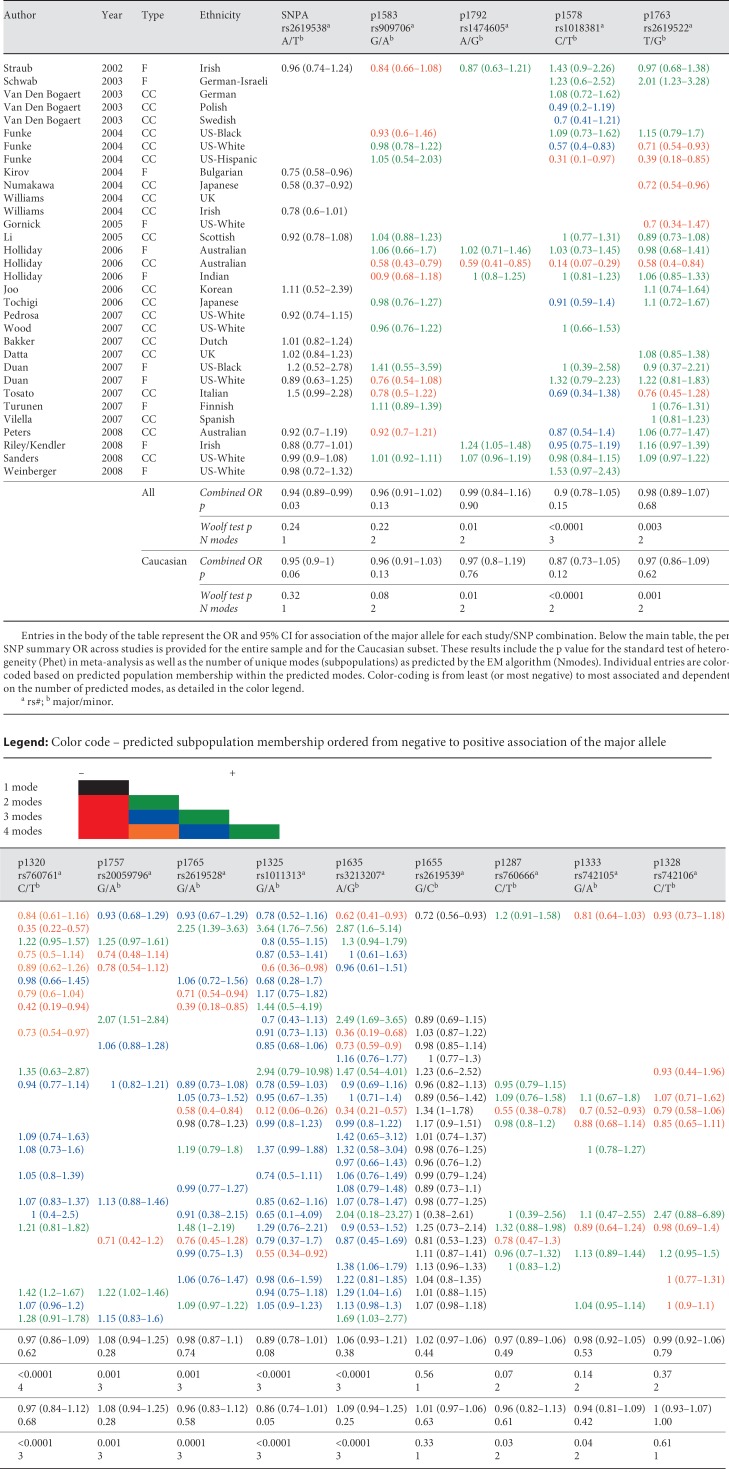
The 32 unique samples included in the present meta-analysis are summarized in table 1. Other than availability of appropriate summary data (either publication of case/control allele counts in population-based studies or transmission/non-transmission data for family-based studies, or availability of raw data), we had no inclusion/exclusion criteria. Raw genotype data were available to us from several family-based studies (Weinberger and colleagues [36], Turunen et al. [37], Straub et al. [29], Duan et al. [38]). In these instances we inferred missing genotypes within families using the gene-dropping [17] approach as implemented in the Merlin package [18]. Inferred genotypes were included in the analysis if the posterior genotype probability was greater than 95%. We included in the meta-analysis 14 SNPs across the DTNBP1 region that had been included in the original report of association. The SNPs span the DTNBP1 locus and are detailed in table 1. In all analyses, the major allele was considered as the target allele.

Table 1.

Results of meta-analysis and studies included

Published reports that used family or population-based methods to test for association and included sufficient raw data to complete a 2 × 2 (allele × case-control status) table were considered for pooling at each SNP via meta-analysis. Although population-based association studies generate concerns regarding population stratification, we included those studies in our combined analysis to bolster power since the bulk of studies of association with DTNBP1 use this approach.

In several of the studies, a transmission disequilibrium test (TDT) design was used in the meta-analysis [19]. In its simplest form (the biallelic case), the TDT tests the null hypothesis of no association by the McNemar test statistic for pairs of transmitted and nontransmitted alleles. Alternatively, one could test that the segregation ratio of the biallelic marker is 0.5 or, for the purpose of this analysis, that the odds ratio of transmission/non-transmission of a specific ‘target' allele to an affected individual equals 1. In other family-based studies, a haplotype-based haplotype relative risk (HHRR) design was used [20, 21]. This is a standard χ² statistic that uses all parental genotype information (heterozygous and homozygous parents). The HHRR statistic compares the number of times a given parental allele (‘target' allele) is transmitted versus non-transmitted. The test statistic is: χ² = [(a/a + c)/(b/b + d)], where a = transmissions of the target allele, c = non-transmissions of the target allele, b = transmissions of all other alleles and d = non-transmissions of all other alleles. The odds ratio is constructed as (a/c)/(b/d). The HHRR can lead to a more powerful statistical test for association than TDT because it uses more information (e.g., homozygous parents); however, under certain conditions, HHRR could be less powerful than the TDT [22]. In population-based samples, which compare case to control allele frequencies, we construct an odds ratio as (a/c)/(b/d) where a is the number of major alleles present in cases, c is the number of target alleles present in cases, b is the number of major alleles in controls and d is the number of target alleles present in controls. We used formal meta-analytic techniques to combine odds ratios across study types. The equivalence of odds ratios generated from family- and population-based studies has been previously addressed [23]. The issue is addressed in the present study by a formal test of the influence of study type on effect estimate in a meta-regression framework.

In order to derive a summary statistic for each SNP, a random-effects meta-analysis model, as described by DerSimonian and Laird [24], is applied to the available data. A random-effects model was selected because it includes both within- and between-study components of variance. Thus, because it will generally yield a wider confidence interval, the random-effects model is more conservative than a fixed-effects model [25]. A random-effects model is particularly germane for this study because between-study variation is expected due to genetic heterogeneity, diagnostic differences and differing ascertainment schemes between the studies. The common odds ratio is determined by:

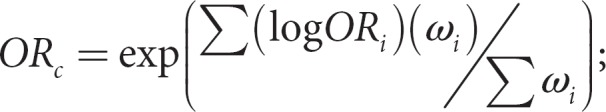
where OR_i is the odds ratio for study i and ω_i is the weight of the trial.

The variance of each trial is determined by the Woolf [26] simple method:

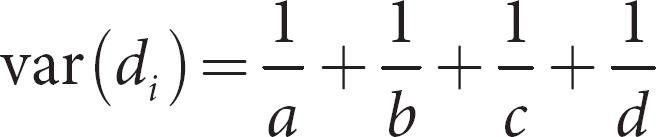
where d_i is the log(OR) for study I. For family-based studies a is the # transmissions of the major allele, b is the # transmissions of other alleles, c is the number of parental target alleles, and d is the number of other parental alleles.

The weight of each study was determined by:

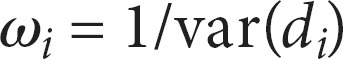
Prior to pooling, we performed a log likelihood χ² test of heterogeneity (Woolf's G) [27] to ensure that each group of studies was suitable for meta-analysis. The general form of Woolf's G is 2Σ [o_ilog(o_i/e_i)] where o_i and e_i are the observed and expected values in each respective cell. G approximates a y² distribution with degrees of freedom equal to one less than the number of studies included in the analysis. The results of the standard meta-analysis are presented in table 1 and online supplementary figures S1–S14 (www.karger.com/doi/10.1159/000264445).

Generally, in meta-analysis, when significant heterogeneity is found, the studies are deemed unsuitable for pooling without proper correction for the between-study variance component via random effects models. However, in meta-analysis of genetic association studies, it may be more interesting to examine the source of such heterogeneity.

In most of our secondary analyses, we dealt with log(OR) as a per study summary effect statistic because taking the natural logarithm of the odds ratio approximates a Gaussian distribution thus meeting the assumptions of most statistical procedures we applied.

We explored the relationship between log(OR) and target allele frequency primarily as a means of quality control. In instances where a target allele outlier was present, we eliminated that study/marker combination from further analysis. The relationship between per study minor allele frequency (MAF) and log(OR) was formally tested using weighted least squares regression, where the weight is equivalent to that used in meta-analysis (online suppl. table S1 and figures S15–S28). This allowed us to eliminate the possibility of a true effect combined with systematic allele misspecification as a potential source of the flip-flop phenomenon at the each of the markers. All analyses were conducted in the full dataset and in the Caucasian subset at each SNP.

Expectation-Maximization

The Expectation-Maximization (EM) algorithm is a frequently used approach for problems involving the maximization of functions of several variables. A particularly common use of the EM is the detection and parameter estimation of a mixture of Gaussian distributions. As stated previously, log(OR)s follow a Gaussian distribution. The log(OR)s generated meta-analytically also provide a variance estimate which is a function of the sample size. We use the log(OR)s and variance estimates as input into the EM algorithm to estimate the number of modes or mixtures in the distribution of log(OR)s for each SNP and the location of each of these modes. Mixtures of 1 through N studies-at-a-marker distributions were tested for each of the markers in both the entire dataset and in the Caucasian subset. We used a minimum of 100 random start values across the N possible modes per SNP. The mixture means, mixing proportions, and per study probability of mode membership were estimated and the likelihood of each model estimated. Models were compared to the null model (unimodality) by Akaike's Information Criterion (AIC). The EM approach seems to be generally consistent with the Woolf test of heterogeneity.

Meta-Regression

While demonstrating heterogeneity between studies is an important exercise, attempting to attribute this heterogeneity to measured covariates is an important step. We performed meta-regression to test the impact of several important covariates on log(OR) estimates using a weighted least squares regression model. In our model, we include per study weights as 1/($$), where τ² is the estimated between-study variance and $$ is the variance of the i-th study. We tested singly the influence of study design (family- vs. population-based), ethnicity (Caucasian vs. Non-Caucasian), and publication date on per study effect size. Study design was included to test for a systematic difference in effect size estimate between family- and population-based studies. This is especially important in this context since several of the family-based samples were ascertained as part of large multiplex pedigrees. Although not an explicit test of the influence of family history, this test provides some indication of the bias (heterogeneity) potentially induced by such samples at any given locus. Ethnicity tests were limited to the single Caucasian versus non-Caucasian test due to the small number of studies in any single non-Caucasian subset. The influence of publication date was assessed to test for a systematic reporting bias over time (online suppl. table S1).

We performed a series of weighted correlation analyses, in the Caucasian subset, of the between-marker log(OR)s. As stated previously, our analyses focus on the major allele as the ‘target' allele. This analysis allows us to compare the pattern of association relationships to the pattern of linkage disequilibrium across the locus. In addition, we calculated delta [28], which is the equivalent of the correlation coefficient of a 2 × 2 contingency table, using the Build 35, Release 21a phased founder haplotype data from the Caucasian of European Ancestry dataset of the HapMap project. For these calculations we again selected the ‘major' allele at each locus as the target allele. Importantly, since delta is not squared, the direction of the association between major alleles is maintained (online suppl. figure 29). Additional details of this analysis are presented in the supplement.

Simulation

We generated simulated study data to test our approaches to exploring marker heterogeneity. The simulated data comprised case and control allele data, generated under a range of allelic odds ratios, for multiple studies within each replicate. We simulated genetic heterogeneity at a given locus by generating subsets of studies with varying odds ratios. Among our heterogeneity models we simulated instances of allelic heterogeneity (i.e., true associations with differential allelic effects in subgroups of data). We also simulated models with a homogeneous effect across all studies and models with no effect across all studies to test the type I error rate of our approach.

Results

We examined 32 distinct studies with data on DTNBP1 and Scz using various subsets of the 14 markers reported in the original association study [29]. The studies included and the results of a standard meta-analysis are summarized in table 1. We present one set of results, with alleles reclassified for several studies where there were significant deviations from HapMap. The complement SNPs, SNPA and P1655, with minor allele frequencies >0.4 were especially problematic. The details of these reassignments are provided in the supplement. The analyses with obvious allele misassignments are presented as our primary analyses (table 1). As can be seen from table 1, SNPA is modestly significant when analyzed using traditional methods (p = 0.04). Forest plots for individual SNPs are presented in the supplement. Of importance, results for many of the markers are characterized by substantial heterogeneity using both standard tests (‘Woolf Test P' in table 1) and our novel approach to elucidating the mixture of studies at a particular allele. Importantly, under the null hypothesis of no allelic heterogeneity, we would expect a single distribution of studies.

We examined, using weighted least squares meta-regression on per study, per SNP log(OR), the influence of covariates (per study minor allele frequency, study design [family- vs. population-based], ethnicity and publication date) on effect size (online suppl. table S1). When significant, this test is considered at least a partial explanation of heterogeneity. After correction for multiple tests, we found evidence for a relationship between MAF and log(OR) at p1325 (p = 0.002) in the Caucasian subset and years since publication was also significant at p1320 in the full dataset (p = 0.006). For p1325 there is little variation in MAF so this is not driven by ethnic heterogeneity. The significant effect at p1320 reflects a trend toward association with the major allele in more recent studies.

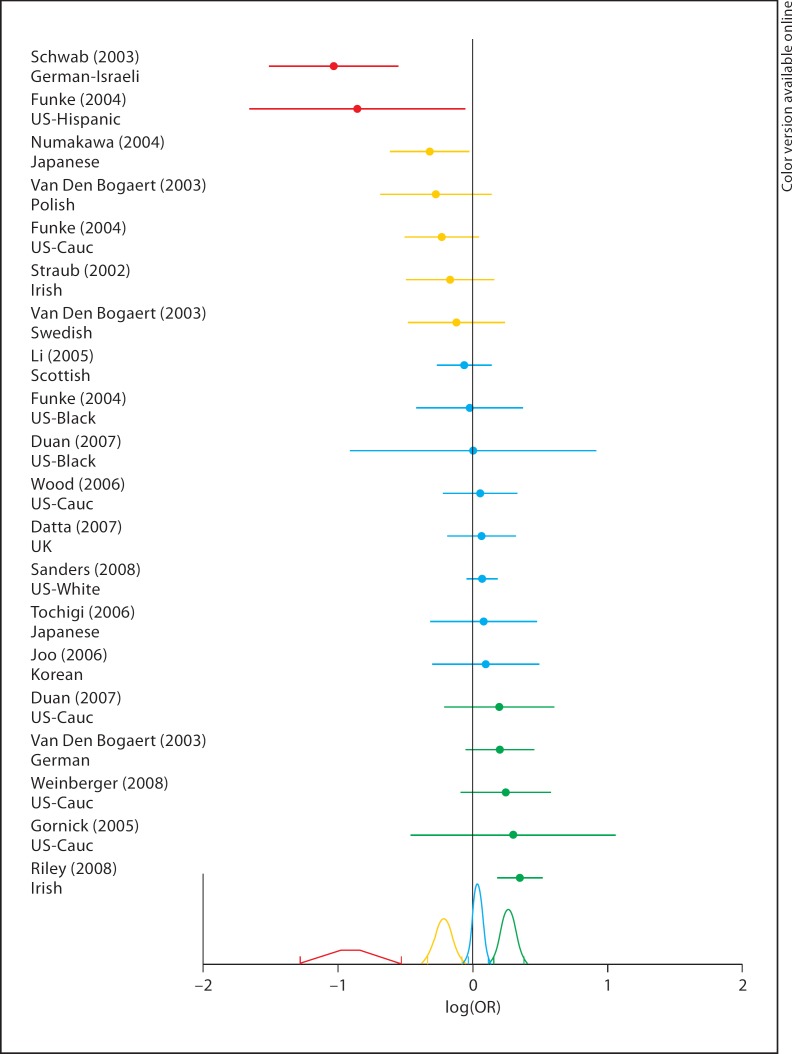
In addition to merely demonstrating cross-study heterogeneity of results at individual markers, we sought to further understand these results by assessing unimodality of the OR distribution across studies via the EM algorithm. Predicted group membership for each study at each SNP is summarized in table 1 as is the number of predicted modes for each SNP with group membership indicated by color. Only two of the 14 SNPs are predicted to have a single distribution. In Caucasians, 3 SNPs have this result. In addition, log(OR)s are plotted, along with the subpopulation distributions, under the best-fitting model from the EM, of the locations of the mixture modes for P1320 (fig. 1). It is clear from figure 1 that the data at P1320 contain 4 distinct subpopulations, 3 of which differ significantly from zero. These analyses provide evidence for significant allelic heterogeneity in the relationship between these SNPs and Scz and suggest that the conclusion of the traditional meta-analysis of no effect across 12 of these 14 SNPs is incorrect.

Fig. 1.

Per study/population log(OR) and 95% CI at SNP P1320 are presented ranked from negative to positive association of the major allele. Studies are color-coded based on predicted subpopulation membership via EM algorithm. Color-coded probability distributions for the predicted subpopulation effects (based on the combined log(OR) and variance) are plotted along the x-axis. Vertical colored ticks represent the upper and lower bounds of the 95% CIs for each distribution. In the print version, colors are replaced by different lines.

Discussion

The DTNBP1 locus, which codes for the dysbindin protein, has generated an inconsistent pattern of association results with Scz. The pattern observed in this gene-disease combination is not unique in the complex disease association literature and has been discussed by others. In an attempt to elucidate our understanding of the relationship between the DTNBP1 locus and Scz, we performed, in addition to standard meta-analytic procedures, a novel set of analyses on 32 distinct samples.

We found evidence for significant heterogeneity and distinct association subpopulations at multiple loci across the DTNBP1 region. While this is an important finding, understanding the source of such heterogeneity would require an investigation into the population history of the DTNBP1 region in each of the studies comprising the association subpopulations. Such an effort would be possible with dense genotype data from each of the studies. It is noteworthy, however, that this heterogeneity is not explainable by any obvious factor such as ethnicity.

In the context of genetic meta-analyses, heterogeneity has been identified as an interesting phenomenon and specific methods for its detection have been developed [6, 7]. Analytic decisions and even suitability for pooling are often determined based on the presence of significant heterogeneity [7]. The issue of allelic heterogeneity will play a more central role in the GWAS era as modest levels of heterogeneity will hamper the replication requirement. In fact, recent successes in replicated GWAS findings have formally demonstrated homogeneity [30, 31]. However, there is some confusion even on the approach to assessing heterogeneity in such large scale studies. For example, in large multi-center, multi-site studies, decisions regarding sample subdivision are difficult. Excess subdivision can induce statistical homogeneity by broadening the confidence intervals around individual studies while failure to do so may lead to pooling of heterogeneous subsamples [7]. In an attempt to address this concern, an approach to identifying meta-analysis datasets whose heterogeneity level may be overly influenced by one or a few samples has been proposed though its authors caution against its use as a post hoc approach to identifying heterogeneous subpopulations [32]. The approach we present addresses this problem and is uniquely suited to identifying and describing heterogeneous subpopulations. Our general approach is, we suggest, applicable to genomewide association data. Although applying our current approach in instances where there are no a priori subdivisions in the data will be challenging, such an approach is feasible.

While the GWAS era proceeds in identifying loci of modest but homogeneous effect, it is important to consider realistically our power to detect loci exhibiting allelic heterogeneity. As has been demonstrated previously, using standard approaches to association analysis, polymorphisms exhibiting realistic degrees of allelic heterogeneity are undetectable even in unrealistically large samples [33]. Thus, the association literature has largely progressed either ignoring allelic heterogeneity or writing it off as just another potential contributor to reduced marginal effects. There may be many interesting variants that exhibit allelic heterogeneity with respect to disease risk or trait variation that are being missed. Substantial methodology work should be done to develop methods that would allow for their detection.

Overall, we propose a useful framework for considering the information at a particular locus in an effort to advance toward gene-based testing [34]. Our approach to detecting and classifying homogeneous subsamples may permit detection of important genomic regions in the context of genomewide association meta analysis (GWAMA). A major weakness of GWAMA has been the inability of current approaches to classify significantly heterogeneous subsamples at particular markers. In the presence of true allelic heterogeneity, effects will be washed away by traditional combination of odds ratios. Some investigators suggest using approaches where p values are combined, using Fisher's method [35]. This approach has been generally viewed as anticonservative and overly influenced by single, highly significant studies. Under our approach, investigators will be able to identify heterogeneous subsets and with further development of the methodology that we are currently pursuing, conduct valid tests of association with each subset.