Modifiers and Subtype-Specific Analyses in Whole-Genome Association Studies: A Likelihood Framework

Abstract

Objective:

We propose new statistical methods for analyzing genetic case/control association data in which cases can be further classified into subtypes, for example, based on clinical features. The primary utility of our work is the ability to distinguish between subtype-specific and modifier effects of genetic variants within a single testing framework.

Methods:

A range of disease/subtype causal models are defined for genetic variants involving subtype-specific and modifier effects. We present a log-linear modeling framework enabling comparison between these causal models and selection of the best-fit model.

Results:

We evaluate and compare the analytic power and model selection performance of the proposed work with standard two-group-based association tests. Simulation studies demonstrate that our approach has similar or greater power than the traditional approach over a range of causal models. We also report empirical findings about the impact of misspecification of subtype frequency during model selection, and extend the application of the proposed work to the cross-disorder association studies of multiple diseases.

Conclusion:

Whether a variant is a disease risk factor, is subtype specific, or modifies disease features has important consequences for the interpretation and follow-up of genetic associations. Our framework provides a simple, systematic way to evaluate and describe associations involving such subtype-specific or modifier effects.

Introduction

The variability in clinical features observed for most complex genetic diseases is almost certainly due, at least in part, to genetic variation. Although there are potentially numerous scenarios by which diverse genetic influences could lead to phenotypic heterogeneity, two main possibilities exist. First, a genetic marker may confer risk for only a specific subtype of the disease. This subtype-specific susceptibility gene, present in a subset of cases, confers liability for a form of illness with a distinct clinical profile. Alternatively, clinical features such as age at onset or the presence or severity of specific symptoms may be altered by a modifier gene which does not impact risk for the disease itself [1]. By loose analogy, one might imagine that wearing a seat belt is not causally related to whether an individual has a car crash, but that it does modify whether the accident is fatal.

The distinction between a subtype-specific susceptibility gene and a modifier gene is meaningful in the attempt to understand the underlying genetic architecture of complex diseases and in selecting methods used to investigate these types of genes. Affected individuals ascertained for genetic case/control association studies are often classified into subtypes based on clinical or other related features. Common, generic examples of ways in which subjects are often classified include early disease onset [2], a positive family history [3], broad versus narrow phenotype definition [4], treatment responsiveness or resistance [5], and neurophysiological outcomes [6]. For specific diseases, classification by disease course, recurrence, or symptomatology is also often of interest [7, 8, 9, 10]. For example, patients with bipolar disorder may be further classified as type 1 or type 2, as psychotic or not, or as rapid or mixed cycling [11].

Analogous to the analysis of disease subtypes, a comparable scenario arises when two or more studies of different but related diseases are combined, possibly sharing the same control sample. For example, whole-genome association studies of schizophrenia [12], bipolar disorder [13], and major depressive disorder [14] all utilized a largely identical control sample. Genetic epidemiological studies [15, 16, 17] suggest there are likely risk genes that are shared across two or more of these disorders. Therefore, as well as detecting association of variants with one of these diseases, pleiotropic cross-disorder variants are also of much interest, as they might give etiological and nosological insights into the relationships between the disorders [18].

In many instances, with this subtype information, investigators wish to explore whether or not disease-gene associations are stronger with respect to such subtypes beyond the search for disease susceptibility genes [19, 20]. This is a perfectly reasonable approach unless the clinical features on which the subtypes are based are actually influenced by modifier genes. In this case, the variants of interest may be present in cases and controls at the same frequency, but in the absence of disease, they are unrelated to the features of illness under study. For example, age of onset of a disorder may be linked to the onset of puberty. Thereby, genes influencing developmental maturation could modify age of onset in individuals already predisposed to the illness but have no disease-related effect on healthy controls, and stratification of subjects by age of onset for comparison against control subjects will not be fruitful. Thus, testing for modifier gene effects necessitates case-only analyses.

Distinguishing between subtype-specific and modifier gene effects is clearly vital to unravel the genetic basis of complex disorders, but as of yet, few analysis methods are available for addressing this problem. In this paper, we present new statistical approaches to identifying and characterizing the genetic influences on observed variability within complex genetic diseases in the context of typical genome-wide association studies. This novel method uses log-linear models to discriminate between the types of genetic effects at work across a range of possible causal models. Simulation studies demonstrate the comparable power of the proposed approach over a series of two group-based standard association tests as well as its model selection performance under a large range of disease/subtype scenarios. We also discuss the impact of the model selection metrics and misspecification of subtype frequencies in the proposed modeling framework.

Methods

Disease/Subtype Models for Genetic Variants

To define disease/subtype causal models for genetic variants, we first introduce basic notations. Suppose that individuals affected with disease D can be classified into those with the subtype of interest, d*, and those without, d. The frequency of the subtype within affected individuals P(d* | D) is labeled s. This frequency can be estimated from given data if case ascertainment is independent of subtype status, or it can be fixed to the population value if known. Unaffected controls (either screened or unscreened) are labeled U. For a genetic variant with alleles A and a, the baseline frequency of A in controls is labeled qU. For convenience, the effect of the A allele is parameterized as a frequency difference Δ between controls and two subtype cases.

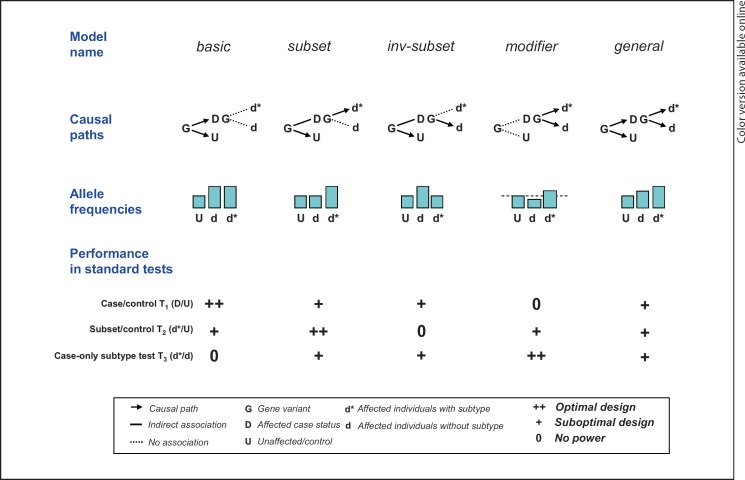
We define the following six disease/subtype causal models for genetic variants, as outlined in table 1. The null model represents a variant with no effect on either disease or subtype risk. In other words, controls and two case subgroups share the same allele frequency qU, The basic model represents a variant that increases disease risk but has no effect on subtype. Such disease-susceptibility variants without subtype effects can be detected in typical case/control association studies. The subset model represents a variant that in the general population specifically increases risk for the d* disease subtype only, not d. In contrast, the inv-subset model represents the opposite scenario, of a subtype-specific effect on d, not d*. Often, one of the two subtypes is thought to represent a more ‘pure' form of disorder, and, therefore, subtype analyses often focus on this one subgroup of interest. As such, the inv-subset model is included to illustrate what happens when this presumption is incorrect (e.g. for a gene that influences late-onset disease only). The modifier model specifies a variant with no association to disease D, as the weighted allele frequency mean in subtypes d and d* is constrained to be equal to the baseline frequency qU. Rather, the variant only influences risk for d versus d* given the individual is affected, D. Finally, the gradient scenario suggests that the variant increases risk for both subtypes, although the population-level association for d* is stronger than for d. This gradient model represents just one of many possible, more general models in which the allele frequency varies between all three groups. We note that definitions of the above disease/subtype causal models can be extended to cases of multiple subtype categories without difficulty.

Table 1.

Definitions for the true simulated disease/subtype models

	True scenario	Population frequency of A allele
	U	d	d*
null	q<LOWER>U</LOWER>	q<LOWER>U</LOWER>	q<LOWER>U</LOWER>
basic	q<LOWER>U</LOWER>	q<LOWER>U</LOWER> + Δ	q<LOWER>U</LOWER> + Δ
subset	q<LOWER>U</LOWER>	q<LOWER>U</LOWER>	q<LOWER>U</LOWER> + Δ
inv-subset	q<LOWER>U</LOWER>	q<LOWER>U</LOWER> + Δ	q<LOWER>U</LOWER>
modifier	q<LOWER>U</LOWER>	q<LOWER>U</LOWER> − Δ (1 − s)	q<LOWER>U</LOWER> + s Δ
gradient	q<LOWER>U</LOWER>	q<LOWER>U</LOWER> + Δ	q<LOWER>U</LOWER> + 2 Δ

For each of the three groups (U, d and d*), the allele frequency is parameterized in terms of qU (baseline frequency), Δ (effect of the variant), and s (subtype frequency).

Log-Linear Modeling of Disease/Subtype Causal Models

We use a data analysis technique called log-linear modeling [21] to explicitly test and compare multiple disease/subtype causal models, while considering all three groups of individuals, U, d*, and d jointly. Log-linear modeling is a powerful statistical tool which enables the exploration of relationships among more than two categorical variables and has been widely used for decades in multiple disciplines [22]. First, we fit a series of log-linear models corresponding to the six disease/subtype models defined in the previous section; table 2 shows the expected allele count parameters in three groups, U, d and d*, for each log-linear model. These parameter-constraints mirror the scenarios used to generate the data, with the exception of the general model (this replaces the gradient model, which is merely one possible instantiation of a general model that is not optimally characterized by any of the other five models, from null to modifier). Each model either has one, two or three estimated parameters (arbitrarily labeled q_x, q_y and q_z), which specify the allele frequencies for the A allele in groups U, d and d*. We denote these estimated frequencies as qU, q_d and q_d*. If for group i = U, d or d*, the observed counts of alleles are labeled A_i and a_i, then the log likelihood L for a model is

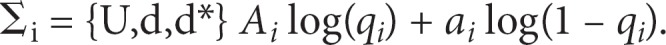
Maximum likelihood parameter estimation is used to obtain the allele frequency parameters, along with two commonly used information criteria, the Akaike information criterion (AIC) and Bayesian information criterion (BIC). For a model with k parameters, the AIC is −2ln(L) + 2k; the BIC is −2ln(L) + kln(n) where n is the total number of observations. These information metrics can be used for selecting a disease/subtype causal model that best-fits to given data [23, 24]. Models with lower values for these metrics are to be preferred over models with higher values: unlike likelihood ratio tests (LRTs), non-nested models can be compared. We thus select the disease/subtype log-linear model with the lowest AIC or BIC score as the causal model for the examined variant. In general, the BIC more heavily penalizes models with more free parameters than the AIC and so tends to select simpler models than does AIC [25]. We also calculate a series of LRTs, LG, LB, LM, LS and LI that compare the test statistics for the goodness of fit of the null model with that of the five non-null models, general, basic, modifier, subset, and inv-subset, respectively. table 3 lists the nested model structure for the LRTs. Note that the general LRT LG can be computed using a simple test of independence on a 3 × 2 allele count table or using multinomial logistic regression, as well.

Table 2.

Parameterization of log-linear models, showing the with-in-model constraints

Model	Parameterization of A allele frequency for groups U, d and d*
q<LOWER>U</LOWER>	qd	qd*
null	qx	qx	qx
basic	qx	qy	qy
subset	qx	qx	qy
inv-subset	qx	qy	qx
modifier	qx (1 − s) qys	qx	qy
general	qx	qy	qz

Table 3.

Likelihood ratio tests constructed within the log-linear modeling framework

Test	Super-model	Sub-model	d.f.
L<LOWER>G</LOWER>	general	null	2
L<LOWER>B</LOWER>	basic	null	1
L<LOWER>M</LOWER>	modifier	null	1
L<LOWER>S</LOWER>	subset	null	1
L<LOWER>I</LOWER>	inv-subset	null	1

Test Strategy for Application in Whole-Genome Association Studies

We propose the following procedure for subtype analyses in the context of whole-genome and large-scale association studies, using the log-linear models described above.

(1) Start with all available markers, as opposed to pre-selecting a subset of markers on the basis of the primary case/control association statistic. Such selection would effectively remove variants with modifier effects and bias towards markers conforming to the basic model.

(2) As the primary screen, for each variant fit the general and null log-linear models to the data and calculate the 2 d.f. LRT statistic, LG.

(3) For variants whose primary screening LG statistic is significant at type I error rate α, proceed to fit the full set of models: general, basic, subset, inv-subset and modifier and null.

(4) Identify the best-fit models based on AIC and BIC; if the two metrics select different models, report both.

(5) In order to control the marker-wise type I error at α, report only the best-fit model and the p value from the general versus null LRT LG calculated in step 2 as the primary result per marker. (Reporting the uncorrected p value for the best-fitting model, e.g. LG, LB, LM, LS or LI, would capitalize on chance and inflate type I error.)

A possible exception to the proposed test approach would be a study of a single disease in which the primary disease association test (T₁) has already been performed and there are multiple subtypes of interest. In this case, it might be preferable to select markers at step 2 on the basis of the subtype-only test T₃ (i.e. simply any evidence of allele frequency differences between subtypes). In this instance, we are not interested in re-selecting SNPs that show strong affected/unaffected effects, implying the basic model, under each subtype analysis, as these would already have been highly ranked. The model comparison procedures described in steps 3–5 can still be used to characterize whichever variants are selected as being significant, as described above. That is, given a significant difference between subtype allele frequencies, information from controls will determine the best-fitting model overall.

Series of Two-Group-Based Standard Association Tests

One approach to the subtype analysis of whole-genome association study is to conduct a series of association tests between two groups. We label the standard case/control test T₁. Two further subtype tests involve comparing a subset of cases against controls (T₂, subset/control) and the remaining cases (T₃, case-only) to clarify the subtype-specific effects. We evaluate and compare the power of these standard two-group-based association tests with our log-linear modeling-based selection approach. For the five non-null models introduced above, figure 1 schematically illustrates the causal paths between genotype and phenotype, the resulting pattern of allele frequency differences between the three groups (U, d and d*) and a broad indication of how well the three basic tests T₁−T₃ might be expected to work (i.e. ‘as well as possible', ‘not at all', or ‘partially depending on the details of study design and genetic variant'). PLINK [26] was used to conduct the three pair-wise tests, T₁⁻T₃.

Fig. 1.

Schematic illustrating some of the models considered here, and the standard tests often applied to subtype data.

Basic Power Calculation and Simulation Study

For each of the five non-null disease/subtype models, we calculate power for the standard pair-wise tests. For a sample of n affected individuals (D) and m unaffected individuals, the corresponding tests T₁−T₃ and their sample sizes are summarized in table 4. Power is calculated based on the expected non-centrality parameter for a χ² test of independence based on each implied 2 × 2 table. In all scenarios, we assume a total of 1,000 cases and 1,000 controls; cases are further subdivided (d* vs. d) for a range of values for s (0.1 ≤ s ≤ 0.9 in 0.1 increments). To control for multiple testing, a Bonferroni-corrected type I error rate is applied to T₁, T₂ and T₃.

Table 4.

Definitions for the three standard tests of association

Test	Cases	Case sample size	Controls	Control sample size
Case/control (T1)	D	n	U	m
Subset/control (T2)	d*	ns	U	m
Case-only (T3)	d*	ns	d	n (1 − s)

U and D represent a group of controls and of cases, respectively. Cases can be further divided into two groups, d* and d, which are a group of cases with the subtype of interest and those without the subtype. For the three standard two-group-based association tests (i.e. T₁, T₂, and T₃), the second (i.e. Cases) and the forth (i.e. Controls) columns list two of the four groups, U, D, d*, and d, that are tested for genetic association. The sample size of each test group is determined by three factors: (1) the number of controls, n; (2) the number of cases, m; and (3) the frequency of the subtype within affected individuals, s.

For a nominal type I error rate of a, we also calculate α series of LRTs, listed in table 3. In particular, we are interested in the power of the 2 d.f. general LRTs, LG, as the statistic is used to select a subset of potential markers to fit a full set of log-linear models. For each disease/subtype model, we simulated 10,000 replicate datasets, fitting the same series of LRTs LG⁻LI and selecting the most parsimonious model based on the AIC and BIC (selecting one of the six models from null to general with the lowest value in each case). We also examined the distribution of best-fit models based on AIC and BIC only for datasets that show a significant LG test at some nominal α. For each set of replicates, the value of s used both to generate and analyze the data was set at 0.1–0.9, in 0.1 increments.

Important points to demonstrate are therefore (1) that LG is an adequate statistic for ranking and selecting markers as associated with a single disease and/or subtype in some way, or with one or more of multiple diseases, and (2) that the model selection procedure, applied to markers with a significant LG test, will show adequate discrimination under realistic scenarios. We also investigate the impact of model misspecification, with respect to subtype frequency, s.

Results

Basic Power Calculation

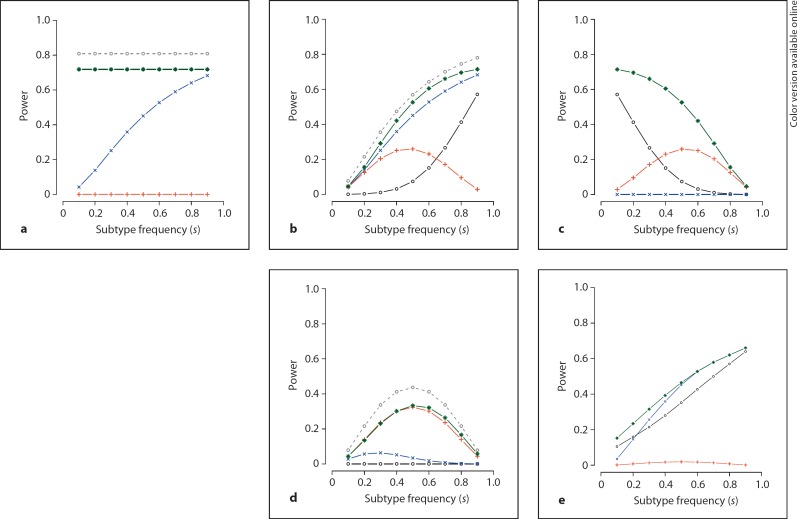
We first examine the relative power of the general likelihood test LG versus the standard tests T₁, T₂ and T₃, under the five disease/subtype causal models: basic, subset, inv-subset, modifier and gradient. Figure 2 shows the results for a control allele frequency of qU = 0.15 and a genetic effect (allele frequency difference) of Δ = 0.05. The nominal type I error rate α is set at 0.001. The five panels a–e correspond to the five models: basic, subset, inv-subset, modifier and gradient, respectively. In all panels, the x-axis represents the simulated value of the subtype frequency s, while the y-axis represents the power of the examined tests, LG, T₁, T₂, and T₃ (green stars = LG; black circles = T₁; blue crosses = T₂; red plusses = T₃). As previously described, the error rate α for T₁, T₂, and T₃ was corrected for three tests (a = 0.001/3), while the single test LG requires no further correction. Note that for panel a (i.e. the basic model) the power of T₁ after correction for multiple testing and LG are identical (and therefore difficult to distinguish on the plot). We also plot the optimal power for the standard pair-wise tests of T₁, T₂ or T₃ using gray circles. As summarized in figure 1, the case/control test T₁ has the best power under the basic model, while the subtype/control test T₂ and the case-only test T₃ perform the best under the subset and the modifier model, respectively.

Fig. 2.

Power analysis results of the two-group-based standard association tests (T_1, T₂, and T₃). Panels a–e represent the five true causal models: basic, subset, inv-subset, modifier and gradient. Black circles = power for T₁, correcting for three tests; blue crosses = power for T₂, correcting for three tests; red plusses = power for T₃, correcting for three tests; green stars = power for LG, no correction necessary; gray circles = power for optimal model (T₁, T₂ or T₃) under corresponding models only (basic, subset and modifier), without any correction.

Overall, the data presented in figure 2 illustrates that in most scenarios the single general LRT LG (a 2 d.f. test) performs at least as well as the basic tests T₁, T₂ and T₃. In particular, the LRT shows substantially increased power for the inv-subset model. Bonferroni correction for three independent tests is conservative, although LG still compares well if T₁, T₂ and T₃ are only corrected for 2 independent tests (data not shown). The competent performance of LG is clear when one considers the additional optimal power curve of the standard pair-wise tests plotted in panels a, b and d (dotted lines with gray circles): these three models correspond directly to the assumed true disease/subtype model underlying T₁, T₂ and T₃, respectively. For these three models only, we thus additionally examined the power for the optimal corresponding test, without any correction for multiple testing. In all cases, we observed that the power of the general test is never, proportionally speaking, very low even compared to the anti-conservative procedure of selecting the best of T₁, T₂ or T₃ uncorrected. In addition to the comparable power under all disease/subtype models, major advantages of the single general LRT LG are that it naturally handles the issue of multiple testing, and that it offers considerably increased power in the inv-subset scenario.

Model Selection Performance

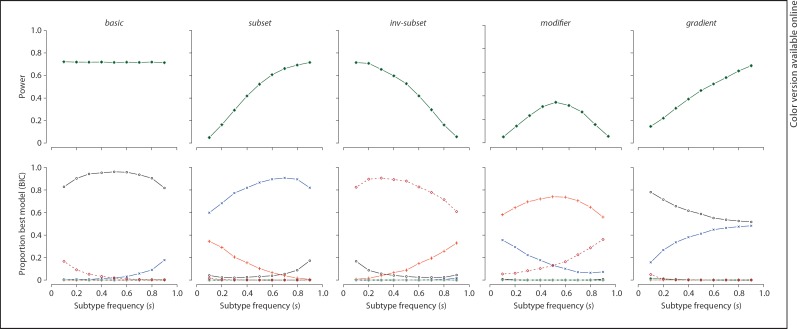
The primary motivation for our approach, however, is not to increase power to detect associations per se, but rather to provide a statistical basis for distinguishing between different classes of associated variant, in particular subtype-specific versus modifier effects. Here we use simulations to investigate the performance of our best-fitting model selection approach based on AIC and BIC metrics. For the five true model scenarios, figure 3 shows the power of the LG test at a type I error rate of 0.001 in the top panels. The simulation parameters are the same as for the analytic power calculations above. The bottom panels show, for replicates in which the LG test is significant, the proportion of times each model is selected by the BIC metric (black circles = basic; blue crosses = subset; brown diamonds = inv-subset; red plusses = modifier; green stars = general).

Fig. 3.

Simulation results. Power (for a type I error rate of 1 × 10⁻³) for the LG test under five different true scenarios (left to right) is shown in the top row; the bottom row shows the proportion of times each model is selected as the best-fit model based on the BIC metric, given the replicate was significant for LG at p < 1 × 10⁻³. Black circles = basic; blue crosses = subset; brown diamonds = inv-subset; red plusses = modifier; green stars = general. See online supplementary figure 1 for full simulation results.

In general, power for the LG test is lower for modifier variants, as simulated under these particular conditions and sample sizes. The bottom panels show good discrimination power of our selection approach, in general. That is, given a significant LG test, the appropriate basic, subset, inv-subset, or modifier model is selected the majority of the time (60–98%). It is important to note that in many cases, the true model may be the most likely to be selected, but it is far from selected 100% of the time. In particular, the modifier model shows a tendency to be confused with subtype-specific effects for relatively rare subtypes (e.g. under 10%). This is because the non-subtype cases (the majority of cases) only need show a small difference in allele frequency from controls in the opposite direction to the subtype, to equate the overall case and control means. We also note that, for this particular set of simulations, the general model is rarely selected, so performance under the gradient scenario is poor in terms of model selection. Naturally, as with any power calculation, all these conclusions are subject to the specific terms under which the data were simulated and the sample sizes: if gradient loci of very large effect existed, then these would be easily detected via the LG test and selected via AIC and BIC measures.

Online supplementary figure 1 shows the full simulation results (www.karger.com/doi/10.1159/000327158) of our model selection performance; the full power curves and the best-fit models selected by AIC and BIC are shown both for all replicates as well as those that are significant for LG at p < 0.001. Note that, in general, it is not a good strategy to select the AIC and BIC best-fit models for all examined variants: that is, under the null hypothesis of no association the rate of non-null best-fit models selected by AIC (in particular) and BIC might be substantially higher than the type I error rate specified for LG. For this sample size, simulating under the null model, a non-null model was selected approximately 1% of the times based on BIC, and the rate was much higher for AIC. This highlights the importance of first using the LG statistic to restrict model selection to a subset of putatively associated SNPs. Overall, these simulations suggest that the BIC metric is to be preferred over the AIC; it tends to display a conservative bias under most conditions, whereas the AIC displays a liberal bias, in terms of selecting more complex models. However, the performance of different model selection metrics can be affected by the size of the data samples and specific simulation settings [27]. Therefore, we suggest to explore both AIC and BIC scores in the model selection procedure. Of course, these two metrics do not provide a perfect means to test and select the different causal models outlined in this article; nonetheless, we would argue that performance is likely to be good for moderate effect sizes in large samples that pass the LG test at a stringent threshold, and that it is better than ad hoc comparisons of p values from the T₁, T₂ and T₃ tests.

As illustrated in figure 1, there is not a direct correspondence between the implied causal models and the power of the three correlated tests, T₁, T₂ and T₃. In practice, the case/control test T₁ will typically be performed first to select a smaller set of SNPs for subtype analysis (e.g. in the context of a whole-genome association study). In this case, the interpretation of the subsequent subset/control test T2 is not straightforward, because the statistics from the T₁ and T₂ tests will be highly correlated even under the null model depending on the relative frequency of d and d*, Simply noting whether or not the T₂ p value (based on a smaller sample) is larger or smaller than the T₁ p value is not a sound basis for concluding anything vis-à-vis subtype-specific or modifier effects. Dissimilarly, under the null hypothesis of no subtype-specific association, T₃ is independent of T₁, which makes the joint interpretation of p values from T₁ and T₃ easier. However, by itself a significant T₃ result is consistent with a number of distinct causal models: in particular, it provides no grounds for deciding between subtype-specific and modifier models of gene effect. In contrast, our modeling framework enables to explicitly test and compare a number of causal models and to distinguish between modifier and subtype-specific effects.

Misspecification of Subtype Frequency

Whether an effect is classified as a modifier versus a subtype-specific effect can clearly depend on accurately specifying the value of s, the subtype frequency, in the general population of individuals with disease. In a large sample of cases, where ascertainment is independent of subtype status, then s can simply be estimated from the sample. If the ascertainment scheme means that the sample estimate of s will be biased from the true population value, then s should be fixed to an independent estimate of its true population value when fitting the modifier model. For example, if the subtype is drug resistance, and drug-resistant cases are more likely to be enrolled in the study, this will bias the sample estimate of s. In general, if one subtype is more severe, it may affect ascertainment via Berkson's bias [28].

This issue is particularly likely to arise if ‘cases' in fact comprise two distinct disorders, such as bipolar disorder and schizophrenia, combined from two original case/control studies. In this case, the relative proportion of bipolar to schizophrenic patients will simply reflect the sample size of the two original studies. Also, if there is a large sex difference in the rate of the subtype, then X chromosome markers should be analyzed separately for males and females with different values of s specified.

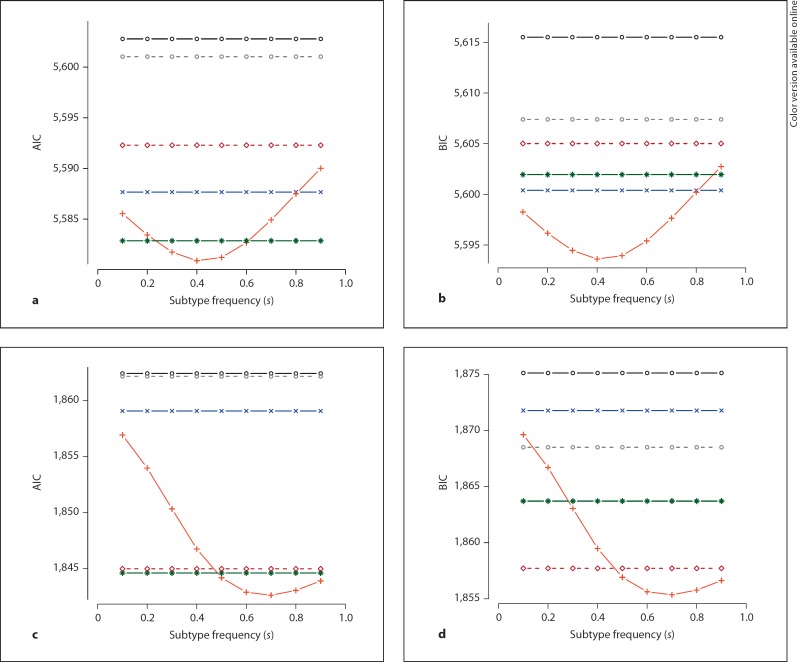
Given that the choice of modifier versus subtype-specific models is affected by the value of s, it is advisable to perform a sensitivity analysis in which s is varied and its impact on model selection is assessed; in other words, to ask how tolerant the result is to possible misspecification of s. figure 4 plots the AIC and BIC scores for the two simulated modifier SNPs (labeled 1 and 2) as a function of different values of s. The true value of s in data generation was 0.5, but for log-linear model fitting, s was set to vary between 0.1 and 0.9. Panels a and b represent the AIC and the BIC scores for SNP 1; panels c and d represent AIC and BIC for SNP 2 (gray circles = null; black circles = basic; blue crosses = subset; brown diamonds = inv-subset; red crosses = modifier; green stars = general).

Fig. 4.

Model misspecification, for SNPs based on AIC and BIC model selection metrics. Gray circles = null; black circles = basic; blue crosses = subset; brown diamonds = inv-subset; red crosses = modifier; green stars = general.a, b AIC and BIC for SNP 1. c, d AIC and BIC for SNP 2.

In all cases, at s = 0.5 (the simulated true value) the modifier model gives the lowest AIC and BIC compared to other models. However, as the misspecification of s arises, the AIC and the BIC score of the modifier model tends to arise, as well. Note that the AIC and the BIC scores of other non-null models (i.e. basic, subset, inv-subset, and general) are invariant regardless of the value of s, because their log-linear model fitting does not depend on s as summarized in table 3. Calculating how the modifier AIC and BIC metrics change relative to the other models (which do not depend on s) will indicate how robust the designation as a modifier is. The precise profile will depend on the frequency of the variant and the nature of the effect. In general, if a change in s of only a few percent would alter the model selection (e.g. if a different model, e.g. general or subset, becomes more likely based on either AIC or BIC) it is not advisable to make any strong conclusions regarding the modifier effects as the best causal model for the examined variant.

Application to Cross-Disease Meta-Analysis

Finally, we consider the joint analysis of data from studies of multiple diseases, rather than subtypes of a single disease. Here, we focus on independent case/control samples for five different diseases, subsets of which are expected to share common genetic risk factors. For example, the Psychiatric GWAS Consortium (PGC) combines genotype data from studies of attention deficit hyperactivity disorder, autism, bipolar disorder, major depression and schizophrenia. As well as detecting association of a variant with one of these diseases, pleiotropic cross-disorder variants are also of interest, as these might give etiological and nosological insights into the relationships between diseases [18]. We assume that the standard, ‘within-disease' analyses have already been performed, but that one question we now want to ask is: by pooling these data across disorder, can we detect novel loci that harbor variants that impact two or more of the five disorders, but were missed by the smaller individual disorder analyses?

In addition to standard meta-analytic approaches, one approach to analysis is to use a log-linear modeling approach describe above. Under the alternate model, 10 allele frequencies would be estimated, for cases and controls separately within each of the five studies. Under the reduced model, only five allele frequencies would be estimated, with case and control estimates constrained to be similar within each study. The 5 d.f. LRT between these two models represents an omnibus test of any association, which does not assume a similar relative risk across groups and allows for different background frequencies.

We assessed the power of this approach by simulation. We assumed that a particular variant increases risk for only two of the five disorders (labeled A and B of A–E). This represents a ‘worst-case scenario' from the point of view of the secondary cross-disease analysis. For each disease, we simulated 2,000 independent case/controls pairs. The genotypic relative risk was set at 1.2; risk allele frequency was randomly generated following a uniform distribution, truncated at 5 and 95%. The power of the 5 d.f. test compares favorably to some of the other obvious alternatives. For a nominal type I error rate of 0.01, the power to detect the effect within a single study, either A or B (N = 2,000 + 2,000), is 80%. At a similar overall type I error rate, the power to detect an effect in both A and B (and therefore conclude pleiotropy) is 88% (i.e. p < 0.1 in both studies, implying a joint 0.1² = 0.01 type I error). If cases and controls from A and B were pooled (N = 4,000 + 4,000), power for the single test is 94%. However, none of these tests account for the fact that we are considering five diseases, and we do not know a priori which diseases, if any, show association. By contrast, the power of the 5 d.f. omnibus test, which does account for all multiple testing across diseases, is 87%. Even though only two of the five diseases show the association, here we have greater power than for a single study test of association of either A or B. Naturally, if three or more of the five diseases showed association, we would expect the omnibus test to perform even better.

Discussion

Heterogeneity in the clinical presentation of complex genetic diseases suggests the existence of subtype-specific and/or modifier genes. Identifying and distinguishing between these types of genes is an important next step in understanding disease pathology. We have outlined a set of log-linear models for testing and describing subtype-specific and modifier effects in the context of genetic case/control association studies. Our approach provides a single testing framework that specifically distinguishes subtype-specific from modifier effects. Of note, recent work by Huang et al. [29] applied our model selection-based testing framework to the cross-disorder analysis of three major psychiatric disorders and identified the genetic variants with subtype-specific effects of genomewide significance. As discussed in the work [29], whether or not a gene variant is a modifier, etiologically distinct from a basic or subtype-specific disease variant, could have important consequences in how one approaches subsequent follow-up.

Genome-wide association studies have successfully identified numerous loci at which common variants influence disease risk or quantitative traits. Despite these successes, the variants identified by these studies have generally explained only a small fraction of the heritable component of disease risk, and have not pinpointed with certainty the causal variants at the associated loci. Furthermore, the mechanisms of action by which associated loci influence disease or quantitative phenotypes are often unclear, because we do not know through which genes the associated variants exert their effects or because these genes are of unknown function or have no clear connection to known disease biology. Thus, the initial set of genome-wide association studies serve as a starting point for future genetic and functional studies.

Some of the variability often observed in association signals across studies could be due to subtype specificity. A gene conferring risk for any subtype is particularly likely to show inconsistent patterns of association in standard case/control studies when ascertainment varies with respect to that subtype (for example, if some studies oversampled severely affected, hospitalized patients, whereas others did not). It is important to note that different SNPs in the same gene, even in the same linkage disequilibrium block, may be associated but with different causal models reported as the most likely. Naturally, this approach will be more powerful when looking at the true causal variant rather than at markers that are only indirectly associated. In this instance, the SNP with the strongest LG test statistic is likely the best SNP upon which to base model selection. However, as with the issue of correctly specifying the subtype frequency, s, one should reserve strong judgment in the absence of a consistent overall pattern of results.

A subtype might represent a co-morbid disorder, or a phenotype which can exist in individuals without disease. For example, if the subtype were bipolar disorder with co-morbid panic disorder, one would not be able to distinguish between a subtype-specific effect for bipolar disorder versus a main, basic effect for panic disorder (i.e. where the variant is completely unrelated to bipolar disorder, per se). However, if one were to sample all four combinations of individuals with and without bipolar and panic disorder, it would be easy to extend the approach presented here to distinguish between this larger set of possible models. A further issue in interpretation is that different subtypes will often be correlated with each other. For example, if psychotic bipolar patients are more likely to be early-onset and male, it may not be clear whether a subtype-specific effect relates to psychosis, age at onset or sex. One advantage of the simple case-only test, T₃, is that other subtypes can easily be included as covariates, for example, in a logistic regression context, whereas this would not be straightforward for the subset/control test, T2 (as the covariates would not be defined in controls). Our log-linear modeling approach could be extended to incorporate case-only covariates (i.e. other subtypes and continuous variables). Similarly, this approach could be easily extended to model genotype or haplotype frequencies instead of allele frequencies, or to be re-parameterized in terms of genotypic relative risks and include affected offspring/parent trio data.

Overall, this novel method offers the capacity to concurrently assess subtype-specific and modifier gene influences to facilitate the goal of better understanding the pathological mechanisms underlying the heterogeneity of complex disorders. We have outlined possible next steps that may help accelerate progress from genetic studies to the biological knowledge that can guide the development of predictive, preventive, or therapeutic measures.