Knowledge-based tradeoff hyperplanes for head-and-neck treatment planning

Abstract

Purpose

To develop a tradeoff hyperplane model to facilitate tradeoff decision-making before inverse planning.

Methods and materials

We propose a model-based approach to determine the tradeoff hyperplanes that allow physicians to navigate the clinically viable space of plans with best achievable dose-volume parameters before planning. For a given case, a case reference set (CRS) is selected using a novel anatomical similarity metric from a large reference plan pool. Then, a regression model is built on the CRS to estimate the expected dose-volume histograms (DVHs) for the current case. This model also predicts the DVHs for all CRS cases and captures the variation from the corresponding DVHs in the clinical plans. Finally, these DVH variations are analyzed using the principal component analysis to determine the tradeoff hyperplane for the current case.

To evaluate the effectiveness of the proposed approach, 244 head-and-neck cases were randomly partitioned into reference (214) and validation (30) sets. A tradeoff hyperplane was built for each validation case and evenly sampled for 12 tradeoff predictions. Each prediction yielded a tradeoff plan. The root-mean-squared-errors (RMSEs) of the predicted and the realized plan DVHs were computed for prediction achievability evaluation.

Results

The tradeoff hyperplane with three principal directions accounts for 57.8%±3.6% of variations in the validation cases, suggesting the hyperplanes capture a significant portion of the clinical tradeoff space. The average RMSE in three tradeoff directions are 5.23±2.46, 5.20±2.52, and 5.19±2.49, as compared to 4.96±2.48 of the KBP predictions, indicating that the tradeoff predictions are comparably achievable.

Conclusions

Clinically relevant tradeoffs can be effectively extracted from existing plans and characterized by a tradeoff hyperplane model. The hyperplane allows physicians and planners to explore the best clinically achievable plans with different OAR sparing goals before inverse planning and is a natural extension of the current KBP framework.

1. Introduction

Knowledge-based planning (KBP) uses a model to predict optimal achievable plan DVHs [1–5] and provides planning guidance that leads to clinically optimal plans. Clinical implementations of KBP models have gained widespread acceptance [6–10]. However, in treatment sites such as head-and-neck (HN), one set of DVH predictions may not be sufficient for clinical planning due to the complexity of tradeoff relations. Physicians usually prescribe OAR dose constraints based on estimates of the best achievable DVHs with desired tradeoffs, and planners often have to interact with the treatment planning system (TPS) and the physicians iteratively to achieve patient-specific optimal OAR-sparing. This iterative tradeoff process forgoes some of the time-saving advantages accomplished by the KBP.

There are two possible approaches to providing decision support for tradeoff considerations: pre-planning and post-planning. In the post-planning approach, the tradeoff decisions are based on alternative plans that are on the Pareto front of a multi-criteria optimization (MCO) search space [11–15]. In a pre-planning approach, tradeoff decisions are based on models that predict such tradeoff scenarios before any inverse planning is performed. This approach has not been previously reported.

This study presents a novel pre-planning approach that aims to support tradeoff decision-making and accelerate HN treatment planning by modeling the clinically viable tradeoff experiences embedded in prior clinical plans. We hypothesize that historical plans are at or close to Pareto-optimal and that for a given case, the clinically feasible Pareto-surface has been sufficiently explored previously in the planning of similar cases. Using a morphological metric, we can identify a set of similar cases, or a case reference set (CRS). If we build a model using this CRS, then the variations observed between the model predictions and clinical DVHs within the CRS should reflect prior tradeoff decisions, and such tradeoff information can be extracted and projected to the current case of interest as a subspace consisting of clinically viable tradeoff plans (i.e. tradeoff hyperplanes).

2. Methods and materials

2.1. KBP model

The workflow of the proposed method starts with building a localized KBP model. First, for a given current case, a case reference set (CRS) consisted of N reference cases is selected from a reference database. The cases in CRS are morphologically similar to the current case and used as the training set for KBP modeling. Thus, we refer this as the localized KBP model, as this modeling only uses a subset of the reference pool (214 cases in this study). The localized KBP model implemented in this study is based on a previously reported localized modeling technique [16, 17] that works effectively for cases with multiple PTVs as are typical in HN cancer treatment. We implemented the same generalized distance-to-target (gDTH) feature with slight modifications. The model previously presented [16] references similar plans in terms of individual OARs. In contrast, this study selects similar plans in terms of all OARs by employing a case similarity metric that is a weighted sum of gDTH Euclidean distances between two cases across all OARs. To take into account the prescription variation in the dataset, we adopt a similarity metric S that takes both prescription ratio and spatial information into account¹⁷:

$$S=\Vert gDT{H}_{\mathit{\text{case}}1}-gDT{H}_{\mathit{\text{case}}2}{\Vert }_F^2+\alpha {\left(\frac{d_{\mathit{\text{case}}1 \mathit{\text{primary}}}}{d_{\mathit{\text{case}}1 \mathit{\text{boost}}}}-\frac{d_{\mathit{\text{case}}2 \mathit{\text{primary}}}}{d_{\mathit{\text{case}}2\mathit{\text{boost}}}}\right)}^2,$$

where $\Vert \cdot {\Vert }_F^2$ denotes Frobenius norm, d denotes prescription dose, and α is a balancing factor set to match the mean values of the first term and the second term in the training dataset.

The CRS size is determined to be 35 based on training-set cross-validation results. The number is consistent with the number of cases previously used for HN knowledge-based planning, which ranges from 12 to 44, as reported in a recent review article [18]. The CRS size is fixed in the current study. However, it may be possible and more advantageous to dynamically vary the CRS size based on similarity metrics to ensure more cases can be selected to the CRS when a case is determined to be very similar to more than a set number of cases in the database.

For all the cases in CRS, dosimetric parameters and anatomical features are extracted to train a regression model using the following formula:

$$\widehat{\beta }={\text{arg min}}_{\beta }\left\{\Vert Y-X\beta {\Vert }_F^2+\lambda |\beta {|}_1\right\},$$

where $X\in {ℝ}^{N\times P}$ denotes P anatomical feature values from N training cases (i.e., N is the size of CRS), $Y\in {ℝ}^N$ denotes OAR DVH principal component scores (PCS) of the N training cases, and $\widehat{\beta }\in {ℝ}^P$ denotes the optimal regression coefficients corresponding to P anatomical features. Here, the PCS is a dimension-reduced representation of the entire DVH curve [19]. Following previous implementations, we retain the first three PCS for the modeling process and use the equation to model the three PCS values separately.[20] The last term, known as the penalty term, helps to prevent overfitting. The penalty hyperparameter λ for adjusting the model bias-variance balance was decided by in-training-set five-fold cross validation results. The results were evaluated using RMSE of predicted DVHs compared to clinical DVHs, and the λ value corresponding to the smallest RMSE value was selected. This localized KBP model is used to predict the OAR DVH for the current case.

2.2. Tradeoff hyperplanes

After the KBP model is built, it is applied to all the cases in the CRS to extract tradeoff related variations. The difference between the model predicted and the actual DVH PCS (from clinical plans) for all OARs is formulated as $E\in {ℝ}^{N\times MP}$, which is essentially the fitting residuals of N training cases in the CRS (N=35 in this study), each with M OARs and P DVH PCS scores per OAR. By retrospectively examining the DVH predictions and comparing them with clinical DVHs, we observed that significant portions of the fitting errors are due to the tradeoff relations. As a result, there is valuable information in the fitting residuals. The purpose of subtracting the predicted PCS is to remove the variations linked to anatomical differences and extract only the discrepancy between the KBP model and the clinical plans that are likely caused by tradeoff decisions. The matrix E of OAR DVH fitting residuals is subsequently processed by principal component analysis (PCA) to further reduce the dimensionality with the first L PCS (L=3 in this study) taken as the principal tradeoff directions. The tradeoff directions effectively reveal the most prominent DVH variation patterns in the CRS after adjusting for anatomy variations. These patterns are representative of the commonly-occurring tradeoffs in the historical reference database. Since the CRS used as training cases in the model building process is selected based on morphological similarity to the current case, the extracted tradeoff directions are thus specific to the current-case. These directions form a tradeoff hyperplane that provides effective guidance for a well-confined and clinically representative tradeoff subspace.

2.3. Data selection

A total of 244 anonymized HN cases were retrieved with IRB approval. These cases were all regularly-fractionated but were of various prescription doses, including 44 Gy/ 70 Gy and 50 Gy/ 60 Gy to the primary and boost PTVs. All cases were planned with IMRT technique using from 7 to 11 beams. Recently, volumetric modulated arc therapy (VMAT) has been increasingly utilized to treat HN cases. However, in this study, the proposed method are evaluated with IMRT cases due to data availability in our historical database. It is expected that the method can be applied to VMAT without major modifications. The cases were treated by three physicians from our institution. OAR constraints were prescribed to limit parotid D_median, oral cavity D_median, larynx D_median, pharynx D_median, mandible D_1cc/D_max, brainstem D_max, and cord+5mm D_max. The prescribed planning constraints were given by physicians based on their estimations of best achievable dose-volume values from past experience. Typical constraints used in our institution are presented in the supplementary materials. Note that in our clinical practice and in this HN dataset, PTV-OAR is not a tradeoff direction. For these patients, the PTV coverage is always normalized to have 100% prescription dose cover at least 95% PTV volume.

2.4. Validation

The validation experiment covers two aspects: (1) to validate the assumption that the clinically desirable tradeoffs can be well-represented by the proposed hyperplanes; and (2) DVHs generated by the hyperplane model can be realized in the actual IMRT plans. From the 244 anonymized cases, we randomly partitioned 214 cases to the reference pool and the remaining 30 cases to the validation pool. For each validation case, we created a total of 14 auto-generated plans. First, a KBP plan was generated from DVH predictions given by the KBP model. This plan represents the baseline scenario before any tradeoff considerations are attempted. Second, the clinical plans’ DVHs in the CRS were analyzed against the KBP model predictions to extract the embedded tradeoff knowledge and construct the tradeoff hyperplane. The tradeoff hyperplane was sampled in all three principal tradeoff directions with the amplitude of $\pm {\sigma }_i^n$ and $\pm 2{\sigma }_i^n$ to generate 12 sets of OAR DVH predictions that represent 12 different tradeoff options. Here ${\sigma }_i^n$, n ∈ [1, 30], i ∈ [1, 3] denotes the standard deviation of the tradeoff vector in the CRS for case n in the i^th direction. These 12 sets of DVH predictions were then used to generate 12 tradeoff plans. Finally, the 14^th plan, called the clinical-DVH-fitted plan, was generated as a fitting of the clinical DVHs on the predicted DVH hyperplanes. Formally, DVH_fitted can be found by solving a linear least-squares problem: $\widehat{\omega }={\mathit{\text{argmin}}}_{\omega }\Vert DV{H}_{\mathit{\text{clinical}}}-DV{H}_{KBP}-\omega \mathrm{\Delta }DVH{\Vert }_2^2$, where $\mathrm{\Delta }DVH\in {ℝ}^{3\times \text{T}}$ denotes the three principal tradeoff directions, and $\omega \in {ℝ}^3$ denotes the fitting parameters corresponding to the three principal tradeoff directions. The clinical-DVH-fitted plan can then be generated by using $DV{H}_{\mathit{\text{fitted}}}=DV{H}_{KBP}+\widehat{\omega }\mathrm{\Delta }DVH$, followed by auto-generation of the plan. This plan is essentially a projection of the clinical plan, it provides a sanity check on the validity of the other 13 auto-generated plans in this experiment. In this closed loop, the difference between the original clinical plan and its clinical-DVH-fitted plan serves another baseline of the achievability of the hyperplane model.

All 14 plans were generated automatically in the Eclipse™ treatment planning system (TPS; Varian Medical Systems, Palo Alto, CA) using the predicted DVHs as optimization objectives. To interface with the TPS and streamline the planning process, we have developed an Eclipse scripting API[21] program to automatically predict DVHs, place optimization objectives, and run optimizations. These auto-generated plans share the same isocenters and beam angles of the clinical plans. The endpoint of the workflow is an ensemble of best achievable plans with various tradeoffs (referred to as “tradeoff plans” in the rest of the paper).

To test the achievability of hyperplane based tradeoff guidance, the realized DVHs of the 14 plans for each validation case were evaluated against their corresponding DVH predictions. Root-mean-squared error (RMSE) values were calculated to quantify the discrepancies between the realized and predicted DVH curves. Furthermore, the distribution of OARs that were involved in tradeoffs along the three principal directions was analyzed. Two OARs with the largest PCS amplitudes in each tradeoff vector were selected and denoted as tradeoff organs. We expect that those more involved OARs along tradeoff directions should correspond to OARs that have more clinical importance in sparing decision making.

3. Results

3.1. Distribution of tradeoff directions

Figure 1 shows the percentages of DVH PCS variations (8 OARs) in the CRS that can be represented by the hyperplane. The variations were quantified by the Euclidean distances between the clinical DVH PCS and the clinical-plan-fitted DVH PCS in a tradeoff subspace with a given number of tradeoff directions n, normalized to the Euclidean distance between clinical DVH PCS and KBP DVH PCS. Using this measurement, the first three directions (n=3) account for 57.8 % ± 3.6 % of the total variations. It confirms the hypothesis that the clinical tradeoffs are of low dimensions and can be effectively represented by hyperplanes. This also means that the validation cases are close to the hyperplanes, with less than half of the variations due to other factors. The OARs involved in tradeoff directions in the validation cases are summarized in Fig. 2. Parotids often appear in the primary tradeoff direction. Oral cavity, larynx, and pharynx are often involved in secondary and tertiary tradeoff directions. This indicates that physicians have made consistent selections of OARs to tradeoff with similar anatomies, albeit tradeoff directions and dose amount were different case-to-case. On the contrary, cord, brainstem, and mandible have not been identified as tradeoff OARs, suggesting that the DVHs of these OARs do not form direct tradeoff relations with any other OARs.

Figure 1.

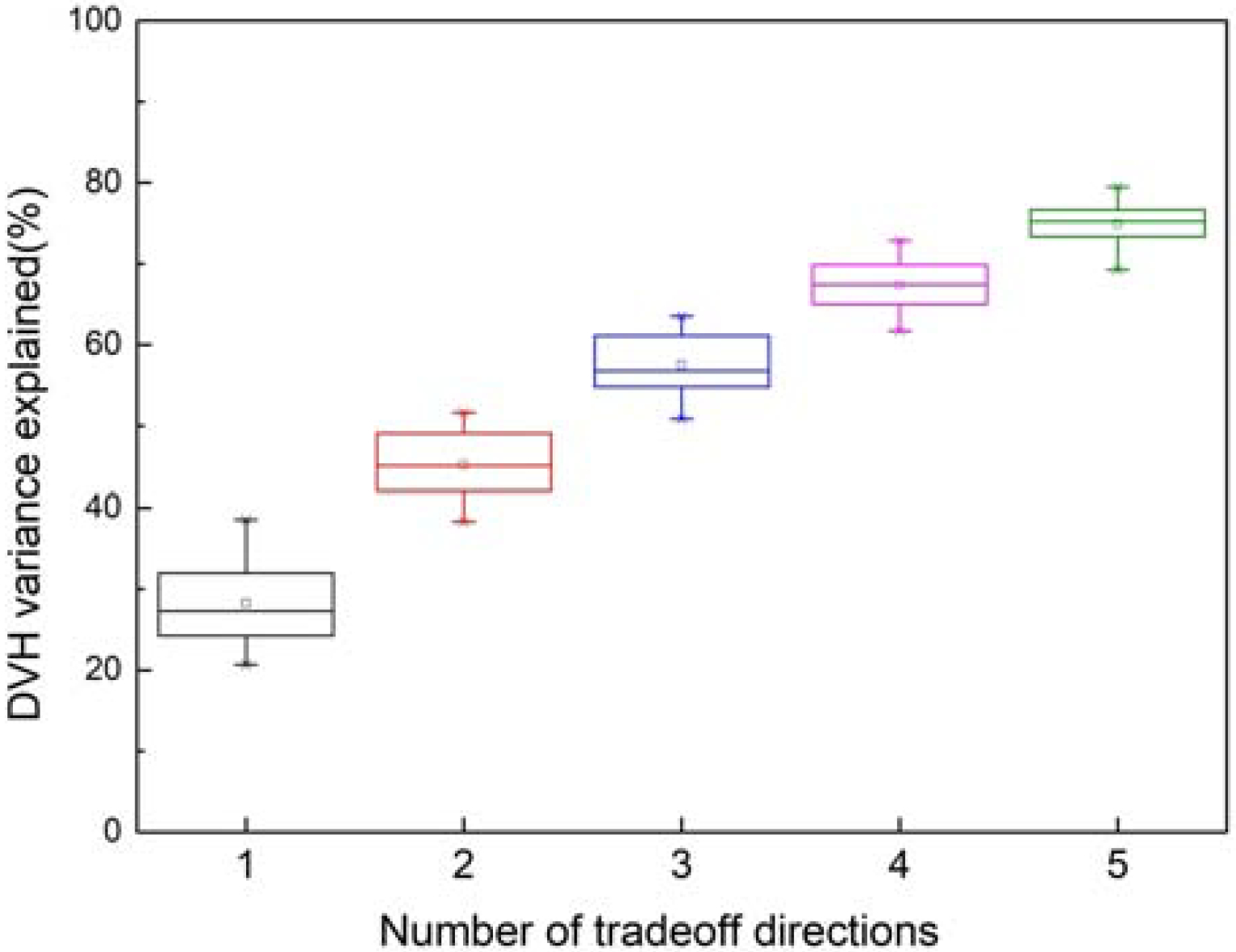
Percentage of DVH PCS variations (8 OARs) in the CRS that can be represented by the hyperplane. The hyperplane in this study is constructed with 3 tradeoff directions.

Figure 2.

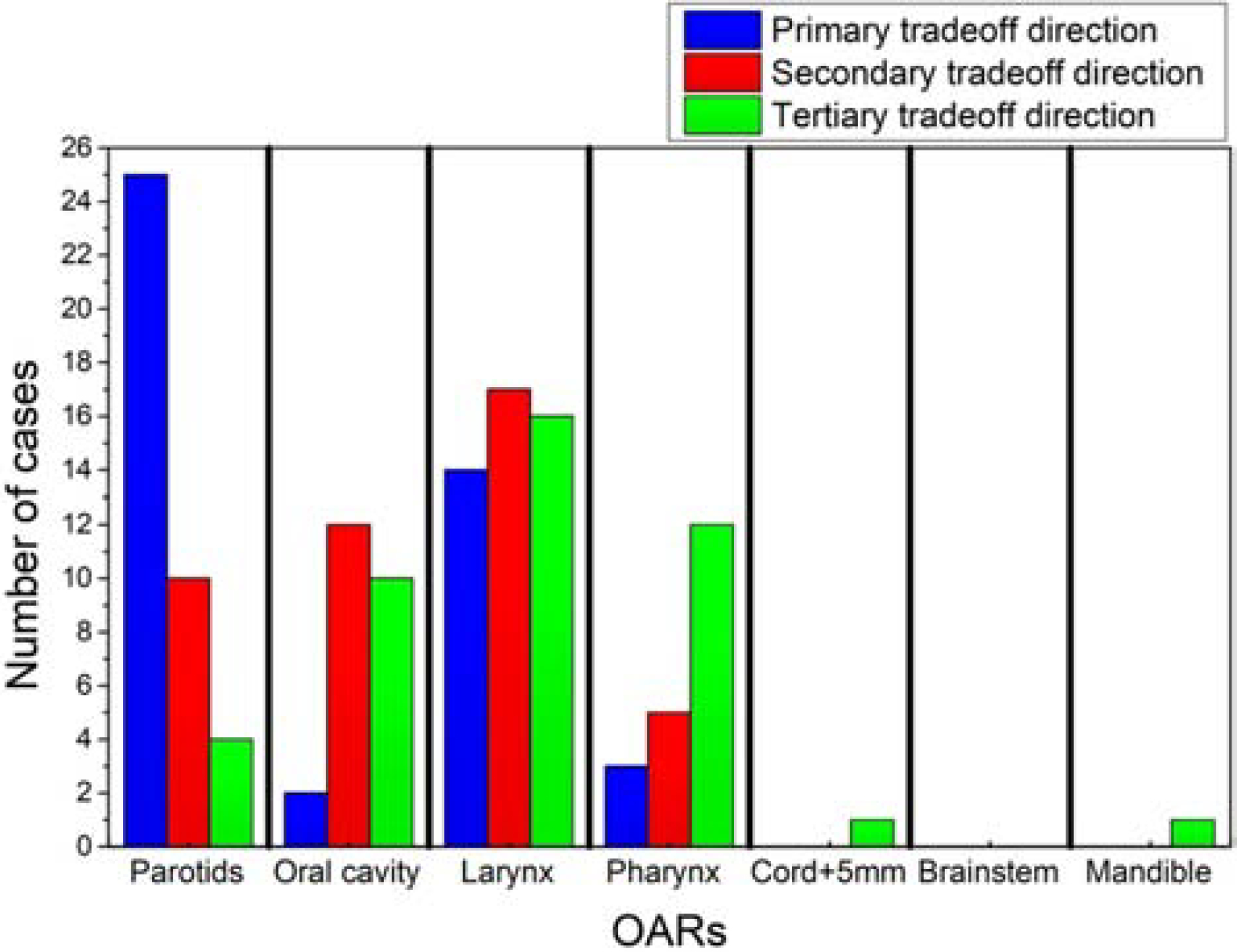
Distribution of involved OARs in the three principal tradeoff directions among validation cases. The values represent the number of cases for which the OARs have appeared in the first three tradeoff directions.

3.2. Achievability of tradeoff predictions

Figure 3 shows the RMSE between the DVHs predicted by the tradeoff hyperplane and the corresponding DVHs realized by the auto-generated tradeoff plans. These RMSE values represent the fidelity of the realized plans compared with predictions. Among these 14 plans, 12 are actual tradeoff plans and two plans are references (the KBP plan and the clinical-DVH-fitted plan). As shown, RMSEs of the max-dose constrained OARs (cord, brainstem, mandible) have higher values compared to dose-volume constrained OARs (e.g. parotid). In clinical planning, when OARs are max-dose constrained, planners tend to place very low priorities on sparing these OARs at dose-volume points other than the D_max. This results in large DVH variations not attributed to anatomy differences. Therefore, these DVH curves are not predicted as accurately as DVHs of other OARs. Due to such variations, RMSE values, even for the KBP plans, are not expected to be zero. However, as it has been shown in the literature that KBP model predicted DVHs are indeed achievable [22], the non-zero RMSE of the KBP model predictions can establish the baseline for the hyperplane model.

Figure 3.

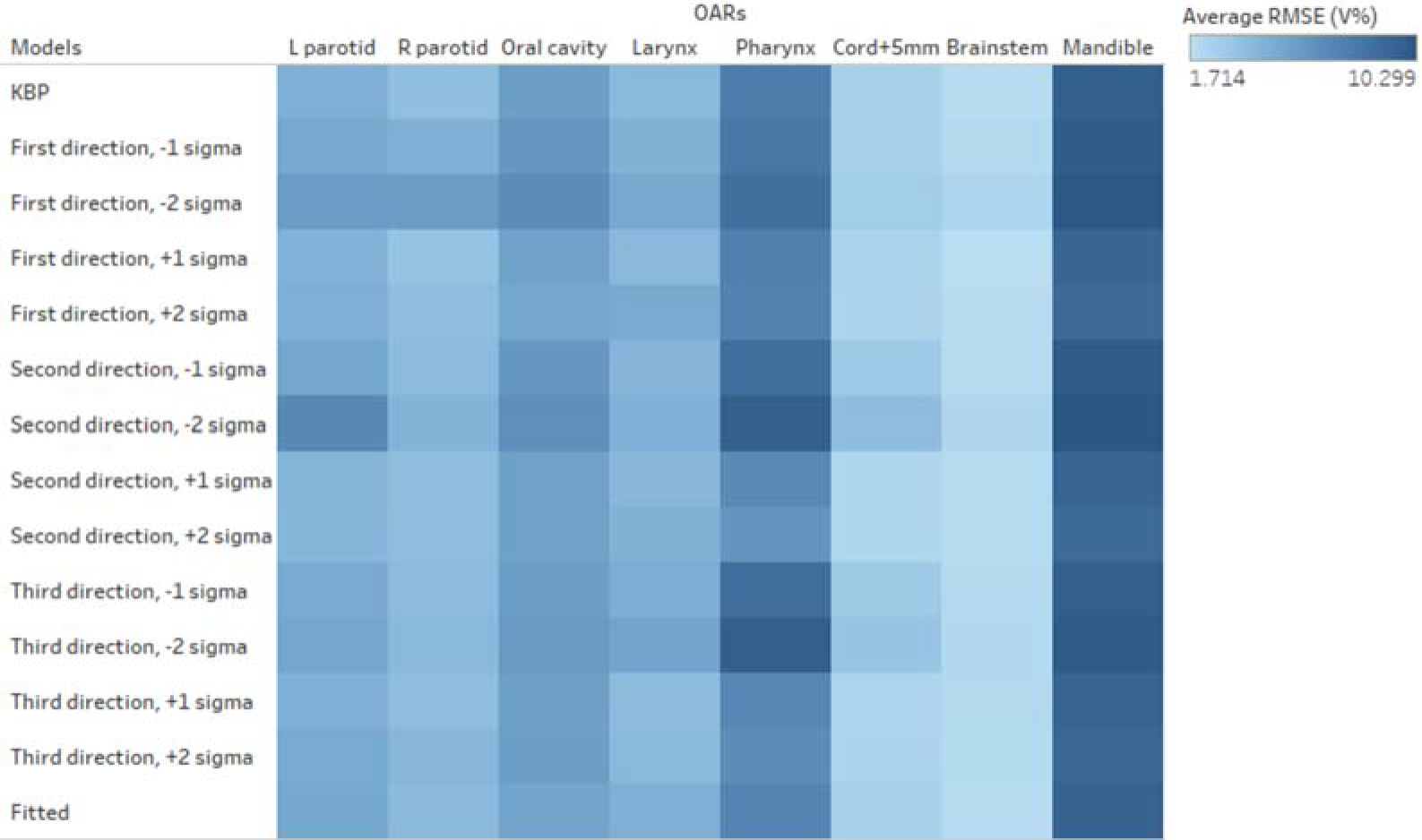
RMSE values for model predicted DVHs measured against corresponding plan-realized DVHs. Small RMSE values indicate that hyperplane predicted DVHs closely resemble the realized DVHs of auto-generated plans and hence provide evidence that the hyperplane DVH predictions are highly achievable. Different colors denote different ranges of RMSE values.

Table 1 shows the dosimetric results of hyperplane-guided tradeoff plans, the KBP plans, and the clinical-DVH-fitted plans, averaged over the validation set. The averaged dose-volume results confirm that the tradeoff plans, as a group, were achievable and of comparable plan quality to KBP plans. It is important to note that tradeoff directions are case-specific and the tradeoff directions of one case can be opposite to that of another case. After taking the average, much of the tradeoff variations are averaged out. Thus the average values listed in this table may not reflect the full range of dosimetric variations. Nevertheless, the primary tradeoff directions are still clearly reflected in the right parotid D_median, oral cavity D_median, and larynx D_median.

Table 1.

Dosimetric results of KBP plans, hyperplane-guided tradeoff plans at various tradeoff locations (±σ, ±2σ) of the three principal tradeoff directions, and the clinical-DVH-fitted plans

	KBP	Primary direction				Secondary direction				Tertiary direction				Clinical-DVH-Fitted
		+σ	−σ	+ 2σ	−2σ	+σ	−σ	+2σ	−2σ	+σ	−σ	+2σ	−σ
Right parotid Dmedian (Gy)	22.2	20.1	24.3	18.8	26.2	21.8	22.7	21.5	23.2	22.2	22.2	22.3	22.3	21.8
Left parotid Dmedian (Gy)	20.4	19.8	20.7	19.3	21.1	19.1	21.5	18.4	22.5	20.2	20.4	20.0	20.6	20.1
Oral cavity Dmedian (Gy)	29.6	29.1	29.9	28.8	30.2	29.2	29.8	28.9	30.1	29.3	29.8	29.1	29.8	29.3
Larynx Dmedian (Gy)	24.0	23.0	25.1	22.1	26.1	24.0	24.1	24.0	24.2	24.3	23.8	24.4	23.6	23.7
Pharynx Dmedian (Gy)	39.3	39.0	39.5	38.5	39.6	38.9	39.6	38.2	39.8	38.9	39.7	38.1	40.1	39.1
Cord+5mm Dmax (Gy)	43.2	43.2	43.0	43.5	43.0	42.5	43.4	40.7	43.8	42.9	43.2	42.1	43.0	42.8
Brainstem Dmax (Gy)	25.7	25.9	25.8	25.9	25.8	25.0	25.6	25.0	26.1	25.8	25.6	25.7	25.6	25.9
Mandible D1cc (Gy)	65.3	65.3	65.3	65.4	65.4	65.2	65.5	65.2	65.5	65.4	65.4	65.5	65.3	65.4

3.2. An example case illustrating the primary tradeoff direction

Figure 4 shows an example case with the original clinical plan, the KBP plan, and two tradeoff plans (sampled in the primary tradeoff direction). DVHs of the clinical plan (blue), KBP model predictions (magenta), and tradeoff predictions (grey) are shown for all contoured OARs, including right parotid, left parotid, oral cavity, larynx, pharynx, cord+5mm, brainstem, and mandible, respectively. The primary tradeoff direction for this case involves right parotid, left parotid, larynx, and pharynx, and the tradeoff DVHs cover a significant dose-volume range. On the contrary, cord, oral cavity, mandible, and brainstem show little involvement in the tradeoff decisions.

Figure 4.

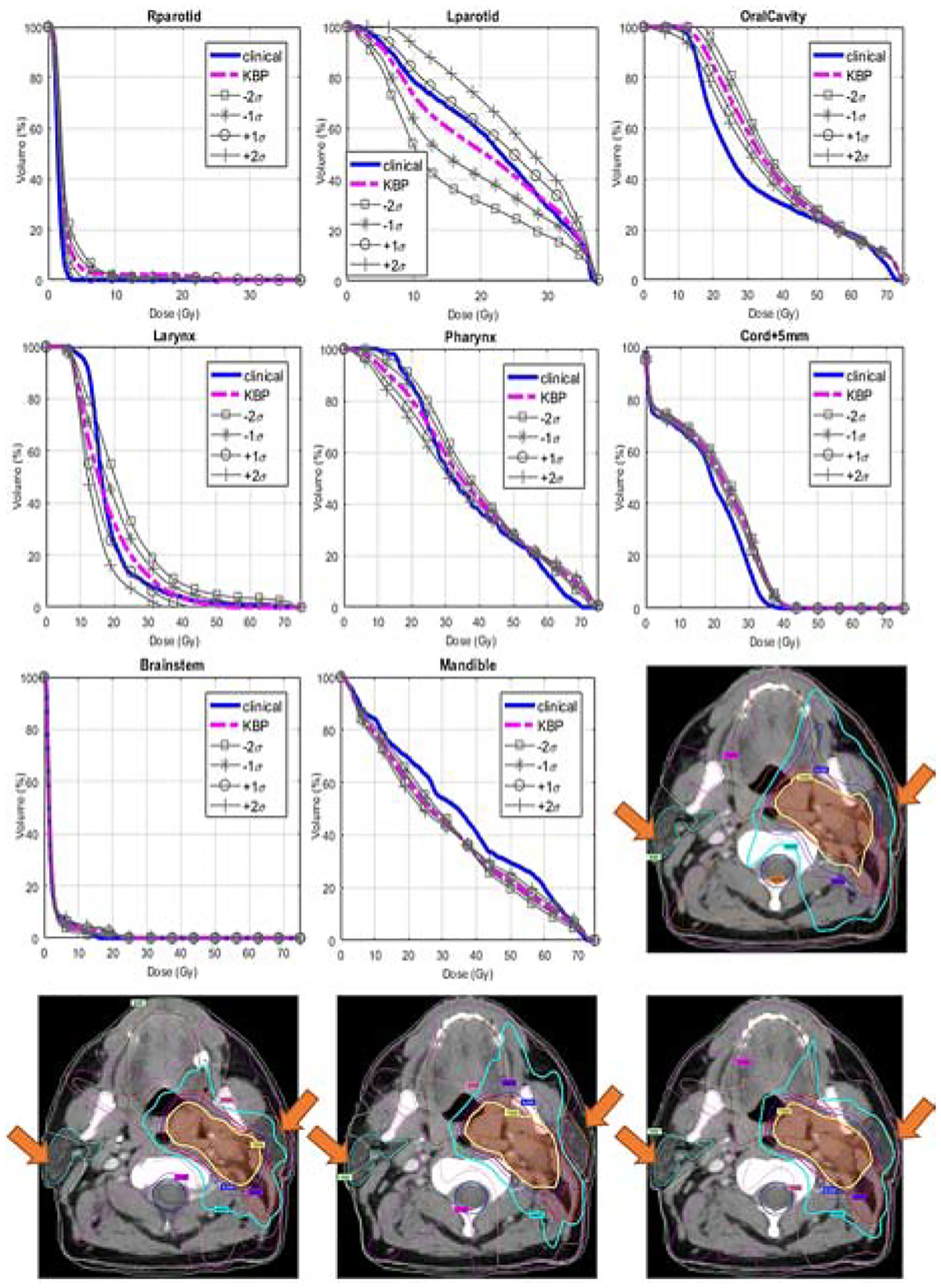
The primary tradeoff direction of an example case. In the first 8 plots, the solid blue lines are clinical DVHs; the dashed magenta lines are KBP predictions; the grey lines with different markers represent various tradeoff predictions in the primary tradeoff direction. The tradeoff direction and amplitude are extracted from the CRS (see text). σ is the standard deviation of DVH variations in this tradeoff direction. The bottom 4 dose distribution plots are, in turn, the clinical plan, the KBP plan, the −2 σ tradeoff plan, and the +2 σ tradeoff plan. Both PTVs and relevant OARs are displayed. The variation in left/right parotid dose is apparent at the locations marked by arrows.

In this case, we notice that the clinical planner traded extra sparing on the right parotid with sparing of the ipsilateral parotid (left parotid). As the figure shows, the right parotid DVH (blue) is lower than KBP prediction (magenta) and is closest to the +σ marked by “o” signs, while the left parotid is higher than KBP prediction and also is closest to the +σ marked by “o” signs. This indicates a significant tradeoff decision favoring the right parotid. The series of tradeoff DVHs in the figure also reveals the fact that if significant improvement of left parotid sparing (as suggested by the DVHs marked with squares) is warranted, then the compromise of the right parotid sparing is necessary. Therefore, providing a series of such hyperplane-guided tradeoff predictions to physicians would help them make informed decisions on the best tradeoff choices. This series of tradeoff plans are shown in the bottom row of Fig. 4, as the gradually enhanced sparing of ipsilateral parotid clearly resulted in the compromise of the contralateral parotid.

4. Discussion

To summarize, the hyperplane presents tradeoff plans that are clinically-relevant and narrows down the search space. The physician could use the hyperplane to effectively navigate the tradeoffs and make tradeoff decisions with other clinical considerations. The proposed method is an extension of previously reported knowledge models [16], which further explores the nature of variation in plans with highly similar anatomies. The RMSE data, shown in Fig. 3, illustrate that parotids and oral cavity have least variations among similar anatomies, while brainstem and mandible vary the most. The result is as expected from the clinical planning point of view. In HN planning, sparing of parotids often carries the highest priority. In order to lower the probability of severe xerostomia correlated with parotid mean dose, physicians and planners carefully examine and paint the dose based on the location of the PTVs with respect to both parotids. On the contrary, brainstems and mandibles are often evaluated for the maximum dose, so different planners have different habits in controlling the overall dose in these organs.

One important insight provided by the proposed modeling approach is the case-specific tradeoff directions. For the planning of HN IMRT, these tradeoff directions provide physicians and planners guidance on the tradeoff candidate OARs and the range of the potential tradeoffs. As shown in Fig. 2, cord and brainstem are the organs rarely involved in tradeoffs as all their tradeoff choices are collapsed onto the expected DVHs. The parotids, on the other hand, are the primary tradeoff candidates, showing the highest frequency in Fig. 2. For a specific case like the one shown in Fig. 4, the prior clinical experience indicating the D_median tradeoff range (one standard deviation) for left parotid is about 7 Gy. And, the gains in left parotid sparing, is mostly coming from the compromise in right parotid sparing, with the corresponding range of 2 Gy. Such information is valuable to physicians and planners as they can examine the feasibility of their sparing goals prior to planning, with the guidance on tradeoff directions and ranges. Further, the predicted hyperplane can be sampled and interpolated, and resulted DVHs are then used to generate the corresponding tradeoff KBP plans, with full potential of automation. This process produces an ensemble of treatment plans that represent past tradeoff experience in the clinical practice.

As mentioned earlier, multi-criteria optimization (MCO) [11–15], which has been successfully implemented in some commercial treatment planning systems [23, 24], provides a post-planning solution to the tradeoff decision problem. Given an initial plan, these systems generate a set of alternative plans based on pre-selected tradeoff criteria and allow users to navigate Pareto surfaces in the vicinity of the initial plan before final dose calculations. Each of the alternative plans represents a tradeoff location on the Pareto surface. In this work, we also provide physicians tradeoff options for each patient. Compared with MCO approaches, the proposed model is different in two aspects. First, the model is directly built with existing clinical plans. Prior knowledge about optimal tradeoffs for different patients embedded in the reference database allows the model to predict the clinically relevant tradeoff hyperplane without inverse planning. Since a unique KBP model and a set of tradeoff directions are built for each patient case, the proposed model allows flexible tradeoff modeling based on patient-specific anatomy. Patients with different sub-type and different PTV sizes may require different tradeoff considerations and such considerations are implicitly modeled during the anatomy-based CRS selection phase. Second, the exploration range of this method is guided by historical plans. From the computational performance perspective, selecting a proper exploration range is important in finding the final tradeoff plan because larger than necessary range will result in decreased efficiency and overly small range will not allow the user to navigate to the desired tradeoff location. In MCO planning, the tradeoff range is usually a fixed template set by the TPS. In comparison, the exploration ranges in the proposed model are proportional to prior plan variations in corresponding tradeoff directions. The proposed model intuitively explores the tradeoff hyperplane based on previous clinicians’ tradeoff decisions and focuses on searching in clinically meaningful tradeoff directions.

We note that successful implementation of this technique requires two conditions. First, the KBP model accurately models the anatomical variations. Improvements in high-order features and advanced modeling techniques ensure patient-specific anatomical features can be well-modeled [16]. To further reduce the effects of anatomical variations, we select only a highly similar subset of cases (CRS) for KBP modeling. Second, all the plans in the reference dataset are planned consistently. Prior evaluations of the plan quality have shown consistent quality among academic institutions. For instance, in a study by Lian et al [25], an HN IMRT KBP model from one institution was compared with a Tomotherapy KBP model from another institution and the authors found the two models were in high agreement, indicating that both institutions’ dosimetry quality are highly consistent, despite the differences in treatment modalities, delivery techniques, and treatment planning procedures. Thus, compared with the conventional knowledge-based models, the proposed model needs more training cases to establish a subset of sufficiently similar cases for plan referencing. A potential limitation of the study is the validation of the proposed model in its predictability of trade-off locations. In this study, we used a surrogate test for validation purposes. As an ensemble, clinical plans from a pool of patients are at different tradeoff locations of their own patient-specific tradeoff surfaces. We have projected each clinical plan to its corresponding tradeoff hyperplane predicted by our model and examined the clinical-DVH-fitted plans, the clinical plans, and the KBP plans and found the discrepancies between the clinical-DVH-fitted plans and the clinical plans are on average 57.8% smaller than the discrepancy between KBP plans and the clinical plans. This shows that the hyperplane model explains most of the variation between clinical plans and the KBP plans.

In addition, the variations of the CRS can be due to both tradeoff considerations and inter-planner or intra-planner plan quality variations. While the former type of variations can be extracted using the proposed method, the latter can potentially present itself as noise and cannot be effectively summarized with PCA. Therefore, the results shown in section 3.1 may vary based on the quality of the available reference database. It is also worth noting that the dataset used in this paper is representative of a single-center experience. Physicians from the same treatment facility tend to take similar and consistent tradeoffs. Therefore, we expect that the tradeoff hyperplane model will capture more variations and potentially become of higher dimensions if applied to a heterogeneous dataset with treatment plans across different cancer centers. Accordingly, the number of cases for CRS and the entire reference pool will likely need to be increased.

5. Conclusions

By taking advantage of a high-dimensional morphological feature and the KBP modeling framework, we have developed a patient-specific pre-planning technique for tradeoff hyperplane estimation to aid clinical decision-making and facilitate an efficient clinical workflow for head-and-neck treatment planning. Experiments show that the proposed hyperplane model predicts an effective subspace of tradeoff DVHs that are both achievable and clinically meaningful.