Identification of Novel RNA Design Candidates by Clustering the Extended RNA-As-Graphs Library

Abstract

Background:

We re-evaluate our RNA-As-Graphs clustering approach, using our expanded graph library and new RNA structures, to identify potential RNA-like topologies for design. Our coarse-grained approach represents RNA secondary structures as tree and dual graphs, with vertices and edges corresponding to RNA helices and loops. The graph theoretical framework facilitates graph enumeration, partitioning, and clustering approaches to study RNA structure and its applications.

Methods:

Clustering graph topologies based on features derived from graph Laplacian matrices and known RNA structures allows us to classify topologies into ‘existing’ or hypothetical, and the latter into, ‘RNA-like’ or ‘non RNA-like’ topologies. Here we update our list of existing tree graph topologies and RAG-3D database of atomic fragments to include newly determined RNA structures. We then use linear and quadratic regression , optionally with dimensionality reduction , to derive graph features and apply several clustering algorithms on our tree-graph library and recently expanded dual-graph library to classify them into the three groups.

Results:

The unsupervised PAM and K-means clustering approaches correctly classify 72–77% of all existing graph topologies and 75–82% of newly added ones as RNA-like. For supervised k-NN clustering, the cross-validation accuracy ranges from 57– 81 %.

Conclusions:

Using linear regression with unsupervised clustering, or quadratic regression with supervised clustering, provides better accuracies than supervised/linear clustering. All accuracies are better than random, especially for newly added existing topologies, thus lending credibility to our approach.

General Significance:

Our updated RAG-3D database and motif classification by clustering present new RNA substructures and RNA-like motifs as novel design candidates.

1. Introduction

The biological functions of macromolecules like proteins and RNA [1, 2] are crucially dependent on their secondary (2D) and tertiary (3D) structures. Studying known RNA structures and their characteristics can improve our understanding of the relationship between RNA structure and function, and also provide us important tools and information for design of novel RNAs for various applications [3, 4, 5].

RNA 2D structure describes the connectivity between double-stranded helical regions and single-stranded loops. This connectivity can be represented mathematically using graphs (pioneering works in [6, 7, 8, 9]). Our lab’s RNA-As-Graphs (RAG) approach represents RNA 2D structures using coarse-grained, undirected, and planar tree and dual graphs [10, 11, 12]. Tree graphs represent RNA loops as vertices, and edges denote the helical regions connecting the loops; dual graphs reverse this definition, translating helices and loop strands as vertices and edges, respectively. Using these representations, we have developed numerous RAG-based tools to study RNA structure modularity; create databases and search utilities for RNA structures and substructures ( RAG-3D [13, 14] and RAG-3Dual [15, 16]); computationally model in-vitro RNA selection [15, 14]; predict RNA graph topology and corresponding atomic models [19, 20, 21]; and develop a computational pipeline for designing RNA sequences that fold onto specific topologies using fragment assembly [22]. A webserver for our structure prediction and design algorithms is now available (http://www.biomath.nyu.edu/ragtop) [23].

Using coarse-grained approaches (recent review in [24]) not only reduces the complexity of RNA structure representation, but coarse-grained graphs also provides us with an opportunity to utilize graph theory tools to study RNA structures [25]. For example, using simple build-up rules for tree and dual graphs that represent RNA structures (Section 2.1), we can enumerate all possible tree and dual graph topologies. Our current RAG library atlas consists of 2,287 possible tree graph topologies up to 13 vertices [26] and 110,667 possible dual graph topologies up to 9 vertices [16]. Using 2D structures derived from RNA 3D structures available on the Protein Data Bank (PDB), we classify tree and dual graphs corresponding to known RNA structures as ‘existing’ topologies. The existing topologies only constitute a small fraction of our entire library. Based on graphical features extracted from the Laplacian matrices of the corresponding tree and dual graphs, we use clustering algorithms to classify as-of-yet undiscovered, or hypothetical, RNA motifs (tree and dual graph topologies) as ‘RNA-like’ or ‘non RNA-like’; the former class more likely corresponds to RNA structures [27, 26]. These RNA-like graph topologies also provide good candidates for designing novel RNA molecules, as we have demonstrated recently with our computational design pipeline [22].

To incorporate the growing library of newly solved RNA structures, we frequently update our existing topologies and graph classification results. Our most recent classifications were performed using RNA structures available in 2014 for tree [26] and 2010 for dual graphs [27]. Since then, we have redefined our definition of known RNA structures [26, 15], updated our RNA structural dataset with structures available on the PDB as of August 2018, and improved our graph enumeration algorithm to double the size of our dual graph library [16]. Here, we use our latest RNA structural dataset to update our list of existing tree graph topologies and corresponding RAG-3D database of RNA substructures and subgraphs (as done for dual graphs and the RAG-3Dual database recently [16]). Our RAG-3D database now consists of 216,398 atomic fragments/substructures corresponding to 1,376 unique tree subgraph topologies. The 80 existing tree graph topologies and list of corresponding RNA structures is available at http://www.biomath.nyu.edu/?q=rag/tree_vertices.php, and our updated RAG-3D database is available at https://github.com/Schlicklab/RAG-3D-Database/tree/Update_2019.

Next we re-evaluate and expand our graph clustering approach to use the updated list for existing tree and dual graph topologies and the recently expanded dual graph library. We apply both unsupervised, or untrained (PAM and K-means) and supervised ¹ (k-NN) clustering algorithms to cluster tree and dual graph topologies, based on features extracted from their Laplacian matrices and associated eigenvalue spectra by linear and/or quadratic regression. Using linear regression, we obtain 4 features corresponding to the slope and y-intercepts of the fitted lines for eigenvalues and squared eigenvalues; using both linear and quadratic regression, we obtain 5 features corresponding to the slope and y-intercept of the fitted line for eigenvalues and co-efficients for the fitted polynomial for squared eigenvalues (see Subsection 2.3). We analyze the linear independence of the derived features (by plotting one feature against another) to better interpret the results. For tree graphs, only 2 of the 4 linear variables and 4 of the 5 quadratic variables are linearly independent; for dual graphs all linear and quadratic variables are linearly independent. We also apply dimensionality reduction to reduce the number of features using Principal Component Analysis (PCA) and use both the full dimensional and reduced features for clustering.

Clustering results with PAM and K-means show 72–77% accuracy, measured as percentage of all existing topologies correctly classified as RNA-like, for both tree and dual graphs. For the newly added existing tree and dual graph topologies (compared to our previous studies [26] and [27], respectively), the accuracy increases to 75–82%. With k-NN clustering, the accuracy (measured by cross-validation analysis) varies significantly between features derived using linear ( 58–62% ) and quadratic regression ( 75–81% ) for tree graphs. For dual graphs, k-NN clustering accuracy is 63–69% using linear variables, increases to 67–73% using reduced quadratic variables and 76–81% using full quadratic variables.

These results confirm the utility of such classifications to predict viable new RNA motifs. That is, many more “RNA-like” RNAs have been solved compared to those we classify as “non RNA-like”. All our clustering accuracies are better than random, especially for newly added existing topologies, thus lending credibility to our approach. Our updated RAG-3D database and classification results present new RNA substructures and new RNA-like motifs as good candidates for novel RNA design.

2. Materials and Methods

2.1. RAG tree and dual graph representation

RNA-As-Graphs (RAG) represents RNA secondary (2D) structure as undirected tree and dual graphs using the following rules [10, 11, 12]:

1. All nucleotides are considered a single chain.

2. Single-stranded RNA loops that are considered in graph construction are: hairpins, dangling ends, junctions, and internal loops and bulges with more than one nucleotide. Single-residue bulges and internal loops are ignored.

3. Base-paired helices or stems with at least two canonical base pairs (AU, GC, and GU wobble) are represented. Isolated base pairs are ignored.

4. For tree graphs:

   • Vertices represent RNA loops.
   • Edges represent RNA helices connecting the loops.
   • Only one edge exists between two vertices; self-edges are not allowed.
5. For dual graphs:

   • Vertices represent RNA helices.
   • Edges represent individual loop strands connecting the helices.
   • Self-edges represent hairpin loops and helical ends; multiple edges can exist between two vertices.
   • Dangling end nucleotides are ignored.

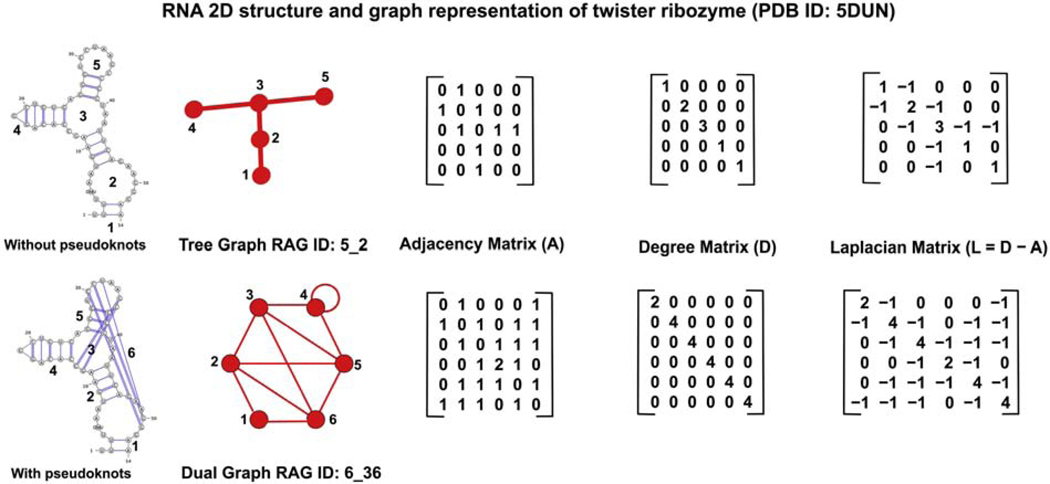
Due to its simplicity, a tree graph is a more intuitive representation of RNA 2D structure. However, tree graphs fail to capture more complicated features of RNA 2D structures, like pseudoknots (non-nested base pairs), which can be represented by dual graphs. Figure 1 shows the 5-vertex tree graph and 6-vertex dual graph representation of the twister ribozyme (PDB ID: 5DUN) without and with pseudoknots, respectively.

Figure 1:

Tree graph (RAG ID: 5_2) and dual graph (RAG ID: 6_36) for the 2D structure of the twister ribozyme (PDB ID: 5DUN) without and with pseudoknots, respectively.

Both tree and dual graphs of n vertices are uniquely defined by three n ×n matrices. The adjacency matrix ( A) indicates the number of connections between vertices, i.e., each element a_ij of A for I, j =1,…,N denotes the number of edges between vertices i and j ; the diagonal elements a_ii equals 0 for tree graphs, and equals 2 for dual graphs if vertex i has a self-edge. The diagonal degree matrix D elements d_ii equals the number of edges indecent on vertex i ; all off-diagonal elements of matrix D are 0. The Laplacian matrix is L=D− A=. For dual graphs, self-edges are ignored when constructing the Laplacian. Figure 1 shows the A, D , and L matrices for the tree and dual graphs of the twister ribozyme. The eigenvalue spectrum of the Laplacian matrix describes the topology of the graph. The first/lowest eigenvalue λ₁ = 0 . The second lowest eigenvalue λ₂, the Fiedler value, describes the connectivity of the graph [28].

2.2. RAG library and graph ID assignment

Based on the rules used to represent RNA 2D structures using graphs, we have previously used graph enumeration to generate possible unique tree and dual graph topologies. Our RAG library consists of 2287 non-isomorphic tree graph topologies for 2–13 vertices (where vertices represent RNA loops) [26] and 110,667 non-isomorphic dual graph topologies for 2–9 vertices (where vertices represent RNA helices) [16]. Each graph is uniquely determined by its Laplacian eigenvalue spectrum and adjacency matrix. Note that some non-isomorphic graphs can have identical eigenvalue spectra. Each unique graph (i.e., different connectivity) is assigned a graph identifier of the form V_n , where V is the number of vertices and n is the unique integer given to each non-isomorphic graph with the same vertex number.

To label the graph of an RNA 2D structure, the tree and/or dual graph is constructed for the 2D structure as per the rules in Section 2.1, and the corresponding adjacency matrix and Laplacian eigenvalue spectrum are determined. If the RAG tree and/or dual graph library contains only one graph with the same eigenvalue spectra as the query RNA, the RNA is assigned its RAG ID. If there are two or more graphs with the same eigenvalue spectra, the RNA is assigned the RAG ID of the graph that is isomorphic to it (determined by generating permutations of the query adjacency matrix and comparing it to the adjacency matrix of the graph in the library). This is important to correctly label RNA 2D structures for subsequent analysis. For dual graphs, we have previously updated our graph ID assignment procedure to distinguish between non-isomorphic graphs with identical spectra [29]. Here we update our tree graph ID assignment procedure to do the same.

2.3. Calculating graph features

To represent each tree and dual graph topology, we use coordinates derived from the corresponding Laplacian eigenvalue spectrum λ₂,…, λ_n (λ₁ is ignored as it is always equal to 0) using least-squared regression. Graphs with only 2 vertices (2_1 for tree graphs and 2_1, 2_2, and 2_3 for dual graphs) are ignored as they have only one non-zero eigenvalue and hence a single point for least-squared regression. See Section S1 in Supplementary Data for more details on least-squared regression. The procedure to calculate the features for all tree and dual graph topologies with number of vertices n > 2 is as follows:

1. For each graph topology, we draw the points (1, λ₂),(2,λ₃),…,(n−1,λ_n) , referred to as ‘eigenvalue points’, on a plane and perform linear least-squared regression to calculate parameters α₁ and β₁, the slope and the y-intercept, respectively. To ensure that the slope parameters are independent of number of vertices, α₁ is scaled as nα₁.

2. For each graph topology, we draw the points $\left(1,{\lambda }_2^2\right),\left(2,{\lambda }_3^2\right),\dots ,\left(n-1,{\lambda }_n^2\right)$ , referred to as ‘squared eigenvalue points’, on a plane and perform one of the following:

   • linear least-squared regression to calculate parameters α₂ and β₂ , the slope and the y-intercept, respectively. To ensure that the slope parameters are independent of number of vertices, α₂ is scaled as nα₂ . In this case, the graphs are represented by four variables [x₁, x₂, x₃, x₄]=[nα₁, β₂,nα₂,β₂].
   • quadratic least-squared regression to calculate parameters a , b , and c , the coefficients of the fitted polynomial ax² + bx+c . In this case, the graphs are represented by five variables $\left[x_1,x_2,x_3,x_4,x_5\right]=\left[n{\alpha }_1,{\beta }_1,a,b,c\right]$ .
3. To ensure each coordinate has an equal contribution, we normalize the above obtained coordinates as follows:

   $$x_m^{*}=\left({\overline{x}}_1/{\overline{x}}_m\right)x_m,\text{where}$$

   $${\overline{x}}_m=\text{average}\text{of}\text{the}m\text{th}\text{coordinate}\text{over}\text{all}\text{tree}\text{or}\text{dual}\text{graph}\text{topologies}$$

   Tree and dual graph features are calculated separately.

4. Additionally, using Principal Component Analysis (PCA), we map the normalized coordinates onto two variables to represent and/or visualize each tree or dual graph topology. Note that this method for dimensionality reduction is different from the Multi-Dimensional Scaling method (MDS) we used previously [26] (as MDS for more than 100,000 dual graphs requires more time and memory), but produce similar results.

In this paper, we will refer to the variables obtained using linear or quadratic regression for squared eigenvalue points (Step 2) as linear or quadratic variables, respectively. We refer to the normalized variables before PCA (Step 3) as full variables and the two variables obtained after PCA (Step 4) as reduced variables. We also analyzed the linear independence of both linear and quadratic variables (by plotting one variable against another) for tree and dual graphs. For tree graphs, the number of linearly independent variables is 2 (of 4) and 4 (of 5) for linear and quadratic variables, respectively; for dual graphs all 4 linear variables and all 5 quadratic variables are linearly independent (see Section S2 in Supplementary Data). Analysis of the linear independence of variables helps us interpret the similarities and/or differences between the results obtained when using full or reduced variables.

We perform graph clustering (described below) on 4 different sets of variables for both tree and dual graphs: linear reduced, quadratic reduced, linear full, and quadratic full. We have only used linear reduced variables (obtained using MDS) previously [29, 27, 26].

2.4. Clustering algorithms

Using the variables for each graph topology calculated in Subsection 2.3, we apply three clustering algorithms, PAM, K-means, and k-NN, to classify all tree and dual graph topologies in our RAG library into two categories/clusters: ‘RNA-like’ (graph topologies likely to correspond to RNA structures) and ‘non RNA-like’ (graph topologies unlikely to correspond to RNA structures). Tree and dual graph topologies are clustered separately. For each clustering techniques, N denotes the total number of graph topologies (2286 for tree graphs and 110,664 for dual graphs, as graphs with 2 vertices are not considered), and K = 2 denotes the number of clusters.

Of the three clustering techniques, PAM and K-means are unsupervised clustering algorithms as they do not require any training data. In contrast, k-NN requires training data (i.e., features of known RNAs); hence the known RNAs are used for training the RNA-like group. The three clustering algorithms are briefly described below. See Section S3 in Supplementary Data for further details.

2.4.1. Partitioning Around Medoids (PAM)

The PAM algorithm divides N points into K clusters by randomly choosing K data points as ‘medoids’ and assigning the remaining N – K points to the closet medoid (using Euclidian distance). Following initialization, in each iteration of PAM, all K medoids are interchanged sequentially with every other point in their corresponding clusters and the cluster identities for all points are re-assigned. The new medoids are kept if the total cost function – the sum of the Euclidian distances of each point from their corresponding medoid – decreases. This procedure is continued until it converges to an optimal solution.

For purposes of this paper, after the data points are divided into two clusters, the cluster with the higher number of existing graph topologies is labeled ‘RNA-like’. The accuracy of the clustering is calculated in two different ways: 1) as the percentage of all existing topologies correctly classified as RNA-like, and 2) as the percentage of newly added existing topologies correctly classified as RNA-like.

2.4.2. K-means clustering

The K-means clustering algorithm divides N points into K clusters by randomly initializing K cluster centers and assigning initial clusters to all N points based on the closet cluster center (using Euclidian distance). In each iteration of the K-means algorithm, the K cluster centers are updated as the average or mean of the points in the corresponding clusters, and the cluster identities of all N points is re-assigned. The process continues until a specified number of iterations is reached or convergence to an optimal solution is achieved (defined by no change in cluster identities).

Similar to PAM clustering, the cluster with the higher number of existing graph topologies is labeled ‘RNA-like’. The accuracy of the clustering is calculated in two different ways: 1) as the percentage of all existing topologies correctly classified as RNA-like, and 2) as the percentage of newly added existing topologies correctly classified as RNA-like.

2.4.3. k-Nearest-Neighbors (k-NN)

k-NN is a supervised clustering algorithm that uses training samples for K clusters to assign cluster identities to all points based on the majority of the cluster identities of their k nearest neighbors from the training sample. Here we use all existing tree and dual graph topologies (see Section 3.2) as training samples for the RNA-like cluster and an equal number of randomly selected hypothetical tree or dual graph topologies as training samples for the non RNA-like cluster. Note that only using the previously existing tree and dual graph topologies as the training sample is not feasible as their number is low (45 for tree graphs and 33 for dual graphs). As the training examples of the non RNA-like cluster are selected randomly, the clustering is performed 10 times, each time with different randomly selected graph topologies. The number of nearest neighbors is varied as all odd values between k= 1 to 19, and the accuracy of clustering is calculated using leave-one-out (LOO) and 10-fold cross validation.

2.4.4. Implementation in Matlab

We use least-squared regression and clustering functions already implemented in Matlab (version R2019a) for calculating graph features and graph clustering. We use the linsolve() function to perform linear regression, the polyfit() function to perform quadratic regression, and the pca() function to perform PCA dimensionality reduction (see Subsection 2.3). We use the kmedoids(), kmeans(), and fitcknn() functions to perform PAM, K-means, and k-NN clustering, respectively, and use the kfoldLoss() function to calculate the cross-validation error for k-NN clustering. All calculations are performed on an iMac machine, with 3.5 GHz Intel Core i7 processor and 32 GB RAM. Typical calculations range from a few seconds for PAM and K-means clustering to a few minutes for multiple k-NN trials.

3. Results

3.1. Updating existing tree graphs topologies and RAG-3D database

In our previous study, we classified tree graph topologies corresponding to RNA structures available on the PDB as of August 2014 as ‘existing’ topologies [26]. To update our list of existing tree graph topologies, we use our latest RNA structural dataset (as of August 31, 2018) described in our recent study to update existing dual graphs [16]. We remove all pseudoknots (as tree graphs cannot represent pseudoknots) in the 2D structures, as well as structures with no or single/isolated base pairs or only one vertex, and then use the remaining 4,488 RNA structure files for further study. See Section S4 in the Supplementary Data for details on the RNA structure files.

Of the 4,488 RNA structure files, 1,293 files have more than 13 vertices and were not assigned graph IDs (as our enumerated tree graph library consists of tree graph topologies between 2–13 vertices). Table 1 shows the number of existing topologies for vertex numbers 2–13, corresponding to the remaining 3,195 RNA 2D structure files. In total, we have classified 80 unique tree graph topologies as existing topologies. These existing topologies are used for supervised graph clustering algorithms in Subsection 3.2. All 80 existing topologies and the corresponding RNA 2D structures are so indicated on our RAG resource http://www.biomath.nyu.edu/?q=rag/tree_vertices.php.

Table 1:

Number of existing tree graph topologies for the updated RNA dataset. For comparison, the number of existing dual graph topologies from our recent paper [16] are also shown.

Vertex Number	Number of Topologies	Number of Existing IDs	Percentage of Existing IDs (%)
Tree Graphs
2	1	1	100
3	1	1	100
4	2	2	100
5	3	3	100
6	6	5	83.33
7	11	10	90.91
8	23	11	47.83
9	47	9	19.15
10	106	14	13.20
11	235	11	4.68
12	551	5	0.90
13	1301	8	0.61
Total	2287	80	3.5
Dual Graphs
2	3	3	100
3	8	7	87.5
4	29	17	58.62
5	110	20	18.18
6	508	22	4.33
7	2551	21	0.82
8	14670	14	0.10
9	92788	17	0.02
Total	110,667	121	0.11

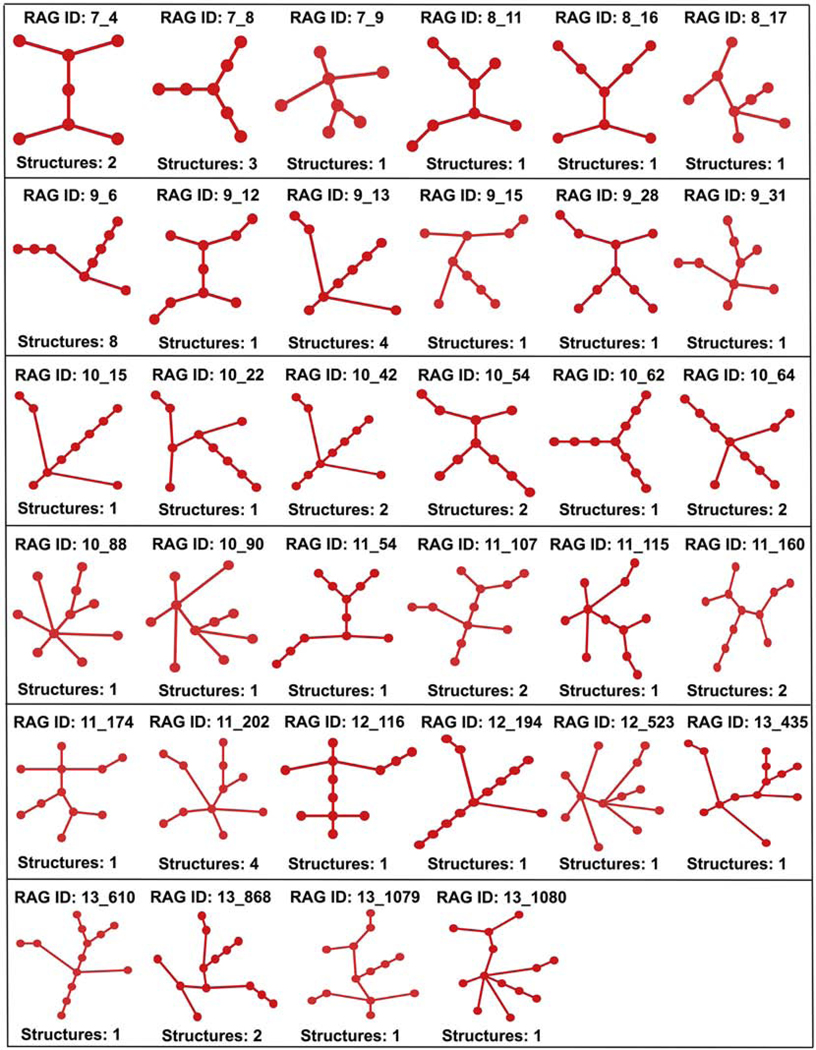
Of the 80 existing tree graph topologies, 46 were part of the 57 graph topologies classified as existing in our previous study (note that we revised our initial number of 85 existing topologies to 57 as 28 were mistakingly labeled as existing in our previous study [26]); the remaining 34 are newly-discovered tree graph topologies (shown in Figure 2). Some of the newly discovered tree graph topologies include: 7_4 (e.g., ci-di-AMP riboswitch, PDB 4W90), 9_13 (e.g., phosphoribosyl pyrophosphate aptamer, PDB 6CK4), 10_22 (e.g. HIV-1 core packaging signal, PDB 2N1Q), 11_115 (e.g., group II intron, PDB 5G2X), and 11_160 (e.g., varkud satellite ribozyme, PDB 4R4V). See Table S3 in Supplementary Data for the 11 of the previous 57 topologies that were removed from the list due to being superseded by updated structures in the PDB, the chain/model being removed from the updated RNA dataset, or assigned a different topology using the consensus 2D structure (see Supplementary Data Section S4 for details on 2D structure files).

Figure 2:

The 34 newly identified existing tree graph topologies, along with the corresponding number of full RNA structures (before graph partitioning). The full list of existing tree graph topologies and their corresponding RNA structures is available at http://www.biomath.nyu.edu/?q=rag/tree_vertices.php.

We also updated our RAG-3D database [14] of RNA subgraphs and corresponding atomic fragments to include all subgraphs up to 13 vertices. Our RAG-3D database now consists of 216,398 atomic fragments corresponding to 1,376 unique tree graph topologies. The updated RAG-3D database provides us with a much larger repertoire of subgraphs and atomic fragments that can be used for RNA structure prediction and design using fragment assembly [21, 22]. The updated RAG-3D database is available at https://github.com/Schlicklab/RAG-3D-Database/tree/Update_2019.

3.2. Graph classification results

To distinguish tree and dual graph topologies that are more likely to correspond to RNA structures, we had previously used graph clustering techniques to classify tree and dual graph topologies into two clusters: ‘RNA-like’ and ‘non RNA-like’ [27, 26]. Using the newly solved RNA structures and our extended dual graph library [29] we repeat the clustering analysis. Four different sets of graph variables (linear reduced, quadratic reduced, linear full, and quadratic full) are calculated as described in Subsection 2.3, and clustering is performed (as described in Subsection 2.4) separately for 2286 tree graphs and 110,664 dual graphs with more than 2 vertices.

For determining the accuracy of unsupervised PAM and K-means clustering as defined in Subsection 2.4, we use the list of 79 existing tree graph topologies (see Subsection 3.1) and 118 existing dual graph topologies (identified recently [16]) with more than 2 vertices. These existing topologies are also used as training samples for the RNA-like cluster for the supervised k-NN clustering. For accessing the accuracy of PAM and K-means against newly added existing topologies, we use the 34 (of 79) tree graph and 85 (of 118) dual graph topologies [15, 16] identified since 2014 [26] and 2010 [27], respectively.

3.2.1. PAM and K-means results

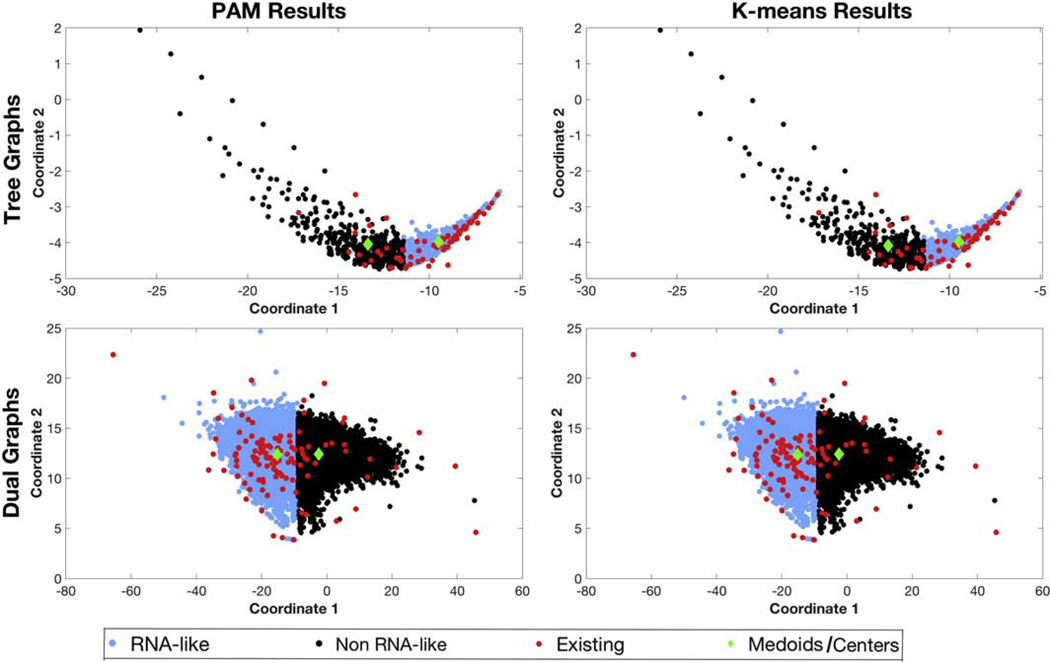
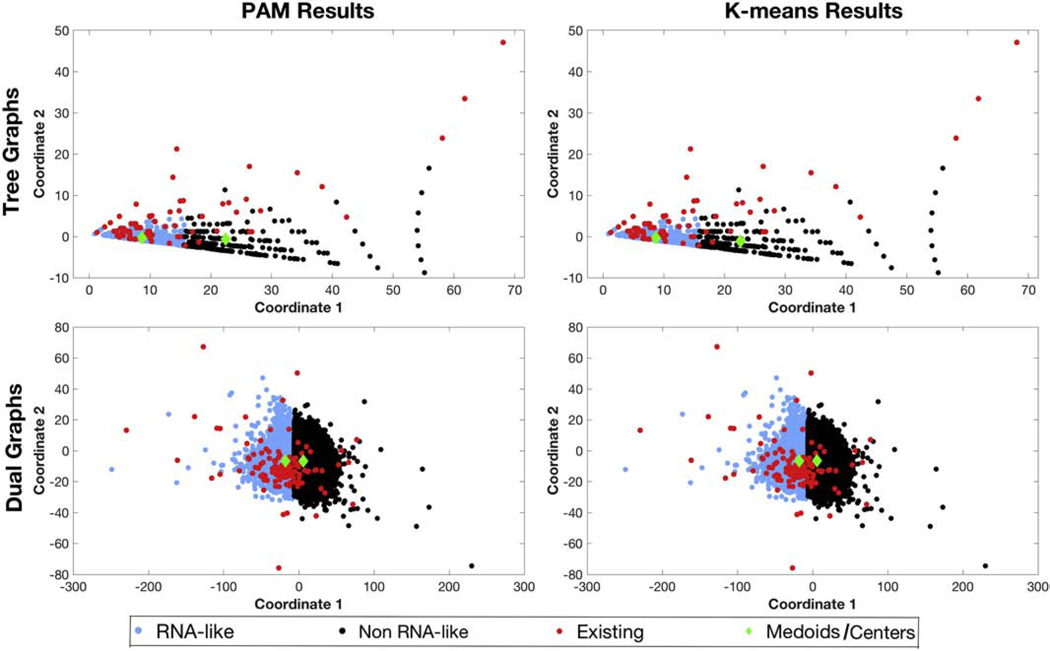
Figure 3 shows the results of the unsupervised PAM and K-means clustering algorithm for tree and dual graph topologies using linear reduced variables. Looking at the distribution of 2286 tree graph topologies in our library (i.e., existing and hypothetical combined), PAM and K-means place ≈ 72% in the RNA-like cluster (shown in blue) and the remaining 28% in the non RNA-like cluster (shown in black). The distribution is more even for dual graphs, with both RNA-like and non RNA-like clusters containing ≈ 50% of 110,664 dual graph topologies. Figure 4 shows the results of PAM and K-means using quadratic reduced variables. Compared to linear reduced variables, there is a significant increase in the total number (from 72% to 82%) of all tree graph topologies in the RNA-like cluster, whereas the distribution remains even for all dual graphs.

Figure 3:

Clustering results using PAM and K-means algorithms for tree and dual graphs with linear reduced variables. The RNA-like topologies are shown in blue and non RNA-like topologies are shown in black. The existing topologies corresponding to known RNA structures are shown in red. The cluster medoids/centers are shown as green diamonds.

Figure 4:

Clustering results using PAM and K-means algorithms for tree and dual graphs with quadratic reduced variables. The RNA-like topologies are shown in blue and non RNA-like topologies are shown in black. The existing topologies corresponding to known RNA structures are shown in red. The cluster medoids/centers are shown as green diamonds.

Accessing the accuracy of the clustering against all existing topologies, both algorithms correctly classify 61 (77%) of the 79 existing tree graphs (ignoring 2_1) and 89 (75%) of the 118 existing dual graphs (ignoring 2_1, 2_2, and 2_3) as RNA-like (Table 2). However, the accuracy drops slightly to ≈ 73% for both tree and dual graphs with quadratic reduced variables. This suggests that quadratic variables may be worse than linear ones for distinguishing RNA-like from non RNA-like tree graph topologies with unsupervised clustering methods.

Table 2:

PAM and K-means clustering accuracy. Shown for all tree and dual graph topologies with 3 or more vertices are the motifs classified as RNA-like and non RNA-like by unsupervised clustering algorithms PAM and K-means using reduced linear and quadratic variables. Also shown are the number and percentage of existing tree and dual graph topologies correctly classified as RNA-like.

	(a) Tree graphs
	All Topologies (Total: 2286)		Existing Topologies (Total: 79)
	RNA-like	non RNA-like	RNA-like	non RNA-like
Method	Linear variables
PAM	1645	641	61	18
	(71.96%)	(28.04%)	(77.22%)	(22.78%)
K-means	1643	643	61	18
	(71.87%)	(28.13%)	(77.22%)	(22.78%)
Method	Quadratic variables
PAM	1889	397	58	21
	(82.63%)	(17.37%)	(73.42%)	(26.58%)
K-means	1890	396	58	21
	(82.68%)	(17.32%)	(73.42%)	(26.58%)
	(b) Dual graphs
	All Topologies (Total: 110,664)		Existing Topologies (Total: 118)
	RNA-like	non RNA-like	RNA-like	non RNA-like
Method	Linear variables
PAM	55,268	55,396	89	29
	(49.94%)	(50.06%)	(75.42%)	(24.58%)
K-means	55,258	55,406	89	29
	(49.93%)	(50.07%)	(75.42%)	(24.58%)
Method	Quadratic variables
PAM	57,078	53,586	86	32
	(51.58%)	(48.42%)	(72.88%)	(27.12%)
K-means	56,994	53,670	86	32
	(51.50%)	(48.50%)	(72.88%)	(27.12%)

Accessing the accuracy against newly added existing topologies, 27 of the 34 (79.41%) tree graph topologies are correctly classified as RNA-like using linear reduced variables, which increases to 28 (82.35%) using quadratic reduced variables. For dual graphs, 67 of 85 (78.82%) topologies are correctly classified as RNA-like using linear reduced variables, dropping to 64 (75.29%) using quadratic reduced variables. However, these accuracies are greater as compared to accuracies for all existing topologies (both previous and new), indicating that our approach is good at predicting viable new RNA motifs.

The results for PAM and K-means clustering using full variables (shown in Supplementary Table S4) are almost identical to results obtained using the corresponding reduced variables.

3.2.2. k-NN results

Table 3 shows the average accuracy over 10 trials for the supervised k-NN clustering algorithm, using full linear and quadratic variables, for different values of number of nearest neighbors ( k ). See Tables S5–S12 in the Supplementary Data for maximum and minimum accuracies over the 10 runs. Using linear full variables, the average accuracy for all values of k for tree graphs is 58–62% , whereas the accuracy is 67–69% for almost all values of k for dual graphs. Using quadratic variables, the accuracy for both tree and dual graphs increases to 76–81% .

Table 3:

Average accuracy (over 10 trial runs) of k-NN clustering algorithm with full linear and quadratic variables using leave-one-out (LOO) and 10-fold cross validation for tree and dual graphs.

	Average Accuracy (%)
	Linear variables		Quadratic variables
	LOO	10-fold	LOO	10-fold
Neighbors	Tree Graphs
1	60.82	60.51	75.63	76.08
3	62.66	62.78	77.28	76.71
5	58.73	59.43	78.61	78.61
7	59.94	60.32	80.25	80.32
9	58.73	59.43	81.08	80.70
11	58.86	58.73	79.68	80.32
13	58.23	59.62	79.24	78.23
15	59.68	59.62	77.66	77.47
17	60.51	60.95	76.52	76.39
19	60.70	59.56	75.70	76.27
Neighbors		Dual Graphs
1	64.24	63.86	78.81	78.81
3	65.55	65.59	81.10	81.06
5	66.74	66.53	80.17	80.17
7	67.84	67.67	79.62	79.24
9	68.64	68.01	79.41	78.81
11	68.86	68.35	78.98	78.94
13	68.35	68.35	78.31	78.22
15	68.60	69.19	77.75	77.50
17	68.52	68.31	77.71	77.25
19	68.69	68.39	76.91	76.57

For tree graphs, the k-NN average accuracies using reduced variables (shown in Supplementary Table S13) are very similar to the ones obtained using corresponding full variables. For dual graphs, the accuracy obtained using quadratic reduced variables (shown in Supplementary Table S13) is 67–73%, which is ≈ 3–8% less than the accuracy obtained using quadratic full variables (Table 3). This may be because all 5 quadratic variables for dual graphs are linearly independent and representing them using 2 reduced variables leads to a decrease in accuracy. However, this difference in accuracy is not observed between full and reduced linear variables for dual graphs or full and reduced quadratic variables for tree graphs, where the number of linearly independent full variables is also more than 2 (Subsection 2.3).

These results indicate that PAM and K-means have a higher accuracy than k-NN clustering results with linear variables, whereas the accuracy percentages are similar with quadratic variables. In addition, PAM and K-means have similar clusters and accuracy for both tree and dual graphs, and k-NN performs better for dual graphs than tree graphs using linear variables. All methods are better than random, lending utility to our approach.

3.3. Misclassified existing topologies with unsupervised methods

We also examine the tree and dual graph topologies that are misclassified as non RNA-like by PAM and K-means clustering. Since the accuracy of PAM and K-means was identical for reduced and full variables, and was higher when using linear as opposed to quadratic variables for both tree (77% vs 73%) and dual graphs (75% vs 73%), we choose the clusters using linear reduced variables for this analysis.

Figure 5 shows the 18 existing tree graph topologies (including 7 newly added ones), along with the corresponding number of RNA structures and one example, that are misclassified as non RNA-like. We see that 13 of 18 graph topologies correspond to only one known structure (not counting substructures obtained via graph partitioning) in our RNA structural dataset. Yet, some tree graph topologies that correspond to more than 10 structures (even as high as 580 for 5_3) are also misclassified. Most of the 18 topologies either contain multiple junctions or higher-order junctions (with 5 or more helices) that are less prevalent in RNA structures. However, the two simplest topologies, 5_3 and 6_5, have multiple representatives.

Figure 5:

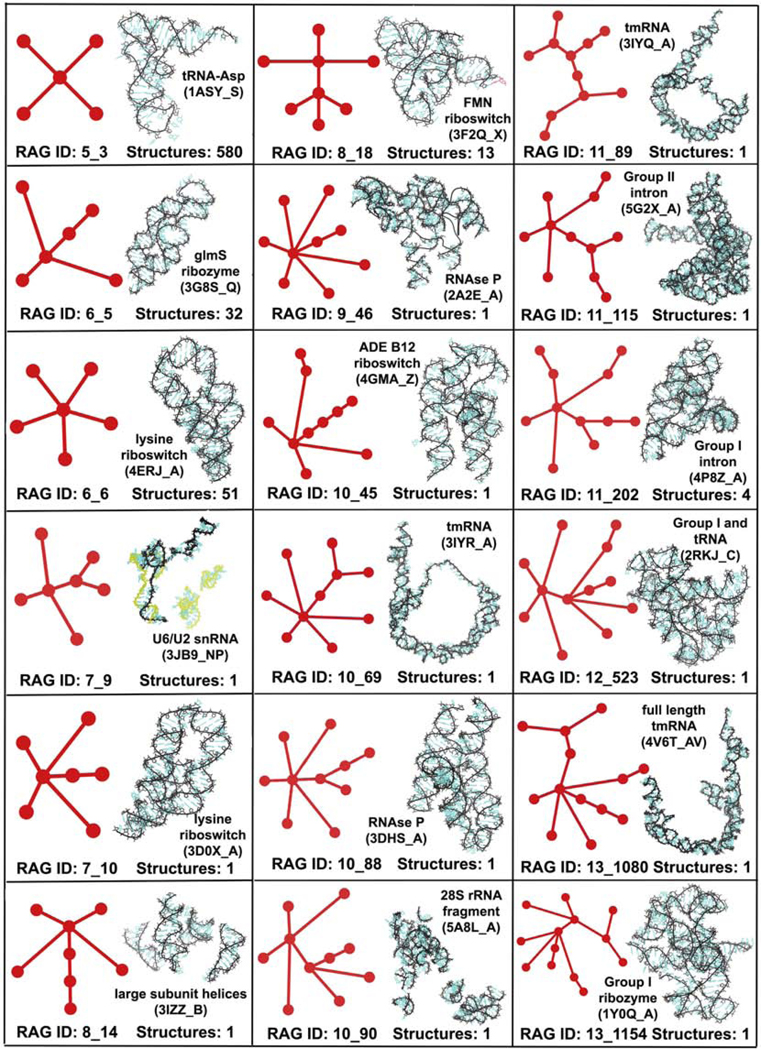
Tree graph topologies that were misclassified as non RNA-like using linear variables with PAM and K-means clustering. The total number of full RNA structures corresponding to these tree graph topologies in our RNA structural dataset are also shown, along with an image (and PDB ID) of one example.

Figure 6 shows the 29 existing dual graph topologies (including 18 newly added ones), along with the corresponding number of RNA structures and one example, that are misclassified as non RNA-like. Unlike tree graphs where the majority of misclassified topologies had only one RNA example, only 10 of the 29 dual graph topologies have only one corresponding known RNA, but 21 of the 29 have less than 10 structures. However, similar to tree graphs, some very common dual graph topologies (e.g., 3_5, 4_19, 4_27, and 5_2) with multiple representatives are also misclassified.

Figure 6:

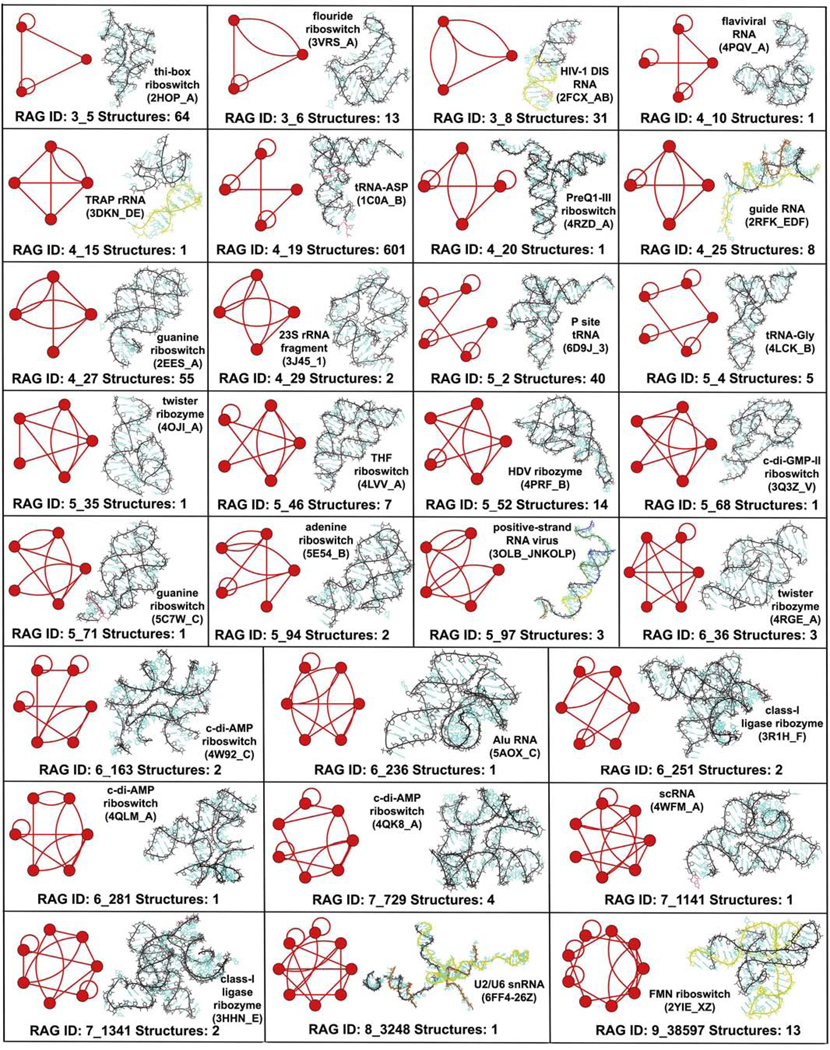
Dual graph topologies that were misclassified as non RNA-like using linear variables with PAM and K-means clustering. The total number of full RNA structures corresponding to these dual graph topologies in our RNA structural dataset are also shown, along with an image (and PDB ID) of one example.

One potential aspect for misclassification of topologies could be the linear regression used to extract graph features (Subsection 2.3). We looked at the difference between the mean squared error (MSE) of the linear regression for correctly classified vs misclassified graph topologies. For tree graphs, the average MSE (for both eigenvalues and squared eigenvalues) for 18 misclassified topologies is ≈ 7–8 times higher than that for the 61 correctly classified topologies (Table S14 in Supplementary Data). This suggests that quadratic regression may represent tree graph features better. However, this is not the case for dual graphs, where the average MSE is similar for misclassified and correctly classified topologies (Supplementary Data Table S15 ).

From the above data, it is difficult to pinpoint the reasons for classifying some RNAs as non RNA-like, but clearly the misclassified motifs are a minority. The complex junctions evident in the tree graphs may explain this behavior. In the future, more refined machine learning approaches trained on known RNAs could improve our classifications (see Discussion).

4. Discussion

Our updated list of existing tree graph topologies, the RAG-3D database of RNA substructures, and updated classifications of tree and dual graphs into RNA-like and non RNA-like topologies support the utility of our graph theoretical approach. Our clustering results using linear variables show that the unsupervised PAM and K-means approaches correctly classify about 75–77% of existing graph topologies as RNA-like for both tree and dual graphs (Table 2) ; the supervised k-NN accuracy increases to a similar or higher range when using quadratic variables (Table 3) . The existing tree graph topologies and list of corresponding RNA structures is available at http://www.biomath.nyu.edu/?q=rag/tree_vertices.php, and our updated RAG-3D database is available at https://github.com/Schlicklab/RAG-3D-Database/tree/Update_2019.

Significantly, both the unsupervised clustering algorithms (PAM and K-means) provide better accuracies for newly added existing topologies as compared to the full list (previous and new motifs combined). This provides us with confidence that this classification, even though based on very simple descriptors of complex data, is reasonable and will continue to improve as our list of existing tree and dual graph topologies is updated in the future. Similar to our previous study [26], the supervised clustering algorithm k-NN has a lower accuracy than the unsupervised algorithms using linear variables, possibly because we have known data only for one class (RNA-like). That is, supervised clustering is, incomplete as it is, based on using known RNAs to train the RNA-like cluster and randomly selected graph topologies for the non RNA-like cluster. However, the k-NN algorithm results are better than our previous study [26], which indicates that the accuracy can improve as we include more RNA structures as they emerge.

Interestingly, the k-NN accuracies are comparable to PAM and K-means when using quadratic variables, and even surpass them for some values of nearest neighbors (Table 3). This improvement highlights the potential advantage of using supervised clustering methods with features derived by polynomial regression. In addition, the unsupervised algorithms distinguish between RNA-like and non RNA-like clusters by an almost straight line (Figures 3 and 4), and may suggest an oversimplified classification, even with the high accuracy. In the future, it may be possible to explore different methods to derive graph features and cluster topologies classified as RNA-like and non RNA-like using various algorithms. Machine learning approaches could also be useful, with training based on the successful (existing RNA) group. Note that although using full dimensional variables was not fruitful before [29, 27], our k-NN results suggest that using them with polynomial regression can be beneficial, and warrants further investigation with enlarged RNA databases. It may also be interesting to pool the tree and dual graph descriptors for a unified clustering and/or weighting the existing topologies based on the number of representative structures.

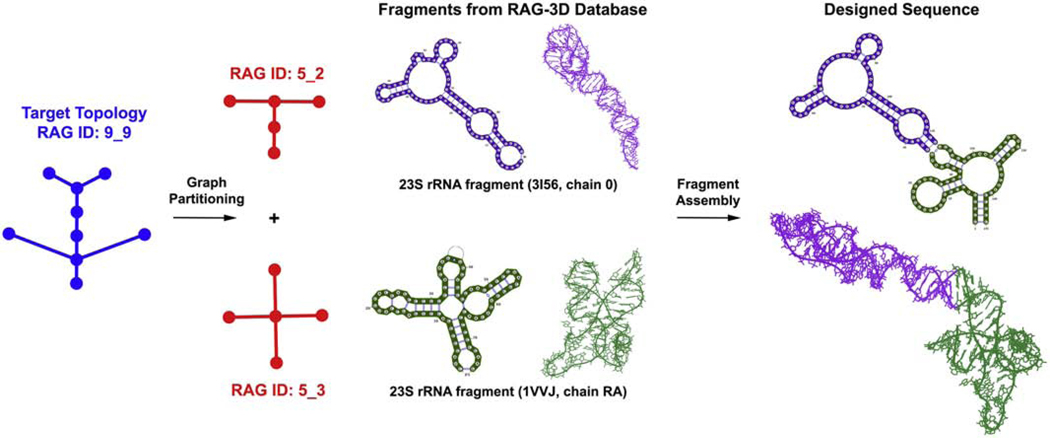
Our updated RAG-3D database of atomic fragments for tree graphs and the classification of RNA-like motifs will benefit our recently developed computational design pipeline. Indeed, initial experimental testing showed the utility of our approach [22]. As sketched in Figure 7, our design pipeline uses graph partitioning to partition the target RNA-like graph into subgraphs, extract corresponding atomic fragments from our RAG-3D database, construct a new RNA sequence/structure using fragment assembly (F-RAG), and screen the top scoring sequences using two RNA 2D structure prediction programs to produce successful sequences that fold onto the target RNA-like topology [22]. The RNA-like topologies identified here provide novel design candidates, especially with the updated RAG-3D database which includes a larger collection of atomic fragments for fragment assembly. Our preliminary results indicate that using only a small fraction of our larger RAG-3D database leads to an increase in the number of initial sequences (before screening) generated for some target tree graph topologies. This insight, combined with our latest protocol for performing automated mutations on unsuccessful sequences ( RAG-IF, manuscript in revision), can potentially increase the yield of our design protocol. Designing RNA-like dual graph topologies and more complex RNA sequences and structures form important future goals. As the universe of solved RNA motifs continues to grow, new computational approaches for design are essential for pursuing important biomedical and technological applications.

Figure 7:

Sketch of our computational pipeline for design of RNA-like tree graph topologies.

Highlights.

• Updated the list of tree graph topologies and RAG-3D fragment database using newly solved RNA structures

• Identified novel RNA-like motifs, with high accuracy, using unsupervised and supervised clustering algorithms

• Updated database and motif classification present new RNA substructures and RNA-like motifs as novel design candidates

List of Abbreviations

RNA

Ribonucleic Acid

2D

secondary structure

3D

three-dimensional/tertiary structure

RAG

RNA-As-Graphs

PDB

Protein Data Bank

PAM

Partitioning Around Medoids

k-NN

k Nearest Neighbors

PCA

Principal Component Analysis

LOO

leave-one-out

MSE

Mean Squared Error

F-RAG

fragment assembly for RNA-As-Graphs

RAG-IF

RNA-As-Graphs inverse folding