Abstract
Recent years have witnessed the tendency of measuring a biological sample on multiple omics scales for a comprehensive understanding of how biological activities on varying levels are perturbed by genetic variants, environments, and their interactions. This new trend raises substantial challenges to data integration and fusion, of which the latter is a specific type of integration that applies a uniform method in a scalable manner, to solve biological problems which the multi-omics measurements target. Fusion-based analysis has advanced rapidly in the past decade, thanks to application drivers and theoretical breakthroughs in mathematics, statistics, and computer science. We will briefly address these methods from methodological and mathematical perspectives and categorize them into three types of approaches: data fusion (a narrowed definition as compared to the general data fusion concept), model fusion, and mixed fusion. We will demonstrate at least one typical example in each specific category to exemplify the characteristics, principles, and applications of the methods in general, as well as discuss the gaps and potential issues for future studies.
Keywords: Multi-omics, Data integration, Data fusion, Model fusion
1. Introduction
1.1. Background
Through various unprecedented breakthroughs in sequencing technologies and a significant reduction in costs, many biological problems have been transformed into sequencing problems, thus prompting an explosion of big biological data. While technical advances have dramatically fostered biological and medical studies, they have also brought substantial challenges on integrating multi-tissue type, multiple genome-wide scale assay data (e.g., ChiP-seq and RNA-seq) for accurate, comprehensive, and effective analyses [1]. The bottleneck in research stems from the integrative analysis of data to understand the biological processes and disease mechanisms, rather than the generation of data.
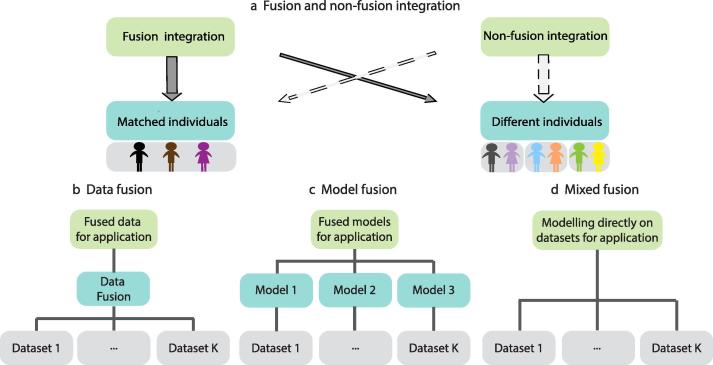
Beginning in the last decade, there has been an emerging tendency to measure the same individual or sample from multi-omics perspectives, thereby providing the opportunity of building predictive models for investigating relationships across biological scales on an individual basis. Relationships of intense interests include interactions and associations between biological entities from different levels of biology, such as interactions among DNA, RNA, proteins, and metabolites [2]. Understanding these interactions are essential to determining complicated, interwoven biological regulatory and protein networks with entities across multi-levels that are a part of normal physiology and influence the pathogenesis of complex diseases [3]. All of these relationships are difficult to unveil from single-scale assays but may be facilitated by the investigation of the penetrating effects of genetic and environmental perturbations in complex diseases, as demonstrated in the TCGA [4] and ENCODE [5] inspired projects. Fusion methods, a special form of integrative analysis, have been developed to meet the demand of scalable and integrative methods based on an overall model, to tackle the complexity of multi-omics datasets characterized by large dimensions and ever increasing scales (e.g., in ENCODE) [6], and to reduce the confounders from heterogeneity of samples. Fusion methods are different from non-fusion ones in that non-fusion integrative methods usually work on distinct biological samples and data sources (e.g., heterogeneous knowledge base and omics data), are conducted in sequence, lack an overall model, or are tailored for specific applications (Fig. 1a). Therefore, non-fusion integration methods are difficult to generalize to other problems and scale up with increasing types of assays, as seen in the Ping-Pong algorithm [7] and kernel-based integration method PreDR [8]. Here, we review the basic principles of sample-matched, multi-omics fusion methods, elaborate on their major challenges and gaps, and discuss the future outlook of fusion analysis for knowledge discovery: the process of identifying novel knowledge from data.
Fig. 1.
Relationship between data integration methods and principles of three types of fusion methods. Panel (a) shows the differences between fusion and non-fusion methods in dealing with their samples. Fusion methods are ideal for matched individual samples although some of them (e.g., network-based model-fusion methods) may also work for different individuals (solid arrow across). While most non-fusion integrations were designed for applications with different individuals, many do work on matched individuals, overlooking the additional information of matched samples (dashed arrow across). Panels (b–d) are our categorization of fusion integration methods, showing the differences in data access and modeling.
1.2. Challenges of multi-omics fusion analytics
A variety of challenges lie within multi-omics fusion analysis. It inherits most of the challenges presented in heterogeneous, non-fusion integrative methods, such as noisy, zero-inflated, and high dimensional (easily in the thousands) data with a relatively much smaller number of samples. In addition, fusion methods have specific challenges that do not occur in sequential and customized non-fusion methods that use multi-staged, filtering based approaches [9]. The challenges usually originate from the overall, scalable model when integrating all data sources, even after the confounding issues from heterogenous samples have been greatly diminished. First of all, from the outset, data scales, or generally speaking, data distributions across distinct scales, may be different, even after uniform pipeline processing with standardized normalization, as initial datasets often follow negative binomial distributions with different parameters, as demonstrated in TCGA and ENCODE. Distributional differences may also be attributed to distinct data preprocessing methods across different types of omics assays (e.g., between ChiP-seq and RNA-seq). Second, the number of dimensions and the multitude of assays of the same type can vary significantly across omics groups. For instance, in ENCODE, the number of assays can vary from one (e.g., DNase-Seq and RNA-seq) to hundreds (ChiP-seq). Thus, a simple concatenation of different types of omics data for direct analysis will tend to favor the assays with more dimensions. Third, although most assays target a particular biological entity (e.g., a genomic region), some search for interactions between biological entities (e.g., Hi-C and ChiA-pet), which further complicates the fusion analysis while potentially limiting the use of many fusion methods and it calls for particular design of fusion methods to adapt to these types of interaction data, such as network-based fusion methods [10]. Fourth, the assays conducted on distinct samples may be different, which causes some parts of the data to become totally inaccessible, i.e. the data sparsity of the input matrix, as seen in ENCODE. Finally, the data may have been collected with a distinct purpose. For instance, many datasets were collected for case-control studies (e.g., TCGA), while others were generated by data-driven projects (e.g., ENCODE), which makes generalized fusion modelling much more difficult to design.
1.3. Current methods and existing reviews
Multi-omics integration problems originated in the biomedical domain more than a decade ago, including the concept of data fusion [6]. However, the studies of the problem from mathematical, statistical and computational perspectives can be traced back much earlier than that. Problems like multiblock regression [11] and simultaneous component identification [12] were reported as early as the 1930s [13] in mathematics and statistics. In computer science, ensemble learning and deep learning-based integration methods were developed in the 2000s and 2010s respectively, which are all related to the fusion analysis through multi-omics datasets. Independently from each data science discipline, a significant number of fusion methods have been developed over the last two decades, which are discussed in this mini-review.
Several reviews have summarized the progress in this field from different perspectives [14]. Deun et al. provided a structured overview of simultaneous component based data integration from multiblock datasets [12], thus providing a general mathematical framework for matrix decomposition of multi-omics datasets. They further categorized the framework into the following three modes after applying weights to each data block (e.g., omics group): common component score decomposition for datasets with common rows, common loading decomposition for datasets with common columns, and the general mode with neither common component scores nor common loadings [12]. Ritchie et al. termed the simultaneous analysis from multi-omics as meta-dimensional analysis and further categorized them into three different approaches: concatenation-based, transformation-based, and model-based methods [9]. Concatenation-based integration combines multi-omics datasets into a large matrix before applying a model. Transformation-based integration converts each omics dataset into an intermediate form (e.g., graph), then applies a model after merging the intermediate forms. Model-based integration applies a model to each omics dataset and then integrates the models [9]. Lin et al. employed similar perspectives but took more of a machine learning approach [15]. Bersanelli et al. summarized the methods from both the problem and method perspectives then reviewed the mathematical models of their representative methods [16]. Huang et al. used a similar angle for review and claimed ‘more is better’, as believed by most scientists [17], [18], since more measurements always carry more information, thus having the potential to unveil relationships that would be impossible for single omics analyses to catch [18]. Other reviews include description of the whole processes of the integration [14] or focus on specific problems such as clustering [19] and outcome prediction [20].
This mini-review, by no means, attempts to provide a systematic review on all existing data integration methods. Instead, we focus on the analysis of multi-omics assays conducted on the same samples, a trend that is increasingly evident recently. This therefore implies that we will not cover heterogenous data integration, such as different sample integration and knowledge-based integration. It is our endeavor to provide a uniquely structured perspective for fusion methods as a specific type of integration and we will summarize the selected methods from multi-dimensional angles, specifically from both methodology and application (problem) perspectives. We will concentrate on basic principles of the methods, many of which are mathematical or statistical, rather than being overwhelmed with the details of biological/biomedical problems and their implications.
2. Review of the methodologies
2.1. Categorization of fusion methods
Suppose we have collected multi-omics datasets from a set of biological samples and multiple omics measurements. Without losing generality and to unify the notation, we may assume these datasets can be assembled as a big data matrix of X (matrices are bolded throughout the paper) consisting of I rows of biological samples and J columns of measurements, where the J columns are further divided into K distinct groups. Each submatrix (Xk; I rows and Jk columns) corresponds to the same type of omics assay data, referred to as an omics data block (or simply data block in this review). Note the difference between biological samples and statistical samples/instances; rows can also be regarded as either variables or features, while columns are regarded as statistical samples, as in the case of Multiple Non-negative Matrix Factorization (MNMF) [21]. By default, we assume rows are statistical samples, while columns are variables and will note where the definition is switched. Then, this data model can be generalized for multiblock datasets with common columns [12], as they can be transposed into the proper format. Also note that the biological samples can be either labeled with phenotypic classes (e.g., in TCGA) or unlabeled (in ENCODE).
Based on the nature of fusion methods, we chose to divide them logically into three exclusive and complementary categories: data fusion approaches, model fusion approaches, and mixed fusion approaches. In data fusion approaches (Fig. 1b; a narrowed view of the concept, rather than the commonly used data fusion term which envelops all the fusion analyses in this review), data from different omics groups are first fused into one single data matrix through fusion strategies, such as scale normalization across data blocks, and dimension reduction. Then, traditional models can be employed as if the data were from a single data source. This type of fusion is similar to the concatenation-based methods from Ritchie et al.’s review. In model fusion methods (Fig. 1c), each omics data block underwent separate and independent modelling, then had the models integrated as one for their application, in which the original data is no longer utilized. This type of fusion is similar to model-based approaches in Ritchie et al.’s review, whereas transformation methods in Ritchie at al.’s review can be regarded either as data fusion methods, if the intermediate form is regarded as data, or as model fusion methods if the intermediate form is regarded as a model. Last, mixed fusion approaches access each omics data block directly and build a comprehensive model across multiple blocks for fusion analysis (Fig. 1d). Note that mixed fusion approaches are not in Ritchie et al.’s review.
For each of the three types of fusion, various methods were developed and formalized from mathematics, statistics, and computer science perspectives. Meanwhile, these methods have been employed for different problems, mainly from three aspects: biological mechanism discovery that aims to unveil relationships between biological entities, clustering problems that partition biological samples and entities, and classification/regression problems that build integrative models for biological/clinical classes or outcomes. Therefore, we classify the methods using a two-dimensional structure of method versus applied problems (Fig. 2) with the goal of providing another perspective of comparison for methods in this field. Of note, many methods were not limited to a particular problem or method and thus can be multipurpose for integrative approaches (e.g., MFA [22] and PARADIGM [23]). In the following sections, we provide more details for each type of fusion methods, discuss the basic ideas, model assumptions, implementation, strengths, as well as limitations.
Fig. 2.
Categorization of fusion methods for multi-omics data integration. Methods are categorized by multiple levels and applied problems. Methods spanning two categories are shown across the corresponding boundaries (e.g., PARADIGM and stSVM), while methods usable for multiple problems are shown repeatedly in the same row (e.g., MNMF/SNMNMF and MFA).
2.2. Data fusion methods
Matrix decomposition is the most common approach for data fusion, using an overarching mathematical and statistical framework to integrate omics datasets. Under the assumption that all the data blocks share rows (identifiers), matrix decompositions can be divided as either common dimensional space based decomposition (or loadings) or common component-score decomposition, depending on whether the rows are regarded as samples or variables.
2.2.1. Common dimensional space based matrix decomposition
Multiple non-negative matrix factorization (MNMF) [21], the multiblock version of NMF [24], is a typical method that decomposes all the data blocks with the same loadings. Non-negative decomposition ensures interpretability of the latent factors and the corresponding coefficients (scores) by only using non-negative values. In MNMF [21], each row is regarded as a variable (each corresponding to a dimension) even though it is an individual biological sample, while the genomic profiles (e.g., DNA methylation, gene expression, and miRNA expression) are regarded as statistical samples in the dimensional space. The basic idea of MNMF is to decompose each omics data block (Xk) into the product of a common but reduced dimensional space (Q in Eq. (1)) and a score matrix (Fk in Eq (1); representing projections into the common space), often resulting in different projections in the common space. MNMF solves both types of matrices by minimizing the squared error subject to the constraints of non-negativity (Eq. (2)). After projecting all measurements (columns, often being genomic entities) into the new common space, clustering is conducted to identify grouping across multi-omics datasets, called as multi-dimensional modules, which indicate possible inter-connections between the genomic entities. The inter-connections may indicate functional associations between genomic variables (e.g., genes and genomic regions) in perturbed cancer pathways, as demonstrated by applying MNMF to clustering multi-scale modules in cancer genomic datasets [21]. It should be noted, MNMF requires careful standardization before integration, as data within the matrix are required to be non-negative.
| (1) |
| (2) |
Other approaches within this framework include Statistical Coupling Analysis-P (SCA-P) [25], which searches for the optimal pattern matrix that reconstructs the original data matrix after dimension reduction. The pattern matrix is a generalization of the loading matrix.
2.2.2. Common component score based matrix decomposition
In contrast to common space decomposition, common score based matrix decomposition searches for latent and consistent scores across multiple data blocks (e.g., common effects among multi-omics datasets). Multiple factor analysis (MFA) is a typical example of this category and assumes common latent factor scores between samples for determining the quantities in all data blocks (F; Eq. (3)). For instance, driving biological factors may influence the measurement of biological entities on varying scales. In this case, the dimensional space for each data block can have variance and not be of critical concern (Qk; Eq. (3)). MFA normalizes the data blocks by dividing each block with the largest singular value in that block, so that the first transformed factor of each block has the uniform variance of 1 [26]. In other words, MFA normalizes each omics data block through its maximal information in a single latent factor. Then, the normalized data block (Xk) is merged for a principal component analysis (PCA) or generalized singular value decomposition (details in Section 2.2.3) to get a solution. Generally, it can use minimum square errors to determine the theoretically optimal solution (Eq. (4)). MFA can be employed to identify simultaneous components, or hidden factors shared among multiple omics datasets. It has been demonstrated in clustering biological samples (e.g., glioma) from microarray data to gene ontology [22] in addition to dealing with missing values in multi-omics data [27].
| (3) |
| (4) |
Unlike MFA which uses the singular value of each data block as the weight, pattern fusion analysis (PFA) estimates the optimal weights directly from all data blocks [28]. Other approaches under this category include SUM-PCA [29], which simply merges all the data blocks and performs a PCA, resulting in common scores across data blocks. It uses an equivalent weight of 1 across the data blocks. Another example is MCIA, which is similar to MFA, but utilizes different strategies for weight [30].
If every data block has the same set of columns, the problem becomes a tensor (three-dimensional matrix can be regarded as a tensor) decomposition (or multi-way decomposition) [31], which is an extension of two-dimensional matrix decomposition and is usually common-score based. Many three-dimensional (3D) matrices exist in biological studies, with dimensions like biological samples (e.g., neurons), variables (e.g., genes or time), and conditions (e.g., assays). Methods using tensor decomposition include decomposing a matrix as a linear combination of basis two-dimensional matrices (e.g., variable and condition) [32] in addition to decomposing a matrix as a linear combination of the product of latent component scores from each of the three dimensions [33].
2.2.3. A common solution for matrix decomposition of the same rows
For matrix decomposition problems without extra constraints (e.g., non-negativity), there is a common solution based on generalized singular value decomposition (GSVD), even though these problems differ in their target on common loadings, common scores, or respective weighting strategies across data blocks. In classic SVD, a matrix is decomposed into diagonal singular values and two singular vectors consisting of unit vectors (referred to as left and right singular vectors). In GSVD, weights can be imposed on rows and columns, with a diagonal row weight matrix (M) or a column weight matrix (A) [26], thus making singular vectors often non-unit vectors (Eq. (5)). In MFA, the weight on each row can be 1 or 1/I, while the weight on each column corresponds to the largest eigenvalue of the respective data block, which is also the square of the corresponding singular value [26]. The problem in GSVD can be solved by converting it into a standard SVD calculation after multiplying the square root of the row weight matrix (M1/2) in the left of data matrix (X) and the square root of the column weight matrix (A1/2) in the right. To solve the problem, one can simply convert the SVD solution back to GSVD by multiplying it with the reverse weight matrix (M−1/2 and A−1/2) [34].
For common score-based decomposition (e.g., MFA), each row is a sample and each column is a variable. Thus, the right singular matrix is the loading matrix interpreted geometrically as new rotated dimension vectors, while the factor scores are contained within the product of the left singular matrix and the singular value matrix (Eq. (6)). The loading matrix Q, with a number of rows equal to the number of columns (J) of the input matrix (X), can be divided into sub-loading matrices corresponding to each data block (K in total) [26] (Eq. (7)). Then, each data block (Xk) can be decomposed as the product of the common score matrix (F) and the distinct loading matrices (Qk), corresponding to the unique dimensional space of each data block (Eq. (7) and Eq. (8)).
For common space decomposition (e.g, SCA-P [25]), the left singular matrix (P) corresponds to the loading matrix (dimension) since each row of the input matrix (X) is one variable. The score matrix (F) is the product of the singular value matrix and the transposed right singular matrix (Eq. (9)). The score matrix has the number of columns corresponding to the original matrix (X) and can be further divided into submatrices with respect to each input data block (Eq. (9)). Then, each input data block (Xk) can be decomposed as the product matrix of the common dimension space (P) and the corresponding score matrix (Fk), as desired in this type of matrix decomposition (Eqs. (8), (9)).
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
The above strategies can be applied to other methods, even in future methods with novel weighting strategies. It guarantees the optimal solution under full-rank decomposition, but can be suboptimal in reduced-dimensional decomposition (less than full-rank of the input matrix) under the object function of minimal square errors.
2.3. Model fusion methods
Model fusion is not a completely new concept, as ensemble learning (clustering and classification) and meta-analysis have similar ideas, particularly in scenarios where the original datasets are inaccessible. An example of model fusion is Bayesian consensus clustering (BCC). BCC first estimates a separate clustering model for each omics data block, then integrates all the models into a unified consensus clustering model without directly accessing the original data [35]. In the first stage, a Finite Dirichlet (extension of a beta distribution) mixture model (πk; Eq. (12)) is applied to partition all the samples (I total) on each data block (K blocks total) into a preset number of clusters (R total) based on Bayes rule (Eqs. (11), (12)). In the second stage, every sample (i) is assumed to be assigned to a consensus cluster (Ci), which is generated through a consensus Finite Dirichlet mixture probability (π; Eq. (13)). Then, a probability (αk; Eq. (14)) that the clustering of a data block (k) is consistent with the overall clustering is assumed and the posterior clustering probability of both the data block clustering and overall clustering is established based on the set of parameters and once again Bayes rules (Eq. (15)). Even though in implementation, the estimation of the parameters during the two stages are simultaneously conducted to get more accurate optimization, the method still follows the model fusion framework. In application, BCC has been employed to identify different subtypes among breast cancer tumor samples [35].
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
Another model fusion example is ENDEAVOUR [6], a pioneer paper on data fusion in the broad sense. ENDEAVOUR first sought to rank each column of a heterogeneous data source about all gene properties, resulting in a rank ratio for each gene, in each column, based on its value or the statistical significance. Then, a global order statistic was defined based on a multivariate cumulative distribution, assuming the rank ratio followed a uniform distribution with a density of 1 (see the integration function in Eq. (16)). ENDEAVOUR finally employed either a beta distribution or a gamma distribution to test the significance of the order statistic, based on whether the number of columns was larger than 5 (an empirical cutoff). The method successfully validated genes causing DiGeorge syndrome that were prioritized through the fusion-based method [6].
| (16) |
An example of mathematical model fusion is Gene Network Reconstruction (GNR) [10]. It first constructed a gene regulatory network from each individual microarray gene expression dataset using singular value decomposition. Then, it employed linear programming to estimate the optimal network structures by minimizing the overall errors over all the networks of the individual datasets, without accessing the original gene expression data.
2.4. Mixed fusion methods
A majority of fusion methods employ a mixed approach, which applies a fusion model that accesses the data of all the omics blocks directly to estimate optimal parameters for the overall fusion model. For example, iCluster (integrative clustering [36]) assumes an overall clustering partition (Eqs. (17), (18), (19)) across multiple data blocks and then estimates the latent variables (partition matrix Z) directly using all the data. This approach is clearly distinct from BCC. Specifically, iCluster represents each data block (Xk) as the product of the partition matrix (Z) and coefficient matrix (Wk), with assumed error terms of a Gaussian distribution (Eq. (19)). Then, it uses maximum likelihood estimation (log-likelihood) to infer the parameters [36]. iCluster+ further generalized iCluster by incorporating discrete variables as well as continuous variables [37]. iCluster has been used to identify known and novel subtypes of breast and lung cancers from concordant DNA copy number changes and gene expression [36] while iCluster+ has accurately grouped cell lines by their cell-of-origin for several cancer types using genomic, epigenomic and transcriptomic profiling [37].
| (17) |
| (18) |
| (19) |
Sparse Multi-Block Partial Least Squares (sMBPLS [20]) regression is another example of a mixed fusion method. sMBPLS applies a weight (wk vector) to each column of an explanatory data block (k) to get a linear combination of all the columns in that data block, resulting in a vector for each block (tk; Eq. (20)). Then, it applies another weight (bk) to each block to get a weighted value for each sample, yielding a combined explanatory vector (t; Eq (21)). Similarly, it applies a weight to each column of the response variables, thus obtaining a response vector (u; Eq. (21)). Then, it tries to get the maximal covariance between the weighted explanatory vector (t) and the response vector (u), as well as two regularization terms for the explanatory and response vectors, respectively [20] (Eqs. (22), (23)). sMBPLS has identified multi-dimensional regulatory modules for ovarian cancers and observed higher functional enrichment than those which only a single type of omics data [20]. Another example in statistics-based mixed fusion is eCAVIAR, which identifies co-location signals of Single Nucleotide Polymorphisms through integration of genome-wide association studies and expression quantitative trait loci [38]. Other statistical-based mixed fusion methods include PSDF [39] and COALESCE [40] for clustering and iBAG [41] for outcome prediction, all of which use Bayesian model-based integration and parameter estimation.
| (20) |
| (21) |
| (22) |
| (23) |
As an example of a network approach, PARADIGM constructs a network based on canonical pathways and the central dogma. It connects different biological entities (DNA, mRNA, protein, and activity) of a gene [23] and uses factors (constraint functions) to represent the relationships among them, both within the same gene and across genes. Then, it takes results from multiple omics datasets and categorizes them as activated (1), neutral (0), and inactivated (−1). Utilizing the categorization of genes and their network structure, it estimates the log likelihood of the unknown status of other genes and uses the status with the largest likelihood as the final status of the biological entities [23]. PARADIGM has identified altered activities in pathogenesis pathways of glioblastoma multiform and breast cancers [23]. Other examples include similarity network fusion (SNF), which fuses a similarity network derived from each data block, then uses a graph diffusion approach on the network to obtain an overall similarity network topology [42].
For a typical example of a machine learning approach, Mobadersany et al. [43] developed an integrative deep learning approach that combined histology images and genomic mutation data to predict cancer survival rates. Image data features were extracted by convolutional layers, and then combined with genomic data using fully connected layers, followed by a Cox model in the output layer. Another machine learning based fusion approach employs a smoothed t-statistic support vector machine model (stSVM) [44]. It does as its name suggests and integrates network information with experimental data by smoothing t-statistics of individual subjects over a target network, before training a support vector machine classifier.
2.5. Comparison of methods
While a comprehensive and comparative study of all fusion methods is out of this scope, we will briefly compare methods from both theoretical and practical perspectives. Readers can refer to comparative studies in research papers such as Liu et al. [45] and a few comparative review papers such as Tini et al. suggested SNF achieved the best clustering for complicated data, seconded by MFA [19].
First, assumptions on the reviewed methods are distinct. Matrix decomposition based data fusion methods are usually model-free unless specific statistical tests are required for the derived parameters. Statistics based model and mixed fusions are usually accompanied by a probability distribution, often a Gaussian distribution [36] for convenience. Thus, non-Gaussian datasets have to undergo data transformation, using either the theoretical relationship between distributions or a log-based transformation. On the other hand, non-statistical machine learning methods, such as support vector machine and deep learning are usually model free.
Second, method performance and practical implementation make a great difference. Multiple omics datasets easily reach tens of thousands of columns and hence trigger the curse of dimensionality. For instance, an optimal SVD/GSVD may become impossible as the intermediate matrices become unable to load into the memory. Due to this, dimension reduction using the first few dimensions is a common practice. For instance, MNMF only uses the first 200 dimensions to facilitate the iterative process of updating the factor and score matrices. Similarly, for SVD based implementation, approximation approaches can be used for fast calculation of the first few singular values for large-scale matrices [46]. See more details in the review of Meng et al. which covers dimension reduction techniques for multi-omics data [47].
Finally, careful consideration in the application of methods should be conducted. First, we should choose the methods based on the nature of scientific problems and data, as many methods are designed for a particular problem (such as clustering). An example is that categorized data in multiple scales (from DNA to protein) are required for PARADIGM, which makes many problems without the specified data inapplicable. Another example is that NMF-based methods require non-negative data, which also limits some applications if transformation to nonnegative data does not make sense. Second, we should understand the implications of the input matrix, such as what corresponds to samples and what corresponds to variables. This will influence interpretation of the results, as seen in NMF-based methods [21]. Last of all, we need think over whether the model makes sense for the problem in hand, and can address questions such as: what do the common scores mean and how do they make sense in the biological or biomedical context?
3. Summary and outlook
While there are a variety of fusion methods on integrating multi-omics datasets, we have categorized them into several groups due to their distinct perspectives. First upon the type of fusion, as in data fusion, model fusion, and mixed fusion, each of which was developed from mathematics, statistics, and computational disciplines, though many are transdisciplinary. From the application perspective, we have divided them into mechanism discovery, clustering, classification and prediction. We demonstrated each specific category with at least one example to exemplify the main characteristics of that category, as well as covering other instances as needed. We focused on the main mathematical and statistical principles while also highlighting certain significant achievements and applications.
It is evident that existing methods are not evenly represented in each category by methodology and application. Most fusion methods are mixed ones, spanning mathematics, statistics, and computational disciplines. Matrix decompositions are enriched in data fusion methods, mainly from the mathematics discipline. Many model fusion methods are both statistical and mathematical. From the application perspective, clustering methods are overrepresented, seconded by mechanistic ones, and least of all by classification and prediction ones. Most methods were motivated by TCGA datasets [4] because of its well-designed control-case sample collection and data generation, availability of multiple omics assays of the same individuals, and a moderate number of samples. Of note, between mechanism discovery and clustering, there is a gap or underrepresentation of problems, which prioritize the pairwise relationships between biological entities from multi-omics perspectives, such as SNP-SNP interactions [48], [49], gene-gene interactions, and sample-sample similarities.
Several facts may explain the current status of method development for fusion methods. Clustering approaches are relatively easier to design and implement, although the validity of the whole partition is harder to assess, and a rigorous measurement of performance is not well established. Enrichment studies can help explain the promise of clustering to some extent. Mechanistic approaches are usually not well-defined and hard to justify due to lack of a benchmark. However, some discoveries can be verified by wet lab experiments and demonstrate high significance, which further drives the advance of these type of discoveries. Classification and prediction problems have well established assessment criteria; however, due to large dimensions and relatively small sample sizes, it is very difficult to reach a sufficient accuracy for many applications.
Current methods are usually problem-specific, bound to and driven by particular problems (e.g., TCGA), rather than providing a general, ubiquitous solution for all fusion problems. Because of this, there are almost no one-size-fits-all, state-of-the-art methods and pipeline for the diverse problems that require multi-omics fusion. This partially hampers the dissemination of information to the final users of these methods, who are often biologists.
Although fusion methods have had significant breakthroughs from both theoretical and practical perspectives, especially from mathematical and statistical fields, caution should be taken during application as heterogeneity may still be an issue for multi-omics datasets. Heterogeneity may arise from distinct sample collection and processing, different measurements across omics types, the presence of other nuisance factors, and covariates that are involved in collecting samples and generating the data. In the future, fusion models are expected to be more flexible for incorporating these factors to reduce false discoveries caused by noisy, missing values [27], and confounders. Heterogeneity is especially prominent when integrating single-cell sequencing data as the matched samples for distinct omics measurements are currently intractable but measurement of similar samples are possible, making anchored [50] or coupled clustering [51], [52] adequate solutions. Without careful modelling and application, more multi-omics data is not necessarily better than single scale omics data. Additionally, most statistical models are based on a Gaussian distribution, whereas omics datasets often follow negative binomial distributions. Thus, future studies should consider a scenario for more accurate modelling. Finally, with ever-increasing sample sizes encountered in modern studies and datasets, the power of most methods should improve, while the influence from noise will significantly diminish. With development of technology and fusion methods advancing, there is great potential to foster further biological and medical studies and their applications.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
We appreciate Zuoguo Yu and Jinyan Li for their critical comments and startup packages from three units of University of Arizona: College of Agriculture and Life Sciences, Research Development Services, and University of Arizona Health Sciences. This work has also been supported in part by NIH U01AI122275.
Contributor Information
Edwin Baldwin, Email: eabaldwi@email.arizona.edu.
Jiali Han, Email: jialih@email.arizona.edu.
Wenting Luo, Email: wentingluo@email.arizona.edu.
Jin Zhou, Email: jzhou@email.arizona.edu.
Lingling An, Email: anling@email.arizona.edu.
Jian Liu, Email: jianliu@email.arizona.edu.
Hao Helen Zhang, Email: haozhang@email.arizona.edu.
Haiquan Li, Email: haiquan@email.arizona.edu.
References
- 1.Bebek G. Network biology methods integrating biological data for translational science. Brief Bioinf. 2012;13(4):446–459. doi: 10.1093/bib/bbr075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hasin Y., Seldin M., Lusis A. Multi-omics approaches to disease. Genome Biol. 2017;18(1):83. doi: 10.1186/s13059-017-1215-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Yan J. Network approaches to systems biology analysis of complex disease: integrative methods for multi-omics data. Brief Bioinf. 2017;19(6):1370–1381. doi: 10.1093/bib/bbx066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Weinstein J.N. The cancer genome atlas pan-cancer analysis project. Nat Genet. 2013;45(10):1113. doi: 10.1038/ng.2764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Consortium, E.P. The ENCODE (ENCyclopedia of DNA elements) project. Science. 2004;306(5696):636–640. doi: 10.1126/science.1105136. [DOI] [PubMed] [Google Scholar]
- 6.Aerts S. Gene prioritization through genomic data fusion. Nat Biotechnol. 2006;24(5):537. doi: 10.1038/nbt1203. [DOI] [PubMed] [Google Scholar]
- 7.Kutalik Z., Beckmann J.S., Bergmann S. A modular approach for integrative analysis of large-scale gene-expression and drug-response data. Nat Biotechnol. 2008;26(5):531. doi: 10.1038/nbt1397. [DOI] [PubMed] [Google Scholar]
- 8.Wang Y. Drug repositioning by kernel-based integration of molecular structure, molecular activity, and phenotype data. PLoS One. 2013;8(11) doi: 10.1371/journal.pone.0078518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ritchie M.D. Methods of integrating data to uncover genotype–phenotype interactions. Nat Rev Genet. 2015;16(2):85. doi: 10.1038/nrg3868. [DOI] [PubMed] [Google Scholar]
- 10.Wang Y. Inferring gene regulatory networks from multiple microarray datasets. Bioinformatics. 2006;22(19):2413–2420. doi: 10.1093/bioinformatics/btl396. [DOI] [PubMed] [Google Scholar]
- 11.Wangen L., Kowalski B. A multiblock partial least squares algorithm for investigating complex chemical systems. J Chemom. 1989;3(1):3–20. [Google Scholar]
- 12.Van Deun K. A structured overview of simultaneous component based data integration. BMC Bioinf. 2009;10(1):246. doi: 10.1186/1471-2105-10-246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Thurstone L.L. Multiple factor analysis. Psychol Rev. 1931;38(5):406. [Google Scholar]
- 14.Yu X.-T., Zeng T. Computational Systems Biology. Springer; 2018. Integrative analysis of omics big data; pp. 109–135. [DOI] [PubMed] [Google Scholar]
- 15.Lin E., Lane H.-Y. Machine learning and systems genomics approaches for multi-omics data. Biomarker Res. 2017;5(1):2. doi: 10.1186/s40364-017-0082-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bersanelli M. Methods for the integration of multi-omics data: mathematical aspects. BMC Bioinf. 2016;17(2):S15. doi: 10.1186/s12859-015-0857-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Huang S., Chaudhary K., Garmire L.X. More is better: recent progress in multi-omics data integration methods. Front Genet. 2017;8:84. doi: 10.3389/fgene.2017.00084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Buescher J.M., Driggers E.M. Integration of omics: more than the sum of its parts. Cancer Metab. 2016;4(1):4. doi: 10.1186/s40170-016-0143-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tini G. Multi-omics integration—a comparison of unsupervised clustering methodologies. Brief Bioinf. 2017 doi: 10.1093/bib/bbx167. [DOI] [PubMed] [Google Scholar]
- 20.Lussier Y.A., Li H. Breakthroughs in genomics data integration for predicting clinical outcome. J Biomed Inform. 2012;45(6):1199. doi: 10.1016/j.jbi.2012.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zhang S. Discovery of multi-dimensional modules by integrative analysis of cancer genomic data. Nucleic Acids Res. 2012;40(19):9379–9391. doi: 10.1093/nar/gks725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.De Tayrac M. Simultaneous analysis of distinct Omics data sets with integration of biological knowledge: multiple factor analysis approach. BMC Genomics. 2009;10(1):32. doi: 10.1186/1471-2164-10-32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Vaske C.J. Inference of patient-specific pathway activities from multi-dimensional cancer genomics data using PARADIGM. Bioinformatics. 2010;26(12):i237–i245. doi: 10.1093/bioinformatics/btq182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lee D.D., Seung H.S. Learning the parts of objects by non-negative matrix factorization. Nature. 1999;401(6755):788. doi: 10.1038/44565. [DOI] [PubMed] [Google Scholar]
- 25.Kiers H.A., ten Berge J.M. Hierarchical relations between methods for simultaneous component analysis and a technique for rotation to a simple simultaneous structure. Br J Math Stat Psychol. 1994;47(1):109–126. [Google Scholar]
- 26.Abdi H., Williams L.J., Valentin D. Multiple factor analysis: principal component analysis for multitable and multiblock data sets. Wiley Interdiscip Rev Comput Stat. 2013;5(2):149–179. [Google Scholar]
- 27.Voillet V. Handling missing rows in multi-omics data integration: multiple imputation in multiple factor analysis framework. BMC Bioinf. 2016;17(1):402. doi: 10.1186/s12859-016-1273-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Shi Q. Pattern fusion analysis by adaptive alignment of multiple heterogeneous omics data. Bioinformatics. 2017;33(17):2706–2714. doi: 10.1093/bioinformatics/btx176. [DOI] [PubMed] [Google Scholar]
- 29.Smilde A.K., Westerhuis J.A., de Jong S. A framework for sequential multiblock component methods. J Chemometr. 2003;17(6):323–337. [Google Scholar]
- 30.Meng C. A multivariate approach to the integration of multi-omics datasets. BMC Bioinf. 2014;15(1):162. doi: 10.1186/1471-2105-15-162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Papalexakis E.E., Faloutsos C., Sidiropoulos N.D. Tensors for data mining and data fusion: Models, applications, and scalable algorithms. ACM Trans Intell Syst Technol (TIST) 2017;8(2):16. [Google Scholar]
- 32.Seely J.S. Tensor analysis reveals distinct population structure that parallels the different computational roles of areas M1 and V1. PLoS Comput Biol. 2016;12(11) doi: 10.1371/journal.pcbi.1005164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hore V. Tensor decomposition for multiple-tissue gene expression experiments. Nat Genet. 2016;48(9):1094. doi: 10.1038/ng.3624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Abdi H. Singular value decomposition (SVD) and generalized singular value decomposition. Encycl Measur Stat. 2007:907–912. [Google Scholar]
- 35.Lock E.F., Dunson D.B. Bayesian consensus clustering. Bioinformatics. 2013;29(20):2610–2616. doi: 10.1093/bioinformatics/btt425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Shen R., Olshen A.B., Ladanyi M. Integrative clustering of multiple genomic data types using a joint latent variable model with application to breast and lung cancer subtype analysis. Bioinformatics. 2009;25(22):2906–2912. doi: 10.1093/bioinformatics/btp543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Mo Q. Pattern discovery and cancer gene identification in integrated cancer genomic data. Proc Natl Acad Sci U S A. 2013;110(11):4245–4250. doi: 10.1073/pnas.1208949110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hormozdiari F. Colocalization of GWAS and eQTL signals detects target genes. Am J Hum Genet. 2016;99(6):1245–1260. doi: 10.1016/j.ajhg.2016.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Yuan Y., Savage R.S., Markowetz F. Patient-specific data fusion defines prognostic cancer subtypes. PLoS Comput Biol. 2011;7(10) doi: 10.1371/journal.pcbi.1002227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Huttenhower C. Detailing regulatory networks through large scale data integration. Bioinformatics. 2009;25(24):3267–3274. doi: 10.1093/bioinformatics/btp588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Wang W. iBAG: integrative Bayesian analysis of high-dimensional multiplatform genomics data. Bioinformatics. 2012;29(2):149–159. doi: 10.1093/bioinformatics/bts655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Wang B. Similarity network fusion for aggregating data types on a genomic scale. Nat Methods. 2014;11(3):333. doi: 10.1038/nmeth.2810. [DOI] [PubMed] [Google Scholar]
- 43.Mobadersany P. Predicting cancer outcomes from histology and genomics using convolutional networks. Proc Natl Acad Sci U S A. 2018;115(13):E2970–E2979. doi: 10.1073/pnas.1717139115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Cun Y., Fröhlich H. Network and data integration for biomarker signature discovery via network smoothed t-statistics. PLoS ONE. 2013;8(9) doi: 10.1371/journal.pone.0073074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Liu Y. Multilevel omic data integration in cancer cell lines: advanced annotation and emergent properties. BMC Syst Biol. 2013;7(1):14. doi: 10.1186/1752-0509-7-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Holmes M, Gray A, Isbell C, Fast SVD for large-scale matrices, in Workshop on Efficient Machine Learning at NIPS. 2007.
- 47.Meng C. Dimension reduction techniques for the integrative analysis of multi-omics data. Brief Bioinf. 2016;17(4):628–641. doi: 10.1093/bib/bbv108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Li H. Integrative genomics analyses unveil downstream biological effectors of disease-specific polymorphisms buried in intergenic regions. NPJ Genomic Med. 2016;1:16006. doi: 10.1038/npjgenmed.2016.6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Manduchi E. Leveraging epigenomics and contactomics data to investigate SNP pairs in GWAS. Hum Genet. 2018;137(5):413–425. doi: 10.1007/s00439-018-1893-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Stuart T. Comprehensive integration of single-cell data. Cell. 2019 doi: 10.1016/j.cell.2019.05.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Duren Z. Integrative analysis of single-cell genomics data by coupled nonnegative matrix factorizations. Proc Natl Acad Sci U S A. 2018;115(30):7723–7728. doi: 10.1073/pnas.1805681115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Zeng W. DC3 is a method for deconvolution and coupled clustering from bulk and single-cell genomics data. Nat Commun. 2019;10(1):1–11. doi: 10.1038/s41467-019-12547-1. [DOI] [PMC free article] [PubMed] [Google Scholar]