System for application of controlled forces on dental implants in rat maxillae: Influence of the number of load cycles on bone healing

Abstract

Experimental studies on the effect of micromotion on bone healing around implants are frequently conducted in long bones. In order to more closely reflect the anatomical and clinical environments around dental implants, and eventually be able to experimentally address load‐management issues, we have developed a system that allows initial stabilization, protection from external forces, and controlled axial loading of implants. Screw‐shaped implants were placed on the edentulous ridge in rat maxillae. Three loading regimens were applied to validate the system; case A no loading (unloaded implant) for 14 days, case B no loading in the first 7 days followed by 7 days of a single, daily loading session (60 cycles of an axial force of 1.5 N/cycle), and case C no loading in the first 7 days followed by 7 days of two such daily loading sessions. Finite element modeling of the peri‐implant compressive and tensile strains plus histological and immunohistochemical analyses revealed that in case B any tissue damage resulting from the applied force (and related interfacial strains) did not per se disturb bone healing, however, in case C, the accumulation of damage resulting from the doubling of loading sessions severely disrupted the process. These proof‐of‐principle results validate the applicability of our system for controlled loading, and provide new evidence on the importance of the number of load cycles applied on healing of maxillary bone.

1. INTRODUCTION

When implants placed in bone are loaded, they are inevitably subjected to some degree of micromotion. The resulting peri‐implant strain and stress distributions will cause deformation of supporting interfacial tissues that can negatively affect bone healing (de Barros et al., 2018; Leucht et al., 2007; Perren, 2002; Perren, Fernandez, & Regazzoni, 2015; Wazen et al., 2013). However, in basic studies of oral implants, there is still no validated method to measure and control tissue deformation and strain fields at the bone‐implant interface. Therefore, design principles about oral implant loading still rely largely on general, empirical experience with implants.

The oral setting represents a challenging environment for investigating the interfacial events that lead to implant osseointegration—or its failure—and there are few experimental models of stable placement of implants that can then be subjected to controlled loading (Karimbux, Sirakian, Weber, & Nishimura, 1995; Nagasawa, Takano, Maeda, & Uoshima, 2013). Consequently, the influence of loading (and related peri‐implant strains) on the bone healing process around dental implants has largely been extrapolated from studies in long bones (Le Cann et al., 2017; Matsuo et al., 2017; Sennerby, Thomsen, & Ericson, 1993). The main reasons for using long bones are: surgical convenience, easy access to the implant to execute the loading, better control of implant stability, and opportunity to use larger implants. While the use of long bones models has provided important information on osteointegration, in general, it has not directly addressed possible differences between maxillofacial and long bones such as (a) developmental origin, (b) turnover rate, (c) the paucity of bone marrow and derived stem cells, and (d) differences in osteoclastogenesis (Aghaloo et al., 2010; Faloni et al., 2011).

The objective of this work was to develop an experimental system for use in the oral environment that shields the implant from external disturbance resulting from typical masticatory activities, yet allows application of controlled forces to the implant when desired. Furthermore, we sought a system that would also allow us to test an implant installed into an over‐sized osteotomy and thus initially surrounded by a gap (i.e., a Bone Implant Gap Interface, BIGI) where possible new peri‐implant bone formation could be studied as a function of biomechanical conditions in the gap. An analogous system has been developed and tested in long bones (Leucht et al., 2007; Wazen et al., 2013), so we used some of the same principles in designing this new system for oral use in rats. It should be emphasized that our use of a relatively large peri‐implant gap (i.e., 100 μm) in the model is meant to be a defined “test bed” for studying mechanobiology; our findings are presented in terms of stress and strain states, which can be computed for differently‐sized gaps that may exist in a given situation.

2. MATERIALS AND METHODS

2.1. Ti implants, implant placement sites, and type of interface

Threaded titanium‐6 aluminum‐4 vanadium alloy “Retopins” (NTI Kahla GmbH, Germany), 0.62 mm diameter and 4.2 mm length, were used as the implant. Before surgery, the implants were washed with 70% ethanol and air‐dried, placed in the edentulous ridge anterior to the first molar (Figure 1d). The 0.62 mm retopins were placed in 0.82 mm holes to create an initial gap between bone and implant of 0.1 mm, which thus comprised a model for study of gap‐healing at an interface (BIGI).

Figure 1.

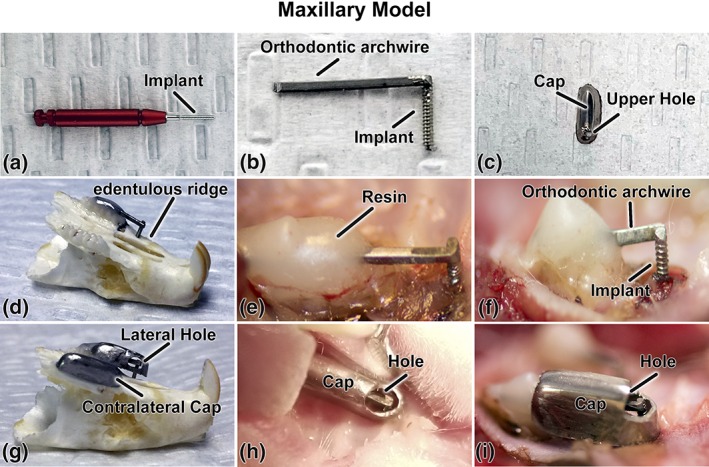
Micromotion system for rat maxillae; (a) photograph of the Retopin implant; (b) the implant welded to a titanium orthodontic arch wire; (c) the protective cap with a loading hole on its upper aspect; (d) implant system adapted and cemented on a dry maxilla and; (e, f) in situ on the edentulous ridge of the maxilla; (g) protective pediatric crown adapted to overhang the implant in a dry maxilla and (h, i) in situ. (c, h, and i) the loading hole can be positioned on the upper or (g) the lateral aspect of the cap. The holes in (g–i) were made bigger for illustration purposes

2.2. Surgical procedure

In total, 15 male Wistar rats weighting 200–225 g (Charles Rivers Canada; St‐Constant, QC, Canada) were used. They were anesthetized with an intraperitoneal injection of a mixture of Ketalean (0.05 mg/g body weight; ketamine hydrochloride; Biomeda‐MTC, Cambridge, ON, Canada), Rompun (0.005 mg/g body weight; xylazine; Bayer Inc., Toronto, ON, Canada), and Acevet (0.001 mg/g body weight; acepromazine maleate; Vetoquinol Inc., Lavaltrie, QC, Canada). For implant installation, a transgingival pilot hole was made 3 mm in front of the first maxillary molar on the edentulous ridge using a 0.35 mm drill bit (Drill Bit City, Prospect Heights, IL, EUA), and followed drill bits of 0.6 and 0.82 mm. (Drill Bit City). All drill holes were made using a low‐speed dental engine (800 rpm, Kavo Dental; Biberach an der Riß, Germany).

2.3. Micromotion system

Since the gap interface does not provide primary stability of the implant, each implant was attached to a 0.016″ × 0.022″ rect 10 titanium orthodontic arch wire (Patterson Dental, Saint Paul, MN, EUA) by spot‐welding at 2.0 kV. (Figure 1a,b). The retopin was placed in the surgical hole and the wire portion was cemented onto the molars using a nano‐optimized flowable composite (Tetric EvoFlow, Ivoclar Vivadent, Schaan Liechtenstein, Figure 1e,f). To protected the implants from external disturbance, a stainless‐steel pediatric crown (3 M, Elyria, OH, EUA) was adapted to overhang the implant and cemented over the wire to the molars using a self‐adhesive resin cement (RelyX™ Unicem 2, 3 M). (Figure 1c,g–i). A small hole (1.1 mm) was made in the upper part of the crown to allow access to and loading of the extremity of the archwire “beam” attached to the implant (described below, Figure 1c). Another crown was cemented on the contralateral side to maintain the occlusal balance (Figure 1g). The animals received an injection of Temgesic (0.2 mL Buprenorphine hydrochloride, Reckitt and Colman, Hull, UK) after surgery, and were fed with soft food containing Temgesic for the entire 14 day duration of the experiment.

2.4. Loading regimen

Three loading regimens were applied; case A no loading (unloaded implant) for 14 days, case B no loading in the first 7 days followed by 7 days of a single, daily loading session, and case C no loading in the first 7 days followed by 7 days of two such daily loading sessions with a 6 hr interval between them. For each of these 3 experimental groups n = 5 animals. The experimental groups and loading protocols are described in Table 1. In the case of the one and two daily loading sessions groups, the animals were anesthetized and kept under AErrane anesthesia (isoflurane USP, Baxter, Mississauga, ON, Canada) maintained at 1–2% during application of force. Hence, these loaded animals were anesthetized one and two times per day, respectively. The surgical site was cleaned once a day with Baxedin (chlorhexidine gluconate; Omega Laboratories, Montreal, QC, Canada) before the loading. The unloaded group was also similarly anesthetized once a day for routine wound cleaning. Each isoflurane anesthesia, including induction, never exceeded 5 min. As discussed in de Barros et al. (2018), such isoflurane anesthesia duration had no impact on the outcome of the results, and the additional anesthesia in the 2× group did not alter significantly the bone healing.

Table 1.

Experimental groups and loading regimen

	Group	Number of animals
1	Unloaded: no loading for 14 days	5
2	Micromotion 1×: no loading in the first 7 days followed by 7 days of one daily loading session of 60 cycles with a peak axial force of 1.5 N.	5
3	Micromotion 2×: no loading in the first 7 days followed by 7 days of two daily loading sessions of 60 cycles with a peak axial force of 1.5 N	5

A hand‐held Force Gauge Series 5, model M7‐2 loading device, (Mark‐10, Copiague, NY) was used to apply, by hand, a controlled waveform lasting about 1 s with a maximum force of 1.5 N (de Barros et al., 2018) to the end of the wire (to which the implant was attached) through a small opening on the top of the protective cap. We used bench‐top testing and FE analyses of prototype designs in order to decide on the appropriate dimensions and length of the archwire beam; the intent was that a 1.5 N force on the end of the beam, acting toward the attached implant and along the implant's long axis, should produce implant micromotion of about 50 μm when there was no tissue in the gap.

2.5. Ethical approval and animal supervision

All animal procedures and experimental protocols were approved by the Comité de déontologie de l'expérimentation sur les animaux of Université de Montréal and followed the ARRIVE guidelines (Animal Research: Reporting of In Vivo Experiments). Animals were under regular observation at the university animal facilities throughout the period of experimentation. They were given food and water ad libitum and left to move around freely in the cages. The animals' appearance, weight, and healing were checked on a daily basis.

2.6. Finite element analysis

The micromotion system was designed so that implant micromotion occurred when the archwire “beam” was deformed under defined loading at its cantilever end. The FE model of the situation included simplified block‐like structures representing the molar teeth, cortical bone of the edentulous ridge mesial to the molars, and a thin cortical bone layer above the sinus—all of which were assigned the properties of cortical bone in the rat (Young's modulus 6 GPa, Poisson's ratio 0.33) (Cory et al., 2010), these structures were all several orders of magnitude stiffer than the tissue that filled the gap interface. The approximate dimensions for each simplified block structure were gathered from micro‐CT scans of rat maxillae (Phillips, Ji, Rivelli, Chapman, & Corboz, 2009). The bucco‐lingual thickness of the entire model was 1.5 mm, and the various other parts of the model had the following dimensions in the mesio‐distal and occluso‐apical directions, respectively: molars near the implant 6 mm × 2 mm; cortical bone near the implant 5 mm × 1.35 mm; sinus 11 mm × 8 mm; and cortical bone above the sinus 11 mm × 0.5 mm. Also, the FE model included a mixture of soft connective tissue and bone within the sinus region, which was assigned a low Young's modulus and Poisson's ratio consistent with soft connective tissue and porous cancellous bone (i.e., Young's modulus E = 50 MPa and a Poisson's ratio = 0.33). There is no cortical bone on the buccal or lingual surfaces of the model. The modulus of the gap interface was parametrically set at three values to simulate the properties of three possible tissues that could “fill” in the peri‐implant gap at 7 days post‐implantation, that is, the values of Young's modulus and Poisson's ratio were 0.28 MPa and 0.33 for simulating fill of the gap by only a blood clot (Munster, Jawerth, Fabry, & Weitz, 2013; Piechocka, Bacabac, Potters, Mackintosh, & Koenderink, 2010), 1 MPa and 0.33 simulating fill of the gap by a mixture of granulation tissue and low density cancellous bone (Wazen et al., 2013), and 18 MPa and 0.33 representing fill of the gap by a mixture of cancellous bone and vascular space as seen at 7 days in a gap interface in a model of implant micromotion in mouse tibiae (Wazen et al., 2013). The beta titanium archwire beam was assigned a Young's elastic modulus of 64.76 GPa and Poisson's ratio = 0.33 (Burstone & Goldberg, 1980), and the retopin implant was assigned a Young's elastic modulus of 110 GPa (and Poisson's ratio = 0.33) for Ti‐6Al‐4V (Brunski, 2013). The model was constrained to prevent translation in x‐, y‐, and z‐ at its mesial and distal surfaces, as well as at the superior surface opposite the archwire beam. In vivo, the top surface of the archwire beam was shielded from loading by the cap cemented over the molar teeth (not shown in the FE model), so in the FE model a force of 1.5 N was applied in the negative z‐direction on the beam's mesial end, to simulate the situation at the start of each in vivo loading protocol. Continuity of displacements was assumed at all interfaces (boundaries) in the model, which is equivalent to assuming bonding exists at these interfaces. The model was meshed in Comsol Multiphysics 5.4 with 98,970 first‐order tetrahedral elements and 411,909 degrees of freedom. The sizes of the elements were about 40–60 μm for the finer parts of the mesh and 600–700 μm for the coarser regions of the mesh. The model was based on linearly elastic material behavior, and a static analysis was performed. FE models were run using both infinitesimal and finite (Green‐Lagrange) strain definitions, with no substantive differences in predicted strain magnitudes or distributions; the presented results are based on finite strains. Results from the FE model included displacements of the archwire and implant (micromotion) as well as maps of the principal, distortional, and hydrostatic strains throughout the gap interface.

The definition of the distortional strain was:

$${\overline{\epsilon }}_{\mathrm{s}}=\frac{1}{3}{\left[{\left({\epsilon }_{\mathrm{I}}-{\epsilon }_{\mathrm{II}}\right)}^2+{\left({\epsilon }_{\mathrm{II}}-{\epsilon }_{\mathrm{III}}\right)}^2+{\left({\epsilon }_{\mathrm{III}}-{\epsilon }_{\mathrm{I}}\right)}^2\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$$

This definition of distortional strain is equal to one‐half of the octahedral shear strain, or 1/√2 times the effective (Von Mises) strain.

The definition of the hydrostatic strain was:

$${\overline{\epsilon }}_{\mathrm{h}}=\frac{\left({\epsilon }_{\mathrm{I}}+{\epsilon }_{\mathrm{II}}+{\epsilon }_{\mathrm{III}}\right)}{3}$$

In addition to sizing the archwire beam that was connected to the implant, the other key aim of the finite element analysis was to estimate the mechanical strain state in the gap interface around the implants during the three loading protocols (Figure 2a,b).

Figure 2.

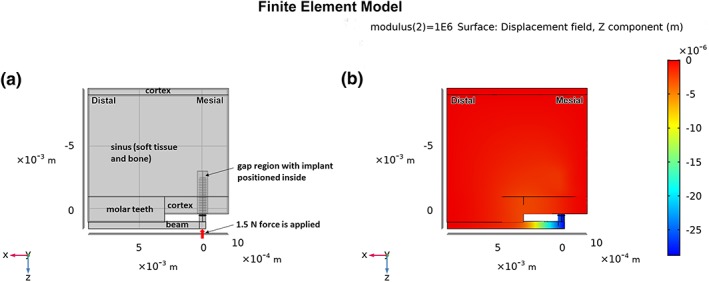
(a) Overall formulation of the FE model, showing idealized regions of molar teeth, cortical bone, sinus, titanium beam, gap, and implant. The thickness of the model is 1.5 mm into the page, with mesio‐distal and occluso‐apical dimensions as noted in the text. The mesial, distal, and superior surfaces of the model are fixed; (b) semi‐transparent view of a portion of the model showing z‐displacements after loading the end of the beam with 1.5 N, and with the modulus of the gap tissue equal to 1 MPa

2.7. Tissue processing for histology

Animals were anesthetized with a mixture of a 20% chloral hydrate solution (0.4 mg/g body weight Sigma‐Aldrich Canada Ltd, Oakville, ON, Canada) and Rompun (0.005 mg/g body weight; xylazine; Bayer Inc.), and sacrificed by an inhalation overdose of AErrane (isoflurane USP, Baxter). Maxillae were dissected and immersed overnight at 4°C in a fixative solution consisting of 4% paraformaldehyde and 0.1% glutaraldehyde in 0.1 M phosphate buffer, pH 7.2. The samples were then decalcified for 3 days at 4°C in Planck‐Rychlo solution consisting of 0.13 M aluminum chloride hexahydrate (Sigma‐Aldrich), 0.2 N hydrochloric acid (Fisher Scientific, Whitby, ON, Canada), 1.35% formic acid (Fisher Scientific). Decalcified samples were washed for 24 hr in 0.1 M phosphate buffer (pH 7.2), dehydrated through graded ethanols, cleared with xylene, embedded in paraffin and sectioned at 5 μm thickness. All the sections were cut in a mesial‐distal orientation. The sections were stained with hematoxylin and eosin for observation by light microscopy.

2.8. Histomorphometric analyses

Three sections per animal were analyzed for a total of 15 sections per group (n = 15). The bone implant distance (BID) was calculated using the mean bone–implant distance over the distal implant periphery based on data taken from 30 evenly spaced points around the periphery of the implant in each section, for a cumulative number of 90 measurements per animal and 450 measurements per group (n = 450). One‐way ANOVA was performed to determine the differences in BID for unloaded and loaded groups. Values of p < .05 were considered statistically different. The power of the study was calculated using the WebPower‐Statistical Power Analysis Online (https://webpower.psychstat.org/wiki/start). Level of power ≥ 80% was considered statistically significant difference.

2.9. Immunohistochemistry

In order to validate the formation of the new bone observed histologically we mapped the localization of Bril, a short transmembrane protein expressed almost exclusively in osteoblasts that correlates with active bone formation (Moffatt et al., 2008), and OPN, an integrin‐binding ligand, expressed by osteoblastic cells that has been associated with the control of mineralization/mineral crystal growth, osteoblastic cell adhesion, and proliferation (de Barros e Lima Bueno et al., 2011).

Sections were deparaffinized with d‐limonene based solvent (Citrisolv®; Fisher Scientific), rehydrated through a descending ethanol series and washed in distilled water. In order to avoid non‐specific sticking, sections were blocked with 0.01 M phosphate‐buffered saline (PBS), pH 7.2, containing 5% skim milk for 30 min at room temperature. After blocking, the sections were incubated overnight at room temperature with rabbit primary antibody raised against rat Bril (1:4000 dilution) (Moffatt et al., 2008) and Osteopontin (OPN) (1:1500 dilution, LF124 kindly provided by Dr. Larry Fisher). Sections were then washed with PBS containing 0.05% (v/v) Tween 20 (Fisher Scientific), pH 7.4, followed by treatment with the Dako Envision TM+ System, HRP labeled polymer anti‐rabbit kit (Dako Corporation, Carpinteria, CA, EUA) as recommended by the manufacturer. Visualization was performed with 3, 3′‐diaminobenzidine and sections were counterstained with 0.5% methyl green (Sigma‐Aldrich).

3. RESULTS

The installation of the maxillary device did not impair the animals' mastication and, in all cases, they gained weight throughout the experiment. Upon dissection of the maxillae and molar cap removal, there were no visible, overt clinical signs of infection or inflammation at the wound site.

3.1. Finite element analysis

Our finite element analysis indicated that for a cantilever length of the archwire of 3 mm, and a force of 1.5 N on the end of the cantilever, the wire and implant moved toward the sinus (negative z‐direction) 42 μm when there was a blood clot in the gap (having a modulus of about ∼0.28 MPa (Munster et al., 2013; Piechocka et al., 2010), 28 μm when the gap's modulus was 1 MPa, and about 6 μm when the gap contained newly‐formed cancellous bone of modulus ∼18 MPa (Wazen et al., 2013). The implant also moved slightly distally (positive x‐direction) by about 7, 3, and 0.16 μm for gap moduli of 0.28, 1, and 18 MPa, respectively.

Of primary interest were strain states for cases B and C, when loading and micromotion started on day 7 and was either applied in one (case B) or two (case C) sessions per day. So, in both cases B and C, and when the modulus of the gap tissue was assumed to be 1 MPa, the principal compressive strain magnitudes were largest on the distal side of the implant (Figure 3a), e.g., about 0.19 (19%) at the crests of the threads, and extended out from each crest through the entire width of the gap. Close to the implant and in between the threads the compressive strain magnitudes were about 0.1 (10%). On the diametrically‐opposite side of the implant—its mesial side—the compressive strain magnitudes were small in most of the gap region for example, 0.05–0.08 (5–8%). At the same time there were small regions right at the crests of the threads where the compressive strain magnitudes reached about 15%, but the spatial extent of these strains was limited compared to what occurred on the distal side of the implant. As for the principal tensile strains (Figure 3b), these were virtually mirror images of the principal compressive strains, for example, the largest and most extensive regions of high strain (15%) occurred on the mesial side, with the highest strains at the crests of the threads and the lower strains in between. On the distal side, the principal tensile strains were generally small, for example, 5–8% except at the crests of the threads where peak strains reached about 15%, with small spatial extent.

Figure 3.

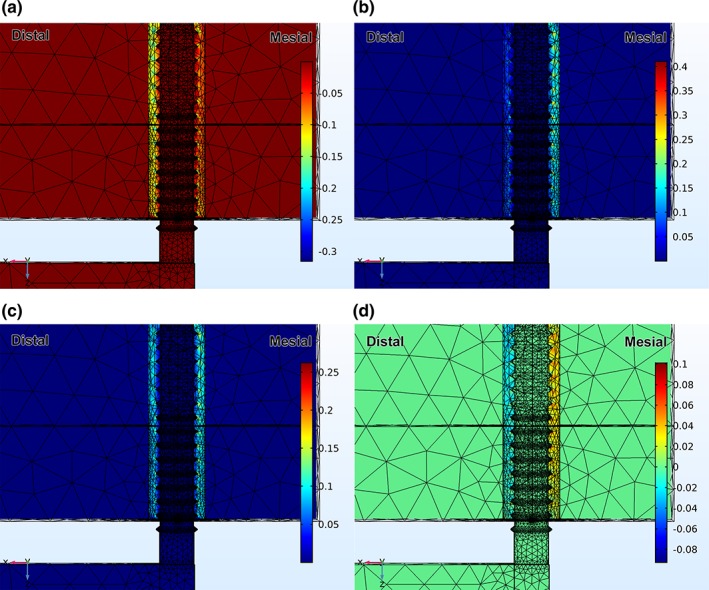
(a) Distribution of 3rd principal strain (compressive) after loading the end of the beam with 1.5 N, and with the modulus of the gap tissue equal to 1 MPa; (b) distribution of 1st principal strain (tensile) after loading the end of the beam with 1.5 N, and with the modulus of the gap tissue equal to 1 MPa; (c) distribution of distortional strain after loading the end of the beam with 1.5 N, and with the modulus of the gap tissue equal to 1 MPa; (d) distribution of hydrostatic strain after loading the end of the beam with 1.5 N, and with the modulus of the gap tissue equal to 1 MPa

Since additional measures of strain are often useful in analyzing the mechanobiology of early tissue differentiation in bone healing studies (Claes & Heigele, 1999; de Barros et al., 2018; Carter & Beaupre, Leucht et al., 2001; Wazen et al., 2013), distributions of distortional and hydrostatic strains were also plotted in the peri‐implant region (Figure 3c,d). The magnitude of the distortional strains reached about 0.10 throughout the majority of the gap on the mesial side of the implant, and peaked at about 0.16 near the crests of the threads. On the distal side of the implant the distortional strains were smaller, for example, between 0.06 in most of the gap region and around 0.1 near the crests of the threads. As for the hydrostatic strains the strains were positive on the mesial side of the implant (ranging from 0 to about 0.08) and negative on the distal side (ranging from 0 to about −0.04.).

3.2. Histology

There was no major inflammatory infiltrate in the immediate proximity to the implants. Some osteoclasts were present at the surgical site; however, in all cases, there was no conspicuous accumulation of these bone resorbing cells near the implant. At 7 days, in all groups there was no evidence of bone formation onto bone surfaces exposed during drilling or within the gap between them and the implant surface (Figure 4a). However, at day 14, bone deposition on the exposed surfaces was evident in rats from the Unloaded and Micromotion 1× groups. The new bone extended into the bone‐implant gap and toward the implant surface (Figure 5a–d). Notably, in both the Unloaded and Micromotion 1× groups, higher bone formation was observed on the distal side of the implants, adjacent to the first molar, while on the mesial side bone deposition appeared patchier (Figure 5a–d). Two loading sessions/day (Micromotion 2×) dramatically reduced bone formation on the distal side and very little or no new bone was observed on the mesial side, and fibro‐cellular tissue surrounded the implants (Figure 5e,f).

Figure 4.

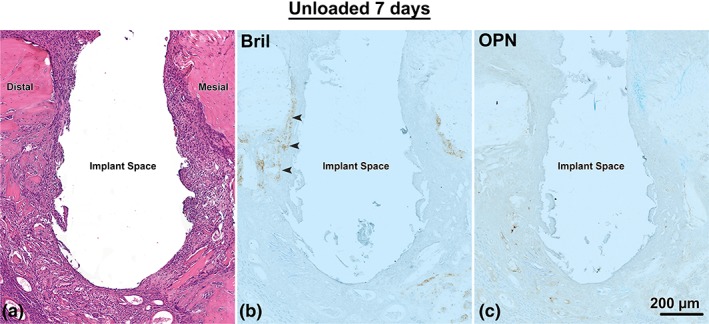
Light micrographs from the Unloaded implant group at 7 days post‐surgery, as shown in a mesial‐distal plane. (a) Histological preparations stained with hematoxylin and eosin and (b) immunolabeled with Bril and (c) OPN. There is some accumulation of Bril (arrowheads) and no accumulation of OPN in the surfaces exposed by osteotomy

Figure 5.

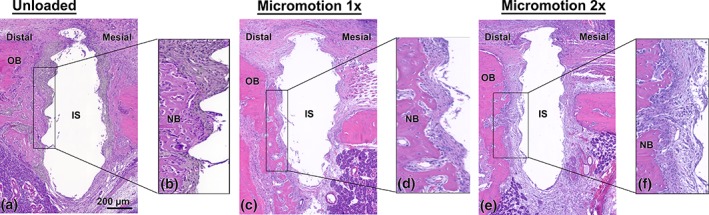
Light microscope images stained with hematoxylin and eosin from the (a, b) Unloaded, (c, d) Micromotion 1× and (e, f) Micromotion 2× groups at 14 days post‐surgery. In the Unloaded and Micromotion 1× groups, new bone extends into the bone‐implant gap and toward the implant surface (b, d). In contrast, in the Micromotion 2× group, there is little or no bone deposition onto the exposed bone surfaces and fibro‐cellular tissue surrounded the implants (f). IS, implant space; NB, new bone; OB, old bone

3.3. Histomorphometric analysis

The power of the study was 86% and there was no significant difference in BID values between the Unloaded control (85 ± 10 μm) and Micromotion 1× the group (90 ± 11 μm). However, consistent with the histology, the micromotion 2× group showed on the average 200% larger bone–implant distances when compared with the other two groups (180 ± 12 μm, p = .01, Figure 6b).

Figure 6.

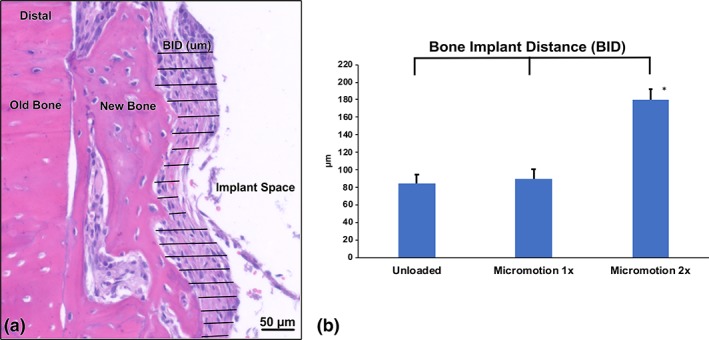
Bone‐implant distance (BID) measurements in Unloaded, Micromotion 1×, and Micromotion 2× groups at 14 days post‐surgery. (a) Histological representation of BID measurements in a Micromotion 1× sample. (b) The Micromotion 2× group shows significantly higher BID values, confirming the interference with osseointegration of this loading regimen

3.4. Immunohistochemistry analysis

In all groups, at 7 days following surgery there was little accumulation of Bril and none for OPN on the bone surfaces exposed by osteotomy (Figure 4b,c). At 14 days, in the Unloaded and Micromotion 1× groups, immunolabeling for both Bril and OPN was observed over newly‐formed bone in close proximity to the implants (Figure 7a,b,d,e). In contrast, in the Micromotion 2× group, there was no such immunoreactivity material near the implants, the area being essentially occupied by fibro‐cellular tissue (Figure 7c,f). However, Bril and OPN were detected over the newly‐formed bone beyond this tissue but the labeling, in general, appeared weaker (Figure 7c,f).

Figure 7.

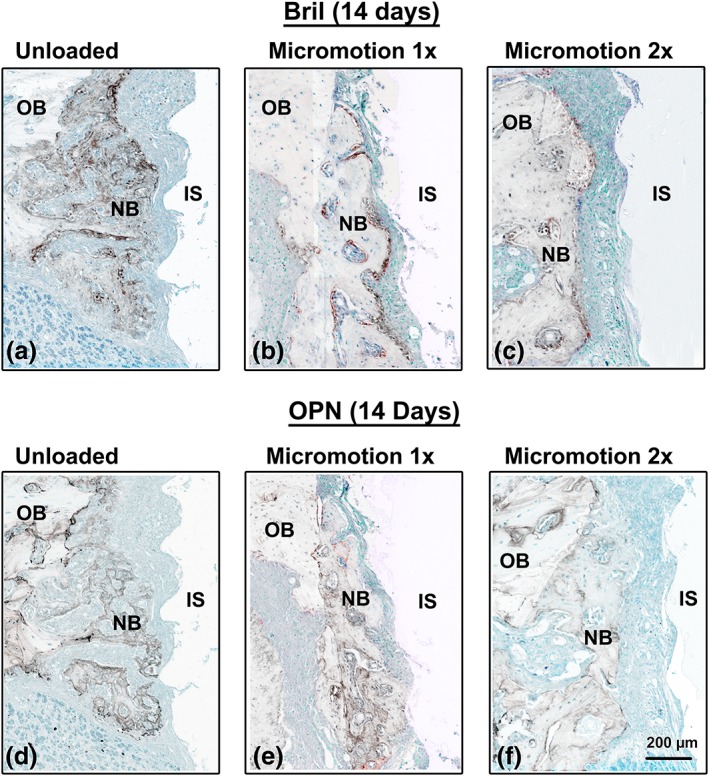
Immunolocalization of Bril and OPN at 14 days post‐surgery. In the Unloaded and Micromotion 1× groups, both Bril (a, b), indicating the presence of active bone formation and OPN (d, e) are detected throughout the new bone deposited on the surgically‐exposed surfaces. In the Micromotion 2×, the newly‐formed bone is found further away from the implant and immunoreactivity for both Bril (c) and OPN (f) is generally weaker. IS, implant space; NB, new bone; OB, old bone

4. DISCUSSION

There are only scattered reports on the osseointegration of implants in the oral cavity of rodents and these are, in general, under conditions of uncontrolled loading that essentially rely on placing the implant under the occlusion plane (Dunn et al., 2005; Ikeda et al., 2018; Lin et al., 2011; Mouraret et al., 2014). While this would shield from direct occlusal forces, it does not protect from tongue movements and food impact. In fact, studies on bone healing under controlled loading are carried out mostly in the tibiae of rodents (de Barros et al., 2018; Jariwala et al., 2017; Leucht et al., 2007; Vandamme et al., 2007; Wazen et al., 2013; Willie et al., 2010), and the results are extrapolated to the oral environment. In a recent report, Uto et al. (2017) used repetitive loading to investigate its impact on bone quality around implants in rat maxillae. Although placed in a tight fit, the implant was not shielded from external interference during the extended loading period. We have developed an experimental system that stably anchors an implant in the rat maxilla, protects it from external influences during healing, and allows application of controlled forces (and related implant micromotion) over single or dual daily loading sessions. By varying the position of the loading orifice on the molar cap (Figure 1g), the system could allow the application of forces in either axial or lateral directions. In this study, the implant was placed on the edentulous ridge to mimic compact, maxillary bone but it could also be positioned in a fresh or healed tooth extraction site (Figure S1).

Rodent models, “rats in particular, are believed extremely useful for conducting basic research involving the skeleton” (Bagi, Berryman, & Moalli, 2011). In addition, rat models have, in general, a closer similarity to humans, including reactions to injury (Iannaccone & Jacob, 2009). In this context, we have used the rat because its size also facilitates surgical and experimental procedures, as well as animal handling. However, our system can also be adapted to mice (Figure S2), particularly in situations where transgenic animal models may be of benefit. Notably, “mice often respond to experimental interventions in ways that differ markedly from humans” (Garcia et al., 2013; Perlman, 2016). Finally, our choice of rats was further motivated by the fact that they are widely‐used for studies of osteoporosis (Chen et al., 2018; Lelovas, Xanthos, Thoma, Lyritis, & Dontasi, 2008), a condition that affects ageing individuals that represent the major recipient group of oral implants.

The focus of our work was not to replicate any particular clinical situation but rather to investigate the basic bone healing response that occurs near the bone‐implant interface where tissue deformation takes place during loading. The rationale for selecting a rather large peri‐implant gap was to allow a closer look at the influence of loading and strains on bone induction and formation in a well‐defined tissue environment that still simulates the gap regions (small or large) that usually exist around any bone implant. As noted earlier, our use of stress and strain parameters allows translation to differently‐sized gaps, since using an appropriate stress analysis, one can compute interfacial stresses and strains in whatever gaps might exist in some different situation with a given implant undergoing loading and micromotion of some other sort. (An analogy is that if one determines an intrinsic stress limit—such as the yield strength or the tensile strength—using a small specimen of a given material, that stress limit can be used in assessing the significance of a computed stress level in some larger, or smaller, sample of the same material; a calculation of stress considers geometry and boundary conditions). Our results indicate that healing of the bony hole created to obtain our peri‐implant gap occurs by osteoconduction from surgically‐exposed bone surfaces. This is different from what we have observed using a tibial model in both mice and rats where marrow disturbance generates new bone induction (de Barros et al., 2018; Wazen et al., 2013). The observed mesial/distal differential in bone deposition in the present case may relate to bone type of the edentulous ridge. On the distal part (near the molar) there is a mixture of compact and trabecular bone while on the mesial part (near the incisor) there is only a thin layer of compact bone with subjacent connective and glandular tissue. As indicated by the Bril labeling, the trabecular bone situated distally and associated with the molar roots shows active bone forming surfaces, whereas there is a paucity of Bril expression over the compact bone situated mesially. As such, it would be expected to have more bone formation on the distal side. Alternatively, the perimolar environment may favor bone formation because it is enriched in cells responsible for periodontal homeostasis (including stem cells), whereas the tissues under the mesial compact are not expected to have any osteogenic capacity. One interesting question is whether osteogenesis could be enhanced both distally and mesially by signals that promote stem cell activity, such as Wnt (Li et al., 2017; Yin et al., 2016).

The histological, histomorphometric and immunohistochemical analyses revealed that two loading sessions/day disrupt bone formation near the implant surface. The BID was significantly larger in the Micromotion 2× group, a result similar to what we have observed in rat tibiae (de Barros et al., 2018). Finite element analysis predicts principal compressive and tensile strain magnitudes of 8–10% in proximity of the implant that, based on our prior work using just one loading session per day (Wazen et al., 2013), are not expected to be a problem for bone formation. Moreover, the magnitudes of principal, distortional, and hydrostatic strain in the gap were also within the limits allowed for membranous bone formation during fracture healing (Claes & Heigele, 1999). Therefore, the observed difference in osseointegration in the Micromotion 2× group—at principal strain magnitudes that were not detrimental in the 1× group—leads to the conclusion that the interference in the 2×/day group results from accumulation of damage beyond a yet‐to‐be‐defined threshold of cycles over the 7 days of loading. In this regard, there is a similarity to what we observed in prior work in the tibia, where strain magnitudes delivered in a 1×/day loading/micromotion regime were permissible for osseointegration while the same magnitudes delivered in multiple sessions/day were not (de Barros et al., 2018). This suggests at least some commonality in mechanobiological factors influencing bone healing around implants in tibial and maxillary sites. The results (Uto et al., 2017) are difficult to compare with the present paper due differences in the total number of loading frequency and the site where the implants were placed. However, it is interesting to note that under acceptable loading, the bone mineral density was increased and also stimulated the bone formation which is in agreement with what Leucht et al. (2007) reported.

Because there was no histologically‐visible, new bone formation at 7 days under stable conditions, it can be presumed that the healing process actively started during the second week and that damage accumulation outpaced regenerative processes during this period. Since there was no convergence of osteoclasts in proximity to the implant, it can be concluded, as confirmed by the BID results, that the accumulation of damage had an influence on the propagation of the wave of bone formation from the exposed bone surfaces.

5. CONCLUSION

We have developed a system that allows, in reliable manner, control over loading conditions, the resulting micromotion, and generated peri‐implant stress and strain states around an oral implant in a rat model. This system opens the door to (a) investigating dental implant loading under various placement conditions (immediate vs. delayed), (b) determining “acceptable” versus “detrimental” loads and peri‐implant strain states that can then be translated to clinical situations, (c) integrating structural and molecular analyses to elucidate the bone healing response in the oral cavity and identify new molecular targets to accelerate and maintain osseointegration, and (d) testing new implant designs and surfaces, and bioactive molecules (Yin et al., 2016) under relevant loading conditions. In addition to validating the applicability of our system, our work provides new evidence on the importance of the total load applied on healing of maxillary bone.

CONFLICT OF INTEREST

The authors have no conflicts of interest to report.

Supporting information

Figure S1 Photographs of (A) the loading system adapted for placement in a rat maxillary first molar extraction site and (B) the protective stainless‐steel pediatric crown with exaggerated top loading holes.

Figure S2. Photographs of (A, B) the micromotion system and protective crown adapted for placement of implants in the edentulous ridge and (C, D) a first molar extraction site in mouse maxillae. In both A and C, the molars are covered with the cement used to attach the arch wire, and therefore not visible.

de Barros e Lima Bueno R, Dias AP, Ponce KJ, Brunski JB, Nanci A. System for application of controlled forces on dental implants in rat maxillae: Influence of the number of load cycles on bone healing. J Biomed Mater Res. 2020;108B:965–975. 10.1002/jbm.b.34449