Machine Learning of Discriminative Gate Locations for Clinical Diagnosis

Abstract

High‐throughput single‐cell cytometry technologies have significantly improved our understanding of cellular phenotypes to support translational research and the clinical diagnosis of hematological and immunological diseases. However, subjective and ad hoc manual gating analysis does not adequately handle the increasing volume and heterogeneity of cytometry data for optimal diagnosis. Prior work has shown that machine learning can be applied to classify cytometry samples effectively. However, many of the machine learning classification results are either difficult to interpret without using characteristics of cell populations to make the classification, or suboptimal due to the use of inaccurate cell population characteristics derived from gating boundaries. To date, little has been done to optimize both the gating boundaries and the diagnostic accuracy simultaneously. In this work, we describe a fully discriminative machine learning approach that can simultaneously learn feature representations (e.g., combinations of coordinates of gating boundaries) and classifier parameters for optimizing clinical diagnosis from cytometry measurements. The approach starts from an initial gating position and then refines the position of the gating boundaries by gradient descent until a set of globally‐optimized gates across different samples are achieved. The learning procedure is constrained by regularization terms encoding domain knowledge that encourage the algorithm to seek interpretable results. We evaluate the proposed approach using both simulated and real data, producing classification results on par with those generated via human expertise, in terms of both the positions of the gating boundaries and the diagnostic accuracy. © 2019 The Authors. Cytometry Part A published by Wiley Periodicals, Inc. on behalf of International Society for Advancement of Cytometry.

Polychromatic flow cytometry technologies quantitatively measure surface and intracellular protein expression and cytokine secretion at the single cell level. They are widely applied in clinical diagnosis of immune system disorders and blood cancers, including leukemia, lymphoma and HIV infection. (David et al. 1; Abraham and Aubert 2; Zare et al. 3; Muchmore et al. 4; Krieg et al. 5). However, due to the heterogeneity of disease phenotypes at the cell population level, the analysis of polychromatic clinical cytometry data remains challenging, without a gold‐standard analysis protocol or a universally applicable gating template to follow. The current approach to the analysis of clinical cytometry data is manual gating, which relies on a human analyst to create gating boundaries hierarchically in measurement space to separate cells into subgroups (cell populations). The process is challenging to carry out in high‐dimensional spaces, as well as being subjective and difficult to reproduce (Aghaeepour et al. 6; Mair et al. 7; Verschoor et al. 8; Saeys et al. 9). In addition, generating gates for multiple samples can be time‐consuming, leading to significant data throughput bottlenecks. For example, Rahim et al. 10 report that the time spent in manual gating analysis can be on the order of 5 to 15 min per sample. Thus, analyzing 100 samples could take 8 to 25 hours.

In this article, we propose a new machine learning approach that automatically searches for interpretable gates in marker space, seeking gates that have high diagnostic accuracy in terms of prediction of class labels at the sample level. The learned gates are optimized for discrimination at the sample level rather than being designed to capture a single and complete cell population. Thus, the proposed approach is not an auto‐gating method for identifying cell populations but instead learns the location of hyper‐rectangular regions in marker space that are optimized for classification of cytometry samples.

In this general context, in order to reduce human bias in the analysis process and improve reproducibility of the analysis results, a variety of different computational approaches have been proposed and developed in prior work to process, analyze, and classify cytometry samples (Pyne et al. 11; Qian et al. 12; Aghaeepour et al. 6, 13; Finak et al. 14; Hassan et al. 15; Saeys et al. 9; Johnsson et al. 16; Lee et al. 17, 18; Arvaniti and Claassen 19; Li et al. 20; Lun et al. 21; Rahim et al. 10; Ko et al. 22; Hu et al. 23; Lux 24; Lee et al. 25). For identification of cell populations, auto‐gating approaches include unsupervised, supervised, semi‐supervised (Lee et al. 18), and constrained unsupervised (Lee et al. 26) methods. The unsupervised methods are typically based on data clustering and/or mixture modeling in high‐dimensional spaces, which can potentially identify novel cell populations but can be difficult for users to interpret. In contrast, supervised, semi‐supervised, and constrained unsupervised methods retain interpretability and are easier to apply in clinical settings to support disease diagnosis. For disease diagnosis, classification of cytometry samples can be achieved without necessarily identifying cell populations (Qiu 27). Many of the supervised learning approaches in the FlowCAP‐II competition (Aghaeepour et al. 6) achieved accurate classification without conducting auto‐gating analysis. However, for interpretation of the classification results, it is necessary to identify the informative features that correspond to characteristics of cell populations. When the results of a learned model can be mapped to these cell population characteristics, both the results and the model are more trustworthy to clinicians.

While there has been significant development of automated techniques in the literature, predicting a classification outcome for disease diagnosis of a subject is still largely a human‐centered process in clinics and hospitals. This process typically includes manual gating analysis for identification of cell populations, extracting features based on proportions of cell populations that lie within selected gates, and applying decision thresholds to these characteristics to make classification decisions. There are subjective decisions involved in the process at multiple stages, including: (1) defining the gating hierarchy, (2) selecting gate boundaries, (3) selecting which features to use for sample‐level diagnosis/prediction, and (4) defining appropriate thresholds on the features for sample or subject classification. The manual nature of this diagnostic process means that it is not easily reproducible and does not scale well to large numbers of markers or cytometry samples or subjects.

The approach proposed in this article focuses on automating and optimizing steps (2) through (4) of this process and it complements existing methods such as RchyOptimyx (Aghaeepour et al. 13) that focus on optimizing the gating hierarchy (Step 1 in the process above). Specifically, we learn and optimize both the gating boundaries and the diagnostic accuracy simultaneously by defining an appropriate objective function that is a function of gate locations in marker space, features based on gate locations, and parameters of diagnostic classifier at the sample level based on those features. Provided the objective function is differentiable, techniques such as gradient descent can be used to find the gate locations, features, and classification parameters that optimize the objective function. The optimization works simultaneously across a set of labeled cytometry samples (the training data) to find a common set of gates that work well for classification across all labeled samples.

An example of where our proposed approach can be used in a practical setting is that of quality control in a clinical diagnostic setting, such as for the leukemia diagnosis problem we discuss in more detail later in the article. In such a setting, discrepancies between a data‐driven diagnosis (such as that proposed in this paper) and the diagnosis from a hematopathologist, can act as an automated tool to alert the hematopathologist to review the subjective manual gating analysis of the flow cytometry data by the diagnostic lab personnel to avoid potential misdiagnosis.

Materials and Methods

Learning Discriminative Gate Features

Notation and approach

Let x _i be the observed single‐cell cytometry data for subject i, a set of multidimensional, multipanel cell‐level measurements, with i = 1, …, N, where N is the number of subjects. More specifically, x _i consists of a set of data matrices, one data matrix per marker panel, where the number of rows in each data matrix corresponds to the number of cells for subject i in that panel, and the number of columns in each data matrix corresponds to the number of marker measurements for that panel.

We focus on binary classification, letting y _i ∈{0, 1} indicate the class label for subject i, such as healthy or disease. The method we propose can be extended to problems with more than two classes through the use of an appropriate multiclass classification model such as a multinomial logistic regression model.

To build a classification model, we need to learn a mapping from x _i to y _i. We follow the usual approach of defining a P‐dimensional feature vector f _i for each subject i, where features are extracted from the cell‐level measurements x _i using a recursive gating process. For cytometry‐based diagnosis, features are typically defined based on appropriate domain knowledge, such as proportions of cell populations and their mean fluorescence intensities (MFI) within gates for subsets of measured markers. In the experiments reported in this article, we focus on classifiers that use features based on cell proportions.

Given a feature representation, each subject can then be represented in feature‐space as a table of N rows (each row containing a feature vector f _i for sample i) and P columns (one per feature). When combined with class labels y _i, this table can then be used to train and evaluate a multivariate classification model using any standard classification method. This is a typical approach (e.g., Aghaeepour et al. 6; Ko et al. 22) for building diagnostic classifiers, consisting of two steps: first, P features are defined, and second, a classification model is constructed given vectors of the P‐dimensional feature values for each subject.

In contrast to this two‐step diagnosis protocol, the approach we pursue in this article is to jointly optimize both the feature definitions and the parameters of the classifier in a single step. This has the goal of producing gates that are well‐suited for differentiating between the classes at the subject level. The vector of feature values f _i = f(x _i; θ) for each subject i is a function of both the set of cell‐level measurements x _i and the gate parameters θ. We focus in this article on parameterizations θ that define rectangular gates, where gates in turn define features that are then used by a classifier to make predictions. Both the parameters of the gate locations (which determine the features) and the parameters of the classifier (the logistic weights) are simultaneously estimated by optimization of a suitably‐defined objective function. In this work, we use logistic regression classifiers, but any classifier whose objective functions are differentiable with respect to their parameters could be used. The optimization of features and classification weights is partly inspired by “end‐to‐end” training of deep neural networks, where early layers are optimized for feature extractions from raw data and later layers are optimized for class prediction given the features (LeCun et al. 28).

Gating tree

Our approach assumes that a fixed gating hierarchy has been determined by domain experts. This gating hierarchy contains a tree‐structured ordering of pairs of dimensions such as those used in manual gating for identifying cell populations of interest, but does not contain the locations of these gates. Figure 1a shows a manually‐determined gating hierarchy for the Chronic Lymphocytic Leukemia (CLL) data used later in the article. Given the gating hierarchy, our model learns the gate locations at each node of the gating hierarchy.

Figure 1.

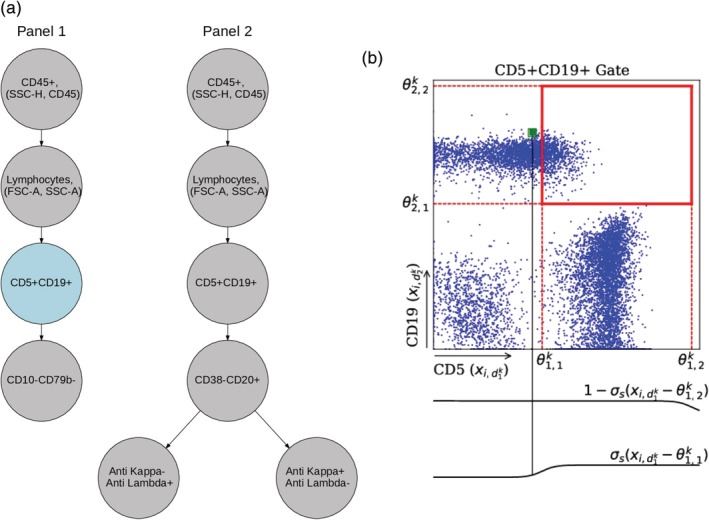
Illustration of a gating hierarchy and one node in the gating tree. (a) Gating hierarchy for two‐panel CLL data (from Scheuermann et al. 29). Each node contains a pair of axes and its gate parameters. We use two gating hierarchies to represent two separate staining panels. Here, we only show θ _k for the CD5 + CD19+ gate in panel 1 in (b) to demonstrate the notation and soft‐gating mechanism. This gate is shown in blue in (a). The four θ parameters here define a rectangular gate, as shown in (b) by the bold red lines. The two sigmoid functions below the green datapoints demonstrate the soft‐gating function applied to this datapoint. Since this point is slightly to the left of ${\theta }_{1,1}^k$, that is, the left side of the box, its corresponding sigmoid function, shown in the bottom sigmoid plot, takes a value less than 0.5. However, since this point is very far from and to the left of the ${\theta }_{1,2}^k$ boundary (the right side of the box), the sigmoid function shown in the top plot for this boundary is very close to 1. [Color figure can be viewed at http://wileyonlinelibrary.com]

We define each node k in the hierarchy as a tuple (d _k, θ _k), where d _k is a two‐dimensional vector that represents a pair of markers over which the data in node k is applied; each entry takes a value between 1 and the number of cell measurements. We parametrize each gate with a 4‐dimensional vector θ _k that characterizes the location of the gate, where ${\theta }_{1,1}^k,{\theta }_{1,2}^k,{\theta }_{2,1}^k,{\theta }_{2,2}^k$ represent the lower and upper boundaries of the gate in dimension $d_1^k$ and $d_2^k$, respectively. We constrain these gate parameters to have the same side length in each dimension but allow the parameters (corners) to be outside the range of the data, which we normalize to lie between [0, 1] per marker. The actual gate boundaries do not extend beyond the [0,1] boundaries of the range, but this gives the algorithm enough freedom to form rectangular gates at the edges, yet still less freedom than unconstrained rectangular gating. We found that this constrained approach led to more robust results than unconstrained optimization of the four parameters.

When a gate g _k is applied to cells of one sample, each individual cell is mapped to a number between 0 and 1, which reflects whether the cell lies within the gate or not. For typical rectangular gates that practitioners use in a manual gating process, the gating function can be defined as a product of indicator functions as follows:

$$g_k\left({\mathbf{x}}_{\mathit{ij}};{\mathbf{\theta }}_{\mathbf{k}},{\mathbf{d}}_{\mathbf{k}}\right)=\left(x_{i,d_1^k}\ge {\theta }_{1,1}^k\right)\times \left(x_{i,d_1^k}\le {\theta }_{1,2}^k\right)\times \left(x_{i,d_2^k}\ge {\theta }_{2,1}^k\right)\times \left(x_{i,d_2^k}\le {\theta }_{2,2}^k\right)$$ (1)

where $x_{i,d_1^k}\hspace{0.17em}/\hspace{0.17em}{x}_{i,\hspace{0.17em}{d}_2^k}$ represent a measurement for markers $d_1^k\hspace{0.17em}/\hspace{0.17em}{d}_2^k$ respectively for a cell in sample i. This counts each cell as being entirely in the gate if it is within the rectangle (value of 1), and entirely outside the box if not (value of 0). However, the discontinuity in the indicator function precludes the use of gradient‐based optimization, since the objective function is not differentiable. To make the gating function differentiable, we replace the indicator functions used in Eq. 1 with sigmoid functions:

$$\begin{array}{l}{g}_k\left({\mathbf{x}}_{\mathit{ij}};{\mathbf{\theta }}_{\mathbf{k}},{\mathbf{d}}_{\mathbf{k}}\right)={\sigma }_s\left(x_{i,d_1^k}-{\theta }_{1,1}^k\right)\times \left(1-{\sigma }_s\left(x_{i,d_1^k}-{\theta }_{1,2}^k\right)\right)\\ \times {\sigma }_s\left(x_{i,d_2^k}-{\theta }_{2,1}^k\right)\times \left(1-{\sigma }_s\left(x_{i,d_2^k}-{\theta }_{2,2}^k\right)\right)\end{array}$$ (2)

where x _ij is the vector of measurements for the jth cell in sample i, $x_{i,d_1^k}\hspace{0.17em}/\hspace{0.17em}{x}_{i,\hspace{0.17em}{d}_2^k}$ is the $d_1^k\hspace{0.17em}/\hspace{0.17em}{d}_2^k$ th component of this vector.

The sigmoid function σ_s(z) = 1/(1 + exp(−sz)), parameterized by a positive constant s, approximates the indicator functions in Eq. 1. The constant s controls the steepness or slope of the logistic function and can be interpreted as the closeness of the sigmoid function to an indicator function, that is, how close the approximation is to hard gates used during manual gating processes. Based on some initial experimentation, we used a value s = 100 in the results reported in this article. This value typically corresponds (in our experiments) to a fairly steep (almost step‐like) sigmoid function, where data points that lie more than about distance of about 0.05 from the boundary (on a 0–1 scale) are included in the gate with a weight of 0.01 or less.

Feature extraction from gating trees

The predictive features for classification are defined as the log proportions of cells that fall within each gate at the leaf nodes of the gating tree, relative to the total number of cells from the subject. Each feature, corresponding to each leaf node in the gating tree, is extracted by applying all the gates along the root to leaf path to each cell in sample x_i, summing over the resulting values, and normalizing to obtain proportions:

$$f_{\mathit{ip}}=\log \left(\frac{1}{N_i}\sum _{x_{\mathit{ij}}\in x_i}\prod _{\hspace{0.17em}k\in \text{Path}\left(p\right)}{g}_k\left(x_{\mathit{ij}};{\mathbf{\theta }}_{\mathbf{k}},{\mathbf{d}}_{\mathbf{k}}\right)\right)$$ (3)

where N _i is the total number of cells in sample x _i, and Path(p) is the root‐to‐leaf path associated with the pth feature. Using the logarithm of proportions of cell populations to define features puts the feature values on a better scale for learning classification weights (compared to using proportions directly), especially in situations with very small proportions.

Modeling multiple panels as gating forests

Flow cytometry data sets often consist of multiple panels each with different numbers of distinct protein markers. These different panels are not matched at the cell level. However, although we cannot merge the raw data at the single cell level across panels directly, we can merge the extracted features of the same subject i from multiple panels by appending them together in feature vector f _i to provide as input to a classifier, allowing our approach to directly handle cytometry measurements from multiple staining panels. The gating parameters across multiple panels and the classifier parameters can all learned simultaneously by extending the loss function to include the data, the gating locations, and the features across multiple staining panels per subject. Experimental results on CLL data, in which cells are stained with two panels of markers, are reported later in Section “Results on Simulated Data”.

Objective function

The classification model and gate features are learned by optimizing (minimizing) an objective function consisting of two parts. The first component of the objective function is the classification loss l(θ, α), which measures the difference between predictions made by the model and the true labels of subjects y _i:

$$l\left(\theta ,\alpha \right)=-\frac{1}{N}\sum _{i=1}^N\left[y_i\log \left(P\left(y_i=1|{\mathbf{x}}_i;\theta ,\alpha \right)\right)+\left(1-y_i\right)\log \left(P\left(y_i=0|{\mathbf{x}}_i;\theta ,\alpha \right)\right)\right]$$

where α is the vector of parameters for the logistic regression model, θ is a vector of parameters for the gate positions, and P(y _i|x _i;θ, α) are the probabilities produced by the model for subject i for some fixed values of θ and α. We seek to minimize l(θ, α) since lower values of this loss function correspond to more accurate predictions by the model. This loss function l(θ, α) is known as the log‐loss and is the standard loss function for binary classification used in machine learning (Friedman et al. 30; Murphy 31). Other differentiable loss functions (such as squared error) could also in principle be used. By optimizing the classification loss l(θ, α) with respect to gate locations and classifier parameters, the sample‐level diagnosis information is backpropagated to model parameters, driving the gates to search the multidimensional marker space to identify cell populations that can discriminate between samples from different classes.

The second part of the objective function consists of regularization terms, which constrain the learned features (the gates) to reflect expert intuition and relevant prior knowledge about cell types and diagnosis. In the work described, here we use two regularization terms that are well‐suited to disease diagnosis where the negative class (y = 0) is typically indicated by the absence of particular cell types (such as cancer cells) and where the positive class has a much larger proportion of the same cells. In particular, the first regularization term r ₁(θ) encourages the model to learn gates with lower proportions for the negative class:

$$r_1\left(\theta \right)=\sum _{i=1}^N\left(1-y_i\right){\mathbf{f}}_i\cdot \mathbf{m}$$ (4)

where m is a binary mask which determines which particular features are encouraged to have lower proportions. The second regularization term r ₂(θ) encourages the model to make the features (proportions) for the positive class be significantly larger than those of the negative class push the features (proportions) from positive samples apart from those of the negative:

$$r_2\left(\theta \right)=-\ln \left({\left|{\mu }_{\mathit{pos}}-{\mu }_{\mathit{neg}}\right|}^2\right),$$ (5)

where μ _pos and μ _neg are both p‐dimensional vectors containing the means of the positive features and negative features, respectively. Note that these two regularization terms are well‐suited for diagnosis problems where the two classes are differentiated by the presence or absence of cells in certain regions of marker space. For other diagnosis problems, other forms of regularization terms, reflecting different types of prior knowledge about each problem, may be more appropriate.

The full objective function then takes the form:

$$L\left(\theta ,\alpha \right)=l\left(\theta ,\alpha \right)+{\lambda }_1{r}_1\left(\theta \right)+{\lambda }_2{r}_2\left(\theta \right)$$ (6)

consisting of the log‐loss plus a weighted combination of the regularization terms, where λ ₁ ≥0 and λ ₂  ≥0 are the weights for each regularization terms. Their values are determined via grid‐search and cross‐validation (see below).

From a Bayesian perspective the full objective function above can be viewed as the negative logarithm of the posterior probability of the parameters given data, which in turn is proportional to the negative log‐probability of the data (the log‐loss term) minus a log‐prior term on the parameters (the regularization terms). Minimizing this function corresponds to seeking the mode of the joint posterior probability of α and θ conditioned on the data and the prior (regularization) terms.

Optimization

The objective function L(θ, α), as defined in Eq. 6 above, is a scalar function of the unknown parameter vectors θ and α. To minimize L(θ, α) with respect to θ and α, gradient‐based search is a computationally practical option and is the standard approach in machine learning for optimization of parameters with differentiable objective functions such as logistic regression and neural networks (Friedman et al. 30; Murphy 31; LeCun et al. 28). It uses iterative local search from an initial starting point in parameter space, then follows the surface of L(θ, α) in small steps, where each step is in the direction opposite of the local gradient, that is, the steepest downhill direction. The search continues until a local minimum of L(θ, α) is found.

We scaled all measurement values to lie within the range [0,1], using the global maximum/minimum measurement values per measurement dimension across all samples. This type of normalization is a standard preprocessing step for gradient‐based optimization in machine learning to help avoid numerical issues due to scaling.

We explored three different approaches for initializing the gradient descent algorithm. The first method puts an initial square gate (of width 0.5) in the center of each two‐dimensional marker space. The second approach runs the gradient descent procedure from 20 different randomly located gate locations (square gates, width 0.5) and selects the solution from the 20 gradient runs with the minimum value of the objective function. The third approach uses the data for initialization in the following manner. Cells across all samples are pooled and an initial gate is determined for each two‐dimensional node by searching over a three‐by‐three grid of equi‐spaced points ([0.25, 0.5, 0.75] in each dimension), extending each point to one of the four corners to create 36 candidate initial gates per node. From these 36 candidate locations, the gate which maximizes the difference in the proportion of cells within the gate, between the positive and negative populations, is chosen independently per node. We found that this third approach was more robust than the other two approaches in terms of consistently finding features (gates) that produced good classification performance and we used this approach in the generation of results reported in the remainder of the article. The grid size was selected to be relatively coarse both for computational reasons and to avoid initializing with very small gates. In practice, other heuristic initialization techniques could also be useful.

The term hyperparameters in machine learning is generally used to refer to algorithmic parameters that a user can set prior to running the algorithm. For our model, the relevant hyperparameters consist of the two regularization weights λ ₁ and λ ₂ and the learning rate ν > 0 for gradient descent. Following standard practice in machine learning, in the results reported below we randomly selected a subset of data called a development set, which was then used to optimize the hyperparameters using cross‐validation and grid search. We used the Adam algorithm (Kingma and Ba 32) in the PyTorch (Paszke et al. 33) software package for optimization. Adam is a widely used gradient‐based optimization algorithm for machine learning algorithms. Apart from the learning rate, default settings for other optimization‐related algorithm parameters were used (β ₁ = 0.9, β ₂ = 0.999). We ran gradient descent for 200 iterations in all of our experiments and this appeared to be sufficient for convergence of the method for the data sets we report on below.

Data sets

Chronic lymphocytic leukemia data

We also evaluated our approach in the context of the clinical diagnosis of CLL. The data set consists of FCS files from peripheral blood mononuclear cell (PBMC) samples from 146 human subjects (98 CLL‐positive and 48 CLL‐negative). Two 10‐color CLL staining panels were used to obtain multidimensional single cell measurements from each individual (i.e., 292 FCS files in total).

The FCS files and the diagnosis were provided by UCSD clinical laboratories under pseudo IDs/file names. Protected health information (PHI) was scrubbed at UCSD by applying the FCS deidentifcation tool downloaded from FlowRepository,¹ followed by manual examination. The scatter parameters and the markers measured in the two panels are Panel 1: FSC‐A, FSC‐H, FSC‐W, SSC‐A, SSC‐H, SSC‐W, CD45, CD22, CD5, CD19, CD79b, CD3, CD81, CD10, CD43, CD38, Time; Panel 2: FSC‐A, FSC‐H, FSC‐W, SSC‐A, SSC‐H, SSC‐W, FMC‐7, Anti‐Lambda, CD5, CD19, Anti‐Kappa, CD23, CD45, CD49d, CD20, CD38, Time. Acquisition was performed on BD FACSCanto 10‐color instruments.

As described in Scheuermann et al. 29, the expert manual gating strategy for identifying the CLL cells from the two UCSD panels is as follows (see also Supplementary Fig. 1). In Panel 1, eight parameters including both scatter and fluorescence markers were used in a sequential gating process to identify the CLL cell population: (1) SSC‐H versus CD45 to identify leukocytes; (2) FSC‐A versus SSC‐A to identify live lymphocytes; (3) CD5 versus CD19 to identify the CD5 + CD19+ abnormal B cell population; (4) CD10 versus CD79b to extract the CLL cells at the left lower corner of the scatter plot (CD79b‐CD10‐). In Panel 2, there are four additional markers involved in the human‐defined gating hierarchy: CD38, CD20, anti‐Kappa and anti‐Lambda, including (1) CD38 versus CD20 to identify the abnormal CD38‐CD20+ B lymphocytes; (2) there are two children nodes following the root node, for identifying either kappa‐lambda+ cells and kappa+lambda‐ cells from the CD38‐CD20+ cells, with the ratio of kappa‐lambda+ cells to kappa+lambda‐ cells being informative. We describe results below for learning gating locations for Panel 1 data alone and also simultaneously learning gating locations for Panel 1 and Panel 2 data together.

Data Availability and Software

Software and simulated data can be found in our github repository². FCS files of the CLL study together with their diagnosis labels have been deidentified and submitted to FlowRepository. Files of Panel 1 and Panel 2 for the 102 samples used for training and development can be found under IDs: FR‐FCM‐Z27S and FR‐FCM‐Z27T. Files of Panel 1 and Panel 2 for the 44 hold out samples used for testing can be found under ID FR‐FCM‐Z27U for the first 24 samples, and the last twenty (in TXT format) can be found at a separate github repository.³

Results

Results on Simulated Data

To help evaluate our approach, we construct a simple two‐class, eight‐dimensional simulated data set that mimics flow cytometry data with a single panel, as shown in Figure 2. The gating hierarchy for this data consists of a single tree, with a left branch of depth two and a right branch of depth three. At each node, we sample from a Gaussian mixture with different weights for each class. At the M3, M4 leaf node the first class has more cells than the second class in the lower left corner, while for the M7, M8 leaf node, the second class has more cells in the upper right corner if the bottom right cluster is selected for the M5, M6 gate, or more cells overall if the top right cluster is selected for the M5, M6 gate. We also add Gaussian noise centered on the optimal gate locations at the leaves, which makes finding the optimal leaf gates harder. The model must filter out the noise at the leaf nodes by placing the non‐leaf gates in the correct positions. In order to evaluate our model performance on these data, we randomly generated 2000 samples with each sample containing 950 cells, and held out 1,000 samples for testing. We learned four gates on this data following the gating hierarchy as shown in Figure 2. The model achieves accuracy of 96% on the holdout data, reaching convergence after 200 iterations.

Figure 2.

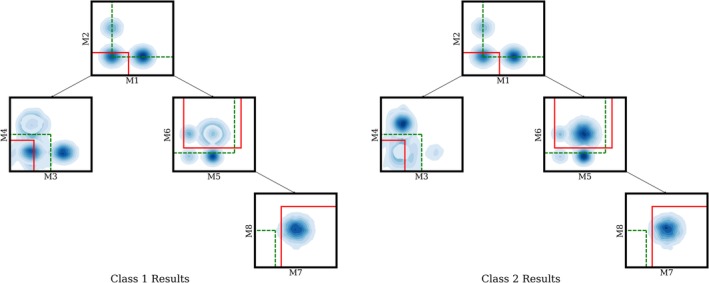
Learning gate locations for simulated data: Green dashed lines show the initialization of gate locations before learning, while solid red lines represent the learned gates after convergence. . The two contour plots shown above are generated by applying kernel density estimation to the pooled data for each respective class. Deeper blue corresponds to higher data density at that region. For class 1, the M3 vs M4 leaf has more data in the bottom left corner. For class 2, the M7 vs M8 leaf has more data overall. Our proposed method successfully locates these two regions, which differ between the two classes starting from the heuristic initialization discussed in 2.1. (The M7 vs M8 leaf gate initialization has no data in it because the plot shows the data at each node filtered by its parents gates. Using the initial instead of final gates to filter the data, there is data in the M7, M8 heuristic initialized gate.) [Color figure can be viewed at http://wileyonlinelibrary.com]

Results on CLL Data

We first describe our results using only Panel 1 data, and in section 'Learning with Multiple Panels' we describe the results using both Panel 1 and Panel 2. In our experiments on CLL PBMC data, the algorithm learned the locations of four gates for Panel 1, for marker‐pairs CD45/SSC‐H, SSC‐A/FSC‐A, CD19/CD5, CD79b/CD10, corresponding to the 4‐level gating hierarchy for Panel 1 in Figure 1a. The algorithm is provided with the structure of the tree (i.e., the sequence of pairs of markers involved in gating) and jointly learns the gate locations across all nodes using the discriminative learning algorithm outlined earlier.

Data partitions, hyperparameter tuning, and runtime

FCS files from 44 of the 146 CLL PBMC samples were set aside as a holdout set for final model evaluation and were not used in any development or training of models. Of the remaining 102 PBMC samples, 34 were randomly selected as a development set for hyperparameter tuning. The 68 remaining samples were designated as a validation set for cross‐validation experiments to compare model performance with baselines. Final predictions were made on the 44 sample holdout set by training a single model on the 102 samples in the combined development and validation sets and then making predictions on each of the 44 holdout samples. When making predictions with the learned model on new samples, we thresholded the class probabilities from the logistic classifier at 0.5 to predict the positive class.

The three hyperparameters of the algorithm, the two regularization weights and the learning rate, were selected by a grid search on the development data by maximizing the average accuracy across a five‐fold cross validation run. The grid values used were [0, 0.001, 0.01, 0.1] for the regularization weights and for the learning rate ν, [0.001, 0.005,0.01, 0.05, 0.1] with the values λ ₁ = 0.001, λ ₂ = 0.001, ν = 0.01 being the values that maximized accuracy and that were used in all subsequent experiments with the CLL data.

The algorithm takes a total of 1,676 s to train on the 102 samples using a GeForce 1,080 Ti GPU.

Baseline prediction methods for comparison

We conducted experiments with two baseline models on the CLL data. Unlike our proposed single‐step approach, the baseline approaches use two‐steps to make sample predictions. First, features are constructed by performing a clustering algorithm (K‐means or FlowSOM) on the pooled training data, followed by calculating proportions of data in the clusters for each individual sample (Shen 34; Gassen 35). A logistic regression classifier is then fit to the training data, using the cluster membership features to predict the probability of CLL. In order to select the optimal number of clusters K, we performed a grid search over the range [5, 10, 30, 50, 100], computing the average testing accuracy across five 80/20 splits of the development data. For K‐means clustering, we found K = 5 and K = 30 both had the highest average testing accuracy across the development folds (73%). So we used both values of K in our experiments below. FlowSOM clustering, for different numbers of clusters K, did not yield features or classifiers that produced classification accuracies that were systematically better than predicting the majority class—this may be because of the relatively small sample sizes. (training sets of with 54 samples for the 80/20 splits on the validation data).

Cross‐validation results

We conducted cross‐validation experiments on the validation set by randomly splitting the set of subjects 50 times into disjoint partitions of 80% for training and 20% for testing. For each run, we trained a classification model on the training data to learn the gate locations to produce the proportion‐based features and to simultaneously learn the weights of the logistic classifier, without using any information about the human‐defined gating boundaries. Separately, we trained a logistic classifier using the features computed from the predefined human‐generated gates as shown in Supplementary Figure 1, which we refer to as “human‐gates+logistic” below. We also evaluated the classification accuracy from human‐generated gates, using a predefined expert rule that classifies a sample as positive if the proportion of cells within the gate exceeded 0.01% of CD45+ leukocytes (a standard rule‐of‐thumb in diagnostic laboratories) and refer to this as the “human‐gates+rule.” The means (and standard deviations) of the classification accuracy of the algorithm gates, the human‐gates+logistic, and the human‐gates+rule were 82.0% (7.1%), 80.7% (9.1%), and 83.47% (8.19%), respectively, relative to a base‐rate classification accuracy of 62% on the validation data. The differences in classification accuracies across the 50 runs, between each of the human gate methods and the algorithmic method, were not statistically significant at the 0.05 level under a Wilcoxon signed‐rank test. That is, our proposed learning approach achieved results that are consistent with the results obtained with human gating (gating boundaries as well as classification accuracy) without knowledge of the location of the human‐defined gates.

We also evaluated the k‐means baseline approach, with both k = 5 and k = 30, on the same 50 cross‐validation train‐test sets, resulting in mean accuracies (and standard deviations) of 65.6% (10.6%) and 73.3% (8.9%) for k = 5 and k = 30, respectively. The differences in classification accuracies across the 50 runs, for each value of k, between k‐means and each of the algorithm gates and the two versions of human‐gates were statistically significant at a 0.001 level under a Wilcoxon signed‐rank test. Thus, the unsupervised k‐means method led to classification accuracies that were significantly lower than those produced by either the algorithmic or human gates.

Classification with hold‐out samples

We fit a single model to the 102 samples in the combined development and test data sets, using the same initialization and optimization methods as used above and the same hyperparameter settings. This model was then used to make classification decisions on the 44 holdout samples that had not been used in any aspect of model development or evaluation prior to making these predictions. We also used the human gates+logistic, human gates+rule, and k‐means methods as reference baselines for comparison. The human gates+logistic used the human‐defined gates (Supplementary Fig. 1) for defining features (proportions) for each of the 102 samples and a logistic classifier was trained on these labeled features. The k‐means method was also trained (clustering followed by logistic regression) on all 102 samples in the combined development and test data sets.

The discriminatively‐trained gates from the algorithm correctly classified 90.9% of the 44 samples (40 correct), the human‐gates+logistic and the human‐gates+rule methods each correctly classified 86.4% (38 out of 44). Thirty two of the 44 samples in the holdout set are positive, so a majority classifier that predicts all samples as positive could achieve an accuracy of 72.7%. The K‐means baselines produced accuracies of 77.0% and 88.6% (K = 5 and K = 30, respectively) for the same holdout data. Although the hold‐out sample size of 44 is small, the results suggest that the discriminatively‐trained gates are at least as accurate as the human‐generated gates for this data. Figure 3 shows a scatter plot of the log‐proportions (the features used by the classifier) for both the samples used to train the model (left) and the holdout samples (right). The x‐axis corresponds to the features from the human‐generated gates and the y‐axis corresponds to features from the algorithm‐generated gates. Decision boundaries for each are also shown. The feature values are well correlated, indicating that proportions from the algorithmic gates and the human‐defined gates are in broad agreement. The algorithmic gates tend to be systematically somewhat smaller than the human gates with mean cell proportions of 5.45% (positive samples) and 0.0053% (negative samples) for the algorithmic gates, compared to proportions of 12.75% (positive) and 0.023% (negative) for the human gates. This reflects the tendency of the algorithmic gates to seek out “discriminative pockets” of cells in the marker space during the gradient‐based training.

Figure 3.

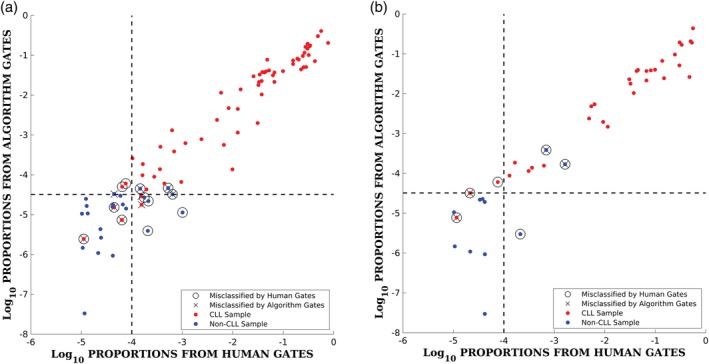
Scatter plot of features (log scale) per sample for the model trained on 102 samples showing results in‐sample on the 102 training samples (left), and out‐of‐sample on the 44 holdout samples (right). Red symbols denote CLL samples and blue symbols denote non‐CLL samples. Samples that are misclassified in each data set are indicated by black open circles for the human gates and black X's for the algorithm gates. The vertical dotted line in each plot corresponds to the decision threshold of 0.01% for the human gates and the horizontal dotted line corresponds to the decision boundary for the logistic regression classifier for the algorithm's gates (the feature value where the two posterior class probabilities equal 0.5). [Color figure can be viewed at http://wileyonlinelibrary.com]

Illustration of gate learning

Figure 4 illustrates how the gates are learned during gradient descent and how they compare to the human‐defined gates. These results correspond to the model that was fit to all 102 samples and used for prediction on the hold‐out data—these gates are typical of the results that were obtained across the 50 cross‐validation runs. Figure 4a shows the locations of the gates after being initialized (using the heuristic procedure described earlier). Figure 4b shows the locations of the gates after they have moved during gradient descent from their initial locations to their final location after 200 gradient descent iterations on the gate parameters. Figure 4c shows the human‐generated gates. The blue points in each plot correspond to cell‐level measurements in each two‐dimensional marker space after gating by the parent node. From a qualitative perspective, the locations of the algorithmic gates in the lower two nodes confirms the finding in Scheuermann et al. 29, namely that the CD5 + CD19 + CD10‐CD79b‐ cell population is diagnostic for CLL.

Figure 4.

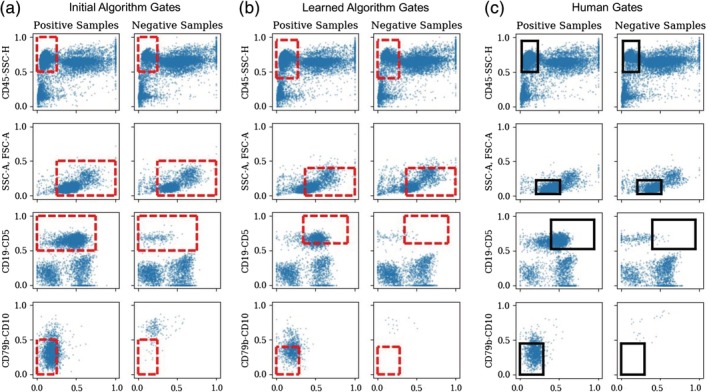
Learning gate locations for panel 1 from the clinical CLL data. Gate locations are shown in red dotted lines (for the algorithm) and in black (for the human gates). Blue points correspond to cells/events pooled across samples with positive (CLL) or negative (non‐CLL) labels and where the cells/events in each row have been filtered by the gates above them. (a) Initial gate locations for the algorithm, (b) final gate locations after 200 iterations of gradient descent, (c) gate locations as drawn independently by human experts. [Color figure can be viewed at http://wileyonlinelibrary.com]

Comparing Figure 4a,c, we see that the initialization places the gates in the general region of the human‐defined gates, but with somewhat different sizes and locations for some of the nodes. The learned gate locations are quite similar to the human‐defined gates, with the exception of the gate at the second node from the top, where the algorithm's gate is considerably larger than the human gate. However, the human gate captures more cells than the algorithm's gate (being centered on more dense regions of cells than the algorithm's gates): approximately 11.1% of all positive cells pass through the human gates, while only 5.0% of the positive cells pass through the (converged) algorithm's gates. In addition, between Figure 4a,b, from the beginning to the end of gradient descent, the proportion of cells passing through the gates decreases from 16.4% to 5.0%. We noticed that this was a common phenomenon when learning of discriminative gates, namely that the gradient procedure tended to converge to gates that captured smaller (and more discriminative) sets of cells, compared to either the human gates or the initial gates—and was also noted above in the features for the holdout data.

There is a corresponding increase in accuracy (and decrease in log‐loss) during gradient descent: the converged gates have a classification accuracy of 91.2% compared to accuracies of 76.5% and 87.3% for the initial and human gates, respectively. For log‐loss, l(θ, α), there is a corresponding decrease (lower is better) with a log‐loss of 0.198 for the gates after gradient descent compared to log‐losses of 0.405 and 0.247 for the initial and human gates. These numbers for accuracy and log‐loss are computed on the training data and, as is typical for discriminative machine learning methods, the training data metrics tend to be optimistic estimates relative to out‐of‐sample values. Nonetheless, the CV and hold‐out results (described above) indicate that the discriminative gate‐learning process is not overfitting by much, that is, that the learned gates perform at least as well as the human gates when evaluated in cross‐validation mode or out‐of‐sample.

Figure 5 plots the increase of classification accuracy during training, as well as the optimization process of classification loss. Accuracy increases quickly during the early iterations, and stays near 90% after 100 iterations as shown in Figure 5a. The classification loss converges around 175 iterations as shown in Figure 5b. Further iterations after 100 may be over‐fitting slightly to the training data as shown by the gap between the train (orange) and blue (test) classification losses, however, the accuracy remains stable on the 44 hold out test data.

Figure 5.

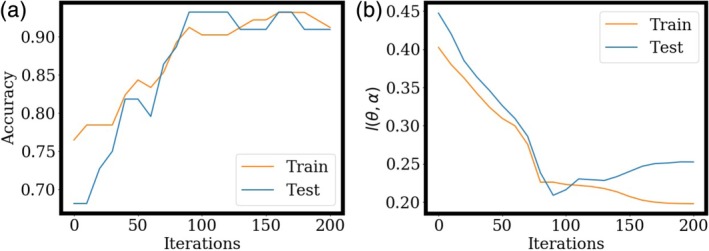
Optimization of accuracy, and classification loss l(θ, α), as a function of iteration number, on the CLL data. The model is trained on all 102 training samples and evaluated on the 44 hold out samples. [Color figure can be viewed at http://wileyonlinelibrary.com]

Learning with multiple panels

As mentioned previously in section “Materials and Methods”, our method can be extended to simultaneously learn gates across multiple staining panels of data that are matched at the sample level, allowing the algorithm to potentially utilize multiple discriminative features from a diverse set of markers. We investigated this approach by including data from Panel 2 into the CLL data set as shown in Figure 1a. We configured the gradient descent algorithm to simultaneously learn one feature (and relevant gates) from the Panel 1 data, and two features (and sets of gates) from the Panel 2 data. We then performed the same set of validation and holdout experiments as describe above for models based on Panel 1 alone. The binary mask, m, in regularization term r₁(θ) for the results with both panels is set to one for the feature from Panel 1 and zero for the Panel 2 features since they are based on the ratio of kappa‐lambda+ cells to kappa+lambda‐ cells, and regularizing these features to zero would inhibit learning the ratio.The addition of the second panel did not improve classification results across the 50 cross‐validation runs on the validation data set or when evaluating a single model on the holdout set, yielding an average accuracy of 80.21% for cross‐validation, and a holdout accuracy of 88.64%. The results are not significantly different from the results with the single panel model described earlier. The slightly poorer results suggest that the addition of a second panel for this problem allowed the model to overfit (given the relatively small amount of labeled data at the sample level), and that the information from the markers in Panel 2 data did not provide the learning algorithm with any additional discriminative information beyond that in the Panel 1 data.

Discussion

The proposed approach provides a machine learning solution for optimizing the locations of hyper‐rectangular discriminative gates for classification of multidimensional cytometry data at the sample level. The resulting algorithm optimizes gating locations by maximizing classification accuracy within a single framework and is applicable to cytometry data analysis problems that (i) have labeled training data at the sample level and (ii) where samples can be classified using features derived from gating boundaries, for example, the number of cell events, the proportions of the cell populations, or their ratios.

The primary strengths of the approach are two fold. The first strength is that the method produces interpretable low‐dimensional gate representations. Unlike the data clusters identified by many existing unsupervised auto‐gating methods in high‐dimensional marker spaces, a hyper‐rectangular gate is simple and easy to translate into marker expression levels for clinical use. The second strength of the approach is that the learning of gate locations is coupled to diagnostic classification at the sample or subject level. Existing auto‐gating methods are largely unable to incorporate discriminative information from the sample level and often rely on the less optimal two‐step approach of first identifying sub‐populations of cells in an unsupervised manner and then using these representations to learn classifiers at the sample level in a second step (Aghaeepour et al. 6; Saeys et al. 9; Rahim et al. 10).

There are a number of potentially useful directions for further development of the approach. For example, in the work described in this article, we assumed that the gating hierarchy is known a priori. In principle, however, one could also learn the structure of a gating hierarchy, given an appropriately defined objective function, potentially leveraging existing methods, such as RchyOptimyx (Aghaeepour et al. 13), that optimize the sequence of steps of the auto‐gating process to correlate with clinical outcome. In a manner analogous to learning of decision tree classifiers in supervised learning, a greedy approach could be used to search over pairs of marker dimensions, using the algorithm described in this article to find discriminative gate locations for each pair, and then selecting the markers and gate locations that have maximal discriminative power.

The process of searching over pairs of markers and gate locations could be applied recursively on the child nodes. Branches could be terminated when there appears to be little additional discriminative power to be found in a node. A potential issue with this approach for learning gating hierarchies is the computational complexity. If K is the number of markers, then this greedy tree search process involves, at each node in the gating hierarchy, O(K ²) instantiations of the algorithm for learning gate locations for each possible pair of markers. For even relatively moderate numbers of markers (e.g., K = 10), this will be computationally demanding. However, it may be possible to reduce this complexity in practice, for example by leveraging prior knowledge available about markers and cell‐types to provide hints to the search algorithm, or by using an initial manual gating as a starting point and then having the algorithm make local changes to the structure to try to improve it in terms of its predictive accuracy. This initialization could also be done in a semisupervised manner based on given phenotype of cell populations of interest, without requiring prior knowledge for the locations of the gates (e.g., using a Bayesian tree method (Ji et al. 36)).

Another direction to extend the current model is to learn nonrectangular polygonal gates, providing more flexibility in terms of capturing dense regions of cells that have discriminative power, based on reparameterization of the parameters θ for each gate. One option, for example, would be to parametrize a six‐sided polygon that is symmetric about its major and minor axes and that can be uniquely specified by the locations of three 2d vertices (i.e., six parameters in all). As long as the loss function is differentiable with respect to the shape parameters then such parametrizations could replace the rectangular representations assumed in this article. In the current approach, density is not directly a factor in where gates are located, allowing the algorithm to include regions that are relatively empty. Polygonal gates can provide a mechanism for taking local cell density into account, by providing more representational power to enclose denser regions of points. This requirement for density could be added as a regularization constraint to encourage the algorithm to find dense and discriminative regions that correspond to distinct cell types, further improving the interpretability of the results.

Another direction for improvement would be to address the limitation that a single set of global gate locations are learned for all samples in our proposed approach. This will not work well if there is significant misalignment of measurements across samples. A potential solution to this would be to first use an existing alignment approach to align the samples. A second option would be to try to learn gates that can vary the location of their boundaries per sample, but nonetheless constrain them to be similar by regularizing the variance of gate locations across different samples, using for example a random effects approach similar to the joint clustering and alignment framework proposed by Lee et al. 17.

Conclusions

In this article, we describe the development of a novel approach that can learn discriminative gate locations given a gating hierarchy. The learning process iteratively optimizes gating locations based on the discriminative power of the events inside the hyperrectangle gate to maximize the predictive power of the classifier. The experimental results show that the algorithm we propose has the ability to learn gate locations that broadly agree with the locations of manually defined gates and have similar accuracy to those gates. Applying the algorithm to a CLL diagnosis data set not only confirms our previous finding (Scheuermann et al. 29) that the CD5 + CD19 + CD10‐CD79b‐ cell population is diagnostic for CLL but also demonstrates the utility and effectiveness of the proposed discriminative learning method, showing that it is possible to simultaneously optimize both the gating location and classification accuracy across multiple cytometry samples and subjects in an interpretable way. Although there are still a number of important next steps to explore, the proposed discriminative gating approach has the potential to impact and benefit both translational research and clinical studies that need objective analysis of cytometry data for identification of interpretable differences in cytometry data between cohorts.

Supporting information

Supplementary Figure 1 DAFi‐based prefiltering and identification of cell populations from (a) Panel 1 and (b) Panel 2 for CLL diagnosis of one CLL positive subject. The DAFi‐gating sequences are, from left to right (a) Singlets (FSC‐A vs FSC‐H), Live Leukocytes (SSC‐H vs CD45), Lymphocytes (FSC‐A vs SSC‐A), CD5 + CD19+, CD10‐CD79b‐, (b) Singlets (FSC‐A vs FSC‐H), Live Leukocytes (SSC‐H vs CD45), Lymphocytes (FSC‐A vs SSC‐A), CD5 + CD19+, CD38‐CD20+, Kappa‐Lambda+, Kappa+Lambda‐.