Statistical prediction of load carriage mode and magnitude from inertial sensor derived gait kinematics

Abstract

Load carriage induces systematic alterations in gait patterns and pelvic-thoracic coordination. Leveraging this information, the objective of this study was to develop and assess a statistical prediction algorithm that uses body-worn inertial sensor data for classifying load carrying modes and load levels. Nine men participated in an experiment carrying a hand load in four modes: one-handed right and left carry, and two-handed side and anterior carry, each at 50% and 75% of the participant’s maximum acceptable weight of carry, and a no-load reference condition. Twelve gait parameters calculated from inertial sensor data for each gait cycle, including gait phase durations, torso and pelvis postural sway, and thoracic-pelvic coordination were used as predictors in a two-stage hierarchical random forest classification model with Bayesian inference. The model correctly classified 96.9% of the carrying modes and 93.1% of the load levels. Coronal thoracic-pelvic coordination and pelvis postural sway were the most relevant predictors although their relative importance differed between carrying mode and load level prediction models. This study presents an algorithmic framework for combining inertial sensing with statistical prediction with potential use for quantifying physical exposures from load carriage.

1.0. Introduction

Prolonged exposure to manual load carriage is a known risk factor for low back disorders (Knapik, Harman, & Reynolds, 1996; Putz-Anderson et al., 1997). Epidemiological findings suggest an increased odds of developing a prolapsed lumbar disc from frequently carrying objects more than 11.3 kg (25 lbs.) (Kelsey et al., 1984). Heavy and frequent load carriage may accelerate spinal degeneration due to an increased loading on the spine and would damage spinal tissues in the vertebral column (Jensen, 1988). While minimizing the frequency and intensity of manual load carriage is ideal, such tasks are still common and inevitable in non-routinized work such as in construction (Anderson et al., 2007), firefighting (Park, Hur, Rosengren, Horn, & Hsiao-Wecksler, 2010), and manufacturing (Cheng & Lee, 2006). Accurate measurement of exposures to biomechanical risk factors is an important step to develop effective musculoskeletal injury prevention and risk reduction programs (David, 2005). Measuring the duration, frequency, and magnitude of hand loads longitudinally is an essential step for assessing the biomechanical impacts to the musculoskeletal system and identifying strategies for intervention.

Measuring longitudinal exposures to load carriage in field settings presents unique challenges. Traditional exposure assessment techniques that rely on direct observations have limitations in non-repetitive job conditions where the work tasks vary considerably in duration, frequency, or intensity levels (Gold, Park, & Punnett, 2006). Direct measurement of task durations and load magnitudes in applied settings would require instrumentation system that is wireless and portable and unrestricted by changes in a worker’s location. In addition to load magnitude, the biomechanical effects of load carriage are influenced by the mode of load carriage (e.g., two-handed anterior, one-handed side). A study by Rose, Mendel, and Marras (2013) demonstrated that carrying the same load with different carrying modes generates a significant difference in the anterior-posterior shear loading at L2/L3. Carrying a two-handed anterior load of 11.3 kg was sufficient to produce an average shear load of 856 N, which exceeded the recommended exposure limits of 700 N (Gallagher & Marras, 2012) and can potentially damage spinal tissues. The same load carried in a backpack produced a lower average shear load of 345 N (Rose et al., 2013). Thus, methods for direct measurement of such exposures need to identify and quantify both dimensions, namely, carrying mode and load magnitude, besides temporal aspects of duration and frequency.

Wearable inertial sensors (or inertial measurement units, IMUs) have gained attention in ergonomics research (Valero, Sivanathan, Bosché, & Abdel-Wahab, 2016) for field-based direct measurement of worker postures. Inertial sensors are light-weight, portable, less obtrusive, and have on-board power and data storage capacity that allows for data collection over a long work period (Bergmann, Mayagoitia, & Smith, 2009; Mayagoitia, Nene, & Veltink, 2002). Typical use of wearable inertial sensors in ergonomics studies to date have focused on posture measurement in occupational tasks (e.g., lifting and pushing/pulling) to estimate the orientation of a body segment or joint angle between segments (Estill, MacDonald, Wenzl, & Petersen, 2000; Nath, Akhavian, & Behzadan, 2017; M. C. Schall Jr., Fethke, Chen, & Gerr, 2015; Valero et al., 2016) relative to a neutral posture (i.e., typically upright standing) in order to quantify the extent and proportion of time spent in a deviated or non-neutral posture. During load carriage, postural deviation relative to an upright standing posture is subtle compared to other occupational tasks and less consequential than the duration, magnitude and mode of load carriage. However, the magnitude and position of hand loads can alter gait kinematics and posture (Ghori & Luckwill, 1985; Goh, Thambyah, & Bose, 1998; Hong & Cheung, 2003; Majumdar, Pal, & Majumdar, 2010; Park et al., 2010; Qu & Yeo, 2011).

Movements of the torso, pelvis, and lower extremities change systematically with external load levels and carrying modes when walking (Kinoshita, 1985; LaFiandra, Wagenaar, Holt, & Obusek, 2003). Kinematic adjustments for maintaining posture and stability during walking are reflected in temporal and kinematic gait parameters, and rotational movement coordination between the torso and pelvis (LaFiandra et al., 2003; van Emmerik & Wagenaar, 1996). Using data from body-worn inertial sensors, a recent study confirmed systematic difference in thoracic and pelvic sway and movement coordination based on load level between two-handed anterior and side carry (Lim & D'Souza, under review). Specifically, in that study, carrying hand-loads that weighed 4.5 kg, 9.1 kg, and 13.6 kg in two-handed anterior vs. side carrying modes were associated with significant differences in coronal and transverse thoracic-pelvic coordination measured using relative phase angles after adjusting for stride length and gait speed. The present study aims to leverage information about changes in gait kinematic patterns for estimating the duration, relative magnitude and mode of load carriage using inertial sensing and predictive modeling.

Predictive modeling or machine-learning (ML) techniques have been used in combination with wearable sensor data to extract contextual task information beyond just quantifying posture. For example, activity recognition is an area of active research where data from body-worn inertial sensors are used for classifying daily activities (Oshima et al., 2010; Ravi, Dandekar, Mysore, & Littman, 2005), detecting gait events (Aminian, Najafi, Büla, Leyvraz, & Robert, 2002; Coley, Najafi, Paraschiv-Ionescu, & Aminian, 2005; Sabatini, Martelloni, Scapellato, & Cavallo, 2005), and predicting safety critical events such as falls (Bagalà et al., 2012; Schwickert et al., 2013; Wu & Xue, 2008). The application of such techniques to occupational ergonomics is still lagging. A few ergonomics studies have combined predictive modeling with the wearable sensor data in activity recognition to classify manual material handling tasks (Kim & Nussbaum, 2014), assembly tasks (Stiefmeier et al., 2006), and patient handling activities (Lin, Song, Xu, Cavuoto, & Xu, 2017), and to detect states of fatigue from gait kinematics during walking (Baghdadi, Megahed, Esfahani, & Cavuoto, 2018; Janssen et al., 2011; Zhang, Lockhart, & Soangra, 2014). Lee (2008) applied linear discriminant analysis (LDA) to gait kinematics data obtained from a 3-D optical motion capture system to distinguish between unloaded versus loaded gait with participants wearing a vest weighing 12.5 kg. Their study showed potential for using gait kinematics to classify carrying load condition but was limited to a single carrying mode and load magnitude. Collectively all of these previous studies suggest the possibility for leveraging information about postural adaptations during load carriage obtained by inertial sensors combined with predictive modeling techniques to create new algorithmic approaches for assessing physical exposures from load carriage in situ.

The aim of this paper was to develop and assess a statistical prediction algorithm as proof-of-concept that uses gait kinematics calculated from body-worn inertial sensor data for classifying hand-load carrying mode and load level. The statistical prediction algorithm implemented in this study incorporates a priori biomechanical knowledge about the effects of load carriage on human gait patterns to inform the data segmentation process, computing and selecting of predictor variables, and the structure of the statistical model. We discuss these steps in the context of leveraging ML techniques for ergonomics exposure assessment.

2.0. Methods

2.1. Study Participants

Nine healthy men were recruited from the university community for the study. Participants had ages ranging from 18 to 25 years with an average ± standard deviation (SD) of 22.0 ± 3.0 years, stature of 1.75 ± 0.05 m, weight of 77.11 ± 9.98 kg, and BMI of 24.87 ± 2.84 kg/m². Participants were screened for pre-existing back injuries or chronic pain with a body discomfort questionnaire adapted from the body mapping exercise by NIOSH (Cohen, Gjessing, Fine, Bernard, & McGlothlin, 1997 for more details). All participants were right-handed and right-footed when tested with the questionnaire adapted from the Edinburgh handedness inventory (Oldfield, 1971). Prior to the study, participants completed a written informed consent approved by the university’s institutional review board.

2.2. Experiment Procedures

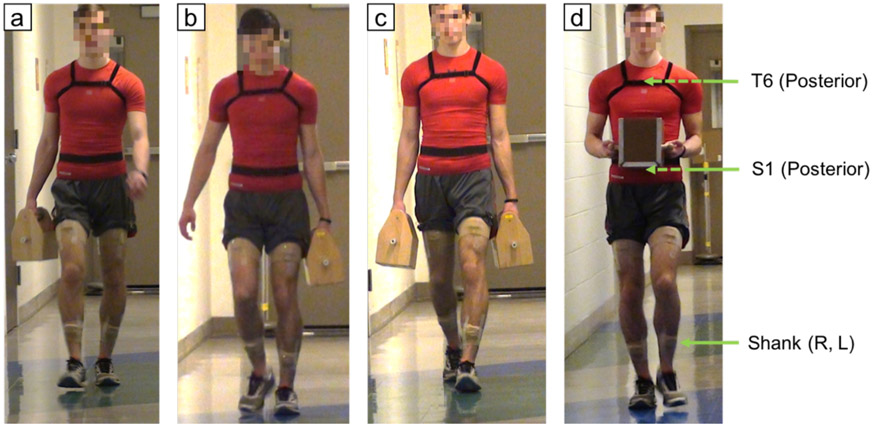
A pre-experimental session was conducted to determine each participants’ Maximum Acceptable Weight of Carry (MAWC; Cheng & Lee, 2006), which was later used to set the normalized load levels in the main experiment. For the measurement of one-handed MAWC, participants were asked to carry a 2.3 kg box with their right hand and walk 5 m back and forth. The box had dimensions of 152.4 mm width x 177.8 mm depth x 127 mm height, and one handle on the top (Figure 1-a). The weight of the box could be increased in increments of 2.3 kg. A method of limits discussed in Snook and Ciriello (1991) was used for determining the maximum acceptable weight that the participant could carry without perceiving unusual tiredness, weakness, overheating, or breathlessness. The procedure was repeated to measure a two-handed MAWC by using a box with dimensions of 177.8 mm width x 228.6 mm depth x 203.3 mm height held anteriorly with both hands using handles located on the side (Figure 1-d).

Figure 1:

Images showing the four carrying modes performed in this study: (a) one-handed right hand carry (1H-R), (b) one-handed left hand carry (1H-L), (c) two-handed side carry (2H-Side), (d) two-handed anterior carry (2H-Anterior) along with the location of four inertial sensors attached on the body at T6, S1, and shank (R, L).

During the main experiment, participants carried a weighted box down a levelled corridor (26.2 m length x 1.6 m width) for a distance of 24 m in four carrying modes commonly used in occupational settings (Figure 1), viz., one-handed right hand carry (1H-R), one-handed left hand carry (1H-L), two-handed side carry (2H-Side), and two-handed anterior carry (2H-Anterior), in addition to a no-load (i.e., empty-handed reference) condition. Two levels of box weights were carried in each mode, namely, 50% MAWC and 75% MAWC. The one-handed MAWC for each participant was used to calculate the normalized load levels of 50% and 75% for the one-handed conditions (i.e., 1H-R and 1H-L). Likewise, the two-handed anterior MAWC was used to calculate the 50% and 75% normalized load levels for the 2H-Anterior and 2H-Side carrying modes. Hand load was equally divided between the right and left boxes in the 2H-Side carry.

Two no-load walk trials were performed first, and subsequently each participant performed two consecutive trials of eight loaded conditions ( = 4 carrying modes x 2 load levels) in random order. Walking speed was self-selected to observe the natural adaptation in walking patterns due to different load carriage conditions. Two-minute rest breaks between each walk trial were given to participants to minimize carry-over effects of fatigue.

2.3. Instrumentation

Four commercial inertial sensors (Opal, APDM Inc, Portland, OR, USA) were attached on the participant at the sixth thoracic vertebra (T6), the first sacral vertebra (S1), and superior aspect of the right and left shank midway between the lateral femoral and malleolar epicondyles (Figure 1-d). Sensor placement was informed by the need for computing specific predictor variables. Sensors attached on the right and left shank were used for detecting key gait events (e.g., heel strike and toe-off) and subsequent temporal gait parameters (Aminian et al., 2002). Sensors placed on the T6 and S1 were used for calculating torso and pelvis postural sway and thoracic-pelvic coordination measures (Lim & D’Souza, 2018) that were related to the objectives of this study. Velcro straps were used to secure the sensors located at T6 and S1, and double-sided hypoallergenic tape and medical wrap were used to attach the sensors to shank (R, L). One of the sensor axes (i.e., x-axis) was attached aligned with the proximal-distal axis of the body segment and pointing downward.

The inertial sensors recorded 3-D accelerometer, gyroscope, and magnetometer sensor data at a sampling frequency of 80 Hz. Accelerometer and gyroscope data were filtered using a second-order low-pass zero-lag Butterworth filter with a cut-off frequency of 2-Hz. Gyroscope data (angular velocity in radians/s) was integrated to obtain angular displacement, and subsequently filtered using a second-order high-pass filter with a cut-off frequency of 0.75 Hz to reduce the effect of drift (Williamson & Andrews, 2001).

2.4. Algorithm to Classify Carrying Mode and Load Level

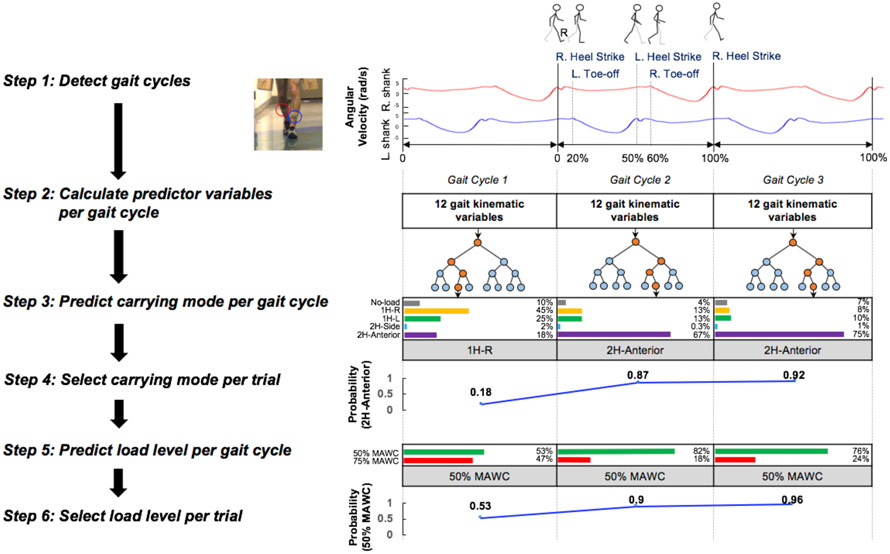
A statistical classification algorithm was developed with six general steps described in the following section (Figure 2). Four carrying modes (i.e., 1H-R, 1H-L, 2H-Side, 2H-Anterior) and no-load and two load levels, 50% MAWC vs. 75% MAWC, were the target outcome variables for each walking trial.

Figure 2:

Overview of the carrying mode and load level classification algorithm developed in the study. The right panel shows example classification results for three consecutive gait cycles at a two-handed anterior carry with 50% MAWC load condition.

2.4.1. Step 1: Detect Gait Cycles

Individual gait cycles were detected using a custom gait detection algorithm adapted from Aminian et al. (2002) and described in detail by Lim and D'Souza (under review). To summarize this process, first, gait events signifying heel strike and toe-off were detected from the angular velocity (rad/s) data obtained from the sensors on the right and left shank (Figure 2). Second, gait cycles were denoted by finding the sequence of the following events: right heel strike → left toe-off → left heel strike → right toe-off → next right heel strike. The algorithm was implemented in MATLAB (MATLAB R2016b, The MathWorks Inc., Natick, MA, USA).

2.4.2. Step 2: Calculate Predictor Variables

Sixteen gait parameters were calculated over each gait cycle, namely, seven temporal gait measures, six torso and pelvis postural sway and three thoracic-pelvic coordination measured in the transverse, sagittal, and coronal planes, respectively (Table 1). Thoracic-pelvic coordination was measured as the relative phase angle of rotational movement between the torso and pelvis segments (Burgess-Limerick, Abernethy, & Neal, 1993; LaFiandra et al., 2003). This particular set of variables were considered based on preliminary work on 2H-Anterior load carriage (Lim & D'Souza, 2018). Swing, left leg (%) and stance, left leg (%) durations were highly correlated with the initial double support (%) duration with a Pearson’s correlation coefficient of ∣R∣ > 0.8. Swing, right leg (%) and stance, right leg (%) durations were also highly correlated with the terminal double support (%) duration. Thus, four temporal parameters, i.e., stance, right and left leg (%) and swing, right and left leg (%) were excluded from further analysis to avoid multi-collinearity, reducing the final set of predictor variables to twelve.

Table 1:

List and definitions of gait parameters calculated from the inertial sensor data for each gait cycle. Excluding stance right and left leg (%) and swing right and left leg (%), all of the remaining 12 parameters were used as predictors in the classification model.

	Parameter	Definition
Temporal parameters (7 nos.)
1	Gait cycle duration (sec)	Duration of one gait cycle (one right plus left step duration).
2,3	Stance, Right and Left Leg (%)	Percentage of the gait cycle for when the right or left foot is on the ground.
4,5	Swing, Right and Left Leg (%)	Percentage of the gait cycle for when the right or left foot is not on the ground.
6	Initial double support (%)	Percentage of the gait cycle for when both feet are on the ground after a right foot heel-strike.
7	Terminal double support (%)	Percentage of the gait cycle for when both feet are on the ground after a left foot heel-strike.
Torso and pelvis postural sway (6 nos.)
8~13	ROM at T6 and S1 in the transverse, sagittal, and coronal planes (deg.)	Range of rotation angle at torso and pelvis in transverse, sagittal, and coronal planes: Max (integrated angular velocity) – min (integrated angular velocity)
Thoracic-pelvic coordination (3 nos.)
14~16	Mean relative phase angle between T6 and S1 in the transverse, sagittal, and coronal planes (deg.)	Average (pelvic phase angle – thoracic phase angle) in transverse, sagittal, and coronal planes. Phase angle (t) = arctan (normalized angular velocity (t) /normalized integrated angular velocity (t))

2.4.3. Step 3: Predict Carrying Mode per Gait Cycle

A two-stage hierarchical model was implemented comprising a first stage classification model for predicting carrying mode (Step 3 in Figure 2), and a second stage classification model for predicting the load level (Step 5 in Figure 2). The design of the hierarchical structure was informed by prior studies demonstrating that the mode of load carriage influences alterations in gait kinematics significantly more than changes in the load levels within the same carrying mode (Ghori & Luckwill, 1985; Kinoshita, 1985). The random forest technique (Breiman, 2001) was chosen as the classification algorithm for both stages because it produced the highest prediction accuracy in a preliminary study on estimating the carrying mode and load level compared to other common multiclass classification algorithms such as classification and regression trees, multinomial logistic regression, linear discriminant analysis, and support vector machines. Random forest is a nonparametric machine-learning technique based on a decision tree that grows recursive binary partitioning at the nodes of the tree. Hundreds of decision trees are grown by random selection of a subset of predictor variables each time. The prediction results across all trees are averaged to obtain the final consensus prediction. In this study, prediction was performed over 500 trees for each gait cycle with a selection of four predictor variables each time. This step was implemented using the randomForest package v.4.6-12 (Liaw & Wiener, 2002) in R v.3.3.1 (R Core Team, 2016).

2.4.4. Step 4: Select Carrying Mode per Trial

Classification results from each gait cycle within a walk trial were used to decide the final classification result for the walk trial. In our algorithm, predictions in Steps 3 and 5 were performed independently for each gait cycle; however, under the assumption that the carrying mode and load level does not change within a walk trial, probabilities of the current gait cycle data belonging to a specific carrying mode were updated based on the prior gait cycles using the method of Bayesian inference (Box & Tiao, 2011). Assume that a prediction model (M) is developed based on the current gait cycle data (Y). When data on new gait cycle (Y*) is obtained, the posterior distribution can be updated using Baye’s theorem as follows:

$$p(M\mid Y^{\ast })=c\ast p(Y^{\ast }\mid M)\ast p(M)$$

where p(M∣Y*) is the posterior distribution updated by the new data (Y*), p(Y*∣M) is the probability that the new data belongs to each class given the prediction model, and p(M) is the prior probability before updating the new data. A normalizing constant, c, ensures that the posterior probabilities of all classes add up to one. Using this method, the classification results from prior gait cycles were cumulatively used to update the classification result of the current gait cycle until the last gait cycle identified in a walk trial. The carrying mode with the highest posterior probability at the final gait cycle within the walk trial was selected as the final prediction outcome for the carrying mode.

2.4.5. Step 5: Predict Load Level per Gait Cycle

Steps 5 and 6 were performed to classify the load level within each predicted carrying mode. While one model was developed for Step 3, four separate models were developed in Step 5 for each carrying mode excluding the no-load condition. Separate load level prediction models were built based on a priori knowledge that the important kinematic parameters to distinguish load levels differ by carrying mode (Ghori & Luckwill, 1985; Kinoshita, 1985). Gait data from each walk trial was subjected to one of four classification models for predicting the load level depending on the carrying mode that was predicted in Step 4. Load levels were predicted for each gait cycle in the walk trial.

2.4.6. Step 6: Select Load Level per Trial

Similar to step 4, Bayesian inference was used to update the classification result of the load level within a walk trial.

2.5. Evaluating Model Performance

The performance of the prediction model was evaluated using 10-fold cross-validation tests. All walk trials were split into ten roughly equal-sized subsamples or folds (k = 1,2, … ,10). In each iteration, one subsample (k) was selected as the validation data for testing the model, and the remaining k-1 subsamples were used for training the model (Hastie, Tibshirani, & Friedman, 2008). This test was iterated k times until all subsamples were used as a validation set. Gait cycles from the same walk trial were grouped when partitioning, so that all of the gait cycles from the same walk trial were included in the same subsample.

An identical test was performed for the classification algorithm without the Bayesian update (Step 4 and 6) as a comparison to investigate the benefit of applying the Bayesian inference to the algorithm. In this model, the final classification result for the walk trial was decided by averaging the classification results from individual gait cycles within the walk trial.

Three performance measures were computed:

• Average prediction accuracy = [# true positives + # true negatives] / [# total walk trials],

• Precision = [# true positives] / [# true positives + # false positives]), and

• Sensitivity = [# true positives] / [# total positives].

2.6. Interpreting the Predictive Model

The relative importance (%) of predictor variables in each model was calculated to investigate the importance of each predictor variable in predicting the response variable (Boulesteix, Janitza, Kruppa, & König, 2012). In a random forest model, variable importance is measured as the impurity of data after it is split at each node. The Gini impurity Index, a common measure of the node impurity, is computed by averaging impurity at a data partition across all classes of the response variable (Strobl, Boulesteix, Zeileis, & Hothorn, 2007). A larger decrease in the Gini index represents a larger decrease in impurity at a data partition and a greater importance of the predictor variable in the classification model. The magnitude of the Gini index can differ by models, so it is a common practice to calculate a normalized index as the relative importance (%) by giving the most important variable a score of 100% in each model.

3.0. Results

A total of 162 walk trials were performed across all participants (9 participants x 9 conditions per participant x 2 walk trials per condition). Excluding three interrupted walk trials during the data collection, 159 walk trials were used for building and testing the algorithm. A total of 2028 gait cycles were recorded across all participants with an average ± standard deviation (SD) of 12.8 ± 1.5 (range: 9 to 17) gait cycles in each repetition of the walk trials.

Across all participants the average ± SD for the MAWC (kg) in the one-handed condition was 32.5 ± 7.9 kg and in the two-handed condition was 31.0 ± 4.5 kg, respectively. Load levels for the walk trials were set to 50% and 75% of the participant’s one-handed and two-handed MAWC value. Average ± SD values of normalized MAWCs were 17.4 ± 3.9 (50% MAWC) and 24.4 ± 6.3 (75% MAWC) for the one-handed conditions, and 16.6 ± 2.3 (50% MAWC) and 23.2 ± 3.53 (75% MAWC) for the two-handed conditions.

3.1. Bayesian Inference Update vs. Averaging

Applying Bayesian inference in Steps 4 and 6 outperformed the averaging approach in terms of the prediction accuracy. The model with the Bayesian inference correctly classified the carrying mode in 96.9% of the walk trials and load level in 93.1% of the walk trials, resulting in an average overall prediction accuracy of 91.8%. In comparison, the averaging approach correctly classified the carrying mode in 95.3% and load level in 72.7% of the walk trials, resulting in an average overall prediction accuracy of 72.2%, which was 19.6% lower compared to the Bayesian approach.

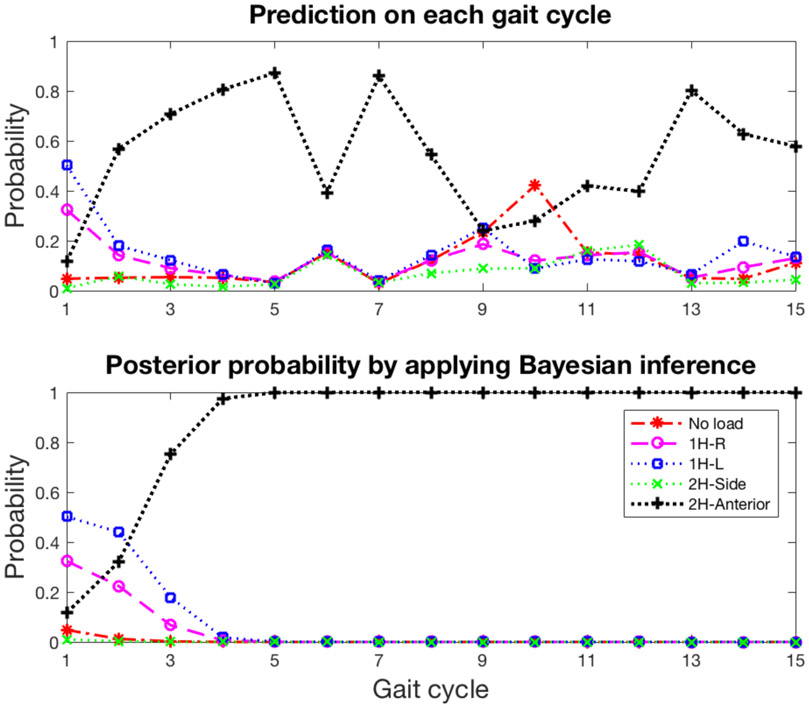
Figure 3 depicts an example model prediction for a walk trial in a 2H-Anterior carry consisting of fifteen consecutive gait cycles. The Bayesian inference approach showed convergence in the posterior probability after four gait cycles in the example described in Figure 3. Across all conditions an average ± SD of 4.5 ± 1.5 gait cycles were needed to correctly classify carrying mode with a posterior prediction over 90%. Since the Bayesian approach demonstrated a clear advantage in prediction performance, we limit the subsequent analysis and discussion to this approach.

Figure 3:

Example results from the random forest classification to predict carrying mode for fifteen consecutive gait cycles from a two-handed anterior carry walk trial without (top-panel) and with (bottom-panel) Bayesian inference applied. In each gait cycle, the mode with the highest predicted probability is labeled as the classification result for that gait cycle. In this example, without Bayesian inference applied (top-panel) 3 of the 15 gait cycles were misclassified as either 1H-L (gait cycle #1) or no-load (gait cycle #9 and #10). In the bottom graph, Bayesian inference was applied to the same data and updated the posterior probability of the gait cycle based on prior gait cycles cumulatively. The probability of the data predicted as the correct class (i.e., two-handed anterior carry in this case) exceeded 0.9 after four gait cycles and converged to 1.0 in subsequent cycles.

3.2. Model Performance

3.2.1. Carrying Mode Classification

Table 2 presents the confusion matrix for the prediction model along with the precision and sensitivity values from the 10-fold cross-validation test. The prediction accuracy for classifying the carrying mode was 96.9%. The precision of the no-load, 2H-Side, and 2H-Anterior conditions were 100% while it was lower in the 1H-R and 1H-L at 91.4% and 94.3% respectively. Sensitivity was also highest for the no-load, 2H-Side and 2H-Anterior conditions at 100%, compared to 1H-R and 1H-L at 94.1% and 91.7% respectively. Five walk trials were misclassified in carrying mode between the 1H-R and 1H-L conditions, and interestingly were all at the load level of 75% MAWC.

Table 2:

Confusion matrix showing the classification result for carrying modes from each walk trial data: No-load = empty-handed reference condition, 1H-R = one-handed right carry, 1H-L = one-handed left carry, 2H-Side = two-handed side carry, 2H-Anterior = two-handed anterior carry.

		Predicted Carrying Mode					Total Walk Trials	Sensitivity
		No-load	1H-R	1H-L	2H-Side	2H-Anterior
Actual Carrying Mode	No-load	18	0	0	0	0	18	100%
	1H-R	0	32	2	0	0	34	94.1%
	1H-L	0	3	33	0	0	36	91.7%
	2H-Side	0	0	0	36	0	36	100%
	2H-Anterior	0	0	0	0	35	35	100%
Total Walk Trials		18	35	35	36	35	159
Precision		100%	91.4%	94.3%	100%	100%

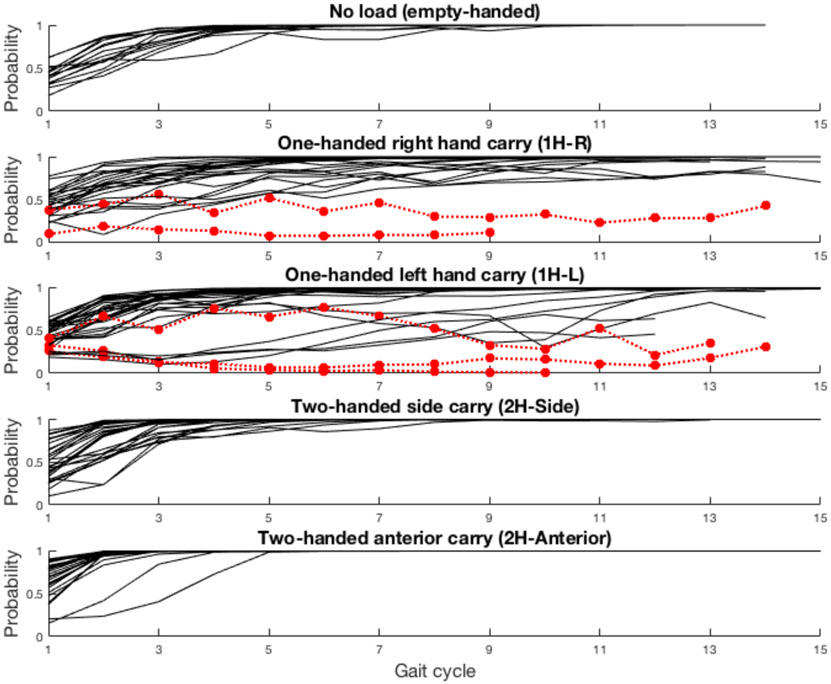
To further investigate the misclassified cases, posterior probabilities of the target carrying mode for individual walk trials were plotted by gait cycle (Figure 4). Consistent with Table 2, there were no misclassified cases for the no-load, 2H-Side, and 2H-Anterior conditions. The posterior probabilities in these conditions (n = 89 walk trials) converged to 1.0 typically after 4 to 5 gait cycles even though the initial probability at the first gait cycle was very low (P < 0.5) in many cases. On the other hand, the posterior probabilities for multiple walk trials in the 1H-R and 1H-L conditions did not converge to 1.0 and fluctuated throughout the walk trial.

Figure 4:

Posterior probabilities of the target carrying mode in each walk trial depicted by gait cycles. Misclassified classes are marked as red dotted lines.

3.2.2. Load Level Classification

The average prediction accuracy for classifying the load level across all carrying modes was 93.1% (n = 148 of 159 walk trials), which was 3.8% lower than the classification of carrying mode. Table 3 summarizes the confusion matrices for the models by carrying mode along with the precision and sensitivity values from the cross-validation test. Prediction accuracies within each carrying mode were 91.4% for 1H-R, 91.4% for 1H-L, 94.4% for 2H-Side, and 91.4% for 2H-Anterior. Among the carrying modes, the model for 2H-Side had the highest prediction accuracy with just 1 out of 18 walk trials misclassified between the 50% MAWC and 75% MAWC load levels each.

Table 3:

Summary of the classification results in terms of sensitivity and precision of predicted load levels for each predicted carrying mode.

Carrying mode	Load level	Sensitivity (%)	Precision (%)
One-handed, Right	50% MAWC	88.9	94.1
	75% MAWC	94.1	88.9
One-handed, Left	50% MAWC	88.9	94.1
	75% MAWC	94.1	88.9
Two-handed, Side	50% MAWC	94.4	94.4
	75% MAWC	94.4	94.4
Two-handed, Anterior	50% MAWC	88.9	94.1
	75% MAWC	94.1	88.9

3.3. Variable importance

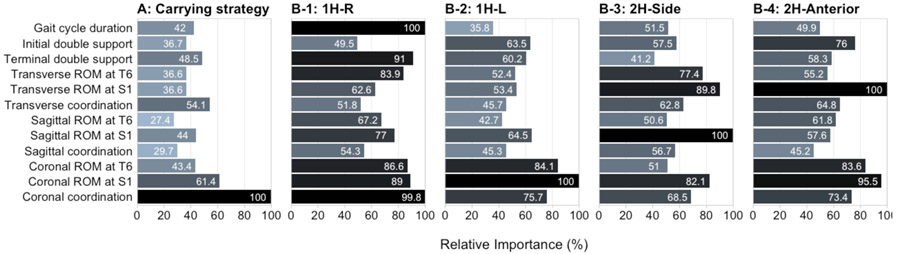
Figure 5 shows the relative importance (%) of the predictor variables in each classification model. Thoracic-pelvic coordination in the coronal plane was the most important predictor in the classification model for carrying mode, followed by postural sway of the pelvis in the coronal plane and transverse thoracic-pelvic coordination in a distant second and third, respectively (Figure 5, panel A). For 1H-R, gait cycle duration and thoracic-pelvic coordination in the coronal plane were nearly equally most important predictors for classifying the load level (Figure 5, panel B-1). However, unlike the classification model for carrying mode with one dominant predictor variable, the load level classification model for 1H-R also indicated terminal double support, torso and pelvis postural sway in the coronal plane, and torso postural sway in the transverse plane as relatively important (i.e., > 75%). Coronal plane measures of torso and pelvis postural sway and thoracic-pelvic coordination were the three most important predictors in the load level classification model for 1H-L compared to the rest of the predictor variables (Figure 5, panel B-2). Pelvis postural sway in the sagittal plane was the most important predictor when classifying the load level in the 2H-Side carry (Figure 5, panel B-3). Pelvis postural sway in the transverse plane and coronal plane were the second and third most important predictors. Pelvic postural sway in the transverse and coronal planes were both equally important when predicting the load level in the 2H-Anterior carry, followed by torso postural sway in the coronal plane (Figure 5, panel B-4).

Figure 5:

Relative importance (%) of the predictor variables computed as the mean decrease in the Gini index relative to the maximum (100%) for each of the five classification models, namely, for carrying mode (panel A) and for load level (Panels B-1 to B-4).

4.0. Discussion

Wearable sensing technology combined with predictive modeling has the potential to advance the science of field-based exposure assessment by providing information about work content beyond just quantifying worker postures. This study assessed the potential for classifying carrying mode and load level using gait kinematics calculated from the inertial sensor-derived data. As an initial investigation, the study was intentionally limited to a small homogenous participant sample (n = 9) with gait data recorded at self-selecting walking speeds over multiple walk trials and conditions, namely 159 walk trials and 2028 gait cycles in total, to build and assess the statistical model. Thoracic and pelvic range of motion and thoracic-pelvic coordination were important predictors in classifying carrying mode and relative load level compared to unloaded gait. The accuracy of statistically classifying carrying mode and load levels were 96.9% and 93.1%, respectively. Use of the Bayesian inference for updating probabilities with the incoming gait cycles improved the overall prediction accuracy by 19.6% with 4 to 5 gait cycles needed to converge on the classification result.

4.1. Methodological Contributions

Biomechanical exposures during physical work are typically characterized by three main dimensions (Winkel & Mathiassen, 1994), i.e., intensity (magnitude or amount of the forces and loads which are also a function of task and posture), frequency (repetition), and duration (the time the physical activity is performed). The algorithm presented provides information on all three dimensions of physical exposures during load carriage. The gait detection algorithm (Step 1) used in this study implements a robust detection of the start and end of walking, so the duration of the walking (either unloaded or loaded) can be accurately estimated. The load level classification (Step 5 & 6) predicts the relative intensity of the load carried, the measurement of which can be obtrusive in work settings that involve carrying loads of different magnitudes (e.g., construction work, distribution centers). The carrying mode classification (Step 3 & 4) combined with the load level classification (Step 5 & 6) quantifies the frequency of load carriage by categorizing the task in terms of its mode and load level.

Developing a successful prediction algorithm requires knowledge of the underlying system or domain when deciding on the structure of the statistical model (e.g., single-stage vs. multi-stage), segmenting the data, and selecting predictor variables or features within the data segment (Hastie et al., 2008). The current study incorporated biomechanical information about the association between human gait kinematics and load carriage to develop and assess the statistical prediction model, which had direct bearing on model performance. We discuss key aspects of the model development and assessment in the subsequent sections.

4.1.1. Data Segmentation and Choice of Predictor Variables

Statistical prediction with continuous time series data requires that the data be restructured into segments. The methods of segmenting a continuous stream of sensor data influences the performance of the prediction model and thus needs consideration (Avci, Bosch, Marin-Perianu, Marin-Perianu, & Havinga, 2010). To be useful, the method of data segmentation needs to represent the data such that the prediction error of all segments across time is minimized (Keogh, Chu, Hart, & Pazzani, 2001). A common approach to segmenting time series data uses sliding windows with a fixed sliding width (e.g., Kim & Nussbaum, 2014). Other approaches include a top-down approach of splitting time-series data into partitions by decreasing the segment length iteratively until the prediction error is below a user-specified threshold (Keogh et al., 2001), and a bottom-up algorithm that starts from the finest possible partition of the time-series data and increases the length of the segment iteratively. Unlike the latter two iterative approaches, use of a sliding window is the most popular form in online applications since the segmentation can be performed while the data is streaming. Another online approach involves segmenting data based on pre-defined events, as was the case in this study.

In this study, inertial sensor data were segmented by first detecting gait cycles, which represents a meaningful segmentation of the data stream. For a given carrying mode and load magnitude, gait cycle duration for a person shows little variability over short bouts of walking; however, the cycle duration can vary significantly between participants and across load carry conditions for the same person (LaFiandra et al., 2003; Martin & Nelson, 1986). For example, in the present study gait cycle duration ranged between 0.93 s to 1.16 s across all participants and carrying conditions. If a fixed window of average gait cycle, for example 1 s, was used for data segmentation instead of the proposed adaptive algorithm, the kinematic variables calculated within a segment would be less representative of the gait patterns relative to a data segment that captures a complete gait cycle. Another advantage of the proposed data segmentation method is that it can be used in online applications in near-real-time. Once a gait cycle is detected from an incoming data stream, predictor variables for the gait cycle can be computed and used as input to the classification algorithm. The delay in the classification output would be just over one gait cycle (~ 1 sec). The detection of an exact start and end of gait cycles resolves an issue of underestimating the task duration reported in previous studies on classifying manual material handling tasks (Kim & Nussbaum, 2014). In that study, task durations were underestimated by about 14% when classifying tasks using inertial sensor data that were segmented by sliding window of fixed duration. The detection of gait events and subsequent data segmentation based on gait cycles used in the current study would produce a more accurate estimate of duration of load carriage compared to a sliding window of fixed duration.

Choice of the predictor variables, which requires computing (i.e., extracting) and selecting features from sensor data, is also an important step towards building a simpler, comprehensible model while ensuring adequate prediction accuracy (Liu, Motoda, Setiono, & Zhao, 2010). Predictor variables need to represent the main characteristics of a data segment, so that it contains important cues for distinguishing levels of outcome variables (Avci et al., 2010). Use of domain specific features such as step detection, step variance, and vertical and horizontal acceleration of the sensor segment were found to increase prediction performance when classifying physical activities such as walking, running, cycling, and resting compared to using only time- and frequency-domain features (Bieber & Peter, 2008). Kim and Nussbaum (2014) used descriptive statistics on whole-body joint angles to classify manual material-handling tasks. The present study used temporal, and thoracic and pelvic kinematic gait parameters as predictor variables. As opposed to using raw sensor data, the use of such domain specific features could significantly reduce the number of feature vectors used in a classification algorithm and also increase prediction accuracy.

4.1.2. Structure of the Model

A two-stage hierarchical model structure was implemented in this study where the carrying mode was classified first followed by classification of load levels within mode. Without the hierarchical structure, nine classes or categories would need to be predicted (i.e., 4 carrying modes x 2 load levels, and 1 no-load condition). With the same number of test datasets, increasing the number of target classes often increases the possibility of misclassification and lowers prediction accuracy. Reducing a k-class problem to a set of k two-class problems by building a separately trained binary classification model for each of the k problems is a common approach to deal with the multiclass classification (Anand, Mehrotra, Mohan, & Ranka, 1995). However, this approach does not provide guidance about which the two classes need to be paired or the effect of having different pairs on model performance. Considering that classification problems in occupational settings may have a high number of potential outcome classes such as task type (e.g., lifting, pushing, pulling, carrying, etc.) and intensity level (e.g., forceful exertions; Mark C Schall Jr., Sesek, & Cavuoto, 2018), multiclass classification models would be more common than two-class classification.

Implementing a hierarchical structure in classification models with multiple target classes has three advantages. First, implementation of the hierarchical model significantly improves the prediction accuracy compared to classifying the combination of different task conditions at one time. In our preliminary testing with the same test dataset, the multiclass prediction model with no hierarchical structure resulted in a prediction accuracy of 48.0%, which was 43.8% lower than the proposed hierarchical model. In a different study aimed at classifying the handle height and force intensity level in a pushing task, the hierarchically structured model produced a 50.0% greater prediction accuracy compared to the multiclass prediction model (Lim & D'Souza, 2017). In both cases, the hierarchy of the models was built with an empirical understanding of the relative influence of different task variables (Ghori & Luckwill, 1985; Kinoshita, 1985; Lim, Case, & D’Souza, 2016; Lim & D'Souza, 2018).

A second advantage of having a hierarchical model structure is the opportunity for optimizing the predictor variable set in each model. The analysis of variable importance (Figure 5) suggests that the important variables in each model differ across classification models. This information can be used to reduce the number of predictor variables in each model thereby decreasing model complexity and computational effort, and increasing model interpretability.

Third, the hierarchical structure allows prediction performance assessment at every level of the hierarchy independently. In addition, the algorithms that occur in the lower level do not affect the performance of the algorithms that occur in the upper levels (Mathie, Celler, Lovell, & Coster, 2004).

4.1.3. Model Interpretability

The random forest method used in this study is flexible in modeling relationships between multiple predictors and outcome classes, without requiring any a priori assumptions about the type of relationships, e.g., linear vs. nonlinear. This flexibility lends to high prediction accuracy as was evident in this study, but comes at some expense of interpretability, i.e., it is difficult to quantify how any individual predictor is associated with the outcome. The primary means for interpreting a random forest model uses the average decrease in the Gini Index as an indicator of the relative importance of predictor variables. Our results on important predictor variables are supported by findings from previous studies that demonstrate that changes in gait from hand-load carriage are evident in the measures of thoracic and pelvic postural sway and thoracic-pelvic coordination (Anderson et al., 2007; Madinei & Ning, 2017, LaFiandra et al., 2003; van Emmerik & Wagenaar, 1996).

The relative importance of thoracic and pelvic sway and intersegment coordination differed across all five prediction models (Figure 5). Specifically, 2H-Side carriage increases angular momentum and moment of inertial in the coronal and transverse planes (Madinei & Ning, 2017). With this increase, postural stability is maintained by an increased but anti-phasic sway (i.e., counter-rotation) of the pelvis in the coronal, transverse, and sagittal planes with increasing loads relative to unloaded gait (Lim and D’Souza, 2018). Similar contributions of thoracic and pelvic sway and intersegment coordination in the coronal plane were also identified in the 1H-R and 1H-L side carry. However, the load prediction models for 1H right vs. left side carry showed differences in relative importance of other temporal gait parameters, namely, gait cycle duration and terminal double support. These differences may be due to bilateral asymmetries in strength and gait, and is a topic of further investigation.

Restricted arm movements and close coupling between the torso and pelvis during 2H-Anterior load carriage is associated with increased pelvic sway in the coronal and sagittal planes, and a decrease in pelvic sway in the transverse plane relative to unloaded gait (Anderson et al., 2007; Madinei & Ning, 2017). Consequently, movement coordination between the thoracic-pelvic segments is more in-phase or synchronized in the coronal and transverse planes with increasing load relative to unloaded gait (Birrell & Haslam, 2008; Majumdar et al., 2010).

4.2. Study Limitations

Certain limitations of this laboratory study are worth emphasizing in order to contextualize the study findings and implications for practice. Given its focus on model development and assessment, the study sample comprised of a relatively small and homogenous sample of healthy, young male participants. Further investigation is needed to test the generalizability of the model across the spectrum of worker demographics on known sources of variability in gait such as age (Ko, Hausdorff, & Ferrucci, 2010), gender (Mazzà, Iosa, Picerno, & Cappozzo, 2009), obesity (Cau et al., 2014; Pamukoff, Dudley, Vakula, & Blackburn, 2016) and strength (Lord et al., 1996; Nigg, Fisher, & Ronsky, 1994). The present study found that a minimum of 4 to 5 gait cycles needed to converge on a prediction result. This finding suggests that in subsequent studies the amount of data collected from each participant can be economized in lieu of a larger and more diverse sample.

For jobs that might involve long duration of manual load carriage, cumulative fatigue from load carriage may induce alterations in gait (Barbieri et al., 2013; Helbostad, Leirfall, Moe-Nilssen, & Sletvold, 2007; Yoshino, Motoshige, Araki, & Matsuoka, 2004). Prior studies have associated fatigue with increased variability in step length, step width, and mediolateral trunk accelerations while walking, and increased double support duration during load carriage. Qu and Yeo (2011) reported hip and torso range of motion to increase while carrying a backpack load immediately following a fatiguing treadmill exercise. Age is also reported to moderate the effects of fatigue on gait (Barbieri et al., 2013; Helbostad et al., 2007). To minimize the confounding effects of fatigue, the present study introduced two-minute rest breaks between each walk trial of 24 m distance. However, subsequent studies will need to account for the effects of cumulative fatigue from long duration exposures to load carriage on thoracic and pelvic range of motion and coordination.

The proposed model also requires that load magnitudes be normalized to individual carrying capacity determined using either biomechanical strength or psychophysical criteria. This may be a limitation in certain work settings that do not have a steady cohort of workers that can be assessed. Additional study is also needed to consider more diverse task conditions that are representative of applied settings (e.g., size and form-factor of the load carried, location of handles, and weight distribution of the load) and over extended periods before the proposed algorithm can be used as a field evaluation tool for manual load carriage work.

4.3. Application and Relevance

Quantifying physical exposures to load carriage can be challenging in non-routinized work settings where load intensity, duration and frequency vary between workers and within worker across time. The present study represents an initial step towards the development of a real-time exposure assessment tool that leverages wearable inertial sensing and predictive modeling for use in occupational settings. Multiple previous studies have used inertial sensors to classify between different types of activities (e.g., walking vs. sitting), however few studies have delved into predicting task demands within a specific activity (i.e., relative changes between load within the same task). The present study is novel in this regard. A key contribution of this study was the reliance on a biomechanical understanding of the effects of load carriage on pelvic and thoracic movement and coordination into a practical framework for predicting carrying mode and relative load conditions. From a practical standpoint, our findings have direct implications for attachment locations of inertial sensors. Leveraging subtle movement patterns of the torso and pelvic implies that the sensors be closely attached to the skin on these segment as opposed to worn on top of loose clothing, helmet, or gloves. Newer forms of wearable sensing embedded in smart clothing may help overcome these potential usability concerns (Esfahani & Nussbaum, 2018).

Extending the proposed approach to include other tasks that are of interest in ergonomics exposure assessment such as lifting and pushing/pulling will require task-specific models that capture intrinsic kinematic adaptations to task demands. For example, findings by Zehr, Howarth, and Beach (2018) indicating that thoracic-pelvic coordination in the sagittal plane is influenced by lifting mode (i.e., freestyle, flexed and neutral spine; Zehr et al., 2018) can be leveraged to develop and assess predictive models of lifting modes using body worn inertial sensors. These task specific models can be envisioned as modules nested within an overarching activity classification model. This framework aligns with our proposed approach of a multi-stage hierarchical model structure led by classification by task type (e.g., lifting, pushing, pulling, carrying, etc.), followed by models that classifying mode and intensity within task type to account for the large number of potential outcome classes in occupational settings.

5.0. Conclusions

This study presents an algorithmic framework for combining wearable inertial sensing, gait kinematics, and statistical prediction for classifying carrying modes and load levels during manual load carriage. Overall, the algorithm was sensitive in discerning loaded from unloaded walk conditions within 4 to 5 gait cycles. Prediction accuracy and the relative importance of thoracic and pelvic measures as predictors were found to differ by models for carrying mode and load level. The few misclassified trials occurred largely in the 1H-R and 1H-L side carrying modes. Further investigation is needed to test the generalizability of the model across the spectrum of worker demographics and load carrying conditions. The present study also provides practical information about locations for inertial sensor placement and the type and amount of data required for distinguishing carrying modes and relative load levels for use in subsequent studies of higher ecological validity and increased generalizability.

Applying statistical classification techniques to movement analysis requires an understanding of machine learning theory, signal processing, and feature extraction. By emphasizing model development and assessment, this study also attempts to explain aspects of classification and predictive modeling towards encouraging the application of these statistical techniques to ergonomics practice.