Protein structure prediction using multiple deep neural networks in the 13th Critical Assessment of Protein Structure Prediction (CASP13)

Abstract

We describe AlphaFold, the protein structure prediction system that was entered by the group A7D in CASP13. Submissions were made by three free‐modeling (FM) methods which combine the predictions of three neural networks. All three systems were guided by predictions of distances between pairs of residues produced by a neural network. Two systems assembled fragments produced by a generative neural network, one using scores from a network trained to regress GDT_TS. The third system shows that simple gradient descent on a properly constructed potential is able to perform on par with more expensive traditional search techniques and without requiring domain segmentation. In the CASP13 FM assessors' ranking by summed z‐scores, this system scored highest with 68.3 vs 48.2 for the next closest group (an average GDT_TS of 61.4). The system produced high‐accuracy structures (with GDT_TS scores of 70 or higher) for 11 out of 43 FM domains. Despite not explicitly using template information, the results in the template category were comparable to the best performing template‐based methods.

1. INTRODUCTION

In this paper, we describe the entry from team A7D to the “human” category in the 13th Critical Assessment of Protein Structure Prediction (CASP13). The A7D system, called AlphaFold, used three deep‐learning‐based methods for free modeling (FM) protein structure prediction, without using any template‐based modeling (TBM). These methods were based around combinations of three neural networks:

1. To predict the distance between pairs of residues within a protein.

2. To directly estimate the accuracy of a candidate structure (termed the GDT‐net).

3. To directly generate protein structures.

The distance predictions and the accuracy predictions were each used to define a potential. We developed a simulated annealing system to optimize these potentials, by assembly of fragments generated by the structure generation network, augmented to track and reuse fragments from low‐potential structures. It was found that the distance‐based potential could also be directly optimized by gradient descent. The A7D submissions were generated by three methods which combined these algorithms:

1. Memory‐augmented simulated annealing with neural fragment generation with GDT‐net potential.

2. Memory‐augmented simulated annealing with neural fragment generation with distance potential.

3. Repeated gradient descent of distance potential.

The main conclusions of this work are that the three systems performed similarly, with the GDT‐net (A) and gradient descent (C) methods giving small improvements over B. Since all systems relied heavily on distance predictions based on coevolutionary data, we believe that potentials based on these predictions were essential to the accuracy of our structure predictions. The good results that A7D obtained in the assessment were due to the fact that deep learning allows extracting features from the data without making heuristic assumptions about the data. For example, none of the systems we developed uses the concept of secondary structure at inference time, but rather we model distances and angles and learn probability distributions for these which implicitly model secondary structure.

2. METHODS

In this section, we give more details on the components of the three systems outlined above, and in particular of the three neural networks that were trained for distance prediction, structure generation, and structure scoring.

2.1. Distance prediction

At the centre of all three methods used in CASP13 is a neural network (1) trained to predict the distances d _ij between the β‐carbon atoms of pairs of residues. Contact prediction has been extensively used in structure prediction16, 20, 29, 31 but previous work has also made residue distance predictions,3, 35 and these were used for structure prediction in CASP13 by other groups in distance geometry approaches.10, 32 While in some cases, these distances are highly constrained by secondary structure or clear coevolutionary signals, in most cases, they will be uncertain. In order to model this uncertainty, the network predicts discrete probability distributions $P\left(d_{\mathit{ij}}\mid S,\mathrm{MSA}\left(S\right)\right)$, given a sequence $S$ and its multiple sequence alignment $\mathrm{MSA}\left(S\right)$. These distance distributions are modeled with a softmax distribution for distances in the range 2 to 22 Å split into 64 equal bins. The network is trained to predict distances between two 64‐residue fragments of a chain, giving a probabilistic estimate of a 64 × 64 region of the distance map. These regions are tiled together to produce distance predictions for the entire protein. The distributions are predicted with a deep, dilated residual convolutional network13 described in detail in another paper.24 The network consists of 220 two‐dimensional (2D) residual blocks with 128 channels and dilated 3 × 3 convolutions, elu nonlinearity with dropout and batch normalization.

A distance potential is created from the negative log likelihood of the distances, summed over all pairs of residues i,j.

$$V_{\text{distance}}\left(\mathbf{x}\right)=-\sum _{i,j,i\ne j}\log P\left(d_{\mathit{ij}}\mid S,\mathrm{MSA}\left(S\right)\right)$$ (1)

With a reference state,27 this becomes the log likelihood ratio of the distances under the full conditional model and under a background model predicting the distance distributions P(d_ij ∣ length) independent of sequence (trained with the same network architecture on the same set of proteins but without sequence or MSA input features):

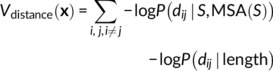(2)

This distance‐based potential is used for our fragment assembly system and our gradient descent system. We substitute it with a learned potential in the GDT‐net model of Section 2.2.

2.2. GDT‐net

In this system, we train a neural network, which we call GDT‐net (2), to predict the GDT_TS33 of a candidate structure. We then use the GDT‐net's accuracy prediction as a scoring function to be optimized by simulated annealing as described in Section 2.3.

The GDT‐net is trained in a distributed and continuous setting,26 summarized in Figure 1, in which actors generate candidate structures by running simulated annealing with the latest GDT‐net for all proteins in the training set while learners train the GDT‐net on candidates sampled from the actors.

Figure 1.

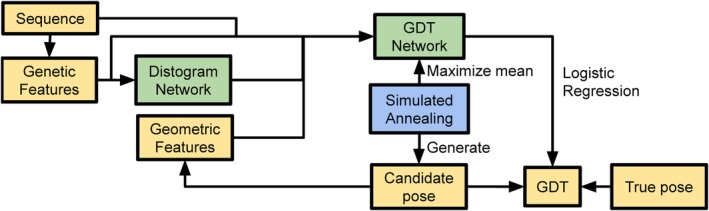
A schematic of the GDT‐net system (A). Feature extraction stages are shown in yellow, structure‐prediction neural network in green, and structure realization in blue

The input of the GDT‐net consists of N × N MSA features similar to the ones used for distance prediction in Section 2.1, the contact map prediction obtained by collapsing the predicted distance distributions into two bins, and geometric features representing the current candidate structure, in the form of the N × N distance matrix and contact map (for both Cα and Cβ atoms) of the candidate structure, as well as the Cβ coordinates and sine/cosine of the torsion angles.

The GDT‐net architecture begins with a deep 2D resnet stack, similar to the one used for the distance predictions, but with strided convolutions to progressively reduce the resolution (18 residual blocks with 3 × 3 dilated convolutions and up to 64 channels per block). After the resnet stack, mean pooling is applied to obtain a single vector whose dimension is agnostic to the number of residues. Pooling is followed by a softmax with 100 bins for the range [0,100]. The network is trained to minimize negative cross entropy of the softmax and the quantized GDT_TS of the candidate with respect to the true structure. During simulated annealing, we use the negative mean of the softmax distribution (with a temperature of 0.3) as a scoring function.

For generating the candidate structure data, we use about 4000 actors that continuously sample from the training set, fetch the latest GDT‐net checkpoint (starting with randomly initialized weights), and run simulated annealing with it, for 40 000 steps, recording candidate structures every 1000 steps. For training the network, we use asynchronous SGD with momentum with batch size 1 on 16 GPUs, sampling uniformly from all the candidate structures. We decay the learning rate every 10 M steps.

2.3. Memory‐augmented simulated annealing

Two out of the three methods (A and B) used a simulated annealing17 based search method. Fragment‐insertion‐based simulated annealing has previously been used6, 15, 27, 34 to predict protein structure. A simulated annealing step consists of inserting a structural fragment into an existing structure and accepting or rejecting the new structure based on the Metropolis‐Hastings acceptance criteria12, 19 and an associated scoring function.

Figure 2 shows an overview of the simulated annealing search system, which consists of a pool of backbone optimizing simulated annealing workers, a pool of side‐chain optimization and full‐atom scoring workers, as well as three databases: a local per‐worker fragment library, a global backbone‐only structural library, and a global full‐atom structural library. The details of these are discussed below.

Figure 2.

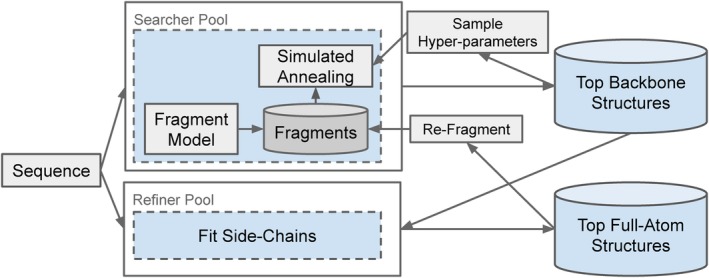
An overview of the simulated annealing framework. A pool of workers runs simulated annealing to optimize the backbone structure. Another pool refines these structures to add side‐chain atoms. Fragments from these full‐atom structures are reused in simulated annealing in a continuous fashion

A few modifications are made to a standard simulated annealing setup. When performing multiple simulated annealing runs, it can be seen that alternative predicted structures can be correct at different positions in the protein. In order to combine these structures, we periodically update the local fragment database using low‐scoring refragmented structures25 found across all the simulated annealing workers. The local fragment database is initialized, and periodically updated, with fragments from the model described in Section 2.4.

Another observation is that often it is significantly faster to score a backbone‐only structure, than it is to score a full‐atom model, as the full‐atom model requires placing all the side‐chain atoms. To get the best of both worlds, a separate set of workers exists, whose job is to continuously take the best backbone‐only structures, fit the side‐chains using the Rosetta relax protocol,5 and perform full‐atom scoring on these structures. These structures are used in two ways. Firstly, the final structure is selected based on the full‐atom scores. Secondly, these structures are refragmented and reused in the simulated annealing workers, biasing selection towards fragments from good full‐atom structures.

There are several hyperparameters in the simulated annealing such as start temperature, run length, and proportion of fragments from the fragment model. Along with structure and score, we also store these hyperparameters in the global databases. When each worker restarts simulated annealing, it samples the hyperparameters proportional to their associated structure scores. This leads to automatic optimization of the hyperparameters over time in a similar way to previous work on population‐based training of neural networks.14

Two versions of simulated annealing were run in CASP13; these differ in the potential used for the backbone only part of the algorithm. The first (A) uses the GDT‐net described in Section 2.2, and the second (B) uses the distance potential described in Section 2.1 to score the structures. Both methods use Talaris201421 combined with the distance potential for the Rosetta relax5 protocol, and in final decoy selection (see Section 2.7).

2.4. Structure prediction

The third neural network (3) was designed to make direct structure predictions using an end‐to‐end trained generative model of protein backbone torsion angles based on the work of Gregor et al.11 Similar to that work, our network, shown in Figure 3, is a convolutional, autoregressive latent model; the key difference is that we need the generative model to be conditioned on the sequence and MSA features. The 2D conditioning data are fed through a 2D residual network (five blocks with 32 channels) and then mean pooled along one dimension before being passed into a one‐dimensional (1D) convolutional LSTM encoder (256 channels) which parameterizes the prior for a set of Gaussian‐distributed latent variables. The latents (two per angle) are decoded by a 1D convolutional LSTM decoder which over 128 iterations incrementally generates a 1D canvas whose values are used to generate the parameters of independent von Mises distributions which describe the backbone torsion angles. The model is trained with a variational upper bound on the true log‐likelihood as is usual in variational autoencoders.23 While this neural network is an end‐to‐end model of protein structure (an alternative formulation of which has been proposed in concurrent work1), it was found to model local structure much better than long‐range interactions, so was not effective for sampling conformations of entire domains. We trained the model on crops of the protein backbones from our training set. While longer crops permit richer modeling of larger fragments, smaller crops allowed us to generate more independent training examples and thus avoid overfitting. We found that training on crops of size 32 led to the best compromise between these two effects. Training used the Adam optimizer and a learning rate of 10⁻⁴.

Figure 3.

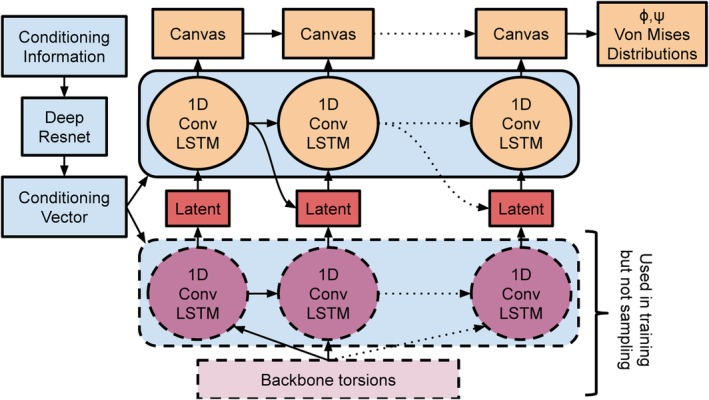
A schematic of the fragment network 3. The blue parts of the network describe the conditioning network, the purple parts are the encoding network used to approximate the posterior, and the orange parts are the generative decoder

Most fragment assembly methods construct fragments by looking up likely fragments based on a database of structures or angles extracted from the Protein Data Bank,15, 27 but previous work has also investigated generative4 and neural‐network36 models of protein structure. In this work, we sampled from the generative network to create libraries of nine‐residue fragments which were used in the memory‐augmented simulated annealing of Section 2.3.

2.5. Repeated gradient descent

As an alternative to simulated annealing, we created a smooth combined potential by adding a torsion potential and Rosetta's score2 to a spline approximation to the log probability of the distance predictions from network 1, (equal weights, as determined by cross validation, were used for the potentials) and used gradient descent (L‐BFGS18) to directly optimize this combined potential with respect to the structure torsion angles. While gradient descent has previously been used to locally minimize the energy of structures predicted from backbone sampling (as in Rosetta's relax protocols, for example5), here, we use it to establish backbone structure. Repeated optimization (5000 repeats) from initial torsion angles sampled from predicted torsion angle distributions was found to converge quickly. Full details of the repeated gradient descent system (C) can be found in another paper.24

2.6. Domain segmentation

Simulated annealing is computationally expensive to run on long protein chains, particularly when using the GDT‐net scoring. For this reason, we used a simple domain segmentation approach to partition a chain into pieces which are modeled independently in parallel. Our approach is based on assuming that domains will have many interresidue contacts whereas there will be fewer contacts between domains. We consider all possible partitions of a chain into two or three segments and score each segmentation, similar to the “Domain Guess by Size” method.30 The score is based on the full‐chain contact map from our distance prediction network and we use four more pieces of information:

• The probability P(n | L) of having n domains in a chain of length L.

• The probability P(l) of having a domain of length l.

• The mean number of contacts per residue for a domain of length l, μ _l.

• The standard deviation of the number of contacts per residue for a domain of length l, σ _l.

These data are all obtained by collecting statistics from PDB9 and CATH.7 The last two pieces of information are used to parametrize the probability p(d | l) of having a certain number of contacts d in a domain of length l as a Gaussian distribution. Note that having the full‐chain contact map makes it straightforward to extract the average number of contacts per residue of a particular segmentation by summing the on‐diagonal blocks of the contact map prediction and dividing by the length of each block. This calculation yields the expected number of contacts d _l. With this information, we can score a particular segmentation of a protein of length L into n segments of length {l ₁,…,l _n} as follows:

$$S\left(L,n,\left\{l_1,\dots l_n\right\}\right)=\log P\left(n\mid L\right)+\sum _{i=1}^n\log P\left(l_i\right)+\log p\left(d_i\mid l_i\right).$$ (3)

The most likely two‐segment partition and the most likely three‐segment partition are used for structure generation, along with a single‐segment for chains shorter than 400 residues. For each segmentation proposal, the domains are folded independently, with domain‐specific distance predictions. The domain structures are combined with simulated annealing optimizing the full‐chain potential over the torsions at the boundary. The best full‐chain structures are then relaxed with Rosetta (using Rosetta's Talaris2014 score plus the full‐chain distogram potential weighted 1:0.02, as found through cross validation) and the lowest‐potential chains considered in decoy selection.

2.7. Decoy selection

For all but five of the targets in CASP13, we used exactly two of the three folding systems. Before target T0975, the two systems based on simulated annealing and fragment assembly (and using 40‐bin distance distributions) were used (five independent runs with the distance potential, three with the GDT‐net). From T0975 on, a newly trained 64‐bin distance prediction network was used and structures were generated by the repeated gradient descent system (three independent runs) as well as the distance‐potential fragment assembly system (five independent runs), while the GDT‐net model was retired. Five submissions were chosen from the eight structures (the lowest potential structure generated by each independent run) with the first submission (“top‐1”) being the lowest‐potential structure generated by GDT‐net (pre‐T0975) or gradient descent (thereafter). The remaining four submissions were the four best other structures, with the fifth being a gradient descent structure/GDT‐net if none had been chosen for position 2, 3, or 4. All submissions for T0999 were generated by gradient descent.

2.8. Data

All the neural network models are trained on structures extracted from the PDB.9 We extract nonredundant domains by utilizing the CATH7 35% sequence similarity cluster representatives (CATH version: 2018‐03‐16). This gives 31 247 domains, which are split into train, and test sets (29 427 and 1820 proteins, respectively) keeping all domains from the same homologous superfamily (H‐level in the CATH classification) in the same partition.

MSAs were generated using HHblits,22 and from these profiles, 1D features were extracted. Potts models were fitted on the MSAs using pseudolikelihood8 to generate 2D coevolutionary features. PSI‐BLAST2 profiles were also used in the distance prediction network.

3. RESULTS

Figure 4 shows the FM performance of the A7D system, showing the number of FM (FM + TBM/FM) domains (out of 43) solved to a given GDT_TS accuracy, which shows that the A7D system is particularly adept at producing 50‐70 GDT_TS structures.

Figure 4.

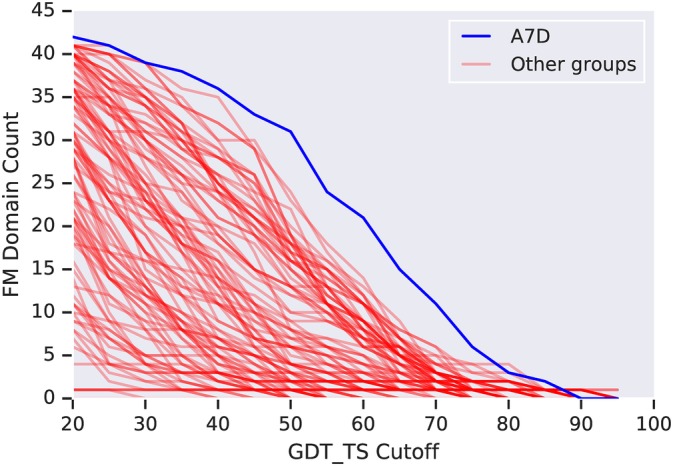
Number of FM + FM/TBM domains (out of 43) solved to a GDT_TS threshold for all groups in CASP13

Figure 5 shows the GDT_TS for each CASP13 submission, colored by the method used to generate it, in the order submitted. Table 1 shows the average performance of the different methods for the targets where more than one method was used. Two direct comparisons (B vs C and B vs A) can be made—fragment assembly after T0975 with gradient descent for that period (both using the distance potential) and, before T0975, distance potential with the GDT‐net scoring (both using fragment assembly). From this comparison, it is apparent that the GDT‐net and gradient descent methods perform slightly better than distance potential fragment assembly. We suspect that the GDT‐net performed better as it was able to look at the likelihood of the whole structure, as opposed to just using the marginal probabilities in the distance predictions. The gradient descent approach is domain‐free, and we suspect this is one of the reasons it performed better. Another interesting observation from Figure 5 is that the fragment assembly method, despite producing similar average results, generates a greater variety of scores than the gradient descent method for each target.

Figure 5.

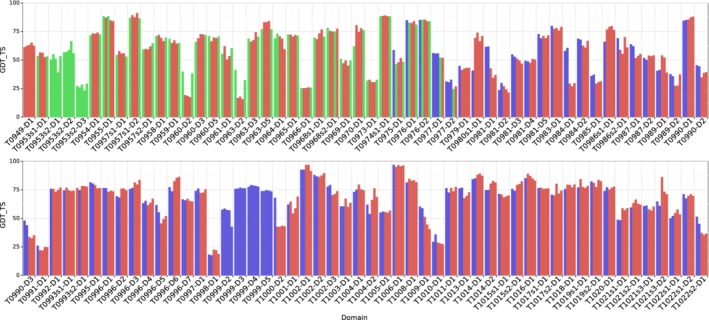
A7D CASP13 submission accuracies by domain. The GDT_TS for each of the five A7D CASP13 submissions are shown. Submissions are colored by method with fragment assembly submissions (B) colored red, GDT‐net submissions (A) colored green, and gradient descent submissions (C) colored blue. T0999 (1589 residues) was manually segmented based on HHpred28 homology matching

Table 1.

A7D CASP13 accuracies by method. Average GDT_TS scores of the A7D CASP13 submissions broken down by method. Since the methods used changed after T0975, we show the means for these two sets separately. Domains in which only one method was used have been excluded to make the numbers comparable

	Mean GDT_TS for targets
Method	Before T0975	T0975 onwards
Fragment assembly with GDT‐net	63.8	N/A
Fragment assembly with distance potential	62.4	63.4
Gradient descent on distance potential	N/A	64.4

Figure 6 shows that, as expected, the system produces more accurate structures when the multiple sequence alignments are deeper, because of the distance predictor's dependence on coevolutionary information. Since the system does not search for templates, the performance on TBM targets is often worse than that for FM targets with similar N_eff. Performance on TBM targets with few alignments can be much worse than for systems which explicitly use templates (eg, T0973‐D1 which was over 40 GDT_TS worse than the best submission). Interestingly, the low‐alignment designed protein T0955‐D1 was solved to high accuracy (GDT_TS 88.4) despite having no alignments, presumably because of its short length and because the design process ensured it had highly typical structure. The raw data for Figures 5 and 6 are provided in the Supplementary information.

Figure 6.

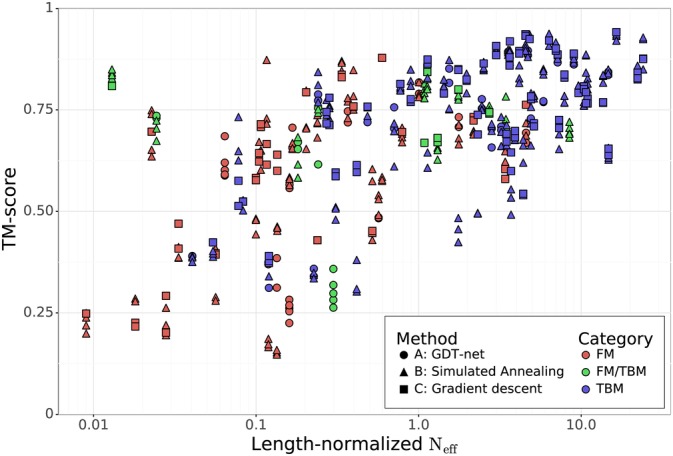
The TM‐score of the A7D submissions plotted against the length‐normalized number of effective sequence alignments found (N_eff). Each domain decoy is colored by difficulty category, with a shape indicating the method by which it was generated

The A7D system was able to generate good structures for several hard targets, for instance, the three‐domain protein T0990, shown in Figure 7. In this case, domain D3 is inserted into domain D2, so our domain segmentation algorithm, which only considers single‐segment domains, was unable to generate a correct segmentation. It can be seen that the gradient descent method which does not use domain segmentation produced better results than the fragment assembly method. For T0980 s1‐D1, on the other hand, fragment assembly produced better models than the repeated gradient descent, which failed to correctly assemble the beta sheet.

Figure 7.

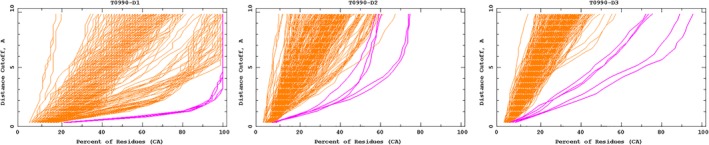
Accuracy curves for three domains of T0990. Curves show the fraction of residues that are correct within a given alignment threshold. All groups' submissions are shown with one curve per submission (396, 396, and 397 models, respectively), highlighting the five A7D submissions in magenta. Graphs from http://predictioncenter.org

4. DISCUSSION

In this work, we have presented the structure prediction system entered by A7D in the CASP13 assessment and detailed the three deep‐learning components which were combined in three different approaches. We have shown in this blind evaluation that deep‐learning‐based methods have excellent performance across a range of targets, including novel folds. All approaches rely heavily on a deep distance prediction neural network which uses coevolution information as inputs. We found that all three approaches performed similarly, but having the diversity of the different methods generating submissions for each target was useful. Despite the differences in the structure assembly methods, we did not find significant differences in accuracy arising from native contact order or other structural features. Our approaches tried to avoid heuristics and hand‐crafted assumptions on the structure of proteins but for the fragment assembly approach we relied on a heuristic method to segment domains as described in Equation (3). In contrast, many fragment assembly approaches rely on secondary structure to limit the types of fragments available in certain regions and to modify the folding potential. The distance prediction network can express ambiguity by predicting distance distributions, which can represent secondary structure in short‐range distances, in a way which is harder to do with three‐way classification of secondary structure. The gradient descent algorithm has even fewer hyperparameters and assumptions than this and performs better.

We note that our method performed well in the TBM + TBM/FM category, despite none of the methods explicitly using template information. This is because proteins that have a template in the PDB also tend to have rich coevolutionary information and can thus be well modeled by the distance prediction potential.

The main weakness of our approach is that it still relies heavily on coevolution. When few alignments are available, distance predictions tend to be uninformative and poor structures are generated (Figure 6). Since there is no explicit template lookup, performance on TBM targets with few homologous sequences was much worse than template‐based methods. Also, we did not attempt to propagate the uncertainty about distance into an uncertainty in residue positions. The B‐factors submitted were incorrect leading to suboptimal performance when A7D models were used for molecular replacement.

CONFLICT OF INTERESTS

The authors have filed patent disclosures relating to the work presented here.

Supporting information

Appendix S1: Supplementary File

Senior AW, Evans R, Jumper J, et al. Protein structure prediction using multiple deep neural networks in the 13th Critical Assessment of Protein Structure Prediction (CASP13). Proteins. 2019;87:1141–1148. 10.1002/prot.25834