Topological bands for ultracold atoms

Abstract

There have been significant recent advances in realizing band structures with geometrical and topological features in experiments on cold atomic gases. This review summarizes these developments, beginning with a summary of the key concepts of geometry and topology for Bloch bands. Descriptions are given of the different methods that have been used to generate these novel band structures for cold atoms and of the physical observables that have allowed their characterization. The focus is on the physical principles that underlie the different experimental approaches, providing a conceptual framework within which to view these developments. Also described is how specific experimental implementations can influence physical properties. Moving beyond single-particle effects, descriptions are given of the forms of interparticle interactions that emerge when atoms are subjected to these energy bands and of some of the many-body phases that may be sought in future experiments.

I. INTRODUCTION

Topology is a mathematical concept that refers to certain properties that are preserved under continuous deformations. One familiar example is the number of twists put into a belt before its buckle is fastened. Usually we aim to fasten a belt without any twists. But if we were to introduce a single twist we would produce a Möbius strip. No continuous deformation of the closed belt would get rid of this uncomfortable twist. The number of twists is said to be a “topological invariant” of the closed belt.

The importance of topological invariants in stabilizing spatial deformations and defects is also well known in physics in diverse areas ranging from cosmology to condensed matter. For a superfluid confined to a ring, the number of times that the superfluid phase ϕ changes by 2π around the ring

$$N=\frac{1}{2\pi }\oint \mathbf{\nabla }\varphi \cdot \text{d}\mathit{l}$$ (1)

is a topological invariant. This winding number cannot change under smooth deformations of the superfluid: a change would require the superfluid density to vanish somewhere—such that ϕ is ill defined—requiring the motion of a quantized vortex line across the ring. Here the topological stability arises from the interplay of the underlying space (the ring) and the form of the local order parameter (the phase of the superfluid wave function).

In recent years it has come to be understood that topology enters physics in another, very fundamental way through the nature of the quantum states of particles moving through crystalline lattices. The energy eigenstates of electrons moving through periodic potentials are well known to form energy bands, a result that follows from the existence of a conserved crystal momentum via Bloch’s theorem. Remarkably, under certain circumstances, each Bloch energy band can be assigned a robust integer-valued topological invariant related to how the quantum wave function of the electron “twists” as a function of crystal momentum. This integer is invariant under continuous changes of material properties, “continuous” meaning that the energy gaps to other bands should not close. The first example of such a topological invariant for Bloch energy bands arose from a highly original analysis of the integer quantum Hall effect in a two-dimensional (2D) lattice (Thouless et al., 1982). Recent theoretical breakthroughs have shown that, once additional symmetries are included, topological invariants are much more widespread. These ideas underpin a recent revolution in our understanding of band insulators and superconductors (Hasan and Kane, 2010; Qi and Zhang, 2011). The topological nature of these materials endows them with physical characteristics that are insensitive to microscopic details, a notable example being the exact quantization of the Hall resistance in 2D irrespective of the presence or form of a random disorder potential.

A great deal of current research focuses on understanding the physical consequences of these new materials, and experimental studies of topological insulators and superconductors in solid state systems continue apace. Furthermore, there is significant activity in exploring the nature of the strongly correlated phases of matter that arise in these materials, notably to construct strong-correlation variants of these topological states of weakly interacting electrons. Theory suggests many interesting possibilities, which are still seeking experimental realization and verification.

Such questions are ideally addressed using realizations with cold atomic gases. Cold atomic gases allow strongly interacting phases of matter to be explored in controlled experimental settings. However, a prerequisite for quantum simulations of such issues is the ability to generate topological energy bands for cold atoms. This poses a significant challenge, even at this single-particle level. Realizing topological energy bands typically requires either the introduction of effective orbital magnetic fields acting on neutral atoms and/or the introduction of a spin-orbit coupling between the internal spin states of an atom and its center-of-mass motion. This is an area of research that has attracted significant attention over the last years, both theoretical and experimental. Much progress has been made in developing techniques to generate artificial magnetic fields and spin-orbit coupling for neutral atoms (Zhai, 2015; Dalibard, 2016; Aidelsburger, Nascimbène, and Goldman, 2017). The use of these techniques in the setting of optical lattices has led to the realization and characterization of topological Bloch bands for cold atoms.

In this review we describe how topological energy bands can be generated and probed in cold atom systems. We focus on existing experimental studies, for which the essential behavior can be understood in terms of noninteracting particles. We start by explaining the concepts underpinning topological energy bands in Sec. II. We describe the key physical effects that are required to generate these bands and how these can be engineered in cold atom systems in Sec. III. Our emphasis is on recent experimental developments. In Sec. IV we describe the principal observables that have been used to characterize the geometrical and topological characters of the resulting energy bands. In Sec. V we move beyond single-particle physics to discuss some of the theoretical understanding of the consequences of interactions in these novel optical lattices and to describe some of the interacting many-body phases that can be sought in future experiments on these systems. We conclude in Sec. VI with comments on the outlook for future work and point out connections to broader research areas.

Throughout this review we explain just the essential physics underlying recent developments, so the content is necessarily incomplete. The review should be used as a starting point from which to explore the literature, rather than as a comprehensive survey of the field. We note that we focus on topological bands for atoms in periodic lattices. Related phenomena can appear for photons and hybrid light-matter objects (cavity polaritons) in novel optical materials, and we refer the interested readers to the review by Ozawa et al. (2018). We note also that all our discussions are based on the notion of band structure, meaning that we ourselves restrict to periodic materials and that we do not address the case of atoms or photons moving in quasiperiodic systems (Kunz, 1986; Kraus et al., 2012; Tanese et al., 2014; Dareau et al., 2017).

II. TOPOLOGY OF BLOCH BANDS

In this section we provide an introduction to how topology enters into band theory for particles moving in periodic potentials. We focus on quantities and models that are relevant to later sections. More comprehensive accounts are available in review articles on topological insulators (Hasan and Kane, 2010; Qi and Zhang, 2011; Chiu et al., 2016).

A. Band theory

Here we describe the essential properties of a quantum particle moving through a periodic lattice potential. Our aim is to understand both the resulting eigenenergies (giving the conventional band structure) along with the underlying structure of the eigenstates (from which the band topology is derived).

Any lattice potential is invariant under displacements by a set of lattice vectors R, which can be written $\mathit{R}={\sum }_i{m}_i{\mathit{a}}_i$ in terms of integer {m_i} multiples of basis vectors {a_i} (with i = 1,...,d in dimension d). From Bloch’s theorem, the energy eigenstates take the form

$${\psi }_{\mathit{q}}^{(n)}(\mathit{r})={\text{e}}^{\text{i}\mathit{q}\cdot \mathit{r}}{u}_{\mathit{q}}^{(n)}(\mathit{r}),$$ (2)

with $u_{\mathit{q}}^{(n)}(\mathit{r})=u_{\mathit{q}}^{(n)}(\mathit{r}+\mathit{R})$ having the periodicity of the lattice. These eigenstates are characterized by the band index n and the crystal momentum q. Although we retain $\hslash$ in equations, we refer to momentum and wave vector inter-changeably. Starting from the Schrödinger equation for the energy eigenstate ${\psi }_{\mathit{q}}^{(n)}(\mathit{r})$:

$$\left[-\frac{1}{2m}{\mathbf{\nabla }}^2+V(\mathit{r})\right]{\psi }_{\mathit{q}}^{(n)}(\mathit{r})=E_{\mathit{q}}^{(n)}{\psi }_{\mathit{q}}^{(n)}(\mathit{r}),$$ (3)

one readily finds that the Bloch states $u_{\mathit{q}}^n(\mathit{r})$ are eigenstates of the q-dependent Hamiltonian

$${\widehat{H}}_{\mathit{q}}=\left[-\frac{1}{2m}{(\mathbf{\nabla }+\text{i}\mathit{q})}^2+V(\mathit{r})\right].$$ (4)

If there are internal degrees of freedom, e.g., spin, then one should replace $u_{\mathit{q}}^n(\mathit{r})$ by $u_{\mathit{q}}^n(\alpha ,\mathit{r})$ with α labeling these additional degrees of freedom.

States that differ in crystal momentum q by a reciprocal lattice vector $\mathit{G}={\sum }_i{m}_i{\mathit{G}}_i$ are physically equivalent. (The reciprocal lattice is constructed from basis vectors {G_i} defined by the condition ${\mathit{G}}_i\cdot {\mathit{a}}_j=2\pi {\delta }_{ij}$.) Thus, q can be chosen to be restricted to the first Brillouin zone (BZ): the locus of points q that are closer to the origin than to any reciprocal lattice vector G. For example, for a 2D lattice with basis vectors ${\mathit{a}}_1=(a_1,0)$ and ${\mathit{a}}_2=(0,a_2)$ the reciprocal lattice has basis vectors ${\mathit{G}}_1=\left(2\pi /a_1,0\right)$ and ${\mathit{G}}_2=\left(0,2\pi /a_2\right)$, and the BZ is the region $-\pi <q_x{a}_1\le \pi$ and $-\pi <q_y{a}_2\le \pi$.

Many of the cases we describe will be tight-binding models, for which there are M single-particle orbitals within each unit cell of the lattice. These could be multiple lattice sites and/or other internal degrees of freedom. The system Hamiltonian $\widehat{H}$ acts on the set of M × N_c single-particle states $|\alpha ,\mathit{R}\rangle =|\alpha \rangle \otimes |\mathit{R}\rangle$ with α = 1,…,M labeling the states within a unit cell and R the position of each of a total of N_c unit cells. For periodic boundary conditions, the energy eigenstates are plane waves

$$|{\psi }_{\mathit{q}}^{(n)}\rangle =\frac{1}{\sqrt{N_c}}\sum _{\mathit{R}}{\text{e}}^{\text{i}\mathit{q}\cdot \mathit{R}}|u_{\mathit{q}}^{(n)}\rangle \otimes |\mathit{R}\rangle ,$$ (5)

where n = 1,…,M is the band index and $|u_{\mathit{q}}^{(n)}\rangle$ are the associated Bloch wave functions in the M-dimensional internal space. The band energies and Bloch wave functions follow from the spectrum of a wave-vector-dependent Hamiltonian ${\widehat{H}}_{\mathit{q}}$ that acts in this internal space. For example, ${\widehat{H}}_{\mathit{q}}$ can be represented by the M × M matrix

$$H_{\mathit{q}}^{\alpha \beta }=\frac{1}{N_c}\sum _{\mathit{R},{\mathit{R}}^{\prime }}{\text{e}}^{\text{i}\mathit{q}\cdot \left(\mathit{R}-{\mathit{R}}^{\prime }\right)}\langle \alpha ,{\mathit{R}}^{\prime }|\widehat{H}|\beta ,\mathit{R}\rangle .$$ (6)

Note that the Bloch Hamiltonian ${\widehat{H}}_{\mathit{q}}$ and thus its matrix representation is not uniquely defined: it can be replaced by ${\widehat{H}}_{\mathit{q}}^{\prime }={\widehat{\mathcal{U}}}_{\mathit{q}}{\widehat{H}}_{\mathit{q}}{\widehat{\mathcal{U}}}_{\mathit{q}}^{†}$, where ${\widehat{\mathcal{U}}}_{\mathit{q}}$ is a wave-vector-dependent unitary transformation. Because the states at wave vectors q and q + G are physically equivalent, one can always choose the Hamiltonian to have the same periodicity as the ${\widehat{H}}_q={\widehat{H}}_{q+G}$. We make this choice throughout this section. However, as will be explained later, some care is required in doing so when considering geometrical properties of the bands. Other choices are discussed in Appendix A.2.

B. Geometrical phase

At its most basic level, the band structure of a periodic potential is specified by the energies $E_{\mathit{q}}^{(n)}$. However, the bands are also characterized by geometrical and topological features. These relate to how the wave functions $|u_{\mathit{q}}^{(n)}\rangle$ vary with wave vector q across the BZ. No variations can occur for simple tight-binding models with one orbital per unit cell M = 1 (i.e., one-band models). However, topological features arise already for two orbitals per unit cell, M = 2. We describe topological classifications of Bloch bands in 1D and 2D and illustrate these using two-band tight-binding models.

Our presentation relies heavily on the concept of the geometrical phase (Berry, 1984), which we briefly review. Consider a Hamiltonian $\widehat{\mathcal{H}}(\mathit{X})$ which depends on a set of parameters X and with nondegenerate spectrum

$$\widehat{\mathcal{H}}(\mathit{X})|{\mathbf{\Psi }}^{(n)}(\mathit{X})\rangle =E^{(n)}(\mathit{X})|{\mathbf{\Psi }}^{(n)}(\mathit{X})\rangle .$$ (7)

The system is prepared in an eigenstate $|{\mathbf{\Psi }}^{(n)}(\mathit{X})\rangle$ at an initial time t_i, and the parameters X_t are changed slowly in time t such that the state evolves adiabatically, following an instantaneous eigenstate of $\widehat{\mathcal{H}}({\mathit{X}}_t)$. The parameters are taken around a cycle such that ${\mathit{X}}_{t_{\text{f}}}={\mathit{X}}_{t_{\text{i}}}$. Since the Hamiltonian returns to the initial form at t_f, so too must any eigenstate up to an overall phase factor (in this case of a nondegenerate spectrum). This phase has both dynamical and geometrical contributions

$$|{\mathbf{\Psi }}_{\text{f}}^{(n)}\rangle ={\text{e}}^{\text{i}\left[{\gamma }_{\text{dyn}}^{(n)}+{\gamma }_{\text{geo}}^{(n)}\right]}|{\mathbf{\Psi }}_{\text{i}}^{(n)}\rangle ,$$ (8)

$${\gamma }_{\text{dyn}}^{(n)}=-\frac{1}{\hslash }{\int }_{t_{\text{i}}}^{t_{\text{f}}}{E}^{(n)}\left({\mathit{X}}_{t^{\prime }}\right)\text{d}{t}^{\prime },$$ (9)

$${\gamma }_{\text{geo}}^{(n)}=\oint \text{i}\langle {\mathbf{\Psi }}^{(n)}|{\partial }_{\mathit{X}}{\mathbf{\Psi }}^{(n)}\rangle \cdot \text{d}\mathit{X}.$$ (10)

The geometrical phase is the integral of the Berry connection

$${\mathit{A}}^{(n)}(\mathit{X})\equiv \text{i}\langle {\mathbf{\Psi }}^{(n)}|{\partial }_{\mathit{X}}{\mathbf{\Psi }}^{(n)}\rangle$$ (11)

around the closed loop in parameter space X. The Berry connection plays a role similar to that of the vector potential for a magnetic field. It is gauge dependent, varying under local gauge transformations $|{\mathbf{\Psi }}^{(n)}\rangle \to {\text{e}}^{\text{i}\mathbf{\Phi }(\mathit{X})}|{\mathbf{\Psi }}^{(n)}\rangle$. However, if X has more than one component, one can define a gauge-invariant Berry curvature

$${\mathrm{\Omega }}_{ij}^{(n)}\equiv {\partial }_{X_i}{A}_j^{(n)}-{\partial }_{X_j}{A}_i^{(n)}.$$ (12)

If the closed loop X can be viewed as the boundary of a 2D surface (X₁, X₂) on which the Berry curvature is everywhere well defined, then the geometrical phase (10) is the flux of the Berry curvature

$${\mathrm{\Omega }}^{(n)}\equiv {ϵ}_{ij}{\partial }_{X_i}{A}_j^{(n)}={ϵ}_{ij}\text{i}{\partial }_{X_i}\langle {\mathbf{\Psi }}^{(n)}|{\partial }_{X_j}{\mathbf{\Psi }}^{(n)}\rangle$$ (13)

through this 2D surface. Here ϵ_ij is the antisymmetric tensor of two indices ${ϵ}_{xy}=-{ϵ}_{yx}=1$ and the summation over repeated indices is assumed.

We apply these concepts to physical situations in which the role of external parameters X is played either by the crystal momentum q or by the real-space position r. In both cases, the Berry connection and Berry curvature define local geometric properties of the quantum states. The integrals of these geometric quantities over a closed manifold—the BZ for q, or the unit cell of the lattice for r—give rise to topological properties. As discussed in later sections, trajectories of q can be imposed in physical systems by the application of external forces, inducing adiabatic dynamics of the Bloch states.

C. Topological invariants

1. The Zak phase

Owing to the periodicity of the BZ under the addition of any reciprocal lattice vector G, a trajectory in wave vector from q_i to ${\mathit{q}}_{\text{f}}={\mathit{q}}_{\text{i}}+\mathit{G}$ is a closed loop. Since the Hamiltonian is periodic, ${\widehat{H}}_{\mathit{q}}={\widehat{H}}_{\mathit{q}+\mathit{G}}$, the ideas of Berry apply directly. The integral of the Berry connection along such closed loops

$${\varphi }_{\text{Zak}}^{(n)}={\int }_{{\mathit{q}}_{\text{i}}}^{{\mathit{q}}_{\text{i}}+\mathit{G}}\text{i}\langle u^{(n)}|{\partial }_{\mathit{q}}{u}^{(n)}\rangle \cdot \text{d}\mathit{q}$$ (14)

was proposed by Zak as a way to characterize the energy bands (Zak, 1989).

The first glimpse of how the mathematics of topological invariants can arise in band theory is provided by computing the Zak phase for simple two-band tight-binding models in one dimension (1D). We illustrate this for the Su-Schrieffer-Heeger (SSH) model.

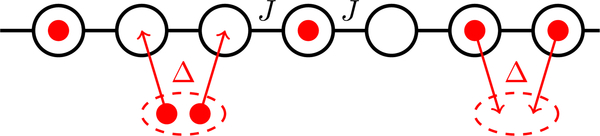
The SSH model is a tight-binding model in which there are two sites in the unit cell labeled A and B. The sites are connected by alternating tunnel couplings J and J′; see Fig. 1. The single-particle Hamiltonian reads

$$\widehat{H}=-\sum _j(J^{\prime }{\widehat{a}}_j^{†}{\widehat{b}}_j+J{\widehat{a}}_j^{†}{\widehat{b}}_{j-1}+\text{H}.\text{c}.),$$ (15)

where ${\widehat{a}}_j^{†}$ and ${\widehat{b}}_j^{†}$ create a particle on the A and B sites of the jth unit cell. For a bulk system with periodic boundary conditions, we look for the energy eigenstates using the Bloch wave form

$$|{\psi }_q\rangle =\sum _j{\text{e}}^{\text{i}jaq}(u_q^A|A_j\rangle +u_q^B|B_j\rangle ),$$ (16)

with a the lattice constant. The problem reduces to finding the eigenvectors ${(u_q^A,u_q^B)}^T$ of the Hamiltonian in reciprocal space, which has matrix representation

$${\widehat{H}}_q=-\left(\begin{array}{cc}0& J^{\prime }+J{\text{e}}^{-\text{i}qa}\\ J^{\prime }+J{\text{e}}^{\text{i}qa}& 0\end{array}\right)$$ (17)

within the $\text{BZ}-\pi /a<q\le \pi /a$.

FIG. 1.

Tight-binding (SSH) model of the polyacetylene molecule. For the SSH model (17), the on-site energies for A and B are supposed to be equal. This constraint will be relaxed for the Rice-Mele model (40).

The Hamiltonian (17) can be written in the general form

$${\widehat{H}}_q=-\mathit{h}(q)\cdot \widehat{\mathit{\sigma }},$$ (18)

where ${\widehat{\sigma }}_{\alpha }$ are the Pauli operators. Throughout this review, we use the conventional matrix representation of the Pauli operators in which ${\widehat{\sigma }}_z$ is diagonal. Then the SSH model has

$$h_x(q)+\text{i}{h}_y(q)=J^{\prime }+J{\text{e}}^{\text{i}qa},h_z=0,$$ (19)

with h_x,y(q) real periodic functions of q. The energy spectrum is composed of the two bands

$$E_q^{(\pm )}=\pm |\mathit{h}(q)|=\pm {\left[J^2+{J\prime }^2+2J{J}^{\prime }\cos (qa)\right]}^{1/2},$$ (20)

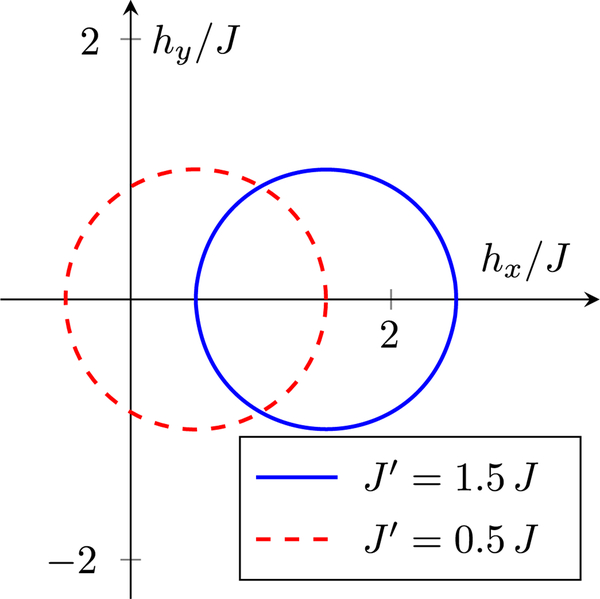
which are separated by a gap provided $|\mathit{h}|$ does not vanish at any q. Assuming $J,J^{\prime }>0$, the gap $2|J-J^{\prime }|$ closes only when $J=J^{\prime }$ for the quasimomentum q = π/a.

Provided there is a nonzero gap, i.e., $|\mathit{h}|\ne 0$ for all q, one can write $h_x+\text{i}{h}_y=|\mathit{h}|{\text{e}}^{\text{i}{\varphi }_q}$ with a well-defined ϕ_q, and the Bloch states are

$$\left(\begin{array}{c}{u}_q^A\\ u_q^B\end{array}\right)=\frac{1}{\sqrt{2}}\left(\begin{array}{c}1\\ \mp {\text{e}}^{\text{i}{\varphi }_q}\end{array}\right).$$ (21)

In this pseudospin representation, the fact that h_z = 0 in Eqs. (18) and (19) for the SSH model entails that these eigenstates lie on the equator of the Bloch sphere. The resulting Zak phases of the bands (14) are

$${\varphi }_{\text{Zak}}^{(\pm )}=-\frac{1}{2}{\int }_{\text{BZ}}\frac{\partial {\varphi }_q}{\partial q}\text{d}q.$$ (22)

Thus,

$$N\equiv -\frac{1}{\pi }{\varphi }_{\text{Zak}}^{(\pm )}=\frac{1}{2\pi }{\int }_{\text{BZ}}\frac{\partial {\varphi }_q}{\partial q}\text{d}q$$ (23)

is the number of times ϕ_q changes by 2π as q runs over the BZ. Since the Hamiltonian is periodic, ϕ_q = ϕ_{q + G} modulo 2π, N is an integer winding number, analogous to that for the phase of a superfluid around a ring (1). It measures the solid angle drawn by the pseudospins $u_q^{(\pm )}$ along the equator of the Bloch sphere when q spans the BZ.

The winding number (23) is a topological invariant of 1D band insulators arising from Hamiltonians of the form (18): N cannot be changed unless $|\mathit{h}(q)|$ vanishes at some q, i.e., unless the band gap closes. The case of the SSH model is illustrated in Fig. 2, which shows the locus of (h_x, h_y) as q runs over the BZ. For $J^{\prime }/J<1$ the curve encircles the origin once, N = 1; while for $J^{\prime }/J>1$ the curve does not encircle the origin, N = 0. These two curves cannot be smoothly interconverted without crossing h_x = h_y = 0, i.e., without the band gap closing. One could evade this conclusion by including terms proportional to ${\widehat{\sigma }}_z$ in the Hamiltonian. Then two gapped states with different N could be continuously deformed into each other. [We explore this later for the Rice-Mele (RM) model.] However, as explained in Sec. II.E, including ${\widehat{\sigma }}_z$ terms would break an underlying “chiral” symmetry of the SSH model. The winding number in 1D is an example of a topological invariant whose existence relies on an underlying symmetry.

FIG. 2.

The winding number for the SSH model. The curves plot the locus of (h_x, h_y) as q runs over the BZ. For $J^{\prime }/J>1$ the vector (h_x, h_y) does not encircle the origin, but for $J^{\prime }/J<1$ it encircles the origin once, indicating that these two cases have winding numbers (23) of N = 0 and 1, respectively.

A perceptive reader will notice that the topological invariant [Eq. (23)] we constructed appears to be rather unphysical. The two parameter regimes of the SSH model which have different winding numbers, at $J^{\prime }/J>1$ and $J^{\prime }/J<1$, could be trivially related by reversing the labeling of the A and B sublattices in Fig. 1, at least deep in the bulk of the system. In what sense are these two parameter regimes topologically distinct? A key point to note is that the winding number (23) has a basis-dependent offset. In place of Eq. (16) we could just as well have sought an energy eigenstate of the form

$$|{\psi }_q\rangle =\sum _j{\text{e}}^{\text{i}jaq}({\tilde{u}}_q^A|A_{j+N_A}\rangle +{\tilde{u}}_q^B|B_{j+N_B}\rangle )$$ (24)

$$=\sum _j{\text{e}}^{\text{i}jaq}({\tilde{u}}_q^A{\text{e}}^{-\text{i}{N}_{A}aq}|A_j\rangle +{\tilde{u}}_q^B{\text{e}}^{-\text{i}{N}_{B}aq}|B_j\rangle ),$$ (25)

associating site A in the cell j + N_A with site B in cell j + N_B. Comparing Eq. (25) with (16) shows that this amounts to replacing ${(u_q^A,u_q^B)}^T$ by ${({\tilde{u}}_q^A{\text{e}}^{-\text{i}{N}_{A}aq},{\tilde{u}}_q^B{\text{e}}^{-\text{i}{N}_{B}aq})}^T$, i.e., to a q-dependent unitary transformation ${\widehat{\mathcal{U}}}_q$. In this new basis ${({\tilde{u}}_q^A,{\tilde{u}}_q^B)}^T$, the eigenstates (21) are replaced by

$$\left(\begin{array}{c}{\tilde{u}}_q^A\\ {\tilde{u}}_q^B\end{array}\right)=\frac{1}{\sqrt{2}}\left(\begin{array}{c}{\text{e}}^{\text{i}qa{N}_A}\\ \mp {\text{e}}^{\text{i}{\varphi }_q}{\text{e}}^{\text{i}qa{N}_B}\end{array}\right).$$ (26)

For N_A = N_B this transformation may be viewed as a reciprocal-space gauge transformation. A direct calculation of the Zak phase for Eq. (26) shows that the winding number $N\equiv -{\varphi }_{\text{Zak}}/\pi$ is increased by N_A + N_B as compared to that for Eq. (21). This example shows that the absolute value of the winding number cannot be physically meaningful. Instead, physical consequences can involve only differences of winding numbers, which are well defined when computed within the same reciprocal-space basis choice. In Sec. II.D we describe how the winding number difference at a boundary between two regions influences the spectrum of states on the edge. However, note that we already found one physical consequence of the winding number difference: the parameter space of microscopic couplings becomes disconnected, in the sense that there is no way to continuously change the physical parameters to evolve between regions of different winding numbers without crossing a critical point at which the band gap closes. Such gap closings between topologically distinct regions have direct physical consequences in measurements of the bulk excitation spectrum. In particular, for a set of noninteracting fermions filling one such band, the gap closing implies a thermodynamic phase transition between two insulating regimes, separated by a semimetallic state. We illustrated this gap closing for the SSH model. However, this also holds for any 1D model in which $\mathit{h}=\left(h_x,h_y,0\right)$ i.e., with chiral symmetry. The requirement of the closing of a band gap in order to change the winding number is a defining feature of a topological invariant of the energy band.

2. The Chern number

A topological classification of (nondegenerate) energy bands in 2D exists without requiring any underlying symmetry and without ambiguities related to the choice of basis in reciprocal space. The topological invariant is the Chern number

$$\mathcal{C}=\frac{1}{2\pi }{\int }_{\text{BZ}}\text{i}{ϵ}_{ij}{\partial }_{q_i}\langle u_{\mathit{q}}|{\partial }_{q_j}|u_{\mathit{q}}\rangle {\text{d}}^{2}q.$$ (27)

We suppress the band index n, but note that a Chern number exists for each band. This topological invariant, and terminology, arises from the mathematics of fiber bundles (Stone and Goldbart, 2009). However, it can be readily interpreted more physically in terms of the Berry curvature (13) of the Bloch states

$$\mathrm{\Omega }(\mathit{q})\equiv {\mathbf{\nabla }}_{\mathit{q}}\times \mathit{A}(\mathit{q})\cdot {\mathit{e}}_z=\text{i}{ϵ}_{ij}{\partial }_{q_i}\langle u_{\mathit{q}}|{\partial }_{q_j}|u_{\mathit{q}}\rangle .$$ (28)

The Chern number is related to the flux of the Berry curvature Ω(q) through the BZ. Just as the Dirac quantization condition requires the magnetic flux through a closed surface to be quantized (in units of h/e), the flux of the Berry curvature through the BZ (a closed surface with the topology of a torus) is quantized (in units of 2π). This follows by using Stokes’s theorem to relate the integral of Ω(q) over the BZ to the line integral of A(q) around its boundary. Since the BZ is a closed surface this line integral must be an integer multiple of 2π. This integer C is the number of flux quanta of Berry curvature through the BZ. Since the Berry curvature is a gauge-invariant quantity, so too is the Chern number.

The Chern number vanishes for systems with time-reversal symmetry (TRS), for which $u_{\mathit{q}}(\mathit{r})\propto u_{-\mathit{q}}^{*}(\mathit{r})$ and hence $\mathrm{\Omega }(\mathit{q})=-\mathrm{\Omega }(-\mathit{q})$. The realization of Chern bands therefore requires a means to break TRS. In Sec. III we describe ways in which this can be achieved for cold atom systems. One class of implementation involves tight-binding models, in which a spinless particle hops on a lattice with complex tunneling matrix elements, e.g., to represent the Peierls phase factors for a charged particle in a magnetic field. TRS is broken if, for some closed loop on the lattice, the phases acquired on encircling the loop in the clockwise (+ϕ_AB) and anticlockwise (−ϕ_AB) directions differ modulo 2π, i.e., provided ϕ_AB is not an integer multiple of π. Another class of implementation exploits internal atomic states, labeled by index α. Quite generally, the nondissipative action of laser light on an atom is to couple state α to state ${\alpha }^{\prime }$ with a well-defined momentum transfer κ. An optical lattice is defined by a set of such couplings $V_{\mathit{\kappa }}^{{\alpha }^{\prime }\alpha }$, which to preserve periodicity must build up a regular lattice in momentum space. The couplings $V_{\mathit{\kappa }}^{{\alpha }^{\prime }\alpha }$ therefore define a tight-binding model in momentum space with amplitudes and phases determined by the laser fields. For shallow lattices, the net phase acquired on encircling a closed loop on this momentum-space lattice determines the integrated Berry curvature through that loop, allowing lattices with broken TRS $\mathrm{\Omega }(\mathit{q})\ne -\mathrm{\Omega }(-\mathit{q})$ to be directly constructed (Cooper and Moessner, 2012).

To illustrate how a nonzero Chern number arises in tight-binding models, we discuss here the key features of the Haldane model (Haldane, 1988). This is a two-band model, so the Bloch Hamiltonian is a 2 × 2 Hermitian matrix

$${\widehat{H}}_{\mathit{q}}=-\mathit{h}(\mathit{q})\cdot \widehat{\mathit{\sigma }}$$ (29)

with h(q) a three-component vector coupled to the Pauli matrices ${\widehat{\sigma }}_{x,y,z}$. Just as in the SSH model, the energy bands are $E_{\mathit{q}}^{(\pm )}=\pm |\mathit{h}(\mathit{q})|$ and there is a gap provided |h_q| does not vanish at any q. However, now the Bloch state of the lower band depends on the three-component unit vector $\mathit{e}(\mathit{q})\equiv \mathit{h}(\mathit{q})/|\mathit{h}(\mathit{q})|$, e.g.,

$$|u_{\mathit{q}}\rangle =\left(\begin{array}{l}\cos \left({\theta }_{\mathit{q}}/2\right)\\ \sin \left({\theta }_{\mathit{q}}/2\right){\text{e}}^{\text{i}{\varphi }_{\mathit{q}}}\end{array}\right)$$ (30)

for e(q) = $(\sin {\theta }_{\mathit{q}}\cos {\varphi }_{\mathit{q}},\sin {\theta }_{\mathit{q}}\sin {\varphi }_{\mathit{q}},\cos {\theta }_{\mathit{q}})$. The Chern number can be written in terms of this unit vector as

$$\mathcal{C}=N_{2\text{D}}\equiv -\frac{1}{8\pi }{ϵ}_{ij}{\int }_{\text{BZ}}\mathit{e}\cdot \frac{\partial \mathit{e}}{\partial q_i}\times \frac{\partial \mathit{e}}{\partial q_j}{\text{d}}^{2}q$$ (31)

N_2D counts the number of times that the unit vector e(q) wraps over the unit sphere as q spans the BZ; it is the 2D analog of the 1D winding number (23).

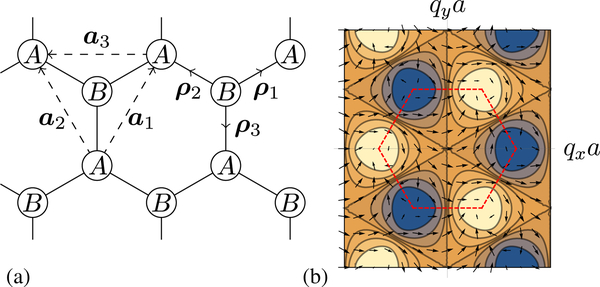
The Haldane model is described in detail in Sec. III. It is defined on a honeycomb lattice, for which the unit cell contains two sites, which we label A and B, as in Fig. 3(a). Nearest-neighbor tunneling is off diagonal in the sublattice index and leads to

$$h_x(\mathit{q})+\text{i}{h}_y(\mathit{q})=J({\text{e}}^{\text{i}\mathit{q}\cdot {\mathit{a}}_1}+{\text{e}}^{\text{i}\mathit{q}\cdot {\mathit{a}}_2}+1)$$ (32)

in Eq. (29), where a_1,2 are the lattice vectors marked on Fig. 3(a). The Hamiltonian has been chosen to be periodic under the addition of reciprocal lattice vectors. Note, however, that other choices can be made, related to the Hamiltonian via unitary transformations ${\widehat{H}}_{\mathit{q}}\to {\widehat{\mathcal{U}}}_{\mathit{q}}{\widehat{H}}_{\mathit{q}}{\widehat{\mathcal{U}}}_{\mathit{q}}^{†}$. Indeed, in Sec. III we replace

$$h_x(\mathit{q})+\text{i}{h}_y(\mathit{q})\to J({\text{e}}^{\text{i}\mathit{q}\cdot {\mathit{\rho }}_1}+{\text{e}}^{\text{i}\mathit{q}\cdot {\mathit{\rho }}_2}+{\text{e}}^{\text{i}\mathit{q}\cdot {\mathit{\rho }}_3})$$ (33)

which arises for ${\widehat{\mathcal{U}}}_q=\exp (-\text{i}{\widehat{\sigma }}_z\mathit{q}\cdot {\mathit{\rho }}_3/2)$, with ρ₃ the nearest-neighbor lattice vector in Fig. 3(a). This transformation does not change the energy spectrum nor the topology of the band. However, it can be more helpful to work with Eq. (33) when considering physical observables (Bena and Montambaux, 2009). As discussed in Appendix D, unitary transformations of the form ${\widehat{\mathcal{U}}}_q$ affect the definition of the force and current operators as well as the local Berry curvature.

FIG. 3.

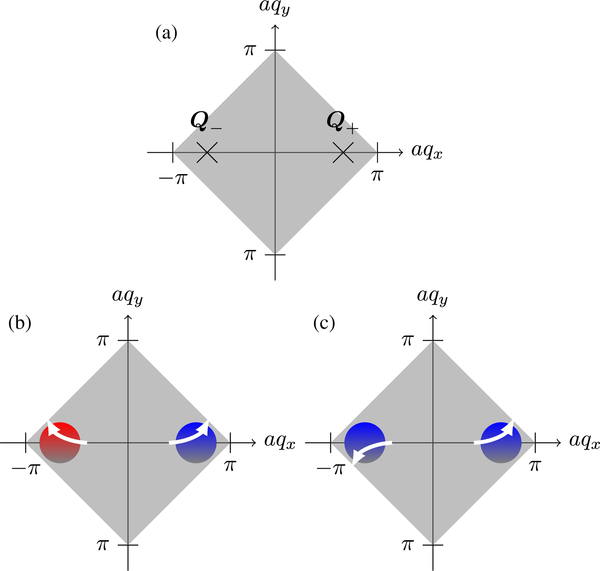
(a) Real-space honeycomb lattice for the Haldane model. (b) Illustration of the unit vector e(q) in the topological phase of the Haldane model. The dashed line shows the conventional BZ, whose corners are the points Q_±. The arrows show the projection of e(q) on the plane (e_x, e_y), while the colors and contours indicate e_z. The unit vector wraps once over the sphere within the BZ, indicating the topological character with $\mathcal{C}$ = 1.

The resulting band structure is well known from studies of graphene: there are two points at the corners of the BZ q = Q_± with

$${\mathit{Q}}_{\pm }=\pm \frac{4\pi }{3\sqrt{3}a}(1,0),$$

at which the bands touch, i.e., h_x + ih_y = 0. Close to either band-touching point, with $\tilde{\mathit{q}}$ ≡ q − Q_±, the Hamiltonian has the 2D Dirac form

$${\widehat{H}}_{\mathit{q}}^{\pm }\approx \hslash v\left[\pm {\tilde{q}}_x{\widehat{\sigma }}_x+{\tilde{q}}_y{\widehat{\sigma }}_y\right]+h_z^{\pm }{\widehat{\sigma }}_z$$ (34)

with velocity $v=(3/2)Ja/\hslash$. The terms $h_z^{\pm }$ arise from effects other than nearest-neighbor tunneling and open gaps at the Dirac points between the two bands. One such effect is an energy splitting Δ between A and B sublattices. In this case the coefficients $h_z^{+}$ and $h_z^{-}$ are both equal to Δ and the gap openings at the two Dirac points are equivalent. This causes the resulting Bloch bands to have vanishing Chern number, so the two resulting bands are nontopological. This is consistent with the fact that this model has TRS. Introducing next-nearest-neighbor hopping with the Aharonov-Bohm phase ${\varphi }_{\text{AB}}\ne 0$ mod π breaks TRS and provides a term with $h_z^{+}=-h_z^{-}$ for which the Chern numbers of the bands are 1 and −1. Figure 3 shows how e(q) varies in reciprocal space in this topological phase.

The preceding discussions are somewhat abstract, focusing on mathematical aspects of the energy bands in 2D. However, the Chern number has direct physical consequences. As first shown by Thouless et al. (1982), a band insulator exhibits the integer quantum Hall effect if the total Chern number of the filled bands is nonzero, with a Hall conductivity quantized at $\mathcal{C}$ times the fundamental unit of conductance e²/h. This result can be extended to systems subjected to disorder and interparticle interactions by defining a Chern number for the many-body ground state in a geometry with periodic boundary conditions (Niu, Thouless, and Wu, 1985). For noninteracting systems without translational invariance, a local Chern marker can be defined (Bianco and Resta, 2011). The quantization of the Hall conductance is intimately related to the existence of edge states, which we now discuss.

D. Edge states

Topological band insulators have the generic feature that although they are bulk insulators—owing to the energy gap between the filled and empty bands—they host gapless states on their surfaces.

The existence of gapless edge modes for 2D systems with nonzero Chern number is well known from studies of the integer quantum Hall effect (Halperin, 1982). Each filled Landau level gives rise to a chiral edge mode. This can be understood semiclassically in terms of the skipping orbit of the cyclotron motion around the edge of the sample; see Fig. 4. These semiclassical skipping orbits consist of two features. The rapid skipping motion at the cyclotron frequency is a feature which in a quantum description arises when the wave function has nonzero amplitude in more than one Landau level, such that its time dependence involves the Landau level energy spacing (cyclotron energy); it is therefore related to the inter-Landau level excitation known as a “magnetoplasmon.” The drift of the guiding center of the orbit around the perimeter of the sample is a feature that exists for quantum states within a single Landau level and that represents the chiral edge mode of that Landau level. The existence of these edge modes is required for consistency of the quantized bulk Hall conductance (Laughlin, 1981).

FIG. 4.

Skipping orbits for a charged particle in a uniform magnetic field. In the bulk, the semiclassical dynamics of a wave packet leads to a circular cyclotron orbit. The reflection of such an orbit from the (hard wall) edge leads to a skipping motion around the sample edge.

More generally, gapless edge states occur at the boundary between two insulating regions with different values of a topological invariant. A simple semiclassical view of these gapless regions is provided by considering the boundary to arise from a smooth spatial variation in the parameters of the Hamiltonian, between two phases with different topological indices. Since the two insulators far to the left and far to the right of the boundary are topologically distinct, at some point in space the gap between the filled and empty bands must close. This gap closing motivates the existence of gapless edge states. While this semiclassical argument applies only for smooth variations in space, the result is a robust feature for any form of boundary, referred to as the bulk-boundary correspondence (Hasan and Kane, 2010). The only restriction is that, in cases where the topological invariant relies on an underlying symmetry, this symmetry must be preserved also in the boundary region. This is illustrated later for the edge state of the SSH model.

We demonstrate the emergence of edge states in the SSH and Haldane models within continuum approximations for which the edge state wave functions take simple analytic forms.

1. SSH model

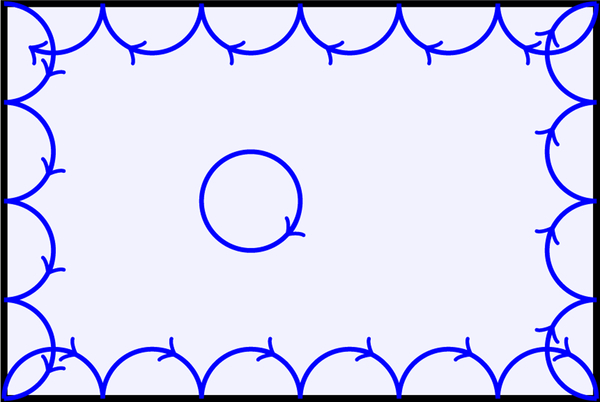
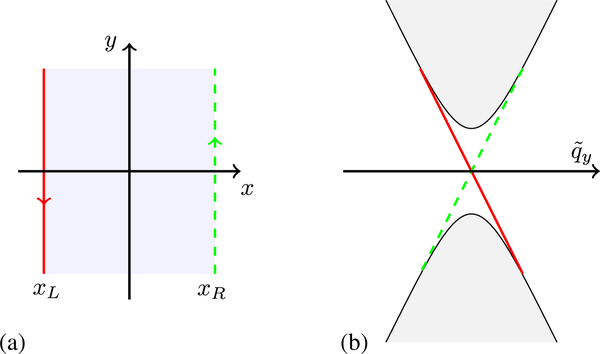
Consider a 1D band insulator formed by filling the lower energy band of a Hamiltonian of the form (18), which is purely nondiagonal in the sublattice basis and parametrized by the two-component vector (h_x, h_y). This restriction on the form of the Hamiltonian arises from the chiral symmetry of the model as discussed further in Sec. II.E. Let the properties of the system depend on some quantity M such that $h_x+\text{i}{h}_y\equiv |h(q,M)|{\text{e}}^{\text{i}\varphi (q,M)}$ is a function of both wave vector q and M. We introduce a boundary between two gapped phases at position x = 0 by allowing M(x) to vary slowly in space, as compared to the lattice constant α and setting $M(x\ll 0)=M_{-}$ and $M(x\gg 0)=M_{+}$. The two phases are characterized by winding numbers N_± (23) computed from ϕ(q, M_±). It is straightforward to show that $h_x+\text{i}{h}_y$ must have N₋ − N₊ vortices within the boundary region; see Fig. 5. So if $N_{+}\ne N_{-}$ then |h(q, M)| must vanish at certain points (q, M): these are the gap-closing points, discussed semiclassically, which lead to gapless edge states.

FIG. 5.

An edge of the SSH model is represented by $h_x+\text{i}{h}_y=|h_{q,M}|{\text{e}}^{\text{i}\varphi (q,M)},$ which depends both on the wave vector q and on some control parameter M that varies smoothly between $M_{-}\text{at}x\ll 0\text{and}{M}_{+}\text{at}x\gg 0.$ The number of vortices of h_x + ih_y within this region can be computed by integrating $\mathbf{\nabla }\varphi (q,M)$ around the boundary. The integrals along $q=\pm \pi /a$ cancel (since the BZ is periodic), leaving only the integrals along M = M_±, which give the difference of winding numbers $N_{-}-N_{\text{+}}.$

For the SSH model, $h_x+\text{i}{h}_y=J^{\prime }+J{\text{e}}^{\text{i}qa}$, the gap-closing point $(J^{\prime }/J=1,qa=\pi )$ hosts a single vortex. Defining $M=1-J^{\prime }/J$ and $\tilde{q}=q-\pi /a$, we expand the Hamiltonian around $M=\tilde{q}=0$ to first order in $\tilde{q}$ (suitable for the continuum limit, $|\tilde{q}|\ll 1/a$) to give

$${\widehat{H}}^{\text{SSH}}/J\approx \tilde{q}a{\widehat{\sigma }}_y+M(x){\widehat{\sigma }}_x$$ (35)

$$=-\text{i}a{\widehat{\sigma }}_y{\partial }_x+M(x){\widehat{\sigma }}_x.$$ (36)

In the last line we replaced $\tilde{q}$ by $-\text{i}{\partial }_x$ to give a 1D Dirac Hamiltonian in which M(x) can be viewed as a spatially varying “mass.” This was a model studied by Jackiw and Rebbi (1976), who showed that, provided M(x) changes sign, there is a solution that is localized at the boundary with exactly zero energy. For $M_{+}>0$ and $M_{-}<0$, this is

$$|\mathrm{\Psi }\rangle =\left(\begin{array}{c}{\text{e}}^{-{\int }_0^{x}M\left(x^{\prime }\right)\text{d}{x}^{\prime }/a}{\text{e}}^{\text{i}\pi x/a}\\ 0\end{array}\right).$$ (37)

That the state is an eigenstate of ${\widehat{\sigma }}_z$ with $|{\sigma }_z=+1\rangle$ indicates that it has nonzero amplitude only on the A sublattice. $M_{+}<0$ and $M_{-}>0$ the nonzero amplitude would be on the B sublattice. This is the gapless edge mode of the SSH model which arises because M_± describe different topological phases. That the state has energy E = 0 is a consequence of a chiral symmetry that protects the relevant 1D topological invariant, as discussed in Sec. II.E. If the Hamiltonian were to depart from this chiral form, for example, by including terms h_z that couple to ${\widehat{\sigma }}_z$, the energy of this subgap state would depart from E = 0. This could occur either by a change of the bulk Hamiltonian or due to breaking of the symmetry near the edge: for example, arising from an on-site potential that shifts the energy of the A site relative to the B site near the edge.

Although we derived this edge state for a continuum model, the properties are robust to lattice effects provided the chiral symmetry is preserved. A derivation of the edge state of the SSH model for a sharp boundary is provided in Appendix A.1.

2. Haldane model

one can use this solution for the edge state of the SSH model to construct a 1D band of edge states on a surface of the topological band insulator formed from the Haldane model. Consider the low-energy theory for the Haldane model (34) in a topological phase with $h_z^{\pm }=\mp |H|$. We impose a boundary to a nontopological phase at x > x_R by adding a spatially dependent energy offset $\mathrm{\Delta }(x){\widehat{\sigma }}_z$, such that $h_z^{\pm }(x)=\mathrm{\Delta }(x)\mp |H|$. The low-energy Hamiltonians close to Q_± become

$${\widehat{H}}_{\mathit{q}}^{\pm }\approx \mp \text{i}\hslash v{\widehat{\sigma }}_x{\partial }_x+h_z^{\pm }(x){\widehat{\sigma }}_z+\hslash v{\tilde{q}}_y{\widehat{\sigma }}_y$$ (38)

where we replaced ${\tilde{q}}_x\to -\text{i}{\partial }_x$. Translational invariance is maintained along the y direction, such that q_y (and therefore ${\tilde{q}}_y=q_y-Q_y^{\pm }$) is conserved.

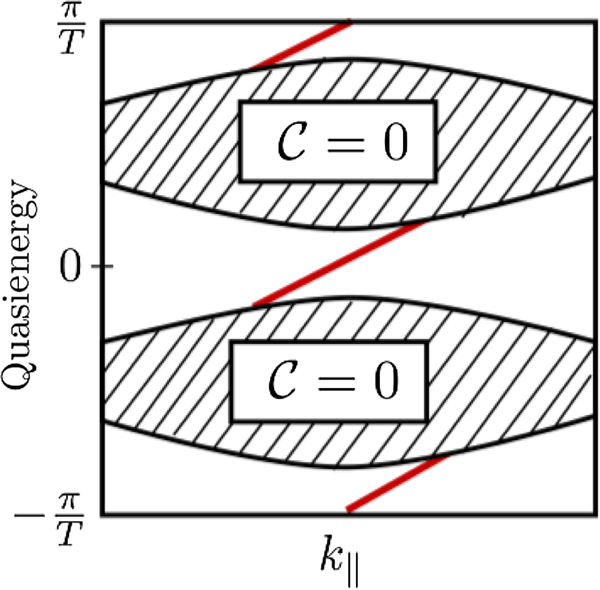
For Δ(x) an increasing function of x at x > 0 there is a boundary between topological (x < x_R) and nontopological (x > x_R) regions where $\mathrm{\Delta }(x_R)=|H|$. At this point, $h_z^{+}(x_R)=0$ so the gap at Q⁺ vanishes. The low-energy Hamiltonian close to Q⁺ (38) takes the form of the Jackiw-Rebbi Hamiltonian (36), just under a permutation of the Pauli matrices $\left[\left({\widehat{\sigma }}_x,{\widehat{\sigma }}_y,{\widehat{\sigma }}_z\right)\to \left({\widehat{\sigma }}_y,{\widehat{\sigma }}_z,{\widehat{\sigma }}_x\right)\right]$, plus a term $\hslash v{\tilde{q}}_y{\widehat{\sigma }}_y$ for which the zero mode (37) is also an eigenstate (noting the permutation of the Pauli matrices), with eigenvalue $E_{q_y}^R=\hslash v{\tilde{q}}_x$. This is the chiral edge mode, which propagates along the right-hand boundary x_R at velocity ve_y. For a finite-width strip, with another boundary to a nontopological phase at x < x_L, there is an edge mode with the opposite velocity $E_{q_y}^L=-\hslash v{\tilde{q}}_y$. The dispersion is illustrated in Fig. 6.

FIG. 6.

The low-energy spectrum of the Haldane model on a finite-width strip. (a) The strip is bounded in the x direction, but uniform along y such that the wave vector ${\tilde{q}}_y=q_y-Q_y^{+}$ is conserved. (b) The spectrum has a continuum of states in the bulk, shown shaded. The bulk bands are topological, with unit Chern number, so a single edge state connects between these bulk bands: the red solid line (green dashed line) shows the band corresponding to the edge mode on the left (right) boundary. We show only the part of the spectrum close to the Q⁺ point, at which the boundaries force a gap closing and at which the edge states appear.

E. Topological insulators

1. Discrete symmetries

The Chern number for 2D systems is an example of a topological invariant for energy bands in a setting where no symmetries constrain the form of the Hamiltonian. The field of topological insulators arose from the realization that, when one constrains the Hamiltonian to have additional symmetries, new topological invariants emerge in various spatial dimensions. The general theory of symmetry-protected topological invariants for gapped fermionic systems concerns global symmetries—time-reversal, particle-hole symmetry, chiral symmetry—which make no reference to spatial structure or dimension (Altland and Zirnbauer, 1997). These define ten distinct symmetry classes which, combined with the spatial dimensionality, determine the possible topological invariants (Chiu et al., 2016). An important example is time-reversal symmetry which leads to the existence of a ${\mathrm{\mathbb{Z}}}_2$ topological invariant in 2D and 3D for electronic systems with spin-orbit coupling. This led to the discovery of materials which behave as topological insulators in these dimensions (Hasan and Kane, 2010; Qi and Zhang, 2011). Furthermore, this formalism also allows a unified description of topological superfluids, formed from the pairing of fermions. Within the Bardeen-Cooper-Schrieffer (BCS) mean-field theory, the spectrum of quasiparticle excitations of such superfluids is obtained from the Bogoliubov–de Gennes (BdG) theory, which takes the form of a noninteracting fermionic system albeit with anomalous terms that mix particle and hole excitations. The intrinsic particle-hole symmetry of the BdG theory stabilizes gapped topological superfluids. We discuss such topological superfluids in Sec. V.B.2.

Here we explore the physics of symmetry-protected topological band insulators in the context of the SSH model previously described. This provides an example of a topological band insulator that arises in 1D when there is an underlying chiral symmetry. This chiral symmetry arises from the existence of a unitary operator $\widehat{U}$ that anticommutes with the Hamiltonian $\widehat{H}$

$$\widehat{H}\widehat{U}=-\widehat{U}\widehat{H}$$ (39)

Then for an energy eigenstate $|\mathbf{\Psi }\rangle$ of eigenvalue E, the state $\widehat{U}|\mathbf{\Psi }\rangle$ is readily shown to be an energy eigenstate with energy −E. Thus, the chiral symmetry enforces a symmetry on the spectrum about E = 0. This rather formal construction arises in tight-binding models, such as the SSH model, in which the Hamiltonian involves only terms that hop between two different sublattices (labeled A and B). Defining ${\widehat{P}}_{A/B}$ as projectors onto the A/B sublattices, then $\widehat{U}\equiv ({\widehat{P}}_A-{\widehat{P}}_B)$ satisfies Eq. (39) if ${\widehat{P}}_A\widehat{H}{\widehat{P}}_A={\widehat{P}}_B\widehat{H}{\widehat{P}}_B=0$ i.e., provided the Hamiltonian $\widehat{H}$ couples only A and B sublattices. The chiral symmetry constrains the Hamiltonian for the SSH model (18) to be off diagonal in the sublattice basis. As described in Sec. II.C.1 this form ensures that the winding number is a topological invariant. Furthermore, the symmetry of the energy spectrum ensures that the edge mode, found in Sec. II.D.1, is at exactly zero energy E = 0 and is also an eigenstate of $\widehat{U}={\widehat{P}}_A-{\widehat{P}}_B$. This implies that there is at least one zero energy in-gap mode, but other nonzero energy in-gap modes are allowed by chiral symmetry provided they come in ±E pairs. For boundaries that break the chiral symmetry, the in-gap states will have no particular relation to zero energy. A disordered potential that acts differently on the two sublattice sites will break chiral symmetry and also shift the energies of in-gap states away from zero energy. However, if the disorder is such that Eq. (39) is preserved, the topology of this model is robust and the in-gap states remain at zero energy.

2. The Rice-Mele model

Since the topological invariant of the SSH model is ensured by a (chiral) symmetry, it is possible to smoothly evolve between states with different topological invariants by breaking this symmetry. To illustrate this, we study the Rice-Mele model which generalizes the SSH model by relaxing the assumption that the A and B sites have the same energy and assigning energy offsets ±Δ. The Hamiltonian (17) is replaced by

$${\widehat{H}}_q^{\text{RM}}=\left(\begin{array}{cc}\mathrm{\Delta }& -J^{\prime }-J{\text{e}}^{-\text{i}qa}\\ -J^{\prime }-J{\text{e}}^{\text{i}qa}& -\mathrm{\Delta }\end{array}\right)$$ (40)

within the $\text{BZ}-\pi /a<q\le \pi /a$. The two bands have energies

$$E_q^{(\pm )}=\pm {[{\mathrm{\Delta }}^2+{|J^{\prime }+J{\text{e}}^{-\text{i}qa}|}^2]}^{1/2},$$ (41)

and so are separated by a gap provided Δ ≠ 0. (For Δ = 0 the gap closes at the topological transition of the SSH model $J^{\prime }/J=1$.) The eigenstate of the lower band can be written as

$$|u_q^{(-)}\rangle =\left(\begin{array}{c}\sin \left({\gamma }_q/2\right)\\ -{\text{e}}^{\text{i}{\varphi }_q}\cos \left({\gamma }_q/2\right)\end{array}\right)$$ (42)

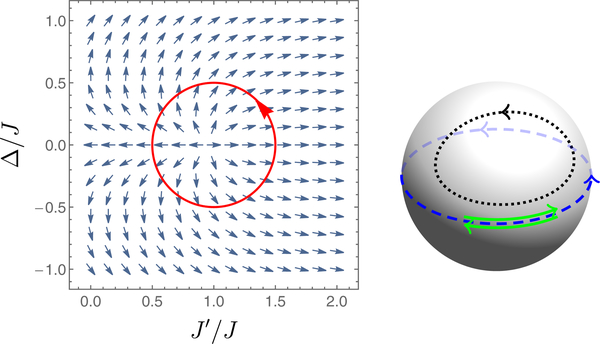
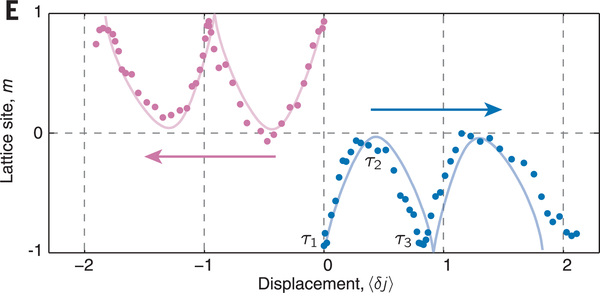
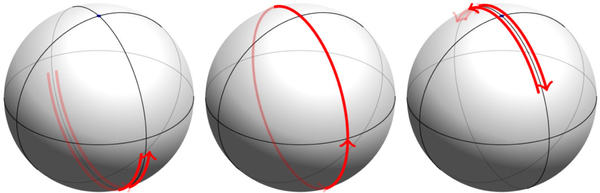
with γ_q and ϕ_q defined by $-\left(J^{\prime }+J{\text{e}}^{-\text{i}qa}\right)/\mathrm{\Delta }\equiv \tan {\gamma }_q{\text{e}}^{-\text{i}{\varphi }_q}$. The resulting Zak phase (14) is shown in Fig. 7 (left) as a function of $J^{\prime }/J$ and $\mathrm{\Delta }/J$. Along the line Δ = 0 the Zak phase steps by π across $J^{\prime }/J=1$, consistent with the change in winding number by one at the topological transition of the SSH model, and Eq. (23). However, note that the gapped band insulators at $\mathrm{\Delta }=0,J^{\prime }/J>1$ and $\mathrm{\Delta }=0,J^{\prime }/J<1$ can now be continuously connected by tracing out a path that has $\mathrm{\Delta }\ne 0$ when $J^{\prime }/J=1$ (Fig. 7, right).

FIG. 7.

Left: Zak phase of the lower band of the Rice-Mele model, represented by the unit vector $\left(\cos {\varphi }_{\text{Zak}},\sin {\varphi }_{\text{Zak}}\right).$ The phase changes by 2π around the point $\mathrm{\Delta }=0\text{and}{J}^{\prime }/J=1$ at which the gap closes. The loop denotes a possible pumping cycle. Right: Representation of the eigenstates (42) on the Bloch sphere. Blue dashed line: Closed trajectory on the equator for the SSH model in the topological case $\left(\mathrm{\Delta }=0,J^{\prime }/J<1\right),$ obtained when q scans the Brillouin zone. The Zak phase, given by half the subtended solid angle, is equal to π. Green solid line: Trajectory in the nontopological case of the SSH model $\left(\mathrm{\Delta }=0,J^{\prime }/J>1\right)$ with a zero subtended solid angle. Black dotted line: Closed trajectory obtained for the Rice-Mele model with a nonzero energy offset Δ. A continuous variation of Δ and $J^{\prime }/J$ in the Rice-Mele model allows one to connect the topological and nontopological SSH trajectories, without going through the singular point $J^{\prime }/J=1,\mathrm{\Delta }=0.$

F. Adiabatic pumping

Consider again the Rice-Mele model, whose Zak phase is illustrated in Fig. 7. There is a vortex in ϕ_Zak around the gap-closing point (Δ = 0 and $J^{\prime }/J=1$) at which the Zak phase is undefined. The winding of ϕ_Zak by 2π around a closed loop encircling the gapless point, such as the loop shown in Fig. 7, is a topological invariant of the model: this winding is preserved under smooth variations of the Rice-Mele Hamiltonian that do not cause the gap to close on this loop.

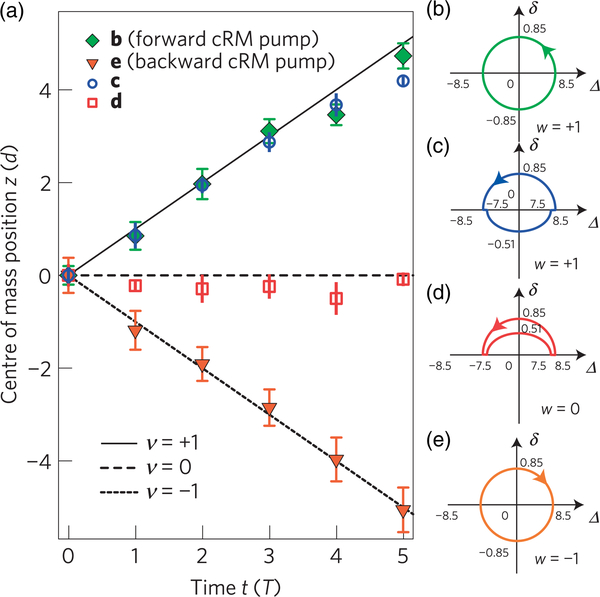
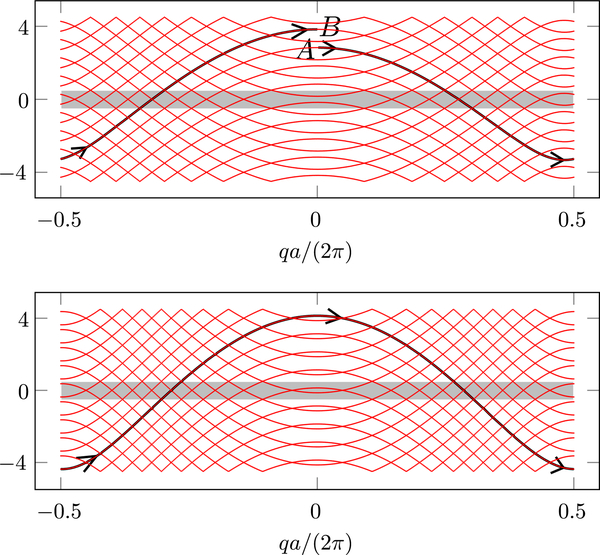
The existence of this invariant is at the basis of the concept of a quantized pump (Thouless, 1983). It describes the generic situation of a crystal with filled bands, which is characterized by parameters that can be externally controlled. When these parameters are varied around a closed loop, the number of particles that are transported is quantized. It is thus a robust quantity that is not affected by a small change of the geometry of the loop in parameter space. Note that at this stage no intuition has been provided on the mechanism at the basis of the transport, nor its direction. For a physical discussion see Sec. IV.C.1, in particular, Fig. 22.

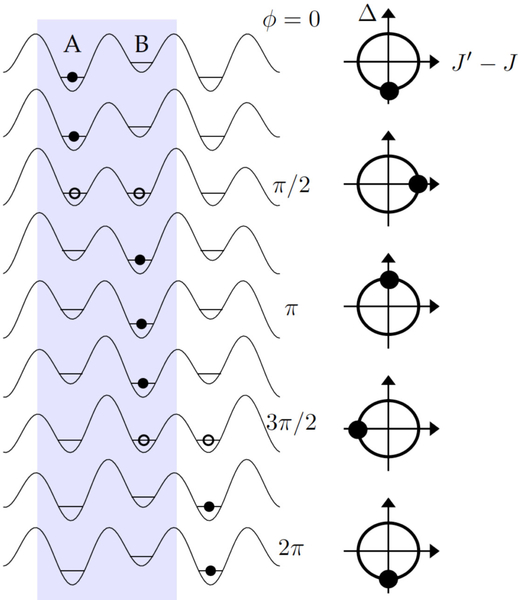
FIG. 22.

Topological pumping with a 1D superlattice described by the potential (50). Left: The phase ϕ of the long lattice [see Eq. (50)] is varied from 0 to 2π from top to bottom. Initially the phase ϕ = 0 and the particle is supposed to be localized on the site A_j of a given lattice cell j. In the limiting case where the energy difference between A and B sites is large compared to the tunnel matrix elements, this state would be stationary if ϕ was kept at the value 0. When ϕ is increased up to π/2, the sites A_j and B_j have the same energy and the particle is adiabatically transferred to B_j. Note that we neglect here the tunneling of the particle from A_j to B_j−1, assuming that it is inhibited by the large barrier between these two sites. The particle then remains in B_j until the phase reaches the value 3π/2, when the particle again undergoes an adiabatic transfer, now from B_j to A_j+1. (Here again we neglect tunneling across the large barrier now present between B_j and A_j.) When the phase ϕ = 2π the potential is back to its initial value and the particle has moved by one lattice site. Note that a motion in the opposite direction occurs if the particle starts for the site B_j when ϕ = 0. Right: In the two-band approximation corresponding to the Rice-Mele model, the system performs a closed loop around the origin in the parameter space (J′ − J, Δ).

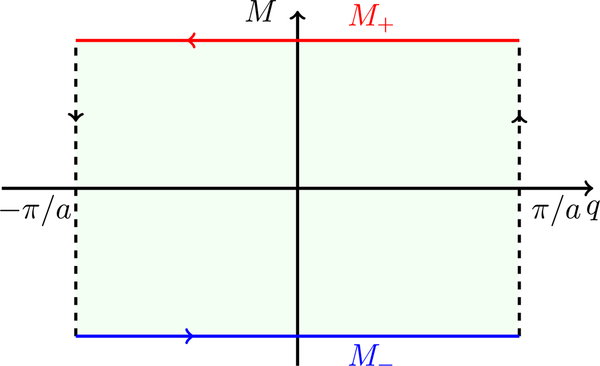
This quantization has the same topological origin as the integer quantum Hall effect. To see this, consider tracing out the closed loop in parameter space as time t varies from t = 0 to t = T. The Zak phase at any given time t is defined by the integral of the Berry connection along the $\text{BZ}-\pi /a<q\le \pi /a$ at that instant. The change in Zak phase between any two times t₁ and t₂ can be written as a line integral

$${\varphi }_{\text{Zak}}\left(t_1\right)-{\varphi }_{\text{Zak}}\left(t_2\right)\equiv {\oint }_{\mathcal{L}}\mathit{A}\cdot \text{d}\mathit{q}$$ (43)

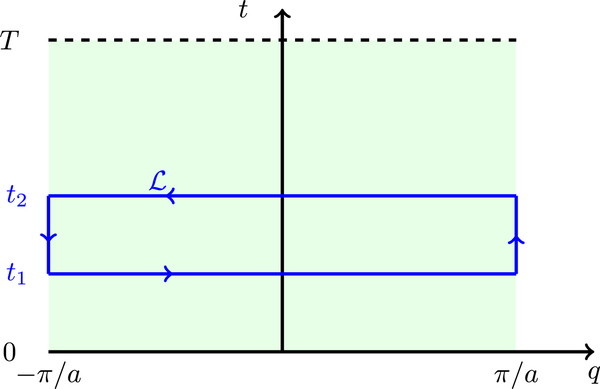
where we label the position in the q–t plane by a two-component vector q = (q₁, q₂) = (q, t) and the associated Berry connection $A_i\equiv \text{i}\langle u_{\mathit{q}}|{\partial }_i|u_{\mathit{q}}\rangle$, with ${\partial }_1\equiv \partial /\partial q$ and ${\partial }_2\equiv \partial /\partial t$. The integration contour $\mathcal{L}$ is shown in Fig. 8. The horizontal lines at fixed t = t₁ and t = t₂ recover ${\varphi }_{\text{Zak}}\left(t_1\right)-{\varphi }_{\text{Zak}}\left(t_2\right)$, while the integrals on the lines at q = ±π/a cancel as a result of the periodicity of the BZ. Applying Stokes’s theorem, the line integral in Eq. (43) can be written as the integral of the Berry curvature $\mathrm{\Omega }={ϵ}_{ij}{\partial }_i{A}_j$ over the area bounded by $\mathcal{L}$. The fact that the parameters of the Hamiltonian return to their original values as t = 0 → T enforces periodicity also in t, such that the q−t plane has the topology of a torus. Thus, extending the contour to enclose the full region from t = 0 to t = T, thereby computing ${\varphi }_{\text{Zak}}(0)-{\varphi }_{\text{Zak}}(T)$, recovers 2π times a Chern number. The relevant integral is entirely analogous to Eq. (27) with the measure d²q replaced by dqdt.

FIG. 8.

The relationship of the change in the Zak phase for a 1D band insulator, with momentum $-\pi /a<q\le \pi /a,$ under adiabatic variation of parameters in time around a cycle of period T, i.e., with time 0 < t ≤ T. The change in Zak phase between times t₁ and t₂ is represented by the line integral around a contour $\mathcal{L}.$ When $\mathcal{L}$ is extended to include the full q–t plane, the periodicity in $q\to q+2\pi /a\text{and}t\to t+T$ ensures that the line integral must by an integer multiple of 2π. This integer is the Chern number defined in the q–t plane.

The link between the winding of ϕ_Zak and the transported particle number for a filled band can be established using arguments detailed in Appendix A.4. The transported particle number is determined by computing the change in the mean particle position Δx over one cycle of the pump, averaged over all states in the band. The result is that this net displacement of particles over one cycle, for example, the closed loop in Fig. 7, is

$$\mathrm{\Delta }x=\frac{a}{2\pi }\left[{\varphi }_{\text{Zak}}(T)-{\varphi }_{\text{Zak}}(0)\right].$$ (44)

Because ϕ_Zak(T) equals ϕ_Zak(0) plus 2π times the winding number corresponding to the vortex of Fig. 7, the displacement is quantized in units of the lattice period α. When the band is filled with exactly one particle per state, this entails the quantization of the number of transported particles.

III. IMPLEMENTATIONS OF TOPOLOGICAL LATTICES

To this point in this review, we have developed our understanding of lattices and discussed how topology presents additional “labels” tied to individual Bloch bands: providing a new way to categorize band structure. This section takes the next step and describes the currently implemented techniques by which 1D and 2D band structures with nontrivial topology have been created.

A. Iconic models

Cold atom experiments are often able to nearly perfectly realize iconic topological models from condensed matter theory. Here we briefly describe two such models—the Harper-Hofstadter model (Harper, 1955; Hofstadter, 1976) and the Haldane model (Haldane, 1988)—as particularly simple examples of topological lattices and explore what is essential about each of these models. This allows us to place experimental approaches in context and to identify what types of new terms must be added to standard optical lattices.

1. Harper-Hofstadter model

The Harper-Hofstadter model, describing charged particles in a square lattice with a uniform of magnetic field, derives from the simple 2D tight-binding Hamiltonian

$$\widehat{H}=-J\sum _{j,m}({\widehat{a}}_{j+1,m}^{†}{\widehat{a}}_{j,m}+{\widehat{a}}_{j,m+1}^{†}{\widehat{a}}_{j,m}+\text{H}.\text{c}.)$$ (45)

for particles hopping in a square lattice with tunneling strength J. Each individual site of this lattice is labeled a pair of integers j and m. The first term in Eq. (45) denotes tunneling along the j direction (horizontal) and the second term marks tunneling along the m direction (vertical). This model results in a single, nontopological, cosinusoidal band with full width 8J.

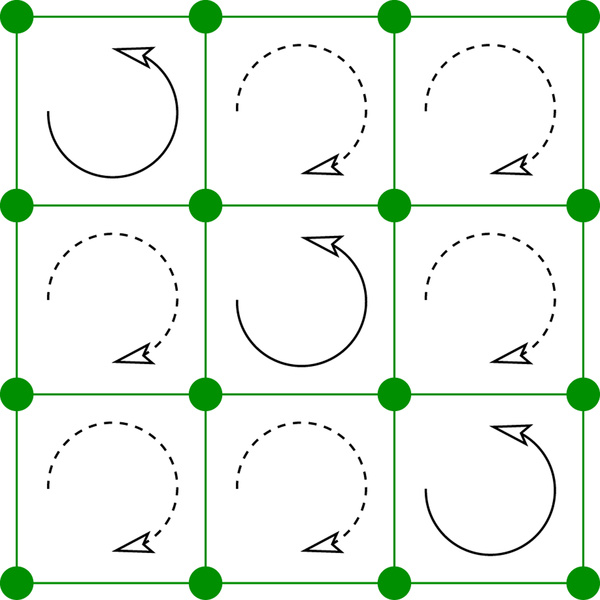
As shown in Fig. 9(a), our task is to imbue the tunneling matrix elements with nonzero Peierls phase factors so that the phase accrued by a particle encircling a single plaquette is ϕ_AB, equivalent to the Aharonov-Bohm phase ${\varphi }_{\text{AB}}=qBA/\hslash$ acquired by a particle with charge q moved around a plaquette of area A. The resulting complex tunneling matrix elements are required to break time-reversal symmetry and allow a nonzero Chern number. As can be confirmed by the phases depicted in Fig. 9(a), the associated Harper-Hofstadter Hamiltonian expressed in the Landau gauge

$$\widehat{H}=-J\sum _{j,m}({\text{e}}^{\text{i}m{\varphi }_{\text{AB}}}{\widehat{a}}_{j+1,m}^{†}{\widehat{a}}_{j,m}+{\widehat{a}}_{j,m+1}^{†}{\widehat{a}}_{j,m}+\text{H}.\text{c}.),$$ (46)

gives a phase ϕ_AB for tunneling around each plaquette. For rational ϕ_AB/2π = p/q, expressed in reduced form, the single band of Eq. (45) fragments into q (generally) topological bands, with zero aggregate Chern number.

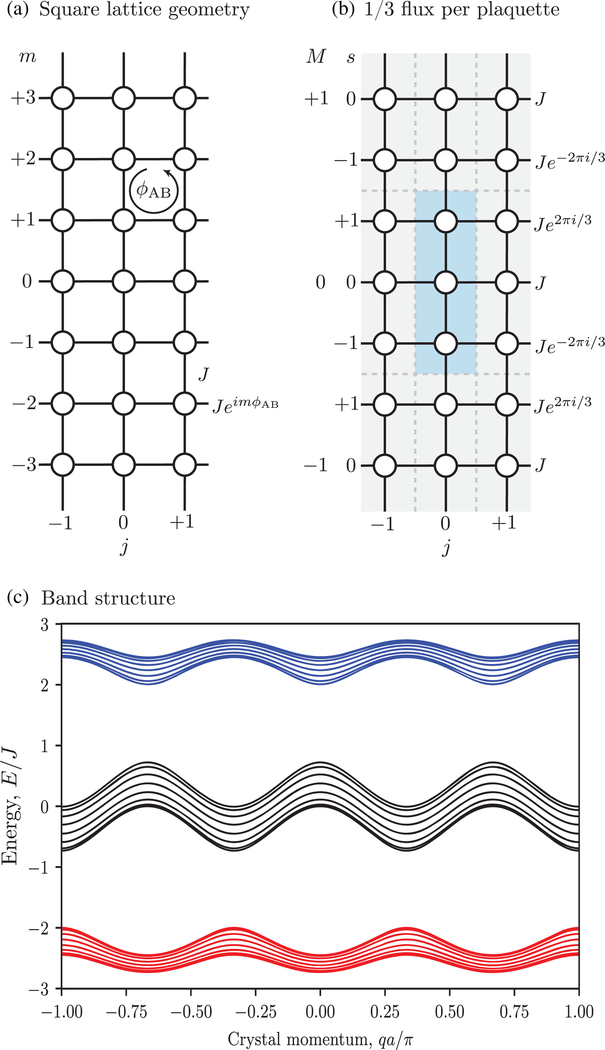
FIG. 9.

The Harper-Hofstadter model. (a) Harper-Hofstadter lattice geometry with symmetric hopping J and a flux ϕ_AB in each plaquette. (b) Harper-Hofstadter lattice geometry with flux ${\varphi }_{\text{AB}}=2\pi /3$ per plaquette. The individual magnetic unit cells are delineated by gray dashed lines with a representative magnetic unit cell set off in blue (dark shading) for clarity. (c) Computed band structure with ${\varphi }_{\text{AB}}=2\pi /3$ showing the three topological bands with Chern numbers +1, −2, and +1 built from the three inequivalent sites within the magnetic unit cell.

We can focus in on the essential features of this model by considering the special case of one-third flux per unit cell, i.e., ${\varphi }_{\text{AB}}=2\pi /3$. First take note of the tunneling phase $e^{im{\varphi }_{AB}}$ for motion along j: As shown in Fig. 9(a), this tunneling phase depends on m and has a spatial period of three lattice sites, implying that the lattice’s unit cell is enlarged beyond the plaquettes of the underlying square lattice (the unit cells without magnetic flux) to three plaquettes at ${\varphi }_{\text{AB}}=2\pi /3$. In Fig. 9(b), these unit cells are graphically indicated by the gray dashed lines, with a representative unit cell shaded (light blue) for clarity. Each of these unit cells is identified by integers j and M. In order to distinguish between the three inequivalent sublattice sites within each unit cell, we introduce also the site index $s=-1,0,+1$, related to the individual plaquette index m via m = 3M + s.

As a result of this expanded unit cell, the associated Brillouin zone is reduced to 1/3 of its initial size along the m direction, and the number of bands correspondingly increases from 1 to 3. Following textbook techniques, we express this Hamiltonian in the Fourier representation, i.e., giving states labeled by their crystal momentum $\mathit{q}=(q_j,q_m)$ along with the sublattice index s, i.e., for ϕ_AB = 2π/3 the states are $\{|\mathit{q},-1\rangle ,|\mathit{q},0\rangle ,|\mathit{q},+1\rangle \}$. For each crystal momentum q the Hamiltonian matrix coupling these sublattice sites together is

$$H_{\mathit{q}}=-J\left(\begin{array}{ccc}2\cos \left(q_{j}a-2\pi /3\right)& 1& \exp \left[\text{i}{q}_m\left(3a_s\right)\right]\\ 1& 2\cos \left(q_{j}a\right)& 1\\ \exp \left[-\text{i}{q}_m\left(3a_s\right)\right]& 1& 2\cos \left(q_{j}a+2\pi /3\right)\end{array}\right),$$ (47)

where a and a_s denote the nearest-neighbor lattice spacings in the directions of increasing j and m, respectively. (Even if m denotes a “synthetic dimension” the notion of length a_s remains a useful bookkeeping device, by which 3a_s is the side of the expanded unit cell.) The three eigenvalues of this matrix define three separate bands. Figure 9(c) shows the resulting band structure, where each of the three bands is endowed with a nonzero Chern number. The expansion of the unit cell to contain three sublattice sites is essential for the formation of topological bands. Recall that Chern numbers are derived from the integrated Berry curvature over the Brillouin zone. For a tight-binding model, the Berry curvature can only be nonzero when each Bloch wave function has a spin or pseudospin degree of freedom, here provided by the sublattice degree of freedom.

In Sec. III.D we describe how to experimentally imprint these hopping phases using tailored laser fields and will comment on the limitations of different experimental approaches.

2. Haldane model

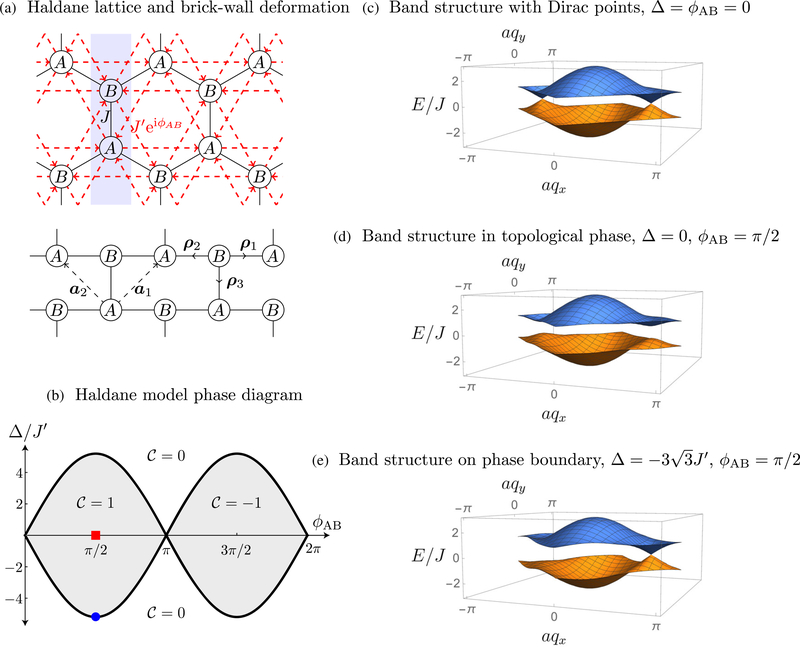
The Haldane model (Haldane, 1988), an extension of the well-known honeycomb lattice, was an early model of topological band structure but without the presence of an overall magnetic field which requires the expansion of the unit cell size. Figure 10(a) plots the Haldane lattice in the conventional honeycomb geometry. We also show its deformation to a “brick-wall” geometry most relevant for its experimental realization with cold atoms. The tunneling matrix elements (black solid lines) with strength J define the underlying honeycomb lattice, along the three nearest-neighbor bonds. As indicated, even the simple honeycomb lattice describes a dimerized lattice with $|A\rangle$ and $|B\rangle$ sublattice sites (possibly offset in energy by ±Δ), making it an ideal starting point for realizing topological band structures. Figure 10(b) shows the resulting two bands kissing at a pair of Dirac points. Haldane’s addition of next-nearest-neighbor tunneling with strength J′ and phase ϕ_AB [pink dashed lines in Fig. 10(a), along bonds connecting sites of the same sublattice] renders this model topological.

FIG. 10.

Haldane model. (a) Haldane lattice geometry showing overall honeycomb lattice structure with the addition of next-nearest-neighbor hopping with Aharonov-Bohm tunneling phases ϕ_AB. The shaded (blue) box marks the two sites comprising a single unit cell. We also show the deformation of the underlying lattice to the brick-wall geometry, used to plot the dispersions with q_xa = q · a₁ and q_ya = q · a₂. (b) Haldane model phase diagram showing the two topological lobes immersed in a nontopological background. (c) Band structure computed with only nearest-neighbor tunneling [black solid lines in (a), showing the familiar pair of Dirac points from this “brick-wall” lattice. (d) Band structure computed in the topological phase at the marked red square in (b), with ϕ_AB = π/2 and “tilt” $\mathrm{\Delta }=0,J^{\prime }=J/10$. (e) Band structure at the topological transition, marked by the blue circle in (b), with ϕ_AB = π/2 and $\mathrm{\Delta }=-3\sqrt{3}{J}^{\prime },$ showing the formation of a single Dirac point.

This Hamiltonian too can be readily expressed in a crystal momentum-dependent matrix, now with two contributions. First the energy offset and nearest-neighbor tunneling from the underlying honeycomb lattice contribute the matrix

$$H_{\mathit{q},0}=\left(\begin{array}{cc}\mathrm{\Delta }& -J\sum _i\exp \left(-\text{i}\mathit{q}\cdot {\mathit{\rho }}_i\right)\\ -J\sum _i\exp \left(\text{i}\mathit{q}\cdot {\mathit{\rho }}_i\right)& -\mathrm{\Delta }\end{array}\right),$$ (48)

and the next-nearest-neighbor links contribute a second term

$$H_{\mathit{q},1}=-2J^{\prime }\left(\begin{array}{cc}\sum _i\cos \left(\mathit{q}\cdot {\mathit{A}}_i-{\varphi }_{\text{AB}}\right)& 0\\ 0& \sum _i\cos \left(\mathit{q}\cdot {\mathit{A}}_i+{\varphi }_{\text{AB}}\right)\end{array}\right).$$ (49)

We have defined A₁ = a₁, A₂ = −a₂, A₃ = a₂ − a₁, with the vectors ρ_i and a_i labeling nearest-neighbor and next-nearest-neighbor separations as indicated in Fig. 3(a). (For practical realizations of the brick-wall lattice, the next-nearest-neighbor coupling, along A₃, is suppressed compared to couplings along A_1,2. However, we use equal strengths for all in Fig. 10.)

Figure 10(b) plots the topological phase diagram associated with this model as a function of the Aharonov-Bohm tunneling phases ϕ_AB and tilt 2Δ. This system supports three distinct topological regions: zones with Chern number ±1, with the majority of parameter space in the topologically trivial phase with Chern number 0.

The Haldane model is particularly amenable to experimental study because tuning experimental parameters such as ϕ_AB can directly drive topological phase transitions. While for the Harper-Hofstadter lattice, tuning ϕ_AB does lead to different Chern numbers, the size of the unit cell also changes, leading to more dramatic changes in the band structure. In Sec. III.C we show how strongly driving the parameters of a brick-wall lattice can break time-reversal symmetry and imbue the lattice’s two bands with nontrivial topology.

In these examples of topological band structure, we identified two common elements that experimentalists need to introduce to create nontrivial topology: complex-valued tunneling matrix elements and unit cells with more than one underlying lattice site or spin degree of freedom.

B. Realization of SSH model

The 1D SSH model of polyacetylene and its generalization the Rice-Mele model are among the most simple topological models to realize. As described in Sec. II.E.2, the Rice-Mele model, Eq. (40), consists of a bipartite 1D lattice with tunneling strengths alternating between $J$ and $J^{\prime }$, and energies of the two sublattice sites, staggered by ±Δ.

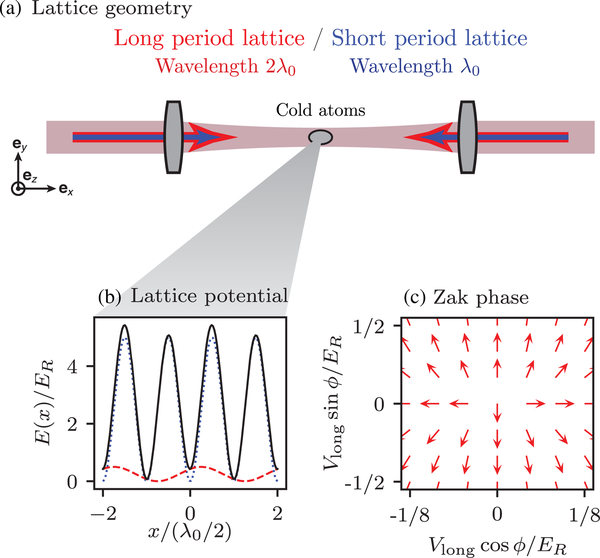
Figure 11(a) depicts a typical laser system required to approximate this idealized model, similar to the experimental realization of Atala et al. (2013). Here a conventional 1D optical lattice with period λ₀/2 is generated by a pair of counterpropagating lasers each with wavelength λ₀. In this lattice, the tunneling is uniform with strength J₀ and the energy minima of the lattice sites are degenerate, as indicated by the pale blue dotted curve in Fig. 11(b). A second, weaker, lattice with period λ₀, generated by a laser with wavelength 2λ₀ [pink dashed curve in Fig. 11(b)], gives a combined potential [black solid curve in Fig. 11(b)] with generally staggered energy minima and alternating tunneling. This gives the overall potential

$$V(x)=V_{\text{short}}{\sin }^2\left(k_{\text{R}}x\right)+V_{\text{long}}{\sin }^2\left[\left(k_{\text{R}}x+\varphi \right)/2\right],$$ (50)

where we defined the single-photon recoil momentum $\hslash k_{\text{R}}=2\pi \hslash /{\lambda }_0$, the associated recoil energy $E_{\text{R}}={\hslash }^2{k}_{\text{R}}^2/2m$, and the atomic mass m of the atom under study.

FIG. 11.

Implementation of the SSH and Rice-Mele models. (a) Representative laser configuration: A pair of overlapping lasers with wavelengths λ₀ and 2λ₀ subject a cloud of ultracold atoms to 1D optical lattices, with periods λ₀/2 and λ₀, respectively, and a spatial relative phase ϕ. (b) Energies of these two lattices and combined potential, showing the long-period lattice shifted in position with respect to the short period lattice by a controllable phase shift ϕ. The SSH model is realized for ϕ = π/2 + nπ (for integer n), in which case all minima have the same energy and are separated by potential barriers with staggered height. An example of band structure in this case is shown in Fig. 12. The choices ϕ = nπ (for integer n) lead to equal barrier heights between adjacent sites, and staggered site energies, but with $J^{\prime }=J,\mathrm{\Delta }\ne 0$. The displayed data are for an intermediate case of ϕ = π/4 where $J^{\prime }\ne J$ and Δ ≠ 0. (c) Zak phase for the lower pair of bands controlled by tuning the phase shift ϕ between the long and short period lattices and the strength of the long-period lattice, as represented by the unit vector (cos ϕ_Zak, sin ϕ_Zak).

Figure 11(c) shows the Zak phase ϕ_Zak, Eq. (14), computed for this physical system in terms of the experimental control parameters. This figure depicts the singularity expected when V_long = 0, which at ϕ = π/2 corresponds to the location of the topological transition in the SSH model when $J=J^{\prime }$.

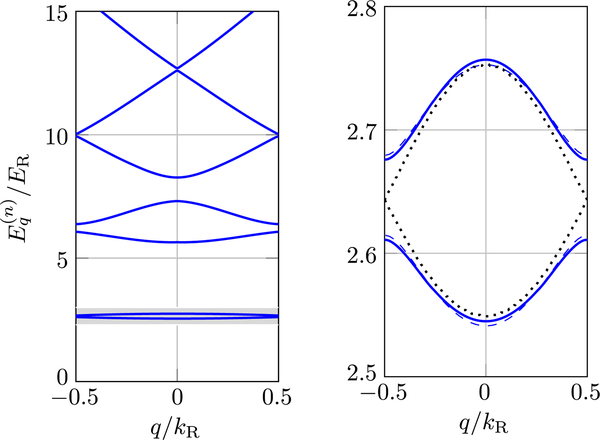
Figure 12 shows the bottom part of the infinite band spectrum for V_short = 6E_R and V_long = 1E_R, with the relative phase set to ϕ = π/2. The right part of this figure shows a zoom on the lowest pair of bands, which are the only relevant ones when the temperature and the interaction energies are comparable to or lower than E_R. The result for V_long = 0 is indicated for comparison with dotted lines. The BZ is reduced in size by a factor of 2 as compared to that of the short period lattice only. This is reflected by the V_long = 0 bands touching at the edge of the BZ; in 1D this marks each such linked pair as truly being one band in a doubled BZ.

FIG. 12.

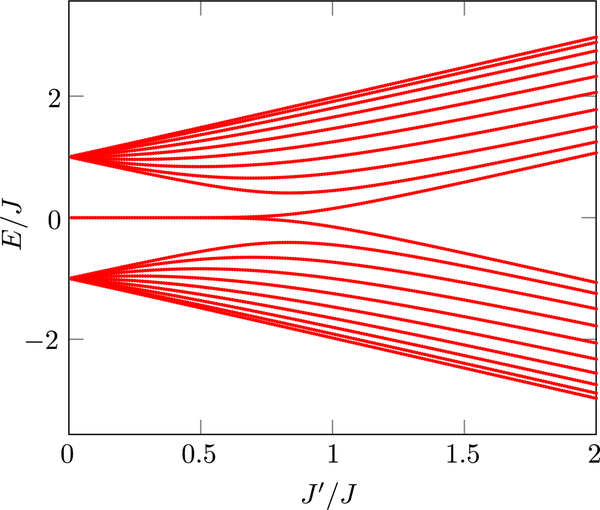
Bipartite lattice band structure compared to the Rice-Mele model. Left: Band structure computed for the superlattice potential given by Eq. (50) with V_short = 6E_R, V_long = E_R, and a relative phase ϕ = π/2 corresponding to the particular case of the SSH model. Right: Zoom on the lower pair of bands (continuous lines). The energy offset between adjacent minima and a fit to the prediction (41) for the band structure of the Rice-Mele model (dashed lines) allow one to extract the practical values of Δ, J, and J′. (Here Δ = 0, J = 0.069E_R, and J′ = 0.037E_R.) The dotted lines show the (folded) lowest band for V_long = 0, up to a global energy shift.

Then the additional independent control of both $J,J^{\prime }$, and Δ requires two additional experimental degrees of freedom. In this realization these parameters are the relative phase ϕ of the long and short period lattices (displacing one lattice with respect to the other) and the depth of the long period lattice V_long. Figure 12 has been calculated for ϕ = π/2, in which case all minima of V(x) have the same energy while the barrier heights between adjacent minima alternate between two values. This realizes the SSH model and the dashed lines in the right panel of Fig. 12 show a fit of the SSH prediction (20) to the two lowest bands, providing thus the relevant values of $J$ and $J^{\prime }$.

Model parameters:

The V_short = 6E_R short period lattice depth used in these simulations, a typical laboratory scale, sets the nominal tunneling strength of J ≈ 0.05E_R. Intuitively, we expect that the energy difference between the minima to be about V_long cos(ϕ). Similarly, the barriers between the sites differ in height by roughly V_long sin(ϕ). The tunneling strength in the effective SSH model has a nontrivial, but monotonically decreasing, exponential-type behavior in the barrier height. This then begs the question of obtaining the parameters of the Rice-Mele model in Eq. (40), including the two tunneling strengths $J$ and $J^{\prime }$ along with the energy difference Δ between sublattice sites.

First, recall that the band structure of simple 1D optical lattice potential $V{\sin }^2\left(k_{\text{R}}x\right)$ only approaches that of a tight-binding model with nearest-neighbor tunneling when $V\gg E_{\text{R}}$. For nearest-neighbor tunneling strength J, the resulting dispersion is simply $-2J\cos \left(\pi q/k_{\text{R}}\right)$. As a result the effective nearest-neighbor tunneling strength can be directly obtained from the lowest term in a Fourier expansion of the band structure of the physical 1D optical lattice. [The higher terms in the series describe longer range tunneling, which becomes negligible for deep lattices; see Jiménez-García and Spielman (2013) for an introduction.] This approach is insufficient for the Rice-Mele band structure $\pm [{\mathrm{\Delta }}^2+\delta J^2+{(4{\overline{J}}^2-\delta J^2){\cos }^2\left(\pi q/k_{\text{R}}\right)]}^{1/2}$, because fits to this dispersion alone cannot effectively disentangle Δ from δJ = J − J′, nor δJ from $\overline{J}=\left(J+J^{\prime }\right)/2$. One practical resolution to this difficulty is to employ symmetry and evaluate the band structure of the bipartite lattice for two cases: first compute the band structure for ϕ = 0 where J and $J^{\prime }$ are manifestly equal, and then compute the band structure for ϕ = π/2 where Δ = 0. This then allows for the independent determination of Δ, J, and J′. For example, for V_short = 6E_R and V_long = E_R this procedure gives $\overline{J}$ = 0.053E_R, almost independent of ϕ. For ϕ = 0, we further find Δ = 0.43E_R and δJ = 0, while for ϕ = π/2, this becomes Δ = 0 and δJ = 0.032E_R.

C. Inertial forces

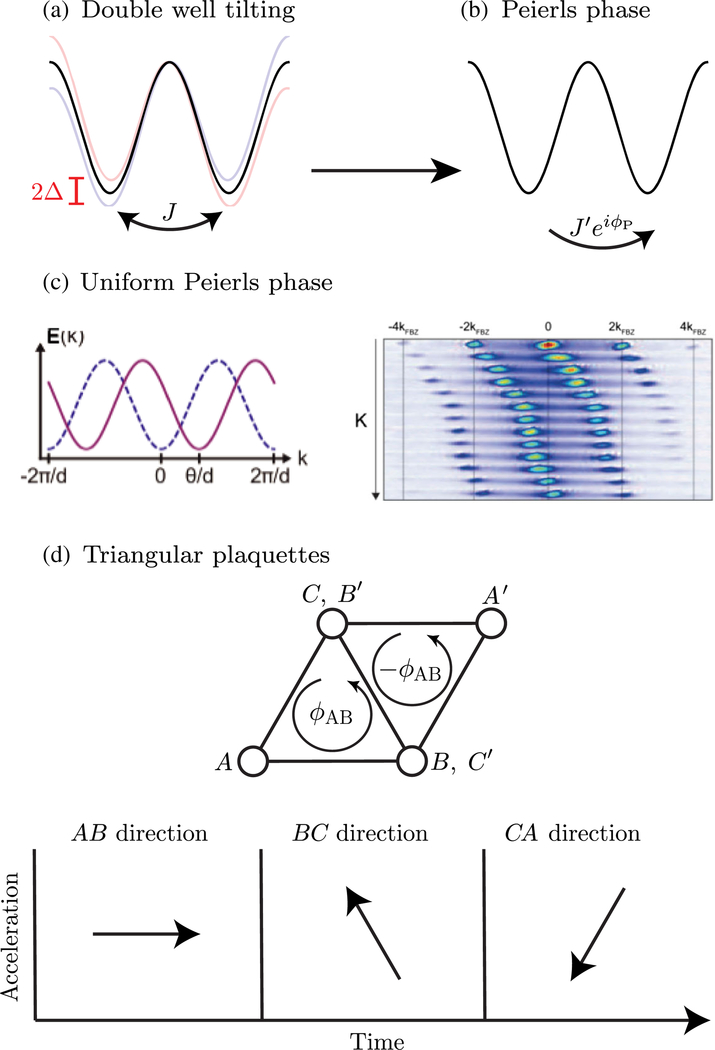
The common experience of starting water in a pail spinning by moving the bucket in a circular manner, not rotating the bucket, suggests that applied inertial forces might produce effects akin to those present in rotating systems: described best by effective Lorentz forces. We see later how these ideas are implemented for ultracold atoms in optical lattices and also come to understand the limitations of these approaches.

The tight-binding model depicted in Eq. (45) is representative of the tunnel-coupling structure present for atoms confined in optical lattices. It is of particular importance that the tunneling matrix elements J are real valued (more specifically, transformations between different gauges can introduce “trivial” complex amplitudes to the tunneling matrix elements, but in these simple lattices there always exists a gauge choice for which the amplitudes are real valued). In this section we develop a simple model illustrating how inertial forces (linear potential gradients or equivalently spatially shaking the lattice potential) can add tunable complex hopping phases to these matrix elements.

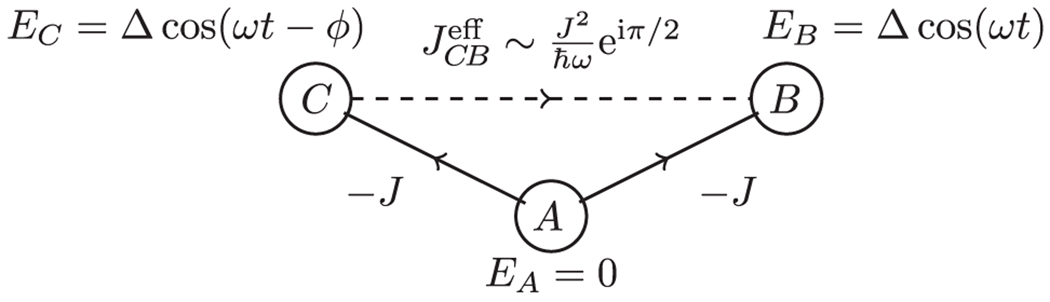
From a quantum mechanical perspective the essential concept is to engineer nontrivial phases acquired by the unitary evolution of a time-periodic Hamiltonian which can be cast as complex hopping amplitudes in an effective time-independent Hamiltonian. This physics is minimally captured by the tunnel-coupled pair of lattices sites shown in Fig. 13, essentially comprising a single unit cell of the Rice-Mele model. We aim for a two-site model described by the Hamiltonian

$$\begin{gathered} \widehat{H}=-J(|r\rangle \langle l|{\text{e}}^{\text{i}{\varphi }_{\text{P}}}+|l\rangle \langle r|{\text{e}}^{-\text{i}{\varphi }_{\text{P}}})+\mathrm{\Delta }(|r\rangle \langle r|-|l\rangle \langle l|) \\ =-J\cos ({\varphi }_{\text{P}}){\widehat{\sigma }}_x+J\sin ({\varphi }_{\text{P}}){\widehat{\sigma }}_y+\mathrm{\Delta }{\widehat{\sigma }}_z, \end{gathered}$$ (51)

including a laboratory-controllable tunneling phase ϕ_P, alas, our lattice is born with ϕ_P = 0. In the second line we expressed this Hamiltonian in terms of the Pauli operators ${\widehat{\sigma }}_{x,y,z}$, allowing us to follow a simple analysis of a spin-1/2 system (Haroche et al., 1970).

FIG. 13.

Inertial forces. (a) A simple double-well lattice subject to modulation, creating (b) experimentally tunable hopping phases. (c) Shaking or tilting in 1D gives rise to a uniform Peierls phase factor that shifts the minima of the tight-binding band structure (Struck et al., 2012). (d) Shaking in 2D can break time-reversal symmetry giving rise to topological lattices.

We earlier noted that gauge transformations can introduce complex-valued tunneling phases. A gauge transformation is simply a position-dependent unitary transformation that adjusts the local phase of the wave function and compensates the Hamiltonian accordingly; in our double-well model, a gauge transformation in the spatial picture becomes a ${\widehat{\sigma }}_z$ rotation in the spin picture. Evidently, the Peierls phase factor ϕ_P can be fixed to a nonzero value by the choice of gauge. Since such a choice is of no physical consequence, it is instead the ability to change ϕ_P (either spatially to induce Aharonov-Bohm fluxes or temporally to induce artificial electric fields) that is the essential content of this discussion. Here we adopt the most straightforward gauge choice that sets ϕ_P = 0 for unadulterated lattices.

In the following, we show how a time-periodic linear gradient provides control over both the tunneling amplitude J and phase ϕ_P. In our two-site model, this modulation (i.e., detuning) is described by Δ(t) = Δ(t + T), with period T, angular frequency $\mathrm{\omega }=2\pi /T$, and with zero per-cycle average ${\langle \mathrm{\Delta }(t)\rangle }_T=0$.

It is straightforward to eliminate the time-dependent Δ(t) term in Eq. (51) (initially, with ϕ_P = 0) by making the unitary transformation

$$|{\psi }^{\prime }(t)\rangle =\exp \left(\frac{\text{i}}{\hslash }{\int }_0^t\mathrm{\Delta }\left(t^{\prime }\right){\widehat{\sigma }}_z\text{d}{t}^{\prime }\right)|\psi (t)\rangle ;$$ (52)

in the language of quantum optics this is akin to the transformation into the time-dependent “interaction” picture. Since this transformation is a ${\widehat{\sigma }}_z$ rotation it is equivalent to a time-dependent gauge transformation, leading to a nonzero, time-dependent Peierls phase factor

$${\varphi }_{\text{P}}(t)=\frac{2}{\hslash }{\int }_0^t\mathrm{\Delta }\left(t^{\prime }\right)\text{d}{t}^{\prime }.$$ (53)

When the modulation frequency’s associated energy $\hslash \omega$ is greatly in excess of the tunneling J, we make a rotating wave approximation to replace the time-dependent terms introduced by this rotation by their time averages, giving the time-averaged interaction picture Hamiltonian

$$\widehat{H}=-J{\langle \cos {\varphi }_{\text{P}}(t)\rangle }_T{\widehat{\sigma }}_x+J{\langle \sin {\varphi }_{\text{P}}(t)\rangle }_T{\widehat{\sigma }}_y,$$ (54)

with a potentially nonzero dc Peierls phase factor

$$\tan ({\varphi }_{\text{P},\text{dc}})=\frac{{\langle \sin {\varphi }_{\text{P}}(t)\rangle }_T}{{\langle \cos {\varphi }_{\text{P}}(t)\rangle }_T}.$$ (55)

Physically, the time-dependent gauge transformation in Eq. (52) allows the system to sample a range of Peierls phase factors and retain a nonzero average. In effect, our task is to make ${\langle \sin {\varphi }_{\text{P}}(t)\rangle }_T$ nonzero, and because sin is an odd function we seek a waveform ϕ_P(t) that takes on positive and negative values in an “imbalanced” manner.

The most simple example to deploy in the laboratory is a monochromatic sinusoidal modulation $\mathrm{\Delta }(t)=\mathrm{\Delta }\cos (\omega t)$ of the tilt. In this case, the Bessel series expansion gives ${\langle \cos {\varphi }_{\text{P}}(t)\rangle }_T={\mathcal{J}}_0(2\mathrm{\Delta }/\hslash \omega )$ and ${\langle \sin {\varphi }_{\text{P}}(t)\rangle }_T=0$. Because the integrated sinusoidal waveform takes on positive and negative values with equal frequency the average tunneling phase is zero; however, this modulation does renormalize the tunneling strength $J\to J\times {\mathcal{J}}_0(2\mathrm{\Delta }/\hslash \omega )$ as was observed experimentally (Lignier et al., 2007). While monochromatic sinusoidal modulation is simple to deploy, it can obscure the underlying physics, rapidly becoming a tangle of Bessel functions.

Instead consider a waveform consisting of two delta-function “kicks” in each drive cycle (Sørensen, Demler, and Lukin, 2005; Anderson, Spielman, and Juzeliūnas, 2013), the first with strength $\mathrm{\Delta }/\omega$ at time t = 0 and the second with strength $-\mathrm{\Delta }/\omega$ at time f × T, a fraction f through the drive period T. Integrating this waveform gives the time-dependent peierls phase factor

$${\varphi }_{\text{P}}(t)=\frac{2\mathrm{\Delta }}{\hslash \omega }\times \{\begin{array}{ll}1-f\hfill & \text{for}0\le t\le fT,\hfill \\ -f\hfill & \text{for}fT<t\le T,\hfill \end{array}$$ (56)

a pulse-width modulated waveform with zero average, with duty cycle $f\in [0,1)$. For $f\notin \{0,1/2\}$, the resulting asymmetric and skewed waveform leads to a nonzero average of ${\langle \sin {\varphi }_{\text{P}}(t)\rangle }_T$.

For the special case $\mathrm{\Delta }/\hslash \omega =\pi$, the time-averaged Peierls phase factor is ${\varphi }_{\text{P},\text{dc}}=-2\pi (f-1/2)$ with tunneling strength unchanged at J. The basic physical picture is that after an atom tunnels between sites it acquires a phase different from what it would have acquired on its initial site, and ${\varphi }_{\text{P},\text{dc}}$ expresses the differential phase acquired upon returning to its initial site. The time-dependent phase ${\varphi }_{\text{P}}(t)$ must break time-reversal symmetry to give a nonzero average of sin ${\varphi }_{\text{P}}(t)$. Figure 13(c) depicts the first experimental realization of a nonzero peierls phase factor imprinted using inertial forces (Struck et al., 2013). Rather than tilting the lattice potential, Struck et al. (2013) found it more convenient to spatially shake the lattice potential by modulating the phase of the lasers creating the optical standing wave, giving the potential $V(\widehat{x},t)=V_0\cos \left[2k_{\text{R}}(\widehat{x}-\delta x(t))\right]/2$. Here V₀ is the lattice depth and k_R is the two-photon recoil momentum from the wavelength λ of the lasers creating the lattice potential.

Although this shaking process is physically quite different from applying a time-dependent gradient, they are functionally equivalent. The connection between the two can be seen clearly in terms of a pair of time-dependent transformations. We begin by using the spatial displacement operator ${\widehat{D}}_x[-\delta x(t)]=\exp [\text{i}\widehat{k}\delta x(t)]$ to transform to the non-inertial frame comoving with the lattice, i.e., ${\widehat{D}}_x[-\delta x(t)]\widehat{x}$ ${\widehat{D}}_x{[-\delta x(t)]}^{†}=\widehat{x}+\delta x(t)$. This exchanges the lattice’s motion for a new time-dependent contribution to the Hamiltonian $-\hslash \widehat{k}{\partial }_t\delta x(t)$. The once-transformed Hamiltonian

$$\begin{gathered} {\widehat{H}}^{(1)}(t)=\frac{{\hslash }^2}{2m}{\left[\widehat{k}-\frac{m}{\hslash }{\partial }_t\delta x(t)\right]}^2+\frac{V_0}{2}\cos \left(2k_{\text{R}}\widehat{x}\right) \\ -\frac{m}{2}{\left[{\partial }_t\delta x(t)\right]}^2 \end{gathered}$$ (57)

contains a new time-dependent vector potential and a global time-dependent energy shift that does not impact the system’s dynamics. Evoking Hamilton’s equation $\dot{x}={\partial }_{\hslash k}\widehat{H}$, we see that the appearance of this vector potential simply describes the fact that in the moving frame the velocity of an object differs from that in the lab frame by the instantaneous velocity of the moving frame $-{\partial }_t\delta x$.

We complete our argument using the time-dependent momentum displacement operator ${\widehat{D}}_k[-\delta k(t)]=\exp [-\text{i}\delta k(t)\widehat{x}]$, a gauge transformation, that converts the time-dependent vector potential into a potential gradient $\widehat{V}=\left[m{\partial }_t^2\delta x(t)\right]\widehat{x}$. This reminds us that inertial forces are present in accelerating frames and informs us that experimenters are free to use either shaken lattices or potential gradients equivalently to produce the inertial forces required to induce ϕ_P.

While this nonzero and uniform peierls phase factor is an essential first step for emulating Aharonov-Bohm fluxes, a uniform peierls phase factor in 1D can be eliminated via a gauge transformation (although any temporal change can still lead to effective electric fields). In contrast by moving to 2D systems such as in modulated and shaken honeycombgeometry lattices, this technique has nontrivial alterations to band structure (Struck et al., 2013) and including those topologically equivalent to the Haldane model (Jotzu et al., 2014).

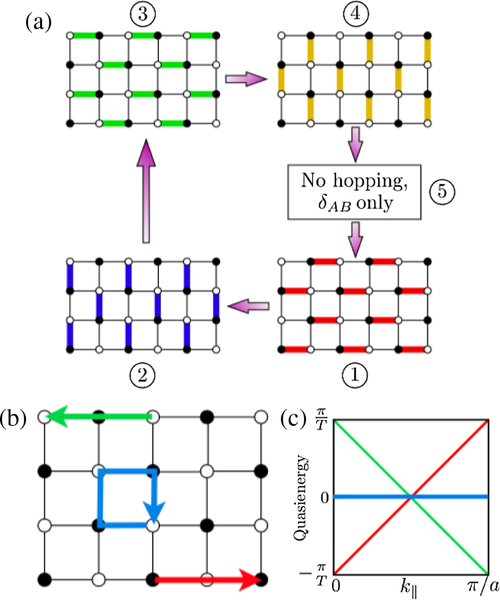
We now extend our discussion to 2D to understand Aharonov-Bohm fluxes. Figure 13(d) depicts a minimal model of shaking in 2D; the top panel illustrates the two triangular plaquettes that make up a single unit cell of a triangular lattice, while the bottom panel graphs a shaking protocol that first accelerates parallel to the A-B link of the left plaquette (i.e., along e_x), then accelerates parallel to B-C, and finally accelerates parallel to C-A. For each link, this protocol leads to the same time-dependent peierls phase factor given in Eq. (53), with each phase shifted in time by 2π/3, giving the same nonzero tunneling phase ϕ_P,dc to each side of the plaquette. This then leads to an overall Aharonov-Bohm ${\mathrm{\Phi }}_{\text{AB}}={\varphi }_{\text{P},\text{dc}}$.

It might appear that our task is complete, but have we truly created a uniform Aharonov-Bohm phase over all plaquettes? Unfortunately Struck et al. (2013) demonstrated that this is not the case. Following the same argument for the second (inverted) plaquette that completes a single unit cell shows that accumulated phases give a negative flux ${\mathrm{\Phi }}_{\text{AB}}=-{\varphi }_{\text{P},\text{dc}}$, leading to a staggered flux. Therefore on average the Aharonov-Bohm flux through this lattice is zero. One way to understand this is that the Peierls phase factors are created with uniform amplitude throughout the lattice, rather than with the linear dependence on position as for our Landau-gauge example of the Harper-Hofstadter Hamiltonian. Sørensen, Demler, and Lukin (2005) proposed remedying this by applying a potential whose gradient itself increased away from the systems center, which they termed a quadrupole potential.

Evidently shaking of this type does not provide a straightforward route for realizing Hamiltonians such as the Harper-Hofstadter model with uniform fields, but it has proven a successful route for creating a Haldane-type Hamiltonian that has a zero average flux but still with topological bands (Jotzu et al., 2014). Important to this realization is the fact that the effective Hamiltonian for the shaken lattice acquires a next-nearest-neighbor hopping with a nonzero Peierls phase factor. Beyond the time-averaged Hamiltonian discussed, perturbative corrections from the time-varying part of the nearest-neighbor tunneling lead to next-nearest-neighbor tunneling of order $J^{\prime }~J^2/\hslash \omega$, arising from a second-order process through an intermediate virtual state detuned by $\hslash \omega$. Such terms are conveniently obtained from the Magnus expansion of this tight-binding model described in Appendix B. An analysis of the effective model for the shaken lattice that goes beyond this Magnus expansion approach was provided by Modugno and Pettini (2017).

D. Resonant coupling: Laser-assisted tunneling

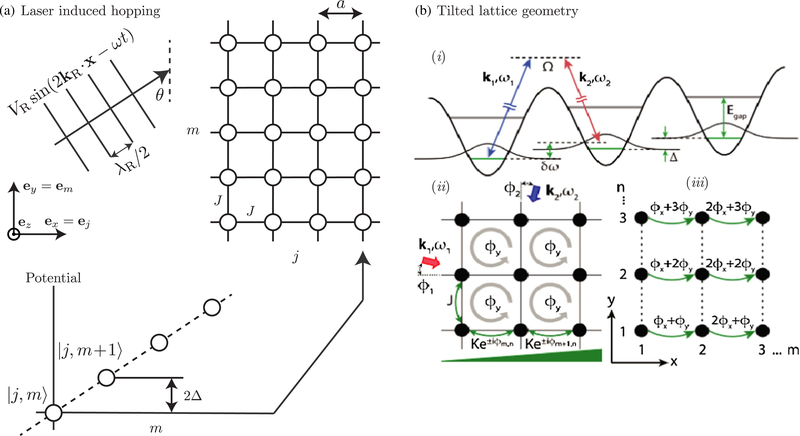
The previous section outlined the broad range of engineered tunnel couplings possible via temporal modulation of the parameters of the lasers underlying the lattice potential. While it was possible to create complex-valued tunneling, it was not possible to independently control the phase and amplitude of tunneling on each lattice link: more control is required. Following the ideas of Jaksch and Zoller (2003), we describe how such a fine-grained control is in principle possible using laser-assisted tunneling and how experimental implementations have approached this task. As we shall see, although this laser-assisted tunneling is effected by temporal modulation, the modulation results from additional lasers, rather than the lasers from which the underlying lattice is assembled.

The essential concept of this technique is straightforwardly illustrated in the 2D square lattice depicted in Fig. 14(a): the native tunneling along the vertical direction is first eliminated by applying a potential gradient (i.e., tilting the lattice), then coupling between neighboring lattices sites is reestablished with a traveling wave potential. Here the spatially nonuniform phase of the traveling wave is imprinted upon atoms as they are moved from site to site described by complex-valued tunneling amplitudes. Because local optical phases are relatively easy to control [for example, by creating higher-order optical modes such as Laguerre-Gauss modes, as was done by Chen et al. (2018)], these techniques in principle allow for more subtle engineering of the local Aharonov-Bohm phases than is possible with whole-scale modulation of lattice parameters. Still, current implementations (Aidelsburger et al., 2013; Miyake et al., 2013) rely only on the uniformly changing phase from plane waves to generate homogeneous fields.

FIG. 14.

Laser-induced hopping. (a) 2D square lattice (right) with a potential gradient along e_m (vertical) illuminated by a traveling wave potential. The coupling of any pair sites of this lattice $|j,m\rangle \text{and}|j,m+1\rangle$ is qualitatively described as a two-level system with detuning 2Δ coupled by the traveling wave. (b) Technique for creating the half-flux Harper-Hofstadter Hamiltonian in tilted spin-dependent lattices as implemented in MIT (Miyake et al., 2013) similar to Aidelsburger et al. (2013).

The basic principle can be understood in terms of the same sort of two-level system discussed in Sec. III.C, but from a perspective in which the rotating wave approximation (RWA) is valid. In the present case, we focus on two neighboring lattice sites in Fig. 14(a), labeled by $|j,m\rangle \text{and}|j,m+1\rangle$ coupled by the traveling wave potential $V_{\text{R}}(\mathit{x})=V_{\text{R}}\sin (2{\mathit{k}}_{\text{R}}\cdot \mathit{x}-\omega t)$ that locally modulates the potential intersecting e_m with angle θ. Physically this is directly realized (Aidelsburger et al., 2013; Miyake et al., 2013) by a pair of interfering lasers giving rise to a moving standing wave with periodicity λ_R/2, and recoil wave vector |k_R| = 2π/λ_R (the wavelength λ_R incorporates all geometric factors present from the intersection angle between these lasers).

Midway between these two sites, at position ${\mathit{x}}_0=a(j,m+1/2)$, this potential is

$$V_{\text{R}}(\mathit{x})\approx \frac{V_{\text{R}}}{2\text{i}}\left\{{\text{e}}^{\text{i}(2k_{\text{R}}\cdot {\mathit{x}}_0-\omega t)}\left[1+2\text{i}{\mathit{k}}_{\text{R}}\cdot (\mathit{x}-{\mathit{x}}_0)\right]-\text{c}.\text{c}.\right\},$$ (58)

to first order in position. In this expression (1) the first term describes a modulated, but spatially uniform shift in the potential with no physical consequence that may therefore be neglected; and (2) the horizontal, e_j dependence drops out at this order because the localized wave functions, both centered at aj, are symmetric and compact in square geometry optical lattices. The remaining terms add a modulated contribution to the detuning

$$\mathrm{\Delta }(t)\approx \left[k_{\text{R}}a\cos (\theta )\right]V_{\text{R}}\cos \left(2{\mathit{k}}_{\text{R}}\cdot {\mathit{x}}_0-\omega t\right):$$ (59)

the same sort of shaking potential we studied in Sec. III.C, now with an overall phase dependent on the center position x₀. Here we focus on the limit in which $\hslash \omega =2\mathrm{\Delta }\gg J$ that leads to the time-independent RWA Hamiltonian

$${\widehat{H}}_{\text{RWA}}=-J_{\text{RWA}}[|j,m+1\rangle \langle j,m|{\text{e}}^{\text{i}{\varphi }_{\text{RWA}}(m,j)}+\text{H}.\text{c}],$$ (60)

with double-well tunneling strength

$$J_{\text{RWA}}=-J\left(\frac{V_{\text{R}}}{2\mathrm{\Delta }}\right)k_{\text{R}}a\cos (\theta )$$ (61)

and phase

$${\varphi }_{\text{RWA}}(m,j)=2k_{\text{R}}a[j\sin \theta +\left(m+\frac{1}{2}\right)\cos \theta ].$$ (62)

Here the local phase of the traveling wave potential $2{\mathit{k}}_{\text{R}}\cdot {\mathit{x}}_{\text{0}}$ at the double well is directly imprinted onto the atoms as they tunnel in the m direction, but not when they tunnel in the j direction. The result of this double-well analysis can be extended to the whole lattice, where the expression for ${\varphi }_{\text{RWA}}$ is unchanged, and J_RWA is qualitatively the same but quantitatively altered.

Summing the tunneling phase around any plaquette gives an Aharonov-Bohm flux

$${\mathrm{\Phi }}_{\text{AB}}=2k_{\text{R}}a\sin \theta ,$$ (63)

with no spatial dependence. As a result, the RWA Hamiltonian is gauge equivalent to the Landau-gauge Harper-Hofstadter Hamiltonian

$$H=-\sum _{j,m}J{\widehat{a}}_{j+1,m}^{†}{\widehat{a}}_{j,m}+J_{\text{RWA}}{\text{e}}^{\text{i}j{\varphi }_{\text{AB}}}{\widehat{a}}_{j,m+1}^{†}{\widehat{a}}_{j,m}+\text{H}.\text{c}\mathrm{..}$$ (64)

This Hamiltonian was realized in the manner described by both the Munich and the Massachusetts Institute for Technology (MIT) groups (Aidelsburger et al., 2013; Miyake et al., 2013), illustrated in Fig. 14. The MIT group used a lattice derived from a 1064 nm laser, with a traveling wave generated by beams from the same laser intersecting the e_m axis at θ = π/4. This geometry gives a flux ${\mathrm{\Phi }}_{\text{AB}}/2\pi =1/2$ per plaquette and illustrates an important practical point of this technique. In a similar manner, but with a different laser geometry the Munich group realized 1/4 flux per plaquette. In both cases, the laser-induced tunneling strength is proportional to cos θ, while the Aharonov-gohm phase is proportional to sin θ, requiring a compromise dependent on the experimental goals. Following this initial experiment, the Munich group retooled their technique as pictured in Fig. 14(c) by using the staggered potential inside individual four-site plaquettes and laser-induced hopping to establish tunneling along all the lattice directions, enabling the measurement of the Chern number (Aidelsburger et al., 2015); see Sec. IV.C.2.

E. Synthetic dimensions

The concept of synthetic dimensions is rooted in the fact that a lattice is no more than a set of states labeled by integers, e.g., j and m in the preceding discussions labeled the atoms at sites described by wave functions $|j,m\rangle$. This insight allows the creation of lattices that use the atoms’ internal or “spin” degrees of freedom as additional synthetic dimensions. Boada et al. (2012) and Celi et al. (2014) described how the techniques discussed in Sec. III.D can be used to create a lattice with one spatial dimension (denoted by j) and one synthetic dimension (denoted by m to evoke the atomic m_F states from which it is built). Large artificial magnetic fields using synthetic dimensions were simultaneously realized at the National Institute of Standards and Technology (NIST) and the European Laboratory for Nonlinear Spectroscopy (LENS) (Mancini et al., 2015; Stuhl et al., 2015) using hyperfine ground states of bosonic ⁸⁷Rb and fermionic ¹⁷³Yb, respectively.

Both synthetic dimension experiments then replaced photon-assisted tunneling with two-photon Raman transitions. Physically, these transitions simultaneously change the internal atomic state and impart the two-photon recoil momentum. For a 1D optical lattice—essentially one chain along e_j of the 1D lattice in Fig. 14—the spatially imprinted phase is ${\varphi }_{\text{syn}}=2k_{\text{R}}aj\sin \theta$. This expression is equivalent to Eq. (62) derived for photon-assisted tunneling, but without any dependence on m since the Raman laser’s k vector is always “perpendicular” to the synthetic m direction, rendering $\cos \theta \to 0$. This thereby eliminates the geometric compromise required to maximize the laser-assisted tunneling strength at simultaneously large flux.

Although synthetic dimension and photon-assisted tunneling experiments can produce the same sort of magnetic lattice geometrics, the techniques have important practical differences. For example, spin selective measurements allow the synthetic dimension lattice site to be measured with near-perfect “spatial” resolution. In addition the limited number of spin states (typically 3 to 5) produce synthetic dimension lattices with striplike geometrics with perfect hard-wall boundary conditions, rather than extended planes as for conventional 2D optical lattices. In addition synthetic dimension lattice sites with the same spatial index j but with different internal index m are in reality spatially overlapping, so that the spatially local atom-atom interactions become anisotropic: long ranged in m and short ranged in j.

Both experimental synthetic dimension realizations [⁸⁷Rb and ¹⁷³Yb in Mancini et al. (2015) and Stuhl et al. (2015), respectively] created large flux, highly elongated strips along j, with just three sites in width along m. More recently two-leg ladder implementations of the synthetic dimension concept have been realized (Livi et al., 2016; Kolkowitz et al., 2017) using the optical clock transition of both ¹⁷³Yb and ⁸⁷Sr, and synthetic dimensions have even been constructed using momentum states in lieu of spin states (Meier, An, and Gadway, 2016).

F. Flux lattices: Intrinsic topology

Each of the topological lattices discussed in the preceding sections was engineered beginning with a nontopological lattice to which modulation or light-assisted tunneling was added to engineer a desired topological model. In this section we focus on a different approach for generating a topological lattice without the need for modulation or light-assisted tunneling. This approach applies to an atom with several internal states and subjected to a combination of three light-matter interactions: those that are independent of internal atomic states, those that depend on internal atomic states, and those that couple between the different internal atomic states. In particular, as we show in Appendix C, the far-detuned light-matter interaction for alkali atoms takes the form

$${\widehat{H}}_{\text{RWA}}=U(\mathit{r})\widehat{1}+\mathit{\kappa }(\mathit{r})\cdot \widehat{\mathit{F}},$$ (65)

where U (r) and κ(r) ⋅ $\widehat{\mathit{F}}$ describe the rank-0 (scalar) and rank-1 (vector) light shifts acting on an atom with internal angular-momentum operator $\widehat{\mathit{F}}$. The possible lattices formed from Eq. (65) have a very rich range of structures, characterized by the spatial variations of U(r) and the three components of κ(r). Because this approach is not tied to a preexisting tight-binding lattice, it is not limited to deep optical lattices and can have topological properties even for very shallow or weak optical coupling strengths.

We discuss the essence of this approach in two ways: (1) we explore “flux lattices” in which the Aharonov-Bohm flux emulated by a Berry phase in real space leads to lattices with nonzero effective magnetic fields, and (2) we explore the connection between spin-dependent lattices and established topological models. Indeed in our initial discussion of the Haldane model, we identified the two sublattice sites in each unit cell with a pseudospin degree of freedom and arrived at a spin-dependent band structure, Eq. (48); we now make this literal.

1. Flux lattices

Before turning to our discussion of flux lattices, we pause to reflect on our discussion of topological lattices to this point. Section II introduced the concept of topological invariants in terms of the Berry connection (Zak phase) or Berry curvature (Chern number) integrated over the BZ. In the latter case, the Chern number can be cast as a momentum-space statement of Gauss’s law, in which the Berry curvature integrated over the toroidal BZ counts an integer number of topological “charges” in the inside of the torus yielding the Chern number.

A “flux lattice” is an optical lattice potential that instead is defined as a lattice in which the integrated Berry curvature in each spatial unit cell is nonzero, suggesting that the atoms might behave as if large magnetic fields are present. This provides an intuitive framework in which to link the physics of Landau levels and lattice bands. Indeed, in general, the atom experiences a combination of a periodic magnetic field (with nonzero average) and a periodic scalar potential. Figure 15(b) depicts a bichromatic laser configuration that gives the same κ used in the initial flux lattice proposals (Cooper, 2011; Cooper and Dalibard, 2011), with four frequency degenerate in-plane lasers and with a single down-going laser at a different frequency. As shown by Juzeliūnas and Spielman (2012), this geometry can be tuned to produce the desired effective magnetic field with vector strength

$$\begin{gathered} \mathit{\kappa }={\kappa }_{\perp }\left[\cos \left(\frac{\pi x}{a}\right){\mathit{e}}_x+\cos \left(\frac{\pi y}{a}\right){\mathit{e}}_y\right] \\ +{\kappa }_{\Vert }\sin \left(\frac{\pi x}{a}\right)\sin \left(\frac{\pi y}{a}\right){\mathit{e}}_z, \end{gathered}$$ (66)

where ${\kappa }_{\perp }$ and ${\kappa }_{\Vert }$ are set by the intensity and polarization of the laser fields, and a = λ is equal to the laser wavelength λ. This result follows directly from the expressions in Appendix C. The right panel of Fig. 15(b) shows the spatial distribution of the Berry curvature in a single unit cell with spatial extent a, with a clear non-negative mean, evaluated for ${\kappa }_{\perp }={\kappa }_{\Vert }$. Thus, it achieves the goal of having a net nonzero effective magnetic field piercing the unit cell. In both the square geometry and a similar three-beam setup with 2π/3 intersection angle, the resulting band structure can have topological bands (Cooper, 2011; Cooper and Dalibard, 2011).

FIG. 15.

Spin-dependent topological lattices. (a) Level diagram for three-level total angular-momentum f = 1 case with m_F states labeled, as is applicable for the common alkali atoms ⁷Li, ²³Na, ³⁹K, ⁴¹K, and ⁸⁷Rb. For reference, the diagram shows the decomposition of these optical fields into ${\sigma }_{\pm }$ and π, but as discussed in the text, this is not an overly useful way of considering this problem. (b) Laser geometry for a typical optical flux lattice (left) producing a real-space Berry curvature with nonzero average (right). (c) Experimental geometry for spin-dependent topological lattice (Sun et al., 2017). (d) Directly observed topological band structure (left) and computed (right). From Sun et al., 2017.

This discussion hides one subtle point: the integrated curvature over each unit cell must be a multiple of 2π. In the present case the integrated curvature is 8πm_F over the complete unit cell. The circles in Fig. 15(b) mark the locations of the minima of the adiabatic potential $\hslash m_F|\mathit{\kappa }|$. For a deep lattice, in which this potential is large compared to the recoil energy, the atoms are strongly confined close to these minima. Their locations define effective lattice sites of a tight-binding description, with the unit cell containing four such sites and therefore divided into four plaquettes. For a spin-1/2 system, with m_F = ±1/2, each of these plaquettes will have a flux $\mathrm{\Phi }=\pi$, while for bosonic alkali atoms, m_F takes on integer values implying $\mathrm{\Phi }=2\pi m_F$ is a multiple of 2π. In either case, nearest-neighbor hopping on this square lattice geometry would not break time-reversal symmetry, so the Berry curvature of the bands must vanish. As a result, for topological band structure to emerge in a straightforward way, longer range hopping as in the Haldane model is required. These considerations indicate that, for this square geometry, the flux lattice would not lead to topological bands in the deep-lattice limit. However, we reiterate that the flux lattice approach is not restricted to deep lattices, but applies also for shallower lattices in which the atoms can move throughout the unit cell and a restriction to nearest-neighbor hopping is inappropriate.

We demonstrated that flux lattices can give rise to a net nonzero magnetic field piercing the real-space unit cell. The comparison with free particles in a uniform magnetic field, which form Landau levels, suggests the appearance of topological Chern bands. However, this is not guaranteed: such lattices may or may not be topological, as defined by the usual Chern number computed in momentum space. (The deep-lattice limit of the square flux lattice described above provides an example in which the bands are not topological despite the nonzero effective magnetic flux.) Moreover, as we now discuss, there can be cases in which the net flux through the unit cell vanishes, yet the bands are topological (Cooper and Moessner, 2012). In general, to determine the band topology requires a full calculation of the band structure, including the atom’s kinetic energy.

2. Fluxless lattices

A key insight from the Haldane model is that a net magnetic field is not a prerequisite for topological band structure. It is sufficient to break time-reversal symmetry, a condition that can readily be achieved for lattices that couple internal states. The appearance of topological bands for zero net flux is readily established for shallow lattices (Cooper and Moessner, 2012). Here we focus on the regime of deep lattices, where an effective (spin-dependent) tight-binding model can be developed. As we made explicit in our discussion of the Haldane model, the two basis sites consisting of a single unit cell can be assigned a pseudospin label, and these pseudospins are then arrayed to form a honeycomb or brick-wall lattice. Building from this understanding, we conclude by discussing the topology of state-dependent lattices, without any explicit reference to Berry phases.

Figure 15(c) displays the phase-stable lattice geometry realized by Sun et al. (2017), which is closely related to the flux lattice geometry, absent the vertical beam and with the in-plane beams driving Raman transitions. A predecessor of this setup described by Wu et al. (2016) generated a 2D optical lattice with spin-orbit coupling with ⁸⁷Rb atoms [a first realization of 2D spin-orbit coupling was reported by Huang et al. (2016) for a bulk geometry]. The two pseudospin states are the Zeeman levels $|F=1,m=-1\rangle \text{and}|F=1,m=0\rangle$ of the lowest hyperfine state of the ground state manifold. The essential concept of this lattice is to first use the scalar light shift from the detuned, counterpropagating beams to create a conventional 2D optical lattice operating in the tight-binding regime, and then to use the vector contribution of the light shift to give a combination of local effective magnetic fields and spin-dependent tunneling. The resulting tight-binding model is very closely related to that of the Haldane model and shares its topological properties. The left panel of Fig. 15(d) shows the experimentally measured band structure in good agreement with the predictions of theory displayed in the right panel.

IV. EXPERIMENTAL CONSEQUENCES

This section presents recent experimental investigations of nontrivial (global or local) topological properties of energy bands, in either 1D or 2D geometries. Interactions play a nonessential role for the experiments described next; hence phenomena addressed here correspond to single-particle (or ideal gas) physics.

This section is divided into three parts. In the first one we describe measurements that are performed on an atomic system at equilibrium, using local probes in momentum space that allow one to reconstruct the topology of the occupied band(s). In the second part we present analyses performed by looking at the dynamics of wave packets. These wave packets are well localized at the scale of the Brillouin zone and one can bring them close to some points of specific interest, Dirac points, for example, using an external force. The last part is devoted to transport measurements, which are closer in spirit to the techniques that are commonly used in condensed matter physics.

A. Characterization of equilibrium properties

1. Time-of-flight measurements

Before entering into a discussion of specific measurements, we briefly comment on implications of the time-of-flight (TOF) measurements commonly used in experiment. In the vast majority of cold atom experiments, the measurement procedure begins with the rapid removal of all applied fields (both those involved in trapping the ensemble and those required to create the topological lattice of interest). After this abrupt, projective, turn-off, the atoms then undergo a period of ballistic expansion followed by a measurement of their density (often in a spin-resolved manner). In many experiments, this procedure gives a direct measurement of the momentum distribution as it was when the applied fields were just removed.

While this sounds simple in principle, this procedure can appear to give measurement results that are gauge dependent. Fortunately any supposed contradiction with general principles of local gauge invariance is illusory. For example, two different experiments might well create a Harper-Hofstadter lattice with the same flux using very different laser geometries, which naturally define the synthetic vector potential in two different gauges. The observed momentum distribution will in general differ in these two cases (Kennedy et al., 2015). As discussed by Möller and Cooper (2010) and LeBlanc et al. (2015) these differences arise because the synthetic vector potential vanishes during TOF when the laser fields are removed: there are physical differences in how exactly the synthetic vector potential returns to zero when TOF begins and physically different effective electric fields present during this turn-off. All physical observables remain invariant to local gauge transformations, provided these are applied consistently, i.e., changing the vector potential both before and during TOF.

2. Local measurement of the Berry curvature

We consider here a cold atomic gas at equilibrium in a 2D optical lattice. With the so-called band-mapping technique one can precisely measure the distribution $\mathcal{N}(\mathit{q})$ of the quasimomentum q for each energy band. With this technique the laser beams forming the lattice are turned off in a controlled manner, so that the populations of the Bloch states forming the various energy bands in the presence of the lattice are transferred to states with a well-defined momentum in the absence of the lattice (Greiner et al., 2001). The measurement of $\mathcal{N}(\mathit{q})$ in combination with a suitable temporal variation of the lattice parameters before the complete turn-off allows one to characterize the band topology, i.e., to access not only the energies, but also the Berry curvature Ω(q).

To illustrate this point we consider a 2D lattice and use the same two-band model as in Sec. II, assuming a unit cell with two nonequivalent sites labeled A and B. The generic Hamiltonian in reciprocal space is ${\widehat{H}}_{\mathit{q}}=h_0(\mathit{q})\widehat{1}-\mathit{h}(\mathit{q})\cdot \widehat{\mathit{\sigma }}$ where (h₀, h) is a 4-vector with real components that are periodic over the BZ. The energies of the two bands are $E_{\mathit{q}}^{\pm }=h_0(\mathit{q})\pm |\mathit{h}(\mathit{q})|$ and the Bloch states $|u_{\mathit{q}}^{\pm }\rangle$ can be written as linear combinations of $|\mathit{q},A\rangle$ and $|\mathit{q},B\rangle$. Using the expression (30) for these Bloch states, one finds

$$\begin{gathered} {\mathbf{\Omega }}^{\pm }(\mathit{q})={\mathbf{\nabla }}_{\mathit{q}}\left(\langle u_{\mathit{q}}^{\pm }|\right)\times {\mathbf{\nabla }}_{\mathit{q}}\left(|u_{\mathit{q}}^{\pm }\rangle \right) \\ =\pm \frac{1}{2}{\mathbf{\nabla }}_{\mathit{q}}\left(\cos {\theta }_{\mathit{q}}\right)\times {\mathbf{\nabla }}_{\mathit{q}}{\varphi }_{\mathit{q}}, \end{gathered}$$ (67)

where (θ_q, ϕ_q) defines the direction of h(q) in spherical coordinates.

A procedure to determine θ_q and ϕ_q, hence the curvature Ω, in such a two-band situation was proposed by Hauke, Lewenstein, and Eckardt (2014) and implemented by Fläschner et al. (2016). The starting point is the momentum distribution ${\mathcal{N}}_{\mathit{q}}(\mathit{k})$ associated with a Bloch state

$${\psi }_{\mathit{q}}^{(-)}(\mathit{r})=\sum _{s=A,B}\sum _{{\mathit{R}}_s}{\alpha }_{\mathit{q},s}w(\mathit{r}-{\mathit{R}}_s){\text{e}}^{\text{i}\mathit{q}\cdot {\mathit{R}}_s}.$$ (68)

Here $w(\mathit{r})$ is the Wannier function of the band, supposed to be identical for the two sublattices s = A, B, and $({\alpha }_{\mathit{q},A},{\alpha }_{\mathit{q},B})=(\cos ({\theta }_{\mathit{q}}/2),{\text{e}}^{\text{i}{\varphi }_q}\sin ({\theta }_{\mathit{q}}/2))$. The momentum distribution ${\mathcal{N}}_{\mathit{q}}(\mathit{k})$ is the square of the Fourier transform of ${\psi }_{\mathit{q}}^{(-)}(\mathit{r})$. For k inside the first BZ, it is peaked around k = q and given by $|\tilde{w}(\mathit{k}){|}^2{|{\alpha }_{\mathit{k},A}+{\alpha }_{\mathit{k},B}|}^2$, where $\tilde{w}(\mathit{k})$ is the Fourier transform of $w(\mathit{r})$. When the lowest band is uniformly filled with independent fermions, the momentum distribution of the gas is obtained by summing the contributions ${\mathcal{N}}_{\mathit{q}}(\mathit{k})$ over all quasimomenta q of the BZ:

$$\mathcal{N}(\mathit{k})=|\tilde{w}(\mathit{k}){|}^2\left[1-\sin {\theta }_k\cos {\varphi }_k\right].$$ (69)

This distribution can be measured using a ballistic expansion after a sudden switch-off of the lattice. The key point of Eq. (69) is that the measured distribution $\mathcal{N}(\mathit{k})$ is sensitive to the relative phase of the contributions ${\alpha }_{\mathit{q},s}$ of the two sites s = A, B in the expression of each Bloch state $|{\psi }_{\mathit{q}}^{-}\rangle$. More precisely, although not sufficient to determine unambiguously the angles θ and ϕ, this measurement already provides the value of the product sin θ cos ϕ. To go one step further, Hauke, Lewenstein, and Eckardt (2014) suggested to apply an abrupt quench to the lattice parameters so that the Hamiltonian becomes ${\widehat{H}}_{\mathit{q}}^{\prime }=\left(\hslash {\omega }_0/2\right){\widehat{\sigma }}_z$. One then lets the gas evolve in the lattice during a time interval t before measuring the momentum distribution. Since the evolution during this time simply consists of adding the phase $\pm {\omega }_{0}t/2\text{to}{\alpha }_{\mathit{q},s}$ the momentum distribution at time t reads

$$\mathcal{N}(\mathit{k},t)=|\tilde{w}(\mathit{k}){|}^2\left[1-\sin {\theta }_k\cos \left({\varphi }_k+{\omega }_{0}t\right)\right].$$ (70)

By repeating this procedure for various times t and measuring the amplitude and the phase of the time-oscillating signal, one can determine simultaneously ϕ and θ at any point in the BZ.

This procedure was implemented by Fläschner et al. (2016) using a hexagonal lattice of tubes filled with fermionic ⁴⁰K atoms. The unit cell for this graphenelike geometry contains two sites and the lattice parameters are chosen such that there is initially a large energy offset $\hslash {\omega }_{AB}$ between the A and B sites, corresponding to essentially flat bands with no tunneling. As explained in Sec. III.D, the dynamics in the lattice can be restored by a resonant, circular shaking of the lattice at a frequency $\mathrm{\Omega }\approx {\omega }_{AB}$. In the experiment of Fläschner et al. (2016), the shaking was produced by a phase modulation of the three laser beams forming the lattice, and it also resulted in a non-negligible value for the Berry curvature. Once the atoms equilibrated in this lattice, the abrupt quench needed for the procedure of Hauke, Lewenstein, and Eckardt (2014) was obtained by simply switching off the modulation. Measured amplitudes and phases of the time oscillation of $\mathcal{N}(\mathit{k},t)$ are plotted in Fig. 16, together with the Berry curvature reconstructed from Eq. (67). One then expects the integral of Ω_q to be an integer $\mathcal{C}$ times 2π, where $\mathcal{C}$ is the Chern index of the populated band. Here the reconstructed Berry curvature leads to a value of $\mathcal{C}$ compatible with 0 (Fläschner et al., 2016). This is in agreement with the expected band topology in this case.

FIG. 16.

(Left column) Amplitude ∝ sin θ_q and (middle column) phase ϕ_q obtained from the fits to the oscillation (70) of the momentum distribution. From those fit results, one can reconstruct the (right column) momentum-resolved Berry curvature given in units of the inverse reciprocal lattice vector length |b| squared. From Fläschner et al., 2016.

The method outlined by Hauke, Lewenstein, and Eckardt (2014) is reminiscent of a previous proposal by Alba et al. (2011). There the two lattice sites A and B are supposed to be occupied by two different internal (pseudospin) states $|a\rangle$ and $|b\rangle$. The momentum distribution measurement can be done in a spin-resolved way, which provides the local spin polarization for the lowest band [see Eq. (30)]:

$$\frac{h_z(\mathit{q})}{|\mathit{h}(\mathit{q})|}=\cos {\theta }_{\mathit{q}}=\frac{{\mathcal{N}}_b(\mathit{q})-{\mathcal{N}}_a(\mathit{q})}{{\mathcal{N}}_a(\mathit{q})+{\mathcal{N}}_b(\mathit{q})}.$$ (71)

The other two components of h/|h| can be obtained by inducing a coherent transition between $|a\rangle \text{and}|b\rangle$. (Raman pulse) with an adjustable phase and duration in order to rotate the pseudospin during the time of flight. Once the direction of h(q) is known at all points of the Brillouin zone, the value of the Berry curvature follows from Eq. (67).

3. Topological bands and spin-orbit coupling

When the considered lattice has some specific geometrical symmetries, the assessment of the topological nature of a band can be notably simplified with respect to the procedure outlined above. One does not need to characterize the eigenstates of the Hamiltonian at all points of the Brillouin zone to determine if the integral of the Berry curvature (67) over this zone is nonzero, and it is sufficient to concentrate on some highly symmetric points. The basis of this simplification, which is discussed in Appendix A for the case of a 1D lattice [see, in particular, Eq. (A6)], was outlined by Liu et al. (2013) for a 2D square optical lattice for pseudospin 1/2 particles in the presence of spin-orbit coupling terms.

Let us briefly outline the main result of Liu et al. (2013). Suppose that the Hamiltonian is invariant under the combined action of the spin operator ${\widehat{\sigma }}_z$ and the spatial operator transforming a Bravais lattice vector R into −R. Consider the energy eigenstates (Bloch states) at the four points of the BZ: $\left\{{\mathbf{\Lambda }}_i\right\}=\{(0,0),(0,\pi ),(\pi ,0),(\pi ,\pi )\},i=1,\dots ,4$. The two Bloch states $|{\psi }_{\pm }\left({\mathbf{\Lambda }}_i\right)\rangle$ at each of these locations are also eigenstates of ${\widehat{\sigma }}_z$, and the corresponding eigenvalues ${\xi }_{i,\pm }$ can take only the values +1 or −1. Now one can show that the sign of the product $P_{\eta }=\prod _i{\xi }_{i,\eta }$ of the four ${\xi }_{i,\eta }$ of a given subband η = ± is directly related to the Chern number of this subband. More specifically, if the sign of P_η is negative, the Chern number of the subband η is odd, hence nonzero: this unambiguously signals a topological band. If P_η has a positive sign, the Chern number of the subband η is even, and this most likely signals a nontopological character for this subband (zero Chern number).

This procedure was realized experimentally by the type of lattice we described in Sec. III.F.1 involving two pairs of retroreflected Raman lasers intersecting at right angles. This configuration can produce the reciprocal-space tight-binding Hamiltonian with the following generic form (29):

$$\begin{gathered} {\widehat{H}}_{\mathit{q}}=2t_{\text{SO}}[\sin (a{q}_y){\widehat{\sigma }}_x+\sin (a{q}_x){\widehat{\sigma }}_y] \\ +[m_z-2t_0(\cos (a{q}_x)+\cos (a{q}_y))]{\widehat{\sigma }}_z, \end{gathered}$$ (72)

where m_z is proportional to the detuning from Raman resonance. The two amplitudes t₀ and t_SO characterize the tunneling amplitudes without and with spin flip, respectively. They can be controlled independently by varying the intensities of the two pairs of laser beams. In particular the term proportional to t_SO can be simplified in the limit of low momenta into $\propto k_y{\widehat{\sigma }}_x+k_x{\widehat{\sigma }}_y$ corresponding to the usual form of the Rashba-Dresselhaus spin-orbit coupling for a bulk material (Galitski and Spielman, 2013).

An interesting feature of this Hamiltonian is the possibility to control the topology of the lowest band: It is nontrivial if and only if $|m_z|<4t_0$. Wu et al. (2016) tested this prediction by loading the ⁸⁷Rb gas at a temperature T ~ 100 nK such that the lowest band was quasiuniformly filled, whereas the population of higher bands remains small. The polarization defined in Eq. (71) was measured by a spin-resolved imaging of the atomic cloud after time of flight, and the product P₋ for the lowest band was found to be negative in the expected range of values of m_z.

4. Momentum distribution and edges states

It is well known from integer quantum Hall physics that the nontrivial topology of a band can give rise to a quantized Hall conductance σ_xy. Applying a voltage difference V_y between the two opposite edges of a rectangular 2D sample gives rise to a global current $I_x={\sigma }_{xy}{V}_y$ along the x direction. This current flows on the edges of the sample in a chiral way, with a positive value $I_x^{(+)}$ on the y > 0 side of the sample and a negative value $I_x^{(-)}$ on the y < 0 side (Hatsugai, 1993). In the absence of an applied voltage (V_y = 0), the edge currents are still nonzero but they exactly compensate each other: $I_x^{(-)}=-I_x^{(+)}$

The possibility to engineer a 2D atomic gas with one real dimension and one synthetic dimension that we discussed in Sec. IV.B.4 offers a way to directly access these edge currents in a cold atom experiment. Indeed when the second dimension (labeled y) is synthetic, i.e., associated with an internal degree of freedom (pseudospin), one expects a given sign of I_x for the largest value of the pseudospin and the opposite sign for its smallest value.

The advantage of a synthetic dimension for observing these edge states is clear: It provides a sharp boundary to the sample, whereas a standard 2D optical lattice would lead to edge states that would be smeared over several lattice sites, and hence much more difficult to observe. In addition, the momentum distribution can be measured individually for each pseudospin value. One thus obtains the value of the current on each “site” of the synthetic direction. The transposition of such a measurement to a real direction y implies a single-site resolving imaging, which is much more demanding from an experimental point of view. However, the use of spin states for synthetic dimensions greatly limits the potential extent of the synthetic dimension: in the extreme limit of just two spin states, the system can even behave as if it were all edge with no bulk (Hügel and Paredes, 2014). For narrow systems with synthetic extent less than q for flux p/q, the states behave more like those in a continuum [with a single guiding center, see the supplementary material in Stuhl et al. (2015)], and as the width further increases, the familiar topological edge modes emerge, but remain slightly gapped at the edge of the 1D Brillouin zone from the bulk bands.

In addition, recent experiments have instead turned to using momentum states for a synthetic dimension, in principle allowing for more extended systems. Indeed the edge states associated with the 1D SSH model have already been observed using a momentum-space lattice (Meier, An, and Gadway, 2016).

We show in Fig. 17 the results of an experiment performed by Mancini et al. (2015). A gas of fermionic ¹⁷³Yb atoms can tunnel between the sites of an optical lattice along the x direction, with an essentially frozen motion along the two other (real) y and z directions. The synthetic direction consists of three Zeeman substates m = −5/2, −1/2, +3/2 selected among the six Zeeman states of the ground level. The “tunneling” along this synthetic direction is provided by a pair of light beams. These beams induce stimulated Raman processes between the Zeeman states, hence the desired laser-induced hopping. These beams also provide an artificial gauge field thanks to the space-dependent phase ±φ(x) printed on the atomic state in a Δm = ±2 transition.

FIG. 17.

Direct visualization of an edge-state current for a two-dimension (one real, one synthetic) lattice in the presence of an artificial magnetic field. Upper row: Momentum distributions n_m (k) along the real direction x for the three values of the pseudospin m corresponding to the synthetic direction. The value m = −1/2 can be viewed as the bulk, whereas m = +3/2 and m = −5/2 corresponding to the opposite edges of the sample along the synthetic dimension. Lower row: Function $h_m(k)=n_m(k)-n_m(-k)$. From Mancini et al., 2015.

The atoms are prepared in a metallic state (less than one atom/lattice site) in the lowest band of the single-particle Hamiltonian. Figure 17 shows the momentum distributions n_m(k) along the x direction for the three values m of the pseudospin. Here the central value of the pseudospin (m = −1/2) plays the role of the bulk of the material. The momentum distribution in this internal state is thus symmetric around 0, corresponding to a null net current. In contrast, a nonzero current is associated with the side values of the pseudospin: The distribution for the largest (smallest) value of m is displaced toward positive (respectively, negative) values. The displacement is made even clearer in the second row of Fig. 17 where the function h_m(k) = n_m(k) − n_m(−k) is plotted. Mancini et al. (2015) also checked that the sign of the edge current is reversed when the sign of the artificial magnetic field is changed.

B. Wave-packet analysis of the BZ topology

Cold atom experiments offer the possibility to prepare the particles in a state described by a wave packet that is well localized in momentum space, in comparison with the size of the Brillouin zone. In this case, the dynamics of the wave packet directly reveals the local properties in the BZ: energy landscape E(q) and Berry curvature Ω(q). These properties can be encoded either on the dynamics of the center of the wave packet or on the interference pattern that occurs when several paths can be simultaneously followed.

1. Bloch oscillations and Zak phase in 1D

Conceptually the simplest example of a wave-packet analysis of the band topology is found in a 1D lattice of period a, for which the BZ extends between q = −π/a and π/a. When an atom initially prepared with the quasimomentum q₀ is submitted to an additional uniform force F, its quasimomentum q(t) periodically spans the Brillouin zone (Bloch oscillation) at a frequency $aF/h:q(t)=q_0+Ft/\hslash$ (mod2π/a). The phase that is accumulated in this periodic motion contains relevant information about the topology of the energy bands.

Since Bloch oscillations play a key role in several instances in the following, we briefly outline the principle of their theoretical description. The Hamiltonian of the particle in the presence of the periodic lattice potential V(x) and of the force F reads $\widehat{H}={\widehat{p}}^2/2m+V(\widehat{x})-F\widehat{x}$. Let us write the initial state of the particle $\psi (x,0)={\text{e}}^{\text{i}x{q}_0}{u}_{q_0}^{(n)}(x)$, where $u_{q_0}^{(n)}(x)$ is the periodic part of the Bloch function associated with the nth band and the quasimomentum q₀. One can look for a solution of the time-dependent Schrödinger equation under the usual Bloch form $\psi (x,t)={\text{e}}^{\text{i}xq(t)}u(x,t)$. The evolution of u is governed by the periodic Hamiltonian ${\widehat{H}}_{q(t)}={[\widehat{p}+\hslash q(t)]}^2/2m+V(\widehat{x})$; therefore the solution u(x, t) remains spatially periodic at any time. If we add the assumption that the force F is weak enough so that interband transitions play a negligible role, the state of the particle will adiabatically follow the corresponding Bloch state of the nth band, i.e., $u(x,t)={\text{e}}^{\text{i}\phi (t)}{u}_{q(t)}^{(n)}(x)$, and the relevant information is encoded in the phase $\phi (t)$. Let us focus on the state of the particle after one Bloch period. At this moment, the quasimomentum is back to its initial value q₀ and the phase is the sum of two contributions: (i) the dynamical phase $-\int E[q(t)]\text{d}t/\hslash$ and (ii) the Zak phase of the band, Eq. (14).

The first measurement of the Zak phase in a cold atom context was performed by Atala et al. (2013). A 1D superlattice was made out of two standing waves with a long and a short period [see Sebby-Strabley et al. (2006) and Trotzky et al. (2008) for two methods for creating double-well superlattice potentials], generating the potential (50) where both the relative phase ϕ and the amplitudes V_long,short are control parameters. As detailed in Sec. III.B, this constitutes a realization of the Hamiltonian proposed by Rice and Mele (1982), reducing to the SSH model (Su, Schrieffer, and Heeger, 1979) for ϕ = π/2. Here we restrict for simplicity to the SSH case and we refer the reader to Atala et al. (2013) for a discussion of the general case. First we recall that, as discussed in Sec. II.C.1, the Zak phase itself is not invariant under gauge transformations in momentum space. Indeed it depends on the choice of the relative phases between Wannier states, i.e., the arbitrariness in deciding if the unit cell is formed by a pair {A_j, B_j} [N_A = N_B in Eq. (24)] or by a pair {B_{j − 1}, A_j} [N_A = N_B + 1 in Eq. (24)]. However, once this choice is made, the gauge-invariant quantity $\delta {\varphi }_{\text{Zak}}\equiv {\varphi }_{\text{Zak}}^{\left(D_1\right)}-{\varphi }_{\text{Zak}}^{\left(D_2\right)}=\pi$, where D₁ and D₂ correspond to the two possible dimerizations of the system, obtained by choosing either ϕ = 0 or ϕ = π.

In order to measure $\delta {\varphi }_{\text{Zak}}$, Atala et al. (2013) first prepared the atoms in a wave packet localized at the bottom of the lowest band. Then using a π/2 microwave pulse the atoms were placed in a superposition of two spin states $|\uparrow \rangle \text{and}|\downarrow \rangle$ which underwent Bloch oscillations in opposite directions in the presence of a magnetic gradient (Fig. 18). At the moment when the two wave packets reach the edges of the BZ, the Zak phase is encoded in the relative phase between these wave packets. In principle it could thus be read using a second π/2 microwave pulse, closing the interferometer in quasimomentum space. However, the magnetic field fluctuations in the lab cause a random dephasing between the two arms of the interferometer and prevent one from performing this direct measurement. To circumvent this problem, Atala et al. (2013) used a spin echo technique. A second microwave pulse flipped the spins as the atoms reached the edges of the BZ and at the same moment, the dimerization was changed by switching ϕ from 0 to π, corresponding to an exchange of states between the lower and the upper bands. Finally the two paths were recombined when the wave packets reached the top of the upper band, and the accumulated phase revealed the value of $\delta {\varphi }_{\text{Zak}}$. The experimental result $\delta {\varphi }_{\text{Zak}}/\pi =0.97(2)$ was in excellent agreement with the expected value.

FIG. 18.

Two-band spectrum of the SSH Hamiltonian and Zak phase measurement. An initial wave packet is prepared at the bottom of the lowest band (left column). Each atom is in the superposition of the $|\pm \rangle$ spin states, which experience opposite forces in the presence of a magnetic field gradient. After a combination of exchanges of the atomic internal state and of the dimerization (middle column), the two wave packets recombine at the top of the highest band (right column). The measurement of the accumulated phase provides the value of the Zak phase. From Atala et al., 2013.

2. Measurement of the anomalous velocity

We now turn to the case of a 2D lattice and we investigate how the semiclassical dynamics of a wave packet can reveal the topological features of a given energy band. The starting point is the set of equations that govern the evolution of the average quasimomentum q and average position r when a constant force F is superimposed to the lattice potential

$$\hslash \stackrel{.}{\mathit{q}}=\mathit{F},$$ (73)

$$\hslash \stackrel{.}{\mathit{r}}={\mathbf{\nabla }}_{\mathit{q}}E(\mathit{q})+\mathbf{\Omega }(\mathit{q})\times \mathit{F}.$$ (74)

This set of equations is valid when the applied force F is weak enough, so that transitions to other bands can be neglected. With the first equation we recover the Bloch oscillation phenomenon: The momentum drifts linearly in time in response to the applied force F. The second equation provides the value of the velocity of the wave packet at a given position in the BZ. It contains two contributions: The first one is the well-known expression for the group velocity [see, e.g., Ashcroft and Mermin (1976) for the case of a periodic potential]. The second contribution, which is sometimes called the “anomalous velocity” (Xiao, Chang, and Niu, 2010), couples the wave-packet dynamics to the local value of the Berry curvature Ω(q). As a result of this contribution, the recording of a given trajectory inside the Brillouin zone allows one to reconstruct the Berry curvature along this trajectory (Price and Cooper, 2012).

This method was implemented by Jotzu et al. (2014) in order to analyze the topology of a 2D optical lattice in the vicinity of Dirac points. The experiment was performed with a brick-wall lattice [Fig. 10(a)], which is topologically equivalent to the hexagonal lattice of graphene, with two sites A and B per unit cell (Tarruell et al., 2012). In such a lattice, when only nearest-neighbor couplings A → B and B → A are taken into account, the spectrum consists of two bands touching at two Dirac points Q₊ and Q₋ in the BZ [Fig. 19(a)]. As explained in Sec. III.C, an additional circular shaking of the lattice breaks the time-reversal symmetry of the system and allows one to lift the degeneracy at the Dirac points, with the two subbands acquiring a nontrivial topology. Another possibility to lift this degeneracy consists of simply introducing an energy offset between sites A and B. However, in this case each subband is topologically trivial (Sec. II.C.2). With this setup one can thus explore the phase diagram of the Haldane model shown in Fig. 10(b).

FIG. 19.

(a) Brillouin zone and Dirac points Q_± for the brick-wall lattice of Fig. 10. (b) When the degeneracy is lifted by introducing an energy offset between the A and B sites, the subbands are topologically trivial. For the lowest band, the Berry curvature has opposite signs in the vicinity of Q_±. The anomalous velocity (white arrows) thus has opposite chirality at these points. (c) Lifting of degeneracy obtained by adding complex next-nearest-neighbor (NNN) couplings (Haldane, 1988). The Berry curvature then keeps a constant sign over the BZ, and the anomalous velocity has the same chirality at both points. Adapted from Jotzu et al., 2014.

Using an analysis of wave-packet dynamics close to the points Q_±, Jotzu et al. (2014) studied the transition between the topological and trivial cases. Starting from a wave packet at the center of the BZ, they dragged it close to Q₊ or Q₋ using the force F created by a magnetic gradient. The curvature of the motion of the wave packet in the BZ revealed the sign of the anomalous velocity, hence of the Berry curvature. In the trivial case, Ω(Q₊) and Ω(Q₋) have opposite signs, hence the Chern number which is proportional to the integral of Ω(q) over the BZ is zero [Fig. 19(b)]. In the topologically nontrivial case, Ω(Q_±) have the same sign [Fig. 19(c)]. The measurements of the drift of the wave packet performed by Jotzu et al. (2014) quantitatively confirmed this scenario.

3. Interferometry in the BZ

We now come back to the simple case of a graphenelike lattice with only nearest-neighbor (NN) couplings, in which case the two subbands touch at two Dirac points Q_±. In this case it is not possible to calculate the Berry curvature Ω for each subband because the definition (67) is singular in Q_±. The situation can be viewed as an equivalent (for momentum space) of an infinitely narrow solenoid (in real space) providing a finite magnetic flux. In the latter case it is known that the presence of the solenoid can be probed by interferometric means. This is indeed a paradigmatic example for the Aharonov-Bohm effect: Using a two-path interferometer such that the solenoid passes through its enclosed area, there exists between the two paths a phase difference proportional to the magnetic flux. In the case of a two-path interferometer enclosing a Dirac point in momentum space, the phase difference between the two paths is π (Mikitik and Sharlai, 1999).

This phase shift was measured in the cold atom context by Duca et al. (2015). The graphenelike structure was generated using an optical lattice with three beams at 120° angles. Initially the external state of the ⁸⁷Rb atoms is a wave packet located at the center of the BZ, and their internal state is a given Zeeman state $|\uparrow \rangle$. A microwave π/2 pulse prepares a coherent superposition of $|\uparrow \rangle$ and $|\downarrow \rangle$, where the magnetic moment of $|\downarrow \rangle$ is opposite to that of $|\uparrow \rangle$. Then the displacements of the two corresponding wave packets are controlled using simultaneously: (i) a lattice acceleration along y which creates the same inertial force on the two Zeeman states; (ii) a magnetic gradient which creates opposite forces on them along x; and (iii) a π microwave pulse which exchanges the atomic spins in the middle of the trajectories, in order to close the interferometer in momentum space. The result obtained by Duca et al. (2015), shown in Fig. 20, shows that a phase difference of ~π between the two paths appears if and only if the enclosed area contains one of the two Dirac points. Using a similar technique Li et al. (2016) could also access the Wilson line regime, which generalizes the Berry phase concept to the case where the state of the system belongs to a (quasi) degenerate manifold. Li et al. (2016) investigated the case where the transport from one place to another in the BZ is done in a time much shorter than the inverse of the frequency width of the bands. In that experiment the transport was characterized by a single phase factor and could be analyzed within the framework of Stückelberg interferometry (Lim, Fuchs, and Montambaux, 2014, 2015). However, in more complex situations, interferometry can also reveal non-Abelian features of the transport (Alexandradinata, Dai, and Andrei Bernevig, 2014).

FIG. 20.

Aharonov-Bohm interferometer around a Dirac point. Starting from a wave packet localized at the center of the BZ of a graphenelike optical lattice, one measures the phase difference φ between the two paths of an interferometer ending at the quasimomentum (k_x = 0, k_y). When one of the Dirac points K or K′ is inside the enclosed area of the interferometer, the measured value for φ is in good agreement with the prediction φ = π. From Duca et al., 2015.

4. Direct imaging of edge magnetoplasmons

Although the synthetic-dimension systems can be described by the same Harper-Hofstadter Hamiltonian as with real-space laser-assisted tunneling approaches, using the spin degree of freedom to encode one spatial direction enables new preparation, control, and measurement opportunities. For example, the finite number of spin states in effect generates infinitely sharp hard-wall boundaries in the synthetic dimension; the synthetic-dimension tunneling can be applied and removed on any experimental time scale; atoms can be initially prepared in any initial synthetic-dimension site; and conventional time-of-flight measurements, along with Stern-Gerlach techniques, allow the near-perfect resolution of “position” in the spin direction.

Recent synthetic-dimension experiments (Mancini et al., 2015; Stuhl et al., 2015) used these techniques to directly image the evolution of edge magnetoplasmons. In a quantum Hall system, an edge magnetoplasmon is the quantum analog to the skipping cyclotron orbits which “bounce” down the edge of a system in a chiral manner, essentially following cyclotron orbits that are interrupted by the system’s edge; see Fig. 4. These dynamical excitations evolve with a characteristic frequency given by the cyclotron frequency and are superposition states between different Landau levels. These should not be confused with the chiral edge modes that underlie quantized conductance: these modes are built from states all within the same Landau level. These modes have not been observed in two-dimensional experiments; however, their analog has been observed in 1D experiments, also using synthetic dimensions, where the end modes of 1D systems have been observed (Meier, An, and Gadway, 2016).

In condensed matter systems, edge magnetoplasmons certainly have been launched and detected, both in steady state, in magnetic focusing experiments (van Houten et al., 1989), and directly in the time domain using electrostatic gates (Ashoori et al., 1992). Cold atom experiments complete the picture by allowing for direct space and time resolution of these skipping orbits.

In these experiments (Mancini et al., 2015; Stuhl et al., 2015), the system was initialized with no hopping along the synthetic dimension, and with all atoms in either one or the other edge along the synthetic dimension. Once this initial state was prepared, tunneling was instantly turned on. The highly localized initial state, described by a superposition of different Landau levels, then began to evolve, skipping down the system’s edge. Following a tunable period of evolution time-of-flight measurements directly imaged the position along the synthetic direction along with velocity in the spatial direction,¹ which gives position by direct imaging. As shown in Fig. 21, this prescription allows for direct imaging of edge magnetoplasmons.

FIG. 21.

Edge-magnetoplasmon trajectories, where the displacement was obtained by integrating the velocity. From Stuhl et al., 2015.

C. Transport measurements

In the last part of this section, we turn to experimental procedures that are closer in spirit to well-established condensed matter techniques. Starting from a uniformly filled band, one can perform a transportlike experiment, measure the displacement of the whole cloud in the lattice after a certain duration, and infer nontrivial topological aspects from this dynamics (Dauphin and Goldman, 2013).

1. Adiabatic pumping

The concept of a quantized pump introduced by Thouless (1983) has been described in general terms in Sec. II.F. It requires a lattice whose shape is controlled by at least two effective parameters, such as Δ and J′ − J for the Rice-Mele model [see Eq. (40)]. One starts with a gas that uniformly fills a band of the lattice. Then one slowly modifies the lattice shape in a way that corresponds to a closed loop in parameter space. As shown in Appendix A, the resulting displacement of the center of mass of the gas is then quantized in units of the lattice spacing.

This concept can be addressed in a 1D geometry, using a superlattice with the potential (50). As explained in Sec. III.B, the motion of atoms in the two lowest bands of this potential for a deep enough lattice can be described by the Rice-Mele Hamiltonian. Suppose that the relative phase ϕ of the long-period lattice is scanned from 0 to 2π, while the lattice depths V_long and V_short are kept fixed; see Fig. 22. Initially when ϕ = 0, the energy of an A site is below that of a B site, i.e., Δ < 0 in the framework of the Rice-Mele model. At this moment the superlattice is symmetric, hence the tunnel matrix elements J′ and J from B_j to A_j and A_{j + 1} are equal. When 0 < ϕ < π, the energy barrier between A_j and B_j is smaller than that between B_j and A_{j + 1}, hence J′ > J. During this time period, Δ increases and changes sign when ϕ = π/2. During the second half of the cycle π < ϕ < 2π, one now finds J′ < J and Δ again changes sign. When ϕ = 2π, the system has performed a closed loop in the parameter space (J′ − J, Δ), encircling the vortex localized in J′ − J = 0, Δ = 0. One can therefore conclude that the center of mass of the cloud has moved by one lattice cell. In the limiting case of a particle initially localized in one of the lattice sites, one can recover this result by a simple reasoning based on the adiabatic following of the instantaneous energy levels; see Fig. 22.

A Thouless pump was implemented in cold atom setups (Lohse et al., 2016; Lu et al., 2016; Nakajima et al., 2016). The experiment by Nakajima et al. (2016) used a superlattice potential similar to that represented in Fig. 22, with V_long = 30E_R and V_short = 20E_R, respectively, with $E_{\text{R}}={\hslash }^2/(8m{a}^2)$. Using a gas of noninteracting ¹⁷¹Yb atoms (fermions), Nakajima et al. (2016) verified that the displacement of the cloud when ϕ varies from 0 to 2π is equal to one lattice period, as expected; see Fig. 23. They also checked that it is topologically robust, i.e., it does not change if one slightly deforms the path in parameter space by adding a time variation modulation of V_long and V_short. However, if the modification is such that the closed trajectory in parameter space (J′ − J, Δ) does not encircle the origin point anymore, the displacement per pump cycle drops to zero.

FIG. 23.

Quantization of the displacement of a cloud of fermionic ¹⁷¹Yb atoms placed in a 1D optical superlattice described by the Rice-Mele Hamiltonian. Depending on the closed loop in parameter space (J′ − J ≡ 2δ, Δ), the displacement can be positive, zero, or negative. The time T represents the duration of a pump cycle. From Nakajima et al., 2016.

2. Centre-of-mass dynamics in 2D

As a last example of a cold atom probe of band topology, let us briefly describe the analysis of the dynamics associated with the Harper-Hofstadter Hamiltonian (46) by Aidelsburger et al. (2015). This Hamiltonian was implemented using the laser-induced hopping method explained in Sec. III.D, producing the flux per plaquette ϕ_AB = π/2. As a result of this applied gauge field, the lowest band of the lattice was split in four subbands, with Chern numbers (+1, −1, −1, +1) with the two intermediate subbands touching at Dirac points. Bosonic ⁸⁷Rb atoms were loaded in majority in the lowest subband of the lattice, at a temperature such that this subband was filled quasiuniformly. Then a weak uniform force along the y axis originating from a gradient of the light intensity of an auxiliary beam was applied to the atoms for an adjustable duration t. The position of the center of mass of the atom cloud was monitored as a function of time and it revealed the topology of the bands. At short times (typically less than 50 ms), the drift of the cloud along the x direction, similar to a Hall current, was found to be linear with t; see Fig. 24. It provided a measurement of the anomalous velocity in good agreement with the expected value for the Chern number of the lowest subband. For longer times t, heating originating from the resonant modulation applied to the lattice induced transitions between the various subbands, which eventually get equally populated. Since the sum of all four Chern numbers is zero, the drift of the center of mass then stopped. A careful analysis of this dynamics, associated with an independent measurement of the population of each subband, provided a measurement of the individual Chern numbers with a 1% precision.

FIG. 24.

Transport measurement in a square lattice with a flux or plaquette ϕ_AB = π/2 (data 1). A Hall-type current is observed through the displacement of the center of mass of the cloud along the x direction, when a uniform force inducing Bloch oscillations (BO) is applied along y for an adjustable time. For short BO times, only the lowest subband is populated, resulting in a linear variation of x(t) with time, in agreement with the expected Chern index of this subband. At longer times, heating processes equalize the populations of the subbands and the Hall drift stops. When the flux is zero, no Hall current is observed (data 2). Adapted from Aidelsburger et al., 2015.

V. INTERACTION EFFECTS

Some of the most interesting directions for future work on cold atoms in topological optical lattices involve studies of collective effects that arise from interparticle interactions. Such studies hold promise for the exploration of novel phases of matter and to elucidate the role of topology in strongly correlated many-body systems.

A. Two-body interactions

The methods previously described for generating topological lattices consist either of periodic modulation of site energies, forming a so-called “Floquet” system (see Appendix B), or of Raman coupling of internal spin states, leading to optically “dressed states” of the atoms. Both of these methods lead to effective interactions between particles in the resulting energy bands that have some novel features.

1. Beyond contact interactions

For ultracold atoms in the continuum, the typical two-body interactions are dominated by the s-wave scattering, which can be represented by a short-range (contact) interaction gδ(r₁ − r₂), where the Dirac δ distribution is supposed to be properly regularized. However, for particles “dressed” by a laser field as in the optical lattices described, the interactions typically acquire nonlocal character.

a. Continuum models

For the continuum setting of optical flux lattices of Sec. III.F with laser plane waves inducing Raman couplings between internal spin states, nonlocal interactions can arise from the momentum dependence of the dressed-state wave functions. For the two-state system described by the Hamiltonian (72), an energy eigenstate in a given band can be written as

$$|{\mathrm{\Psi }}_{\mathit{q}}\rangle =|{\psi }_{\mathit{q}}\rangle \otimes |{\mathrm{\Sigma }}_{\mathit{q}}\rangle ,$$ (75)

i.e., the product of an orbital Bloch state $|{\psi }_{\mathit{q}}\rangle$ of quasimomentum q and of a q-dependent spin state $|{\mathrm{\Sigma }}_{\mathit{q}}\rangle$ written in the basis $|\pm {\rangle }_z$. The dependence of the spin component $|{\mathrm{\Sigma }}_{\mathit{q}}\rangle$ on a wave vector has direct consequences on the two-body scattering matrix elements within this band.

Let us first recall the simple case of spinless or fully polarized particles. For the contact interaction $\widehat{V}=g\delta (\widehat{\mathit{r}})$, the matrix element of $\widehat{V}$ for a pair of free distinguishable particles transitioning from (q₁, q₂) → (q₁ + Q, q₂ − Q) is equal to g (up to a normalization factor) and it is independent of the momentum transfer Q. Here we neglect for simplicity energy-dependent corrections of the s-wave scattering amplitude, which is valid when Q⁻¹ is larger than the s-wave scattering length, a criterion usually satisfied in quantum gases. For two indistinguishable particles, physical observables involve the sum over the two permutations

$$\left({\mathit{q}}_1,{\mathit{q}}_2\right)\to \left({\mathit{q}}_1+\mathit{Q},{\mathit{q}}_2-\mathit{Q}\right)\text{or}\left({\mathit{q}}_2-\mathit{Q},{\mathit{q}}_1+\mathit{Q}\right)$$ (76)

with a relative sign of ε = ±1 for bosons or fermions. The matrix element of $\widehat{V}$ is doubled for polarized bosons and vanishes for polarized fermions: the latter result simply reflects the fact that single-component fermions are insensitive to the contact interaction, since the Pauli principle precludes them from having the same spatial position.

Consider now the scattering of atoms in the dressed-state band with wave functions (75) and assume for simplicity that the contact interaction is independent of the internal states $|\pm \rangle$. For bosons and fermions (ε = ±1), the transition matrix element of $\widehat{V}$ for the two-path process (76) is now

$$\begin{gathered} \langle {\psi }_{{\mathit{q}}_1+\mathit{Q}},{\psi }_{{\mathit{q}}_2-\mathit{Q}}|\widehat{V}|{\psi }_{{\mathit{q}}_1},{\psi }_{{\mathit{q}}_2}\rangle \langle {\mathrm{\Sigma }}_{{\mathit{q}}_1+\mathit{Q}}|{\mathrm{\Sigma }}_{{\mathit{q}}_1}\rangle \langle {\mathrm{\Sigma }}_{{\mathit{q}}_2-\mathit{Q}}|{\mathrm{\Sigma }}_{{\mathit{q}}_2}\rangle \\ +\epsilon \langle {\psi }_{{\mathit{q}}_2-\mathit{Q}},{\psi }_{{\mathit{q}}_1+\mathit{Q}}|\widehat{V}|{\psi }_{{\mathit{q}}_1},{\psi }_{{\mathit{q}}_2}\rangle \langle {\mathrm{\Sigma }}_{{\mathit{q}}_2-\mathit{Q}}|{\mathrm{\Sigma }}_{{\mathit{q}}_1}\rangle \langle {\mathrm{\Sigma }}_{{\mathit{q}}_1+\mathit{Q}}|{\mathrm{\Sigma }}_{{\mathit{q}}_2}\rangle . \end{gathered}$$

For fermions, this matrix element no longer vanishes in general. For example, for Q = 0, it is $\propto g(1-{|\langle {\mathrm{\Sigma }}_{{\mathit{q}}_2}|{\mathrm{\Sigma }}_{{\mathit{q}}_1}\rangle |}^2)$. This is an important result that shows that starting from contact-interacting fermions occupying a nondegenerate band, the optical dressing leads to an interacting one-component Fermi gas, more precisely to effective p-wave interactions (Zhang et al., 2008). The possibility of interaction between two identical fermions can be viewed as arising from nonadiabatic corrections to the optical dressing, allowing two particles to coincide in real space by being in different internal dressed states, dependent on their momentum (Cooper and Dalibard, 2011). The momentum dependence of the dressed-state wave functions converts the contact interactions into a momentum-dependent interaction for atoms, thereby allowing effective p-wave scattering even at ultralow temperatures. Similarly, dressed-state bosons can acquire a momentum-dependent interaction allowing the appearance of d-wave and higher angular-momentum channels in the scattering (Williams et al., 2012).

b. Tight-binding models

For tight-binding lattice systems, we described in Sec. III how periodic driving at frequency $\omega$ can be used to tailor the amplitudes and phases of the hopping matrix elements between the sites. We demonstrated how, at rapid driving frequencies, an effective Hamiltonian with potentially complex modified tunneling amplitudes arises. This is the effective Floquet Hamiltonian for the modulated system, which governs the dynamics of the particles on time scales large compared to the period of the modulation, $T=2\pi /\omega$, as described in Appendix B. In the presence of interparticle interactions, e.g., Hubbard interaction U between particles on the same lattice site, new terms appear in this effective Floquet Hamiltonian, including nonlocal interactions (Eckardt, 2017). To understand the origin of the nonlocal interactions, consider the modulated two-site system described in Sec. III.C under a harmonic drive of the energy offset between the sites Δ(t) = (Δ/2) $\cos \omega t$. The unitary transformation Eq. (52) leads to a Hamiltonian

$${\widehat{H}}^{\prime }=-J[{\text{e}}^{\text{i}{\varphi }_{\text{P}}(t)}|r\rangle \langle l|+{\text{e}}^{-\text{i}{\varphi }_{\text{P}}(t)}|l\rangle \langle r|],$$ (77)

$${\varphi }_{\text{P}}(t)=\frac{\mathrm{\Delta }}{\hslash \omega }\sin (\omega t).$$ (78)

It is convenient to expand this Hamiltonian in its harmonics

$${\widehat{H}}^{\prime }=-J\sum _{m=-\infty }^{\infty }{\mathcal{J}}_m\left(\frac{\mathrm{\Delta }}{\hslash \omega }\right){\text{e}}^{\text{i}m\omega t}|r\rangle \langle l|+\text{H}.\text{c}$$ (79)

where ${\mathcal{J}}_m(z)$ are Bessel functions of the first kind. The m = 0 term gives the time-averaged Hamiltonian discussed in Sec. III: it describes intersite tunneling with an effective tunneling rate that is modified from the bare rate J by ${\mathcal{J}}_0(\mathrm{\Delta }/\hslash \omega )$. For $\hslash \omega$ large compared to all other energy scales (tunneling J and any on-site-interaction energy U) the higher-order terms |m| > 0 are far off resonant, so are rapidly oscillating and have small effects on the wave function. Still these terms do perturb the atomic wave function, leading to the new features we are interested in here. For a particle that is initially in the right well $|r\rangle$, a rapidly oscillating perturbation ${\widehat{V}}_m{\text{e}}^{\text{i}m\omega t}$ (i.e., m ≠ 0) causes a first-order correction to the wave function of

$$|{\psi }^{\prime }\rangle \approx |r\rangle +|l\rangle \langle l|{\widehat{V}}_m|r\rangle {\text{e}}^{\text{i}m\omega t/2}\frac{\sin (m\omega t/2)}{m\hslash \omega }$$ (80)

$$\approx |r\rangle -J{\mathcal{J}}_m(\mathrm{\Delta }/\hslash \omega ){\text{e}}^{\text{i}m\omega t/2}\frac{\sin (m\omega t/2)}{m\hslash \omega }|l\rangle .$$ (81)

Thus, these terms induce a small nonzero probability for the particle to be in the left well,

$$p_l=\sum _{m\ne 0}\frac{J^2}{2{(m\hslash \omega )}^2}{\left[{\mathcal{J}}_m\left(\frac{\mathrm{\Delta }}{\hslash \omega }\right)\right]}^2,$$ (82)

after averaging over the rapid oscillations and summing over all such terms. If in addition to the tunneling (78) the static Hamiltonian has an on-site interaction between particles in the left well, which we consider to be a Hubbard interaction $U{\widehat{n}}_l\left({\widehat{n}}_l-1\right)/2$ (with ${\widehat{n}}_l$ the number operator in the left well), then these rapidly oscillating terms that move particles from the right to the left well will give rise to effective nonlocal interactions $U_{lr}^{\text{eff}}{\widehat{n}}_l{\widehat{n}}_r$, with

$$U_{lr}^{\text{eff}}=U{p}_l\propto \frac{U{J}^2}{{(\hslash \omega )}^2}.$$ (83)

A similar nonlocal term will arise from interactions in the right well. A full analysis of such effects is best achieved through a construction of the Floquet Hamiltonian at high drive frequency via the Magnus expansion (Goldman and Dalibard, 2014) or other systematic approach (Eckardt and Anisimovas,2015). An overview of the Magnus expansion is given in Appendix B.

c. Synthetic dimensions

An extreme example of nonlocal interactions arises for systems involving synthetic dimensions (Celi et al., 2014; Mancini et al., 2015; Stuhl et al., 2015). There interactions are typically long ranged among the set of s = 1, N_s internal states which form the synthetic dimension and short ranged in the d spatial coordinates. For a synthetic dimension formed from an internal spin degree of freedom, the interactions are of infinite range in the synthetic dimension and of conventional short range in position. For example spin-exchange interactions can be viewed as a correlated tunneling, such as $\left(m,m^{\prime }\right)\to \left(m-1,m^{\prime }+1\right)$. Such systems realize interesting intermediate situations in which the single-particle physics can be viewed as d + 1 dimensional (for N_s is large) while the interactions remain d dimensional. For a synthetic dimension formed from simple harmonic oscillator subband states (Price, Ozawa, and Goldman, 2017) the interactions fall off with increasing spacing along the synthetic dimension. Interactions in an effective two-leg ladder, formed from spin-orbit coupled strontium atoms, have been studied experimentally by Bromley et al. (2018).

d. Current-density coupling

Finally, we note that the novel two-body interactions that are induced by Raman coupling or Floquet modulation can also include terms that are not just density-density interactions, but that couple the particle motion to particle density. These effects arise naturally in photon-assisted tunneling between lattice sites as a consequence of interaction-induced energy shifts. The imposed energy offset between two adjacent lattice sites is modified by the on-site interactions U in such a way that the photon-assisted tunneling can be brought into or out of resonance depending on the occupations of the sites by other particles. This leads to a density-dependent tunneling term of the form

$$\sum _i\left[J\left({\widehat{n}}_i,{\widehat{n}}_{i+1}\right){\widehat{b}}_i^{†}{\widehat{b}}_{i+1}+\text{H}.\text{c}.\right],$$ (84)

shown here for spinless bosons. Such situations were analyzed by Aidelsburger et al. (2015), Bermudez and Porras (2015), and Račiūnas et al. (2016). The density-dependent corrections are typically a small modification of the photon-assisted hopping in current experimental setups of gauge fields on optical lattices [see supplementary information in Aidelsburger et al. (2015)]. However, they can be made to dominate in regimes where U is large, such that the photon drive frequency $\omega$ is not resonant with the bare detuning Δ but with Δ ± U. Such situations have been explored in experiments on two-component Fermi systems (Görg et al., 2018; Xu et al., 2018). Analogous coupling between current and density arises also in the continuum if interactions lead to detunings that influence the local dressed states, thus causing the induced vector potential A to be density dependent (Edmonds et al., 2013). Density-mediated hopping can also arise in settings where the single-particle energy bands are flat (dispersionless). Then individual particles do not move, being localized to a region of size of the Wannier orbital, and particle motion arises only through interparticle interactions. Such settings include the flat energy bands of frustrated lattices, such as the Creutz ladder (Creutz, 1999; Mazza et al., 2012; Jünemann et al., 2017) in 1D, and the kagome (Huber and Altman, 2010) and dice lattices (Möller and Cooper, 2012) in 2D, as well as for particles in dressed states of internal spin states in which the direct nearest-neighbor tunneling can be made to vanish (Bilitewski and Cooper, 2016).

2. Floquet heating

The explicit time dependence of the Hamiltonian in periodically driven systems relaxes energy conservation and leads to forms of inelastic scattering and heating not present in the time-independent case. For a Floquet system at frequency $\omega$, these correspond to the absorption (or emission) of an integer number of “photons” of energy $\hslash \omega$ from the external drive. For the “Floquet-Bloch” waves of a spatial- and time-periodic potential, such inelastic scattering could occur even for a single particle that scatters from a defect in the lattice, which allows a momentum transfer. However, an important source of potential inelastic scattering is for pairs of particles via the interparticle interactions, i.e., inelastic two-body collisions.

A general description of the inelastic scattering of Floquet-Bloch waves was provided by Bilitewski and Cooper (2015b). Consider a time-periodic Hamiltonian of frequency $\omega$ and denote the single-particle energy band, with band index ν, by the energies ϵ_ν(q) defined as continuous functions of q over the Brillouin zone. Owing to the time periodicity, this can be viewed as one member of a sequence of Floquet energy bands ${ϵ}_{\nu }^{(m)}(\mathit{q})={ϵ}_{\nu }(\mathit{q})+m\hslash \omega$ (Eckardt, 2017). We define inelastic scattering to be those processes in which m or ν, or both, change under a scattering event. For weak scattering from state i to state f, the inelastic rate can be computed through a “Floquet Fermi golden rule” (Kitagawa et al., 2011)

$${\gamma }_{\text{i}\to \text{f}}={\frac{2\pi }{\hslash }\sum _m|\langle \langle {\mathrm{\Phi }}_{\text{f}}^{(m)}|\widehat{V}{\mathrm{\Phi }}_{\text{i}}^{(0)}\rangle \rangle |}^2\delta \left(E_{\text{i}}-E_{\text{f}}-m\hslash \omega \right),$$ (85)

where $|{\mathrm{\Phi }}_{\text{f},\text{i}}^{(m)}(t)\rangle \equiv {\text{e}}^{-\text{i}m\omega t}|{\mathrm{\Phi }}_{\text{f},\text{i}}^{(0)}(t)\rangle \text{and}\langle \langle {\mathrm{\Phi }}_1|{\mathrm{\Phi }}_2\rangle \rangle \equiv (1/T){\int }_0^T\langle {\mathrm{\Phi }}_1|{\mathrm{\Phi }}_2\rangle \text{d}t$. Here $\widehat{V}$ can denote a one-body potential (e.g., a lattice defect) or a two-body interaction. Processes with nonzero Δm correspond to the exchange of Δm quanta from the drive field, changing the energy of the atom by $m\hslash \omega$. This provides a simple prescription by which to calculate the inelastic (Δm ≠ 0) contribution to the two-body scattering of Floquet-Bloch states. Stepping beyond the two-body calculation to a many-body setting can be achieved by analyzing instabilities within the Gross-Pitaevskii description (Choudhury and Mueller, 2014, 2015; Lellouch et al., 2017).

Calculations for the parameters used in the experimental studies of weakly interacting bosons in the Harper-Hofstadter model (Aidelsburger et al., 2015) show that the heating rates observed in those experiments are consistent with the expected inelastic two-body scattering processes dominated by single-photon absorption (Bilitewski and Cooper, 2015a). This analysis emphasizes the role played by the motion transverse to the 2D plane along the weakly confined third dimension. The application of an optical lattice to confine this motion and open up gaps at the one-photon resonance is expected to significantly reduce the heating rate in such experiments (Bilitewski and Cooper, 2015a; Choudhury and Mueller, 2015). The excitation of motion along tubes, transverse to the optical lattice, has been argued to also be responsible for heating rates in an experimental study of a periodically modulated 1D lattice (Reitter et al., 2017). In strongly driven systems (Weinberg et al., 2015) particle transfer to higher bands can arise from multiphoton resonances at the single-particle level (Sträter and Eckardt, 2016).

Floquet heating in the full, many-body system presents an interesting theoretical issue which remains an active area of investigation. That energy is not conserved leads to the expectation that the system will be driven to an infinite temperature state at long times (Lazarides, Das, and Moessner, 2014). This expectation relies on the assumption that energy is redistributed between all degrees of freedom through the interparticle interactions. There can, however, arise situations in which many-body systems show steady states that are not at infinite temperature (D’Alessio and Polkovnikov, 2013; Chandran and Sondhi, 2016), or in which there form prethermalized states on intermediate time scales (Bukov et al., 2015; Canovi, Kollar, and Eckstein, 2016). Furthermore, in settings involving disorder, it has been shown that many-body localized (MBL) phases can be robust to Floquet modulations, allowing the existence of nonthermal steady states to arbitrarily long times (Abanin, De Roeck, and Huveneers, 2016). A striking example of such a “Floquet MBL” phase is the Floquet time crystal (Moessner and Sondhi, 2017).

B. Many-body phases

The topological optical lattices described support an array of many-body phases. Novel features arise for weakly interacting gases through the geometrical and topological characters of the underlying band structure. Furthermore, there can arise interesting strongly correlated phases, driven by strong interparticle interactions.

1. Bose-Einstein condensates

For an optical lattice loaded with a gas of noninteracting bosons one expects the ground state to be a Bose-Einstein condensate (BEC), in which all particles condense at the minimum of the lowest energy band. This expectation applies just as well to the topological optical lattices as to regular optical lattices. However, topological optical lattices can bring several novel features.

• (1)For systems without time-reversal symmetry (as required to generate a Chern band), the individual Bloch wave functions have phase variations which in general give rise to nonzero local current density. Since the Bloch wave functions are stationary states, these currents must be divergenceless, but this still allows the BEC to support circulating currents in dimensions d > 1. These currents take the form of the local current density of a vortex lattice. An example is shown in Fig. 25.
• (2)For topological optical lattices in d > 1 the energy minimum in which the BEC forms will, in general, be characterized by a nonzero Berry curvature. As described in Sec. V.C this Berry curvature affects the collective modes of the BEC.
• (3)There can arise situations in which there are a set of degenerate energy minima. An important example is provided by the Harper-Hofstadter model, for which the energy band typically has multiple degenerate minima. For example, at flux ϕ_AB= 2π/q the band has q degenerate minima in the magnetic Brillouin zone. For noninteracting particles, there is a macroscopic degeneracy associated with the occupation of these q degenerate single-particle states: a BEC could form in any linear superposition of these states; or indeed a “fragmented” condensate could form (Mueller et al., 2006). The inclusion of interactions U ≠ 0 is required to resolve this macroscopic degeneracy. The simplest way to include interactions is via Gross-Pitaevskii mean-field theory. This is valid for sufficiently weak interactions $U\ll J$ and at high mean particle density $\overline{n}\gg 1$. Studies of the mean-field ground state (in regimes of both weak and strong interactions, $U\overline{n}\ll J$ and $U\overline{n}\gg J$) show that repulsive interactions stabilize a simple BEC with the form of a vortex lattice (Straley and Barnett, 1993; Zhang et al., 2010; Powell et al., 2011). This state breaks the underlying translational symmetry of the lattice, so there are several discrete (symmetry-related) states that are degenerate. For example, for flux ϕ_AB = 2π/3 it has the form of vortex lines along diagonals of the lattice; see Fig. 25. Numerical studies of the vortex lattice ground states for $U\overline{n}\gg J$ have been conducted for a wide range of flux ϕ_AB: these show complex behavior with many competing vortex lattice structures (Straley and Barnett, 1993).

FIG. 25.

A vortex lattice configuration for weakly interacting bosons in the Harper-Hofstadter model at flux ϕ_AB = 2π/3. The gauge-invariant currents flow on the links between the sites of the square lattice. The pattern of current breaks the translational invariance of the system. The strongly circulating currents (shown as solid lines and arrows) are around plaquettes that lie along diagonal lines. These are the lattice equivalents of the “vortex cores,” now distorted from the triangular lattice expected in the continuum models, to be pinned to the plaquettes of the square lattice. There are weak countercirculating currents around other plaquettes, such that the net particle flow vanishes, when coarse grained on scales large compared to the lattice spacing.

Similar vortex lattice states appear in ladder systems. In experiments on weakly interacting bosons on a two-leg ladder with flux, Atala et al. (2014) demonstrated a transition between a uniform superfluid phase with Meissner-like chiral currents and a vortex phase (with broken translational symmetry along the ladder) as a function of the tunneling strength across the rungs of the ladder, akin to the Meissner and vortex lattice phases of a type-II superconductor.

2. Topological superfluids

In both the tight-binding lattices and the Raman-dressed flux lattices, situations can arise in which there are nonlocal interactions between fermions in a single band. This allows attractive p-wave pairing and can lead to interesting forms of topological superfluidity with “Majorana” excitations. Here we discuss the general features of these topological superfluids.

Their properties are understood within mean-field theory, as described by the BdG Hamiltonian. This takes the form

$$\widehat{H}-\mu \widehat{N}=\sum _{\alpha ,\beta }\left[{\epsilon }_{\alpha \beta }{\widehat{c}}_{\alpha }^{†}{\widehat{c}}_{\beta }+\frac{1}{2}({\mathrm{\Delta }}_{\alpha \beta }{\widehat{c}}_{\alpha }^{†}{\widehat{c}}_{\beta }^{†}+{\mathrm{\Delta }}_{\alpha \beta }^{*}{\widehat{c}}_{\beta }{\widehat{c}}_{\alpha })\right],$$ (86)

where ${\widehat{c}}_{\alpha }^{(†)}$ are fermionic creation or annihilation operators for the single-particle states labeled by α = 1,...,N_s, which encodes both positional and internal (spin) degrees of freedom. They obey the fermionic anticommutation relations $\{{\widehat{c}}_{\alpha },{\widehat{c}}_{\beta }\}=\{{\widehat{c}}_{\alpha }^{†},{\widehat{c}}_{\beta }^{†}\}=0,\{{\widehat{c}}_{\alpha },{\widehat{c}}_{\beta }^{†}\}={\delta }_{\alpha \beta }$. The N_s × N_s matrix $\underset{\_}{\underset{\_}{\epsilon }}$ describes the conventional particle motion and potentials and must be Hermitian ${\epsilon }_{\alpha \beta }^{*}={\epsilon }_{\beta \alpha }$; the N_s × N_s matrix $\underset{\_}{\underset{\_}{\mathrm{\Delta }}}$ represents the superconducting pairing and is antisymmetric ${\mathrm{\Delta }}_{\alpha \beta }=-{\mathrm{\Delta }}_{\beta \alpha }$.

It is convenient to express the Bogoliubov–de Gennes Hamiltonian as (up to a constant shift)

$$\widehat{H}-\mu \widehat{N}=\frac{1}{2}({\widehat{\underset{¯}{c}}}^{†}\widehat{\underset{¯}{c}}){\mathcal{H}}^{\text{BdG}}\left(\begin{array}{c}\widehat{\underset{\_}{c}}\\ {\widehat{\underset{\_}{c}}}^{†}\end{array}\right),$$ (87)

$${\mathcal{H}}^{\text{BdG}}=\left(\begin{array}{cc}\underset{\_}{\underset{\_}{\epsilon }}& \underset{\_}{\underset{\_}{\mathrm{\Delta }}}\\ -{\underset{\_}{\underset{\_}{\mathrm{\Delta }}}}^{*}& -{\underset{\_}{\underset{\_}{\epsilon }}}^{*}\end{array}\right),$$ (88)

where ${(\widehat{\underset{\_}{c}},{\widehat{\underset{\_}{c}}}^{†})}^{\text{T}}$ is a 2N_s-component column vector formed by listing all fermionic destruction ${\widehat{c}}_{\alpha =1,\dots ,N_s}$ and creation ${\widehat{c}}_{\alpha =1,\dots ,N_s}^{†}$ operators. The quasiparticle excitations are determined by the spectrum of the 2N_s × 2N_s matrix ${\mathcal{H}}^{\text{BdG}}$

$$E_{\lambda }\left(\begin{array}{l}{\underset{\_}{u}}^{(\lambda )}\hfill \\ {\underset{\_}{v}}^{(\lambda )}\hfill \end{array}\right)={\mathcal{H}}^{\text{BdG}}\left(\begin{array}{l}{\underset{\_}{u}}^{(\lambda )}\hfill \\ {\underset{\_}{v}}^{(\lambda )}\hfill \end{array}\right)$$ (89)

in terms of the 2N_s-component vector of amplitudes $u_{\alpha =1,\dots ,N_s}^{(\lambda )}$ and $v_{\alpha =1,\dots ,N_s}^{(\lambda )}$, where λ labels the 2N_s eigenvalues. The matrix BdG Hamiltonian (88) has a special symmetry:

$${\mathcal{H}}^{\text{BdG}}=-\left(\begin{array}{cc}\underset{\_}{\underset{\_}{0}}& \underset{\_}{\underset{\_}{I}}\\ \underset{\_}{\underset{\_}{I}}& \underset{\_}{\underset{\_}{0}}\end{array}\right){[{\mathcal{H}}^{\text{BdG}}]}^{*}\left(\begin{array}{cc}\underset{\_}{\underset{\_}{0}}& \underset{\_}{\underset{\_}{I}}\\ \underset{\_}{\underset{\_}{I}}& \underset{\_}{\underset{\_}{0}}\end{array}\right),$$ (90)

where $\underset{\_}{\underset{\_}{0}}$ and $\underset{\_}{\underset{\_}{I}}$ are the N_s × N_s null and identity matrices, respectively. This has the consequence that for any eigenstate ${({\underset{\_}{u}}^{(\lambda )},{\underset{\_}{v}}^{(\lambda )})}^{\text{T}}$ with eigenvalue E_λ there is another eigenstate

$$\left(\begin{array}{c}{\underset{\_}{u}}^{(\overline{\lambda })}\\ {\underset{\_}{v}}^{(\overline{\lambda })}\end{array}\right)=\left(\begin{array}{c}{\underset{\_}{v}}^{(\lambda )*}\\ {\underset{\_}{u}}^{(\lambda )*}\end{array}\right)$$ (91)

with eigenvalue $E_{\overline{\lambda }}=-E_{\lambda }$: i.e., the spectrum is symmetric in energy around E = 0. (Note that energies have been defined relative to the chemical potential μ.) This intrinsic particle-hole symmetry represents an inherent redundancy in the theory, by which the eigenstates of ${\mathcal{H}}^{\text{BdG}}$ must include both the destruction and the creation operator of any quasiparticle state (Bernevig and Hughes, 2013). Specifically, defining the operator associated with each eigenvector λ = 1,...,2N_s

$${\widehat{C}}_{\lambda }=\sum _{\alpha }{u}_{\alpha }^{(\lambda )}{\widehat{c}}_{\alpha }+v_{\alpha }^{(\lambda )}{\widehat{c}}_{\alpha }^{†}$$ (92)

the Hamiltonian may be expressed in the diagonalized form

$$\widehat{H}-\mu \widehat{N}=\frac{1}{2}\sum _{\lambda =1}^{2N_s}{E}_{\lambda }{\widehat{C}}_{\lambda }^{†}{\widehat{C}}_{\lambda }.$$ (93)

The symmetry (91) allows this to be written as

$$\widehat{H}-\mu \widehat{N}=\frac{1}{2}\sum _{\lambda =1}^{N_s}{E}_{\lambda }{\widehat{C}}_{\lambda }^{†}{\widehat{C}}_{\lambda }+E_{\overline{\lambda }}{\widehat{C}}_{\overline{\lambda }}^{†}{\widehat{C}}_{\overline{\lambda }}$$ (94)

$$=\frac{1}{2}\sum _{\lambda =1}^{N_s}{E}_{\lambda }\left({\widehat{C}}_{\lambda }^{†}{\widehat{C}}_{\lambda }-{\widehat{C}}_{\lambda }{\widehat{C}}_{\lambda }^{†}\right)$$ (95)

$$=\sum _{\lambda =1}^{N_s}{E}_{\lambda }\left({\widehat{C}}_{\lambda }^{†}{\widehat{C}}_{\lambda }-\frac{1}{2}\right),$$ (96)

where the sum is now over just N_s eigenstates. These are conventionally chosen to be states for which E_λ ≥ 0, such that the ground state $|0\rangle$ is defined by ${\widehat{C}}_{\lambda }|0\rangle =0$, and ${\widehat{C}}_{\lambda }^{†}$ are the quasiparticle creation operators.

For spinless fermions in translationally invariant settings we can use the plane-wave operators ${\widehat{\tilde{c}}}_{\mathit{q}}\propto {\sum }_{\alpha }{\text{e}}^{-\text{i}\mathit{q}\cdot {\mathit{r}}_{\alpha }}{\widehat{c}}_{\alpha }$ to write

$$\widehat{H}-\mu \widehat{N}=\frac{1}{2}\sum _{\mathit{q}}\left({\widehat{\tilde{c}}}_{\mathit{q}}^{†}{\widehat{\tilde{c}}}_{-\mathit{q}}\right)\left(\begin{array}{cc}{\epsilon }_{\mathit{q}}& {\mathrm{\Delta }}_{\mathit{q}}\\ {\mathrm{\Delta }}_{\mathit{q}}^{*}& -{\epsilon }_{\mathit{q}}\end{array}\right)\left(\begin{array}{c}{\widehat{\tilde{c}}}_{\mathit{q}}\\ {\widehat{\tilde{c}}}_{-\mathit{q}}^{†}\end{array}\right)$$ (97)

with the superconducting gap required to satisfy Δ_−q = −Δ_q. The BdG matrix (88) reduces to a momentum-dependent 2 × 2 matrix ${\mathcal{H}}_{\mathit{q}}^{\text{BdG}}$. An important example is the Kitaev model of a p-wave superfluid in 1D, described in detail in Appendix A, for which

$${\mathcal{H}}_q^{\text{BdG}}=\left(\begin{array}{cc}-2J\cos (qa)-\mu & -2\text{i}\mathrm{\Delta }\sin (qa)\\ 2\text{i}\mathrm{\Delta }\sin (qa)& \mu +2J\cos (qa)\end{array}\right)$$ (98)

$$\equiv -\mathit{h}(q)\cdot \mathit{\sigma }.$$ (99)

The energy eigenvalues show the above particle-hole symmetry $E_q^{\pm }=\pm |\mathit{h}(q)|$. Furthermore, as shown in Appendix A, the bands are characterized by a winding number relating to how h(q) encircles the origin, analogous to the winding number of the SSH model. This winding number can be used to identify a topological superconducting phase.

On a finite geometry this topological phase hosts an exact zero-energy state on its boundary, i.e., with E_λ0 = 0 in Eq. (96). The prescription that we used to define the form (96) is ambiguous for such zero modes. Consider the operator ${\widehat{C}}_{{\lambda }_0}$ constructed via Eq. (92) from the eigenvector of such a zero mode λ₀. The particle-hole symmetry implies that there is another zero-energy state with label ${\overline{\lambda }}_0$, which, using Eq. (91), would lead to an operator ${\widehat{C}}_{{\overline{\lambda }}_0}={\widehat{C}}_{{\lambda }_0}^{†}$. Together, these two operators ${\widehat{C}}_{{\lambda }_0}^{†}\text{and}{\widehat{C}}_{{\overline{\lambda }}_0}$ describe the destruction or creation of a fermionic quasiparticle at $E_{{\lambda }_0}=E_{{\overline{\lambda }}_0}=0$. Since this excitation has zero energy, it describes a ground state that is twofold degenerate depending on whether this zero-energy mode is occupied or filled. It is therefore immaterial which of these operators we choose to view as a particle creation or destruction. Indeed, we could also choose to work in terms of operators that are linear superpositions. One particular choice is to define the Majorana operators

$${\widehat{\gamma }}_1\equiv \left({\widehat{C}}_{{\lambda }_0}+{\widehat{C}}_{{\lambda }_0}^{†}\right),$$ (100)

$${\widehat{\gamma }}_2\equiv \text{i}\left({\widehat{C}}_{{\lambda }_0}-{\widehat{C}}_{{\lambda }_0}^{†}\right),$$ (101)

which obey anticommutation relations $\left\{{\widehat{\gamma }}_i,{\widehat{\gamma }}_j\right\}=2{\delta }_{ij}$. Since the Majorana operators are self-adjoint ${\widehat{\gamma }}_i^{†}={\widehat{\gamma }}_i$, they can be viewed as describing particles that are their own antiparticles.

The above transformation to Majorana operators appears rather arbitrary: from a mathematical perspective one can always choose to work either in terms of the two Majorana operators ${\widehat{\gamma }}_1,{\widehat{\gamma }}_2$ or in terms of ${\widehat{C}}_{{\lambda }_0}$ and its adjoint ${\widehat{C}}_{{\lambda }_0}^{†}$. For topological superconductors there is a clear physical reason to prefer the Majorana operators: the Majoranas are spatially localized, each one tied to a single boundary or defect. Thus, local probes couple directly to the Majorana operators. In contrast, the quasiparticle operators ${\widehat{C}}_{{\lambda }_0}^{(†)}$ are nonlocal. The locality of the Majorana operators is shown explicitly in Appendix A for the Kitaev model, where one Majorana operator acts on the right boundary and one acts on the left boundary.

That the Majorana modes are spatially localized causes the system to have properties that are robust to external perturbations, including disorder potentials: the exact particle-hole symmetry enforces the mode to have E = 0. Departures from E = 0 can arise only from mixing with other Majorana modes; since the intervening superconducting state is gapped these corrections are suppressed exponentially in the distance between the local Majorana modes, e.g., the length of the 1D Kitaev chain. Note that the two Majorana modes—one at each end of the 1D Kitaev chain—describe a single fermionic excitation, such that one should view the Majorana as a fractionalized quasiparticle. In contrast, the zero-energy edge states of the SSH model correspond to two separate fermionic excitations, one at each end of the chain. As discussed in Sec. II.E.1 the edge states of the SSH model are sensitive to local perturbations which break the chiral symmetry.

The above example for the 1D topological superconductor has a very natural generalization to 2D. There, the bulk spectrum is of the form

$${\mathcal{H}}_{\mathit{q}}^{\text{BdG}}=\left(\begin{array}{cc}{ϵ}_{\mathit{q}}-\mu & {\mathrm{\Delta }}_{\mathit{q}}\\ {\mathrm{\Delta }}_{\mathit{q}}^{*}& \mu -{ϵ}_{\mathit{q}}\end{array}\right)\equiv -\mathit{h}(\mathit{q})\cdot \mathit{\sigma },$$ (102)

where q now runs over a 2D Brillouin zone. Topological superconducting states can appear in situations where the h(q) acquires all three components, such as in the continuum $p_x+\text{i}{p}_y$ superfluid, for which

$$h_z={\hslash }^2|\mathit{q}{|}^2/2m-\mu ,h_x+\text{i}{h}_y={\mathrm{\Delta }}_0(q_x+\text{i}{q}_y).$$ (103)

For μ > 0, the quasiparticle spectrum is fully gapped, and the unit vector h(q)/|h(q)| wraps the sphere as q runs over all values, indicating that this is a topological phase (Read and Green, 2000). At μ = 0 there is a gap-closing transition to a superconducting phase at μ < 0 which is nontopological. The 1D surface of this topological 2D superconductor has an edge mode that has Majorana character, albeit in a setting in which there is a continuum of edge modes. In this 2D setting localized Majorana modes arise as bound states on the cores of quantized vortices, i.e., point defects localized in the bulk of the system (introduced by rotation or other external means).

It is natural to search for topological superfluids using cold atoms. Many routes to p-wave pairing of single-component fermions have been suggested. These include methods involving a p-wave Feshbach resonance (Gurarie and Radzihovsky, 2007), long-range dipolar interactions (Baranov et al., 2012), or induced interactions via a background BEC (Wu and Bruun, 2016). In the context of this review, the connections arise through the use of spin-orbit coupling (optical dressing) to allow contact interactions (e.g., s-wave pairing) to lead to effective p-wave interactions between single-component fermions. Proposals of this kind have been presented in 3D, 2D (Zhang et al., 2008), and 1D (Nascimbène, 2013; Yan, Wan, and Wang, 2015).

3. Fractional quantum Hall states

The conditions for realizing fractional quantum Hall (FQH) states in 2D semiconductor systems are well understood (Prange and Girvin, 1990). The application of a strong magnetic field breaks the single-particle energy spectrum into degenerate Landau levels. When a Landau level is partially filled with electrons, the large number of ways in which the electrons can occupy the single-particle states gives a very high degeneracy. This degeneracy is lifted by repulsive interparticle interactions, leading to strongly correlated FQH ground states at certain ratios of particle density to flux density ν = n/n_ϕ. FQH states are characterized by a nonzero energy gap to making density excitations in the bulk. For temperatures below this gap they behave as incompressible liquids: with a bulk energy gap, but carrying gapless edge modes. In this sense they resemble integer quantum Hall states. However, the edge modes are not simply described as single-particle states but involve fractionalized quasiparticles (Wen, 1995). Similarly, the gapped particlelike excitations in the bulk of the system have fractional charge and are predicted to have fractional quantum exchange statistics (Stern, 2008).

The achievement of similar regimes with ultracold atoms would allow the exploration of several novel variations of FQH physics.

a. Bosons

Cold atom experiments have the potential to allow the first exploration of FQH states for bosons. Theory shows that contact-interacting bosons in the lowest Landau level exhibit FQH states provided the filling factor is not too large. These states include robust variants of interesting phases—the Moore-Read and Read-Rezayi phases—which are expected to exhibit non-Abelian particle exchange statistics (Cooper, 2008). The stabilization, and exploration, of non-Abelian phases is a much sought after goal, in part to find the first evidence that nature does exhibit this exotic possibility of many-body quantum theory and in part in connection with the possible relevance for quantum information processing (Nayak et al., 2008).

The physics of interacting bosons in the lowest Landau level can be accessed in the Harper-Hofstadter model at relatively low flux density $|{\varphi }_{\text{AB}}|\lesssim 2\pi /3$ for which the lowest band is similar to the continuum Landau level and where similar FQH states appear for bosons (Sørensen, Demler, and Lukin, 2005; Palmer and Jaksch, 2006; Hafezi et al., 2007; Möller and Cooper, 2009). Optical flux lattices, involving spin-orbit coupling, can lead to 2D energy bands that are very similar to the lowest Landau level: topological bands with unit Chern number and with very narrow energy dispersion. An advantage of this approach is that the flux density n_ϕ can be high, so FQH states are expected at high particle density n where interactions are strong. Exact diagonalization studies have established stable FQH states of bosons including exotic non-Abelian phases (Cooper and Dalibard, 2013; Sterdyniak et al., 2015).

b. Lattice effects

The use of optical lattices to generate topological energy bands naturally causes cold atomic gases to explore new aspects of FQH physics. The underlying lattice makes the single-particle states differ from those of the continuum Landau level and can influence the nature of the many-body ground states. For the Harper-Hofstadter model, the FQH states found at low flux density, where the bands resemble the continuum Landau level, are replaced by other strongly correlated phases at high flux densities where lattice effects become relevant.

It has been shown that states of the same form as FQH states of the continuum Landau level, the so-called “fractional Chern insulator” (FCI) states, can be formed, for bosons and fermions, in a variety of topological energy bands starting from models (such as the Haldane model) which are far removed from the continuum Landau level (Parameswaran, Roy, and Sondhi, 2013). Typically such models require the introduction of further-neighbor tunneling terms to flatten the lowest energy band, such that one can enter a regime of strong correlations (mean interaction energy larger than bandwidth) without mixing with higher bands. Indeed, it has been shown that by tailoring the tunneling Hamiltonian, one can construct models for which the exact many-body ground states are FQH states (Kapit and Mueller, 2010) or FCI states (Behrmann, Liu, and Bergholtz, 2016). No general theorem exists concerning the nature of the many-body ground state in a given Chern band. However, beyond flatness of the energy band, it is believed that flatness of the geometry of the states, as measured by the Berry curvature and by a quantity known as the Fubini-Study metric, is advantageous in stabilizing topological many-body phases (Parameswaran, Roy, and Sondhi, 2013).

A particularly interesting aspect of the topological energy bands in lattices is that these can differ qualitatively from a continuum Landau level, specifically if their Chern number differs from unity. Indeed, for the Harper-Hofstadter model at flux ϕ_AB = π + ϵ, with ϵ small, the lowest energy band has Chern number of 2, and so is topologically distinct from the lowest Landau level. Numerical calculations show the appearance of FQH phases for particles occupying this energy band. These are examples of FQH states that have no counterpart in the continuum Landau level but that are stabilized by the lattice itself (Möller and Cooper, 2009, 2015; He et al., 2017).

c. Symmetry-protected topological phases

The topological states of noninteracting Fermi systems (topological insulators and superconductors) are now viewed as examples of a more general class of a symmetry-protected topological (SPT) phase, which allows for interparticle interactions and bosonic statistics. SPT phases are defined by the conditions that they are gapped phases, with gapless edge modes, but unlike the FQH effect they do not involve particle fractionalization. Hence these states have a unique ground state on a periodic geometry, and the many-body ground state has only short-range entanglement (Senthil, 2015). The phases of strongly interacting bosons in Chern bands include cases of “integer” quantum Hall states of the bosons, which provide one of the cleanest realizations of SPT phases (Möller and Cooper, 2009, 2015; He et al., 2017). Here integer refers to the fact that the Hall conductance is an integer as opposed to fractional. Such phases still arise from strong interparticle interactions, albeit without fractionalized quasiparticles.

d. Ladders

Cold atomic gases provide ways in which to study ladderlike systems which are quasi-1D variants of FQH systems. These arise both in Harper-Hofstadter models with superlattices to create ladder geometries, and in systems involving a synthetic dimension for which there is naturally tight confinement. Both situations have been shown theoretically to support strongly correlated states that are closely related to FQH states (Cornfeld and Sela, 2015; Petrescu and Le Hur, 2015; Calvanese Strinati et al., 2017). A precise connection between FQH states on an infinite 2D system and the states in these quasi-1D settings can be made by considering the quantum Hall wave functions on a cylindrical geometry which is infinite in one direction but has finite circumference L in the other. Studies of the evolution of the ground state from 2D ($L\gg \overline{a}$, with $\overline{a}$ the mean interparticle spacing) into the “squeezed geometry” $(\text{small}L\lesssim \overline{a})$ show that many FQH states of the 2D systems evolve smoothly into charge-density-wave (CDW) states of the quasi-1D geometry. For example, the bosonic Laughlin state, at filling factor ν = 1/2, evolves into a CDW state which breaks translational symmetry to double the unit cell to give two degenerate ground states of the CDW. The fractionally charged quasiparticles of the FQH states map onto domain walls between the different symmetry-related CDW states.

4. Other strongly correlated phases

a. Chiral Mott insulator

For the Harper-Hofstadter-Hubbard model at strong interactions $U\gtrsim J$ the Gross-Pitaevskii approach fails. Just as in the case of vanishing magnetic field, there can be incompressible Mott phases, with n_i = integer. However, other strongly correlated phases are predicted to appear. One striking example is the chiral Mott insulator: an incompressible phase at integer filling (like the Mott insulator), but which carries a nonzero local current in the ground state (as does a vortex lattice). Numerical calculations indicate that, within a region of stability between Mott insulator and superfluid, the chiral Mott insulator can form the ground state of the Bose-Hubbard model with external flux on a variety of 2D lattices (Dhar et al., 2013; Zaletel et al., 2014; Vasić et al., 2015). In ladder systems the Mott-vortex phase found in numerical calculations (Greschner et al., 2015; Petrescu and Le Hur, 2015; Piraud et al., 2015) can be viewed as the 1D analog of the chiral Mott insulator.

b. Chiral spin states

For hard-core interactions U → ∞, interesting many-body states can still arise in the Harper-Hofstadter-Hubbard model for bosons provided n_i ≠ integer so the hard-core bosons are mobile. These bosons can be viewed as a spin-1/2 quantum magnet, with the phases of the tunneling matrix elements introducing frustrated magnetic interactions (Möller and Cooper, 2010). Thus, the FQH (or FCI) phases of these hard-core bosons can be viewed as quantum spin liquids (Kalmeyer and Laughlin, 1987). Other predicted quantum spin liquids may also find realization with these Bose-Hubbard models (Läuchli and Moessner, 2015). The phases of interacting fermions in Hubbard-like models with tunneling phases have also been studied theoretically. Much of the focus has been on the Haldane model for spin-1/2 fermions with on-site repulsion U. For systems close to half filling there is a competition between the band insulator, the Mott insulator, and various spin-symmetry-broken phases (Zheng et al., 2015; Imriška, Wang, and Troyer, 2016; Vanhala et al., 2016). The Mott insulating state naturally leads to frustrated spin models, with possible unconventional forms of ordering at very low temperatures, at the superexchange energy scale J²/U or below, including chiral spin states (Arun et al., 2016) and chiral spin liquids (Hickey et al., 2016).

c. Number-conserving topological superfluids

The theory of topological superfluids, Sec. V.B.2, is based on the mean-field treatment of pairing described by the Bogoliubov–de Gennes theory. In this theory, the number of pairs of fermions is not conserved. For a 1D system, such a mean-field theory can be appropriate in settings in which the superfluid pairing is proximity induced, e.g., by coupling to a bulk superfluid of fermion pairs with which pairs of particles can be exchanged and which can impose a fixed superconducting order parameter. However, in the absence of such a proximitizing medium the quantum fluctuations in 1D systems preclude the existence of any long-range order in the superconducting pairing and the structure of the mean-field theory should fail. Theoretical work has shown how 1D topological superfluids can still arise in such number-conserving settings. Models with microscopic symmetry can give rise to zero-energy modes, arising as exact degeneracies in the spectrum of an open chain in the topological phase (Fidkowski et al., 2011; Sau et al., 2011; Iemini et al., 2015, 2017; Lang and Buachler, 2015). This degeneracy is the many-body counterpart of the Majorana modes of the mean-field 1D topological superconductor. In settings without such a symmetry, topological degeneracies can arise in geometries in which modulation of the parameters along the chain lead to multiple interfaces between topological and nontopological phases (Ruhman, Berg, and Altman, 2015; Ruhman and Altman, 2017).

C. Experimental perspectives

Many of the experimental consequences of topological bands described in Sec. IV rely on the interactions between the particles being sufficiently weak that they can be treated as noninteracting. It is therefore important to consider what experimental observables can be used to characterize the properties of atoms in topological bands when interactions cannot be neglected.

1. Equilibrium observables

Some of the most important observables for characterizing the properties of the atoms are well established from studies of atomic gases in other settings without topological character. Measurements of the equation of state and observations of density-density correlations in time-of-flight imaging will be crucial for establishing the existence and forms of strongly correlated phases such as fractional quantum Hall states. Similarly, the possibility to image at the single-site level in quantum gas microscopes (Bakr et al., 2009; Sherson et al., 2010) will allow precise characterization of microscopic structure in these phases, including of the local currents, for example, in the chiral Mott insulator phase. A method for detecting local currents was presented in experiments from the Munich group (Atala et al., 2014).

2. Collective modes

Observations of the collective mode frequencies provide a sensitive way to detect properties of many-body systems (Dalfovo et al., 1999). For BECs formed in bands with geometrical character, the collective mode frequencies are sensitive to the Berry curvature at the band minimum (Price and Cooper, 2013). Consider a weakly interacting BEC in a single band minimum. We take the minimum to have isotropic effective mass M* and a local Berry curvature Ωe_z. The effect of Berry curvature on the collective modes can be readily determined by adapting the standard hydrodynamics approach (Pethick and Smith, 2002) to include the anomalous velocity from the Berry curvature. For a spherical harmonic trapping potential $V(\mathit{r})=(1/2)\mathrm{\Lambda }|\mathit{r}{|}^2,$ the collective modes have the same spatial structure as for Ω = 0 (Stringari, 1996), but the frequencies depend on the Berry curvature. For example, for small Ω the three angular-momentum components of the dipole mode are split by Δω = ΛΩ/2ℏ, leading to a precessional motion of the center-of-mass oscillation of the cloud at this frequency.

3. Edge states

For incompressible fluids that are topological, e.g., a topological insulator of noninteracting fermions, or a FQH fluid, there exists a special class of low-energy collective modes, which are the gapless edge states of the fluid. For noninteracting particles in Chern bands, these are the edge states discussed in Sec. II.D. For interacting systems these may not be easily described as single-particle excitations, but can still appear as long-lived surface excitations. Measurements of the propagation of surface waves can directly probe the edge-state structure, for example, allowing one to detect the number of edge channels and their respective velocities (Cazalilla, Barberán, and Cooper, 2005). The edge states also lead to highly characteristic dynamics in far-from-equilibrium situations in which the confining potential is removed (Goldman et al., 2013). Edge states appear also at interfaces between bulk regions of differing topologies, prepared, for example, by spatial modulation of the lattice potential (Goldman et al., 2016) and have been probed experimentally for the SSH model (Leder et al., 2016). Experiments using a quantum gas microscope have shown the influence of strong interparticle interactions on the chiral edge states in Harper-Hofstadter ladders (Tai et al., 2017).

4. rf excitation

Another natural probe of the edge states is to measure the spectrum for the removal of particles via rf excitation, ideally performed with single-site resolution (Bakr et al., 2009; Sherson et al., 2010) to focus on the boundary. Such spectra have been proposed as a means to detect localized Majorana modes in topological superfluids, appearing as a near zero-energy contribution inside the spectral gap (Grosfeld et al., 2007; Nascimbène, 2013). A definition of fractional statistics is provided by Haldane’s exclusion statistics (Haldane, 1991): a generalized version of Pauli blocking, by which the fractional quasiparticles reduce the number of available states for other quasiparticles in a well-defined, but fractional, manner. An observation of this effect requires counting many-body states and may be possible in precision spectroscopy of small FQH clusters (Cooper and Simon, 2015) in which the exclusion statistics reveal themselves in the count of spectral lines.

5. Adiabatic pumping

For topologically ordered systems, the existence of fractional low-energy particlelike excitations allows for new features in Thouless pumping. Specifically, under one full cycle of the adiabatic evolution of the pump, it is possible to transfer a fractional particle number across the system. (In the examples discussed above, the number of particles transferred was constrained to be an integer, set by the Chern number.) This fractional pumping is related to the existence of a ground state degeneracy: one cycle of the adiabatic pump converts one ground state into another degenerate ground state, and multiple cycles (transferring multiple fractional particles) are required before the system returns to its starting state. This picture forms the basis for understanding of the quantization of the Hall conductance in the fractional quantum Hall effect of 2D systems (Laughlin, 1981; Halperin, 1982). For narrow strips of quantum Hall systems, this physics smoothly evolves into the pumping of fractional charges in commensurate charge-density waves. The manifestation of such pumping for 1D fermionic systems with synthetic dimension was described by Mazza et al. (2015), Zeng, Wang, and Zhai (2015), and Taddia et al. (2017).

6. Hall conductivity from “heating”

An interesting way in which to measure the Hall conductivity σ_xy of a system, i.e., the transverse current density in response to a uniform force, is to measure the heating rate, as set by the rate of power absorption P_±(ω) caused by the application of a circularly polarized force F_±(t) = F₀(cos ωt, ± sin ωt). The dc Hall conductivity is found to be set by

$${\sigma }_{xy}=\frac{2}{\pi F_0^2{A}_{\text{syst}}}{\int }_0^{\infty }\text{d}\omega \frac{1}{\omega }\left[P_{+}(\omega )-P_{-}(\omega )\right],$$ (104)

i.e., the difference of the power absorption rates divided by frequency and integrated over all drive frequencies (Tran et al., 2017; Asteria et al., 2019). For noninteracting particles the power absorption can be found from measurements of the rates of depletion of initially occupied states Γ_±, via $P_{\pm }=(\hslash \omega ){\mathrm{\Gamma }}_{\pm },$ allowing the Hall conductivity to be determined via measurements of this depletion rate. For a filled Chern band, the integrated difference of depletion rates (104) is therefore expected to recover the quantized Hall conductivity of the filled bands. Equation (104) is however valid even for interacting particles, arising from a general sum rule for the linear response functions, and so provides a possible way to measure the Hall conductivity also in strongly correlated phases.

VI. OUTLOOK

A. Turning to atomic species from the lanthanide family

In this review we explored several classes of lattice schemes for which a nontrivial topology originates from a two-photon Raman coupling between various sublevels of the electronic ground state manifold. So far most experiments of this type were performed with atoms from the alkali-metal family, which are relatively easy to manipulate and cool down to quantum degeneracy. However, for such atoms, recoil heating due to spontaneous emission of photons may cause severe problems. Indeed the desired Raman coupling is significant only when the laser is detuned from the resonance by less than the fine-structure splitting Δ_f.s. of the resonance line (see Appendix C). Because of this relatively small detuning, spontaneous emission of photons occurs with a non-negligible rate γ. More precisely, one can define the merit factor $\mathcal{M}=\kappa /\gamma ,$ where κ is the desired Raman matrix element. Taking as an example the case of the fermionic alkali-metal atom ⁴⁰K, one finds after optimization $\mathcal{M}~{\mathrm{\Delta }}_{\text{f}.\text{s}.}/\mathrm{\Gamma }~{10}^5,$ where Γ stands for the natural width of the electronic excited state [see, e.g., Dalibard (2016) for details]. If one takes as a typical value ℏκ equal to the recoil energy, the photon scattering rate is γ ~ 0.3 s⁻¹, leading to the heating rate $\dot{E}~k_{\text{B}}\times 100\text{nK}/\text{s}.$ This may be too large for a reliable production of strongly correlated topological states.

A more favorable class of atoms is the lanthanide family, with species such as erbium or dysprosium. These atoms have two outer electrons and an incomplete inner shell (6s² and 4f¹⁰ for Dy). Because of this inner shell, the electronic ground state has a nonzero orbital angular momentum (L = 6 for Dy). The lower part of the atomic spectrum contains lines corresponding to the excitation either of one of the outer electrons or of one electron of the inner shell. By choosing a laser excitation close to a narrow line resonance and thus with a large detuning Δ_b from the closest broad line, one reaches after optimization $\mathcal{M}~{\mathrm{\Delta }}_b/{\mathrm{\Gamma }}_b.$ Because Δ_b is now of the order of an optical frequency, the merit factor is $\mathcal{M}~{10}^7,$ leading to γ ~ 10⁻³ s⁻¹ and to the residual heating $\dot{E}$ ~ k_B × 0.1 nK/s.

B. Topological lattices without light

Laser fields constitute a common element for all of the techniques described herein, and in virtually all of these cases these fields lead to unwanted off-resonant scattering leading to heating, atom loss, or both. As discussed in the previous section, these scattering processes might be mitigated or eliminated by suitable selection of different transitions or working with different atoms; however, fundamentally different approaches are also possible.

Of particular interest is the possibility to replace the laser fields with rf or microwave magnetic fields generated by a microfabricated atom chip. Unlike optical fields, these fields have practically no off-resonant emission, solving the inprinciple atomic physics limitation, in exchange for the technical complexity of working in the vicinity of an atom chip.

In one category of proposals, the atom chip serves simply as the source of a large time-modulated gradient magnetic field (Anderson, Spielman, and Juzeliunas, 2013). This produces in effect a series of pulses that generates spin-dependent gauge fields; the most simple implementation of this technique was realized in the lab (Luo et al., 2016), and although spontaneous scattering was eliminated, the fairly low frequency of their drive led to significant micromotion induced heating effects.

In a second category of proposals (Goldman et al., 2010), the atom chip consists of a large array of microfabricated parallel wires which give a near-field radio-frequency magnetic field that drives transitions in the same way as Raman lasers, as described here in the context of synthetic dimensions or intrinsic spin-dependent lattices. Because these fields are structured at the micrometer scale, far below the free-space wavelength of rf fields, these are near-field structures and the atomic ensemble must be on the micrometer scale from the chip’s surface.

C. Other topological insulators and topological metals

We have focused on specific recent experimental realizations of topological energy bands using cold gases: in 2D systems and in 1D systems with chiral symmetry. Routes to achieving topological superfluid phases in cold gases, arising from BCS pairing of fermions, have also been described in Sec. V.B.2.

As discussed in Sec. II.E other forms of topological energy bands can arise depending on dimensionality and the global symmetries that are imposed, according to the tenfold way (Chiu et al., 2016). Important cases in solid state systems are the ${\mathrm{\mathbb{Z}}}_2$ topological insulators that arise in spin-orbit coupled systems with time-reversal symmetry, in 2D and 3D. There are proposals for how to realize bands with this topology for cold gases. The required TRS can be implemented by fine-tuned engineering of the relevant terms in the Hamiltonian (Goldman et al., 2010). TRS can also be established as an intrinsic property for cold gases: in the absence of Zeeman splittings and of any circularly polarized light fields (Béri and Cooper, 2011). In 2D, the insulating state formed by filling a ${\mathrm{\mathbb{Z}}}_2$ topological band exhibits a quantized Hall effect for the spin current. A similar quantized spin Hall response also arises in a related setting without spin-orbit coupling, in which spin up and spin down fill Chern bands with equal and opposite Chern number: such energy bands have been realized for bosons in cold atoms (Aidelsburger et al., 2013) using laser-assisted tunneling to generate a Harper-Hofstadter model with equal and opposite fluxes for the two spin states (Kennedy et al., 2013).

Cold atomic gases provide a natural setting with which to explore certain forms of topological band that are more difficult to implement in solid state materials. The sublattice (chiral) symmetry is very fragile in solid state systems, as it is typically broken by any disorder potential. However, it can readily arise for optical lattice potentials in cold atom gases for which disorder can be negligible (Essin and Gurarie, 2012; Wang, Deng, and Duan, 2014). Similarly, there are predicted to be topological insulators beyond those classified in the tenfold way, arising from lattice symmetries which rely on a high spatial regularity that can arise in cold gases. These include topological invariants stabilized by crystalline lattice symmetries (Fu, 2011), and the Hopf insulator (Moore, Ran, and Wen, 2008; Deng et al., 2013), which also relies on a form of translational symmetry for stability (Liu, Vafa, and Xu, 2017). Note also that cold gases allow topology in dimensions higher than d = 3 to be explored, through the use of synthetic dimensions provided by internal degrees of freedom or by viewing a phase degree of freedom as an additional quasimomentum. Recent experimental work (Lohse et al., 2018) used pumping to demonstrate the topological response of an effective 4D quantum Hall system (Zhang and Hu, 2001) based on the theoretical proposal by Price et al. (2015).

An area of growing interest in solid state settings concerns so-called topological metals, or semimetals (Chiu et al., 2016). (There exist analogous topologically stable forms of gapless superconductors.) As for topological insulators, the classification of topological metals depends also on the dimensionality and the existence (or absence) of symmetries. However, since metals involve bands that are only partially filled by fermions, they cannot be characterized by the topological invariants used for insulators, which involve integrals over the filled energy bands. Instead, topological metals can be characterized by topological invariants defined in terms of integrals over the Fermi surface which separates filled from empty states (Volovik, 2003). One example of a topological metal is provided by the 2D honeycomb lattice with nearest-neighbor hopping. This realizes the band structure of graphene in which there are two Dirac points in BZ, each of which leads to a Fermi surface when the Fermi energy lies close to the Dirac point. Each of these Fermi surfaces is a topological metal, characterized by the Berry phase of Bloch states around the Fermi surface, which is π. This value is a topological invariant, i.e., it is robust to continuous changes of the underlying parameters, provided the system retains both time-reversal symmetry and inversion symmetry. (These symmetries ensure that the Berry curvature of the bands vanishes, except for singular delta-function contributions at the Dirac nodes which lead to the π Berry phases.) The Dirac node is topologically stable and can only be created or annihilated if it merges within another Dirac point. A related example that arises in 3D is the “Weyl point.” This can be viewed as a point source of Berry curvature in reciprocal space. The integral of the flux of Berry curvature through any closed 2D surface in reciprocal space is 2π$\mathcal{C}$, where $\mathcal{C}$ is required to be an integer. If this surface encloses a Weyl point, $|\mathcal{C}|=1.$ The Weyl point is topologically stable to deformations of the Hamiltonian, without any symmetry requirements, unless it annihilates with a second Weyl point of opposite charge. Optical lattice with Weyl points can be constructed using the laser-induced tunneling methods described in Sec. III.D (Dubček et al., 2015).

D. Far-from-equilibrium dynamics

Cold atomic gases readily allow the study of coherent quantum dynamics in far-from-equilibrium settings. Starting with a cold gas at thermal equilibrium, a sudden change of the Hamiltonian, a so-called “quantum quench,” typically leaves the system in a far-from-equilibrium state. Here we discuss some of the consequences of quantum quenches between Hamiltonians for which the ground states have different topological character. We focus on cases of noninteracting particles in topological energy bands.

Consider first an optical lattice potential which is varied slowly in time, such that the topological invariant of the lowest energy band differs between initial and final Hamiltonians. If the relevant topological invariant is symmetry protected, it is possible to have a smooth evolution between these two cases provided that the Hamiltonian breaks the symmetry at intervening times. An example of this is the pumping sequence of the RM model, which breaks the chiral symmetry of the SSH model and therefore allows a smooth evolution between the topologically distinct phases of the SSH model. When there is no symmetry protection (e.g., Chern bands in 2D), then the change in band topology requires the band gap to close at some intermediate time, as illustrated in Fig. 26. For a BEC formed close to the band minimum, such a change in band topology need not induce any phase transition: the Bloch wave functions of those states which the bosons occupy can evolve smoothly, allowing adiabatic evolution of the BEC, albeit into a very different local wave function. This allows, for example, the adiabatic formation of a dense vortex lattice (Baur and Cooper, 2013). However, for noninteracting fermions that fill the lowest energy band, the ground states of the initial and final Hamiltonians have different topological characters, so these two states must be separated by a phase transition.

FIG. 26.

The change of band Hamiltonian that causes the topological index of the lowest band v to change, via the closing of a band gap.

The far-from-equilibrium dynamics following a quantum quench between Hamiltonians whose ground states have different topologies has been explored for noninteracting fermions which fill a band. One striking result is that the topological invariant of the many-body state is often preserved under unitary time evolution. This has been shown for topological superfluids (Foster et al., 2013, 2014; Sacramento, 2016), and for Chern bands (Caio, Cooper, and Bhaseen, 2015; D’Alessio and Rigol, 2015). [Different behavior can arise for symmetry-protected topological invariants (McGinley and Cooper, 2018).] In interpreting this result it is crucial to distinguish between the topology of the Hamiltonian and the topology of the many-body state. The former is defined as the topological invariant constructed for the lowest energy band of the Hamiltonian, with Bloch wave functions $|u_q^{(0)}\rangle ,$ while the latter is defined as the topological invariant constructed from the wave functions which the fermions occupy $|u_{\mathit{q}}^s\rangle .$ These two sets of wave functions need only coincide if the many-body wave function is the ground state of the Hamiltonian. Out of equilibrium, for example, following a quantum quench, the Bloch wave function occupied by the particle at momentum q need not be an eigenstate of the Hamiltonian, so it becomes time dependent $|u_{\mathit{q}}^{\text{s}}(t)\rangle .$ We consider situations in which the periodicity of the lattice is preserved, such that wave vector q remains a good quantum number. That the topological invariant of the state is preserved is guaranteed provided the unitary evolution of the Bloch states $|u_{\mathit{q}}^{\text{s}}(t)\rangle ={\text{e}}^{-\text{i}{\widehat{H}}_{\mathit{q}}t/\hslash }|u_{\mathit{q}}^{\text{s}}(0)\rangle$ is smooth in momentum space q, which is true for short-range hopping. [For topological invariants that are symmetry protected, it is also required that the symmetry is not broken either explicitly or dynamically (McGinley and Cooper, 2018).] That said, at long times, the Bloch wave functions of the many-body state $|u_{\mathit{q}}^s(t)\rangle$ will become rapidly varying as a function of q. When the variation in q is so fast that this cannot be viewed as smooth on the scale of 2π/L, with L the typical sample dimension, then the bulk topological invariant becomes ill defined. Thus for any finite system, there is an upper time scale after the quench for which it is meaningful to expect the Chern number to be preserved. Simple estimates lead to the conclusion that this time is of order L/ν, with ν a characteristic group velocity of the final Hamiltonian (Caio, Cooper, and Bhaseen, 2016). Such systems can still be characterized by the Bott index (Loring and Hastings, 2010), which provides a real-space formulation of the Chern index applicable also to finite-sized systems. This has been used to find protocols for preparing nonequilibrium (Floquet) systems by which the Bott index undergoes transitions between topological values (D’Alessio and Polkovnikov, 2013; Ge and Rigol, 2017).

Although the topological invariant of the wave function is unchanged following the quench to a new Hamiltonian with different topology, this does not mean that there are no observable consequences of the new Hamiltonian. Local physical observables can be strongly influenced by the new Hamiltonian, despite the fact that the nonlocal topological invariant of the state is unchanged. Indeed, theory shows that under a quantum quench of the Haldane model the edge current quickly adapts to become close to that of the ground state of the final Hamiltonian (Caio, Cooper, and Bhaseen, 2015). Furthermore, by following the dynamics of the Bloch wave functions $|u_{\mathit{q}}^s(t)\rangle$ detailed information on the final Hamiltonian can be recovered (Gong and Ueda, 2017; Wang et al., 2017). This has been demonstrated in experiments by the Hamburg group (Tarnowski et al., 2017; Fläschner et al., 2018), using the band-mapping techniques described in Sec. IV.A.2 to reconstruct the dynamical evolution of the occupied wave functions $|u_{\mathit{q}}^s(t)\rangle .$ The experiments use a two-band model, for which the Hamiltonian at q may be written as

$${\widehat{H}}_{\mathit{q}}=h_0(\mathit{q})\widehat{1}-\mathit{h}(\mathit{q})\cdot \widehat{\mathit{\sigma }}.$$ (105)

The wave function of the fermion with q can be represented by a three-component unit vector e(q). If e(q) is aligned with h(q), then this is an energy eigenstate of the Hamiltonian. In the quench experiment, the system is prepared with e^initial(q) = (0,0, −1) for all wave vectors [the ground state of an initial Hamiltonian with h^initial(q) = (0,0,1)] and then the Hamiltonian is changed to its final value h(q). For general q this is not aligned with e^initial(q) so the wave function evolves in time, precessing around the local h(q). This leads to the appearance of nonzero components of the vector (e_x, e_y) which indicate interband coherences. The evolution can lead to the creation of vortex-antivortex pairs in these components (e_x, e_y). The appearance of each vortex-antivortex pair was shown to be associated with a cusp in the Loschmidt echo, hence giving rise to the characteristic feature of a “dynamical phase transition” (Heyl, 2018). Such singular features can arise even for quenches within a single topological phase, and so are not connected to the topological phase transition itself. Instead, the change in the topology of the Hamiltonian can be found by tracing the time evolution of e(q, t) and constructing the linking number of the trajectories (in q and t) of any two values of e [e.g., e = (1,0,0) and (0,0,1)] (Wang et al., 2017). This linking number is the Hopf index of the map e(q, t). This procedure has been successfully carried out in experiments (Tarnowski et al., 2017). A related approach has recently been used to demonstrate the topological character of the effective Hamiltonian in a spin-orbit coupled BEC (Sun et al., 2018).

The above considerations rely on the assumption that the fermions are noninteracting. It will be of interest to explore the extent to which these, or similar, approaches can be applied in the presence of interparticle interactions. Being gapped phases of matter, associated with filled bands, the ground states of the Hamiltonian are expected to be robust to weak interactions. However, even weak interactions can lead to the generation of entanglement between single-particle states at different wave vectors under far-from-equilibrium dynamics, which may be viewed as a form of decoherence.

Moving beyond the phases of noninteracting fermions in topological bands, it will be of interest to explore similar quench dynamics in topological phases that arise only because of strong interparticle interactions. This is an area where results remain limited. Recent work on the Haldane phase of a spin-1 chain (a symmetry-protected topological phase of this interacting quantum spin system) has shown that the “string order” that characterizes the topological phase is lost following the quench (Calvanese Strinati et al., 2016), suggesting a difference from the noninteracting fermion cases described above. One important difference concerns the role of symmetry protection under dynamical evolution (McGinley and Cooper, 2018).

E. Invariants in Floquet-Bloch systems

The topological invariants we focused on are those of static single-particle Hamiltonians, in which the spatial periodicity leads to the existence of a Bloch Hamiltonian that depends on a quasimomentum q within a BZ. If the Hamiltonian is time varying, but periodic with period $T\equiv 2\pi /\omega ,$ then energy is replaced by a Floquet quasienergy that is defined up to the addition of integer multiples of ℏω. The combination of both temporal and spatial periodicities causes Floquet-Bloch systems to have topological invariants that are distinct from those of static Hamiltonians.

(1) The periodicity of the Floquet spectrum allows the Floquet bands to wind in quasienergy, by an integer multiple of h/T as q runs over the BZ. This winding in quasienergy gives rise to topological invariants of Floquet-Bloch bands (Kitagawa et al., 2010) that are absent in static settings. Figure 27 shows an example of a Floquet-Bloch band in a 1D system that winds in quasienergy once across the BZ.

FIG. 27.

Floquet energy spectrum in units of $\hslash \omega$ for the driven Rice-Mele model in the topological (top) and nontopological (bottom) cases. The parameters $\left(J^{\prime }/J,\mathrm{\Delta }/J\right)$ are varied along a circle of radius 0.5 with angular frequency ω = 0.23 $J/\hslash$. The circle is centered on the point (2,0) in the nontopological case and on the point (1,0), i.e., the vortex in Fig. 7, in the topological one. In the topological case a particle starting in state A at momentum q = 0 arrives in B after an adiabatic motion across the full BZ, leading to the net current (107) for a filled band. The gray areas highlight given “temporal Brillouin zones,” of energy width ℏω.

To understand the physical significance of such situations, it is instructive to consider the band of Fig. 27 (top) to be filled with noninteracting fermions. [How one might prepare such a state is itself an interesting question (Dauphin et al., 2017; Lindner, Berg, and Rudner, 2017). Indeed, nonadiabatic effects associated with the switch-on of a pump can lead to deviation from quantization (Privitera et al., 2018).] The net current carried by the filled band is

$$I\equiv \frac{L}{2\pi }{\int }_{-\pi /a}^{\pi /a}\frac{1}{\hslash }\frac{\text{d}{ϵ}_q}{\text{d}q}\text{d}q=\frac{L}{T},$$ (106)

where a is the lattice constant and L is the total length of the system. The number of particles in the filled band is N = L/a, so the current per particle is

$$\frac{I}{N}=\frac{a}{T}.$$ (107)

Thus, the current is equivalent to a displacement of each particle by a lattice constant a in each period of the cycle T. For a band that winds in quasienergy s times, the current is quantized at sa in each cycle T. For a band that winds in quasienergy s times, the current is quantized at sa in each cycle T. The quantized current from a filled Floquet-Bloch band that winds s times in quasienergy precisely matches the current expected from an adiabatic pump, as described in Sec. II.F, operated cyclically with period T and with Chern number s. Indeed, settings in which adiabatic Thouless pumping occurs give rise to Floquet-Bloch spectra in which a band winds in quasienergy. (The adiabaticity condition corresponds to the relevant Floquet-Bloch band crossing with all Floquet-Bloch bands that wind in the opposite sense.) However, the general structure of the Floquet-Bloch states and the associated topological invariants (Kitagawa et al., 2010) are not restricted to such adiabatic settings.

(2) New features also arise when one considers the edge states on systems with a boundary. One finds that finite-size systems can have protected edge states, at quasienergies between the bulk bands, even if the topological invariants constructed from the Floquet Hamiltonian ${\widehat{H}}_{\mathit{q}}^F$ are trivial for all of the bulk energy bands (Kitagawa et al., 2010). A simple example of a 2D model which exhibits such “anomalous edge states” is illustrated in Fig. 28. One period T is broken into four subperiods T/4, during which the tunneling amplitude J is turned on only for a subset of the bonds. This tunneling is chosen to satisfy (J/ℏ)(T/4) = π such that a particle that starts on one side of the active bond is transferred to the other side of the bond during the time T/4. For particles in the bulk, the net action after all four parts of the cycle is to return the particle to its starting point (up to some overall phase). Thus the Floquet operator for time evolution over one cycle [see Eq. (B2)] is proportional to the identity and has a bulk Floquet-Bloch band structure with constant quasienergy and whose wave functions have trivial topological character. However, a particle that starts on the edge of the system is transported along the edge over one period; this motion appears as dispersive (chiral) edge states in the Floquet spectrum of the finite-size system; see Fig. 28(c). The understanding of such anomalous edge states is that the topological invariant of a band constructed from the Floquet operator determines the change in the number of edge states as the quasienergy passes through the band (Rudner et al., 2013). An edge state can pass through a set of topologically trivial bands and satisfy periodicity in quasienergy and quasimomentum; see Fig. 29. To compute the number of anomalous edge states requires one to know not just the stroboscopic evolution defined by the Floquet operator, but also the full time-evolution operator at intermediate times, from which an additional invariant can be constructed (Rudner et al., 2013). Anomalous edge states have not yet been seen in atomic systems, but have been observed in experiments on light propagation in photonic structures (Maczewsky et al., 2017; Mukherjee et al., 2017).

FIG. 28.

A simple model that shows anomalous edge states. (a) A cycle consists of four steps in which specific sets of bonds are active and one step in which there is only a sublattice energy offset δ_AB. (b) Trajectories of particles initially in the bulk (blue closed loop) or on the edges [green (red) lines on top (bottom) edges]. (c) Floquet spectrum showing the dispersionless bulk band and the two anomalous edge states with equal and opposite nonzero velocities. From Rudner et al., 2013.

FIG. 29.

For Floquet-Bloch systems, the topological invariant of the bulk band determines the change in the number of edge modes as quasienergy passes through the band. The periodicity in quasienergy allows the existence of edge states even in settings where the bulk bands are all topologically trivial. From Rudner et al., 2013.

(3) The concept of particle-hole symmetry needs be generalized for Floquet-Bloch systems. For static Hamiltonians, particle-hole symmetry (E → −E) stabilizes (edge) modes at energies E = 0 (SSH model or Majorana mode in the Kitaev model). The periodicity of the Floquet quasienergy ϵ under ϵ → ϵ + ℏω means that symmetry ϵ → −ϵ arises for ϵ = 0 or ϵ = ℏω/2. Indeed, topologically stable edge modes at quasienergies ϵ = ℏω/2 have been theoretically demonstrated in periodically driven lattice models with sublattice (chiral) symmetry analogous to the SSH model (Asbóth, Tarasinski, and Delplace, 2014), and in Floquet superfluid systems where they appear as Majorana modes (Jiang et al., 2011).

Recent works have constructed a general theory of the topological classification of time-varying single-particle Hamiltonians (Nathan and Rudner, 2015; Fruchart, 2016; Roy and Harper, 2016). Extensions of these ideas to interacting, many-body phases is an active area of theoretical research.

F. Open systems

So far we focused our studies on the topological properties of the ground state of an isolated system. The possibility to introduce a coupling between this system and an environment opens new possibilities and raises new questions that we now discuss. We restrict our presentation to studies in direct relation with atomic gas implementations.

Consider first the case where the environment is at a nonzero temperature T. If the coupling is sufficiently weak, the energy levels of the system remain relevant and its steady state is now a statistical mixture of these levels. Since bands with various topologies that were empty at T = 0 now acquire a finite population, the Chern number calculated via a thermal average will not be an integer anymore. One could naively conclude that the system loses all its topological properties when T becomes non-negligible with respect to the gap protecting the bands that are populated at zero temperature.

However, one may look for more subtle topological invariants that can be associated with the density matrix describing the system at nonzero T. A possible direction consists of generalizing the notion of geometric phase, using the concept of parallel transport for density matrices introduced by Uhlmann (1986). This line was investigated by Huang and Arovas (2014) and Viyuela, Rivas, and Martin-Delgado (2014), who could derive in this way a classification of topological phases at nonzero T. It was subsequently revisited with a somewhat different perspective by Budich and Diehl (2015), who pointed out possible ambiguities of the previous approaches for a model 2D system. Another direction consists of establishing an equivalence between classes of density matrices using local unitary operations (Chen, Gu, and Wen, 2010), and deducing from this equivalence the desired classification of topological phases. It was developed for the particular case of mixed Gaussian states of free fermions by Diehl et al. (2011) and Bardyn et al. (2013), and recently generalized by Grusdt (2017) [see also van Nieuwenburg and Huber (2014) for the specific case of 1D systems]. Independently of the tool that is used to define the topological class of density matrices, it is worth emphasizing that on the one hand these topological features are in principle observable, but on the other hand their relation with usual physical quantities associated with the response of the system is still the subject of ongoing research (Budich, Zoller, and Diehl, 2015).

Working with open systems also offers the possibility of creating novel topological states that emerge from the dissipative coupling itself. Here we take the reservoir at T = 0 for simplicity. In the conceptually simplest version of the scheme, the coupling is engineered so that the system ends up after some relaxation time in a pure state, often called a dark state. “Topology by dissipation” is achieved when this dark state possesses nontrivial topological properties. For a coupling compatible with the Born-Markov approximation (Gardiner and Zoller, 2004; Daley, 2014), the master equation describing the evolution of the density operator ρ of the system can be written in the Lindblad form (Lindblad, 1976) $\dot{\rho }=\mathcal{L}(\rho )$ where the linear operator $\mathcal{L},$ the Liouvillian, acts in operator space:

$$\mathcal{L}(\rho )=\text{i}[\rho ,H]+\frac{1}{2}\sum _j(2L_j\rho L_j^{†}-L_j^{†}{L}_j\rho -\rho L_j^{†}{L}_j).$$ (108)

Here H is the Hamiltonian of the system in the absence of coupling to the reservoir, and the L_j’s are the Lindblad operators describing the various coupling channels to the bath. If one neglects for simplicity the Hamiltonian evolution of the system (H = 0), one finds that a pure state $|\psi \rangle$ satisfying $L_j|\psi \rangle =0$ for all j is an eigenstate of the Liouvillian with eigenvalue 0 and thus a dark state. The topology associated with this state can be readily inferred from the fact that it is the ground state of the parent Hamiltonian $H^{\prime }={\sum }_j{L}_j^{†}{L}_j.$ Conditions for the existence and uniqueness of such dark states were discussed in the context of fermionic setups by Bardyn et al. (2012, 2013).

The steady state of the master equation will be protected against small perturbations if it is an isolated point in the spectrum of the Liouvillian. One defines in this case the “damping gap” as the smallest rate at which deviations from the steady state are washed out. In this dissipative context, the damping gap plays a role that is formally equivalent to the energy gap in the Hamiltonian context.

The concepts of topology by dissipation and damping gap can be generalized to the case where the steady state of the master equation associated to Eq. (108) is a mixed state. Its analysis is relatively simple for free fermion systems on a lattice, assuming that the Lindblad operators L_j are linear functions of the on-site creation and annihilation operators. This corresponds, for example, to the case where dissipation occurs via an exchange of particles with a reservoir that is described by a classical mean field. In this case, the system density operator is Gaussian and the already mentioned tools developed by Bardyn et al. (2013) can be used to characterize its topological properties. Interestingly for such systems, a change of the topological properties of the system can occur either when the damping gap closes or when the “purity gap” closes. This notion of purity gap closure, first introduced by Diehl et al. (2011) and later generalized by Budich and Diehl (2015), corresponds to a situation where there exist bulk modes associated with a subspace (e.g., a given q in momentum space) in which the state is completely mixed.

Examples of topologically nontrivial pure or mixed states and their corresponding edge modes were presented by Diehl et al. (2011) and Bardyn et al. (2012) in a 1D and a 2D setup, respectively. Budich, Zoller, and Diehl (2015) pointed out a remarkable property of steady states involving a mixed state: they may possess a nontrivial topological character even when all Lindblad operators L_j are local in space. This cannot occur when the steady state is pure, an impossibility that is reminiscent from the fact that in the Hamiltonian framework, Wannier functions of a topologically nontrivial filled band (nonzero Chern number) must decay slowly, i.e., algebraically, in space (Thouless, 1984).

The concept of topological pumping can also be extended to the case of open systems, as shown by Linzner et al. (2016) and Hu et al. (2017). Using a proper engineering of the Liouvillian (108) of a fermionic 1D chain, Linzner et al. (2016) could generalize the result of Sec. IV.C.1 for the Rice-Mele model and prove the quantization of the variation of the many-body polarization after a closed loop in parameter space. As for the other topological features described in this section, this quantization holds even when the steady state of the master equation is a mixed state.

Finally we note that dissipation also offers a new route for revealing an existing topological order. Rudner and Levitov (2009) considered the motion of a single particle on a 1D bipartite (AB) lattice similar to the one at the basis of the SSH model. Here dissipation corresponds to a nonzero decay rate of the particle when it resides on the sites of sublattice A. The particle is assumed to start on site B₀, i.e., the B sublattice site in the lattice cell m = 0. Here one is interested in the average displacement $\langle \mathrm{\Delta }m\rangle ={\sum }_{m}m{P}_m,$ where P_m is the probability that the particle decays from the A site of the mth lattice cell. Quite remarkably this average displacement is quantized and can take only the values 0 and 1. This binary result corresponds to the two topological classes that we identified above for the SSH model within the Hamiltonian framework. This result holds for any values of the decay rate and on-site energies, but it stops being valid if one introduces a dissipative component in the hopping process between the two sublattices. It was confirmed experimentally with a setup in the photonic context by Zeuner et al. (2015). They used a lattice of evanescently coupled optical waveguides, in which losses and dissipation were engineered by bending the waveguides. The scheme of Rudner and Levitov (2009) was recently generalized theoretically to multipartite lattices by Rakovszky, Asbóth, and Alberti (2017), who used a weak measurement of the particle position as the source of dissipation.

VII. SUMMARY

We have summarized the methods that have been used to engineer topological bands for cold atomic gases, and the main observables that have allowed characterizations of their geometrical and topological properties. Most experimental studies so far have been at the single-particle level. Theory suggests many interesting possibilities for novel many-body phases in regimes where interparticle interactions become strong. Such systems are in regimes where theoretical understanding is very limited, so experimental investigation will be particularly valuable. Accessing this regime for large gases will require careful management of heating—from lattice modulation methods or from Raman coupling of internal states—as well as the development of robust detection schemes to uncover the underlying order. There is already progress in this direction. It seems likely to provide a rich vein to explore, with much scope for experimental discoveries and surprises.

APPENDIX A: TOPOLOGICAL BANDS IN ONE DIMENSION

1. Edges states in the SSH model

The Su-Schrieffer-Heeger (SSH) model was introduced to describe the electronic structure of polyacetylene (Su, Schrieffer, and Heeger, 1979). This molecule has alternating single and double bonds along the carbon chain, which are represented in a tight-binding model with one orbital per carbon atom (site) by alternating tunnel couplings J and $J^{\prime }$ between the sites; see Fig. 1. There are two sites in the unit cell, which we label A and B and that are assigned the same energy in the SSH model (this constraint is relaxed in the Rice-Mele model). The single-particle Hamiltonian is given in Eq. (15), and we emphasized in the main text the existence of two distinct topological classes, corresponding to J < J′ (winding number N = 0) and J > J′ (N = 1).

This classification may appear rather formal for an infinite chain, since the labeling in terms of A and B sites is arbitrary and one can exchange the roles of J and $J^{\prime }$ without changing the physical system. However, its physical relevance appears clearly if one considers a finite or semi-infinite chain. Then the two classes correspond to different possibilities for the edge state(s) of the chain, as an illustration of the general bulk-edge correspondence. In the following we first describe the case of a semi-infinite chain for which analytical calculations are straightforward and then discuss the case of a finite chain.

a. Semi-infinite chain

We consider a semi-infinite lattice, with unit cells labeled by j = 1, 2, 3, 4, .... Such a boundary could be formed by imposing a very large potential on the unit cells at j ≤ 0 on an infinite lattice. However, to retain the chiral symmetry it is convenient to view this as a boundary to a region, at j ≤ 0, where the intercell tunneling J = 0: this causes the J = 1 unit cell to be disconnected from any sites with j ≤ 0; see Fig. 30. The region on the left j ≤ 0 has J = 0 so its winding number is N = 0.

FIG. 30.

A semi-infinite SSH model. The left region (gray area) has J = 0, hence a winding number N = 0. The right region may have N = 0 or 1, depending on the ratio $J/J^{\prime }.$ In the latter case a zero-energy edge state resides close to the boundary between the two domains.

For the semi-infinite SSH chain (with j ≥ 1) the eigenvalue condition is

$$E{\psi }_j^A=\{\begin{array}{ll}-J^{\prime }{\psi }_j^B-J{\psi }_{j-1}^B\hfill & j>1,\hfill \\ -J^{\prime }{\psi }_j^B\hfill & j=1,\hfill \end{array}$$ (A1)

$$E{\psi }_j^B=-J{\psi }_{j+1}^A-J^{\prime }{\psi }_j^{B}j\ge 1.$$ (A2)

Assuming that there is only one edge state in this problem (which can be checked analytically), the chiral symmetry entails that it has a zero energy. Setting E = 0 in Eqs. (A1) and (A2) one readily finds the solution

$$\left(\begin{array}{c}{\psi }_j^A\\ {\psi }_j^B\end{array}\right)\propto \left(\begin{array}{c}{\left(-J^{\prime }/J\right)}^j\\ 0\end{array}\right).$$ (A3)

This is a localized (normalizable) state provided $J^{\prime }<J,$ i.e., provided the insulator to the right of the boundary j ≥ 1 is in the topological phase with N = 1. Recalling that the boundary is to a region with J = 0, and hence N = 0, we establish the existence of an E = 0 edge state if and only if the insulators on either side have differing topological index N. The length $\xi$ over which this edge state is localized is $\xi ~a\ln \left(J/J^{\prime }\right).$ Note that this edge state occupies only one type of site (here the A sites), in agreement with the general requirement of the chiral symmetry for a state $|\psi \rangle$ at zero energy: $\widehat{U}|\mathbf{\Psi }\rangle =({\widehat{P}}_A-{\widehat{P}}_B)|\mathbf{\Psi }\rangle \propto |\mathbf{\Psi }\rangle .$ This solution is the discrete version of the edge mode, Eq. (37), of the continuum model derived in Sec. II.D.1.

b. Finite chain

One can also consider a chain with M unit cells; see Fig. 31. For $J^{\prime }<J$ and a length Ma much larger than the extension $\xi$ of the edge state found for a semi-infinite chain, we expect now two edge states of energy ~0, each localized at one end of the chain. When $J^{\prime }/J$ increases and approaches unity, this pair of edge states gradually hybridize and they finally merge into the quasicontinua corresponding to the two bands for $J^{\prime }/J$ above unity.

FIG. 31.

Energy spectrum of a SSH chain of M = 10 dimers. A pair of edge states close to zero energy exists when $J^{\prime }/J$ is notably below 1. When $J^{\prime }/J$ increases above 1, these edge states are gradually transformed into bulk states. Adapted from Delplace, Ullmo, and Montambaux, 2011.

In practice, generating a boundary that preserves chiral symmetry could be delicate to achieve. Thus edge states of cold atom implementations of the SSH model are likely to be shifted away from zero energy. In contrast, the topological protection of the Majorana modes of the Kitaev chain described next (Appendix A.5) does not require any such local fine-tuning. There the protecting symmetry is the exact particle-hole symmetry of the Bogoliubov–de Gennes Hamiltonian (90).

2. Gauge invariance and Zak phase

Strictly speaking the Zak phase is not a gauge invariant quantity. Here we illustrate this point using again the SSH model. In a local gauge transform, one can redefine the positions of the sites A_j and B_j to be $ja+{\xi }_A\text{and}jb+{\xi }_B,$ leading to the following modified form of the Bloch wave form:

$$|{\psi }_q\rangle =\sum _j{\text{e}}^{\text{i}\left(ja+{\xi }_{\text{A}}\right)q}{u}_q^A|A_j\rangle +{\text{e}}^{\text{i}\left(ja+{\xi }_B\right)q}{u}_q^B|B_j\rangle .$$ (A4)

The vector h(q) defining the Hamiltonian in reciprocal space (18) is then changed into

$$h_x(q)+\text{i}{h}_y(q)=\left(J^{\prime }+J{\text{e}}^{\text{i}qa}\right){\text{e}}^{\text{i}q\left({\xi }_A-{\xi }_B\right)},$$ (A5)

so that the Hamiltonian ${\widehat{H}}_q$ is not q periodic anymore. The phase $q\left({\xi }_A-{\xi }_B\right)$ is added to ϕ_q in the definition (21) of the eigenstates of ${\widehat{H}}_q.$ This in turn adds the quantity $\pi \left({\xi }_B-{\xi }_A\right)/a$ to the Zak phase [see, e.g., Atala et al. (2013)].

To decrease the ambiguity in the definition of the Zak phase, one may insist on keeping the q periodicity of $\widehat{H}(q)$, and thus h(q), over the BZ. This restricts the local gauge transform described above to ${\xi }_B-{\xi }_A=N^{\prime }a,$ where N′ is an integer. The Zak phase then recovers the structure π × integer, but the corresponding winding number is increased by N′. In practice this has no impact because physical consequences involve only differences of winding numbers or phases between regions of possibly different topology, which are gauge invariant.

3. Time-reversal symmetry of the SSH model

Additional symmetries can be exploited to simplify the calculation (or measurement) of the topological invariant. The SSH model has time-reversal symmetry, such that ${\widehat{H}}_q={\widehat{H}}_{-q}^{*}$ and therefore ϕ_q = −ϕ_−q. This allows the winding number (23) to be written as an integral over half of the BZ

$$N=\frac{1}{\pi }{\int }_0^{\pi /a}\frac{\partial {\varphi }_q}{\partial q}\text{d}q=\frac{1}{\pi }\left({\varphi }_{\pi /a}-{\varphi }_0\right).$$ (A6)

Thus, information on the winding number N can be obtained by measuring ϕ_q at just two points, q = 0 and π/a. Since the angle ϕ_q. is defined only mod2π, this method can determine only if N is even or odd. Nevertheless, this partial information can be useful, notably for ${\mathrm{\mathbb{Z}}}_2$ topological invariants (Fu and Kane, 2007).

4. Adiabatic pumping for the Rice-Mele model

The Rice-Mele model generalizes the SSH model to the case where the energies of sites A and B may differ by a quantity 2Δ. As explained in Sec. II.F, the vortex in ϕ_Zak around the gap-closing point (Δ = 0 and J′/J = 1) is a topological invariant which can be viewed as a Chern number in the periodic 2D space formed from crystal momentum −π/a < q ≤ π/a and time 0 < t ≤ T. This Chern number counts the number of particles that are pumped through the system under this adiabatic cycle (Thouless, 1983).

To establish the link between the winding of ϕ_Zak and the transported mass, we start from the fact that the lattice remains at any time periodic, so that the Bloch theorem ensures that the quasimomentum q is conserved during the evolution. Let us assume a slow evolution and a nonclosing gap, so that transitions to upper bands are negligible. The evolution operator $\widehat{U}(T)$ for a closed cycle of duration T in parameter space $\left(J^{\prime }/J,\mathrm{\Delta }/J\right)$ is diagonal in the Bloch state basis $|{\psi }_q\rangle :|{\psi }_q\rangle \to \widehat{U}(T)|{\psi }_q\rangle ={\text{e}}^{\text{i}\gamma (q)}|{\psi }_q\rangle .$ Using the canonical commutation relation, the evolution of the position operator $\widehat{x}$ follows: ${\widehat{U}}^{†}(T)\widehat{x}\widehat{U}(T)=\widehat{x}-{\partial }_q\gamma (\widehat{q}),$ from which we can deduce the global displacement Δx of the atomic cloud by averaging over all states in the band. Now there are two contributions to γ(q): (i) The dynamical phase related to the energy E(q), which has a vanishing contribution to Δx because the average of the group velocity ${\partial }_{q}E(q)$ over the band is zero; (ii) Zak phase $\text{i}{\int }_0^T\langle u_q|{\partial }_t{u}_q\rangle \text{d}t$ which leads after average over the band to

$$\mathrm{\Delta }x=\frac{a}{2\pi }{\int }_0^T{\partial }_t{\varphi }_{\text{Zak}}(t)\text{d}t.$$ (A7)

Because ϕ_Zak(T) equals ϕ_Zak(0) plus the winding number corresponding to the vortex of Fig. 7, this proves the quantization of the displacement in units of the lattice period a.

5. The Kitaev model for topological superconductors

In this model one considers spinless fermions moving on a 1D chain of identical sites with the hopping coefficient J between nearest neighbors; see Fig. 32. We assume that the chain is coherently coupled to a superfluid reservoir that can inject and remove pairs of fermions on neighboring sites. This coupling is characterized by the real parameter Δ, which stands for the p-wave superconducting gap induced by the reservoir. It also sets the chemical potential μ which controls the total population of the chain. We are therefore interested in the eigenstates and the corresponding energies of

$$\begin{gathered} \widehat{H}-\mu \widehat{N}=\sum _j\{-J({\widehat{c}}_j^{†}{\widehat{c}}_{j+1}+{\widehat{c}}_{j+1}^{†}{\widehat{c}}_j)-\mu {\widehat{c}}_j^{†}{\widehat{c}}_j \\ +\mathrm{\Delta }({\widehat{c}}_j{\widehat{c}}_{j+1}+{\widehat{c}}_{j+1}^{†}{\widehat{c}}_j^{†})\}. \end{gathered}$$ (A8)

FIG. 32.

Kitaev model: A 1D chain of identical sites with nearest-neighbor hopping and a coherent coupling to a superfluid reservoir that injects and removes pairs of fermions on neighboring sites.

For an infinite chain (or a finite chain with periodic boundary conditions), translation invariance ensures that $\widehat{H}-\mu \widehat{N}$ takes a simple form in momentum space. It can be written in the standard Bogoliubov-de Gennes form

$$\widehat{H}-\mu \widehat{N}=\frac{1}{2}\sum _q({\widehat{\tilde{c}}}_q^{†},{\widehat{\tilde{c}}}_{-q}){\mathcal{H}}_q^{\text{BdG}}\left(\begin{array}{c}{\widehat{\tilde{c}}}_q\\ {\widehat{\tilde{c}}}_{-q}^{†}\end{array}\right),$$ (A9)

where the operator ${\widehat{\tilde{c}}}_q^{†}\propto \sum _j{\text{e}}^{\text{i}qja}{\widehat{c}}_j^{†}$ creates a particle with quasimomentum q and each Hamiltonian ${\mathcal{H}}_q^{\text{BdG}}$ is a 2 × 2 matrix:

$${\mathcal{H}}_q^{\text{BdG}}=-\mathit{h}(q)\cdot \mathit{\sigma }\text{with}\{\begin{array}{l}{h}_y(q)=-2\mathrm{\Delta }\sin (qa),\hfill \\ h_z(q)=2J\cos (qa)+\mu ,\hfill \end{array}$$ (A10)

and h_x = 0. Although the present physical problem is different from the SSH and Rice-Mele models, we recover in Eq. (A10) a Hamiltonian in reciprocal space which has a similar structure. In particular, the search for distinct topological phases can be performed by analyzing the trajectory of the vector h(q) when q travels across the BZ.

More precisely we see from Eq. (A10) that the vector h always lies in a plane (here y-z), which makes the discussion formally similar to the SSH model. The quasiparticle excitation spectrum is set by |h(q)|: this is gapped for all q in the BZ provided $|\mu |\ne 2J.$ However, there are two topologically distinct phases; see Fig. 33. For |μ| < 2J the two-component vector h(q) encircles the origin, winding by 2π as q runs over the BZ: this is the topological superconducting phase, for which there exist localized (Majorana) modes on the boundaries of a finite sample. For |μ| > 2J the vector h(q) does not encircle the origin and has a vanishing winding number: this is the nontopological superconducting phase. These two topological phases cannot be smoothly connected without causing |h(q)| = 0 at some point in the BZ, i.e., a closing of the quasiparticle gap.

FIG. 33.

Distinct topological phases of the Kitaev model, evidenced by the trajectory of h(q)/|h(q)| on the unit sphere, as q scans the Brillouin zone. Left (μ < −2J) and right (μ > 2J): topologically trivial phases, with a zero winding around the origin. Middle (|μ| < 2J): topological phase.

The existence of edge states for an open chain of M sites can be simply revealed by taking the particular case Δ = J and μ = 0 (Kitaev, 2001) (the energy spectrum as a function of μ is shown in Fig. 34). In this case, one can perform a canonical transformation using the new fermionic operators:

$${\widehat{C}}_j=\frac{\text{i}}{2}({\widehat{c}}_j^{†}-{\widehat{c}}_j+{\widehat{c}}_{j+1}^{†}+{\widehat{c}}_{j+1})$$ (A11)

for j = 1,...,M − 1 and

$${\widehat{C}}_M=\frac{\text{i}}{2}({\widehat{c}}_M^{†}-{\widehat{c}}_M+{\widehat{c}}_1^{†}+{\widehat{c}}_1)$$ (A12)

so that the $\{{\widehat{C}}_j,{\widehat{C}}_j^{†}\}$ satisfy canonical fermionic commutation rules. The Hamiltonian (A8) can then be written

$$\widehat{H}-\mu \widehat{N}=2J\sum _{j=1}^{M-1}\left({\widehat{C}}_j^{†}{\widehat{C}}_j-\frac{1}{2}\right).$$ (A13)

FIG. 34.

Quasiparticle spectrum of $\widehat{H}-\mu \widehat{N}$ [Eq. (A8)] for an open chain of 20 sites and Δ = J. The pair of solutions (E, −E) with E ≈ 0 that appears in the topological region |μ| < 2J represents the Majorana zero energy modes at the two ends of the chain.

A ground state of $\widehat{H}-\mu \widehat{N}$ is obtained by solving

$${\widehat{C}}_j|{\psi }_0\rangle =0,j=1,\dots ,M-1.$$ (A14)

It is separated from the excited states by the gap 2J, as expected from the above analysis for the infinite chain: For J = Δ and μ = 0, |h(q)| = 2J is indeed independent of q. The existence of edge states in this case originates from the fact that the nonlocal fermion mode $({\widehat{C}}_M,{\widehat{C}}_M^{†}),$ acting on both ends of the chain, does not contribute to the Hamiltonian (A13). It can therefore be filled or emptied at no energy cost, leading to two independent ground states. More precisely, if $|{\psi }_0\rangle$ is the ground state satisfying ${\widehat{C}}_M|{\psi }_0\rangle =0,\text{then}|{\psi }_1\rangle ={\widehat{C}}_M^{†}|{\psi }_0\rangle$ is also a ground state. The states $|{\psi }_0\rangle \text{and}|{\psi }_1\rangle$ correspond to different global parities of the total fermion number. The situation is thus different from a usual superconductor, where the ground state is nondegenerate and represents a condensate of Cooper pairs, hence a superposition of states with an even number of fermions.

As discussed in the main text, the gapless edge modes of the topological superconductor are better viewed in terms of the Majorana operators

$${\widehat{\gamma }}_1\equiv {\widehat{C}}_M+{\widehat{C}}_M^{†}=\text{i}({\widehat{c}}_M^{†}-{\widehat{c}}_M),$$ (A15)

$${\widehat{\gamma }}_2\equiv \text{i}({\widehat{C}}_M-{\widehat{C}}_M^{†})=-({\widehat{c}}_1^{†}+{\widehat{c}}_1)$$ (A16)

in view of the fact that these Majorana operators are spatially localized on each end of the chain.

APPENDIX B: FLOQUET SYSTEMS AND THE MAGNUS EXPANSION

We mention here several key results for Floquet systems of use in the main text. We refer the interested reader to Eckardt (2017) for a comprehensive recent account.

Consider a Floquet system, defined by a time-varying Hamiltonian $\widehat{H}(t)$ that is periodic $\widehat{H}(t+T)=\widehat{H}(t)$ with period $T=2\pi /\omega .$ The time evolution over an integer number of periods, from t₀ to t₀ + NT, is described by the unitary operator

$$\widehat{U}\left(t_0,t_0+NT\right)\equiv \mathcal{T}\exp \left[-\frac{\text{i}}{\hslash }{\int }_{t_0}^{t_0+NT}\widehat{H}\left(t^{\prime }\right)\text{d}{t}^{\prime }\right],$$ (B1)

where $\mathcal{T}$ denotes time ordering. This can be written

$$\widehat{U}\left(t_0,t_0+NT\right)={\left[\widehat{U}\left(t_0,t_0+T\right)\right]}^N\equiv {\text{e}}^{-(\text{i}/\hslash ){\widehat{H}}_{t_0}^{F}T},$$ (B2)

which defines the effective Floquet Hamiltonian ${\widehat{H}}_{t_0}^F$ in terms of the logarithm of the time evolution operator over a single period T. Clearly ${\widehat{H}}_{t_0}^F$ is undefined up to the addition of integer multiples of $2\pi \hslash /T=\hslash \omega ,$ so its eigenvalues—defining the Floquet spectrum—have a periodicity in energy of The Floquet Hamiltonian describes the “stroboscopic” evolution of the system, i.e., at the selected times t = t₀, t₀ + T,...,t₀ + NT. This is relevant for understanding the dynamics over time scales long compared to the drive period T.

In addition to this stroboscopic evolution, the system undergoes a “micromotion” on a time scale of the period T. This causes the Floquet Hamiltonian ${\widehat{H}}_{t_0}^F$ to depend on the time during the cycle, via a t₀-dependent unitary transformation (the Floquet spectrum is therefore invariant). A convenient way to account for this micromotion is to write the general time-evolution operator, from time t_i to t_f, as (Goldman and Dalibard, 2014)

$$\widehat{U}\left(t_{\text{i}},t_{\text{f}}\right)={\text{e}}^{-\text{i}\widehat{K}\left(t_{\text{f}}\right)}{\text{e}}^{-(\text{i}/\hslash ){\widehat{H}}^{\text{eff}}\left(t_{\text{f}}-t_{\text{i}}\right)}{\text{e}}^{\text{i}\widehat{K}\left(t_{\text{i}}\right)}.$$ (B3)

This can be achieved with a time-independent effective Hamiltonian ${\widehat{H}}^{\text{eff}}$ and a “kick” operator that is periodic in time $\widehat{K}(t)=\widehat{K}(t+T)$ and that has vanishing average over one period (Goldman and Dalibard, 2014). The kick operator takes account of the micromotion (related to how t_i and t_f fall in the period T) and the time-independent effective Hamiltonian ${\widehat{H}}^{\text{eff}}$ controls the long-time behavior.

In general, the determination of the effective Hamiltonian ${\widehat{H}}^{\text{eff}}$ (or the closely related ${\widehat{H}}_{t_0}^F$) is a difficult task. However, for a drive frequency $\omega$ that is large compared to other frequency scales, the effective Hamiltonian can often be approximated by the Magnus expansion in powers of $1/\omega$ (Eckardt, 2017). Writing the Hamiltonian in terms of its harmonics

$$\begin{gathered} \widehat{H}(t)=\sum _{m=-\infty }^{\infty }{\widehat{H}}_m{\text{e}}^{\text{i}m\omega t} \\ ={\widehat{H}}_0+\sum _{m=1}^{\infty }{\widehat{H}}_m{\text{e}}^{\text{i}m\omega t}+{\widehat{H}}_{-m}{\text{e}}^{-\text{i}m\omega t} \end{gathered}$$ (B4)

where ${\widehat{H}}_m^{†}={\widehat{H}}_{-m},$ the Magnus expansion leads to (Goldman and Dalibard, 2014)

$$\begin{gathered} {\widehat{H}}_{\text{eff}}={\widehat{H}}_0+\frac{1}{\hslash \omega }\sum _{m=1}^{\infty }\frac{1}{m}[{\widehat{H}}_m,{\widehat{H}}_{-m}] \\ +\frac{1}{2{(\hslash \omega )}^2}\sum _{m=1}^{\infty }\frac{1}{m^2}[[{\widehat{H}}_m,{\widehat{H}}_0],{\widehat{H}}_m] \\ +[[{\widehat{H}}_{-m},{\widehat{H}}_0],{\widehat{H}}_m]+\cdots . \end{gathered}$$ (B5)

The Magnus expansion underpins several results used in the main text as follows:

• (i)The leading term ${\widehat{H}}_0$ is the time-averaged Hamiltonian, as used in our discussion of inertial forces in Sec. III.C to construct nonzero Peierls phase factors for tunneling.
• (ii)
  The first-order term is important in generating the next-nearest-neighbor hopping from circular shaking of the honeycomb lattice, as required to simulate the Haldane model. Consider the three-site system shown in Fig. 35 with on-site energies E_α, α = A, B, C, a constant tunnel matrix element −J along the links AB and AC, and no “bare” tunneling between B and C:

  $$\widehat{H}=-J(|B\rangle \langle A|+|C\rangle \langle A|+\text{H}.\text{c}.)+\sum _{\alpha }{E}_{\alpha }{\widehat{P}}_{\alpha }$$ (B6)

  with the projectors ${\widehat{P}}_{\alpha }=|\alpha \rangle \langle \alpha |.$ Shaking at a frequency $\omega$ leads to sinusoidally varying energy offsets that we model as E_B (t) = Δ cos $(\omega t)$ and E_C (t)= Δ cos $(\omega t-\varphi ),$ whereas E_A(t) is set to zero by convention. The phase offset ϕ arises from the circular shaking and the angle between the two nearest-neighbor bonds (typically ϕ = 2π/3). Using the unitary transformation generalizing Eq. (52)

  $$\widehat{U}(t)=\sum _{\alpha }{\text{e}}^{\text{i}{\int }_0^t{E}_{\alpha }(t^{\prime })\text{d}{t}^{\prime }/\hslash }{\widehat{P}}_{\alpha },$$ (B7)

  we convert these energy modulations into time-varying phase factors on the hopping:

  $$\begin{gathered} \frac{\widehat{\tilde{H}}(t)}{-J}={\text{e}}^{\text{i}(\mathrm{\Delta }/\hslash \omega )\sin \omega t}|B\rangle \langle A| \\ +{\text{e}}^{\text{i}(\mathrm{\Delta }/\hslash \omega )\sin (\omega t-\varphi )}|C\rangle \langle A|+\text{H}.\text{c}. \end{gathered}$$ (B8)

  Expanding in terms of the harmonics leads to

  $$\begin{gathered} \frac{{\widehat{H}}_m}{-J}={\mathcal{J}}_m(\mathrm{\Delta }/\hslash \omega )|B\rangle \langle A|+{\mathcal{J}}_{-m}(\mathrm{\Delta }/\hslash \omega )|A\rangle \langle B| \\ +{\text{e}}^{-\text{i}m\varphi }\left[{\mathcal{J}}_m(\mathrm{\Delta }/\hslash \omega )|C\rangle \langle A|+{\mathcal{J}}_{-m}(\mathrm{\Delta }/\hslash \omega )|A\rangle \langle C|\right], \end{gathered}$$ (B9)

  where ${\mathcal{J}}_m$ are Bessel functions. Computing the first-order correction to the effective Hamiltonian (B5), one finds

  $${\widehat{H}}_{\text{eff}}^{(1)}\equiv \frac{1}{\hslash \omega }\sum _{m=1}^{\infty }\frac{1}{m}\left[{\widehat{H}}_m,{\widehat{H}}_{-m}\right]$$ (B10)

  $$=-J^{\text{eff}}\left[{\text{e}}^{\text{i}\pi /2}|B\rangle \langle C|+{\text{e}}^{-\text{i}\pi /2}|B\rangle \langle C|\right]$$ (B11)

  $$J^{\text{eff}}=\frac{2J^2}{\hslash \omega }\sum _{m=1}^{\infty }\frac{\sin (m\varphi ){\left[{\mathcal{J}}_m(\mathrm{\Delta }/\hslash \omega )\right]}^2}{m}.$$ (B12)

  This describes a next-nearest-neighbor tunneling term, between B and C sites, which inherits a Peierls phase factor of π/2. A particle that encircles the plaquette A → B → C → A picks up a gauge-invariant phase ${\psi }_{\text{AB}}=-\pi /2,$ placing the system in the regime where the Haldane model has topological bands. It is interesting to note that for this $1/\omega$ expansion, the leading term in J_eff corresponds to the m = 1 contribution in Eq. (B12), hence scales as $1/{\omega }^3.$ Had we directly used the Magnus expansion (B5) for the initial Hamiltonian (B6), this would have required us to go up to the third order of the expansion, which would have been quite involved. Fortunately the unitary transformation (B7) involves an integral of the on-site energies over time, which provides a gain of a factor $1/\omega$. The Magnus expansion at order 1 applied to $\widehat{\tilde{H}}$ is then sufficient to obtain the relevant effective Hamiltonian.
• (iii)The second-order term in Eq. (B5), of order $1/{\omega }^2,$ is responsible for the nonlocal interactions discussed in Sec. V.A.1. These arise from the contribution of the Hubbard interaction U to ${\widehat{H}}_0,$ and from the oscillating tunneling matrix elements in ${\widehat{H}}_{m\ne 0}$ in the double commutator, leading the term of order $J^{2}U/{(\hslash \omega )}^2$ of Eq. (83). We refer the interested reader to Eckardt and Anisimovas (2015) for a comprehensive analysis of such terms.

FIG. 35.

Hopping on three sites of the honeycomb lattice, with time-varying on site energies. The unitary transformation (B7) maps this problem to time-varying tunneling matrix elements between nearest neighbors A ↔ B and A ↔ C. Then the first-order correction in $1/\omega$ from the Magnus expansion leads to a tunneling term of order $J^2/\hslash \omega$ between next-nearest neighbors B ↔ C, with nonzero Peierls phase factor; see Eq. (B12).

APPENDIX C: LIGHT-MATTER INTERACTION

Here we describe the general form that the light-matter interaction must take for two-photon interactions and describe the specific structure of this interaction for alkali atoms. To briefly summarize what follows, the light-matter interaction can be divided into contributions from irreducible rank-0, −1, and −2 spherical tensor operators. In alkali atoms the rank-0 and −1 contributions dominate, but in heavier atoms (or sufficiently close to atomic resonance) the rank-2 contribution can be large. In addition, a similar description of single photon transitions (as would be relevant to systems coupling ground and metastable excited states) gives only the rank-0 and rank-1 contributions.

Now consider a system of ultracold alkali atoms in their electronic ground state manifold illuminated by one or several laser fields which nonresonantly couple the ground states with the lowest electronic excited states. In the presence of an external magnetic field only, the light-matter Hamiltonian for the atomic ground state manifold is

$${\widehat{H}}_0=A_{\text{hf}}\widehat{\mathit{I}}\cdot \widehat{\mathit{J}}+\frac{{\mu }_B}{\hslash }\mathit{B}\cdot (g_{\mathit{J}}\widehat{\mathit{J}}+g_{\mathit{I}}\widehat{\mathit{I}}),$$ (C1)

where A_hf is the magnetic dipole hyperfine coefficient, and μ_B is the Bohr magneton. The Zeeman term includes separate contributions from $\widehat{\mathit{J}}=\widehat{\mathit{L}}+\widehat{\mathit{S}}$ (the sum of the orbital $\widehat{\mathit{L}}$ and electronic spin $\widehat{\mathit{S}}$ angular momentum) and the nuclear angular momentum $\widehat{\mathit{I}}$, along with their respective Landé g factors. We next consider the additional contributions to the atomic Hamiltonian resulting with off-resonant interaction with laser fields.

As Deutsch and Jessen (1998), Dudarev et al. (2004), and Sebby-Strabley et al. (2006) observed, conventional spinindependent (scalar U_s) optical potentials acquire additional spin-dependent terms near atomic resonance: the rank-1 (vector U_ν) and rank-2 tensor light shifts (Deutsch and Jessen, 1998). For the alkali atoms, adiabatic elimination of the excited states labeled by J = 1/2 (D1) and J = 3/2 (D2) yields an effective atom-light coupling Hamiltonian for the ground state atoms (with J = 1/2):

$${\widehat{H}}_L={\widehat{H}}_0+{\widehat{H}}_1+{\widehat{H}}_2=u_s\left({\mathit{E}}^{*}\cdot \mathit{E}\right)+\frac{\text{i}{u}_v\left({\mathit{E}}^{*}\times \mathit{E}\right)}{\hslash }\cdot \mathit{J}+{\widehat{H}}_2.$$ (C2)

The rank-2 term ${\widehat{H}}_2$ is negligible for the parameters of interest and henceforth neglected. Here E is the optical electric field $u_v=-2u_s{\mathrm{\Delta }}_{\text{FS}}/3\left(\omega -{\omega }_0\right)$ determines the vector light shift, ${\mathrm{\Delta }}_{\text{FS}}={\omega }_{3/2}-{\omega }_{1/2}$ is the fine-structure splitting, $\hslash {\omega }_{1/2}\text{and}\hslash {\omega }_{3/2}$ are the D1 and D2 transition energies, and ${\omega }_0=\left(2{\omega }_{1/2}+{\omega }_{3/2}\right)/3$ is a suitable average. u_s sets the scale of the light shift and proportional to the atoms ac polarizability.

The contributions from the scalar and vector light shifts featured in H_L can be independently specified with informed choices of laser frequency $\omega$ and intensity. Evidently, the vector light shift is a contribution to the total Hamiltonian acting like an effective magnetic field

$${\mathit{B}}_{\text{eff}}=\frac{\text{i}{u}_v\left({\mathit{E}}^{*}\times \mathit{E}\right)}{{\mu }_B{g}_J}$$ (C3)

that acts on $\widehat{\mathit{J}}$ and not the nuclear spin $\widehat{\mathit{I}}$. Instead of using the full Breit-Rabi equation (Breit and Rabi, 1931) for the Zeeman energies, we assume that the Zeeman shifts are small in comparison with the hyperfine splitting—the linear, or anomalous, Zeeman regime—in which case, the effective Hamiltonian for a single manifold of total angular momentum $\widehat{\mathit{F}}=\widehat{\mathit{J}}+\widehat{\mathit{I}}$ states is

$$H_0+H_L=u_s\left({\mathit{E}}^{*}\cdot \mathit{E}\right)+\frac{{\mu }_B{g}_F}{\hslash }\left(\mathit{B}+{\mathit{B}}_{\text{eff}}\right)\cdot \widehat{\mathit{F}}.$$ (C4)

Note that B_eff acts as a true magnetic field and adds vectorially with B, and since $|g_I/g_J|\approx 0.0005$ in the alkali atoms, we safely neglected a contribution $-{\mu }_B{g}_I{\mathit{B}}_{\text{eff}}\cdot \widehat{\mathit{I}}/\hslash$ to the atomic Hamiltonian. We also introduced the hyperfine Landé g factor g_F. In ⁸⁷Rb’s lowest energy manifold with F = 1, for which J = 1/2 and I = 3/2, we get $g_F=-g_J/4\approx -1/2.$ In the following, we always consider a single angular momentum manifold labeled by F and select its energy at zero field as the zero of energy.

Bichromatic light field:

Consider an ensemble of ultracold atoms subjected to a magnetic field B = B₀e_z. The atoms are illuminated by several lasers with frequencies $\omega \text{and}\omega +\delta \omega ,\text{where}\delta \omega \approx |g_F{\mu }_B{B}_0/\hslash |$ differs by a small detuning $\delta =g_F{\mu }_B{B}_0/\hslash -\delta \omega$ from the linear Zeeman shift between m_F states $(\text{where}|\delta |\ll \delta \omega ).$ In this case, the complex electric field $\mathit{E}={\mathit{E}}_{{\omega }_{-}}\exp (-\text{i}\omega t)+{\mathit{E}}_{{\omega }_{+}}\exp [-\text{i}(\omega +\delta \omega )t]$ contributes to the combined magnetic field, giving

$$\begin{gathered} \mathit{B}+{\mathit{B}}_{\text{eff}}=B_0{\mathit{e}}_z+\frac{\text{i}{u}_v}{{\mu }_{\text{B}}{g}_J}[\left({\mathit{E}}_{{\omega }_{-}}^{*}\times {\mathit{E}}_{{\omega }_{-}}\right)+\left({\mathit{E}}_{{\omega }_{+}}^{*}\times {\mathit{E}}_{{\omega }_{+}}\right) \\ +\left({\mathit{E}}_{{\omega }_{-}}^{*}\times {\mathit{E}}_{{\omega }_{+}}\right){\text{e}}^{-\text{i}\delta \omega t}+\left({\mathit{E}}_{{\omega }_{+}}^{*}\times {\mathit{E}}_{{\omega }_{-}}\right){\text{e}}^{\text{i}\delta \omega t}]. \end{gathered}$$ (C5)

The first two terms of B_eff add to the static bias field B₀e_z, and the remaining two time-dependent terms describe transitions between different m_F levels. Provided $B_0\gg |{\mathit{B}}_{\text{eff}}|$ and $\delta \omega$ are large compared to the kinetic energy scales, the Hamiltonian can be simplified by time averaging to zero the time-dependent terms in the scalar light shift and making the rotating wave approximation (RWA) to eliminate the time dependence of the coupling fields. The resulting contribution to the Hamiltonian

$${\widehat{H}}_{\text{RWA}}=U(\mathit{r})\widehat{1}+\mathit{\kappa }(\mathit{r})\cdot \widehat{\mathit{F}},$$ (C6)

where we identify the scalar potential

$$U(\mathit{r})=u_s\left({\mathit{E}}_{{\omega }_{-}}^{*}\cdot {\mathit{E}}_{{\omega }_{-}}+{\mathit{E}}_{{\omega }_{+}}^{*}\cdot {\mathit{E}}_{{\omega }_{+}}\right)$$ (C7)

and the RWA effective magnetic field. This expression is valid for g_F > 0 (for g_F < 0 the sign of the e_x and ie_y terms would both be positive, owing to selecting the opposite complex terms in the RWA)

$$\begin{gathered} \mathit{\kappa }=\left[\delta +\text{i}\frac{u_v}{\hslash }\left({\mathit{E}}_{{\omega }_{-}}^{*}\times {\mathit{E}}_{{\omega }_{-}}+{\mathit{E}}_{{\omega }_{+}}^{*}\times {\mathit{E}}_{{\omega }_{+}}\right)\cdot {\mathit{e}}_z\right]{\mathit{e}}_z \\ -\frac{u_v}{\hslash }\mathrm{Im}\left[\left({\mathit{E}}_{{\omega }_{-}}^{*}\times {\mathit{E}}_{{\omega }_{+}}\right)\cdot \left({\mathit{e}}_x-\text{i}{\mathit{e}}_y\right)\right]{\mathit{e}}_x \\ -\frac{u_v}{\hslash }\mathrm{Re}\left[\left({\mathit{E}}_{{\omega }_{-}}^{*}\times {\mathit{E}}_{{\omega }_{+}}\right)\cdot \left({\mathit{e}}_x-\text{i}{\mathit{e}}_y\right)\right]{\mathit{e}}_y. \end{gathered}$$ (C8)

Although this effective coupling is directly derived from the initial vector light shifts, κ is composed of both static and resonant couplings in a way that goes beyond the restrictive ${\mathit{B}}_{\text{eff}}\propto \text{i}{\mathit{E}}^{*}\times \mathit{E}$ form. This enables topological state-dependent lattices.

APPENDIX D: BERRY CURVATURE AND UNIT CELL GEOMETRY

As noted in the main text, it can be convenient to perform a unitary transformation of the Bloch Hamiltonian ${\widehat{H}}_q^{\prime }={\widehat{\mathcal{U}}}_q{\widehat{H}}_q{\widehat{\mathcal{U}}}_q^{†},$ with a ${\widehat{\mathcal{U}}}_q$ wave-vector-dependent unitary operator. Such transformations can be used to render the Hamiltonian periodic in the BZ, but also can relate different choices of unit cell without change of periodicity. They must leave all physical observables unchanged. The energy spectrum is invariant under this unitary transformation E′_q = E_q, while the Bloch states transform as $|u_{\mathit{q}}^{\prime }\rangle ={\widehat{\mathcal{U}}}_{\mathit{q}}|u_{\mathit{q}}\rangle .$ (In this Appendix we drop the band index for clarity.) The new Berry connection in reciprocal space is

$${\mathit{A}}^{\prime }=\text{i}\langle u_{\mathit{q}}^{\prime }|{\mathbf{\nabla }}_{\mathit{q}}|u_{\mathit{q}}^{\prime }\rangle =\mathit{A}+\text{i}\langle u_{\mathit{q}}|{\widehat{\mathcal{U}}}_{\mathit{q}}^{†}[{\mathbf{\nabla }}_{\mathit{q}}{\widehat{\mathcal{U}}}_{\mathit{q}}]|u_{\mathit{q}}\rangle .$$ (D1)

It is interesting to note that, in general, this transformation causes the Berry curvature to change. How can one reconcile this with the fact that the Berry curvature has measurable physical consequences, e.g., within semiclassical dynamics (Sec. IV.B.2)? As we shall see, the answer lies in noting that these unitary transformations can lead to changes of the positions of the orbitals within the unit cell, i.e., changing the internal geometry of the unit cell.

We illustrate this for a two-band model, with a unitary transformation

$${\widehat{\mathcal{U}}}_{\mathit{q}}=\exp (\frac{1}{2}\text{i}\mathit{q}\cdot \mathit{\rho }{\widehat{\sigma }}_z).$$ (D2)

This is the transformation used in our discussion of the Haldane model (33). It leads to the change

$${\mathit{A}}^{\prime }(\mathit{q})=\mathit{A}(\mathit{q})-\frac{1}{2}\mathit{\rho }\langle {\widehat{\sigma }}_z\rangle$$ (D3)

of the Berry connection, where we defined $\langle {\widehat{\sigma }}_z\rangle \equiv \langle u_{\mathit{q}}|{\widehat{\sigma }}_z|u_{\mathit{q}}\rangle .$ Hence, the Berry curvature becomes

$${\mathbf{\Omega }}^{\prime }(\mathit{q})\equiv {\mathbf{\nabla }}_{\mathit{q}}\times {\mathit{A}}^{\prime }=\mathbf{\Omega }(\mathit{q})-\frac{1}{2}\left[{\mathbf{\nabla }}_{\mathit{q}}\langle {\widehat{\sigma }}_z\rangle \right]\times \mathit{\rho }.$$ (D4)

In general, the Berry curvature changes, ${\mathbf{\Omega }}^{\prime }(\mathit{q})\ne \mathbf{\Omega }(\mathit{q}).$ However, since the difference is a total derivative, its integral over the BZ vanishes, so there is no change in the Chern number of the band.

For a consistent application of the unitary transformation, one must consider how all relevant physical quantities transform. Semiclassical dynamics describes the velocity of a wave packet centered on q and r in response to a uniform force. A uniform force in the original basis arises from a potential

$$\widehat{V}=-\mathit{F}\cdot \widehat{\mathit{r}}.$$ (D5)

Under the unitary transformation this becomes

$${\widehat{\mathcal{U}}}_{\mathit{q}}\widehat{V}{\widehat{\mathcal{U}}}_{\mathit{q}}^{†}=-\mathit{F}\cdot \widehat{\mathit{r}}-\frac{1}{2}\mathit{F}\cdot \mathit{\rho }{\widehat{\sigma }}_z.$$ (D6)

We used the fact that, with q replaced by the momentum operator, the unitary operator (D2) effects translations in real space, albeit in a spin-dependent manner, $\widehat{\mathit{r}}\to \widehat{\mathit{r}}+(1/2)\mathit{\rho }{\widehat{\sigma }}_z.$ Indeed, this transformation encodes the important physical effect of the unitary transformation: it amounts to spatial displacement of the orbitals within the unit cell, here separating ${\sigma }_z=\pm 1$ by ρ. In the new basis the force F has two effects. First, it provides a uniform potential gradient which leads to $\hslash \stackrel{.}{\mathit{q}}=\mathit{F}$ as usual. Second, it applies a state-dependent potential that shifts the energy of the wave packet by $-(1/2)\mathit{F}\cdot \mathit{\rho }\langle {\widehat{\sigma }}_z\rangle$ with the expectation value taken for the wave packet’s momentum q. This second contribution can be incorporated as an F-dependent change in the dispersion relation

$$E_{\mathit{q}}^{\prime }=E_{\mathit{q}}-\frac{1}{2}\mathit{F}\cdot \mathit{\rho }\langle {\widehat{\sigma }}_z\rangle .$$ (D7)

The displacement of orbitals within the unit cell also changes the velocity operator. In the new basis the velocity is

$${\widehat{\mathit{v}}}^{\prime }\equiv \frac{1}{\hslash }{\mathbf{\nabla }}_{\mathit{q}}{\widehat{H}}_{\mathit{q}}^{\prime }=\frac{1}{\hslash }{\mathbf{\nabla }}_{\mathit{q}}\left[{\widehat{\mathcal{U}}}_{\mathit{q}}{\widehat{H}}_{\mathit{q}}{\widehat{\mathcal{U}}}_{\mathit{q}}^{†}\right]$$ (D8)

$$=\frac{1}{\hslash }{\widehat{\mathcal{U}}}_{\mathit{q}}\left[{\mathbf{\nabla }}_{\mathit{q}}{\widehat{H}}_{\mathit{q}}\right]{\widehat{\mathcal{U}}}_{\mathit{q}}^{†}-\frac{\text{i}}{2\hslash }\mathit{\rho }\left[{\widehat{H}}_{\mathit{q}}^{\prime },{\widehat{\sigma }}_z\right]$$ (D9)

$$={\widehat{\mathcal{U}}}_{\mathit{q}}\widehat{\mathit{v}}{\widehat{\mathcal{U}}}_{\mathit{q}}^{†}-\frac{1}{2}\mathit{\rho }{\widehat{\stackrel{.}{\sigma }}}_z.$$ (D10)

There is a correction to the velocity $\widehat{\mathit{v}}\equiv (1/\hslash ){\mathbf{\nabla }}_{\mathit{q}}{\widehat{H}}_{\mathit{q}}$ beyond the mere unitary transformation ${\widehat{\mathcal{U}}}_{\mathit{q}}\widehat{\mathit{v}}{\widehat{\mathcal{U}}}_{\mathit{q}}^{†}.$ In the last line this correction is written in terms of the rate of change of ${\widehat{\sigma }}_z$ (in the Heisenberg picture) to indicate its physical origin: the motion of a particle between orbitals within the unit cell corresponds to motion through space with nonzero velocity. In the semiclassical dynamics of the wave packet, this gives the correction

$${\mathit{v}}^{\prime }=\mathit{v}-\frac{1}{2}\mathit{\rho }\langle {\widehat{\stackrel{.}{\sigma }}}_z\rangle =\mathit{v}-\frac{1}{2}\mathit{\rho }\dot{\mathit{q}}\cdot {\mathbf{\nabla }}_{\mathit{q}}\langle {\widehat{\sigma }}_z\rangle .$$ (D11)

Starting from the standard semiclassical dynamics (74) in the original (unprimed) basis, and using the transformations (D4), (D7), and (D11), one recovers the correct semiclassical dynamics in the new (primed) basis

$${\mathit{v}}^{\prime }=\frac{1}{\hslash }{\mathbf{\nabla }}_{\mathit{q}}{E}_{\mathit{q}}^{\prime }+{\mathbf{\Omega }}^{\prime }\times \stackrel{.}{\mathit{q}}.$$ (D12)

Thus, unitary transformations of this form lead to changes in the positions of the orbitals within the unit cell: these changes in cell geometry modify the effect of the forces applied and the velocity on the scale of the unit cell. These modifications compensate the change in the Berry curvature to recover the correct semiclassical dynamics.