Revealing Developmental Regionalization of Infant Cerebral Cortex Based on Multiple Cortical Properties

Abstract

The human brain develops dynamically and regionally heterogeneously during the first two postnatal years. Cortical developmental regionalization, i.e., the landscape of cortical heterogeneity in development, reflects the organization of underlying microstructures, which are closely related to the functional principles of the cortex. Therefore, prospecting early cortical developmental regionalization can provide neurobiologically meaningful units for precise region localization, which will advance our understanding on brain development in this critical period. However, due to the absence of dedicated computational tools and large-scale datasets, our knowledge on early cortical developmental regionalization still remains intact. To fill both the methodological and knowledge gaps, we propose to explore the cortical developmental regionalization using a novel method based on nonnegative matrix factorization (NMF), due to its ability in analyzing complex high-dimensional data by representing data using several bases in a data-driven way. Specifically, a novel multi-view NMF (MV-NMF) method is proposed, in which multiple distinct and complementary cortical properties (i.e., multiple views) are jointly considered to provide comprehensive observation of cortical regionalization process. To ensure the sparsity of the discovered regions, an orthogonal constraint defined in Stiefel manifold is imposed in our MV-NMF method. Meanwhile, a graph-induced constraint is also included to improve the compactness of the discovered regions. Capitalizing on an unprecedentedly large dataset with 1,560 longitudinal MRI scans from 887 infants, we delineate the first neurobiologically meaningful representation of early cortical regionalization, providing a valuable reference for brain development studies.

1. Introduction

The human brain undergoes a protracted course of development after birth, while maintains an exceptionally high rate of development in the first two years [1, 2]. There is a growing consensus that early development strongly affects brain cognition and function throughout the entire lifespan, suggesting that exploring the early brain developmental patterns is of great importance in understanding both ordered and disordered brains [1, 3]. Due to the non-uniformities in underlying cortical microstructures, which are closely related to functional principles of the cortex, the infant cerebral cortex grows in regionally heterogeneous manners, thus forming a unique landscape of cortical developmental regionalization. Prospecting such developmental regionalization could potentially provide neurobiologically meaningful units to facilitate precise region localization, inter-subject and inter-study comparison, and effective feature reduction for early brain disorder identification [4], thus advancing our understanding on brain development in this critical early period. However, due to the absence of dedicated computational tools and large-scale datasets, our knowledge of such infantile cortical developmental regionalization still remains intact.

To fill the methodological gap and hence to advance our knowledge towards this critical early postnatal period, we are motivated to explore cortical developmental regionalization in the first two postnatal years, by leveraging a novel multi-view nonnegative matrix factorization (MV-NMF) method and an unprecedentedly large-scale infant MRI dataset. The utilization of NMF to analyze complex high-dimensional cortical data is mainly motivated by three reasons. 1) It can naturally discover different groups of vertices varying in similar manners across different subjects and ages, thus providing a part-based cortical representation to facilitate the interpretability of the cortical regionalization. 2) By varying the desired number of output components/parts, NMF can reveal the regionalization at different resolutions in a hierarchical manner. 3) It is more flexible than other development-based analyses [5], as there is no strict requirement of longitudinal data with multiple time points. On the other hand, the motivation to use multiple views, i.e., multiple cortical attributes (e.g., cortical thickness and surface area), is to provide comprehensive and complementary characterizations of the cortical regionalization process, as different cortical attributes have distinct neurobiological mechanisms and thus reflect distinct aspects of the regionalization progress.

Therefore, in our proposed MV-NMF method, we minimize an objective function to jointly decompose multi-view data matrices (of cortical attributes) for grouping cortical vertices into hierarchical regions. Specifically, apart from the conventional reconstruction error in each view, a multi-view regularization is included in our objective function to iteratively fuse multi-view information to encourage the consistency of regionalization results between different views. To improve the sparsity of the discovered regions, the orthogonal constraint is effectively imposed during the alternative optimization procedure by computing the gradient in the Stiefel manifold [6]. Moreover, a graph-induced regularization is also incorporated in our objective function to further improve the compactness of the results. The proposed MV-NMF method has been applied to an unprecedentedly large dataset with 1,560 longitudinal MRI scans from 887 typically developing infants. The revealed landscape of early cortical regionalization provides a reliable reference for studying early postnatal cortical organization and progression.

2. Materials and Methods

2.1. Dataset and Image Processing

Totally 1,560 longitudinal MRI scans were collected from 887 typically developing infants (466 males / 421 females) with age at scan ranging from 0.2 months to 29.3 months. Using a Siemens 3T head-only scanner, T1w images with the resolution of 1 × 1 × 1 mm³ were acquired with the parameters: TR=1,900 ms, TE=4.38 ms, inversion time=1,100 ms, and flip angle= 7°. T2w images with the resolution of 1.25 × 1.25 × 1.95 mm³ were acquired with the parameters: TR=7,380 ms, TE=119 ms, and flip angle=150°.

All MR images were preprocessed following a standard procedure [7], including skull stripping, cerebellum and brain stem removal, intensity inhomogeneity correction, rigid alignment of each scan to the age-matched infant brain atlas, tissue segmentation, non-cortical structure masking and filling, and left-right hemisphere separation. Inner and outer cortical surfaces were reconstructed for each hemisphere and mapped onto a spherical space. To establish cortical correspondences across subjects and ages, we employed a longitudinally consistent registration strategy. Specifically, first, for each subject, longitudinal cortical correspondences were established by spherical registration of surfaces at the early time points to the corresponding surface at the last time point [8]. Then, inter-subject cortical correspondences were established by groupwise registration of all spherical cortical surfaces at the last time point. All cortical surfaces were finally resampled to a standard mesh tessellation, and computed with surface area and cortical thickness for each vertex [8], which will be used as cortical attributes for discovering cortical developmental regionalization.

2.2. Nonnegative Matrix Factorization (NMF)

In a data-driven way, the NMF method approximates complex high-dimensional data by representing them as the linear combinations of limited bases, with each basis corresponding to a part/component. Taking cortical thickness as an example, the data matrix $X\in {ℝ}^{M\times N}$ is a large nonnegative matrix constructed by cortical thickness values from all scans (data samples), where M and N are the numbers of vertices and scans, respectively. Each column of X includes cortical thickness values from one scan. The NMF method decomposes X into two smaller non-negative matrices, i.e., the bases matrix $W\in {ℝ}^{M\times K}$ and the coefficients matrix $H\in {ℝ}^{K\times N}$, by satisfying X ≈ WH. The number of bases (components/parts) should be small, i.e., K ≪ M and K ≪ N. As a result, each column of W is a basis that represents one distinct region/part, which indicates a group of cortical vertices jointly developing across subjects and ages. Each data sample (i.e., each column in X) can be approximately reconstructed by a linear combination of bases from W, using the corresponding column from H as the coefficients. By minimizing the Frobenius norm of the reconstruction error $||X-{W|H||}_F^2$, W and H can be found through an iterative multiplication [9].

2.3. Multi-View NMF

Multiple cortical attributes, e.g., cortical thickness, surface area and myelin content, have distinct biological mechanisms and provide rich complementary information on cortical development, thus improving the reliability and meaningfulness of discovered basis matrices. Hence, we propose a multi-view NMF (MV-NMF) framework, with each view corresponding to a cortical attribute, to discover early cortical developmental regionalization. Besides the multi-view regularization, our MV-NMF also imposes an orthogonal constraint by computing the true gradient in an orthogonal parameter space, namely Stiefel manifold. To further improve the compactness of the final solutions, a graph regularization is also included.

Objective Function.

Let $X_v\in {ℝ}^{M\times N_v}$ be the data matrix for the v-th view in total V views, while $W_v\in {ℝ}^{M\times K}$ and $H_v\in {ℝ}^{K\times N_v}$ denote, respectively, the basis and coefficient matrices decomposed from X_v. Scalar N_v is the total number of samples in the v-th view. The objective function of our MV-NMF method is defined as

$$\mathcal{J}=\underset{W_v^T{W}_v=I}{\underset{W_v,H_v\ge 0}{\text{min}}}\frac{1}{2}\sum _{v=1\dots V}{\lambda }_v\Vert X_v-W_v{H}_v{\Vert }_F^2+{\mathcal{R}}_{MV}+\alpha \cdot {\mathcal{R}}_G.$$ (1)

Herein, alongside the reconstruction error in the first term, we introduce two additional terms, i.e., the multi-view regularization ${\mathcal{R}}_{MV}$ and the graph-based regularization ${\mathcal{R}}_G$. Parameters λ_v and α control the influences of their corresponding terms.

The multi-view regularization is defined as

$${\mathcal{R}}_{MV}=\frac{1}{2}\sum _{u=1\dots V}\sum _{v=1\dots V}{\theta }_{uv}\Vert W_u-W_v{\Vert }_F^2,$$ (2)

which aims to minimize the dissimilarity between the bases of different views. Parameter θ_uv controls the influence of the inconsistency between any two paired views.

The graph-based regularization ${\mathcal{R}}_G$ is introduced to improve the compactness and remove small artifacts of discovered regions. Denoting matrix A as a symmetric adjacent matrix, which defines the one-ring connections of vertices on the cortical surface. Matrix D is a diagonal matrix, where each element D_ii represents the sum of the i-th row (or column) of A. Let Tr(·) denote the trace of a matrix, the graph-based regularization is defined in terms of the graph Laplacian [10], i.e.,

$${\mathcal{R}}_G=\frac{1}{2}\sum _{v=1\dots V}Tr\left(W_v^T(A-D)W_v\right)).$$ (3)

Updating Rule.

First, the partial gradient of $\mathcal{J}$ toward H_v is found to be

$${\nabla }_{H_v}\mathcal{J}=-{\lambda }_v{W}_v^T{X}_v+{\lambda }_v{W}_v^T{W}_v{H}_v.$$ (4)

Thus, it is straightforward to have the form of updating rule for H_v, with ⨀ representing the elementwise multiplication:

$$H_v\leftarrow H_v\odot \frac{W_v^T{X}_v}{W_v^T{W}_v{H}_v}.$$ (5)

To update W_v, we first compute the corresponding partial gradient:

$${\nabla }_{W_v}\mathcal{J}=-{\lambda }_v{X}_v{H}_v^T-\sum _{u=1\dots V}{\theta }_{uv}{W}_u+\sum _{u=1\dots V}{\theta }_{uv}{W}_v+{\lambda }_v{W}_v{H}_v{H}_v^T+\alpha (A-D)W_v.$$ (6)

Then, in Stiefel manifold, which is a parameter space with the orthogonality constraint $W_v^T{W}_v=I$, the true gradient ${\tilde{\nabla }}_{W_v}\mathcal{J}$ (with orthogonality) [6] is computed by

$${\tilde{\nabla }}_{W_v}\mathcal{J}={\nabla }_{W_v}\mathcal{J}-W_v{\left[{\nabla }_{W_v}\mathcal{J}\right]}^T{W}_v=\left[{\lambda }_v{W}_v{H}_v{X}_v^T{W}_v+\sum _{u=1,\dots ,V}{\theta }_{uv}{W}_v{W}_u^T{W}_v+\alpha D{W}_v+\alpha W_v{W}_v^{T}A{W}_v\right]-\left[{\lambda }_v{X}_v{H}_v^T+\sum _{u=1,v}{\theta }_{uv}{W}_u+\alpha A{W}_v+\alpha W_v{W}_v^{T}D{W}_v\right].$$ (7)

Accordingly, the multiplicative update rule for W_v is of the form

$$w_v\leftarrow w_v\odot \frac{{\lambda }_v{X}_v{H}_v^T+{\sum }_{u=1}^v{\theta }_{uv}{W}_u+\alpha A{W}_v+\alpha W_v{W}_v^{T}D{W}_v}{{\lambda }_v{W}_v{H}_v{X}_v^T{W}_v+{\sum }_{u=1}^v{\theta }_{uv}{W}_v{W}_u^T{W}_v+\alpha D{W}_v+\alpha W_v{W}_v^{T}A{W}_v}.$$ (8)

Iterative Optimization.

To generate meaningful solutions, an appropriate initialization for NMF-based methods is necessary. Many single-view NMF methods employ the nndsvd initialization method [11], which has shown faster reduction of the residual error than random initialization. Herein, we also apply nndsvd algorithm for initialization, but with some modifications to adapt our proposed multi-view scheme. Specifically, we first obtain initializations from each view separately, which encode the potential jointly developing vertices on each view. Second, we explicitly look for the intersections from the initializations of different views to generate new components in the initialization, since their intersections encode the potential jointly developing vertices on all views. Third, according to the desired number of initialization components, the smallest components are removed. In this way, the multi-view NMF scheme can be appropriately initialized. The optimal bases matrices W_v and coefficients matrices Hv of each view were obtained by iteratively calling Equations (8) and (5). The final regions discovered using MV-NMF were the average of regions from different views.

3. Experiments

In this paper, cortical thickness and surface area were used in our MV-NMF scheme to explore cortical regionalization, since they are two important cortical morphological attributes with distinct neurobiological/genetic mechanisms and growth patterns during infancy [4]. The data matrix of each view is normalized so that each column averages to 1. In our experiments, parameters of the proposed MV-NMF method were empirically set as: λ₁ = λ₂ 1, θ_uv 1000, and α = 500.

Effectiveness of MV-NMF.

To integrate information from multiple views, one straightforward solution is to concatenate the multiple data matrices into a single matrix. Specifically, assume $X_1\in {ℝ}^{M\times N_1}$ and $X_2\in {ℝ}^{M\times N_2}$ are two data matrices in term of cortical thickness and surface area, respectively. One can directly concatenate X₁ and X₂ (as [X₁, X₂]), and then apply the conventional NMF on the concatenated big matrix for exploring cortical regionalization. We refer this method as rig-NMF, since it rigidly imposes the bases from different views to be identical. Hence, we compared the rig-NMF with our MV-NMF using the same data and initialization. For a fair comparison, we employed an orthogonal projective version of NMF [9] for the rig-NMF method, given its state-of-the-art performance with high orthogonality and compactness [12].

We assume that the effectiveness of a method can be reflected by the border consistency of its discovered regionalization across different resolutions. That is, if a border is more consistently preserved along the change of K (i.e., the number of output components), the result is more likely to reflect the stable hierarchical regionalization of the underlying microstructures. Accordingly, by increasing K from 2 to 7, the border consistencies obtained by rig-NMF and our MV-NMF are compared in Fig. 1. Note that, each component highlighted by black block in a specific row (e.g., K = 2) means that it is hierarchically decomposed into two finer components in the next row (e.g., K = 3). Based on the inconsistent borders pointed by blue arrows, it can be observed that our MV-NMF discovers borders with higher consistency, indicating the effectiveness and rationality of our MV-NMF.

Fig. 1.

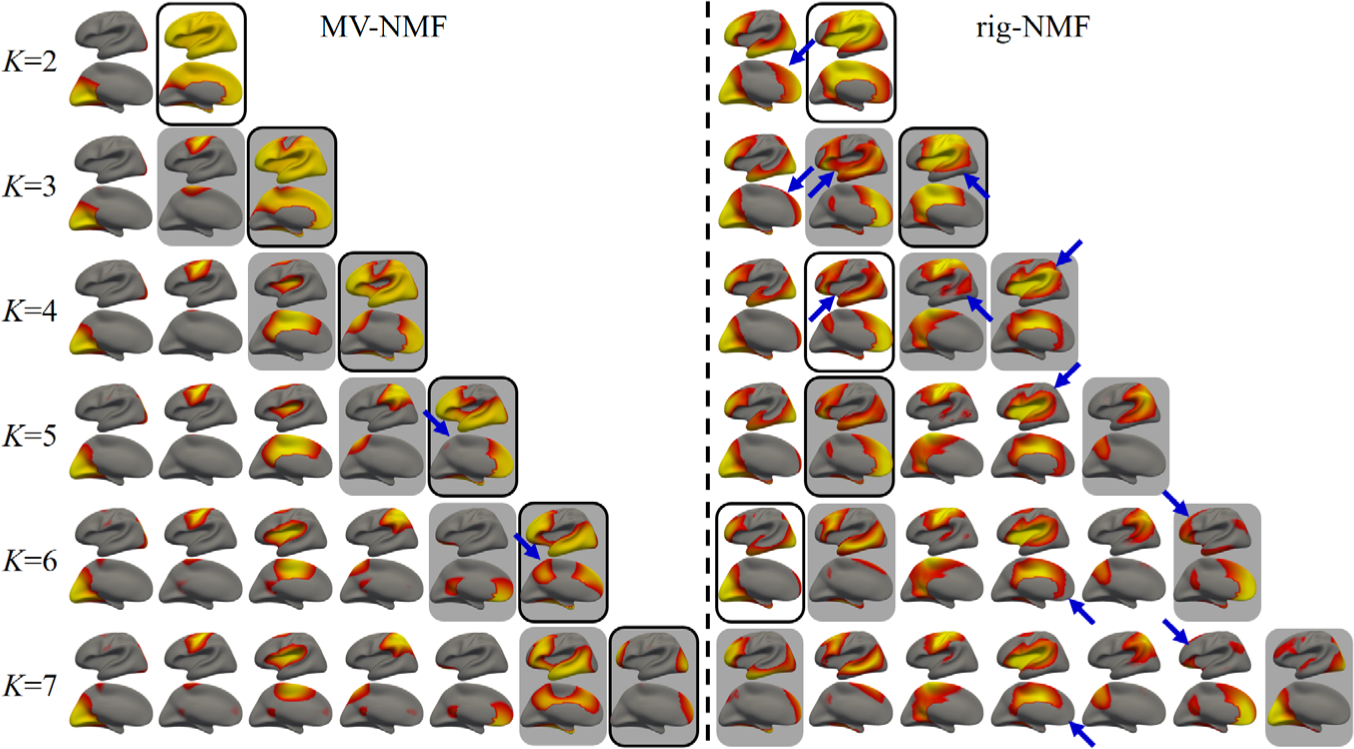
The layers of hierarchical structures obtained by MV-NMF and rig-NMF, by increasing the component number K from 2 to 7. The inconsistent borders across different layers are pointed out with blue arrows.

Robustness of MV-NMF.

The proposed MV-NMF does not require different views to have the same number of samples. To show the robustness of the MV-NMF, we designed an imbalanced testing dataset, where we randomly removed half of the cortical thickness samples to check if our method can still produce similar results as using all samples. This situation could happen when estimated cortical thickness values are not reliable for some subjects, since cortical thickness (between 1 and 5 mm) is much more sensitive to cortical surface reconstruction results, compared to surface area. This process was repeated five times. By calculating the Dice coefficient between each imbalanced test and the case of using all samples, we finally summarized the mean Dice coefficients at different numbers of components in Fig. 2 (a). It can be observed that, compared with rig-NMF, our MV-NMF yields similar performance when K is between 2 and 8, but much better performance when K is larger. Across all resolutions, the Dice coefficients of our MV-NMF are always larger than 0.9, demonstrating the robustness of our proposed method.

Fig. 2.

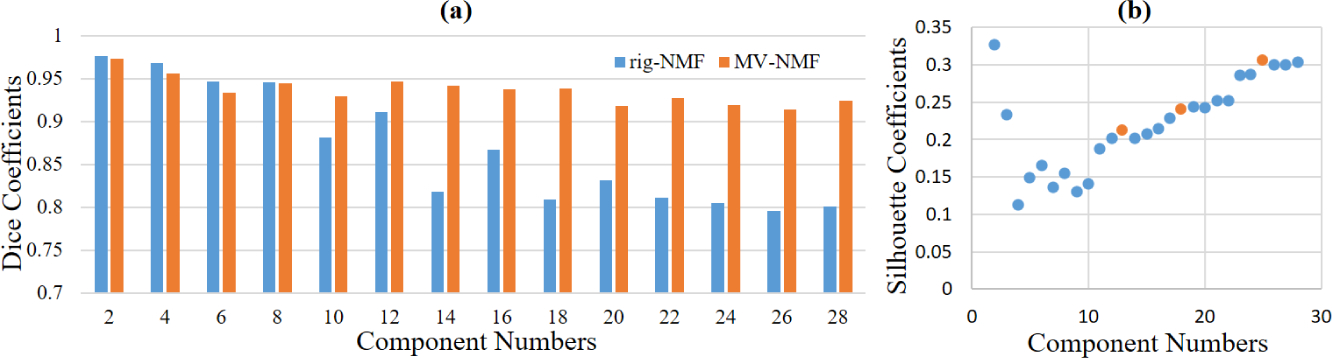
(a) Mean Dice coefficients by performing five times imbalanced sample test. (b) Silhouette coefficients in terms of different resolutions. K = 13, 25 are local peaks. K = 18 shows a start of a plateau (i.e., K = 18 to 22).

Determination of Resolution K.

Whereas MV-NMF provides hierarchical regions while increasing the resolution, we need to select some representative resolutions for the best representation of the studied data. To this end, a silhouette value was computed for each resolution K. It measures the intra-region similarity against inter-regions similarity. High silhouette values indicate better results. In each view, the similarity of two vertices i and j is evaluated using the correlation coefficient between X_v(i,·) and X_v(j,·). The multi-view silhouette value is the average of the values from all views, as shown in Fig. 2 (b). Naturally, higher resolutions lead to higher silhouette values. Yet we can still observe local peaks, such as for K = 13 and 25. Meanwhile, when resolution increases from 18 to 22, a plateau is shown. We thus chose 13, 18, and 25 as the most appropriate resolutions for the landscape of early cortical regionalization.

Discovered Regions.

Although 13, 18 and 25 are all shown to be appropriate resolutions, we prefer relatively finer ones when considering network/region-based analyses. Fig. 3 shows the discovered regions with K = 25 and their topography with sharp boundaries, which correspond well with existing neuroscience knowledge according to the name of each region given in the figure. Besides, these regions are also consistent with previous findings. For example, regions 2, 11, 13, 15, 17, 18, 21, 22 and 25 are found in the genetic-based cortical topography [4]. Regions 2, 6, 7, 11, 13, 14, 15, 18, 23, 24 are found in the cortical thickness based remodeling patterns in adolescents [12].

Fig. 3.

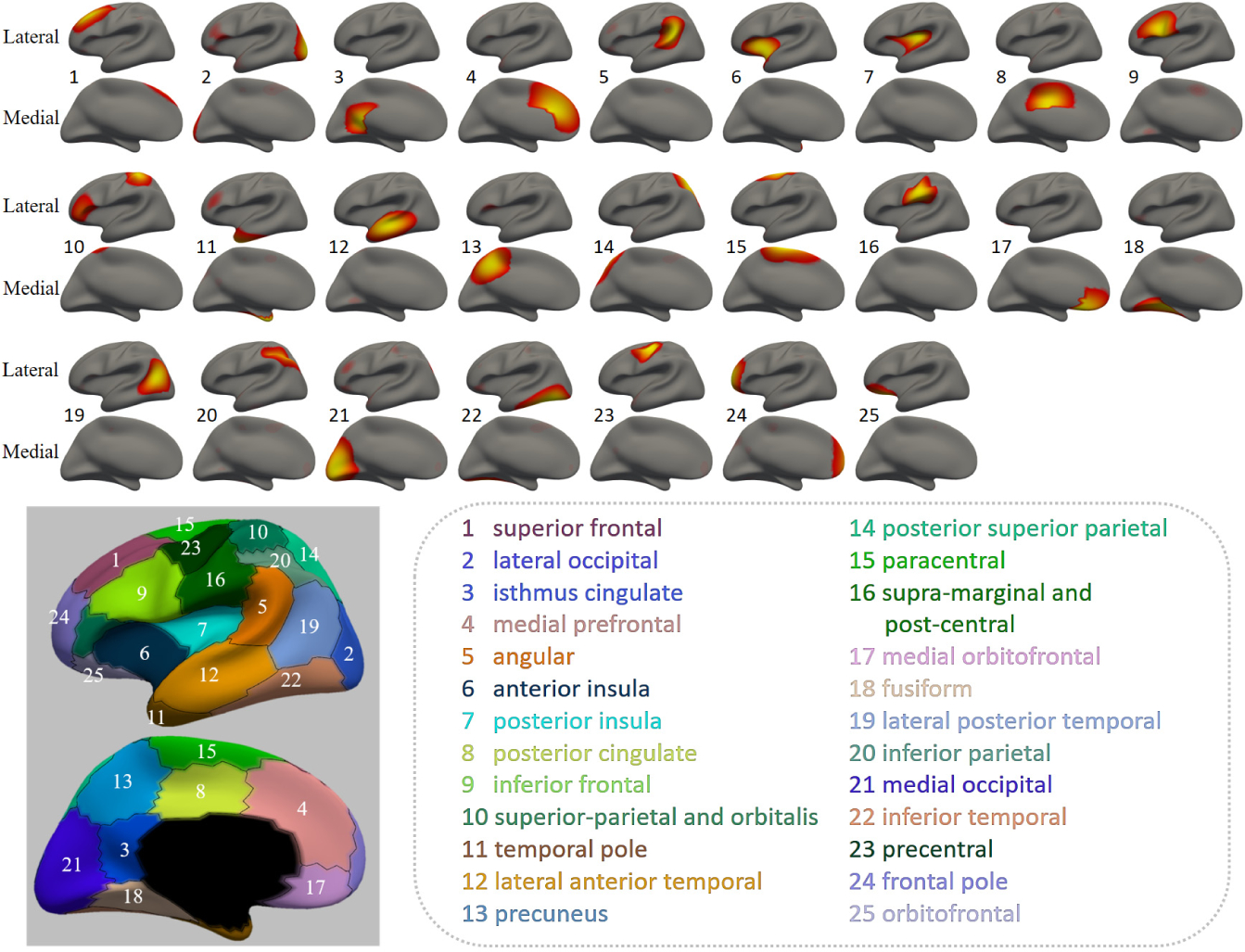
The 25 regions and their topography with sharp boundaries.

4. Conclusion

We have proposed a novel multi-view NMF scheme to jointly consider cortical thickness and surface area for exploring the early cortical developmental regionalization. Capitalizing on an unprecedentedly large infant MRI dataset, we have provided valuable references of region topography that encodes multi-view cortical developmental patterns. Our discovered regionalizatoin reflects co-developing vertices across ages and subjects on multi-views, which differs markedly from previous cortical atlases. These references will later be publicly released to facilitate other infant-related studies, thus boosting our knowledge in the early brain development. As an important future work, we will include more cortical attributes to discover regionalization patterns based on more than two views, which will provide more insights into early brain development.