The Mortality and Medical Costs of Air Pollution: Evidence from Changes in Wind Direction

Abstract

We estimate the causal effects of acute fine particulate matter exposure on mortality, health care use, and medical costs among the US elderly using Medicare data. We instrument for air pollution using changes in local wind direction and develop a new approach that uses machine learning to estimate the life-years lost due to pollution exposure. Finally, we characterize treatment effect heterogeneity using both life expectancy and generic machine learning inference. Both approaches find that mortality effects are concentrated in about 25 percent of the elderly population.

Exposure to high levels of air pollution negatively affects human health, leading many countries to regulate air pollution levels. Accurately quantifying the health effects of marginal pollution reductions matters greatly for determining optimal environmental policy, especially for rich countries where pollution levels are relatively low and further reductions may be very costly. However, estimating the causal effect of pollution on health is complicated due to well-documented challenges, including omitted variable bias, measurement error, and separately identifying the effects of different pollutants. Quasi-experimental studies that use a plausibly exogenous source of pollution variation are typically confined to narrow geographic and temporal scales, raising questions of external validity. Such studies also lack power to detect changes in important but rare outcomes like adult mortality due to relatively small sample sizes. This problem is exacerbated when characterizing which groups are most vulnerable to pollution.

We conduct the first large-scale, quasi-experimental investigation of the effects of acute (short-term) fine particulate matter (PM 2.5) exposure on elderly mortality, health care use, and medical costs. We overcome the challenges described above by combining administrative data on the universe of elderly Medicare beneficiaries, comprising approximately 97 percent of the US population aged 65 and older, with daily pollution data covering much of the United States for the years 1999 through 2013. We then estimate the causal impact of PM 2.5 on health by exploiting variation in pollution attributable to changes in daily wind direction. We also employ machine learning techniques to estimate life-years lost due to acute pollution exposure and to systematically quantify treatment effect heterogeneity.

The identifying assumption of our instrumental variables (IV) approach is that, after flexibly controlling for many fixed effects and climatic variables, changes in a county’s daily wind direction are unrelated to changes in the county’s mortality or health care use except through their influence on air pollution. A key innovation of our study relative to previous quasi-experimental designs exploiting wind variation is that our approach does not require understanding the detailed layout of an area (e.g., locations of roads, rivers, and population centers) or identifying the sources of air pollution. This allows us to harness variation in PM 2.5 across a broad geographic scale and over a long time period, enabling us to estimate effects on rare health outcomes like mortality and to explore treatment effect heterogeneity.

We estimate that a 1 microgram per cubic meter (μg/m³) (about 10 percent of the mean) increase in PM 2.5 exposure for one day causes 0.69 additional deaths per million elderly individuals over the three-day window that spans the day of the increase and the following two days. Our IV estimates are significantly larger than both our ordinary least squares (OLS) estimates and estimates reported in the prior literature, demonstrating the potential for substantial bias in observational studies of pollution exposure. The IV estimate is robust to simultaneously instrumenting for PM 2.5, carbon monoxide, and ozone.

Increases in PM 2.5 also lead to more emergency room (ER) visits, more hospitalizations, and higher inpatient spending, driven almost entirely by admissions that originate in the ER. Each 1 μg/m³ increase in PM 2.5 increases three-day ER visits by 2.7 per million beneficiaries and inpatient ER spending by over $16,000 per million. OLS estimates are again much smaller and sometimes significantly negative. As a placebo test, we find no effect of PM 2.5 on planned (non-ER) hospital admissions.

A central concern that arises when estimating mortality effects is whether those who die from pollution exposure would have died soon anyway, a phenomenon referred to in the literature as “mortality displacement” or “harvesting.” If the mortality effects of pollution are concentrated among the relatively old or sick, then the number of life-years lost will be much smaller than if the effects were evenly distributed across the population. Some studies address mortality displacement by including pollution lags to investigate whether mortality effects decrease as the length of time under consideration increases or by averaging pollution fluctuations over longer time periods. We show that the effect of one-day PM 2.5 exposure on mortality grows if we expand the time window over which we measure mortality from 3 days to 5, 14, or 28 days, suggesting that our main results are not artifacts of short-term mortality displacement.

Traditional approaches to mortality displacement such as those described above cannot account for displacement that occurs outside the time window spanned by the dependent variable or included lags of treatment. They also cannot account for differences in remaining life expectancy among those who die. We therefore develop a new approach to directly estimate the number of life-years lost due to pollution exposure. We estimate a Cox-Lasso machine learning model that incorporates numerous individual- and neighborhood-level variables from Medicare health histories and the American Community Survey and use the results to predict remaining life expectancy at the individual level. For purposes of comparison, we also develop and implement a survival random forest model of life expectancy and find that it yields similar results. We aggregate our individual-level estimates to the county level and use them to estimate the number of life-years lost due to pollution exposure.

Our analysis reveals that accounting for age and sex reduces estimates of life-years lost by 33 percent compared to a naïve estimate that controls for nothing. Accounting for a person’s medical history reduces the life-years lost estimate by an additional 40 percent relative to using only age and sex. Our preferred estimate is that a 1 μg/m³ increase in PM 2.5 causes the loss of 2.99 life-years per million beneficiaries over 3 days. Using a conventional value of $100,000 per life-year (Cutler 2004), this estimate implies that the social mortality cost of a 1 μg/m³ increase in PM 2.5 is $299,000 per million beneficiaries. The accompanying increase in hospital payments is $19,000 per million beneficiaries. These estimates do not include the cost of any defensive investments or avoidance behaviors undertaken by people (e.g., Graff Zivin and Neidell 2009, 2013; Neidell 2009; Deschênes, Greenstone, and Shapiro 2017). A back-of-the-envelope calculation based on these results values the mortality benefit from the reduction in average US PM 2.5 concentrations during our study period (see Figure 1) at $24 billion per year.¹

Figure 1. Trends in PM 2.5 Air Pollution and Monitoring, 1999–2013.

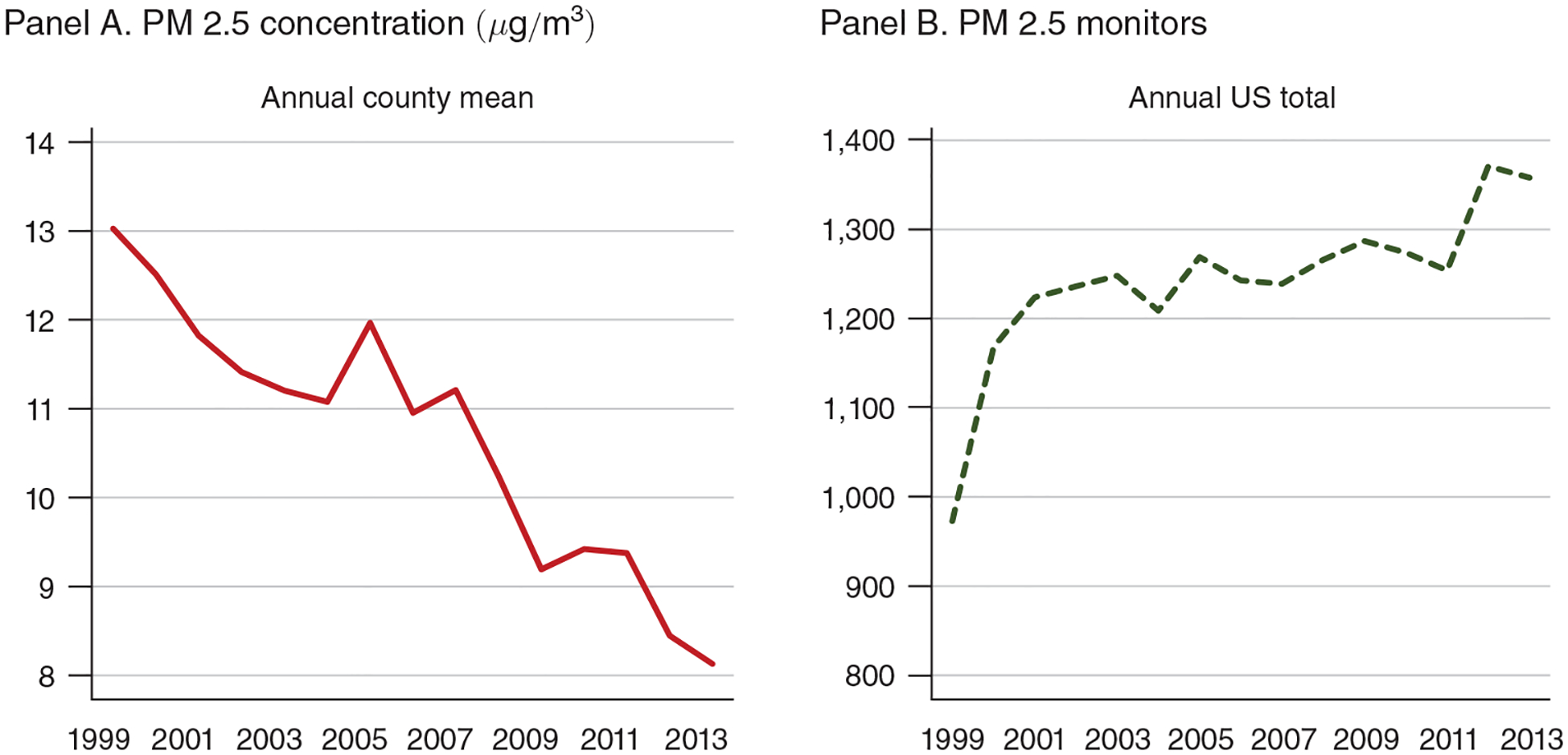
Note: The figure displays annual county means for PM 2.5 concentration (panel A) and the nationwide total number of PM 2.5 monitors (panel B).

Expressed in levels, our estimated mortality effect increases with age. However, the effect relative to each age group’s average mortality is nonmonotonic in age, suggesting that age alone is a noisy predictor of vulnerability to air pollution. We show that life expectancy is a better measure of vulnerability to pollution. For example, those with a life expectancy of less than 1 year are over 30 times more likely to die from pollution than the typical beneficiary, who has a life expectancy of 11 years. Although the number of people in this short-lived group is small, this effect is so large that, despite their high mortality rates, these beneficiaries lose the largest number of life-years per capita in both absolute (10.1 per million) and relative terms. The aggregate mortality burden of PM 2.5 is concentrated among the elderly with five to ten years of remaining life expectancy, followed by those with two to five years remaining, because these groups represent a large fraction of the Medicare population and are also vulnerable to acute particulate matter exposure.

These estimates of treatment effect heterogeneity will be incomplete if some determinants of pollution vulnerability are not relevant predictors of life expectancy. To examine heterogeneity more systematically, we adapt the machine-learning approach of Chernozhukov et al. (2018) to our setting. Using a sample of over 40 billion person-day observations, we recover a pattern of heterogeneous treatment effects that is similar to what we find using predicted life expectancy. Acute PM 2.5 exposure has a near-zero effect on mortality for about 75 percent of the elderly population and increases mortality substantially for about 5 percent of this population. The life expectancy of the most vulnerable group (top 1 percent) is 7.9 years less than the least vulnerable group (bottom 75 percent), and the means of important predictors of life expectancy vary significantly between these two groups. The most vulnerable group of beneficiaries is 7.2 years older, 6 percentage points more likely to have lung cancer, and 38 percentage points more likely to suffer from Alzheimer’s disease or dementia than the least vulnerable group. Overall, we conclude that life expectancy accurately indexes elderly vulnerability to air pollution.

The Environmental Protection Agency (EPA) has tightened its regulation of particulates over the past several decades, focusing increasingly on small particulates. Evidence supporting fine particulate matter regulation has come primarily from associational studies that have consistently found a relationship between PM 2.5 and increased morbidity and mortality, even after controlling for various confounding factors (e.g., Dockery et al. 1993, Laden et al. 2000, Samet et al. 2000, Pope and Dockery 2006). Most of these studies focus on the effects of short-term (usually daily) exposure (Pope 2000), suggesting that even transient increases in particulate matter can have significant consequences. However, concerns about bias in associational estimates have caused both the scientific community and regulators to question how many deaths are avoided from reductions in particulate matter (OMB 2012; Dominici, Greenstone, and Sunstein 2014). While randomized controlled laboratory trials have shown negative effects of acute pollution exposure on cardiovascular performance, these studies face issues of external validity and are too small to draw conclusions about mortality effects (Brook et al. 2009, Langrish et al. 2013).

Our study provides the first quasi-experimental estimates of the causal effect of acute PM 2.5 exposure on adult mortality, health care use, and medical costs. We contribute to the recent quasi-experimental literature in economics on the health effects of air pollution. Much of this work has focused on the effect of pollutants other than fine particulate matter, such as TSP, PM 10, ozone, sulfur dioxide, or nitrogen oxides (Chay, Dobkin, and Greenstone 2003; Chay and Greenstone 2003; Currie and Neidell 2005; Currie, Neidell, and Schmieder 2009; Moretti and Neidell 2011; Chen et al. 2013; Schlenker and Walker 2016; Knittel, Miller, and Sanders 2016; Deschênes, Greenstone, and Shapiro 2017). Of these studies, only four consider non-infant mortality (Chay, Dobkin, and Greenstone 2003; Chen et al. 2013; Deschênes, Greenstone, and Shapiro 2017; Deryugina and Reif 2019), but they do not estimate the effects of fine particulate matter. Ward (2015) focuses on PM 2.5 but only considers hospitalizations from respiratory causes in the province of Ontario. Anderson (2015) uses variation in wind direction across a highway in Los Angeles to proxy for changes in air pollution but does not directly measure which pollutants are changing and focuses on chronic (long-term), rather than acute, pollution exposure.

Our study moves beyond these papers in three important ways. First, we estimate mortality costs more accurately by developing and applying a novel machine-learning-based method to estimate the life-years lost associated with air pollution exposure. We are not aware of any other study that has incorporated information beyond age and sex when accounting for life-years lost, or of any other paper in economics that has estimated a survival model using machine learning. Second, we are the first to apply the Chernozhukov et al. (2018) method of generic machine learning inference on heterogeneous treatment effects to a quasi-experimental study design. Third, our approach allows us to separately identify the causal effects of multiple pollutants on mortality. We find that the PM 2.5-mortality relationship is more robust than that of other pollutants.

Our methods can be applied in a wide variety of contexts. For example, whether health insurance reduces mortality is an important question in health economics (Finkelstein and McKnight 2008; Card, Dobkin, and Maestas 2009; Huh and Reif 2017). As in our study, estimating the social value of that mortality reduction depends on the number of life-years saved, which can be quantified using our life-years lost approach together with datasets containing information on demographics, health status, and mortality, such as the Health and Retirement Study or the Panel Study of Income Dynamics. In addition, our heterogeneity approaches can identify which populations benefit most from health insurance, another longstanding question in health economics (Levy and Meltzer 2008, Black et al. 2019).

The rest of the paper is organized as follows. Section I provides a brief background on fine particulate matter, summarizes how wind transports air pollution, and gives a preview of our estimation strategy. Section II describes our data. Section III describes our empirical strategy in detail. Section IV presents results, and Section V concludes.

I. Background

Fine particulate matter, PM 2.5, is a mixture of various particles with diameters of 2.5 micrometers or less, including nitrates, sulfates, ammonium, and carbon (Kundu and Stone 2014).² The PM 2.5 present in a given location consists of both locally produced pollution and pollution produced elsewhere that is transported into the region by the wind.³ The amount of transported pollution is significant (Zhang et al. 2017). For example, the EPA estimates that most of the PM 2.5 in the Eastern United States was transported from hundreds of miles away (EPA 2004). Pollution transport patterns depend on a host of factors, including the pollutant, the location of the pollution source, wind direction and speed, precipitation, and other atmospheric conditions.

Although sophisticated atmospheric science models (e.g., Muller and Mendelsohn 2007) can simulate pollution transport and the resulting estimates can be used as instruments for pollution, simulating pollution transport is computationally infeasible at the daily level. However, a valid instrumental variables approach requires only that the instruments (i) be sufficiently correlated with the endogenous variable of interest and (ii) not be correlated with any unobserved determinants of the outcome of interest. We instrument for changes in a county’s daily average PM 2.5 concentrations using changes in the county’s daily average wind direction, which we show is by itself an important determinant of pollution levels.⁴

Wind may affect pollution measured by a particular monitor either by redistributing locally produced pollution (e.g., from traffic or local power plants) or by transporting externally produced pollution into the county. We construct our empirical specification to exploit primarily the wind-induced variation in pollution exposure that affects the whole county in a similar manner. This variation, which is more likely to arise from transport of externally produced pollution, reduces the potential for measurement error in residents’ pollution exposure due to within-county transport.

We now illustrate the type of variation used to estimate the causal effects of PM 2.5, relegating the details to Section III. Figure 2 shows the relationship between the estimated daily wind direction at pollution monitors, in 10-degree bins, and PM 2.5 concentrations measured by these monitors in and around the San Francisco Bay Area, CA. Figure 3 shows the same relationship for pollution monitors in and around Greater Boston, MA. All estimates are relative to 260–270 degrees, where 270 degrees corresponds to a “westerly” (blowing from the west) wind direction. The figures display results from a regression that controls for county, month-by-year, and state-by-month fixed effects, as well as a flexible set of controls for maximum and minimum temperatures, precipitation, wind speed, and the interactions between them.

Figure 2. Relationship between Daily Average Wind Direction and PM 2.5 Concentrations for Counties in and around the Bay Area, CA.

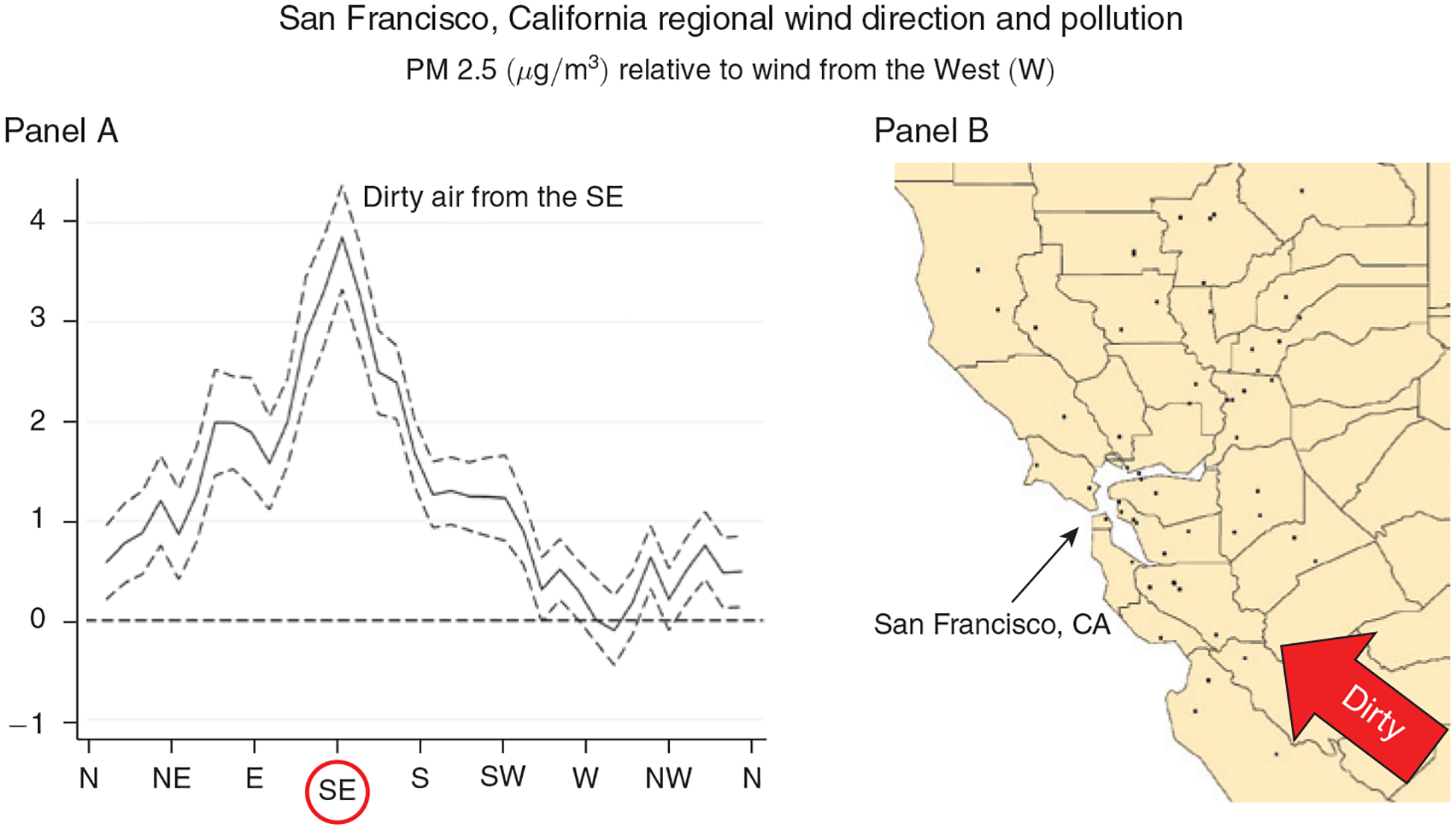
Notes: Panel A shows regression estimates of equation (A1) from the online Appendix, where the dependent variable is the county average daily PM 2.5 concentration and the key independent variables are a set of indicators for the daily wind direction falling into a particular 10-degree angle bin. Controls include county, month-by-year, and state-by-month fixed effects, as well as a flexible function of maximum and minimum temperatures, precipitation, wind speed, and the interactions between them. The dashed lines represent 95 percent confidence intervals based on robust standard errors. Panel B shows the location of the PM 2.5 pollution monitors (black dots) in the Bay Area that provided the pollution measures for this regression.

Figure 3. Relationship between Daily Average Wind Direction and PM 2.5 Concentrations for Counties in and around the Greater Boston Area, MA.

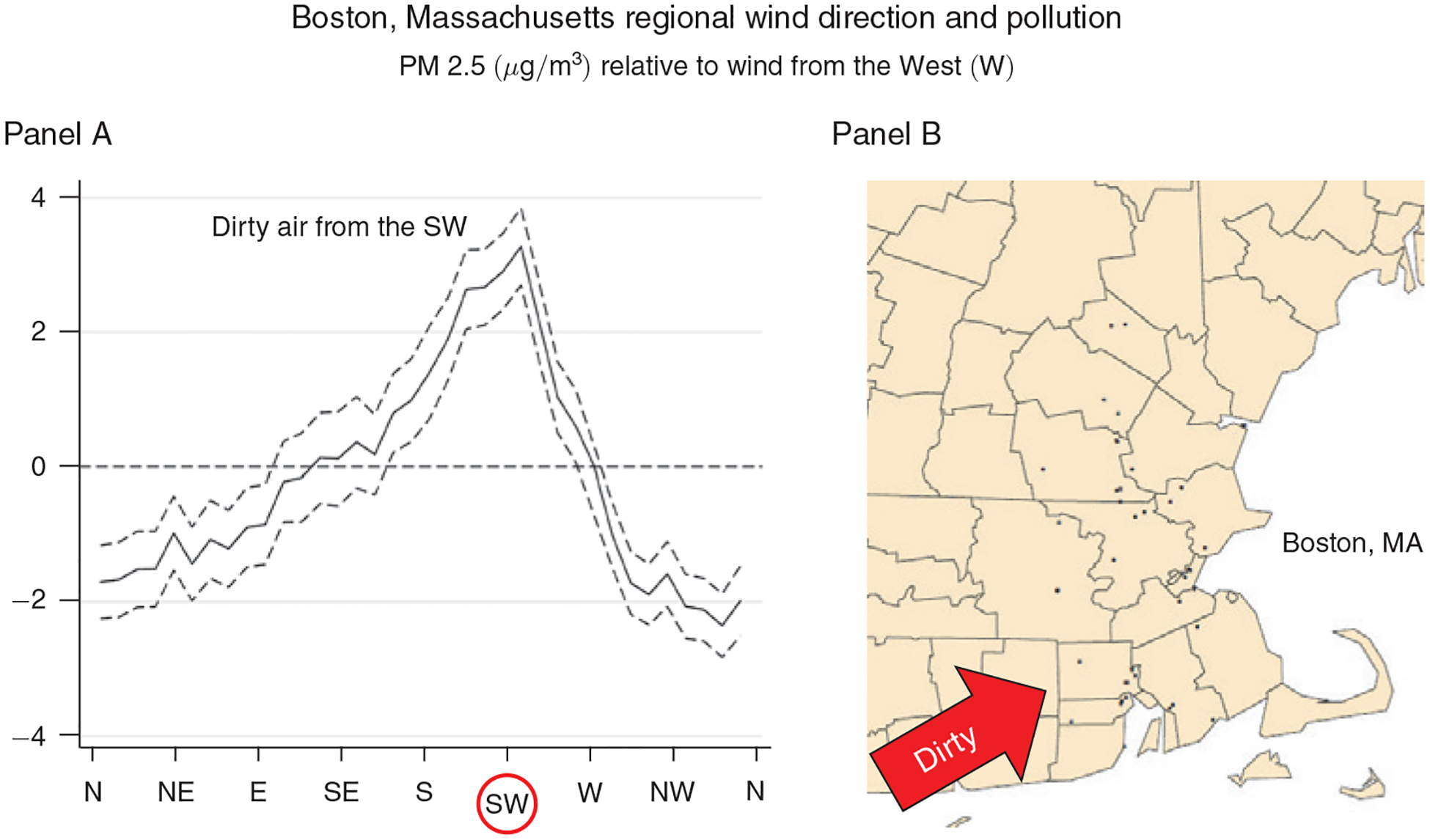
Notes: Panel A shows regression estimates of equation (A1) from the online Appendix, where the dependent variable is the county average daily PM 2.5 concentration and the key independent variables are a set of indicators for the daily wind direction falling into a particular 10-degree angle bin. Controls include county, month-by-year, and state-by-month fixed effects, as well as a flexible function of maximum and minimum temperatures, precipitation, wind speed, and the interactions between them. The dashed lines represent 95 percent confidence intervals based on robust standard errors. Panel B shows the location of the PM 2.5 pollution monitors (black dots) in the Boston area that provided the pollution measures for this regression.

In both figures, the local wind direction is a strong predictor of local PM 2.5, and the patterns are consistent with local geography. In and around the Bay Area, PM 2.5 is highest when the wind is blowing from the southeast and lowest when the wind is blowing from the west and the north. In other words, more pollution is blown in from Southeast California than from the ocean or less densely populated states like Oregon and Washington. In and around Boston, pollution is highest when the wind is blowing from the southwest, where New York City is located, and lowest when it is blowing from the east, north, northeast and northwest, where the ocean and sparsely populated areas dominate.

II. Data

A. Air Pollution

We obtain air pollution data from the EPA’s Air Quality System database, which provides hourly data at the pollution-monitor level for pollutants that are regulated by the Clean Air Act. Comprehensive data for PM 2.5 are available beginning in 1999. We also obtain data on four other criteria pollutants: ozone (O₃), carbon monoxide (CO), sulfur dioxide (SO₂), and nitrogen dioxide (NO₂).⁵ As with PM 2.5, past literature has linked these air pollutants to adverse health outcomes (Currie and Neidell 2005, Moretti and Neidell 2011, Ward 2015, Schlenker and Walker 2016). We aggregate monitor readings to the daily level by averaging across hourly observations and then construct county-level pollution measures by averaging all available pollution readings on a given day across all monitors located within the county.

Figure 1 displays aggregate trends in PM 2.5 over time. Average concentrations of PM 2.5 fell steadily from 13.0 micrograms per cubic meter (μg/m³) in 1999 to 8.13 μg/m³ in 2013. One unit of PM 2.5 thus represents about 10 percent of the average concentration during our time period. Figure 1 also shows that the number of PM 2.5 monitors has remained fairly constant since 2001. However, the set of monitored counties does change over time, and Grainger, Schreiber, and Chang (2016) finds evidence that counties strategically place their pollution monitors in relatively clean areas. Because our instrumental variables approach exploits variation in pollution that is almost surely independent of monitor placement, our estimates should not be biased by changes in monitor composition. However, for completeness we test the robustness of our results to imposing various continuity requirements on the sample of included pollution monitors and obtain very similar estimates (see discussion in Section IVD).

B. Atmospheric Conditions

Wind speed and wind direction data for the years 1999–2013 are obtained from the North American Regional Reanalysis (NARR) daily reanalysis data.⁶ NARR incorporates raw data from land-based weather stations, aircraft, satellites, radiosondes (essentially weather balloons), dropsondes (weather instruments dropped from aircraft), and other meteorological datasets. Wind conditions are reported on a 32-by-32 kilometer grid and consist of vector pairs, one for the east-west wind direction (u-component) and one for the north-south wind direction (v-component). We first interpolate between grid points to estimate the daily u- and v-components at each pollution monitor. We then convert the average u- and v-components into wind direction and wind speed and average up to the county-day level. We define “wind direction” as the direction the wind is blowing from.

Finally, we obtain temperature and precipitation data from Schlenker and Roberts (2009), which produces a daily weather grid using data from PRISM and weather stations.⁷ Total daily precipitation and daily maximum and minimum temperatures are reported for each point on a 2.5-by-2.5 mile grid covering the contiguous United States for the years 1999–2013. We average the daily measures across all grid points in a particular county to obtain a county-day measure.

C. Mortality, Morbidity, and Medical Costs

Our data on mortality, morbidity, and medical costs come from Medicare administrative data. Our sample includes all beneficiaries between 65 and 100 years old, accounting for over 97 percent of US elderly. Dates of death, age, sex, and county of residence are obtained for all beneficiaries from the 1999–2013 Medicare enrollment files. Health care use and costs are derived from the Medicare Provider Analysis and Review (MedPAR) File, which reports information on each inpatient stay in a hospital or skilled nursing facility for any beneficiary enrolled in fee-for-service (FFS) Medicare.⁸ MedPAR observations are derived from facility (Medicare Part A) service claims corresponding to that stay and include the date of admission, length of stay, and total cost of the stay.⁹ The cost of these inpatient stays accounts for about 70 percent of all Medicare Part A spending and about 43 percent of all Medicare Parts A, B, and D spending on elderly FFS beneficiaries over 1999–2013. We also use Medicare outpatient claims to measure outpatient ER visits that do not result in a hospital admission, although we do not observe their cost. We aggregate hospital visit records to the county-day level using patients’ county of residence and the admission date (for inpatient stays) or date of service (for outpatient ER visits).

Individual-level indicators for the presence of 27 chronic conditions, such as heart disease, chronic obstructive pulmonary disease (COPD), diabetes, and depression, are obtained from the chronic conditions segment of the Master Beneficiary Summary File. Professional medical coders infer these conditions from detailed claims data, which are only available for beneficiaries enrolled in FFS Medicare. Because it may take some time for a relevant claim to appear in the data, information about chronic conditions will be most reliable for those who have been enrolled in FFS Medicare for multiple years.

Table 1 presents summary statistics for our main estimation sample, which consists of 1,980,549 county-day observations.¹⁰ The mean daily concentration of PM 2.5 is 10.48 micrograms per cubic meter, with a standard deviation of 7.13. There are, on average, 49,106 Medicare beneficiaries in each county, and about one-half of them are between the ages of 65 and 74. Because we focus on the elderly, the three-day mortality rate in our sample is high, ranging from 135 per million for those aged 65–69 to nearly 1,200 per million for those aged 85 and over.

Table 1—

Summary Statistics, 1999–2013

	Mean	Standard deviation	Observations
PM 2.5 (μg/m3)	10.48	7.13	1,980,549
Number of beneficiaries
65+	49,106	78,983	1,980,549
65–69	13,173	20,910	1,980,549
70–74	11,672	18,802	1,980,549
75–79	9,658	15,767	1,980,549
80–84	7,452	12,183	1,980,549
85+	7,151	11,818	1,980,549
Number of FFS beneficiaries	34,196	52,182	1,898,236
Continuously enrolled FFS beneficiaries	26,901	39,335	1,898,236
Three-day mortality rate
65+	388.25	247.60	1,980,549
65–69	135.37	264.38	1,980,549
70–74	201.83	369.19	1,980,549
75–79	320.70	487.38	1,980,549
80–84	526.38	787.33	1,980,549
85+	1,168.68	1,118.87	1,980,549
All FFS	404.84	274.51	1,898,236
Continuously enrolled FFS	456.06	317.66	1,898,236
Three-day inpatient spending, planned and ER	34,598,644	15,236,367	1,898,236
Three-day inpatient ER spending	13,793,534	7,831,989	1,898,236
Three-day admissions rate, planned and ER	3,270	1,207	1,898,236
Three-day ER admissions rate	1,547	707	1,898,236
Three-day ER (inpatient and outpatient) visit rate	4,185	1,206	1,898,236

Notes: Table reports unweighted statistics for the estimation sample. Unit of observation is county-day. All rates are per million Medicare beneficiaries in the relevant group. Spending and admissions variables are only available for fee-for-service (FFS) beneficiaries. Continuously enrolled refers to beneficiaries who have been continuously enrolled in FFS for at least two years. Life-years lost analysis uses variables only available for continuously enrolled FFS beneficiaries. All FFS samples begin in 2001 instead of 1999.

We observe hospital spending only for beneficiaries who are enrolled in FFS; these comprise 70 percent of the people in our sample. For the life-years lost analysis, we focus on the subset of beneficiaries who have been continuously enrolled in FFS for at least two years (55 percent of the people in our sample) to ensure well-measured chronic conditions. On average, there are 26,901 such individuals in each county, and their three-day mortality rate is higher than the overall mortality rate in the Medicare population.¹¹

Three-day hospital spending for the FFS population averages about $35 per beneficiary, in nominal terms. About 40 percent of this spending originates from ER admissions. On average, there are 3,270 hospital admissions per million FFS beneficiaries over any given three-day period, and 47 percent (1,547) of these admissions are through the ER. Many ER visits do not result in admissions: the overall ER visit rate is 4,185 per million FFS beneficiaries.

III. Empirical Strategy

A. Mortality and Health Care Use

Our objective is to estimate the effect of short-run exposure to fine particulate matter on mortality, health care use, and health care spending, net of any potentially confounding factors. We model this relationship using the following regression equation:

$$Y_{\mathit{\text{cdmy}}}=\beta \text{PM}{2.5}_{\mathit{\text{cdmy}}}+X_{\mathit{\text{cdmy}}}^{\prime }\gamma +{\alpha }_c+{\alpha }_{sm}+{\alpha }_{my}+{ϵ}_{\mathit{\text{cdmy}}},$$ (1)

where the dependent variable is the outcome of interest in county c on day d in month m and year y. The parameter of interest is β, the coefficient on daily PM 2.5 levels. We first examine the effect of PM 2.5 on the death rate, measured in deaths per million beneficiaries. The other outcome variables measure health care use and medical costs. We calculate these measures for all hospital admissions and also for the subset of hospital admissions that originate through the ER. We also estimate the effect of PM 2.5 on the total ER visit rate per million beneficiaries, which includes visits that did not result in a hospital admission. As a placebo test, we consider non-ER (planned) admissions, which should not be affected by short-run fluctuations in fine particulate matter.

The dependent variable, Y_cdmy, is a three-day total, based on the day d and the following two days. For example, we estimate the effect of PM 2.5 on May 1 on the death rate calculated across May 1–3. This aggregation nets out short-run mortality displacements: a death that occurs one to two days earlier because of an increase in pollution exposure (e.g., on May 1 instead of May 2) does not affect our three-day measure. A three-day measure also allows for lagged effects (e.g., exposure to pollution on May 1 could cause a death on May 2). To ensure that β is not capturing the effects of weather conditions over the following two days, we include two leads of our weather variables. Our OLS estimates also include two leads of PM 2.5, while our IV estimates include two leads of the instruments.¹² To minimize concerns about autocorrelation, we also control for two lags of PM 2.5 (OLS) or two lags of the instruments (IV).¹³

The high granularity and comprehensive scope of our data allow us to include multiple sets of high-dimensional fixed effects. We generate indicators for daily maximum temperatures falling into 1 of 17 bins, ranging from −15 degrees Celsius (5°F) or less to 30 degrees Celsius (86°F) or more, with 15 intermediate bins each spanning 3 degrees Celsius (5.4°F). We do the same for minimum temperatures. For daily precipitation and wind speed, we generate indicators for deciles of these variables. We then generate a set of indicators for all possible interactions of these temperature, precipitation, and wind speed variables and include it in all our regressions as $X_{\mathit{\text{cdmy}}}^{\prime }$.¹⁴ Our estimates are robust to less flexible weather controls or omitting weather controls entirely (Table 10). Those results reinforce the assumption that our estimates are not driven by unobserved climatic factors that are correlated with both wind direction and mortality.

Table 10—

Robustness of Mortality IV Estimates to Including Different Fixed Effects and Weather Controls

	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
PM 2.5 (μg/m3)	0.425	0.647	0.270	0.344	0.413	0.670	0.712	0.643
	(0.040)	(0.061)	(0.041)	(0.044)	(0.039)	(0.059)	(0.060)	(0.061)
Type of weather controls	None	Separate	None	None	None	Full	Full	Full
County fixed effects	X	X	X	X		X	X
Month fixed effects			X			X
Year fixed effects			X			X
Year-by-month fixed effects	X	X		X	X		X	X
State-by-month fixed effects	X	X
County-by-month fixed effects					X			X
F-statistic	460	333	439	449	474	288	292	309
Dependent variable mean	385	385	385	385	385	385	385	385
Observations	1,982,529	1,982,529	1,982,529	1,982,529	1,982,495	1,980,549	1,980,549	1,980,515

Notes: Table reports IV estimates of equation (1) from the main text when varying the inclusion of different weather controls and fixed effects. The dependent variable is the three-day mortality rate per million Medicare beneficiaries. Estimates are weighted by the number of beneficiaries. Standard errors, clustered by county, are reported in parentheses.

Our estimates also include county (α_c), state-by-month (α_sm), and month-by-year (α_my) fixed effects. The county fixed effects control for geographic differences in health and pollution. State-by-month fixed effects control for any seasonal correlation between pollution, wind direction, and population health, allowing this correlation to vary by state. Finally, month-by-year fixed effects control flexibly for common time-varying shocks, such as those induced by any Medicare or environmental policy changes during our sample period. As with weather controls, we estimate alternative specifications with varying fixed effects to demonstrate the robustness of our results. We cluster all standard errors at the county level and weight all estimates by the relevant population in cases where the dependent variable is in per capita terms.¹⁵ Our results are robust to different clustering choices, including clustering by pollution-monitor group.¹⁶

OLS estimates of equation (1) are prone to bias because exposure to PM 2.5 is not randomly assigned and is likely to be measured with error.¹⁷ We therefore employ an IV strategy, using daily wind direction in the county as an instrument for pollution and allowing the effect of the wind instruments on PM 2.5 to vary by geography. The specification for our first stage is

$$\text{PM}{2.5}_{\mathit{\text{cdmy}}}=\sum _{g\in G}\sum _{b=0}^2{\beta }_b^{g}1\left[G_c=g\right]\times WINDDI{R}_{\mathit{\text{cdmy}}}^{90b}+X_{\mathit{\text{cdmy}}}^{\prime }\sigma +{\alpha }_c+{\alpha }_{sm}+{\alpha }_{my}+{ϵ}_{\mathit{\text{cdmy}}}.$$ (2)

The excluded instruments are the variables $1\left[G_c=g\right]\times WINDDI{R}_{\mathit{\text{cdmy}}}^{90b}$. Each variable in the set $WINDDI{R}_{\mathit{\text{cdmy}}}^{90b}$ is equal to 1 if the daily average wind direction in county c falls in the 90-degree interval [90b, 90b + 90) and 0 otherwise. The omitted category is the interval [270, 360). We use the k-means cluster algorithm to classify all the pollution monitors in the United States into 100 spatial groups based on their location.¹⁸ Intuitively, neighboring monitors are more likely to be assigned to the same group than distant monitors. The variable 1 [G_c = g] is an indicator for county c being classified into monitor group g from the set of monitor groups G. The coefficient on the interaction between these two variables, ${\beta }_b^g$, is thus allowed to vary across geographic regions. The other control variables (the included instruments), $X_{\mathit{\text{cdmy}}}^{\prime }$ and the fixed effects, are defined as in equation (1).

A county’s pollution-monitor readings may not adequately measure the average pollution exposure for county residents due to the sparse placement of monitors within counties. We structure equation (2) to mitigate this problem by restricting the effect of county wind direction on pollution to be the same for all monitors within each of the geographic areas, all of which span multiple counties. This restriction reduces the influence of pollution variation emitted by local sources from our estimates, thereby reducing measurement error. Locally produced pollution is likely to have different effects on monitors within a monitor group depending on the relative location of the source and monitor. In contrast, nonlocal sources that are systematically located to one side or another of the entire monitor group are more likely to have a similar effect on all (or most) monitors in the group. Consequently, the nonlocal sources are more likely to drive the pollution variation captured by equation (2).¹⁹ This is beneficial because pollution from local sources is unlikely to reach all individuals residing within the area encompassed by a monitor group, thereby generating measurement error.

Consider a pollution source located in the center of a county. Suppose an air pollution monitor is located to the east of this source. When the wind blows from the west, the monitor will record high levels of pollution, and when it blows from the east, it will record low levels of pollution. Yet, in either case, pollution exposure increases for only one-half of the county; in the other half of the county, pollution exposure decreases. On net, there may not be any health effects at the county level, leading a researcher who uses such variation to conclude that short-term fluctuations in air pollution have no effect on health. More generally, measurement error and subsequent bias is generated by pollution transport that affects measured pollution concentrations in a manner that is not representative of the average individual residing in the area. By contrast, we provide evidence in Section IVD and online Appendix Section A that the pollution variation we employ is largely driven by nonlocal transport and thus should have a uniform effect on the entire county. Online Appendix Section A also provides evidence that our first-stage variation is not driven by a few monitors located close to local pollution sources.

Equation (2) restricts the effect of wind direction to be constant within each of the four WINDDIR bins. We employ only four bins because increasing the number of instruments is computationally burdensome. The specification presented in equation (2) includes hundreds of instruments and tens of thousands of control variables and fixed effects and is estimated using over one million observations.²⁰ The main cost of restricting the number of bins is the loss of potentially useful variation in wind direction. We have investigated the effect of increasing the number of WINDDIR bins on our estimates; those results, shown in the robustness section, are very similar to our preferred specification.

Weak instrument bias is not a concern in our setting. As illustrated by Figures 2 and 3, wind direction is a strong predictor of air pollution levels, and this is confirmed by the large first-stage F-statistics presented in our tables.²¹ As a robustness check, we also estimate our IV model using the limited information maximum likelihood (LIML) estimator, which is approximately median unbiased even when using many weak instruments, and obtain results similar to two-stage least squares (2SLS; see online Appendix Table A3).

Our identifying variation depends on how frequently the wind changes and how much those changes matter for local pollution levels. To investigate the latter, we plot in online Appendix Figure A8 the difference in PM 2.5 between the most and least polluted wind directions based on our first-stage estimates for each monitor group. The difference is larger than 1 μg/m³ (about 10 percent of the sample average) in most areas and is generally largest in the Midwest and Northeast. By contrast, the difference is small in most of Arizona and New Mexico.

Online Appendix Table A5 presents results of regressions where the outcome is a local characteristic (e.g., number of beneficiaries), and the right-hand-side variable of interest is the difference in PM 2.5 between the most and least polluted wind directions for each monitor group (as shown in online Appendix Figure A8). Areas with a larger difference are more populous and have higher PM 2.5 concentrations, higher rates of hospitalizations, and higher spending. They have slightly higher mortality rates, but the magnitudes of the differences are small. Online Appendix Table A6 reports the corresponding relationships between these same local characteristics and PM 2.5 levels. While each characteristic varies significantly with PM 2.5 levels, the magnitudes of the differences are much smaller than in Table A5.

B. Life-Years Lost

The previous section describes how we estimate the causal effect of PM 2.5 on the number of lives lost. To monetize the social cost of this mortality, one could multiply the estimated number of lost lives by the value of a statistical life (VSL), which is the approach currently used by the EPA. However, using the same VSL for all deaths may overstate the economic cost if the individuals who die as a result of pollution exposure are relatively sick and have short life expectancies, a concern that may be particularly relevant for the elderly. An alternative approach commonly used in the empirical literature is to estimate life-years lost (LYL) rather than lives lost and then to monetize this using the value of a statistical life-year.

However, estimating life-years lost is challenging because counterfactual life expectancy is unobserved. The standard approach approximates counterfactual life expectancy using population life tables (Gardner and Sanborn 1990, Fontaine et al. 2003, Steenland and Armstrong 2006, CDC 2008, Deschênes and Greenstone 2011, Rapsomaniki et al. 2014) or using estimated changes in cause- and age-specific mortality over time (Finkelstein and McKnight 2008, Huh and Reif 2017). All previous studies that we are aware of use only age, or age and sex, to calculate counterfactual life expectancies. However, this approach will overstate life-years lost if individuals who are more affected by pollution also have shorter life expectancies than average, conditional on these variables. As we show in detail in online Appendix E, the key factor driving this bias is the covariance between the propensity to die from pollution exposure and measurement error in remaining life expectancy, conditional on observables. Our strategy is to use the Medicare data to control for the rich set of observable health and non-health characteristics in our machine-learning-based estimation of remaining life expectancy in order to minimize this covariance.

A challenge with estimating counterfactual life expectancy is that not everybody dies during the period we observe them. We therefore employ the semiparametric Cox proportional hazards survival model, which assumes that the hazard rate of death for individual i can be factored into two functions:²²

$$h\left(t_i|x_i,\beta \right)=h_0\left(t_i\right)\text{exp}\left[x_i^{\prime }\beta \right].$$

The hazard rate at time t_i, h(t_i|x_i, β), depends on the baseline hazard rate, h₀(t_i), and on a vector of individual characteristics, x_i. The parameter vector β is estimated by maximizing the log partial likelihood function:

$$\text{ln\hspace{0.17em}}L(\beta )=\sum _{i=1}^N{\delta }_i\left[x_i^{\prime }\beta -\text{ln\hspace{0.17em}}\sum _{j\in R\left(t_i\right)}\text{exp}\left[x_j^{\prime }\beta \right]\right],$$ (3)

where δ_i is equal to 1 for individuals whose deaths we observe (uncensored observations) and equal to 0 otherwise. The risk set R(t_k) = {l : t_l ≥ t_k} is the set of observations at risk of death at time t_k. We nonparametrically estimate the baseline hazard function, h₀ (t_i), following Breslow (1972). See online Appendix Section C.1 for details.

We estimate this Cox proportional hazards model using the 2002 cohort of Medicare beneficiaries.²³ We observe all deaths that occur among this cohort between January 1, 2002, and December 31, 2013. During this ten-year time period, 50 percent of the sample dies. To ensure accurate measures of beneficiaries’ chronic conditions, we limit the sample to Medicare beneficiaries who as of January 1, 2002, had been continuously enrolled in FFS Medicare for at least two years.²⁴ For computational ease, we further limit the analysis to a random 5 percent sample of these beneficiaries. The final estimation sample for our survival analysis includes about 1.2 million individuals.

To assess the value of accounting for individual characteristics and using machine learning over simpler approaches, we estimate the survival model several times, using increasingly large sets of characteristics. First, we use no individual characteristics, assuming a homogeneous survival function. A second specification controls for age and sex, and then a third specification additionally controls for the presence of 27 preexisting chronic conditions. Our last two specifications, estimated with either Cox-Lasso or survival random forest, incorporate over 1,000 variables derived from individual-level Medicare data and zip code-level data from the American Community Survey. These models include information on prior medical spending; outpatient and inpatient visits; length of stay for inpatient, skilled nursing facility, and hospice events; number of hospital readmissions; and average commute times, median income, median housing values, and employment in the beneficiary’s five-digit zip code of residence (see online Appendix Section C for details). To avoid reverse causality, all Medicare variables are based on medical histories from the previous year (2001).

Including so many control variables creates two challenges. First, some variables may be significant predictors of survival for the 2002 cohort by chance, even if they are not good predictors of survival in general. This may cause bias due to overfitting (Harrell, Lee, and Mark 1996). Second, computational limitations prevent us from including a large set of regressors when performing conventional maximum likelihood estimation on a large sample using standard numerical procedures.

Recent advances in machine learning techniques help us overcome these challenges, and we use all 1,062 variables when predicting individual-level life expectancies (Athey and Imbens 2017). Our first approach employs survival random forest, a nonparametric, nonlinear method for predicting outcomes (Breiman 2001, Ishwaran and Kogalur 2007, Ishwaran et al. 2008). Our second approach applies the least absolute shrinkage and selection operator (Lasso) to the Cox model (Tibshirani 1997). Lasso can be implemented by maximizing a penalized version of objective function (3):

$$\text{ln\hspace{0.17em}}L(\beta )=\left(\sum _{i=1}^N{\delta }_i\left[x_i^{\prime }\beta -\text{ln}\sum _{j\in R\left(t_i\right)}\text{exp}\left[x_j^{\prime }\beta \right]\right]\right)-\lambda \sum _{i=1}^k\left|{\beta }_i\right|,$$ (4)

where |β_i| is the absolute value of β_i (where β_i is element i of the vector β), and k is the number of included regressors. We select the optimal penalty parameter λ using five-fold cross-validation.²⁵ We then use estimates of β and observable characteristics x_i to predict the life expectancy of each Medicare beneficiary who was continuously enrolled in fee-for-service for at least two years at some point during our sample period. Additional details for both the Cox-Lasso and the survival random forest methodologies are provided in online Appendix Section C.

To integrate these estimates into the county-level empirical strategy in Section IIIA, we aggregate life-years lost over all individuals in the county and replace the dependent variable in equation (1) with the estimated daily number of life-years lost per capita in county c, ${\widehat{L}}_{\mathit{\text{cdmy}}}$. The variable ${\widehat{L}}_{\mathit{\text{cdmy}}}$ is equal to the sum of the estimated counterfactual life expectancies for all decedents divided by the total number of beneficiaries in the county and thus is analogous to how we calculate the mortality rate.

We now demonstrate the increase in explanatory power that accompanies the inclusion of additional demographic and health variables in estimating life-years lost. We first identify the Medicare beneficiaries who died between 2001 and 2013. We then use our model to predict their counterfactual life expectancy using increasing numbers of explanatory variables, lagged by one year from their death date. The results are shown in Figure 4. The green bar, Medicare FFS average, reports the average life expectancy for all Medicare fee-for-service beneficiaries (11.36 years) and serves as a baseline. This value would be an accurate measure of counterfactual life expectancy if Medicare beneficiaries died randomly. However, it is well known that individuals who die are older and sicker than the general population, on average. Intuitively, if a model could perfectly predict life expectancy, then the average predicted life expectancy for this sample of individuals (who all died within one year) should be below 1. However, to the extent that there is an idiosyncratic component to mortality (e.g., some individuals who suffer a heart attack survive purely by chance), even the most complete model may produce estimates above 1.

Figure 4. Average Life Expectancy for Continuously Enrolled FFS Medicare Beneficiaries Who Later Die within One Year, 2001–2013.

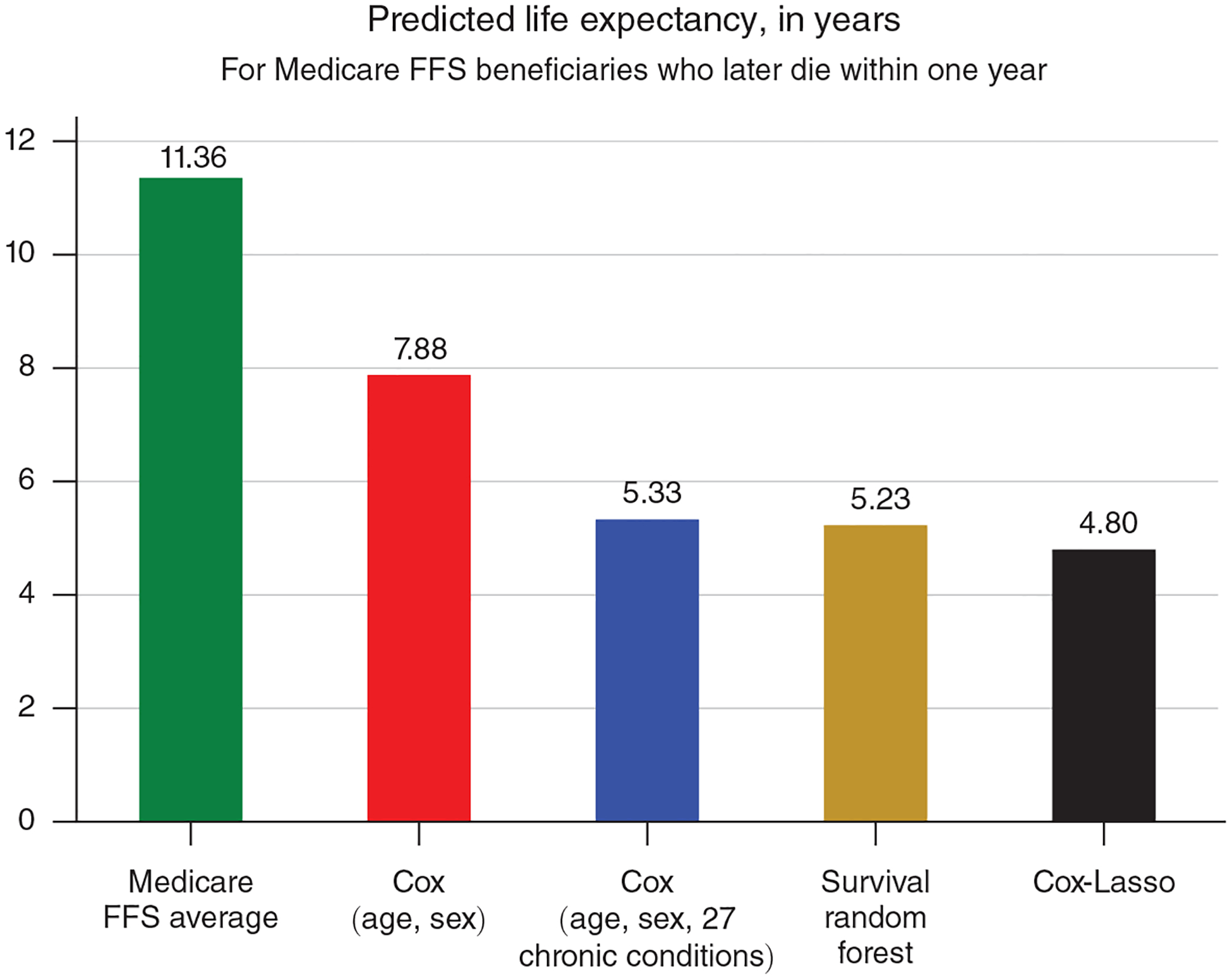
Notes: Life expectancy for each beneficiary is estimated as of January 1 of the calendar year of death. Estimates for Medicare FFS average are produced by MLE estimation of survival model (3) with no covariates. Estimates for Cox (age, sex) and Cox (age, sex, 27 chronic conditions) are produced by estimating the survival model (3) using age and sex, and age, sex, and 27 chronic conditions, as predictors, respectively. Estimates for Cox-Lasso are produced by machine learning estimation of the survival model (4) with 1,062 predictors (including interactions). Estimates for Survival random forest are produced by machine learning estimation using the same predictors as Cox-Lasso.

The rest of Figure 4 reports the performance of four increasingly detailed survival models. The red bar, Cox (age, sex), adjusts life expectancy for age and sex, similar to the age group analysis performed by Deschênes and Greenstone (2011), and predicts an average life expectancy of 7.88 years. The blue bar, Cox (age, sex, 27 chronic conditions), additionally controls for 27 different chronic conditions, which reduces predicted life expectancy by over two additional years. The last two bars display predicted life expectancy using two machine learning methodologies, both incorporating data from all 1,062 variables in our dataset.²⁶ The gold bar, Survival random forest, reports a predicted life expectancy slightly smaller than the Cox model with age, sex, and 27 chronic conditions. The black bar, Cox-Lasso, reports an even smaller predicted life expectancy of 4.80 years per decedent.

The Cox-Lasso method does not predict life expectancy perfectly, but precise predictions are not necessary for identification. For example, if air pollution kills people at random, then one does not need to have precise individual-level estimates of life expectancy; the population mean will suffice. The only way to know whether additional precision matters is to see how estimates change when using different predictions. Those results are presented in Section IV.

C. Treatment Effect Heterogeneity

The rich set of characteristics in the Medicare data provides an excellent opportunity to thoroughly investigate heterogeneity in vulnerability to dying from acute air pollution exposure. We pursue a two-pronged approach. First, we characterize how our estimated treatment effect differs across populations with different life expectancies. We hypothesize that beneficiaries with low estimated life expectancies are more likely to be killed by air pollution. However, this method may overlook relevant heterogeneity if, conditional on our prediction of life expectancy, there exist additional factors that matter for pollution vulnerability. Our second strategy employs a method recently developed by Chernozhukov et al. (2018)—henceforth, CDDF—for estimating heterogeneous treatment effects using machine learning techniques. We summarize the estimation procedure below and provide full details in online Appendix Section D. Because county-day units do not adequately reflect individual heterogeneity, this analysis employs person-day as the unit of observation. For simplicity, we focus on one-day mortality as the outcome.

The CDDF method requires a binary treatment; thus, we partition our person-day observations into “treatment” and “control” groups by assigning an observation to the treatment group if the wind direction on that day is associated with an above-median level of pollution, conditional on fixed effects.²⁷ Otherwise, the observation is assigned to the control group. We also randomly partition the data evenly into an “auxiliary” sample (used to estimate our prediction models) and a “main” sample (used to estimate our regressions).

Next, we predict one-day mortality, Died_it, using a gradient-boosted decision tree algorithm (Chen and Guestrin 2016) that incorporates: weather, as specified in equation (1); leads and lags of the treatment variable; and individual-level characteristics, all denoted by Z_it.²⁸ We estimate the model separately for auxiliary sample observations in the treatment and control groups, resulting in two prediction models. We then predict mortality for each person-day observation in the main sample using both the treatment group and control group prediction models. Let $\widehat{{\mathit{\text{Died}}}^T}\left(Z_{it}\right)$ denote the predicted probability of dying formed using the treatment group prediction model, and let $\widehat{{\mathit{\text{Died}}}^C}\left(Z_{it}\right)$ denote the corresponding prediction derived from the control group model. The difference between these two predictions, $\widehat{S}\left(Z_{it}\right)=\widehat{{\mathit{\text{Died}}}^T}\left(Z_{it}\right)-\widehat{{\mathit{\text{Died}}}^C}\left(Z_{it}\right)$, represents the change in the observation’s predicted likelihood of death due to being exposed to a high pollution wind direction and is referred to as a proxy predictor of the (true) conditional average treatment effect, s₀(Z_it). Although this proxy predictor may be biased, researchers can still use it to conduct valid inference about key features of s₀(Z_it), such as the presence of heterogeneity (Chernozhukov et al. 2018).

After constructing the proxy predictor, Ŝ(Z_it), we estimate the following weighted regression using a pooled sample of control and treatment group observations from the main sample:

$${\mathit{\text{Died}}}_{it}=\alpha +{\beta }_1\left(T_{it}-\widehat{p}\left(Z_{it}\right)\right)+{\beta }_2\left(T_{it}-\widehat{p}\left(Z_{it}\right)\right)\left(\widehat{s}\left(Z_{it}\right)-\overline{\widehat{s}}\right)+\theta \widehat{{\mathit{\text{Died}}}^C}\left(Z_{it}\right)+{\epsilon }_{it},$$ (5)

where the weights are equal to

$$w(Z)=\frac{1}{\widehat{p}\left(Z_{it}\right)\left(1-\widehat{p}\left(Z_{it}\right)\right)}.$$

The outcome variable, Died_it, is equal to 1 if individual i died on date t and 0 if individual i survived. We drop observations for individuals who died prior to date t. The indicator T_it equals 1 if the person-day observation was assigned to the treatment group and 0 otherwise. The propensity score, $\widehat{p}\left(Z_{it}\right)$, denotes the predicted probability of treatment. We estimate the propensity score in the same manner as Ŝ(Z_it) but with the treatment indicator T_it as the outcome rather than Died_it. To reduce noise, we trim our sample using a threshold of 5 percent. That is, we omit individual-day observations with propensity scores below 0.05 or above 0.95.²⁹ The variable $\overline{\widehat{S}}$ is the average of Ŝ(Z_it) across the estimation sample. We include the control variable $\widehat{{\mathit{\text{Died}}}^C}\left(Z_{it}\right)$ to improve precision.

CDDF show that ${\beta }_1+{\beta }_2\left(\widehat{S}\left(Z_{it}\right)-\overline{\widehat{S}}\right)$ is the best linear predictor of the conditional average treatment effect, s₀(Z_it), under general conditions. In this case, $E\left[{\widehat{\beta }}_1\right]$ is an unbiased estimate of the average treatment effect, E[s₀(Z_it)]. In addition, rejecting the null hypothesis that ${\widehat{\beta }}_2=0$ implies that heterogeneity is present and that the proxy predictor, Ŝ(Z_it), captures a relevant component of this heterogeneity.

Next, we estimate sorted group average treatment effects, E[s₀(Z_it)|G], where the groups G are defined as disjoint intervals of the proxy predictor, Ŝ(Z_it). Specifically, we estimate the following weighted regression on our trimmed sample:

$${\mathit{\text{Died}}}_{it}=\alpha +\sum _{k=1}^7{\gamma }_k\left(T_{it}-\widehat{p}\left(Z_{it}\right)\right)\cdot 1\left(G_k\right)+\theta \widehat{{\mathit{\text{Died}}}^C}\left(Z_{it}\right)+{ϵ}_{it}.$$ (6)

The indicator 1 (G_k) is equal to 1 if the prediction of the observation’s conditional average treatment effect, Ŝ(Z_it), lies within the kth interval and 0 otherwise. We again include the control variable $\widehat{{\mathit{\text{Died}}}^C}\left(Z_{it}\right)$ to improve precision, and we use the same weights as in equation (5). The coefficients of interest, γ_k, correspond to the average treatment effect for each group k. To form groups, we use 25-percentile intervals for the bottom 75 percent of Ŝ(Z_it) values and then use the seventy-fifth, eighty-fifth, ninety-fifth, and ninety-ninth percentiles as the lower cut points for the remaining intervals.

We must overcome two additional challenges in order to implement the CDDF methodology in our setting. First, the daily probability of dying is very small. Standard machine learning algorithms perform poorly in such settings because the algorithm will often never predict death for anybody. We follow Einav et al. (2018) and address this by “downsampling” the data. Downsampling increases the death rate in the sample used to train the prediction model by omitting a large fraction of the person-day observations where Died_it = 0. The resulting predictions are later rescaled to match the average death rate in the full sample.

Second, our auxiliary and main samples each contain over 20 billion person-day observations. Because of computational constraints, we are unable to include county, state-by-month, and month-by-year fixed effects in our regressions. Instead, we replace them with month, year, and division fixed effects.³⁰ To estimate equations (5) and (6) on a sample this large, we partition the main sample into 250 subsets, estimate the equations for each subset, and then take the appropriate average of the coefficients and standard errors.³¹

Finally, we note that our estimation procedure does not account for the measurement error introduced by the generation of the treatment variable. Permutation tests described in online Appendix D.2 suggest that this omission does not cause us to significantly understate the magnitude of our standard errors.

IV. Results

A. Mortality and Health Care Use

Panel A of Table 2 reports OLS estimates of the relationship between daily PM 2.5 and three-day mortality rates for different age groups. As reported in column 1, each 1 μg/m³ increase in daily PM 2.5 exposure is associated with 0.095 additional deaths per million elderly over the following three days, or a 0.025 percent increase relative to the average three-day mortality rate. Columns 2–6 report results estimated separately for each of five age groups. The absolute and relative increases in mortality are nonmonotonic across age groups, with those aged 70–79 experiencing lower (and insignificant) increases in death rates than those aged 65–69 despite having higher mean death rates.

Table 2—

OLS and IV Estimates of Effect of PM 2.5 on Elderly Mortality, by Age Group

	65+	65–69	70–74	75–79	80–84	85+
	(1)	(2)	(3)	(4)	(5)	(6)
Panel A. OLS estimates
PM 2.5 (μg/m3)	0.095	0.041	0.029	0.022	0.142	0.425
	(0.021)	(0.014)	(0.018)	(0.022)	(0.036)	(0.072)
Dependent variable mean	385	131	197	312	508	1,127
Effect relative to mean, percent	0.025	0.032	0.015	0.007	0.028	0.038
Observations	1,980,549	1,980,549	1,980,549	1,980,549	1,980,549	1,980,549
Adjusted R2	0.254	0.080	0.085	0.082	0.077	0.110
Panel B. IV estimates
PM 2.5 (μg/m3)	0.685	0.267	0.329	0.348	0.877	2.419
	(0.061)	(0.066)	(0.068)	(0.098)	(0.159)	(0.246)
F-statistic	298	285	292	303	309	315
Dependent variable mean	385	131	197	312	508	1,127
Effect relative to mean, percent	0.178	0.204	0.167	0.111	0.173	0.215
Observations	1,980,549	1,980,549	1,980,549	1,980,549	1,980,549	1,980,549

Notes: Table reports OLS and IV estimates of equation (1) from the main text. Dependent variable is the three-day mortality rate per million beneficiaries in the relevant age group. All regressions include county, month-by-year, and state-by-month fixed effects; flexible controls for temperatures, precipitation, and wind speed; and two leads of these weather controls. OLS (IV) estimates also include two lags and two leads of PM 2.5 (instruments). Estimates are weighted by the number of beneficiaries in the relevant age group. Standard errors, clustered by county, are reported in parentheses.

Panel B of Table 2 presents the corresponding IV estimates of the causal effect of daily PM 2.5 on three-day mortality. These are substantially (6–17 times) larger than the estimates in panel A, suggesting that OLS estimation suffers from significant bias. The IV estimates imply that each 1 μg/m³ increase in daily PM 2.5 exposure causes 0.69 additional deaths per million elderly over the following three days, or a 0.18 percent increase relative to the average three-day mortality rate. The corresponding estimate for a one standard deviation increase in daily PM 2.5 is a 1.3 percent increase in three-day mortality. Columns 2–6 show a monotonic relationship between the mortality effect of PM 2.5 and age, with each 1 μg/m³ increase in daily PM 2.5 causing 0.27 additional deaths per million among the 65–69 population and 2.4 additional deaths per million among the 85 and over population. However, because the average mortality rate is also much higher for the older age groups, the relative mortality effects across age groups follow a U-shaped pattern: each 1 μg/m³ increase in daily PM 2.5 exposure increases three-day mortality by 0.20 percent among ages 65–69, by 0.11 percent among ages 75–79, and by 0.22 percent among ages 85 and over. This pattern is somewhat unexpected: if sicker individuals are more vulnerable to pollution shocks, and if age is a good proxy for health, then we might expect relative mortality to increase monotonically with age. We return to this point when discussing our estimates of life-years lost due to PM 2.5, where we will find that relative mortality does increase monotonically with counterfactual life expectancy.

Next, we estimate the effect of daily PM 2.5 on three-day hospitalization rates and associated medical spending per million beneficiaries enrolled in FFS Medicare.³² For reference, we show the all-age mortality response to PM 2.5 for this population in column 1 of Table 3; it is very similar to what we find for the overall Medicare population in Table 2. The OLS results in panel A of Table 3 show that the association between PM 2.5, hospitalization, and medical spending is mixed: each 1 μg/m³ increase in daily PM 2.5 exposure is associated with significantly less inpatient spending and fewer hospital admissions, is not associated with spending on ER admissions, and is associated with significantly more ER admissions and visits.

Table 3—

OLS and IV Estimates of Effect of PM 2.5 on Medicare Hospitalization Outcomes

	FFS all-age mortality	All inpatient spending	Inpatient ER spending	Inpatient admissions rate	Inpatient ER admissions rate	Inpatient + outpatient ER rate	Non-ER admissions rate (placebo)
	(1)	(2)	(3)	(4)	(5)	(6)	(7)
Panel A. OLS estimates
PM 2.5 (μg/m3)	0.130	−11,489	84	−0.717	0.091	0.329	−0.809
	(0.023)	(2,242)	(972)	(0.157)	(0.081)	(0.112)	(0.124)
Dep. var. mean	402	37,984,768	16,805,670	3,366	1,749	3,984	1,617
Effect relative to mean, percent	0.032	−0.030	0.001	−0.021	0.005	0.008	−0.050
Observations	1,898,236	1,898,236	1,898,236	1,898,236	1,898,236	1,898,236	1,898,236
Adjusted R2	0.233	0.511	0.679	0.544	0.694	0.648	0.336
Panel B. IV estimates
PM 2.5 (μg/m3)	0.727	19,339	16,446	2.207	2.060	2.693	0.148
	(0.071)	(9,346)	(4,266)	(0.671)	(0.317)	(0.444)	(0.441)
F-statistic	300	300	300	300	300	300	300
Dep. var. mean	402	37,984,768	16,805,670	3,366	1,749	3,984	1,617
Effect relative to mean, percent	0.181	0.051	0.098	0.066	0.118	0.068	0.009
Observations	1,898,236	1,898,236	1,898,236	1,898,236	1,898,236	1,898,236	1,898,236

Notes: Table reports OLS and IV estimates of equation (1) from the main text. All dependent variables are three-day measures per million fee-for-service (FFS) beneficiaries. All regressions include county, month-by-year, and state-by-month fixed effects; flexible controls for temperatures, precipitation, and wind speed; and two leads of these weather controls. OLS (IV) estimates also include two lags and two leads of PM 2.5 (instruments). Estimates are weighted by the number of FFS beneficiaries. Standard errors, clustered by county, are reported in parentheses.

A more consistent story emerges from our IV approach (panel B), which shows that increases in daily PM 2.5 increase both hospitalizations and inpatient spending, driven primarily by encounters that originate in the ER.³³ The IV estimates imply that each 1 μg/m³ increase in daily PM 2.5 causes a highly significant increase in ER inpatient spending of $16,400 per million beneficiaries (relative to a mean of $16.8 million). This increase is almost as large as the increase in total inpatient spending, and we cannot reject that the latter is driven entirely by increases in ER spending. The overall inpatient admissions rate increases by 2.21 per million beneficiaries, an increase that can also be almost entirely explained by the 2.06 additional admissions originating in the ER. Overall, PM 2.5 increases total ER visits, including visits that do not result in a hospital admission, by 2.69 per million beneficiaries. Finally, we consider the non-ER admissions rate, which largely consists of planned hospitalizations and thus serves as a natural placebo test. The point estimate is very small and insignificant, further lending credence to our identification strategy.

Comparing the OLS estimates to the IV estimates in Tables 2 and 3 provides strong evidence that observational studies of the relationship between air pollution and health outcomes suffer from significant bias: virtually all our OLS estimates are smaller than the corresponding IV estimates. If the only source of bias were classical measurement error, which causes attenuation, we would not expect to see significantly negative OLS estimates. Thus, other biases, such as changes in economic activity that are correlated with both hospitalization patterns and pollution, appear to be a concern even when working with high-frequency data.

It is natural to attempt to compare the magnitudes of our IV estimates to those from the epidemiological literature, which are often used to calculate the benefits of various environmental policies. However, while many epidemiology papers estimate the health effects of acute pollution exposure, few of them focus on the effect of PM 2.5 on the elderly. Furthermore, studies that do estimate the health effects of acute PM 2.5 exposure often focus on specific causes of death or hospitalization, which makes a direct comparison difficult.³⁴ We are also not aware of any other study that uses three-day mortality as an outcome variable.

To facilitate comparison to two studies from the epidemiological literature with settings similar to ours, we have also estimated the effect of PM 2.5 on one-day mortality and hospitalizations (see online Appendix Table A10). Using data from 27 large US cities from 1997 to 2002, Franklin, Zeka, and Schwartz (2007) reports that a 10 μg/m³ increase in daily PM 2.5 exposure increases all-cause mortality for those aged 75 and above by 1.66 percent. Our one-day IV estimate for 75+ year-olds (column 1 of online Appendix Table A10) is an increase of 2.97 percent (an additional 6.1 deaths per million beneficiaries for a 10 μg m³ increase in daily PM 2.5), which is over 70 percent larger. Employing three-day mortality as the outcome for this age group (column 2 of online Appendix Table A10), which allows for delayed effects, further raises our estimated effect of PM 2.5 by over 80 percent (11 deaths per million). On the hospitalization side, Dominici et al. (2006) uses Medicare claims data from US urban counties from 1999 to 2002 and finds an increase in elderly hospitalization rates associated with a 10 μg/m³ increase in daily PM 2.5 exposure ranging from 0.44 percent (for ischemic heart disease hospitalizations) to 1.28 percent (for heart failure hospitalizations). We estimate that a 10 μg/m³ increase in daily PM 2.5 increases one-day all-cause hospitalizations by 2.22 percent (column 3 of online Appendix Table A10), which is 70 percent larger than the heart failure estimate and over five times larger than the ischemic heart disease estimate. Overall, these comparisons suggest that observational studies may systematically underestimate the health effects of acute pollution exposure.

B. Life-Years Lost and the Value of Mortality Reductions

We now consider the mortality cost of acute PM 2.5 exposure, as measured by life-years lost (Section IIIB). Table 4 displays estimates of equation (1) when the outcome variable is the estimated three-day life-years lost per million beneficiaries $\left({\widehat{L}}_{\mathit{\text{cdmy}}}\right)$. For reference, column 1 of Table 4 shows the estimated effect of PM 2.5 on the three-day mortality rate among the two-year FFS population. This estimate is slightly larger in absolute terms than the IV estimate from Table 2 in part because the two-year FFS restriction mechanically excludes individuals aged 65–66, causing this sample to be older on average. The effects relative to average three-day mortality are very similar for both populations.

Table 4—

IV Estimates of Effect of PM 2.5 on Elderly Life-Years Lost, Using Different Survival Models

	Life-years lost regressions
	All-age mortality	None	Age, sex	Age, sex, chronic conditions	Survival random forest	Cox-Lasso
	(1)	(2)	(3)	(4)	(5)	(6)
PM 2.5 (μg/m3)	0.850	9.657	6.509	3.901	3.048	2.991
	(0.079)	(0.893)	(0.700)	(0.520)	(0.542)	(0.487)
F-statistic	304	304	304	304	304	304
Dependent variable mean	459	5,208	3,556	2,398	2,401	2,224
Effect relative to mean, percent	0.185	0.185	0.183	0.163	0.127	0.134
LYL per decedent	NA	11.357	7.755	5.230	5.236	4.850
LYL per compiler	NA	11.357	7.655	4.587	3.585	3.517
Observations	1,898,236	1,898,236	1,898,236	1,898,236	1,898,236	1,898,236

Notes: Table reports IV estimates of equation (1) from the main text. The dependent variable in column 1 is the three-day mortality rate per million continuously enrolled fee-for-service (FFS) Medicare beneficiaries. The dependent variable in columns 2–6 is life-years lost (LYL) over three days for the same group. The headings in columns 2–4 display the variables used to predict life expectancy when using a traditional Cox proportional hazards model. Column 5 displays results when life expectancy is predicted using a survival random forest model that is estimated using over 1,000 predictors. Column 6 displays results when using a Cox-Lasso model with those same predictors. LYL per decedent is calculated by dividing the average LYL (dependent variable mean) by the average mortality rate (dependent variable mean reported in column 1). LYL per complier is calculated by dividing the column’s estimate by the mortality effect reported in column 1. All regressions include county, month-by-year, and state-by-month fixed effects, as well as flexible controls for temperatures, precipitation, and wind speed; two leads of the weather controls; and two leads and lags of the instruments. Estimates are weighted by the number of continuously enrolled FFS beneficiaries. Standard errors, clustered by county, are reported in parentheses.

Column 2 of Table 4 displays results when every decedent’s counterfactual life expectancy is set equal to the mean for the two-year FFS population (11.4 years). This estimate implies that each 1 μg/m³ increase in daily PM 2.5 increases life-years lost by 9.7 years per million beneficiaries. This same effect can also be obtained directly by multiplying the mortality effect of 0.850 in column 1 by the mean life expectancy of 11.4. However, this estimate is accurate only if beneficiaries killed by PM 2.5 are representative of the overall two-year FFS population. If decedents have a lower counterfactual life expectancy than those who remain alive, then the estimate in column (2) will be biased upward.

Columns 3–6 of Table 4 illustrate this bias by progressively expanding the set of covariates used to predict life expectancy. For columns 2–4, those covariates are reported in the column headers. Column 3 displays estimates when life expectancy is modeled solely as a function of age and sex. This approach is comparable to studies that estimate age- and sex-specific mortality effects and multiply them by the corresponding life expectancies from population life tables (e.g., Deschênes and Greenstone 2011). In our setting, accounting for decedents’ age and sex reduces the estimated impact of PM 2.5 on life-years lost by 33 percent, from 9.7 to 6.5 life-years per million beneficiaries. This decrease is consistent with the results presented in Table 2: older beneficiaries, who have lower life expectancies, are also more likely to be killed by PM 2.5. The estimate decreases by another 40 percent when we account for previously diagnosed chronic conditions (column 4), implying significant heterogeneity in the mortality effect of PM 2.5 even among individuals of the same age and sex.

Our last two specifications employ life expectancy predictions generated by two different machine-learning algorithms that incorporate over 1,000 additional predictors, as described in Section IIIB. The survival random forest estimate reported in column 5 is 22 percent smaller than the estimate that accounts for age, sex, and 27 chronic conditions and implies that each 1 μg/m³ increase in daily PM 2.5 increases life-years lost by 3.0 years per million beneficiaries. The Cox-Lasso estimate reported in column 6 is very similar. The richness of our controls suggests this final estimate is about as good an approximation to the true value as can be obtained empirically. Importantly, Table 4 demonstrates that common methods for calculating life-years lost that control only for basic demographic characteristics significantly overstate the effect of pollution on life-years lost.

The sequential reductions in the estimate of life-years lost reported in Table 4 occur for two reasons. First, better survival models should predict lower remaining life expectancy for decedents on average. For example, Table 4 reports that the mean life-years lost per decedent (LYL per decedent) decreases from 11.36 in the model with no predictors to 4.85 in the Cox-Lasso model. Second, a better survival model should also predict a more accurate distribution of predicted life expectancies among decedents. This increased accuracy matters if air pollution selectively kills individuals in this population who are systematically healthier (or sicker) than the average decedent. Table 4 demonstrates that this second channel also plays a role in reducing the estimated life-years lost from improved survival modeling. For example, while the average LYL per decedent decreases by only 7 percent (= 0.38/5.23) when moving from LYL estimates based on age, sex, and chronic conditions to those based on the Cox-Lasso model, the estimated effect of PM 2.5 on LYL decreases by 23 percent (= 0.91/3.901). This drop indicates that the mortality effects of PM 2.5 tend to be larger among individuals with characteristics that Cox-Lasso associates with lower life expectancy, even after conditioning on age, sex, and chronic conditions.

We can also calculate the number of life-years lost among those individuals who died because of increases in wind-driven PM 2.5 (i.e., the compliers) from the estimates reported in Table 4. Comparing this value to the average number of life-years lost among all decedents can shed light on whether those dying from increased pollution are differentially healthy or frail compared to those who die on a typical day. We calculate the LYL per complier by dividing the estimated effect of increased PM 2.5 on life-years lost by the estimated mortality effect reported in column 1.³⁵ When life expectancy is modeled as a function of age and sex alone, those dying from pollution appear to have about the same life expectancies (7.7 years) compared to the average decedent (7.8 years). However, estimates that rely on chronic conditions or the machine learning models show that those dying from pollution (compliers) have lower life expectancy than the average decedent. For example, column 6 reports that the average life expectancy of a complier is just 3.5 years, compared to the decedents’ average of 4.9 years.

A back-of-the-envelope calculation illustrates the policy implications of these results. The average level of PM 2.5 decreased by 4.9 μg/m³ nationwide between 1999 and 2013, as shown in Figure 1. The estimate reported in column 6 of Table 4 implies that such a decrease saved 235,374 life-years annually among the 44 million Medicare beneficiaries alive in 2013.³⁶ If we assign each life-year a standard value of $100,000 each (Cutler 2004), the mortality reduction benefits of this decrease added up to about $24 billion in 2013. The EPA’s calculation of the annual costs of meeting the 1990 Clean Air Act Amendment air quality standard increased from $19.9 billion to $43.9 billion between 2000 and 2010 (EPA 2011). Thus, the estimated $24 billion in annual mortality reduction benefits approximately equals the estimated annual costs of complying with new air pollution standards during this period. By contrast, the reduction in hospital payments implied by our estimates is an order of magnitude smaller, about $1.5 billion annually.³⁷

Our estimate of the mortality reduction benefits is nearly 70 percent lower than the estimate of $76 billion obtained from ignoring heterogeneity in the effect of pollution on elderly mortality. Estimated benefits that account for age and sex are $51 billion, still more than double the $24 billion estimate based on our most comprehensive model. This contrast demonstrates the importance of properly accounting for counterfactual life expectancy when calculating the mortality benefits of reductions in air pollution.

We note that these cost calculations do not account for the costs of any behavioral responses to pollution. Prior studies have found that short-run (daily) increases in ambient air pollution cause people to stay indoors (Graff Zivin and Neidell 2009, Neidell 2009), buy indoor air purifiers (Ito and Zhang 2016), and buy facemasks (Zhang and Mu 2018). There is some evidence that this avoidance behavior is greater among the elderly than for the population as a whole. Neidell (2009) shows that the elderly (and children) reduce their outdoor activity in response to a smog alert to a greater degree than do other adults, and Graff Zivin and Neidell (2009) show that the elderly respond more to consecutive smog alerts. The cost of avoidance behaviors is omitted from our calculations because we can neither directly observe nor credibly infer such responses. This omission means that our mortality and hospitalization cost estimates are lower bounds for the total costs of pollution to the US elderly.

C. Treatment Effect Heterogeneity

We next estimate the effects of PM 2.5 on mortality and life-years lost separately for groups of beneficiaries with different life expectancies. Table 5 reports mortality rate and life-years lost estimates separately for five groups of beneficiaries: those with a predicted life expectancy of over 10 years, 5–10 years, 2–5 years, 1–2 years, and less than 1 year. The column headers report the percent of all beneficiaries falling into each group: 55 percent of our sample has a life expectancy that exceeds 10 years, while only 0.7 percent has a life expectancy of less than 1 year. Panel A of Table 5 illustrates that the mortality rate effect of PM 2.5 decreases monotonically with life expectancy. A 1 μg/m³ increase in daily PM 2.5 increases deaths among those with life expectancy of less than 1 year by 18.5 per million. By contrast, the effect on those with life expectancies of 5 to 10 years is over 30 times smaller (0.52 deaths per million), and the mortality rate effect for those with life expectancies exceeding 10 years is a small and insignificant 0.06. Relative mortality decreases monotonically with life expectancy, which is consistent with the notion that the sickest individuals are most vulnerable to pollution shocks.

Table 5—

IV Estimates of Effect of PM 2.5 on Elderly Life-Years Lost, by Remaining Life Expectancy

	> 10 years (54.6%)	5–10 years (29.8%)	2–5 years (12.7%)	1–2 years (2.24%)	< 1 year (0.69%)
	(1)	(2)	(3)	(4)	(5)
Panel A. Mortality
PM 2.5 (μg/m3)	0.06	0.52	2.72	6.96	18.51
	(0.05)	(0.13)	(0.37)	(1.30)	(3.13)
F-statistic	296	313	318	323	304
Dependent variable mean	88	418	1,405	2,952	4,629
Effect relative to mean, percent	0.06	0.12	0.19	0.24	0.40
Observations	1,898,236	1,898,236	1,898,236	1,895,485	1,852,853
Panel B. Life-years lost
PM 2.5 (μg/m3)	0.80	3.74	8.63	10.38	10.06
	(0.60)	(0.91)	(1.26)	(2.05)	(2.09)
F-statistic	296	313	318	323	304
Dependent variable mean	1,133	2,938	4,705	4,508	2,708
Effect relative to mean, percent	0.07	0.13	0.18	0.23	0.37
Aggregate burden, percent	14.79	37.80	37.17	7.89	2.36
Observations	1,898,236	1,898,236	1,898,236	1,895,485	1,852,853

Notes: Table reports IV estimates of equation (1) from the main text. The dependent variable is either deaths (panel A) or life-years lost (panel B) over three days per million continuously enrolled fee-for-service (FFS) beneficiaries for those with remaining life expectancy in the range given by the column heading. Column headings also display (in parentheses) the percent of beneficiaries falling into each range. Life expectancy is predicted using a Cox proportional hazards model that is estimated using a Cox machine learning algorithm with over 1,000 predictors. All regressions include county, month-by-year, and state-by-month fixed effects, as well as flexible controls for temperatures, precipitation, and wind speed; two leads of the weather controls; and two leads and lags of the instruments. Estimates are weighted by the number of continuously enrolled FFS beneficiaries. Standard errors, clustered by county, are reported in parentheses.

Table 5 shows that, although beneficiaries with a life expectancy of less than one year are the most likely to be killed by air pollution, beneficiaries with a life expectancy of up to ten years are also vulnerable. Beneficiaries with a life expectancy of less than 1 year make up less than 1 percent of our sample, while those with life expectancies of 5 to 10 years make up almost 30 percent. Therefore, the absolute number of deaths caused by PM 2.5 varies less across these two groups than does the relative number of deaths.

Panel B of Table 5 shows the effect of PM 2.5 on life-years lost in each of these five groups. Although beneficiaries in column 5 have less than one year of life expectancy, their high mortality rate causes their number of life-years lost due to pollution be relatively large: 10.1 life-years per million beneficiaries. This is larger than any other group except for those in column 4, who have a life expectancy of 1–2 years and who lose 10.4 life-years per million beneficiaries for each 1 μg/m³ increase in daily PM 2.5. Thus, even for individuals where the “harvesting critique” is most likely to apply, there are still significant benefits to reducing pollution on a per capita basis. By contrast, among beneficiaries with a life expectancy of 5–10 years (column 2), the life-years lost from pollution is only 3.74 years per million. Although their life expectancy is high relative to those in column 5, their mortality rate is much lower, resulting in a smaller loss of life-years. The life-years lost estimate for those with 2–5 years of life expectancy (column 3) lies in between, at 8.7 life-years per million beneficiaries per 1 μg/m³ increase in daily PM 2.5.

Weighting the life-years lost coefficients from Table 5 by the respective sizes of the groups, we see that the largest portion of the social cost of pollution in terms of life-years lost is borne by those with a life expectancy of 5 to 10 years (30 percent of sample, 38 percent of aggregate burden), followed closely by those with a life expectancy of 2 to 5 years (12.7 percent of sample, 37 percent of aggregate burden).³⁸ While the per capita burden is highest for those in the two lowest life expectancy bins (less than 2 years), the majority of the aggregate burden falls on those with intermediate life expectancy (2 to 10 years).

This life expectancy approach identifies vulnerable populations better than an approach that uses age alone. In Table 2, we found significant mortality effects of pollution across all age groups, but there was no clear relationship between age and the relative mortality effect. In contrast, our life expectancy-based approach has identified a group of beneficiaries (those with over ten years of predicted life expectancy) who are quite resilient to pollution shocks. In addition, the health-vulnerability gradient is much stronger in both absolute and relative terms when health is measured by life-years remaining rather than life-years lived (i.e., age). Overall, these findings suggest that a precise measure of life expectancy may be useful not only for characterizing mortality costs but also in identifying heterogeneity in vulnerability to pollution.

If there are factors that affect vulnerability to pollution even after conditioning on our prediction of life expectancy, then our life expectancy analysis may miss meaningful treatment effect heterogeneity. We investigate this possibility by employing the method developed by CDDF. Table 6 presents estimates of equation (5), the best linear predictor of the conditional average treatment effect. Our preferred estimate in column 1 indicates that being assigned to the treatment (high pollution) group increases one-day mortality by 1.15 deaths per million beneficiaries. This is consistent with reduced-form estimates of approximately 1.2 deaths per million from the corresponding county-day specifications (panel B of online Appendix Table A13). We also strongly reject the null hypothesis of no heterogeneity (i.e., ${\widehat{\beta }}_2$ is significantly different from zero). We obtain similar results for the Horvitz-Thompson transformation (presented in column 2) and when we omit individuals with propensity scores below 0.01 or above 0.99, with or without applying the Horvitz-Thompson transformation (columns 3 and 4).

Table 6—

Best Linear Prediction of the Conditional Average Treatment Effect

Parameter	(1)	(2)	(3)	(4)
β1 (average treatment effect)	1.15	1.06	1.08	1.11
	(0.221)	(0.200)	(0.263)	(0.247)
β2 (heterogeneity)	0.0148	0.0133	0.0137	0.0126
	(0.003)	(0.00268)	(0.00346)	(0.00317)
Horvitz-Thompson transformation		X		X
Trimming threshold	5%	5%	1%	1%
Observations (millions)	21,724	21,724	23,075	23,075

Notes: Columns 1 and 3 present regression estimates of equation (5) from the main text. Columns 2 and 4 present estimates of equation (A6) from the online Appendix. The dependent variable is the one-day mortality rate per million beneficiaries. The parameter β₁ measures the average mortality effect of being exposed to one day of air when the wind that day is blowing from a direction associated with high air pollution. Rejecting the null hypothesis that β₂ = 0 implies that heterogeneity is present and that the proxy predictor, Ŝ(Z_it), captures a component of this heterogeneity. These regressions omit observations with estimated propensity scores less than the trimming threshold or greater than 1 minus the threshold. Standard errors, clustered by county, are reported in parentheses.

Figure 5 shows how the average treatment effect varies across groups of observations with different predicted conditional average treatment effects, Ŝ(Z_it), as estimated by equation (6). We estimate small and statistically insignificant treatment effects for beneficiaries in the bottom 75 percent of the Ŝ(Z_it) distribution. The treatment effect for those falling in the seventy-fifth to eighty-fifth percentile is slightly larger and marginally significant. Similarly, those in the eighty-fifth to ninety-fifth percentiles are subject to a small but statistically significant treatment effect. The estimated treatment effect becomes much larger for observations in the top 5 percent of the distribution, with the most vulnerable 1 percent suffering an increase in their mortality rate of almost 20 deaths per million beneficiaries on “treated” days, when PM 2.5 is about 2.4 units higher than on “control” days.³⁹

Figure 5. Average Treatment Effects for Disjoint Intervals of the Proxy Predictor, Ŝ(Z_it).

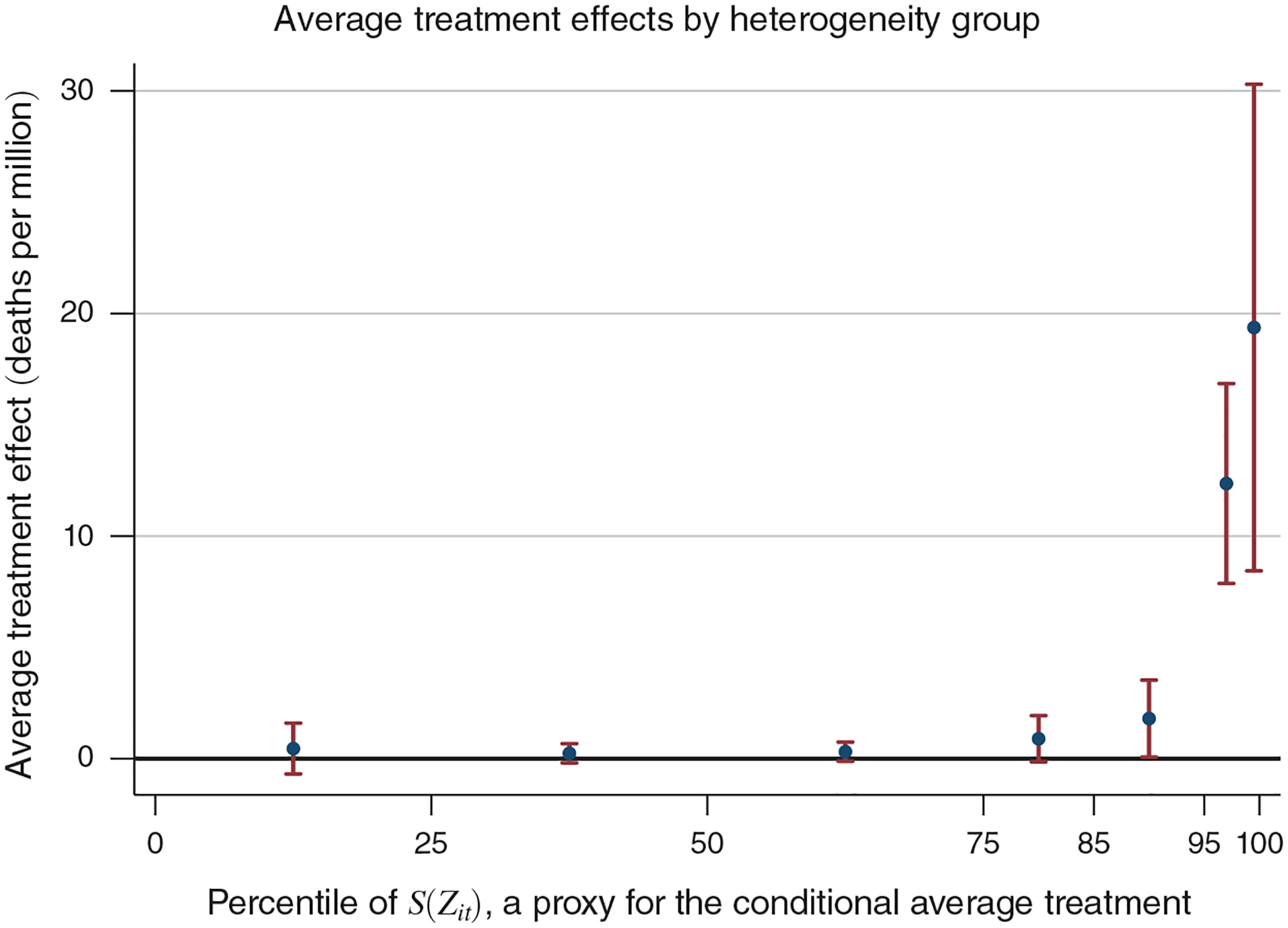
Notes: This figure illustrates heterogeneity in pollution vulnerability among the Medicare population by plotting estimates of β_q, q = 1, …, 7 from equation (6). Each estimate of β_q represents the average treatment effect for observations with predicted conditional average treatment effects lying within the qth interval. The percentile ranges of Ŝ(Z_it) corresponding to each interval are [0, 25), [25, 50), [50, 75), [75, 85), [85, 95), [95, 99), and [99, 100]. The average treatment effect for the entire sample is 1.15 deaths per million (reported in Table 6). The red bars report 95 percent confidence intervals. Standard errors are clustered by county. Values for the point estimates and standard errors are reported in online Appendix Table A14.

The pattern of heterogeneous treatment effects displayed in Figure 5, where observations are grouped according to their predicted conditional average treatment effect, is similar to the pattern of heterogeneity shown in Table 5, where beneficiaries are grouped according to their predicted life expectancy. In both cases, PM 2.5 exposure has near-zero effects on a majority of the population and large, positive effects concentrated among a small group.⁴⁰ Table 7 provides further evidence on this point by comparing the characteristics of those in the top 1 percent of the Ŝ(Z_it) distribution to those in the bottom 75 percent. We examine predicted life expectancy along with 17 different variables that are important determinants of remaining life expectancy and find significant differences for each one. For example, beneficiaries in the top 1 percent are 7.2 years older than those in the bottom 75 percent, are 6.3 percentage points more likely to have lung cancer, are 38.5 percentage points more likely to suffer from Alzheimer’s or dementia, have significantly larger Medicare Part B expenditures in the previous year, and are more likely to have visited a hospice. Overall, our results suggest that remaining life expectancy, a measure of general health, is also a good proxy for vulnerability to acute air pollution exposure in this population.

Table 7—

Summary Statistics for the Medicare Beneficiaries Most and Least Affected by Pollution

Outcome:	Bottom 75%	Top 1%	Difference
	(1)	(2)	(3)
Life expectancy (years)	11.6	3.65	−7.91
			(0.00192)
Demographics
Age (years)	75.7	82.9	7.20
			(0.00321)
Male	0.399	0.441	0.042
			(0.000108)
Chronic conditions
Alzheimer’s or dementia	0.0849	0.470	0.385
			(0.000155)
Chronic kidney disease	0.113	0.422	0.309
			(0.000164)
COPD	0.169	0.495	0.326
			(0.000197)
Heart failure	0.187	0.650	0.463
			(0.000128)
Lung cancer	0.00781	0.0705	0.0627
			(0.0000601)
Medical spending {dollars)
Durable medical equipment	136	785	648
			(1.05)
Hospice	63.8	1,126	1,062
			(2.90)
Hospital outpatient	750	3,767	3,018
			(2.92)
Part B drug	238	1,613	1,375
			(2.43)
Part B other	85	779	694
			(2.06)
Medical events
Dialysis	0.051	0.884	0.833
			(0.00158)
Durable medical equipment	1.76	8.28	6.52
			(0.00696)
Hospice stays	0.0012	0.0236	0.0224
			(0.0000613)
Part B drug	2.60	8.78	6.18
			(0.00914)
Part B evaluation and management	4.65	25.3	20.7
			(0.040)

Notes: Column 1 presents means for person-day observations predicted to have treatment effects in the bottom 75 percent. Column 2 presents means for those with treatment effects in the top 1 percent. Column 3 reports the difference between columns 2 and 1. Life expectancy is predicted using the Cox-Lasso model described by equation (7). All demographic, chronic condition, medical spending, and medical event variables listed in this table are the most significant predictors of remaining life expectancy within their respective categories. Medical spending and medical events are measured over the calendar year prior to the date of the observation. Hospice stays are defined as the number of unique admissions. For all other medical events, the event is defined as each line item on the insurance claim that contains the relevant service. COPD stands for chronic obstructive pulmonary disease. Standard errors, clustered by county, are reported in parentheses.

D. Extensions and Robustness Checks

One concern with interpreting our estimates as the causal effects of PM 2.5 is that other air pollutants like ozone (O₃) and carbon monoxide (CO) can be co-transported with fine particulate matter (PM 2.5). Because these pollutants are not perfectly co-transported, they can be produced by sources located in different places and are carried differently by the wind, our empirical strategy allows us to instrument separately for each pollutant. Two other pollutants, sulfur dioxide (SO₂) and nitrogen dioxide (NO₂), are precursors to PM 2.5 but also may have independent health effects. SO₂ converts to ${\text{SO}}_4^{2-}$, an important component of particulate matter, on the order of several percent per hour (Luria et al. 2001). NO₂ converts to particulate nitrate at a similar rate (Lin and Cheng 2007). Recall that we are considering the effect of a one-day change in average pollution concentrations on three-day outcomes. Because the majority of SO₂ and NO₂ converts to particulate matter within two to three days, it is impossible to distinguish their independent effects from those of PM 2.5 with a three-day specification.⁴¹ We therefore focus on whether our previous estimates change after controlling for CO and O₃.

We restrict the sample to county-days where readings for CO, O₃, and PM 2.5 are simultaneously available and then sequentially add the endogenous variables CO and O₃ to our main estimating equation. The results are shown in Table 8. The estimated effects of PM 2.5 are always significant and fairly stable. This suggests that the mortality effects we found are indeed primarily attributable to PM 2.5 and not these other pollutants. The coefficient on O₃ is negative in column 3, reflecting the well-known finding that it is negatively correlated with other pollutants that affect mortality (Currie and Neidell 2005), such as CO. When we also add CO as a control (column 4), we get slightly different O₃ and CO results depending on whether we consider the entire Medicare population or just FFS beneficiaries (panel A versus panel B). Nevertheless, our conclusions about the impacts of PM 2.5 are the same for both populations.

Table 8—

IV Estimates of Effect of PM 2.5 on Elderly Mortality When Controlling for Other Pollutants

	(1)	(2)	(3)	(4)
Panel A. All beneficiaries
PM 2.5 (μ/m3)	0.490	0.337	0.642	0.394
	(0.109)	(0.108)	(0.099)	(0.137)
CO (parts per billion)		0.025		0.023
		(0.008)		(0.009)
Ozone (parts per billion)			−0.310	−0.093
			(0.106)	(0.118)
F-statistic	137	35	56	29
Dependent variable mean	382	382	382	382
Observations	652,218	652,218	652,218	652,218
Panel B. Fee-for-service beneficiaries
PM 2.5 (μg/m3)	0.699	0.572	0.903	0.779
	(0.118)	(0.134)	(0.124)	(0.190)
CO (parts per billion)		0.018		0.011
		(0.010)		(0.011)
Ozone (parts per billion)			−0.427	−0.328
			(0.148)	(0.180)
F-statistic	134	34	53	27
Dependent variable mean	457	457	457	457
Observations	590,263	590,263	590,263	590,263

Notes: Table reports IV estimates of equation (1) from the main text, with the addition of the endogenous variables CO and/or ozone, which are instrumented for using wind direction. The dependent variable is the three-day mortality rate per million beneficiaries (panel A) or per million fee-for-service (FFS) beneficiaries (panel B). The sample is restricted to county-days where readings for CO, ozone, and PM 2.5 are simultaneously available. All regressions include county, month-by-year, and state-by-month fixed effects; flexible controls for temperatures, precipitation, and wind speed; two leads of the weather controls; and two leads and lags of the instruments. Estimates are weighted by the number of Medicare beneficiaries in panel A and by the number of FFS beneficiaries in panel B. Standard errors, clustered by county, are reported in parentheses.

Our baseline mortality specification employs a three-day window. The effect of employing a longer time window on our mortality estimates is theoretically ambiguous. On the one hand, a longer time window can increase estimates if PM 2.5 reduces people’s life expectancy but does not kill them quickly. For example, if acute exposure reduces an individual’s life expectancy to five days, that would not be reflected in our three-day window specification but could be captured by a fiveday specification. On the other hand, a longer time window will reduce estimates if the three-day specification suffers from short-term mortality displacement. We investigate these possibilities by estimating how a one-day increase in fine particulate matter affects mortality over the next 5 to 28 days (see Figure 6), controlling for the appropriate number of weather and instrument leads. We find that our estimate weakly increases with the length of the time window, which suggests that our results are not driven by short-term mortality displacement. The increase in the effect of a 1-day shock appears to level off after about 14 days, suggesting that the effects of acute exposure do not cause additional deaths beyond this point.

Figure 6. Effect of One-Day Increase in Fine Particulate Matter (PM 2.5) on Mortality over Different Time Periods.

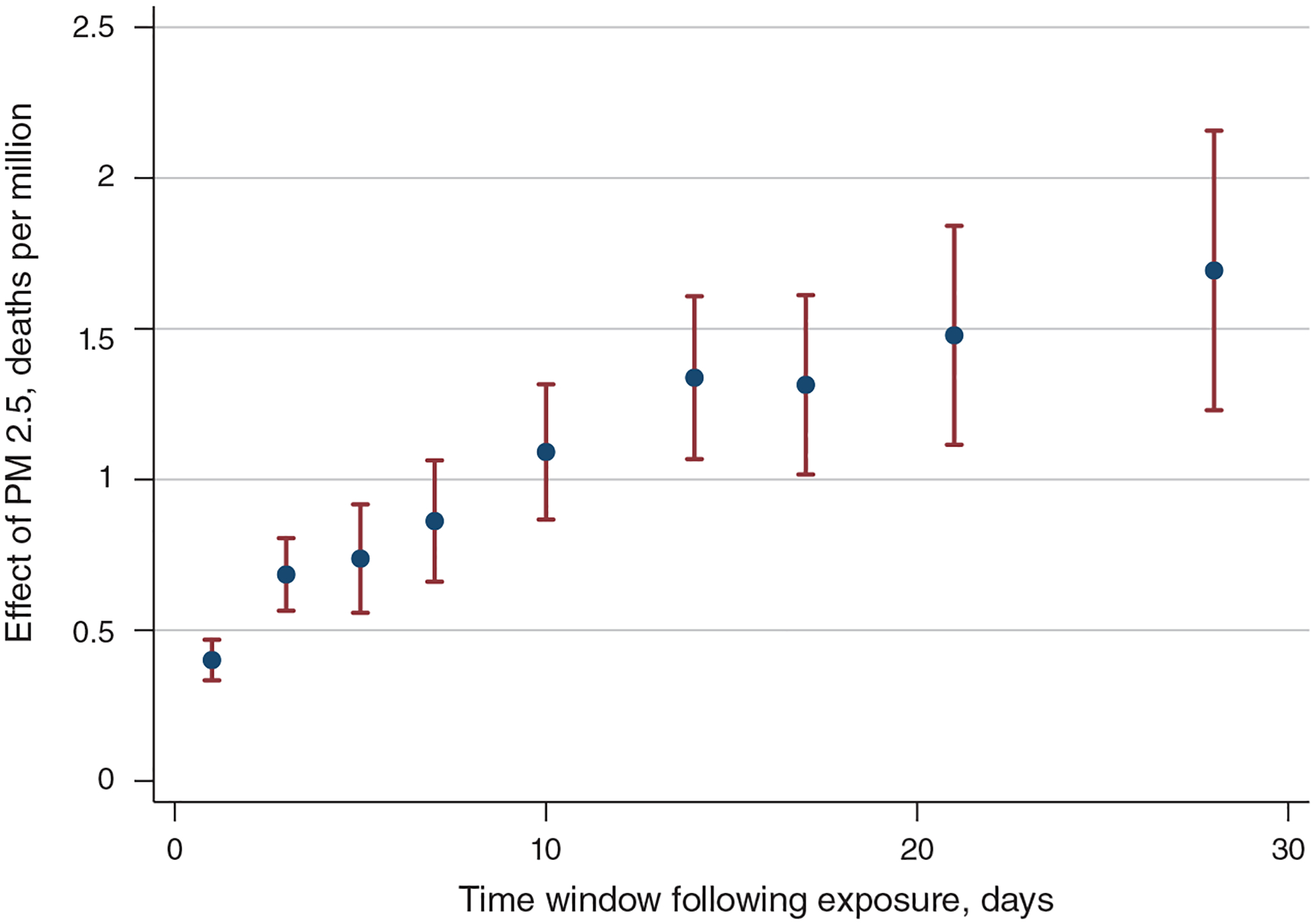
Notes: This figure plots IV estimates of equation (1) from the main text for outcome windows ranging from 1–28 days. Dependent variable is the mortality rate per million beneficiaries over the number of days indicated on the x-axis. Estimates are shown for outcome windows of 1 day, 3 days, 5 days, 7 days, 10 days, 14 days, 17 days, 21 days, and 28 days. The three-day window estimate shown in this figure corresponds to the point estimate reported in column 1, panel B of Table 2. All regressions include county, month-by-year, and state-by-month fixed effects; two lags of the instrument; flexible controls for temperatures, precipitation, and wind speed; and the appropriate number of leads of these weather controls and instruments (number of days minus 1). Estimates are weighted by the number of beneficiaries.

IV estimates are generally interpreted as a local average treatment effect (LATE). This interpretation requires imposing a monotonicity assumption (Imbens and Angrist 1994). In our setting, this assumption requires that PM 2.5 always (weakly) increases in a county when the wind blows from a high pollution direction and vice versa. Because our instruments are indicator variables and the coefficients vary at the level of the pollution-monitor group, the monotonicity assumption means that every county in each monitor group should experience a change in pollution in the same direction as every other county in that monitor group, for each 90-degree wind angle bin. The assumption may be violated if, for example, some counties in a monitor group respond differently to wind than do the others within its group, if the direction of the change in pollution varies within a 90-degree angle bin, or if the wind direction-pollution relationship within a monitor group differs by time of year.

To investigate the validity of the monotonicity assumption in our setting, we estimate alternative specifications that allow our instruments to vary over a larger number of wind direction bins, over smaller or larger geographic areas, and over the calendar year (Table 9).⁴² If these variations change our results, then it would indicate a violation of the monotonicity assumption. Column 1 of Table 9 decreases the size of the wind direction bins from 90 to 60 degrees. Column 2 reduces the number of monitor groups from 100 to 50. Column 3 increases the number of groups to 200. Finally, column 4 interacts our baseline monitor-group-wind-direction indicators with four season-of-year indicators. In all four cases we obtain estimates similar to those from our main specification. We conclude that violations of the monotonicity assumption, if they exist, have little effect on our ability to interpret our results as LATE.

Table 9—

Robustness of Mortality IV Estimates to Instrument Choices

	(1)	(2)	(3)	(4)
PM 2.5 (μg/m3)	0.690	0.719	0.652	0.603
	(0.054)	(0.056)	(0.063)	(0.067)
Size of wind angle bins (degrees)	60	90	90	90
Number of monitor groups	100	50	200	100
Interactions with season	No	No	No	Yes
F-statistic	197	554	161	NA
Dependent variable mean	385	385	385	385
Observations	1,980,549	1,980,549	1,980,547	1,980,549

Notes: Table reports IV estimates of equation (1) from the main text. The baseline specification reported in other tables aggregates pollution monitors into 100 groups and wind angles into 90-degree intervals. This table demonstrates that our estimates are not sensitive to the chosen level of aggregation or to interacting our instruments with seasonal indicators. The dependent variable is the three-day mortality rate per million Medicare beneficiaries. Estimates are weighted by the number of beneficiaries. Standard errors, clustered by county, are reported in parentheses.

To minimize measurement error, our empirical strategy employs variation in pollution that affects all pollution monitors within a geographic area in the same way, by restricting the coefficient on wind direction to be the same for all monitors in the same group. We argued that this approach filters out local variation in pollution, leaving primarily variation in pollution that is transported into a county from other regions. This assertion is supported by Table 9, which shows that varying the number of monitor groups, i.e., increasing or decreasing their average size, yields estimates very similar to our preferred specification. If local pollution transport was an important component of overall variation in pollution, our first stage would suffer from measurement error, and our results would be sensitive to the number of monitor groups used. In particular, we would obtain a different estimate when we increased the size of the monitor groups since the group-specific first stage would be averaged over a larger area.⁴³

Another consequence of employing pollution variation due to nonlocal transport is that our wind direction instrument should be weakest on days with low wind speeds. By contrast, an approach that relies on local pollution emissions should yield an instrument that would be strongest on days with low wind speeds, when pollution does not travel far from where it was emitted. Thus, we can test the validity of our approach by estimating the first stage separately by deciles of daily wind speed. Those results are reported in Figure 7. Because each regression uses only 10 percent of our sample, the F-statistics are lower than the ones reported in our main specification. Nevertheless, the F-statistics are largest for samples that employ days with high wind speeds, providing strong evidence that the variation we employ comes primarily from pollution that is transported into counties by the wind rather than generated locally.

Figure 7. Relationship between the Strength of the First Stage and Wind Speed.

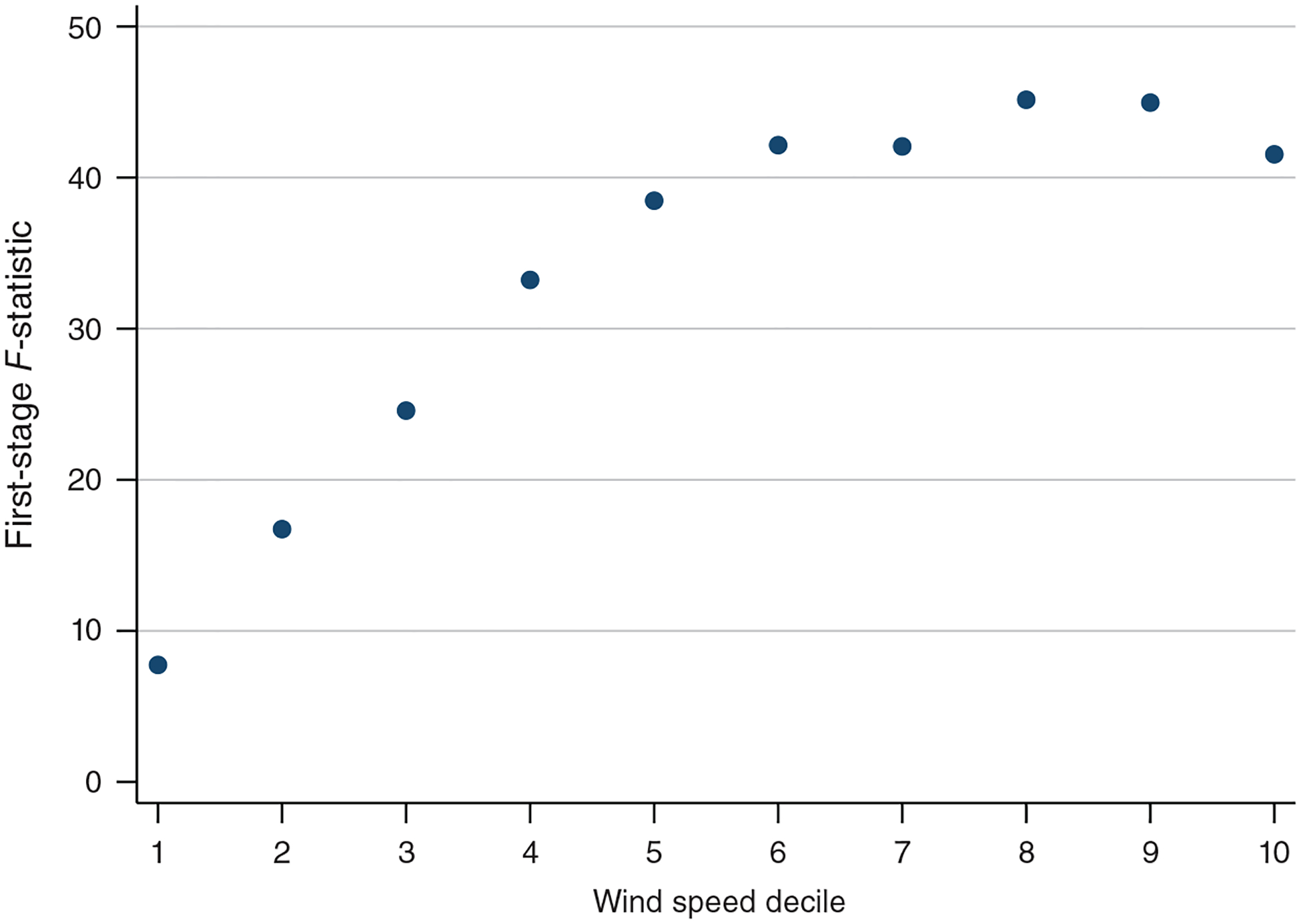
Notes: This figure reports the F-statistic for our first stage (equation (2)) for ten different subsamples that each include only days that fall within a particular wind speed decile. The F-statistic is lowest when the sample is limited to days with low wind speeds.

Tables 10 and 11 show the robustness of our primary empirical specification to including different types of fixed effects and weather controls and to varying the number of instrument lags. Table 10 demonstrates that our results are robust to varying the weather controls, suggesting that unobserved interactions between wind direction, weather, and mortality are not driving our results. It also illustrates the invariance of our estimates to more or less stringent fixed effects, providing evidence that our results cannot be explained by seasonal or regional patterns. Table 11 demonstrates that our estimates are not driven by lagged effects from PM 2.5 on preceding days and thus can be properly interpreted as the effect of a one-unit change in daily PM 2.5 levels.

Table 11—

Robustness of Mortality and Life-Years Lost IV Estimates to Including Fewer or More Instrument Lags

	No lags	1 lag	3 lags	4 lags	5 lags
	(1)	(2)	(3)	(4)	(5)
Panel A. Mortality
PM 2.5 (μg/m3)	0.602	0.730	0.687	0.683	0.680
	(0.077)	(0.061)	(0.061)	(0.061)	(0.061)
F-statistic	389	304	298	298	297
Dependent variable mean	385	385	385	385	385
Observations	1,980,549	1,980,549	1,977,622	1,974,768	1,971,974
Panel B. Life-years lost
PM 2.5 (μg/m3)	2.737	3.267	2.997	2.993	2.978
	(0.488)	(0.477)	(0.487)	(0.485)	(0.480)
F-statistic	392	310	304	304	303
Dependent variable mean	2,224	2,224	2,224	2,224	2,224
Observations	1,898,236	1,898,236	1,895,565	1,892,953	1,890,387

Notes: Table reports IV estimates of equation (1) from the main text. Column headings report the number of instrument lags included in the regression. (The specification reported in other tables includes two lags.) Dependent variable in panel A is the three-day mortality rate per million beneficiaries. Dependent variable in panel B is the life-years lost over three days per million continuously enrolled fee-for-service (FFS) beneficiaries. Estimates are weighted by the number of Medicare beneficiaries in panel A and by the number of FFS beneficiaries in panel B. Standard errors, clustered by county, are reported in parentheses.

The remaining robustness checks and extensions are relegated to the online Appendix. In online Appendix Table A2, we estimate the effect of PM 2.5 on four cause-of-death categories: cardiovascular, cancer, other internal, and external.⁴⁴ Over 80 percent of the deaths caused by PM 2.5 can be attributed to cardiovascular and other internal causes (roughly equally divided between the two).⁴⁵ However, we also see increases in deaths attributed to cancer, consistent with our overall conclusion that acute pollution exposure causes death among already weak individuals. As expected, deaths from external causes are unaffected by changes in pollution.

Our main empirical specification employs 300 instruments. Although our reported F-statistics are generally large, and our IV and OLS estimates are quite different, we nevertheless undertake two sets of robustness exercises to ensure that our estimates do not suffer from weak instrument bias. First, we estimate our IV model using LIML, which is approximately median unbiased even in the presence of many weak instruments, and obtain results that are very similar to the 2SLS estimates presented in Table 2 (online Appendix Table A3). Second, we conduct a placebo exercise where we generate a set of random wind directions and use those in our first stage instead of the actual wind direction (online Appendix Table A4). The first-stage F-statistics for those estimates are very small, which provides strong evidence that our wind direction instrument is picking up meaningful rather than spurious variation in PM 2.5 levels.

We conduct another falsification test where we include future measures of PM 2.5 that lie outside the three-day mortality window. Online Appendix Table A8 reports IV results that include PM 2.5 three days into the future (columns 1 and 2) and seven days into the future (columns 3 and 4). In column 1, there is a significant negative coefficient on the three-day lead of pollution. However, once we include the three-day leads of the weather controls as well (column 2), this negative coefficient shrinks and becomes insignificant. Most importantly, none of these additions substantially affects the coefficient on contemporaneous PM 2.5.

Another potential concern is that windy days may cause behavioral responses among the elderly that are correlated with health (for example, staying indoors or traveling less). Online Appendix Table A9 lists the statistics of the average wind speed by deciles of wind speed. The Beaufort Wind Scale describes wind speeds of 3.5–5 m/s as a “gentle breeze” and 5.5–8 m/s as a “moderate breeze.”⁴⁶ The American Society of Civil Engineers (ASCE 2004) lists wind speeds of 0–3.9 m/s as a comfortable range for standing and 0–5.4 m/s as a comfortable range for walking. Thus, for many of the observations in our sample where the instrumental variables are quite strong (wind speed deciles 5–8), the corresponding wind speeds can be best described as a “gentle breeze.” We therefore do not expect the wind speed itself to affect behavior much. Nonetheless, as a robustness check, we have estimated our main results excluding all observations where the wind speed is greater than 3.9 meters per second (i.e., those that the ASCE would not consider comfortable for standing). Our result is robust to this exclusion (column 4 of online Appendix Table A10).

Finally, our estimates should not be affected by monitor entry and exit, as these are plausibly unrelated to daily wind direction. Nonetheless, we probe the robustness of our results to imposing various continuity requirements on the sample of included monitors. About one-quarter of PM 2.5 monitors in our sample are online during our entire 13-year sample period; the median number of years online is 8. Most monitors do not operate every day, as the EPA does not require it.⁴⁷ As a robustness check, we restrict our sample of monitors to (i) those that exist for at least five years of our sample period; (ii) those that exist for at least seven years; (iii) those that are online for at least 120 days per year, on average, regardless of how many years they are online; or (iv) those that are online for at least 240 days per year. Our estimates (not reported) vary little under each of these four restrictions.

V. Conclusion

Understanding how air pollution affects mortality, health care use, and medical costs is essential for crafting efficient environment policies, such as Pigouvian pricing, but endogeneity and measurement error make it challenging to identify the causal effects of pollution. It is also difficult to quantify the mortality cost of air pollution when mortality effects are heterogeneous. If deaths caused by pollution occur disproportionately among the least healthy, then ignoring this heterogeneity will lead to upward bias when estimating the social cost of pollution.

Our study exploits daily variation in acute fine particulate pollution exposure driven by changes in wind direction. We find significant average treatment effects of exposure on mortality, hospitalizations, and medical spending. Our preferred estimate of the total number of life-years lost, obtained using a machine learning algorithm and health information from detailed Medicare data, is less than one-half of the magnitude of an estimate that accounts for age and sex alone, and less than one-third of the magnitude of an estimate based solely on the life expectancy of an average Medicare beneficiary. This result shows that failure to adjust for the health of those who die will overstate mortality reduction benefits of decreases in air pollution. Nonetheless, we calculate that the reduction in PM 2.5 experienced nationwide between 1999 and 2013 resulted in elderly mortality reductions worth $24 billion annually by the end of that period.

We investigate heterogeneity by estimating how the mortality effect of air pollution varies by predicted life expectancy. Individuals with low levels of life expectancy are the most vulnerable, whether we measure vulnerability using total mortality risk, relative mortality risk, or expected number of life-years lost. We expand our examination of heterogeneity by adapting a recent machine learning method for heterogeneous treatment effects (CDDF) to our quasi-experimental setting. This method identifies approximately 25 percent of the elderly population as vulnerable to acute pollution exposure. Many key determinants of low life expectancy (e.g., advanced age, presence of serious chronic conditions, and high medical spending) also vary systematically with pollution vulnerability, and individuals identified as most vulnerable to pollution have significantly lower life expectancies than those identified as least vulnerable. Overall, life expectancy seems to accurately index vulnerability to acute air pollution exposure.

The methods we use to estimate mortality costs and to identify vulnerable populations are general and could be applied to other contexts. A benefit of using life expectancy as a measure of vulnerability is that it is easily interpreted, can be compared across studies, and is a useful input into welfare calculations. However, if the primary goal is to characterize the magnitude of treatment effect heterogeneity in a particular context, then the additional flexibility offered by the CDDF approach may justify the reduction in interpretability that typically arises with machine learning approaches. Although both the life-expectancy and CDDF approaches reveal similar patterns of heterogeneity in our context, the performance of the two approaches may diverge in other settings where specific vulnerability does not align as well with general health.