Abstract
Objective
To determine whether the exclusion of patients who die from adjusted 30‐day readmission rates influences readmission rate measures and penalties under the Hospital Readmission Reduction Program (HRRP).
Data Sources/Study Setting
100% Medicare fee‐for‐service claims over the period July 1, 2012, until June 30, 2015.
Study Design
We examine the 30‐day readmission risk across the three conditions targeted by the HRRP: acute myocardial infarction (AMI), congestive heart failure (CHF), and pneumonia. Using logistic regression, we estimate the readmission risk for three samples of patients: those who survived the 30‐day period after their index admission, those who died over the 30‐day period, and all patients who were admitted to see how they differ.
Data Collection/Extraction Methods
We identified and extracted data for Medicare fee‐for‐service beneficiaries admitted with primary diagnoses of AMI (N = 497 931), CHF (N = 1 047 552), and pneumonia (N = 850 552).
Results
The estimated hospital readmission rates for the survived and nonsurvived patients differed by 5%‐8%, on average. Incorporating these estimates into overall readmission risk for all admitted patients changes the likely penalty status for 9% of hospitals. However, this change is randomly distributed across hospitals and is not concentrated amongst any one type of hospital.
Conclusions
Not accounting for variations in mortality may result in inappropriate penalties for some hospitals. However, the effect of this bias is low due to low mortality rates amongst incentivized conditions and appears to be randomly distributed across hospital types.
Keywords: hospitals, mortality, pay‐for‐performance, quality, readmissions
What this Study Adds.
What is already known on this topic: Hospitals are currently penalized for excess readmissions for a number of clinical conditions. There are concerns about the extent to which hospital's mortality rates influence their performance on readmission rates, as death nonrandomly excludes patients who die within the initial 30‐day window from readmission rate calculations. Previous work has examined this relationship through correlations of risk‐adjusted mortality and readmissions, which do not allow for the examination of sample selection bias. This paper explores a simple method to examine whether the relationship between mortality and readmissions leads to sample selection bias, and how this influences hospital penalty status under HRRP.
What this study adds: 30‐day hospital mortality rates and 30‐day hospital readmission rates are not independent; sample selection bias does result from the relationship between mortality and readmissions. The extent of the sample selection bias differs by clinical condition and therefore should be explored separately by condition. For conditions initially penalized through HRRP, adjusting for this bias would influence the penalty status of just over 2% of hospitals.
1. INTRODUCTION
Improving hospitalized patients’ outcomes has been a major focus for US policy makers. Of these outcomes, readmissions have received considerable attention, initially when the Centers for Medicare & Medicaid Services (CMS) started publicly reporting hospital performance on this metric, and later through the Hospital Readmissions Reduction Program (HRRP). The HRRP penalizes hospitals up to 3% of their base Medicare payments for higher‐than‐expected 30‐day readmission rates for Acute Myocardial Infarction (AMI), Congestive Heart Failure (CHF) and pneumonia, and more recently for Chronic Obstructive Pulmonary Disease (COPD), hip and knee arthroscopy, and Coronary Artery Bypass Grafting (CABG).
Critics of the policy have raised concerns about the way readmissions are estimated.1, 2 One concern relates to the relationship between mortality and readmissions. Currently, 30‐day readmission rate calculations exclude patients who die within the initial 30‐day window in two ways: First, anyone who dies in the hospital is not eligible to be considered for readmission (they are excluded from the denominator) and, second, anyone who dies after discharge without coming back to the hospital is, by definition, not eligible to be readmitted and therefore, excluded from the numerator. This has the potential to create sample selection bias because people do not die at random: The sickest patients are the likeliest to die, and this population is nonrandomly distributed across hospitals3, 4; had these patients survived, they likely would have been at a higher risk of readmission. Therefore, hospitals with high mortality rates may have readmission rates that are artificially attenuated by the removal of these high‐risk patients.
In 2013, Krumholz et al5 estimated the correlation between 30‐day risk‐adjusted mortality and 30‐day risk‐adjusted readmission rates for the three conditions incentivized through the Affordable Care Act. They found a weak correlation between mortality and readmissions for patients admitted with heart failure though no association in AMI and pneumonia patients. However, they estimated hospital risk‐adjusted mortality and readmission rates from patient‐level regressions separately, assuming independence between these two variables. Their approach does not consider the linkages between readmission and mortality rates described above, and thus does not account for the potential sample selection bias, which may ensue as a result. However, we do not know to what degree this risk is theoretical or whether the relationship between mortality and readmissions is empirically verifiable.
Therefore, we sought estimate the readmission risk for patients who died and were excluded from the standard readmission rate calculations. If these patients have significantly different readmission risks than those who survive, not accounting for them may result in current policies targeting and penalizing the wrong hospitals. Empirical evidence here would be critically helpful. We sought to answer three questions. First, what is the readmission risk for patients who survived and patients who died across the three initially targeted conditions? Second, if the readmission risks are different, does re‐estimating the readmission rates to include the readmission risk of the patients who died change the relative performance of hospitals? Finally, which hospitals are more affected by this potential sample selection bias?
2. METHODS
2.1. Data
Using 100% inpatient fee‐for‐service Medicare claims data, we examined all admissions from July 1, 2012, until June 30, 2015, for the three conditions initially targeted by the HRRP (AMI, CHF, and pneumonia) as identified by CMS to inform the Fiscal Year (FY) 2017 penalties.6 We purposefully chose these dates as they are prior to the rollout of the ICD‐10 codes, which may influence our estimates due to coding changes, and after the change in the number of secondary conditions recorded by Medicare which can also influence the estimation of readmission rates, as documented elsewhere.7 To be consistent with the CMS criteria, we only looked at patients above the age 65 who are continuously enrolled in the fee‐for‐service program. The group of hospitals we investigated consisted of the HRRP‐incentivized hospitals and was composed of acute care hospitals that participated in the HRRP. We excluded other ineligible hospitals including children's hospitals, psychiatric and cancer‐specialty hospitals, and federal hospitals, as well as hospitals from Maryland who have been subject to a different set of readmission incentives, and matched the remaining hospitals to those listed on the CMS website for FY 2017.8
2.2. Outcomes
Our main outcome of interest is the probability of being readmitted for the three conditions. Over the study period, our data contain detailed patient‐level information on the patient's episode of care, including their admission location, diagnoses, and discharge location. Using the patient‐level data, we are able to construct a binary variable for readmission status, which indicates whether each patient was readmitted within 30 days following their index admission for one of the targeted conditions. To be consistent with the CMS method for constructing readmission rates, we excluded any index admissions that were discharged against medical advice, and, for AMI, any patients who had a same‐day discharge. We coded a readmission as any‐cause admission occurring within 30 days of discharge from an index visit except planned admissions for chemotherapy, transplant, or rehab, based on the CCS categories specified by CMS. For any transfers, we kept only the receiving hospital as the index admission, which is consistent with the CMS approach.
2.3. Statistical analysis
We first estimated the readmission rates for the patients who survived, and the patients who died, for each of the three conditions. To do this, we estimated a logistic regression using the data from the survived patients, separately for each condition. We controlled for patient characteristics including age, gender, and patient comorbidities as identified by the Hierarchical Condition Categories (HCC) developed by CMS, and included a hospital fixed effect. Using the coefficients estimated by this model, we predicted the average probability of readmission for each observation in the dataset, including for patients who died in the first 30 days. We then plotted a histogram with these values for each condition, separately for the population who survived and the population who died, to compare the probability of being readmitted across the two populations.
Next, using the coefficients from the previous regression detailed above, we predicted the average probability of being readmitted to each of the hospitals in our sample, separately for the patients who survived and for those who died at some point between admission and 30 days after discharge. We then computed the difference between these two probabilities for each hospital by subtracting the probability of being readmitted for those who survived from the probability of being readmitted for those who died. Using a scatterplot, we illustrate the differences across hospitals and examine how they vary by risk‐adjusted mortality rate. The risk‐adjusted mortality rates represent the average predicted probability of dying for each hospital, using the same model as above, but with 30‐day mortality as our dependent variable. Next, we compare the average predicted probability of being readmitted to each of the hospitals as estimated for the survived patients and the patients who died to the full sample of admitted patients using a Pearson's correlation coefficient.
To better understand how our estimates are influenced by mortality at different intervals and by the duration of time outside the hospital, we further construct three additional outcome measures for hospitals using the same methodology. We then compare these outcome measures to the average predicted probability of readmission using a Spearman rank correlation. These outcomes reflect a composite measure of death or readmission, defined in the following three ways: (a) death or readmission at any point from admission to 30 days postdischarge; (b) death or readmission from discharge to 30 days postdischarge, and (c) death or readmission from discharge to 15 days postdischarge. We also compare the Spearman correlation coefficient from our readmission measures for each hospital to the hazard rates for hospitals produced from a Fine/Gray competing risk model, with readmission as the variable of interest and death as the competing event.
Finally, using the two risk‐adjusted readmission rates, for the survived and admitted populations, we examine how many hospitals would receive (or not receive) penalties given the adjustment for the deceased patients. To do this, we calculate the difference between each hospital's risk‐adjusted readmission rate and the average readmission rate as a measure of their excess readmission rate, and examine how many move from below average to above average when looking at the admitted population, and vice versa, by condition. Finally, we examine which characteristics are associated with the hospitals that were likely to experience a change in their penalty status when adjusting for the omitted patients, looking at: hospital size, teaching status, ownership, region, urban/rural location, and presence of a medical intensive care unit (MICU).
All analyses were performed using Stata version 14 (STATCorp), with the exception of the competing risk analysis, which was performed with SAS version 9.4 (SAS Institute Inc). This study was granted exemption by the Harvard T. H. Chan School of Public Health Office of Human Research Administration.
3. RESULTS
3.1. Hospital and patient characteristics
Our study cohort included all Medicare fee‐for‐service patients admitted to HRRP‐participating hospitals for each of the three initially targeted conditions over the time period used to estimate the FY 2017 penalties: July 1, 2012, until June 30, 2015. Over our study period, we examined a total of 497 931 patients admitted with a primary diagnosis of AMI; 1 047 522 patients admitted with a primary diagnosis of CHF; and 850 552 patients admitted with a primary diagnosis of pneumonia (Tables 1a, 1b, 1ca‐c). Of the AMI patients, 31 907 (6.4%) of the sample died before discharge; 65 439 (13.1%) died within 30 days after discharge; and 79 613 (16.0%) were readmitted (Table 1a). Of the CHF patients, 36 181 (3.5%) of the sample died before discharge; 134 124 (12.8%) died within 30 days after discharge; and 217 466 (20.8%) were readmitted (Table 1b). Of the pneumonia patients, 34 761 (4.1%) of the sample died before discharge; 106 869 (12.6%) died within 30 days after discharge; and 131 952 (15.5%) were readmitted (Table 1c). Patient characteristics varied by condition: 47.6% of the population was female for AMI, 54.8% for CHF, and 55.4% for pneumonia. The distribution of patients was slightly younger for AMI and slightly older for pneumonia. Approximately 85% of the population was non‐Hispanic white across conditions. These patients were seen in a total of 2977 HRRP‐participating hospitals for AMI, 3040 for CHF, and 3046 for pneumonia (Table 2).
Table 1a.
Characteristics of patient sample (AMI)a
| Admitted patients | Inpatient death | Death 30 d | Readmission 30 d | |||||
|---|---|---|---|---|---|---|---|---|
| N | % | N | % | N | % | N | % | |
| Total | 497 931 | 100.0 | 31 907 | 6.4 | 65 439 | 13.1 | 79 613 | 16.0 |
| Sex | ||||||||
| Female | 236 799 | 47.6 | 15 656 | 6.6 | 33 332 | 14.1 | 40 274 | 17.0 |
| Male | 261 132 | 52.4 | 16 251 | 6.2 | 32 107 | 12.3 | 39 339 | 15.1 |
| Age, years | ||||||||
| 65‐70 | 106 911 | 21.5 | 4193 | 3.9 | 6898 | 6.5 | 14 029 | 13.1 |
| 71‐85 | 92 033 | 18.5 | 4441 | 4.8 | 7705 | 8.4 | 13 906 | 15.1 |
| 76‐80 | 88 965 | 17.9 | 5440 | 6.1 | 10 051 | 11.3 | 14 888 | 16.7 |
| 81‐85 | 85 963 | 17.3 | 6420 | 7.5 | 12 999 | 15.1 | 15 154 | 17.6 |
| 85‐90 | 72 959 | 14.7 | 6331 | 8.7 | 14 474 | 19.8 | 13 171 | 18.1 |
| 91+ | 51 109 | 10.3 | 5082 | 9.9 | 13 312 | 26.0 | 8465 | 16.6 |
| Race | ||||||||
| Non‐Hispanic white | 438 908 | 88.1 | 28 014 | 6.4 | 57 919 | 13.2 | 69 112 | 15.7 |
| Black | 35 197 | 7.1 | 2200 | 6.3 | 4413 | 12.5 | 6604 | 18.8 |
| Hispanic | 7317 | 1.5 | 523 | 7.1 | 1056 | 14.4 | 1394 | 19.1 |
| Other | 14 320 | 2.9 | 1085 | 7.6 | 1906 | 13.3 | 2324 | 16.2 |
| Comorbidity | ||||||||
| Diabetes | 205 275 | 41.2 | 12 823 | 6.2 | 26 515 | 12.9 | 39 972 | 19.5 |
| Stroke | 17 634 | 3.5 | 1600 | 9.1 | 3880 | 22.0 | 4994 | 28.3 |
| COPD | 133 394 | 26.8 | 8931 | 6.7 | 20 190 | 15.1 | 31 385 | 23.5 |
| Sepsis | 37 879 | 7.6 | 4783 | 12.6 | 9483 | 25.0 | 13 036 | 34.4 |
| Renal failure | 217 951 | 43.8 | 21 616 | 9.9 | 43 633 | 20.0 | 49 561 | 22.7 |
Abbreviation: AMI, acute myocardial infarction.
2977 HRRP‐eligible hospitals.
Table 1b.
Characteristics of patient sample (CHF)a
| Admitted patients | Inpatient death | Death 30 d | Readmission 30 d | |||||
|---|---|---|---|---|---|---|---|---|
| N | % | N | % | N | % | N | % | |
| Total | 1 047 552 | 100.0 | 36 181 | 3.5 | 134 124 | 12.8 | 217 466 | 20.8 |
| Sex | ||||||||
| Female | 573 701 | 54.8 | 17 395 | 3.0 | 70 773 | 12.3 | 118 949 | 20.7 |
| Male | 473 851 | 45.2 | 18 786 | 4.0 | 63 651 | 13.4 | 98 517 | 20.8 |
| Age, years | ||||||||
| 65‐70 | 135 849 | 13.0 | 3331 | 2.5 | 10 110 | 7.4 | 29 959 | 22.1 |
| 71‐85 | 146 630 | 14.0 | 3957 | 2.7 | 13 192 | 9.0 | 32 308 | 22.0 |
| 76‐80 | 174 862 | 16.7 | 5429 | 3.1 | 18 773 | 10.7 | 38 013 | 21.7 |
| 81‐85 | 212 874 | 20.3 | 7689 | 3.6 | 28 004 | 13.2 | 44 685 | 21.0 |
| 85‐90 | 214 704 | 20.5 | 8487 | 4.0 | 33 416 | 15.6 | 42 976 | 20.0 |
| 91+ | 162 633 | 15.5 | 7288 | 4.5 | 30 629 | 18.8 | 29 525 | 18.2 |
| Race | ||||||||
| Non‐Hispanic white | 885 593 | 84.5 | 31 784 | 3.6 | 119 075 | 13.4 | 181 660 | 20.5 |
| Black | 116 051 | 11.1 | 2834 | 2.4 | 10 035 | 8.6 | 26 020 | 22.4 |
| Hispanic | 17 558 | 1.7 | 562 | 3.2 | 1961 | 11.2 | 3955 | 22.5 |
| Other | 25 930 | 2.5 | 920 | 3.5 | 2775 | 10.7 | 5345 | 20.6 |
| Comorbidity | ||||||||
| Diabetes | 499 555 | 47.7 | 15 159 | 3.0 | 57 175 | 11.4 | 116 647 | 23.4 |
| Stroke | 31 446 | 3.0 | 1239 | 3.9 | 4940 | 15.7 | 10 146 | 32.3 |
| COPD | 470 194 | 44.9 | 15 398 | 3.3 | 59 892 | 12.7 | 120 562 | 25.6 |
| Sepsis | 115 416 | 11.0 | 6072 | 5.3 | 20 666 | 17.9 | 42 564 | 36.9 |
| Renal failure | 686 046 | 65.5 | 27 136 | 4.0 | 99 963 | 14.6 | 169 499 | 24.7 |
Abbreviation: CHF, congestive heart failure.
3040 HRRP‐eligible hospitals.
Table 1c.
Characteristics of patient sample (Pneumonia)a
| Admitted patients | Inpatient death | Death 30 d | Readmission 30 d | |||||
|---|---|---|---|---|---|---|---|---|
| N | % | N | % | N | % | N | % | |
| Total | 850 552 | 100.0 | 34 761 | 4.1 | 106 869 | 12.6 | 131 952 | 15.5 |
| Sex | ||||||||
| Female | 471 125 | 55.4 | 16 247 | 3.4 | 55 974 | 11.9 | 70 955 | 15.1 |
| Male | 379 427 | 44.6 | 18 514 | 4.9 | 50 895 | 13.4 | 60 997 | 16.1 |
| Age, years | ||||||||
| 65‐70 | 127 109 | 14.9 | 3691 | 2.9 | 10 829 | 8.5 | 20 068 | 15.8 |
| 71‐85 | 132 884 | 15.6 | 4291 | 3.2 | 12 987 | 9.8 | 21 659 | 16.3 |
| 76‐80 | 149 006 | 17.5 | 5572 | 3.7 | 16 613 | 11.1 | 24 257 | 16.3 |
| 81‐85 | 165 728 | 19.5 | 7096 | 4.3 | 21 400 | 12.9 | 25 987 | 15.7 |
| 85‐90 | 154 540 | 18.2 | 7389 | 4.8 | 23 048 | 14.9 | 23 512 | 15.2 |
| 91+ | 121 285 | 14.3 | 6722 | 5.5 | 21 992 | 18.1 | 16 469 | 13.6 |
| Race | ||||||||
| Non‐Hispanic white | 754 949 | 88.8 | 30 648 | 4.1 | 95 316 | 12.6 | 115 973 | 15.4 |
| Black | 56 106 | 6.6 | 2471 | 4.4 | 7062 | 12.6 | 10 061 | 17.9 |
| Hispanic | 14 647 | 1.7 | 560 | 3.8 | 1706 | 11.6 | 2231 | 15.2 |
| Other | 22 753 | 2.7 | 1023 | 4.5 | 2316 | 10.2 | 3359 | 14.8 |
| Comorbidity | ||||||||
| Diabetes | 297 160 | 34.9 | 11 095 | 3.7 | 34 760 | 11.7 | 55 565 | 18.7 |
| Stroke | 19 084 | 2.2 | 1111 | 5.8 | 3659 | 19.2 | 5411 | 28.4 |
| COPD | 421 500 | 49.6 | 16 495 | 3.9 | 53 873 | 12.8 | 83 402 | 19.8 |
| Sepsis | 106 496 | 12.5 | 6910 | 6.5 | 19 797 | 18.6 | 34 496 | 32.4 |
| Renal failure | 344 194 | 40.5 | 18 616 | 5.4 | 54 767 | 15.9 | 73 416 | 21.3 |
3046 HRRP‐eligible hospitals.
Table 2.
Hospital characteristics
| AMI | CHF | PN | ||||
|---|---|---|---|---|---|---|
| N | % | N | % | N | % | |
| Size | ||||||
| Small | 866 | 29.1 | 922 | 30.3 | 929 | 30.5 |
| Medium | 1672 | 56.2 | 1678 | 55.2 | 1678 | 55.1 |
| Large | 439 | 14.8 | 440 | 14.5 | 439 | 14.4 |
| Region | ||||||
| Northeast | 478 | 16.2 | 479 | 15.9 | 479 | 15.8 |
| Midwest | 699 | 23.6 | 709 | 23.5 | 708 | 23.4 |
| South | 1235 | 41.8 | 1267 | 42.0 | 1273 | 42.1 |
| West | 545 | 18.4 | 564 | 18.7 | 565 | 18.7 |
| Ownership | ||||||
| For profit | 605 | 20.3 | 629 | 20.7 | 634 | 20.8 |
| Nonprofit | 1921 | 64.5 | 1944 | 64.0 | 1946 | 63.9 |
| Public | 451 | 15.2 | 467 | 15.4 | 466 | 15.3 |
| Teaching status | ||||||
| Nonteaching | 242 | 8.1 | 243 | 8.0 | 242 | 7.9 |
| Minor | 769 | 25.8 | 774 | 25.5 | 774 | 25.4 |
| Major | 1966 | 66.0 | 2023 | 66.6 | 2030 | 66.6 |
| RUCA | ||||||
| Urban | 1848 | 62.3 | 1871 | 61.8 | 1876 | 61.8 |
| Suburban | 138 | 4.7 | 144 | 4.8 | 145 | 4.8 |
| Large rural | 604 | 20.4 | 611 | 20.2 | 611 | 20.1 |
| Small rural | 377 | 12.7 | 402 | 13.3 | 402 | 13.3 |
| MICU | ||||||
| Yes | 2352 | 79.0 | 2368 | 77.9 | 2369 | 77.7 |
| No | 625 | 21.0 | 672 | 22.1 | 677 | 22.2 |
Abbreviations: AMI, acute myocardial infarction; CHF, congestive heart failure; MICU, medical intensive care unit; PN, pneumonia; RUCA, rural urban commuting area.
3.2. Probability of readmission by survival
We first examined whether the average predicted probability of being readmitted to an HRRP hospital varied amongst the admitted patient population. In particular, we were interested in understanding whether the average probability would be different for the patients excluded from the denominator, because they did not survive the first 30 days after their index admission, or the numerator, because they died in the days postdischarge before being readmitted. Figure 1 compares the distributions of the predicted probability of being readmitted within 30 days for the patients who survived the first 30 days following their index admission to the predicted probability of being readmitted within 30 days of the patients that died in this period.
Figure 1.
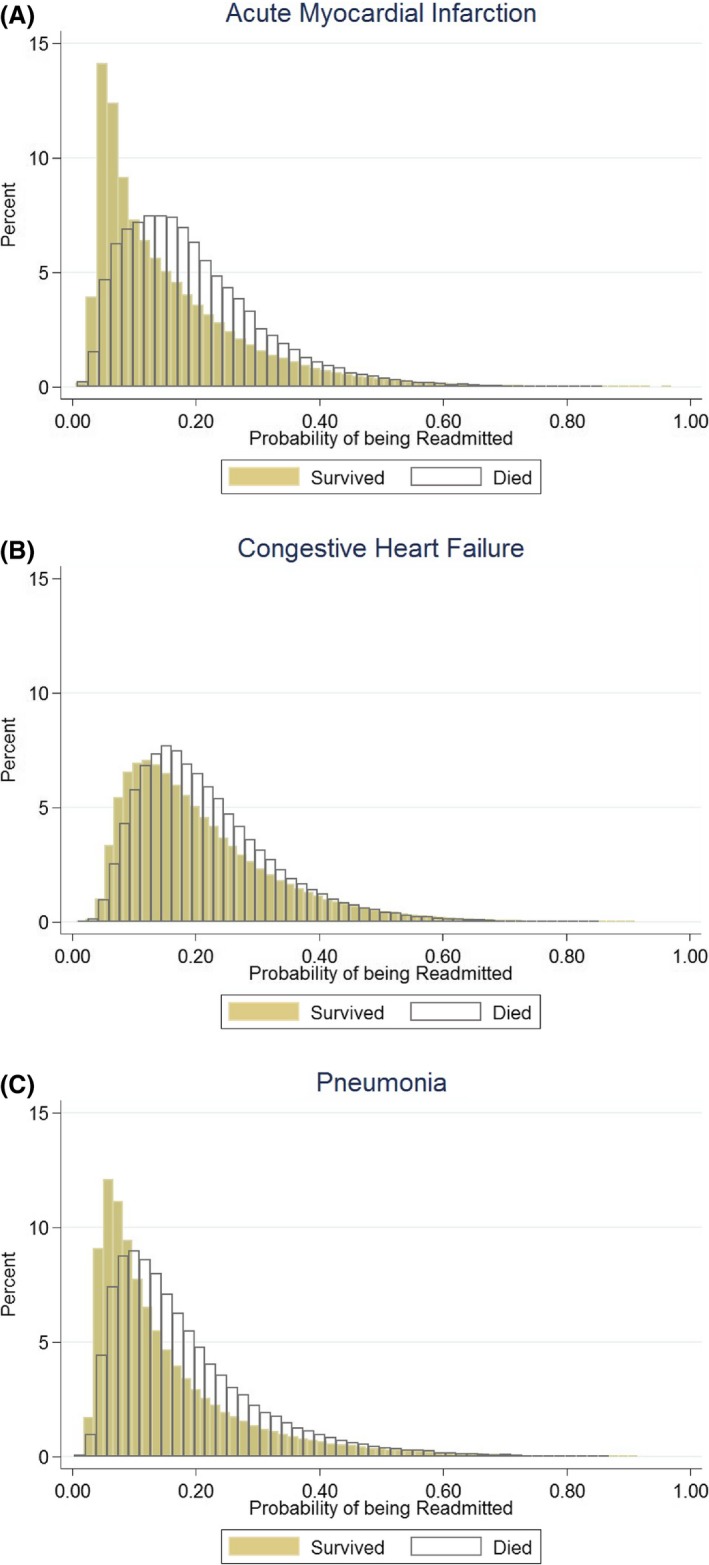
A, Probability of readmission for patients who survived versus those who died (AMI). B, Probability of readmission for patients who survived versus those who died (CHF). C, Probability of readmission for patients who survived versus those who died (Pneumonia). AMI, acute myocardial infarction; CHF, congestive heart failure [Color figure can be viewed at http://wileyonlinelibrary.com]
We found that the differences between the distributions of these two populations varied across conditions. AMI had the greatest difference between the distributions (survived: mean probability of readmission = 0.15, SD = 0.11; died: mean probability of readmission = 0.20, SD = 0.12), followed by pneumonia (survived: mean probability of readmission = 0.15, SD = 0.12; died: mean probability of readmission = 0.18, SD = 0.12), and CHF (survived: mean probability of readmission = 0.21, SD = 0.12; died: mean probability of readmission = 0.22, SD = 0.11). These results indicate that across the three conditions, the population that died would have had a higher probability of being readmitted had they survived, adjusting for patient gender, age, comorbidity, and the hospital at which they were treated.
3.3. Hospital probability of readmission by survival
Next, we examined the difference between the average probabilities of being readmitted to each hospital for the survived and deceased populations. To do this, we plotted the difference in these probabilities by hospital in relation to the average mortality rate (Figure 2A‐C). On average, across hospitals, the difference was 2.3 percentage points for AMI, 1.1 percentage points for CHF, and 2.9 percentage points for pneumonia, with greater variation amongst providers with lower mortality rates. We also observe that on average, amongst providers with lower mortality rates, the difference between the two readmission rates is such that the probability of readmission for those who died is greater than that of those who survived.
Figure 2.

A, Difference in readmission rates between those who survived and those who died, by mortality (AMI). B, Difference in readmission rates between those who survived and those who died, by mortality (CHF). C, Difference in readmission rates between those who survived and those who died, by mortality (Pneumonia). AMI, acute myocardial infarction; CHF, congestive heart failure [Color figure can be viewed at http://wileyonlinelibrary.com]
Given the different probability of readmission for the two groups of patients, we are interested in examining how risk‐adjusted hospital readmission rates would change if we estimated them for the full sample of patients who were admitted to the hospitals. To do this, we compared the average predicted probability of being readmitted to each of the hospitals for the survived patient sample to the average predicted probability for the full sample of admitted patients (Appendix S2). The Spearman rank correlation of the two readmission rates is high: CHF (0.989), pneumonia (0.996), and AMI (0.994), as the readmission rate for the full population is essentially a weighted average of the survived and deceased populations.
We carry out a number of sensitivity analyses to examine the extent to which modeling readmissions for the entire admitted population using the parameters estimated from the survived population may create additional bias (Appendix S2). First, we compare the readmission estimate for the entire admitted population and the readmission estimate for the survived population to the readmission rate for the deceased population. The Spearman rank correlation is high for the readmission rates constructed from both the full‐admitted population and the survived population, but higher for those constructed from the full‐admitted population: AMI (0.773 vs 0.702), CHF (0.824 vs 0.786), and pneumonia (0.802 vs 0.752).
Next, we compare the readmission rates to the three additional outcome measures for hospitals, which are constructed as a composite outcome encompassing both mortality and readmissions at different time periods (Appendix S2). The Spearman correlation between the three composite measures and readmission rates constructed from the full‐admitted sample, and those constructed from only the patients who survived, is very similar. The correlation between the readmission rate for the survived population and the composite outcome that encompasses death or readmission within 30 days for the entire admitted population is 0.512 for AMI, 0.719 for CHF, and 0.707 for pneumonia. The correlation of this composite measure to the readmission rate for the admitted population corresponds to 0.561 for AMI, 0.721 for CHF, and 0.724 for pneumonia. The correlations for the 30‐day composite outcome estimated from discharge onwards are the same, likely because such a small percentage of the population dies during the inpatient stay.
Finally, the correlation between the readmission rate for the survived population and the composite outcome that encompasses death or readmission within 15 days from discharge is positive but weaker, at 0.358 for AMI, 0.301 for CHF, and 0.386 for pneumonia. The correlation of the readmission rate estimated for the admitted population to this composite measure is very similar, corresponding to 0.344 for AMI, 0.297 for CHF, and 0.397 for pneumonia. This suggests that the characteristics influencing outcomes closer to discharge are likely different from those influencing readmissions further from discharge.
In addition, we compare the two readmission rates to the hazard rates produced by a Fine/Gray competing risk model that focuses on all admitted patients and accounts for death. Again, we find quite similar correlations between these estimates and the readmission rates estimated for the admitted and survived populations, at 0.782 vs 0.771 for AMI, 0.795 vs 0.801 for CHF, and 0.741 vs 0.748 for pneumonia, respectively.
Using the above risk‐adjusted readmission rates for the admitted and survived populations, we are also able to examine how many hospitals would move from readmission rates that were below average to readmission rates that are above average, and vice versa, when adjusting for the deceased patients (Table 3). This is important as it has the potential to influence whether or not hospitals receive a penalty payment under the HRRP. Our results show that amongst hospitals with more than 25 cases per condition, approximately 2% of hospitals would switch in this way. A total of 52 hospitals (2.48%) would switch from being either above or below average for AMI, 61 (2.16%) for CHF, and 69 (2.38%) for pneumonia.
Table 3.
Change in hospitals receiving penalties when adjusting for the full populationa
| AMI | CHF | PN | ||||
|---|---|---|---|---|---|---|
| N | % | N | % | N | % | |
| Hospitals with more than 25 admissions | 2093 | 70.3 | 2826 | 92.96 | 2897 | 95.11 |
| Hospitals who switch to excess readmissions | 42 | 2.01 | 41 | 1.45 | 38 | 1.31 |
| Hospitals who switch from excess readmissions | 10 | 0.48 | 20 | 0.71 | 31 | 1.07 |
| Total number of hospitals who switch status | 52 | 2.48 | 61 | 2.16 | 69 | 2.38 |
Abbreviations: AMI, acute myocardial infarction; CHF, congestive heart failure; PN, pneumonia.
Total number of HRRP‐eligible hospitals for AMI = 2977, CHF = 3040, and PN = 3046.
Considerably, more hospitals would see their penalty status influenced if the readmission measure was replaced by one of the alternative composite measures of hospital outcome, which take into account both mortality and readmissions at different time periods. Using a 30‐day composite measure taking into account both mortality and readmissions, 34.97% of AMI hospitals, 47.56% of CHF hospitals, and 47.46 of pneumonia hospitals would move away from having excess readmissions, thus no longer receiving a penalty. There was no difference in the number of hospitals affected when either of the 30‐day measures—measured from patient admission or patient discharge—were used. If a 15‐day composite measure taking into account both mortality and readmission 15‐days postdischarge were used, then we estimate that 23.98% of the AMI hospitals, 45.56% of the CHF hospitals, and 17.47% of the pneumonia hospitals would no longer receive a penalty.
Finally, we explore the average predicted readmission rates for the survived and admitted populations, by a number of hospital characteristics, including hospital size, profit status, teaching status, region, urbanity, and whether or not the hospital has a MICU (Appendix S1a‐c). Our results show that across hospital characteristics, we would see an increase in readmission rates when accounting for the entire admitted population. However, this increase is very small and influences hospitals across the board, not appearing to be particularly concentrated amongst any subgroup.
4. DISCUSSION
We found that mortality rates and readmission rates are not independent, and that sample selection bias does result from the relationship between mortality and readmissions. The hospital readmission rate estimated for the survived and omitted patient populations differed between 1 percentage point for CHF to 5 percentage points for AMI, on average. However, including the omitted populations in the readmission estimation has a negligible effect on overall hospital readmission rates. As a result, we found that only about 2% of hospitals would see their readmission metric switch from being above average to below average, or vice versa, when accounting for this sampling bias. Taken together, these findings suggest that variations in mortality do influence readmission rates, in ways that vary by condition. While this effect is small for the three initial conditions targeted by the HRRP, policy makers may want to explore this relationship when choosing to incentivize readmission rate for other conditions, as the magnitude of the effect varies based on the condition.
Our findings hold important implications for policy makers as we continue to incentivize readmission reduction and expand HRRP penalties to more conditions. In particular, our study illustrates that patients who die before they can be readmitted are different than those who survive and removing them from the denominator when constructing readmission rates will result in sample selection bias. Our study shows that the magnitude of this bias varies by condition; we saw the difference to be much more pronounced for AMI and pneumonia than for CHF patients. This may be related to a number of factors beyond the capabilities of the risk‐adjustment models used, including the pathology of the disease or the heterogeneity amongst patients.
While these data show that the hospital readmission rates predicted for the omitted population are different from readmission rates for the population that survived, we also find that risk‐adjusted readmission rates change only modestly by accounting for them. This is because the readmission rate of the admitted sample is mostly made up of the survived population, approximately 85% of admitted patients. Moreover, the hospitals that are most affected from this sample selection bias are not concentrated by particular characteristics. This is reassuring for policy makers who may be concerned that adjusting for this difference may unduly penalize or reward particular subgroups of hospitals. However, given that the penalized hospitals are determined by relative performance, even this small change can impact which hospitals receive financial penalties. We find that when we adjust for this bias, approximately 2% of hospitals would move from having readmission rates above average to rates below average, or vice versa, for each condition.
Our findings contribute to the existing work that has examined the relationship between mortality and readmissions in the past decade. Krumholtz and colleagues examined the correlation between 30‐day risk‐adjusted mortality and 30‐day risk‐adjusted readmission rates for the same three targeted conditions, assuming independence between these outcomes.5 They found no correlation between the two quality measures for AMI and pneumonia, and a small negative correlation for heart failure. Our findings contribute to this work by examining the underlying assumption that these outcomes are independent, showing that excluding the patients who die introduces a systematic bias.
Our results are consistent with other recent work by Sabbatini and colleagues who find evidence supporting this mechanism in the emergency department (ED), showing that patients who experienced an ED return visit that was associated with admission shortly after ED discharge had significantly lower rates of in‐hospital mortality as compared to patients who were hospitalized during the index ED visit.9 Similarly, Laudicella and colleagues showed sample selection bias of this sort to exist amongst hip fracture patients in England.10 However, we find a noticeably smaller effect on hospital readmission rates when correcting for this bias. Our findings also complement the work of Haneuse and colleagues who illustrate different ways to model joint readmission and mortality variance across hospitals.11, 12, 13
Our study has several limitations. First, as we do not observe readmissions for the sample of patients that did not survive, our estimates of the probability of readmission for the patients that died are based on a model of the survived population. Thus, some of our hospital estimates will be less than perfectly predictive. For example, while we find that across conditions, the majority of hospitals have a higher estimated readmission rate amongst the dead population than the survived population, and in some instances, this readmission rate is lower. This may represent limitations of the model's ability to estimate the probability of readmissions for the deceased population, as the coefficients used to estimate average readmissions are based on the survived population. For instance, many patients of pneumonia die of sepsis, and thus, sepsis is likely to be associated with a low probability of readmission, and our estimation of the probability of readmissions for this population may be underestimated. However, we carry out a number of checks to determine the extent to which this is an issue and find that while these estimates are less than perfectly predictive, they do not introduce a large bias.
As it is impossible to accurately estimate the probability of readmissions for those who die, we also examine the performance of an alternative measure of hospital outcome that combines mortality and readmissions. The benefit of a composite measure that takes into account both outcomes would be to bypass the problem of sample selection, as it would capture both the patients who die as well as those who are readmitted. As expected, the composite measure, while positively correlated with readmission rates, correlates more weakly than our adjusted measure of readmissions that uses the admitted population. Using this measure to penalize hospitals would thus result in a substantial change in the number of hospitals receiving a penalty.
Another limitation of the study is that we used administrative data, which may be limited in its ability to account for the medical severity of patients. However, this is the data used by CMS to construct the readmission rates and thus is likely adequate for the purposes of this analysis. In addition, we only observed patients admitted to the Medicare fee‐for‐service program, and not those in Medicare Advantage. As Medicare Advantage enrollment increases over time, this may influence mortality and readmission rates observed in the future. Finally, we are not able to use the exact methods that CMS uses to construct readmission rates given that we are trying to include all patients that were admitted to the hospital. We do control for the same characteristics that CMS does, and we use the same underlying data to be as consistent with their approach as possible. Additionally, our aim is not meant to replicate their approach but rather to consider the biases that result from the exclusion of a group of patients from this quality metric.
5. CONCLUSION
We find that 30‐day readmission rates and 30‐day mortality rates of the three HRRP‐targeted conditions are not independent. While accounting for mortality has a negligible effect, it is critically important in order to ensure that the proper hospitals are being penalized. As HRRP continues, making changes to ensure proper measurement is critical to ensuring that we incentivize the right behaviors and minimize unintended consequences.
Supporting information
Papanicolas I, Orav EJ, Jha AK. Is mortality readmissions bias a concern for readmission rates under the Hospital Readmissions Reduction Program?. Health Serv Res. 2020;55:249–258. 10.1111/1475-6773.13268
REFERENCES
- 1. Hawn MT. Unintended consequences of the hospital readmission reduction program. Ann Surg. 2015;261:1032‐1033. [DOI] [PubMed] [Google Scholar]
- 2. Joynt KE, Jha AK. A path forward on medicare readmissions. N Engl J Med. 2013;368:1175‐1177. [DOI] [PubMed] [Google Scholar]
- 3. Gorodeski EZ, Starling RC, Blackstone EH. Are all readmissions bad readmissions? N Engl J Med. 2010;363:297‐298. [DOI] [PubMed] [Google Scholar]
- 4. Ong MK, Mangione CM, Romano PS, et al. Looking forward, looking back: assessing variations in hospital resource use and outcomes for elderly patients with heart failure. Circ Cardiovasc Qual Outcomes. 2009;2:548‐557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Krumholz HM, Lin Z, Keenan PS, et al. Relationship between hospital readmission and mortality rates for patients hospitalized with acute myocardial infarction, heart failure, or pneumonia. JAMA. 2013;309:587‐593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Centers for Medicare and Medicaid Services . Measure methodology: hospital quality initiative. 2019.
- 7. Ibrahim AM, Dimick JB, Sinha SS, Hollingsworth JM, Nuliyalu U, Ryan AM. Association of coded severity with readmission reduction after the hospital readmissions reduction program. JAMA Intern Med. 2018;178:290‐292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Centers for Medicare and Medicaid Services . FY 2017 IPPS final rule homepage 2017.
- 9. Sabbatini AK, Kocher KE, Basu A, Hsia RY. In‐hospital outcomes and costs among patients hospitalized during a return visit to the emergency department. JAMA. 2016;315:663‐671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Laudicella M, Li Donni P, Smith PC. Hospital readmission rates: signal of failure or success? J Health Econ. 2013;32:909‐921. [DOI] [PubMed] [Google Scholar]
- 11. Haneuse S, Lee KH. Semi‐competing risks data analysis: accounting for death as a competing risk when the outcome of interest is nonterminal. Circ Cardiovasc Qual Outcomes. 2016;9:322‐331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Lee KH, Dominici F, Schrag D, Haneuse S. Hierarchical models for semi‐competing risks data with application to quality of end‐of‐life care for pancreatic cancer. J Am Stat Assoc. 2016;111:1075‐1095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Lee KH, Haneuse S, Schrag D, Dominici F. Bayesian semi‐parametric analysis of semi‐competing risks data: investigating hospital readmission after a pancreatic cancer diagnosis. J R Stat Soc Ser C Appl Stat. 2015;64:253‐273. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials


