Abstract
Purpose:
In current clinical practice, administered activity (AA) for pediatric molecular imaging is often based on the North American expert consensus guidelines or the European Association of Nuclear Medicine dosage card, both of which were developed based on best clinical practice. These guidelines were not formulated using a rigorous evaluation of diagnostic image quality relative to AA. In the guidelines, AA is determined by a weight-based scaling of the adult AA, along with minimum and maximum AA constraints. In this study, we use task-based image quality assessment methods to rigorously evaluate the efficacy of weight-based scaling in equalizing image quality using a population of pediatric patients of different ages and body weights.
Methods:
A previously developed projection image database was used. We measured task-based image quality (IQ), with respect to the detection of a renal functional defect, at six different AA levels (AA relative to the AA obtained from the guidelines). IQ was assessed using an anthropomorphic model observer. Receiver-operating characteristics (ROC) analysis was applied; the area under the ROC curve (AUC) served as a figure-of-merit for task performance. In addition, we investigated patient girth (circumference) as a potential improved predictor of the IQ.
Results:
The data demonstrate a monotonic and modestly saturating increase in AUC with increasing AA, indicating that defect detectability was limited by quantum noise and the effects of object variability were modest over the range of AA levels studied. The AA for a given value of the AUC increased with increasing age. The AUC vs. AA plots for all the patient ages indicate that, for the current guidelines, the newborn and 10-year and 15-year phantoms had similar image quality for the same AA suggested by the North American expert consensus guidelines, but the 5-year and 1-year phantoms had lower image quality. The results also showed that girth has a stronger correlation with the needed AA to provide a constant AUC for 99mTc-DMSA renal SPECT.
Conclusions:
The results suggest that (1) weight-based scaling is not sufficient to equalize task-based image quality for patients of different weights in pediatric 99mTc-DMSA renal SPECT; (2) patient girth should be considered instead of weight in developing new administration guidelines for pediatric patients.
Keywords: dose reduction/optimization, administered activity guidelines, DMSA, pediatric imaging, SPECT, task-based image quality
I. INTRODUCTION
Historically, many pediatric imaging centers developed their own administered activity (AA) guidelines, giving rise to large variations (5 to 20-fold) [1], and consequently, large differences in radiation exposure to pediatric patients undergoing nuclear medicine examinations. At present, prescribed AA for pediatric nuclear medicine in North America is based on the 2010 North American Consensus guidelines [2, 3]. Consensus, in this context, means that a majority of pediatric nuclear medicine practitioners agree that the guidelines are reasonable to promote dose reduction and consistent across different institutions. Image quality for these guidelines was characterized primarily by expert consensus rather than quantitative, objective measures.
The development of the expert consensus guidelines undoubtedly helped normalize recommended AA [4]. However, in a previous study, we showed that weight alone is not sufficient to determine an optimal patient-specific AA accurately, and other factors such as body habitus need to be taken into consideration [5]. In that work, we evaluated the image quality as a function of AA for two pediatric phantoms having the same weight but different heights. There was substantial difference in image quality for the guideline-recommended AA. Furthermore, as shown in [6], patients with the same weight but different body habitus can have considerable differences in effective dose (patient risk and its relationship to image quality will be discussed in a forthcoming paper). One candidate parameter for improving image quality in renal scintigraphy is girth (patient circumference) at the level of the kidneys. Thus, the goal of this study was to calculate objective task-based image quality metrics for a wide range of AA’s employing a more complete set of pediatric phantoms to determine the efficacy of the consensus guidelines for equalizing image quality for patients with different weights and body habitus. We also used the data derived in this study to perform a preliminary investigation of the correlation between patient girth and image quality.
II. MATERIALS AND METHODS
Image quality was measured in this work in terms of performance on the task of detecting renal function defects in Tc-99m DMSA SPECT. The images used were simulated from a series of anthropomorphic digital phantoms. Task performance was assessed for a range of AAs using an anthropomorphic model observer. The area under the ROC curve (AUC) served as a figure of merit for task performance.
A. Series of realistic digital phantoms
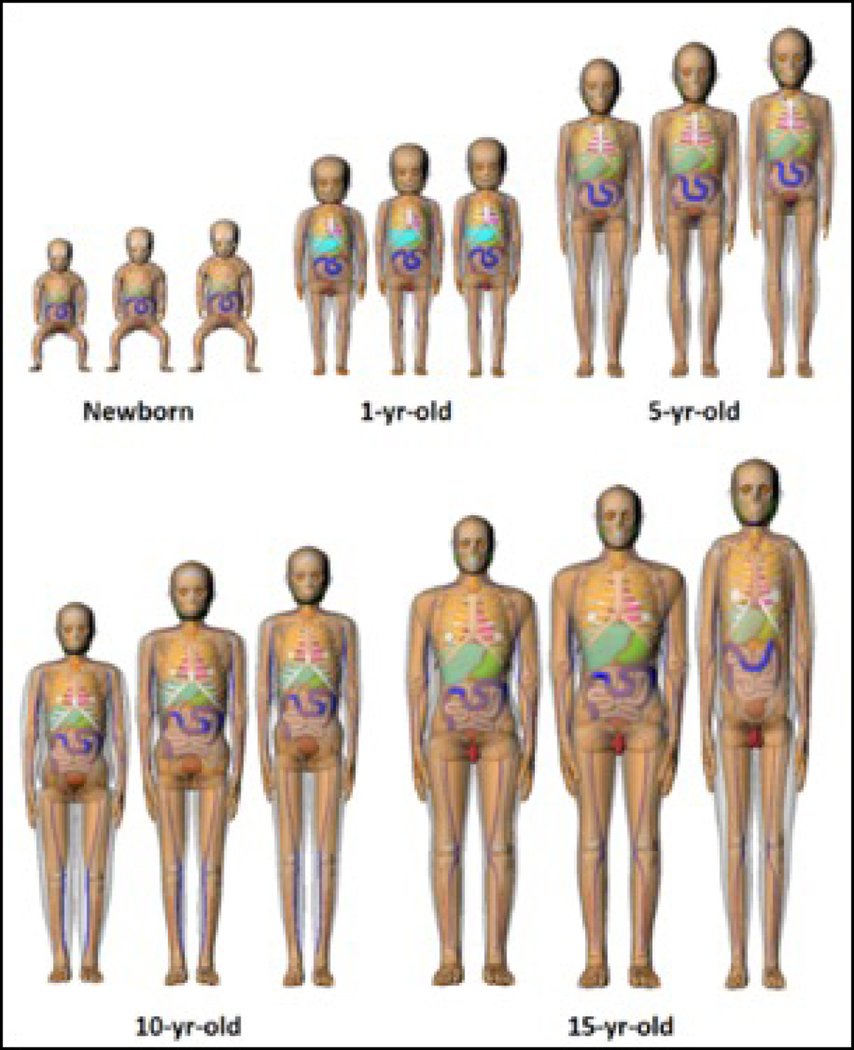
The series of pediatric phantoms used was developed at the University of Florida and is based on demographic data from the CDC’s National Health and Nutrition Examination Survey (NHANES) data [7]. The series consists of 90 phantoms that include variations in age, gender, height, and kidney mass. For each gender, five groups are modeled: 0, 1, 5, 10, and 15 years of age. All phantoms at a given age have a weight equal to the 50th percentile weight for that age and one of three height percentiles: 10th (short), 50th (average) and 90th (tall). The phantoms for each height percentile and age group are shown in Figure 1. The targeted weights for each age are provided in Table 1. For each height percentile, the phantoms have 3 kidney sizes: the average size and 15% larger and smaller than the average. The variation in kidney size models the effects of anatomical variation [7] that would not be externally observable. The phantoms were digitized using 0.1 cm cubic voxels.
Figure 1.
Renderings of 10th, 50th, and 90th percentile height at constant 50th percentile weight newborn, 1-yr-old, 5-yr-old, 10-yr-old, and 15-yr-old hybrid phantoms.
Table 1.
Summary of phantom masses
| Age (year) | Male | Female |
|---|---|---|
| Newborn | 3.5 kg | 3.4 kg |
| 1y | 10.4 kg | 9.5 kg |
| 5y | 20 kg | 20 kg |
| 10y | 30 kg | 35 kg |
| 15y | 55 kg | 50 kg |
B. Activity Distribution
A previously-described pharmacokinetic (PK) model for 99mTc-DMSA was used in this study to model kidney uptake [8, 9]. The PK model is based on literature data and was validated using 47 patient datasets acquired at the Boston Children’s Hospital (BCH). A single mixed-age population sample, instead of an age-specific PK model, was used for estimating uptake of activities in the organs at the time of the imaging study. The patient datasets were reconstructed using five iterations with eight subsets per iteration of a quantitative ordered-subsets expectation-maximization (OS-EM) reconstruction method that included attenuation, scatter and collimator-detector response compensation. Attenuation maps estimated based on automated intensity thresholding of images reconstructed from scatter windows were used for attenuation compensation as CT scans of these patients were not available. Intensity thresholding was used to obtain kidney volumes-of-interest (VOIs); the reasonability of the kidney VOIs and body contours used to generate the attenuation maps were reviewed visually. Tracer uptake (in units of activity) in individual organs (i.e., the kidneys, spleen, liver, and body remainder) at a single imaging time point (3 hours post injection) was computed by converting the mean count density inside the VOIs to units of activity concentration using the measured camera sensitivity. The percent of the decay-corrected AA in the kidneys in these VOIs is referred to as the percent kidney uptake. In addition, we computed the ratio of activity concentrations (sum of activity values divided by volume of the VOI) in the cortex to the medulla/pelvis using segmentations of the kidney cortex and pelvis/medulla VOIs obtained by intensity thresholding. This ratio is referred to as the cortex-to-medulla plus pelvis activity concentration ratio. The results obtained from the above procedure are summarized in Table 2, and were used as estimates of the percent tracer uptakes in the patient’s kidneys. Variations in tracer uptake based on those seen in the 47 patient datasets were modeled using the coefficient of variation (percent standard deviation) from those data and assuming a truncated normal distribution.
Table 2.
Summary of population parameters
| Kidney Uptake Fraction | Cortex-to-Medulla + Pelvis Act. Conc. Ratio | |
|---|---|---|
| Maximum | 0.393 | 2.00 |
| Minimum | 0.329 | 1.36 |
| Sample mean | 0.361 | 1.68 |
| Sample standard deviation | 0.025 | 0.25 |
C. Defect model
We used a defect model described in [10]. In the model, a defect volume of 0.3 cm3 for a newborn patient with the average kidney size and 50th height percentile was deemed, by an experienced pediatric nuclear medicine specialist, clinically relevant and at the limits of clinical detectability in the newborn phantom. Defect volumes for other ages were determined so that the defect contrast for each age and kidney size at the 50th height percentile was the same as for the newborn phantom with the same corresponding relative kidney size (average or 15% larger or smaller than average) [10]. The sizes of these defects were thus different for each age group. Using this model, focal renal lesions consisting of areas of reduced uptake were created to simulate focal acute pyelonephritis in three locations (lower pole, upper pole and lateral aspect of the kidney) along the cortical wall.
D. Projection data simulation
For each phantom in the population, we simulated noise-free projection data for the renal cortex, medulla, pelvis, liver, spleen, and background (including all other organs), modeling the physics and acquisition parameters appropriate for Tc-99m renal SPECT. The projections were generated using an analytic projection code that modeled attenuation, spatially varying collimator-to-detector response [11], and object-dependent scatter [12]. The code has been previously validated by comparison to Monte Carlo and experimental projection data for imaging of a variety of radionuclides [13–21]. The projections were simulated for a Siemens low-energy, ultra-high-resolution (LEUHR) collimator at 120 projection views over a 360° body-contouring orbit and a 0.2-cm projection bin size. Prior to simulation, each computational phantom was placed on a patient bed obtained from a CT scan of the bed on a Siemens Symbia SPECT/CT system. This bed constrained the orbit in the lateral direction, especially for small computational phantoms.
The renal activity and relative activity concentrations for structures inside the kidney (the renal cortex, medulla, and pelvis) were randomly sampled from truncated Gaussian distributions with the means, standard deviations, minima, and maxima derived from the PK model and 47 sets of patient data acquired at the Boston Children’s hospital. These parameters are summarized in Table 2. Each individual organ projection was scaled by its relative uptake value and the product of AA, acquisition duration, and scanner sensitivity.
A projection set of the entire phantom was generated by summing these individual sets of scaled organ projections. Simulated projections were scaled to represent various AA-levels. In this context, the AA-level is the AA simulated divided by the weight-based AA. Thus, an AA-level of 50% represents the case where the simulated activity was half of the standard, weight-based AA. The AA-levels varied from 25% to 150% in increments of 25%. The standard, weight-based AA (weight-based scaling) is calculated by multiplying the patient weight by a scaling factor subject to constrains on minimum and maximum AA:
| (1) |
where is the patient weight in kilograms and is a scaling factor. For DMSA, is 1.85 and the AAmin and AAmax are 18.5 and 99.9 , respectively.
Poisson noise was simulated using a Poisson distributed random number generator. A total of 207,360 sets of projection images were thus generated comprised of 64 uptake realizations × 6 AA levels × 5 ages × 3 height percentiles × 2 genders × 3 kidney sizes × 3 defect locations × 2 defect statuses (present or absent). Note that even for a given age, height percentile, weight and kidney size, and defect location, the mean (noise-free) activity distribution was statistically independent since the kidney uptake and cortex to medulla+pelvis activity concentration ratios were randomly sampled.
E. Image reconstruction and post-reconstruction processing
Images were reconstructed using filtered backprojection (FBP) and post-filtered with 3D Butterworth filters with an order of 8. We determined the optimal cutoff frequency for the 3D post-reconstruction Butterworth filter based on the AA giving the highest AUC at each AA level. The optimal cutoff frequency was 0.6 cycles per cm for all the AA levels investigated. This cutoff frequency was used for all the AUC values presented below. The reconstructed images had cubic voxels with a side of length of 0.2 cm. Images centered on the defect with a size of 128×128 pixels were extracted from the coronal, transaxial, and sagittal slices containing the defect centroid and used in the image quality evaluation. Samples of these images are shown in Figure 2.
Figure 2.
From top to bottom the images show upper, lateral, and lower pole (from left to right) defects for the 50th height percentile for the 1- and 5-year-old female and 10- and 15-year-old male phantoms. Inside each of the small block of images, top and bottom row shows coronal, sagittal, and tran-saxial slices for the defect-free and defect present images, respectively.
F. Model observer
The channelized Hotelling observer (CHO), first proposed by Myers and Barrett [22] has been shown to provide good predictions of human performance on detection tasks for a variety of nuclear medicine imaging applications[23–26]. The CHO uses a set of frequency channels applied to input images that model the human visual system combined with the Hotelling Observer, which approximates the Ideal Observer in cases where the input data are multi-variate normally (MVN) distributed with equal covariance matrices.
As noted, the Hotelling Observer is strictly optimal only when the input data (i.e., the vectors of channel outputs) are MVN distributed; conversely, it performs poorly when the input data are multimodally distributed [27, 28]. The data used in this study, as discussed below, included both background and signal variations and were non-MVN. Thus, instead of the traditional CHO, we used a multi-template strategy proposed in [28]. to handle the non-MVN data. This strategy involves partitioning the data into sub-ensembles that are approximately MVN and applying the optimal linear discriminant to each sub-ensemble [28]. We used a leave-one-out training-testing strategy. In this strategy, one feature vector was left-out (i.e., not used in the training), and the remaining vectors were used to train the observer. The observer was then applied to the left-out vector to produce a test statistic. This process was repeated with each vector in the ensemble being left-out once. This process was applied to each sub-ensemble and produced a number of test statistics equal to the size of the sub-ensemble. The resulting test statistics produced by this strategy were pooled and analyzed, using ROC analysis to estimate the AUC, which served as a figure of merit (FOM) for task performance.
G. Channel model
We used seven non-overlapping rotationally-symmetric difference-of-mesa channels[29]. The starting frequency and width of the first channel was 0.5 cycles per pixel, and subsequent channels had widths that doubled and abutted the previous channel. The frequency domain channels and corresponding spatial templates (i.e., the analytical inverse Fourier transform of the frequency channels sampled at the pixel size) are shown in Figure 3.
Figure 3.
Images of the seven anthropomorphic DOM channels used in this work. The top and bottom rows show, respectively, the frequency channels and the spatial domain templates. From left to right, the start frequencies and widths of the channels were 0.5, 1, 2, 4, 8, 16, and 32 cycles/pixel. The spatial templates are the analytic inverse Fourier Transforms of the frequency channels sampled at the image pixel size.
Each of the seven spatial domain templates was applied to each of the 3 images (transaxial, sagittal, and coronal) to give a 21-element feature vector. Each element in the resulting feature vector was obtained by taking the dot product of a spatial domain template with an input image, representing the total energy in this frequency band contained in that image. The input images were those described in Section E and had the defect centroid at the center of the image. These feature vectors served as inputs to the observer described below.
H. Evaluation of the multivariate normality assumption of the channel outputs
In the multi-template channelized linear discriminant observer (MTCLDO) strategy, channel output vectors were sorted into sub-ensembles from one defect location, age, and height percentile. We verified visually that the resulting distributions of the channel output vectors in each sub-ensemble were not multi-modal and were nearly MVN distributed, as illustrated in Figure 4 below.
Figure 4.
Sub-ensemble histograms of the test statistic distributions for the no-defect (green) and with-defect (blue) cases for each of the seven channels. These data are for an upper pole defect in the 50th height percentile 1-year-old phantom (including both male and female). This illustrates the near-MVN distribution of the feature vectors.
I. ROC and statistical analysis
We applied the MTCLDO to feature vectors in the sub-ensembles described above. Because younger ages have minimal anatomical differences between genders, we combined the sub-ensembles for the two genders. Thus, for newborn and 1-, and 5-year old phantoms, we had 27 sub-ensembles, and each sub-ensemble was comprised of 768 channel output vectors (64 realizations × 2 genders × 3 kidney sizes × 2 defect statuses × 1 height percentile × 1 defect location). The sub-ensembles for the 10- and 15-year old phantoms were half as large as separate sub-ensembles were used for each gender. The test statistics for all the sub-ensembles for all the height percentiles, genders and defect locations for a given age were pooled, ROC analysis was performed using the LABROC4 code [30], and the AUC calculated. This produced a total 30 AUC values, one for each of the ages (5) and AA levels (6). Bootstrapping and nonparametric analysis were used to compute 95% confidence intervals for each of these AUC values.
J. A model of AUC versus AA
The goal of the following is to derive an approximate empirical relationship between the AUC and AA that can be used to fit the data from the model observer studies. When the test statistics are normally distributed under both hypotheses, the AUC under the ROC for the CHOs is related to the Hotelling SNR by [31]
| (2) |
Rearranging the formula to express SNR as a function of AUC, we have
| (3) |
In a binary classification task if the two classes have the same covariance matrix, , the SNR of the Hotelling Observer test statistics can be expressed as
| (4) |
where is the difference in the ensemble mean difference of the two classes. Then, we can re-write the above formula using formalism introduced by Barrett [32] to replace the total covariance as a sum of the object covariance matrix and quantum noise covariance matrix:
| (5) |
where represents the object variability, which includes the effects of anatomical and uptake variability from patient to patient for a particular AA times acquisition duration (AD). In (4), denotes the contribution of quantum noise to the ensemble covariance matrix of the reconstructed images. The subscript denotes averaging over all objects in the sub-ensemble.
Suppose we now change the noise level by scaling the AA×AD by , such that . Then, the SNR can be estimated as follows: [26]
| (6) |
We now replace n with AA (dropping AD for simplicity but without loss of generality) and assume that the vector can be replaced with a scalar , representing the mean signal difference, , and the proportionality constant relating n and AA. Similarly, we assume that the two covariance matrices can be replaced by the scalars , representing the object variability noise, and , representing the quantum noise, . This gives
| (7) |
Combining equations 1 and 7 gives an expression for AUC as a function of AA:
| (8) |
Inverting the above formula to express AA in terms of AUC yields:
| (9) |
Note that the relative size of the constants K2 and K3 indicates the degree to which the SNR is limited by quantum noise rather than anatomical variability. It should also be noted that (9) is not a rigorous relationship in the sense that it ignores the vector and matrix natures of the defect and covariance matrices. However, as will be shown below, it is suitable for fitting AUC values as a function of the AA, and thus is practically useful.
III. RESULTS
The results from the IQ studies are summarized in Figure 5, which shows the AUC for each age group plotted as a function of the % AA level, i.e., the percentage of the AA obtained from the consensus guidelines [3]. Note that the guidelines do not result in the same IQ (as measured by the AUC) for the 100% AA level. In this sense, they do not provide the same level of image quality for patients with different weights with respect to detecting defects having the same contrast. The ultimate goal of this work was to provide the pediatric nuclear medicine practitioner with the AA needed to give the desired objectively-measured task-based image quality, as specified by the AUC, prior to patient imaging. The data in Figure 5 provides a way to do this. The analytic expression relating AUC to AA derived above and given by Equation (8) was fit to the data in Figure 5. The results of this fit are shown in Figure 6 for all the patient ages. Note that the fits are visually quite good, and the correlation coefficients are better than 0.99. These fitted functions provide an analytical relationship between AUC and AA, and could potentially be used to determine the AA required to give a desired AUC for a given patient weight.
Figure 5.
The area under the ROC curve (AUC) vs. percent AA plot for all the patient ages. The error bars are the 95% confidence intervals estimated using bootstrapping.
Figure 6.
AUC vs. AA curves and their fitted functions. The AUC was fitted to a model of AUC versus AA, as specified in equation 8, relating AUC to the mean signal difference (K1), object variability noise (K2) and quantum noise (K3), and AA.
The data demonstrate a monotonic and modestly saturating increase in AUC with increasing AA, indicating that defect detectability is limited by quantum noise, and the effects of object variability are modest over the range of AA levels studied. The AA for a given value of the AUC increases with increasing age. The curves in Figure 5 indicate that, for the current guidelines, the newborn and 10-year and 15-year phantoms have similar image quality for the same fraction of the AA suggested by the North American expert consensus guidelines, but the 5-year and 1-year phantoms have lower image quality. The fact that the AUC is higher at the weight-based injected activity for the newborn is due to the fact that there is a minimum activity of 18.5 MBq specified by the consensus guidelines. The result of this limit is that the newborn phantoms has an AA per unit weight of 5.55 MBq/kg, compared to 2.59 MBq/kg for the other ages. This higher AA per unit weight contributes to the higher AUC for this age group, and suggests that the activity limit might need to be revisited.
In previous work [8], we have shown that there are variations in image quality among phantoms with different weights but the same height. In [9], we showed data that suggested that height was not sufficient to explain variations in image quality for phantoms with the same weight over a range of anatomical variations. However, girth (circumference) at the level of the kidneys provides a more consistent correlation. To demonstrate the correlation between girth and the AUC values, we measured the patient girth of each of the phantoms and averaged them over height percentiles within one age. In clinical practice, patient girth could be estimated prior to imaging using a tape measure or from a previous CT image, if available. Figure 7 shows a comparison of AA vs. girth and AA vs. weight at a fixed AUC for all the patient ages. The colored lines connect the nearest phantoms in age. These data indicate that the relationship between girth and AA is more robust than it is between weight and AA. The Pearson product-moment correlation coefficients between AA and weight and girth are 0.941 and 0.985, respectively. This further supports the observation that girth may be more robust for estimating the AA needed to provide a constant image quality. The data, combined with the more direct physical relationship between girth and factors affecting image quality suggests that girth should be considered as an alternative to weight in the development of future guidelines.
Figure 7.
AA vs. patient girth (top) and weight (bottom) at a fixed AUC of 0.84.
IV. DISCUSSION
One limitation of this paper is that current clinical practice in DMSA SPECT has moved toward the use of iterative reconstruction rather than FBP. However, the Consensus guidelines were created based on images reconstructed with FBP. Thus, the data here are relevant to those guidelines. Further exploration of the impact of iterative reconstruction on these guidelines is important. Nevertheless, the work in this paper suggest that future guidelines should consider AA administration guidelines based on something other than weight-based scaling.
A second limitation of this paper is that, while a substantial improvement over the methods that form the basis for previous guidelines, the variability in the present phantom database does not match that of true patient populations. The phantom database included, for a given weight, variability in patient height (and hence girth), kidney size (3 sizes), kidney depth (different depths for each height), and kidney uptake (different for each phantom). However, the phantoms were created by scaling data from a single patient [7]. Increased object variability would increase K2 in equations 8 and 9, resulting in saturation of the AUC vs AA curves at lower values of the AUC. However, this would have little effect on the shape of this curve in the regime where quantum noise dominates. Since the curves in Figure 6 for the different weights are clearly different, the observation that weight does not equalize AA would likely remain true in that region. The best AA would be in the region where there is a balance between object variability and quantum noise, i.e., in where the curve starts to saturate. Thus, even if there were more objects, it seems unlikely that weight-based scaling would succeed in providing equal image quality.
Another limitation of the paper is that only a Butterworth filter was investigated, and the post-reconstruction filtering cutoff frequency was optimized over the range from 0.6 to 0.15 cycles/cm with 0.01 cycles/cm increment. We did this search for all six AA levels; the cutoff frequency of the 3D post-reconstruction Butterworth giving the highest AUC was deemed optimal. The optimal cutoff frequency was found to be 0.6 cycles/cm for all the AA levels.
This paper provides data to support the use of girth instead of weight in specifying AA. The finding is consistent with intuition that girth at the location of the kidney would be a better parameter than weight to use for patient-specific dosing. To understand this, consider that an increase in patient weight can be manifested by changes in size in areas that are distant from the organ being imaged and thus have little effect on image quality. For example, increased leg length would increase weight, but would not cause additional attenuation, scatter or loss of resolution. By contrast, change in girth at the position of the kidney has a direct effect on attenuation, scatter, and resolution (by increasing the radius of rotation). Based on this argument, and supported by the data in Figure 7, girth would seem to be a reasonable parameter to consider in developing new administered activity guidelines for Tc-99m DMSA. In addition, we have also investigated correlations between rankings of AUC and height percentile for each age. However, we did not find robust relationships with respect to height.
One alternative parameter to girth that could be explored is body mass index (BMI). This is readily calculated from height and weight and would not require an additional measurement. This has the additional advantage that it could likely be calculated prior to the patient arriving in the clinic based on the height and weight in the patient’s medical record. However, the relationship between BMI and girth as a function of height is not one-to-one, and there is not as direct a relationship to the image degrading factors mentioned above as there is for girth. Nevertheless, this remains a parameter that could be considered in the development of new guidelines.
V. CONCLUSIONS
This study demonstrates that the current consensus guidelines, which scale activities based on patient weight subject to minimum and maximum activity constraints, do not give the same image quality for patients with different weights. Further, this study provides a relationship between diagnostic image quality, as measured by AUC, and AA for 99mTc-DMSA pediatric SPECT for a set of phantoms having different weights. These fitted functions could potentially be used to determine the appropriate AA for desired level of image quality for a given patient weight. However, the data suggest that patient girth at the level of the kidney may be a better factor to use than weight when selecting AA for this imaging task.
Acknowledgements
This work was supported by National Institute of Biomedical Imaging and Bioengineering of the National Institutes of Health under grant number R01-EB013558. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Footnotes
Disclosure statement
No potential conflicts of interest relevant to this article exist.
References
- 1.Treves ST, Davis RT, and Fahey FH, Administered radiopharmaceutical doses in children: a survey of 13 pediatric hospitals in North America. J Nucl Med, 2008. 49(6): p. 1024–7. [DOI] [PubMed] [Google Scholar]
- 2.Gelfand MJ, et al. , Pediatric radiopharmaceutical administered doses: 2010 North American consensus guidelines. J Nucl Med, 2011. 52(2): p. 318–22. [DOI] [PubMed] [Google Scholar]
- 3.Treves ST, et al. , 2016 Update of the North American Consensus Guidelines for Pediatric Administered Radiopharmaceutical Activities. J Nucl Med, 2016. 57(12): p. 15N–18N. [PubMed] [Google Scholar]
- 4.Fahey FH, et al. , Effects of Image Gently and the North American guidelines: administered activities in children at 13 North American pediatric hospitals. J Nucl Med, 2015. 56(6): p. 962–7. [DOI] [PubMed] [Google Scholar]
- 5.Sgouros G, et al. , An approach for balancing diagnostic image quality with cancer risk: application to pediatric diagnostic imaging of 99mTc-dimercaptosuccinic acid. J Nucl Med, 2011. 52(12): p. 1923–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Fahey FH, et al. , Dose Estimation in Pediatric Nuclear Medicine. Semin Nucl Med, 2017. 47(2): p. 118–125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.O’Reilly SE, et al. , A risk index for pediatric patients undergoing diagnostic imaging with (99m)Tc-dimercaptosuccinic acid that accounts for body habitus. Phys Med Biol, 2016. 61(6): p. 2319–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Plyku D, et al. , Pharmacokinetic modeling of pediatric imaging agents. Journal of Nuclear Medicine, 2014. 55(supplement 1): p. 1134–1134. [Google Scholar]
- 9.Li Y, et al. , A projection image database to investigate factors affecting image quality in weight-based dosing: application to pediatric renal SPECT. Phys Med Biol, 2018. 63(14): p. 145004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Li Y, et al. Development of a defect model for renal pediatric SPECT imaging research. in Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC), 2015 IEEE 2015. IEEE. [Google Scholar]
- 11.Frey EC, Ju ZW, and Tsui BMW, A Fast Projector-Backprojector Pair Modeling the Asymmetric, Spatially Varying Scatter Response Function for Scatter Compensation in Spect Imaging. Ieee Transactions on Nuclear Science, 1993. 40(4): p. 1192–1197. [Google Scholar]
- 12.Frey EC and Tsui BMW, A new method for modeling the spatially-variant, object-dependent scatter response function in SPECT. 1996 Ieee Nuclear Science Symposium - Conference Record, Vols 1–3, 1997: p. 1082–1086. [Google Scholar]
- 13.Du Y, et al. , Combination of MCNP and SimSET for Monte Carlo simulation of SPECT with medium- and high-energy photons. IEEE Transactions on Nuclear Science, 2002. 49(3): p. 668–674. [Google Scholar]
- 14.Du Y, Tsui BMW, and Frey EC, Model-based compensation for quantitative I-123 brain SPECT imaging. Physics in Medicine and Biology, 2006. 51(5): p. 1269–1282. [DOI] [PubMed] [Google Scholar]
- 15.Du Y, Tsui BMW, and Frey EC, Model-based crosstalk compensation for simultaneous Tc-99m/I-123 dual-isotope brain SPECT imaging. Medical Physics, 2007. 34(9): p. 3530–3543. [DOI] [PubMed] [Google Scholar]
- 16.He B, et al. , A Monte Carlo and physical phantom evaluation of quantitative In-111SPECT. Physics in Medicine and Biology, 2005. 50(17): p. 4169–4185. [DOI] [PubMed] [Google Scholar]
- 17.Mok GSP, et al. , Development and Validation of a Monte Carlo Simulation Tool for Multi-Pinhole SPECT. Molecular Imaging and Biology, 2010. 12(3): p. 295–304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Rong X, et al. , Development and evaluation of an improved quantitative (90)Y bremsstrahlung SPECT method. Med Phys, 2012. 39(5): p. 2346–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Song N, et al. , Development and evaluation of a model-based downscatter compensation method for quantitative I-131 SPECT. Med Phys, 2011. 38(6): p. 3193–204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Song N, et al. , EQPlanar: a maximum-likelihood method for accurate organ activity estimation from whole body planar projections. Phys Med Biol, 2011. 56(17): p. 5503–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wang WT, et al. , Parameterization of Pb X-ray contamination in simultaneous Tl-201 and Tc-99m dual-isotope imaging. IEEE Transactions on Nuclear Science, 2002. 49(3): p. 680–692. [Google Scholar]
- 22.Myers KJ and Barrett HH, Addition of a channel mechanism to the ideal-observer model. J Opt Soc Am A, 1987. 4(12): p. 2447–57. [DOI] [PubMed] [Google Scholar]
- 23.Yao J and Barrett HH, Predicting Human-Performance by a Channelized Hotelling Observer Model. Mathematical Methods in Medical Imaging, 1992. 1768: p. 161–168. [Google Scholar]
- 24.Sankaran S, et al. , Optimum compensation method and filter cutoff frequency in myocardial SPECT: a human observer study. J Nucl Med, 2002. 43(3): p. 432–8. [PubMed] [Google Scholar]
- 25.Gifford HC, et al. , Channelized hotelling and human observer correlation for lesion detection in hepatic SPECT imaging. J Nucl Med, 2000. 41(3): p. 514–21. [PubMed] [Google Scholar]
- 26.He X, Links JM, and Frey EC, An investigation of the trade-off between the count level and image quality in myocardial perfusion SPECT using simulated images: the effects of statistical noise and object variability on defect detectability. Physics in Medicine and Biology, 2010. 55(17): p. 4949–4961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Elshahaby FEA, et al. , Factors affecting the normality of channel outputs of channelized model observers: an investigation using realistic myocardial perfusion SPECT images. Journal of Medical Imaging, 2016. 3(1). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Li X, et al. , Use of Sub-Ensembles and Multi-Template Observers to Evaluate Detection Task Performance for Data That are Not Multivariate Normal. IEEE Trans Med Imaging, 2017. 36(4): p. 917–929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Burgess AE, Li X, and Abbey CK, Visual signal detectability with two noise components: anomalous masking effects. J Opt Soc Am A Opt Image Sci Vis, 1997. 14(9): p. 2420–42. [DOI] [PubMed] [Google Scholar]
- 30.Metz CE, Herman BA, and Shen JH, Maximum likelihood estimation of receiver operating characteristic (ROC) curves from continuously-distributed data. Stat Med, 1998. 17(9): p. 1033–53. [DOI] [PubMed] [Google Scholar]
- 31.Barrett HH and Myers KJ, Foundations of image science Wiley series in pure and applied optics. 2004, Hoboken, NJ: Wiley-Interscience; xli, 1540 p. [Google Scholar]
- 32.Barrett HH, Objective Assessment of Image Quality - Effects of Quantum Noise and Object Variability. Journal of the Optical Society of America a-Optics Image Science and Vision, 1990. 7(7): p. 1266–1278. [DOI] [PubMed] [Google Scholar]