Machine Learning in Drug Discovery and Development Part 1: A Primer

Abstract

Artificial intelligence, in particular machine learning (ML), has emerged as a key promising pillar to overcome the high failure rate in drug development. Here, we present a primer on the ML algorithms most commonly used in drug discovery and development. We also list possible data sources, describe good practices for ML model development and validation, and share a reproducible example. A companion article will summarize applications of ML in drug discovery, drug development, and postapproval phase.

Application of artificial intelligence (AI; Box 1) in drug discovery and development has emerged as a key promising pillar. Its importance has been consolidated by the need of new strategies to overcome the high failure rate in drug development of ~ 90%.1, 2 As such, pharmaceutical companies are beginning to explore how various AI frameworks can supplement or be integrated into the current drug discovery and development processes.1

Box 1. History of AI.

AI was pioneered by British mathematician Alan Turing in the 1950s with the idea of training a machine to think like a human. He introduced the Turing test, which has been used to determine if a machine has intelligence.3 The first demonstration of the fundamental concept of AI was introduced by American electrical engineer Arthur Samuel. Mr. Samuel developed the self‐learning Samuel Checkers‐Playing Program, which won the 1952 world championship.4, 5 He also first coined the term machine learning, a subgroup within AI, in 1959.6

In 2011, Apple Inc. (Cupertino, CA) introduced virtual AI assistant “Siri” on iPhone 4S, which uses a natural‐language user interface to return contextual information and performance according to users’ requests.7 Google Brain, which is an AI research team at Google (Mountain View, CA), trained a neural network to recognize a cat from randomly selected YouTube videos in 2012.8 In 2014, a chatbot “Eugene Goostman” passed the Turing test at a contest by convincing 33% of the judges.9 In 2015, the first formal match occurred between AlphaGo10, an AI‐based software developed by Google DeepMind Technologies Limited, and a professional human Go player; AlphaGo won 5–0.

An executive order on maintaining American leadership in AI was issued in early 2019.11 The American Medical Association has supported the use of AI in medical practice and training since mid‐2019.12

Machine learning (ML), a branch of AI (Figure 1), is “based on the idea that systems can learn from data, identify patterns and make decisions with minimal human intervention.”13 AI frameworks may contain several different ML methods applied together. For example, an AI framework in drug discovery may optimize drug candidates through a combination of ML models that predict favorable physicochemical characteristics (e.g., solubility and permeability), pharmacokinetics (PK), safety, and possibly efficacy.14, 15, 16, 17, 18, 19, 20, 21 An AI framework in drug development may use ML methods to prescreen covariates in PK‐pharmacodynamic data, identifying patient subpopulations, predicting clinical outcomes, informing clinical trial design, and investigating novel therapeutic purpose for existing drugs (i.e., drug repositioning or drug repurposing).22, 23, 24, 25 However, ML methods have been utilized more often in drug discovery than in development.

Figure 1.

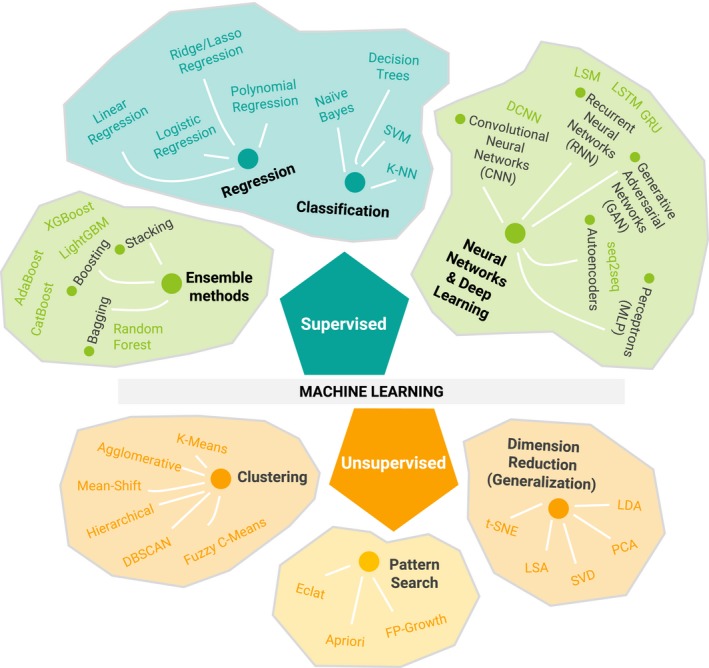
Overview of the types of machine learning and algorithms. Only the most commonly used algorithms are described in this tutorial. AdaBoost, adaptive boosting; DBSCAN, density‐based spatial clustering of applications with noise; DCNN, deep convolutional neural networks; Eclat, equivalence class transformation; FP‐Growth, frequent pattern growth; GRU, gated recurrent unit; K‐NN, K‐nearest neighbors; LDA, linear discriminant analysis; LightGBM, light gradient boosting machine; LSA, latent semantic analysis; LSM, liquid state machine; LSTM, long short‐term memory; MLP, multilayer perceptron; PCA, principal component analysis; seq2seq, sequence‐to‐sequence; SVD, singular value decomposition; SVM, support vector machine; t‐SNE, t‐distributed stochastic neighbor embedding; XGBoost, extreme gradient boosting.

ML can support a range of different drug discovery and development applications. To be a fit‐for‐purpose approach, the application of ML should be guided by answers to the following three questions: (i) What is the drug discovery and/or development need? (ii) What ML methods are most appropriate to address this need? and (iii) What data can be used to support these ML methods? Data quality is as critical as data quantity in that data should be unbiased and diverse to support robust models. In addition, researchers should prepare to validate and interpret the models and results.

This work consists of two parts. The first part is a tutorial on the most commonly used ML algorithms along with possible data sources, good practices for ML model development and validation, and a reproducible example. The second part, published in a companion article, is an overview of applications of ML in drug discovery, drug development, and the postapproval phase.

Data sources for building ML models

The amount of data being generated today is staggering. An estimated 2.5 quintillion bytes are created every single day.26 However, it is not the quantity of data but it is the opportunity to generate knowledge that matters most. Some common examples of large data sets include chemical structure data, gene expression and genetic data, high throughput in vitro data, clinical trial data, and electronic medical records. Data may be freely available public data, commercially available data, internal companies’ data, or data shared among participating institutions.27 The reader can refer to Conrado et al.28 for examples of individual data‐sharing initiatives.

“Big data” and advances in technologies for data science have paved the way for the applications of ML in drug discovery and development. Recent advances in ML technology, in turn, allow us to make use of large data sets on a scale that was previously unrealizable. A rapidly emerging field is the use of wearable technology and sensors, which provide a wealth of real‐time data that can be leveraged to assess patient health and detect trends for potential health risks.29 For example, wearable sensors that can be adhered directly to patients’ body surfaces can provide detailed movement data.30 Alternatively, small, wearable devices, such as sensors embedded into a ring or wristband, enable pulse wave, arterial blood flow, physical activity, and sleep pattern data to be monitored continuously.31, 32 Technological advances in computer‐aided diagnosis and detection systems created the fields of radiomics and radiogenomics.33, 34 These advances enable researchers to convert medical images into quantitative data7, 23, 24 that can be used to develop ML models to generate hypotheses and inferences as well as support decision making beyond visual interpretation.35 Postmarket surveillance data such as adverse drug reaction (ADR) reports from the U.S. Food and Drug Administration (FDA) Adverse Event Reporting System36 are also vital sources in that they can inform drug discovery and development by back translating to the molecular mechanisms and targets of the adverse events.37 The Adverse Event Reporting System contains rich sources of ADR information submitted voluntarily by drug manufacturers, healthcare professionals, and consumers in the United States. More than 9 million ADR reports were submitted from 1969 to the present, and the number of reports increases every year.

Data can be either structured or unstructured.28 Structured data could occur through a user‐friendly online data repository including a description of the data, tools for data querying, a data dictionary, summary tables, and some means of support.28 Examples of structured data are the Alzheimer's Disease Neuroimaging Initiative (ADNI), the Parkinson's Progression Markers Initiative (PPMI), and the Coalition Against Major Diseases (CAMD) consortium database.28 Unstructured data as the name suggests are everything else. Unfortunately, most data are unstructured and require substantial amounts of time and effort to curate. Within drug development, efforts have been underway through the Clinical Data Interchange Standards Consortium (CDISC) to standardize clinical research data.38 The Coalition for Accelerating Standards and Therapies (CFAST; https://c-path.org/programs/cfast) was initiated in 2012 as a partnership between CDISC and the Critical Path Institute (C‐Path) to accelerate clinical research by creating and maintaining therapeutic area data standards. Integrated and standardized data sets can catalyze biomedical discoveries and drug development28 as well as help the regulatory agencies to review new drug applications more efficiently. These standardized structured data sets are ideal for use as “training data sets” (refer to the ML Algorithms section) in ML. Together, data standardization and ML modeling could revolutionize drug discovery and development in these and other disease areas.

ML algorithms

ML algorithms may involve fitting data to statistical models or the algorithms may be more heuristic in nature. Unlike traditional model fitting, the goal of an ML algorithm is usually to make accurate predictions about outcomes for new data when the covariates are provided. The parameters returned by the model are generally of secondary interest, and statistical hypothesis testing is not usually performed.

Supervised ML

A supervised ML algorithm requires an input data set, which can be split into a “training” data set and a “test” or “validation” data set. The process of fitting (or “calibrating”) the model to the training data set is called “model training.” The “trained” ML model can then be validated—having its predictive performance assessed—using the test or validation data set. The “validated” ML model can then be applied to new data sets (i.e., not used for model development) to make predictions or decisions based on the new data set covariates.

With supervised ML, the training data set contains both covariates and outcomes. Such a data set is called “labeled”39, 40 because it includes the outcomes. The outcome may be continuous or categorical. After a supervised ML model is trained, it can be used to predict outcomes for new data set based on its covariates. Several widely used algorithms in supervised ML are described in the next sections.

Linear and logistic regression

Multiple linear regression is a widely used algorithm in supervised ML when a continuous outcome varies linearly with the independent variables or covariates. An outcome or dependent variable can be represented as follows:

$$Y={\beta }_0+{\beta }_1{x}_1+\dots +{\beta }_n{x}_n$$

where $Y$ is the outcome prediction, ${\beta }_{1-n}$ are the coefficients and $x_{1-n}$ are the covariates. Ordinary least squares, which is based on the principle of maximum likelihood, is the simplest and most common way of estimating the coefficients. This model is not designed to handle strong collinearities between covariates. Severe multicollinearity greatly reduces the precision of the estimated coefficients. In such cases, principal component analysis may be used to reduce the number of features to a smaller set of unrelated components.

Logistic regression is a widely used supervised ML method for modeling binary outcomes, such as yes/no, success/failure, and survived/died. The logistic regression model estimates the probability that the outcome belongs to a particular binary category. The probability curve is sigmoid or S‐shaped and constrained between 0 and 1.

$$P\left(Y=1\right)=\frac{1}{1+e^{-\left({\beta }_0+{\beta }_1{x}_1+\dots +{\beta }_n{x}_n\right)}}.$$

Ridge regression, least absolute shrinkage and selection operator (LASSO), and elastic net

Some data sets, such as genetic data sets, have large numbers of features (covariates) relative to the number of observations, but most features are expected to have minimal association with the outcome. Including all of the features in a linear or logistic regression model would add noise to the model and potentially result in a nonidentifiable model when the number of features is greater than the number of observations. Instead of reducing the number of features for multiple linear regression, we can fit a model starting with all predictors using a technique that constrains the coefficient estimates, or equivalently, that shrinks the coefficient estimates toward zero. The two best‐known techniques for shrinking the regression coefficients toward zero are ridge regression and LASSO.41 Multiple linear regression is the underlying model used for these techniques. However, the fitting procedure is not based on maximum likelihood. Instead, these techniques work by applying a “penalty” to the fitting procedure that depends on the magnitude of the coefficients. All coefficients are usually penalized equally. Therefore, before applying ridge regression or other shrinkage methods, the analyst will typically rescale the covariates to prevent covariates with numerically wider ranges from being excessively penalized.

Ridge regression shrinks the regression coefficients by imposing a penalty on their size. Instead of minimizing only the residual sum of squares, as ordinary least squares does, ridge regression minimizes:

$$Y-\beta X^2+\gamma {\beta }^2.$$

Here, the first term is simply the residual sum of squares. In the second term, $\gamma$ is a weight factor, and ${\beta }^2$ is the sum of the squared coefficients. Thus, when $\gamma =0$ the ordinary least squares coefficients are returned, and when $\gamma =\infty$, the coefficients will approach zero. However, a disadvantage is that it includes all predictors in the final model. As with the ridge regression, the LASSO shrinks the coefficient estimates toward zero:

$$Y-\beta X^2+\lambda {\beta }_1.$$

Here, in the second term, $\lambda$ is a weight factor, and ${\beta }_1$ is the sum of the absolute values of the coefficients. This penalty has the effect of forcing some of the coefficient estimates to be exactly equal to zero. LASSO performs variable selection, yielding models that involve only a subset of the variables. As a result, models generated from the LASSO are generally much easier to interpret than those generated from the ridge regression. For a data set with N observations, LASSO will select at most N features.42 LASSO can also be adapted to fit logistic regression models.

Elastic net is another shrinkage‐based method that linearly combines the penalties from ridge and LASSO to minimize:

$$Y-\beta X^2+\gamma {\beta }^2+\lambda {\beta }_1.$$

Compared with LASSO, the elastic net can yield a model including more features than number of observations, but with possibly far fewer than would be selected via the ridge penalty alone. In addition, the elastic net exhibits a grouping effect, where highly correlated features will have similar estimated coefficients.

Decision trees and random forest

Decision trees41, 43, 44, 45 are a commonly used group of nonlinear ML methods. Each model is a set of rules organized in the form of a tree. Starting at the base or “root node,” the algorithm selects a “branch” based on the decision rule at the root node. The decision rule is generally based on a single covariate and a specified threshold (e.g., if the third covariate is greater than five, take the left branch). The algorithm then reaches the next node and follows the next decision rule. Eventually, the algorithm reaches a “leaf node,” which represents a specific output decision, returned as a result. Decision trees can be used for building both classification models for making qualitative predictions and regression models for making quantitative predictions. One reason for the popularity of single decision trees is their ease of interpretation and representation. However, they are outperformed by more advanced ML algorithms, such as random forest or gradient boosting modeling.

Random forest41, 46 is a method that creates a large collection of decision trees, where each decision tree makes a prediction or “vote” for a certain outcome. For each tree, typically one third of the training data set is randomly selected and set aside, and the remaining two thirds of the training data set is used for model development. When these decision trees are being built, each time a split in a tree is considered, a random sample of predictors is chosen as split candidates from the full set of predictors. A single predictor and a corresponding decision rule threshold are identified that maximize the accuracy of the decision tree. When all of the trees are completed, the model is ready to make predictions about new data. The prediction is defined by majority voting from this collection of decision trees. To evaluate the accuracy of the model, the trained forest can be used to predict the remaining one‐third of the observations and calculate the out‐of‐bag (OOB) error.

Random forest is a type of ensemble modeling because it involves combining multiple ML models to improve the overall performance of the model. Ensemble models generally combine the results by voting or taking the mode, mean, or weighted mean of the results from different models. More advanced techniques include bagging and boosting. Bagging involves creating random subsamples, or bootstrapping, of training data with replacement and building a model for each subset. For boosting, see the Gradient Boosting section.

Gradient boosting

Gradient boosting41, 47 differs from bagging methods in that the trees are trained and combined sequentially. This algorithm generates models by computing a sequence of trees in which each successive tree is built from the prediction residuals of the preceding tree. A simple partitioning of the data is determined at each step in the boosting tree algorithm, and the deviations of the observed values from the respective residuals for each partition are computed. Given the preceding sequence of trees, the next tree will then be fitted to the residuals to find another partition that will further reduce the error in the model.

Neural networks (NNs)

NNs48 are composed of units called artificial neurons. Each connection between neurons can transmit a signal to another neuron. All neurons have multiple inputs and one output. The receiving neuron can process the signals and then signal downstream neurons connected to it. Each input is associated with a weight that varies as learning proceeds, which can increase or decrease the strength of the signal that is sent downstream. A general formula for the output Y of a neuron is:

$$Y=f\left(\sum _i{W}_i{X}_i\right).$$

where f is a specified function, X _i is the i ^th input, and W _i is the weight associated with the i ^th input. Neurons are typically organized in the following three types of layers: (i) the input layer (i.e., the bottom layer), where the predictors are entered; (ii) the hidden (middle) layers; and (iii) the output layer (i.e., the top layer), where the predictions are generated.

Deep NN (DNN), also known as deep learning, refers to a model with more than one hidden (middle) layer. Recent advances of DNN‐based algorithms have been implemented in various fields from automatic speech recognition49 to medical image recognition.50 DNNs can be further categorized based on model architectures; convolution NN, recurrent NN, and long short‐term memory‐based recurrent NN.

Genetic algorithm

The genetic algorithm is inspired by the process of natural selection and belongs to the larger class of evolutionary algorithms. The genetic algorithm works as following:22

• First, the solution space is defined and corresponds to a set of models to test.

• The search for the best model is initialized by randomly creating an initial population, defined as a set of individuals with a genome (model structures). These model structures can then be fitted to the data, and the best model is identified based on a goodness‐of‐fit statistic criterion (e.g., Akaike information criterion).

• Then, the next generation can be created by first selecting sets of “parents.” Parents are selected randomly, with replacement and probability of selection proportional to fitness.

• Next, the genomes of the parents are lined up and “crossover” occurs, i.e., some user‐defined fraction of the parent sets (e.g., 60%), at a single, random location in the genome. For instance, if the genome contains four genes (model characteristics: one compartment PK model + first‐order absorption + presence of lag time + proportional residual error), then a 50% split would generate the left part with “one compartment PK model + first‐order absorption” and the right part with “presence of lag time + proportional residual error.” Then, the left part of the first parent is combined with the right part of the second parent and vice versa.

• Subsequently, a mutation is randomly applied based on a prespecified small proportion. For instance, the “presence of lag time” feature is reversed to “absence of lag time.”

• This process is repeated until no further improvement is seen (i.e., a model with an improved goodness‐of‐fit criterion is no longer obtained).

A reproducible example can be found in Bies et al.,22 where a genetic algorithm–based, hybrid ML approach to model selection has been developed and applied.

Unsupervised ML

Unsupervised ML deals with unlabeled data51 defined as data that include the covariates, but not the outcomes. This technique is used to identify patterns and associations between data points. Dimensionality reduction methods may be applied as a first step in the analysis.52 Principal component analysis is among the most widely used dimensionality reduction techniques. In addition, the data may also be normalized to facilitate comparison between data points. Several widely used algorithms in unsupervised ML are described in the next sections.

K‐means

K‐means groups data points with similar properties or features into a fixed number of clusters (K). K‐means is commonly applied to gene expression or clinical lab data to identify similar groups of samples or subjects. The algorithm can be initialized by randomly selecting K “centroids” from the data set. A centroid is a data point (imaginary or real) at the center of a cluster, i.e., the mean value of the points assigned to the cluster. Hence, “means” in the “K‐means” expression corresponds to the centroid.53 Each data point is assigned to the nearest cluster. Each centroid is then updated (i.e., iteration) so that the total within‐cluster variation is minimized. There are several K‐means algorithms, and the standard algorithm defines the total within‐cluster variation as the sum of squared Euclidean distances between points and the corresponding centroid.54 Most often, a local optimum is achieved; hence, it is suggested to run the algorithm multiple times with randomized starting centroids for better outcome. Systematically, the steps are the following:54

1. Define K, the number of clusters to be created.

2. Select randomly K centroids from the data set (i.e., the initial cluster centers).

3. Assign each data point to the nearest centroid based on the Euclidean distance between the point and the centroid.

4. Recompute the centroid for each of the K clusters by calculating the new mean value of all the data points in the cluster.

5. Iteratively minimize the sum of squared Euclidean distances. Repeat Step 3 and Step 4 until the centroids do not change.

To select the number of clusters, the total within‐cluster distance to the centroid may be compared for increasing K values. The point where the average within‐cluster distance to the centroid levels off may be chosen as the value of K.

K‐means is relatively fast, robust, and easy to interpret. It is also relatively efficient when the data set are well separated from each other. However, some drawbacks of K‐means include (i) a priori selection of K, (ii) distinguish data that are close or overlapping, (iii) obtain different results produced by non‐linear transformation, and (iv) inability to handle categorical data.

Hierarchical

This algorithm creates a set of nested clusters structured as a hierarchical tree. Unlike K‐means, hierarchical clustering starts with considering each observation as an individual cluster. Then iterations are performed to merge similar clusters until all the clusters are merged. A dendrogram (i.e., a tree diagram that shows the taxonomic relationship between covariates) is obtained to show the hierarchical relationship between the clusters. This technique is also known as agglomerative hierarchical clustering. Another less commonly used hierarchical technique is called divisive hierarchical clustering, where all the observations are grouped into one cluster and then successively split into multiple clusters.

Hierarchical clustering offers several advantages including easy implementation and the lack of a need to specify the number of clusters. However, limitations include sensitivity to outliers and greater computation resource requirements.

Active learning

Active learning is a ML method where the algorithm can interactively request labeled data to train themselves. Active learning can be used when a full labeled data set has not yet been collected and cost constraints prevent full labeling. For example, if one wishes to predict affinity to a protein based on selected chemical features, it may be too expensive to run experiments with a full compound library. An active learning algorithm would design a series of experiments to learn the relationship between the chemical features and affinity. Each experiment would be designed based on the previous data obtained. The algorithm would select the most informative compounds for future experiments. Although there are many different approaches to active learning, these methods often use a supervised ML algorithm to process the data that have already been collected.55 To select new data for labeling, an active learning algorithm may identify unlabeled samples that have the greatest prediction uncertainty. These samples will be more informative compared with samples with high prediction certainty, thus allowing greater improvement in prediction accuracy.

Good practices for ML model development and validation

Data curation and preparation

Every ML experiment begins with data curation on the data required to build a model (i.e., training data); indeed, a common saying is that a model will be only as good as the data from which it is derived.56, 57 Modelers typically rely on data generated (and, more recently, even compiled) by other scientists. Therefore, data quality is often highly dependent on the data providers. Although often an overlooked aspect, data curation and preparation are cornerstone to develop reliable models. Common issues related to data curation and preparation are described in the next sections. Good practices for the curation of chemical data sets in drug discovery are presented in Box 2.

Box 2. Good practices for curation of chemical data sets in drug discovery.

The curation of chemical data sets involves removing duplicates and checking that the molecular representations are appropriate and correct. The required degree of curation depends on the molecular predictors that will be used in the models. For instance, if only conformation‐independent descriptors are to be used, geometry optimization or considerations on the stereochemistry of the training samples might be avoided. The opposite is true if methods that consider molecular geometry are employed. During curation, the modeler may resort to cheminformatic tools that perform some of the previous steps in an automated manner but complementing such automated procedures with manual curation would be ideal. Studies show that, on average, there are two structural errors per medicinal chemistry article.57 In 2008, Young et al. 58 examined six databases (both public and private) to collect structural information on 8,530 chemicals. They observed that the databases had error rates ranging from 0.1% to 3.4% and concluded that small errors in structural representations can lead to significant errors in predictions. Recently, Maeda et al. 59 examined the database of Natural Product Updates 2010 and 2011 published by Royal Society of Chemistry. From the listed literature, the articles reporting newly isolated or structurally updated natural products were individually investigated. Among about 2,500 compounds requiring confirmation in the primary source, 63% showed unclear drawing and not well‐defined chiral atoms, 3.7% had the correct name but the wrong structure, and 0.4% showed discrepancies to nuclear magnetic resonance data. The previous examples, which coincide with our experience managing data sets from online resources, illustrate the importance of prior curation before applying ML methodologies.

When intending to build ligand‐based models for virtual screening applications, the following specific considerations must be taken into account: (i) Ideally, the dependent variable (i.e., the modeled biological activity) should cover at least two or three orders of magnitude,60, 61, 62 from the least to the most active compound; (ii) the available biological data on the training set compounds should, preferably, be uniformly distributed across the range of activity, or at least follow a normal distribution, and the same applies to the independent variable60 (in the case of classificatory models, a balanced training set is recommended to avoid bias toward the prediction of a particular category); and (iii) the biological activities of all the training examples should be of similar quality. Preferably, they should have been measured in the same laboratory using the same conditions61, 62 so that the variability in the measured biological activity only reflects treatment differences. To mitigate the influence of noisy data points associated to large experimental errors or variability, data sources should be sensibly examined, disposing of training examples extracted from inadequate or dubious experimental protocols. Some public databases flag bioassay data to warn the user on possible reliability issues. For instance, ChEMBL (https://en.wikipedia.org/wiki/ChEMBL) has incorporated a “Data Validity” column to the interface, which warns from potential or confirmed author errors and bioactivity values outside usual range and missing data, among other issues. Lastly, classification models can be used to lessen the impact of data heterogeneity.

A wide coverage of the activity space allows the model not only to capture essential molecular features needed to elicit the desired activity but also to identify those characteristics that reduce activity and sometimes to detect nonlinear behavior. Data distribution should be studied to avoid poorly populated regions within the examined chemical and biological space as well as densely populated narrow intervals.60 It is often stated that data extrapolation should be avoided; however, interpolation could also be dangerous if too sparsely populated regions exist within the task space. Histograms can be of help for visualizing the distribution of the dependent and the independent variables; however, examination of the multivariate space can reveal empty or poorly occupied regions that a separate analysis of the independent variables may not.63

Concerning data set size, historically it has been said that the number of compounds in the training data set should be at least 20 (in the case of classifiers, at least 10 compounds of each class are required), and at least 10, in each of the test and external evaluation data sets (with a minimum of 5 compounds per class for classifiers). Therefore, the total minimum number of compounds is recommended to be at least 40.57 Nevertheless, a minimum of 150 compounds is preferred when available.

Outliers

Data entry or experimental errors can introduce observations that appear to be inconsistent with the rest of the data. Data curation includes identifying and potentially removing or correcting outliers.64 The modeler could also perform a sensitivity analysis by rerunning the model without the outliers and comparing the model results.

Because many data sets for ML are large, manually identifying and handling outliers may not be possible. However, one may be able to summarize the covariate ranges and visually inspect the distributions to identify outliers or ranges where outliers fall. Heuristic or statistical/mathematical methods to detect and handle data outliers can be performed in a semiautomated manner.65, 66

Missing data

Another challenge with data preparation is handling missing data. Missing data are not unusual, often the result of missed data collection or entry and issues with data processing. Although some ML algorithms, such as random forest, can handle missing data, most algorithms do not perform well with missing data.

There are several strategies to handle missing data. The first step should be to find the number of the missing values and visualize their distribution. Packages in R and Python such as VIM67 and missingno68 can aid in this process. As a rule of thumb, and depending on the importance of the variable, one could consider removing variables with 70% or more missing data, as often they do not provide information toward predictability. For the remaining covariates, the simplest strategy is to remove data points for which any covariate is missing. Another simple alternative is to replace missing values with the median value for continuous variables or with the mode for categorical variables. For time‐dependent variables, similar statistical measures could be considered across time points. Although these strategies allow ML models to be fit by various algorithms, they may also introduce bias.

More sophisticated approaches to handle missing data for time‐dependent variables include model‐based imputation (e.g., regression model of height and weight in children). Another model‐based imputation is the K‐nearest neighbor. The assumption with K‐nearest neighbor is that a missing point value can be approximated by the values of the nonmissing points that are closest to it based on other variables.

For established pharmacometric analyses, several effective strategies to handle missing data have been described in the literature.69 Handling missing data is usually quite challenging, and strategies to address it need to be executed in the context of the problem at hand. Often, a combination of different methods might be required to effectively manage missing data.

Overfitting

Overfitting is gaining explanatory power of the training data by sacrificing generalizability (i.e., predictive ability for relevant data sets not used in the model building). As in any learning task, memorizing peculiarities of the training data (i.e., fitting noise) is discouraged because the goal of learning is to envision a general principle that can be later applied to other scenarios or cases. According to the principle of parsimony, one should use the simplest model or method that delivers the pursued performance level (e.g., avoid using NN or random forest if a single linear model provides an adequate solution). This also means to avoid including more parameters and/or covariates than required.70 Models that explain too well the training data usually experience a sharp drop in performance when making predictions for new data.

Overfitting may be addressed in a retrospective manner (i.e., after model development) using adequate model validation procedures (refer to the Model Validation section) or in a prospective manner (i.e., before model development). The distinction between retrospective and prospective approaches to avoid overfitting is philosophically similar to the distinction between quality control and quality assurance. In the context of computer‐aided drug discovery and development of ML models, both prospective and retrospective approaches are utilized.

Prospective avoidance of overfitting usually involves a rule of thumb regarding the ratio of training observations to covariates included in the model. A minimum ratio of 5:1 is often recommended for multivariate regression approaches,60, 71 but a more conservative ratio of 10:1 is safer.

An approach called regularization can help avoid overfitting when using complex, flexible ML approximations.72 Regularization techniques are neither prospective nor retrospective, but somewhat in the middle, as they are applied “on the fly” while training the model. For example, dropout is a regularization technique used in the context of DNN; it consists of removing or ignoring randomly selected neurons during training, resulting in a network that is capable of better generalization.73 Moreover, for complex ML approaches that require tuning hyperparameters (e.g., learning rate and number of hidden units in a neural network), the models are usually interrogated by a third data set (besides traditional training and holdout sets), which is called a “test data set.” Test data sets can be used for regularization by early stopping, i.e., stopping further training when the error on the validation data set increases, as this is a warning of overfitting.74

Overfitting can depend on the number of tested covariates in the model.75 If covariates are added in an univariate or stepwise manner, then one must consider the inflation of the false positive rate or Type I error as a result of multiple comparison, i.e., the larger the number of covariate models tested, the greater the probability of finding significant covariates by chance. For instance, if one statistical test is performed at the 0.05 α level and the null hypothesis is true, there is a 5% chance of incorrectly rejecting the null hypothesis (i.e., false positive or Type I error); however, if 10 independent statistical tests are performed and the null hypotheses are true, the family‐wise error rate is 40%. If these “false positive” covariates are then included in model, this will contribute to overfitting. We have observed that the use of small random subsets of descriptors (a “random subspace” approximation) is a useful strategy to mitigate the chance of spurious correlations.76 Ensemble learning, which is the combination of individuals models into a meta‐model (e.g., random forest), can also improve model robustness.

Model validation

Model validation is performed to assess the model’s predictive performance when it is used to make predictions for relevant data that were not used for model building. A validated model is expected to make sufficiently accurate predictions for the intended use (i.e., to have sufficient predictive performance). Model validation includes a series of techniques for quantitative assessment of the model stability and predictive power;77, 78 it serves to detect the occurrence of overfitting and chance correlations (when no cause–effect relationship is encoded in the correlation). Validation techniques can be roughly classified into internal and external validation approaches.

External validation

External validation is the most stringent type of model validation.77, 79 Here, the validation data set should be completely independent from the training data set—e.g., a different study altogether. For instance, a model was developed using a sample of subjects with disease X (training data set), and the intended use for the model is to make predictions of any sample of subjects with disease X outside of the training data set. A successful external validation may rely on the following assumptions: (i) the training data set is representative of the general population with disease X, and (ii) the validation data set is a sample of the population with disease X, consequently, a sample of the training data set.

The validation data set must not be used at any stage of the model development or selection. If this condition is not met, then an additional external validation data set would be required as a more definitive proof of the model predictive ability.57 For instance, if multiple models are built and the best models are selected based on the predictive performance for the validation data set, then this is not an external validation. Something similar occurs when a model ensemble is built using a selective ensemble procedure based on the performance on a holdout set; in this case, a third validation sample should be included as solid proof of the ensemble predictive power.

Internal validation

Cross‐validation is one of the most frequently used internal validation procedures. It can be used when an external validation data set is not available or is prohibitively expensive to obtain. However, it is important to understand that internal validation methods can be considered overoptimistic in the sense that a successful internal validation does not guarantee transportability.

The simplest type of cross‐validation is the holdout method.80 The analysis data set is split into two subsets called the training subset and the holdout subset. The model is developed using the training subset only and used to make predictions for the holdout subset. Then, at the minimum, a measure of the residuals (e.g., difference between the observed and model predicted values) could be used to evaluate the model performance. However, evaluation results can have a high variability, depending on which data points end up in the training vs. the test subset.80 Ensuring that the data set is split randomly and relevant variables are balanced among the subsets can help mitigate this issue.

K‐fold cross‐validation is an improvement of the holdout method.80 The training data set is randomly divided into K equal or nearly equal subsets (also called “folds”) and then K‐1 parts of it are systematically used for model development and the remaining fraction is reserved for model evaluation. The process is repeated until each part has been once removed from the training data set. Averaging the predictive performance on the folds allows computing a confidence interval for the parameter estimates, for instance. Although the training data set should be randomly divided into K parts, one may want to ensure that relevant variables are balanced among the K parts. The advantage of this method is that the variability in evaluation results as a result of the splits of the data set is attenuated, with the reduction magnitude being directly proportion to the size of K.80 Leave‐one‐out cross‐validation is a K‐fold cross‐validation with K equal to N, where N is the number of independent experimental units (i.e., subjects within a study). Although K‐fold cross‐validation methods are more computationally intensive, they can be automated using packages such as caret (refer to the Resources section). Cross‐validation has also been implemented in Perl‐speaks NONMEM as part of the stepwise covariate modeling procedure.81

Data leakage

Data leakage is a common and critical mistake when developing ML models. Definitions for data leakage include the following: (i) it is “when information from outside the training data set is used to create the model”82 or (ii) “when the data you are using to train a ML algorithm happen to have the information you are trying to predict.”83 Data leakage may reduce the generalization of the model (overfitting), overestimate model performance, and/or completely invalidate the model. A common example of data leakage is leaking data from the test or validation data set into the training set:82, 83, 84

• Perform data preparation (e.g., variables normalization) or featuring engineer in the whole data set before splitting into training and validation data sets

• In time‐series data:

  1. Sample time points instead of experimental units (e.g., subjects) when setting aside the validation data set

  2. Include time‐varying predictors that are correlated with time and have a similar distribution between the training and validation data sets

Other examples are:82, 83, 84

• Leaking the correct prediction into the test data (e.g., use the response itself as a predictor)

• Leaking of information from the future into the past

• Reversing randomization or anonymization of data that were intentionally included

• Include information from data that is outside of the application scope for the model

Recommendations to avoid data leakage include:82, 83, 84

• Remove incremental identification fields from the data set

• When possible, remove predictors that are correlated with time from time‐series data sets

• Conduct data preparation and feature engineering separately for the training and validation data sets. In the case of cross‐validation, this should be done within the cross‐validation folds

• In time‐series data, perform nested cross‐validation to evaluate performance: select a particular time value (t) and, for instance, establish that all data points lower than (or equal to) t will be part of the training set, and all data points greater than (or equal to) t will be part of the validation data set

• Use an unseen validation data set as a final check

A reproducible example

ML model to guide drug repurposing: Searching for novel inhibitors of putrescine uptake in Trypanosoma cruzi (T. cruzi)

This example is an adaptation of the work of Alberca et al. 76 to obtain a ML model for the subsequent search for drugs against T. cruzi, i.e., putrescine uptake inhibitors. T. cruzi is a parasite that is transmitted to animals and people by insect vectors and causes Chagas disease, a neglected tropical infectious disease endemic to Latin America.85 Putrescine is a low‐molecular‐weight polyamine with crucial importance for the parasite survival.76 Different from humans, T. cruzi cannot synthesize putrescine and must uptake it from the human host via a high‐affinity putrescine transporter; this makes putrescine uptake an attractive target for drugs against T. cruzi.76

Alberca et al.76 developed a linear regression model using small random subsets of descriptors (a random subspace approximation) followed by an ensemble‐learning procedure to combine the results (Supplementary Material S1 ).76 Although we follow the data set preprocessing (i.e., creation of the training and validation data sets) of Alberca et al., a random forest model and a LASSO model are developed for demonstration (Supplementary Material S2 ).

For model development and validation, a data set composed of 256 polyamine analogs (previously assayed against T. cruzi) was compiled from literature.76 The 256 compounds were labeled as “active” or “inactive” according to their half‐maximal effective concentrations against T. cruzi. The active group were compounds with half‐maximal effective concentrations of less than 20 µM (n = 116), and the remaining compounds were considered inactive (n = 140).

For reproducibility, Supplementary Material S3 carries the data set with the 256 compounds (polyamines_dataset.csv). The first column of the data set contains a code for each compound, with the compounds labeled as “AXXX” belonging to the active class, and the compounds labeled as “IXXX” belonging to the inactive class. The second column is a binary dependent variable (named “ActivityClass”) that takes values of 0 for the inactive compounds and values of 1 for the active compounds. Other data set columns are the 3,668 molecular descriptors that were computed with Dragon 6.0 (commercial software, Milano Chemometrics & QSAR Research Group, Syracuse, Italy); these descriptors can be used to evaluate molecular structure‐activity relationships as well as high‐throughput screening of molecule databases.86 Common examples of molecular descriptors are molecular weight and number of atoms.

The procedure for the analysis is the following:

• 1A series of packages required for data analysis purposes are installed
• 2Working directory is set
• 3Data set with the 256 compounds is read
• 4A random and balanced training data set with 87 active and 87 inactive compounds is obtained. The data set consisting of 256 polyamine analogs was divided into two groups using a representative sampling procedure: (i) training data set, which was used to develop or “train” the models, and (ii) test data set, which was used to internally validate the models. Of the compounds, 75% (n = 87) in the active group were kept for the training data set; an equal number of compounds (n = 87) were taken from the inactive group (62.1% of the inactive group). To obtain a balanced training data set, we have undersampled the inactive group. A balanced training data set prevents model bias toward predicting a specific category (i.e., active vs. inactive). In the original article, Alberca et al.76 sampled the 87 compounds from the active and inactive groups through a two‐step clustering approach (hierarchical clustering followed by K‐means) to ensure representativity. For simplicity, we have omitted this sampling approach in this example.

# Obtain a random and balanced training data set with 87 active
# and 87 inactive compounds
set.seed(123)
random_sample <- strata(data = data set, stratanames = "ActivityClass",
size = c(87, 87), method = "srswor" )
training_set <- data set[random_sample$ID_unit, ]

• 5Columns (i.e., variables) with missing values or scarcely informative descriptors (constant or almost constant values) are then removed to yield the final training data set with 1,608 predictors:

# Columns containing non‐available descriptor values for at
# least one compound are removed (i.e., keep only descriptor
# with information available for all compounds)
training_set <‐ training_set[ , apply(training_set, 2,
function(x) !any(is.na(x)))]
# Columns displaying no variance (sd = 0) or almost no variance
# are indexed. Applied to numeric columns only.
index_low_variance <‐ nearZeroVar(x = training_set)
# Remove the previously indexed columns
training_set <‐ training_set[ , ‐index_low_variance]

• 6The remaining 29 active and 53 inactive compounds were assigned to the validation data set. For simplicity, a holdout cross‐validation (internal validation) is being used.

# Create the validation set
testing_set <‐ data set[‐random_sample$ID_unit, ]
testing_set <‐ subset(testing_set, select = names(training_set))

• 7Then we develop a random forest model using default parameters. Among the “randomForest” arguments are “mtry” and “ntree”: (i) mtry is the number of variables tried at each split. The default values are different for classification (sqrt(p) where p is number of predictors) and regression (p/3). (ii) ntree is the number of trees to grow with a default of 500. Note that this should be set to a reasonable large number to ensure that every input row gets predicted at least a few times.

# Develop a random forest model using default parameters
set.seed(123)
rf_model <‐ randomForest(ActivityClass ~ ., data = training_set,
importance = TRUE)
rf_model
# Call:
# randomForest(formula = ActivityClass ~ ., data = training_set, importance = TRUE)
# Type of random forest: classification
# Number of trees: 500
# No. of variables tried at each split: 40
#
# OOB estimate of error rate: 23.56%
# Confusion matrix:
# 0 1 class.error
# 0 72 15 0.1724138
# 1 26 61 0.2988506
# Predicting on validation set and check classification accuracy
pred_testing_rf <‐ predict(rf_model, testing_set, type = "class")
mean(pred_testing_rf == testing_set$ActivityClass)
# 0.804878
table(pred_testing_rf, testing_set$ActivityClass)
# pred_testing_rf 0 1
# 0 43 6
# 1 10 23

• 8In the previous model, a few metrics can be looked at to evaluate this forest classification model, such as OOB estimate of error rate (23.6%) for the training data set and the classification accuracy (80.5%) and confusion matrix for the validation data set—(i) OOB error rate: for each tree, one third of the training data set is randomly selected and set aside (do not confuse it with the validation or holdout data set), hence the trained forest model makes predictions on the remaining one third of the observations and calculate the OOB error; (ii) classification accuracy is the proportion in which the model predicted the correct classification of the validation data set (i.e., the number of correct predictions divided by the total number of predictions); and (iii) the outputted confusion matrix can be interpreted as following:

	True classification
	0	1
Predicted classification
0	True negative (TN)	False negative (FN)
1	False positive (FP)	True positive (TP)

where 0 and 1 correspond to the inactive and active classifications, respectively. From this, the positive predictive value (PPV) and the negative predictive value (NPV) can be derived:

$$PPV=\frac{\mathit{TP}}{TP+FP}=\frac{23}{23+6}=0.793\text{or}79.3\%.$$

$$NPV=\frac{\mathit{TN}}{TN+FN}=\frac{43}{43+10}=0.811\text{or}81.1\%.$$

Hence, PPV is the proportion of positive predictions that are true positives, and NPV is the proportion of negative predictions that are true negatives.

As we mentioned previously, random forest is a type of ensemble modeling in that it combines multiple ML models to improve the overall performance of the model. This along with the fact that the random forest model is interrogated "on the fly" by a test data set (one third of the training data set) make for a powerful ML algorithm. In this example, however, interpreting an ensemble of 500 trees with more than a thousand predictors is rather cumbersome, and the modeler may want to investigate the performance of a simpler model.

Therefore, we also developed a logistic regression model:

# 10‐fold cross‐validation
set.seed(123)
fitControl <‐ trainControl(
method = "cv",
number = 10)
# Logistic regression model training
logistic_model <‐train(ActivityClass ~ .,
data = training_set,
method = "glm",
family = "binomial",
maxit = 100,
trControl = fitControl)
## Predicting on training set and checking classification accuracy
pred_training_logistic <‐ predict(logistic_model, training_set)
mean(pred_training_logistic == training_set$ActivityClass)
# 1
table(pred_training_logistic, training_set$ActivityClass)
# pred_training_logistic 0 1
# 0 87 0
# 1 0 87
## Predicting on testing set and checking classification accuracy
pred_testing_logistic <‐ predict(logistic_model, testing_set)
mean(pred_testing_logistic == testing_set$ActivityClass)
# 0.5609756
table(pred_testing_logistic, testing_set$ActivityClass)
# pred_testing_logistic 0 1
# 0 31 14
# 1 22 15

As we expected, the accuracy of the logistic model in predicting the training data set (100%) is higher than that of the random forest model. However, it performs poorly in predicting the validation data set (i.e., close to a random classification). This is an example of overfitting, as logistic regression cannot handle a large number of covariates.

We then perform a multiple linear regression model with the LASSO algorithm, a relative simple model that can work with many covariates by performing variable selection:

# Format x and y variables as required (x as a matrix, y as a list of # values)
x <‐ as.matrix(training_set[ , ‐1]) # Removes ActivityClass
y <‐ as.double(as.matrix(training_set[ , 1])) # Only ActivityClass
x_test <‐ as.matrix(testing_set[ , ‐1]) # Removes ActivityClass
y_test <‐ as.double(as.matrix(testing_set[ , 1])) # Only ActivityClass
# Use default parameters
# alpha=1 is the lasso penalty, and alpha=0 the ridge penalty.
# Logistic regression (family=’binomial’), as we have a
# binary response. Here, we already perform 10‐fold cross
# validation to choose the best λ.
set.seed(123)
cv_lasso <‐ cv.glmnet(x, y, family = 'binomial', alpha = 1,
type.measure = 'class')
# lengthy output suppressed
# best lambda
cv_lasso$lambda.min
# 0.02904885
# extract only non‐zero coefficients
extract.coef(cv_lasso)
# or equivalent
coef(cv_lasso, s = "lambda.min")[which(coef(cv_lasso,
s = "lambda.min") != 0)]
# results 44 non‐zero coefficients
# Predicting on validation set and check classification accuracy
pred_testing_lasso <‐ predict(cv_lasso, newx = x_test,
type = "class",
s = "lambda.min")
mean(pred_testing_lasso == y_test)
# 0.7682927
table(pred_testing_lasso, y_test)
# y_test
# pred_testing_lasso 0 1
# 0 44 10
# 1 9 19

LASSO selected 40 predictors for the final model. For the validation data set, the classification accuracy, PPV, and NPV are 76.8%, 65.5% and 83.0%, respectively. Although the classification accuracy and NPV are comparable with those of the random forest model, the PPV is lower (65.5% vs. 79.3%). Whether the percent reduction in PPV with LASSO justifies the choice of the random forest model though will depend of the context in which the model will be applied. Herein, the fit‐for‐purpose context goes beyond knowing that the model will be applied to screen for potential drug candidates to treat against T. cruzi. For instance, let us assume that an “active” classification from the model will be the gold standard on deciding whether to translate the compound to a clinical trial in the disease population. In this case, having a model with a higher PPV is probably warranted. On the other hand, if the model will be used to generate a short list of compounds (i.e., getting rid of probable inactive compounds) to be tested in a series of more definitive in vitro tests, then the LASSO would be expected to perform similarly to the random forest model (NPV of 83% and 81% for LASSO and random forest, respectively). In summary, there is no absolute best ML algorithm.

Resources

The popularity and widespread adoption of ML across industry has helped create versatile tools and resources for researchers to build a variety of ML models. For the benefit of our readers, we have compiled a list of open source tools and learning resources related to ML (Table 1). Although the list is not exhaustive, it contains a useful collection of tools based on our experience with building ML models.

Table 1.

Open source tools and learning resources on ML

Resource name	Description	What is this good for?	Reference
Machine Learning in R for beginners	A short tutorial that introduces you to implementing ML using R	To get started with ML using R	87
Stanford ML Tips and Tricks	A quick reference guide to ML concepts and algorithms	A cheat sheet for understanding the concepts and algorithms in ML	88
Kaggle Data sets	A repository of data sets to build ML model	It contains numerous data sets that can be used to build ML models	89
WEKA	An open source user interface ML tools	A great tool to get started with ML	90
Google Colaboratory	It’s an online Python Jupyter notebook environment that requires no setup to use	An easy‐to‐use online tool with no installation necessary on your local machine. It is also a great tool for ML education	91
Caret R package	R package for ML analysis	For researchers comfortable with R who want to perform ML analysis	92

ML, machine learning.

Additional considerations

Models used by ML algorithms may be much more complex than traditional statistical models, thus limiting interpretability. In some cases, the model could be interpreted based on the relative importance of the covariates. This could be determined, for example, by refitting the model without a given covariate and computing the reduction in model accuracy. Another way of interpreting the effect of a covariate is to plot the predicted outcome vs. the covariate, setting the other covariates equal to their medians within the data set.

In pharmacometric analysis, models are often used to simulate new data. However, many ML models do not describe the variability in the outcome as a model parameter, thus making the simulation process more difficult. If new simulated outcome data are required, and the covariates are provided, one approach is to start with the model predictions and add random noise with a variance determined by the model accuracy for the test or validation data set. However, this approach may not work when there are repeated measurements within subjects because model accuracy alone does not distinguish between intersubject and intrasubject variability.

This first part of our work presented a tutorial on ML concepts and technical aspects. With such knowledge, the reader will be able to follow the second part of our work, which is an overview on applications of ML in drug discovery, drug development, and the postapproval phase.

Funding

No funding was received for this work.

Conflict of Interest

The authors declared no competing interests for this work.

Supporting information

Supplementary Material S1.

Supplementary Material S2.

Supplementary Material S3.