Abstract
The increasing accessibility of data to researchers makes it possible to conduct massive amounts of statistical testing. Rather than follow specific scientific hypotheses with statistical analysis, researchers can now test many possible relationships and let statistics generate hypotheses for them. The field of genetic epidemiology is an illustrative case, where testing of candidate genetic variants for association with an outcome has been replaced by agnostic screening of the entire genome. Poor replication rates of candidate gene studies have improved dramatically with the increase in genomic coverage, due to factors such as adoption of better statistical practices and availability of larger sample sizes. Here we suggest that another important factor behind the improved replicability of genome-wide scans is an increase in the amount of statistical testing itself. We show that an increase in the number of tested hypotheses increases the proportion of true associations among the variants with the smallest P-values. We develop statistical theory to quantify how the expected proportion of genuine signals among top hits depends on the number of tests. This enrichment of top hits by real findings holds regardless of whether genome-wide statistical significance has been reached in a study. Moreover, if we consider only those “failed” studies that produce no statistically significant results, the same enrichment phenomenon takes place: the proportion of true associations among top hits grows with the number of tests. The enrichment occurs even if the true signals are encountered at the logarithmically decreasing rate with the additional testing.
Keywords: probability of a true finding, genuine signal, true association, Bayesian analysis, multiple testing, variability of P-values, genome-wide association studies, sequencing studies
Introduction
Transparency of the research process and corroboration of previous findings are basic principles of the scientific method. Transparency, or reproducibility of research refers to the ability of researchers to reproduce findings of a previous study using the same procedures and data as were used in that study. If the findings are real, analysis of independent data sets should corroborate these findings. Replicability refers to independent confirmation of the findings, to the ability to reproduce findings of a previous study, if similar design and procedures are followed but new data are collected. [Bollen et al., 2015; Goodman et al., 2016] Replicated findings are more credible than those that have yet to be independently confirmed. Consistent with the idea that science aims to create generalizable knowledge, robustness of findings to statistical variability between independent data permits researchers to extrapolate conclusions from a sample to a population. The nature and the amount of within and between sample variability vary greatly between disciplines. In the fields of observational research, sources of statistical variability are often difficult to understand or control, and proper statistical analysis can be far from routine, which may explain in part why researchers have had mixed success replicating results of observational studies.[Ioannidis, 2014; Sweeney et al., 2017] Emergence of large, complex data sets, such as next generation sequencing data expanded the role of statistical analysis, but misuse of statistics raised new concerns [Wasserstein and Lazar, 2016], [Greenland et al., 2016]. Publication of a novel scientific result backed by statistical analysis has been traditionally accompanied by a P-value, a commonly used measure of statistical significance. The pressure to publish or perish, coupled with the requirement for results to be significant, may encourage researchers to try various analyses of data, test multiple hypotheses, and report only those P-values that reach statistical significance – a phenomenon coined as P-hacking [Simonsohn et al., 2014]. As a result, P-values have come under fire and non-transparency of multiple testing has become associated with the promotion of false findings [Cumming, 2008; Halsey et al., 2015; Johnson, 2013; Lai et al., 2012; Lazzeroni et al., 2014; Nuzzo et al., 2014].
A field where extensive multiple testing is common is genetic epidemiology. With genome-wide association studies (GWAS) that use modern high-throughput technologies, millions of tests are performed in an agnostic manner in search of genetic variants that may be associated with a phenotype of interest. The best results with the smallest P-values are commonly compared to a genome-wide significance threshold (e.g., association P-value ≤ 5 × 10−8). This criterion protects against the type-I error, but does not readily translate into a measure of reliability for a particular association. Consequently, this approach is likely to omit real associations that do not reach the significance threshold or fall on a borderline. Investigators may choose to use P-values to rank genetic variants in their study and then decide which genetic variants are worthy of further investigation based on subjective and practical considerations in addition to the P-value magnitude. Variability of P-values in replication studies and their inadequacy as predictors of future performance have been questioned [Halsey et al., 2015; Lazzeroni et al., 2014], making these decisions even more challenging. Furthermore, adhering to more stringent genome-wide significance thresholds than those currently in use to safeguard against a lack of replicability may increase sample sizes required to impractical levels, and a gain in power may be counterbalanced by a potential decrease in quality of phenotypic measurements.
Interestingly, despite the shortcomings of P-values as measures of support for a research hypothesis, a high fraction of the borderline genetic associations have been reliably replicated [Panagiotou et al., 2012]. This has been attributed to the adoption of replication practices and improvement of statistical standards, including stringent significance thresholds [Ioannidis et al., 2011]. Here we suggest that another important factor is a drastic increase in the number of tests in a single study compared to the pre-GWAS era, which leads to quantifiable enrichment of the smallest set of P-values in an experiment by genuine signals. Our analysis gives statistical support to the argument that it is illogical to pay a higher penalty for exploring additional, potentially meaningful relations in a study [Rothman, 1990; Williams and Haines, 2011].
The main problem we study here can be illustrated with the quantile-quantile (QQ) plots of P-values from genetic association studies. When there is an excess of small P-values, compared to what would be expected if none of the studied genetic variants had any effect on the outcome, such a plot on a log scale would have a hockey stick shape, with a set of the smallest P-values deviating from the 45◦ line. In actuality, some of these smallest P-values correspond to genuine signals, which we would depict as red, and others to false signals, which we would depict as blue. If we had access to the information about which effects are genuine and to multiple QQ plots from many different genetic studies, we could focus on colors of a single P-value, e.g., the minimum P-value (minP) in each study. Some of the minP’s would be red, others blue, and the average would be a combination of these (purple). The hue of the purple would represent the frequency that the minimum P-value corresponds to a genuine signal, taken across studies. We illustrate such an “averaged” QQ plot in Figure 1 where we overlaid 1,000 QQ plots from 1,000 simulated genetic association studies (details of how this figure was generated can be found in Appendix C). Each smaller dot represents one of the 10 smallest P-values out of 1,000 separate tests in each of these 1,000 association studies (10 × 1,000, so 10,000 dots in total). The color of the smaller dots is either blue or red, depending on whether its P-value corresponds to a false or a true signal. Only a minority of the P-values passed the Bonferroni-corrected multiple testing threshold (note the excess of red dots in the upper right corner of Figure 1 above the green multiple threshold line). The ten larger dots represent averages of the smaller dots. The average is taken over P-values of the same order, e.g., the larger dot on the far right of Figure 1 represents the average of 1,000 minP’s. The shade of purple of the larger dots represents the empirical probability that the i-th ordered P-value, i = 1, …, 10, is a genuine signal. On the average, the top 10 P-values tend to deviate upwards from the 45° line.
Figure 1.
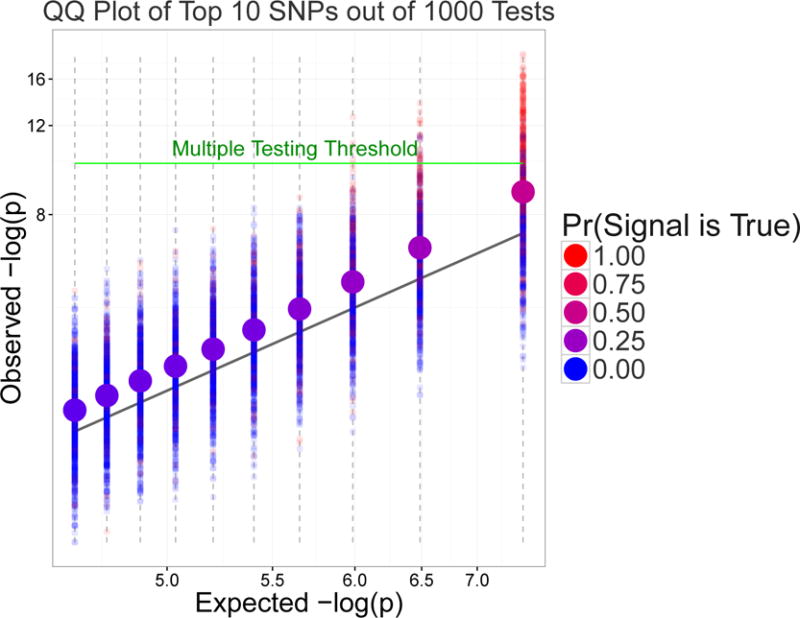
An average QQ plot over 1000 genetic associations studies. Smaller points represent top 10 P-values (on a logarithmic scale) from a given study. Larger points are averages of smaller points. The color of larger points highlights the empirical probability that the i-th ordered P-value, i = 1, …, 10, is a genuine signal.
In a particular study, the probability that a signal is genuine can be estimated using the Bayesian approach. With the Bayesian approach, one must provide prior information or external knowledge, such as the chances that a randomly-selected genetic variant is genuine. After observing data, the posterior probability that a given minP corresponds to a genuine signal can be determined. This probability reflects the degree of assurance and corresponds to a shade of purple somewhere between blue and red, though in reality, the color is either red or blue. Despite this uncertainty due to estimation based on data, the average of these posterior probabilities over multiple genetic studies turns out to be exactly the same as the true degree of the purple shade, provided the prior information is specified without error by the effect size distribution across loci in the genome. This thought experiment provides the intuition for the model that we will evaluate more formally in the remainder of this paper. Through this model, we find that on average, the top-ranking P-values become steadily saturated with genuine effects as more testing is done in every study; even among studies in which no P-values cleared a multiple testing adjusted significance threshold.
Methods
Expected proportion of genuine signals (EPGS) among ordered P-values
It is illustrative to describe our model in terms of a genome-wide association scan, where single nucleotide polymorphisms (SNPs) or more generally, alleles of genetic loci, carry signals that reflect the strength of association with an outcome, for example, the susceptibility to disease. Various effect sizes across the genome occur with different frequencies, that is, the SNP-specific effect size (magnitude of a signal) across the genome forms a distribution. Consider the example of testing which SNPs have an effect size that is at least γ0 in magnitude, and define the null hypothesis H0 that a particular effect size is smaller than γ0 with the alternative H, that it is larger than γ0. This model is an extension of a commonly used, simpler “point-null” model, where non-associated SNPs are assumed to have the zero effect size. The effect size definition we will use is the standardized form of the effect size, due to our focus on ranked P-values. We consider P-values derived from commonly-used test statistics, such as chi-squared and normal Z statistics. The distribution of these P-values and the ranks of sorted P-values from a multiple-testing experiment is a function of the standardized effect size. More specifically, the distribution of P-values for commonly used test statistics depends on the product of the sample size, (N or ) and a measure of effect size, δ, scaled by the variance σ2 (or σ). For example, when the outcome is a case/control classification and the predictor is also binary, the standardized effect size can be expressed in terms of the squared correlation:
| (1) |
or the log of the odds ratio:
| (2) |
where p1 and p2 are frequencies of exposure in cases and controls respectively, is the pooled frequency of exposure, and w is the proportion of cases. The value p2 is determined by the values p1 and OR as p2 = [1 − OR(1 − 1/p)]−1. The standardized effect size in Eq. (2) can be interpreted as the contribution of a given SNP to the additive component of the genetic variance of the trait, assuming the Hardy-Weinberg equilibrium. In this generalization of the point-null model, the effect sizes of all SNPs can be divided into two sets: the null set, Γ0, and the set, ΓA, in which the effects of SNPs in this set that are larger than γ0. The proportion of SNPs that fall into Γ0 can be regarded as the prior probability of H0, π = Pr(H0); then Pr(HA) = 1 − π. In two-sided versions of test statistics, P-values are for the test γ0 = 0, that is, the effect size is assumed to be exactly zero under H0 (point null hypothesis). Even though the computation of a P-value may be carried out under the point H0, we can still define the sets Γ0 and ΓA without the point null assumption (γ0 = 0). We can then ask the question of whether the originating, actual effect size falls into ΓA and by our definition, is genuine.
Having obtained a particular P-value, we can evaluate the probability of a signal to be genuine as the posterior probability Pr(HA | P-value) = Pr(γ ∈ ΓA | P-value) via Bayesian approaches, such as the local false discovery rate (local FDR) [Efron and Tibshirani, 2002; Efron et al., 2001], or other methods based on summary statistics [Kuo et al., 2015; Wakefield, 2007]). This requires prior information, which is summarized in our model by the distribution of the effect size γ across all SNPs in the genome. The computation does not change by the fact that the minimum P-value is selected out of all P-values in a genome-wide scan: the probability Pr(HA | minP) is computed the same way as for a random P-value that was not subject to selection. This highlights the resistance of the Bayesian approach to selection bias [Dawid, 1994; Senn, 2008]. If the effect size distribution is known precisely, these posterior probabilities are exact in the sense that the average Pr(HA | minP) taken across a large number of additional studies from the same population and with the same set of SNPs yields a correct chance that the minimum P-value originates from a genuine signal. Thus, we can talk about the average of such computed probabilities that the minimum P-value stems from a genuine signal. This average (expectation), taken across many replication studies is also equal to the expected proportion of genuine signals (EPGS), due to dichotomization of the effect size distribution into the null and the alternative groups, Γ and ΓA. Extending this from the minimum P-value to the top u smallest P-values, we define EPGS as the expected proportion of genuine signals among the u smallest P-values within a list of k sorted P-values, {p(1), … p(k)}. To draw an analogy, posterior probabilities, such as those estimated by the local FDR are related to EPGS as P-values are related to statistical power.
As noted above, the posterior probability that a signal with the minimum P-value is genuine, Pr(H | minP), does not depend on the number of tests, k, and does not require a correction for multiple testing. If one had access to a large number, B, of independent studies and took the minP from each, the empirical estimate of EPGS would simply be the average:
| (3) |
A more practical equation for EPGS can be derived using the theory of order statistics. It is useful to model a continuous effect size distribution for γ as a finite mixture with a large number of components, t. Then the marginal cumulative distribution function (CDF) of P-values is a weighted sum:
| (4) |
for some weights w1, …, wt. Next, we can partition t effect sizes into Γ0: (γ1, …, γo) and ΓA: (γo+1, …, γt) and define the null hypothesis as H0: max(γ) ≤ γo. To derive the expected probability that a finding is genuine, we let
Further, we assume that k = L + m tests were performed with being a set of L P-values generated by signals from Γ0: (γ1, …, γo) and being a set of m P-values generated from ΓA: (γo+1, …, γt). We use the notation to denote the j-th smallest P-value out of m in total, that originated from an effect in the set ΓA. We apply a similar notation to the distribution functions, for example, denotes the marginal CDF of the j-th ordered P-value among m in total.
Next, we consider the expectation of the probability that T is equal to one. For the minimum P-value,
where q(1:L)(·) is a function such that with being the marginal CDF for the minimum P-value that originated from a signal of the set Γ0, i.e., and is the marginal probability density function (PDF) of P-values over ΓA: (γo+1, …, γt). Further,
where is a quantile function, i.e., , and U is a uniform (0,1) random variable.
Extending this to the higher order statistics, we define
| (5) |
It is worth noting that is simply an expectation of a function of a uniform random variable and thus it is straightforward to evaluate numerically.
Finally, the values from Eq. 5 define the distribution of ordered P-values in the set ΓA. Specifically, is the expected chance that at least j genuine signals will rank among top u smallest P-values. Therefore the expected proportion of genuine signals among u smallest P-values is given by their average:
| (6) |
We would like to draw the reader’s attention to the fact that the theoretical derivation of EPGS reveals its dependency on the number of tests. An apparent paradox is that the average of posterior probabilities in Eq. 3 can be computed without knowing the number of tests in any of B studies and yet the average in its theoretical form in Eq. 5 depends on the number of tests. An intuition for this can be gained by looking at the posterior probability as an expectation, that is, the average of an indicator, E {I(γ ∈ ΓA) | minP}. If a random P-value was substituted in place of the minP, then, by the rule of iterated expectation, EPGS would be equal to the expected value of the prior distribution. However, the distribution of P-values is modified due to selection in a way that depends on the number of tests, k. EPGS would similarly depend on k if it was evaluated over a threshold, α, and corrected for multiple testing as α/k.
Expected effect size of ordered P-values
So far, we have adopted the framework that makes a distinction between effect sizes that are large enough to be considered genuine (i.e., they correspond to the set HA) and a set of smaller effect sizes that correspond to H0. Such dichotomization allows us to directly obtain the theoretical form of EPGS. A conceptually different approach is to model all k tested signals as arising from a single effect size distribution. Such a distribution may be L-shaped and have a sizable spike around zero to reflect the preponderance of signals carrying small effects. In terms of the genome wide association scans, such a distribution reflects the prior knowledge that a randomly chosen SNP has a small effect size with high probability. The advantage of modeling k effect sizes simultaneously is that it allows for thresholding, i.e., to estimate the expectation taken across top hits (smallest P-values) of random experiments and to allow for experiments themselves to be subject to selection. For example, it allows one to theoretically evaluate EPGS as in Eq. 3, but under the condition that none of the B minPs reach the Bonferroni threshold (minP > 0.05/k). The expected effect size for ordered P-values can then serve as a measure of enrichment of top hits by genuine signals. This measure is not the same as the expected value of the observed (estimated) effect sizes for top hits, because the latter is subject to selection bias, the so-called “winner’s curse” and thus overestimates the actual average effect size.
To estimate the expected effect size corresponding to the j-th smallest P-value, P(j:k), we let X(i:k) denote the test statistic that corresponds to it. In terms of the statistics, X(i:k) is the i-th largest value, i = k − j + 1. For the thresholding process just described, we are interested in the expectation for statistics whose respective P-values did not reach the critical value α/k. For positively-valued statistics, such as the chi-squared, the expected value under thresholding can be derived as:
| (7) |
where Q(·) is the inverse CDF of the test statistic. Using this fact, the expectation for the effect sizes that correspond to this i-th largest thresholded statistic can now be approximated as:
| (8) |
For a fixed value of i, the expectation in Eq. (7) increases with k, reflecting the winner’s curse phenomenon. A simple function of k can be obtained by applying the monotone transformation to ordered values of X. Then U(i:k) is the i-th smallest value. Without thresholding, E(U(i:k)) = i/(k + 1), and this expectation is decreasing with k. The expectation for the effect size in Eq. (8) is non-decreasing, and for statistics with the strict monotone likelihood ratio densities (e.g., the normal and chi-square) it is increasing to the maximum possible value of the assumed effect size distribution. Thus, the enrichment of top hits by genuine signals with increasingly large effect sizes is to be expected even among multiple testing experiments without statistically significant findings.
Locally dependent statistics
Our results above were obtained by utilizing the theory for behavior of the order statistics under the independence assumption. We have not assumed identically-distributed statistics, because our approach allows us to deal with sequences of variables that follow any distribution that can be characterized by a fine grid of values matched to their respective probabilities. Nonetheless, in genetic association studies, association statistics and P-values are expected to be non-independent as a consequence of linkage disequilibrium between alleles of SNPs. Linkage disequilibrium (LD), measured as the correlation between alleles of two SNPs, does not necessarily translate to the same correlation between association statistics or P-values for that pair of SNPs [Zaykin and Kozbur, 2010]. While this creates a level of complication, the fact remains that association statistics are expected to be locally correlated in the genome. However, as long as the dependence structure does not exhibit long-range behavior, the independence assumption may not be particularly restrictive. For statistics this condition can be described informally as asymptotic independence of joint sets of values that are sufficiently distant from each other. There are conditions, including stationarity, that lead to the existence of asymptotic distributions that govern extreme values of such dependent sequences, as the number of observations approaches infinity [Smith, 1992]. We do not expect the LD patterns in the human genome to follow a well-behaved stationary distribution. In practice, association statistic values for the extremes can fit quite well under a distribution that is expected for a smaller number of tests under independence. In other words, although there may not be a set of parameters describing the asymptotic behavior, the effective number of tests ke may exist in the sense that the distribution of the largest statistic (or the associated minimum P-value) of k statistics in total is well approximated by the distribution of the largest statistic for a smaller set k of independent statistics; [Dudbridge and Gusnanto, 2008; Kuo and Zaykin, 2011] i.e., ke = θ × k for some 0 < θ ≤ 1, with θ = 1 implying independence. Although our primary concern is the underlying distribution of all effect sizes that gives rise to these extreme statistics, and not the distribution of extreme statistics themselves, we demonstrated a relationship earlier between these distributions that utilizes two simplifying assumptions: (i) point H0, and (ii) independence between genuine and false signals [Kuo and Zaykin, 2011]. The second assumption is reasonable if we assume that the proportion of genuine signals is very small and that signals locally-correlated with any genuine signal are proxy associations that are worth discovering and pursuing (thus they are arguably not “false” associations). In this model, the probability that the i-th smallest P-value represents a genuine signal depends on expected values of ordered P-values for spurious signals. The expected value for the j-th ordered spurious P-value, j = 1, …, L, is approximately je/(Le + 1), where L is θ × L and j is the “effective rank.” For je, the equally-spaced scale between 1 and k leads to je/(L + 1) ≈ j/(L + 1) when j is not too small. Even though such scaling can be justified for certain cases as an asymptotic property, in genetic applications it is a useful heuristic approximation. Empirically, the common practice of using QQ plots in genome-wide studies confirms that in the absence of biases, such as confounding by population stratification, null associations closely fit the expected line in the presence of LD, thus approximating the behavior under independence.
To describe briefly a justification for “squeezing” the rank j of P-values into je, 1 ≤ je ≤ ke, note that under independence,
| (9) |
| (10) |
and under certain conditions, similar to those for θ to be the asymptotic parameter of the distribution for the maximum, the terms in Eq. 10 are multiplied by weights, w(i)′, which are sums of probabilities for consecutive values of extremes to occur in groups (clusters) of different sizes [Beirlant et al., 2006],
| (11) |
Using the relation between Eq. 9 and 10,
| (12) |
where . The equally spaced values of je can then be related approximately to reasonable assumptions that the probability of a cluster of size X, p(X = x), quickly approaches zero as x increases and that the dominant probability is p(1) ≈ θ.
Simulations
To validate our analytical EPGS derivation, we compared theoretical values based on Eq. 5 to empirical expectations computed based on B=1,000,000 simulations. Table 1 summarizes the results of several comparisons for different values of k (the total number of tests) and m (the total number of true signals). Effect sizes, γ1, …, γt, t = 200, were derived from a discretized Gamma distribution, Gamma(1/shape, shape), where the shape was randomly chosen to fall between 1/4 and 4 for each row in the table. Empirical values were obtained by assuming normally distributed statistics with noncentralities γ1, …, γt, where the boundary between the null, Γ0, and the alternative set, ΓA was placed at the median value. After obtaining L + m = k statistics in each simulation, the P-values were sorted and the count, C, was incremented by one, if the j-th ordered P-value, originated from the set, ΓA, was among the u smallest P-values. The empirical estimate of was then simply C/B. Table 1 indicates an excellent agreement between the theoretical and the empirical expectations.
Table 1.
Comparison of theoretical and empirical values of .
| j | u | k | m | Shape | Empirical | Theoretical |
|---|---|---|---|---|---|---|
|
| ||||||
| 1 | 1 | 179 | 53 | 1.19 | 0.603 | 0.603 |
| 1 | 1 | 142 | 42 | 1.73 | 0.593 | 0.593 |
| 2 | 14 | 122 | 11 | 0.34 | 0.766 | 0.767 |
| 2 | 26 | 263 | 10 | 0.35 | 0.621 | 0.621 |
| 3 | 26 | 219 | 14 | 1.55 | 0.750 | 0.751 |
| 3 | 16 | 165 | 14 | 2.14 | 0.667 | 0.667 |
| 4 | 6 | 111 | 17 | 0.46 | 0.404 | 0.404 |
| 4 | 12 | 106 | 22 | 0.4 | 0.909 | 0.910 |
| 4 | 75 | 1M | k=103 | 0.34 | 0.007 | 0.007 |
| 4 | 75 | 5M | k=103 | 0.34 | 0.011 | 0.012 |
| 4 | 75 | 10M | k=103 | 0.34 | 0.014 | 0.014 |
| 4 | 75 | 20M | k=103 | 0.34 | 0.017 | 0.017 |
| 5 | 13 | 111 | 19 | 3.87 | 0.768 | 0.768 |
| 5 | 25 | 168 | 15 | 4.00 | 0.595 | 0.596 |
| 6 | 9 | 166 | 33 | 0.51 | 0.671 | 0.672 |
| 6 | 14 | 176 | 42 | 0.35 | 0.946 | 0.946 |
| 7 | 11 | 191 | 40 | 0.53 | 0.767 | 0.766 |
| 7 | 9 | 150 | 35 | 3.07 | 0.771 | 0.771 |
| 8 | 17 | 268 | 27 | 0.97 | 0.197 | 0.197 |
| 8 | 11 | 159 | 32 | 0.32 | 0.547 | 0.547 |
| 9 | 17 | 222 | 38 | 0.62 | 0.656 | 0.656 |
| 9 | 13 | 157 | 19 | 2.68 | 0.080 | 0.080 |
| 10 | 30 | 292 | 34 | 0.26 | 0.373 | 0.373 |
| 10 | 22 | 252 | 35 | 0.85 | 0.496 | 0.496 |
| 11 | 15 | 268 | 44 | 0.58 | 0.384 | 0.383 |
| 11 | 13 | 199 | 34 | 0.26 | 0.195 | 0.195 |
| 12 | 13 | 291 | 63 | 2.43 | 0.696 | 0.695 |
| 12 | 17 | 278 | 54 | 0.44 | 0.617 | 0.617 |
To validate our approximation to the expected effect size of the ordered P-values, we calculated empirical averages based on B=10,000 simulation experiments and compared them to the theoretical approximation provided in Eq. 8. Table 2 summarizes the results under the assumption of the point null. Allowing for zero effect sizes in this table was achieved by setting the smallest of the ordered effect sizes γ1, …, γt, to zero, that is, γ1 = 0, and the notation Pr(min(γ)=0)=0.95 reflects that the corresponding mixture weight was w = 0.95. Further, Table 3 summarizes the results without the point null assumption. Both tables support that the approximation is suitable.
Table 2.
Comparison of theoretical and empirical values of E(γ | χ(i:k)) allowing for zero effect sizes.
| Allow point H0: Pr(min(γ)=0)=0.95 | ||||||
|---|---|---|---|---|---|---|
|
| ||||||
| i ⇒ | 1 | 25 | 1 | 25 | 1 | 25 |
|
| ||||||
| k ⇓ | Simulated E(γ) | Analytical E(γ) | E(χ2) | |||
|
| ||||||
| 1K | 1.52 | 0.28 | 1.53 | 0.27 | 14.00 | 5.45 |
| 5K | 2.28 | 0.64 | 2.30 | 0.63 | 18.20 | 8.78 |
| 10K | 2.51 | 0.86 | 2.60 | 0.87 | 20.09 | 10.34 |
| 100K | 3.31 | 1.92 | 3.36 | 1.91 | 26.57 | 16.04 |
| 150K | 3.42 | 2.14 | 3.46 | 2.11 | 27.73 | 17.13 |
| 200K | 3.47 | 2.27 | 3.52 | 2.24 | 28.55 | 17.90 |
| 350K | 3.59 | 2.45 | 3.64 | 2.50 | 30.14 | 19.44 |
| 400K | 3.67 | 2.54 | 3.66 | 2.55 | 30.52 | 19.81 |
| 500K | 3.68 | 2.67 | 3.70 | 2.65 | 31.16 | 20.43 |
| 550K | 3.69 | 2.67 | 3.72 | 2.69 | 31.43 | 20.70 |
| 650K | 3.73 | 2.74 | 3.75 | 2.75 | 31.90 | 21.17 |
| 1M | 3.79 | 2.91 | 3.79 | 2.93 | 33.13 | 22.38 |
| Thresholding: minP > 0.05/k; Allow point H0: Pr(min(γ)=0)=0.95 | ||||||
|---|---|---|---|---|---|---|
|
| ||||||
| i ⇒ | 1 | 25 | 1 | 25 | 1 | 25 |
|
| ||||||
| k ⇓ | Simulated E(γ) | Analytical E(γ) | E(χ2) | |||
|
| ||||||
| 1K | 1.30 | 0.27 | 1.29 | 0.27 | 12.75 | 5.43 |
| 5K | 1.99 | 0.63 | 1.98 | 0.63 | 16.43 | 8.75 |
| 10K | 2.28 | 0.86 | 2.27 | 0.86 | 18.05 | 10.30 |
| 100K | 3.00 | 1.89 | 3.04 | 1.89 | 23.43 | 15.95 |
| 150K | 3.15 | 2.10 | 3.14 | 2.09 | 24.36 | 17.01 |
| 200K | 3.23 | 2.24 | 3.21 | 2.22 | 25.02 | 17.78 |
| 350K | 3.33 | 2.49 | 3.33 | 2.47 | 26.29 | 19.29 |
| 400K | 3.34 | 2.50 | 3.36 | 2.53 | 26.59 | 19.65 |
| 500K | 3.41 | 2.63 | 3.40 | 2.62 | 27.09 | 20.26 |
| 550K | 3.42 | 2.63 | 3.42 | 2.66 | 27.30 | 20.52 |
| 650K | 3.44 | 2.73 | 3.45 | 2.73 | 27.67 | 20.98 |
| 1M | 3.52 | 2.88 | 3.53 | 2.90 | 28.63 | 22.17 |
Table 3.
Comparison of theoretical and empirical values of E(γ | χ(i:k)) without allowing for zero effect sizes.
| Pr(min(γ)=0.05)=0.95 | ||||||
|---|---|---|---|---|---|---|
|
| ||||||
| i ⇒ | 1 | 25 | 1 | 25 | 1 | 25 |
|
| ||||||
| k ⇓ | Simulated E(γ) | Analytical E(γ) | E(χ2) | |||
|
| ||||||
| 1K | 1.42 | 0.30 | 1.40 | 0.31 | 14.28 | 5.68 |
| 5K | 2.09 | 0.63 | 2.12 | 0.63 | 18.43 | 9.08 |
| 10K | 2.39 | 0.82 | 2.42 | 0.83 | 20.29 | 10.65 |
| 100K | 3.16 | 1.75 | 3.23 | 1.76 | 26.67 | 16.31 |
| 150K | 3.27 | 1.95 | 3.34 | 1.94 | 27.81 | 17.37 |
| 200K | 3.37 | 2.08 | 3.41 | 2.07 | 28.62 | 18.13 |
| 350K | 3.50 | 2.31 | 3.54 | 2.32 | 30.20 | 19.64 |
| 400K | 3.55 | 2.37 | 3.57 | 2.37 | 30.58 | 20.00 |
| 500K | 3.59 | 2.47 | 3.62 | 2.47 | 31.21 | 20.61 |
| 550K | 3.61 | 2.48 | 3.64 | 2.51 | 31.48 | 20.87 |
| 650K | 3.64 | 2.58 | 3.67 | 2.57 | 31.95 | 21.33 |
| 1M | 3.73 | 2.73 | 3.75 | 2.74 | 33.17 | 22.53 |
| 5M | 3.98 | 3.24 | 4.00 | 3.27 | 37.7 | 27.05 |
| 10M | 4.09 | 3.43 | 4.09 | 3.45 | 39.65 | 29.01 |
| 20M | 4.16 | 3.59 | 4.16 | 3.60 | 41.58 | 30.97 |
| Thresholding: minP > 0.05/k; Pr(min(γ)=0.05)=0.95 | ||||||
|---|---|---|---|---|---|---|
|
| ||||||
| i ⇒ | 1 | 25 | 1 | 25 | 1 | 25 |
|
| ||||||
| k ⇓ | Simulated E(γ) | Analytical E(γ) | E(χ2) | |||
|
| ||||||
| 1K | 1.19 | 0.28 | 1.19 | 0.31 | 12.98 | 5.66 |
| 5K | 1.80 | 0.64 | 1.81 | 0.62 | 16.61 | 9.05 |
| 10K | 2.10 | 0.83 | 2.08 | 0.82 | 18.20 | 10.61 |
| 100K | 2.88 | 1.76 | 2.87 | 1.74 | 23.50 | 16.21 |
| 150K | 2.95 | 1.91 | 2.98 | 1.92 | 24.42 | 17.26 |
| 200K | 3.07 | 2.05 | 3.06 | 2.05 | 25.07 | 18.01 |
| 350K | 3.23 | 2.31 | 3.20 | 2.29 | 26.33 | 19.49 |
| 400K | 3.23 | 2.34 | 3.23 | 2.35 | 26.63 | 19.85 |
| 500K | 3.26 | 2.46 | 3.28 | 2.44 | 27.13 | 20.44 |
| 550K | 3.30 | 2.47 | 3.30 | 2.48 | 27.34 | 20.70 |
| 650K | 3.32 | 2.52 | 3.33 | 2.55 | 27.71 | 21.15 |
| 1M | 3.41 | 2.71 | 3.40 | 2.72 | 28.66 | 22.31 |
We also performed simulation experiments with high levels of local dependence to study the closeness of predictions using the independence theory. We modeled the dependencies by the autoregressive-moving-average (AR + MA) model with two AR components, 0.87, 0.1 and three MA components, 0.75, 0.50, 0.25. Although this model is stationary, it does not have θ as an asymptotic parameter, because the extremes of this process behave as if θ was an increasing function of k. For example, if T are observations from this process with F (·) being the stationary CDF of T, then at k = 103, the minimum of the values transformed to the uniforms, p = 1 − F (max(T)), behaves as if θ(k) ≈ 0.08. At larger values of k, the values slowly increase. However, even at k = 106, the effect of dependence on p(1) is still substantial, e.g., θ(k = 104) ≈ 0.12; θ(k = 105) ≈ 0.18; θ(k = 106) ≈ 0.20.
The effect of dependence on extremes as well as the effect of corrections by k and j can be visualized by QQ plots. Figure 2 shows a substantial downward bias for an uncorrected expected QQ plot (k = 105). The bias is largely removed when using the effective numbers, ke, je. The expected axes of the plots were constructed as E(−ln [p] ≈ Ψ(k + 1) − Ψ(je) (substituting je and k with j and k for the first plot), where Ψ(·) is the digamma function. The locally dependent, marginally uniform values, U = 1 − F (T), were used as a generating process to produce sequences of dependent statistics, Z, via a quantile transformation, using a specified mixture distribution for the effect size (derived from Gamma(1,10) with an added 95% mass about zero to model a high probability of small effect sizes). The relation between consecutive values of U and Z is shown in Figure 3. Note the occasional spikes present in the plot for the Z-statistics in Figure 3 that occur when Z happens to be generated from a large underlying effect size value. These spikes are relatively rare: in terms of P-values, this model generates only a small excess at the tail, e.g. Pr(P-value < 10−4) ≈ 3 × 10−4. As already noted, our interest is the expectation of the generating effect sizes of the extreme statistics, γ, rather than the expectation of values of these statistics. It is important to note that the larger the variance of γ values, the less influence the dependence between statistics will have on the distribution of γ in the extremes. Table 4 illustrates this point by summarizing results of simulations by the AR + MA-induced dependence just described and confirms close correspondence of the theoretical values to the empirical values obtained by simulations.
Figure 2.
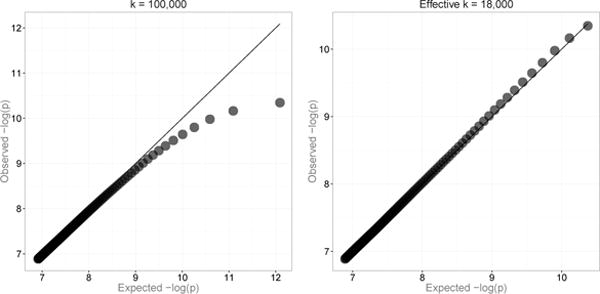
The expected QQ plot bias due to local dependence (left) and the effect of correction by using effective numbers of tests and ranks (right).
Figure 3.
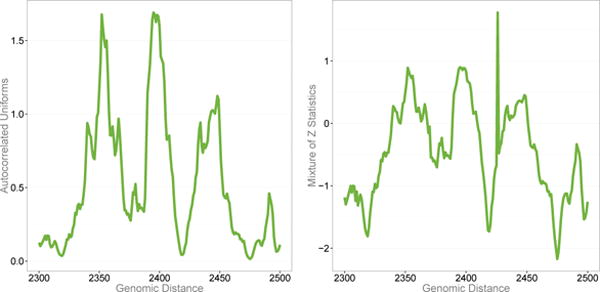
The generating uniform distribution (left), transformed as , and the resulting locally correlated mixture of statistics (right).
Table 4.
Comparison of theoretical and empirical values of E(γ | Z(j:k)) and E(Z(j:k))under ARMA-induced dependence.
| i ⇒ | 1 | 25 | 50 | 1 | 25 | 50 | 1 | 25 | 50 | 1 | 25 | 50 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||||
| k ⇓ | Simulated E(γ) | Analytical E(γ) | Simulated E(Z) | Analytical E(Z) | ||||||||
|
| ||||||||||||
| 1K | 0.63 | 0.10 | 0.07 | 0.73 | 0.10 | 0.07 | 3.15 | 1.91 | 1.62 | 3.51 | 2.03 | 1.70 |
| 5K | 1.46 | 0.24 | 0.16 | 1.59 | 0.23 | 0.16 | 4.03 | 2.64 | 2.39 | 4.15 | 2.69 | 2.41 |
| 10K | 1.89 | 0.33 | 0.23 | 2.06 | 0.33 | 0.23 | 4.37 | 2.90 | 2.65 | 4.44 | 2.95 | 2.68 |
| 100K | 3.21 | 1.09 | 0.77 | 3.29 | 1.09 | 0.76 | 5.45 | 3.80 | 3.5 | 5.45 | 3.81 | 3.54 |
| 5M | 4.17 | 3.36 | 3.07 | 4.19 | 3.36 | 3.07 | 6.95 | 5.53 | 5.21 | 6.96 | 5.53 | 5.22 |
Results
Our methods can be applied to evaluate the behavior of EPGS as the number of tests, k, increases. We first considered changes in the probability that the smallest P-value corresponds to a true signal as increasingly more tests are performed, i.e., we considered changes in Pr(H | minP) as the number of tests, k, approaches infinity. The condition k → ∞ and the resulting approach of the probability to one is an abstraction that is not meant to be actualized in practice. It is rather a benchmark model that gives the upper bound for Pr(HA | minP), and assures that, given some assumptions, this probability is increasing with k. Important assumptions include: (1) the prior probability of the alternative hypothesis, Pr(HA), is constant, or decreasing with k to either a non-zero value, or decreasing to zero at a rate that is at least as slow as logarithmic and (2) for the probability to reach one rather than being simply non-decreasing, the test statistic should have a distribution with a strict monotone likelihood ratio, e.g., this includes the chi-square and the normal statistics (Appendix A). The assumption of constant Pr(HA) is not necessarily unreasonable with high-throughput sequencing data because the chance of finding a causal variant in a discovery study does not necessarily decrease if a larger number of variants is tested. Therefore, our theoretical findings justify a carry-forward of the most-significant association variant from discovery to replication stage.
We can also evaluate the degree of enrichment by genuine signals for the next ordered P-values (second, third, and so on). To determine how the chances of the top j-th P-value being a true finding vary with the number of tests, we calculated the empirical probabilities Pr(HA | p), j = 1, …, 50, for the top 50 P-values. The results are summarized by QQ plots in Figure 4 (simulation details are given in Appendix C). Each panel of Figure 4 is similar to Figure 1 but with the smaller dots removed and only the larger dots remain. Specifically, each panel shows the observed −log (pj), j = 1, …, 50 versus the expected −log (p) under the point H for k = 500, 10,000 and 1,000,000 tests. The green line corresponds to the Bonferroni-corrected significance threshold at the 5%/k level. The color of the dots represents the empirical probability of a true positive result out of 1,500 simulations, ranging from blue (Pr(HA | p) = 0) to red (Pr(HA | p) = 1). Figure 4 shows enrichment of the top P-values by true signals and illustrates how the rate of enrichment depends on the rate of occurrence of genuine signals.
Figure 4.
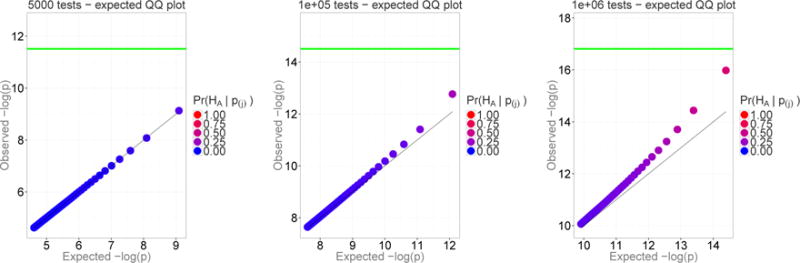
The proportion of genuine signals among top 50 P-values with the prior probability of a true finding of 0.1%. The color of the dots represents the posterior probability of a genuine result, ranging from blue (Pr(H | p) = 0) to red (Pr(H | p) = 1). The green line indicates Bonferroni-adjusted significance threshold.
It is evident from Figure 4 that the probability of a P-value to be a true association is increasing even among P-values that do not reach the 5%/k significance level (note the change in the color of the dots below the green threshold line). Thus, we modified our simulations in a way in which experiments where the minimum P-value was significant were discarded. A practice to keep only those studies where no significances were found would clearly go against common sense. Figure 5 shows that the enrichment of top hits by genuine signals still occurs. Note that it is not possible in these graphs for the dots to cross the Bonferroni green line because experiments with significance were discarded. Still, even among these experiments without any significant P-values, the chance that the top hits represent true findings increases with the number of tests. For instance, with one million tests and among the top 50 P-values, none of which reached statistical significance, the empirical probability of a true association ranges from ~ 35% for p to ~ 92% for p1. Moreover, the magnitude of the effect size, γ, increases with both the order of P-values and with the number of tests. This behavior would only be more apparent for multiple testing adjustments that are not as stringent as the Bonferroni. The results presented in Figure 5 can also be obtained analytically by using the expectations provided in Eq. 7 and 8.
Figure 5.
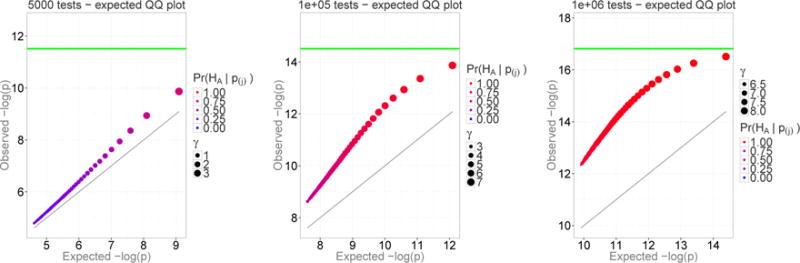
The proportion of genuine signals among the top 50 P-values, none of which passed a significance threshold (min(p) > 0.05/k). The color of the dots represents the posterior probability of a genuine result, the size of the dots represents the magnitude of the effect size, and the green line indicates the Bonferroni-adjusted significance threshold.
Figures 1, 4, 5 were constructed according to the traditional point null hypothesis assumption of zero effect size. However, more realistically, the null hypothesis may be represented by a set of non-zero, negligibly small effect sizes. For this scenario, we used effect size estimates from Park et al. [2010] who provided the number of susceptibility loci and the distribution of their effect sizes measured as a function of the odds ratio (OR) for breast, prostate and colorectal (BPC) cancers. Signals that correspond to H0 were defined as those with the OR in the range of 1/1.01 to 1.01 with the prior probability of H0 equal to one minus the estimated proportion of susceptibility loci for BPC cancers. Table 5 summarizes the results and shows how the average odds ratio (OR) corresponding to the smallest P value changes with an increase in the number of tests. From Table 5, it is clear that even without the assumption of the point null hypothesis, there is an enrichment of true signals with high effect size magnitude among the top hits.
Table 5.
Comparison of the average odds ratios without the point null assumption.
| Number of tests | Pr(HA | minP) |
|
|
|---|---|---|---|
|
| |||
| k = 100 | 0.0102 | 1.0105 | |
| k = 1,000 | 0.0538 | 1.0164 | |
| k = 10,000 | 0.2596 | 1.0454 | |
| k = 50,000 | 0.6234 | 1.1101 | |
| k = 100,000 | 0.8135 | 1.1507 | |
| k = 500,000 | 0.9946 | 1.2235 | |
The results displayed in Figures A.1–5 and Table 5 are for the condition of constant rate of encountering a true positive. The assumption of constant rate of Pr(HA) regardless of the number of tests may not always be reasonable. When the rate decreases and eventually reaches a positive constant, EPGS will still increase to one, although at a slower pace compared to the starting rate. However, it is also possible for the of Pr(HA) to approach zero slowly enough so that EPGS will still increase with k. These results are summarized in Appendix B, in which we investigated the limiting behavior of EPGS when Pr(HA) is a decreasing function of k, h(k). In particular, if the probability of a genuine signal vanishes with k, i.e., limk→∞ h(k) = 0, but
| (13) |
where c is a constant, then EPGS → 0 as k → ∞. However, when the rate of occurrence of genuine signals is slowly decreasing with k, EPGS may still increase, with one example being a logarithmic decrease, h(k) = Pr(H)/ln(k).
Discussion
Misinterpretation and abuse of significance testing and P-values have been put in the center of the scientific research controversy as major culprits responsible for poor replicability of studies. Multiple statistical testing as a form of ‘P-hacking’ is believed to promote false findings that fail to be replicated in subsequent investigations. In this article, we show that paradoxically, massive multiple testing, exemplified by large scale genetic association studies, does not promote spurious findings. The more tests are performed, the higher the proportion of real findings is expected in a set of the smallest P-values of a predefined size. This remains the case even among those studies where no P-values reached statistical significance.
It is hard to overstate the importance of the statistical analysis as a key factor affecting replicability of research. Relatively high rates of replicability are observed in genetic association studies compared to other fields of observational research and have been attributed to several factors. These factors include increased awareness of researchers about the dangers of multiple testing and to the subsequent adoption of appropriately stringent significance thresholds. A factor overlooked to date may be that the selection of the top smallest P-values out of many tests leads to enrichment of these top hits with genuine signals as the number of tests increases.
Our basic model for this enrichment is when the rate of occurrence of genuine signals is constant. The rate of occurrence can be allowed to decrease with the number of tests for the enrichment to take place. However, the decrease should either be sufficiently slow or stabilize at some non-zero baseline level. In the latter case the rate becomes constant, although lower than the rate for the small number of tests.
While we are primarily motivated by genetic association studies, our model is general. As an illustration, imagine a completely uninformed epidemiologist studying effects of various predictors on susceptibility to a disease. The epidemiologist is oblivious to any external knowledge regarding possible effects of predictors on the outcome and simply tests every predictor available. In this scenario, the rate with which truly associated predictors are tested does not diminish as additional predictors are tested. In the end, the predictor yielding the smallest P-value is reported as a potentially true association. This strategy is often perceived with disdain as ‘data torturing.’ However, a predictor with the smallest P-value in such a study becomes increasingly less likely to be a spurious association as more tests are performed. Therefore, an epidemiologist that tested the effects of one hundred random exposures on a disease and reported the smallest of one hundred P-values with no regard to their significance is more likely to be correct in identifying a truly-associated effect than a colleague who tested only ten exposures. Conversely, a knowledgeable epidemiologist would study most plausible predictors first and consequently the rate of occurrence of genuine signals would drop with any additional testing. However, it is reasonable to suppose that as the prior, subject matter expertise is exhausted, he/she would settle at a lower, yet constant rate scenario. This constant rate scenario is the basis of our model.
Our observations regarding the enrichment of top hits with true positives model a sequential testing of potential predictors. A very different scenario would be testing for all possible higher-order interactions among predictors. In such a scenario, the number of tests would grow exponentially, and it is possible that the rate of genuine signals Pr(HA) would quickly approach zero because of a steep increase in the number of tested combinations.
Our analysis reflects limitations of P-values as summary measures of effect size. Distribution of P-values for commonly used test statistics depends on the product of the sample size, (N or ) and a measure of effect size, δ, scaled by the variance σ2 (or σ). Scaling of δ by σ itself limits interpretability, and the second major limitation is the conflation of this standardized measure of effect with N. Thus, the interpretation of our results is most straightforward for studies where P-values are derived from statistics with similar sample sizes, such as in genome wide association scans.
Our model is not to be viewed as one that would faithfully reflect reality. Rather, it serves as a benchmark by allowing one to make predictions for a range of scenarios, including idealized scenarios. For example, we describe how the rate of true positives for the top-ranked P-values would have reached one if the number of tests had been steadily increasing, but that is only the limiting behavior, never to be met in real studies, let alone genetic studies, due to the finite set of variants in the genome. Predictions of our model correspond most closely to the expected rate of true findings by the “uninformed epidemiologist” from the example above, who takes every predictor available for testing and then reports the smallest P-value. There are additional assumptions in that example, including the absence of unknown confounding factors, or validity of the asymptotic distribution assumed for the test statistic at very small P-values.
Theoretical results developed here allow researchers to quantify the expected enrichment of the smallest P-values by genuine signals as a function of the number of tests, given external information about the effect size distribution. Qualitatively, we demonstrate that the expected proportion of genuine associations among the smallest P-values of multiple testing experiments is expected to increase with the number of tests. Far from promoting P-values as measures of hypothesis credibility, our analysis centers around the balance of true and false findings among extreme P-values averaged over similarly designed studies. This averaging is to data analysis as climate is to weather, and may be viewed as an expectation of Bayesian posterior probabilities given P-values as summaries of data. Implicit in that view is the preference of analysis based on posterior inference, where P-values can serve as ranking measures for standardized effect size, subject to subsequent careful evaluation. An argument had been made, due to implausibility of the global null hypothesis, that scientists should not be reluctant to explore potentially wrong leads due to fear of a penalty for peeking and scientific curiosity [Rothman, 1990; Williams and Haines, 2011]. We make this argument more formal and describe how more testing should lead to more real findings in quantifiable terms. Our approach allows one to put it in numbers, to calculate what rate of real findings should be expected for a given number of tests and how this rate depends on other parameters, such as the sample size or the effect size distribution. Moreover, in studies with an excessive hypotheses testing the use of study-wise significance thresholds is now commonplace. What happens among those failed studies where there were no significant findings, however, has been largely unknown. We show that the same enrichment phenomenon takes place: the proportion of true associations among the top hits grows with the number of tests, and the rate of enrichment is quantifiable in this case as well. An implementation of our approach available in R at https://github.com/dmitri-zaykin/Top_Hits
Acknowledgments
This research was supported in part by the Intramural Research Program of the NIH, National Institute of Environmental Health Sciences. Also, we thank Dr. Dawn Richards, for proofreading and stylistic suggestions.
A Appendix
Limiting behavior of the expected probability that a finding is genuine with constant prior probability of a true association
In this appendix, we describe a limiting behavior of the E [Pr(HA | minP)] as the number of tests, k, goes to infinity. In our previous work we considered a special case of the results in Eq. 7, by setting the effect size under H0 to zero, i.e., by assuming the point null hypothesis [Kuo and Zaykin, 2011]. This simplification leads to approximations that are useful for studying dependency of EPGS on the number of tests. Let π = Pr(H0) be the prior probability of the null hypothesis and 1 − π = Pr(HA) be the probability of the alternative hypothesis. Let G0 (·) and Gγ (·) denote the cumulative distribution function (CDF) of the test statistic under the null and the alternative hypothesis respectively. The CDF of the P-value derived from the continuous test statistics where the deviation from the null can be described by a single parameter γ can be written as
| (14) |
Assuming that γ follows the distribution Γ(γ) and averaging over all possible values of the effect size for genuine signals, the marginal CDF of a true association P-value is:
| (15) |
Futher, the CDF of the jth-ordered true association P-value has the form:
| (16) |
where Bin denotes the binomial CDF evaluated at j − 1 successes in m true associations with success probability . Assuming that the effect size is zero under H0, the expected proportion of genuine signals among u smallest out of k total sorted list of P-values, {p(1), … p(k)} is:
| (17) |
Here, we focus on the limiting behavior of EPGS for u = 1 (i.e., the probability that one of the true associations will have the smallest P-value in a study) under the assumption that the rate of occurrence of true signals does not depend on k. Considering minP, we define the expected false discovery rate (EFDR) as EFDR = 1-EPGS. Then
| (18) |
For a fixed value of γ, the P-value density is the derivative of Fγ (p), that can be expressed as a ratio of two densities that differ in the value of the noncentrality: , where g(·) is the density that corresponds to the CDF, G(·), as defined above. Thus, for the test statistic densities with the strict monotone likelihood ratio, which includes the chi-square and the normally distributed statistics, fγ (p) → ∞, as p → 0. For the Student t and the F statistics the ratio of densities is increasing asymptotically in the sample size (N) and is non-decreasing for a fixed value of N. Therefore, the limit of the expression in Eq. 18 as k → ∞
and EPGS → 1. At γ = 0, EFDR ≈ exp(− π/(1 − π)) ≈ 1 − π = Pr(H0), as it should be, since the distinction between genuine and false signals merely becomes a label.
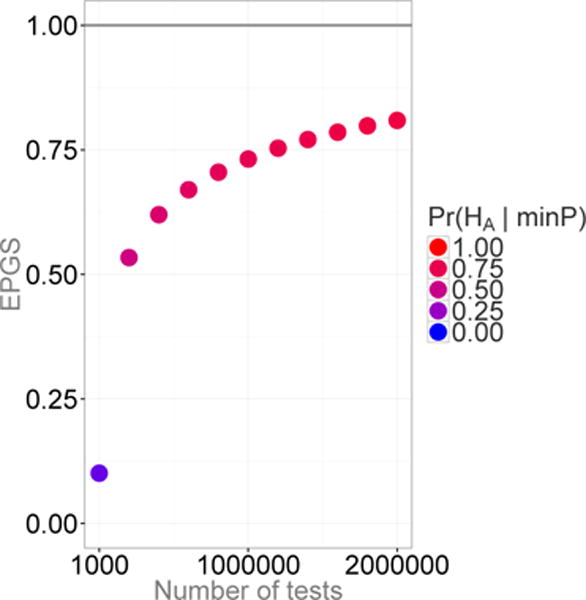
This result is illustrated graphically in Figure A.1 with Pr(HA) = 0.1% and the number of tests ranging from 1,000 to 2 million (additional details of how this figure was constructed can be found in Appendix C). Figure A.1 illustrates the convergence of the probability for the strongest signal to be a true finding to one, as more tests are performed.
Figure A1.

The proportion of genuine signals versus the number of tests (k) under the assumption of constant Pr(HA) = 0.1%. The plot depicts how the chance that the smallest P-value is a true finding converges to 1 with increased numbers of tests.
B Appendix
Decreasing prior probability of a true association
We now discuss how the limiting behavior of EPGS=E [Pr(HA | minP)] changes if Pr(HA) is a decreasing function of k, 1 − π = h(k), with
From Eq. 18, it follows that
| (19) |
Regardless of the specific form of h(k), in Eq. 19 as k approaches infinity. Therefore, if
| (20) |
where c is a positive constant, then E [Pr(HA | minP)] → 0 as k → ∞. For example, (1 − π1/k) · k initially increases with k, but reaches a constant, limk→∞ (1 − π1/k) · k = −ln(π) > 0.
If limk→∞ h(k) · k = ∞, the limit in Eq. 19 may or may not go to infinity, depending on the steepness of decrease in the rate of Pr(HA). To examine specific cases we make further simplifications: by noting that EPGS increases with γ, we consider a lower bound on the effect size and assume a single value γ > 0. One example of a slow decreasing rate is a logarithmic decrease in the rate of true associations with k,
Futher,
and
Accordingly, by L’Hospital’s Rule, limA→∞ (ln{EFDR}) in Eq. 19 is
| (21) |
| (22) |
The first term of the product in Eq. 22 goes to zero as k → ∞ but the second term, approaches infinity faster, assuming k tests were based on a normal statistic (computed with Wolfram Mathematica Wolfram [2008]).
As in the case of constant Pr(HA), ln{EFDR} → − ∞ implies that EPGS → 1. Therefore, even if the probability of finding a causal variant decreases logarithmically with the number of variants considered, the probability that the smallest P-value is a true finding still approaches 1 as more tests are performed.
As an illustration, we modified Figure A.1 by assuming h(k) = 0.1%/ln(k) and presented the results in Figure B.1. This modified figure highlights the idea that even though EPGS may not reach 1 (in contrast to the convergence behavior obtained at about one million tests in Figure A.1), the top P-values are becoming increasingly likely to represent true findings with increased numbers of tests.
Figure B1.
The proportion of genuine signals versus the number of tests (k) under the assumption of Pr(H) = 0.1%/ln(k). The plot depicts how the chance that the smallest P-value is a true finding converges to 1 even if the rate of true findings vanishes with k.
C Appendix
Simulation Details
In this section, we provide details for simulations used for construction of the figures. P-values can be viewed as random variables [Boos and Stefanski, 2011; Murdoch et al., 2008; Sackrowitz and Samuel-Cahn, 1999] and can be simulated directly for statistics with a known analytic distribution, such as the one degree chi-square. To obtain 1,000 QQ plots in Figure 1, we first assumed that in each study 2.5% of 1000 tests contain true signals and 97.5% of P-values correspond to the point null hypothesis of no association. Under the point null hypothesis, P-values are independent uniform (0,1) random variables so we generated 975 observation from uniform (0,1). For the effect size distribution, γ ~ Γ(γ), we assumed an L-shaped distribution as suggested by the population genetics theory [Otto and Jones, 2000]. Specifically, we assumed Gamma(0.25, 5) and generated 25 non-centrality parameters, γ. Then, using the inverse of Eq. 14, we generated the remaining 25 P-values (corresponding to the true effects) as functions of the uniform random numbers and sorted the resulting 1,000 P-values. QQ-plots were created for the top 10 ranked P-values with color highlighting whether they were corresponding to a false signal (and were generated from the uniform distribution) or not. Figure 4 was generated in a similar fashion but with a modified rate of occurrence of true associations (0.1% versus 2.5%) and for a different number of tests (k = 5,000, k = 100,000 and k = 1,000,000). Figure 5 was generated under the same scenario as Figure 4 (i.e., γ ~ Γ(0.25, 5) and Pr(HA) = 0.1%) but under rejection sampling where all experiments with a significant minP were discarded. In Figure A.1, we plotted the empirical values of EPGS = Pr(HA | minP). Figure B.1 replicates Figure A.1 but with Pr(HA) = 0.1%/ln(k).
Our figures that feature the effect of an increase in k under the constant rate of Pr(HA) are constructed with the assumption that the effect size distribution does not change with k. This assumption would be plausible if the variants were always picked at random, however, as was pointed out by a reviewer, genome-wide studies with a very large k would include a large fraction of rare variants. The allele frequency itself as well as its inverse relationship with the risk of disease would result in changes to the effect size distribution in studies with a dense coverage of rare variants.
The sample size in our model is included as a part of the non-centrality parameter, which is a product of the sample size times the standardized effect size (Eqs. 1), 2. An increase in the sample size results in the proportional increase of γ and leads to a faster rate of enrichment of the top-ranking SNPs with true positives. As an illustration, Figure C.1 shows the effect of a ten-fold increase in the sample size. The distribution of the non-centrality parameter in simulations for the top row of Figure C.1 followed the Gamma(0.05, 2) distribution, with the mean non-centrality equal to 0.1. This non-centrality may correspond to different combinations of parameters, for example, it may be obtained by Eq. 2 with the sample size of 750 cases, 750 controls, the mean odds ratio for the associated variants equal to 1.03, and the mean allele frequency among the cases equal to 0.2.
The ten-fold increase in N was modeled by a ten-fold increase in the scale parameter which gave the ten-fold increase for the mean of the non-centrality distribution.
Figure C1.
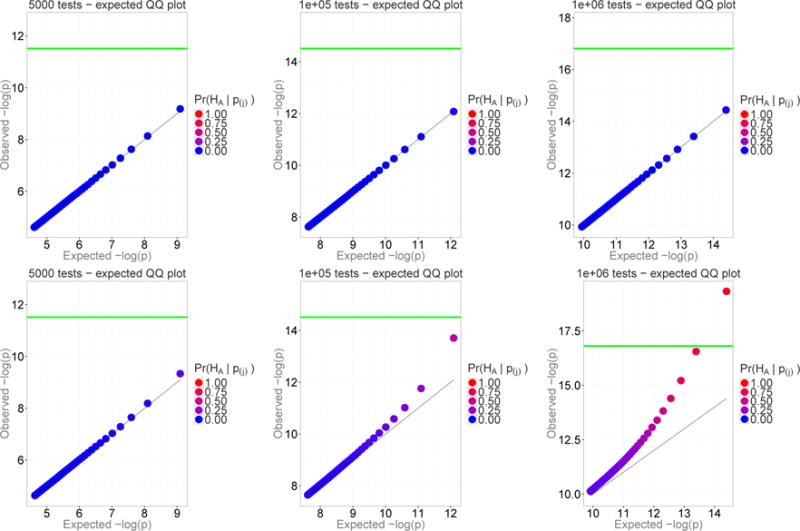
The proportion of genuine signals among the top hits increases with sample size. In these QQ plots, the prior probability of genuine signal is 0.1%. The bottom row replicates the model of the top row but for a ten-fold increases in the sample size.
Footnotes
Conflict of Interests
We have no conflicts of interest to declare.
References
- Beirlant J, Goegebeur Y, Segers J, Teugels J. Statistics of extremes: theory and applications. John Wiley & Sons; 2006. [Google Scholar]
- Bollen K, Cacioppo J, Kaplan R, Krosnick J, Olds J. Social, behavioral, and economic sciences perspectives on robust and reliable science: Report of the Subcommittee on Replicability in Science, Advisory Committee to the National Science Foundation Directorate for Social, Behavioral, and Economic Sciences. 2015 Retrieved from the National Science Foundation Web site: www.nsf.gov/sbe/ACMaterials/SBERobust_and_ReliableResearchReport.pdf.
- Boos DD, Stefanski LA. P-value precision and reproducibility. Am Stat. 2011;65(4):213–221. doi: 10.1198/tas.2011.10129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cumming G. Replication and P-intervals: P-values predict the future only vaguely, but confidence intervals do much better. Perspect Psychol Sci. 2008;3(4):286–300. doi: 10.1111/j.1745-6924.2008.00079.x. [DOI] [PubMed] [Google Scholar]
- Dawid A. Selection paradoxes of Bayesian inference. Multivariate Analysis and Its Applications. 1994;24:211–220. [Google Scholar]
- Dudbridge F, Gusnanto A. Estimation of significance thresholds for genomewide association scans. Genet Epidemiol. 2008;32(3):227–234. doi: 10.1002/gepi.20297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efron B, Tibshirani R. Empirical Bayes methods and false discovery rates for microarrays. Genet Epidemiol. 2002;23(1):70–86. doi: 10.1002/gepi.1124. [DOI] [PubMed] [Google Scholar]
- Efron B, Tibshirani R, Storey J, Tusher V. Empirical bayes analysis of a microarray experiment. J Am Statist Assoc. 2001;96(456):1151–1160. [Google Scholar]
- Goodman SN, Fanelli D, Ioannidis JP. What does research reproducibility mean? Science translational medicine. 2016;8(341):341ps12–341ps12. doi: 10.1126/scitranslmed.aaf5027. [DOI] [PubMed] [Google Scholar]
- Greenland S, Senn SJ, Rothman KJ, Carlin JB, Poole C, Goodman SN, Altman DG. Statistical tests, P-values, confidence intervals, and power: a guide to misinterpretations. Eur J Epidemiol. 2016;31(4):1–14. doi: 10.1007/s10654-016-0149-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halsey LG, Curran-Everett D, Vowler SL, Drummond GB. The fickle P-value generates irreproducible results. Nat Method. 2015;12(3):179–185. doi: 10.1038/nmeth.3288. [DOI] [PubMed] [Google Scholar]
- Ioannidis JP. Discussion: why an estimate of the science-wise false discovery rate and application to the top medical literature is false. Biostatistics. 2014;15(1):28–36. doi: 10.1093/biostatistics/kxt036. [DOI] [PubMed] [Google Scholar]
- Ioannidis JP, Tarone R, McLaughlin JK. The false-positive to false-negative ratio in epidemiologic studies. Epidemiology. 2011;22(4):450–456. doi: 10.1097/EDE.0b013e31821b506e. [DOI] [PubMed] [Google Scholar]
- Johnson VE. Revised standards for statistical evidence. Proc Natl Acad Sci. 2013;110(48):19313–19317. doi: 10.1073/pnas.1313476110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuo CL, Vsevolozhskaya OA, Zaykin DV. Assessing the probability that a finding is genuine for large-scale genetic association studies. PLOS ONE. 2015;10(5):e0124107. doi: 10.1371/journal.pone.0124107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuo CL, Zaykin DV. Novel rank-based approaches for discovery and replication in genome-wide association studies. Genetics. 2011;189(1):329–340. doi: 10.1534/genetics.111.130542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lai J, Fidler F, Cumming G. Subjective p intervals. Methodology. 2012;8(2):51–62. [Google Scholar]
- Lazzeroni L, Lu Y, Belitskaya-Levy I. P-values in genomics: apparent precision masks high uncertainty. Mol Psychiatry. 2014;19(12):1336–1340. doi: 10.1038/mp.2013.184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murdoch DJ, Tsai YL, Adcock J. P-values are random variables. Am Stat. 2008;62(3):242–245. [Google Scholar]
- Nuzzo R, et al. Statistical errors. Nature. 2014;506(7487):150–152. doi: 10.1038/506150a. [DOI] [PubMed] [Google Scholar]
- Otto SP, Jones CD. Detecting the undetected: estimating the total number of loci underlying a quantitative trait. Genetics. 2000;156(4):2093–2107. doi: 10.1093/genetics/156.4.2093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panagiotou OA, Ioannidis JP, et al. What should the genome-wide significance threshold be? empirical replication of borderline genetic associations. Int J Epidemiol. 2012;41(1):273–286. doi: 10.1093/ije/dyr178. [DOI] [PubMed] [Google Scholar]
- Park JH, Wacholder S, Gail MH, Peters U, Jacobs KB, Chanock SJ, Chatterjee N. Estimation of effect size distribution from genome-wide association studies and implications for future discoveries. Nat Genet. 2010;42(7):570–575. doi: 10.1038/ng.610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rothman KJ. No adjustments are needed for multiple comparisons. Epidemiology. 1990;1(1):43–46. [PubMed] [Google Scholar]
- Sackrowitz H, Samuel-Cahn E. P values as random variables–expected P values. Am Stat. 1999;53(4):326–331. [Google Scholar]
- Senn S. A note concerning a selection “paradox” of Dawid’s. Am Stat. 2008;62(3):206–210. [Google Scholar]
- Simonsohn U, Nelson LD, Simmons JP. P-curve and effect size correcting for publication bias using only significant results. Perspect Psychol Sci. 2014;9(6):666–681. doi: 10.1177/1745691614553988. [DOI] [PubMed] [Google Scholar]
- Smith RL. The extremal index for a Markov chain. J Appl Prob. 1992;29(1):37–45. [Google Scholar]
- Sweeney TE, Haynes WA, Vallania F, Ioannidis JP, Khatri P. Methods to increase reproducibility in differential gene expression via meta-analysis. Nucleic Acids Research. 2017;45(1):e1–e1. doi: 10.1093/nar/gkw797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wakefield J. A Bayesian measure of the probability of false discovery in genetic epidemiology studies. Am J Hum Genet. 2007;81(2):208–227. doi: 10.1086/519024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wasserstein RL, Lazar NA. The ASA’s statement on p-values: context, process, and purpose. Am Stat. 2016;70(2):129–133. [Google Scholar]
- Williams SM, Haines JL. Correcting away the hidden heritability. Ann Hum Genet. 2011;75(3):348–350. doi: 10.1111/j.1469-1809.2011.00640.x. [DOI] [PubMed] [Google Scholar]
- Wolfram S. Institutional homepage. Wolfram Research, Inc.; 2008. Wolfram mathematica. URL (last accessed 20 July 2016) https://www.wolfram.com/mathematica/ [Google Scholar]
- Zaykin DV, Kozbur DO. P-value based analysis for shared controls design in genome-wide association studies. Genet Epidemiol. 2010;34(7):725–738. doi: 10.1002/gepi.20536. [DOI] [PMC free article] [PubMed] [Google Scholar]


