Admission Laboratory Values Accurately Predict In-hospital Mortality: a Retrospective Cohort Study

Abstract

Background

The greater the severity of illness of a patient, the more likely the patient will have a poor hospital outcome. However, hospital-wide severity of illness scores that are simple, widely available, and not diagnosis-specific are still needed. Laboratory tests could potentially be used as an alternative to estimate severity of illness.

Objective

To evaluate the ability of hospital laboratory tests, as measures of severity of illness, to predict in-hospital mortality among hospitalized patients, and therefore, their potential as an alternative method to severity of illness risk adjustment.

Designs and Patients

A retrospective cohort study among 38,367 adult non-trauma patients admitted to the University of Maryland Medical Center between November 2015 and November 2017 was performed. Laboratory tests (hemoglobin, platelet count, white blood cell count, urea nitrogen, creatinine, glucose, sodium, potassium, and total bicarbonate (HCO₃)) were included when ordered within 24 h from the time of hospital admission. A multivariable logistic regression model to predict in-hospital mortality was constructed using a section of our cohort (n = 21,003).

Main Measures

Model performance was evaluated using the c-statistic and the Hosmer-Lemeshow (HL) test. In addition, a calibration belt was constructed to determine a confidence interval around the calibration curve with the purpose of identifying ranges of miscalibration.

Key Results

Patient age and all laboratory tests predicted mortality with good discrimination (c = 0.79). Patients with abnormal HCO₃ levels or leukocyte counts at admission were twice as likely to die during their hospital stay as patients with normal results. A good model calibration and fit were observed (HL = 13.9, p = 0.18).

Conclusions

Admission laboratory tests are able to predict in-hospital mortality with good accuracy, providing an objective and widely accessible approach to severity of illness risk adjustment.

INTRODUCTION

Severity of illness refers to the degree of organ system derangement in a patient.¹ The greater the severity of illness of a patient is, the more likely the patient will have a poor hospital outcome. Available severity of illness scoring systems can be divided into those that are specific for an organ or disease (e.g., Glasgow Coma Scale) and those that are applicable to specific patient populations (e.g., Acute Physiology and Chronic Health Evaluation II (APACHE) score).² However, hospital-wide severity of illness scores that are simple, widely available, and not diagnosis-specific are still needed.

Laboratory tests could potentially be used as an alternative to estimate a hospital-wide severity of illness. Laboratory tests are routinely ordered upon patient hospital admission, are objective, and are easily accessible from electronic medical records. Leveraging the results of admission laboratory tests to generate a hospital-wide severity of illness score has the potential for a number of important applications. This study focused particularly on two important ones: (a) severity of illness confounding adjustment in epidemiological studies and (b) hospital-level pay-for-performance risk adjustment.

The Centers for Medicare and Medicaid Services (CMS) use risk adjustment to account for differences in beneficiary-level risk factors that can affect quality outcomes or medical costs when comparing hospitals. One of the main components used by CMS to account for patient severity is the Medicare Severity Diagnosis Related Group (MS-DRG).³ MS-DRGs classify each patient based on principal diagnosis, specific secondary diagnosis, procedures, gender, and discharge status.⁴ Each DRG is assigned a unique weight, which is later multiplied by the hospital’s payment rate per case.⁵ This approach to classifying illness severity is limited by its diagnosis-specific nature, which is highly dependent on accurate hospital coding of International Classification of Diseases (ICD) codes. Poor to fair ICD-10 coding accuracy and MS-DRG-assignment accuracy (61% and 71% respectively in 2017) have been consistently reported by the Annual National ICD-10 Coding Contests.⁶ Furthermore, MS-DRG is a proprietary coding system; therefore, this system is not always affordable or accessible to every hospital or researcher. Use of admission laboratory tests to predict severity of illness can circumvent many of these issues.

The objective of this study was to evaluate the ability of hospital admission laboratory tests to predict in-hospital mortality among hospitalized patients. If accurate, evaluation of laboratory tests could provide an alternative method for severity of illness risk adjustment.

METHODS

Study Cohort and Database

We conducted a retrospective cohort study among all non-trauma adult patients admitted to the University of Maryland Medical Center (UMMC), a 755-bed tertiary care hospital located in Baltimore, MA, between November 7, 2015, and October 31, 2017. Patients with multiple hospital admissions during this time period were included in the dataset. Institutional Review Board approval was obtained with a waiver of informed consent. The cohort was created using the hospital’s central data repository, which is a relational database containing administrative, pharmacy, clinical, and laboratory data obtained from electronic medical records. Validation of a random sample of 50 patients and their laboratory variables was performed by chart review and was greater than 99% accurate. Additionally, general validation of this data repository has previously demonstrated positive and negative predictive values greater than 99%.^7–10

We chose to analyze laboratory tests that are commonly ordered early during hospital admission (only laboratory tests ordered in at least 80% of patients upon hospital admission at UMMC) and that have been associated with severity of illness (imminent death, in-hospital mortality, adverse events, etc.).^11–18 Laboratory values selected included hemoglobin, platelet count, leucocyte count, blood urea nitrogen (BUN), serum creatinine, glucose, sodium, potassium, and total bicarbonate (HCO₃). As our purpose was to assess severity of illness at admission, laboratory tests were only included if they were ordered within 24 h of admission. In cases of multiple tests obtained during this 24 h period, only the first laboratory result was selected.

Statistical Analyses

The association of each predictor with the outcome was assessed graphically. When this association was found to be linear, laboratory test results were analyzed as continuous variables. However, in the absence of linearity, variables were categorized as abnormally low, normal, and abnormally high based on standard clinical ranges reported by the UMCC’s Clinical Laboratory. Furthermore, continuous test results are difficult to interpret as clinically relevant unit changes are not consistent across laboratory tests (e.g., a one-unit increase in serum creatinine has a different clinical significance from a one-unit increase in serum glucose). Therefore, we developed another model for the outcome using only categorized laboratory tests (abnormal vs. normal) in order to improve clinical interpretation.

The dataset was randomly split into one development dataset (60% of the original dataset) and one validation dataset (40% of the original dataset). All laboratory tests significantly associated (p < 0.05) with the outcome in the bivariate analysis were considered for inclusion into the multivariable model. As patient’s age is associated with in-hospital mortality ¹⁹ and standardized ranges of laboratory values are commonly gender-specific,²⁰ these two variables were also considered for entry into the multivariable model. Additionally, interaction terms between gender and specific laboratory tests were evaluated. Stepwise selection was used to construct multivariable logistic regression models using generalized estimating equations (GEE) to account for the correlation of multiple outcomes from the same patient. If a variable’s p value was < 0.15 when adjusted for the rest of the variables in the model, the variable was kept in the final multivariable model.

Model performance was tested using the validation dataset as follows. For all the records in the validation set, outcomes were predicted using the predictive equation derived from the development subset. The c-statistic evaluated the models’ discriminatory power (i.e., their ability to discriminate between those with the outcomes and those without).²¹ A c-statistic of 0.50 indicates that the model is no better than flipping a coin in predicting the outcome. Values ≥ 0.70 are considered good, while values ≥ 0.80 are considered excellent.²¹ The Hosmer-Lemeshow test was used to evaluate the model’s calibration (i.e., how closely the predictions of our model match the observed outcomes in our study population).²¹ The Hosmer-Lemeshow test with a non-significant p value demonstrates that there is no evidence of a poor model fit.^{22, 23} Additionally, a GiViTi calibration belt was constructed to determine a confidence interval around the calibration curve.^{24, 25} The calibration plot contains the bisector, which represents the line of perfect calibration between the predicted and the observed proportions. The calibration belt around the bisector represents the 80% and 95% confidence level calibration of the model. If the belt does not contain the bisector, it indicates a significant lack of fit. The model is either under- or overestimating the outcome.^{24, 25}

RESULTS

Our development dataset had 26,857 admitted patients with a 3.6% mortality rate. Our validation dataset had 11,510 admitted patients with a 3.3% mortality rate. All analyzed laboratory tests were significantly associated with in-hospital mortality in the bivariate analysis and all laboratory tests remained in the first multivariable model (Table 1). The patients missing any of the laboratory tests included in the final multivariate model were automatically excluded from the final model. Twenty-two percent of the observations in the development dataset were excluded in the final model due to missing tests, i.e., not all patients having all the lab tests. The patients excluded were not different than the ones included in the model with respect to mortality. The model’s discriminatory power was good (c = 0.79 (95% CI 0.76–0.81)). After adding patient’s age and gender to the multivariable model, only age and the laboratory tests remained, leading to a slightly increased c-statistic (c = 0.81 (95% CI 0.78–0.83)) (Table 1). Additionally, as some included laboratory tests have gender-specific clinical cutoffs, we considered the interaction terms between gender and these laboratory tests; however, none of them remained in the final model.

Table 1.

In-hospital Mortality Predictive Model Evaluating Admission Laboratory Results

Variables†	Bivariate OR (95%CI)	Multivariable OR (95%CI)
Hemoglobin (g/dL)	0.85 (0.82–0.88)	0.93 (0.90–0.97)
Leukocyte count (K/μL)	1.02 (1.01–1.02)	1.01 (1.01–1.02)
Glucose (mg/dL)	1.00 (1.00–1.00)	1.00 (1.00–1.00)‡
Platelets
Abnormally low (< 153,000 cells/μL)	3.03 (2.65–3.48)	2.25 (1.93–2.62)
Abnormally high (> 367,000 cells/μL)	1.04 (0.79–1.38)	0.76 (0.55–1.05)
Urea nitrogen (mg/dL)	1.02 (1.02–1.03)	1.01 (1.00–1.01)
Serum creatinine
Abnormally low (< 0.52 mg/dL)	0.99 (0.72–1.35)	1.02 (0.73–1.43)
Abnormally high (> 1.04 mg/dL)	3.84 (3.34–4.41)	1.78 (1.48–2.14)
Sodium
Abnormally low (< 136 mmol/L)	2.18 (1.88–2.52)	1.58 (1.34–1.87)
Abnormally high (> 147 mmol/L)	2.79 (2.21–3.51)	2.04 (1.58–2.64)
Potassium
Abnormally low (< 3.5 mmol/L)	1.59 (1.31–1.92)	1.39 (1.09–1.79)
Abnormally high (> 5.2 mmol/L)	3.46 (2.80–4.28)	0.87 (0.64–1.17)
Bicarbonate
Abnormally low (< 21 mmol/L)	4.40 (3.81–5.08)	2.45 (2.05–2.93)
Abnormally high (> 30 mmol/L)	1.58 (1.24–2.00)	1.43 (1.11–1.86)
Age (years)	1.03 (1.03–1.04)	1.02 (1.02–1.03)

*Analysis Was Evaluated Using the Dataset Used for Model Development. The Final Sample Size Included in the Final Multivariate Model is 21,003.

†Laboratory results were analyzed as continuous variables when their association with the outcome was linear. In the absence of linearity with the outcome, variables were categorized as abnormally low (levels below the reference ranges), normal (levels within the reference ranges), and abnormally high (levels above the reference ranges) based on standardized clinical ranges reported by the clinical laboratory. The normal category was defined as the reference category when categorical data were used

‡Glucose association was significantly associated (p < 0.0001) with mortality (OR = 1.003 (1.002–1.003))

In our second multivariate model where all the laboratory variables were categorized, having any of these abnormal tests at admission was associated on average with a 26 to 115% increase in the odds of dying during the hospital stay (Table 2). Patients with abnormal levels of HCO₃ or leucocyte counts at admission were twice as likely to die during their hospital stay as patients with normal levels. However, due to the categorization of continuous variables, this model had a minimal decrease in discriminatory power (c = 0.79 (95%CI 0.77–0.81)). The Hosmer-Lemeshow test demonstrated a good model fit (X² = 13.85, p = 0.18) (Fig. 1a). The calibration belt also demonstrated good calibration, as the belt consistently includes the bisector. Nevertheless, due to the small sample size at medium and high ranges of the predicted probabilities, the calibration belt is wider among probabilities above 0.40 (Fig. 1b).

Table 2.

In-hospital Mortality Final Predictive Model Using Only Categorized Laboratory Results (Abnormal vs. Normal) and Age

Variables*	Multivariable OR (95%CI)
Hemoglobin
Abnormal	1.26 (1.06–1.50)
Females: < 11.9 or > 15.7 g/dL
Males: < 12.6 or > 17.4 g/dL
Leukocytes count
Abnormal (< 4, 500 or > 11, 000 cells/μL)	2.01 (1.74–2.34)
Glucose
Abnormal (< 70 or > 99 mg/dL)	1.52 (1.74–2.34)
Platelets
Abnormal (< 153,000 or > 367,000 cells/μL)	1.80 (1.55–2.08)
Urea nitrogen
Abnormal	1.46 (1.23–1.73)
Females: < 6 or > 17 mg/dL
Males: < 8 or > 20 mg/dL
Serum creatinine
Abnormal (< 0.52 or > 1.04 mg/dL)	1.78 (1.51–2.11)
Sodium
Abnormal (< 136 or > 147 mmol/L)	1.62 (1.40–1.88)
Potassium
Abnormal (< 3.5 or > 5.2 mmol/L)	1.49 (1.26–1.75)
Bicarbonate
Abnormal (< 21 or > 30 or mmol/L)	2.15 (1.84–2.50)
Age (years)	1.03 (1.02–1.03)

*Analysis was evaluated using the dataset used for model development. The final sample size included in the final multivariate model is 21,003. Laboratory variables were categorized as either abnormal (levels outside the reference ranges) or normal (levels within the reference ranges). The normal category was considered the reference category. The US traditional unit system is mostly used in our laboratory; therefore, this is the unit system reported in this manuscript. We detailed here the necessary SI unit conversions: hemoglobin (F, < 119 or > 157 g/L; M, < 126 or > 174 g/L); leukocytes (< 4.5 or > 11 × 10⁹ cells/L); glucose (< 3.9 or > 5.5 mmol/L); platelets (< 153 or > 367 × 10⁹ cells/L); urea nitrogen (F, < 2.1 or > 6.1 mmol/L; M, < 2.6 or > 7.1 mmol/L); serum creatinine (< 46.0 or > 91.9 μmol/L)

Figure 1.

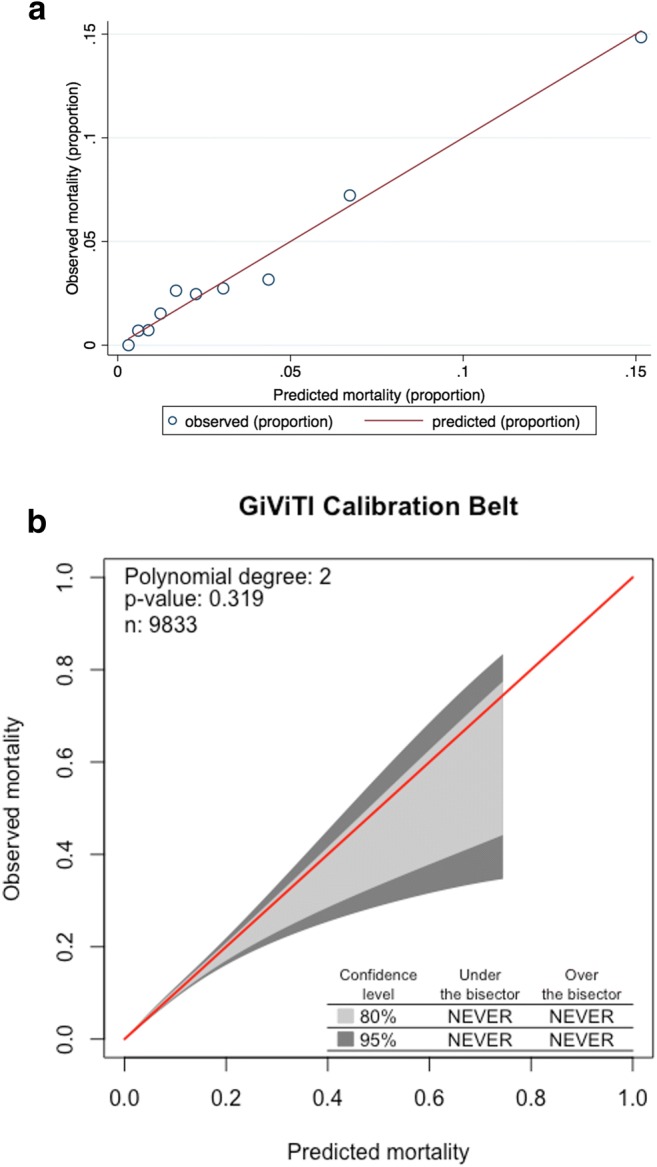
a Calibration plot comparing the observed and predicted proportions for mortality within the Hosmer-Lemeshow test groups. b GiViTi calibration belt demonstrating the confidence interval around the calibration curve. The calibration curve contains the bisector (red line), which represents the line of perfect calibration between the predicted and the observed proportions. The calibration belt around the bisector represents the 80% (light gray) and 95% (dark gray) confidence level calibration of the model. If the belt does not include the bisector, it indicates a significant lack of fit. The model is either under or overestimating the outcome.

DISCUSSION

Our results demonstrate that admission laboratory tests can be used to predict severity of illness among hospitalized patients, suggesting their use as an alternative to the currently used CMS-DRGs. An admission laboratory–based method is more accessible, user-friendly, and more objective. Additionally, as it is not diagnosis-specific, it does not depend on the accuracy of ICD-10 coding in hospitals, which continues to pose challenges.

Previous investigators have evaluated the use of routine laboratory data to predict in-hospital mortality. In 1995, Pine and colleagues evaluated patients admitted with acute myocardial infarction, congestive heart failure, or pneumonia (n = 5966) to several acute care hospitals in Missouri to develop a predictive model for hospital mortality. These investigators included laboratory tests (blood chemistry, hematology, and arterial blood gases) and administrative data (age, sex, admission source, principal and secondary diagnoses based on ICD-9-CM codes) in their predictive model (c = 0.86).¹⁸ In 2005, Prytherch et al. used 1 year of adult hospital discharges from general medicine floors (n = 9497) to predict in-hospital mortality from routine laboratory tests (urea, sodium, potassium, albumin, hemoglobin, white blood cell count, creatinine), age, gender, and mode of admission (elective or emergency) (average c = 0.77).¹⁶ Limitations with both of these studies include small sample sizes and restriction to specific medical floors or services.

Froom et al. also developed a predictive model for hospital mortality among 10,308 patients hospitalized in internal medicine wards in a regional hospital over a 1-year period. Froom’s final model included age and admission laboratory tests (albumin, alkaline phosphatase, aspartate aminotransferase, urea, glucose, lactate dehydrogenase, neutrophil count, total leukocyte count) (c = 0.89).¹⁵ The investigators validated their model using data from the subsequent year; however, the investigators did not evaluate the model’s calibration, which is essential to assess the utility of a predictive model. Assadollahi et al. used a case-control design (550 cases and 1100 controls) to develop a simple clinical scoring system predicting in-hospital patient mortality at admission using seven laboratory variables (age, urea, hemoglobin, white blood cell count, platelet count, sodium, glucose) (c = 0.87).¹³ Although they selected both medical and surgical patients, they did restrict their study population to only patients admitted through the emergency room. They observed a lower score calibration in the highest score strata, likely as there were only small numbers of patients in this group, a similar phenomenon to what was observed in our model. To our knowledge, this study is the first to predict hospital-wide patient severity of illness using admission laboratory values.

We evaluated a large cohort of patients across several years. However, future validation of our results across other hospitals is necessary. Also, we were unable to include other laboratory tests that are potentially associated with mortality (i.e., albumin, alkaline phosphate, alanine aminotransferases, aspartate aminotransferases, coagulation tests, lactate dehydrogenase) as they were not ordered within 24 h of admission for the majority (> 80%) of patients during our study period. This limitation likely exists in all hospital datasets; furthermore, our model incorporates commonly ordered laboratory tests and is therefore applicable to most hospitalized patients and less likely to be affected by missing data in real-world use. Additionally, our outcome was a rare event in the study population, which may explain our lower model calibration particularly among those patients with higher mortality risk as the sample size used to inform this prediction was limited. Our database is also limited by the availability of MS-DRG codes for the totality of our cohort. As the majority of national hospitals, MS-DRG codes are only available for Medicare and Medicaid patients, as hospitals are required by CMS to report these codes only for this particular group of patients. Although it is beyond the scope of this manuscript, future studies could compare our approach with the CMS-DRG system. Future research using admission laboratory tests could include additional statistical techniques such as machine learning and the use of prediction rules/tools built into electronic medical records.

In conclusion, our findings suggest admission laboratory tests can predict severity of illness in a simple, widely available, and diagnosis non-specific manner assisting both clinicians with patient prognosis and healthcare researchers with adjusting for severity of illness in clinical studies.

Funders

K24AI079040 from the National Institutes of Health (NIH) (Dr. A.D. Harris)

Compliance with Ethical Standards

University of Maryland Baltimore Institutional Review Board approved this study (HP-00040458).

Conflict of Interest

The authors declare that they do not have a conflict of interest.