Methods for Evaluating Causality in Observational Studies

Abstract

Background

In clinical medical research, causality is demonstrated by randomized controlled trials (RCTs). Often, however, an RCT cannot be conducted for ethical reasons, and sometimes for practical reasons as well. In such cases, knowledge can be derived from an observational study instead. In this article, we present two methods that have not been widely used in medical research to date.

Methods

The methods of assessing causal inferences in observational studies are described on the basis of publications retrieved by a selective literature search.

Results

Two relatively new approaches—regression-discontinuity methods and interrupted time series—can be used to demonstrate a causal relationship under certain circumstances. The regression-discontinuity design is a quasi-experimental approach that can be applied if a continuous assignment variable is used with a threshold value. Patients are assigned to different treatment schemes on the basis of the threshold value. For assignment variables that are subject to random measurement error, it is assumed that, in a small interval around a threshold value, e.g., cholesterol values of 160 mg/dL, subjects are assigned essentially at random to one of two treatment groups. If patients with a value above the threshold are given a certain treatment, those with values below the threshold can serve as control group. Interrupted time series are a special type of regression-discontinuity design in which time is the assignment variable, and the threshold is a cutoff point. This is often an external event, such as the imposition of a smoking ban. A before-and-after comparison can be used to determine the effect of the intervention (e.g., the smoking ban) on health parameters such as the frequency of cardiovascular disease.

Conclusion

The approaches described here can be used to derive causal inferences from observational studies. They should only be applied after the prerequisites for their use have been carefully checked.

The fact that correlation does not imply causality was frequently mentioned in 2019 in the public debate on the effects of diesel emission exposure (1, 2). This truism is well known and generally acknowledged. A more difficult question is how causality can be unambiguously defined and demonstrated (box 1). According to the eighteenth-century philosopher David Hume, causality is present when two conditions are satisfied: 1) B always follows A—in which case, A is called a “sufficient cause” of B; 2) if A does not occur, then B does not occur—in which case, A is called a “necessary cause” of B (3). These strict logical criteria are only rarely met in the medical field. In the context of exposure to diesel emissions, they would be met only if fine-particle exposure always led to lung cancer, and lung cancer never occurred without prior fine-particle exposure. Of course, neither of these is true. So what is biological, medical, or epidemiological causality? In medicine, causality is generally expressed in probabilistic terms, i.e. exposure to a risk factor such as cigarette smoking or diesel emissions increases the probability of a disease, e.g., lung cancer. The same understanding of causality applies to the effects of treatment: for instance, a certain type of chemotherapy increases the likelihood of survival in patients with a diagnosis of cancer, but does not guarantee it.

BOX 1. Causality in epidemiological observational studies (modified from Parascondola and Weed [34]).

1. ausality as production: A produces B. Causality is to be distinguished from mere temporal sequence. It does not suffice to note that A is always followed by B; rather, A must in some way produce, lead to, or create B. However, it remains unclear what ’producing’, ‘leading to’, or ‘creating’ exactly means. On a practical level, the notion of production is what is illustrated in the diagrams of cause-and-effect relationships that are commonly seen in medical publications.

2. Sufficient and necessary causes: A is a sufficient cause of B if B always happens when A has happened. A is a necessary cause of B if B only happens when A has happened. Although these relationships are logically clear and seemingly simple, this type of deterministic causality is hardly ever found in real-life scientific research. Thus, smoking is neither a sufficient nor a necessary cause of lung cancer. Smoking is not always followed by lung cancer (not a sufficient cause), and lung cancer can occur in the absence of tobacco exposure (not a necessary cause, either).

3. Sufficient component cause: This notion was developed in response to the definitions of sufficient and necessary causes. In this approach, it is assumed that multiple causes act together to produce an effect where no single one of them could do so alone. There can also be different combinations of causes that produce the same effect.

4. Probabilistic causality: In this scenario, the cause (A) increases the probability (P) that the effect (B) will occur: in symbols, P (B | A) > (B | not A). Sufficient and necessary causes, as defined above in (2), are only those extreme cases in which P (B | A) = 1 and P (B | not A) = 0, respectively. When these probabilities take on values that are neither 0 nor 1, causality is no longer deterministic, but rather probabilistic (stochastic). There is no assumption that a cause must be followed by an effect. This viewpoint corresponds to the method of proceeding in statistically oriented scientific disciplines.

5. Causal inference: This is the determination that a causal relationship exists between two types of event. Causal inferences are made by analyzing the changes in the effect that arise when there are changes in the cause. Causal inference goes beyond the mere assertion of an association and is connected to a number of specific concepts: some that have been widely discussed recently are counterfactuals, potential outcomes, causal diagrams, and structural equation models (36, 37).

6. Triangulation: Not all questions can be answered with an experiment or a randomized controlled trial. Alternatively, methodological pluralism is needed, or, as it is now sometimes called, triangulation: confidence in a finding increases when the same finding is arrived at from multiple data sets, multiple scientific disciplines, multiple theories, and/or multiple methods (35).

7. The criterion of consequentiality: The claim that a causal relationship exists has consequences on a societal level (taking action or not taking action). Olsen has called for the formulation of a criterion to determine when action should be taken and when not (7).

In many scientific disciplines, causality must be demonstrated by an experiment. In clinical medical research, this purpose is achieved with a randomized controlled trial (RCT) (4). An RCT, however, often cannot be conducted for either ethical or practical reasons. If a risk factor such as exposure to diesel emissions is to be studied, persons cannot be randomly allocated to exposure or non-exposure. Nor is any randomization possible if the research question is whether or not an accident associated with an exposure, such as the Chernobyl nuclear reactor disaster, increased the frequency of illness or death. The same applies when a new law or regulation, e.g., a smoking ban, is introduced.

When no experiment can be conducted, observational studies need to be performed. The object under study—i.e., the possible cause—cannot be varied in a targeted and controlled way; instead, the effect this factor has on a target variable, such as a particular illness, is observed and documented.

Several publications in epidemiology have dealt with the ways in which causality can be inferred in the absence of an experiment, starting with the classic work of Bradford Hill and the nine aspects of causality (viewpoints) that he proposed (box 2) (5) and continuing up to the present (6, 7).

BOX 2. The Bradford Hill criteria for causality (modified from [5]).

1. Strength: the stronger the observed association between two variables, the less likely it is due to chance.

2. Consistency: the association has been observed in multiple studies, populations at risk, places, and times, and by different researchers.

3. Specificity: it is a strong argument for causality when a specific population suffers from a specific disease.

4. Temporality: the effect must be temporally subsequent to the cause.

5. Biological gradient: the association displays a dose–response effect, e.g., the incidence of lung cancer is greater when more cigarettes are smoked per day.

6. Plausibility: a plausible mechanism linking the cause to the effect is helpful, but not absolutely required. What is biologically plausible depends upon the state-of-the-art knowledge of the time.

7. Coherence: the causal interpretation of the data should not conflict with biological knowledge about the disease.

8. Experiment: experimental evidence should be adduced in support, if possible.

9. Analogy: an association speaks for causality if similar causes are already known to have similar effects.

Aside from the statistical uncertainty that always arises when only a sample of an affected population is studied, rather than its entirety (8), the main obstacle to the study of putative causal relationships comes from confounding variables (“confounders”). These are so named because they can, depending on the circumstances, either obscure a true effect or simulate an effect that is, in fact, not present (9). Age, for example, is a confounder in the study of the association between occupational radiation exposure and cataract (10), because both cumulative radiation exposure and the risk of cataract rise with increasing age.

The various statistical methods of dealing with known confounders in the analysis of epidemiological data have already been presented in other articles in this series (9, 11, 12). In the current article, we discuss two new approaches that have not been widely applied in medical and epidemiological research to date.

Methods of evaluating causal inferences in observational studies

The main advantage of an RCT is randomization, i.e., the random allocation of the units of observation (patients) to treatment groups. Potential confounders, whether known or unknown, are thereby distributed to the treatment groups at random as well, although differences between groups may arise through sample variance. Whenever randomization is not possible, the effect of confounders must be taken into account in the planning of the study and in data analysis, as well as in the interpretation of study findings.

Classic methods of dealing with confounders in study planning are stratification and matching (13, 14), as well as so-called propensity score matching (PSM) (11).

The best-known and most commonly used method of data analysis is regression analysis, e.g., linear, logistic, or Cox regression (15). This method is based on a mathematical model created in order to explain the probability that any particular outcome will arise as the combined result of the known confounders and the effect under study.

Regression analyses are used in the analysis of clinical or epidemiological data and are found in all commonly used statistical software packages. However, they are often used inappropriately because the prerequisites for their correct application have not been checked. They should not be used, for example, if the sample is too small, if the number of variables is too large, or if a correlation between the model variables makes the results uninterpretable (16).

Regression-discontinuity methods

Regression-discontinuity methods have been little used in medical research to date, but they can be helpful in the study of cause-and-effect relationships from observational data (17). Regression-discontinuity design is a quasi-experimental approach (box 3) that was developed in educational psychology in the 1960s (18). It can be used when a threshold value of a continuous variable (the “assignment variable”) determines the treatment regimen to which each patient in the study is assigned (box 4).

BOX 3. Terms used to characterize experiments (18).

• Experiment/trial A study in which an intervention is deliberately introduced in order to observe an effect.

• Randomized experiment/trial An experiment in which persons, patients, or other units of observation are randomly assigned to one of two or more treatment groups (or intervention groups).

• Quasi-experiment An experiment in which the units of observation are not randomly assigned to the treatment/intervention groups.

• Natural experiment A study in which a natural event (e.g., an earthquake) is compared with a comparison scenario.

• Non-experimental observational study A study in which the size and direction of the association between two variables is determined.

BOX 4. Regression-discontinuity methods.

In the simplest case, that of a linear regression, the parameters in the following model are to be estimated:

y_i = ß ₀ + ß ₁ z _i + ß ₂ (x _i - x _c) + e _i,

where:

i from 1 to N represents the statistical units

y is the outcome

ß ₀ is the y-intercept

z is a dichotomous variable (0, ) indicating whether the patient was treated (1) or not treated (0)

x is the assignment variable

x _c is the threshold

ß ₁ is the effect of treatment

ß ₂ is the regression coefficient of the assignment variable

e is the random error

A possible assignment variable could be, for example, the serum cholesterol level: consider a study in which patients with a cholesterol level of 160 mg/dL or above are assigned to receive a therapy. Since the cholesterol level (the assignment variable) is subject to random measurement error, it can be assumed that patients whose level of cholesterol is close to the threshold (160 mg/dL) are randomly assigned to the different treatment regimens. Thus, in a small interval around the threshold value, the assignment of patients to treatment groups can effectively be considered random (18). This sample of patients with near-threshold measurements can thus be used for the analysis of treatment efficacy. For this line of argument to be valid, it must truly be the case that the value being measured is subject to measuring error, and that there is practically no difference between persons with measured values slightly below or slightly above threshold. Treatment allocation in this narrow range can be considered quasi-random.

This method can be applied if the following prerequisites are met:

• The assignment variable is a continuous variable that is measured before the treatment is provided. If the assignment variable is totally independent of the outcome and has no biological, medical, or epidemiological significance, the method is theoretically equivalent to an RCT (19).

• The treatment must not affect the assignment variable (18).

• The patients in the two treatment groups with near-threshold values of the assignment variable must be shown to be similar in their baseline properties, i.e., covariables, including possible confounders. This can be demonstrated either with statistical techniques or graphically (20).

• The range of the assignment variable in the vicinity of the threshold must be optimally set: it must be large enough to yield samples of adequate size in the treatment groups, yet small enough that the effect of the assignment variable itself does not alter the outcome being studied. Methods of choosing this range appropriately are available in the literature (21, 22).

• The treatment can be decided upon solely on the basis of the assignment variable (deterministic regression-discontinuity methods), or on the basis of other clinical factors (fuzzy regression-discontinuity methods).

Example 1: The one-year mortality of neonates as a function of the intensity of medical and nursing care was to be studied, where the intensity of care was determined by a birth-weight threshold: infants with very low birth weight (<1500 g) (group A) were cared for more intensively than heavier infants (group B) (23). The question to be answered was whether the greater intensity of care in group A led to a difference in mortality between the two groups. It was assumed that children with birth weight near the threshold are identical in all other respects, and that their assignment to group A or group B is quasi-random, because the measured value (birth weight) is subject to a relatively small error. Thus, for example, one might compare children weighing 1450–1500 g to those weighing 1501–1550 g at birth to study whether, and how, a greater intensity of care affects mortality.

In this example, it is assumed that the variable “birth weight” has a random measuring error, and thus that neonates whose (true) weight is near the threshold will be randomly allocated to one or the other category. But birth weight itself is an important factor affecting infant mortality, with lower birth weight associated with higher mortality (23); thus, the interval taken around the threshold for the purpose of this study had to be kept narrow. The study, in fact, showed that the children treated more intensively because their birth weight was just below threshold had a lower mortality than those treated less intensively because their birth weight was just above threshold.

Example 2: A regression-discontinuity design was used to evaluate the effect of a measure taken by the Canadian government: the introduction of a minimum age of 19 years for alcohol consumption. The researchers compared the number of alcohol-related disorders and of violent attacks, accidents, and suicides under the influence of alcohol in the months leading up to (group A) and subsequent to (group B) the 19^th birthday of the persons involved. It was found that persons in group B had a greater number of alcohol-related inpatient treatments and emergency hospitalizations than persons in group A. With the aid of this quasi-experimental approach, the researchers were able to demonstrate the success of the measure (24). It may be assumed that the two groups differed only with respect to age, and not with respect to any other property affecting alcohol consumption.

Interrupted time series

Interrupted time series are a special type of regression-discontinuity design in which time is the assignment variable. The cutoff point is often an external event that is unambiguously identifiable as having occurred at a certain point in time, e.g., an industrial accident or a change in the law. A before-and-after comparison is made in which the analysis must still take adequate account of any relevant secular trends and seasonal fluctuations (box 5).

BOX 5. Interrupted time series.

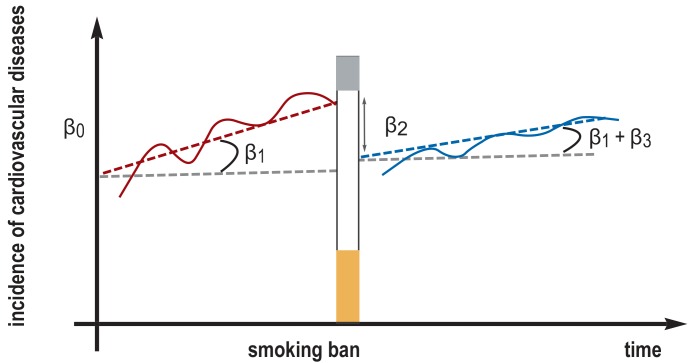
In the simplest case of a study involving an interrupted time series, the temporal sequence is analyzed with a piecewise regression. The following model is used to study both a shift in slope and a shift in the level of an outcome before and after an intervention, e.g., the introduction of a law banning smoking (figure 2):

y = ß ₀ + ß ₁ × time + ß ₂ × intervention + ß ₃ × time × intervention + e,

where:

y is the outcome, e.g., cardiovascular diseases

intervention is a dummy variable for the time before (0) and after (1) the intervention (e.g., smoking ban)

time is the time since the beginning of the study

ß ₀ is the baseline incidence of cardiovascular diseases

ß ₁ is the slope in the incidence of cardiovascular diseases over time before the introduction of the smoking ban

ß ₂ is the change in the incidence level of cardiovascular diseases after the introduction of the smoking ban (level effect)

ß ₃ is the change in the slope over time (cf. ß ₁) after the introduction of the smoking ban (slope effect)

e is the random error

The prerequisites for the use of this method must be met (18, 25):

• Interrupted time series are valid only if a single intervention took place in the period of the study.

• The time before the intervention must be clearly distinguishable from the time after the intervention.

• There is no required minimum number of data points, but studies with only a small number of data points or small effect sizes must be interpreted with caution. The power of a study is greatest when the number of data points before the intervention equals the number after the intervention (26).

• Although the equation in Box 5 has a linear specification, polynomial and other nonlinear regression models can be used as well. Meticulous study of the temporal sequence is very important when a nonlinear model is used.

• If an observation at time t—e.g., the monthly incidence of cardiovascular diseases—is correlated with previous observations (autoregression), then the appropriate statistical techniques must be used (autoregressive integrated moving average [ARIMA] models).

Example 1: In one study, the rates of acute hospitalization for cardiovascular diseases before and after the temporary closure of Heathrow Airport because of volcanic ash were determined to investigate the putative effect of aircraft noise (27). The intervention (airport closure) took place from 15 to 20 April 2010. The hospitalization rate was found to have decreased among persons living in the urban area with the most aircraft noise. The number of observation points was too low, however, to show a causal link conclusively.

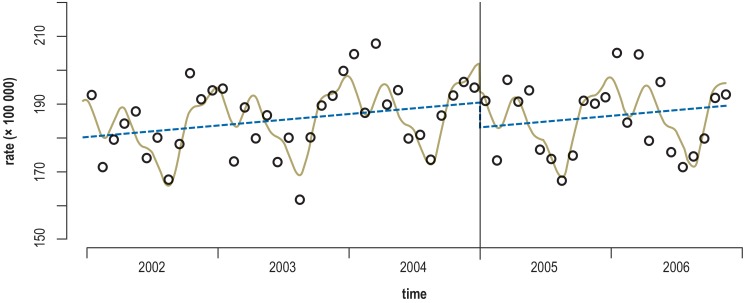
Example 2: In another study, the rates of hospitalization before and after the implementation of a smoking ban (the intervention) in public areas in Italy were determined (28). The intervention occurred in January 2004 (the cutoff time). The number of hospitalizations for acute coronary events was measured from January 2002 to November 2006 (figure 1). The analysis took account of seasonal dependence, and an effect modification for two age groups—persons under age 70 and persons aged 70 and up—was determined as well. The hospitalization rate declined in the former group, but not the latter.

Figure 1.

Age-standardized hospitalization rates for acute coronary events (ACE) in persons under age 70 before and after the implementation of a smoking ban in public places in Italy, studied with the corresponding methods (30). The observed and predicted rates are shown (circles and solid lines, respectively). The dashed lines show the seasonally adjusted trend in ACE before and after the introduction of the nationwide smoking ban.

Discussion

The necessary distinction between causality and correlation is often emphasized in scientific discussions, yet it is often not applied strictly enough. Furthermore, causality in medicine and epidemiology is mostly probabilistic in nature, i.e., an intervention alters the probability that the event under study will take place. A good illustration of this principle is offered by research on the effects of radiation, in which a strict distinction is maintained between deterministic radiation damage on the one hand, and probabilistic (stochastic) radiation damage on the other (29). Deterministic radiation damage—radiation-induced burns or death—arises with certainty whenever a subject receives a certain radiation dose (usually a high one). On the other hand, the risk of cancer-related mortality after radiation exposure is a stochastic matter. Epidemiological observations and biological experiments should be evaluated in tandem to strengthen conclusions about probabilistic causality (box 1).

While RCTs still retain their importance as the gold standard of clinical research, they cannot always be carried out. Some indispensable knowledge can only be obtained from observational studies. Confounding factors must be eliminated, or at least accounted for, early on when such studies are planned. Moreover, the data that are obtained must be carefully analyzed. And, finally, a single observational study hardly ever suffices to establish a causal relationship.

In this article, we have presented two newer methods that are relatively simple and which, therefore, could easily be used more widely in medical and epidemiological research (30). Either one should be used only after the prerequisites for its applicability have been meticulously checked. In regression-discontinuity methods, the assumption of continuity must be verified: in other words, it must be checked whether other properties of the treatment and control groups are the same, or at least equally balanced. The rules of group assignment and the role played by the continuous assignment variable must be known as well. Regression-discontinuity methods can generate causal conclusions, but any such conclusion will not be generalizable if the treatment effects are heterogeneous over the range of the assignment variable. The estimate of effect size is applicable only in a small, predefined interval around the threshold value. It must also be checked whether the outcome and the assignment variable are in a linear relationship, and whether there is any interaction between the treatment and assignment variables that needs to be considered.

In the analysis of interrupted time series, the assumption of continuity must be tested as well. Furthermore, the method is valid only if the occurrence of any other intervention at the same time point as the one under study can be ruled out (20). Finally, the type of temporal sequence must be considered, and more complex statistical methods must be applied, as needed, to take such phenomena as autoregression into account.

Observational studies often suggest causal relationships that will then be either supported or rejected after further studies and experiments. Knowledge of the effects of radiation exposure was derived, at first, mainly from observations on victims of the Hiroshima and Nagasaki atomic bomb explosions (31). These findings were reinforced by further epidemiological studies on other populations exposed to radiation (e.g., through medical procedures or as an occupational hazard), by physical considerations, and by biological experiments (32). A classic example from the mid-19^th century is the observational study by Snow (33): until then, the biological cause of cholera was unknown. Snow found that there had to be a causal relationship between the contamination of a well and a subsequent outbreak of cholera. This new understanding led to improved hygienic measures, which did, indeed, prevent infection with the cholera pathogen. Cases such as these prove that it is sometimes reasonable to take action on the basis of an observational study alone (6). They also demonstrate, however, that further studies are necessary for the definitive establishment of a causal relationship.

Figure 2.

The effect of a smoking ban on the incidence of cardiovascular diseases

Key messages.

• Causal inferences can be drawn from observational studies, as long as certain conditions are met.

• Confounding variables are a major impediment to the demonstration of causal links, as they can either obscure or mimic such a link.

• Random assignment leads to the even distribution of known and unknown confounders among the intervention groups that are being compared in the study.

• In the regression-discontinuity method, it is assumed that the assignment of patients to treatment groups is random with, in a small range of the assignment variable around the threshold, with the result that the confounders are randomly distributed as well.

• The interrupted time series is a variant of the regression-discontinuity method in which a given point in time splits the subjects into a before group and an after group, with random distribution of confounders to the two groups.