Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2020 Mar 6;5(10):5529–5533. doi: 10.1021/acsomega.0c00167

Modeling of Nanoscale Electromagnets Based on Gold Finite Nanosolenoids

Pavel N D’yachkov 1,*, Evgeny P D’yachkov 1
PMCID: PMC7081633  PMID: 32201845

Abstract

graphic file with name ao0c00167_0004.jpg

Magnetic fields generated by the nanosolenoids based on the (5, 3) and (10,7) gold nanotubes (AuNTs) 12–600 Å long with numbers of Au atoms 20–2000 are calculated. The electron energy levels of the finite length tubules were determined using the linearized augmented cylindrical waves method with Born–von Karman cyclic boundary conditions and on account of a helical symmetry of the AuNTs. Using these data, the numbers of conducting channels NF and the low-temperature ballistic electron currents in the finite AuNTs are determined, and finally, the magnetic fields B of the gold nanosolenoids are obtained. Due to the increase in the number of conduction channels with the increase in the length of the tubes, the internal magnetic field gradually increases from 1.6 T/V in a tubule with L = 12 Å up to 12 T/V in a tube with L = 600 Å, slowly approaching the magnetic field of 14 T/V of the infinite (5, 3) AuNT. At a distance of 5 Å from the ends of the tubes (near z = L/2 – 5 Å), this field decreases rapidly, halving at z = L/2 and almost zeroing near z = L/2 + 5 Å. The field from the outside of the tubes is weak but not zero as in the infinite tubule. It is minimal at z = 0 and reaches a maximum at the edge of the AuNTs, where it is about 3–4 times less than the internal field. These results pave the way for a more realistic design of the nanosolenoids.

I. Introduction

Advancement of nanotechnology has greatly accelerated the miniaturization of electronic components and devices. This progress resulted in growing interest in a design of the nanoscale electromagnets and inductors, in which a helicoidal electron flow through a nanowire generates the magnetic fields. However, to date, a very small number of such elements have been proposed outside the framework of conversional silicon technology. It was suggested that the chiral graphene nanoribbons or nanotubes can be properly organized in a form of nanosolenoids to yield the helicoidal currents and magnetic fields strong, confined, and tunable by the nanomaterial composition, chirality, and diameter.1−8 However, the ideal carbon (n1, n2) nanotubes are not quite suitable for this since the nanosolenoids require materials with a metallic type of conductivity, but such tubules with n1 – n2 indivisible by 3 are dielectrics and those with n1 – n2 divisible by 3 are essentially metallic, but the band gaps usually emerge in this case due to the effects of the cylindrical surface curvature.8−11 Thus, the chemically modified tubules are to be used for these purposes. For example, the nanosolenoids based on a hetero-nanotube consisting of the spiral carbon and boron nitride strips were proposed, and their electrical and magnetic properties were calculated.1 An electromagnetic conversion in the solenoid in a form of the helical graphene nanostructures joined in a single layer wound around a dislocation line was suggested and theoretically studied, too.2 As examples of pure carbon-based materials, one can also cite the nanometer-sized graphite helical structures, which behave as a collection of individual, closely packed nanosolenoids,4 some graphene spiral structures,5 and the various helically coiled nanotubes with very complex structures.6,7 The large magnetic fields are anticipated to be realized using solenoids with the carbon nanotubes-copper composite materials.8 Finally, our previous calculations show that much more efficient nanosolenoids are possible if one turns from carbon to the chiral gold nanotubes (AuNTs).12 Note that, in all previous calculations, the not quite realistic models of the infinite nanosolenoids were considered when the end effects were neglected.

Back in 2003, the 5 nm long (5, 3) AuNTs were successfully synthesized by electron beam thinning of a gold foil in an electron microscope.13 The atomic geometry of single-walled AuNTs resembles that of the carbon tubules, where the honeycomb network of the C atoms is replaced by the triangular network of the Au atoms with a Au–Au bong length equal to 2.9 Å. Over the past years, there was great progress in the synthesis of AuNTs. The single-walled and multiwalled tubules and rings were obtained;14−19 in the latter, the length and diameter are of the same order of magnitude. Knowledge of their properties expanded very significantly. They exhibit distinct electrical, optical, electrochemical, transport, and catalytic properties.14−25 Their use for solving the problems of enantioseparation, protein and immunosensing, DNA detection, and photothermal cell ablation is discussed in a recent review.17

The purpose of this work is to calculate and plot the radial and axial magnetic fields within and outside the finite chiral AuNT nanosolenoids. The analysis was carried out on the example of (5, 3) AuNTs 12–600 Å long with the numbers of Au atoms between 20 and 1000. For comparison, the analogous data for the (10, 7) AuNTs are presented in the Supporting Information. We hope that these results pave the way for a more realistic design of the nanosolenoids. To the best of our knowledge, this is the first study of the finite-length nanosolenoid where the fringe effects were not ignored.1−12 It is shown that the magnetic fields of the finite nanosolenoids can be an order of magnitude smaller than the field of infinite ones, and spatial distribution of fields is more complex.

II. Results and Discussion

Figure 1 shows a nanotube in contact with two electrodes. According to Ampère’s law, for the infinite-length solenoids, the magnetic field B = μnj inside the tubules does not depend on their diameters and on the distance from the axis but only on the current j and the number n of its turns per unit length, the field lines being parallel the tube axis. This is not so for the finite continuous solenoids, and the formulas for magnetic field in this case are somewhat more complex. They are presented below in the Method of Calculation section.

Figure 1.

Figure 1

Open in a new tab

Finite-length gold nanosolenoid and magnetic field created described using field lines.

Figure 2 shows the energy level diagrams of the finite (5, 3) AuNTs. The energy reference point is located at the highest occupied levels. The highest levels play a role of the Fermi level in the finite-length nanotubes; the ballistic electronic transport is carried out through these levels at low temperatures and applied voltages. In tubes with lengths L = 12 and 24 Å, there is one such level (NF = 1), and NF = 2 and 3 in tubes with L = 60 and 120 Å, respectively, which in all cases is significantly smaller than NF = 8 for the infinite (5, 3) AuNT.12 In proportion to the decrease in the NF values by 8, 4, and 2.7 times, the current should decrease when switching to the short tubes. In the (5, 3) gold tubule 600 Å long, the value of NF = 7 approaches the NF = 8 value of the infinite tube.

Figure 2.

Figure 2

Open in a new tab

Electron energy levels of finite AuNTs.

Figure 3 shows the dependences of the magnetic field on the coordinates z and ρ of (5, 3) AuNTs with lengths L of 12–600 Å. Due to the increase in the number of conduction channels with the increase in the length of the tubules, the internal magnetic field gradually increases from 1.6 T/V in tubes with lengths L = 12 and 24 Å to the 3, 5, and 12 T/V in tubes with L = 60, 120, and 600 Å, slowly approaching the magnetic field of 14 T/V of the infinite (5, 3) AuNT.12 In the free space inside the finite tubules, the magnetic field depends on the distance ρ from the tube’s axis and z coordinate. At a distance of about 5 Å from the end of the tubes (near z = L/2 – 5 Å), this field begins to decrease rapidly, halving at z = L/2 and almost zeroing near z = L/2 + 5 Å. The field from the outside of the tubes is weak but not zero as in the case of the infinite tubule. It is minimal at z = 0 and reaches a maximum at the edge of the AuNTs at z = L/2, where it is about 3–4 times less than the internal field.

Figure 3.

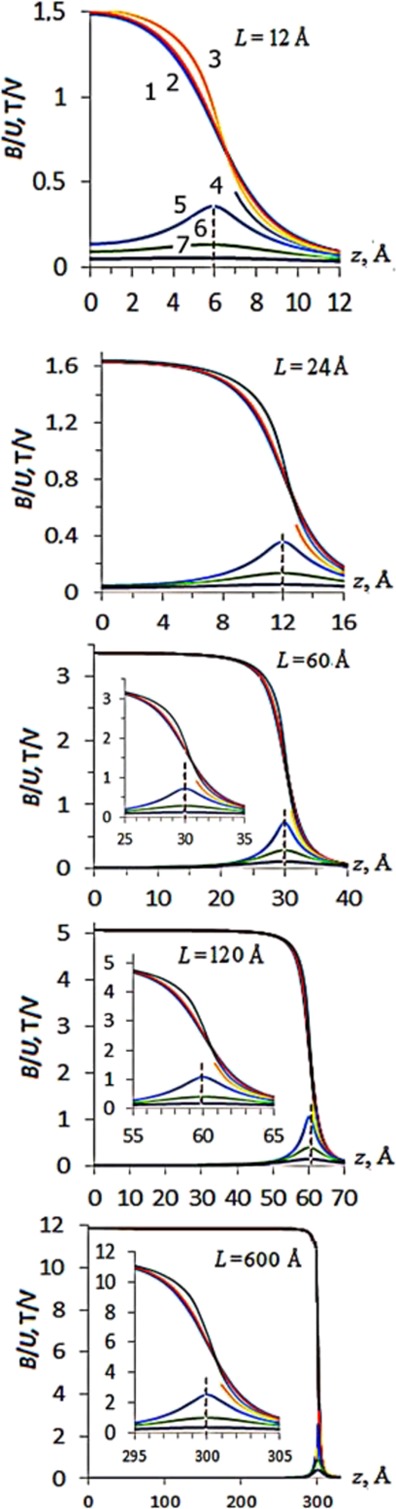
Figure 3

Open in a new tab

Magnetic fields of (5, 3) AuNTs; insets show the fields near the edges of three longer tubules. Field lines are calculated for free space bounded by van der Waals tube dimensions. The dotted lines indicate the edges of tubes. Here, (1) ρ = 0 corresponds to the nanotube center; (2) ρ = (a – rvdW)/2 = 1.15 Å corresponds to the space between the axis and inner van der Waals border of the tubule (here, rvdW = 0.9 Å is the van der Waals radius of the gold atom); (3) ρ = a – rvdW = 2.3 Å is the inner van der Waals boundary; (4) for ρ = a, the field is calculated outside the fringe of tubes for z ≥ L/2 + 0.9 Å; (5) ρ = a + rvdW = 4.1 Å is the outer van der Waals boundary; (6) ρ = 6 Å; (7) ρ = 9 Å.

In addition to the magnetic field, the finite solenoids are characterized by a self-induction Inline graphic, which is calculated by the formula Inline graphic = μn2SL. The self-induction depends only on the length L and cross section area S = πa2 of the solenoids but not on the current or operational voltage; for example, Inline graphic is equal to about 10–13 H for the tubule with L = 60 Å having about the 100 Au atoms.

III. Concluding Remarks

The magnetic fields generated by the chiral (5, 3) AuNT-based nanosolenoids are calculated. The relationships between the tubule’s length, their electron energy levels, ballistic transport, and magnetic fields of solenoids are analyzed. The transition from the infinite to finite tubes is accompanied by the change of the dispersion electron curves in the Fermi level region for the discrete electronic spectrum, by the decrease in the number of electron transport channels, and by the weakening of the magnetic field of the solenoids. These results can be considered as yet another manifestation of the fundamental mechanism of the change in the metallic properties of an extended material to the molecular properties of nanoparticles, which has been noted recently in ref (34). In the 12 Å long (5, 3) AuNTs containing about 100 Au atoms, the magnetic field is 8 times smaller than that in the infinite tubule. The magnetic field reaches the maximum in the center of the finite tubes and quickly decreases at a distance of ±5 Å from their edges. The data for the (10, 7) AuNTs presented in the Supporting Information reasonably agree with magnetic properties of the (5, 3) tubules.

IV. Method of Calculation

Following the methods described elsewhere,26,27 consider a single circular current on a surface of an imaginary cylinder of radius a and length L, with its centroid at the origin of a cylindrical coordinate system ρ, θ, z and its axis aligned with the z direction (Figure 4).

Figure 4.

Figure 4

Open in a new tab

Single circular current j on an imaginary cylindrical surface.

The magnetic field B due to this coil is given in terms of the vector potential A by

IV. 1

Only the Aθ component can be nonzero due to the cylindrical symmetry; therefore, eq 1 for the radial and axial components yields

IV. 2

and Bθ = 0. For a single circular current j, one has

IV. 3

where R is the distance from the local point on the current circle to the field point. For the continuous solenoids made up of a series of n circular currents per unit length

IV. 4

where l is the axial distance from the coordinate origin. On integrating with respect to l, there follows

IV. 5

where ξ± = z ± L/2. From this equation, the field components can now be directly found26,27

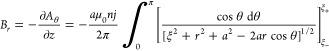IV. 6
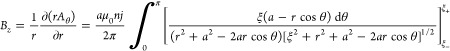IV. 7

Equations 6 and 7 describe the magnetic field in terms of the geometry characteristics a, L, and n of the solenoid. For the (5, 3) AuNTs, a = 2.3 Å, n = 1.74,12 and the nanotube lengths L were varied between 12 and 600 Å in this work. The numerical results were found by integrating these equations on a computer. It remains to find out the electron current j.

The length of AuNTs determines the electrons tunneling between the cathode and anode through the nanomaterial. According the Landauer formalism28,29 applied successfully to the gold nanowires and tubules in refs (30) and (31), at low temperatures, the current j depends on the numbers of conducting channels at the Fermi level NF and applied voltage U

IV. 8

The constant G0 = 7.748 × 10–5 Ω–1 is called the conduction quantum. It remains to obtain the NF values for the AuNTs. For this, we calculated the electronic energy levels of the tubules of various lengths. (Recall that NF = n1 + n2 for the infinite (n1, n2) AuNTs12).

As in the previous calculation of the band structure of infinite AuNTs, the energy levels of the finite-length tubules were calculated by the linearized augmented cylindrical waves (LACW) method.11,32,33 The Born–von Karman cyclic boundary conditions and helical symmetry of the AuNTs were used, which allows one to determine the monatomic unit cell and describe the geometry of finite tubes as a result of helical translations of only one Au atom. The LACW method described in detail elsewhere is just a reformulation of the linear augmented plane-wave (LAPW) technique well-known in the theory of solids for the case of tubular multiatomic systems. It applies the muffin-tin and local density approximations for the electron potential, and the nanotube electronic structure is determined by the free electron movement in the cylindrical monoatomic layer and by electrons scattering on the atomic potentials, the structural information being used as input data.

Acknowledgments

This work was supported by IGIC RAS state assignment and by the Russian Basic Research Foundation (Grant 19-43-340005).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c00167.

  • Here, the electron energy levels and magnetic fields of the finite (10, 7) AuNTs are presented (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao0c00167_si_001.pdf (173.8KB, pdf)

References

  1. Zhang Z. Y.; Miao C.; Guo W. Nano-solenoid: Helicoid Carbon–Boron Nitride Hetero-Nanotube. Nanoscale 2013, 5, 11902–11909. 10.1039/c3nr02914j. [DOI] [PubMed] [Google Scholar]
  2. Xu F.; Sadrzadeh A.; Xu Z.; Yakobson B. I. XTRANS: An Electron Transport Package for Current Distribution and Magnetic Field in Helical Nanostructures. Comput. Mater. Sci. 2014, 83, 426–433. 10.1016/j.commatsci.2013.11.043. [DOI] [Google Scholar]
  3. Xu F.; Yu H.; Sadrzadeh A.; Yakobson B. I. Riemann Surfaces of Carbon as Graphene Nanosolenoids. Nano Lett. 2016, 16, 34–39. 10.1021/acs.nanolett.5b02430. [DOI] [PubMed] [Google Scholar]
  4. Mitran T. L.; Nemnes G. A. Helical Graphite Metamaterials for Intense and Locally Controllable Magnetic Fields. RSC Adv. 2017, 7, 49041. 10.1039/C7RA08247A. [DOI] [Google Scholar]
  5. Avdoshenko S. M.; Koskinen P.; Sevinçli H.; Popov A. A.; Rocha C. G. Topological Signatures in the Electronic Structure of Graphene Spirals. Sci. Rep. 2013, 3, 1632. 10.1038/srep01632. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Popović Z. P.; Vuković T.; Nikolić B.; Damnjanović M.; Milošević I. Current Distribution Dependence on Electric Field in Helically Coiled Carbon Nanotubes. Contemp. Biomater. 2017, 8, 121–127. 10.7251/cm.v2i8.4405. [DOI] [Google Scholar]
  7. Brazhe R. A.; Savin A. F. Coiled Supracrystalline Nanotubes as Solenoids for Nanoelectronics. Phys. Wave Processes Radio Eng. Syst. 2015, 18, 50–54. (in Russian). [Google Scholar]
  8. James C. R.; Long J. E.; Manning D. E. Significant Multi Tesla Fields within a Solenoid Encircled by Nanostructure Windings. Sci. Rep. 2019, 9, 3143. 10.1038/s41598-018-38306-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Ouyang M.; Huang J.-L.; Cheung C. L.; Lieber C. M. Energy Gaps in “Metallic” Single-Walled Carbon Nanotubes. Science 2001, 292, 702–705. 10.1126/science.1058853. [DOI] [PubMed] [Google Scholar]
  10. Hartmann R. R.; Saroka V. A.; Portnoi M. E. Interband Transitions in Narrow-Gap Carbon Nanotubes and Graphene Nanoribbons. J. Appl. Phys. 2019, 125, 151607. 10.1063/1.5080009. [DOI] [Google Scholar]
  11. D’yachkov P. N.Quantum Chemistry of Nanotubes: Electronic Cylindrical Waves; CRC Press. Taylor and Francis: London and New York, 2019, 212 p. [Google Scholar]
  12. D’yachkov E. P.; D’yachkov P. N. Gold Nanosolenoids Based on Chiral Nanotubes Calculated Using the Relativistic Linearized Augmented Cylindrical Wave Method. J. Phys. Chem. C 2019, 123, 26005–26010. 10.1021/acs.jpcc.9b07610. [DOI] [Google Scholar]
  13. Oshima Y.; Onga A.; Takayanagi K. Helical Gold Nanotube Synthesized at 150 K. Phys. Rev. Lett. 2003, 91, 205503. 10.1103/PhysRevLett.91.205503. [DOI] [PubMed] [Google Scholar]
  14. Bridges C. R.; DiCarmine P. M.; Fokina A.; Huesmann D.; Seferos D. S. Synthesis of Gold Nanotubes with Variable Wall Thicknesses. J. Mater. Chem. A 2013, 1, 1127–1133. 10.1039/C2TA00729K. [DOI] [Google Scholar]
  15. Bridges C. R.; DiCarmine P. M.; Seferos D. S. Gold Nanotubes as Sensitive, Solution-Suspendable Refractive Index Reporters. Chem. Mater. 2012, 24, 963–965. 10.1021/cm203184d. [DOI] [Google Scholar]
  16. Hendren W. R.; Murphy A.; Evans P.; O’Connor D.; Wurtz G. A.; Zayats A. V.; Atkinson R.; Pollard R. J. Fabrication and Optical Properties of Gold Nanotube Arrays. J. Phys.: Condens. Matter 2008, 20, 362203. 10.1088/0953-8984/20/36/362203. [DOI] [Google Scholar]
  17. Shamraiz U.; Raza B.; Hussain H.; Badshah A.; Green I. R.; Kiani F. A.; Al-Harrasi A. Gold Nanotubes and Nanorings: Promising Candidates for Multidisciplinary Fields. Int. Mater. Rev. 2018, 478–512. 10.1080/09506608.2018.1554991. [DOI] [Google Scholar]
  18. Ye S.; Marston G.; McLaughlan J. R.; Sigle D. O.; Ingram N.; Freear S.; Baumberg J. J.; Bushby R. J.; Markham A. F.; Critchley K.; et al. Engineering Gold Nanotubes with Controlled Length and Near-Infrared Absorption for Theranostic Applications. Adv. Funct. Mater 2015, 2117–2127. 10.1002/adfm.201404358. [DOI] [Google Scholar]
  19. Ye S.; Marston G.; Markham A. F.; Coletta P. L.; Evans S. D. Developing Gold Nanotubes as Photoacoustic Contrast Agents. J. Phys.: Conf. Ser. 2019, 1151, 012018 10.1088/1742-6596/1151/1/012018. [DOI] [Google Scholar]
  20. Kondo Y.; Takayanagi K. Synthesis and Characterization of Helical Multi-Shell Gold Nanowires. Science 2000, 289, 606–608. 10.1126/science.289.5479.606. [DOI] [PubMed] [Google Scholar]
  21. Kohl J.; Fireman M.; O’Carroll D. M. Surface Plasmon and Photonic Mode Propagation in Gold Nanotubes with Varying Wall Thickness. Phys. Rev. B 2011, 84, 235118. 10.1103/PhysRevB.84.235118. [DOI] [Google Scholar]
  22. Wang J.; Zhang C.; Zhang J.; Song H.; Wang P.; Lu Y.; Fei G.; Xu W.; Xu W.; Zhang L.; Kivshar Y. S.; et al. Hybrid Plasmonic Cavity Modes in Arrays of Gold Nanotubes. Adv. Opt. Mater. 2016, 5, 1–11. 10.1002/adom.201600731. [DOI] [Google Scholar]
  23. Zhu L.; Wang J.; Ding F. Gold Nanotube Encapsulation Enhanced Magnetic Properties of Transition Metal Monoatomic Chains: An ab initio study. J. Chem. Phys. 2009, 130, 064706 10.1063/1.3055520. [DOI] [PubMed] [Google Scholar]
  24. Sen A.; Lin C. J.; Kaun C. C. Single-molecule Conductance through Chiral Gold Nanotubes. J. Phys. Chem. C 2013, 117, 13676–13680. 10.1021/jp402531p. [DOI] [Google Scholar]
  25. Zhang K.; Zhang H. Plasmon coupling in Gold Nanotube Assemblies: Insight from a Time-Dependent Density Functional Theory (TDDFT) Calculation. J. Phys. Chem. C 2014, 118, 635–641. 10.1021/jp410056u. [DOI] [Google Scholar]
  26. Callaghan E.; Maslen S.. The Magnetic Field of a Finite Solenoid; National Aeronautics and Space Administration: Washington, 1960. [Google Scholar]
  27. Caciagli A.; Baars R. J.; Philipse A. P.; Kuipers B. W. M. Exact Expression for the Magnetic Field of a Finite Cylinder with Arbitrary Uniform Magnetization. J. Magn. Magn. Mater. 2018, 456, 423–432. 10.1016/j.jmmm.2018.02.003. [DOI] [Google Scholar]
  28. Landauer R. Electrical Resistance of Disordered One-Dimensional Lattices. Philos. Mag. 1970, 21, 863–867. 10.1080/14786437008238472. [DOI] [Google Scholar]
  29. Chen A.-B.Basic Theory of Electron Tunneling and Ballistic Transport in Nanostructures. In Handbook of Theoretical and Computational Nanotechnology; Rieth M., Schommers W., Eds.; American Scientific Publishers: California, 2006; Vol. 1, pp 311–377. [Google Scholar]
  30. Ohnishi H.; Kondo Y.; Takayanagi K. Quantized Conductance through Individual Rows of Suspended Gold Atoms. Nature 1998, 395, 780–783. 10.1038/27399. [DOI] [Google Scholar]
  31. Oshima Y.; Mouri K.; Hirayama H.; Takayanagi K. Quantized Electrical Conductance of Gold Helical Multishell Nanowires. J. Phys. Soc. Jpn. 2006, 75, 053705 10.1143/JPSJ.75.053705. [DOI] [Google Scholar]
  32. D’yachkov P. N.; Makaev D. V. Account of Helical and Rotational Symmetries in the Linear Augmented Cylindrical Wave Method for Calculating the Electronic Structure of Nanotubes: Towards the Ab Initio Determination of the Band Structure of a (100, 99) Tubule. Phys. Rev. B 2007, 76, 195411. 10.1103/PhysRevB.76.195411. [DOI] [Google Scholar]
  33. D’yachkov P.; Makaev D. Ab Initio Spin-Dependent Band Structures of Carbon Nanotubes. Int. J. Quantum Chem. 2016, 116, 316–324. 10.1002/qua.25030. [DOI] [Google Scholar]
  34. Malola S.; Kaappa S.; Häkkinen H. Role of Nanocrystal Symmetry in the Crossover Region from Molecular to Metallic Gold Nanoparticles. J. Phys. Chem. C 2019, 123, 20655–20663. 10.1021/acs.jpcc.9b05863. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao0c00167_si_001.pdf (173.8KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES