Abstract
Despite medical advances, the emergence and re-emergence of infectious diseases continue to pose a public health threat. Low-dimensional epidemiological models predict that epidemic transitions are preceded by the phenomenon of critical slowing down (CSD). This has raised the possibility of anticipating disease (re-)emergence using CSD-based early-warning signals (EWS), which are statistical moments estimated from time series data. For EWS to be useful at detecting future (re-)emergence, CSD needs to be a generic (model-independent) feature of epidemiological dynamics irrespective of system complexity. Currently, it is unclear whether the predictions of CSD—derived from simple, low-dimensional systems—pertain to real systems, which are high-dimensional. To assess the generality of CSD, we carried out a simulation study of a hierarchy of models, with increasing structural complexity and dimensionality, for a measles-like infectious disease. Our five models included: i) a nonseasonal homogeneous Susceptible-Exposed-Infectious-Recovered (SEIR) model, ii) a homogeneous SEIR model with seasonality in transmission, iii) an age-structured SEIR model, iv) a multiplex network-based model (Mplex) and v) an agent-based simulator (FRED). All models were parameterised to have a herd-immunity immunization threshold of around 90% coverage, and underwent a linear decrease in vaccine uptake, from 92% to 70% over 15 years. We found evidence of CSD prior to disease re-emergence in all models. We also evaluated the performance of seven EWS: the autocorrelation, coefficient of variation, index of dispersion, kurtosis, mean, skewness, variance. Performance was scored using the Area Under the ROC Curve (AUC) statistic. The best performing EWS were the mean and variance, with AUC > 0.75 one year before the estimated transition time. These two, along with the autocorrelation and index of dispersion, are promising candidate EWS for detecting disease emergence.
Author summary
Emerging and re-emerging infectious diseases, such as Ebola and measles, present urgent public health challenges and threaten the progress made towards eliminating the global burden of disease. Consequently, a crucial activity in modern epidemiology is developing methods of anticipating (re-)emerging disease outbreaks. Early-warning signals (EWS) are a proposed method for detecting disease (re-)emergence, based on critical slowing down (CSD), a dynamical phenomenon present in systems approaching transition points. The presence of CSD preceding disease (re-)emergence has been comprehensively demonstrated in a range of low-dimensional epidemiological models. For EWS to be useful, however, CSD needs to be a generic feature of (re-)emerging disease transmission dynamics, rather than being limited to specific models. To assess the generality of CSD, we carried out a simulation study of a hierarchy of models of a re-emerging measles-like infectious disease. We found that CSD is present in the dynamics of all the models studied, supporting its generality. In addition, we studied seven candidate EWS, and found that four are strong candidates for use in monitoring systems to detect disease (re-)emergence.
Introduction
Critical slowing down (CSD) is a dynamical feature of systems approaching phase transitions, and has been investigated both theoretically [1–7] and experimentally [8–14] across the natural sciences. As the transition is approached, the stability of the systems’ equilibrium weakens, causing an increasing persistence of perturbations away from the equilibrium (the eponymous “slowing down”) [4]. The ubiquity of CSD has led to suggestions that the phenomenon may be exploited to develop mechanism-independent methods of anticipating impending transitions [5]. This has spurred the examination of various summary statistics that can detect the presence of CSD in time series data and may serve as early-warning signals (EWS) [5–7, 9–14]. Anticipating the emergence of novel pathogens (such as H7N9 avian influenza virus [15]) and the re-emergence of historically controlled infectious diseases (such as measles [16]) is an urgent problem for global public health [17, 18], to which EWS are potentially well suited [6, 7].
The key parameter that influences the threat posed by a (re-)emerging pathogen is the effective reproductive number, Reff, defined as the number of secondary cases a typical infectious individual causes [19]. Reff can increase via multiple mechanisms, including changes in contact rates [20] and population immune profile [21, 22], environmental variation such as climate change [23], pathogen evolution (leading to evasion of immunity [24, 25] and host adaptation [26]), and declining vaccine uptake [16]. As Reff increases the transmission dynamics undergo a phase transition (Fig 1a). Below the epidemic threshold, Reff = 1, there is limited secondary transmission of the disease, however above the threshold large-scale epidemics and endemicity become possible (Fig 1b). The existence of CSD as Reff approaches 1 has been comprehensively demonstrated in a range in low-dimensional epidemiological models (see for instance Fig 1c), including those with: seasonality in transmission [27], imperfectly reported data [28, 29], declining vaccine uptake [6] and vector-borne transmission [30]. One gap where the presence of CSD has not been demonstrated is in high-dimensional epidemiological models. For the purposes of this paper, we define a high-dimensional model as one possessing a large number of state variables (this is in contrast to dynamical definitions of dimensionality, which may be lower due to a separation of dynamical time-scales [31] or weak coupling between state variables [32]). By sacrificing analytical tractability, high-dimensional models are designed to provide a more realistic representation of the actual transmission dynamics of disease in nature [33–36] and thus serve as a bridge between low-dimensional models and the real world.
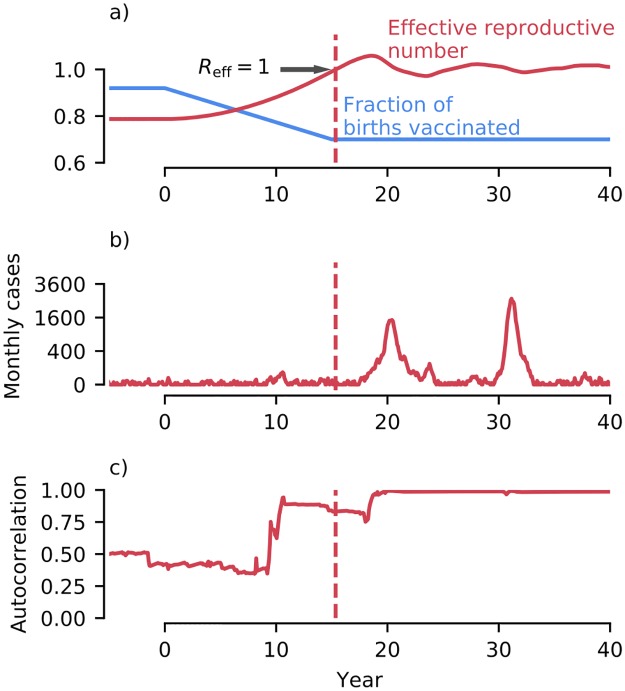
Fig 1. Example simulation of disease re-emergence using the nonseasonal SEIR model.
Parameters were set to mimic transmission of a measles-like disease in a population of 106 individuals, see Methods for model details and the full parameterization. a) The simulation was initialised above the herd immunity threshold, with 92% vaccine coverage. Starting in year 0, vaccine uptake of new born individuals drops linearly from 92% to 70% over 15 years. As vaccine uptake drops, Reff increases, crossing the critical threshold Reff = 1 shortly after 15 years. b) After the herd immunity threshold is crossed large outbreaks become possible, and endemicity is reestablished. c) Increases in early-warning signals (autocorrelation shown) precede the epidemic transition, enabling possible forewarning.
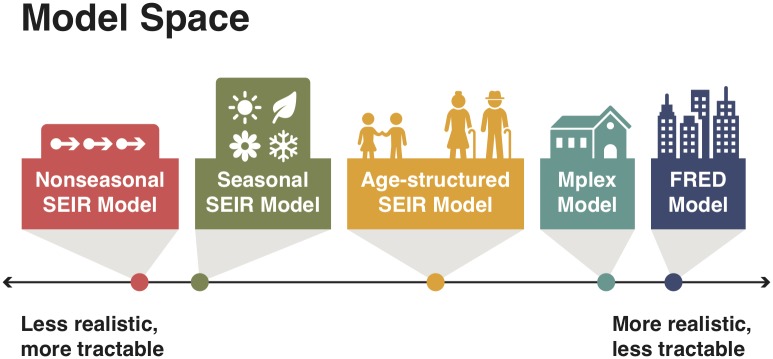
The aims of this paper are to i) ascertain whether CSD is present in high-dimensional epidemiological models and ii) evaluate the performance of a range of EWS at detecting (re-)emergence. We studied five different transmission models, of varying dimensionality and structure (Fig 2). Three models were variants of the Susceptible-Exposed-Infectious-Recovered (SEIR) model, a canonical model of mathematical epidemiology: the basic nonseasonal SEIR model, the SEIR model with seasonality, and an age-structured SEIR model which has assortative mixing between age groups. In addition we considered i) a multiplex contact network model parameterised using socio-demographic data (referred to in this paper as the Mplex model) [37] and ii) FRED (A Framework for Reconstructing Epidemiological Dynamics), an agent-based modeling system [35]. We simulated a comparable re-emergence scenario with each model and, from the resulting time series, calculated seven candidate EWS (the autocorrelation, coefficient of variation, index of dispersion, kurtosis, mean, skewness and variance) previously proposed in the literature [28]. To assess whether the epidemic transition was preceded by CSD and detectable EWS, we first estimated the time of emergence (when Reff = 1) for each model by fitting a Poisson transmission model using Bayesian MCMC. The presence of CSD prior to re-emergence was then established by inspecting the autocorrelation at lag 1 month. We assessed the operational performance of EWS, finding that four out of seven EWS (the autocorrelation, index of dispersion, mean and variance) are credible candidates for detecting disease re-emergence.
Fig 2. Representation of the trade off between tractability and realism in model construction.
Models are positioned along the axis based on the relative complexity of the model, as determined by the number of state variables (the dimensionality) and model structure (the interactions between state variables). The nonseasonal SEIR model is the simplest model, with the FRED and Mplex models being the most complex. Simpler models lend themselves to mathematical analysis, while sacrificing realism. More complex models better represent reality, at the expense of analytical tractability.
Results
Simulated time series
Representative simulated time series of monthly cases using each model are shown in Fig 3 (for experiment design and model details see Methods). During the herd immunity era (vaccine coverage at 95%, t < 0 years), monthly incidence was low in all models, with averages ranging from 1.42 cases for the age-structured SEIR model to 3.74 cases for FRED.
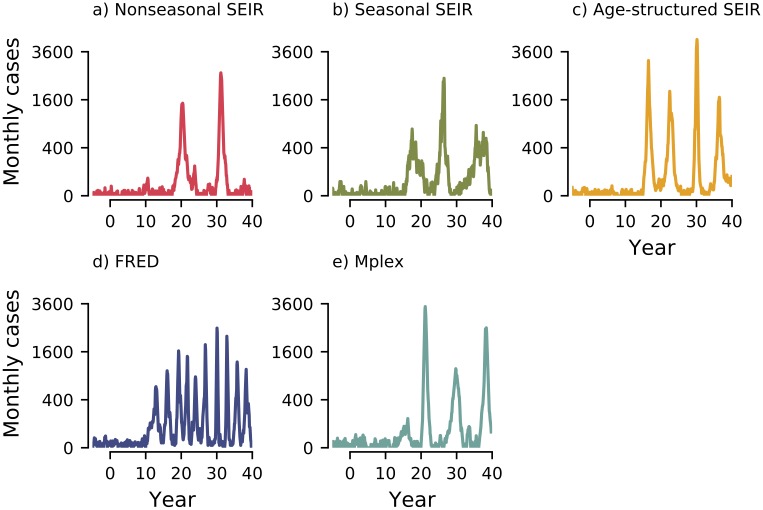
Fig 3. Example simulated time series of monthly cases for the five models (panels a–e).
Each model was parameterised to have a herd immunity threshold around 90% vaccine coverage, and experienced the same decrease in vaccine coverage over the same time span as Fig 1a. Qualitatively, we see that the effect of declining vaccine coverage is model-structure dependent. For the time series shown, the time to the first major outbreak varies between 10 years for FRED (panel d) to 18 years for the nonseasonal SEIR model (panel a).
As vaccine coverage dropped (via a linear decrease in vaccine uptake from 95% to 70% over 15 years), incidence gradually rose until herd immunity was lost, and there was a transition to large outbreaks. We refer to the time of this transition as the time of emergence. Both the time of emergence and the outbreak dynamics after the transition varied among models. The nonseasonal and seasonal SEIR model both had long multi-year outbreaks, whereas all other models had more intense, short-lived epidemics.
Time of emergence
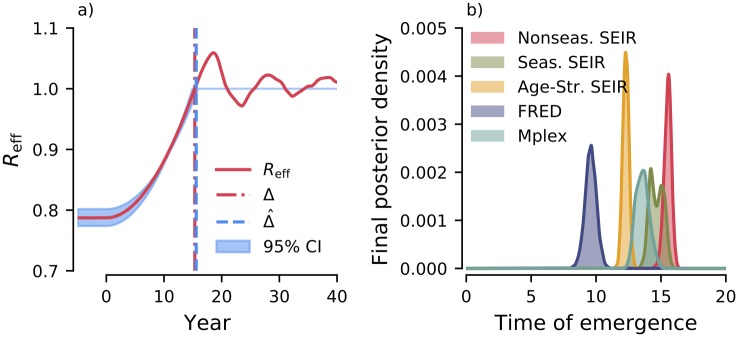
In Fig 4a we show the effective reproductive number, Reff(t), and time of emergence, Δ, for the nonseasonal SEIR model. After fitting the Poisson transmission model to all 100 time series (see Methods), the maximum a posteriori (MAP) for the time of emergence is years after vaccination started decreasing. The posterior density for Δ is sharply peaked, with a 95% credible interval (CI) of [14.92, 15.95]. The MAP lies within 4 months of the true time of emergence, Δ = 15.3 years.
Fig 4. Estimating of time of emergence from case reports data.
a) The Poisson transmission model assumes Reff is a piecewise linear function of time, with a quadratic increase from at t = 0 to Reff = 1 at t = Δ. The time of emergence, Δ, is estimated from the simulated data using Bayesian MCMC (see Methods). b) Final posterior density of the time of emergence. The MAP values of for each model are listed in Table 1.
The remaining models have no analytical solution for Δ; the posterior densities after fitting the Poisson transmission model are shown in Fig 4b. The MAP estimates of and are summarised in Table 1. Including seasonality in the SEIR model results in a bimodal posterior density (Fig 4b) with the MAP ( years) roughly 1 year before that of the nonseasonal SEIR model. For the age-structured SEIR model, years. The posterior density is more sharply peaked around the MAP. The agent-based simulator FRED has the earliest time of emergence, years, whereas the Mplex model has an intermediary time of emergence, years. The posterior densities for both models are less sharply peaked than the age-structured SEIR model.
Table 1. Estimates of the time to emergence (Δ; in years) and initial reproductive number () for each model (MAP point estimate and 95% credible interval).
| Model | Δ | |||
|---|---|---|---|---|
| MAP | 95% CI | MAP | 95% CI | |
| Nonseasonal SEIR | 15.59 | [14.92, 15.95] | 0.79 | [0.77, 0.80] |
| Seasonal SEIR | 14.20 | [13.78, 15.47] | 0.78 | [0.76, 0.79] |
| Age-structured SEIR | 12.28 | [11.83, 12.67] | 0.75 | [0.73, 0.76] |
| FRED | 9.61 | [8.68, 10.30] | 0.89 | [0.88, 0.90] |
| Mplex | 13.63 | [12.67, 14.44] | 0.81 | [0.79, 0.82] |
Detection of critical slowing down
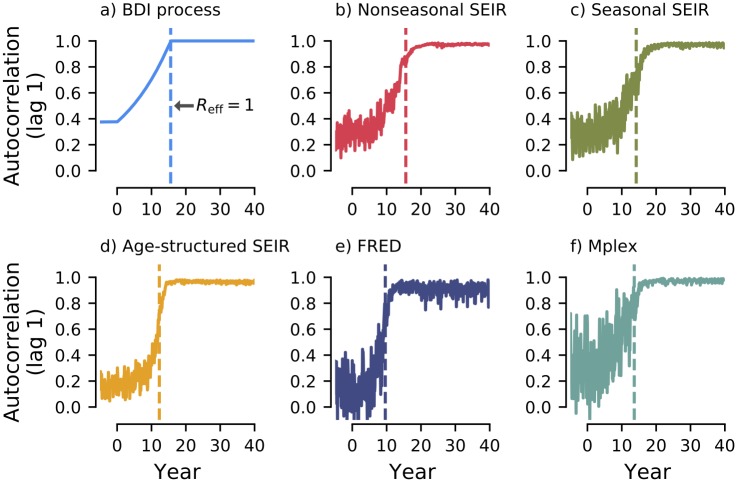
As a theoretical benchmark, the autocorrelation of the Birth-Death-Immigration (BDI) process (see Methods) using a parameterization matched to the simulated SEIR model is shown in Fig 5a. As Reff → 1, the autocorrelation increases and approaches 1, indicative of CSD.
Fig 5. The autocorrelation at lag one month through time.
a) Theoretical benchmark using the BDI process, given by Eq 11. b-f) Estimates for the autocorrelation calculated for each month from the ensemble of realisations. MAP estimates of the time of emergence, , are indicated by dashed vertical lines. For all models, the autocorrelation increases as the time of emergence is approached, indicative of CSD.
For the five models studied in this paper (Fig 5b–5f) we also saw an increasing trend in the autocorrelation for . Unlike for the BDI process, the autocorrelation did not reach 1 at the transition in any of these models, due to the effects of susceptible depletion and the speed of emergence [7]. Models with a faster speed of emergence (such as FRED, Fig 5e) had a lower autocorrelation at the time of emergence. The observed increase in autocorrelation for all models studied supports the hypothesis that CSD is a generic feature of epidemiological dynamics approaching the epidemic transition.
Performance at detecting disease emergence
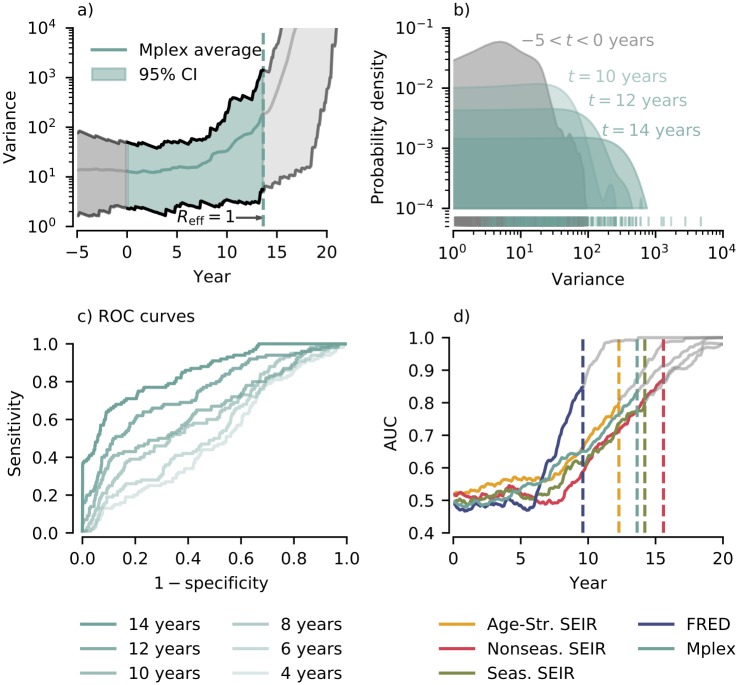
Fig 6a shows the variance calculated using an exponentially weighted moving average for the Mplex model. Probability densities for the variance during the period −5 < t < 0 years (null period) and at the time points t = 10, 12, 14 years are shown in Fig 6b. As coverage dropped, the average over 100 realizations and the 95% confidence interval both shifted to higher values and the overlap of the null (−5 < t < 0 years) and test distributions decreased.
Fig 6. Performance of the variance at detecting emergence.
a) Variance for the Mplex model calculated using an exponentially weighted moving window with a half life of 3 years. Mean and 95% credible interval calculated using 100 realizations. b) Test (green) and null (grey) probability densities for the variance. Probability densities found using kernel density estimation (see Methods). Null probability density calculated using all data points in the interval −5 < t < 0 years. Test probability densities shown for t = 10, 12, 14 years. c) ROC curves for the variance for the Mplex model shown for 2 year intervals. d) Area Under the ROC Curve (AUC) through time for the variance for each model. Vertical lines indicate the time of emergence.
The decrease in distribution overlap is reflected in the Receiver Operator Characteristics (ROC) curve (for details see Methods). As t increased, the ROC curve moved towards the top left corner (Fig 6c) implying emergence became easier to detect using the variance. For all models the Area Under the ROC Curve (AUC) rose from 0.5 (uninformative classifier) after vaccine uptake started declining (Fig 6d). The AUC through time for the remaining EWS are presented in S1 Fig.
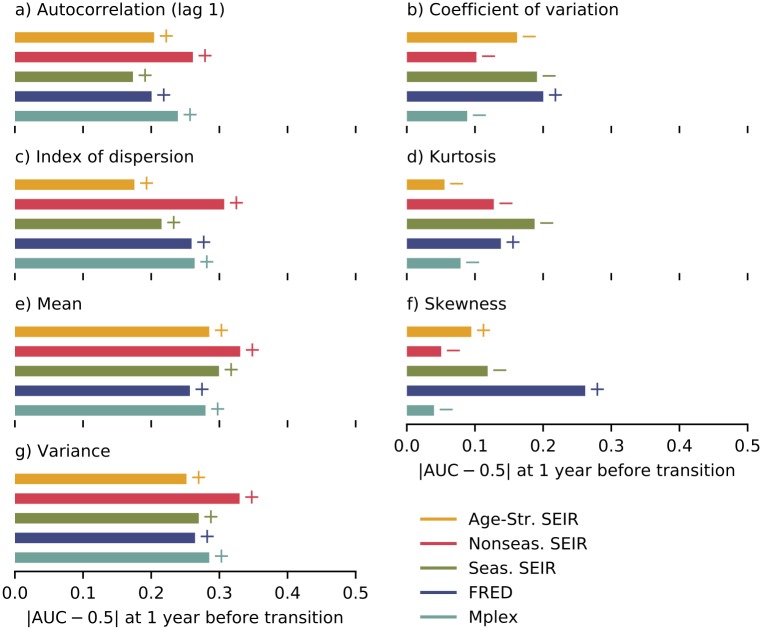
Performance at detecting emergence depended on both the EWS and the model. AUC values one year before the estimated time of emergence are summarised for each combination of EWS and model in Fig 7.
Fig 7. Summary of the AUC values one year before the transition.
a–g) AUC values for each model for the EWS indicated in the panel. The + (−) symbols next to each bar indicate that the AUC is greater (less) than 0.5.
Most EWS consistently increased before the transition (indicated by a “+” in Fig 7). The exceptions were the coefficient of variation, kurtosis and skewness. For the coefficient of variation and kurtosis, one model (FRED) had AUC > 0.5 one year before the transition, whereas the remaining four models had AUC < 0.5. For the skewness, two models (FRED and the age-structured SEIR model) had AUC > 0.5. The inconsistency in the trends of these three EWS prior to the epidemic transition make them poor indicators of emergence.
For the other EWS (the mean, variance, index of dispersion and autocorrelation), performance was generally similar for each model. Using any of these EWS, emergence was easiest to detect in the nonseasonal SEIR model (which had the latest time of emergence), however there was no consistent order for the remaining models. Performance was generally slightly higher for the mean and variance (with AUC values ranging from 0.75 to 0.83) than for the autocorrelation and index of dispersion (AUC ranging from 0.67 to 0.81).
Our quantification of EWS performance is sensitive to i) the estimated time of emergence and ii) the lead time before the transition (chosen to be 1 year in Fig 7). Sensitivity to both these factors can be inferred from S1 Fig. For the four reliable EWS, the AUC rises with time after year 0 (when vaccine uptake started decreasing), as expected. The faster the change in AUC, the greater the sensitivity to both the estimate of the time of emergence and the lead time relative to the time of emergence. FRED, which has the earliest time of emergence, has the fastest rate of increase in AUC. For the remaining models, the rate of increase in AUC is comparable.
Discussion
Research into critical slowing down and EWS preceding emerging disease outbreaks has, up to this point, focused on low-dimensional models that can be studied analytically [6, 7]. In formulating these models, a large number of simplifying assumptions are made, leaving open the question of whether CSD and EWS are unique to simple models, or are a more generic feature of epidemiological dynamics. In this paper, we addressed this question by studying five models with very different structures: two well-mixed models (the seasonal and nonseasonal SEIR model), an age-structured SEIR model with age-dependent contact rates, the Mplex model which explicitly modelled a contact network of schools and households, and FRED which simulates a synthetic population of interacting agents. We used each of these models to simulate the transmission dynamics of a measles-like vaccine preventable disease that was re-emerging due to declining vaccine uptake.
The first aim of this paper was to ascertain whether CSD was present in high-dimensional epidemiological models prior to the epidemic transition Reff = 1. We detected CSD in all models before the critical transition. The observed ubiquity of CSD suggests it is intrinsic to re-emerging disease dynamics. In simple terms, we expect this is due to all of our models (and also infectious disease transmission in nature) sharing a common causal relationship: as vaccination coverage drops towards the herd-immunity threshold, the probability of longer chains of transmission increases. As explained in a previous study [7], this forms the dynamical basis for CSD in low-dimensional epidemiological models. Our study demonstrates that the additional dynamical complexities introduced in high-dimensional models do not serve to mask [38] or negate [39] the existence of CSD. Model structure did, however, have an impact on the time of emergence (the lag between vaccine coverage starting to decline and the effective reproductive number Reff reaching unity).
The second aim was to evaluate the performance of a range of EWS, which we quantified using the AUC statistic. For most EWS (the autocorrelation, index of dispersion, mean and variance), performance increased as the time of emergence was approached. Performance of the other three EWS (the skewness, kurtosis and coefficient of variation) did not have a consistent relationship with time; whether the AUC for these three EWS increased or decreased prior to the transition was found to be model-dependent. These findings corroborate those of a previous study into the detectability of emergence using imperfect data [28], confirming that these three are, in isolation, unreliable EWS. Overall, the best performing EWS were the mean and variance, with AUC > 0.75 one year before the transition for all models. These two, along with the autocorrelation and index of dispersion, are promising candidate EWS for detecting disease emergence.
We focused in this study on the impact of dimensionality and model structure on the detectability of re-emergence, considering models in which the interactions between individuals were clustered in various ways (e.g. by age, school, neighborhood). However, to simplify the comparison, we did not consider social clustering of vaccine status—i.e. in the models studied, all new born individuals had an identical probability of receiving the vaccine. One factor that has been clearly implicated in recent measles outbreaks in high-vaccination countries is that unvaccinated individuals tend to be socially clustered [40]. As vaccine uptake declines, these clusters will change in size and composition, which can lead to different re-emergent dynamics [41]. Investigating whether CSD is present in settings with heterogeneous vaccine uptake, and what the impacts are for potential early-warning, is an pressing topic for further study.
There are many mechanisms that can drive disease (re-)emergence. Here, we have concentrated only on declining vaccine uptake, however CSD is theoretically predicted to be independent of the mechanism causing Reff to increase. One particularly challenging mechanism of emergence that warrants further study are changes in the population structure itself [42]. For instance, rapid increases in population density and connectivity in West and Central Africa have been suggested to enhance the risk of emerging disease outbreaks such as Ebola [43]. High-dimensional models may play a key role in understanding these changing risks and EWS in monitoring them.
Our findings confirm that CSD is present in high-dimensional models, bridging a key gap between previous theoretical results for low-dimensional systems and the real world. Our results add further support to the hypothesis that CSD is a generic feature of (re-)emerging epidemiological dynamics driven by increases in Reff, and that the epidemic transition is preceded by detectable EWS. Developing detection methods that operationalise EWS and can inform public health bodies presents a clear future step.
Methods
Experiment design
To investigate the generality of CSD, we studied five transmission models with very varied structures undergoing the same epidemic transition: the loss of herd immunity in a population due to declining vaccine uptake. To provide a meaningful comparison, where possible all five models were assigned identical epidemiological and demographic parameters.
For all models, infection followed an SEIR-type sequence: upon infection susceptible (S) individuals enter a latent non-infectious stage (E), followed by an infectious stage (I), followed by eventual recovery (R). The mean latent period and infectious period are set to values appropriate for measles, 1/ρ = 8 days and 1/γ = 5 days, respectively [44]. We assume that infection is non-virulent (i.e. all individuals recover) and confers perfect life-long immunity. In each of the models, presence of the pathogen in the population was maintained by individuals contracting the infection from external sources (referred to as importation). In a fully susceptible population, on average one importation occurred per week, ζ = 1 week−1. The per capita rate of importation is given by the ratio ζ/N0 where N0 is the population size, and was uniform for all susceptible individuals. All models output weekly cases reports over the interval t = −10 to t = 40 years. We assumed perfect reporting (i.e. case reports equal the true number of weekly cases).
All models bar FRED had a mean population size N0 = 106, a per capita annual birth rate of 0.013 and mean life expectancy of 75 years. The values for FRED were similar, matching those of Allegheny county, PA, USA (see below), specifically: N0 = 1.2 × 106, a per capita annual birth rate of 0.011 and mean life expectancy of about 78 years.
The primary difference between the models was in the structure of the populations, i.e. in the dynamics of contacts between individuals. It is these contacts that facilitate disease transmission from infectious to susceptible individuals, with a probability given by the pathogens transmissibility. The details of the contact structures for each model are described in the following sections. While the contact structure varied widely between models, the basic reproductive number R0 (the average number of secondary cases an infectious individual causes in a fully susceptible population) was set to be roughly the same for all models to ensure comparability of results.
The models were driven through the epidemic transition via the same decline in vaccine uptake. The probability that a new born individual receives the vaccine v(t) decreased linearly from 0.92 to 0.70 over 15 years, starting in year 0. We assumed immunised individuals receive a perfect vaccine (i.e. with no primary vaccine failure, leakiness or waning of immunity [45]) at birth. By tuning the pathogen’s transmissibility, we fixed the herd immunity immunization threshold of each model to be around 90% coverage (in line with R0 ≈ 10). All models were therefore initialised above the herd immunity threshold. The timing of the epidemic transition depended on the details of the model structure (see below).
Our models all incorporated the effects of demographic stochasticity [46], hence we examined 100 realizations for each.
Nonseasonal SEIR model
The first model considered was the nonseasonal SEIR model with birth and death. The model included the effects of demographic stochasticity, modeling the transmission dynamics as a discrete sequence of jumps between states [44, 46]. Simulations were performed using the Next-Reaction Method (NRM) algorithm [47]. Unvaccinated individuals were born with rate {1 − v(t)}αN0. All individuals died with per capita rate α, meaning individuals had a Type II (exponential) survivorship curve. We set the mean life expectancy to be 1/α = 75 years. The SEIR model has exact solutions for the basic reproductive number and herd immunity threshold [44], we used these to set the transmissibility of the pathogen β(t) = β0, ensuring that R0 = 10 and the herd immunity threshold was at 90% vaccine coverage.
A summary of the transition rates and effects of the SEIR model are listed in Table 2.
Table 2. Transitions of the SEIR process model.
At the beginning of each aggregation period the number of new cases, C, is reset to 0.
| Name | (ΔS, ΔE, ΔI, ΔR, ΔC) | Propensity |
|---|---|---|
| unvaccinated birth | (1, 0, 0, 0, 0) | α{1 − v(t)}N0 |
| vaccinated birth | (0, 0, 0, 1, 0) | αv(t)N0 |
| death of S | (−1, 0, 0, 0, 0) | αS |
| death of E | (0, −1, 0, 0, 0) | αE |
| death of I | (0, 0, −1, 0, 0) | αI |
| death of R | (0, 0, 0, −1, 0) | αR |
| importation | (−1, 1, 0, 0, 0) | ζS/N0 |
| transmission | (−1, 1, 0, 0, 0) | β(t)SI/N0 |
| becoming infectious | (0, −1, 1, 0, 0) | ρI |
| recovery | (0, 0, −1, 1, 1) | γI |
Seasonal SEIR model
The seasonal SEIR model is identical in all respects to the nonseasonal SEIR model, apart from seasonality in the transmission term, with β varying over the course of a year dependent on whether schools were open or closed. Using the dates for term times in England listed in [48], the transmission rate was β(t) = β0 − b1 on days when schools were shut and β(t) = β0 + b1l/(1 − l) when schools were open. The amplitude of seasonality was b1 = 0.3 (appropriate for measles [44]). The parameter l = 0.26 is a normalization constant, and is equal to the fraction of days schools were shut.
Age-structured SEIR model
The Age-structured SEIR model used contact rate data from the POLYMOD study [49] to model disease transmission in a population with age-assortative mixing. The model included effects of demographic stochasticity, and was implemented as a discrete time Euler-multinomial process [48]. The simulation time step was set to one day.
The survivorship curve was assumed to be a step function (Type I), with all mortality occurring at age 75 years. The birth rate was fixed to give a constant population size of N0 = 106 individuals, meaning all ages classes i = 1, …, 75 consisted of Ni = N0/75 individuals.
The force of infection experienced by a susceptible individual in age class i was
| (1) |
where ζ/N0 is the per capita importation rate, βij(t) is the transmission probability, Kij is the rate an individual of age class i contacts individuals in age class j and Ij is the number of infectious individuals in age class j. If either i or j were of school age (5-15 years old) then the transmission rate βij(t) was subject to the same term time forcing as the seasonal SEIR model, otherwise it is constant βij = β0. The transmission coefficient β0 was set to give an R0 = 10 (calculated using the next-generation matrix [50]), matching the SEIR model.
The contact matrix Kij was derived from the POLYMOD matrix for Great Britain (Table S8.3 of [49]) via two steps. First, the POLYMOD matrix, with elements Qa,b, was symmetrised to correct for reciprocity via [48]
| (2) |
where a and b label the age categories of the POLYMOD matrix (14 5-year increments ranging from 0–70 and 70+). Second, the contact matrix Ki,j was constructed from
| (3) |
where ai and bj label the age categories of the POLYMOD matrix that i and j respectively belong to. Given the flat population profile from ages 0 to 75, and for all i = 0…, 75.
FRED model
FRED is an open-source agent-based simulator that simulates disease transmission in synthetic populations [35]. The simulator is designed to capture the spatial and demographic heterogeneities of a specific population by constructing a synthetic population matched to census data for a given geographic region [51]. We used the pre-constructed synthetic population for Allegheny county (Pittsburgh), Pennsylvania, USA [35].
FRED explicitly represents each individual in the population as an agent, who each have a record of demographic traits (e.g. age, employment status, family income), health status (e.g. vaccine status, infectivity) and locations of social activity (e.g. household, school, workplace). FRED implements demographic dynamics, with individuals born, aging, and dying according to the synthetic population’s birth rates and age-specific mortality rates [35]. Infection status follows the SEIR pattern, as used in the other models studied in this paper. At each time step (fixed to one day) infectious agents visit the various locations of social activity and can transmit the infection to other agents also present. Transmission is only possible between agents present at the same location, and occurs with a probability dependent on the ages of the two agents. Transmission is seasonal, with schools closed during the summer holidays and on weekends, and most workers do not attend workplaces at the weekend. The transmissibility of the pathogen was tuned to ensure a similar herd immunity threshold to the SEIR model.
A complete description of the simulator is beyond the scope of this paper, we refer the reader to [35] and the FRED documentation, available online at https://fred.publichealth.pitt.edu. All FRED configuration parameters necessary to reproduce the results of this paper are listed in S1 Table.
Mplex model
The Mplex model [37] simulated disease transmission on a multiplex network consisting of three layers (the household, school, and community layers), following the SEIR scheme adopted by the other models presented in this work. The multiplex network comprises of about 106 nodes and was constructed using Italian socio-demographic data [52]. A brief description of the model is presented here, with a full description provided in S1 Text.
Each individual in the population was represented by a unique node in the network. Individuals were assigned an age, resolved in years and days. At each simulation time step (corresponding to 1 day), three demographic events were simulated [53]: i) individuals could die with a probability given by the age-specific daily mortality rate of the Italian population; ii) for each deceased individual a newborn individual was introduced to the population, guaranteeing that the population size remains constant and at a demographic equilibrium; iii) the age of all (alive) individuals was increased by 1 day. Once per year, school-age individuals were reassigned to a school appropriate for their age. In addition to the demographic process, at each time step of the simulation the Mplex model simulated disease transmission dynamics. During regular school days, the transmission can occur in each of the three layers, while during the summer holidays no transmission at school is possible. Layer-specific weights regulating the transmission process in each layer were estimated from the Italian time-use data by assuming that the transmission probability is proportional to the time spent in contact with other individuals [54]. The latent period, the infectious period, and the case importation rate were the same as for the other models. The transmission rate was set to obtain R0 = 10.
Estimating the time of emergence
To establish whether CSD was present prior the epidemic transition, we needed to determine the timing of the epidemic transition, i.e. the time at which Reff = 1. For the nonseasonal SEIR model, an analytical expression exists for Reff(t) allowing the time of emergence to be found algebraically. For higher-dimensional models with seasonality we found the time of emergence by fitting a Poisson transmission model using Bayesian MCMC.
Poisson transmission model
The Poisson transmission model is a one-dimensional non-Markovian Poisson process that models the number of new cases through time, based on the renewal equation [55]. Versions of this model have been used to model the transmission of Ebola [36, 56] and Influenza [37].
The model assumes that the number of new cases at time step t + δ, denoted Ct+δ, follows a Poisson distribution Ct+δ ∼ Poisson(λt) with rate parameter
| (4) |
where Reff(t) is the effective reproductive number, ϕ(t − s) is the infectiousness kernel and η is the rate cases are imported. The infectiousness kernel ϕ(t − s) is given by
| (5) |
where χ(t′) is the probability that an individual is infectious t′ after infection. We assumed exponentially distributed latent and infectious periods, giving
| (6) |
where ρ and γ are the rates of the latent and infectious period distributions, respectively.
Cases stemming from external importation occur with rate weighted by the fraction of the population susceptible, initially η = (1 − v(0))ζ. As vaccination decreases the importation rate will rise, however this increase is much less relative to the increase in secondary transmission. To reduce the number of parameters estimated by MCMC, we therefore fixed the importation rate at the initial value.
The effective reproductive number was modeled using the piecewise function
| (7) |
where vaccine uptake starts to decreased at time t = 0. The parameter ϵ controls the curvature of Reff(t). The analytical solution for susceptible replenishment in the nonseasonal SEIR model with declining vaccine uptake can be well-approximated by a quadratic function, therefore we set ϵ = 2. The two model parameters which required estimation were the time of emergence, Δ, and the initial reproductive number .
Bayesian Markov Chain Monte Carlo
The two unknown parameters ( and Δ) were estimated by sequentially fitting the Poisson transmission model to each simulated realisation using Bayesian MCMC. Each time series was of weekly case reports (i.e. δ = 1 week) between t0 = −10 years and T = 40 years. Using the Poisson transmission model, the probability of observing a time series is
| (8) |
where is a Poisson distribution with rate parameter given in Eq 4 and . We assumed that before t = t0 there are no cases, for t0 ≪ 0 this has negligible effect on parameter estimates.
By applying Bayes’ rule iteratively, the joint posterior density for the parameters, given the first i simulated time series, is
| (9) |
where Ci = {Ci,t}t is the i-th time series of cases and P(Ci|Θ) is given in Eq 8. For i ≥ 2, the prior is equal to the preceding posterior . We assumed the initial prior, q1, was uniform for Δ ∈ (0, T] years and .
We generated 30000 samples from the posterior by running Hamiltonian Monte Carlo with the No-U-Turn Sampler [57] implemented in the python package pymc3 [58]. We then constructed a smoothed posterior distribution from the samples using Gaussian kernel density estimation [59]. This smoothed posterior was then fed back into the MCMC algorithm as the subsequent prior, and the procedure was repeated.
We obtained point estimates from the maximum a posteriori of the final posterior given all M = 100 time series,
| (10) |
Critical slowing down and early-warning signals
Critical slowing down
In a previous theoretical study using the Birth-Death-Immigration (BDI) process, a simple transmission model that ignores any effects of susceptible depletion, the presence of CSD was shown using the autocorrelation [7]. For a subcritical (Reff < 1) disease, the BDI process can be solved to give an expression for the autocorrelation in the number of individuals infected at lag δ [2, 7],
| (11) |
As Reff increases the autocorrelation also increases, approaching one as Reff → 1. The increase in the autocorrelation is caused by the increasing persistence of perturbations that defines CSD [6, 7]. In line with this theoretical result, we took an increasing trend in the autocorrelation prior to the epidemic transition as evidence for the presence of CSD. Using 100 simulated time series, we numerically calculated the autocorrelation at lag one month through time for each model.
Estimating EWS
A range of EWS have been proposed to anticipate dynamical transitions [5–7, 10, 28, 30]. We considered seven: the autocorrelation (at lag 1 month), coefficient of variation, index of dispersion, kurtosis, mean, skewness and variance. EWS were calculated for each simulated time series of case counts. Prior to calculating the EWS we grouped the weekly counts into 4-weekly counts, as a previous study into EWS using imperfect data found that this resulted in more robust performance [28].
Each EWS was calculated longitudinally from a single realization using a moving window estimator [6, 7]. We chose to use exponentially weighted moving averages; for example the estimator for the mean is
| (12) |
| (13) |
and for the variance is
| (14) |
The decay rate is specified by the half-life t1/2 = ln(2)/κ. We set t1/2 = 39 4-week intervals, which is approximately 3 years. The estimators for the remaining EWS were constructed similarly, and are shown in Table 3.
Table 3. List of early-warning signals and estimators.
| EWS | Estimator |
|---|---|
| Mean | |
| Variance | |
| Coefficient of variation | |
| Index of dispersion | |
| Skewness | |
| Kurtosis | |
| Autocorrelation at lag δ |
Quantifying performance using the AUC statistic
Following a previous study [28], we scored performance using the Area Under the ROC Curve (AUC) statistic, which quantifies how successfully a particular EWS classifies whether or not a disease is approaching an epidemic transition [60].
The Reciever Operator Characteristics (ROC) curve is a parametric plot of the sensitivity and specificity of a classification method as a function of the detection threshold [60]. As null (not emerging) data we took all EWS values in the interval −5 < t < 0 years, i.e. immediately before vaccine uptake started dropping and the pathogen started re-emerging. The test data were then the EWS values for t > 0 years. We calculated the ROC and AUC using data for each time point separately, to show how the detectability of emergence changes with time.
The AUC statistic quantifies the overlap of test and null distributions, and may be interpreted as the probability that the EWS at time t from a randomly chosen realisation is higher than a randomly chosen value from the null interval −5 < t < 0 years, AUC = P(τtest > τnull) [60].
An AUC = 0.5 implies that an observed EWS value conveys no information about whether or not the disease is re-emerging. An AUC greater than (less than) 0.5 implies that test values are typically larger (smaller) than null values. Given AUC values further from 0.5 imply better performance, and some EWS may increase or decrease as the transition is approached, we compared performance using the absolute distance |AUC − 0.5|. Performance is maximised if |AUC − 0.5| = 0.5. We also calculated the sign of (AUC − 0.5), to see whether an EWS consistently increased/decreased for all models and times.
Supporting information
(PDF)
a–g) AUC through time for each model for the EWS indicated in the panel. Vertical lines indicate the estimated time of emergence.
(TIFF)
(PDF)
Data Availability
All data files and code to reproduce analysis are available from the Zenodo database (doi:10.5281/zenodo.3663086).
Funding Statement
TB, JMD, and PR received funding from the National Institute of General Medical Sciences of the National Institutes of Health (https://www.nigms.nih.gov/, Award Number U01GM110744). MA and AV acknowledge support from the Models of Infectious Disease Agent Study, National Institute of General Medical Sciences Grant U54GM111274. Q-HL acknowledges the support from the Fundamental Research Funds for the Central Universities. JJG received funding from the National Institute of General Medical Sciences of the National Institutes of Health Award Number 2U54GM08849106. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Hohenberg PC, Halperin BI. Theory of dynamic critical phenomena. Reviews of Modern Physics. 1977;49(3):435 10.1103/RevModPhys.49.435 [DOI] [Google Scholar]
- 2. Bailey NTJ. The Elements of Stochastic Processes with Applications to the Natural Sciences. vol. 25 John Wiley & Sons; 1990. [Google Scholar]
- 3. van Kampen NG. Stochastic Processes in Physics and Chemistry. North Holland; 1981. [Google Scholar]
- 4. Strogatz SH. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry and Engineering. Westview Press; 2001. [Google Scholar]
- 5. Scheffer M, Bascompte J, Brock WA, Brovkin V, Carpenter SR, Dakos V, et al. Early-warning signals for critical transitions. Nature. 2009;461(7260):53–59. 10.1038/nature08227 [DOI] [PubMed] [Google Scholar]
- 6. O’Regan SM, Drake JM. Theory of early warning signals of disease emergence and leading indicators of elimination. Theoretical Ecology. 2013;6(3):333–357. 10.1007/s12080-013-0185-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Brett TS, Drake JM, Rohani P. Anticipating the emergence of infectious diseases. Journal of The Royal Society Interface. 2017;14(132):20170115 10.1098/rsif.2017.0115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Djurberg C, Svedlindh P, Nordblad P, Hansen MF, Bødker F, Mørup S. Dynamics of an interacting particle system: evidence of critical slowing down. Physical review letters. 1997;79(25):5154 10.1103/PhysRevLett.79.5154 [DOI] [Google Scholar]
- 9. Carpenter SR, Cole JJ, Pace ML, Batt R, Brock W, Cline T, et al. Early warnings of regime shifts: a whole-ecosystem experiment. Science. 2011;332(6033):1079–1082. 10.1126/science.1203672 [DOI] [PubMed] [Google Scholar]
- 10. Kéfi S, Rietkerk M, Alados CL, Pueyo Y, Papanastasis VP, ElAich A, et al. Spatial vegetation patterns and imminent desertification in Mediterranean arid ecosystems. Nature. 2007;449(7159):213–217. 10.1038/nature06111 [DOI] [PubMed] [Google Scholar]
- 11. Dakos V, Scheffer M, van Nes EH, Brovkin V, Petoukhov V, Held H. Slowing down as an early warning signal for abrupt climate change. Proceedings of the National Academy of Sciences. 2008;105(38):14308–14312. 10.1073/pnas.0802430105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Dakos V, Kéfi S, Rietkerk M, van Nes EH, Scheffer M. Slowing Down in Spatially Patterned Ecosystems at the Brink of Collapse. The American Naturalist. 2011;177(6):E153–E166. 10.1086/659945 [DOI] [PubMed] [Google Scholar]
- 13. Drake JM, Griffen BD. Early warning signals of extinction in deteriorating environments. Nature. 2010;467:456 EP –. 10.1038/nature09389 [DOI] [PubMed] [Google Scholar]
- 14. Dai L, Vorselen D, Korolev KS, Gore J. Generic Indicators for Loss of Resilience Before a Tipping Point Leading to Population Collapse. Science. 2012;336(6085):1175–1177. 10.1126/science.1219805 [DOI] [PubMed] [Google Scholar]
- 15. Lam TTY, Wang J, Shen Y, Zhou B, Duan L, Cheung CL, et al. The genesis and source of the H7N9 influenza viruses causing human infections in China. Nature. 2013; p. 1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Sundaram ME, Guterman LB, Omer SB. The True Cost of Measles Outbreaks During the Postelimination Era. JAMA. 2019;321(12):1155–1156. 10.1001/jama.2019.1506 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Webby RJ, Webster RG. Are we ready for pandemic influenza? Science. 2003;302(5650):1519–1522. 10.1126/science.1090350 [DOI] [PubMed] [Google Scholar]
- 18. Morens D, Folkers G, Fauci A. The challenge of emerging and re-emerging infectious diseases. Nature. 2004;430(6996):242–249. 10.1038/nature02759 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Anderson RM, May RM. Infectious Diseases of Humans: Dynamics and Control. Oxford University Press; 1991. [Google Scholar]
- 20. Wilson ME. Travel and the emergence of infectious diseases. Emerging Infectious Diseases. 1995;1(2):39 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Gostic KM, Ambrose M, Worobey M, Lloyd-Smith JO. Potent protection against H5N1 and H7N9 influenza via childhood hemagglutinin imprinting. Science. 2016;354(6313):722–726. 10.1126/science.aag1322 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Domenech de Cellès M, Magpantay FMG, King AA, Rohani P. The impact of past vaccination coverage and immunity on pertussis resurgence. Science Translational Medicine. 2018;10(434). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Mordecai EA, Cohen JM, Evans MV, Gudapati P, Johnson LR, Lippi CA, et al. Detecting the impact of temperature on transmission of Zika, dengue, and chikungunya using mechanistic models. PLoS Neglected Tropical Diseases. 2017;11(4):e0005568 10.1371/journal.pntd.0005568 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Łuksza M, Lässig M. A predictive fitness model for influenza. Nature. 2014;507(7490):57–61. 10.1038/nature13087 [DOI] [PubMed] [Google Scholar]
- 25. Gouma S, Vermeire T, Van Gucht S, Martens L, Hutse V, Cremer J, et al. Differences in antigenic sites and other functional regions between genotype A and G mumps virus surface proteins. Scientific Reports. 2018; p. 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Antia R, Regoes RR, Koella JC, Bergstrom CT. The role of evolution in the emergence of infectious diseases. Nature. 2003;426(6967):658 10.1038/nature02104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Miller PB, O’Dea EB, Rohani P, Drake JM. Forecasting infectious disease emergence subject to seasonal forcing. Theoretical Biology and Medical Modelling. 2017;14(1):17 10.1186/s12976-017-0063-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Brett TS, O’Dea EB, Marty É, Miller PB, Park AW, Drake JM, et al. Anticipating epidemic transitions with imperfect data. PLoS Computational Biology. 2018;14(6):e1006204 10.1371/journal.pcbi.1006204 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. O’Dea EB, Drake JM. Disentangling reporting and disease transmission. Theoretical Ecology. 2018; p. 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. O’Regan SM, Lillie JW, Drake JM. Leading indicators of mosquito-borne disease elimination. Theoretical ecology. 2016;9(3):269–286. 10.1007/s12080-015-0285-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Kuehn C. Multiple time scale dynamics. vol. 191 Springer; 2015. [Google Scholar]
- 32. Bjørnstad ON, Sait SM, Stenseth NC, Thompson DJ, Begon M. The impact of specialized enemies on the dimensionality of host dynamics. Nature. 2001;409(6823):1001 10.1038/35059003 [DOI] [PubMed] [Google Scholar]
- 33. Eubank S, Guclu H, Kumar VA, Marathe MV, Srinivasan A, Toroczkai Z, et al. Modelling disease outbreaks in realistic urban social networks. Nature. 2004;429(6988):180 10.1038/nature02541 [DOI] [PubMed] [Google Scholar]
- 34. Ajelli M, Gonçalves B, Balcan D, Colizza V, Hu H, Ramasco JJ, et al. Comparing large-scale computational approaches to epidemic modeling: agent-based versus structured metapopulation models. BMC infectious diseases. 2010;10(1):190 10.1186/1471-2334-10-190 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Grefenstette JJ, Brown ST, Rosenfeld R, DePasse J, Stone NT, Cooley PC, et al. FRED (A Framework for Reconstructing Epidemic Dynamics): an open-source software system for modeling infectious diseases and control strategies using census-based populations. BMC Public Health. 2013;13(1):940 10.1186/1471-2458-13-940 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Ajelli M, Merler S, Fumanelli L, y Piontti AP, Dean NE, Longini IM, et al. Spatiotemporal dynamics of the Ebola epidemic in Guinea and implications for vaccination and disease elimination: a computational modeling analysis. BMC medicine. 2016;14(1):130 10.1186/s12916-016-0678-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Liu QH, Ajelli M, Aleta A, Merler S, Moreno Y, Vespignani A. Measurability of the epidemic reproduction number in data-driven contact networks. Proceedings of the National Academy of Sciences. 2018;115(50):12680–12685. 10.1073/pnas.1811115115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Perretti CT, Munch SB. Regime shift indicators fail under noise levels commonly observed in ecological systems. Ecological Applications. 2012;22(6):1772–1779. 10.1890/11-0161.1 [DOI] [PubMed] [Google Scholar]
- 39. Hastings A, Wysham DB. Regime shifts in ecological systems can occur with no warning. Ecology letters. 2010;13(4):464–472. 10.1111/j.1461-0248.2010.01439.x [DOI] [PubMed] [Google Scholar]
- 40. Omer SB, Salmon DA, Orenstein WA, Dehart MP, Halsey N. Vaccine refusal, mandatory immunization, and the risks of vaccine-preventable diseases. New England Journal of Medicine. 2009;360(19):1981–1988. 10.1056/NEJMsa0806477 [DOI] [PubMed] [Google Scholar]
- 41. Truelove SA, Graham M, Moss WJ, Metcalf CJE, Ferrari MJ, Lessler J. Characterizing the impact of spatial clustering of susceptibility for measles elimination. Vaccine. 2019;37(5):732–741. 10.1016/j.vaccine.2018.12.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Merler S, Ajelli M. Deciphering the relative weights of demographic transition and vaccination in the decrease of measles incidence in Italy. Proceedings of the Royal Society B: Biological Sciences. 2014;281(1777):20132676 10.1098/rspb.2013.2676 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Munster VJ, Bausch DG, de Wit E, Fischer R, Kobinger G, Muñoz Fontela C, et al. Outbreaks in a Rapidly Changing Central Africa—Lessons from Ebola. New England Journal of Medicine. 2018;379(13):1198–1201. 10.1056/NEJMp1807691 [DOI] [PubMed] [Google Scholar]
- 44. Keeling MJ, Rohani P. Modeling infectious diseases in humans and animals. Princeton University Press; 2008. [Google Scholar]
- 45. Magpantay F, Riolo M, de Cellès M, King A, Rohani P. Epidemiological Consequences of Imperfect Vaccines for Immunizing Infections. SIAM Journal on Applied Mathematics. 2014;74(6):1810–1830. 10.1137/140956695 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Black AJ, McKane AJ. Stochastic formulation of ecological models and their applications. Trends in ecology & evolution. 2012;27(6):337–345. 10.1016/j.tree.2012.01.014 [DOI] [PubMed] [Google Scholar]
- 47. Gibson MA, Bruck J. Efficient exact stochastic simulation of chemical systems with many species and many channels. The journal of physical chemistry A. 2000;104(9):1876–1889. 10.1021/jp993732q [DOI] [Google Scholar]
- 48. Riolo MA, Rohani P. Combating pertussis resurgence: One booster vaccination schedule does not fit all. Proceedings of the National Academy of Sciences. 2015;112(5):E472–E477. 10.1073/pnas.1415573112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Mossong J, Hens N, Jit M, Beutels P, Auranen K, Mikolajczyk R, et al. Social contacts and mixing patterns relevant to the spread of infectious diseases. PLoS medicine. 2008;5(3):e74 10.1371/journal.pmed.0050074 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Diekmann O, Heesterbeek JAP, Metz JA. On the definition and the computation of the basic reproduction ratio R 0 in models for infectious diseases in heterogeneous populations. Journal of mathematical biology. 1990;28(4):365–382. 10.1007/bf00178324 [DOI] [PubMed] [Google Scholar]
- 51. Cooley P, Brown S, Cajka J, Chasteen B, Ganapathi L, Grefenstette J, et al. The role of subway travel in an influenza epidemic: a New York City simulation. Journal of Urban Health. 2011;88(5):982 10.1007/s11524-011-9603-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Fumanelli L, Ajelli M, Manfredi P, Vespignani A, Merler S. Inferring the structure of social contacts from demographic data in the analysis of infectious diseases spread. PLoS computational biology. 2012;8(9):e1002673 10.1371/journal.pcbi.1002673 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Ajelli M, Merler S. An individual-based model of hepatitis A transmission. J Theor Biol. 2009;259(3):478–488. 10.1016/j.jtbi.2009.03.038 [DOI] [PubMed] [Google Scholar]
- 54. Ajelli M, Poletti P, Melegaro A, Merler S. The role of different social contexts in shaping influenza transmission during the 2009 pandemic. Sci Rep. 2014;4:7218 10.1038/srep07218 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Grassly NC, Fraser C. Mathematical models of infectious disease transmission. Nature Reviews Microbiology. 2008;6(6):477 10.1038/nrmicro1845 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Team WER. Ebola virus disease in West Africa—the first 9 months of the epidemic and forward projections. New England Journal of Medicine. 2014;371(16):1481–1495. 10.1056/NEJMoa1411100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Hoffman MD, Gelman A. The No-U-Turn sampler: adaptively setting path lengths in Hamiltonian Monte Carlo. Journal of Machine Learning Research. 2014;15(1):1593–1623. [Google Scholar]
- 58. Salvatier J, Wiecki TV, Fonnesbeck C. Probabilistic programming in Python using PyMC3. PeerJ Computer Science. 2016;2:e55 10.7717/peerj-cs.55 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Friedman J, Hastie T, Tibshirani R. The Elements of Statistical Learning Springer series in statistics New York, NY, USA:; 2001. [Google Scholar]
- 60. Fawcett T. An introduction to ROC analysis. Pattern Recognition Letters. 2006;27(8):861–874. 10.1016/j.patrec.2005.10.010 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(PDF)
a–g) AUC through time for each model for the EWS indicated in the panel. Vertical lines indicate the estimated time of emergence.
(TIFF)
(PDF)
Data Availability Statement
All data files and code to reproduce analysis are available from the Zenodo database (doi:10.5281/zenodo.3663086).