Predicting individual clinical trajectories of depression with generative embedding

Highlights

• •Patients with major depressive disorder (MDD) show variable clinical trajectories.
• •Generative embedding (GE) is used to predict clinical trajectories in MDD patients.
• •GE classifies patients with chronic depression vs. fast remission with 79% accuracy.
• •GE provides mechanistic interpretability and outperforms conventional measures.
• •Proof-of-concept that illustrates the potential of GE for clinical prediction.

Abstract

Patients with major depressive disorder (MDD) show heterogeneous treatment response and highly variable clinical trajectories: while some patients experience swift recovery, others show relapsing-remitting or chronic courses. Predicting individual clinical trajectories at an early stage is a key challenge for psychiatry and might facilitate individually tailored interventions. So far, however, reliable predictors at the single-patient level are absent. Here, we evaluated the utility of a machine learning strategy – generative embedding (GE) – which combines interpretable generative models with discriminative classifiers. Specifically, we used functional magnetic resonance imaging (fMRI) data of emotional face perception in 85 MDD patients from the NEtherlands Study of Depression and Anxiety (NESDA) who had been followed up over two years and classified into three subgroups with distinct clinical trajectories. Combining a generative model of effective (directed) connectivity with support vector machines (SVMs), we could predict whether a given patient would experience chronic depression vs. fast remission with a balanced accuracy of 79%. Gradual improvement vs. fast remission could still be predicted above-chance, but less convincingly, with a balanced accuracy of 61%. Generative embedding outperformed classification based on conventional (descriptive) features, such as functional connectivity or local activation estimates, which were obtained from the same data and did not allow for above-chance classification accuracy. Furthermore, predictive performance of GE could be assigned to a specific network property: the trial-by-trial modulation of connections by emotional content. Given the limited sample size of our study, the present results are preliminary but may serve as proof-of-concept, illustrating the potential of GE for obtaining clinical predictions that are interpretable in terms of network mechanisms. Our findings suggest that abnormal dynamic changes of connections involved in emotional face processing might be associated with higher risk of developing a less favorable clinical course.

1. Introduction

Major depressive disorder (MDD) is one of the most burdening mental disorders with a lifetime prevalence of 10–30% (Andrade et al., 2003; de Graaf et al., 2012). Up to a fourth of MDD patients are at risk of developing a chronic disease (Penninx et al., 2011), characterized by severe negative impact on quality of life and high rates of psychiatric comorbidities (Kohler et al., 2019). The diagnostic criteria of MDD in ICD and DSM-5 (American Psychiatric Association, 2013) are not grounded in pathophysiology, but refer to symptoms and signs (e.g., depressed mood, anhedonia, fatigue) that could have various causes. The diagnostic label MDD likely subsumes patients with different disease mechanisms and has limited predictive validity: MDD patients show highly variable clinical trajectories over time (Gueorguieva et al., 2011; Musliner et al., 2016; Muthen et al., 2011), and the absence of mechanistically interpretable predictors turns therapy into a trial-and-error procedure (Cuthbert and Insel, 2013; Kapur et al., 2012; Rush et al., 2006). This is not only costly and frustrating for patients, but also bears the risk of long-term adverse events (McMahon and Insel, 2012) and reduced treatment adherence (Velligan et al., 2010).

This emphasizes the need for novel prognostic approaches to depression that furnish predictors for clinical trajectories and treatment outcomes. Predicting symptom trajectories in MDD at an early stage is of high clinical relevance because identifying patients at risk of chronic disease might guide the deployment of intensified early interventions (MacQueen, 2009). To achieve this, successful tools may benefit from being grounded in biology to enable a mechanistically relevant stratification of the heterogeneous MDD spectrum (Stephan et al., 2017). Using neuroimaging, some studies demonstrated that disease onset and short-term treatment response prediction may be possible (Dunlop et al., 2017; Mayberg et al., 1997; Pan et al., 2017; Phillips et al., 2015). By contrast, it has proven more challenging to predict long-term clinical outcome, such as symptom trajectories over several years.

Schmaal et al. (2015) assessed the prognostic value of structural and functional magnetic resonance imaging (fMRI) to classify disease trajectories in MDD patients from the NEtherlands Study of Depression and Anxiety (NESDA; Penninx et al., 2008), a multi-site longitudinal study in a large naturalistic cohort. The authors demonstrated that fMRI data from an emotional face perception paradigm allowed discriminating patients who, over the course of two years, showed a chronic disease trajectory from patients showing rapid remission of depressive symptoms, with up to 73% accuracy. This result was obtained by applying a supervised machine learning (ML) method, Gaussian Process Classifiers (GPCs; Rasmussen and Williams, 2005), to contrast images.

While an encouraging initial result, developing this approach further with conventional ML techniques and towards clinically required levels of accuracy faces several challenges (Brodersen et al., 2011). First, achieving high classification accuracy robustly from whole-brain fMRI data can be difficult, given the high dimensionality of the data relative to the small sample sizes. Second, the results from “black-box” ML operating on descriptive features (e.g., contrast images) do not easily allow for mechanistic interpretations. The latter, however, is increasingly recognized as critical for clinical applications of ML (Itani et al., 2019; Woo et al., 2017), both to derive novel treatment ideas from successful predictions but also to detect cases when ML goes awry, e.g., predictions that derive from artefacts in the data.

Generative embedding (GE) represents a potentially attractive alternative to “classical” ML (Shawe-Taylor and Cristianini, 2004). The idea is simple but powerful: instead of selecting features from the original data, one applies a generative model to the data and uses the ensuing model parameter estimates as features. Generative models describe how observed data may have been “generated” from latent (hidden) system states and thus often embody some degree of mechanistic interpretability. For example, in neuroimaging, GE uses model-based estimates of physiological or cognitive parameters, such as connection strengths (Brodersen et al., 2014, 2011), ion channel conductances (Symmonds et al., 2018), prediction errors (Paulus, 2015), or response inhibition (Wiecki et al., 2016). More technically, GE views a generative model as a theory-driven dimensionality reduction device that projects high-dimensional data onto neurobiologically meaningful parameters that define a low-dimensional and interpretable space for classification. Provided a plausible model exists, GE frequently yields more accurate results than conventional ML (Brodersen et al., 2014, 2011), likely because the generative model separates signal (reflecting the process of interest) from (measurement) noise.

Model-based estimates of brain connectivity might be particularly informative for predicting clinical trajectories in MDD, given that dysconnectivity has been postulated as a hallmark of depression (Greicius et al., 2007; Mayberg, 1997; Wang et al., 2012). Here, we used a generative model of fMRI data, dynamic causal modeling (DCM; Friston et al., 2003), to infer effective (directed) connectivity and test the utility of GE for predicting individual clinical trajectories in MDD patients from the NESDA study. For this purpose, we combined DCMs of the emotional face perception network with linear support vector machines (SVMs). We then compared the cross-validated predictive accuracy of GE with more conventional approaches, such as classification based on functional connectivity and local BOLD activity, testing whether a biologically plausible generative model would be superior for predicting naturalistic disease courses from fMRI data.

We emphasize that the present work is not meant to provide an ultimate prognostic tool for outcomes in MDD since this may require a substantially larger dataset than currently available. Instead, the present study provides proof-of-concept that illustrates the potential benefits of GE relative to conventional approaches in neuroimaging studies of MDD, with regard to predictive power and interpretability.

2. Materials and methods

2.1. Participants

The data used here were acquired in the NESDA study (Penninx et al., 2008), a multi-site longitudinal study on the long-term course of depression and anxiety disorders in a large naturalistic cohort. In total, 2981 participants (18–65 years) were recruited from community, primary care and specialized mental health organizations. From this cohort, 301 participants (156 with MDD diagnosis) were included in the MRI experiment. For detailed descriptions of the full sample, see van Tol et al. (2010). For the current study, only those participants were included that had: (i) a DSM-IV diagnosis of MDD, as established using the structured Composite International Diagnostic Interview (CIDI; Robins et al., 1988) in the 6 months prior to baseline, (ii) reported symptoms in the month before baseline as confirmed by either the CIDI or the Life Chart Interview (LCI; Lyketsos et al., 1994), (iii) availability of 2-year follow-up of depressive symptoms from the LCI, and (iv) no other exclusion criteria related to, e.g., poor data quality, non-compliance with task instructions, or deficient performance. For details, see Schmaal et al. (2015). This yielded a final sample of 85 participants (for an overview of the demographic and clinical characteristics, see Table 1).

Table 1.

Demographic and clinical characteristics of participants included in the generative embedding analyses.

Characteristic	REM (n = 39)	IMP (n = 31)	CHR (n = 15)	Statistic	p-value
Age, Years	35.90 (11.50)	35.03 (10.00)	44.00 (10.01)	F = 3.92	0.02
Gender, n (%)
Female	28 (72)	20 (65)	9 (60)	χ2=0.83	0.66
Male	22 (28)	11 (35)	6 (40)
Education, Years	11.74 (3.30)	12.26 (3.00)	12.00 (2.36)	F = 0.25	0.78
Scan Location, n (%)
AMC Amsterdam	5 (13)	5 (16)	4 (27)	χ2=3.81	0.43
LUMC Leiden	13 (33)	15 (48)	5 (33)
UMCG Groningen	21 (54)	11 (35)	6 (40)
IDS Total T1	31.44 (10.76)	32.77 (8.35)	33.72 (7.91)	F = 0.37	0.69
IDS Total T2	14.72 (9.06)	22.29 (9.93)	29.60 (7.17)	F = 15.87	< 0.001
IDS Change (T2-T1)	−16.72 (11.33)	−10.48 (10.56)	−4.13 (8.10)	F = 8.35	< 0.001
BAI Total T1	14.90 (9.25)	15.77 (9.42)	14.27 (6.93)	F = 0.16	0.85
Antidepressant Use T1, n (%)
No	27 (69)	22 (71)	8 (53)	χ2=1.58	0.45
Yes	12 (31)	9 (29)	7 (47)
Antidepressant Use T2, n (%)
No	25 (64)	22 (71)	9 (60)	χ2=0.64	0.73
Yes	14 (36)	9 (29)	6 (40)

Based on the two-year follow-up clinical trajectories derived from CIDI and LCI information, MDD patients were divided into different categories with distinct courses of symptom severity. This division was informed by a latent class growth analysis (Rhebergen et al., 2012), as reported by Schmaal et al. (2015). The three classes were: (i) MDD-remitted, showing a rapid remission of symptoms (REM: n = 39), (ii) MDD-improved, showing a slow but gradual improvement of symptoms from baseline to follow-up (IMP: n = 31), and (iii) MDD-chronic, showing no improvement of symptoms from baseline to follow-up (CHR: n = 15).

2.2. Experimental procedure

For fMRI, an event-related emotional face perception paradigm was used. Participants viewed color images of angry, fearful, sad, happy, and neutral facial expressions, as well as scrambled faces. Stimuli were shown for 2.5 s, with an inter-stimulus interval varying between 0.5–1.5 s. Participants were instructed to indicate the gender of the presented face via button press. For scrambled images, participants had to press buttons in accordance with an arrow pointing to the left or right. Stimuli were presented using E-prime (Psychological Software Tools, Pittsburgh, PA; https://pstnet.com/products/e-prime/). For details, see Demenescu et al. (2011).

2.3. Functional magnetic resonance imaging

2.3.1. Image acquisition

For NESDA, structural and functional MRI data were acquired at the University Medical Center Groningen (UMCG), Amsterdam Medical Center (AMC), and Leiden University Medical Center (LUMC). Participants were scanned on 3-Tesla MR scanners (Philips Healthcare, Best, The Netherlands) with SENSE 8-channel (LUMC, UMCG) or 6-channel (AMC) receiver head coils. For details, see Supplementary Material S1.

2.3.2. Image data processing

Some of the functional images were affected by a “column” or “pencil beam” artifact caused by imperfect fat suppression pulses. The artifact was most apparent in temporal signal-to-noise ratio (tSNR) maps and manifested as vertical stripes, primarily in frontal gyrus and anterior temporal lobe (see https://github.com/dinga92/stripe_cleaning_scripts). This was corrected by regressing out artifact-related independent components prior to the routine preprocessing steps. Artifact correction was done within FMRIB's Software Library (FSL; http://www.fmrib.ox.ac.uk/fsl) as follows: First, the Multivariate Exploratory Linear Optimized Decomposition into Independent Components (melodic) algorithm was used to identify independent components associated with the artifact, and second, regfilt was used to regress out the artifact-related components.

After artifact correction, functional images were analyzed using SPM12 (version R7487, Wellcome center for Human Neuroimaging, London, UK, http://www.fil.ion.ucl.ac.uk) and Matlab (Mathworks, Natick, MA, USA). Individual images were realigned to the mean image, coregistered with the high-resolution anatomical image, and normalized to the Montreal Neurological Institute (MNI) standard space using the unified segmentation-normalization approach. During spatial normalization, functional images were resampled to a voxel size of 2 × 2 × 2 mm³. Finally, normalized functional images were spatially smoothed using an 8 mm FWHM Gaussian kernel.

Preprocessed and artifact-corrected functional images from each participant entered first-level General Linear Model (GLM) analyses. Each condition (i.e., angry, fearful, happy, sad, neutral, and scrambled faces) was modeled as an individual regressor, consisting of a train of stimulus onsets convolved with a canonical hemodynamic response function (HRF). Additionally, temporal and dispersion derivatives of the canonical HRF were included to account for variability in shape and timing of hemodynamic responses (Friston et al., 1998). Realignment parameters were included as nuisance regressors to control for movement-related artifacts. Importantly, we assessed whether groups differed in the amount of head movements as this could potentially confound subsequent classification analyses. However, using a one-way between-subject analysis of variance (ANOVA) with the factor group, we found that the MDD groups did not significantly differ in their mean framewise displacement (FD; Power et al., 2012) computed from the six realignment parameters (F_(2,82) = 0.68, p = 0.51). Additionally, low-frequency fluctuations in the data were removed using a high-pass filter (cut-off 1/128 Hz).

2.3.3. Time series extraction

We selected six regions of interest (ROIs) that represent key components of the extended face perception network (Haxby et al., 2000), bilateral occipital face area (OFA; Puce et al., 1996), fusiform face area (FFA; Kanwisher et al., 1997), and amygdala (Breiter et al., 1996). To account for inter-subject variability in their exact location, center coordinates were defined for each participant individually: First, we identified the most likely MNI coordinates of these regions from a meta-analysis of 720 studies using Neurosynth (Yarkoni et al., 2011) with the search criterion “face”. Relying on this external information from Neurosynth helped ensure independence of feature selection (i.e., definition of ROI coordinates) and subsequent prediction. Generally, we prevented any cross-talk between training and test samples which might otherwise positively bias classification accuracy (see Supplementary Material S2). Second, individual peak activation coordinates were defined as the subject-specific local maximum closest to the Neurosynth coordinates within a 12 mm sphere for the linear contrast comparing faces (regardless of emotional valence) against scrambled images. Individual coordinates are illustrated in Supplementary Figure S1. While no group information was used to define ROI coordinates, in principle, some bias could still exist if the identification of individual peak activation coordinates had been influenced by systematic group differences. We examined this potential issue for the present analysis, using a multivariate analysis of variance (MANOVA), but did not find any significant group differences in the subject-specific peak activation coordinates for any of the regions (all p > 0.05). Third, BOLD signal time series were extracted from the subject-specific ROIs as the first eigenvariate of all voxels within an 8 mm sphere centered around the individual coordinates. Time series were mean-centered and movement-related variance was removed (by regression using the realignment parameters).

2.4. Dynamic causal modeling

Dynamic causal modeling (DCM; Friston et al., 2003) is a generative model that enables inference on hidden (latent) neuronal states from measured neuroimaging data. For fMRI, dynamics of neuronal activity are described as a function of the effective (directed) connectivity among neuronal populations:

$$\frac{dx}{dt}=\left(A+\sum _j{B}^{\left(j\right)}{u}_j\right)x+Cu$$ (1)

where x represents neuronal states, A encodes endogenous connectivity among brain regions, B^(j) represents the modulatory influence that input u_j exerts on endogenous connections, and C quantifies the strength of experimentally controlled inputs (perturbations) on brain regions. Integrating Eq. (1) yields a predicted neuronal time course which is then passed through a nonlinear hemodynamic model that translates neuronal signal into predicted BOLD signal (Buxton et al., 1998; Friston et al., 2000; Stephan et al., 2007). This yields a complete forward mapping from hidden neuronal states to observable fMRI data and, under Gaussian assumptions about the measurement noise, specifies the likelihood function. By specifying prior distributions over model parameters (neuronal, hemodynamic) and hyperparameters (measurement noise), DCM becomes a fully generative model. Model inversion then proceeds with approximate Bayesian schemes, most commonly variational Bayes under the Laplace approximation (VBL; Friston et al., 2007).

2.4.1. Definition of model space

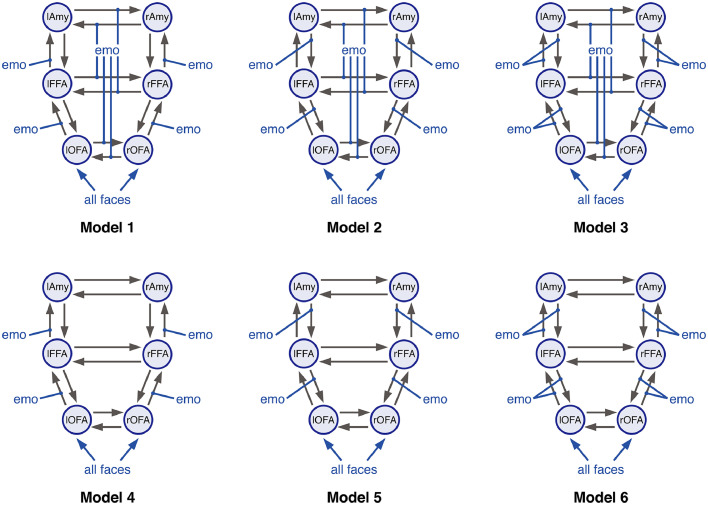
Inference on effective connectivity is conditional on the underlying model (e.g., assumptions about the network architecture). However, there typically exist several a priori hypotheses about the likely network structure. This model uncertainty leads to defining a model space, a set of alternative plausible candidate models. Here, a total of seven models were constructed, representing different possible connectivity structures in the above-mentioned emotional face perception network. For all models, endogenous connectivity and driving inputs were identical. Driving inputs were set to elicit face-sensitive activation (i.e., containing all face stimuli regardless of whether an emotional or neutral face was presented, but excluding scrambled faces) in left and right OFA, consistent with their proposed role as the first stage in the face perception network (Haxby et al., 2000; Pitcher et al., 2011). The stimulus-evoked activity then propagated through the network via intra- and interhemispheric connections. We assumed forward and backward intrahemispheric connections between OFA and FFA, and between FFA and amygdala, but not between OFA and amygdala – consistent with the notion of a hierarchy in the face perception network (Fairhall and Ishai, 2007; Haxby et al., 2000). Additionally, reciprocal interhemispheric connections were set between homotopic regions (Catani and Thiebaut de Schotten, 2008; Clarke and Miklossy, 1990; Van Essen et al., 1982; Zeki, 1970; Zilles and Clarke, 1997), but omitted between heterotopic regions (Catani and Thiebaut de Schotten, 2008; Hofer and Frahm, 2006).

For this basic structure, seven different modulatory input patterns were defined (Fig. 1), representing distinct hypotheses of how emotion processing could modulate intra- and interhemispheric connections in the extended face perception network (Fairhall and Ishai, 2007; Frässle et al., 2016). Emotion processing could modulate either (i) forward, (ii) backward, or (iii) forward and backward intrahemispheric connections. Similarly, emotion processing could modulate interhemispheric connections or not. This yielded six different models, representing all possible combinations of the above effects. Furthermore, we included a “null” model (model 7) where none of the connections were modulated.

Fig. 1.

Different plausible hypotheses of the effective connectivity pattern in the network mediating emotional face perception. Forward and backward intrahemispheric endogenous connections were set between OFA and FFA, and between FFA and amygdala (Amy). Additional, reciprocal interhemispheric connections were set between bilateral OFA, bilateral FFA and bilateral amygdala. Driving inputs comprised all faces, regardless of the emotional valence, and were allowed to drive neuronal activity in the left and right OFA. While endogenous connectivity and driving inputs were identical for all models, they differed in the assumed modulatory influences of emotion processing. Emotion processing could either modulate (i) forward (models 1&4), (ii) backward (models 2&5), or (iii) forward and backward intrahemispheric connections (models 3&6). Additionally, emotion processing (i) modulated (models 1–3) or (ii) did not modulate interhemispheric connections among homotopic brain regions (models 4–6). Systematically varying all combinations resulted in six distinct models. Finally, we also included a “null” model (i.e., model 7, not shown) where none of the intra- and interhemispheric connections was modulate by emotion processing.

Driving and modulatory inputs were not mean-centered. Model inversion was performed using DCM12 (SPM12, version R7487). For details, see Supplementary Material S3.

2.4.2. Bayesian model averaging

We computed individual parameter estimates by means of Bayesian model averaging (BMA; Penny et al., 2010) across all models in our model space within a pre-specified Occam's window (${\pi }_{occ}=0.05$). For details, see Supplementary Material S4. BMA parameter estimates represent a weighted average across the models considered, where each model contributes according to its posterior model probability. In order to prevent any cross-talk between training and test sample, BMA parameters were computed for each participant individually.

2.5. Generative embedding

The posterior means of BMA parameter estimates (78 in total) from each participant were used to create a generative score space for a discriminative classification method. Within this space, a linear kernel representing the inner product $k(x_i,x_j)=<x_i,x_j>$ was used to compare two instances (participants). A support vector machine (SVM) was applied for binary classification of pairwise combinations of the three MDD groups (i.e., REM, IMP, and CHR). Specifically, we used the fitcsvm routine in Matlab. Estimates of classification performance were obtained by leave-one-out cross-validation. Here, in each fold, the classifier is trained on $n-1$ participants (the training set) and tested on the left-out participant. Using the training set only, the hyperparameters of the SVM (box constraint and kernel scale; see Supplementary Material S5) were optimized using in-built routines of fitcsvm. This computes Bayes-optimal hyperparameters using the expected improvement acquisition function (Frazier, 2018) based on (inner) five-fold cross validation. This approach is known as nested cross-validation (Cawley and Talbot, 2010; Stone, 1974). By default, fitcsvm solves SVMs using the Sequential Minimal Optimization algorithm (SMO; Fan et al., 2005). Significance of the classification result was assessed using permutation tests. Here, an empirical null distribution of the balanced accuracy is computed by randomly permuting the participant labels and re-fitting the entire classification model (i.e., training and testing) based on these new labels (Good, 2000; Ojala and Garriga, 2010). For each permutation, the balanced accuracy is re-evaluated. Here, we used 1000 permutations. The p-value is then computed as the rank of the original balanced accuracy in the distribution of permutation-based balanced accuracies, divided by the total number of permutations.

3. Results

3.1. Group differences in effective connectivity

Effective connectivity among the regions of the extended face perception network (i.e., OFA, FFA, and amygdala, each in both hemispheres) was assessed using DCM for fMRI (Friston et al., 2003). First, we provide a brief summary of the group differences in DCM parameter estimates as assessed using classical statistics (a comprehensive description of the classical analyses is provided in Supplementary Material S7).

Random-effects Bayesian model selection (Rigoux et al., 2014; Stephan et al., 2007) suggested model 3 to be the winning model at the group level with an expected posterior probability of 0.49 and a protected exceedance probability close to 1 (Supplementary Figure S4B). Nevertheless, at the single-subject level, other models received non-negligible posterior probabilities as well. To account for this variability, individual connectivity parameters were estimated using BMA (Penny et al., 2010) over all seven models in the model space within the default Occam's window (${\pi }_{occ}=0.05$).

When testing for group differences in the BMA parameter estimates (two-sample t-tests), no significant differences were found when correcting for multiple comparisons based on the false discovery rate (Benjamini and Yekutieli, 2001). At a more liberal threshold (p < 0.05, uncorrected), some differences between the patient subgroups were observed (see Supplementary Figure S6). In brief, effective connectivity patterns differed mainly in how emotions modulated functional integration among the face-processing (i.e., bilateral OFA and FFA) and emotion-sensitive regions (i.e., bilateral amygdala). Overall, emotions tended to exert stronger modulatory influences in patients showing fast remission as compared to patients with a chronic disease trajectory (Supplementary Figure S6, left) and patients with gradual improvement of symptoms (Supplementary Figure S6, right). For the comparison between CHR and IMP patients, the pattern was more ambiguous (Supplementary Figure S6, middle).

While – as highlighted above – none of the group differences survived multiple comparisons correction, these findings suggest that small alterations of different effective connectivity strengths exist between CHR, IMP and REM patients, which enable classification when jointly considered as features.

3.2. Classification of clinical trajectories

3.2.1. Predictive accuracy of effective connectivity parameters

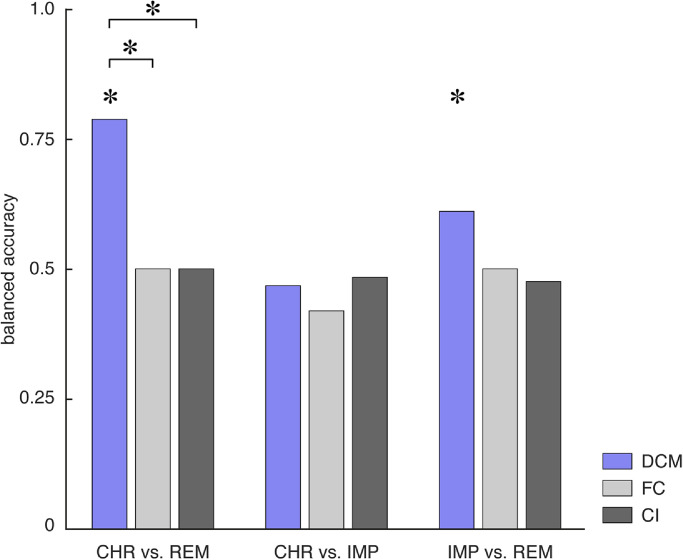
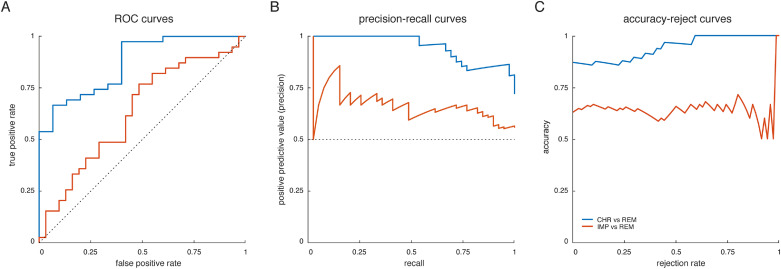
Our results suggest that DCM parameter estimates discriminated patients with chronic disease trajectory from patients showing fast remission, with a balanced accuracy of 79% (p < 0.001; Fig. 2, blue). We then evaluated the underlying receiver-operating characteristic (ROC) and precision-recall (PR) curves (Fig. 3A+B). From the ROC curve, the area under the curve (AUC) for discriminating CHR from REM patients evaluated to 0.87 (blue curve). Notably, high recall (sensitivity) might come at the expense of low positive predictive value (PPV; also known as “precision”) – particularly, in the presence of class imbalances. This is problematic for clinical applications where one strives to maximize sensitivity while at the same time keeping PPV high. Hence, we also inspected the PR curves and found that our classifier achieved 97% sensitivity at a PPV of 86% when discriminating CHR from REM patients.

Fig. 2.

Balanced accuracy for the binary classifiers as assessed using leave-one-out cross validation for the three different subgroup comparisons – that is, CHR vs. REM (left), CHR vs. IMP (middle), and IMP vs. REM (right). Balanced accuracies are shown for the different features – namely, effective connectivity parameters (DCM; blue), functional connectivity (FC; light grey), and local BOLD activity (CI, dark grey). Asterisks above the bars indicate significant classification performance as assessed by means of permutation tests where an empirical null distribution of the balanced accuracy is computed by randomly permuting the participant labels and re-evaluating the classifier based on these new labels. Additionally, asterisks above the lines connecting two bars indicate significant differences in classification performance between different data features as assessed using the asymptotic McNemar test.

Fig. 3.

Performance curves for the two binary classifiers that achieved above-chance balanced accuracies – that is, CHR vs. REM (blue curve) and IMP vs. REM (red curve). (A) receiver-operating characteristic (ROC) curves, illustrating the trade-off between the true positive rate (sensitivity) and the false positive rate (1-specificity) across the entire range of detection thresholds, (B) precision-recall (PR) curves, illustrating the trade-off between the precision (positive predictive value) and recall (true positive rate) for different thresholds, and (C) accuracy-reject curves, representing the accuracy of a classifier as a function of the rejection rate (Nadeem et al., 2010). For a comprehensive summary of all classification results, see Table 2. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Effective connectivity parameter estimates also discriminated between IMP and REM patients, with a balanced accuracy of 61% (p = 0.03; Fig. 2), although this did not reach significance when correcting for multiple comparisons (α_Bonf = 0.0056). The AUC was 0.63 (Fig. 3A+B; red curve). In contrast, CHR patients could not be differentiated from IMP patients above-chance level (balanced accuracy: 47%, p = 0.92; Fig. 2), corresponding to an AUC of 0.35. Table 2 provides a comprehensive summary of all classification results.

Table 2.

Classification results for the generative embedding procedure. Shown are key performance measures of the classification algorithm, including: balanced accuracy, area under the curve, sensitivity (recall), specificity, positive predictive value (precision), and negative predictive value. Performance measures are shown for the three different binary classifications (i.e., CHR vs. REM, CHR vs. IMP, and IMP vs. REM).

Classification	CHR (n = 15) vs. REM (n = 39)	CHR (n = 15) vs. IMP (n = 31)	IMP (n = 31) vs. REM (n = 39)
Accuracy	0.87	0.63	0.63
Balanced accuracy	0.79	0.47	0.61
Area under the curve (AUC)	0.87	0.35	0.63
Sensitivity (recall)	0.97	0.94	0.77
Specificity	0.60	0	0.45
Positive predictive value (Precision)	0.86	0.66	0.64
Negative predictive value	0.90	0	0.61

Since groups differed significantly in age (but no other variable; Table 1), we repeated the analysis after regressing out age as a confound from the DCM parameter estimates. We found results to be highly consistent (although with slightly decreased accuracies), suggesting that our results are not confounded by age (Supplementary Material S8).

3.2.2. Comparison to functional connectivity and fMRI activity

We compared the GE results to a conventional approach in which the classifier operates on estimates of functional connectivity (FC). Following standard practice, FC was computed in terms of Pearson's correlations among the same BOLD signal time series that had previously been used for the DCMs. However, FC measures did not discriminate between the different clinical trajectories above chance, with balanced accuracies of 50% (p = 0.77) for CHR vs. REM patients, 42% (p = 0.996) for CHR vs. IMP patients, and 50% (p = 0.37) for IMP vs. REM patients (Fig. 2, light grey). Importantly, for discriminating CHR from REM patients, GE significantly outperformed FC estimates (p = 0.01; asymptotic McNemar test1 as implemented in MATLAB's testcholdout function).

In addition, we tested whether the different clinical trajectories could be distinguished based on measures of BOLD activity (CI) from the same ROIs as utilized for the connectivity-based analyses. Local BOLD activity was quantified in terms of the mean and standard deviation of the contrast estimates within the 8 mm spheres for all face-related contrasts (i.e., contrasts representing the individual regressors of angry, fearful, happy, sad, and neutral faces; see Methods). Under this approach, the different clinical trajectories were indistinguishable, with balanced accuracies of 50% (p = 0.72) for CHR vs. REM patients, 48% (p = 0.81) for CHR vs. IMP patients, and 48% (p = 0.51) for IMP vs. REM patients (Fig. 2, dark grey). As for FC, GE significantly outperformed local BOLD activity for distinguishing CHR from REM patients (p = 0.01).

Notably, these analyses are not meant to represent an optimal prediction approach based on FC or CI measures. Higher accuracies for classification based on FC/CI might be achieved by taking into account the whole-brain information (e.g., Crowther et al., 2015; Fu et al., 2008; Schmaal et al., 2015). Furthermore, it is worth pointing out that the number of features that enter classification are different for GE, FC and CI. However, the purpose of the above analysis was to compare predictions based on different fMRI-based features derived from the exact same data (i.e., the BOLD activity from the ROIs of the emotional face processing network).

3.3. Assessment of predictive confidence

Next, to assess the predictive confidence of our GE approach, we computed accuracy-reject curves for the two binary classifiers that achieved above-chance balanced accuracies (i.e., CHR vs. REM, IMP vs. REM). Accuracy-reject curves illustrate a classifier's accuracy when only predictions greater than a certain (relative) confidence threshold are considered (Nadeem et al., 2010). Hence, this resembles classification with a reject option (Bishop, 2006), where cases that do not meet a certain confidence criterion can be deferred to a clinician. We found that for distinguishing CHR from REM patients, the classifier yielded perfect classification accuracy at a rejection threshold of 60% of participants (Fig. 3C; blue curve). Furthermore, the accuracy-reject curve overall increased as function of rejection rate, suggesting that participants further away from the decision hyperplane were more likely to be assigned correctly to their respective class. In contrast, for distinguishing IMP from REM patients no such cut-off could be identified, and the curve did not reveal a steady increase as a function of rejection rate (Fig. 3C; red curve).

3.4. Inspection of the generative score space

One benefit of GE is that features represent model parameter estimates, which, depending on the model, may be neurobiologically interpretable. Hence, in a next step, we interrogated our generative score space to illustrate which features contributed most to the classification performance.

3.4.1. Inspection of individual predictive features

In a first step, we aimed to pinpoint the individual contribution of each feature (i.e., DCM parameter estimate) separately for the two significant classifiers (i.e., CHR vs. REM, IMP vs. REM). Importantly, individual feature weights of linear classifiers are not directly interpretable because high magnitudes of feature weights might either indicate an association with the label or a “suppressor” variable that cancels out noise or mismatch in other colinear variables (Haufe et al., 2014; Naselaris et al., 2011). Therefore, we followed the procedure described by Haufe et al. (2014) and first transformed all feature weights into patterns based on a corresponding forward mapping.

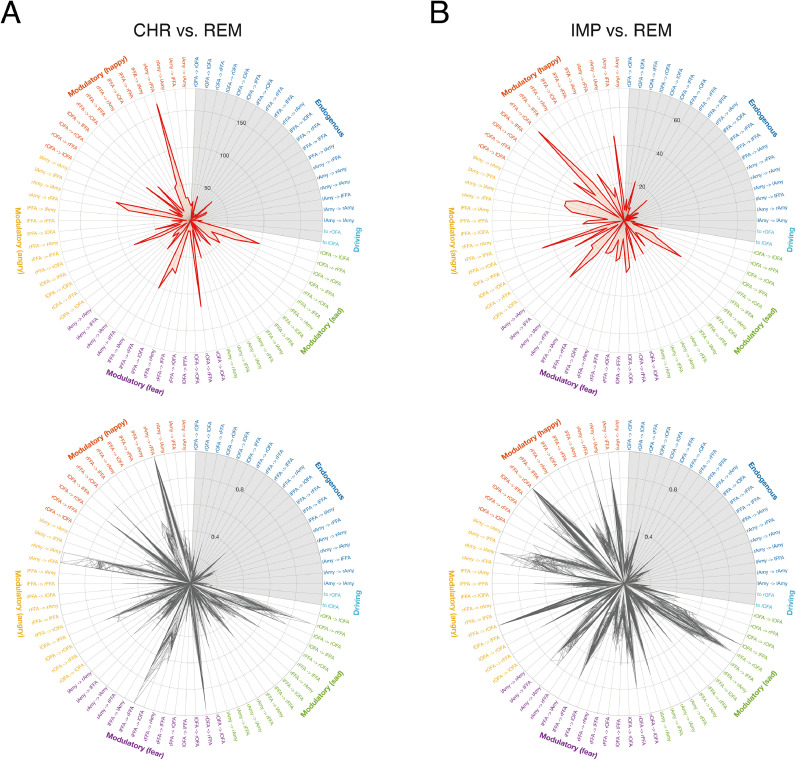
For both classifiers, the features with the highest average (across cross-validation folds) scores were situated along the dimension of modulatory (emotional) influences (Fig. 4, top; for an alternative visualization, see Supplementary Figure S8), whereas the endogenous connectivity and driving input parameters did not distinguish strongly between the groups. Importantly, since averaging over cross-validation folds might artificially smooth the weights due to correlations among folds, we inspected the variability of the observed results across the individual cross-validation folds. This suggested that the observed pattern was highly consistent for both classifiers (Fig. 4, bottom).

Fig. 4.

Illustration of the relevance of individual features. First, feature weights were transformed into feature patterns to allow for interpretability (Haufe et al., 2014). The respective score of each individual feature (DCM parameter) is then shown as a polar plot for the classifier distinguishing (A) patients with a chronic disease trajectory from patients that showed fast remission (CHR vs. REM), and (B) patients with gradual improvement of symptom severity from patients that showed fast remission (IMP vs. REM). (Top) Magnitude of scores computed as the average across all cross-validation folds, (bottom) magnitude of scores for each cross-validation fold individually, normalized to the maximum score within each fold for displaying purposes. The grey area represents endogenous connectivity and driving input parameters, showing less pronounced scores as the modulatory parameters. Endogenous connectivity is colored in blue, modulatory influences of happy faces in red, modulatory influences of angry faces in yellow, modulatory influences of fearful faces in violet, modulatory influences of sad faces in green, and driving inputs (related to all faces regardless of the emotional valence) in cyan. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

In brief, for distinguishing CHR from REM patients, the modulatory influence of happy faces on the connection from right amygdala to right FFA received the highest score (Fig. 4A and Supplementary Figure S8A). Furthermore, scores were high for modulatory influences of negative emotions (i.e., fear, anger, and sadness) on connections among face-processing and emotion-sensitive regions. For instance, modulatory influences by angry faces on the connection from right amygdala to right FFA and left amygdala, and on the connection from left OFA to left FFA showed high loads. Similarly, the modulation of connections from right OFA and left FFA to right FFA, as well as the connection from right FFA to right amygdala by fearful faces received high scores.

For distinguishing IMP from REM patients, the modulatory influence of happy faces on the connection from right FFA to right OFA received the highest score (Fig. 4B and Supplementary Figure S8B). Modulatory influences by angry and sad faces on this connection also showed high loads. Similarly, modulation of connections among FFA and amygdala in both hemispheres by angry faces scored highly, as well as modulation of various endogenous connections (e.g., left amygdala to left FFA, left to right OFA, left FFA to left OFA) by happy faces.

Overall, the most consistently important connections – that is, the connections for which modulations received high scores for all emotional valences and both classifiers – are the connections from left to right OFA, right FFA to right OFA, right amygdala to right FFA, as well as the reciprocal interhemispheric connections between bilateral FFA.

In summary, the model-based distinction between CHR/IMP patients from REM patients relied on the expression of trial-by-trial modulation of connections (by emotional contents) within the face perception network. Put simply, our results suggest that abnormal dynamic changes of connections involved in processing emotional faces are associated with higher risk of developing a less favorable clinical course (see also Supplementary Figure S6).

4. Discussion

This paper examines the utility of GE for predicting individual clinical trajectories of MDD patients over a two-year period. Using fMRI data from the NESDA study and DCM to infer effective connectivity within the emotional face perception network, model parameter estimates served as features for supervised learning. This GE approach enabled the prediction of whether a given patient would show a chronic disease course or fast remission, with a balanced accuracy of 79%. Additionally, patients with gradual improvement in symptom severity could be distinguished from those who remitted quickly with a balanced accuracy of 61%. GE outperformed SVM-based classification based on more conventional (descriptive) features, i.e., FC or local activation estimates derived from the same data within the network of interest. Similar to previous studies (Brodersen et al., 2014, 2011), these findings demonstrate that using a plausible generative model as the basis for classification can enhance classification accuracy significantly.

Apart from the superior classification accuracy, another advantage of GE is that results can be interpreted in terms of the mechanisms represented by the underlying generative model. To this end, one can interrogate the generative score space to identify the features that are most discriminative between the different classes (Brodersen et al., 2011). Here, we addressed this by first transforming the feature weights of the linear SVM into patterns, following previous recommendations (Haufe et al., 2014). Inspecting these scores then allowed to pinpoint those features contributing most to the classification between the different naturalistic courses (Fig. 4 and Supplementary Figure S8). This analysis suggested that groups differed primarily along the dimension encoded by the modulatory parameters, which represent trial-by-trial changes in endogenous connections by emotional valence of faces. Put differently, it is the dynamic modulation of connections by emotional contents of faces that allows for predicting the clinical trajectory of an individual patient – not the average connectivity across all trials. In conclusion, our analysis implies that it is the reactivity of the face processing network to emotional stimuli – in terms of reconfiguring its connection strengths trial-by-trial – which enables predicting future clinical trajectories of individual patients.

These results are consistent with conventional group comparisons of the connectivity patterns (see Results and Supplementary Material S7), which, however, do not allow for single-subject predictions. Our results are also consistent with previous work suggesting aberrant processing and regulation of emotions as a key pathomechanism in MDD (Harmer et al., 2009; Rive et al., 2013). For instance, an fMRI meta-analysis demonstrated valence-dependent effects of emotional stimuli on amygdala and fusiform gyrus in depression, with hyperactivation for negative and hypoactivation for positive stimuli (Groenewold et al., 2013; but see Muller et al., 2017). Reduced amygdala activity to positive emotional stimuli has also been associated with anhedonia (Stuhrmann et al., 2013). Similarly, functional integration of the emotion processing network is altered in MDD (Almeida et al., 2009; Greicius et al., 2007; Mayberg, 1997). Alterations in emotion processing have also been suggested to have some clinical utility. For instance, implicit processing of affective facial expressions related to a diagnosis of MDD (Fu et al., 2007), and longitudinal neuroimaging studies reported normalization of activations by emotion processing under pharmacotherapy (Ai et al., 2019; Anand et al., 2007; Fu et al., 2004; Godlewska et al., 2012; Murphy et al., 2009; Robertson et al., 2007; Sheline et al., 2001).

Our classification accuracies are comparable to the results obtained by Schmaal et al. (2015). For CHR vs. REM patients, GE yielded a higher predictive accuracy than the best result reported by Schmaal and colleagues (balanced accuracy: 73%) when not accounting for age. When age was regressed out as a confound, the predictive accuracy of GE (balanced accuracy: 74%) was on par with the result reported in Schmaal et al. (2015). Otherwise, our procedure yielded somewhat complementary results: while Schmaal and colleagues could distinguish CHR from IMP patients but not IMP from REM patients, the opposite held for GE. This may be due to differences in classification procedure and features: Schmaal et al. used GPCs on whole-brain contrast images, whereas we applied linear SVMs to DCM parameter estimates from a small (six-region) network. Furthermore, their analysis used the artifact-confounded MR data (see Methods); hence, it remains to be tested whether classification accuracy would change when the artifact-corrected images are used.

Previous attempts to obtain single-patient predictions in MDD have almost exclusively concerned short-term treatment responses to specific interventions. For instance, seminal PET work demonstrated that cingulate metabolism differentiated distinct treatment responses (Mayberg et al., 1997). For fMRI, brain activity during the processing of sad faces allowed predicting treatment outcome to antidepressant medication in individual (Fu et al., 2008). Graph-theoretical measures based on FC in the default mode network at baseline was associated with changes in symptom severity after two weeks of medication (Shen et al., 2015). Furthermore, activation (Siegle et al., 2012) and FC (Crowther et al., 2015; Walsh et al., 2017) were predictive of psychotherapy outcome. Similarly, FC of subcallosal cingulate cortex with insula, dorsal midbrain and ventromedial prefrontal cortex was differentially associated with remission and treatment failure to cognitive-behavioral therapy and antidepressant medication (Dunlop et al., 2017). Finally, clinical responses to transcranial direct current stimulation of left prefrontal cortex could be predicted in unmedicated MDD patients (Nord et al., 2019).

Arguably, the attempt to predict outcome after two years in a naturalistic setting, as in NESDA, represents a greater challenge than predicting short-term response to a particular treatment. NESDA (1) recruited patients from a wide spectrum, including community, primary care and specialized mental health organizations, (2) encompassed a wide range of depressive phenotypes from very mild to severe, and (3) did not standardize treatments or occurrence of life events over the 2-year follow-up period (Penninx et al., 2008). This represents a strength of the NESDA dataset since it allows testing the course of MDD in a realistic setting which reflects the clinical heterogeneity that physicians face on a daily basis.

Existing attempts to predict MDD trajectories have focused on clinical or cognitive features (Gueorguieva et al., 2017; Kessler et al., 2016; Vogelzangs et al., 2014; Vreeburg et al., 2013). Recently, Dinga et al. (2018) systematically assessed the predictive value of non-imaging data, using clinical, psychological and biological measures from the NESDA study. They found that clinical measures performed best with balanced accuracies around 66%, while endocrine and immunological measures (e.g., cortisol, inflammatory markers, metabolic syndrome markers) did not distinguish between clinical trajectories. Interestingly, consistent with our GE results, they could primarily discriminate REM patients from the other two groups.

Our study is subject to several limitations. First, while our sample size (n = 85) does not fare badly compared to previous imaging-based prediction studies on MDD, the sample size is too modest for establishing predictions that can be expected to generalize robustly; particularly, the chronic group is small, comprising only 15 patients. Unfortunately, we do not have access to a separate validation set at the present time. Hence, our results should be understood as a proof-of-concept regarding the potential benefits of GE for clinical predictions, not as providing a mature prognostic tool for MDD. Second, the NESDA sample utilized in the present work was acquired at multiple sites. While the proportion of patients in the three clinical trajectory groups did not significantly differ across sites (see Table 1) – rendering any potential bias on the reported classification results unlikely – prediction might still benefit from a more thorough data harmonization (Fortin et al., 2017; Yu et al., 2018). Third, we here adopted the classical view on hierarchical processing in the face perception network (Fairhall and Ishai, 2007; Haxby et al., 2000). This view could be extended, given that recent work suggested a direct subcortical pathway, from the superior colliculus to the amygdala via the pulvinar, for rapid threat detection during emotional face perception (McFadyen et al., 2019). This could be accounted for by expanding the present model space and allowing for additional driving inputs into the amygdala. Fourth, the classical DCM approach employed here is restricted to small networks to keep model inversion computationally feasible (Daunizeau et al., 2011; Frässle et al., 2018b). Consequently, we focused on a six-region network comprising only core regions of the face perception network. However, depression is characterized by more widely distributed network organization (Greicius et al., 2007; Mayberg, 1997; Wang et al., 2012) and, hence, inferring whole-brain effective connectivity represents a promising next step. This could be achieved by exploiting recent advances in generative models that are computationally highly efficient (Frässle et al., 2018a, 2017).

Furthermore, in line with Schmaal et al. (2015), we used binary classifiers which can only distinguish between two disease trajectories. However, this approach does not allow for single-class predictions, which rests on multi-class classification (Bishop, 2006). Extending our classification scheme beyond binary classification is likely to be of clinical relevance, as multi-class prediction more faithfully resembles the decision process that physicians routinely engage in. In addition, an attractive alternative for future analyses is to predict continuous measures, such as time-to-recovery, rather than the discrete classes defined by the latent class growth analysis (Rhebergen et al., 2012). On a similar note, we anticipate that predicting the entire disease trajectories rather than discrete classes or continuous outcome measures will constitute an important future test of the predictive utility of effective connectivity patterns in MDD.

Finally, on a more general note, any biomarker in psychiatry will always yield imperfect predictions. This is because the course of psychiatric disorders is affected by a plethora of environmental factors which cannot be foreseen from physiological data, including the occurrence of stressful life events like loss, bereavement, or trauma (Horesh et al., 2008). Such external perturbations likely upper-bound the predictive accuracy of any biomarker, whether derived from neuroimaging or genetics.

Despite these limitations, the present study demonstrates the potential of GE for predicting clinical outcomes of MDD in a way that combines enhanced accuracy with biological interpretability of predictions. More generally, as illustrated by recent successful clinical applications (Symmonds et al., 2018), generative models offer an attractive strategy for establishing computational assays that could inform clinical decision-making in psychiatry (Frässle et al., 2018b). A critical condition for the future success (or failure) of this strategy will be the availability of large prospective patient datasets that, like NESDA, offer clinically relevant outcome data and allow for testing the generalizability and robustness of model-based clinical predictions in real-world settings.

Data availability

The data used in this study can be obtained via the standard NESDA data access procedure (see https://www.nesda.nl/nesda-english/). This requires researchers to file a data request (analysis plan) which has to be approved by the NESDA consortium in order to be granted access to the data. NESDA fully adheres to the FAIR (Findable, Accessible, Interoperable, and Re-usable) data principles. Furthermore, we will make all analysis code publicly available on the GIT repository of ETH Zurich (https://gitlab.ethz.ch/tnu/code/generative-embedding-nesda).

CRediT authorship contribution statement

Stefan Frässle: Conceptualization, Formal analysis, Funding acquisition, Methodology, Software, Visualization, Writing - original draft, Writing - review & editing. Andre F. Marquand: Conceptualization, Funding acquisition, Data curation, Resources, Writing - review & editing. Lianne Schmaal: Conceptualization, Funding acquisition, Data curation, Resources, Writing - review & editing. Richard Dinga: Data curation, Writing - review & editing. Dick J. Veltman: Funding acquisition, Resources, Writing - review & editing. Nic J.A. van der Wee: Funding acquisition, Resources, Writing - review & editing. Marie-José van Tol: Funding acquisition, Resources, Writing - review & editing. Dario Schöbi: Formal analysis, Validation, Writing - review & editing. Brenda W.J.H. Penninx: Conceptualization, Funding acquisition, Project administration, Resources, Writing - review & editing. Klaas E. Stephan: Conceptualization, Funding acquisition, Resources, Supervision, Writing - review & editing.

Declaration of Competing Interest

The authors report no conflict of interest.