All tests are imperfect: Accounting for false positives and false negatives using Bayesian statistics

Abstract

Tests with binary outcomes (e.g., positive versus negative) to indicate a binary state of nature (e.g., disease agent present versus absent) are common. These tests are rarely perfect: chances of a false positive and a false negative always exist. Imperfect results cannot be directly used to infer the true state of the nature; information about the method's uncertainty (i.e., the two error rates and our knowledge of the subject) must be properly accounted for before an imperfect result can be made informative. We discuss statistical methods for incorporating the uncertain information under two scenarios, based on the purpose of conducting a test: inference about the subject under test and inference about the population represented by test subjects. The results are applicable to almost all tests. The importance of properly interpreting results from imperfect tests is universal, although how to handle the uncertainty is inevitably case-specific. The statistical considerations not only will change the way we interpret test results, but also how we plan and carry out tests that are known to be imperfect. Using a numerical example, we illustrate the post-test steps necessary for making the imperfect test results meaningful.

Conditional probability; False negative; Uncertainty; False positive; Bayes' rule; Statistics; Environmental assessment; Environmental risk assessment; Bioinformatics; Epidemiology

1. Introduction

In both scientific research and routine daily decision-making, we depend on results of various tests. Tests come in all forms and shapes. For example, doctors may test a patient's blood for the presence of a disease marker, environmental engineers may test a sample of drinking water for the presence of cyanobacterial toxin microcystins and determine whether the concentration is above the public health safety threshold, ecologists may survey for invasive species, a geologist may drill a test well exploring for oil, a pollster may take an opinion poll to evaluate the viability of a political candidate, and so on. A unifying feature of these tests is that they are imperfect: the test result is likely correct but not always. In most cases, test results are reported to be or can be simplified as either positive or negative. For example, a positive blood test indicates the existence of the disease marker and a positive opinion poll result indicates that the candidate is likely to win (with more than 50% popular support). A test result is imperfect because (1) most measured values are associated with inevitable measurement error and (2) a test is always based on measurements from a sample (e.g., a blood sample, a water sample, or a sample of 1,000 potential voters). A sample can misrepresent the population. A water sample from a polluted water source may contain no fecal coliform bacteria by chance, thereby leading to a false negative result. Likewise, a water sample from a clean water source may be contaminated unintentionally by researchers during the sampling process or in the lab. The subsequent positive result is then classified as a false positive (i.e., the water source is incorrectly classified as “polluted”). Almost all tests used in scientific research are imperfect and, therefore, such sampling, measurement, and experimental errors are unavoidable. Given this imperfection of tests, we face a challenge when interpreting the test result: how can we use a potentially incorrect result to draw inference or make a decision? Is a positive fecal coliform test result truly indicating that the water is polluted by domestic sewage, or is it a false positive? How we interpret the result will affect how we decide, for example, when to issue a public health warning for an affected recreational beach.

The imperfection of a test is routinely quantified with two error rates: the rate of a false positive (also known as a type I error) and the rate of a false negative (a type II error). Scientists in all fields recognize the imperfection, and used various terms to describe the two types of errors. For example, in the early days of World War II, the US Army developed the receiver operating characteristic (ROC) curve to identify the optimal threshold for determining whether a radar signal was from a Japanese aircraft. The two axes of the ROC curve are errors of omission (false negative) and commission (false positive). The decision threshold is selected to properly balance and minimize the two types of errors when interpreting a signal. When such uncertainty is unknown, decisions based on test results are often controversial. In 2014, the City of Toledo, Ohio faced such a decision when the measured microcystin concentration from one water sample exceeded Ohio's drinking water safety standard of 1 μg/L. Because the standard measurement method is highly variable [9], a measured concentration that exceeds the standard may not mean that the actual concentration is also above the standard. However, information about the measurement uncertainty was not available to the decision makers at the time and a “Do-Not-Drink” advisory was issued. When the subsequent tests of the same water sample returned below standard concentrations, the decision of advising Toledo residents not to drink their tap water became controversial.

For simplifying the discussion, we will define the following terms. First, we use present or absent to represent the state of the world we are trying to infer: a present indicates the presence of an agent of interest (e.g., microcystin concentration exceeding the standard, more than 50% popular support, an enemy aircraft, and so on) and an absent means the absence of the agent. When conducting a test, the test result is either positive (indicating the state of the world is likely present) or negative (likely absent). A false positive rate tells us how likely it is that a test would lead to a positive result when the true state of the world is absent and a false negative rate is the likelihood of a negative result when the true state of the world is present. When a test is carried out, we want to use the test result (either positive or negative) to infer the true state of the world. The imperfection of the test leads to uncertainty in the subsequent interpretation and inference. To make our discussion less abstract, we use a study of fungal disease in a Michigan rattlesnake population as an example.

2. Example: snake fungal disease in Michigan

Snake fungal disease (SFD), caused by the fungus Ophidiomyces ophiodiicola, is an emergent pathogen known to affect at least 30 snake species from 6 families in eastern North America and Europe [1], [6]. SFD was detected in eastern massasaugas (Sistrurus catenatus), a small, federally-threatened rattlesnake species, in Michigan in 2013 [10]. The estimated SFD prevalence ranges from 3-17% in three Michigan populations [5].

A commonly used method for detecting SFD is quantitative PCR (qPCR) to identify the fungal DNA using a skin swab. The method often leads to a false negative because swabbing can miss the disease agent. Hileman et al. [5] show that a single swab of an eastern massasauga with clinical signs of SFD (skin lesions) can often result in a false negative; a positive result (detecting fungal DNA on an individual snake) does not always indicate that the individual has SFD (false positive).

For the purpose of discussion, we used a sample of 20 snakes, 5 which tested positive for SFD. As the effectiveness of using qPCR for testing SFD is still under study, we use optimistic hypothetical rates of false positive (5%) and false negative (3%).

3. Conditional probability and Bayes' rule

Properly handling the uncertainty of the test result is the realm of probability and statistics. We use probability to quantify the uncertainty and use rules of probability to make inferences. Using the probability language to describe an imperfect test, the rate of a false positive is the probability of a positive test result when the underlying true state of the world is absent. Likewise, the rate of a false negative is the probability of a negative test result when the true state of the world is present. These two probabilities are examples of a conditional probability. To summarize the rules of conditional probabilities, we use “p” to represent the state of the world being present, “a” to represent absent (Fig. 1(i)), “+” to represent a positive test result, and “−” to represent a negative result (Fig. 1(ii)). A false positive probability is symbolized as $\mathrm{Pr}(+|a)$, and a false negative probability is $\mathrm{Pr}(-|p)$. These two conditional probabilities characterize the quality of the test.

Figure 1.

A graphical depiction of an imperfect test. The true state of the world is either p (present, the black circle) or a (absent, the white space outside the circle) (i), and the test result is either + (the green circle) or − (the white space outside the circle) (ii). The imperfection of the test makes the interpretation of a test result contingent on information regarding the accuracy of the test and $\mathrm{Pr}(p)$ (the non-overlapping portion of the green circle is the false positive rate and the non-overlapping portion of the black circle is the false negative rate) (iii). Changes in the relative size of p and a (iv) and/or $\mathrm{Pr}(p)$ (v) will lead to a different interpretation of a test result (vi).

When a test is carried out, we observe either a “+” or a “−”. What we want to know is how likely the true state of the world is p when observing a + and how likely the true state of the world is a when observing a “−”. These are also conditional probabilities: $\mathrm{Pr}(p|+)$ and $\mathrm{Pr}(a|-)$. These two conditional probabilities are the basis for interpretation and inference of imperfect tests.

Bayes' rule [2] connects these two groups of conditional probabilities (Fig. 1(iii)):

$$\mathrm{Pr}(p|+)=\frac{\mathrm{Pr}(p)\mathrm{Pr}(+|p)}{\mathrm{Pr}(p)\mathrm{Pr}(+|p)+\mathrm{Pr}(a)\mathrm{Pr}(+|a)}$$ (1)

and

$$\mathrm{Pr}(a|-)=\frac{\mathrm{Pr}(a)\mathrm{Pr}(-|a)}{\mathrm{Pr}(a)\mathrm{Pr}(-|a)+\mathrm{Pr}(p)\mathrm{Pr}(-|p)}$$ (2)

Bayes' rule has been used successfully in many fields. The popular book by Sharon McGrayne [8] documents many mesmerizing stories of Bayes' rule from cracking the enigma code in World War II and hunting down Soviet submarines in the Cold War to settling the disputed authorship of federalist papers, nearly all these stories are related to binary decisions.

We will focus on equation (1). The test result is either positive or negative; consequently, $\mathrm{Pr}(+|p)=1-\mathrm{Pr}(-|p)$. In addition, $\mathrm{Pr}(a)=1-\mathrm{Pr}(p)$. The Bayes' rule (eq. (1)) suggests that in addition to the false positive and false negative probabilities we must also know $\mathrm{Pr}(p)$ in order to calculate $\mathrm{Pr}(p|+)$. In statistics, $\mathrm{Pr}(p)$ is a marginal probability – the probability of the true state of the world being present regardless of the test result (or before we carried out the test). This probability can be interpreted as, for example, the prevalence of a disease in a population or our uncertainty with regard to the true state of the world before a test is carried out. For example, when testing snakes for a snake fungal disease, we can interpret $\mathrm{Pr}(p)$ as the prevalence of the disease in the population. The Bayes' rule suggests that $\mathrm{Pr}(p)$ is necessary when interpreting the test result (see Box-A.).

4. The prior probability and statistical inference

A point of contention in using Bayes' rule is the meaning of the prior probability $\mathrm{Pr}(p)$. In Box-A., we interpreted the prior as the fraction of individual snakes in the population that are infected with the fungal disease. When this fraction changes, the proportion of true positives (infected individuals among positive tests) also changes. When the prior has a clear physical meaning and can be measured, the use of Bayes' rule is widely accepted [3]. When the prior is difficult to specify or the physical meaning is ambiguous, the use of a prior used to be controversial. Increasingly, we recognize that eliciting the prior is a means for proper use of relevant information in an analysis (Box-B.). Regardless of the meaning of the prior, the Bayes' rule highlights the need of quantifying the prior $\mathrm{Pr}(p)$ in order to properly interpret a test result; whether we call the quantity a prior, a marginal probability, or the prevalence is irrelevant. The proper interpretation of the test result and the use of the test result for inference requires a proper statistical treatment. As in all statistical applications, the first step is to represent the scientific hypothesis using a statistical model (with parameters). The proposed statistical model, in turn, will decide how we use data to estimate model parameters and how the model can be verified.

5. The purpose of a test

Understanding and defining the objective of a test is the key to deciding what statistical model to use. When analyzing results from an imperfect test, there are at least two different objectives: (1) testing for an individual subject, that is, to estimate $\mathrm{Pr}(p|+)$ (e.g., whether a patient has a particular disease agent), and (2) testing to learn about a population, that is, to estimate $\mathrm{Pr}(p)$ (e.g., the prevalence of snake fungal disease in the rattlesnake population in Michigan).

5.1. Tests for individual subjects

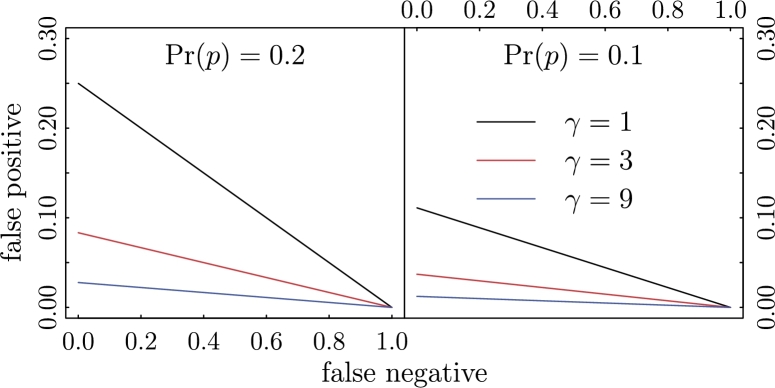
When a doctor tests a patient for a disease, the objective is to determine the likelihood that the patient has the disease. With known characteristics of the test (i.e., $\mathrm{Pr}(+|a)$ and $\mathrm{Pr}(-|p)$) and the prevalence of the disease in the population, we can use Bayes' rule to calculate the conditional probability $\mathrm{Pr}(p|+)$ for a positive result. In this situation, a useful test will result in a $\mathrm{Pr}(p|+)$ larger than a specific number (e.g., 0.5 or a threshold selected as an optimal binary classifier based on an ROC curve). That is, a positive result should suggest that the patient is more likely to have the disease than not. Another way to express this condition is that the odds ratio should be larger than 1 (when the threshold is 0.5): $\frac{\mathrm{Pr}(p|+)}{1-\mathrm{Pr}(p|+)}>1$. More generally, we can require that $\frac{\mathrm{Pr}(p|+)}{1-\mathrm{Pr}(p|+)}>\gamma$ before we consider the test to be useful (e.g., prescribe treatment upon a positive result). Using Bayes' rule, we can express this requirement in terms of the rates of false positive and false negative, as well as the prevalence.

$$\mathrm{Pr}(+|a)<\frac{1-\gamma }{\gamma }\frac{\mathrm{Pr}(p)}{1-\mathrm{Pr}(p)}(1-\mathrm{Pr}(-|p))$$ (3)

In other words, a useful test must satisfy the inequality set by equation (3) (Fig. 2).

Figure 2.

A graphical representation of (3): a test is represented by a dot in the graph and useful tests are those located below the respective lines.

5.2. Tests for estimating population parameter(s)

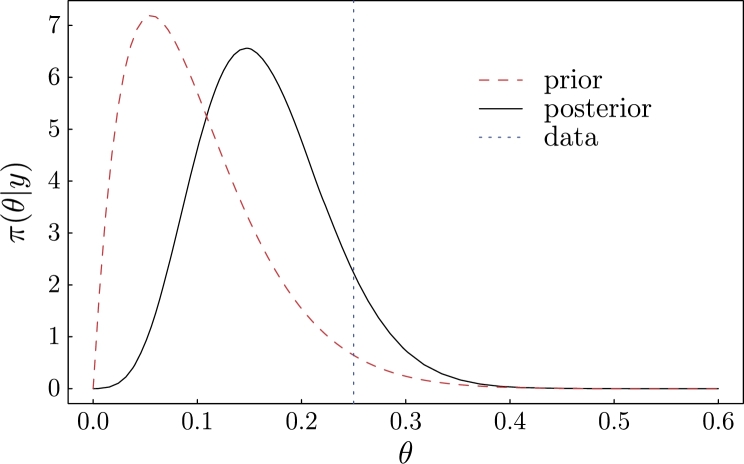
In many cases, we test multiple individuals of a population in order to understand the characteristics of the population. In the snake example, researchers are interested in estimating the prevalence of the fungal disease in the population. That is, we want to specify the prior $\theta =\mathrm{Pr}(p)$, a continuous variable, based on observed number of positives and negatives. In statistical terms, we tested n snakes and observed y positives, from which we wish to estimate the prevalence θ. We start the process by proposing a statistical model describing the data generating process. In the case of analyzing test results, the data are the number of positive results from a total number of subjects. The statistical model describing the distribution of the data is the binomial distribution. The model is parameterized by a single parameter – the probability of observing a positive result. The quantity of interest is the probability of infection. How the parameter of interest and the binomial model parameter are linked depends on what we know (Box-C.). If the test is perfect, that is, we know the rates of false positive and false negative are both 0, we have a simple binomial-beta model and the parameter can be easily estimated. This model is often the first model in an introductory Bayesian statistics textbook [7]. When the complexity of the data generation process increases, the simple model needs to be modified. If the test is imperfect and rates of false positive and false negative are known, the posterior distribution of θ cannot be represented by a commonly seen probability distribution. But the posterior distribution can be numerically evaluated and graphed for inference (Box-C. and D.). For example, suppose we tested 20 snakes for fungal disease and 5 were positive. If the test has a false negative rate of 5% and a false positive rate of 2%, and our initial guess of the prevalence is 10% based on a previous study of 20 snakes (our prior of the prevalence is a beta distribution with parameters $\alpha =2$ and $\beta =18$), the posterior distribution is numerically estimated and shown in Fig. 3.

Figure 3.

Numerically estimated probability density function of the posterior distribution of the population prevalence/prior (θ).

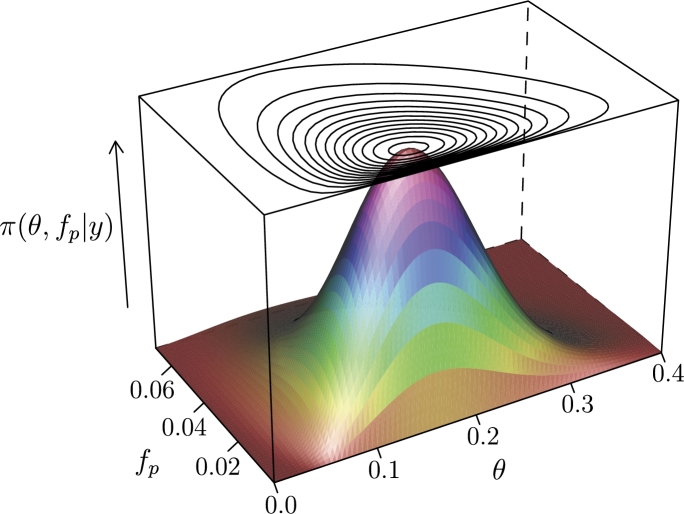
When one of the two error rates is unknown and needs to be estimated, we must specify a two-dimensional joint probability distribution. Computation is more intense, although we can still graphically display the joint distribution. If we are uncertain about the false positive probability in the case shown in Fig. 3, we can use a beta distribution to describe the uncertainty. For example, we may use a $beta(2,100)$ to represent a false positive rate with mean about 0.02 and a standard ard deviation of 0.014 (a middle 95% range of 0.0024 and 0.054). The numerically estimated joint posterior distribution is shown in Fig. 4.

Figure 4.

A perspective plot of the numerically estimated joint distribution of the false positive probability (f_p) and population prevalence/prior (θ).

When both rates are unknown, the posterior distribution becomes a three-dimensional joint distribution, and we must resort to a modern Bayesian computation method to estimate the parameters and a numerical summary of these parameters to understand the distribution (Box-D.).

The steps of moving from the simplest binomial-beta model to the model simultaneously estimating three parameters are typical in statistical learning. These steps should also be taken in applying statistics. When using imperfect tests, we need to understand why and how the test is imperfect and derive the appropriate model accordingly. Such a process is often tedious and iterative, a message we almost always miss when teaching or taking a statistics course.

6. Practical implications

Although our discussions were made with specific examples, the problem of an imperfect test is universal. How we interpret results from an imperfect test depends on how the data were collected and for what purpose. When individual test subjects are of concern, the uncertainty should be presented in terms of a conditional probability (i.e., $\mathrm{Pr}(p|+)$). The quality of the test is the key for proper interpretation of the test result. This is not just a problem of medical diagnostic tests. The statistical principle is the same in any situation where results from an imperfect test are applied to a specific subject.

When an imperfect test is used to infer a population parameter such as the prevalence of snake fungal disease in rattlesnake populations in Michigan, test results are raw data to be further processed to estimate the parameter of interest. The uncertainty associated with the imperfect test is represented by the posterior probability distribution. Depending on the nature of the test and the ease of determining the true status of a test subject, we have different computational needs. In other words, the proper use of an imperfect test requires us to fully consider all available information and properly structure the statistical analysis based on the objective of the study, just as the interpretation of the p-value from a null hypothesis test with low power [4] should be case-specific.

6.1. Summary – a guide to practitioners

Our discussion does not change how a practitioner conducts a test in most cases. Rather, we argued that the test result should be properly interpreted based on the quality of the test procedure, the objective of the test, and the state-of-the art understanding of the subject matter, and report the result accordingly (perhaps to avoid headline-catching, yet erroneous, statements). The knowledge of the two types of error will also help with better study design.

Test Target	Individual subject	Population
Test objective	Estimating $\mathrm{Pr}(p|+)$	Estimating $\mathrm{Pr}(p)$
(questions)	Does the subject	The disease prevalence
	have the disease?	in the population

Test result	+/-	+/- (multiple subjects)
Knowledge needed	$\mathrm{Pr}(p)$,	$\mathrm{Pr}(+|a),\mathrm{Pr}(-|p)$, and
to interpret test	quality of the test	an educated guess of
results	$\mathrm{Pr}(+|a),\mathrm{Pr}(-|p)$	$\mathrm{Pr}(p)$
Additional steps	Bayes' rule	IBF if subject's true
(beyond test		state can be ascertained, or
results)		Bayesian computation when
		true state is infeasible
How can the test be	improved testing	... and a better guess of
improved?	method	$\mathrm{Pr}(p)$

7. Text boxes

• A.
  A simple explanation of Bayes' rule

  • •
    Bayes' rule is a rule about conditional probability. We use a simple numeric example to explain equation (1). In our example of using the qPCR method to detect SFD in a snake, the test is imperfect. Suppose that the false positive rate is 5% and the false negative rate is 3% (much improved over the current test). Suppose we also know, based on similar studies on the same snake species in the Midwest, the prevalence of the fungus is about 4%. In order to interpret a positive or negative test result, we use Bayes' rule. We can explain Bayes' rule as a straightforward account of the expected number of true positives and false positives. Assuming there are 10,000 snakes in this population, our prior knowledge suggests that about 400 snakes have the disease and 9,600 snakes do not. (We used an unrealistically large population number to avoid non-integer numbers.) With a false negative probability of 3%, we expect to have 12 false negatives and 388 true positives. Likewise, among the 9,600 healthy snakes, a 5% false positive rate will result in 480 false positives. If we test all 10,000 snakes, we would expect about 868 positives, and only 388 of them are truly infected. For a randomly caught snake, a positive result would suggest that the chance that the snake is truly infected is 388/(388+480) or 0.447. In other words, a snake with a positive test result is (slightly) less likely to be infected with the disease than not infected. Bayes' rule leads to the same result. The numerator of Bayes' rule is $\mathrm{Pr}(p)\mathrm{Pr}(+|p)$, where $\mathrm{Pr}(p)$ is the prevalence (4%), and $\mathrm{Pr}(+|p)=1-\mathrm{Pr}(-|p)=1-0.03=0.97$. That is, the numerator is 0.0388. We can easily verify that the denominator is 0.0388 + 0.048. Multiplying the population number with both the numerator and denominator, we see that Bayes' rule simply tallies the number of true positives and total positives.
  • •
    When the test is imperfect, we are uncertain about the result. The posterior probability $\mathrm{Pr}(p|+)$, the probability of present after observing a positive result, is used to summarize the uncertainty we have on the result. The uncertainty, however, is a function of the prior and the two probabilities characterizing the performance of the test. In the numerical example here, if the prior is 1%, the posterior would be $\mathrm{Pr}(p|+)=0.164$. This outcome is expected as the number of true positives is now a smaller fraction of the total number of positives (Fig. 1(iv)-(vi)).
• B.
  The meaning of a prior

  • •
    Different people may have different prior probabilities for the same event. This is likely because they use different references. For example, when a doctor tests for a disease in a public health exhibition at a county fair, her prior should be the prevalence of the disease in the population because she would consider the test subject a random sample from the population. To the patient, the general population may not be a good reference because he knows more about himself. In this case, he knows which risk factors apply to him. As a result, the relevant population would be people with the same risk factors (e.g., smokers).
  • •
    The meaning of the prior to the patient and to the doctor may be the same (e.g., prevalence of the disease in a population). But deciding which population to use to form the prior requires more information. The supposedly subjective nature of a Bayesian prior is often criticized. We contend that a prior is simply a means for scientists to properly sort out the relevant facts/information using their knowledge of their study system. In this regard, when we define the prior probability as a degree of belief, we are really trying to make use of all our knowledge to ensure the outcome is most relevant.
  • •
    When we cannot confidently identify a sub-population for inference, we must step back to a larger population. The resulting prior is likely less relevant. As a result, the estimated posterior probability is less accurate. For example, in the numerical example in Box-A., the posterior probability of present given a positive results is less than 0.5. But the test result puts the snake into a smaller population (the 388+480 would-be positive snakes). If we choose to conduct a follow-up test, our prior would be the posterior from the first test. This iterative process is an appealing characteristic of the Bayesian method for many applied scientists.
• C.
  Bayesian inference

  • •
    Using Bayesian statistics to estimate an unknown variable consists of three steps.

    • (a)
      Propose a statistical model that describes the data. This model includes the unknown variable as a parameter. For example, the statistical model we use to estimate the prevalence of SFD in the Michigan rattlesnake population is a binomial model.
    • (b)
      Using the statistical model, we derive the likelihood function of the data – the likelihood of observing the data if the proposed model is correct. If the test is perfect, that is, both false positive and false negative rates are 0, the prevalence is the probability of observing a positive result. The statistical model of observing y positive in n snakes is

      $$\mathrm{Pr}(y|\theta )=\left(\begin{array}{c}n\\ y\end{array}\right){\theta }^y{(1-\theta )}^{n-y}$$ (4)
      This is the likelihood of observing the data if the prevalence is θ. In classical statistics, the estimated parameter $\hat{\theta }$ is the value that maximizes the likelihood.
    • (c)
      Specifying the posterior distribution of θ using the Bayes' rule of a continuous variable:

      $$\pi (\theta |y)=\frac{\pi (\theta )\mathrm{Pr}(y|\theta )}{{\int }_{\theta }\pi (\theta )\mathrm{Pr}(y|\theta )d\theta }$$ (5)

      where $\pi ()$ represent a probability density function. $\pi (\theta )$ is the prior distribution, representing the uncertainty we have about θ and $\pi (\theta |y)$ is the posterior distribution of θ after observing data.
  • •
    The derivation of posterior distribution parameters is often the difficult part of Bayesian inference because of the integral in the denominator. In some cases, the derivation can be simplified if we choose a suitable prior distribution. For example, when we choose a beta distribution as the prior for θ, the prior density (with parameters α and β) is $\pi (\theta )=\frac{\mathrm{\Gamma }(\alpha )\mathrm{\Gamma }(\beta )}{\mathrm{\Gamma }(\alpha +\beta )}{\theta }^{\alpha -1}{(1-\theta )}^{\beta -1}$. This distribution has a mean of $\alpha /(\alpha +\beta )$ and variance of $\alpha \beta /({(\alpha +\beta )}^2(\alpha +\beta +1))$. From the mean and variance formulae we can estimate the likely values of α and β based on what we know about the parameter. The posterior distribution of θ is estimated by multiply the prior distribution density function and the likelihood function. With some tedious algebraic maneuvering, we can often identify the posterior distribution as one of the standard probability distributions. For this case, the posterior distribution is

    $$\begin{array}{ccc}\hfill \pi (\theta |y)& \hfill =\hfill & \frac{\frac{\mathrm{\Gamma }(\alpha )\mathrm{\Gamma }(\beta )}{\mathrm{\Gamma }(\alpha +\beta )}{\theta }^{\alpha -1}{(1-\theta )}^{\beta -1}\left(\begin{array}{c}n\\ y\end{array}\right){\theta }^y{(1-\theta )}^{n-y}}{{\int }_{\theta }\frac{\mathrm{\Gamma }(\alpha )\mathrm{\Gamma }(\beta )}{\mathrm{\Gamma }(\alpha +\beta )}{\theta }^{\alpha -1}{(1-\theta )}^{\beta -1}\left(\begin{array}{c}n\\ y\end{array}\right){\theta }^y{(1-\theta )}^{n-y}d\theta }\hfill \\ \hfill & \hfill \propto \hfill & {\theta }^{y+\alpha -1}{(1-\theta )}^{(n-y)+\beta -1}\hfill \end{array}$$ (6)
    It is the beta distribution with parameters ${\alpha }^{\prime }=y+\alpha$ and ${\beta }^{\prime }=(n-y)+\beta$. The mean of the posterior is $\frac{{\alpha }^{\prime }}{{\alpha }^{\prime }+{\beta }^{\prime }}=\frac{y+\alpha }{n+\alpha +\beta }$. From this distribution, we can also calculate the credible interval to summarize the uncertainty.
  • •
    When the test is imperfect and we know the rate of false positive ($f_p=\mathrm{Pr}(+|a)$) and rate of false negative ($f_n=\mathrm{Pr}(-|p)$), the model becomes more complicated because the probability of observing a positive result is now ${\theta }^{\star }=\theta (1-f_n)+(1-\theta )f_p$. The statistical model of the data is still the binomial distribution, but the probability of observing a positive result is now ${\theta }^{\star }$. As a result, the posterior distribution is:

    $$\begin{array}{ccc}\hfill \pi (\theta |y)& \hfill \propto \hfill & {\theta }^{\alpha -1}{(1-\theta )}^{\beta -1}\times \hfill \\ \hfill & \hfill \hfill & {(\theta (1-f_n)+(1-\theta )f_p)}^y\times \hfill \\ \hfill & \hfill \hfill & {(1-\theta (1-f_n)-(1-\theta )f_p)}^{n-y}\hfill \end{array}$$ (7)

    This distribution is not one of the many probability distributions with a name (known characteristics). In other words, we cannot summarize the features of the distribution (e.g., mean, standard deviation) analytically, at least not easily.
• D.
  Bayesian computation

  • •
    In Box-C. we derived two posterior distributions of the parameter θ. One is summarized by a standard probability distribution, of which we know how to derive needed statistics to summarize the uncertainty about the parameter. The other is an algebraic expression that cannot be represented by a known form of probability distribution. Because θ is the only unknown parameter (in (7)), we can graphically draw the posterior distribution on a two dimensional space. By numerically re-scaling the curve such that the area under the curve is 1, we have a graphical representation of the probability distribution (Fig. 3), from which we can draw inference about the parameter. Specifically, we evaluate the posterior density $\pi (\theta |y)$ in equation (7) over a series values of θ (e.g., 1000 evenly spaced values between 0 and 1) and graph the results. We included an example using the snake fungal disease example in Additional information.
  • •
    When one of the two error rates (e.g., the false positive rate $f_p$) is unknown, the problem is to estimate the joint distribution (specified up to a normalizing constant) of the two unknown parameters. We can still use the same numerical approximation method and graphically present the posterior using a contour plot (Fig. 4). The same computational framework can be used if both error rates are unknown. But graphical display of the distribution is no longer feasible. Frequently, we use the modern Bayesian computational method based on Monte Carlo simulation for this type of problem. We included a detailed example in Additional information.

Declarations

Author contribution statement

Song Qian: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.

Jeanine Refsnider: Conceived and designed the experiments; Analyzed and interpreted the data; Wrote the paper.

Jennifer Moore: Performed the experiments; Contributed reagents, materials, analysis tools or data.

Gunnar Kramer, Henry Streby: Analyzed and interpreted the data; Wrote the paper.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Competing interest statement

The authors declare no conflict of interest.

Additional information

Included in our GitHub repository (https://github.com/songsqian/imperfect) are detailed examples used in this paper, alone with computer code for estimating the various posterior distributions and code for generating all figures.