Temporal Dynamics of Memory-guided Cognitive Control and Generalization of Control via Overlapping Associative Memories

Goal-directed behavior can benefit from proactive adjustments of cognitive control that occur in anticipation of forthcoming cognitive control demands (CCD). Predictions of forthcoming CCD are thought to depend on learning and memory in two ways: First, through direct experience, associative encoding may link previously experienced CCD to its triggering item, such that subsequent encounters with the item serve to cue retrieval of (i.e., predict) the associated CCD.

Abstract

Goal-directed behavior can benefit from proactive adjustments of cognitive control that occur in anticipation of forthcoming cognitive control demands (CCD). Predictions of forthcoming CCD are thought to depend on learning and memory in two ways: First, through direct experience, associative encoding may link previously experienced CCD to its triggering item, such that subsequent encounters with the item serve to cue retrieval of (i.e., predict) the associated CCD. Second, in the absence of direct experience, pattern completion and mnemonic integration mechanisms may allow CCD to be generalized from its associated item to other items related in memory. While extant behavioral evidence documents both types of CCD prediction, the neurocognitive mechanisms giving rise to these predictions remain largely unexplored. Here, we tested two hypotheses: (1) memory-guided predictions about CCD precede control adjustments due to the actual CCD required; and (2) generalization of CCD can be accomplished through integration mechanisms that link partially overlapping CCD-item and item-item associations in memory. Supporting these hypotheses, the temporal dynamics of theta and alpha power in human electroencephalography data (n = 43, 26 females) revealed that an associative CCD effect emerges earlier than interaction effects involving actual CCD. Furthermore, generalization of CCD from one item (X) to another item (Y) was predicted by a decrease in alpha power following the presentation of the X-Y pair. These findings advance understanding of the mechanisms underlying memory-guided adjustments of cognitive control.

SIGNIFICANCE STATEMENT Cognitive control adaptively regulates information processing to align with task goals. Experience-based expectations enable adjustments of control, leading to improved performance when expectations match the actual control demand required. Using EEG, we demonstrate that memory for past cognitive control demand proactively guides the allocation of cognitive control, preceding adjustments of control triggered by the demands of the present environment. Furthermore, we demonstrate that learned cognitive control demands can be generalized through mnemonic integration processes, enabling the spread of expectations about cognitive control demands to items associated in memory. We reveal that this generalization is linked to decreased alpha oscillation in medial frontal channels. Collectively, these findings provide new insights into how memory-control interactions facilitate goal-directed behavior.

Introduction

Cognitive control refers to a collection of neurocognitive functions that align behavior with internal goals through top-down modulations on neural information processing, and hence plays a key role in adaptive behavior (Miller and Cohen, 2001; Waskom et al., 2014; Egner, 2017). One key feature of cognitive control is that it adjusts to meet the cognitive control demand (CCD) of the present environment (Botvinick et al., 1999; Kerns et al., 2004). For example, a driver reacts to worsened driving conditions by flexibly increasing attention to the road and suppressing irrelevant information and behavior. A second key feature of control is that adjustments can be proactive, preparing an individual to meet anticipated imminent demands (Braver, 2012). Emerging data indicate that proactive adaptations are often guided by associative learning and memory (Egner, 2014; Abrahamse et al., 2016; Braem et al., 2019; Chiu and Egner, 2019). For instance, an experience-based association between a busy overpass and high CCD could lead to memory-guided proactive engagement of control the next time one approaches the overpass. The modulation of item-CCD association on cognitive control has been demonstrated in human behavior (Jacoby et al., 2003; Bugg et al., 2011), with the encoding of item-CCD associations modeled by temporal difference learning across trials (Chiu et al., 2017).

A central open question is as follows: how does memory guide adjustments of cognitive control to align control with imminent CCDs? Intuitively, learning the CCD associated with an item should allow an organism to proactively adapt cognitive control to the predicted CCD before the actual demands are detected. To date, this idea has been modeled in computational simulations (Blais et al., 2007; Verguts and Notebaert, 2008), yet empirical tests are scarce. Thus, the first goal of this study is to test this hypothesis by examining the temporal dynamics of association-guided cognitive control.

While the acquisition of item-CCD associations depends, in part, on striatal mechanisms (Chiu et al., 2017), learning often occurs in multiple neural systems that support distinct memory types and processes (Poldrack and Packard, 2003; Kumaran et al., 2016). Hippocampal-dependent mechanisms may support the generalization of expectations about control to related items in memory. For example, the high CCD associated with the busy overpass may be generalized to the roads near the overpass without directly experiencing high CCD on those roads. Indeed, the generalization of CCD has been documented in human behavior (Crump and Milliken, 2009; King et al., 2012; Weidler and Bugg, 2016; Surrey et al., 2017; Bejjani et al., 2018), although the neurocognitive mechanisms remain poorly understood. As a second goal, we tested the hypothesis that the generalization of CCD can be achieved through integrative encoding (Shohamy and Wagner, 2008; Kuhl et al., 2010), wherein partially overlapping associations (e.g., overpass-road and overpass-CCD) result in the formation of an integrated representation (e.g., overpass-road-CCD) that supports direct retrieval of CCD expectations for an item (e.g., road as cue) that have been inherited from another associated item (e.g., overpass).

To test these hypotheses, we leveraged the high temporal resolution of EEG along with a learning and generalization paradigm. Similar to previous studies of generalization (Zeithamova and Preston, 2010; Kuhl et al., 2011; Wimmer and Shohamy, 2012; Zeithamova et al., 2012; Bejjani et al., 2018), the task consisted of three phases (Fig. 1): an association phase establishing tool–landmark associations, a training phase introducing tool–CCD associations, and a test phase assessing the generalization of CCD from tools to landmarks. To preview the results, in the training phase EEG data, the observed temporal dynamics of neural responses are consistent with associative-memory driven proactive engagement of control that precedes further adjustments of control in response to the actual CCD required by the trial. These findings were cross-validated using the independent test phase EEG data. Moreover, the behavioral data at test and EEG data during the association and test phases provide strong evidence of generalization of CCD via associative memory.

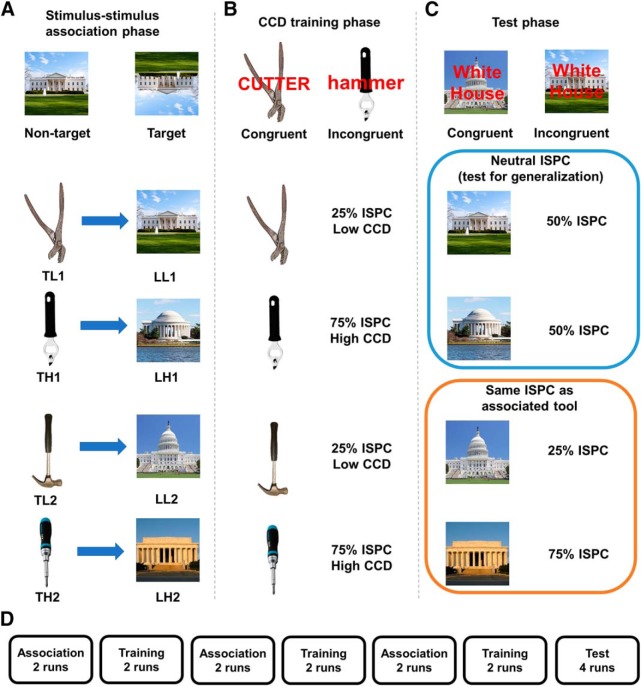
Figure 1.

Experimental design of the three phases in the task. A, In the association phase, participants incidentally formed tool–landmark associations by viewing successively presented tools followed by their respective associative landmarks. Participants responded to rare inverted images. B, In the training phase, participants performed a variant of the Stroop task, wherein they identified the tool and tried to ignore the superimposed word. This phase induced associations between tools and CCDs by manipulating how frequently each tool was used in incongruent trials. Each stimulus is coded by its category (T, Tool; L, landmark), associated/transferred CCD (H, High; L, low), and a number to ensure uniqueness. For example, LL1 indicates a landmark whose associated tool was paired with low CCD. Two tools (TL1 and TL2) were presented mostly in congruent trials (25% of ISPC), whereas the other two tools (TH1 and TH2) were used mostly in incongruent trials (75% of ISPC). C, In the test phase, participants performed the Stroop task but encountered the landmarks as stimuli. Two landmarks (LL1 and LH1) were presented using 50% ISPC. The other two landmarks (LL2 and LH2) were presented using with the same ISPC as their associated tools in the training phase. D, There were 6 interleaved association and training runs, followed by 4 test runs.

Materials and Methods

Subjects.

Fifty-three subjects gave informed written consent, in accordance with procedures approved by the Stanford University Institutional Review board. Data from 4 subjects were excluded due to low behavioral performance (accuracy was ≥3 SDs lower than the group median) in at least one experimental condition of at least one of the three phases (see below) (Leys et al., 2013). Data from 6 additional subjects were excluded due to excessive EEG artifacts. The final sample consisted of 43 participants (18–29 years old, mean = 22.1 years; 26 females) with normal or corrected-to-normal vision and no history of psychiatric or neurological disorders.

Stimuli and experimental design.

The stimuli consisted of eight color images: four tools and four landmarks (Fig. 1A). The images were presented on a 23-inch LCD display at 60 Hz using Psychtoolbox 3 and covered ∼7.7° of visual angle. The task consisted of three phases: an association phase, a training phase, and a test phase.

The association phase (Fig. 1A) aimed to elicit the incidental encoding of tool–landmark associations. To do so, the association phase comprised 6 runs of 60 trials each. Each trial consisted of the pairing of a specific tool followed by a specific landmark; the pairings were repeated throughout the association phase, creating four unique tool–landmark associations. The specific pairings were randomized across participants. Throughout, each image was displayed for 800 ms and the tool–landmark images were separated by a uniformly jittered interstimulus interval (900–1100 ms). To temporally separate the trials and promote the encoding of the tool–landmark associations, the intertrial intervals were uniformly jittered between 2250 and 2750 ms (i.e., the intertrial intervals were substantially longer than the interstimulus intervals). Participants were not instructed to intentionally encode the tool–landmark associations. Instead, to ensure that participants attended to the images, their task was to press a response button using their right index finger whenever the encountered image was inverted. A tool image was defined as inverted when its handle was shown in the bottom half of the image; landmarks were inverted when their base was above their roof. There were four presentations of inverted tools and four inverted landmarks in each run.

The goal of the training phase was to associate each of the four tools with either a high or low CCD. To this end, participants performed a variant of the Stroop task (Fig. 1B). On each trial, a compound stimulus, consisting of a tool image (target) and a superimposed tool name (distractor), was presented for 800 ms. The participants were required to identify the tool in the image by pressing a response button while trying to ignore the tool name. Participants used four fingers of the same hand to separately respond to the four tools. The response mapping was counterbalanced across participants. Trials were separated by uniformly jittered intertrial intervals (2700–3100 ms). It is well established that, compared with congruent trials in which the target and distractor lead to the same response, incongruent trials require higher CCD to resolve the response conflict between the target and distractor (Cohen et al., 1990; Botvinick et al., 2001).

The CCD associated with each of the four tools was varied using an item-specific proportion of conflict (ISPC) manipulation during training. Specifically, two tools were associated with high CCD (denoted as TH1 and TH2) by being presented in incongruent trials 75% of the time (i.e., ISPC = 75%), whereas the other two tools were associated with low CCD (denoted as TL1 and TL2) by being presented in incongruent trials 25% of the time (i.e., ISPC = 25%). The training phase comprised 6 runs of 48 trials each, with 12 trials per tool image per run. As such, the manipulations resulted in a 2 (associative CCD, manipulated by ISPC) × 2 (actual CCD, manipulated by congruency) factorial design. To foster integration (Zeithamova and Preston, 2010), the association and training phase runs were interleaved in sets of 2 (Fig. 1D); as detailed below, we investigated how neural activity in the association phase changed after exposure to the tool–CCD associations in the training phase.

A final test phase was used to assess the generalization of CCD from tool–CCD associations (established in the training runs) to landmark–CCD associations mediated through the tool–landmark associations (induced in the association phase). The task in the test phase was similar to the task in the training phase. Participants were required to identify the image of the landmark while trying to ignore the word label superimposed on the image (Fig. 1C). The trial structure and image presentation times were identical to the training phase. To avoid any potential confound due to the overlap in stimulus–response mappings, participants responded using the other hand than the one used in the training phase. Across the 4 test runs, two landmarks (LL2 and LH2) were presented in the same ISPC as their associated tool. Crucially, the other two landmarks (LL1 and LH1) were presented in a neutral (50%) ISPC and were used to test the generalization of CCD without the potential confound of experiencing a biased (low or high) ISPC across the test phase. As such, any ISPC effects for these landmarks must be inherited from their associated tools. Having biased landmarks (e.g., LL2 and LH2) is not necessary for generalization to occur (Bejjani et al., 2018).

Behavioral analysis.

To test whether the participants were engaged during the association phase, we calculated the hit rate (responding when the image was inverted) and overall accuracy (correctly making/withholding a response based on task instructions).

In the training phase, we analyzed accuracy and response time (RT). Accuracy was analyzed using a repeated-measures ANOVA, including the factors, associated CCD (high/low) and congruency (congruent/incongruent). RTs were analyzed using a model-based approach (Chiu et al., 2017) to assess learning of the tool–CCD associations. Specifically, the learning of the CCD associated with a tool was modeled using a temporal difference learning algorithm (Sutton and Barto, 2018) as follows:

where C(t) represents the congruency (1 = incongruent; 0 = congruent) at Trial t; P_i quantifies the model-belief of the CCD associated with tool i; α is the learning rate that determines how strongly P_i is influenced by experienced congruency. α was determined using a grid search (see below) and shared across all four tools. Given α and the trial sequence experienced by a participant, the model produces trial-by-trial estimates of P_i (i.e., the probability that the forthcoming trial is incongruent) and PE_i, which denotes the unsigned prediction error at Trial t (i.e., the absolute difference between P_i(t) and C(t)). These model estimates were used to explain the variance in trialwise RTs as detailed below.

Trials accompanied by nuisance cognitive processes (e.g., unsuccessful conflict resolution and posterror slowing), such as error trials and posterror trials, were excluded from RT analyses. In addition, trials with RTs outside of the grand median ±2.5 SD range were excluded. For each participant, the remaining trialwise RTs were regressed against a linear model with 7 regressors (congruency, predicted control demand, control prediction error, and 4 regressors representing each of the 4 tools). The shared variance between the predicted CCD and the congruency regressors ranges from 0.01 and 0.18 (0.14 ± 0.01) across subjects. Low shared variance (e.g., ∼0.01) is possible with extreme learning rates (e.g., 1). Control prediction error shared little variance with congruency (<0.002 for all subjects) and predicted CCD (< 0.001 for all subjects). The learning rate was determined by a grid search (range: 0–1, step size = 0.01) that minimized the sum of squared errors of the model fit using trial-level RTs. The estimated coefficients in the winning model were normalized using error terms from model fitting and were then passed to group-level analyses, which used one-sample t tests to examine whether the mean of a coefficient was significantly different from 0. The grid search does not constrain the sign of the estimated coefficients for the regressors and was thus orthogonal to group-level analysis.

For the test phase, the generalization of an associated tool's CCD to its landmark was analyzed using the items with neutral ISPCs (i.e., LL1 and LH1). The model-based analysis was not used because the focus of this analysis was the generalization of the CCD through tool–landmark associations rather than the learning of a new CCD–landmark association from the trial sequence in the test phase. Instead, we performed repeated-measures ANOVAs with the factors CCD of the associated tool (high/low) and congruency (congruent/incongruent) on accuracy and on the median of RT in each condition.

EEG data acquisition and preprocessing.

EEG data from 128-channel HydroCell Sensor Nets (Electrical Geodesics) were recorded at a sampling rate of 1000 Hz while participants performed the experiment. An impedance threshold was set to 50k ohms and was checked approximately every 12 min. EEG data were preprocessed using EEGlab (https://sccn.ucsd.edu/eeglab/index.php) and in-house MATLAB scripts. EEG recordings were downsampled to 500 Hz and then went through an automatic channel rejection procedure based on magnitude and variance using EEGlab. A high-pass filter of >0.1 Hz was applied to the remaining data. For all three task phases, the continuous recorded data were divided into epochs of 1500 ms, ranging from −500 ms to 1000 ms poststimulus onset. Trial-level data went through the automatic epoch rejection of EEGlab using the “all methods” option and default settings. Remaining trials went through another manual epoch rejection process. Trials that survived the rejection procedures were transformed using independent component analysis for further manual rejection of components reflecting eye movements and noise. Independent component analysis-filtered data were rereferenced to the average across all remaining channels. Missing channels were reconstructed using interpolation. Preprocessed data were then used in both event-related potential (ERP) and time-frequency analyses. For ERP analysis, preprocessed EEG data were low-pass filtered (cutoff = 30 Hz), and the 200 ms before stimulus onset was used for baseline correction. ERP data ranged from −200 ms to 800 ms. Statistical analyses were performed at each node in a 2D (channel × time point) grid. For time-frequency analysis, preprocessed EEG data were low-pass filtered (cutoff = 50 Hz). Event-related (log) spectral perturbation (ERSP) was calculated using Morlet wavelets (Delorme and Makeig, 2004) at each frequency in theta (4–7 Hz, 3 cycles), alpha (8–13 Hz, 6 cycles), and beta (14–30 Hz, 10 cycles) bands. ERSP was computed at the trial level and was then grouped and averaged based on experimental conditions. The ERSP data spanned from −80 ms to 590 ms after the onset of the stimulus, with a sampling rate of 100 Hz. Statistical analyses were performed at each of the nodes in a 3D (channel × time point × frequency) grid.

EEG data analysis.

ERP and time-frequency data were divided into conditions for each task phase. For the association phase, trials with inverted images were excluded. The remaining trials were divided into 16 conditions, representing the 8 stimuli (4 tools and 4 landmarks) × 2 run bins (Runs 1 and 2 and Runs 3–6). At the individual subject level, the mean trial numbers were 257 (range: 208–312) and 247 (range: 194–314) for tools and landmarks, respectively. By contrasting the EEG signals in the early (i.e., Runs 1 and 2) with the late part of the association task (i.e., Runs 3–6; Fig. 1D), we investigated neural signals related to the generalization of associated CCD from tools to landmarks via the tool–landmark associations. The training phase data (219 trials on average, range: 150–260) were partitioned into 4 conditions, representing the 2 (associated CCD level: high vs low) × 2 (congruency) factorial design. CCD level was divided into 2 levels rather than a trial-level continuous variable as in the model-based analysis. This approach was adopted out of concern that the signal-to-noise ratio in the EEG data at single channels, time points, and frequency may be insufficient to ensure robust signal in each node on each trial and hence may reduce statistical power. As shown in Figure 2A, model-estimated CCD shows a clear distinction between tools with high and low CCD levels; thus, the 2 CCD levels provided a good approximation of the distribution of the model-derived CCDs, and simultaneously enhanced sensitivity by averaging across multiple trials within each condition. The test phase data (mean trial number: 144, range: 86–167) were grouped based on a 2 (associated CCD of paired tool: high/low) × 2 (congruency/incongruency) factorial design. To avoid bias in ISPC, only landmarks with neutral ISPC (i.e., LL1 and LH1) were used in tests for generalization of CCD (mean trial number: 72, range: 45–84).

Figure 2.

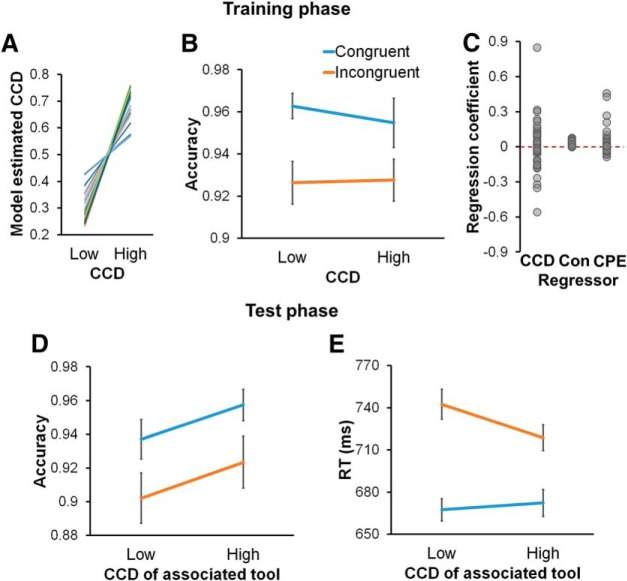
Behavioral results. A–C, Training phase results. A, Individual model-estimated associated CCD levels, measured as the mean P_i across all trials sharing the same CCD level, plotted as a function of CCD levels. Each line indicates one participant. B, Group mean ± SEM of accuracy, plotted as a function of associated CCD and congruency. C, Individual estimated coefficients for the associated CCD, congruency (Con), and control prediction error (CPE) regressors of the model-based analysis on RT. D, E, Group mean ± SEM of accuracy (D) and RT (E) in the test phase, plotted as a function of the CCD of the associated tool and congruency.

One main goal of this study is to test the temporal order of associated and actual CCD effects. To avoid bias, we chose not to use predefined time windows for different effects, and instead adopted a data-driven approach that searched the whole temporal span of EEG data following the onset of the stimulus. Specifically, the statistical analyses of the effects of interest were conducted using nonparametric cluster-based permutation tests (Maris and Oostenveld, 2007). Dependent-sample t tests were performed to compare the conditions at every data node (electrode, time point, and frequency). Clusters of significant (p < 0.01, one-tailed tests) adjacent nodes were identified and grouped together. Two nodes were considered adjacent when they only differed in one dimension, with the difference being within 4 cm Euclidean distance between channels, 1 time point (10 ms), or 1 Hz. We then used the maxsum statistics, defined as the sum of the t statistics across all nodes within a cluster, as a summary quantification of both the statistical significance within nodes and the span of the cluster. The nonparametric cluster-based permutation tests were conducted separately for positive and negative statistics because difference in sign may indicate different neural processes. To determine p values that controlled for multiple comparisons, the maxsum of clusters were compared with a null distribution, which was comprised of the maxsum of the clusters from 6000 simulations that repeated the same analysis with randomly shuffled condition labels (e.g., Bramão and Johansson, 2017; Bramão et al., 2017). Due to the distinct neural processes represented by and the different number of cycles used for the theta, alpha, and beta bands, statistical analyses were conducted on these bands separately. The same threshold for statistical significance was applied to all frequency bands, allowing for comparison of temporal span across clusters from different frequency bands.

To test trial-level brain–behavior correlations, we extracted cluster-mean EEG data (e.g., theta power) for a given cluster from the nonparametric cluster-based permutation tests at each trial as a regressor, which was combined with a constant regressor to form a GLM. Then the trial-wise RT was regressed against this GLM to obtain the coefficient for the EEG data regressor, providing a quantification of the EEG data's modulation on RT. Critically, because a significant CCD × congruency interaction effect (i.e., the difference between when the [generalized] associated CCD matched the actual CCD and when they did not) was used to identify the cluster for this analysis, we prevented double-dipping by performing this analysis separately for each condition of the CCD × congruency factorial design. The mean of the coefficients from the four conditions was calculated for each participant and was passed on to a group-level t test against 0 (i.e., no modulation of EEG data on behavior).

For two clusters found in the nonparametric cluster-based permutation tests, we compared their temporal distributions marginalized over channel and frequency (i.e., the likelihood of finding a data node in the cluster for a given time) to test which cluster emerged earlier. To this end, we formed the null hypothesis that variable A (representing a marginalized temporal distribution) with distribution P_A precedes another random variable B with distribution P_B. To test this hypothesis, we calculated the probability that P_A precedes a time point b randomly sampled from P_B. Once b is drawn, we computed the probability of P(A < b) = ∫₀^bP_A(a)da. Plugging P(A < b) into the random sampling of b based on P_B, we obtained the p value as the probability of the null hypothesis being supported (i.e., P(A < B)), which takes the following form:

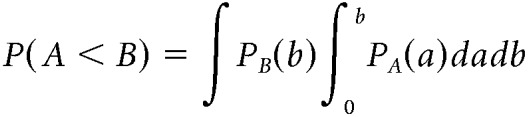In other words, P(A < B) denotes the probability of observing a < b by randomly drawing a and b for infinite times. To avoid confusion with the inferential statistics (see below), P(A < B) is henceforth referred to as “precedence index,” which ranges from 0 to 1. The lower the precedence index, the less likely A precedes B. In particular, a precedence index of 0.5 indicates that A and B are equally likely to precede each other.

To account for sampling error, we estimated the distribution of the precedence index using bootstrap resampling. Specifically, we randomly resampled (with replacement) the subjects to form a new sample of 43 subjects. We then performed the group-level nonparametric cluster-based permutation tests and identified the clusters showing highest maxsum statistics for each of the CCD effect and the CCD × congruency interaction effect. These two clusters were then submitted to the aforementioned temporal distribution comparison. This bootstrap resampling procedure was repeated for 1000 times and resulted in a distribution of the precedence index that the CCD × congruency interaction effect preceded the CCD effect.

Results

Behavioral data

Participants performed the inversion detection task in the association phase with high accuracy (group mean ± SEM: 0.99 ± 0.004). On the rare trials in which participants needed to respond to inverted stimuli, the hit rate was 0.97 ± 0.01. These results indicate that participants followed the task instructions and were attentive to the images.

In the training phase, we first validated the model by comparing its prediction of P_i with the experimental manipulation of tool–CCD associations. Consistent with the task design, model belief of CCD for tools with high ISPC (0.68 ± 0.01) was significantly higher than for those with low ISPC (0.32 ± 0.01, paired t test: t₍₄₂₎ = 16.14, p < 0.001; Fig. 2A). Because the predictions also included the learning process, the model belief of ISPC is expected to fall below the theoretical value (i.e., 0.25 and 0.75). Next, analysis of the effect of congruency on participant accuracy revealed a significant main effect (F_(1,42) = 36.43, p < 0.001), driven by higher accuracy on congruent (0.96 ± 0.01) compared with incongruent trials (0.93 ± 0.01). Neither the main effect of ISPC (F_(1,42) = 0.20) nor the interaction between ISPC and congruency (F_(1,42) = 1.13, p = 0.29) was significant (Fig. 2B). Moreover, a model-based analysis on RT data replicated the classic finding that incongruent trials were slower than congruent trials, evidenced by incongruency positively modulating RT (0.32 ± 0.02, t₍₄₂₎ = 11.67, p < 0.001; Fig. 2C, middle column).

More importantly, in the training phase, we expected that the presentation of the tool would initiate retrieval of its associated CCD, guiding conflict resolution. Thus, when the associated CCD deviates from the actual CCD experienced as a function of congruency on the trial (i.e., when control prediction error is large), retrieved CCD will mislead conflict resolution, resulting in slower responses (Jiang et al., 2014, 2015; Chiu et al., 2017; Muhle-Karbe et al., 2018). These predictions were confirmed by a significant positive modulation of control prediction error on RT (0.32 ± 0.12, t₍₄₂₎ = 2.66, p = 0.01; Fig. 2C, right column). This finding indicates successful encoding of the item-specific CCD–tool associations and the influence of these associations in guiding cognitive control in the training phase. Finally, the modulation of associated CCD on RT was not significant (−0.11 ± 0.28, t₍₄₂₎ = −0.38, p = 0.71). This null result is consistent with previous studies using ISPC manipulations (Chiu et al., 2017; Bejjani et al., 2018), and was expected based on aforementioned theory. This is because the difference between different levels of associated CCD is short-lived and will be replaced by actual CCD, leading to limited influence on the main effect of associated CCD in behavior. As a comparison, we also performed a repeated-measures 2 × 2 ANOVA on training phase RTs. There was a significant main effect of congruency (F_(1,42) = 151.13, p < 0.001). Neither the main effect of associated CCD nor the interaction was significant (both F values < 1; low ISPC/congruent: 640 ± 12 ms; low ISPC/incongruent: 680 ± 13 ms; high ISPC/congruent: 640 ± 11 ms; high ISPC/incongruent: 676 ± 13 ms). Compared with the model-based analysis that specifically examined the learning-related effect, the interaction effect may be confounded by other factors, such as feature-binding (Mayr et al., 2003), perhaps contributing to this null result.

In the test phase, accuracy on landmarks with 50% ISPC (i.e., LL1 and LH1) exhibited a significant main effect of congruency (F_(1,42) = 15.59, p < 0.001; Fig. 2D), driven by higher accuracy on congruent (0.95 ± 0.01) than incongruent trials (0.91 ± 0.01). Additionally, a marginally significant main effect of the ISPC of the associated tool (F_(1,42) = 3.88, p = 0.06) evidenced a trend for higher accuracy in the high CCD (LH1: 0.94 ± 0.01) than low CCD condition (LL1: 0.92 ± 0.01). The interaction between the two factors was not significant (F_(1,42) = 0.004). In RT data, there again was a significant main effect of congruency (F_(1,42) = 98.75, p < 0.001; Fig. 2E), driven by faster responses in the congruent (670 ± 11 ms) than incongruent condition (730 ± 14 ms). The main effect of the ISPC of the associated tool was not significant (F_(1,42) = 1.07, p = 0.31).

Crucially, in the test phase, we observed a significant interaction between the CCD of the associated tool and congruency (F_(1,42) = 9.82, p = 0.003). Similar to the control prediction error effect found during the training phase, the interaction exhibited a pattern wherein mismatched CCD of the associated tool and actual congruency (i.e., LL1 in incongruent trials and LH1 in congruent trials), which corresponded to larger prediction error, led to slower RTs than matched conditions (i.e., LL1 in congruent trials and LH1 in incongruent trials). Critically, the fact that the directly experienced ISPC in the test phase was the same for LL1 and LH1 landmarks rules out the possibility that this interaction was attributable to the test phase. Consistent with recent behavioral findings (Bejjani et al., 2018), this interaction effect indicates that the CCD linked to a tool was transferred to its associated landmark.

EEG results: validation

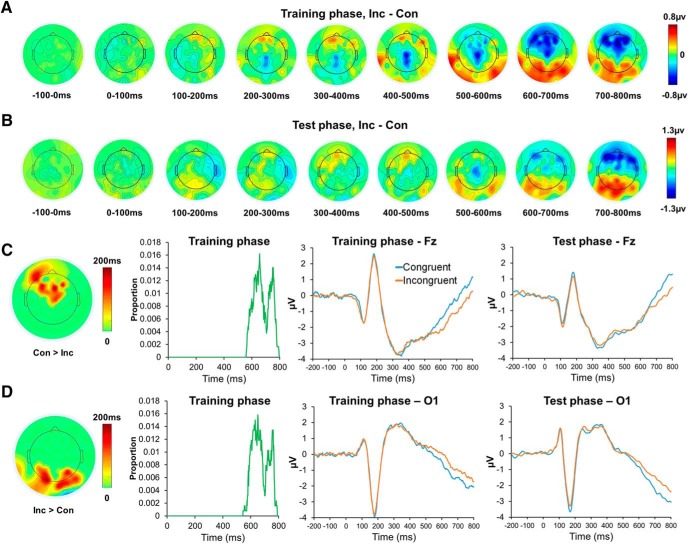
As the first step of EEG analysis, we validated the data by testing whether they replicate the congruency effect (specifically, stronger mid-frontal negativity, sometimes followed by stronger posterior positivity on incongruent than congruent or neutral trials) found in previous ERP studies (Liotti et al., 2000; Folstein and Van Petten, 2008; Hanslmayr et al., 2008). Consistent with these studies, in the present experiment, ERP analyses revealed a main effect of congruency in both the training (Fig. 3A) and test (Fig. 3B) phases. Specifically, in the training phase, a cluster of midline and frontal channels (Fig. 3C, leftmost panel, corrected p < 0.05) showed significantly greater positivity on congruent relative to on incongruent trials, starting ∼550 ms poststimulus onset (Fig. 3C, second panel from left) and continuing until the end of the stimulus presentation (i.e., 800 ms). The ERP time courses across these channels were similar in the test phase (Fig. 3C, right). Indeed, when testing the congruency effect in this cluster using test phase data, the pattern of greater positivity on congruent than incongruent trials persisted (t₍₄₂₎ = 2.53, p = 0.008). Complementing the frontal, midline effect, a cluster of occipital channels showed greater positivity on incongruent compared with congruent trials (Fig. 3D, leftmost panel, corrected p < 0.05), diverging from ∼550 ms to ∼800 ms poststimulus onset in both the training (Fig. 3D, second panel from left) and test phases (Fig. 3D, second panel from right; t₍₄₂₎ = 3.10, p = 0.002).

Figure 3.

Replication of congruency effect in ERP data. A, B, Spatiotemporal distribution of congruency effect in the training and test phases, respectively. C, D, From left to right: Topographic maps of the duration over which the congruency effect was significant in each channel of the cluster identified by the nonparametric cluster-based permutation tests; temporal distribution of significant congruency effects in nodes in the cluster; ERP time courses of representative channels, plotted by experimental conditions, in the training and test phases, respectively. Con, Congruent trials; Inc, incongruent trials. For all time course plots, the temporal resolution is 2 ms.

EEG results: temporal dynamics of memory-guided cognitive control

Our behavioral data revealed the involvement of associated CCD in guiding cognitive control (Fig. 2C). Based on the dual mechanisms of cognitive control theory (Braver et al., 2007; Braver, 2012) and computational simulations (Blais et al., 2007; Verguts and Notebaert, 2008), we hypothesized that, within a trial in the training and the test phases, cognitive control will first be guided by the retrieved/predicted CCD and then gradually shift to the actual CCD (i.e., the experienced [in]congruency). Accordingly, in the EEG data, we expected that, within a trial, a main effect of associated CCD would be first observed, reflecting the retrieval of the associated CCD to guide cognitive control. Subsequently, on trials in which the retrieved associated CCD conflicted with the actual CCD required to guide cognitive control, a mismatch effect would signal the need and engagement in adjustment of control. In other words, neural activity was expected to differ between the scenario when the associated and actual CCDs were consistent (i.e., high CCD in incongruent trial and low CCD in congruent trial) and when they were inconsistent (i.e., low CCD in incongruent trial and high CCD in congruent trial), leading to an interaction effect between associated CCD and congruency (Fig. 4). We did not consider the main effect of congruency because it may reflect reactive cognitive control (i.e., withholding adjustment of cognitive control until the detection of actual CCD), rather than the proactive cognitive control focused on in this study.

Figure 4.

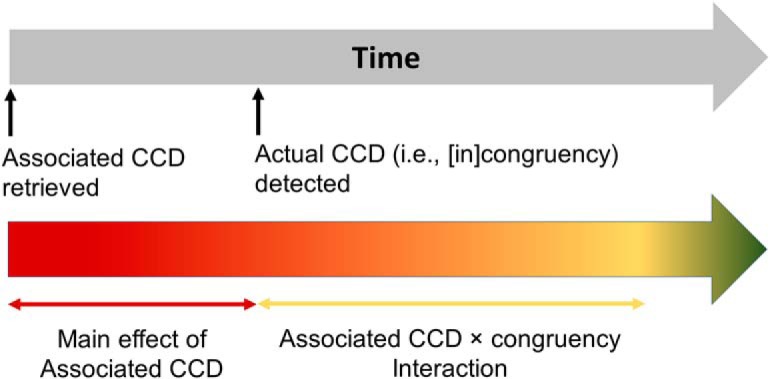
Hypothetical time course of processes driving the engagement of cognitive control (top) and of the underlying EEG effects (bottom).

To test these predictions, we performed 2 (associated CCD: high/low) × 2 (congruency/incongruency) repeated-measures ANOVAs on the ERP data and the time-frequency signals (theta, alpha, and beta bands) from the training phase. Multiple comparisons were corrected for using nonparametric cluster-based permutation tests. To test the neural processes shared by both training and test phase data (e.g., the generalization of the associated CCD) and to examine the validity of the findings, we used clusters detected in the training phase as ROIs and repeated the analyses using the ROIs in the test phase data. To be consistent with the hypothetical chronological order shown in Figure 4, we first present the results of the main effect of associated CCD and then the results of the associated CCD × congruency interaction.

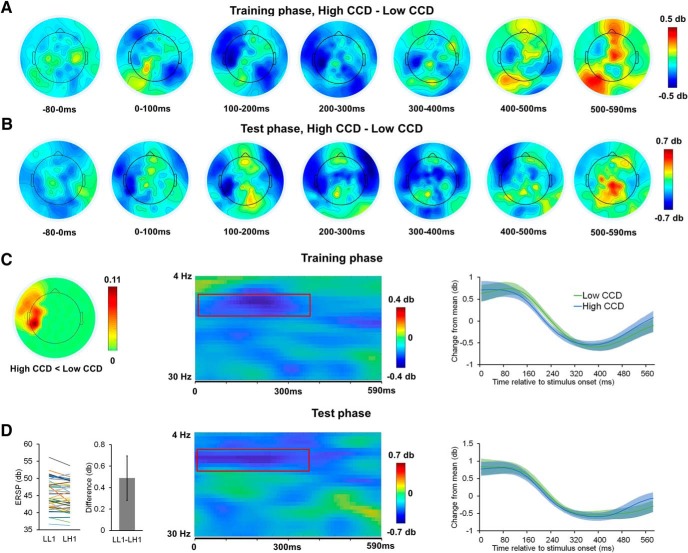
Early in the training phase (peaking at ∼200 ms), we observed lower alpha-band ERSP on high associated CCD trials than on low associated CCD trials (Fig. 5A). A nonparametric cluster-based permutation test statistically confirmed that the high CCD condition was associated with lowered ERSP in the alpha-band in a group of left frontal and middle channels (corrected p = 0.048; Fig. 5C, left) and peaked at ∼200 ms after stimulus onset (Fig. 5C, middle, right). No other clusters passed the nonparametric cluster-based permutation tests.

Figure 5.

Alpha-band oscillations show early (generalized) CCD effects in left middle and frontal channels. A, B, Spatiotemporal distribution of alpha-band CCD effect (high vs low) in the training and test phases, respectively. C, A cluster showing the associated CCD effect in the training phase. Left, Visualization of channel-wise proportion of significant observations (each observation is defined as a combination of channel, time point, and frequency) in the cluster showing a significant associated CCD effect. Middle, Size of the associated CCD effect in the cluster, plotted as a function of frequency and time. The cluster is highlighted by the red box. Right, Time course of cluster-mean (± SEM) ERSP change relative to time course grand mean, plotted as a function of associated CCD levels. D, Leftmost panel, Test phase individual ERSP averaged within the cluster plotted as a function of generalized CCD levels (left) and group mean (± SEM) ERSP difference between LL1 and LH1 (right). The other two panels are organized similar to C.

We next turned to the test phase data and used this cluster to test the generalization of the CCD to landmarks. A similar spatiotemporal pattern was found in the test phase when comparing high and low transferred CCD trials (i.e., LH1 vs LL1; Fig. 5B). Consistent with the training phase data, we observed statistically significant lower alpha-band ERSP for the high transferred CCD landmark (i.e., LH1) compared with low transferred CCD landmark (i.e., LL1, t₍₄₂₎ = 2.13, p = 0.04; Fig. 5D, left). In the channels showing an associated CCD effect in the training phase (Fig. 5C, left), the generalized CCD effect at test demonstrated temporal and frequency spans similar to those in the training phase (Fig. 5D, middle, right). As such, the (generalized) CCD effects presently observed in two independent sets of EEG data (i.e., training and test phases) strongly support the notion that this cluster represents engagement of the (generalized) associated CCD.

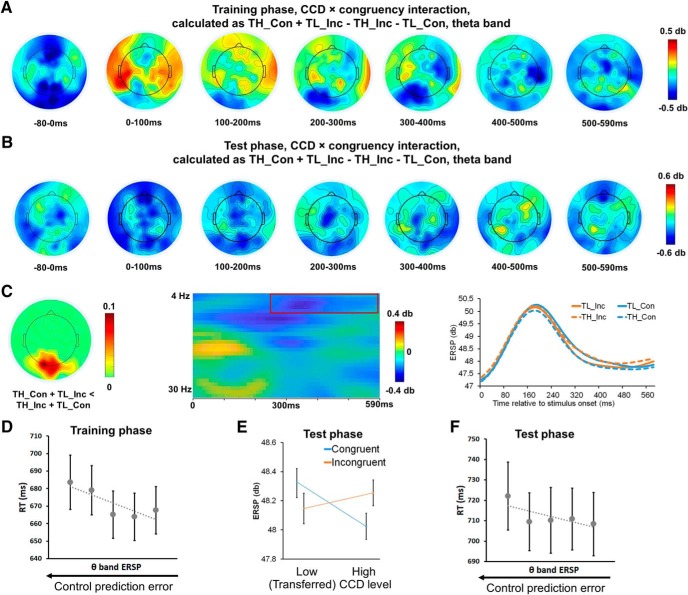
Later within trials during the training phase, we observed an interaction between associated CCD × congruency in the theta-band ERSP (Fig. 6A), revealing a cluster that included posterior midline channels that peaked at ∼350 ms after stimulus onset (Fig. 6C, left; corrected p = 0.044). Numerically, the test phase data displayed a similar interaction in the posterior midline channels (Fig. 6B), which reflected lower ERSP for trials with mismatched associated CCD and congruency (i.e., incongruent trials with low associated CCD and congruent trials with high associated CCD) compared with trials with matched associated CCD and congruency (i.e., incongruent trials with high associated CCD and congruent trials with low associated CCD; Fig. 6C, middle, right). We further found that, at the trial level, theta-band power in the cluster in Figure 6C explained variance in RT, such that lower theta power (reflecting mismatch between associated CCD and congruency, or larger control prediction error) was accompanied by slower responses (collapsed across conditions in the CCD × congruency factorial design to deconfound the shared variance in the CCD × congruency interaction found in both behavioral and EEG data, t₍₄₂₎ = −3.31, p = 0.002; Fig. 6D). When applying this cluster to test phase data, the interaction effect, which was defined following Figure 6A to preserve the sign of the effect, was also significant (t₍₄₂₎ = −2.13, p = 0.04; Fig. 6E), and the interaction effect also predicted test phase RT at the trial level (t₍₄₂₎ = −2.18, p = 0.03; Fig. 6F). The behavioral relevance of this cluster suggests that it is involved in the online adjustment of cognitive control that shifts from memory-guided to actual CCD-guided control.

Figure 6.

Theta-band oscillations show interaction between associated CCD and congruency in posterior midline channels. A, B, Spatiotemporal distribution of theta-band associated CCD × congruency interaction in training phase (A) and test phase (B). C, A posterior midline cluster showing significant theta-band associated CCD × congruency interaction. From left to right: Visualization of channel-wise proportion of significant observations in the cluster; size of interaction effect with the cluster highlighted in red box, plotted as a function of frequency and time; time course of cluster-mean ERSP, plotted as a function of associated CCD levels. D, Group mean RT (± SEM) in the training phase, plotted as a function of quintiles of the theta-band associated CCD × congruency interaction effect. RTs in the test phase are visualized similarly in F. E, ERSP when applied to the cluster in C on test phase data, plotted as a function of congruency and (transferred) associated CCD level.

In the training phase, one other posterior midline cluster displayed a significant CCD × congruency interaction effect in the alpha-band; this effect peaked at ∼300 ms after stimulus onset (corrected p = 0.006; compare Fig. 6C, middle). However, when replicating the aforementioned brain–behavior analysis, alpha-band power in this cluster did not significantly explain variance in RT in training phase data (t₍₄₂₎ = −1.79, p = 0.08). Furthermore, when we repeated these analyses using the test phase data, neither the interaction effect (t₍₄₂₎ = −1.51, p = 0.14) nor the brain–behavior analysis was significant (t₍₄₂₎ = −0.12, p > 0.9). Due to the lack of replicability and behavioral relevance, we conclude that activity in this cluster does not reflect the adjustment of cognitive control following the detection of the actual CCD. No other clusters passed the nonparametric cluster-based permutation tests.

ERP analyses revealed neither a main effect of associated CCD nor an associated × actual CCD interaction that survived the nonparametric cluster-based permutation tests. These null results may reflect phase incoherence in event-induced activity across trials (Bastiaansen and Hagoort, 2003). When repeating the analyses of main effect of associated CCD and CCD × congruency interaction using test phase data, the nonparametric cluster-based permutation tests did not reveal any significant results. This was possibly due to the low trial count and subsequent low signal-to-noise ratio at the node level.

None of the three frequency bands showed a significant effect of congruency. Given that the time window of the time-frequency analyses ended at 590 ms after stimulus onset, the lack of a significant effect here does not contradict the ERP findings showing a congruency effect after 550 ms after stimulus onset. We speculate that the relatively late congruency effects reflect the dominance of actual CCD, after correcting the associative CCD, in guiding cognitive control (reflected in the associated × actual CCD interaction).

To determine whether proactive control adjustments in response to anticipated CCD precedes further control adjustments in response to actual CCD, we quantitatively tested whether the associated CCD effect temporally preceded the CCD × congruency interaction. For each of the clusters showing the associated CCD effect (Fig. 5C) and the CCD × congruency interaction (Fig. 6C), we calculated their marginalized probabilistic density functions on the temporal dimension (Fig. 7) and calculated the precedence index that the distribution of the associated CCD effect followed the distribution of the interaction effect (see Materials and Methods). A resulting precedence index of 0.02 suggested a high chance that the CCD × congruency interaction effect occurred after the CCD effect. We also estimated the distribution of the precedence index by percentile bootstrapping 1000 times (see Materials and Methods). The nonparametric 95% CI of the precedence index was [0.0048, 0.4464], which lay outside of the baseline value of 0.5. This result indicates a p value <0.05 for the null hypothesis that the CCD effect did not precede the CCD × congruency interaction effect.

Figure 7.

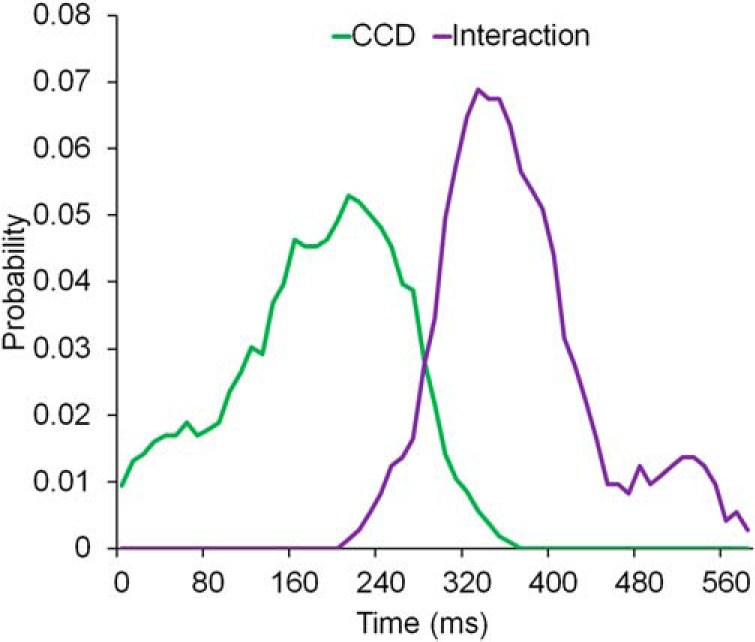
Temporal distribution of the clusters showing main effect of associated CCD and associated CCD × congruency interaction.

EEG results: generalization of CCD through tool–landmark association

As reported above, even when landmarks LL1 and LH1 were presented with the same neutral ISPC (50% congruency) during the test phase, behavioral analyses of RT revealed a significant interaction between the indirectly paired CCD (i.e., through the landmark's associated tool) and congruency (Fig. 2E), and neural analyses revealed a main effect of the indirectly paired CCD on alpha-band oscillations (Fig. 5D). These results provide strong evidence that participants generalized the learned CCD from tools to their associated landmarks.

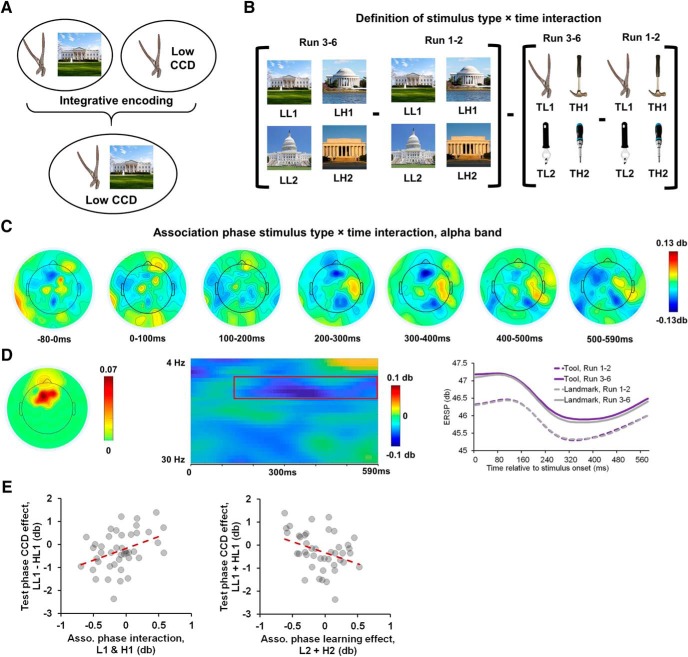
In a final set of analyses, we explored the possible mechanisms supporting this generalization. In particular, we hypothesized that, during the interleaved presentations of tool–landmark pairs in the association phase and tool–CCD pairs in the training phase, these two associations become integrated in memory, forming a tool–landmark–CCD representation that enables the generalization of CCD to the landmark (Fig. 8A).

Figure 8.

Time-frequency analysis and results in the association phase. A, The integrative encoding hypothesis. B, The contrast for the stimulus category × time interaction. C, Spatiotemporal distribution of the interaction effect following the onset of the stimulus. D, A mediofrontal cluster showing significant alpha-band stimulus category × time interaction. From left to right: Visualization of channel-wise weights in the cluster; size of interaction effect plotted as a function of frequency and time with the cluster highlighted in red box; time course of cluster-mean (± SEM) ERSP plotted as a function of experimental conditions. E, Transferred CCD effect in the test phase, measured by the alpha-band ERSP difference between LL1 and LH1 in the cluster shown in Figure 5C, plotted out as a function of the stimulus category × time interaction effect for the same items (left) and different items (right) in the association phase.

One potential task phase during which integrative encoding may occur is in Runs 3–6 of the association phase (i.e., after initial exposure and encoding of the tool–CCD associations; Fig. 1D). During the time course of a trial in these runs, presentation of the tool may reactivate the learned tool–CCD association, which can then be associated with the subsequent landmark upon its presentation. To test this possibility, we compared EEG data following the presentation of landmark images to that following the presentation of tool images in Runs 3–6. The tool image data were used as a baseline to tease apart EEG data reflecting nuisance processes, such as perceptual processing. Data from the first 2 runs of the association phase were included as an additional baseline when tool–CCD associations were not available. This baseline filters out neural activity of the encoding of the tool–landmark association and helps isolate signal potentially reflecting integrative encoding. Therefore, the test for integrative encoding took the form of an interaction between stimulus category (tool vs landmark) and time (Runs 1 and 2 vs Runs 3–6), as shown in Figure 8B.

Across the ERP data and the time-frequency data, the nonparametric cluster-based permutation tests revealed an alpha-band, mediofrontal cluster centered at ∼300 ms after onset of the landmark image (corrected p = 0.036; Fig. 8C,D, left, middle). This effect was driven by data from Runs 3–6, which showed reduced alpha-band ERSP following the onset of the landmarks, compared with following the presentation of the tools (Fig. 8D, right). Given that memory retrieval is accompanied by alpha desynchronization (Hanslmayr et al., 2012, 2016), the increased alpha-band ERSP in tools than landmarks was unlikely to reflect the retrieval of the tool–CCD association. Critically, to test whether this interaction effect was linked to the generalization of CCD to the landmarks, we performed a cross-participant correlation analysis between the cluster-average interaction effect for each participant and the cluster-mean of the transferred CCD effect in the test phase (Fig. 5D) for that participant. Similar to the behavioral analysis, this analysis was performed on items with neutral test phase ISPC (i.e., LL1 and LH1), to deconfound the ISPC in the test phase. Results revealed a significant positive relationship (r = 0.38, p = 0.01; Fig. 8E, top), indicating that participants with stronger post-landmark alpha power decrease in the association phase tended to show a stronger alpha-band transferred CCD effect in the test phase. To examine whether this effect was item-specific (i.e., only occurring within the same items), we repeated this analysis by keeping test phase data unchanged while replacing association phase items LL1 and LH1 with different items LL2 and LH2, thus forming a cross-item design. A positive correlation coefficient would be evidence against the item-specific claim. However, a negative correlation (r = −0.35, p = 0.02; Fig. 8E, bottom) was observed, thus supporting the item-specific claim. The negative correlation shows that post-landmark alpha power decreased in the association phase between LL1-LH1 and LL2-LH2 (r = −0.71, p < 0.001), which may reflect interference between individual associations during generalization.

An alternative interpretation of the stimulus category × time interaction may be that it reflects differential processing of or attention to the tool images relative to the landmark images. Specifically, because each landmark appears 15 times in each association phase run and each tool appears 15 times in each association phase run and 12 times in each training phase run (which were interleaved with association phase runs), a change in the EEG response to a stimulus between association phase Runs 1 and 2 and Runs 3–6 can be viewed as an adaptation effect. From this perspective, the interaction effect might reflect stronger adaption effects for tools than landmarks, given that tools were encountered more often (due to their presentation in the interleaved training phase runs). At the individual level, stronger adaptation for tools than landmarks (compare Fig. 8D, right) might be attributed to more attention to the tool images in the training phase; such attention should impact tool processing during the training phase and thus impact the magnitude of the congruency effect (e.g., attention-enhanced processing of the task-relevant stimulus [i.e., the tool image] might reduce the congruency effect). In short, this alternative interpretation predicts that a stronger stimulus category × time interaction in the association phase will be related to a weaker congruency effect in the training phase. To test this prediction, we used cross-subject correlational analyses between the stimulus category × time interaction effect in the association phase and the congruency effect in the training phase. Given that significant training phase congruency effects were observed in the ERP (clusters identified in Fig. 3C,D), behavioral accuracy, and RT data (Fig. 2), we conducted four analyses, each using one effect as a measure of the congruency effect. None of the correlations reached significance (all p values > 0.18). Therefore, the stimulus category × time interaction effect appears less likely to reflect differential adaptation to the tools than the landmarks.

Another possibility is that the cluster reflected the change in the predictability/association strength between tool and landmark. If this were true, we would predict that this effect (reflecting tool–landmark association) and the main effect of associated CCD in the training phase (reflecting tool–CCD association; Fig. 5C) will jointly predict the main effect of generalized CCD in the test phase EEG data (Fig. 5D). To test this prediction, we conducted cross-subject rescaling (range: 0–1) separately on the effect of tool minus landmark in the cluster reported in Figure 8D and the training phase associated CCD effect. These rescaled effects for TL1, TH1, LL1, and LH1 were combined and correlated with the main effect of generalized CCD for LL1 and LH1 in the test phase. For the joint prediction, we tested whether the strength of generalized CCD relates to either (1) the sum of the two predictor effects or (2) the product of the two predictor effects. Neither yielded a significant correlation with the generalized CCD effect (both p values > 0.18). Thus, it is unlikely that this effect reflects the predictability/association strength between the tool and the landmark.

Discussion

How cognitive control is regulated is of key interest in understanding goal-directed behavior (Botvinick et al., 2001; Botvinick and Cohen, 2014; Waskom et al., 2017). Recent theoretic advances propose that cognitive control can be proactively adjusted based on prediction of future CCD (Botvinick et al., 2001; Brown and Braver, 2005; Braver et al., 2007; Braver, 2012). A wealth of data indicate that such predictions can be based on temporal information (e.g., Logan and Zbrodoff, 1979; Botvinick et al., 1999; Carter et al., 2000; Kerns et al., 2004; Egner and Hirsch, 2005; Egner, 2007; Hazeltine et al., 2011; Aben et al., 2019; De Loof et al., 2019). Here, we explored another important source of CCD predictions: learned associations between items and CCD (e.g., Jacoby et al., 2003; Bugg et al., 2011; Chiu et al., 2017). To advance understanding of (1) how item-CCD associative memories proactively guide the regulation of cognitive control and (2) the neurocognitive mechanisms supporting the generalization of CCD, we leveraged behavioral and EEG measures acquired while participants performed a three-phase task that involved the learning of tool–landmark and tool–CCD associations and the assessment of the generalization of CCD from tools to landmarks (Fig. 1). Our findings provide novel evidence for memory-guided proactive adjustments of control that precede adjustments due to actual demands, and the generalization of CCD via associative memory.

Temporal dynamics of memory-guided adjustments of cognitive control

We first applied a reinforcement learning model (Chiu et al., 2017) to the behavioral data to quantify how associated CCD and actual CCD jointly affect behavior. Analyses revealed that training phase RT scaled with the degree of discrepancy between associated and actual CCD. Based on the theory of proactive cognitive control (Braver et al., 2007; Braver, 2012) and computational simulations (Blais et al., 2007; Verguts and Notebaert, 2008), this observation suggests that the retrieval of associated CCD leads to proactive adjustments of control that speed goal-directed behavior when predicted and actual CCD align; by contrast, when misaligned, additional reactive adjustments are required based on actual CCD following its detection. Consistent with this interpretation, analyses of the EEG data indicated that the effect of associated CCD emerged earlier than the effect of actual CCD. Specifically, lower alpha-band ERSP, at left channels and peaking at ∼200 ms after stimulus onset, was found in trials with higher associated CCD (Fig. 5C). This decrease in alpha oscillations may reflect the increased involvement of selective attention (Klimesch, 1999; Sadaghiani and Kleinschmidt, 2016) in anticipation of the forthcoming incongruent trial predicted by the higher associated CCD. This converges with fMRI data demonstrating that higher associative CCD was accompanied by greater activation in dorsolateral PFC and ACC (Blais and Bunge, 2010).

Subsequent to the associated CCD effect (Fig. 7), we observed an interaction between associated and actual CCD in theta-band ERSP in posterior channels (Fig. 6C). This interaction effect is consistent with similar interactions in ERP when participants perform the Stroop (Shedden et al., 2013) and Simon (Whitehead et al., 2017) tasks. In our data, this interaction appears to be driven by increased theta-band oscillations when the associated CCD matched the actual CCD (Fig. 6C, right). While speculative, compared with a mismatch that requires further adjustment of cognitive control, a match may lead to elevated readiness of information processing, which has been associated with higher theta oscillation (Basar et al., 2001). Crucially, the theta-band ERSP in these channels was negatively correlated with RT at the trial level (Fig. 6D). This result is consistent with previous findings that increased task-elicited theta is accompanied by better performance (Klimesch, 1999), and suggests that this interaction relates to resolution of the discrepancy between associated and actual CCD (as slower RTs indicate larger discrepancies that must be resolved). Importantly, we cross-validated these findings, observing similar results using the independent data from the test phase (Figs. 5B,D, 6B, 8B,D).

Generalization of CCD through item-item associations

Our behavioral and EEG data provide strong evidence of transfer of CCD from tool images to their associated landmarks. Behaviorally, we found an interaction between the CCD of the associated tool and congruency in LL1 and LH1 trials (Fig. 2E) in the test phase. This finding replicates recent work (Bejjani et al., 2018). In the EEG data, we observed a significant main effect of the associated tool's CCD on landmark-triggered alpha oscillations during the test phase (Fig. 5D). Critically, neither finding can be attributed to test-phase learning processes, given that the ISPCs for LL1 and LH1 items were identical in the test phase. The only difference between LL1 and LH1 items was the level of CCD previously bound to their associated tools; as such, these behavioral and EEG differences between these landmarks document the generalization of CCD from tools to landmarks.

Regarding the neurocognitive mechanisms of generalization, one possibility is that generalization occurred through integrative encoding (Shohamy and Wagner, 2008) that merged tool–CCD associations and tool–landmark associations into conjunctive tool–landmark–CCD memories (Fig. 8A). Supporting this idea, we observed differential alpha-band ERSP in medial frontal channels following repeated presentation of landmarks and tools in the association phase (tool/landmark × Runs 1 and 2/Runs 3–6; Fig. 8D). This decrease may be linked to generalization because it emerged following exposure to the tool–CCD associations in the training phase (Fig. 8D), and it predicted the magnitude of the generalized CCD effect in the test phase (Fig. 8E). Prior work has linked decreases in alpha oscillations to memory encoding and retrieval (Hanslmayr et al., 2012), and have been posited to reflect desynchronization in cortical activation that signals a shift from processing present inputs to memory operations (Hanslmayr et al., 2012, 2016). Moreover, prior observations indicate that hippocampal processes support memory generalization (Shohamy and Wagner, 2008; Zeithamova and Preston, 2010; Kuhl et al., 2011; Wimmer and Shohamy, 2012; Zeithamova et al., 2012). Thus, our findings provided new insights about the electrophysiological mechanisms in the generalization of abstract concepts, such as CCD, through partially overlapping memories.

As an additional but nonexclusive mechanism, integrative encoding may also occur in the training phase of the present paradigm. Specifically, as the tool–CCD pairings were experienced, presentation of the tool may have triggered retrieval of the associated landmark, providing an opportunity for forming an integrative memory. The present experimental design is not suitable for examining whether integrative encoding also occurs in the training phase because this phase lacks baseline conditions that are required to deconfound nuisance effects (e.g., there were no training runs that occurred before initial exposure of tool–landmark associations). We also did not find a direct correlation between the sizes of training phase-associated CCD effect and those of the test phase-transferred CCD effect across participants (r = −0.19, p = 0.21). Future studies can examine this hypothesis by moving the first training runs before the first association runs. Alternatively, generalization during the training phase could be tested by examining neural evidence for reinstatement of the to-be-generalized item (Wimmer and Shohamy, 2012; Kurth-Nelson et al., 2015).

Another possibility is that generalization of CCD occurs at retrieval (i.e., the test phase) through inference over partially overlapping associations, which requires additional time to sequentially activate multiple overlapping associations for generalization to occur (Kumaran and McClelland, 2012; Horner et al., 2015; Koster et al., 2018). Whereas Shohamy and Wagner (2008), among others, provided evidence that integration can occur during learning and before the critical generalization test, a recent study reported slower responses when participants made judgments based on retrieval of direct associations relative to those based on inferred associations (Koster et al., 2018). In the present study, our finding that the associated CCD effect preceded actual CCD effects in guiding cognitive control suggests that generalization occurred via integration. Furthermore, the neural timing of the observed CCD effect in the training phase was similar to that of the generalized CCD effect in test phase (Fig. 5A,C,D). This result suggests a direct retrieval of the already generalized landmark–CCD association, thus favoring an integrative encoding account.

A potential confound in the experimental design is that the generalization effect may co-occur with other processes that also change over time. Although we ruled out two confounds (adaptation and tool–landmark association strength), future studies should explore the possible influence of other processes that vary over time.

In conclusion, this study provided new insights into the mechanisms of associative memory-guided adjustment of cognitive control. Specifically, supporting the hypothesis of an earlier involvement of associated CCD than actual CCD in guiding cognitive control, we found an early-onset–associated CCD effect in alpha oscillations. This effect was temporally followed by an interaction between associative and actual CCD in theta oscillations, possibly reflecting their competition in guiding cognitive control. Furthermore, supporting an integrative encoding account, a generalized associated CCD effect in alpha oscillations in the test phase was linked to a decrease in alpha oscillation during the encoding of item–item associations. These findings advance understanding of the neurocognitive mechanisms supporting memory-guided cognitive control during goal-directed behavior.