Blood group and size dependent stability of P. falciparum infected red blood cell aggregates in capillaries

Abstract

For Plasmodium falciparum related malaria (B50), one of the outstanding host factors for the development of severe disease is the ABO blood group of malaria patients, where blood group O reduces the probability of severe disease as compared to individuals of groups A, B, or AB. In this report, we investigate the stability of rosette aggregates in malaria caused by Plasmodium falciparum in microflows. These flows are created in microfluidic channels with stenosis-like constrictions of different widths down to ones narrower as the rosette's diameter. High speed videos were recorded and analyzed by a MATLAB© based tracking software (SURF: SUrvival of Rosettes in Flow). We find a correlation of rosette size, channel diameter, and blood group regarding the mobility of the rosettes. Following the concept of a thermodynamic model, we find a critical width of the stenosis for rosette rupture during their passage. Our data reveal that under physiologically relevant conditions, rosettes in blood group A have a higher rosette frequency and stability as compared to blood group O (BG O), which constitutes a crucial factor promoting the observed protection in BG O individuals against severe malaria in non-O individuals.

INTRODUCTION

A relationship between the ABO blood groups and malaria was first suggested in 1967.¹ Studies finding a prevalence of blood group O in malaria endemic regions² indicated that the malaria parasite Plasmodium falciparum not only has an impact on the distribution of blood groups but also on the evolution of ABO blood groups itself.³ Recently, the underlying interactions between the parasite and the ABO blood group antigens have been studied to develop new approaches for antimalarial drugs or vaccines.⁴ The difference in malaria pathogenesis in individuals of different ABO blood groups is the higher tendency of the non-O red blood cells (RBCs) to form aggregates, so-called rosettes.^5–8 Rosetting is suggested to protect the parasitized cell from the immune system.⁹ Rowe et al.¹⁰ found reduced rosetting in blood group O patient isolates in compliance with a 66% lower chance of severity of blood group O patients, and variable rosetting levels in relation to the ABO blood type of the RBCs have been reported in in vitro studies.^9,11,12

The cohesion within rosettes and their formation was studied during the 1990s by Nash et al. using cone-and-plate viscometers^13,14 or micropipets.¹³ They found strong binding between infected and uninfected RBCs and assumed that rosettes can both survive¹³ and even form¹⁴ in the circulation. Physiological shear conditions in those large flow systems are achieved by adapting the flow rate, which does not take the physical confinement of the blood flow into account, while downsizing to a microfluidic setup does. A more recent work of Adams and Rowe combined a rosette flow assay and image analysis¹⁵ in microchannels of 800 μm height with manual analysis of micrographs. They show comparable performance of rosette-disrupting agents under both static and flow conditions.¹⁵ Moreover, Kaul et al. found rosettes in a rat model only in venules with slow flow conditions.¹⁶ Thus, it has been discussed whether rosettes disrupt under high shear stress as in arterioles or to pass capillaries and reform rapidly. The precise behavior during passage and their role in cytoadhesion is still unclear.¹⁷ However, there is a lack of systematic studies with both good statistics and high time resolution of rosette rheology at the same time, especially for the interesting case of channels mimicking capillaries. Here, we combine those tasks by automated analysis of high speed videos to study individual rosettes in both blood groups O and A and compare their stability size-resolved passing different constrictions. While the experimental approach in Ref. 15 is somehow similar to our approach presented here, the dimensions of the microfluidic systems differ by a factor of about 100 and micrographs were analyzed manually. In contrast, we here track large numbers of individual aggregates and analyze their development over a series of images. The use of a customized automated image analysis like ARAM¹⁸ or SURF (SUrvival of Rosettes in Flow) does not only allow for higher sample sizes but also ensures operator independent and unbiased assessment of rosetting in the respective blood groups. Employing these advantages, we study the stability of rosettes in capillaries with multiple stenoses.

RESULTS

Figure 1 shows micrographs of typical rosettes categorized into six classes of increasing size, the relative frequency of rosettes for BG O and BG A, as well as a schematic representation of the setup consisting of a microchannel, a pipet tip serving as the cell suspension reservoir, and a syringe pump. With a high speed camera, we recorded videos of cells moving through microchannels with one or multiple stenoses.

FIG. 1.

(a) Categorization of rosettes in classes referring to their size in ascending order. The size is being measured in pixels after binarization of the micrographs and normalized to the area of a single RBC A_RBC in each measurement. Gray circles represent the equivalent area for an object of the respective class. (b) Relative frequency of rosettes of each class referring to the total number of rosettes traced by SURF before passing a stenosis, comparison of blood groups O and A. Error bars indicate 95% confidence intervals. (c) Experimental setup consisting of a PDMS block containing the microfluidic channel, a pipet tip as reservoir at the channel inlet, and PTFE tubing being connected to a syringe pump at the channel outlet. Channel length L = 7 mm, height h is set to the constant height h = 8 μm. The channel width w = 50 μm decreases at the constrictions to the stenosis diameter d.

After tracing and analyzing the cells using SURF, one video comprised about 500–1000 traced rosettes. For further analysis, these traces are categorized according to the initial rosette size being normalized to the area of a single red blood cell A_RBC. The histogram edges used are set to 1.11, 2.22, 3.33, 4.44, 5.56, 7.78, and 30 A_RBC, and classified into classes 1–6 in the following part of the manuscript [see Fig. 1(a)]. This approach ensures a consistent categorization of rosettes during the entire sequence of a measurement. A categorization of objects before tracing them or a simple comparison of the size distributions at different positions along the channel would, for instance, allow rosettes to slip to other categories from one observation point to the next by losing cells or by their deformation in the flow. By following the objects through the whole flow system, changes in area can be precisely monitored and events like the loss of a cell become distinguishable from a size decrease due to deformation. The obvious strength of our approach is the possibility to compare rosettes of equal size under different flow conditions and particularly in different blood groups. This allows us to distinguish between longer survival due to a mere bigger size and actual stronger binding between aggregated cells.

Initial size distribution in blood groups O and A

The already mentioned initial size distribution of traced rosettes is shown in Fig. 1(b). The histogram allows us to compare between relative frequencies of rosettes of the respective classes in the two examined blood groups O and A. Differences in rosette frequency between blood groups become most apparent in the smallest (1) and largest (6) rosette class. For identical preparation conditions, at 1% hematocrit and 20% parasitemia, classes 1 and 2 are significantly higher for BG O, classes 3 and 4 exhibit similar values, and classes 5 and especially 6 are significantly higher in BG A, as expected from the literature.^9–11

In Fig. 1(a), depicting our classification scheme, we also show class 1 “aggregates,” being as small as two conjoined cells at most. Reference measurements using solely uninfected RBCs with no aggregation tend to also show a considerable amount of class 1 “false positive” counts from closely adjacent but not aggregated cells (data not shown). Considering the possible occurrence of such artifacts and the definition of a rosette (one infected cell plus at least two uninfected cells), from here on and for the following figures, we only take rosettes of class 2 and larger into account.

Behavior of rosettes passing different constrictions

As described in the methods section and depicted in Fig. 1(c), the blood cell suspension is drawn through the microfluidic channel providing various constrictions. If a rosette is being traced along the channel, main events such as ruptures and total disruption are identified and listed [compare the SURF tracing section and Fig. 2(b)]. Following a rosette squeezing through a stenosis, one of three possible scenarios can be observed: (i) a rosette can either pass undamaged or (ii) slightly damaged, i.e., suffering from a certain cell loss but still being large enough to be considered to be a rosette, or (iii) become totally disrupted, meaning more specifically loosing so many cells that the remaining aggregate falls into class 1. The colored bars in Figs. 3 and 4 depict the distribution of rosette states directly behind each stenosis. The colored bars in Figs. 3 and 4 depict the distribution of rosette states directly behind each stenosis, which are (i) undamaged (green), (ii) damaged (orange), and (iii) totally disrupted (red) as introduced above. Both figures summarize the results of 500–1500 traced rosettes being classified into category 2–6. The experiments shown result in 90% confidence intervals of a width of under 5% on average, for exact values see Tables S1 and S2 (supplementary material). These intervals are shown as error bars in Fig. 5, which is based on the same data. In Figs. 3 and 4, error bars were omitted for the sake of legibility. Experiments were conducted using five different stenoses and red blood cells from both blood groups O and A. The difference between Figs. 3 and 4 is the setup of the constrictions. First (Fig. 3), so-called “cascaded” channels were used, comprising consecutively smaller stenoses to be able to follow the individual rosettes through increasingly demanding areas of shear stress. In Fig. 4, rosettes pass only a single stenosis independently, providing the same starting conditions before each stenosis.

FIG. 2.

Example of a cascaded channel experiment. The widths of the stenoses are 11 μm, 7 μm, and 5 μm in direction of flow from left to right. (a) A BG A rosette of class 4 is passing the first stenosis intact and eventually ruptured in the second one. The depicted micrographs are recorded at a frame rate of 2000 fps. (b) Example of the SURF result for rosettes of class 4. Top: the markers display the ends of the traces. Bottom: the markers indicate “real rupture events” with the size of the marker scaling with the area of the lost part of the rosette.

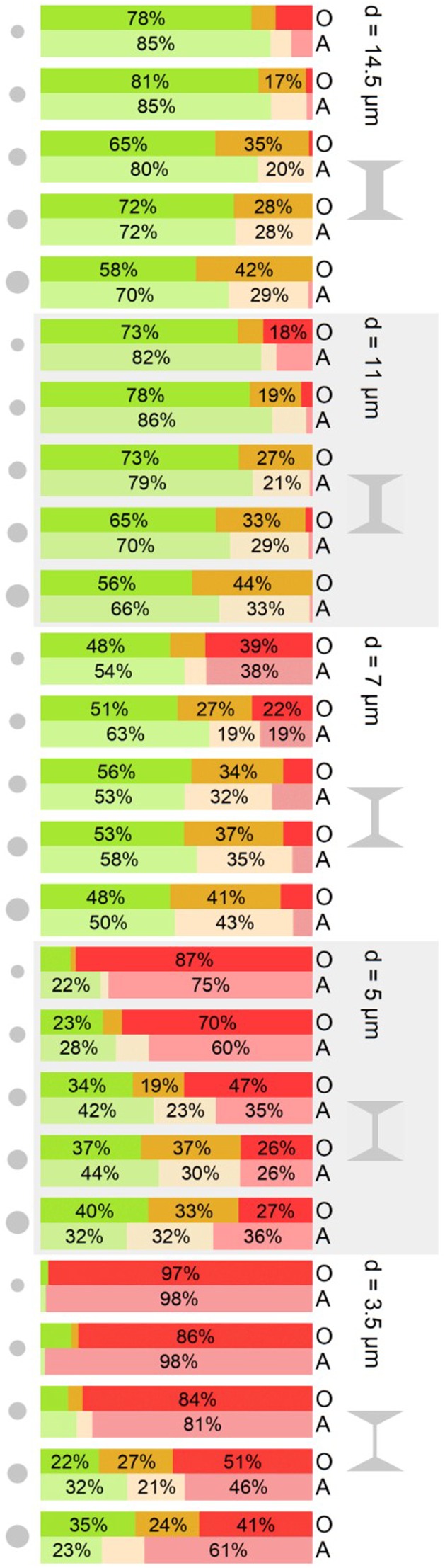
FIG. 3.

State of rosettes after passing a stenosis of width d in a cascaded channel. The experimental findings are categorized in the three categories “undamaged” (green), “damaged” (orange), and “total disruption” (red) as described in the text. The individual stenosis in question is marked by a red, dashed line in the schematic on the right of the figure. Gray circles on the left indicate the equivalent aggregate area of rosettes of class 2–6 from top to bottom, for classification of the rosettes [compare Fig. 1(a)]. Blood groups are labeled O and A on the right.

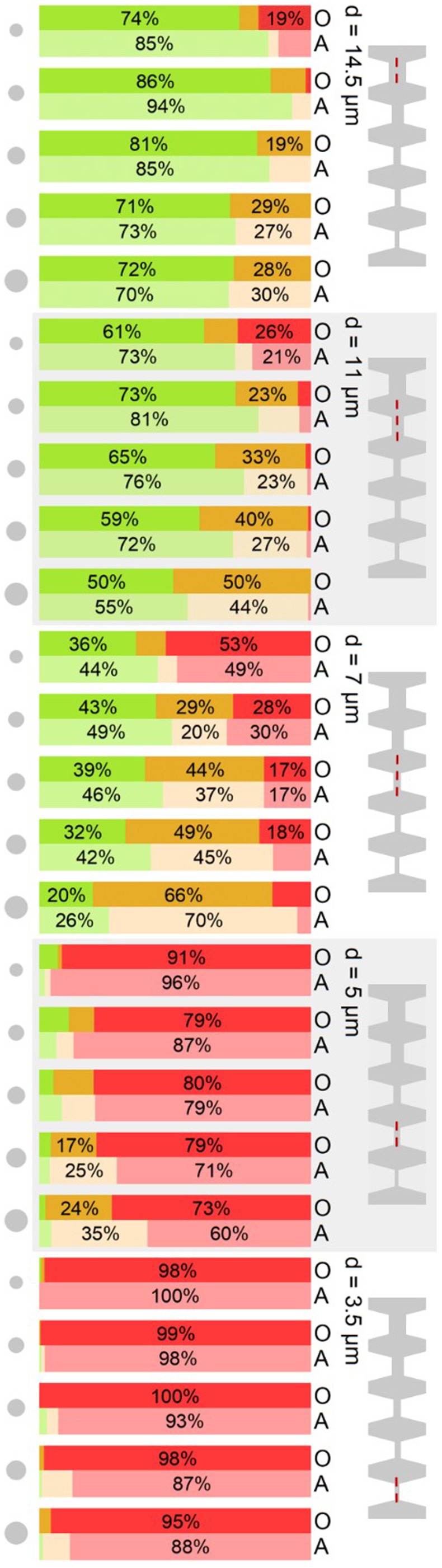
FIG. 4.

State of rosettes after passing a single stenosis (width in μm on the right of each block) being categorized in the three categories “undamaged” (green), “damaged” (orange), and “total disruption” (red). The gray circles on the left indicate the equivalent aggregate area of rosettes of class 2–6 from top to bottom. Blood groups are labeled O and A, respectively, on the right.

FIG. 5.

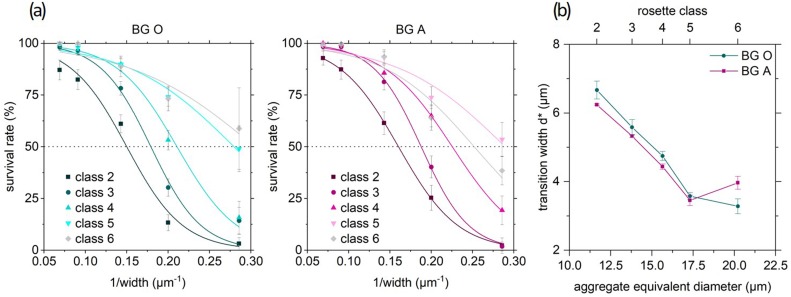
(a) Survival rate as function of the inverse width of the stenosis in blood group O (left) and A (right) fitted according to Eq. (6). Numbers indicate the classification of the rosettes. Error bars are 90% confidence intervals. (b) Critical width $d^{\ast }$ of a stenosis calculated from the fit functions shown in (a), where 50% of the rosettes “survive” the passage. For both blood groups O and A and for each size class of rosettes, we expressed this behavior with an aggregate's equivalent diameter taken from equivalent circles as described in Fig. 1(a). Error bars are standard errors from fit.

The stacked bar charts show the correlation of the stenosis size and the size of rosettes and their “fate” (Fig. 3). The survival rate s is understood as the opposite of total disruption, i.e., the sum of undamaged and slightly damaged rosettes. First focusing on blood group O, from wider to narrower stenosis, we observe that the survivors cover the whole range from almost 100% in the widest constriction (14.5 μm) decreasing to almost 0% (3.5 μm). Looking at the differences between differently sized rosettes, the undamaged rate decreases with size, as one would expect, while the damaged ratio increases to the extent that the survival rate even increases from smaller to larger rosettes. This is in contrast to what one might predict intuitively. We explain this finding by an increased flexibility of the rosettes with a growing number of constituting cells. This argument also applies to the larger proportion of damaged rosettes with increasing size: the more cells there are, the more cells can a rosette lose without becoming totally disrupted.

Finally, for a comparison of the two different blood groups in various scenarios, several arguments for the apparent higher stability in blood group A compared to blood group O during the passage of the smallest two stenoses arise: we observe a lower rate of total disruption up to 24% and consistently, about 10% higher values of undamaged rate in the 14.5, 11, and 7 μm stenoses. In the experiments presented in Fig. 3, the rosettes were passing several progressively smaller stenoses in one channel. In contrast to the above experiments, here the channels are now composed of one single stenosis of the respective width. The stacked bar charts in Fig. 4 thus illustrate the state of the rosettes after passing the stenosis leaving it undamaged, damaged, or totally disrupted.

Looking at the two largest channels, 14.5 μm and 11 μm, the results of the cascaded channel and single stenosis are almost exchangeable, which is consistent with the scenarios of a single stenosis and the first stenosis in a cascade being almost identical.

Looking at the results for the 7 μm stenosis, we find more survivors after a single stenosis as compared to the cascade. This suggests that a rosette, that did not have to pass a stenosis before, is more stable than one previously stressed, despite the larger size of the preceding stenosis.

The most noticeable difference appears for the smallest stenoses: Instead of maintaining almost constant values through all rosette classes, as in Fig. 3, we find a significant increase in survival with increasing size after a single 5 μm or 3.5 μm stenosis.

The distinction between undamaged and damaged rosettes is important to understand what happens in the stenosis. Considering the “parasite's interest,” it is only relevant whether the infected RBC is in a rosette, but not necessarily maximizing the number of cells surrounding it in total. This condition is met by the survival rate or the sum of the undamaged and damaged rate, as introduced earlier.

The obvious parameter that changes with the diameter of the stenosis would be the shear rate. The average shear rate is 250 s⁻¹ in the wide part of the channel and increases in the stenosis toward a maximum of 3500 s⁻¹ (14.5 μm) up to 30 000 s⁻¹ (3.5 μm). Our results show that identical values of the shear rate in different geometric confinements lead to different results, while we identified 1/width as representing the relevant parameter instead. Figure 5 shows the survival rate as a function of the inverse width of the stenosis based on the same data set as Fig. 4.

The progression of the curves in Fig. 5 resemble temperature or force induced unfolding of proteins or RNA.^19–21 Consequently, we follow the idea to describe the breakup of a rosette similarly to such a process. In the real experiment, the breakup of a rosette is most likely a process that includes various microstates (rosettes of different sizes) summarizing the classifications undamaged and damaged introduced above. We here condense those states to a single macrostate A (rosette). Together with the opposite macrostate B (totally disrupted rosette), this results in a two state system. The earlier defined survival rate s can now be calculated as

$$s={\displaystyle \frac{[A]}{[A]+[B]}.}$$ (1)

In analogy to temperature induced protein unfolding, we conclude from the dependence of the survival rate s on the inverse width 1/d [Fig. 5(a)] that the Gibbs free energy difference $\mathrm{\Delta }G$ of the two states scales linearly with 1/d:

$$\mathrm{\Delta }G=G_B-G_A\sim -{\displaystyle \frac{1}{d}.}$$ (2)

Moreover, we approximate

$$\mathrm{\Delta }G(d)=\mathrm{\Delta }{G}_0-c{\displaystyle \frac{1}{d},}$$ (3)

where $\mathrm{\Delta }{G}_0$ reflects the Gibbs free energy difference of the states A and B without flow through a constriction and c is a proportionality constant. For the transition width $d^{\ast }$, it holds

$$\mathrm{\Delta }G(d^{\ast })=0,$$ (4)

and thus,

$$c=\mathrm{\Delta }{G}_0{d}^{\ast }.$$ (5)

Assuming a Boltzmann distribution then results in

$$s={\displaystyle \frac{[A]}{[A]+[B]}={\displaystyle \frac{1}{1+[B]/[A]}={\displaystyle \frac{1}{1+\exp \left(-{\displaystyle \frac{\mathrm{\Delta }G}{k_{B}T}}\right)}={\displaystyle \frac{1}{1+\exp \left(-{\displaystyle \frac{\mathrm{\Delta }{G}_0\left(1-{\displaystyle \frac{d^{\ast }}{d}}\right)}{k_{B}T}}\right)}.}}}}$$ (6)

The transition width $d^{\ast }$ is determined by fitting Eq. (6) to the data in Fig. 5(a) and plotted as a function of the aggregate equivalent diameter in Fig. 5(b). The second fitting parameter $\mathrm{\Delta }{G}_0$ ranges between $4k_{B}T$ and $6k_{B}T$ as shown in Table I. In the following, we focus on $d^{\ast }$ as it reflects the parameter being less susceptible to changes of the ansatz of $\mathrm{\Delta }G$.

TABLE I.

Fitting parameter ΔG₀ for the survival rate in BG O and BG A shown in Fig. 5(a).

$\mathrm{\Delta }{G}_0/k_{B}T$	Class 2	Class 3	Class 4	Class 5	Class 6
BG O	4.41 ± 0.65	5.89 ± 1.25	5.79 ± 0.78	4.40 ± 0.47	4.01 ± 0.76
BG A	4.44 ± 0.06	6.49 ± 0.33	5.44 ± 0.40	4.47 ± 0.72	4.61 ± 0.86

Figure 5(b) clearly shows that the correlation between the transition width $d^{\ast }$ and the aggregate size is much stronger than the observed differences between the blood groups. As described above, a larger, more flexible aggregate can survive smaller constrictions. Coherently, larger transition widths for BG O or transitions already at larger stenosis diameters correlate with higher stability in BG A. Results for $d^{\ast }$ from class 6, however, abandon the systematics. But these originate from survival rates with considerable insecurities of ∼20% (90% confidence interval). In both classes 5 and 6, the survival rate merely reaches the 50% mark. Considering the number of RBCs involved in class 5 and 6 aggregates being 7–20 cells, we have to be aware of a growing percentage of aggregates, which do not involve only one but two or more infected RBCs. This may alter the results due to their different nature.

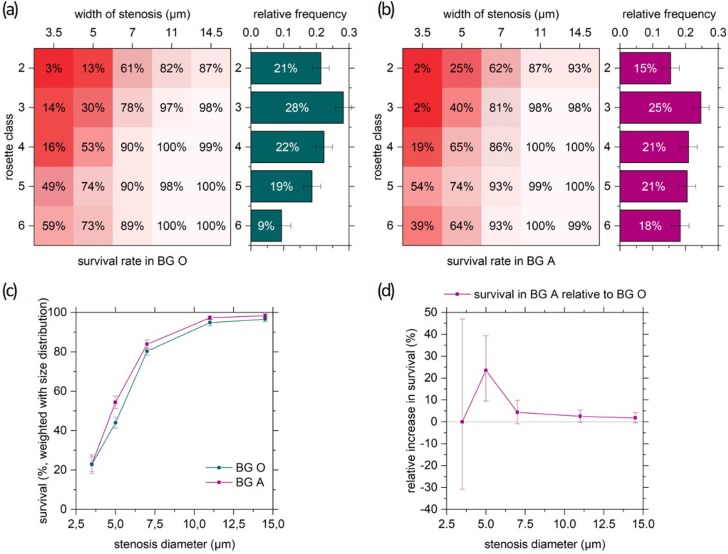
For a quantification of the observed, actual longer survival of blood group A aggregates, we now calculate the total survival in each blood group. The total survival [Fig. 6(c)] for a certain stenosis width is given by the sum over the size-dependent survival rates [Figs. 6(a) and 6(b)], weighted with the initial relative frequency of rosettes of the respective class [bar charts in Figs. 6(a) and 6(b)]. The resulting “effective population survival” [Fig. 6(c)] increases with the stenosis width, and the BG A survival exceeds the survival in BG O consistently. To point out the superior survival in BG A, Fig. 6(d) shows the relative increase of survival in BG A with respect to BG O. At d = 5 μm, the predominance of BG A is most obvious. This specific width matches the transition width $d^{\ast }$ for medium sized rosettes (see Fig. 5) and may be the crucial difference between BG O and A deciding not only about the fate of a single rosette but also the one of the patient. In extreme cases of almost no survival (smallest stenosis) and predominantly undamaged passage (largest stenosis), the difference between blood groups almost vanishes.

FIG. 6.

Relative total survival in BG A with respect to BG O. Top: survival rates for all rosette classes and widths of stenosis, and initial size distribution over rosette classes (a) in blood group O and (b) in blood group A. (c) Size distribution weighted sum of survival rates from (a) and (b) over all classes of rosettes for each width of stenosis. The error bars represent 95% confidence intervals. (d) Relative increase in survival in BG A with respect to BG O from Fig. 6(c). The error bars stand for the extreme values based on the confidence interval limits in Fig. 6(c).

DISCUSSION

While investigating the rosette response to the subjection to their spatial constraint in stenoses, we developed a customized software to analyze the statistics of the trajectories of rosettes in microchannels under flow. SURF enabled us to measure the blood group, aggregate size, and stenosis size-dependent behavior of rosettes passing constrictions.

We demonstrate important physical differences of rosettes in the different ABO blood groups critical for the outcome of severe disease, which support and extend previous in vitro observations to conditions representing in vivo settings.

Concentrating on one rosette class and one blood group, the rosette survival decreases comprehensibly with decreasing width of the stenosis (Fig. 5). On the other hand, with increasing size of the rosettes, the survival does not increase but even decreases (Figs. 3 and 4). Hence, a larger aggregate apparently seems to pass a stenosis more easily. Following the same lines as shown for the dependence of lifetimes of focal adhesion sites of adherent cells,^22,23 larger aggregates could show a higher survival rate because of their larger number of adhesion clusters. Within one cluster of bonds or within one attached cell, the connection or separation of the single bonds usually happens cooperatively.²³ While a small aggregate does not “survive” the loss of one red blood cell, a large aggregate still remains in the aggregate state. The possibility of rearrangement of cells within the aggregate becomes larger with the number of cells involved and thus increases the aggregate's flexibility. If the aggregate is so large that it temporarily fully crowds the stenosis, it self-facilitates its passage by slowing down the flow. The highest survival seems to comply with optimizing the balance of strength and flexibility.

The physical difference in terms of rosettes between blood groups O and A is not only their size distribution but also the binding strength between the RBCs. Our software SURF allows us to compare rosettes of the same size and thus uncover the binding strength specific differences between O and A. The combination of the superiority in blood group A in first, frequency of large aggregates, and second, higher binding strength, leads effectively to higher rosetting (Fig. 6) and presumably to more severe consequences in blood group A patients. Nevertheless, the rosette size distribution has a larger effect on total rosette survival than the blood group specific binding strength. A larger percentage of larger rosettes would even more dramatically enhance the effect. Unfortunately, to the best of our knowledge, the actual rosette size distribution in vivo has never been addressed in the literature up to now. Apart from that, it is not clear what happens to the rosettes after passage and breakup. We found very low change in rosetting size distribution during their passage of simple, straight channels with a constant cross section (unpublished data). For the present study, we thus developed the above stenosis design to apply varying and sufficiently large forces on the passaging rosettes to eventually break them and to actually observe the loss of cells. We chose to develop and apply a tracking algorithm to uncover events on the trajectories of individual rosettes rather than comparing size distributions before and after a constriction. On the basis of our experimental findings, especially from a physicist’s point of view, subsequent experiments should include a variation of the elongational flow to further elucidate the rosettes' resistivity. Whether aggregates reform after their breakup, however, is presently difficult to assess. However, due to the low hematocrit in our experiments, it is not very likely for cells to come close enough to again interact. A higher hematocrit, on the other hand, impedes distinction of aggregated and simply adjacent RBCs, which move side by side in laminar flow. In microscopy based experiments, we always have to rely on a trade-off between a high hematocrit and sufficient resolution. Here, fluid dynamical simulations of rosettes in channels with constrictions at high hematocrit certainly bear the potential to answer this exciting question.^24,25

Another thrilling question deals with the potential of rosettes to actually clog narrow capillaries. In the present study, we intentionally employed channels without a bypass to determine the rosette stability. However, in vivo, in most cases, there will be several vessels in parallel allowing for rosette induced clogging of the narrow ones. Larger flexibility or longer survival might in fact prolong the time of a rosette in the vascular circulation and hereby foster cytoadhesion and the parasite's survival in the patient. This hypothesis could be a highly interesting subject to extend our studies in the future.

This study revealed a crucial factor promoting the observed protection in BG O individuals against severe malaria compared to BG A. In this matter, this is the first study that investigates rosetting under physiological relevant conditions looking on the impact of the ABO blood groups.

METHODS

Sample preparation

We cultivated the P. falciparum laboratory strain S1.2²⁶ according to standard methods and synchronized it using 5% sorbitol.²⁶ Prior to experiments, we identified the stage of the parasite by staining of fresh culture with Acridine Orange and subsequent microscope analysis. We enriched infected red blood cells (iRBCs) around 32–38 h post invasion by magnetically activated cell sorting (Miltenyi Biotec), as described earlier²⁶ resulting in 70%–90% parasitemia. We resuspended the enriched iRBCs with uninfected RBCs in MCMS, malaria culture medium containing 10% filtered human serum, to reach a final parasitemia of 20% and a hematocrit of 1%. The added uninfected RBCs were of blood groups O and A for the measurements in the respective blood groups, while blood group O RBCs were used for cultivation of the parasite. Erythrocytes and sera from Swedish donors used for parasite cultures were collected from the Karolinska University Hospital blood bank (ethical permit number: 2009/668-31/3) as approved by the Regional Ethical Review Board in Stockholm, Sweden.

Microchannel design and measurement setup

The microchannel consisted of a polydimethylsiloxane (PDMS) single layer fabricated by standard soft lithography,²⁷ which was bonded on a glass slide by plasma activation. Generally, all channels were 7 mm long, 8 μm in depth, and 50 μm in width. The central part of interest comprised a single stenosis [Fig. 1(c)] in which the channel width was reduced from 50 μm to one of the five chosen values 3.5 μm, 5 μm, 7 μm, 11 μm, and 14.5 μm. Alternatively, we employed a cascaded sequence of four stenoses of decreasing width. Two different designs of cascaded channels were used, one was chosen such that the cells pass four constrictions starting with 14.5 μm down to 5 μm and a second one starting from 11 μm going to 3.5 μm. The camera field of vision captured only three of the four stenoses (see the example images in Fig. 2). The results in Fig. 3 show the combined results from both cascaded designs and measurements analyzing the first or the last three stenoses.

The setup as depicted in Fig. 1(c) consisted of the microchannel, a pipet tip serving as the cell suspension reservoir, and a syringe pump (Harvard PHD2000, Harvard Apparatus). A Hamilton Gastight Syringe (Hamilton Bonaduz AG) containing phosphate-buffered saline (PBS, pH = 7.4) was connected to the microchannel via a polyfluoroethylene (PTFE) tube. The pump was operated in reverse mode to provide a controlled flow by drawing the suspension from the reservoir through the microfluidic channel. We observed the cells using the 20× objective of an inverted microscope (Nikon Diaphot 300) equipped with a high speed video camera (FASTCAM Mini UX50 type 160K-M-16G, Photron). The videos were recorded with the software Photron Fastcam Viewer PFV from Photron at 2000 frames per second, 1280 × 120 pixel resolution, 1/32 000 s exposure resulting in a maximum total of 74 531 frames or 37 s in real time covering an area of 704 × 66 μm². For analysis, we developed the customized software SURF (see below).

SURF tracing

SURF (SUrvival of Rosettes in Flow) is a MATLAB© based tracking algorithm to follow and analyze rosettes along a microfluidic channel. Figure 2(a) shows examples of video frames where a rosette is eventually disrupted in a stenosis. The first step is to binarize the images to identify moving objects. The objects, either cells or cell aggregates, are darker than the background and can be localized by contour plots using a distinct gray value as threshold to divide each frame in black background pixels and white areas at the locations of the cells. More precisely, the background is calculated as the median of the first 1000 frames and then being subtracted from each frame. The contour plot is obtained after smoothing the images and provides closed lines around objects that are filled with white pixels. For each frame, the objects' area, position, and the parameters of the surrounding ellipse are documented in a tabular form. A histogram of the areas of those objects is used to determine the area of a single red blood cell A_RBC as the most frequent size. Objects larger than 1.5 A_RBC are considered and finally labeled as “rosettes” according to the definition of an aggregate as a rosette, containing at least one iRBC and two RBCs.

To initiate the tracing algorithm, the entrance of the channel or, more precisely, a window from 50 to 75 pixels from the left border of the frame is checked frame by frame for the presence of a rosette to ensure that the rosette is not partially out of the camera's field of view. If a rosette is present, its trace is initiated and the following frame is checked successively for the nearest rosette in the downstream direction first. If the rosette remains intact, its center will certainly move in the direction of the flow from frame to frame. However, if it changes its shape drastically or loses cells in the front, the center of the remaining part might “jump” upstream. To take account for that, and to make sure to find and further follow the main rosette and not a smaller offspring, the search for the matching rosette on the following frame is enlarged upstream by the current rosette's diameter if there is no rosette to be found close downstream that changes its area by less than 50%. The detected traces end if there is no matching remaining part of the rosette found, which means that the rosette was totally disrupted or exited the camera's field of vision.

The basic results of such examinations consist of the rosettes’ size, shape, and position or velocity along the trace. More elaborate is the recognition of events like ruptures and total disruption [Fig. 2(b)]. To distinguish between a change in area by losing cells from a change through mere deformation, the objects surrounding a rosette in an area as large as the full length of the stenosis is documented. An event is only considered a true rupture event whenever a rosette's area decreases by more than 0.65 A_RBC and additional surrounding objects appear at the same time. However, false positives can still occur due to cells flowing nearby without being actually attached. To eliminate such false findings, we define “connect events” analogously to “rupture events” at an increase in area by more than 0.65 A_RBC and vanishing surrounding objects. Looking for patterns of events along the trace, we can pinpoint occurring “pass-by events” (connect event followed by a rupture event) or “reconnections” (rupture event followed by a connect event) and sort those out to identify “real rupture events.”

SUPPLEMENTARY MATERIAL

See the supplementary material for the data used in Figs. 3–5 for “survival” and “undamaged” rate of rosettes in the cascaded channel (Table S1) and after passing a single stenosis (Table S2). For both blood groups, each stenosis and rosette classes 2–6, the raw results, the count numbers of tracked rosettes and the 90% confidence intervals are listed.