Magnetization Transfer in Magnetic Resonance Fingerprinting

Abstract

Purpose:

To study the effects of magnetization transfer (MT, in which a semi-solid spin pool interacts with the free pool), in the context of magnetic resonance fingerprinting (MRF).

Methods:

Simulations and phantom experiments were performed to study the impact of MT on the MRF signal and its potential influence on T₁ and T₂ estimation. Subsequently, an MRF sequence implementing off-resonance MT pulses and a dictionary with an MT dimension, generated by incorporating a two-pool model, were used to estimate the fractional pool size in addition to the B₁⁺, T₁, and T₂ values. The proposed method was evaluated in the human brain.

Results:

Simulations and phantom experiments showed that an MRF signal obtained from a cross-linked bovine serum sample is influenced by MT. Using a dictionary based on an MT model, a better match between simulations and acquired MR signals can be obtained (NRMSE 1.3% versus 4.7%). Adding off-resonance MT pulses can improve the differentiation of MT from T₁ and T₂. In-vivo results showed that MT affects the MRF signals from white matter (fractional pool-size ~16%) and gray matter (fractional pool-size ~10%). Furthermore, longer T1 (~1060 ms versus ~860 ms) and T2 values (~47 ms versus ~35 ms) can be observed in white matter if MT is accounted for.

Conclusion:

Our experiments demonstrated a potential influence of MT on the quantification of T₁ and T₂ with MRF. A model that encompasses MT effects can improve the accuracy of estimated relaxation parameters and allows quantification of the fractional pool size.

1. Introduction

Quantitative magnetic resonance (MR) measurements strive to estimate tissue-specific parameters with minimal experimental bias. Until recently, such methods have mostly focused on relatively simple spin evolutions for which analytic signal solutions can be derived. Early techniques to measure the relaxation time, for example, relied on a series of inversion-recovery measurements to estimate the longitudinal relaxation time (T₁)^1,2 and on spin-echo measurements to estimate the transverse relaxation time (T₂)^3,4. Although such measurements can provide accurate and reliable results, they are generally too time-consuming to be used in routine clinical examinations.

For years, the search for faster methods has strived to achieve a balance between acquisition speed, model simplicity, accuracy, and precision^5–7. One of the most widely used approaches in recent years is the combination of DESPOT1 and DESPOT2 techniques⁸, integrating four (or more) fast measurements to quantify both T₁ and T₂. Although these techniques are fast and SNR efficient, they are also sensitive to experimental imperfections^9,10 and magnetization transfer (MT) effects¹¹.

The effect of MT on T₁ and T₂ quantification is especially strong in the brain, where it is highly correlated with myelin content and axonal count¹². Therefore, MT effects can also be repurposed as a biomarker for neurological diseases in which the myelination of the brain is altered, e.g. in multiple sclerosis¹³. However, MT effects cannot be described by the basic Bloch equations, which are used for the signal description in most rapid quantitative MRI techniques. When the signal evolutions of these MRI techniques are simulated using comprehensive models, a dependency of the model on additional experimental factors, such as properties of the RF pulses, becomes apparent. This dependency can influence the T₁ or T₂ estimation accuracy¹⁴.

Recently, a new framework for quantitative MRI – magnetic resonance fingerprinting (MRF) – was proposed¹⁵. MRF moves away from comparatively simple steady state sequences and from straightforward analytic solutions. Instead, it combines more diverse sequence patterns, which produce transient states, with a numerical signal model that describes the corresponding spin dynamics. The additional degrees of freedom available with MRF enable faster imaging and provide the opportunity to deliberately encode multiple tissue properties and experimental conditions within a single measurement. The role of MT effects on MRF, however, has not been fully investigated yet^14,16.

In this work, we explore the effect of MT on the quantification of T₁ and T₂ values based on MRF measurements. Specifically, a two-pool model is compared to a conventional single-pool model in phantom samples that are known to exhibit MT effects. The possibility to use this two-pool model in MRF for quantifying the fractional pool size of the semi-solid pool is studied in vivo.

2. Methods

All numerical simulations, data analysis, and visualizations were performed using MATLAB 8.5 (The MathWorks Inc., Natick, MA, USA).

2.1. Sequence Design

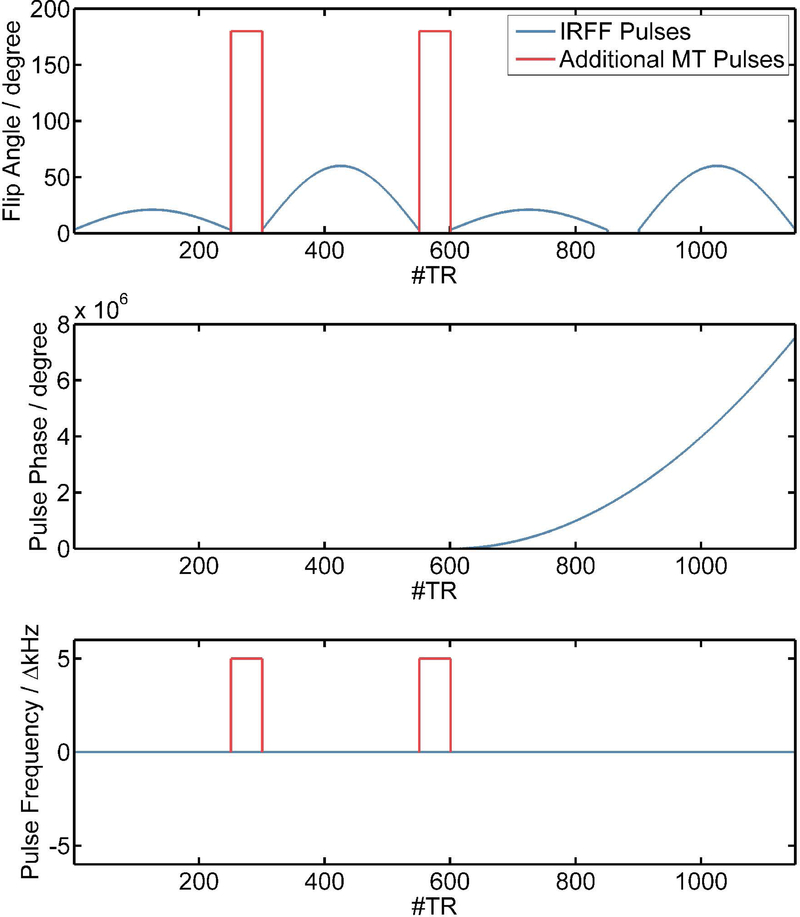
To study the impact of MT, we used an MRF sequence design proposed by Cloos et al.¹⁷ as a starting point. This baseline sequence will be referred to as “Inversion Recovery FISP FLASH (IRFF)”. The IRFF sequence (see also Figure 1) consists of an adiabatic inversion pulse followed by four segments of RF pulse trains with flip angles up to 60° played out with constant repetition time TR of 7.5 ms. The first and second segments are steady state free precession RF trains (FISP-type). In the third and last segments, the transverse magnetization is spoiled using a quadratically increasing RF phase (FLASH-type, 50° phase increment). Gaps between the segments with a duration of 50 x TR allow spin ensembles to relax. In this work, the first and second gaps were used to optionally play out 50 off resonant pulses (each with 7ms duration, 180° flip angle at 5kHz off-resonance frequency with Gaussian waveform). The hypothesis is that the additional pulses will only have an impact on the measured magnetization in the presence of a semi-solid pool and, thus, may improve the encoding of MT effects within the fingerprint. In the following, we will refer to the sequence without MT pulses as IRFF and to the sequence with MT pulses as IRFF-MT.

Figure 1:

Sequence design used in this study with a train of flip angles (top) for each TR according to the IRFF sequence (blue) and optional MT pulses for the IRFF-MT design (red). The RF pulse train is separated into four segments (2x FLASH and 2x FISP) with gaps that allow for relaxation or to provide the space to play out the MT pulses. The phase of the pulses is shown in the middle with a quadratically increasing pulse phase for the last two FLASH segments. The off-resonance frequencies for the pulses are shown on the bottom.

2.2. Image Reconstruction

Quantitative maps were reconstructed from the data using the reconstruction algorithm described by Cloos et al.¹⁷. However, a different Extended Phase Graph^18,19 algorithm was employed. Specifically, the EPG-X framework¹⁴ was used to simulate fingerprints based on a single-pool or a two-pool model.

For the single-pool model, the simplest EPG-X model was used to simulate the MR signal based on the IRFF sequence design and a range of T₁, T₂, and B₁⁺ values. To this end, the complex slice profile was discretized into 16 bins, and the signal was simulated for each bin. Subsequently, all fingerprints across the slice profile were summed, which yields the final fingerprint for the combination of quantitative values.

In order to account for MT effects, the two-pool model of the EPG-X framework was used. This model requires additional information about the deposited RF pulse power. To this end, the pulse power of each individual pulse (including the initial inversion pulse) in the IRFF sequence was calculated using the pulse duration, waveform, and flip angle (depending on B₁⁺). Besides T₁, T₂, and B₁⁺, the simulation with a two-pool model requires additional tissue parameters. Specifically, the relaxation parameters of the semi-solid pool T_1,ss, T_2,ss, the fractional semi-solid pool size F, and the exchange rate of magnetization from the free to the semi-solid pool k are required. This would result in four additional dimensions for the dictionary in order to address MT effects, which would yield large dictionaries and impractical reconstruction times. Furthermore, there may not be enough MT information encoded within the fingerprints to resolve these four additional parameters accurately without confounds. Therefore, several assumptions were made to model MT with only one additional dimension in the dictionary. First, it was assumed that the longitudinal relaxation times of the free and semi-solid pool are identical (T_1,ss = T₁)²⁰. Second, the transverse relaxation of the semi-solid pool, which only affects the shape of the frequency spectrum, was set to a fixed value according to literature²⁰ (T_2,ss = 12 μs). Third, the magnetization exchange rate was fixed to a value that is expected in white matter (WM) (k = 4.3 s⁻¹)²⁰. By introducing these assumptions, the fractional pool size F remains the only parameter to model MT. The systematic bias that is introduced by fixing the above model parameters was studied in more detail in Supporting Information Figure S1.

Using the models described above, three dictionaries were created and used throughout this paper:

1. Single-Pool IRRF Dictionary: 190,527 entries (70 x T₁ ranging from 0.1 – 4.3 s, 70 x T₂ ranging from 15 – 430 ms and 41 x nominal B₁⁺ ranging from 0.7 – 1.3, corresponding to 2.9 GB of memory; entries with T₂ > T₁ were excluded).

2. Two-Pool IRRF Dictionary: 3,048,432 entries (46.8 GB of memory) resulting from an additional 16 values in the F dimension (ranging from 0 – 30%, logarithmically spaced).

3. Two-Pool IRRF-MT Dictionary: This dictionary has the same number of entries as the two-pool IRRF dictionary above, but accounts for the off-resonance pulses in the IRRF-MT sequence.

2.3. In Vitro Experiments

All in vitro experiments were performed using a whole-body 3-Tesla MRI system (MAGNETOM Prisma, Siemens Healthcare, Erlangen, Germany). A QED (Quality Electrodynamics, Mayville, OH, USA) 15-channel TX/RX knee coil was used for excitation and reception.

Both prototype sequence configurations, IRFF and IRFF-MT, were acquired without phase-encoding gradients to directly sample the MRF signal (i.e., the fingerprints) from two phantoms. The first phantom was a tube filled with water that was doped with Manganese (II) Chloride Tetrahydrate (Cl₂Mn₄H₂0, Sigma-Aldrich, St Louis, MO, USA) to serve as a sample without MT. For the second phantom, cross-linked bovine serum albumin (xl-BSA) with a final concentration of 20% (w/w) was prepared using phosphate-buffered saline and Glutaraldehyde²¹ to serve as a sample that exhibits MT. The hypothesis is that fingerprints from IRFF and IRFF-MT should be identical in both water and xl-BSA samples if there were no MT effect. Conversely, if the fingerprints are affected by MT, the signal should decrease in the second and third segments due to the MT pulses employed.

MR signals were plotted for comparison between both samples with different sequence types, respectively. Furthermore, all three dictionaries were used to match the signals acquired from both water and xl-BSA samples. The measured signals and the corresponding best match were plotted for each dictionary (all normalized by the l₂ norm), and the corresponding quantitative parameters (T₁, T₂, B₁⁺, F) were compared. Furthermore, the normalized root-mean-square error (NRMSE) between the measured and best matched simulated signal was calculated as follows:

$$NRMSE=\frac{{\Vert s-f\Vert }_2}{{\Vert s\Vert }_2},$$ [1]

where s denotes a vector of measured signal intensities and f a vector of simulated signal intensities.

To test various ranges of T1, T2, and MT values, an additional phantom experiment was performed. Four tubes with different concentrations of xl-BSA (5%, 10%, 15%, 20%) and three tubes filled with doped water (different concentrations of Manganese (II) Chloride Tetrahydrate) were placed in a cylinder filled with lightly doped water. The two MRF sequence configurations, IRFF and IRFF-MT, were used to acquire images of a 2D slice in the middle of the phantom. Both the single-pool and two-pool models were used to obtain quantitative maps from the MRF acquisitions. Furthermore, an inversion-recovery spin-echo (IR-SE) sequence was used to acquire nine images at different inversion times (TI). A mono-exponential recovery curve was fit to these images to obtain reference T1 values. Additionally, eleven images at different echo times (TE) from a spin-echo sequence were used in a mono-exponential fit to obtain reference T2 values. Finally, reference MT values were obtained from an MTR acquisition (two FLASH acquisitions). All sequence parameters are summarized in Table 1.

Table 1:

Sequence parameters for all sequences that were used in this work.

Parameter	IRRF/IRRF-MT	SE	IR-SE	MP2RAGE	CPMG	B1 FLASH	MTR FLASH	MPRAGE
Resolution	1×1×4 mm3	1×1×4 mm3	1×1×4 mm3	1×1×4 mm3	1×1×4 mm3	1×1×4 mm3	1×1×4 mm3	1×1×1.2 mm3
Matrix Size	256×256×1	256×256×1	256×256×1	256×256×32	256×256×1	256×256×1	256×256×1	256×256×176
TR	7.5 ms	8 s	8 s	5 s	3 s	2 s	100 ms	2.3 s
TE	2.8 ms	12, 24, …, 278 ms	12 ms	3.38 ms	10, 20, …, 320ms	2.16 ms	10 ms	2.9 ms
TI	-	-	25, 50, …, 3200 ms	700/2500 ms	-	-	-	900 ms
TA	3:10 min	11× 25:28 min	9× 25:28 min	3:02 min	12:53 min	4 s	54 s (2 × 27s)	5:12 min

The quantitative values obtained with MRF were compared to the reference values in a bar plot. To validate each model, including the mono-exponential decay/recovery of the reference methods, the NRMSE was calculated in each voxel according to Eq. 1.

2.4. In Vivo Experiments

All in vivo experiments were performed using a whole-body 3-Tesla MRI system (MAGNETOM Skyra, Siemens Healthcare, Erlangen, Germany). The built-in birdcage body coil was used for excitation, and a commercially available 64-channel head/neck coil was used for reception.

The IRRF and IRFF-MT prototype sequences were used to acquire datasets from five healthy volunteers (two female, age range 21–33 years) after written informed consent was obtained prior to the examination. A single axial slice through the brain was imaged using a matrix size of 256×256, 256 mm FOV, 4 mm slice thickness, TR of 7.5 ms, and 10 radial spokes per time point of the fingerprint series, resulting in TA = 3:10 min scan time for each dataset. The study was approved by our institutional review board.

All datasets were reconstructed using the three dictionaries as described above. The IRFF dataset was reconstructed with both the single-pool and the two-pool model, whereas the IRFF-MT dataset was reconstructed with the two-pool model only.

For comparison, a reference T₁ map was acquired using an MP2RAGE sequence, and reference T₂ values were acquired using a Carr-Purcell-Meiboom-Gill (CPMG)⁴ sequence and a dictionary matching that accounts for stimulated echoes²². Reference MT values were obtained from an MTR acquisition (two FLASH acquisitions), and reference B₁⁺ values were obtained with two saturation-prepared FLASH acquisitions. It should be noted that these techniques are not gold-standard methods since they are also affected by model assumptions, such as considering a single compartment with no MT effects, and no diffusion effects. However, a comparison to existing methods should help to put the results obtained here into context.

In order to compare the quantitative values of different brain regions, a 3D MPRAGE sequence was used as input for tissue segmentation with the MorphoBox prototype²³. Detailed sequence parameters are provided in Table 1.

After the acquisition, the maps obtained from the IRFF/IRFF-MT sequences and different dictionaries as well as from the reference sequences were compared. To this end, the MPRAGE image was registered to the images of all sequences, and the same transformation was applied to the label map of the MorphoBox segmentation to have the same segmentation in the native spaces of all quantitative maps. The median values of T₁, T₂, and F/MTR within eight bilateral regions (frontal WM, parietal WM, frontal GM, parietal GM, Corpus Callosum, Thalamus, Caudate, Putamen) were extracted for each subject. Here, the median was used instead of the mean because the relaxation values typically do not show a normal distribution within the ROI (see also Supporting Information Figure S2). The mean and standard deviation across subjects from the different medians of the regions were compared between the different dictionaries and reference methods.

Since MTR and F are different measures, their absolute values cannot be directly compared. Instead, the Pearson correlation between F and MTR was calculated across the median values obtained from the ROIs.

Finally, the values that were obtained in vivo were compared to a previous study that reported T₁, T₂, and MT properties at 3T²⁴.

3. Results

3.1. Simulated Fingerprints and Dictionaries

The creation of the dictionaries took approximately 10 h for the single-pool and 7 days for the two-pool model using 24 cores on an Intel® Xeon® Gold 6126 CPU at 2.60 GHz. The dictionary matching required approximately 5:49 min for the single-pool and 1 h 42 min for the two-pool model using a single CPU core (same specification as above).

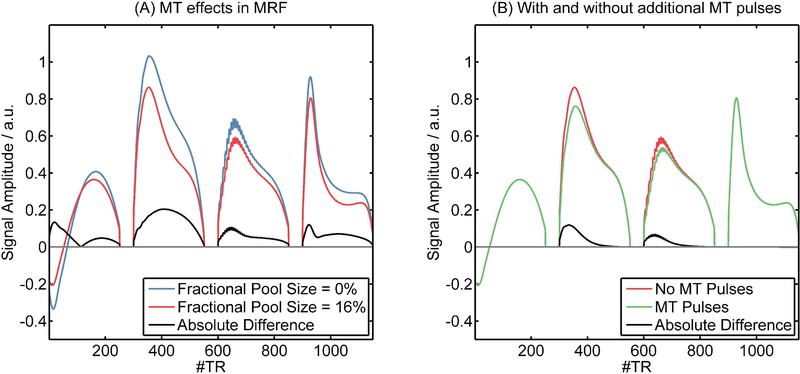
Example dictionary entries are shown in Figure 2. Figure 2a demonstrates the impact of MT on the fingerprint by comparing dictionary entries with the same relaxation parameters but different fractional pool size (F = 0 % versus F = 10 %). The largest differences were observed at the beginning after the high-power adiabatic inversion pulse and in the second and last segments where higher flip angles were used. Figure 2b compares dictionary entries from the IRFF and IRFF-MT sequence designs at a fractional pool size of 16 % (an expected value in WM). The first and last segments were almost identical. However, in the second and third segments, lower signal intensity was observed in the IRFF-MT sequence due to the MT effect of the semi-solid pool, which is amplified by the off-resonant MT pulses during the gaps between the segments.

Figure 2:

(A) Example dictionary entries that show the difference in fingerprints due to MT (no MT versus a fractional pool size of 16%) for a typical WM voxel (T₁ = 800 ms, T₂ = 60 ms, B₁⁺ = 1) without MT pulses. (B) Differences in fingerprints (T₁ = 800 ms, T₂ = 60 ms, B₁⁺ = 1) that experience MT (fractional pool size = 16 %) due to adding off-resonance MT pulses in the first and second gaps in the sequence design.

3.2. In Vitro Experiments

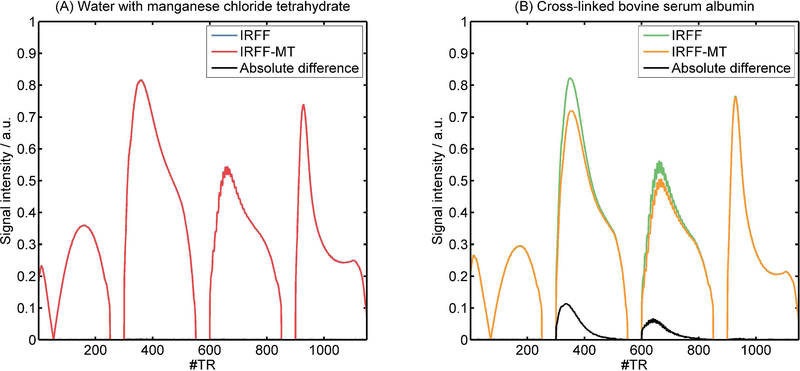
The MR signals from doped water and xl-BSA that were acquired with IRFF and IRFF-MT are shown in Figure 3. In the water sample, where no MT effects are expected, the additional off-resonance MT pulses did not show an effect. The measured signals from IRFF and IRFF-MT were almost identical. In contrast, in the xl-BSA sample, the signal in the second and third segments was lower for the IRFF-MT sequence compared to the IRFF sequence, similar to the comparison of dictionary entries in Figure 2b.

Figure 3:

Four different acquired MR signals (fingerprints) from the water (left, no MT effect) and xl-BSA (right, MT effect) samples using the conventional fingerprinting sequence design (IRFF) and one with off resonant MT pulses in the gaps of the sequence (IRFF-MT).

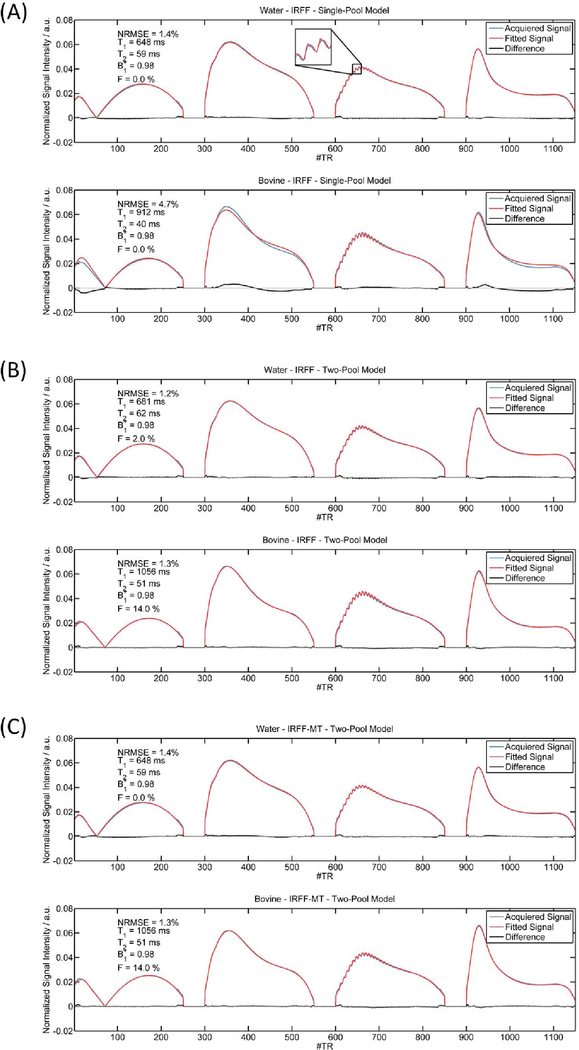
Figure 4a shows fingerprints that were acquired with the IRFF sequence and their corresponding best matches from the single-pool dictionary. In the water sample, the best matching dictionary entry corresponded well to the acquired data (NMRSE = 1.4 %), and even the oscillations in the third segment agreed well. However, in the xl-BSA sample, the best matching single-pool dictionary entry showed large differences at the beginning (after the inversion pulse), and in the segments with larger flip angles (second and fourth segments), thus, resulted in an overall larger NRMSE of 4.7 %. A much lower NRMSE of 1.3 % can be achieved if a two-pool model is matched to the xl-BSA sample (Figure 4b, bottom). Notably, in comparison to the single-pool model, the two-pool model resulted in longer T₁ (1056 ms versus 912 ms) and T₂ (51 ms versus 40 ms) estimates. The best matching two-pool entry for the water sample showed an even lower NRMSE than the single-pool model (1.2 % versus 1.4%). However, also a fractional pool size F = 2 % was observed. This means that a better matching dictionary entry was found with MT than without MT. Assuming that there should be no MT in water, this could indicate that MT effects cannot be well separated from relaxation effects in the signal of the IRFF sequence. Figure 4c shows fingerprints and best matching signals of the two-pool model from the IRFF-MT sequence. After the introduction of the off-resonance pulses in the sequence design, the model describes the fingerprint of the xl-BSA sample well and resulted in the same sample properties (T₁ = 1056 ms, T₂ = 51 ms, B₁⁺ = 0.98, F = 14 %). In the water sample, however, the introduction of the MT pulses resulted in a better differentiation between relaxation and MT effects, yielding a 0 % fractional pool size and the same sample properties as for the single-pool model (T₁ = 648 ms, T₂ = 29 ms, B₁⁺ = 0.98).

Figure 4:

Measured MR signals from doped water (no MT effect) and xl-BSA (MT effect) and corresponding best matching dictionary entries from the different dictionaries: (A) single-pool model, (B) two-pool model, (C) two-pool model with MT pulses (IRFF-MT).

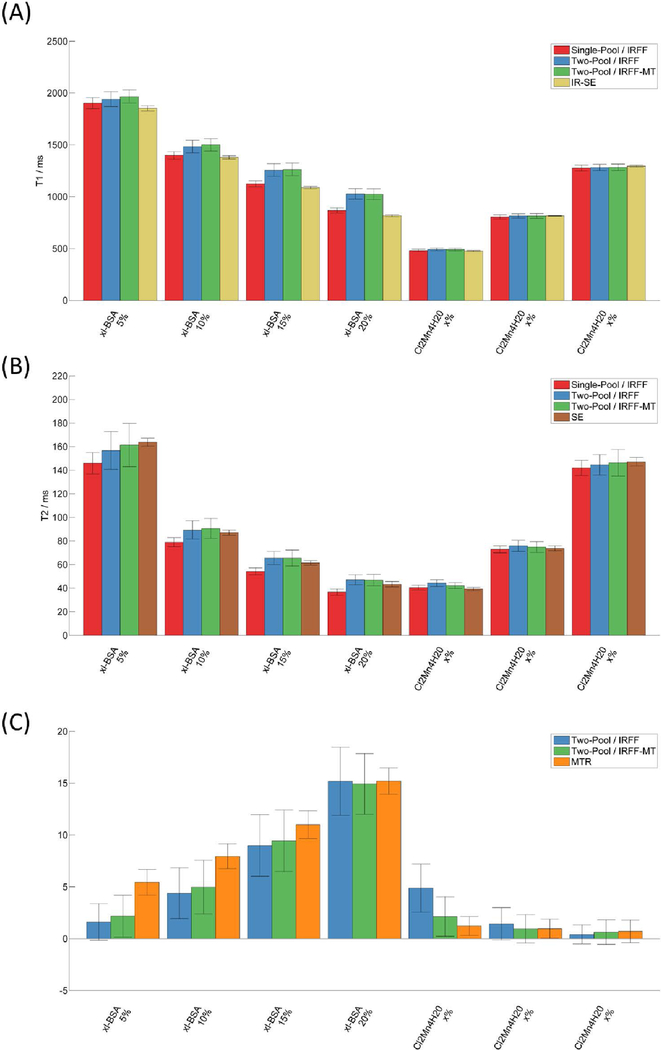
The bar plots in Figure 5 show quantitative values from the imaging experiment using the phantom with multiple tubes of different T1, T2, and MT. The full maps can be found in Supporting Information Figure 3. NRMSE maps which represent the goodness of fit for each approach are shown in Figure 6.

Figure 5:

Mean quantitative values for T₁ (A), T₂ (B), and MT (C) obtained within the compartments of the phantom experiment using all MRF sequence types, models, and reference methods (Spin Echo SE, Inversion Recovery Spin Echo IR-SE, Magnetization Transfer Ratio MTR). Error bars indicate the standard deviation.

Figure 6:

Maps of the Normalized Root Mean Squared Error (NRMSE) of the models fitted to the respective data. The different compartments correspond to (A) xl-BSA 5%, (B) xl-BSA 10%, (C) xl-BSA 15%, (D) xl-BSA 20%, (E) Water Tube 1, (F) Water Tube 2, (G) Water Tube 3.

The T1 values within the water tubes (Figure 5A) appeared coherent across the different MRF acquisitions. However, in the tubes with MT effect, there were discrepancies between methods. The two-pool models resulted in higher T1 values than the single-pool model, and the single-pool model agreed best with the reference values from the IR-SE sequence. This may lead to the conclusion that the single-pool model produces the most reliable T1 measure. However, when comparing the NRMSE maps, the NRMSE increases with higher xl-BSA concentrations for both the reference IR-SE method (up to ~9%) and the single-pool model (up to ~7%), whereas the NRMSE remains low (<4% within the tubes) and is more uniform across all samples when using the two-pool model. This suggests that even the IR-SE method may be biased due to MT.

With regards to T2 values (Figure 5B), all values appear to agree well with the SE reference method except for the single-pool model in tubes with xl-BSA. The T2 values of the single-pool model are increasingly underestimated with higher concentration of xl-BSA, which is also reflected in the poor NRMSE of the respective tubes. The NRMSE of the reference T2 values obtained with a SE sequence is low in all tubes (<1%), indicating a potentially more reliable reference than the T1 values obtained with the IR-SE.

The fractional pool sizes obtained with the two-pool models were higher with increasing concentration of xl-BSA, similar to the MTR value. Erroneously, the two models also found low fractional pool sizes (<5%) in the tubes with water, especially in the tube with the lowest T1 value (~500 ms). This error was smaller (~2%) when the additional MT pulses of the IRFF-MT sequence were employed. Notably, the three values associated with MT -- fractional pool size, MTR concentration, and xl-BSA concentration -- are three different measures of the same effect. Therefore, the general trend should be compared instead of the absolute values. The NRMSE maps of the two-pool MRF methods show an approximately residual error throughout the phantom, which may be attributed to a low effective SNR and pseudo-noise from incoherent undersampling artifacts. However, when a single-pool model is used, the individual xl-BSA tubes standout in the NRMSE maps, which may indicate residual effects that are not incorporated in the model.

3.3. In Vivo Experiments

Example quantitative maps obtained from one volunteer using the three different dictionaries are shown in Figure 5. Regardless of the applied dictionary, all PD maps were affected by receive-field inhomogeneity and, unlike other parameter maps, should not be considered fully quantitative. Nevertheless, contrast between white and gray matter was observed in the PD maps reconstructed from the single-pool model, with lower PD in gray matter in comparison to white matter. Unexpectedly, all PD maps showed lower values for CSF in comparison to white and gray matter. Furthermore, in both T₁ and T₂ maps, lower relaxation values were observed when a single-pool model was used. Since this effect is stronger in white matter, the contrast between white and gray matter was reduced when using a two-pool model. Of note, the increase in T₁ and T₂ when accounting for MT was observed in vitro as well (see Figure 4a–b). Qualitatively, the fractional pool size of the semi-solid pool (F) corresponds to a contrast with the highest fractional pool size in white matter, lower fractional pool size in gray matter, and no MT effect in CSF. When comparing IRFF versus IRFF-MT for the two-pool model, the latter, which employs MT pulses, resulted in lower fractional pool size (~15% versus ~20%). This may be linked to an overestimation of F if MT effects are not sufficiently encoded in the IRFF fingerprint, as also demonstrated in vitro (see Figure 4b–c). The obtained B₁⁺ maps showed high flip angles in the center of the FOV with a smooth transition to lower flip angles in the periphery of the FOV. The B₁⁺ field maps obtained from the different dictionaries appeared similar. Of note, anatomical structures are still visible in the B₁⁺ map in all MRF reconstructions. First, low B₁⁺ values are observed in vessels because flow is not modeled in the dictionaries. Second, B₁⁺ values appear slightly lower in CSF. Besides the high T₁ and T₂, the model fails in CSF, presumably, because diffusion is not modeled.

Quantitative values obtained from all subjects using the three different dictionaries and reference sequences are shown in Table 2. In WM, the single-pool model estimated similar T₁ values compared to the reference MP2RAGE sequence (ranging from 759 – 860 ms). In contrast, both two-pool models yielded higher T₁ values (ranging from 996 – 1087 ms). T₁ values of GM were between 1334 ms and 1377 ms for the single-pool model and the MP2RAGE. Again, higher T₁ values were found for the two-pool models (ranging from 1515 ms - 1530 ms).

Table 2:

Quantitative values (mean ± standard deviation) across subjects obtained using the different dictionaries and MRF sequences together with reference values in various regions of interest. Of note, some standard deviations are zero because the same dictionary entry was found for each subject.

	T1 / ms				T2 / ms				F or MTR / %
	Single Pool IRFF	Two-Pool IRFF	Two-Pool IRFF-MT	MP2RAGE	Single Pool IRFF	Two-Pool IRFF	Two-Pool IRFF-MT	CPMG	Two-Pool IRFF	Two-Pool IRFF-MT	MTR
White Matter
Frontal	852±22	1087±28	1066±23	827±16	35.1±0.9	47.0±1.3	46.5±1.0	74.1±1.8	17.6±0.9	16.0±0.0	23.8±0.3
Parietal	860±18	1077±28	1056±0	820±6	37.2±1.0	48.9±2.0	48.9±1.1	80.4±2.0	17.2±1.1	16.0±0.0	25.9±0.2
Corpus Callosum	803±21	1035±27	996±21	759±11	34.1±0.7	45.2±1.2	45.2±1.2	77.6±3.2	19.2±1.1	17.2±1.1	26.1±0.5
Gray Matter
Frontal	1334±28	1530±40	1515±40	1377±23	47.9±2.0	57.1±1.5	57.7±1.5	84.8±2.1	10.0±0.0	10.0±0.0	18.8±0.3
Parietal	1334±28	1530±40	1515±40	1334±32	47.5±2.1	57.7±2.6	57.1±1.5	82.6±0.0	10.0±0.0	9.6±0.9	20.9±0.6
Deep Gray Matter
Thalamus	1250±109	1445±94	1421±149	1059±57	40.6±2.3	50.6±2.2	51.4±3.3	87.9±13.1	9.2±1.8	10.0±0.0	23.0±1.2
Caudate	1222±0	1388±36	1347±0	1208±33	44.3±1.8	53.4±1.8	52.8±1.1	72.8±2.7	10.0±0.0	8.4±0.9	20.4±1.0
Putamen	936±59	1104±61	1088±60	938±68	38.7±1.0	49.1±2.0	48.7±2.1	75.0±5.6	14.4±0.9	13.2±1.1	23.3±1.3

For T₂ values, the single-pool model provided the lowest values (ranging 34.1 ms – 47.9 ms), which increased once MT was accounted for (ranging from 45.2 – 57.7 ms). The T₂ values obtained with the CPMG sequence were always higher (ranging from 74.1 – 87.9 ms).

The measured fractional pool size in WM was always lower when MT pulses were employed in the sequence (17% for IRFF and 16% for IRFF-MT). The fractional pool size was lower in gray matter (~10%). The MTR, which is the ratio between two images, with and without MT pulses, was higher than the estimated fractional pool size. However, the fractional pool size correlated well with MTR, with slightly better Pearson correlation for IRFF-MT (0.84 and 0.87 for IRFF and IRFF-MT respectively).

B1+ values were not listed in Table 2 since a brain-region-wise analysis of B1+ values is not particularly meaningful (given that B1+ represents a system parameter rather than a tissue property per se). Instead, a comparison of B1+ histograms can be found in Supporting Information Figure S4.

A standard deviation of zero was found for some values of the approaches using dictionary fitting (e.g., T₁ values in the parietal WM for the IRFFT-MT two-pool model). This does not mean that the values were perfectly reproducible across subjects, but it indicates that all values were within the same bin of the dictionary. In the example of the parietal WM, the next lower/higher T₁ values were approximately 50 ms away.

Certain discrepancies can be found when comparing the in-vivo values obtained in this study with reference literature²⁴. In the WM, our approach yielded comparable T1 values (1087±28 ms vs. 1084±45), lower T2 values (46.5±1 ms vs. 69±3 ms), and higher fractional pool size (16% vs. 13.9±2.8%). In GM, a different trend can be observed with lower T1 values (1515±40 ms vs. 1820±114 ms), lower T2 values (57±1.5 ms vs. 95±8), and higher fractional pool size (10% vs. 5±0.5%).

4. Discussion

Our results provide evidence of the possible influence of MT when using MRF to quantify T₁ and T₂ values in the brain. Based on these results, we propose using a two-pool model to make the estimation of relaxation parameters less susceptible to eventual MT effects and attempt to quantify the fractional pool size.

Simulations showed that the fingerprinting sequence used in this study showed the largest differences between a single-pool and a two-pool model at the beginning of the sequence and at timepoints with large flip angles. We speculate that these larger differences originate from the increased saturation of the semi-solid pool since larger flip angles deposit more pulse power. The differences at the beginning of the sequence can be explained by a large saturation of the semi-solid pool by the initial high-power inversion pulse. This MT effect caused by the inversion pulse was also observed by Malik et al.¹⁴.

When using a two-pool model, a better match between measured and simulated fingerprints can be achieved, as demonstrated for in vitro MR signals. However, without modification of the sequence design, MT effects cannot be fully separated from relaxation effects in the presence of undersampling artifacts and noise. We included off-resonance MT pulses to improve the encoding of MT in the fingerprints, which resulted in an overall better match. Of note, the match for signals without MT is still improved in the presence of MT pulses since it is less likely that relaxation effects can be mistaken for MT effects. The two-pool model used in this study was simplified by fixing two of the model parameters to literature values. It was assumed that brain tissue does not have more than two pools, that it involves no inhomogeneous MT²⁵ and it is well represented by a single compartment^26,27. Moreover, physiological effects, such as diffusion and perfusion, were neglected. The proposed model is, thus, still an approximation of the actual microstructural and biochemical environment. These assumptions may also explain the discrepancies with literature. Therefore, the resulting quantitative fractional pool sizes should be interpreted with caution. Ideally, the simulation of the fingerprints should use a complete model of the tissue microstructure. However, such a model might require a large number of dimensions for the dictionary, which could reduce the practicality of fingerprinting and impede routine clinical use until or unless new approaches to dictionary matching are found. Apart from the computation time needed to calculate large dictionaries, the matching robustness would likely suffer because subtle microstructural effects may be poorly encoded in the fingerprint. For example, although MT could be encoded in the fingerprint by including MT pulses in the sequence, the effect on the fingerprint was small, which resulted in unstable matching, as shown by the relatively noisy F maps.

In a wider context, one open research question is, therefore, how much detail is required to model tissue microstructure and how well these effects can be encoded within a fingerprint. Besides employing MT off-resonance pulses, there may be other acquisition techniques that will improve the encoding of MT. In an early stage of this work, we attempted to encode MT by varying the pulse duration¹⁶. However, the signal behavior was rather difficult to model, presumably due to relaxation during the RF pulse. For instance, the fingerprints changed even in the water sample when the pulse duration was varied (see Supporting Information Figure S3). Nevertheless, other studies have presented different approaches to encode off-resonance effects, e.g. by measuring different timepoints after an off-resonance preparation pulse²⁸, randomly varying the pulse power of the used MT pulses²⁹, or more completely varying the off-resonance frequency, saturation power, and repetition time of a MT pulse preparation³⁰. Therefore, the sequence design proposed here may be further improved or changed to better encode MT while avoiding SAR limitations.

Alternatively, one could also attempt to minimize MT bias effects by desensitizing the sequence to MT. For example, a longer TR would allow the semi-solid pool to recover more longitudinal magnetization between excitation pulses. However, this would lead to less efficient data acquisition. Longer pulse durations with a narrower saturation profile in the frequency domain could also be considered to minimize the effect on the semi-solid pool. However, longer pulse duration would also require longer TR, leading again to a less efficient data acquisition. The sequence design, i.e., flip angles and spoilers, has an impact on the MT effect as well. Here, the experiments used the IRFF sequence design. Other sequence designs may be more or less sensitive to MT and may result in a different bias in terms of the effect strength and direction (overestimation vs. underestimation). For example, the MT effect may be negligible in sequence designs that omit the adiabatic preparation and only employ small flip angles. Therefore, the sensitivity of other sequence designs and their potential to sufficiently mitigate or encode MT should be further investigated.

The reference methods (MP2RAGE, CPMG) also use simplified models to accommodate feasible acquisition times and to condition fitting procedures, as is typically the case for quantitative mapping approaches. Therefore, these methods may also suffer from a systematic bias due to MT or other contrast mechanisms. This may explain the relatively large discrepancy of quantitative values across the literature³¹. More specifically, for the discrepancies in T₂ between the values from the two-pool model and the CPMG reference, there is likely still a systematic bias due to diffusion and other microstructural effects, which lead to inaccuracies in the fingerprinting T₂ values. However, also the CPMG sequence is prone to MT effects^32,33, leading to T₂ overestimation. Furthermore, hyperintensities can be observed in T₂ maps obtained with a CPMG sequence at locations with high axonal density. It has been shown that these hyperintensities depend on the angle between the axon’s main direction and the main magnetic field B₀³⁴. These effects affect both CPMG-based and fingerprinting-based approaches, but potentially to different degrees and in different direction (over- vs. underestimation). For T₁ values, the single-pool model agreed better with the reference method (MP2RAGE) than the two-pool model. This may indicate that the MP2RAGE is also biased by MT, coincidentally resulting in the same bias as the single-pool model. This theory is also based on the knowledge that the MP2RAGE uses an adiabatic inversion pulse that deposits a large amount of power, resulting in a resonant saturation of the semi-solid pool. This yields a non-exponential recovery depending on MT which not only affects MP2RAGE measurements but every IR-based T₁ mapping sequence, leading to increased NRMSE as seen in the phantom experiment. It has already been shown that this effect can be modulated by changing the power deposition of the adiabatic pulse³⁵ and the effect has been exploited to quantify MT in vivo³⁶.

For simplicity, all experiments were performed using single-slice acquisitions. The acquisition of multiple slices, interleaved or sequential, will introduce saturation of the semi-solid pool that needs to be accounted for in the spin history: the on-resonant pulse from a slice causes off-resonance saturation of the semi-solid pool in other slices, depending on the relative slice distance and the slice-selection gradient^37,38. The model proposed here can be easily extended to interleaved multi-slice acquisition by applying additional shifted saturation profiles, according to the slice order. This modification will, however, restrict the slice parameters of the acquisition protocol to the trained dictionary. Moreover, the large number of long, high flip-angle MT pulses may exceed SAR limitations.

A major limitation of the proposed method is the current acquisition time of 3:10 min for a single slice, which corresponds to a 1 h 35 min protocol for whole-brain coverage (assuming 30 slices). However, with advanced reconstruction techniques^39,40, k-space trajectories⁴¹, and 3D acquisitions^42,43, it may be possible to achieve clinically acceptable acquisition times. The long reconstruction time is another limitation of the proposed method. However, different methods have been proposed recently to drastically reduce reconstruction times by using either non-linear kernels⁴⁴ or neural networks⁴⁵, which will be investigated in future work.

5. Conclusion

Our work demonstrates that MRF relaxation-parameter estimation can be influenced by MT effects and shows that the MT contrast mechanism should not be ignored. To alleviate the impact of MT, instead of a conventional single-pool model, we evaluated a two-pool model to match the data. In addition, we modified the original IRFF sequence to include off-resonance MT pulses in the RF train, in order to better differentiate between MT and relaxation effects in the fingerprint. This work shows that different T₁ and T₂ values are obtained when accounting for MT effects and, furthermore, that fractional pool size (F) maps can be estimated along with other parameters in an MRF context.

Supplementary Material

Supp figS1-5

Supporting Information Figure S1: Absolute estimation errors in T₁, T₂, B₁⁺ and fractional pool size F if the assumption of the fixed T₂ of the semisolid pool (T_2,SS) and exchange rate (k) is not met. The cross indicates the location where the assumption is true.

Supporting Information Figure S2: Distribution of T₁ values obtained from the MP2RAGE in the frontal white matter of one example subject. The green and red lines indicate the median and mean of the distribution respectively.

Supporting Information Figure S3: Quantitative maps obtained from the phantom experiment with different compartments which were used to compare the values of the different models/sequences to the reference values.

Supporting Information Figure S4: Histograms of B1+ values for the different methods from all voxels within the brain of all subjects. The MRF appear to agree well with each other whereas the GRE based mapping resulted in lower values.

Supporting Information Figure S5: Acquired MR signals (fingerprints) from the water and xl-BSA samples using the IRFF sequence with two different pulse durations of 2 ms and 0.5 ms.

Figure 7:

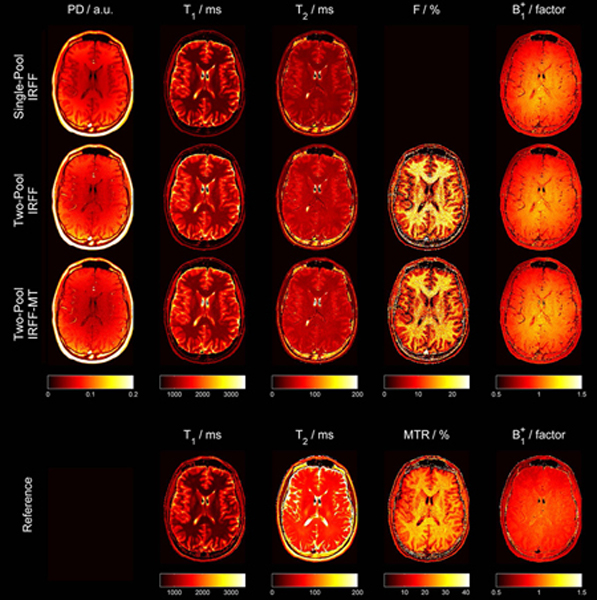
Example quantitative maps obtained from one volunteer using a single-pool model (first row), a two-pool model (second row), a two-pool model with MT pulses in the sequence (IRFF-MT, third row), and reference methods (bottom). Of note, the color bar of the fractional pool size (F) and MTR have a different scaling since they represent different measures which both depend on MT.