Improved pulmonary ¹²⁹Xe ventilation imaging via 3D-spiral UTE MRI

Abstract

Purpose

Hyperpolarized ¹²⁹Xe MRI characterizes regional lung ventilation in a variety of disease populations, with high sensitivity to airway obstruction in early disease. However, ventilation images are usually limited to a single breath-hold and most-often acquired using gradient-recalled echo sequences with thick slices (~10–15 mm), which increases partial-volume effects, limits ability to observe small defects, and suffers from imperfect slice selection. We demonstrate higher-resolution ventilation images, in shorter breath-holds, using FLORET (Fermat Looped ORthogonally Encoded Trajectories), a center-out 3D-spiral UTE sequence.

Methods

In vivo human adult (N = 4; 2 healthy, 2 with cystic fibrosis) ¹²⁹Xe images were acquired using 2D gradient-recalled echo, 3D radial, and FLORET. Each sequence was acquired at its highest possible resolution within a 16-second breath-hold with a minimum voxel dimension of 3 mm. Images were compared using ¹²⁹Xe ventilation defect percentage, SNR, similarity coefficients, and vasculature cross-sections.

Results

The FLORET sequence obtained relative normalized SNR, 40% greater than 2D gradient-recalled echo (P = .012) and 26% greater than 3D radial (P = .067). Moreover, the FLORET images were acquired with 3-fold-higher nominal resolution in a 15% shorter breath-hold. Finally, vasculature was less prominent in FLORET, likely due to diminished susceptibility-induced dephasing at shorter TEs afforded by UTE sequences.

Conclusion

The FLORET sequence yields higher SNR for a given resolution with a shorter breath-hold than traditional ventilation imaging techniques. This sequence more accurately measures ventilation abnormalities and enables reduced scan times in patients with poor compliance and severe lung disease.

1. INTRODUCTION

Hyperpolarized ¹²⁹Xe ventilation imaging quantifies regional ventilation and is sensitive to airway obstruction in a wide variety of diseases.^1–12 The technique is safe and well-tolerated for many populations, including pediatrics.^1,13,14 Ventilation imaging relies on obtaining reliable, spin density–weighted images to quantify xenon regionally in the lung. A standard approach to ventilation imaging incorporates 2D gradient-recalled echo (2D-GRE) sequences limited to a single breath-hold (<16 seconds). Due to the breath-hold and gradient limitations, the lung is typically acquired with thick slices (~10–15 mm), which may suffer from imperfect slice selection.³ Additionally, each slice is acquired at different times during the breath-hold, causing undesired T₁ weighting in later slices. These limitations suggest that HP ¹²⁹Xe imaging using true 3D acquisitions could yield superior performance and quantitative accuracy.

Previously, ¹²⁹Xe ventilation imaging with 3D-radial was compared with a standard multislice 2D-GRE sequence.⁷ The 3D-radial acquisitions captured magnetization dynamics and physiologically relevant characteristics such as gravitationally dependent ventilation gradients, but experienced a nearly 2-fold reduction in SNR. The decreased SNR partially resulted from sampling inefficiency, requiring many acquisitions and thus a flip angle approximately 5-fold smaller for the limited total magnetic moment. However, the center-out nature was advantageous, allowing correction/manipulation of the data to obtain a more accurate image of xenon density and dynamic ventilation.^15–17

Thus, the ideal acquisition would combine the advantages of center-out 3D radial with efficient k-space encoding, to allow larger flip angles and shorter breath-holds. Relative to 3D radial, center-out spiral acquisitions are more efficient in their sampling of k-space. Higher sampling efficiency permits the use of fewer magnetization-consuming excitations and shorter breath-holds, avoiding 2 main disadvantages of 3D radial.¹⁸ One such example, FLORET (Fermat Looped ORthogonally Encoded Trajectories), is a center-out 3D-spiral sequence that has been shown to have a superior performance and efficiency compared with that of 3D radial for ${\mathrm{T}}_2^{*}\mathrm{s}$ greater than approximately 0.8 ms,^18,19 much lower than that expected for hyperpolarized gases (>8 ms).²⁰

Here, FLORET is compared with 2D GRE and 3D radial to determine the potential improvements FLORET may provide for ¹²⁹Xe ventilation imaging. We demonstrate that FLORET provides increased SNR, increased resolution, and shorter breath-holds. Additionally, agreement in identification of regional ventilation defects and overall quantification provides substance to the improvements provided by FLORET ¹²⁹Xe ventilation.

2. METHODS

2.1. In vivo imaging

Human studies were performed with approval from the internal review board of Cincinnati Children’s Hospital Medical Center and with oversight from the U.S. Food and Drug Administration (USFDA) under an investigational new drug (IND 123,577) protocol. Isotopically enriched xenon (83% ¹²⁹Xe; Linde Specialty Gases) was polarized to approximately 30% using a Polarean 9820 ¹²⁹Xe hyperpolarizer. By the time of imaging, polarization decayed to 23% ± 7%.

Hyperpolarized ¹²⁹Xe ventilation images were acquired in 2 healthy volunteers (ages 27 and 33 years) and 2 patients with cystic fibrosis (ages 28 and 48 years) using a Philips 3T Achieva MRI scanner (Best, Netherlands) (maximum gradient amplitude = 80 mT/m; max gradient slew rate = 200 mT/m/ms) and a homebuilt xenon coil.²¹ Subjects were imaged in the supine position during a breath-hold (maximum of 16 seconds) after inhaling a 1-L dose from functional residual capacity. For each subject, 5 doses of xenon were inhaled (1 calibration dose: 700 mL N₂, 300 mL ¹²⁹Xe; 4 imaging doses: 1 L ¹²⁹Xe). The calibration dose was used to ascertain the precise center frequency of the xenon signal and to calibrate the flip angle.

Three comparative ventilation sequences were completed for each subject: 300-mm isotropic FOV, shortest possible TE, and a flip angle calculated to maximize the signal of the central acquisition according to θ = atan(√[2/N_ex]), where N_ex is the number of effective excitations.²² The number of effective excitations for 2D slice-selective scans was equivalent to the number of phase encodings, whereas the 3D scans used a nonselective pulse, making the number of effective excitations equivalent to the number of projections acquired. Because scan duration is the primary limitation, all scans were acquired with identical undersampling factors: 62.5% partial echo and 62.5% half Fourier factors (39% of k-space acquired) for 2D-GRE; 39% of Nyquist radial spokes (equally spaced spokes, maximum undersampling factor, R_max = 2.56) for 3D-radial; and R_max value of 2.56 (intertrajectory spacing linearly increasing with k-space radius up to 2.56 times the Nyquist distance^18,19) for FLORET. The FLORET sequence was implemented with a readout duration of approximately 8 ms, similar to the global ${\mathrm{T}}_2^{*}$ (spectroscopy-based lower limit) of xenon gas in the lung at 3 T²³ and with 2 hubs with a maximum cone angle of 45°. The voxel volumes were smaller for FLORET (27 mm³) compared with 3D radial and 2D GRE (86 mm³ and 79 mm³, respectively). Although 2D GRE acquired identical in-plane resolution to FLORET (3 mm), the 2D GRE sequence required almost 3-fold-thicker slices (8.82 mm). The scan time was shortest for FLORET (12.5 seconds) compared with 15.5 seconds for 3D radial and 15.7 seconds for 2D GRE. Additionally, a fully sampled FLORET was acquired using a readout duration of approximately the local (imaging-based) ${\mathrm{T}}_2^{*}$ of xenon (18 ms).²⁰ Both FLORET sequences used 30.38 mT/m maximum gradient strengths and 102 mT/m/ms slew rate maximums. The FLORET sampling trajectories and additional information can be found in the Supporting Information. Acquisition parameters can be found in Table 1. A proton 3D-radial image was acquired with the same FOV (300-mm isotropic) and 3.0-mm isotropic resolution during a 1-L breath-hold of room air to obtain an anatomical lung mask (flip angle = 5°, TE = 0.156 ms, bandwidth = 498 Hz/pixel, TR = 2.12 ms, scan duration = 15.6 seconds).

TABLE 1.

Sequence parameters implemented for each ventilation scan

	2D GRE (comparison)	3D radial (comparison)	FLORET (comparison)	FLORET (fully sampled)
Resolution (mm)	3.00 × 3.00 × 8.82 (79 mm3)	4.41 × 4.41 × 4.41 (86 mm3)	3.00 × 3.00 × 3.00 (27 mm3)	3.26 × 3.26 × 3.26 (35 mm3)
FOV (mm)	300 × 300 × 300	300 × 300 × 300	300 × 300 × 300	300 × 300 × 300
Matrix size	100 × 100 × 34	68 × 68 × 68	100 × 100 × 100	92 × 92 × 92
Effective excitations (Nex)	63	3600	1088	612
Encoding method	Phase: −ky to +ky Slice: head to foot	Ten-interleave Archimedean spiral	Two-hub minimal angular difference18	Two-hub minimal angular difference18
Flip angle	10.1°	1.4°	2.5°	3.3°
TE (ms)	1.98	0.149	0.118	0.118
Dwell time (us)	31.5	31.6	7.3	7.4
Readout (ms)	3.93	2.18	7.78	19.0
TR (ms)	6.70	4.08	10.0	21.2
Scan duration (seconds)	15.7	15.5	12.5	14.5

2.2. Image reconstruction

Images were reconstructed offline using Graphical Programming Interface (GPI).²⁴ The 2D-GRE reconstruction consisted of Fourier transformation of raw k-space data. For center-out trajectories (3D radial and FLORET), all points in a projection were scaled by the magnitude of their k₀ intensities, removing signal decay due to T₁ relaxation and flip angle, reducing potential artifacts at the potential cost of SNR.²⁵ The data were corrected for gradient delays but not any other gradient imperfections. The resulting data were formatted into a Cartesian matrix using the default GPI density compensation and gridding settings, including iterative density compensation^26,27 and gridding using an exponentially decaying Hanning window with a radius of 2.5 points. The center-out trajectories were corrected for off-resonance frequencies following the method presented by Robison et al,¹⁸ which were negligible due to the low gyromagnetic ratio of xenon and an accurate center frequency from the calibration scan.

2.3. Data analysis

Resulting images were imported into MATLAB 2019a (MathWorks, Natick, Massachusetts) for further analysis. Due to the varying matrix dimensions, each ventilation scan was interpolated onto a 100 × 100 × 100 matrix using the nearest-neighbor method to retain the true resolution. Lung masks were generated from the proton image using a combination of intensity-based thresholding and active-contour region-growing segmentation.

The proton image and lung mask were registered to each ventilation image to account for movement. Ventilation defect percentages (VDPs) were determined using a threshold of 60% of the mean ¹²⁹Xe signal intensity within the lung mask.¹⁰ A background mask was generated containing voxels over 10 voxels away from a voxel above the ventilation threshold. The SNR was determined by $\left[\left(S_{lung}-S_{BG}\right)/{\sigma }_{BG}\right]\times \sqrt{2-\frac{\pi }{2}}$, which accounts for the Rician nature of the magnitude noise,²⁸ where S_lung is mean signal amplitude within the lung mask; S_BG is the mean signal amplitude within the background mask; and σ_BG is the SD of the noise in the background mask. Normalized SNR (SNR_n) was calculated according to $SN{R}_n=\frac{SNR}{V_{vox}\times {\mathrm{f}}_{129}\times {\mathrm{P}}_{129}\times {\mathrm{V}}_{\mathrm{Xe}}}$, where V_vox is the voxel volume, f₁₂₉ is the isotopic fraction of ¹²⁹Xe, P₁₂₉ is the spin polarization, and V_Xe is the xenon volume.⁷ Additionally, SNR_n was made relative to the subjects’ ventilating lung volume to account for varying amounts of functioning lung despite a fixed xenon volume: relative SNR_n = SNR_n(mL⁻²) × V_lung(L).

Lung masks were used to obtain ventilation masks, areas within the lung mask above the defect threshold (60%).¹⁰ All images and masks were registered to the 2D-GRE ventilation image. The ventilation masks were compared using Dice scores (for region-based similarities),²⁹ boundary F1 scores (for edge/contour-based similarities),³⁰ and structural similarity index (SSIM, for signal amplitude-based similarities).³¹ Dice calculates the percent of overlap between the 2 masks, whereas F1 is the percent of boundaries in image 1 that are within x voxels of a boundary in image 2, where x is defined as 0.75% of the image diagonal. The SSIM is more complex, ranging from −1 to 1, and is a measurement of image similarity taking into consideration differences in luminance, contrast, and structure, where a value of 1 is an identical image. For similarity comparisons, the 2D-GRE image was taken as ground truth, as it is the most standard and commonly used technique. Finally, the images were corrected using N4ITK bias correction,³² permitting more accurate cross-section line profiles of areas lacking ventilation due to vasculature. These line profiles were then qualitatively compared among the 3 techniques.

Comparisons among the acquisition groups were compared using a repeated-measures analysis of variance with a Tukey’s honestly significant difference ad hoc test to determine which group differences were significant. Linear regressions were performed among the VDPs of the different acquisition techniques.

3. RESULTS

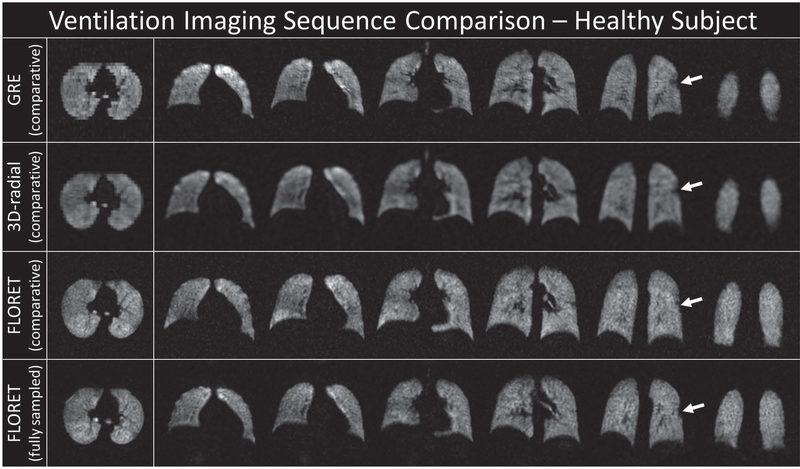
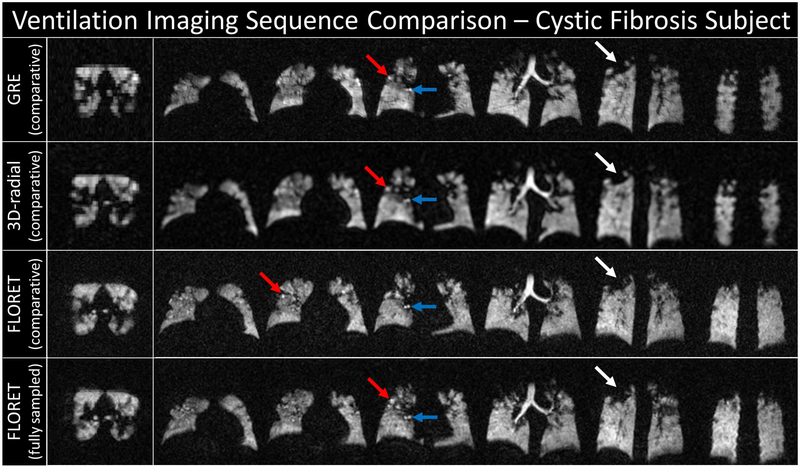
Representative slices from each sequence are shown in Figures 1 and 2. Note that the 2D-GRE sequence is nonisotropic, and while the in-plane resolution is high (3 × 3 mm), the slice thickness is approximately twice as thick as the 3D-radial images and 3 times as thick as the FLORET images. Figure 1 shows the images for a healthy subject. All 4 images (before registration and bias correction) show homogenous ventilation and good correlation of structural features. Figure 2 shows a subject with cystic fibrosis. Many ventilation defects are visible in all images and are predominantly in the middle/upper portions of the lung. Regions of hyperintensity and airway are also observable. This heterogeneity is captured across all sequences (i.e., defects and hyperintensity in the same regions consistently).

FIGURE 1.

Representative slices from the reconstructed images for a healthy subject before registration and bias correction. The white arrows point to the small defect in the left lung. Each row corresponds to 1 of 4 sequences/settings used: top, 2D gradient-recalled echo (GRE) (comparative); upper middle, 3D radial (comparative); lower middle, FLORET (Fermat Looped ORthogonally Encoded Trajectories) (comparative); and bottom, FLORET (fully sampled). Note that the 2D-GRE slices are approximately 3 times thicker than the corresponding in-plane resolution and the resolution in all planes for the comparative FLORET. All other images are fully isotropic

FIGURE 2.

Representative slices from the reconstructed images for a subject with cystic fibrosis before registration and bias correction. White arrows point to a defect; blue arrows point to a hyperintense region of airway; and red arrows point to a hyperintense region likely caused by a defect shunting xenon into other regions of the lung. Each row corresponds to 1 of 4 sequences/settings used: top, 2D GRE (comparative); upper middle, 3D radial (comparative); lower middle, FLORET (comparative); and bottom, FLORET (fully sampled). Note that the 2D-GRE slices are approximately 3 times thicker than the corresponding in-plane resolution and the resolution in all planes for the comparative FLORET. All other images are fully isotropic

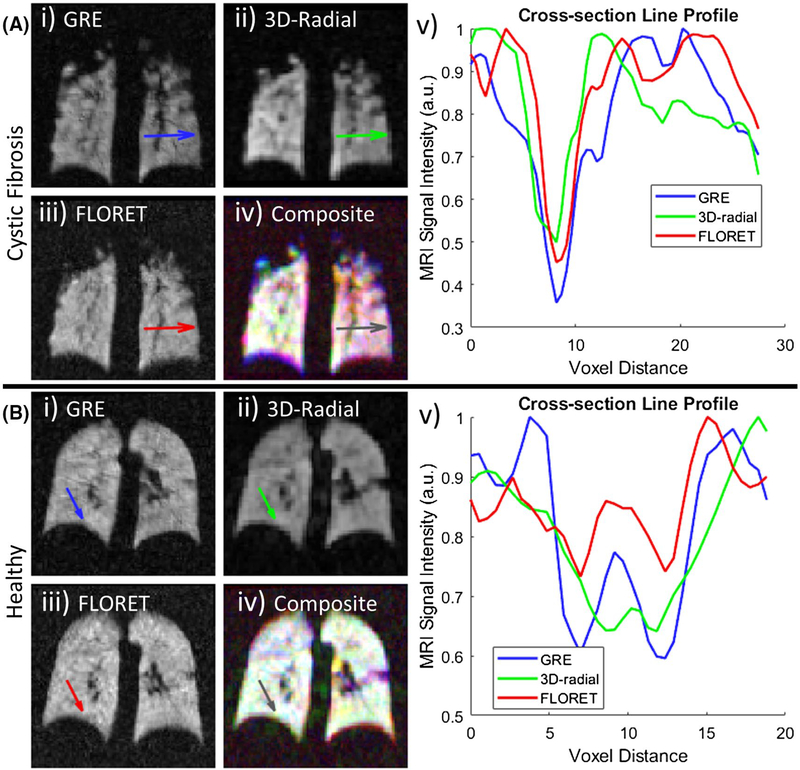
Vasculature cross sections were qualitatively compared among the 3 sequences as shown in Figure 3. Figure 3A illustrates the signal intensity loss due to a larger and more prominent portion of vasculature, whereas Figure 3B illustrates the same for a pair of small vessels, which are difficult to discern by eye, but decrease the signal intensity by about 15%−40%, depending on the sequence and its resolution. The signal amplitude appears to drop more severely and for larger distances in the 2D-GRE images than the FLORET images. This suggests that the longer TE necessary for 2D GRE leads to increased susceptibility-induced signal dephasing in regions adjacent to vasculature, resulting in an overestimation of vessel size. The 3D-radial sequence should benefit from shorter TEs as well, but the effect appears to be lessened by increased partial-volume effects.

FIGURE 3.

Example vasculature cross sections in ventilation images of a subject with cystic fibrosis (CF) (A) and a healthy subject (B). The 3 gray-scale images (i, ii, iii) correspond to 2D GRE, 3D radial, and FLORET, respectively. (iv) Overlay of 3 slices with 2D GRE (blue), 3D radial (green), and FLORET (red) illustrating the excellent agreements among the images following registration. Areas of white indicate relative voxel intensity agreement among all sequences. Areas of color indicate a larger relative intensity for that given sequence. For example, the healthy subject shows excellent agreement within the lung volume with the presence of 3D-radial signal between the lungs. The subject with cystic fibrosis illustrates excellent agreement in the right lung, but a lack of green indicates a lower relative intensity in the 3D-radial sequence. (v) Line profiles (arrows) for each cross section shown in (i)-(iv), illustrating narrower and shallower drops in signal due to vasculature for FLORET, which will reduces the amount of voxels with vasculature classified as ventilation defects

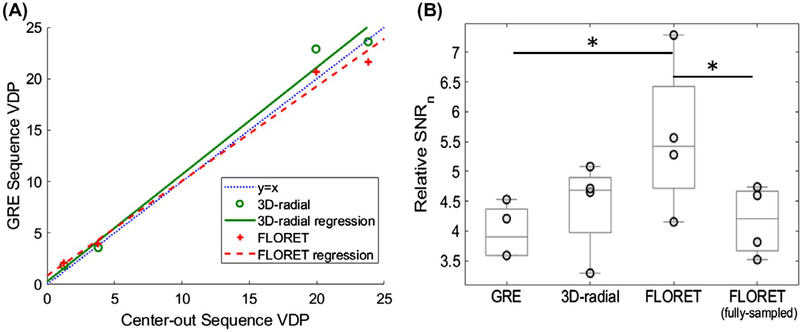
The resulting VDPs for the center-out trajectories were compared with the calculated VDP from the standard 2D-GRE sequence (Figure 4A). This was completed to confirm similar results regardless of the sequence implemented. The 2D-GRE sequence resulted in 1.3% and 3.8% VDPs for the healthy subjects and 19.9% and 23.8% for the subjects with cystic fibrosis. The VDPs from 2D GRE had a linear correlation with 3D radial (y = 1.04x + 0.3, R² = 0.99) and FLORET (y = 0.92x + 0.85, R² = 0.99). Thus, all 3 imaging sequences strongly correlate for measuring VDP, as expected. However, future studies will be required to assess any potential bias among the calculated VDPs for each sequence and whether the image-quality improvements result in additional sensitivity to disease severity and progression.

FIGURE 4.

Whole-lung comparisons among the ventilation sequences. A, Comparison of ventilation defect percentage (VDP) derived from center-out sequences and those derived from the standard 2D-GRE sequence. B, Relative SNR_n each sequence. The comparable FLORET sequence has a significant 40% increase (P = .012) in SNR_n over the 2D-GRE sequence and a significant 34% increase (P = .024) over the fully sampled FLORET

To confirm similar defect locations, quantitative image-space metrics were used, including Dice coefficients, boundary F1 scores, and SSIM indexes. Taking 2D GRE as ground truth, 3D radial had Dice similarity scores of 0.93 ± 0.05, FLORET had scores of 0.94 ± 0.05, and fully sampled FLORET had a score of 0.95 ± 0.03, indicating large overlap of the areas determined as ventilating among all techniques (all P >.72). The 3D-radial sequence had boundary F1 scores of 0.83 ± 0.07, FLORET had scores of 0.885 ± 0.07, and fully sampled FLORET had scores of 0.85 ± 0.06. The boundary F1 score demonstrates that more than 80% of the ventilation boundaries occur in close proximity with each other, regardless of the imaging technique (all P > 0.89). As for SSIM, 3D radial had scores of 0.63 ± 0.08, FLORET had scores of 0.61 ± 0.03, and fully sampled FLORET had scores of 0.66 ± 0.03 (all P > .63). Generally, lower SSIM scores occurred in areas of poorer registration/partial-volume effects and in the anterior portions of the lung. Despite lower SSIM scores, all 3 center-out sequences obtained similar scores, indicating similar intensity discrepancies when compared with 2D GRE. If 3D radial is instead taken as ground truth for the FLORET images, the Dice scores increased by 0.6% and the boundary F1 scores increased 4.3%, while the SSIM scores decreased by 3.4%.

The SNRs were 12.9 ± 1.2 for 2D GRE, 17.8 ± 1.0 for 3D radial, 10.0 ± 1.4 for FLORET, and 12.7 ± 2.2 for the fully sampled FLORET. All images had SNRs much greater than the Rose criterion,³³ allowing for accurate analysis. However, because SNR does not account for polarization or voxel volume, SNR_n is more informative for comparisons. The value of SNR_n was 1.30 ± 0.24 mL⁻² for 2D GRE, 1.40 ± 0.24 mL⁻² for 3D radial, 1.78 ± 0.50 mL⁻² for FLORET, and 1.45 ± 0.28 mL⁻² for the fully sampled FLORET. The FLORET sequence provides higher SNR_n but with higher SD. This fails to account for functional lung volume: Given the same volume of xenon, a subject with smaller lungs or more ventilation defects will have a larger xenon density in his or her ventilating regions, increasing the signal and SNR. This intersubject variation can be accounted for by calculating a relative SNR_n. The resulting relative SNR_ns is shown in Figure 4B. Using relative SNR_n, there are significant differences among the acquisitions (P = 0.011), with comparable FLORET having a 40% larger relative SNR_n than 2D GRE (P = .012) and 34% larger relative SNR_n than the fully sampled FLORET (P = .024). All other comparisons were not statistically significant.

4. DISCUSSION

The quantitative comparisons (VDP, Dice, F1, and SSIM) illustrate similar amounts of disagreement between the traditional 2D-GRE sequence and the center-out sequences (which show increased ventilation region/boundary agreement with each other). The VDPs were strongly correlated among the techniques, indicative of similar information with regard to ventilation defects. There was strong correlation of ventilating regions using the Dice and F1 boundary scores, and moderate correlation of intensities using SSIM scores. Much of the discrepancies appear to be due to the varying voxel dimensions and separate breath-holds. However, 3D radial and FLORET achieved very similar scores with regard to 2D GRE, indicating a similar amount of discrepancies, independent of the acquisition technique. Additionally, decreased prevalence of vasculature with FLORET would lead to fewer vasculature regions misclassified as ventilation defects, depending on the lung mask. This, and the reduced partial-volume effects, likely lead to more accurate VDP quantifications for FLORET.

Previous results showed approximately half the SNR for 3D-radial ventilation images compared with 2D GRE.⁷ Here, we observe a slightly higher SNR_n (~11%) for 3D radial over 2D GRE. The difference likely is due to the offline reconstruction implemented here for both sequences and removal of the native Fermi filter that, in the previous comparison, had been applied to the 2D-GRE images but not the 3D-radial images. Additionally, kernel/gridding approaches may also play a significant role in the different SNRs we observed compared with the previous 3D-radial results.

Because the FLORET sequence has a higher sampling and SNR efficiency than 3D radial, fewer excitations were necessary, allowing for higher flip angles and thus higher SNR. This is despite the shorter dwell time used in the FLORET sequences. The fully sampled version of FLORET had a significant decrease in SNR_n, due to the increased number of excitations, indicating that undersampling could provide noticeable SNR and/or timing gains, as long as undersampling artifacts can be mitigated.

The FLORET sequence efficiency increases with longer readout durations. The comparative sequence used a theoretically optimized readout duration assuming the global ${\mathrm{T}}_2^{*}$ of 8 ms at 3 T.^18,20 Higher efficiency would be gained if a local ${\mathrm{T}}_2^{*}$ of 18 ms is assumed. Additionally, implementation of FLORET has shown little to no effect in image quality/sharpness and only minor decreases in SNR by using longer than optimal readout durations $(~2\times {\mathrm{T}}_2^{*})$.³⁴ For hyperpolarized imaging, a slight reduction in SNR would likely be overcome with larger flip angles and fewer projections. Thus, the FLORET sequences implemented here may be further.

5. CONCLUSIONS

The use of FLORET for ventilation imaging results in similar ventilation structure to traditional techniques, providing corroboration of FLORET ventilation imaging. Like 3D radial, the center-out nature allows FLORET to more accurately capture physiological gradients and permits advanced reconstruction techniques. The sampling efficiency of FLORET provides fewer excitations and larger flip angles, resulting in higher SNR_n when compared with 2D GRE and 3D radial. Perhaps most importantly, the FLORET sampling pattern results in higher-resolution images and/or shorter breath-holds, without the need for high-performance gradients. The FLORET images obtained demonstrate an approximate 3-fold higher resolution and a 40% higher relative SNR_n in a 15% shorter breath-hold duration compared with 2D GRE. This should result in higher sensitivity, more accurate quantification of ventilation, and make ¹²⁹Xe ventilation imaging more feasible for subjects with more advanced lung disease or less compliant subjects who are unable to complete longer-duration breath-holds.

Supplementary Material

Supplemental Figures

FIGURE S1 Base Fermat spirals (kz = 0) for the comparative (left) and fully sampled (right) FLORET sequences. Note that the longer readout samples more of k-space within a single excitation/acquisition

FIGURE S2 Trajectory endpoints for the comparative (left) and fully sampled (right) FLORET sequences. Each hub is colored differently, allowing them to be distinguished. Additionally, endpoints further away in the kx dimension are smaller, to provide depth. Despite the fully sampled nature of the sequence on the right, the left is denser due to its shorter readout duration

FIGURE S3 Complete trajectory sampling for the comparative (left) and fully sampled (right) FLORET sequences. Red to yellow indicates the first hub, with the red indicating the first acquisition of the hub and yellow indicating the final acquisition of the hub. Similarly, the second hub is ordered blue to green. Note that the spirals are acquired relatively randomly in the cone dimension

FIGURE S4 Approximate sampling density maps for the comparative (left) and fully sampled (right) FLORET sequences. Note the cones of increased sampling density due to the overlap of the hubs and the similar amount of undersampling in the cone and spiral dimensions. The minimum undersampling values (at the edges where no hub overlap occurs) is consistent with the reported sampling densities for each sequence